Open Access Article
Open Access ArticleMild decarboxylation of neat muconic acid to levulinic acid: a combined experimental and computational mechanistic study†
Siddhant Bhardwaj a,
Deep M. Patel
a,
Deep M. Patel ab,
Michael J. Forrester
ab,
Michael J. Forrester a,
Luke T. Roling
a,
Luke T. Roling ab and
Eric W. Cochran
ab and
Eric W. Cochran *a
*a
aDepartment of Chemical and Biological Engineering, Iowa State University, Ames, IA 50011, USA. E-mail: ecochran@iastate.edu; Tel: +1-515-294-0625
bCenter for Biorenewable Chemicals (CBiRC), Ames, IA 50011, USA
First published on 13th December 2024
Abstract
Levulinic acid (LA) is a key platform molecule with current applications in the synthesis of several commodity chemicals, including amino-levulinic acid, succinic acid, and valerolactone. In contrast to existing petroleum-based synthesis pathway, biomass-derived cis–cis-muconic acid (MA) offers a sustainable route to synthesize LA. Here, we show the complete decarboxylation of neat MA to LA without solvent at atmospheric pressure and mild temperature. In a series of sulfuric acid catalyzed experiments, we used a suite of one and two-dimensional NMR techniques along with gas chromatography-mass spectrometry (GCMS) analysis and density functional theory (DFT) calculations to elucidate the intermediates involved in LA synthesis. Experimental kinetic studies revealed rate constants for the consumption of MA and the formation of LA, with activation energies calculated to be 16.10 kJ mol−1 and 158.18 kJ mol−1, respectively.
1. Introduction
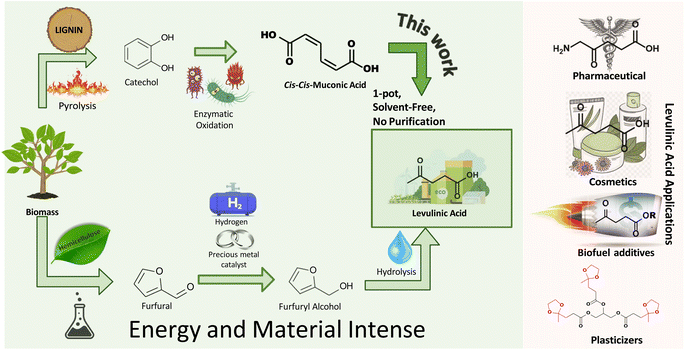
The petrochemical industry is vital for various household and industrial applications, and is expected to grow at a 4.8% CAGR to $858 billion by 2032.1 This anticipated growth highlights concerns regarding finite resource depletion and the environmental impact of non-recyclable waste. Transitioning to recyclable biomass for synthesizing high-value chemicals is increasingly recognized as essential. Levulinic acid (LA), a key platform chemical, stands out for its versatility, acting as a precursor for numerous chemicals such as amino-levulinic acid, succinic acid, levulinate esters, valerolactone, and angelica lactone.2,3 Its broad utility spans solvents,4 food and fragrances,2,4 plasticizers,5–7 biofuel additives,8–10 pharmaceuticals,3,11,12 cosmetics,11,13 herbicides,11,14 and polymers.6,15 The adaptability of LA emphasizes its potential to offer a sustainable alternative to petrochemicals across numerous sectors.Levulinic acid (LA) can be derived from polysaccharide (pentose and hexose sugars) fractions,16,17 with pentose conversion being more atom-efficient.16,18 This process typically involves converting pentose sugars (hemicelluloses) to furfural, then to furfuryl alcohol (FAL), and finally hydrolyzing to LA (Fig. 1).
Various mechanisms for LA synthesis from FAL exist – experimentally detected intermediates include ethoxymethyl furan (EMF), triethoxy pentan-2-one (TEP), and diethyl ether (DEE).19 Density functional theory (DFT) calculations revealed that these intermediates are rather energetically stable, and the formation of EL is more favorable through a different pathway involving a single esterification reaction from FAL (pathway B).19 While Guo et al. focused on the 1,4-ethanol addition to EMF as the primary route for ethyl levulinate (EL) production, avoiding DEE,20 Fan et al. explored pathways involving both EMF and TEP.21,22 The exact roles of EMF and TEP in LA and EL synthesis pathway from FAL remain uncertain, with the current industrial production of FAL relying on furfural hydrogenation using costly catalysts like Pt and Pd,23,24 highlighting the significant energy and material demands of state-of-the-art LA/EL synthesis process. Life cycle assessment (LCA) studies have highlighted the substantial energy requirements for ethyl levulinate synthesis from sugars.25
Given the increasing demand for polysaccharides in the food industry,25,26 lignin, an abundant waste byproduct from the paper and forestry industries, offers a sustainable feedstock alternative for LA production. This strategy supports circular economy principles by converting waste into valuable chemicals and could enhance LA production scalability using readily available industrial byproducts.
Recent efforts have revealed the potential of lignin extracted from agricultural residues including corn stover, wheat straw, rice straw, and bagasse to synthesize valuable platform chemicals, such as muconic acid (MA) and keto adipic acid.27–31 For example, keto adipic acid can be produced at yields reaching 44.5 g L−1, and can be efficiently decarboxylated to afford LA.32 Great strides have also been achieved in the manufacture of MA, with titers up to 85 g L−1 using Corynebacterium glutamicum33 and 81.5 g L−1 from engineered Escherichia coli strains.34 MA serves as a key platform chemical that readily affords a plethora of critical commodity chemicals, including adipic acid, terephthalic acid, ε-caprolactam, and 1,6-hexamethylene diamine, and novel monomers like cyclohex-1-ene-dicarboxylic acid (CH1DA).35–41
The versatility of MA has prompted studies like Carter et al.’s synthesis of tunable nylon-6,6 copolymer from trans,trans-muconic acid through Diels–Alder cycloaddition, improving hydrophobicity and flame retardancy.42 CH1DA composites have significantly enhanced flame retardancy and reduced water absorption.42 Furthermore, the application of ccMA in succinate-based polyesters for fiberglass panels has been demonstrated, achieving shear moduli of 30 GPa, comparable to commercial standards.43 The diverse applications of MA underscore its significance for commercialization in the production of polymers and chemicals.
This work demonstrates a novel, solvent-free method for producing levulinic acid (LA) from muconic acid (MA) derived from lignin, a sustainable waste product. Unlike conventional methods, which typically involve high temperatures and elevated pressures to convert furfuryl alcohol (FAL) to LA, results in side products like formic acid that requires additional purification steps.16,25,44 However, our approach achieves 100% selectivity to LA under mild conditions (80 °C and atmospheric pressure). The solvent-free nature of this process further simplifies production by eliminating the need for costly separation and purification steps, thus reducing environmental impact, material, and energy costs. This streamlined method provides a simpler and more scalable alternative to traditional LA production from cellulose-derived fractions. This finding expands the repertoire of chemicals accessible from MA, reinforcing its status as a platform chemical. Additionally, this study elucidates MA's chemical pathways and identifies critical intermediates using experimental methods and DFT calculations, providing key insights for enhancing LA selectivity and yield in future studies.
2. Experimental section
Catechol, formic acid, hydrogen peroxide (30%), ammonium iron(III) sulfate hexahydrate, sulfuric acid, chloroform, and ethanol were purchased from Fisher Scientific. Deuterated sulfuric acid and deuterated water were obtained from Sigma-Aldrich. Deuterated chloroform was procured from Cambridge Isotope Laboratories.2.1 cis,cis-Muconic acid synthesis
The synthesis of ccMA was adapted from the work of Coupe et al.45 25 g of catechol was dissolved in 125 mL of formic acid. In a separate round-bottom flask, 235.22 g of formic acid (5.11 mol) and 115.79 g of H2O2 (30% wt, 1.02 mol) were stirred together for 1 h at room temperature. The mixture was then cooled in an ice bath, and the catechol solution was added dropwise throughout 2 h. The mixture was stirred overnight at room temperature. The precipitate formed was filtered, washed several times with water, and dried in a vacuum oven overnight. 1H-NMR analysis in DMSO-d6 confirmed the complete conversion of catechol to ccMA.2.2 Levulinic acid synthesis and characterization
| Entries | Reaction parameters | Selectivity (%) | |||
|---|---|---|---|---|---|
| Temperature (°C) | Sulfuric acid (wt%) | MLac | Dilac | LA | |
| a Bulk and solvent-free reaction of ccMA carried out in catalytic amount of sulfuric acid with only stoichiometric amount of water for levulinic acid (LA) synthesis for 16 h. | |||||
| 1 | 80 | 30.5 | 0.00 | 0.00 | 100.00 |
| 2 | 80 | 8.40 | 7.44 | 31.02 | 61.53 |
| 3 | 100 | 1.00 | 11.93 | 24.85 | 63.21 |
| 4 | 110 | 1.00 | 0.00 | 0.00 | 100.00 |
| 5 | 120 | 1.00 | 0.00 | 0.00 | 100.00 |
Gas chromatography-mass spectrometry (GCMS) further characterized LA and other products using an Agilent 7250 GC/Q-TOF system equipped with a 30 m long GC DB5-MS column. Agilent's Mass Hunter software was used for data analysis. GCMS spectra for LA are available in the ESI.†
2.3 Computational details
Computational analyses were performed using the Gaussian 09 software package.46 Gibbs free energies were calculated using the B3LYP functional and the 6-311++G(d,p) basis set for all atoms.47,48 The zero-damped DFT-D3 method was applied to account for dispersion corrections.49,50 Geometry optimizations were carried out with “verytight” convergence criteria. Activation free energies (Ga) were calculated using an explicit H2O and H3O+ molecule through the Berny optimization algorithm.51 All transition states were identified as first-order saddle points based on a single imaginary vibrational frequency. Since multiple solvent molecules are known to participate in such reaction steps,52 we anticipate that our computational framework may overestimate Ga. To model the solvent environment of chloroform, we used the SMD variant of the polarizable continuum model (PCM) employing the integral equation formalism variant.53 Free energy extrapolations were performed at a temperature of 353.15 K. An isolated H3O+ ion was used as a reference for the free energies of proton addition steps through eqn (1) and (2).| A + H3O+ → B + H2O | (1) |
| ΔG = GB + GH2O − GA − GH3O+ | (2) |
Here, Gi denotes the formation free energy of respective isolated species i in the implicit chloroform solvent at 353.15 K. Previous work by Van Lehn et al. suggested that explicit treatment of the solvent phase may change the identities of preferred species predicted by computations.52 Since we did not detect Cl2, HCl, or any chlorinated reaction intermediates in our experimental GCMS or NMR spectra, we do not anticipate the direct participation of solvent molecules (CHCl3) in this system. Additional calculations were performed with the CBS-QB3 composite method (Table S1†), showing a similar trend in the reaction energetics as calculated by our current functionals and basis set.54 We additionally emphasize the consistency of computed reaction energetics and experiments as presented in this work.
3. Results and discussion
We first conducted the solvent-free decarboxylation of neat ccMA in a batch reactor with 30.5 wt% of sulfuric acid (SA) at 80 °C for 16 h. LA was the only product observed through GCMS (Fig. S4†) apart from residual char formation resulting from dissociative water extraction from ccMA by SA owing to it's strong dehydration nature55 and required by the decarboxylation reaction stoichiometry. The addition of stoichiometric water yielded 100% selectivity to LA in 16 h with negligible char residue as shown in entry 1, Table 1; 1H-NMR is available in Fig. S3.†At 80 °C, we found that the high SA concentration was necessary to maintain LA selectivity: the reduction to 8.4 wt% SA at 80 °C in entry 2 shows the production of a mixture of LA, muconolactone (MLac), and dilactone (Dilac). LA selectivity strongly increased with temperature, with entry 3 showing similar MLac and Dilac formation at 100 °C with only 1 wt% SA. At 110 and 120 °C, we observed 100% LA selectivity with 1 wt% SA, entries 4/5, thereby making this an easily scalable process. The final LA mass was about 28% that of the reactants, consistent with the mass loss anticipated through CO2 evolution.
In solvent-free conditions, the reaction to LA was notably rapid, complicating detailed analysis. To elucidate the reaction mechanism, we used chloroform as a solvent in sulfuric acid-catalyzed reactions of ccMA, maintaining a catalyst to ccMA mass ratio of 0.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in the presence of various amounts of ethanol and water, shown in Table 2. Under these conditions, ccMA undergoes esterification, lactonization, and decarboxylation, producing diverse products influenced by ethanol and water concentrations (Fig. S1†). Excess ethanol led to esterification, yielding cis,cis- and cis,trans-diethyl muconate (ccMAT, ctMAT), shown in entry 1, Table 2 and 1H-NMR in Fig. S5.† Higher water concentrations shifted the reaction towards lactonization, producing muconolactone (MLac) and dilactone (Dilac), corroborating Tessonnier et al.’s findings.41
1 in the presence of various amounts of ethanol and water, shown in Table 2. Under these conditions, ccMA undergoes esterification, lactonization, and decarboxylation, producing diverse products influenced by ethanol and water concentrations (Fig. S1†). Excess ethanol led to esterification, yielding cis,cis- and cis,trans-diethyl muconate (ccMAT, ctMAT), shown in entry 1, Table 2 and 1H-NMR in Fig. S5.† Higher water concentrations shifted the reaction towards lactonization, producing muconolactone (MLac) and dilactone (Dilac), corroborating Tessonnier et al.’s findings.41
| Entries | Molarity | Moles | ||||||
|---|---|---|---|---|---|---|---|---|
| ccMAb (M) | Ethanol (M) | Water (M) | ccMATc (%) | ctMATd (%) | MLace (%) | Dilacf (%) | LA/ELg (%) | |
| a Reactions were conducted at constant sulfuric acid concentration (30.5 wt% w.r.t. ccMA), chloroform (4.1 g) and 80 °C temperature for 16 h. b ccMA – cis,cis muconic acid. c ccMAT – cis,cis-diethyl muconate. d ctMAT – cis,trans-diethyl muconate. e MLac – muconolactone. f Dilac – dilactone. g LA/EL – levulinic acid/ethyl levulinate. h Only levulinic acid present. | ||||||||
| 1 | 0.47 | 8.47 | 0 | 57.80 | 24.85 | 17.30 | 0 | 0 |
| 2 | 0.61 | 5.01 | 0.81 | 52.60 | 28.42 | 18.94 | 0 | 0 |
| 3 | 0.71 | 2.88 | 1.86 | 31.44 | 23.58 | 44.96 | 0 | 0 |
| 4 | 0.79 | 0.64 | 4.15 | 12.04 | 8.79 | 72.13 | 5.90 | 1.12 |
| 5 | 0.86 | 0.35 | 0.22 | 11.00 | 8.58 | 65.89 | 9.40 | 5.06 |
| 6 | 0.83 | 0.34 | 2.20 | 7.67 | 7.97 | 60.00 | 9.13 | 15.21 |
| 7 | 0.85 | 0.34 | 1.12 | 4.83 | 4.68 | 46.67 | 30.24 | 13.56 |
| 8 | 0.86 | 0.35 | 0.22 | 7.84 | 0 | 6.51 | 6.98 | 78.65 |
| 9 | 0.93 | 0 | 0 | 0 | 0 | 0 | 0 | 100h |
Additional experiments with small concentrations of ethanol and water revealed LA and EL production. Adjusting these concentrations allowed for control over product selectivity. At 8.47 M ethanol, after 16 hours, the conversion was 57.8 mol% to cis,cis-diethyl muconate, 24.85 mol% to cis,trans-diethyl muconate, and 17.3 mol% to MLac (entry 1, Table 2). Lowering ethanol to 2.88 M and increasing water to 1.86 M increased MLac conversion to 45 mol% (entry 3, Table 2). Further reducing ethanol and adding more water achieved the highest MLac conversion at 72.13 mol% (entry 4, Table 2). This demonstrates that the role of water is crucial in hydrolyzing ester linkages and pushing the equilibrium towards ccMA, with higher water concentrations promoting MLac formation as detailed in Table 2. At reduced ethanol and water concentrations (0.35 M and 0.22 M), the reaction yielded LA and EL, with MLac and dilactone conversions dropping to 6.51 mol% and 6.98 mol%, respectively (entry 8, Table 2), suggesting MLac as a possible intermediate for LA and EL. To further corroborate the role of MLac as an intermediate, we investigated temperature effects on MLac formation under the same reaction conditions mentioned in entry 4 of Table 2. The plot (Fig. S2†) shows the equilibrium product distribution for ccMA to MLac/Dilac at different temperatures. We note that MLac conversion rose from 71.4 mol% to 80 mol% with a temperature increase from 50 °C to 60 °C, then gradually declined at higher temperatures. At 60 °C, LA and EL were not formed, appearing only at higher temperatures with increased consumption of MLac and dilactone, supporting their roles as potential intermediates. Further time-resolved experiments at 80 °C revealed rapid MLac formation within the first 5 minutes, plateauing after 10 hours (Fig. S11†).
3.1 Statistical analysis of the reaction parameters
The statistical analysis of ccMAT, ctMAT, MLac, Dilac, and LA/EL with respect to changes in solvent concentrations (ethanol and water) and ccMA is summarized in Fig. S18† and Table S3.† Confidence intervals were calculated at the 95 level to assess the precision of the means. The narrow intervals for ccMAT (4.06 to 37.09) and ctMAT (3.50 to 20.24) indicate high precision. Similarly, MLac has a reasonable estimate with a confidence interval of 16.29 to 57.57 (Table S3†). In contrast, Dilac and LA/EL show wider confidence intervals, reflecting greater variability, likely due to their dependence on intermediates like MLac, rather than directly on solvents or reactant concentrations.To support this hypothesis, a bivariate analysis was conducted, revealing statistically significant effects of changing experimental parameters (solvent concentrations and reactant) on product concentrations. The analysis showed statistically significant influences of ccMA and ethanol on ccMAT and ctMAT concentrations (p < 0.001), with strong positive correlations for ethanol (r = 0.96 for ccMAT; r = 0.84 for ctMAT) and strong negative correlations for ccMA (r = −0.91 for ccMAT; r = −0.89 for ctMAT), as shown in Table S3.† These results indicate that increasing the concentrations of ethanol leads to higher production of ccMAT and ctMAT, which corresponds to higher consumption of ccMA. Based on these results, it can be inferred that higher ethanol levels inhibit the formation of MLac and subsequent products as also shown in Table 2 (entries 1–4).
MLac production was significantly affected by water (p = 0.0342, r = 0.70), showing an increase in MLac with rising water concentrations, consistent with the data in Table 2 (entries 1–9). Meanwhile, Dilac and LA/EL concentrations were not significantly influenced by ccMA, ethanol, or water (p ≫ 0.05), suggesting their formation depends more on intermediates like MLac, as reflected in Table 2. Additionally, non-significant results (p < 0.05) for other parameters (e.g., water's effect on ccMAT) indicated statistical consistency, as no substantial variation was observed due to these factors. This suggests that the observed variability is well-controlled and predictable, with the effects of solvent and reactant concentrations on the measured compounds being clearly delineated.
“Tautomer” characteristic peaks are identified by ‘e’, ‘f’, and ‘g’ in Fig. 3. Peaks ‘e’ and ‘f’ are attributed to the two alkenes that were formed after MLac tautomerization. The downshift of these peaks indicates the loss of conjugation present in MLac (peaks ‘a’, ‘b’). The “tautomer” is further corroborated in 13C-NMR through the presence peaks of ‘b’, ‘e’, ‘f’, and ‘g’ (Fig. 4).
3.2 Identification of intermediates and mechanistic pathway
In light of the rapid MLac formation and its minimal conversion to LA under the conditions of entry 4, Table 2, we shifted our focus to studying LA synthesis in the absence of added water or ethanol, entry 9, Table 2. To facilitate the identification of reactive intermediate species, the reaction was carried out in D2SO4 and CDCl3 at 75 °C for 3 h. Heavy isotopes reduce the proton exchange rate and hence lower the rate of reaction. With this adaptation, we were able to isolate intermediates at concentrations sufficient for identification via both proton and carbon NMR.1H-NMR spectra (Fig. 3) showed a pair of alkene peaks assigned at 7.6 ppm and 6.2 ppm and a pair of peaks at 2.8 ppm and 2.65 ppm confirmed MLac formation under such reaction conditions.
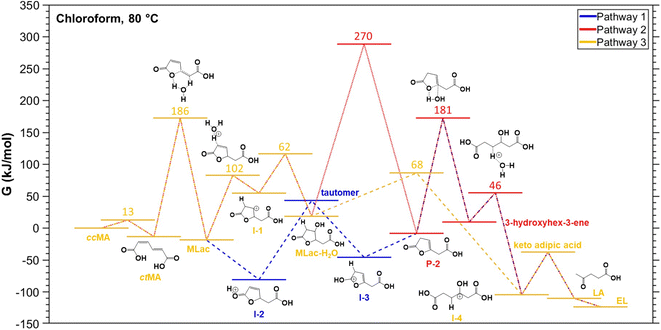
A reaction mechanism consistent with the new species identified in the 1H-NMR is shown in Fig. 2: ccMA first isomerizes to ctMA via proton exchange, followed by cyclization to form MLac; MLac subsequently establishes an equilibrium with Dilac. This is consistent with earlier reports of ccMA isomerization to cis,trans-muconic acid (ctMA) under acidic conditions.41 The pathway to LA synthesis is evidently activated under conditions where tautomerization of MLac is favorable.
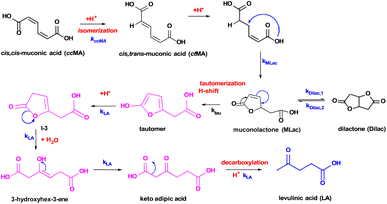 | ||
| Fig. 2 Proposed reaction pathway for levulinic acid synthesis. Pink intermediates are short-lived and highly unstable. | ||
The “tautomer” transforms to 3-hydroxyhex-3-ene. Peaks ‘i’ and ‘h’ in Fig. 3 correspond to its alkene and methylene groups, which were conspicuously absent when the reaction duration was extended. This suggests the short-lived nature of 3-hydroxyhex-3-ene, which likely undergoes rapid tautomerization and decarboxylation to form LA. 13C-NMR peaks ‘j’, ‘k’, and ‘p’ lend additional support to the structural assignment (Fig. 4).
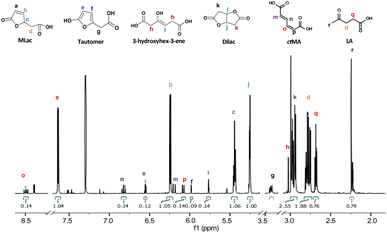 | ||
| Fig. 3 1H-NMR (600 MHz, CDCl3) of the intermediates formed under deuterated reaction conditions at 75 °C for 3 h. | ||
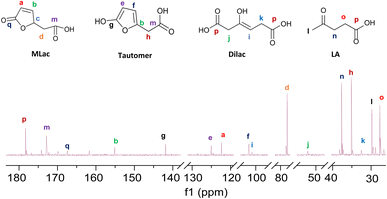 | ||
| Fig. 4 13C-NMR (600 MHz, CDCl3) of the intermediates formed under deuterated reaction conditions at 90 °C for 2 h. | ||
To build on these observations, 2D-HSQC NMR was conducted to correlate the 1H- and 13C-NMR spectra (Fig. S8†). For example, the alkene protons of MLac at 7.6 ppm and 6.2 ppm, and those of the tautomer at 6.5 ppm and 5.9 ppm, showed direct correlations with carbon peaks at 154 ppm, 122 ppm, 125 ppm, and 101 ppm, respectively. Similarly, the proton assignment for the alkene of 3-hydroxyhex-3-ene at 5.7 ppm was correlated with the carbon peak at 97 ppm. The identities of these intermediates were further confirmed by GC-MS analysis, as shown in Fig. S9.† Collectively, these findings strongly validate the presence of intermediates, including MLac, the “tautomer”, and 3-hydroxyhex-3-ene in the mechanistic pathway for LA formation.
Additionally, the protons for the Dilac at 2.9 ppm and 5.2 ppm and for the LA at 2.65 ppm and 2.72 ppm (Fig. 3) were found to be coupled with each other in 2d-HCOSY NMR (Fig. S10†) indicating these protons to be coupled with each other. This provides further evidence that these proton assignments correspond to Dilac and LA.
3.3 Density functional theory calculations
To validate the experimentally observed mechanisms leading to the formation of LA and EL, we calculated the reaction free energies (ΔG) and activation free energies (Ga) of elementary steps in three possible pathways (Figs. S13–S15†). The thermodynamically most favorable elementary steps in the respective pathways for LA and EL formation are summarized in Fig. 5. Additional computational data including zero-point energies, entropies, and formation free energies of individual intermediates are provided in Table S2.†The elementary steps considered in Figs. S13–S15† are based on the 1H-NMR and 13C-NMR predicted most probable reaction mechanism in Fig. 3C. From Fig. 5, isomerization of ccMA to ctMA (ΔG = −13 kJ mol−1, Ga = 13 kJ mol−1) is energetically facile compared to the water-assisted ring-closing of ctMA to MLac (ΔG of −5 kJ mol−1, Ga = 186 kJ mol−1). Such close-to-zero ΔG and small activation barrier for the ccMA isomerization suggest that ccMA isomerization to ctMA could be in thermodynamic equilibrium (ccMA ⇌ ctMA) in the absence of water and sulfuric acid. Additionally, while the DFT-calculated Ga for ctMA isomerization to MLac is in good agreement with previous experiments by Tessonnier et al.,41 it is higher than the expected Ga from our current experiments (see Fig. 7A). This could be due to our DFT-calculated Ga having only one explicit water molecule, which could be in-sufficient to accurately sample the proton transfer process from –COOH group of ctMA to –CH– group of MLac.52 Despite this dis calculated the barrierless addition of H+ to C–O (ΔG = −62 kJ mol−1, Ga = 0 kJ mol−1) to be more favorable than H+ addition to C–C (ΔG = 74 kJ mol−1, Ga = 102 kJ mol−1) of the five membered ring in MLac. The low barrier for C–O hydrogenation compared to C–C of the five-member ring aligns with the previous calculations for furfural hydrogenation.56–59 The reaction intermediate formed by adding H+ to C–O of MLac (I-2) has a 124 kJ mol−1 barrier for further deprotonation to form the tautomer. Comparing the overall barrier for different possible H+ addition at MLac: MLac → I-2 → tautomer (124 kJ mol−1) and MLac → I-1 → MLac−H2O (163 kJ mol−1), the energetically preferred pathway for the further reaction of MLac is through the experimentally observed tautomer (MLac → I-2 → tautomer).
The other experimentally observed product inferred by Fig. 3A and B is 3-hydroxyhex-3-ene, which can be formed by two possible pathways: (i) pathway-1, shown in blue in Fig. 5, in which protonation of the C–C near the –OH group is followed H+ elimination from the –OH to form P-2, followed by H2O-assisted ring-opening; or (ii) pathway-2, red in Fig. 5, in which H-shift and hydration of tautomer forms MLac-H2O, followed by dehydration to P-2 and H2O-assisted ring opening. Due to the insurmountable activation free energy barrier for dehydration of MLac−H2O (Ga = 270 kJ mol−1), we expect negligible reaction flux through (ii) compared to (i). Therefore, the energetically preferred pathway to form 3-hydroxyhex-3-ene is: tautomer → I-3 → P-2 → 3-hydroxyhex-3-ene. Similar to previous calculations by Gorte and Nimlos,60,61 such a high barrier for (ii) compared to (i) could be due to relatively difficult con-certed C–H and C–OH bond dissociation event in a relatively stable MLac−H2O molecule, compared to tautomer involving the sequential C–H bond formation and O–H bond dissociation events. As shown in Fig. 5, 3-hydroxyhex-3-ene can further tautomerize to form experimentally observed keto adipic acid with the overall exergonic energetics (ΔG = −47 kJ mol−1) and overall barrier of 112 kJ mol−1. The major contribution to this high barrier event is the O–H bond dissociation in the intermediate I-4. The keto adipic acid has further downhill energetics to release CO2 and thereby form LA (ΔG = −72 kJ mol−1), which can further esterify to EL in the presence of ethanol with exergonic energetics (ΔG = −13 kJ mol−1).
Overall, our DFT calculations suggest that the energetically preferred pathway for ccMA reduction to LA and EL is Pathway 1: ccMA ⇌ ctMA → MLac → I-2 → tautomer → I-3 → P-2 → 3-hydroxyhex-3-ene → I-4 → ketoadipicacid → LA → EL, with the anticipated highest Ga for P-2 → 3-hydroxyhex-3-ene.
This is in line with our experimental 1H-NMR (Fig. 3A) and 13C-NMR (Fig. 3B) analysis of reaction mixtures under deuterated conditions (CDCl3 + D2SO4) at 75–90 °C, and experimentally expected highest activation energy step being LA formation (Fig. 7A).
3.4 Reaction kinetics
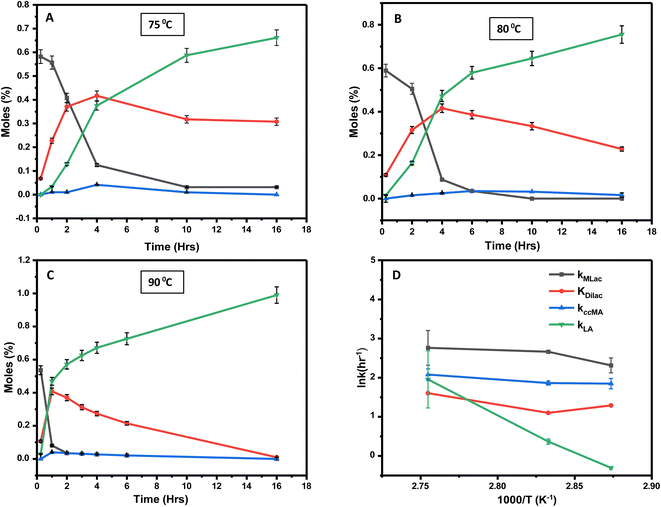
Time-resolved experiments were performed at three distinct temperatures: 75 °C, 80 °C, and 90 °C at constant deuterated sulfuric acid and deuterated chloroform concentration to further elucidate the process. The Dilac peak in the 1H-NMR spectrum at 5.2 ppm served as the reference for quantitative analyses of MLac, Dilac, tautomer, and LA concentrations.Within 15 minutes at 75 °C, MLac rapidly accumulates, constituting 58 mol% of the mixture. However, its concentration waned over time, with a concomitant increase in both Dilac and LA (Fig. 6A). Notably, the Dilac formation rate initially exceeded that of LA, as evidenced by a steeper slope in Fig. 6A. The rate of tautomer formation remained low, plateauing at about 2% within the first 4 hours. Similar trends were observed at higher temperatures. At 80 °C, Dilac consumption increased, thereby promoting LA formation (Fig. 6B). Even more strikingly, at 90 °C, LA yields soared to 72% within 6 h (Fig. 6C). Dilac peaked at around 40% conversion at all temperatures before declining, which corresponded with an uptick in LA formation. Interestingly, once this conversion threshold is surpassed at 90 °C, the rate of LA formation accelerated relatively swiftly compared to that at other temperatures. Finally, complete MLac consumption within 4 hours (Fig. 6C) suggests that the majority of MLac converted to Dilac before forming LA. Combined, these observations imply a high activation barrier for MLac to LA, compared to that for ccMA to MLac.
The time vs. concentration data collected at each temperature were then fit to the first-order rate equations (eqn (3)–(7)) for predicting the rate constants using the least-squares regression in MATLAB. The differential rate equations (eqn (3)–(7)) and their corresponding rate constants are based on the reaction scheme reported as a mechanism (Fig. 3C). The predicted rate constants presented an excellent fit with the experimental observations (Fig. S16† and 7A).
The error bars for the experimental values were calculated by non-linear regression, with a fixed 5% uncertainty applied to reflect potential measurement inaccuracies. The uncertainty in the rate constants was quantified using the Hessian matrix approach, which provided error bars based on the model's sensitivity to parameter changes. This methodology addresses both the experimental variability and the confidence in the fitted model parameters, providing a comprehensive assessment of the uncertainties inherent in the data and the model obtained.
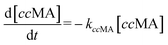 | (3) |
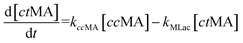 | (4) |
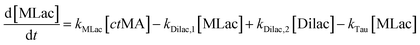 | (5) |
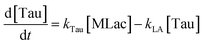 | (6) |
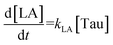 | (7) |
 is the equilibrium constant for MLac ⇌ Dilac, with kDilac,1 being the rate constant for the Dilac formation and kDilac,2 being the rate constant for the Dilac disappearance.
is the equilibrium constant for MLac ⇌ Dilac, with kDilac,1 being the rate constant for the Dilac formation and kDilac,2 being the rate constant for the Dilac disappearance.
In Fig. 6A–C, Tautomer concentration was observed to be quite low, possibly due to its fast conversion to P-2 (ΔG = −40.6 kJ mol−1, Fig. 5). Therefore, while the tautomer formation reaction was taken into consideration (eqn (3) and (4)) for macroscopic modeling, and the corresponding rate constant kTau is not reported in Fig. 7A. The kinetic rate constants evaluation in MAT-LAB assumed the same rate constant of LA (kLA) for all the pink intermediates-involved reaction steps after tautomer formation (Fig. 3C). This can be attributed to the short-lived nature of these compounds reacting instantly to form LA.
The rate constant for MLac formation (kMLac) exceeded that for LA (kLA), consistent across all temperatures (Fig. 7A). Furthermore, kLA values were significantly higher at 90 °C compared to those at 75 °C and 80 °C, corroborating the extremely fast LA formation observed at this elevated temperature (Fig. 6C).
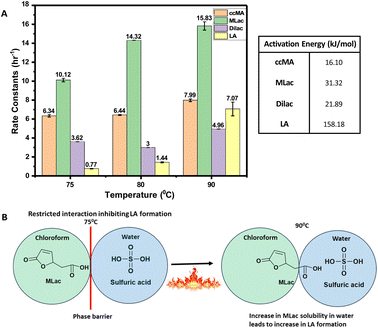
The activation energies were calculated as follows: 16.10 kJ mol−1 for ccMA, 31.32 kJ mol−1 for MLac, and 158.18 kJ mol−1 for LA (Fig. 7A). The lower activation energies observed Fig. 7A indicate that the isomerization of ccMA to MLac proceeds readily, whereas the conversion of MLac to LA necessitates significantly higher energy input.
The high apparent activation energy for LA formation can be ascribed to the hindered interaction among MLac and sulfuric acid phase. This hindrance arises due to the immiscibility of chloroform and sulfuric acid phases (Fig. 7B). However, at a temperature of 90 °C, this diffusion barrier of MLac from chloroform to sulfuric acid phase might be surmountable, and thereby enabling the sulfuric acid to catalyze the tautomerization of MLac to ultimately form LA. Consequently, we hypothesize that the high activation energy for LA formation could result from the hindered diffusion of MLac between chloroform and sulfuric acid phase. Overall, these observations imply that MLac tautomerization could be the rate-determining step for LA formation under the studied reaction conditions.
The kinetic results of our study are comparable to a previous work by Haider et al. and Dumesic et al., where the combined decarboxylation and ring-opening of 2-pyrones substituents in different solvents were calculated to be the highest activation energy step.62,63 This parallels our results, where the immiscibility of chloroform and sulfuric acid led to calculated high activation energy of decarboxylation step for LA formation (158.18 kJ mol−1). Both studies emphasize the critical role of solvent effects, supporting our hypothesis that diffusion barriers in our system could be elevating the apparent activation energy for LA formation.
4. Conclusions
This study presents the solvent-free synthesis of levulinic acid (LA) from bulk cis,cis-muconic acid (ccMA), elucidating the reaction mechanism through experimental and computational analysis. Key parameters influencing reaction kinetics and selectivity include [ethanol]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [water] ratio and temperature. Remarkably, LA selectivity reached 100% in the absence of ethanol, water, and chloroform. The intermediates MLac, dilactone, tautomer, and 3-hydroxyhex-3-enedioic acid were identified using 1H-NMR, 13C-NMR, HSQC, HCOSY, and GCMS, with their formation pathways supported by DFT calculations. Kinetic studies highlighted dilactone as a preferential intermediate over tautomers, impacting the LA formation rate. Tautomerization of MLac, constrained by mass transfer limitations, was identified as the rate-determining step for LA formation. Raising the temperature from 75 °C to 90 °C increased the LA formation rate constant by tenfold, thereby breaching the chloroform to sulfuric acid diffusion barrier of MLac. Combined, these results showcase a complex interplay of chemical reaction kinetics and mass transfer process during the solution-phase chemical transformation of bioderived organic molecules to value-added chemicals.
[water] ratio and temperature. Remarkably, LA selectivity reached 100% in the absence of ethanol, water, and chloroform. The intermediates MLac, dilactone, tautomer, and 3-hydroxyhex-3-enedioic acid were identified using 1H-NMR, 13C-NMR, HSQC, HCOSY, and GCMS, with their formation pathways supported by DFT calculations. Kinetic studies highlighted dilactone as a preferential intermediate over tautomers, impacting the LA formation rate. Tautomerization of MLac, constrained by mass transfer limitations, was identified as the rate-determining step for LA formation. Raising the temperature from 75 °C to 90 °C increased the LA formation rate constant by tenfold, thereby breaching the chloroform to sulfuric acid diffusion barrier of MLac. Combined, these results showcase a complex interplay of chemical reaction kinetics and mass transfer process during the solution-phase chemical transformation of bioderived organic molecules to value-added chemicals.
The mild and solvent-free reaction conditions with high LA selectivity of the proposed synthetic route are promising for future scale-up considerations. However, the scalability could be restricted by the energy requirements of muconic acid synthesis, maintaining consistent reaction conditions, and the mass transfer limitations observed in the muconic acid decarboxylation process to LA. Future techno-economic analyses and life cycle assessments are needed to fully evaluate the feasibility of the proposed LA synthesis route at an industrial scale.
Data availability
All the data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge support from the National Science Foundation, award \#2132200. Also, we wish to thank ISU Chemical Instrumentation Facility staff members (Dr Sarah Cady and Dr Shu Xu) for training and assistance pertaining to the AVIII-600 results included in this publication.Notes and references
- Y. Zhang, E. Xing, W. Han, P. Yang, S. Zhang, S. Liu, D. Cao and M. Li, Engineering, 2024 DOI:10.1016/j.eng.2024.06.017.
- G. C. Hayes and C. R. Becer, Polym. Chem., 2020, 11, 4068–4077 RSC.
- D. W. Rackemann and W. O. Doherty, Biofuels, Bioprod. Biorefin., 2011, 5, 198–214 CrossRef CAS.
- C. G. Lima, J. L. Monteiro, T. de Melo Lima, M. Weber Paixão and A. G. Corrêa, ChemSusChem, 2018, 11, 25–47 CrossRef CAS PubMed.
- A. Sinisi, M. Degli Esposti, S. Braccini, F. Chiellini, S. Guzman-Puyol, J. A. Heredia-Guerrero, D. Morselli and P. Fabbri, Mater. Adv., 2021, 2, 7869–7880 RSC.
- W. Xuan, M. Hakkarainen and K. Odelius, ACS Sustainable Chem. Eng., 2019, 7, 12552–12562 CAS.
- E. Melro, A. Filipe, A. J. Valente, F. E. Antunes, A. Romano, M. Norgren and B. Medronho, Int. J. Biol. Macromol., 2020, 164, 3454–3461 CrossRef CAS PubMed.
- J. C. Serrano-Ruiz, D. J. Braden, R. M. West and J. A. Dumesic, Appl. Catal., B, 2010, 100, 184–189 CrossRef CAS.
- D. J. Braden, C. A. Henao, J. Heltzel, C. C. Maravelias and J. A. Dumesic, Green Chem., 2011, 13, 1755–1765 RSC.
- S. M. Sen, E. I. Gürbüz, S. G. Wettstein, D. M. Alonso, J. A. Dumesic and C. T. Maravelias, Green Chem., 2012, 14, 3289–3294 RSC.
- J. J. Bozell, L. Moens, D. Elliott, Y. Wang, G. Neuenscwander, S. Fitzpatrick, R. Bilski and J. Jarnefeld, Resour., Conserv. Recycl., 2000, 28, 227–239 CrossRef.
- T. Hille, German patent, 4446600, 1996.
- J. Tsucha and K. Yoshida, Japanese patent, 5320023, 1994.
- C. Sasikala, C. V. Ramana and P. R. Rao, Biotechnol. Prog., 1994, 10, 451–459 CrossRef CAS.
- A. S. Amarasekara, U. Ha and N. C. Okorie, J. Polym. Sci., Part A: Polym. Chem., 2018, 56, 955–958 CrossRef CAS.
- E. Ahmad, M. I. Alam, K. Pant and M. A. Haider, Green Chem., 2016, 18, 4804–4823 RSC.
- S. H. Pyo, S. J. Glaser, N. Rehnberg and R. Hatti-Kaul, ACS Omega, 2020, 5, 14275–14282 CrossRef CAS PubMed.
- P. A. Russo, M. M. Antunes, P. Neves, P. V. Wiper, E. Fazio, F. Neri, F. Barreca, L. Mafra, M. Pillinger and N. Pinna, et al. , Green Chem., 2014, 16, 4292–4305 RSC.
- G. M. G. Maldonado, R. S. Assary, J. Dumesic and L. A. Curtiss, Energy Environ. Sci., 2012, 5, 6981–6989 RSC.
- B. Lu, S. An, D. Song, F. Su, X. Yang and Y. Guo, Green Chem., 2015, 17, 1767–1778 RSC.
- S. Zhu, C. Chen, Y. Xue, J. Wu, J. Wang and W. Fan, ChemCatChem, 2014, 6, 3080–3083 CrossRef CAS.
- S. Zhu, Y. Cen, J. Guo, J. Chai, J. Wang and W. Fan, Green Chem., 2016, 18, 5667–5675 RSC.
- H. E. Hoydonckx, W. M. Van Rhijn, W. Van Rhijn, D. E. De Vos and P. A. Jacobs, Ullmann's Encyclopedia of Industrial Chemistry, 2007 Search PubMed.
- X. Chen, L. Zhang, B. Zhang, X. Guo and X. Mu, Sci. Rep., 2016, 6, 28558 CrossRef PubMed.
- G. Fiorentino, M. Ripa, S. Mellino, S. Fahd and S. Ulgiati, J. Clean. Product., 2014, 66, 174–187 CrossRef CAS.
- Z. Persin, K. Stana-Kleinschek, T. J. Foster, J. E. Van Dam, C. G. Boeriu and P. Navard, Carbohydr. Polym., 2011, 84, 22–32 CrossRef CAS.
- C. W. Johnson, D. Salvachúa, N. A. Rorrer, B. A. Black, D. R. Vardon, P. C. S. John, N. S. Cleveland, G. Dominick, J. R. Elmore and N. Grundl, et al. , Joule, 2019, 3, 1523–1537 CrossRef CAS.
- Y. Okamura-Abe, T. Abe, K. Nishimura, Y. Kawata, K. Sato-Izawa, Y. Otsuka, M. Nakamura, S. Kajita, E. Masai and T. Sonoki, et al. , J. Biosci. Bioeng., 2016, 121, 652–658 CrossRef CAS PubMed.
- N. A. Rorrer, S. F. Notonier, B. C. Knott, B. A. Black, A. Singh, S. R. Nicholson, C. P. Kinchin, G. P. Schmidt, A. C. Carpenter and K. J. Ramirez, et al. , Cell Rep. Phys. Sci., 2022, 3, 100791 CrossRef.
- Y. Chen, B. Fu, G. Xiao, L.-Y. Ko, T.-Y. Kao, C. Fan and J. Yuan, ACS Food Sci. Technol., 2021, 1, 382–387 CrossRef CAS.
- Dawnbreaker, DOE Market Research Study: Adipic Acid and Nylon 66, United States Department of Energy Technical Report, 2023 Search PubMed.
- A. Z. Werner, W. T. Cordell, C. W. Lahive, B. C. Klein, C. A. Singer, E. C. Tan, M. A. Ingraham, K. J. Ramirez, D. H. Kim and J. N. Pedersen, et al. , Sci. Adv., 2023, 9, eadj0053 CrossRef CAS PubMed.
- J. Becker, M. Kuhl, M. Kohlstedt, S. Starck and C. Wittmann, Microb. Cell Fact., 2018, 17, 1–14 CrossRef PubMed.
- R. Sillers, T. Hermann, M. Spencer, R. Udani and R. R. Yocum, United States Patent and Trademark Office, US11685938B2, PTT Global Chemical PCL, 2023.
- D. R. Vardon, N. A. Rorrer, D. Salvachúa, A. E. Settle, C. W. Johnson, M. J. Menart, N. S. Cleveland, P. N. Ciesielski, K. X. Steirer and J. R. Dorgan, et al. , Green Chem., 2016, 18, 3397–3413 RSC.
- D. R. Vardon, M. A. Franden, C. W. Johnson, E. M. Karp, M. T. Guarnieri, J. G. Linger, M. J. Salm, T. J. Strathmann and G. T. Beckham, Energy Environ. Sci., 2015, 8, 617–628 RSC.
- R. Lu, F. Lu, J. Chen, W. Yu, Q. Huang, J. Zhang and J. Xu, Angew. Chem., Int. Ed., 2016, 128, 257–261 CrossRef.
- R. Beerthuis, G. Rothenberg and N. R. Shiju, Green Chem., 2015, 17, 1341–1361 RSC.
- L. Coudray, V. Bui, J. W. Frost and D. Schweitzer, US Pat., 9073867, Process for Preparing Caprolactam and Polyamides Therefrom, 2015 Search PubMed.
- C. Mueller, M. Bock, M. Da Silva, R. Fischer, B. Blank, A. Kindler, J. Melder, B. Otto, M. Schelwies and A. Henninger, WO Patent, WO2015086819A1, 2015.
- J. M. Carraher, P. Carter, R. G. Rao, M. J. Forrester, T. Pfennig, B. H. Shanks, E. W. Cochran and J.-P. Tessonnier, Green Chem., 2020, 22, 6444–6454 RSC.
- P. Carter, J. L. Trettin, T.-H. Lee, N. L. Chalgren, M. J. Forrester, B. H. Shanks, J.-P. Tessonnier and E. W. Cochran, J. Am. Chem. Soc., 2022, 144, 9548–9553 CrossRef CAS PubMed.
- N. A. Rorrer, J. R. Dorgan, D. R. Vardon, C. R. Martinez, Y. Yang and G. T. Beckham, ACS Sustainable Chem. Eng., 2016, 4, 6867–6876 CrossRef CAS.
- M. J. Climent, A. Corma and S. Iborra, Green Chem., 2014, 516–547 RSC.
- F. Coupe, L. Petitjean, P. T. Anastas, F. Caijo, V. Escande and C. Darcel, Green Chem., 2020, 22, 6204–6211 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, H. P. Li X. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Norm, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, Wallingford CT, 2013 Search PubMed.
- A. McLean and G. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and H. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- H. B. Schlegel, J. Comput. Chem., 1982, 3, 214–218 CrossRef CAS.
- A. K. Chew, T. W. Walker, Z. Shen, B. Demir, L. Witteman, J. Euclide, G. W. Huber, J. A. Dumesic and R. C. Van Lehn, ACS Catal., 2019, 10, 1679–1691 CrossRef.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- J. A. J. Montgomery, J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 1999, 110, 2822–2827 CrossRef CAS.
- D. A. Dolson, R. Battino, T. M. Letcher, K. H. Pegel and N. Revaprasadu, J. Chem. Educ., 1995, 72, 927 CrossRef CAS.
- A. Banerjee and S. H. Mushrif, ChemCatChem, 2017, 9, 2828–2838 CrossRef CAS.
- B. Liu, L. Cheng, L. Curtiss and J. Greeley, Surf. Sci., 2014, 622, 51–59 CrossRef CAS.
- L. Gong, N. Agrawal, A. Roman, A. Holewinski and M. J. Janik, J. Catal., 2019, 373, 322–335 CrossRef CAS.
- V. Vorotnikov, G. Mpourmpakis and D. G. Vlachos, ACS Catal., 2012, 2, 2496–2504 CrossRef CAS.
- S. Roy, G. Mpourmpakis, D.-Y. Hong, D. G. Vlachos, A. Bhan and R. J. Gorte, ACS Catal., 2012, 2, 1846–1853 CrossRef CAS.
- S. Kim, D. J. Robichaud, G. T. Beckham, R. S. Paton and M. R. Nimlos, J. Phys. Chem. A, 2015, 119, 3604–3614 CrossRef CAS PubMed.
- M. Chia, M. A. Haider, G. Pollock III, G. A. Kraus, M. Neurock and J. A. Dumesic, J. Am. Chem. Soc., 2013, 135, 5699–5708 CrossRef CAS PubMed.
- S. Gupta, M. I. Alam, T. S. Khan, N. Sinha and M. A. Haider, RSC Adv., 2016, 60433–60445 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Additional NMR data, DFT calculation results, and kinetic data. See DOI: https://doi.org/10.1039/d4ra05226a |
| This journal is © The Royal Society of Chemistry 2024 |