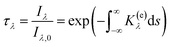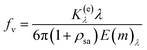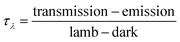Experimental and numerical research on the effects of pressure and CO₂ dilution on soot formation in laminar co-flow methane/air diffusion flames

Abstract

An experimental and numerical investigation was conducted to examine the formation of soot in methane/air laminar diffusion flames under varying CO₂ dilution ratios, ranging from 0% to 40%, and pressures between 5 and 10 atm. The experimental methodology incorporated diffuse-light two-dimensional line-of-sight attenuation (diffuse 2D-LOSA) to ascertain the volume fraction and peak temperature distribution of soot within the flames. For the numerical methodology, CoFlame—an open-source computational code—was utilized to calculate the detailed flame temperature, soot volume fraction, and the mole fractions of key intermediate species pivotal to soot generation. The study reveals that an increased dilution ratio of CO₂ can reduce flame temperature and the molar fraction of hydrogen (H), while simultaneously increasing the molar fraction of hydroxyl (OH). This shift in chemical composition results in a reduced rate of soot nucleation and an intensified oxidation process during the later stages of soot development, thereby diminishing the overall soot volume fraction. An increase in pressure significantly boosts the processes of soot nucleation, HACA surface growth, and PAH condensation, thereby promoting the formation of soot. Elevated pressure corresponds to an increase in flame temperature and a narrower soot formation region. Additionally, the inhibitory effect of CO₂ dilution on soot formation is mitigated under increased pressure. The findings from this research are expected to provide valuable insights and strategic guidance for the management and control of pollutants in the context of hydrocarbon fuel combustion, particularly when CO₂ dilution is employed.

---

1. Introduction

Exhaust Gas Recirculation (EGR) is recognized as an effective strategy for mitigating exhaust emissions from compression ignition engines, particularly concerning pollutants such as soot and NO_x.¹ Significant advancements have been made in the research concerning the mechanisms of NO_x generation and the methods for its control.^2–6 Nonetheless, the production mechanism of soot remains intricate. A consensus has yet to be reached on the competitive and facilitative mechanisms of the key elementary reactions involved in the formation of soot. Further investigation is necessary to better understand the characteristics of soot formation within flames.

Soot formation is a common occurrence in the combustion of various hydrocarbon fuels, predominantly stemming from the incomplete combustion or thermal cracking of these compounds.^7–9 Soot is a deleterious pollutant that not only diminishes the combustion efficiency of fuel but also, through its emission, carries away heat, impacting the thermal efficiency of combustion systems. Prolonged suspension of soot particles in the atmosphere can precipitate a variety of environmental concerns, notably photochemical smog. Soot particles are a significant constituent of Particulate Matter (PM), with polycyclic aromatic hydrocarbons (PAHs) adsorbed on their surfaces posing substantial health risks.^10,11 Research has identified soot as a potent contributor to the greenhouse effect, ranking second only to carbon dioxide in its impact.¹² Consequently, the suppression of soot formation is typically a priority. However, there are instances where soot production can be advantageous, such as within the combustion chamber of a boiler, where it can enhance flame radiation heat transfer.¹³ Additionally, soot particles are utilized as additives in the rubber industry to bolster the wear resistance of materials.

Studies have demonstrated that the introduction of CO₂, either on the oxidant or fuel side, can significantly reduce the temperature and quantity of soot formed during the combustion of hydrocarbon fuels.^14–17 The incorporation of a diluent into the diffusion flame on either side can influence the combustion process and pollutant formation through three primary mechanisms: dilution, thermal, and chemical effects.¹⁸ Yang et al.¹⁹ employed a combination of numerical simulation and experimental methods to study soot formation in co-flow diffusion ethylene flame with CO₂ supplementation to the fuel (the CO₂–F), oxidizer (the CO₂–O), and fuel/oxidizer (the CO₂–F/O) streams. Their findings indicated that the CO₂–F/O was the most effective in inhibiting soot formation and flame temperature, followed by the CO₂–O, and the CO₂–F. Chen et al.²⁰ experimentally investigated the influence of CO₂ addition on the soot particle sizes in axisymmetric laminar co-flow ethylene/air diffusion flames. They discovered that CO₂ addition could compress the nucleation diameter of soot particles and alter the boundary between the flame surface growth zone and the oxidation zone.

However, the majority of these studies have been conducted under atmospheric pressure conditions. Given that most practical combustion devices operate under elevated pressures, examining soot formation under high-pressure conditions is of greater practical relevance.²¹ Currently, there is a scarcity of research that integrates experimental and simulation methodologies to study the impact of diluents on soot formation under high-pressure conditions. Liu et al.²² explored the influence of CO₂/CH₄ ratios on soot formation in laminar inverse coflow diffusion flames under pressures ranging from 1 to 10 atmospheres, at conditions close to ATR (autothermal reforming of methane). Their results indicated that a higher CO₂/CH₄ ratio could inhibit soot formation, but as pressure increased, the extent of soot reduction diminished, and the peak soot volume fraction rose with flame height before stabilizing. Karatas et al.²³ conducted experimental research on the effects of N₂ and CO₂ dilution on soot volume fraction and temperature in ethylene/air laminar diffusion flames. They observed that the maximum soot volume fraction in CO₂-diluted flames was consistently lower, and beyond 15 atm pressure, the relationship between soot formation, flame temperature, and pressure underwent changes, suggesting that the effects of pressure and CO₂ dilution on soot formation are not isolated but rather are superimposed and coupled.

Extensive research has revealed that the underlying mechanisms influencing soot formation due to variations in pressure and CO₂ dilution remain elusive. Consequently, there is a pressing need for more in-depth and meticulous investigation. Moreover, due to its high hydrogen content, methane combustion results in lower soot production, making experimental studies on soot formation in methane flames more challenging. This complexity contributes to the current incomplete understanding of soot formation in methane combustion flames. In light of this, the present study aims to provide an in-depth analysis of the effects of CO₂ dilution on soot formation in methane laminar diffusion flames under high-pressure conditions through a combination of experimental and simulation approaches. The outcomes of this research are anticipated to offer guidance for the control of pollutants during the combustion of hydrocarbon fuels with CO₂ dilution.

2. Experimental setup

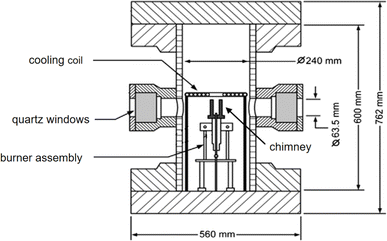
The experimental work was undertaken at the National Research Council Canada, utilizing a high-pressure combustion chamber and a laminar diffusion flame burner, both of which are extensively detailed in the existing literature.²⁴ As depicted in Fig. 1, the combustion chamber boasts a total height of 0.6 m and an internal diameter of 0.24 m. Engineered to endure pressures up to 10 MPa, it is equipped with optical access ports that facilitate a range of diagnostic measurements. These ports are strategically positioned at three distinct angles: 0°, 90°, and 180° to accommodate viewing measurements, as well as to perform 90-degree scattering and imaging experiments. The fuel nozzle of the employed burner is constructed from stainless steel, featuring an exit diameter of 3.06 mm. Complementary to the fuel nozzle, the air outlet is designed using a concentric tube nozzle, which has an internal diameter of 25.4 mm. This configuration ensures a controlled and efficient mixing of fuel and air for the combustion process.

Fig. 1 Schematic of the experimental setup.

In the high-pressure dilution combustion experiment, CO₂ was introduced as a diluent on the fuel side. The mass flow rates of the air mixture (comprising 79% N₂ and 21% O₂) and methane were consistently maintained at 1.118 g s⁻¹ and 0.5975 mg s⁻¹, respectively. Under a pressure of 10 atmospheres, the CO₂ dilution ratio—defined as the volume ratio of CO₂ to the total volume of CO₂ and methane—was systematically varied to 10%, 20%, 30%, and 40%. For pressures of 5 and 7 atmospheres, the CO₂ dilution ratios were incrementally set to 5%, 10%, 15%, 20%, and 25%. It is important to note that the dilution ratio of CO₂ can be maximized at 25% under pressures of 5 and 7 atmospheres. Any attempt to augment the CO₂ dilution beyond this threshold would lead to a soot concentration that is insufficient for reliable measurement.

In this work, the diffusion 2D-LOSA (diffuse-light two-dimensional line-of-sight attenuation) technique was employed to ascertain the volume fraction of soot and to map the flame temperature distribution. Within the diffusion 2D-LOSA system, a mercury arc lamp served as the light source for the experiments. The light emitted from the lamp was directed through an integrating sphere to ensure uniform illumination. A pair of lens doublets was utilized to capture the image of the flame's core, which was then projected onto a CCD array equipped with a 450 nm narrow-band filter.²⁵ During this optical analysis, the capability of light to pass through a medium containing soot aerosol is quantified by measuring its transmissivity across a chord. For a given wavelength λ, the transmissivity, represented as τ_λ, is calculated using the following formula:

The light intensity at the entry point of the medium is represented by I_λ,0, while I_λ denotes the intensity after the light has passed through the medium, which attenuates the light. The local extinction coefficients, indicated by K^(e)_λ, describe the medium's capacity to diminish light. The concentration of soot, symbolized as f_v, is determined by the following formula:

The soot absorption function is represented by E(m)_λ. The term ρ_sa refers to the ratio of the scatter coefficient to the absorption coefficient, which can be negligible for certain aerosols. In our experimental setup, τ_λ was not obtained by directly measuring I_λ,0 and I_λ. Instead, it was ascertained through a series of four monochromatic measurements. These measurements were designed to capture the intensity in the following scenarios: with the lamp but without the attenuation medium (lamp), with neither the lamp nor the attenuation medium (dark), with the lamp and the attenuation medium (transmission), and with the attenuation medium but without the light source (emission). The value of τ_λ is subsequently calculated using the following formula:

Once τ_λ has been established, an inversion algorithm is applied to deduce the local extinction coefficients, K^(e)_λ. With these coefficients in hand, the concentration of soot can be readily calculated. The temperature of the soot is associated with its incandescent emission, which can be ascertained through emission measurements once the absorption coefficient has been determined from the transmission data.^26,27 Throughout the experiment, flame imagery at varying levels of CO₂ enrichment was captured using a high-definition digital video camera. The measurement uncertainty for the soot volume fraction using the diffuse 2D-LOSA technique is projected to lie within a range of 20% to 30%, representing a 95% confidence interval.²⁸ This uncertainty is primarily driven by inaccuracies in determining the magnitude of E(m), the soot refractive index function, and the variability associated with the scattering contribution to light attenuation measurements.

3. Numerical setup

3.1 Methodology

The simulations of the CH₄ laminar diffusion flame presented in this article are conducted using the open-source flame code CoFlame. Developed by Eaves and colleagues,²⁵ CoFlame is a comprehensive suite of tools designed for the simulation of laminar diffusion flames. Accurately simulating soot formation necessitates a dual focus on the gas-phase chemical kinetics and the dynamics of solid-phase particles.

The gas-phase mechanism integrated into the CoFlame simulation in this study is derived from the literature of Chernov, Thomson, and other contributors.^29–34 It encompasses an extensive reaction mechanism for the combustion of C1–C2 fuels, often referred to as the C1–C2 mechanism. In the subsequent series of studies, this mechanism has been iteratively refined and it offers enhanced accuracy over other gas-phase reaction models. The mechanism encompasses 94 chemical reaction components and involves 733 elementary reactions. It includes the pyrolysis of fuel under high-temperature conditions, leading to the formation of gas-phase small molecules and free radicals such as C₂H₂, CH₃, C₃H₃, and C₄H₄. Additionally, it covers the oxidation processes of the components C1 and C2, as well as the formation of higher-order alkanes or alkenes. The mechanism also encompasses the formation of the first benzene ring (A₁), and the generation of larger polycyclic aromatic hydrocarbons (PAHs), including naphthalene (A₂), phenanthrene (A₃), and pyrene (A₄).

For the simulation of soot particle formation and dynamics, a detailed sectional model^35–39 is employed. This model divides the mass range of soot particles into multiple discrete logarithmic segments and solves the particle population balance equation for each segment. The model uses 35 discrete sections, which is deemed sufficient as the average soot morphology parameters stabilize with this number of sections. It is assumed that soot aggregates consist of spherical primary particles of uniform diameter, with a fractal dimension of 1.8.^40,41 The model solves two transport equations per section: one for the soot aggregate number density and another for the soot primary particle number density. The specific sectional control equations are detailed in the literature,²⁵ and the model addresses the particle population balance equation, also known as the particle dynamics equation. It includes key processes in soot formation such as nucleation, PAH condensation and surface growth, surface oxidation, coagulation, collision, particle diffusion, and thermophoresis.

3.2 Numerical conditions

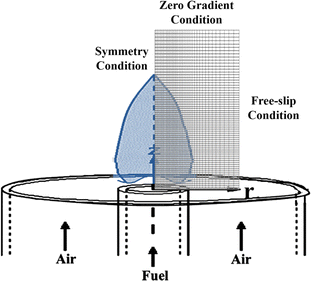
The computational domain for the simulation, depicted in Fig. 2, represents an axisymmetric laminar diffusion flame. The simulation conditions are consistent with the experimental conditions. The fuel nozzle has an inner diameter of 3.06 mm and a wall thickness of 0.5 mm, while the air outlet is configured by a concentric tube with an inner diameter of 25.4 mm. The computational domain spans 4.327 cm axially and 0.387 cm radially, discretized into a non-uniform grid matrix of 72(z) × 60(r) cells. The fuel and air outlets are located at z = 0 cm, with the flame's centerline defined by r = 0 cm. At the domain's axial boundary (z = 4.327 cm), a zero gradient condition is applied, and a free-slip condition is established at the radial boundary (r = 0.387 cm). Following a sensitivity analysis, it was confirmed that the computational domain's size is adequate, with boundary positions exerting no influence on the simulation outcomes. Convergence for a given scenario is achieved when the relative change in output variables, such as soot volume fraction, remains below 10⁻⁵ after every 100 pseudo-time steps.

Fig. 2 Schematic of the flame configuration and computational mesh.

The simulation parameters are meticulously aligned with their experimental counterparts, with CO₂ introduced as a diluent on the fuel side, while the oxidizer is supplied as air, composed of 79% N₂ and 21% O₂. The mass flow rate of methane is rigorously controlled at 0.5975 mg s⁻¹, and the air mass flow rate is set at 1.118 g s⁻¹. Both the fuel and oxidizer inlets are maintained at a temperature of 300 K. The simulation accounts for variations in pressure and the CO₂ addition ratio, which consequently affect the velocities at the fuel and oxidizer outlets. These variations and their corresponding outlet velocities are detailed in Table 1.

Table 1 Simulation conditions

Pressure (atm)	CO2 dilution rate (%)	Fuel outlet velocity (cm s^−1)	Air outlet velocity (cm s^−1)
10	0	1.131	17.552
10	10	1.264	17.552
10	20	1.422	17.552
10	30	1.625	17.552
10	40	1.896	17.552
7	0	1.616	25.074
7	20	2.031	25.074
5	0	2.262	35.104
5	20	2.844	35.104

---

4. Experimental and numerical results

4.1 Soot formation

Fig. 3 presents the experimental findings on the radial distribution of soot volume fraction at distinct flame heights, specifically at 6.0 mm, 6.5 mm, and 7.0 mm. These measurements were uniformly conducted at a constant pressure of 10 atm. Despite the low soot volume fraction values observed in the flames, the secondary repeated measurements demonstrated minimal relative error, affirming the high sensitivity and stability of the diffuse 2D-LOSA technology used for these measurements. As depicted in Fig. 3, the radial distribution of soot volume fraction follows a consistent trend across the various flame heights, showing an initial increase followed by a decrease with radial distance. At a specific radial position within the flame, the soot volume fraction attains its maximum value (S_max). Notably, an increase in CO₂ concentration correlates with a reduction in S_max. Furthermore, the soot concentration asymptotically approaches zero towards the flame's outer edge.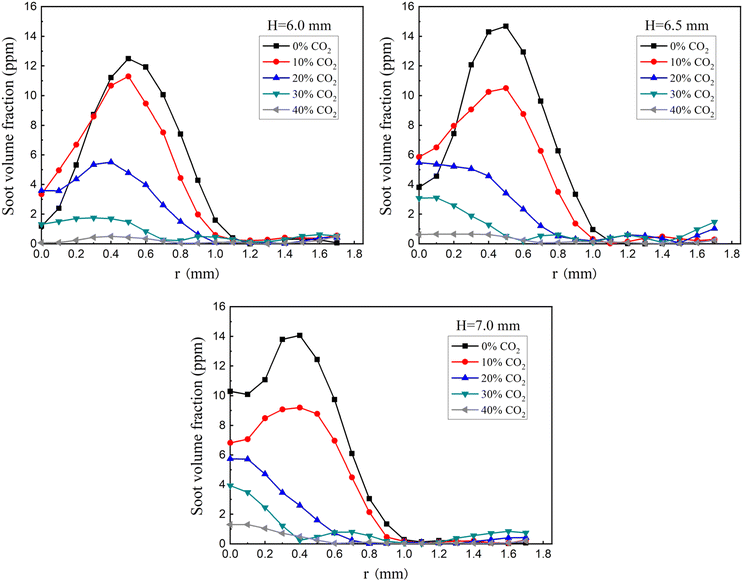

Fig. 3 Radial distributions of soot volume fraction at different flame heights (6.0, 6.5 and 7.0 mm) in flames with different CO₂ dilution rates at 10 atm (experimental results).

Fig. 4 illustrates the variation in average soot volume fraction at different flame heights under varying CO₂ dilution ratios, all at a constant pressure of 10 atm. A distinct trend is observable in the data presented: the average soot volume fraction increases with flame height up to a certain point, after which it decreases. This phenomenon can be attributed to the fact that as the flame height increases, conditions become more conducive to soot formation, leading to an increase in the soot volume fraction that reaches a maximum value. Beyond this peak, the soot particles encounter an environment with heightened oxidative potential at greater heights, which accelerates their oxidation and consequently leads to a reduction in soot concentration. Furthermore, it is evident that the average soot volume fraction progressively diminishes with an increasing proportion of CO₂ dilution. The flame region spanning heights from 5 mm to 8 mm is characterized by a heightened concentration of soot, with a pronounced peak in soot volume fraction occurring at a height of about 7 mm. At this specific height, the average soot volume fraction within the methane flame decreases consistently with the increment of the CO₂ dilution ratio. This trend underscores the significant suppressive impact of CO₂ on soot formation within the flame. Additionally, the curves representing the relationship between soot content and flame height across different CO₂ dilution ratios exhibit similar patterns. This consistency aligns with experimental outcomes achieved by Thomson and colleagues using the extinction method,²⁸ further substantiating the reliability of the diffuse 2D-LOSA technology in the measurement of soot volume fraction in flames.

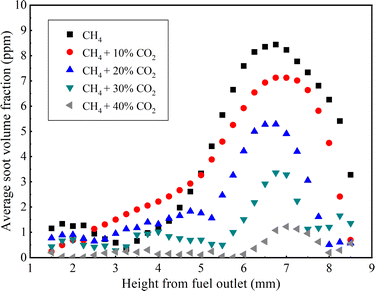Fig. 4 Average soot volume fraction at different flame heights with different dilution ratios of CO₂ at 10 atm (experimental results).

Fig. 5 presents a comparative analysis of the maximum soot volume fraction in methane flames across different CO₂ dilution ratios at pressures of 5 and 10 atm, incorporating both experimental measurements and numerical simulation outcomes utilizing the CoFlame software. It is shown that there is good agreement between the experimental data and the simulation results, which serves to confirm the reliability of the numerical model. A discernible trend emerges from Fig. 5: the maximum soot volume fraction escalates with an increase in pressure and diminishes with a rise in CO₂ concentration. Furthermore, integrating both experimental and simulation outcomes, it is observed that the suppressive effect of CO₂ dilution on soot production seems to weaken with the rise in pressure. For instance, referring to the experimental data depicted in Fig. 5, at 5 atm, a 25% CO₂ dilution ratio is adequate to sustain a relatively low maximum volume fraction of soot. Conversely, at the same dilution rate of 25%, the maximum volume fraction of soot at 7 atm exceeds that at 5 atm. At a pressure of 10 atm, a 40% CO₂ dilution ratio is necessary to maintain the maximum volume fraction of soot at a reduced level. The simulation outcomes mirror this trend, affirming the findings. Collectively, these results suggest that the extent of soot reduction diminished as pressure increases, and the dilution capability of CO₂ is mitigated. This is consistent with the conclusions reached by Liu et al.²² This indicates that to effectively suppress the generation of soot at higher pressures, a more substantial CO₂ dilution ratio is imperative.

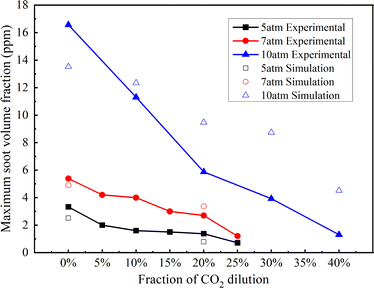Fig. 5 Maximum soot volume fraction with different dilution ratios of CO₂ at 5 and 10 atm (experimental and simulation results).

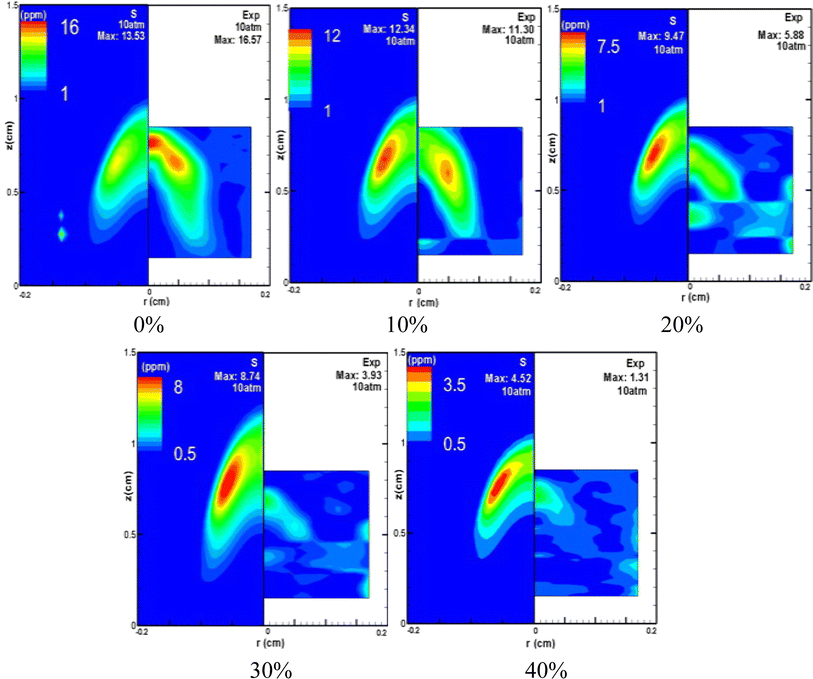
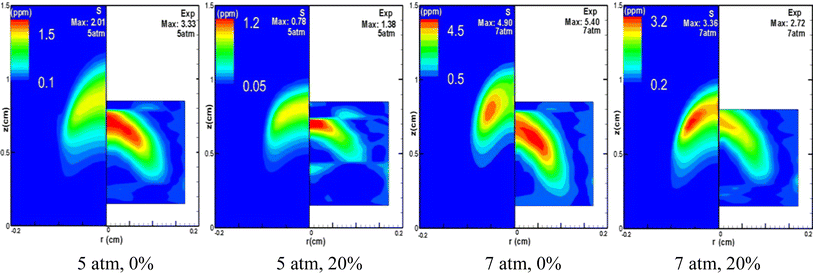
Fig. 6 presents the distribution of soot volume fraction across a spectrum of CO₂ dilution ratios, all at a constant pressure of 10 atm. A clear trend is observed: the formation of soot is attenuated with an increasing ratio of CO₂ dilution. The experimental data depicted on the right side of Fig. 6 highlight that the addition of CO₂ leads to a less uniform and more chaotic distribution of soot generation, causing a perceptible perturbation in the flame. This disruption is likely due to the combined effects of pressure changes and varying CO₂ dilution ratios on the fuel's outlet velocity, which subsequently influences the distribution of soot volume fraction within the flame. Fig. 7 shows the pressure's impact on soot formation by juxtaposing undiluted and 20% CO₂ diluted methane flames under pressures of 5 atm and 7 atm. The comparative results demonstrate that an elevation in pressure generally acts to augment soot formation. Furthermore, an analysis of the experimental data presented in Fig. 7 reveals that at 5 atm, the soot volume fraction drops from 3.33 ppm to 1.38 ppm, a decrease of 58.6%, as the CO₂ dilution rate rises from 0 to 20%. At 7 atm, under identical conditions, the soot volume fraction falls from 5.40 ppm to 2.72 ppm, a reduction of 49.6%, and the simulation outcomes corroborate this trend. Moreover, a comparison of the figure at 5 atm and 7 atm indicates that at 5 atm, the area of soot generation in the flame is notably diminished after a 20% CO₂ dilution, compared to the area without CO₂ dilution. In contrast, at 7 atm, the impact of a 20% CO₂ dilution on the extent of the soot region is minimal. Collectively, these observations validate that the inhibitory effect of CO₂ on soot formation lessens with increasing pressure, aligning with the aforementioned findings.

Fig. 6 The distribution of soot volume fraction in a CH₄ flame with CO₂ dilution ratios ranging from 0% to 40% at 10 atm (with the left side labeled “S” representing simulation results, and the right side labeled “Exp” representing experimental results).

Fig. 7 The distribution of soot volume fraction in CH₄ flames at CO₂ dilution ratios of 0% and 20% under pressures of 5 and 7 atm (with the left side labeled “S” for simulation results, and the right side labeled “Exp” for experimental results).

4.2 Effects of pressure and CO₂ dilution on flame temperature

Fig. 8 compares the peak temperature values derived from numerical simulations with those obtained from experimental measurements across various CO₂ dilution ratios, all at a constant pressure of 10 atm. The numerical calculation results exhibit good agreement with the experimental findings. Specifically, it is observed that the peak temperature of the flame declines with an increasing CO₂ dilution ratio, ranging from 0% to 40%.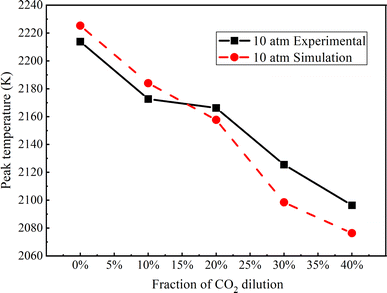

Fig. 8 Peak flame temperature at 10 atm with different dilution ratios of CO₂ (experimental and simulation results).

Fig. 9 delineates the distribution of maximum flame temperatures in methane flames, as ascertained from experimental data, under varying pressures and CO₂ dilution ratios. It is important to note that the maximum CO₂ dilution ratio considered is 25% at pressures of 5 and 7 atm, as increasing the CO₂ dilution rate beyond this threshold results in soot volume fractions that are too low to yield measurable temperature values. At 5 atm, the maximum temperature difference between a pure methane flame and one with 10% CO₂ dilution is 29.7 K, equating to a relative difference of approximately 1.4%. Similarly, the temperature difference between a pure methane flame and a flame with 20% CO₂ dilution is 58 K, which is about a 2.6% relative difference. Analysis of these data points to a generally minor impact of CO₂ dilution on flame temperature, a finding that is in line with results obtained by CARS method.⁴² Furthermore, at pressures of 5, 7, and 10 atm, the maximum temperatures of pure methane flames differ by 11.5 K (about 0.5%), 35.2 K (about 1.5%), respectively. For methane flames with 20% CO₂ dilution, the maximum temperature differences at pressures of 5, 7, and 10 atm are 35.1 K (about 1.5%) and 22.9 K (about 1%), respectively. These variations imply that the overall effect of pressure on flame temperature is modest. Upon closer examination of Fig. 9, it is observed that the maximum flame temperature tends to rise with increasing pressure and fall with increasing CO₂ concentration. This trend mirrors the influence of pressure and CO₂ concentration on soot formation, suggesting a correlation between flame temperature and soot generation. The data suggest that higher temperatures may be conducive to the formation of soot.

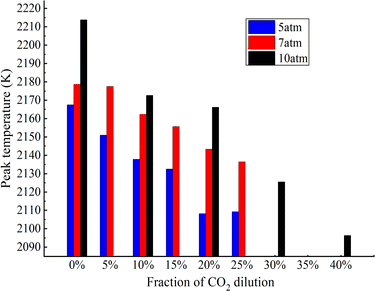Fig. 9 Peak temperature of flames at 5, 7 and 10 atm with different dilution ratio of CO₂ (experimental results).

Fig. 10 graphically represents the numerical simulation results for temperature variations at a constant pressure of 10 atm across different CO₂ dilution ratios. The visual depiction of temperature distribution within the figure clearly illustrates that as the proportion of CO₂ added to the methane flame increases, the flame temperature progressively decreases. A collective analysis of the temperature changes presented in Fig. 8–10 suggests that the thermal impact of CO₂ dilution on the flame temperature is relatively minor. Given the minimal thermal effect, it is prudent to delve deeper into the chemical effects of CO₂ dilution.

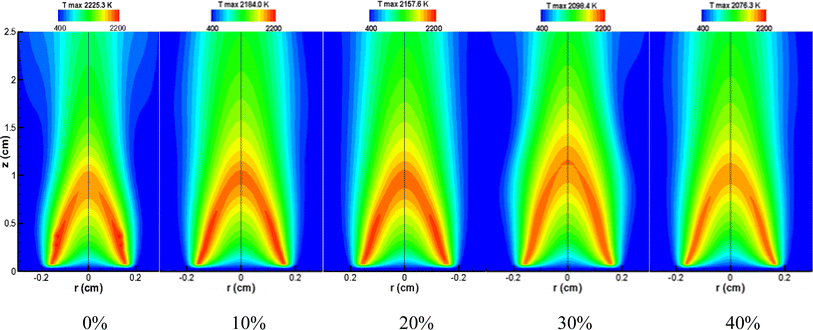Fig. 10 Temperature distributions of CH₄/air diffusion flames with different dilution ratios of CO₂ at 10 atm (simulation results).

5. Result analysis and discussion

Fig. 11 illustrates the distribution of H and OH molar fractions within methane/air laminar diffusion flames under 10 atm pressure, across varying CO₂ dilution ratios. An increase in the CO₂ dilution ratio from 0% to 40% results in a decline of the maximum H mole fraction from 0.00146 to 0.00055, and a corresponding rise in the maximum OH mole fraction from 0.0024 to 0.0040. This trend indicates that higher CO₂ concentrations in the fuel lead to a decrease in H and an increase in OH levels within the flame, which significantly impacts soot formation. The chemical interplay is highlighted by the chain reaction: CO₂ + H ⇌ CO + OH. With added CO₂, the reaction shifts towards the consumption of H and the production of OH. Hydrogen radicals are crucial for both the nucleation and growth phases of soot. Consequently, a decrease in H concentration diminishes soot nucleation and its rate of formation. Furthermore, an elevated OH concentration enhances soot oxidation during the later stages, further preventing soot formation. The chemical effect of CO₂ addition is thus identified as a suppressant to soot generation, aligning with both experimental observations and simulation data presented earlier.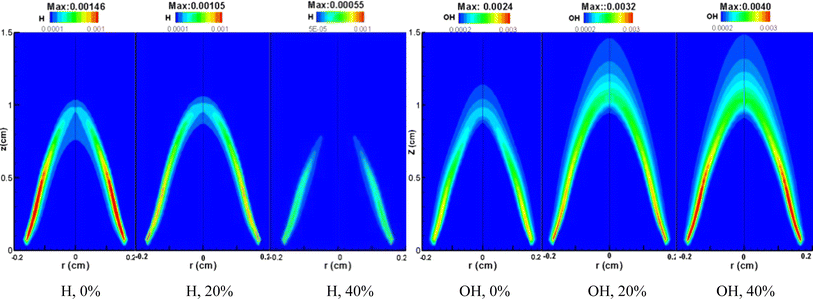

Fig. 11 H and OH mole fraction distribution in laminar CH₄/air diffusion flames with different CO₂ dilution ratios at 10 atm.

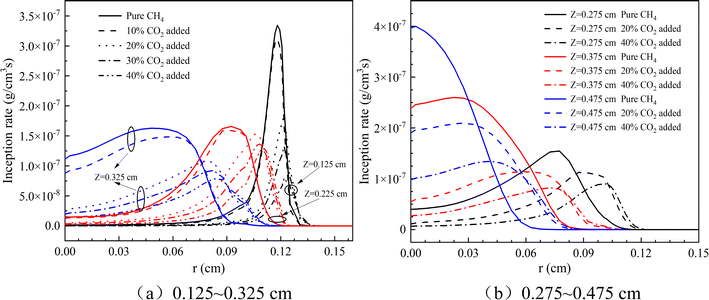
Fig. 12 depicts the initial nucleation rate of soot at varying heights within a flame, under different CO₂ dilution ratios at a constant pressure of 10 atm. Observably, with an increase in height, the peak soot nucleation rate tends to migrate towards the flame's centerline. This trend is consistent across both lower (0.125 to 0.325 cm) and higher (0.275 to 0.475 cm) flame heights. Notably, the soot nucleation rate attenuates as the CO₂ dilution ratio escalates, indicating that CO₂ enrichment acts as an inhibitor to soot nucleation. Fig. 13 complements this analysis by detailing the PAH condensation rate and surface growth rate of soot particles at different flame heights under the same CO₂ dilution conditions and pressure. The data indicate that both the PAH condensation rate and HACA surface growth rate diminish with an increase in the CO₂ dilution ratio, a finding that corroborates the earlier observation regarding the nucleation rate's sensitivity to CO₂ levels.

Fig. 12 Soot nucleation inception rate at different flame heights with different dilution ratios of CO₂ at 10 atm. Soot nucleation inception rates at varying flame heights ((a) 0.125 to 0.325 cm and (b) 0.275 to 0.475 cm) with different CO₂ dilution ratios at 10 atm.

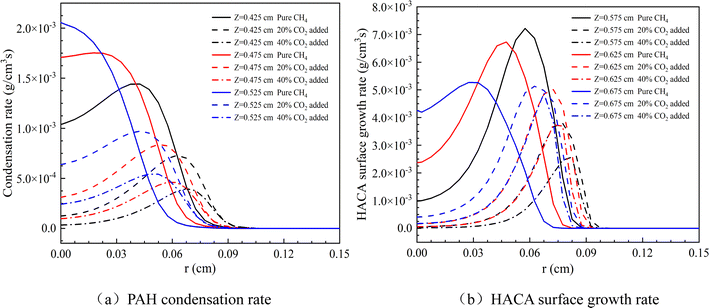Fig. 13 (a) PAH condensation rate and (b) HACA surface growth rate at different flame heights with different dilution ratios of CO₂ at 10 atm.

Analysis of Fig. 10–12 reveals that the chemical influence of CO₂ has a retarding effect on the critical processes of soot formation, namely nucleation, PAH condensation, and HACA surface growth. Compared to low CO₂ dilution levels, methane flames with high CO₂ dilution have an increased concentration of OH radicals. This elevated presence of OH radicals significantly aids in the oxidation of soot, effectively mitigating the accumulation of soot within the combustion process.

Fig. 14 displays the soot nucleation inception rate, PAH condensation rate and HACA surface growth rate in methane flames at various heights under different pressures. The figure indicates that as the pressure increases, the nucleation rate, HACA surface growth rate, and PAH condensation rate of soot all increase, suggesting that higher pressure promotes the nucleation and surface growth of soot. Simultaneously, an increase in pressure leads to a radial narrowing of the soot formation region.

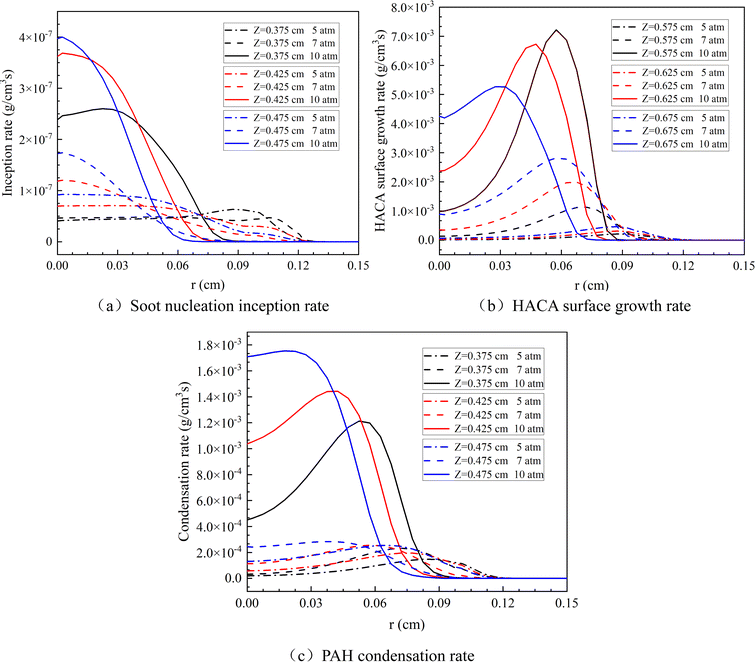Fig. 14 (a) Soot nucleation inception rate, (b) HACA surface growth rate and (c) PAH condensation rate at different flame heights under different pressures.

Synthesizing the above analysis, it is observed that at elevated pressures, the peak volume fraction of soot increases. This indicates that increased pressure is conducive to the formation of soot. This is due to the presence of a positive feedback mechanism⁴² where the condensation rate of PAH and the surface growth rate of HACA are enhanced with the increase in pressure, as depicted in Fig. 14. This enhancement leads to an expansion of the soot surface area, which in turn further facilitates the condensation of PAH and accelerates the growth of HACA. Specifically, as pressure increases, the condensation rate of PAH and the formation rate of precursor molecules also accelerates. These molecules, including C₂H₂, A₁, and A₄, see a significant enhancement in their formation rates, which plays a vital role in promoting the nucleation, growth, and condensation of soot. Consequently, the rise in pressure not only speeds up the condensation of PAH and the growth of HACA but also, by accelerating the formation of these critical molecules, enhances the overall process of soot formation.⁴³

Besides, under elevated pressures, the chemical effect of CO₂ dilution becomes distinct. With the increase in pressure, the rates of the three soot formation steps (soot nucleation inception, PAH condensation and HACA surface growth) are observed to intensify, as depicted in Fig. 14. The enhanced three-body recombination reactions lead to a decrease in the concentration of H.⁴⁴ The equation CO₂ + H ⇌ CO + OH, which represents the chemical reaction pathway for CO₂, suggests that CO₂ continues to react with H to produce CO and OH under elevated pressure. As a result, the decrease in H concentration weakens the chemical role of CO₂ within the system and consequently, the suppressive effect of CO₂ dilution on the generation of soot is less evident at higher pressures.

6. Conclusions

A comprehensive study integrating experimental measurements and numerical simulations was performed to explore the influence of pressure and CO₂ dilution on soot formation within methane/air laminar diffusion flames. The experimental segment of the study employed diffuse 2D-LOSA technology to measure the soot volume fraction and the spatial distribution of flame temperatures. Simultaneously, computational analysis was conducted using the open-source program, CoFlame, to determine the soot volume fraction, flame temperature, and the mole fractions of O and OH. The study also examined the variation characteristics of nucleation, HACA surface growth, and PAH condensation in soot under varying pressures and levels of CO₂ dilution. The synthesis of experimental and computational findings yields the following insights:

An augmentation in the CO₂ dilution ratio is observed to diminish both the soot volume fraction and the flame temperature. This increase in CO₂ dilution ratio exerts a suppressive effect on soot formation within methane flames. As the CO₂ dilution ratio increases, the flame experiences a certain degree of disturbance, resulting in a more dispersed distribution of soot. The chemical impact of CO₂ dilution is significant in mitigating soot generation. The introduction of CO₂ effectively inhibits the nucleation, HACA surface growth, and PAH condensation processes of soot. Specifically, the dilution reduces the hydrogen(H) content essential for soot nucleation, while simultaneously increasing the concentration of OH, which enhances soot oxidation and further limits soot formation.

Conversely, an elevation in pressure leads to an increase in the soot volume fraction and flame temperature. The elevation in pressure effectively promotes the nucleation, HACA surface growth, and PAH condensation processes of soot, which enhance the formation of soot collectively. With the escalation of pressure, the radial width of the soot formation zone becomes constricted. Besides, elevated pressure diminishes the inhibitory effect of CO₂ on soot formation. Therefore, compared to pressures of 5 atm and 7 atm, a higher dilution ratio of CO₂ is required at 10 atm to effectively suppress soot formation.

Data availability

The data supporting this article have been included within the manuscript.

Author contributions

Yinggui Zhou: investigation, methodology, validation, writing – original draft, writing – review & editing. Pengxiang Zhang: investigation, validation, methodology, writing – review & editing. Shengfu Wang: investigation, methodology, conceptualization. Jie Cai: methodology, conceptualization. Jianfei Xi: resources, funding acquisition, supervision.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Funding for school-level research projects of Yancheng Institute of Technology (No. xjr2023043).

References

1. X. Li, Z. Xu, C. Guan and Z. Huang, Appl. Therm. Eng., 2014, 68, 100–106,  DOI:10.1016/j.applthermaleng.2014.04.029.
2. M. R. Kotob, T. Lu and S. S. Wahid, RSC Adv., 2021, 11, 25575–25585,  10.1039/D1RA03541J.
3. Y. Peng, H. Peng, W. Liu, X. Xu, Y. Liu, C. Wang, M. Hao, F. Ren, Y. Li and X. Wang, RSC Adv., 2015, 5, 42789–42797,  10.1039/C5RA05306D.
4. P. Sabnis and S. K. Aggarwal, Renewable Energy, 2018, 126, 844–854,  DOI:10.1016/j.renene.2018.04.007.
5. K. Ekramul Hoque, T. Hossain, A. B. M. Mominul Haque, A. Karim and M. Azazul Haque, J. Energy Resour. Technol., 2024, 146, 1–31,  DOI:10.1115/1.4065200.
6. Y.-T. Gu, S. Marino, M. Cortés-Reyes, I. S. Pieta, J. A. Pihl and W. S. Epling, Ind. Eng. Chem. Res., 2021, 60, 6455–6464,  DOI:10.1021/acs.iecr.0c05186.
7. Y. Hua, F. Liu, H. Wu, C.-F. Lee and Y. Li, Int. J. Engine Res., 2020, 22, 1395–1420,  DOI:10.1177/1468087420910886.
8. H. Chu, R. Hong, W. Dong, H. Zhang, X. Ma and L. Chen, Fuel, 2024, 371, 132046,  DOI:10.1016/j.fuel.2024.132046.
9. H. Chu, S. Feng, R. Hong, X. Ma, F. Qiao and L. Chen, Fuel, 2024, 360, 130569,  DOI:10.1016/j.fuel.2023.130569.
10. M. Xu, M. Wu, Y. Zhang, H. Zhang, W. Liu, G. Chen, X. Guan and L. Guo, Int. J. Environ. Sci. Technol., 2021, 19, 3833–3844,  DOI:10.1007/s13762-021-03284-4.
11. C. C. Ogbunuzor, P. R. Hellier, M. Talibi and N. Ladommatos, Environ. Sci. Technol., 2020, 55, 571–580,  DOI:10.1021/acs.est.0c05561.
12. T. C. Bond, S. J. Doherty, D. W. Fahey, P. M. Forster, T. Berntsen, B. J. DeAngelo, M. G. Flanner, S. Ghan, B. Kärcher, D. Koch, S. Kinne, Y. Kondo, P. K. Quinn, M. C. Sarofim, M. G. Schultz, M. Schulz, C. Venkataraman, H. Zhang, S. Zhang and N. Bellouin, J. Geophys. Res.: Atmos., 2013, 118, 5380–5552,  DOI:10.1002/jgrd.50171.
13. M. O. Andreae and A. Gelencsér, Atmos. Chem. Phys., 2006, 6, 3131–3148,  DOI:10.5194/acp-6-3131-2006.
14. Y. Yang, Q. Li, J. Zhu and B. Zhou, Therm. Sci., 2023, 27, 1325–1335,  DOI:10.2298/tsci220604136y.
15. M. Zhang, J. Cai Ong, K. M. Pang, X.-S. Bai and J. H. Walther, Fuel, 2022, 312, 122700,  DOI:10.1016/j.fuel.2021.122700.
16. M. Gu, H. Chu and F. Liu, Combust. Flame, 2016, 166, 216–228,  DOI:10.1016/j.combustflame.2016.01.023.
17. Q. Tang, J. Mei and X. You, Combust. Flame, 2016, 165, 424–432,  DOI:10.1016/j.combustflame.2015.12.026.
18. R. Kumar, T. L. B. Yelverton, T. Fang and W. L. Roberts, Combust. Flame, 2013, 160, 656–670,  DOI:10.1016/j.combustflame.2012.11.004.
19. Y. Yang, S. Zheng, Y. He, H. Liu, R. Sui and Q. Lu, Fuel, 2023, 353, 129181,  DOI:10.1016/j.fuel.2023.129181.
20. L. Chen, J. Zhou, X. Zheng, J. Wu, X. Wu, X. Gao, G. Gréhan and K. Cen, Aerosol Air Qual. Res., 2017, 17, 2522–2532,  DOI:10.4209/aaqr.2017.08.0271.
21. H. Chu, J. Qi, S. Feng, W. Dong, R. Hong, B. Qiu and W. Han, Fuel, 2023, 345, 128236,  DOI:10.1016/j.fuel.2023.128236.
22. P. Liu, J. Guo, H. G. Im and W. L. Roberts, Combust. Flame, 2022, 112379,  DOI:10.1016/j.combustflame.2022.112379.
23. A. E. Karatas and O. L. Gulder, 52nd Aerospace Sciences Meeting, 2014 DOI:10.2514/6.2014-0652.
24. X. He, Y. Dai, L. Zheng, Y. Qi and J. Wang, Proc. Chin. Soc. Electr. Eng., 2012, 32, 57–64,  DOI:10.13334/j.0258-8013.pcsee.2012.26.003.
25. N. A. Eaves, Q. Zhang, F. Liu, H. Guo, S. B. Dworkin and M. J. Thomson, Comput. Phys. Commun., 2016, 207, 464–477,  DOI:10.1016/j.cpc.2016.06.016.
26. F. Cignoli, S. D. Iuliis, V. Manta and G. Zizak, Appl. Opt., 2001, 40, 5370–5378,  DOI:10.1364/ao.40.005370.
27. D. Snelling, K. Thomson, G. Smallwood, O. G€ulder, E. € Weckman and R. Fraser, AIAA J., 2012, 40, 1789–1795,  DOI:10.2514/3.15261.
28. K. A. Thomson, Ö. L. Gülder and E. J. Weckman, Combust. Flame, 2005, 140, 222–232,  DOI:10.1016/j.combustflame.2004.11.012.
29. K. A. Thomson, M. R. Johnson, D. R. Snelling and G. J. Smallwood, Appl. Opt., 2008, 47, 694–703,  DOI:10.1364/ao.47.000694.
30. J. Appel, H. Bockhorn and M. Frenklach, Combust. Flame, 2000, 121, 122–136,  DOI:10.1016/s0010-2180(99)00135-2.
31. N. M. Marinov, W. J. Pitz, C. K. Westbrook, A. M. Vincitore, M. J. Castaldi, S. Senkan and C. F. Melius, Combust. Flame, 1998, 114, 192–213,  DOI:10.1016/s0010-2180(97)00275-7.
32. V. Chernov, M. J. Thomson, S. B. Dworkin, N. A. Slavinskaya and U. Riedel, Combust. Flame, 2014, 161, 592–601,  DOI:10.1016/j.combustflame.2013.09.017.
33. A. Raj, I. D. C. Prada, A. A. Amer and S. H. Chung, Combust. Flame, 2012, 159, 500–515,  DOI:10.1016/j.combustflame.2011.08.011.
34. Y. Wang, A. Raj and S. H. Chung, Combust. Flame, 2013, 160, 1667–1676,  DOI:10.1016/j.combustflame.2013.03.013.
35. M. D. Smooke, C. S. McEnally, L. D. Pfefferle, R. E. Hall and C. Iii, Combust. Flame, 1999, 117, 117–139,  DOI:10.1016/s0010-2180(98)00096-0.
36. S. H. Park, S. N. Rogak, W. K. Bushe, J. Z. Wen and M. J. Thomson, Combust. Theory Modell., 2005, 9, 499–513,  DOI:10.1080/13647830500195005.
37. M. Sirignano, J. Kent and A. D'Anna, Energy Fuels, 2013, 27, 2303–2315,  DOI:10.1021/ef400057r.
38. H. Richter, S. Granata, W. H. Green and J. B. Howard, Proc. Combust. Inst., 2005, 30, 1397–1405,  DOI:10.1016/j.proci.2004.08.088.
39. T. Blacha, M. Di Domenico, P. Gerlinger and M. Aigner, Combust. Flame, 2012, 159, 181–193,  DOI:10.1016/j.combustflame.2011.07.006.
40. R. Puri, T. F. Richardson, R. J. Santoro and R. A. Dobbins, Combust. Flame, 1993, 92, 320–333,  DOI:10.1016/0010-2180(93)90043-3.
41. A. G. Yazicioglu, C. M. Megaridis, A. Campbell, K.-O. Lee and M. Y. Choi, Combust. Sci. Technol., 2001, 171, 71–87,  DOI:10.1080/00102200108907859.
42. Ö. L. Gülder, D. R. Snelling and R. A. Sawchuk, Symp. (Int.) Combust., [Proc.], 1996, 26, 2351–2358,  DOI:10.1016/s0082-0784(96)80064-6.
43. J. Guo, P. Liu, E. Quadarella, S. R. Gubba, S. Saxena, O. Chatakonda, J. W. Kloosterman, X. He, W. L. Roberts and H. G. Im, Combust. Flame, 2023, 254, 112853,  DOI:10.1016/j.combustflame.2023.112853.
44. F. Liu, A. E. Karataş, Ö. L. Gülder and M. Gu, Combust. Flame, 2015, 162, 2231–2247,  DOI:10.1016/j.combustflame.2015.01.020.

---