A series of blue phosphorescent iridium complexes with thermally activated delayed fluorescence and efficiency roll-off properties

Abstract

Six iridium complexes were designed and studied using the DFT approach, (ppy)₂Ir(pic) (1), (f₄ppy)₂Ir(pic) (2), (ppy)₂Ir(tmd) (3), (f₄ppy)₂Ir(tmd) (4), (ppy)₂Ir(tpip) (5) and (f₄ppy)₂Ir(tpip) (6). Here ppy denotes phenylpyridine, f₄ppy denotes 2-(2,3,4,5-tetrafluorophenyl) pyridine, pic denotes benzoic acid, tmd denotes 5-hydroxy-2,2,6,6-tetramethylhept-4-en-3-one and tpip denotes tetraphenylimido-diphosphinate. The geometries, absorptions, emissions, frontier molecular orbitals, and spin–orbit coupling (SOC) constants of the 6 complexes were evaluated. An intriguing phenomenon was observed during the excitation process of these molecules. It was discovered that, in the ground state, the Frontier Molecular Orbitals (FMOs) of these molecules were loosely arranged throughout the molecule. However, in the Lowest Unoccupied Molecular Orbitals (LUMO) of the triplet excited state, the FMOs become concentrated around the metal core and a maximum of two ligands. Furthermore, the analysis of the energy difference between the lowest singlet excited state and the lowest triplet excited state (ΔE_S1T1) of these complexes in conjunction with their spin–orbit coupling performance indicated that complex 1 exhibits characteristics consistent with Thermally Activated Delayed (TAD) fluorescence. We hope that this research can serve as a reference for practical experimental synthesis.

---

1. Introduction

Organic Light Emitting Devices (OLEDs) have garnered significant interest due to their potential applications in flat panel displays and solid-state lighting.¹ Transition metal complexes, such as those containing Pt, Ir, Os and Rh, are critical in OLED research^2–10 due to their strong spin–orbit coupling, which facilitates intersystem crossing (ISC) and reverse intersystem crossing (RISC) processes.^11–14 Ir complexes are of particular interest due to their three-dimensional spatial structure and low turn-on voltage (less than 3 V).¹⁵ TAD fluorescence has been observed not only in Thermally Activated Delayed Fluorescence (TADF) materials, but also in Ir complexes.¹⁶ As widely used electroluminescent phosphorescent materials, octahedral Ir complexes have applications in red, green and blue OLEDs. A large number of theoretical and experimental studies have been reported on Ir(piq)₃, Ir(ppy)₃ and FIrpic in the field of red, green and blue electroluminescent materials.^17–25 The Ir complex exhibits an exceptionally high transient efficiency,²⁶ yet its pronounced efficiency roll-off remains a pressing issue that requires urgent resolution. At the same time, research on TAD characteristics in Ir complexes remains sparse.

In this article, based on FIrpic with its excellent performance, we designed highly symmetric complex 1.^27–30 In order to increase axial symmetry and reduce the steric hindrance of the whole molecule, especially the auxiliary ligands, complexes 3 and 5 were designed. As the previous research of our group observed that axially symmetric ligands were useful for enhancing the transitions between the Ir metal core and ligands in LUMO,^31–37 the effects of the two auxiliary ligands acac and tpip on the FMOs of the LUMO are shown in Table 2 in ref. 32. Complexes 2, 4, and 6 were also designed by substituting F atoms for the four free H atoms upstream of the benzene ring of the ppy ligands. Due to the involvement of F atoms, which act as powerful electron withdrawing groups, the distances for charge transitions and the efficiency roll-off in the emission process were reduced. Then, combining the FMOs of the different energy levels of the single and triple excited states and SOC characteristics, we found a promising complex, complex 1, with lower ΔE_st and higher SOC characteristics, indicative of TAD characteristics.³⁸ We hope that our research can provide insight into the synthesis of highly efficient electroluminescent materials and promote the development of OLED technology.^39–41

2. Methodology

The ground state geometric structures were calculated by Gaussian 09 software with DFT and TD-DFT methods at the Becke'Slyp (B3LYP) functional level. The calculation basis set employed was 3-21G (for short period elements), while the LanL2DZ pseudopotential was applied to iridium only, later marked as (B3LYP/3-21G & LanL2DZ). The absorptions and emissions of these 6 complexes were calculated in the CH₂Cl₂ environment using the implicit solvent model PCM in the Gaussian 09 software. The absorption, singlets and triplets excited state geometric structures of 6 Ir complexes were calculated using Gaussian 09 under B3LYP/6-31G(d) & LanL2DZ. The emissions were calculated by Gaussian09 under M06-2X/6-31G(d) & LanL2DZ. The SOC constants of the 6 Ir complexes between the singlet excited states and triplet excited states were calculated utilizing the DKH-def2-TZVP all-electron basis set with the DFT and TD-DFT methods at B3LYP function and Douglas–Kroll Hamiltonian matrix elements by ORCA version 5.0.3.^37–44

3. Results and discussion

3.1 Geometries of the ground state S₀ and the lowest-lying triplet state T₁

The names and geometry structures of complexes 1–6 are shown in Fig. 1. Complexes 1–6 consist of an Ir metal core with three ligands, which include two main ligands and one auxiliary ligand. The symmetry of the geometric structure is enhanced by the two main ligands and the auxiliary ligand of complexes 3–4 and 5–6 (tmd and tpip), which are strongly symmetrical.^31–33 The effects of the symmetry on the chemical properties were studied by comparing complexes 1–2 whose auxiliary ligands are widely used in blue and green luminescent materials, and the auxiliary ligands of complexes 3–4 and 5–6. The optimized S₀ molecular geometric structures of complexes 1–6, which provide a clearer description of the changes between the S₀ state and the T₁ state of the important atom of complexes 1–6 are shown in Fig. S1 and Tables S1–S6.†

Fig. 1 The structures of 1–6.

The main ligand ppy is composed of a pyridine ring with a benzene ring substituted for one of the hydrogen atoms. The ligand f₄ppy is derived from ppy, where the four free H atoms on the benzene ring are replaced by four F atoms. The active N atoms on the pyridine rings enhance the electron transfer capabilities between the ligands and the metal core.^42–44

In the S₀ state, because complexes 3–6 have two main ligands and a symmetrical auxiliary ligand. The lengths of the Ir–N1 and Ir–N2 bonds of complexes 3 and 5 are similar to the lengths of complexes 4 and 6, as shown in Table 1. A comparison between the S₀ and T₁ of the 6 complexes reveals that almost all the R2, R5, R6, A1, A2, A3 and A4 tend to increase, while nearly all of the R1, R3, R4 and A4 tend to decrease. In contrast, the auxiliary ligands of complexes 1 and 2 (ppy) are unsymmetrical, so the bond lengths of complexes 1 and 2 are different. This also leads to different levels of steric hindrance on the two main ligands; the main ligand near the benzene ring of ppy is pushed away. After comparing the S₀ and T₁ state data, we found that the two main ligands and the metal core are different in that one is closer to the metal core and the other is far away from the Ir atom. The FMOs of these compounds in the T₁ state are more concentrated in the main ligand, which makes more bonding orbitals concentrated in this position. Denser bonding orbitals often mean stronger interaction forces, which will lead to closer distances. Although the ground and excited states of complexes 1–6 exhibited so many geometric changes, their excitation processes and charge transitions were not affected. This shows that these complexes were stable.

Table 1 Bond lengths and angles for the ground (S₀) and lowest excited states (T₁) of complexes 1–6^a

Complex	States	Selected bond distances (Å)						Selected bond angles (deg.)
		R1	R2	R3	R4	R5	R6	A1	A2	A3	A4	A5
a R1 = RIr-N1, R2 = RIr-N2, R3 = RIr-C1, R4 = RIr-C2, R5 = RIr-N3/O1, R6 = RIr-O1/N2, A1 = angle N1–Ir–N2, A2 = angle N1–Ir–C1, A3 = angle N1–Ir–C2, A4 = angle N1–Ir–N3/O1, A5 = angle N–Ir–O1/N2.
1	S0	2.046	2.062	2.019	2.022	2.168	2.157	175.2	80.7	95.0	89.6	91.4
	T1	2.036	2.080	1.939	1.986	2.256	2.256	176.0	82.7	95.4	87.9	92.5
2	S0	2.052	2.064	2.020	2.023	2.150	2.132	177.5	79.9	97.7	87.7	91.7
	T1	2.038	2.076	1.959	1.995	2.217	2.176	177.9	81.8	98.4	85.5	92.6
3	S0	2.049	2.049	2.009	2.009	2.170	2.169	176.6	80.8	96.9	89.5	92.9
	T1	2.036	2.071	1.934	1.980	2.229	2.214	177.8	82.7	97.0	87.6	93.8
4	S0	2.053	2.053	2.010	2.010	2.144	2.144	179.2	80.1	99.4	87.6	93.0
	T1	2.038	2.068	1.954	1.986	2.199	2.185	179.3	81.8	99.6	85.6	93.7
5	S0	2.049	2.049	2.007	2.007	2.225	2.226	175.3	80.9	95.8	94.3	89.0
	T1	2.035	2.073	1.923	1.975	2.302	2.273	177.8	82.9	97.0	91.2	90.7
6	S0	2.052	2.052	2.006	2.006	2.194	2.194	178.5	80.3	98.7	91.2	89.9
	T1	2.040	2.067	1.950	1.981	2.267	2.247	179.9	82.0	99.6	89.0	91.3

---

3.2 Frontier molecular orbital properties

Differences in molecular structures and functional groups are bound to lead to different properties. Certain substituents tend to have impacts on the electrochemical properties, luminescent properties and the FMOs of the entire molecule. Some of these effects are desirable, but some are minimal or unavoidable. In this section, the changes in the energy levels, energy gaps and FMOs of the S₀ and T₁ states of the complexes will be mainly discussed. We obtained the energy levels and energy gaps of the ground and excited states of these complexes and these are shown in Fig. S2 and Tables S1–S6† (these tables can be found in the ESI†). The details of the FMOs are shown in Table 2. The oscillator strength is the main reference data used to measure the molecular excitation. The larger oscillator strength often means a greater probability of excitation. When f < 0.01, the transition is very unlikely, it is effectively forbidden.

Table 2 Simulated calculated absorption data of the 6 complexes in the CH₂Cl₂ environment, showing the excited state with the longest wavelength and 4 excited states with higher oscillator strengths, along with their energy, oscillator values, orbital contribution of each state and charge transfer between ligands

Complex	States	Energy (nm eV^−1)	Oscillator	Main configurations	Assignation
1	S1	440/2.82	0.047	HOMO → LUMO (70%)	Bz1/Bz2/pic → pic
	S7	347/3.58	0.126	HOMO−1 → LUMO+2 (55%)	pic → Bz1/Mp1/Bz2/Mp2
	S25	283/4.37	0.064	HOMO−4 → LUMO+2 (37%)	Bz1/Mp1/Bz2/Mp2 → Bz1/Mp1/Bz2/Mp2
	S27	279/4.44	0.063	HOMO−5 → LUMO+2 (45%)	Bz1/Bz2/pic →Bz1/Mp1/Bz2/Mp2
	S29	269/4.60	0.470	HOMO−3 → LUMO+4 (45%)	Bz1/Mp1/Bz2/Mp2 → Bz1/Mp1/Bz2/Mp2
2	S1	399/3.11	0.006	HOMO → LUMO (70%)	FBz1/FBz2/pic → Mp1/pic
	S6	334/3.72	0.094	HOMO−1 → LUMO+2 (66%)	FBz1/Mp1/FBz2/Mp2/pic → FBz1/Mp1/pic
	S19	292/4.24	0.073	HOMO−4 → LUMO+1 (62%)	FBz1/Mp1/FBz2/Mp2 → FBz2/Mp2
	S20	290/4.27	0.077	HOMO−4 → LUMO+2 (53%)	FBz1/Mp1/pic → FBz1/Mp1/pic
	S27	270/4.59	0.232	HOMO−1 → LUMO+5 (50%)	FBz1/Mp1/FBz2/Mp2/pic → FBz1/Mp1/Mp2/pic
3	S1	436/2.84	0.051	HOMO → LUMO+1 (70%)	Bz1/Bz2/tmd → Bz1/Mp1/Bz2/Mp2
	S18	342/3.63	0.073	HOMO−4 → LUMO+1 (53%)	Bz1/Mp1/Bz2/Mp2 → Bz1/Mp1/Bz2/Mp2
	S19	308/4.02	0.095	HOMO−1 → LUMO (69%)	tmd → Bz1/Mp1/Bz2/Mp2
	S20	285/4.35	0.165	HOMO → LUMO+5 (50%)	Bz1/Bz2/tmd → Bz1/Bz2/tmd
	S27	269/4.61	0.119	HOMO−2 → LUMO+4 (47%)	Bz1/Mp1/Bz2/Mp2/tmd → Bz1/Mp1/Bz2/Mp2
4	S1	404/3.07	0.047	HOMO → LUMO+1(70%)	FBz1/tmd → FBz1/Mp1/FBz2/Mp2
	S18	288/4.31	0.126	HOMO−4 → LUMO+1 (54%)	FBz1/Mp1/FBz2/Mp2 → FBz1/Mp1/FBz2/Mp2
	S19	286/4.33	0.064	HOMO−1 → LUMO (69%)	FBz2/tmd → FBz1/Mp1/FBz2/Mp2
	S20	283/4.37	0.063	HOMO → LUMO+5 (50%)	FBz1/tmd → FBz1/FBz2/tmd
	S27	265/4.68	0.107	HOMO−2 → LUMO+4 (47%)	FBz1/Mp1/FBz2/Mp2/tmd → FBz1/Mp1/FBz2/Mp2
5	S1	443/2.80	0.038	HOMO → LUMO (69%)	Bz1/Bz2/tpip → Bz1/Mp1/Bz2/Mp2/tpip
	S6	357/3.48	0.130	HOMO−2 → LUMO (44%)	Mp1/Mp2/tpip → Bz1/Mp1/Bz2/Mp2/tpip
	S17	300/4.14	0.091	HOMO−3 → LUMO+1 (44%)	Bz1/Mp1/Bz2/Mp2 → Bz1/Mp1/Bz2/Mp2
	S24	286/4.33	0.123	HOMO−4 → LUMO (44%)	Bz1/Mp1/Bz2/Mp2 → Bz1/Mp1/Bz2/Mp2/tpip
	S29	280/4.43	0.098	HOMO−6 → LUMO+2 (50%)	Bz1/Bz2 → tpip
6	S1	412/3.01	0.036	HOMO → LUMO+1 (69%)	FBz1/FBz2/tpip → FBz1/Mp1/FBz2/Mp2
	S5	345/3.59	0.106	HOMO−2 → LUMO+1 (55%)	Mp1/Mp2/tpip → FBz1/Mp1/FBz2/Mp2
	S11	299/4.15	0.069	HOMO−3 → LUMO (46%)	FBz1/Mp1/FBz2/Mp2 → FBz1/Mp1/FBz2/Mp2/tpip
	S25	275/4.50	0.269	HOMO−2 → LUMO+4 (33%)	Mp1/Mp2/tpip → Mp1/Mp2/tpip
	S26	274/4.91	0.139	HOMO → LUMO+4 (53%)	Bz1/Bz2/tpip → Mp1/Mp2/tpip

---

Thus, we devoted greater attention to the excitation process with f > 0.01. In the excitation process of complex 1, there is an interesting phenomenon in that this molecule seems to prefer to transition to LUMO+2 and LUMO+4 levels, as shown in Table 1 (the upper left corner of the picture is the auxiliary ligand, the middle is the Ir core, and the lower right part is the main ligands). This is contrary to our expectation that the main transition of the molecule is from the HOMO to LUMO. Analysis of the molecular orbitals of these energy levels reveals that oscillator strength transitions with larger oscillator strengths tend to occur between orbitals such as HOMO−1, HOMO−4 to LUMO+2, HOMO−5 to LUMO+2 and HOMO−3 to LUMO+4. The frontier molecular orbitals of HOMO−1, HOMO−4 and HOMO−5 are mainly located on the metal core Ir and the main ligands, and the same is true of the FMOs of LUMO+2. The distribution of the FMOs of HOMO−3 and LUMO+4 also have large overlaps, as shown in Table 3 and Fig. 2. Therefore, we can speculate that complex 1 is more likely to undergo these transitions to the LUMO+2 energy level, rather than LUMO or other non-occupied orbitals for the following reasons: (1) the energy required for the transition from HOMOs to LUMO+2 is small, only 3.58 eV, so the transition is more likely to occur. (2) The molecular orbital of LUMO+2 is closer to that of the HOMOs.

Table 3 The initial orbital and final orbitals of the 5 states in complex 1 with higher oscillator strengths

State	Initial orbital	Final orbital	Oscillator strength
1	HOMO	LUMO	0.0055
7	HOMO−1	LUMO+2	0.1018
25	HOMO−4	LUMO+2	0.1210
27	HOMO−5	LUMO+2	0.1195
29	HOMO−3	LUMO+4	0.2055

---

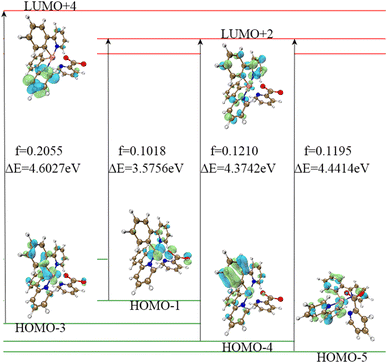Fig. 2 The FMOs which participated in the S₀–S₁ transition of complex 1. The figures of frontier molecular orbital are all made using multifwn software.⁴⁵

Although the transitions of complexes 1–6 are metal-to-ligand charge transfer (¹MLCT) and ligand-to-ligand charge transfer (¹LLCT), the data indicate that the transitions occur preferentially on more reactive chemical bonds and groups. They act like a bridge, which allows electronic transitions to take place. Combined with the data of the previous section, the Ir–N bond and the Ir–C bond are between Ir and the main ligands, and the Ir–N bond and the Ir–O bond are between Ir and the auxiliary ligand.^36,37 The N and C atoms are more active than the O atom, and electron transfer occurs more easily on the Ir–N and Ir–C bonds.^46–48 The same situation also occurs in complexes 3 and 5. The frontier molecular orbital distribution of HOMOs and LUMOs of complex 5 is concentrated on the Ir and two main ligands, which are very similar and dense, as shown in Table 2. In the process of transitions with greater oscillator strength, the distribution of FMOs between energy levels is often more similar. On complexes 2, 4, and 6, this phenomenon still exists. Due to the strong electron-donating ability of F atoms, the FMOs of the fluorinated complexes have undergone some changes, that is, the FMOs is closer to the center of the main ligands and away from the metal atom and auxiliary ligand. A comprehensive overview of this information can be found in Tables S1–S6.† Due to the similarity in the molecular orbitals between the energy levels, the distribution of oscillator strength is no longer fragmented, but smoother and more continuous.

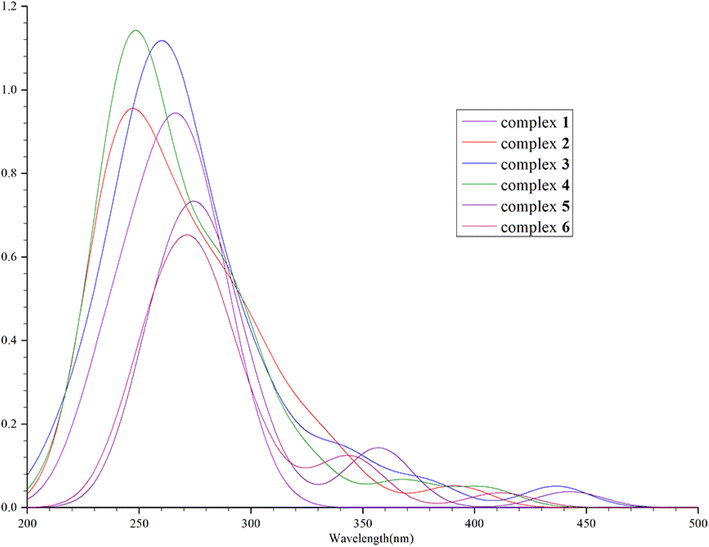
3.3 Absorption and emission in CH₂Cl₂ media

We calculated that the emission spectrum of FIrpic is 472 nm, which is close to the 470–494 nm reported by E. Baranoff and B. F. E. Curchod in 2014, thus verifying the feasibility of this method.^23–25 We calculated the absorption wavelength and oscillator strength of complexes 1–6 in the absorption process. It was found that their absorption spectra were mainly concentrated around 300–375 nm, with a main and strong absorption peak near 300 nm and a weak absorption peak near 400 nm. The absorption of complexes 1–6 is shown in Fig. 3. In the vicinity of 500 nm, the oscillator strength of complexes 1–6 is extremely low (<0.01), indicating minimal absorption in this region.

Fig. 3 The absorption spectra fitted through simulations of complexes 1–6.

The emission spectra of complexes 1–6 were evaluated and determined to be 464 nm, 465 nm, 470 nm, 469 nm, 479 nm and 476 nm, and they displayed a distribution within the band ranging from 460–480 nm, which corresponded to blue-green light. Combining Table 4 and Fig. 4, the F atoms do not significantly contribute to the FMOs, so the emission spectra of complexes 1, 2, 3, 4, 5 and 6 are similar. Concerning the FMOs at the S₀ state and T₁ state energy levels of complexes 1–6, it was found that the molecular orbitals of complexes 1–2 are mainly distributed on the Ir metal core with an identical ppy/f₄ppy. The molecular orbitals of the S₀ state of complexes 3–6 are mainly concentrated on the Ir metal core and two ppy/f₄ppy, while the molecular orbitals of the T₁ state of complexes 3–6 are mainly concentrated on the Ir metal core and one ppy/f₄ppy. The FMOs of complexes 1–6 exhibit a considerable overlap in the S₀ and T₁ states, with these overlaps concentrated on the main ligand, thereby reducing the distance of the electron transition. The contribution of the LUMO of Ir in complexes 1–6 is minimal, both singlet excited states and triplet excited states, which is not as prominent as that in HOMO. Concurrently, this showed that these complexes exhibited ¹MLCT and ³MLCT when shifting from the LUMO to the HOMO. The main ligands nearly make up the entirety of the LUMO of the triplet excited state of complexes 1–6, particularly, complexes 3–6, this showed these complexes exhibited ³LLCT.

Table 4 Emission spectra, energy gaps, orbital participation rates and transition modes of complexes 1–6

Complex	Emissions (nm eV^−1)	Major contribution	Character
a Ref. 23.
1	464/2.67/467^a	L → H (57%); L → H−1 (34%)	^3MLCT/^3LLCT
2	465/2.67	L → H (55%); L → H−1 (40%)	^3MLCT/^3LLCT
3	470/2.64	L → H (58%); L → H−2 (34%)	^3MLCT/^3LLCT
4	469/2.64	L → H (56%); L → H−2 (39%)	^3MLCT/^3LLCT
5	479/2.59	L → H (59%); L → H−1 (34%)	^3MLCT/^3LLCT
6	476/2.60	L → H (57%); L → H−1 (37%)	^3MLCT/^3ILCT

---

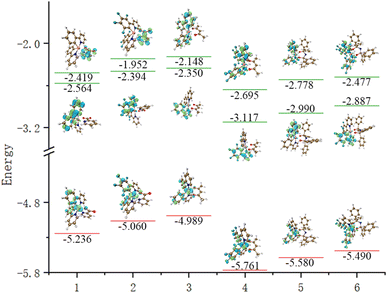Fig. 4 The energy levels and FMOs of S₀, T₁ and S₁ for complexes 1–6 (from left to right: complexes 1–6, from top to bottom: S₁, T₁, and S₀).

The reason for this is that, on the one hand, auxiliary ligands with strong electron-donating ability, such as methyl groups and benzene rings on the auxiliary ligands (acac, tpip) of complexes 3–6, lead to a higher concentration of molecular orbitals on the principal ligand of the molecule. On the other hand, the active Ir–N bond and π-conjugation on the main ligand pyridine ring result in a substantial number of active electrons on the main ligand. The greater the number of active electrons, the stronger the ability for electron transition and the lower the energy dissipation during the transition process, which is helpful for the effective operation of the device in the high current density environment. The characteristics of low efficiency roll-off of the materials are realized.

3.4 Thermally activated delayed (TAD) characteristics and spin–orbit coupling (SOC) coefficients

The energy levels of the singlet and triplet states of complexes 1–6 were calculated. It is 0.369 eV in complex 1, which is close to the value of ΔE_st of thermally activated delayed fluorescence materials. Therefore, we speculate that complex 1 may have similar properties to TADF materials. At the same time, the SOC constants of complexes 1–6 were evaluated and are shown in Tables 5 and 6. The spin–orbit coupling constant of S₁ to T₁ is the sum of the square roots of the modes of the spin–orbit coupling matrix elements of the three sub-states of the S₁ state and T₁ state with triple state spin–magnetic quantum numbers of 0, 1 and −1 respectively, as:

〈S₁|H_SO|T₁〉 = sqrt((Re₀)² + (Im₀)² + (Re₁)² + (Im₁)² + (Re₋₁)² + (Im₋₁)²) (2)

Table 5 The energy levels and gaps of complexes 1–6

Complex	ES0	ES1	ET1	ΔET1S0(eV)	ΔES1S0(eV)	ΔET1S1(eV)
1	−5.23602	−2.41882	−2.56442	2.6716	2.8172	0.1456
2	−5.05996	−1.95196	−2.39366	2.6663	3.108	0.4417
3	−4.98867	−2.14757	−2.34957	2.6391	2.8411	0.202
4	−5.76093	−2.69493	−3.11673	2.6442	3.066	0.4218
5	−5.5797	−2.7783	−2.9896	2.5901	2.8014	0.2113
6	−5.48963	−2.47703	−2.88683	2.6028	3.0126	0.4098

---

Table 6 The sum of the square roots of the modes of the spin–orbit coupling matrix elements of S₁ and T₁ of complexes 1–6 and the spin–orbit coupling constant

Complex	MS = 0		MS = 1		MS = −1		〈S1|Ĥ soc|T1〉
	Re	Im	Re	Re	Im	Re
1	0	34.04	9.77	−27.02	9.77	27.02	53.01
2	0	44.18	−0.48	−28.19	−0.48	28.19	59.51
3	0	−51.52	−27.64	−19.23	−27.64	19.23	70.16
4	0	23.03	12.39	8.58	12.39	−8.58	31.38
5	0	−0.06	−0.05	−5.63	−0.05	5.63	7.96
6	0	−0.07	−0.29	46.5	−0.29	−46.5	65.76

---

The value of complex 1 is 53.01, which also shows that it is very possible to carry out the interstice channeling from the S₁ state to the T₁ state and reverse interstice channeling. It is possible for complex 1 to carry out delayed fluorescence radiation.^48–50 Smaller ΔE_ST and larger SOC constants were the effective parameters to characterize whether the complex exhibited TAD characteristics. The data indicate that complex 1 shows great potential in TAD performance.

4. Conclusions

This report demonstrates how different auxiliary ligands affect absorption and emission. We obtained more ideal blue-phosphorescent materials by analyzing the performance of the auxiliary ligands. The molecular emission spectra of the six complexes designed in this paper are 464, 465, 470, 469, 479, and 476 nm, the charge transfer transition characteristics were mainly ³MLCT and ³ILCT with minimal ³LLCT. In the case of complexes 2, 4 and 6, it was found that the introduction of any strong electron-withdrawing group, such as fluorine, will affect the FMOs. However, the emission spectrum of a molecule containing a fluorine atom will not undergo a blue shift. The emission spectra of molecules whose fluorine atoms occupy only a very small number of orbitals contested only by neighboring carbons will not be blue-shifted. At the same time, some complexes exhibit high SOC constants and properties similar to TADF materials, and we believe that these complexes are promising candidates for luminescent materials in OLEDs. We hope that our theoretical research can provide insight into designing phosphorescent light-emitting materials with TAD properties.

Data availability

Details on the calculation methods used in this study are provided in the ESI, including Fig. S1, S2 and Tables S1–S6,† which show the ground states of the complexes.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Science and Technology Development of Jilin Province of China (No. 20220101039JC) and the Education Department of Jilin Province (Grant No. JJKH20230506KJ).

References

1. L. Flamigni, A. Barbieri, C. Sabatini, B. Ventura and F. Barigelletti, in Photochemistry and Photophysics of Coordination Compounds II, 2007, vol. 131, pp. 143–203,  DOI:10.1007/128_2007_131.
2. Z. Zhang, J. Deng, Q. Sun, H. Zhao, D. Hu, B. Shen, X. Meng, B. Zong, B. Kang and S. R. P. Silva, Org. Electron., 2022, 104, 106472.
3. M. Z. Shafikov, R. Daniels and V. N. Kozhevnikov, J. Phys. Chem. Lett., 2019, 10, 7015–7024.
4. H. J. Choi, M. H. Hyun, H. J. Park and U. C. Yoon, J. Lumin., 2017, 188, 323–330.
5. S. Aghazada, A. J. Huckaba, A. Pertegas, A. Babaei, G. Grancini, I. Zimmermann, H. Bolink and M. K. Nazeeruddin, Eur. J. Inorg. Chem., 2016, 5089–5097.
6. C.-L. Ho and W.-Y. Wong, New J. Chem., 2013, 37, 1665.
7. A. Salehi, X. Fu, D. H. Shin and F. So, Adv. Funct. Mater., 2019, 29, 1808803.
8. T.-T. Feng, F.-Q. Bai, L.-M. Xie, Y. Tang and H.-X. Zhang, RSC Adv., 2016, 6, 11648–11656.
9. X. Wang, H. Yang, Y. Wen, L. Wang, J. Li and J. Zhang, Inorg. Chem., 2017, 56, 8986–8995.
10. X. Wang, C. Chen, Y. Li, P. Ning, W. Wu and L. Wang, Org. Electron., 2017, 49, 360–367.
11. M. X. Song, Z. M. Hao, Z. J. Wu, S. Y. Song, L. Zhou, R. P. Deng and H. J. Zhang, Int. J. Quantum Chem., 2013, 113, 1641–1649.
12. M. X. Song, G. Q. Xi, H. Y. Chi, K. C. He, P. Lü, Z. K. Qin, Y. L. Zhang, S. Q. Lü and H. J. Zhang, Appl. Organomet. Chem., 2020, 34, e5525.
13. P. Tao, Y. Miao, H. Wang, B. Xu and Q. Zhao, Chem. Rec., 2018, 19, 1531–1561.
14. J. P. Clancy, N. Chen, C. Y. Kim, W. F. Chen, K. W. Plumb, B. C. Jeon, T. W. Noh and Y.-J. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195131.
15. L. Wang, Z. Gao, C. Liu, Y. Chen, W. Tao and L. Lu, Tetrahedron, 2020, 76, 131390.
16. M. Y. Wong and E. Zysman-Colman, Adv. Mater., 2017, 29, 1605444.
17. S. H. Kim, J. Jang and J. Y. Lee, Synth. Met., 2007, 157, 228–230.
18. J. Huang, T. Watanabe, K. Ueno and Y. Yang, Adv. Mater., 2007, 19, 739–743.
19. S. Reineke, K. Walzer and K. Leo, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 125328.
20. S. Koseki, N.-o. Kamata, T. Asada, S. Yagi, H. Nakazumi and T. Matsushita, J. Phys. Chem. C, 2013, 117, 5314–5327.
21. S. Sanderson, B. Philippa, G. Vamvounis, P. L. Burn and R. D. White, J. Chem. Phys., 2019, 150, 094110.
22. T. Hofbeck and H. Yersin, Inorg. Chem., 2010, 49, 9290–9299.
23. E. Baranoff and B. F. E. Curchod, Dalton Trans., 2015, 44, 8318–8329.
24. L. Jiang, S. S. Li, M. Z. Tidrow, W. R. Dyer, W. K. Liu, J. M. Fastenau and T. R. Yurasits, Appl. Phys. Lett., 2001, 79, 2982–2984.
25. C. Adachi, M. A. Baldo, S. R. Forrest, S. Lamansky, M. E. Thompson and R. C. Kwong, Appl. Phys. Lett., 2001, 78, 1622–1624.
26. Y. C. Zhu, L. Zhou, H. Y. Li, Q. L. Xu, M. Y. Teng, Y. X. Zheng, J. L. Zuo, H. J. Zhang and X. Z. You, Adv. Mater., 2011, 23, 4041–4046.
27. P. T. Chou and Y. Chi, Chem. –Eur. J., 2007, 13, 380–395.
28. Y. Chi and P.-T. Chou, Chem. Soc. Rev., 2010, 39, 638–655.
29. C. Adachi, R. C. Kwong, P. Djurovich, V. Adamovich, M. A. Baldo, M. E. Thompson and S. R. Forrest, Appl. Phys. Lett., 2001, 79, 2082–2084.
30. M. X. Song, Z. M. Hao, Z. J. Wu, S. Y. Song, L. Zhou, R. P. Deng and H. J. Zhang, J. Phys. Org. Chem., 2013, 26, 840–848.
31. M.-X. Song, G.-F. Wang, J. Wang, Y.-H. Wang, F.-Q. Bai and Z.-K. Qin, Spectrochim. Acta, Part A, 2015, 134, 406–412.
32. Z.-K. Qin, H.-Y. Chi, G.-Q. Xi, X. Liu, M.-X. Song, J. Wang, Y.-L. Zhang, S.-Q. Lü and H.-J. Zhang, Mol. Phys., 2020, 118, e1718229.
33. Y. Ji, X.-L. Guo, J.-Y. Yang, H.-H. Zhang, X.-H. Liu, M.-X. Song, Z.-K. Qin, J. Wang and F.-Q. Bai, Mol. Phys., 2023, 121, e2217781.
34. G. N. Lewis and M. Calvin, Chem. Rev., 1939, 273–328.
35. H. Y. Chi, Y. Ji, Y. K. Zhang, X. M. Zhao, S. J. Qu, F. D. Jiang, C. H. Lu, B. Xiao, M. X. Song and D. F. Li, Appl. Organomet. Chem., 2023, 38, e7322.
36. H. Y. Chi, G. Q. Xi, X. Liu, H. H. Zhang, Y. Ji, X. H. Liu, M. X. Song, Y. L. Zhang, Z. K. Qin and H. J. Zhang, J. Phys. Org. Chem., 2022, 36, e4472.
37. B. C. De Simone, G. Mazzone, J. Pirillo, N. Russo and E. Sicilia, Phys. Chem. Chem. Phys., 2017, 19, 2530–2536.
38. M.-X. Song, Y. Ji, H.-H. Zhang, X.-H. Liu, J.-Y. Yang, X.-L. Guo, J. Wang, Z.-K. Qin and F.-Q. Bai, Chem. Phys. Lett., 2023, 820, 140465.
39. G. Yumoto, H. Hirori, F. Sekiguchi, R. Sato, M. Saruyama, T. Teranishi and Y. Kanemitsu, Nat. Commun., 2021, 12, 3026.
40. Y. Wang, X. Yang, C. Liu, Z. Liu, Q. Fang, F. Bai, S. Wang, X. Hou, B. Feng, B. Chen and B. Zou, Angew. Chem., Int. Ed., 2022, 61, e202210836.
41. F. Neese, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2017, 8, e1327.
42. J. Zhao, P. Song, L. Feng, X. Wang and Z. Tang, J. Mol. Liq., 2023, 380.
43. Y. Li, X.-W. Fan, J. Chen, F.-Q. Bai and H.-X. Zhang, RSC Adv., 2019, 9, 31621–31627.
44. H.-W. Fan, F.-Q. Bai, Z.-X. Zhang, Y. Wang, Z.-X. Qu, R.-L. Zhong and H.-X. Zhang, RSC Adv., 2017, 7, 17368–17376.
45. T. Lu and F. Chen, J. Comput. Chem., 2011, 33, 580–592.
46. Y. Zhang, P. Heng, H. Su, J. Li, J. Guo, P. Ning, W. Wu, T. Ren, L. Wang and J. Zhang, Chem. Rec., 2018, 19, 938–946.
47. J. Xu, X. Wu, J. Guo, Z. Zhao and B. Z. Tang, J. Mater. Chem. C, 2021, 9, 15505–15510.
48. C. M. Marian, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2011, 2, 187–203.
49. F.-Q. Bai, J. Wang, B.-H. Xia, Q.-J. Pan and H.-X. Zhang, Dalton Trans., 2012, 41, 8441.
50. L.-M. Xie, F.-Q. Bai, W. Li, Z.-X. Zhang and H.-X. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 10014–10021.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra05828c

---