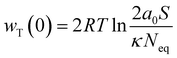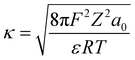DOI:
10.1039/D4RA05988C
(Paper)
RSC Adv., 2024,
14, 35275-35285
Carbonate weakens the interactions between potassium and calcareous soil
Received
18th August 2024
, Accepted 22nd October 2024
First published on 5th November 2024
Abstract
The ion interfacial transport driven by ion–surface interactions in calcareous soil has a profound impact on the nutrient storage and environmental buffer capacity of the main agricultural soils in dry and semi-arid areas. The roles that carbonate plays in preserving the soil's inorganic carbon pool and soil structure stability have been widely investigated, but its significance in the aforementioned microscopic processes, especially the influence of carbonate on the interfacial reaction kinetics of nutrient elements, is yet to be determined. In this study, potassium (K) was used as an indicator ion to investigate its affinity in carbonate-removed (CREM) and carbonate-reserved (CRES) calcareous soil using the general theory of ion diffusion in an external electric field. We discovered that (1) at a given initial K concentration, the carbonate in CRES soil retards the adsorption rate and diminishes the adsorption amount of K in calcareous soil, reducing the interfacial transport properties of nutrient ions at the solid–liquid interface of calcareous soils compared with CREM soil; and (2) this weakening of the interfacial transport effect on nutrient K originates from the soil carbonate, which prefers to weaken the electrostatic interaction intensity between K and the calcareous soil surface. Furthermore, this is due to the carbonate shielding effect on the surface adsorption sites of other soil components and the competitive relationship between K+ and cations released by carbonate dissolution. The influence of carbonate on the nutrient ion transport at the solid–liquid interface of calcareous soil has been investigated by soil electrochemistry theory-based ion adsorption kinetics, and the links between kinetic features and ion–surface binding energy have been clarified.
1. Introduction
Soil nutrient ion is a crucial indication of soil quality, the content and saturation of which reflect nutrients' transport capacity, reserves, circulation, and bioavailability.1 The reaction of ions at the soil solid–liquid interface involves critical physical and chemical mechanisms that control soil structure and function. In a way, it exerts a vital predictive role in preventing and managing soil degradation as well as boosting the quality and efficiency of agricultural outputs.2,3 On the one hand, it is the balance between the leaching loss and enrichment of cations from the soil environment that determines the level of soil acidity;4 on the other hand, the abnormally higher Na+ accumulation in the soil will impair crop growth, lower yields, and limit agricultural expansion.5,6 In these pervasive connections, understanding the interaction between cations and the soil surface under different scenarios is key to disclosing the underlying mechanism of their interfacial reaction.
Carbonate is the main source of inorganic carbon in the soil of China's Loess Plateau. In addition to serving as an inorganic carbon sink or regulating organic carbon accumulation, it also plays a crucial role in preserving soil fertility and removing environmental contaminants.7–9 For example, carbonate can bind soil skeletal particles by coating and bridging, and its strong cementation prevents soil particles from dispersing in water, which effectively regulates soil available potassium levels by trapping potassium within the carbonate-cemented coarse aggregates.10 It can also efficiently remove lead from wastewater at a wide range of initial concentrations via heterogeneous nucleation and surface co-precipitation on its surface.9 If the carbonate is removed, the cementing effect between soil particles is lost, resulting in a decrease in the specific surface area, adsorption capacity, and structural stability loss.11 The impact of carbonate on the structure and function of soils primarily stems from the complexity of its surface properties, which are associated with its surface electric charges. It is generally known that the three-phase equilibrium relationship between solid–liquid–gas (CaCO3–H2O–CO2) governs the surface charge characteristics of soil carbonate.12 Serving as a key characterization of carbonate surface charge, the magnitude of zeta potential is deeply influenced by the adsorption density of lattice ions (e.g., Ca2+, Mg2+, and HCO3−) within the Stern layer, particularly at the outer Helmholtz plane.13 Stated differently, the interaction between the carbonate's surface and the adjacent inner layer ions determines the magnitude of the carbonate's zeta potential. Due to the non-uniformity of the surface charge distribution of carbonate and the inconsistency between zeta potential and surface charge measurements, the zeta potential may not be the most suitable approach for characterizing ion–carbonate bonding interactions.14
Soil's K availability under agronomic management is inextricably linked to its reaction mechanism occurring at the soil solid–liquid interface, which is predominantly mirrored by K adsorption in soil.15,16 It is not hard to figure out that K adsorption and equilibrium partitioning in the solid and liquid phases of soil or clay have been one of the principal focuses of recent decades of research on K interface behavior.17 Typically, ion equilibrium, ion diffusion, and kinetic models have been used in conjunction to clarify the mechanisms of ionic interface reactions in sophisticated heterogeneous soil.18 However, the bulk of them are possibly devoid of adequate mechanism descriptions. For instance, although the Donnan equilibrium has been frequently used to assess ionic exchange, theoretically calculating the distribution of ions between the exchanger and solution phases remains problematic owing to the complexity of obtaining the activity coefficient of the exchanger phase.19,20 According to Fick's law, ion diffusion is primarily controlled by the ion concentration gradient. Any adsorbed cations are regarded as stationary, with no differentiation between different sites or forms of adsorption, implying that the freely moving cations in the electric double layer (EDL) do not contribute to the total flux of ion diffusion in clay.21 Besides, the effect of soil surface charges on ion migration under Fick's law has been overlooked.22 The Elovich equation has been ideally adapted to represent chemical adsorption processes involving multiple reaction mechanisms but may be unsatisfactory for those involving a single reaction mechanism, such as K kinetics;23 the parabolic diffusion equation has been mainly used to describe the intra-particle diffusion of K in the soil, as opposed to the diffusion process on the particle surface or within the soil's liquid film.17 While reactive transport modeling and surface complexation models have been successfully used to characterize ionic interfacial reactions, these methods are most suited to pure soil mineral research environments.24,25 For heterogeneous soils composed of different mechanical compositions, organic matter, and carbonates, it is necessary to make simple assumptions to meet the application conditions.26 To gain a preliminary and general understanding of the interfacial adsorption behavior of K in multiphase complex soil systems, empirical or semi-empirical adsorption isotherm models were typically employed to bridge the cognitive gap regarding the effects of soil components on K adsorption.27 However, aside from the statistical correlation study of K adsorption and soil components using model parameters with no physical significance, there appears to be little new insight into the role played by soil components in ion–surface interactions. Furthermore, the relevance of carbonate in studies of interactions between calcareous soils and potassium ions are yet to be revealed.28 How does carbonate alter the interactions between K and calcareous soil particles?
To answer the concerns above, it is primarily required to determine where the forces between K and calcareous soil particles come from and how the presence or absence of carbonate affects these forces. It is widely accepted that the vast amount of electric charge carried on the soil surface serves as the material basis for a significant number of chemical reactions occurring in the soil.29 Li, et al.30 proved that ion adsorption driven by the interaction forces generated between charged surfaces and ions could be essentially viewed as a diffusion process. This indicates that in addition to the routinely considered effect of ion concentration gradients, ion mobility in charged soil must be influenced by potential gradients created by the charges on the soil surface.31,32 As previously stated, current advances in research indicate that the zeta potential is insufficient to characterize the interactions between ions and charged carbonate surfaces.14 The measurement of zeta potential often presumes a homogeneous particle surface and disregards the possible existence of local charge heterogeneity. The intricacy of ion binding on the carbonate surface constrains current zeta potential measuring techniques in accurately depicting this complexity. The zeta potential may considerably underestimate the true charge on the particle surface. Indeed, Ding et al.33 predicted that the zeta potential at the shear plane of the EDL surrounding charged particles might be just one-third to one-sixth of the real surface potential in various electrolyte solutions. Further study by Liu et al.34 suggested that not only is the zeta potential at the slip plane substantially lower than the surface potential, but the potential at the Stern layer, which is closer to the actual surface, is only one-seventh of the surface potential. This confirms that prior research may have exaggerated the relevance of zeta potential in defining ion–surface interactions. Given that the surface of carbonate is likewise charged and has an effect on a natural solid's surface charge,35 we hypothesize that carbonate in calcareous soil can cause a shift in the interaction between K and soil particles as well as the kinetics of K adsorption. As a result, a generalized theory of ion diffusion in external fields,36 together with a miscible displacement technique without external disturbance,30 have been jointly employed in this study to probe the response of K adsorption kinetics in calcareous soil as carbonate is present or absent. This study's approach surpasses the approximate descriptions of particle surface charge characteristics and ion–surface interactions found in zeta potential measurement methods by considering the actual charge on the soil surface and offering an integrated account of the coupling driving forces between surface charge properties and molecular interactions influencing ions. This approach efficiently characterizes the time-dependent behavior of the potential and the dynamic distribution of ions in an external field. Plus, based on the kinetic model, the interaction energy between the adsorbed K ions and the calcareous soil surface is quantified.
2. Materials and methods
2.1. Soil sampling and characterization
The calcareous soil samples were collected from traditional agricultural farming areas in Yangling (108°2′30′′E, 34°18′14′′N) and Ansai (109°19′21′′E, 36°51′50′′N), which are located in the Loess Plateau, China. Lou soil and Loessial soil to be studied are developed from the Loess parent material and classified as Cumulic Anthrosol and Calcaric Regosols by FAO soil taxonomy, respectively. Two types of soil at 0–20 cm depth were collected by triplicate sampling in locations with similar site circumstances using the random distribution approach. Using the zigzag sampling method, soil samples were collected from 15 points across an agricultural field with an area of around 200 m2. Each point utilized a triplicate random sampling method to collect 0–20 cm of topsoil with a soil auger, totaling approximately 6 kilograms. The collected soil samples were thoroughly mixed and then gradually separated into about 500 grams of soil using the quartering method. Then, 500 grams of each kind of mixed soil sample were air-dried and ground (the two types of soil samples were passed through a 2 mm soil sieve to measure their physical indices and a 0.25 mm soil sieve to determine their chemical indices). In this study, the samples were analyzed using a Rigaku Ultima IV X-ray diffractometer (XRD). The experiment utilized a Cu-target X-ray tube with a tube voltage of 40 kV and a current of 40 mA, and a graphite monochromator was employed to filter the radiation, enhancing signal strength. The scanning step size was set at 0.02°, with a scanning speed of 1° per min per step. Initially, the samples were treated with a glycerol aqueous solution to form the oriented films. After placing these films in a KNO3-saturated desiccator for 24 hours, the samples were directly loaded into a glass sample holder and lightly pressed for the X-ray diffraction analysis. The obtained diffraction data (d-values and relative intensities) were compared with standard data from the Powder Diffraction File (PDF) provided by the International Centre for Diffraction Data (ICDD) to identify the mineral types. The relative percentages of each mineral were estimated by comparing the ratio of the strongest diffraction peak of the sample to that of the standard mineral. The dominant clay minerals (X-ray diffraction method) for the two types of soil were quartz (∼30%), feldspars (∼23%), hydromica (∼15%), kaolinite (∼10%), chlorite (∼10%), calcite (∼7%) and vermiculite (∼4%). While both typical calcareous soils have a similar clay mineral makeup percentage, they differ in their mechanical composition. This also contributes to their differing levels of soil fertility. The mechanical compositions (hydrometer method), pH (pH meter), soil organic matter (SOM, potassium dichromate external heating method), and carbonate content (calcium carbonate equivalent, gasometry) were measured, and the specific surface area (SSA) was analyzed with the combined determination method.37 These parameters are listed in Table 1 below for the two types of soil.
Table 1 Basic physical and chemical properties of the tested soil samples
| Soil type |
Mechanical compositions |
pH |
SOM (g kg−1) |
SSA (m2 g−1) |
CaCO3 (g kg−1) |
| Clay (%) |
Silt (%) |
Gravel (%) |
| Loessial soil |
10.21 |
54.54 |
35.25 |
8.60 |
4.60 |
23.0 |
112.1 |
| Lou soil |
16.32 |
34.56 |
49.12 |
8.01 |
6.10 |
41.5 |
89.19 |
2.2. Sample treatments
Here, CREM treatment of calcareous soil with a standard protocol38 was performed. Briefly speaking, 1 mol L−1 sodium acetate (adjusted to pH 5 with acetic acid) in the ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 (w:v) was added to 20 g of the two types of soil samples, and the two mixed soil suspensions were separately transferred to an Erlenmeyer flask and continuously shaken for 24 hours at 220 rpm. Then, the suspensions were centrifuged at 5000 rpm for 5 minutes, and the supernatants were discarded. The repetitions of the above operation should be done until no carbon dioxide was measured in the sample by the gasometric method.39 To thoroughly remove the ions released by the decomposition of carbonate and residual sodium acetate in the calcareous soil, the sodium acetate solution was replaced by ultrapure water, and the above operation was repeated several times. During this procedure, the Na-saturated sample was adequately prepared by measuring the pH of the rinse solution (approaching neutrality) and its conductivity (approaching that of ultrapure water). Then, the deposited Na+-saturated sample was dried at 70 °C, ground, and passed through a 0.25 mm soil sieve for later use. The Na+-saturated sample of CRES calcareous soil should be prepared as a control experiment. Considering the partial dissolution of carbonate, 1 mol L−1 sodium acetate saturating solution with pH 8.2 was used to suppress carbonate dissolution.40 Similarly, ultrapure water was utilized to swiftly rinse off any residual sodium acetate solution on the surface of CRES calcareous soil while ensuring that the ambient pH around the CRES calcareous soil solution was similar to the pH of the CREM calcareous soil solution.
25 (w:v) was added to 20 g of the two types of soil samples, and the two mixed soil suspensions were separately transferred to an Erlenmeyer flask and continuously shaken for 24 hours at 220 rpm. Then, the suspensions were centrifuged at 5000 rpm for 5 minutes, and the supernatants were discarded. The repetitions of the above operation should be done until no carbon dioxide was measured in the sample by the gasometric method.39 To thoroughly remove the ions released by the decomposition of carbonate and residual sodium acetate in the calcareous soil, the sodium acetate solution was replaced by ultrapure water, and the above operation was repeated several times. During this procedure, the Na-saturated sample was adequately prepared by measuring the pH of the rinse solution (approaching neutrality) and its conductivity (approaching that of ultrapure water). Then, the deposited Na+-saturated sample was dried at 70 °C, ground, and passed through a 0.25 mm soil sieve for later use. The Na+-saturated sample of CRES calcareous soil should be prepared as a control experiment. Considering the partial dissolution of carbonate, 1 mol L−1 sodium acetate saturating solution with pH 8.2 was used to suppress carbonate dissolution.40 Similarly, ultrapure water was utilized to swiftly rinse off any residual sodium acetate solution on the surface of CRES calcareous soil while ensuring that the ambient pH around the CRES calcareous soil solution was similar to the pH of the CREM calcareous soil solution.
2.3. Potassium adsorption experiments
To simulate K adsorption reactions in soils and obtain the ion–surface interactions realistically, the miscible displacement technique,17,30 an experimental method used to study ion exchange adsorption in soils without external disturbance, was carried out at 25 °C to examine the ion adsorption capacity of calcareous soil as carbonate was removed and the initial ion concentration was changed. This method provides the benefit of utilizing a soil-to-solution ratio that closely resembles field conditions, facilitates measurements at the reaction's initial phase, ensures the elimination of displaced species from the reaction site to avert re-adsorption, and sustains a constant adsorbate concentration throughout the process.30 Additionally, it reduces the dilution or leaching effects caused by the retention of the solution, thereby minimizing the overestimation of ion adsorption amounts. Specifically, approximately, 0.5 g of the CREM Na+-saturated sample was evenly spread in the sample chamber of the exchange column as thinly as possible to avoid the influence of a longitudinal concentration gradient of diffusion during the experiment. The potassium acetate electrolyte of 0.1, 1, and 10 mmol L−1 was prepared to flow through the Na+-saturated sample at a constant flow rate of 1 mL min−1 controlled by a peristaltic pump (HL-2, Shang-Hai QPHX Instrument Co., Ltd, Shanghai, China). The effluent liquid was collected every 5 minutes with an automatic partial collector (DBS-100, Shang-Hai QPHX Instrument Co., Ltd, Shanghai, China). A flame photometer (AP1500, Shang-Hai AP Analysis Instrument Co., Ltd Shanghai, China) was used to measure the concentration of K ions in the effluent liquid and compute the amount of adsorbed K ions by the calcareous soil sample. As a control treatment, the K ion adsorption experiment was also performed in the CRES Na+-saturated sample under the above conditions.
2.4. Modeling potassium adsorption kinetics
Given that gradients such as concentration and electric potential could drive the spontaneous flow of ions from the bulk solution to the EDL, the generalized linear theory was used.30 The actual flux Φ(x,t) for ions is:| |
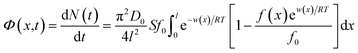 | (1) |
where N(t) is the amount of ion adsorbing at time t during the adsorption/diffusion process; S is the sample's specific surface area; π is the circular constant; D0 represents the ionic diffusion coefficient; f0 represents the initial ionic concentration in bulk solution; l represents the ionic diffusion distance; R and T denote the gas constant and absolute temperature, respectively; f(x) denotes the ionic concentration at x in EDL; w(x) represents the apparent total interaction energies between ions and the soil particle surface at a location of x.
Interactions between ions and the soil particle surface cannot be exclusively attributed to the electrostatic effect, contributions of ion polarization effect,41 polarization-induced covalent bond,42,43 dispersion force44 and ionic hydration,45 etc. should also be incorporated, and these effects are linked and influence the affinity of ions with the soil particle surface cooperatively. It should be emphasized that the contributions of the above components to the ion–surface interactions in this study were all integrated into the electrostatic bonding of ions on the particle surface to conveniently and quantitatively describe the affinity between ions and soil particle surfaces.46 If the total potential energy w(x) is comparatively higher, f(x)ew(x)/RT → 0 and the term 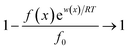 in eqn (1).46,47 In this instance, eqn (1) can be mathematically transformed into:
in eqn (1).46,47 In this instance, eqn (1) can be mathematically transformed into:
| |
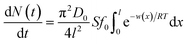 | (2) |
From eqn (2), it can be derived:
| |
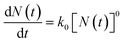 | (3) |
where
| |
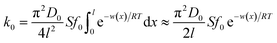 | (4) |
The mathematical derivation from eqn (1)–(4) shows that if the total potential energy w(x) is comparatively higher, the ion adsorption process could be characterized by strong adsorption of zero-order kinetic with eqn (3), and its apparent adsorption rate constant k0 at this stage could be formulated by eqn (4). Because the ion adsorption rate does not alter with its adsorbed amounts variations in consideration of eqn (3), ion adsorption kinetic could be characterized by a straight line parallel to the x-axis in this stage.
While if the total potential energy w(x) is comparatively lower, the term 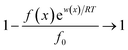 in eqn (1) will no longer be valid, and eqn (1) will change into:
in eqn (1) will no longer be valid, and eqn (1) will change into:
| |
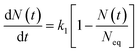 | (5) |
where
| |
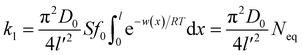 | (6) |
and
| |
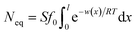 | (7) |
where
Neq is the equilibrium adsorption amount of ion at
t → ∞ in soil and
l′ denotes the ionic diffusion distance driven by the comparatively lower total potential energy
w(
x). The process of derivation described above demonstrates that comparatively lower
w(
x) in eqn
(1) results in the ion adsorption that could be characterized by weak adsorption of first-order kinetic with eqn
(5), and apparent adsorption rate constant
k1 of which at this stage could be formulated by eqn
(6). Because ion adsorption rate is affected by changes in the amount adsorbed according to eqn
(5), ion adsorption kinetics could be characterized by a straight line whose slope is 1 −
N(
t)/
Neq and intersects with the
x-axis in this stage.
Because the results of the ion adsorption studies are continuous (rather than discrete) variables that change over time, statistical analysis of repeated data is frequently unnecessary.48,49 However, it should be noted that the repeatability of the experimental results in this work has been confirmed by multiple trials.
3. Results and discussion
3.1. Accumulation characteristics of adsorbed potassium before and after carbonate removal
The curves of the accumulative adsorbed amounts of K+ versus time are displayed in Fig. 1, from which the following could be intuitively observed: first, the adsorption capacity of CREM Loessial and Lou soil to K+ was superior to that of CRES soil in almost all cases of identical ion concentration. For example, the accumulative adsorbed amounts of K+ for CREM Loessial soil at 0.1, 1, and 10 mmol L−1 during 40 minutes were 9.411, 63.99, and 320.5 mmol kg−1, respectively, while those for CRES Loessial soil at identical conditions were 7.293, 48.45, and 156.5 mmol kg−1, respectively. Likewise, the accumulative adsorbed amounts of K+ for CREM Lou soil at 0.1, 1, and 10 mmol L−1 during 40 minutes were 7.667, 50.06, and 246.6 mmol kg−1, respectively, while for CRES Lou soil at identical conditions, were 8.563, 37.89, and 52.48 mmol kg−1, respectively. Second, for a given initial K concentration and soil type, the discrepancy of adsorbed K amounts between CREM and CRES soil has considerably expanded as ion concentration increases. For instance, the accumulative adsorbed amounts of K for CREM Loessial soil at 0.1, 1, and 10 mmol L−1 during 40 minutes were 1.290, 1.321, and 2.048 times larger than those of CRES Loessial soil at corresponding conditions. The above observations indicate that calcareous soil's adsorbability to K is closely related to carbonate, and the carbonate in calcareous soil has a relatively negative influence on K adsorption. Furthermore, the cumulative adsorption of K+ on Loessial soil surpasses that of Lou soil during the same duration, irrespective of the removal of carbonates. To further dissect the effect of carbonate on the interaction between K and calcareous soil particles, the kinetic process of K adsorption is discussed as follows.
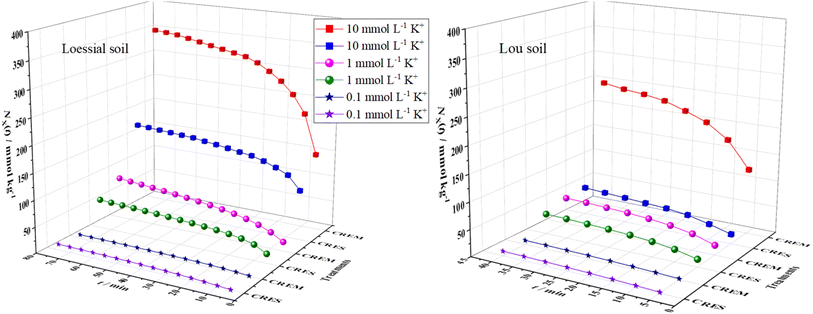 |
| | Fig. 1 Time-dependent changes in the cumulatively adsorbed K+ in CREM and CRES calcareous soil. | |
3.2. Links between potassium adsorption kinetics and carbonate
To be consistent with discrete experimental data, eqn (3) and (5) can be approximately transformed into the differential forms shown below:| |
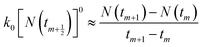 | (8) |
| |
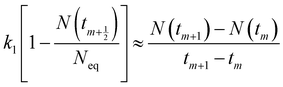 | (9) |
where m is the positive integer 1, 2, 3, …50 Therefore, the relationship curves [N(tm+1) − N(tm)]/(tm+1 − tm) vs. N(tm+1/2) for K adsorption at different experimental conditions are shown in Fig. 2 and 3 based on the experimental results from Fig. 1. Following that, the details of the links between the K adsorption kinetic parameters and carbonate removal will be gone through.
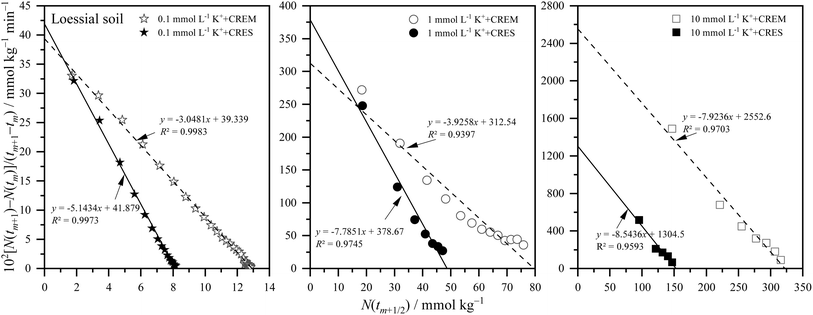 |
| | Fig. 2 Kinetic curves of [N(tm+1) − N(tm)]/(tm+1 − tm) vs. N(tm+1/2) for potassium adsorption in Loessial soil at different treatments. | |
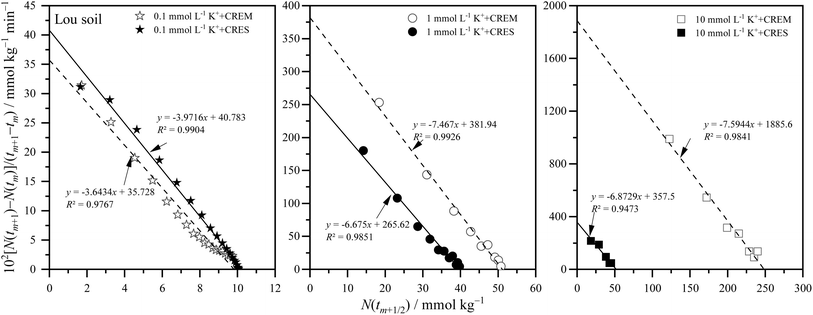 |
| | Fig. 3 Kinetic curves of [N(tm+1) − N(tm)]/(tm+1 − tm) vs. N(tm+1/2) for potassium adsorption in Lou soil at different treatments. | |
3.2.1. Kinetic reaction order of potassium adsorption. From Fig. 2 and 3, and combined with the physical meaning of eqn (5), the first-order kinetic characteristic was observed for weak force adsorption of K in Loessial and Lou soil at all treatments, which implied that the apparent total potential energy w(x) between K ions and calcareous soil particle surface was comparatively lower regardless of carbonate removal or not. To the best of our knowledge, cations can interact with negatively charged soil particle surfaces in three ways: inner-sphere surface complexation, outer-sphere surface complexation, and diffuse adsorption driven by electrostatic attraction and thermal motion. In which diffuse adsorption and outer-sphere surface complex adsorption involve almost exclusively electrostatic bonding, inner-sphere complex adsorption is likely to involve covalent bonds.51 Thus, the strength of the interaction between ions and soil surfaces generally declines in the following order: inner sphere > outer sphere > diffuse adsorption. In light of the lower apparent total potential energy between K ions and calcareous soil particle surfaces, it can be presumably assumed that: (1) K ions primarily bind to the soil surface via diffuse and outer-sphere surface complex adsorption; and (2) the removal of carbonate will not fundamentally change the type of bond between K ions and the soil surface. Molecular dynamics simulation, in effect, has proved the validity of the above hypotheses for K adsorption in soil minerals, and additionally, the confinement effect arising from the soil pore configuration has considerably influenced the weak force adsorption of potassium.52,53
3.2.2. Apparent adsorption rate constant of potassium. Because of the weak ion–surface interaction, the magnitude of the K adsorption rate was indicated by the intercept value of the y-axis of the K adsorption kinetics curves, shown in Fig. 2 and 3, and recapitulated in Table 2. From which, the following characteristics of K adsorption rate changing with carbonate treatment were included: (1) regardless of whether carbonate is removed or not from the calcareous soil, the apparent adsorption rate of K gradually increases with increasing K concentration; and (2) K adsorption rate in CREM soil grows quicker than that in the CRES soil as the initial concentration of K increases.
Table 2 Potassium adsorption rate constant at different ion concentrations in CREM and CRES calcareous soils
| K+ adsorption rate constant (102 mmol kg min−1) |
Treatments |
Loessial soil |
Lou soil |
| K+ concentration (mmol L−1) |
K+ concentration (mmol L−1) |
| 0.1 |
1 |
10 |
0.1 |
1 |
10 |
| k1 |
CREM |
39.34 |
312.5 |
2553 |
35.73 |
381.9 |
1886 |
| CRES |
41.88 |
378.7 |
1305 |
40.78 |
265.6 |
357.5 |
Ion adsorption in heterogeneous soil is a complex interface reaction involving multiple processes of physical chemicals simultaneously. Although potassium ions are primarily distributed on the surface of soil particles via electrostatic force-driven diffusion and outer-sphere coordination, as described in Section 3.2.1, a small amount of potassium exists in various inner-sphere coordination forms due to differences in affinity with surface-O atoms and water-O atoms.52 In other words, the apparent adsorption rate of potassium is regulated by its kinetic diffusion and surface complexation processes. For kinetics diffusion, both film and intraparticle diffusion can become rate-limiting processes in ion adsorption, which is closely associated with the soil's specific surface area and microporosity.51 For the surface complexation rate of aqueous ions, the rate-limiting step is the discharge of water molecules from their coordination sphere.54 According to the preceding viewpoints, the factors influencing the ion adsorption rate are intricate. The calcareous soil's specific surface area and microporosity, along with the hydration degree of potassium ions at the solid–liquid interface, are possibly intertwined in the process of changes in the soil carbonate content and jointly participate in and play a role in regulating the adsorption rate of potassium. Based on the framework developed for ion adsorption kinetics in this study, the theoretical prediction from eqn (6) shows that the apparent ion adsorption rate is proportional to the ionic diffusion coefficient but inversely proportional to the square of the ionic diffusion distance. Although the ionic diffusion coefficient differs in different coordination environments in soil,52,55 the apparent diffusion coefficient of ions typically decreases as ion concentration increases.56 Therefore, the acceleration in potassium adsorption rate is mainly attributed to the sharply decreasing ion diffusion distance as ion concentration increases. According to the Gouy–Chapman theory, the thickness of the EDL is always regarded as the ion diffusion distance to some extent, which is traditionally determined by the solution's dielectric constant and ion intensity, and an increase in ionic strength will result in a progressive drop in the solution's dielectric constant and thickness of the EDL.51,56,57 Based on the above views and taking into account the difference in potassium adsorption rate before and after carbonate removal, we believe that the CRES calcareous soil probably dissolved the carbonate during the process of potassium ion adsorption,58 resulting in the released base cations inhibiting potassium ion adsorption by the soil. Actually, previous studies indicate that carbonates in calcareous soils dissolve instantaneously upon contact with distilled water,59 with their solubility principally influenced by pH, temperature, and the saturation state of minerals in solution.60 The carbonate saturation index (SI) indicates whether carbonate minerals (such as calcite) are saturated, supersaturated, or unsaturated in a body of water. It is widely used for predicting mineral deposition or dissolution in water. Unfortunately, this study only assessed the potassium ion concentration and did not evaluate the constituents of the effluent solution post-experiment, such as the activity of salt ions and carbonate ions. Consequently, the direct acquisition of the SI value of the tested materials during the experiment is unfeasible.
3.2.3. Equilibrium adsorption amount of potassium. The ion equilibrium adsorption amount at the charged soil particle surface is a capacity index of soil nutrients. Here, the equilibrium adsorption amounts of potassium at different ion concentrations before and after eliminating carbonate from calcareous soil are displayed in Table 3, which was obtained from the potassium adsorption kinetic curves of Fig. 2 and 3.
Table 3 Equilibrium adsorption amounts of potassium at different ion concentrations before and after the elimination of carbonate from calcareous soil
| K+ equilibrium adsorption amounts (mmol kg−1) |
Treatments |
Loessial soil |
Lou soil |
| K+ concentration (mmol L−1) |
K+ concentration (mmol L−1) |
| 0.1 |
1 |
10 |
0.1 |
1 |
10 |
| Neq |
CREM |
12.91 |
79.61 |
322.2 |
9.806 |
51.15 |
248.3 |
| CRES |
8.142 |
48.64 |
152.7 |
10.27 |
39.79 |
52.02 |
From Table 3, it can be observed that (1) equilibrium adsorbed potassium in soil is proportional to the potassium concentration and (2) the potassium adsorption capacity of the CREM soil is greater than that of the CRES soil at the identical potassium concentration. These observations indicate that whether or not carbonate is eliminated, the adsorbed potassium by the soil does not quite achieve its maximum adsorption capacity when the potassium concentration is low, revealing that the potassium adsorption capability of calcareous soil is initial-ion-concentration-dependent.61 Potassium ion hydration is thought to have increased the interlayer space of the soil clay, resulting in a greater number of binding sites being available for ion adsorption.61,62 As a result, we speculate that an increase in potassium ion concentration in soil solution leads to more hydrated potassium ions penetrating soil mineral interlayers. The continuous swelling of the soil mineral interlayer space exposes more adsorption sites, resulting in increased adsorbed potassium levels in the soil. In addition, CRES soil has inferior potassium adsorption performance than CREM soil. This could be because the presence of carbonate obscures the accessible sorption sites on clay, silt, and organic matter fractions,40,63 as well as because the base cations released from carbonate dissolution compete with potassium ions for surface binding sites. The adsorption capacity differences (ΔNeq) of K+ before and after soil carbonate removal were depicted in Fig. 4, which implied that the removal of soil carbonate could increase the soil's responsiveness to the initial potassium concentration. Also, the excellent linear relationship between ΔNeq and the initial potassium concentration in Fig. 4 confirmed that the initial K+ concentration was more influential than the carbonate removal on K+ adsorption in calcareous soil.
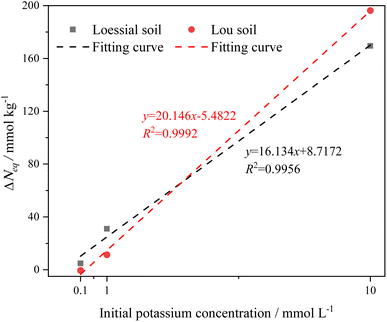 |
| | Fig. 4 Adsorption capacity differences (ΔNeq) of K+ before and after soil carbonate removal changes with the initial potassium concentration. | |
3.3. Interaction energy between potassium ions and soil particle surface
There is a consensus that soil adsorption toward ions is always accompanied by interaction energy changes between ions and particle surfaces. As mentioned and discussed in Sections 3.2.1 and 3.2.2, electrostatic force-driven diffusion and outer-sphere coordination are the primary interactions between K+ and soil particles; inner-sphere coordination is a secondary form of their interactions. The interaction between K and the soil particle surface primarily occurs through nonspecific adsorption mechanisms that depend on electrostatic forces, such as diffuse ion adsorption and outer-sphere surface complexation. In diffuse ion adsorption, K+ screens the surface charge of soil particles by electrostatic interactions and remains dissolved in the soil solution. In outer-sphere surface complexation, K+ retains a specific distance from the soil particle surface without establishing covalent or ionic interactions.51 In the interaction between K+ and the surface –O groups (oxygen atoms bonded to Si) of soil minerals, both the outer orbitals of K+ and –O are in a saturated octet configuration. Consequently, according to classical chemical bonding theory, the formation of covalent bonds between K+ and –O is improbable, indicating that K+ is largely incapable of establishing inner-sphere coordination on soil surfaces.20 Recent research indicates that in the absence of a strong electrostatic field on the soil surface, K+ does not establish covalent inner-sphere coordination with soil particles.42 A substantial surface charge can generate a robust electric field at the soil surface.22 The adsorption potential of K on soil mineral surfaces is influenced by three components: (1) diffusion-adsorption driven by classical electrostatic forces; (2) outer-sphere coordination induced by ion polarization in an external electric field; and (3) covalent interactions resulting from asymmetric hybridization of atomic orbitals.64 Upon the establishment of covalent interactions between K and soil particles, inner-sphere coordination of K on the soil surface ensues. It is crucial to acknowledge that while K+ can participate in covalent interactions with the surface groups of soil minerals under sufficiently strong electric fields, the resultant covalent bonds are weaker than the traditional covalent bonds.47,65 We therefore estimated the ion–surface interaction energies while accounting for the previously indicated interactions. For the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 type of electrolyte solution in the present study, the total interaction energies between K+ and the charged soil surface are as follows:46,47
1 type of electrolyte solution in the present study, the total interaction energies between K+ and the charged soil surface are as follows:46,47| |
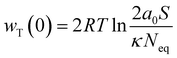 | (10) |
in which| |
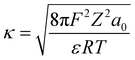 | (11) |
where wT(0) denotes the total adsorption energies of K+ at the charged soil surface of x = 0; a0 denotes the activity of K+ in the bulk solution; κ is the Debye–Hückel parameter and F is the Faraday constant; Z is the ionic valence; and ε is the dielectric constant.
Fitting the experimental results into eqn (10) and (11), the total adsorption energies of K+ in calcareous soil at different test conditions were evaluated, as shown in Fig. 5. The following critical message could be conclusively captured: the K+ adsorption energies in CREM soil were quantitatively larger than those in CRES soil at an identical initial K+ concentration. This energy differential will be steadily magnified as the initial K+ concentration rises. For instance, the K+ adsorption energy differences between CREM and CRES loess soil rose from −2.28 to −3.70 kJ mol−1 as the K+ concentration gradually increased from 0.1 to 10 mmol L−1. In conjunction with the analysis in Section 3.2.3, the rise in the initial K+ concentration and the removal of soil carbonates increase the number of ion-binding sites in the soil, resulting in a difference in the K+ adsorption energies and its adsorption quantities. According to the EDL theory, increasing K+ concentration will significantly compress the thickness of the soil colloidal particles' EDL, presumably leading to a continuous increase in the interaction energies between K+ and the negatively charged soil surface. For CRES calcareous soil, the partially dissolved base cations released by carbonate dissolution will compete with K+ for ion-binding sites, thus lowering K+ adsorption energies in the soil. Furthermore, because the dissolution of soil carbonates progressively increases with increasing background ionic strength,58 the difference in K+ adsorption energy between CREM and CRES soil gradually expands with increasing ion concentration.
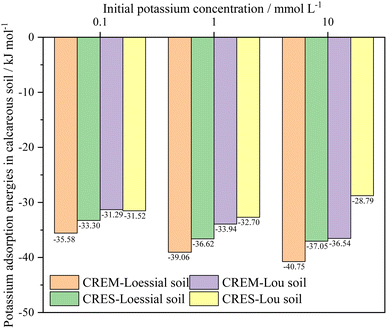 |
| | Fig. 5 Adsorption energies of K+ in calcareous soil at different treatments. | |
The model introduced in this study offers an enhanced theoretical comprehension of ion adsorption kinetics on charged soil particle surfaces; nonetheless, it possesses several possible limitations. Firstly, the charged interface electrostatic field theory used in this study is based on the average effect, which depicts the electric field and potential distribution on the surface of charged particles under ideal conditions while ignoring the heterogeneity of the surface charge distribution. Secondly, the surface properties of charged soil particles, including surface roughness and pore architecture, may influence the distribution and migration pathways of charged ions on the particle surface; however, these elements have not been well addressed in the existing theoretical model. Future studies should address these limitations by incorporating more environmental parameters and particle properties, and by formulating a more comprehensive theoretical model of charged ion diffusion in external fields, which should be substantiated through further experimental investigations.
4. Conclusions
In this study, K adsorption kinetics was used as an example to explore the effects of carbonate on ion–surface interactions in calcareous soils. It can be conclusively said that K is largely bound to the surface of calcareous soil via outer-sphere coordination and diffusion adsorption, with little effect from the presence of carbonate on the type of K bonding on soil particle surfaces. While the increase in K concentration decreased the K diffusion distance and accelerated the K adsorption rate, the CRES soil might dissolve and release base cations, reducing the K adsorption rate. As a result, after removing carbonate, the adsorption rate of K in calcareous soil is more susceptible to changes in its concentration. The adsorption amount of K in calcareous soil rose as K concentration increased, which may be related to the entry of the hydrated K ions into the soil that causes the swelling of the soil mineral layers and more adsorption sites to be exposed. However, for CRES soil, due to the screen effect of carbonate on other adsorption sites of soil components, the amount of K adsorption in the CRES soil under the same ion concentration was less than that of CREM soil. Further studies revealed that increasing K levels in the soil or removing carbonate from calcareous soil could raise the electrostatic binding energy of K on the soil particle surface. The model adopted in this study offers significant applications in soil nutrient management and environmental buffering capacity. The characteristic parameters describing chemical reaction kinetics, such as the ion adsorption rate and adsorption energy, can enhance the understanding of cation interfacial transport behavior in soil, thereby allowing for more effective soil nutrient management, optimized crop nutrient utilization efficiency, and reduced dependence on fertilizers. Additionally, the equilibrium adsorption parameter involved in the model assists in evaluating soil buffering capacity, providing a scientific basis for soil conservation and sustainable management.
Data availability
The data supporting the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (42107332, 42077135), the General Project of the Natural Science Foundation of Shaanxi Province, China (2023-JC-YB-263), the Doctoral Research Startup Project of Northwest A&F University, China (2452018041), and the Key Research and Development Program of Shaanxi Province, China (2024NC-ZDCYL-02-14).
References
- B. Chen, J. Fang, S. Piao, P. Ciais, T. A. Black, F. Wang, S. Niu, Z. Zeng and Y. Luo, New Phytol., 2024, 241, 154–165 CrossRef PubMed.
- S. Li, B. Wang, X. Zhang, H. Wang, Y. Yi, X. Huang, X. Gao, P. Zhu and W. Han, Geoderma, 2023, 429, 116285 CrossRef.
- X. Li, Y. Xing, L. Tang, N. Liu, Q. Chang and J. Zhang, Eur. J. Soil Sci., 2022, 73, e13155 CrossRef.
- N. Bolan, A. K. Sarmah, S. Bordoloi, S. Bolan, L. P. Padhye, L. Van Zwieten, P. Sooriyakumar, B. A. Khan, M. Ahmad and Z. M. Solaiman, Environ. Pollut., 2023, 317, 120632 CrossRef PubMed.
- M. Duan, G. Liu, B. Zhou, X. Chen, Q. Wang, H. Zhu and Z. Li, J. Soils Sediments, 2021, 21, 2192–2202 CrossRef.
- L. Du, L. Ding, X. Huang, D. Tang, B. Chen, H. Tian, Z. Kang and H. Mao, Plant, Cell Environ., 2024, 47, 540–556 CrossRef PubMed.
- Y. Yang, P.-p. Zhang, Y. Song, Z.-m. Li, Y.-y. Zhou, H. Sun, J. Qiao, Y.-q. Wang and S.-s. An, Carbon Neutrality, 2024, 3, 1–17 CrossRef.
- X. Dou, J. Zhang, C. Zhang, D. Ma, L. Chen, G. Zhou, J. Li and Y. Duan, Catena, 2023, 231, 107327 CrossRef.
- E. Fiorito, G. E. Porcedda, L. Brundu, C. Passiu, D. Atzei, G. Ennas, B. Elsener, M. Fantauzzi and A. Rossi, Chemosphere, 2022, 296, 133897 CrossRef PubMed.
- M. Najafi-Ghiri and A. Abtahi, Soil Water Res., 2013, 8, 49–55 CrossRef.
- J. Meng and X.-A. Li, Bull. Eng. Geol. Environ., 2019, 78, 4965–4976 CrossRef.
- M. Ban, T. Luxbacher, J. Lützenkirchen, A. Viani, S. Bianchi, K. Hradil, A. Rohatsch and V. Castelvetro, Colloids Surf., A, 2021, 624, 126761 CrossRef.
- D. Al Mahrouqi, J. Vinogradov and M. D. Jackson, Adv. Colloid Interface Sci., 2017, 240, 60–76 CrossRef.
- M. Bonto, A. A. Eftekhari and H. M. Nick, Adv. Colloid Interface Sci., 2022, 301, 102600 CrossRef.
- D. Das, B. Dwivedi, S. Datta, S. Datta, M. Meena, A. K. Dwivedi, M. Singh, D. Chakraborty and S. Jaggi, Geoderma, 2021, 393, 114983 CrossRef.
- J. P. M. Flores, L. A. Alves, L. G. de Oliveira Denardin, A. P. Martins, E. C. Bortoluzzi, A. V. Inda, P. C. de Faccio Carvalho and T. Tiecher, Soil Tillage Res., 2021, 213, 105070 CrossRef.
- D. L. Sparks, B. Singh and M. G. Siebecker, Environmental Soil Chemistry, Elsevier, 2022 Search PubMed.
- N. Barrow, Eur. J. Soil Sci., 2023, 74, e13355 CrossRef.
- H. Li and L. Wu, Soil Sci. Soc. Am. J., 2007, 71, 1694–1698 CrossRef.
- Q. Li, R. Tian and Q. Yang, Appl. Clay Sci., 2023, 231, 106746 CrossRef.
- P. Krejci, T. Gimmi and L. R. Van Loon, Geochim. Cosmochim. Acta, 2021, 298, 149–166 CrossRef.
- X. Liu, W. Chen, Y. Tang, S. Xiao, Q. Li, W. Ding, L. Wu, R. Tian, R. Li and H. Li, J. Hazard. Mater., 2024, 468, 133718 CrossRef PubMed.
- D. Das, A. K. Nayak, V. Thilagam, D. Chatterjee, M. Shahid, R. Tripathi, S. Mohanty, A. Kumar, B. Lal and P. Gautam, J. Soils Sediments, 2018, 18, 1806–1820 CrossRef.
- E. Tertre, F. Hubert, S. Bruzac, M. Pacreau, E. Ferrage and D. Pret, Geochim. Cosmochim. Acta, 2013, 112, 1–19 CrossRef.
- J. Xiong, L. Weng, L. K. Koopal, M. Wang, Z. Shi, L. Zheng and W. Tan, Environ. Sci. Technol., 2018, 52, 1348–1356 CrossRef PubMed.
- S. Goldberg, L. J. Criscenti, D. R. Turner, J. A. Davis and K. J. Cantrell, Vadose Zone J., 2007, 6, 407–435 CrossRef.
- M. Kassa, W. Haile and F. Kebede, Commun. Soil Sci. Plant Anal., 2019, 1–14 Search PubMed.
- M. Jalali, T. M. Arian and F. Ranjbar, Environ. Monit. Assess., 2020, 192, 1–14 CrossRef.
- X. Liu, W. Chen, Y. Tang, S. Xiao, Q. Li, W. Ding, L. Wu, R. Tian, R. Li and H. Li, J. Hazard. Mater., 2024, 133718 CrossRef.
- H. Li, R. Li, H. Zhu and L. Wu, Soil Sci. Soc. Am. J., 2010, 74, 1129–1138 CrossRef.
- H. Li, L. Wu, H. Zhu and J. Hou, J. Phys. Chem. C, 2009, 113, 13241–13248 CrossRef CAS.
- D. Liu, R. Tian, X. Liu and H. Li, J. Soils Sediments, 2023, 1–10 Search PubMed.
- W. Ding, X. Liu, L. Song, Q. Li, Q. Zhu, H. Zhu, F. Hu, Y. Luo, L. Zhu and H. Li, Surf. Sci., 2015, 632, 50–59 CrossRef.
- X. Liu, F. Hu, W. Ding, R. Tian, R. Li and H. Li, Analyst, 2015, 140, 7217–7224 RSC.
- L. Zhang, D. Mishra, K. Zhang, B. Perdicakis, D. Pernitsky and Q. Lu, Water Res., 2020, 186, 116415 CrossRef PubMed.
- H. Li and L. Wu, New J. Phys., 2007, 9, 357 CrossRef.
- W. Du, Y. Yang, L. Hu, B. Chang, G. Cao, M. Nasir and J. Lv, Colloids Surf., A, 2021, 626, 127067 CrossRef.
- V. Antoniadis, S. M. Shaheen, C. D. Tsadilas, M. H. Selim and J. Rinklebe, Appl. Geochem., 2018, 88, 49–58 CrossRef.
- S. Bao, Soil Agrochemical Analysis, China Agricultural Press, Beijing, 2000, pp. 202–204 Search PubMed.
- F. Razzaghi, E. Arthur and A. A. Moosavi, Geoderma, 2021, 400, 115221 CrossRef CAS.
- D. Liu, W. Du, X. Liu, R. Tian and H. Li, J. Phys. Chem. C, 2019, 123, 2157–2164 CrossRef CAS.
- Q. Li, S. Yang, Y. Tang, G. Yang and H. Li, J. Phys. Chem. C, 2019, 123, 25278–25285 CrossRef CAS.
- Q. Li, W. Shi and Q. Yang, J. Hazard. Mater., 2021, 412, 125168 CrossRef CAS PubMed.
- D. F. Parsons, M. Boström, P. L. Nostro and B. W. Ninham, Phys. Chem. Chem. Phys., 2011, 13, 12352–12367 RSC.
- B. J. Teppen and D. M. Miller, Soil Sci. Soc. Am. J., 2006, 70, 31–40 CrossRef CAS.
- W. Du, R. Li, X. Liu, R. Tian, W. Ding and H. Li, Appl. Clay Sci., 2017, 146, 122–130 CrossRef CAS.
- Q. Li, R. Li and W. Shi, Appl. Clay Sci., 2021, 213, 106245 CrossRef CAS.
- S. Carrick, P. Almond, G. Buchan and N. Smith, Eur. J. Soil Sci., 2010, 61, 1056–1069 CrossRef.
- F. Hu, J. Liu, C. Xu, Z. Wang, G. Liu, H. Li and S. Zhao, Geoderma, 2018, 320, 43–51 CrossRef.
- W. Du, R. Li, X.-M. Liu, R. Tian and H. Li, Colloids Surf., A, 2016, 509, 427–432 CrossRef CAS.
- G. Sposito, The Chemistry of Soils, Oxford University Press, 2008 Search PubMed.
- X. Li, C. Zhu, Z. Jia and G. Yang, J. Colloid Interface Sci., 2018, 523, 18–26 CrossRef CAS.
- X. Li, N. Liu, L. Tang and J. Zhang, Appl. Clay Sci., 2020, 198, 105814 CrossRef CAS.
- H. P. van Leeuwen, Langmuir, 2008, 24, 11718–11721 CrossRef CAS PubMed.
- X. Liu, S. Yang, P. Gu, S. Liu and G. Yang, Appl. Clay Sci., 2021, 201, 105957 CrossRef.
- W. Du, X. Liu, R. Tian, R. Li, W. Ding and H. Li, RSC Adv., 2020, 10, 15190–15198 RSC.
- M. S. Santos, M. Castier and I. G. Economou, Fluid Phase Equilib., 2019, 487, 24–32 CrossRef.
- B. Coto, C. Martos, J. L. Peña, R. Rodríguez and G. Pastor, Fluid Phase Equilib., 2012, 324, 1–7 CrossRef.
- D. Suarez and J. Rhoades, Soil Sci. Soc. Am. J., 1982, 46, 716–722 CrossRef.
- G. Romero-Mujalli, J. Hartmann, J. Börker, J. Gaillardet and D. Calmels, Chem. Geol., 2019, 527, 118634 CrossRef.
- P. Buragohain, S. Sreedeep, P. Lin, J. Ni and A. Garg, J. Soils Sediments, 2019, 19, 186–197 CrossRef.
- X. Li, Q. Li, S. Yang and G. Yang, Phys. Chem. Chem. Phys., 2019, 21, 1963–1971 RSC.
- E. Arthur, Eur. J. Soil Sci., 2017, 68, 365–373 CrossRef CAS.
- D. Liu, R. Tian, X. Liu and H. Li, J. Soils Sediments, 2024, 24, 722–731 CrossRef CAS.
- X. Liu, Y. Tang, R. Tian, R. Li, W. Ding, W. Chen and H. Li, Appl. Surf. Sci., 2024, 656, 159689 CrossRef CAS.
Footnote |
| † Wei Du and Shifeng Wang are contributing equally to this work. |
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
Shifeng Wang†c,
Yizhe Yangd,
Chenyang Xuab,
Feinan Hue,
Wuquan Dingf and
Jialong Lv*ab
*ab,
Shifeng Wang†c,
Yizhe Yangd,
Chenyang Xuab,
Feinan Hue,
Wuquan Dingf and
Jialong Lv*ab
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 (w:v) was added to 20 g of the two types of soil samples, and the two mixed soil suspensions were separately transferred to an Erlenmeyer flask and continuously shaken for 24 hours at 220 rpm. Then, the suspensions were centrifuged at 5000 rpm for 5 minutes, and the supernatants were discarded. The repetitions of the above operation should be done until no carbon dioxide was measured in the sample by the gasometric method.39 To thoroughly remove the ions released by the decomposition of carbonate and residual sodium acetate in the calcareous soil, the sodium acetate solution was replaced by ultrapure water, and the above operation was repeated several times. During this procedure, the Na-saturated sample was adequately prepared by measuring the pH of the rinse solution (approaching neutrality) and its conductivity (approaching that of ultrapure water). Then, the deposited Na+-saturated sample was dried at 70 °C, ground, and passed through a 0.25 mm soil sieve for later use. The Na+-saturated sample of CRES calcareous soil should be prepared as a control experiment. Considering the partial dissolution of carbonate, 1 mol L−1 sodium acetate saturating solution with pH 8.2 was used to suppress carbonate dissolution.40 Similarly, ultrapure water was utilized to swiftly rinse off any residual sodium acetate solution on the surface of CRES calcareous soil while ensuring that the ambient pH around the CRES calcareous soil solution was similar to the pH of the CREM calcareous soil solution.
25 (w:v) was added to 20 g of the two types of soil samples, and the two mixed soil suspensions were separately transferred to an Erlenmeyer flask and continuously shaken for 24 hours at 220 rpm. Then, the suspensions were centrifuged at 5000 rpm for 5 minutes, and the supernatants were discarded. The repetitions of the above operation should be done until no carbon dioxide was measured in the sample by the gasometric method.39 To thoroughly remove the ions released by the decomposition of carbonate and residual sodium acetate in the calcareous soil, the sodium acetate solution was replaced by ultrapure water, and the above operation was repeated several times. During this procedure, the Na-saturated sample was adequately prepared by measuring the pH of the rinse solution (approaching neutrality) and its conductivity (approaching that of ultrapure water). Then, the deposited Na+-saturated sample was dried at 70 °C, ground, and passed through a 0.25 mm soil sieve for later use. The Na+-saturated sample of CRES calcareous soil should be prepared as a control experiment. Considering the partial dissolution of carbonate, 1 mol L−1 sodium acetate saturating solution with pH 8.2 was used to suppress carbonate dissolution.40 Similarly, ultrapure water was utilized to swiftly rinse off any residual sodium acetate solution on the surface of CRES calcareous soil while ensuring that the ambient pH around the CRES calcareous soil solution was similar to the pH of the CREM calcareous soil solution.
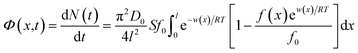
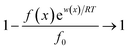 in eqn (1).46,47 In this instance, eqn (1) can be mathematically transformed into:
in eqn (1).46,47 In this instance, eqn (1) can be mathematically transformed into: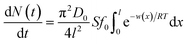
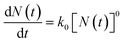
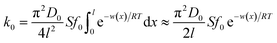
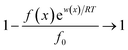 in eqn (1) will no longer be valid, and eqn (1) will change into:
in eqn (1) will no longer be valid, and eqn (1) will change into: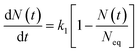
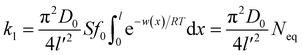
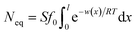
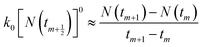
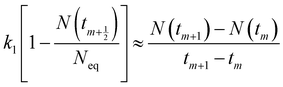


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 type of electrolyte solution in the present study, the total interaction energies between K+ and the charged soil surface are as follows:46,47
1 type of electrolyte solution in the present study, the total interaction energies between K+ and the charged soil surface are as follows:46,47