Open Access Article
Open Access ArticleEnhancing protein aggregation prediction: a unified analysis leveraging graph convolutional networks and active learning†
Jiwon Sun‡
a,
JunHo Song‡a,
Juo Kim‡ a,
Seungpyo Kang
a,
Seungpyo Kang a,
Eunyoung Parkb,
Seung-woo Seo*b and
Kyoungmin Min
a,
Eunyoung Parkb,
Seung-woo Seo*b and
Kyoungmin Min *a
*a
aSchool of Mechanical Engineering, Soongsil University, 369 Sangdo-ro, Dongjak-gu, Seoul 06978, Republic of Korea. E-mail: kmin.min@ssu.ac.kr
bAinB, 160 Yeoksam-ro, Gangnam-gu, Seoul 06249, Republic of Korea. E-mail: seungwoo.seo@ainbsci.com
First published on 3rd October 2024
Abstract
Protein aggregation (PA) is a critical phenomenon associated with Alzheimer's and Parkinson's disease. Recent studies have suggested that factors like aggregation-prone regions (APRs) and β-strand interactions are crucial in understanding such behavior. While experimental methods have provided valuable insights, there has been a shift towards computational strategies, particularly machine learning, for their efficacy and speed. The challenge, however, lies in effectively incorporating structural information into these models. This study constructs a Graph Convolutional Network (GCN) to predict PA scores with the expanded and refined Protein Data Bank (PDB) and AlphaFold2.0 dataset. We employed AGGRESCAN3D 2.0 to calculate PA propensity and to enhance the dataset, we systematically separated multi polypeptide chains within PDB data into single polypeptide chains, removing redundancy. This effort resulted in a dataset comprising 302![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 032 unique PDB entries. Subsequently, we compared sequence similarity and obtained 22
032 unique PDB entries. Subsequently, we compared sequence similarity and obtained 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774 Homo sapiens data from AlphaFold2.0. Using this expanded and refined dataset, the trained GCN model for PA prediction achieves a remarkable coefficient of determination (R2) score of 0.9849 and a low mean absolute error (MAE) of 0.0381. Furthermore, the efficacy of the active learning process was demonstrated through its rapid identification of proteins with high PA propensity. Consequently, the active learning approach achieved an MAE of 0.0291 in expected improvement, surpassing other methods. It identified 99% of the target proteins by exploring merely 29% of the entire search space. This improved GCN model demonstrates promise in selecting proteins susceptible to PA, advancing protein science. This work contributes to the development of efficient computational tools for PA prediction, with potential applications in disease diagnosis and therapy.
774 Homo sapiens data from AlphaFold2.0. Using this expanded and refined dataset, the trained GCN model for PA prediction achieves a remarkable coefficient of determination (R2) score of 0.9849 and a low mean absolute error (MAE) of 0.0381. Furthermore, the efficacy of the active learning process was demonstrated through its rapid identification of proteins with high PA propensity. Consequently, the active learning approach achieved an MAE of 0.0291 in expected improvement, surpassing other methods. It identified 99% of the target proteins by exploring merely 29% of the entire search space. This improved GCN model demonstrates promise in selecting proteins susceptible to PA, advancing protein science. This work contributes to the development of efficient computational tools for PA prediction, with potential applications in disease diagnosis and therapy.
Introduction
Protein aggregation (PA) is recognized as the physical association of misfolded or unfolded proteins, influenced by factors such as aging, genetic mutations, and environmental stressors, including pH and temperature.1–3 This phenomenon is associated with various human diseases, including neurodegenerative disorders (such as Alzheimer's disease, Huntington's disease, and Parkinson's disease), certain types of cancers, and type II diabetes.4–6 Extensive research has focused on exploring the relationship between the aggregation of specific protein species and the onset-staged mechanism of these diseases.7,8 Understanding the inherent vulnerability of proteins in their soluble form to aggregation is crucial, as this knowledge could shed light on the diagnosis and therapy of amyloid-related diseases.9,10 Recent studies have not only extensively investigated the relationship between specific protein aggregations and related diseases, such as the correlation between amyloid-β aggregation and Alzheimer's disease but have also examined deeper into understanding the underlying causes of these aggregations.11,12 These investigations reveal that each protein domain typically possesses at least one aggregation-prone region (APR).2 Furthermore, it is identified that the interaction between identical or homologous APRs through β-strand interactions is the most prevalent structural mechanism driving protein aggregation.The methodology of investigation in PA is mainly divided into two streams including experimental observation and theoretical calculation. From the perspective of experiments, information about 3D protein aggregate structure can be obtained from X-ray diffraction (XRD) spectroscopy and the evolutionary stages of aggregation also can be detected from small-angle X-ray scattering (SAXS).13 In addition, calorimetric-based methods such as isothermal titration calorimetry (ITC) allow researchers to quantitatively measure PA.14 However, the X-ray scattering-based methods require crystal production, which is time-consuming and expensive. Similarly, the calorimetric-based methods have limits associated with the requirement of large-volume samples. From the viewpoint of theoretical calculation, atomistic scale simulations such as molecular dynamics (MD) enable a sophisticated understanding of the early stages of aggregation, finding clues identifying possible aggregation-prone structures by differentiating the aggregation-prone monomeric structure. 15 However, this simulation model requires force-fields which necessitates a compromise between accuracy and simulation scale.
There is a diverse range of research dedicated to numerically quantifying the extent of PA propensity and aggregation-prone regions (APRs) using various computational algorithms with much reduced time than conventional MD. These techniques mainly adopt sequence-based methods. In detail, PA is quantified numerically using amino acid (AA) physiochemical properties, sequence patterns, and knowledge-based score functions. 16–20 In recent times, machine learning (ML) models utilizing sequences as input have begun to be employed in distinguishing sequences that are likely to lead to protein aggregation. The exemplary cases are (1) Budapest Amyloid Predictor web server predicts amyloid protein using a linear support vector machine (SVM), adopting amino acid sequence which originated experimental hexapeptide Waltz database as input. 16 This model achieves prediction accuracy higher than 84% when it classifies whether the input sequence has a propensity to become amyloid or not. (2) Amyloidogenicity Propensity Prediction Neural Network (APPNN) predicts the amyloidogenic polypeptide sequence, achieving 84.9% prediction accuracy against an external validation of experimental sequences using key features for peptides and proteins forming amyloids, focusing on β-sheet frequency, isoelectric point, and hydrophobicity.19 (3) Hot spot found in amyloid-versed (FISH amyloid) introduces an innovative ML approach for amino acid sequence classification, which hinges on detecting segments exhibiting distinctive patterns among sequence elements.21 While numerous previous ML-based studies have predicted aggregation tendencies through sequence-based features, there is a notable need for ML models that incorporate structural information. This gap is significant because the clustering of hydrophobic residues would form structural aggregation-prone regions (STAPs) in their native state. These regions are often undetectable by linear predictors.22 The absence of machine learning models capable of incorporating protein structures is believed to resolve the gap between experimentally observed protein aggregation propensities and the structure embeddings that can be derived from sequences.
Fortunately, there has been a significant turning point in protein science recently. AlphaFold and its subsequent studies have accelerated the structure analysis process that traditionally required a long time based on the protein sequence.23–26 This allows researchers to adopt structural information in their works, increasing the prediction accuracy of protein properties. The exemplary cases are (1) utilizing the AlphaFold2.0 database as an additional dataset on the training of the protein function prediction model.27 This study demonstrates that prediction models only trained on virtual protein structures from AlphaFold2.0 achieved comparable performance to the model trained on experimental structures, implying that the virtual structures were comparably effective in predicting protein functionality. (2) The structural analysis of 26 hereditary cancer proteins was conducted using AlphaFold2.0 protein structures.28 The confidence scores from AlphaFold2.0 structures were more effective in predicting variant pathogenicity than other stability prediction tools. (3) The backbone NMR N–H S2 order parameter was predicted by adopting the information returned from AlphaFold2.0.29 This study combines AlphaFold2's confidence scores with a local contact model to estimate dynamic features at the residue level, successfully capturing experimental NMR order parameter profiles. Demonstrated on nine proteins, the method accommodates diverse sizes and levels of dynamics and disorder. As demonstrated in various studies, the adoption of structure or structural information from AlphaFold can improve the prediction model's performance. Similarly, adopting virtual protein structures demonstrates to increase in the performance of prediction on PA of proteins, making the use of protein structures in ML models a more practical strategy.
In this study, we developed the graph convolutional neural network (GCN) model for predicting PA by incorporating the AlphaFold database with the protein data bank (PDB) dataset. The superior performance of the suggested model is validated using Homo sapiens protein data (21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 873 structures) from AlphaFold2.0 (hAF2.0). The improved model achieved a remarkable prediction accuracy although it was trained using only one 0.1% of the PDB dataset. It is anticipated that this model will serve as a tool for selecting proteins susceptible to PA and will lay a foundational stone in the field of protein science.
873 structures) from AlphaFold2.0 (hAF2.0). The improved model achieved a remarkable prediction accuracy although it was trained using only one 0.1% of the PDB dataset. It is anticipated that this model will serve as a tool for selecting proteins susceptible to PA and will lay a foundational stone in the field of protein science.
Methods
The overall schematic flow of the study is illustrated in Fig. 1. In this study, the GCN-based model was first trained with PDB data whose aggregation score was calculated by AGGRESCAN3D 2.0 (A3D) dynamic mode, then its performance was validated on the hAF2.0 database. As shown in Fig. 1(a), the training data was adopted from the PDB, while the test data constituted the hAF2.0. Subsequently, the protein structures with a multi-polypeptide chain form were divided into each single polypeptide chain.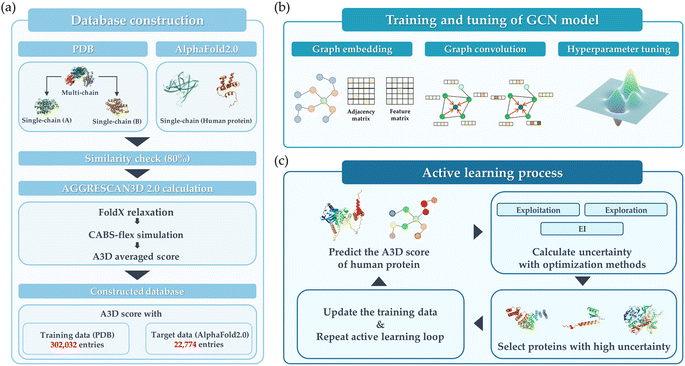 | ||
| Fig. 1 Schematic overview of this study. (a) Database construction, (b) training and tuning of the GCN model, and (c) active learning process. | ||
Fig. 1(b) illustrates the training and tuning process to develop the optimal GCN model using the database constructed in the previous step. In this step, the extensive hyperparameter optimization was performed. Then, the model exhibiting the best performance for train data was implemented to predict the hAF2 data. As a final step, the active learning process is employed as shown in Fig. 1(c), whose purpose is to improve the model's predictive performance and adaptability in extreme conditions. Active learning was implemented through an iterative feedback loop to identify and prioritize protein structures that are most likely to aggregate. Several types of acquisition functions such as Efficient Global Optimization (EGO) and exploitation were employed to compare the performance. This active learning process not only enhanced the model's ability to generalize across diverse datasets but also proposed an optimized process for rapidly and accurately identifying proteins with high A3D scores. Detailed explanations for each of the steps are provided.
Database construction
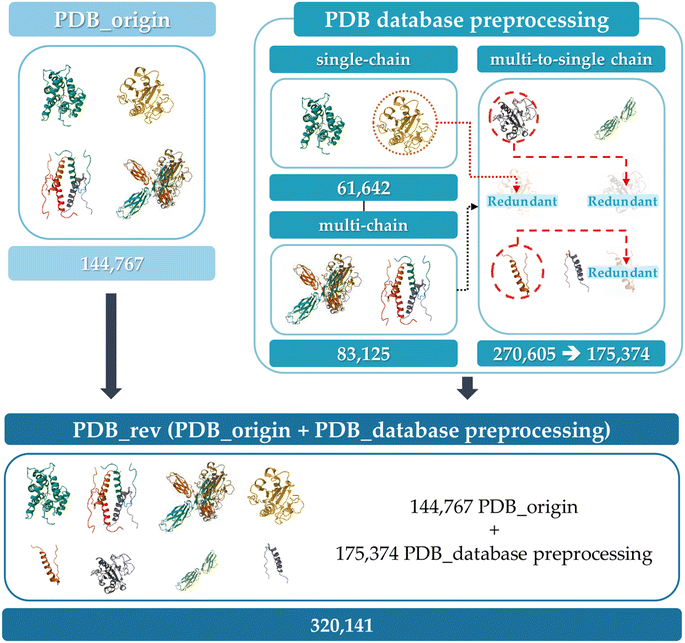
As shown in Fig. 1(a), the database construction method consists of the following steps: (1) to improve the prediction accuracy of PA for the hAF2.0 database, data from PDB with more than half of them having multi polypeptide chains were split into single polypeptide chain and merged with the existing PDB data. (2) Comparison of sequence similarity between the converted PDB data and hAF2.0 data. The similarity between data from PDB and hAF2.0 data is calculated, and proteins that have a similarity of more than 80% are removed from the test data of hAF2.0 to avoid data overlapping which could lead to an overestimation of the model's performance. By selecting proteins distinct from those in the PDB training set, we also emphasize the independence of our datasets. (3) To assess the PA propensity between the PDB and hAF2.0 data, the A3D, which utilizes the structure and AA for calculating PA propensity, was used. Detailed information about the data construction can be found in the later section.Aggregation calculation
The PA propensity values of train and test data were calculated using A3D.30 3D structure-based A3D offers a significant advantage over existing linear sequence-based algorithms such as SOLpro31 and PROSO II32 when analyzing the folded states of globular proteins in a specific structural context. It demonstrates a higher level of accuracy by capturing structural variations that influence PA, considering dynamic changes in protein structure. In addition, in terms of comparison to the other 3D-based algorithms, A3D is one of the most promising methods capable of considering dynamic mutations, leading to the more accurate prediction of PA propensity. Although the spatial aggrecan propensity (SAP) provides a similar method for considering the dynamic fluctuation of protein structure, SAP takes a long time to simulate the time-consuming molecular simulation, which is not reasonable to accumulate the large size of training datasets.33 For this reason, many studies use A3D as a method for predicting PA propensity.34–36 It is also noted that two modes (static and dynamic mode) are available for calculating the PA propensities of protein structures. In contrast to the static mode, where the input structure is energy-minimized by FoldX37 force field to ensure the stability of proteins, the dynamic mode involves using the energy-minimized structure as the input and predicts the flexibility of the protein structure through CABS-flex simulation.38 By considering this, it is possible to reflect the dynamic changes that proteins undergo in solution, thereby allowing for a more accurate determination of protein aggregation tendencies.30 Additionally, in the dynamic mode, the A3D score is calculated as the average of A3D scores extracted from trajectory files generated during the CABS-flex simulation process. Consequently, only the average A3D scores calculated through the dynamic mode were used in the final training data for the GCN model.Architectures of GCN model
A GCN architecture originating from a previous study was utilized to predict the PA propensity of protein structure.35 This model employed the PyTorch Geometric package, and the GCN Conv algorithm served as the basis for the graph convolution process.39,40 As illustrated in Fig. 2(a), protein representation was constructed using 3D atomic coordinates from PDB files. In this graphical representation, denoted as G = (V, E), V represents the nodes, each corresponding to an amino acid (AA), and E symbolizes the edges, indicative of the interactions between AAs. For this study, an edge E is established between two AAs if the distance between their α-carbons is less than a specified threshold (7 Å). The protein graph G encompasses a node feature matrix, X, and an adjacency matrix, A. The matrix X is a 20-dimensional feature matrix (sized N × 20, where N is the count of AAs), generated through one-hot encoding of the 20 AA types. On the other hand, matrix A is an N × N square matrix, where each dimension equals the number of AAs, representing the connections between AAs (1 for connected, 0 for disconnected). Fig. 2(b) illustrates the structure of the GCN model, which includes a GCN for feature extraction from the protein graph, and a dense layer for predicting the A3D dynamic score. The number of dense layers was fixed as 2, and the number of GCN layers varied from 1 to 3 depending on the hyperparameter. The dimension of the GCN layers was maintained constant. The reason for employing shallow and linear GCN layers originated from the consideration that excessive stacking and non-linearity could lead to over-smoothing, which potentially diminishes performance. Given that the number of GCN layers considered is sufficiently small, it is anticipated that the representation of nodes in the GCN process will not converge to a specific value.41,42 The mean squared error (MSE) function was selected as the loss function, with a linear function for the final activation. Batch normalization (BN) was implemented to mitigate internal covariant shift issues, placed after the rectified linear unit (ReLU) activation function.43,44 After the GCN layer, the graph pooling layer was added and the dropout layer was adopted to avoid overfitting. The dense layer also employs ReLU activation functions and the dropout layer. Adaptive moment estimation (Adam) was chosen for the optimizer.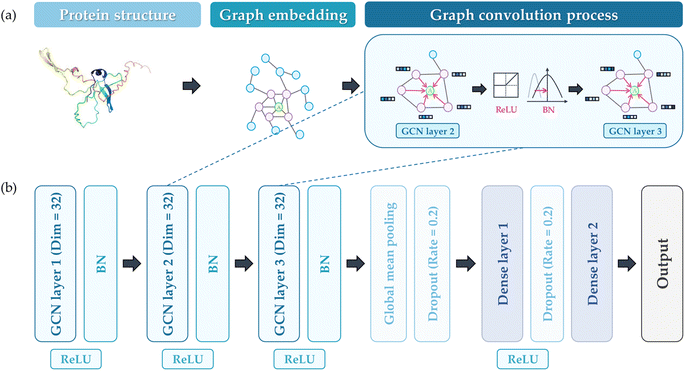 | ||
| Fig. 2 (a) The process of embedding proteins for GCN training, (b) the constructed GCN architecture to predict the output (A3D value). | ||
Hyperparameter tuning
To find the optimal parameters of the GCN model, the extensive hyperparameter combination was investigated using the grid search method. The types and values of explored hyperparameters are listed in Table 1. Three values are explored for each of the six types of hyperparameters, resulting in a total of 729 hyperparameter combinations. It is noted that epoch was not considered in hyperparameter tuning but early stopping was implemented to prevent overfitting. However, to avoid the model being underfitted due to abrupt fluctuations of initial loss values, a minimum of 20 epochs of training was enforced. Subsequently, with a patience setting of 10, the training continued until just before the onset of overfitting, at which point the performance was measured. The number of GCN layers and the pooling method were also utilized as types of hyperparameters.| Hyperparameter | Values |
|---|---|
| Learning rate | [0.001, 0.0005, 0.0001] |
| Dimension | [8, 16, 32] |
| Batch size | [32, 64, 128] |
| Number of GCN layers | [1, 2, 3] |
| Pooling method | [global_add_pool, global_mean_pool, global_max_pool] |
| Dropout rate | [0.0, 0.1, 0.2] |
Active learning process
The primary purpose of active learning in this study is to effectively pinpoint proteins with the highest A3D scores. To accomplish this goal, we have implemented an optimization process that strategically guides the data exploration direction. This is achieved by determining which datasets are prioritized for inclusion in our training set. Several methods are used in the optimization process: exploration based on prediction uncertainty, Efficient Global Optimization (EGO), exploitation utilizing the mean of predicted values, and random selection.First, exploration uses the standard deviation value of predicted values as an acquisition function thus reducing the model's prediction uncertainty. Second, exploitation prioritizes proteins with the highest average predicted A3D scores, and this means the user solely believes in the performance of the surrogate model. Third, efficient global optimization employs an expective improvement (EI) value45 as an acquisition function, which balances exploration and exploitation to prevent biased sampling. Eqn (1) shows how to compute the EI value for a given material x:
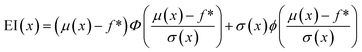 | (1) |
As depicted in Fig. 1(c), we constructed an active learning platform and compared the performances of four different optimization processes: exploration, exploitation, EGO, and random selection. The GCN model is constructed using 80% of the initial database as the training set and the remaining 20% is used as the validation set. A random split of the dataset was performed for cross-validation. Based on 80% of the randomly chosen training set, 20 distinct models were constructed for each iteration of the active learning process. By repeating this process 100 times, the mean and standard deviation of the predicted values were obtained. In each iteration, 200 new entries (about 1% of the hAF 2.0 database) were recommended and thus added to the training set.
Results and discussions
Database construction
The initial database consists of 144![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 768 PDB protein structure (PDB_origin) data for training a graph-based model and 23
768 PDB protein structure (PDB_origin) data for training a graph-based model and 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 391 hAF2.0 data for active learning and model performance validation. The PDB_origin data include thousands of species of protein from Homo sapiens, Mus musculus, and Gallus gallus to synthetically constructed proteins, and exist in a single polypeptide chain (single-chain) or multi polypeptide chain (multi-chain) form.46 In contrast, the hAF2.0 data consists of only single polypeptide chains. It is noted that in single-chain proteins, PA occurs due to interactions between AA within the same polypeptide chain. However, in multi-chain proteins, aggregation arises from interactions between several polypeptide chains. This structural difference, even within the same polypeptide chains, leads to varying tendencies in PA.47 Therefore, it is essential to examine the structural differences and select data that reflects structural variations according to the type. To verify the structural difference within the same polypeptide chains, Fig. S1 (ESI†) represents the box plot of randomly selected protein's A3D score across 12 different protein structures in dynamic mode with the same AA sequence when they exist as sing-polypeptide chains (light blue box), as multi-polypeptide chains (pink box), and when multi-polypeptide chains are divided into single-polypeptide chains (cyan box). Table S1† also represents the average and standard deviation of the A3D score. In Fig. S1,† proteins with the same AA sequences were categorized by the AA lengths plotted at the top of the graph. The pink box represents a single-polypeptide chain that exists within multi-polypeptide chains. Thus, cyan and pink boxes mean the same polypeptide chain but differ depending on whether they exist independently (e.g. 6LML for pink box, 6LML_E for cyan box). When compared to other proteins who have the same AA sequences, most proteins have similar A3D scores and standard deviations. However, for certain proteins (e.g., 6LML, 6TXX), there is a significant difference in mean A3D score when they exist as multi-chains (in 87 AA lengths, −0.3692 average A3D score for 6LML compared to −0.5945 average A3D score for 1KX6 and −0.5820 average A3D score for 6LML_E, and in 378 AA lengths, −0.5698 average A3D score for 6TXX compared to −0.4735 average A3D score for 4TW7 and −0.4942 average A3D score for 6TXX_A). Additionally, some proteins (e.g., 6LML_E, 1D5G_A) show a large standard deviation, indicating that even with the same amino acid sequences, different PA propensities can arise from dynamic changes in the protein structure. Therefore, using various polypeptide chain data from the PDB for predicting PA in single-chain hAF2.0 data, the possibility that even identical AA sequences could adopt different folded states was accounted for. Furthermore, the model's capacity to predict protein aggregation that is not observed in a single-polypeptide chain may improve prediction reliability. In this respect, we separated multi-chain data from the PDB_origin into single-chain and incorporated them into PDB_origin data set as shown in Fig. 3. Initially, the 144
391 hAF2.0 data for active learning and model performance validation. The PDB_origin data include thousands of species of protein from Homo sapiens, Mus musculus, and Gallus gallus to synthetically constructed proteins, and exist in a single polypeptide chain (single-chain) or multi polypeptide chain (multi-chain) form.46 In contrast, the hAF2.0 data consists of only single polypeptide chains. It is noted that in single-chain proteins, PA occurs due to interactions between AA within the same polypeptide chain. However, in multi-chain proteins, aggregation arises from interactions between several polypeptide chains. This structural difference, even within the same polypeptide chains, leads to varying tendencies in PA.47 Therefore, it is essential to examine the structural differences and select data that reflects structural variations according to the type. To verify the structural difference within the same polypeptide chains, Fig. S1 (ESI†) represents the box plot of randomly selected protein's A3D score across 12 different protein structures in dynamic mode with the same AA sequence when they exist as sing-polypeptide chains (light blue box), as multi-polypeptide chains (pink box), and when multi-polypeptide chains are divided into single-polypeptide chains (cyan box). Table S1† also represents the average and standard deviation of the A3D score. In Fig. S1,† proteins with the same AA sequences were categorized by the AA lengths plotted at the top of the graph. The pink box represents a single-polypeptide chain that exists within multi-polypeptide chains. Thus, cyan and pink boxes mean the same polypeptide chain but differ depending on whether they exist independently (e.g. 6LML for pink box, 6LML_E for cyan box). When compared to other proteins who have the same AA sequences, most proteins have similar A3D scores and standard deviations. However, for certain proteins (e.g., 6LML, 6TXX), there is a significant difference in mean A3D score when they exist as multi-chains (in 87 AA lengths, −0.3692 average A3D score for 6LML compared to −0.5945 average A3D score for 1KX6 and −0.5820 average A3D score for 6LML_E, and in 378 AA lengths, −0.5698 average A3D score for 6TXX compared to −0.4735 average A3D score for 4TW7 and −0.4942 average A3D score for 6TXX_A). Additionally, some proteins (e.g., 6LML_E, 1D5G_A) show a large standard deviation, indicating that even with the same amino acid sequences, different PA propensities can arise from dynamic changes in the protein structure. Therefore, using various polypeptide chain data from the PDB for predicting PA in single-chain hAF2.0 data, the possibility that even identical AA sequences could adopt different folded states was accounted for. Furthermore, the model's capacity to predict protein aggregation that is not observed in a single-polypeptide chain may improve prediction reliability. In this respect, we separated multi-chain data from the PDB_origin into single-chain and incorporated them into PDB_origin data set as shown in Fig. 3. Initially, the 144![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 767 PDB_origin protein data has 61
767 PDB_origin protein data has 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 642 single-chain and 83
642 single-chain and 83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 125 multi-chain data. The multi-chain data can be separated into 270
125 multi-chain data. The multi-chain data can be separated into 270![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 605 single polypeptide chains (multi-to-single chains). Then, the single chains with the same sequence are removed, leading to a total of 176
605 single polypeptide chains (multi-to-single chains). Then, the single chains with the same sequence are removed, leading to a total of 176![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 374 multi-to-single chains remaining in the dataset. Finally, from the initial 144
374 multi-to-single chains remaining in the dataset. Finally, from the initial 144![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 768 single or multi-polypeptide chains, a total of 320
768 single or multi-polypeptide chains, a total of 320![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 141 polypeptide chains (PDB_rev) were prepared for GCN model training.
141 polypeptide chains (PDB_rev) were prepared for GCN model training.
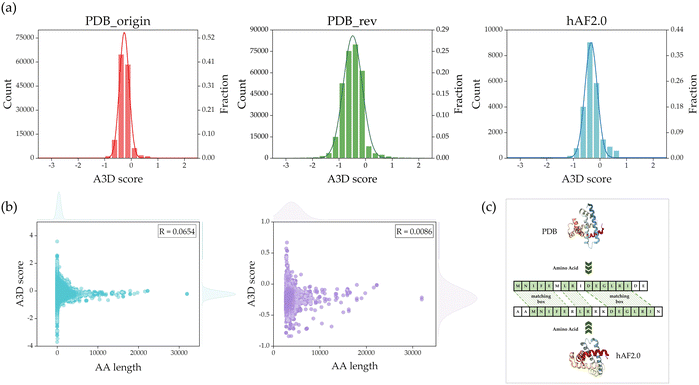
Fig. 4(a) shows the count and fraction weight distributions of A3D scores for PDB_origin, PDB_rev, and hAF2.0 in each dataset. The average A3D scores for PDB_origin, PDB_rev, and hAF2.0 are −0.4915, −0.2604, and −0.2917, respectively, with standard deviations of 0.3912, 0.2040, and 0.3056. As demonstrated in Fig. 4(a), the protein data distribution in the PDB_rev divided dataset closely approximates a normal distribution when compared to the PDB_origin dataset. Compared with the hAF2.0 dataset, the distribution of PDB_rev dataset was more similar to that of PDB_origin. This is a critical consideration in the training process of the GCN model, as an imbalanced data distribution during training could make the model sensitive to specific patterns or outliers, posing challenges for achieving optimal performance and generalization.48 In the process of A3D calculations, protein structures that contained non-standard amino acids due to residue deformations had excessively short sequence lengths or did not converge within 100 steps in the dynamic mode's CABS-flex simulation were removed from the final database. As a result, a total of 304![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 059 PDB datasets were used as the final database for this study.
059 PDB datasets were used as the final database for this study.
Fig. S2† shows a box plot of the AA length for the PDB_rev data and for those in PDB_rev with an AA length of over 2700. The average length of AA in the entire PDB_rev data is 434.522, with the longest protein having an AA length of 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 018. It was observed that the average value of the lower 75% of data is 493, indicating that some proteins have exceptionally long AA lengths. In the case of AlphaFold2.0 protein data, for AA longer than 2,700, the protein data is divided into multiple overlapping fragments, and each structure is predicted separately to address exceptionally long AA proteins. It is challenging to predict the entire structure at once when a specific protein has such a long AA length, and it also demands a high computational cost for training the GCN model. In this regard, we applied the method used in AlphaFold to reduce computational costs by removing PDB_rev data with over 2700 AA.
018. It was observed that the average value of the lower 75% of data is 493, indicating that some proteins have exceptionally long AA lengths. In the case of AlphaFold2.0 protein data, for AA longer than 2,700, the protein data is divided into multiple overlapping fragments, and each structure is predicted separately to address exceptionally long AA proteins. It is challenging to predict the entire structure at once when a specific protein has such a long AA length, and it also demands a high computational cost for training the GCN model. In this regard, we applied the method used in AlphaFold to reduce computational costs by removing PDB_rev data with over 2700 AA.
Before removing the data, if there is a significant correlation between AA and PA, removed data could impact the prediction of PA. Therefore, the correlation between AA and PA was examined. In Fig. 4(b), scatter plots are shown based on AA length and A3D score. In Fig. 4(b), the left represents the distribution of the PDB_rev data that was used as the final database after the previous steps. A Pearson correlation (R) analysis showed that there is no significant correlation (R = 0.0654) between AA length and A3D score. In addition, Fig. 4(b), right shows the scatter plot of AA length and A3D scores with AA lengths exceeding 2700 proteins, among 304![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 059 data, and its R value is 0.0086. Consequently, this observation led to the conclusion that there is no meaningful correlation between AA length and PA. This justifies that the length of AA does not significantly impact PA. After excluding 2027 entries with AA lengths exceeding 2,700, we established a final dataset comprising 302
059 data, and its R value is 0.0086. Consequently, this observation led to the conclusion that there is no meaningful correlation between AA length and PA. This justifies that the length of AA does not significantly impact PA. After excluding 2027 entries with AA lengths exceeding 2,700, we established a final dataset comprising 302![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 032 entries for the PDB database. Notably, the exclusion of data led to a significant reduction in the GCN model's training time, decreasing from approximately 1400 seconds per epoch to about 500 seconds per epoch when using one RTX3090 GPU.
032 entries for the PDB database. Notably, the exclusion of data led to a significant reduction in the GCN model's training time, decreasing from approximately 1400 seconds per epoch to about 500 seconds per epoch when using one RTX3090 GPU.
Sequence similarity
When the sequences of protein polypeptide chains are similar, there is a higher likelihood that the physical and chemical properties of the proteins are also comparable. In the training process, a high degree of similarity between the training and validation data would lead to overfitting the GCN models. To address this issue, a comparison of protein sequence similarity between the PDB_rev and hAF2.0 was performed as shown in Fig. 4(c). Firstly, each sequence of proteins was extracted from PDB and hAF2.0 data, and each of the sequences is aligned such that two or more consecutive AA form a matching box, resulting in a match. The sequence similarity is calculated through Q = 2 × Nmatch/Lsequence, where Nmatch represents the total number of AA forming the matching box, and Lsequence is the total sum of the AA count in the two compared sequences. Table 2 represents the results of comparing sequence similarity, indicating that as the similarity increases by 10%, approximately 400 proteins share that level of similarity. It is noted that proteins with a similarity threshold of 80% were removed from the hAF2.0 data. This process led to the removal of 1518 Homo sapiens protein data. As a result, 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 873 Homo sapiens protein data were used as the final test data.
873 Homo sapiens protein data were used as the final test data.
| Similarity (%) | Count |
|---|---|
| 50 | 2973 |
| 60 | 2385 |
| 70 | 1916 |
| 80 | 1518 |
Hyperparameter tuning
After the hyperparameter tuning, the learning rate: 0.0005, dimension: 32, batch size: 64, number of convolution layers: 3, pooling method: global_mean_pool, and dropout rate: 0.2 were confirmed as an optimal hyperparameter combination in Table 1. With the selected hyperparameter combination, an R2 score of 0.9525 and an MAE of 0.0338 were achieved for the training dataset (PDB_rev). All the hyperparameter combinations and their performance are provided as a separate CSV file in ESI.‡ To identify the dependency of each parameter (learning rate, dimension, batch size, number of GCN layers, pooling method, and dropout rate), the hyperparameter of the top ten percent (72) models was analyzed. It is noteworthy that all the top ten percent of models adopt global_mean_pool as their pooling method. It demonstrates that the choice of graph pooling method plays a significant role in performance enhancement and that the global_mean_pool method is the most suitable. In addition, as shown in Fig. S3,† the developed GCN architecture shows a tendency to be sensitive to learning rate and dimension, while demonstrating less sensitivity towards the other hyperparameters. From these results, it is believed that determining optimal values of the learning rate and the dimension is the most significant to achieving the best performance.Validation of generalization performance
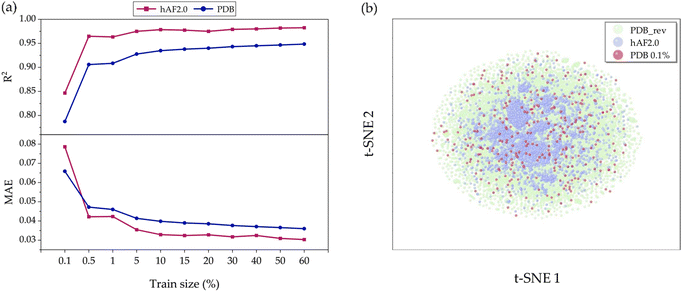
To validate the model's generalization, we constructed a predictive model, aiming to investigate the sensitivity of prediction uncertainty with varying training set sizes. As depicted in Fig. 5(a) it is generally observed that smaller training sets tend to degrade the performance in predicting the test set. Fig. S3(a) and (b)† show detailed results for how each true versus predicted A3D score is distributed when the training set ratio is 80% and 0.1%, respectively. In Fig. 5(a), it is observed that as the training set range increases from 0.1% (302 structures) to 60% (181![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 219 structures), the R2 value is still unexpectedly high at about 0.78 and achieves a high performance above 0.96 in both the PDB_rev and hAF 2.0 databases. In other words, we demonstrate that only 0.1% of the total database is used for training, and the trained model can predict the remaining 99.9% with low MAE values of 0.067 and 0.079 for PDB_rev and hAF 2.0, respectively, despite the large error rate shown in Fig. S4.† This is possible because when the training set is randomly selected from the entire database structure, there is a likelihood of including proteins with high A3D scores, as the training domain is not limited to a specific range of values as shown in Fig. S5.† Consequently, this largely reduces the extrapolation risk, which is often the most vulnerable aspect of ML models, thereby enhancing prediction accuracy and generalizability. Therefore, the constructed prediction model can be utilized as a rough screening tool. As shown in Table S2,† while A3D typically requires 21
219 structures), the R2 value is still unexpectedly high at about 0.78 and achieves a high performance above 0.96 in both the PDB_rev and hAF 2.0 databases. In other words, we demonstrate that only 0.1% of the total database is used for training, and the trained model can predict the remaining 99.9% with low MAE values of 0.067 and 0.079 for PDB_rev and hAF 2.0, respectively, despite the large error rate shown in Fig. S4.† This is possible because when the training set is randomly selected from the entire database structure, there is a likelihood of including proteins with high A3D scores, as the training domain is not limited to a specific range of values as shown in Fig. S5.† Consequently, this largely reduces the extrapolation risk, which is often the most vulnerable aspect of ML models, thereby enhancing prediction accuracy and generalizability. Therefore, the constructed prediction model can be utilized as a rough screening tool. As shown in Table S2,† while A3D typically requires 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240 seconds to complete (over 12 calculations), the GCN model only takes 0.5 seconds during inference after training. This means that the GCN model can predict protein aggregation approximately 42
240 seconds to complete (over 12 calculations), the GCN model only takes 0.5 seconds during inference after training. This means that the GCN model can predict protein aggregation approximately 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 times faster than A3D, making it highly efficient.
480 times faster than A3D, making it highly efficient.
To further verify the origin of such superior performance, we conducted a t-SNE49 analysis. As seen in Fig. 5(b), the data distribution of the PDB_rev (green points) encompasses and is more diverse than that of hAF 2.0 (blue points). This explains why the predictive performance for hAF 2.0 (test data) is better than that for PDB to the most of training set ratios. In other words, the current GCN model could perform better due to being trained on more comprehensive data. Additionally, even though the number of data points (red points) in the 0.1% training set is limited, they are evenly distributed over the green area and not biased towards one side; thus, such behavior leads to an increase in the generalization performance.
Performance of active learning
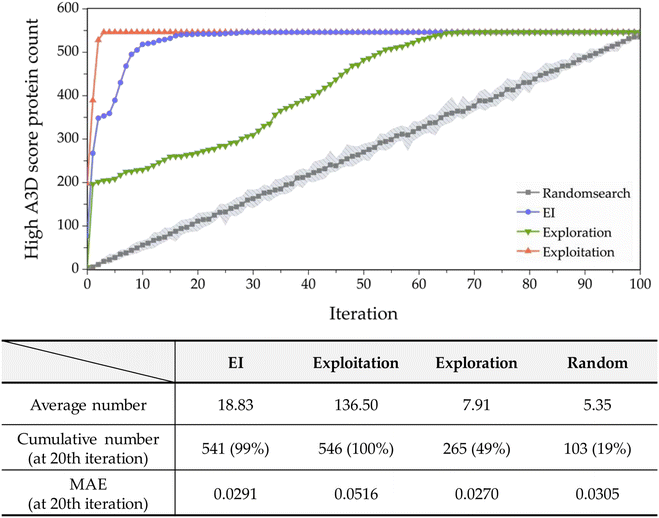
In most studies that aim to build a predictive model, starting with an extensive database is not common. Moreover, the values in the constructed databases are often not uniformly distributed and frequently lack sufficient data to represent the targeted chemical space adequately. Biased or unbalanced data distributions in available databases can complicate the construction of machine learning predictive models. Therefore, in this study, to validate the practical functionality of active learning, we chose the dataset whose predictive performance is the least among the 20 conducted with a 0.1% training set ratio, as shown in Fig. S6.† The performance of this model exhibits an R2 of 0.1870 and an MAE of 0.2870 with an A3D score ranging from −1.2903 to 0.5. Such a dataset suggests that while the initial predictive model may perform reasonably within the trained areas, it fails outside these regions like high A3D score (A3D score ≥ 0.5), leading to extrapolation.The performance of the implemented active learning is evaluated in Fig. 6 by comparing the cumulative number of structures satisfying the criteria within the target domain (A3D score ≥ 0.5). As shown in Fig. 6, EI, exploration, and exploitation strategies outperform random search. At the 20th iteration, the EI approach identified 541 target proteins via active learning, accounting for 99% of the hAF 2.0 database's 546 entire proteins. Furthermore, using the EI strategy, on average, approximately 18.83 proteins are obtained with each iteration up to the 20th cycle. In terms of MAE, exploration, and EI optimization methods surpass random, but exploitation is not satisfactory. In addition, EI identifies fewer target proteins in a shorter time compared to the exploitation strategy but shows more accurate prediction performance with an MAE of 0.0291. These results confirm that EI is an efficient optimization method with good prediction performance in a smaller number of trials to effectively identify proteins with high PA properties.
Moreover, exploitation theoretically should prioritize the highest A3D score to rapidly identify proteins. As presented in Fig. 6, exploitation found all the target proteins during four iterations, and it is more efficient than any optimization process. However, as mentioned earlier, the prediction performance (MAE) is 0.0516, which is the lowest among the five methods.
Next, in the case of exploration, 7.91 target proteins were selected on average, and a total of 265 structures (49% of the total space) were selected at the 20th iteration. This acquisition function is better than random search, but worse than EI and exploitation. Although this is far from what we are aiming for (finding proteins with high A3D scores), it is still important to note that the prediction performance is the best (MAE of 0.027) among all acquisition functions. As discussed before, this is likely due to the addition of proteins with a larger predictive uncertainty.
Conclusions
This study presents the development and evaluation of a new GCN model for predicting PA, a phenomenon associated with various diseases, including neurodegenerative disorders like Alzheimer's and Parkinson's disease. The advancement in predicting such phenomena is highlighted. The dataset, enhanced with data from the RCSB PDB and AlphaFold2.0, includes 302![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 032 unique PDB entries and 22
032 unique PDB entries and 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774 Homo sapiens data. The GCN model, trained on this dataset, achieved high accuracy in PA prediction, with a coefficient of determination (R2) of 0.99 and a low MAE. Developed GCN model effectively identified proteins with a high propensity for PA through an active learning approach, successfully predicting 99% of PA by exploring only 29% of the entire search space. This achievement surpasses previous methods and significantly contributes to protein science. Integration of structural information from PDB and AlphaFold2.0 underscores the necessity for ML models that consider protein structure, enhancing PA prediction accuracy. The developed GCN model emerges as an invaluable tool for selecting proteins susceptible to PA, offering significant applications in protein science, and the diagnosis and treatment of related diseases.
774 Homo sapiens data. The GCN model, trained on this dataset, achieved high accuracy in PA prediction, with a coefficient of determination (R2) of 0.99 and a low MAE. Developed GCN model effectively identified proteins with a high propensity for PA through an active learning approach, successfully predicting 99% of PA by exploring only 29% of the entire search space. This achievement surpasses previous methods and significantly contributes to protein science. Integration of structural information from PDB and AlphaFold2.0 underscores the necessity for ML models that consider protein structure, enhancing PA prediction accuracy. The developed GCN model emerges as an invaluable tool for selecting proteins susceptible to PA, offering significant applications in protein science, and the diagnosis and treatment of related diseases.
Future researchers could build upon this work by exploring several avenues to further refine and expand the capabilities of the GCN model. One potential direction is the fine-tuning of the GCN model with more specific experimental datasets, particularly those that exclude intrinsically disordered proteins/peptides (IDPs).50 Numerous studies have already reported that IDPs lack stable and well-defined structures, making it challenging for AlphaFold to accurately predict their structures.51,52 Consequently, the inclusion of IDPs in the hAF 2.0 database used in this study could impact the GCN model's accuracy in predicting protein aggregation propensity. Addressing this challenge is crucial for improving the model's predictive accuracy, but it also presents significant difficulties. Therefore, future researchers could consider constructing an hAF 2.0 database that excludes IDPs and retraining the GCN model to enhance its accuracy in predicting protein aggregation (PA).
In addition, performance could be further improved by employing advanced machine learning techniques. For example, incorporating semi-supervised learning techniques, such as positive-unlabeled (PU) learning, could further improve prediction accuracy, particularly in situations where labeled data is scarce or imbalanced.53 Moreover, expanding the dataset to include a wider variety of protein types and environmental conditions could make the GCN model even more versatile and applicable to a broader range of biological contexts. These future enhancements would not only improve the current model's performance but also broaden its application scope, ultimately it could serve as an important tool for efficiently predicting PA before experiments by reducing the costs and time with reliability. This advancement could significantly contribute to the development of more effective diagnostic and therapeutic strategies for PA-related diseases.
Data availability
The source code, partial train data, and example notebooks of AP value prediction GCN model are available at https://github.com/sunjiwon/2APGCNN.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2022R1F1A1074339, No. 2022R1C1C1009387). This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2021R1A6A1A10044154).References
- A. M. Morris, M. A. Watzky and R. G. Finke, Protein Aggregation Kinetics, Mechanism, and Curve-Fitting: A Review of the Literature, Biochim. Biophys. Acta, Proteins Proteomics, 2009, 1794(3), 375–397, DOI:10.1016/j.bbapap.2008.10.016.
- J. A. J. Housmans, G. Wu, J. Schymkowitz and F. Rousseau, A Guide to Studying Protein Aggregation, FEBS J., 2023, 290(3), 554–583 CrossRef CAS PubMed.
- E. Lévy, N. El Banna, D. Baïlle, A. Heneman-Masurel, S. Truchet, H. Rezaei, M. E. Huang, V. Béringue, D. Martin and L. Vernis, Causative Links between Protein Aggregation and Oxidative Stress: A Review, Int. J. Mol. Sci., 2019, 20(16), 3896, DOI:10.3390/ijms20163896.
- A. J. Espay, J. A. Vizcarra, L. Marsili, A. E. Lang, D. K. Simon, A. Merola, K. A. Josephs, A. Fasano, F. Morgante, R. Savica, J. T. Greenamyre, F. Cambi, T. R. Yamasaki, C. M. Tanner, Z. Gan-Or, I. Litvan, I. F. Mata, C. P. Zabetian, P. Brundin, H. H. Fernandez, D. G. Standaert, M. A. Kauffman, M. A. Schwarzschild, S. P. Sardi, T. Sherer, G. Perry and J. B. Leverenz, Revisiting Protein Aggregation as Pathogenic in Sporadic Parkinson and Alzheimer Diseases, Neurology, 2019, 92(7), 329–337, DOI:10.1212/WNL.0000000000006926.
- C. A. Ross and M. A. Poirier, Protein Aggregation and Neurodegenerative Disease, Nat. Med., 2004, 10(7), S10–S17, DOI:10.1038/nm1066.
- M. Jouanne, S. Rault and A. S. Voisin-Chiret, Tau Protein Aggregation in Alzheimer's Disease: An Attractive Target for the Development of Novel Therapeutic Agents, Eur. J. Med. Chem., 2017, 139, 153–167, DOI:10.1016/J.EJMECH.2017.07.070.
- G. Invernizzi, E. Papaleo, R. Sabate and S. Ventura, Protein Aggregation: Mechanisms and Functional Consequences, Int. J. Biochem. Cell Biol., 2012, 44(9), 1541–1554, DOI:10.1016/J.BIOCEL.2012.05.023.
- G. B. Irvine, O. M. El-Agnaf, G. M. Shankar and D. M. Walsh, Protein Aggregation in the Brain: The Molecular Basis for Alzheimer's and Parkinson's Diseases, Mol. Med., 2008, 14(7), 451–464, DOI:10.2119/2007-00100.IRVINE.
- C. J. Roberts, Therapeutic Protein Aggregation: Mechanisms, Design, and Control, Trends Biotechnol., 2014, 32(7), 372–380, DOI:10.1016/J.TIBTECH.2014.05.005.
- H. C. Mahler, W. Friess, U. Grauschopf and S. Kiese, Protein Aggregation: Pathways, Induction Factors and Analysis, J. Pharm. Sci., 2009, 98(9), 2909–2934, DOI:10.1002/JPS.21566.
- D. R. Thal and M. Fändrich, Protein Aggregation in Alzheimer's Disease: Aβ and τ and Their Potential Roles in the Pathogenesis of AD, Acta Neuropathol., 2015, 129(2), 163–165, DOI:10.1007/S00401-015-1387-2/FIGURES/1.
- L. Dumery, F. Bourdel, Y. Soussan, A. Fialkowsky, S. Viale, P. Nicolas and M. Reboud-Ravaux, β-Amyloid Protein Aggregation: Its Implication in the Physiopathology of Alzheimer's Disease, Pathol. Biol., 2001, 49(1), 72–85, DOI:10.1016/S0369-8114(00)00009-2.
- B. Frka-Petesic, D. Zanchi, N. Martin, S. Carayon, S. Huille and C. Tribet, Aggregation of Antibody Drug Conjugates at Room Temperature: SAXS and Light Scattering Evidence for Colloidal Instability of a Specific Subpopulation, Langmuir, 2016, 32(19), 4848–4861, DOI:10.1021/ACS.LANGMUIR.6B00653/SUPPL_FILE/LA6B00653_SI_001.PDF.
- T. I. Chandel, M. Zaman, M. V. Khan, M. Ali, G. Rabbani, M. Ishtikhar and R. H. Khan, A Mechanistic Insight into Protein-Ligand Interaction, Folding, Misfolding, Aggregation and Inhibition of Protein Aggregates: An Overview, Int. J. Biol. Macromol., 2018, 106, 1115–1129, DOI:10.1016/J.IJBIOMAC.2017.07.185.
- A. Morriss-Andrews and J. E. Shea, Computational Studies of Protein Aggregation: Methods and Applications, Annu. Rev. Phys. Chem., 2015, 66(1), 643–666, DOI:10.1146/annurev-physchem-040513-103738.
- L. Keresztes, E. Szögi, B. Varga, V. Farkas, A. Perczel and V. Grolmusz, The Budapest Amyloid Predictor and Its Applications, Biomolecules, 2021, 11(4), 500, DOI:10.3390/BIOM11040500.
- G. G. Tartaglia and M. Vendruscolo, The Zyggregator Method for Predicting Protein Aggregation Propensities, Chem. Soc. Rev., 2008, 37(7), 1395–1401, 10.1039/B706784B.
- C. Kim, J. Choi, S. J. Lee, W. J. Welsh and S. Yoon, NetCSSP: Web Application for Predicting Chameleon Sequences and Amyloid Fibril Formation, Nucleic Acids Res., 2009, 37(suppl_2), W469–W473, DOI:10.1093/NAR/GKP351.
- C. Família, S. R. Dennison, A. Quintas and D. A. Phoenix, Prediction of Peptide and Protein Propensity for Amyloid Formation, PLoS One, 2015, 10(8), e0134679, DOI:10.1371/JOURNAL.PONE.0134679.
- S. O. Garbuzynskiy, M. Y. Lobanov and O. V. Galzitskaya, FoldAmyloid: A Method of Prediction of Amyloidogenic Regions from Protein Sequence, Bioinformatics, 2010, 26(3), 326–332, DOI:10.1093/BIOINFORMATICS/BTP691.
- P. Gasior and M. Kotulska, FISH Amyloid - a New Method for Finding Amyloidogenic Segments in Proteins Based on Site Specific Co-Occurrence of Aminoacids, BMC Bioinf., 2014, 15(1), 1–8, DOI:10.1186/1471-2105-15-54/TABLES/3.
- S. Navarro and S. Ventura, Computational Methods to Predict Protein Aggregation, Curr. Opin. Struct. Biol., 2022, 73, 102343, DOI:10.1016/J.SBI.2022.102343.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek, A. Potapenko, A. Bridgland, C. Meyer, S. A. A. Kohl, A. J. Ballard, A. Cowie, B. Romera-Paredes, S. Nikolov, R. Jain, J. Adler, T. Back, S. Petersen, D. Reiman, E. Clancy, M. Zielinski, M. Steinegger, M. Pacholska, T. Berghammer, S. Bodenstein, D. Silver, O. Vinyals, A. W. Senior, K. Kavukcuoglu, P. Kohli and D. Hassabis, Highly Accurate Protein Structure Prediction with AlphaFold, Nature, 2021, 596(7873), 583–589, DOI:10.1038/s41586-021-03819-2.
- A. W. Senior, R. Evans, J. Jumper, J. Kirkpatrick, L. Sifre, T. Green, C. Qin, A. Žídek, A. W. R. Nelson, A. Bridgland, H. Penedones, S. Petersen, K. Simonyan, S. Crossan, P. Kohli, D. T. Jones, D. Silver, K. Kavukcuoglu and D. Hassabis, Improved Protein Structure Prediction Using Potentials from Deep Learning, Nature, 2020, 577(7792), 706–710, DOI:10.1038/s41586-019-1923-7.
- B. Kuhlman and P. Bradley, Advances in Protein Structure Prediction and Design, Nat. Rev. Mol. Cell Biol., 2019, 20(11), 681–697, DOI:10.1038/s41580-019-0163-x.
- D. E. Kim, D. Chivian and D. Baker, Protein Structure Prediction and Analysis Using the Robetta Server, Nucleic Acids Res., 2004, 32(suppl_2), W526–W531, DOI:10.1093/NAR/GKH468.
- W. Ma, S. Zhang, Z. Li, M. Jiang, S. Wang, W. Lu, X. Bi, H. Jiang, H. Zhang and Z. Wei, Enhancing Protein Function Prediction Performance by Utilizing AlphaFold-Predicted Protein Structures, J. Chem. Inf. Model., 2022, 62(17), 4008–4017, DOI:10.1021/ACS.JCIM.2C00885/SUPPL_FILE/CI2C00885_SI_001.PDF.
- H. Keskin Karakoyun, Ş. K. Yüksel, I. Amanoglu, L. Naserikhojasteh, A. Yeşilyurt, C. Yakıcıer, E. Timuçin and C. B. Akyerli, Evaluation of AlphaFold Structure-Based Protein Stability Prediction on Missense Variations in Cancer, Front. Genet., 2023, 14, 1052383, DOI:10.3389/FGENE.2023.1052383/BIBTEX.
- P. Ma, D. W. Li and R. Brüschweiler, Predicting Protein Flexibility with AlphaFold, Proteins: Struct., Funct., Bioinf., 2023, 91(6), 847–855, DOI:10.1002/PROT.26471.
- R. Zambrano, M. Jamroz, A. Szczasiuk, J. Pujols, S. Kmiecik and S. Ventura, AGGRESCAN3D (A3D): Server for Prediction of Aggregation Properties of Protein Structures, Nucleic Acids Res., 2015, 43(W1), W306–W313, DOI:10.1093/NAR/GKV359.
- P. Smialowski, A. J. Martin-Galiano, A. Mikolajka, T. Girschick, T. A. Holak and D. Frishman, Protein Solubility: Sequence Based Prediction and Experimental Verification, Bioinformatics, 2007, 23(19), 2536–2542, DOI:10.1093/BIOINFORMATICS/BTL623.
- C. N. Magnan, A. Randall and P. Baldi, SOLpro: Accurate Sequence-Based Prediction of Protein Solubility, Bioinformatics, 2009, 25(17), 2200–2207, DOI:10.1093/BIOINFORMATICS/BTP386.
- V. Voynov, N. Chennamsetty, V. Kayser, B. Helk and B. L. Trout, Predictive Tools for Stabilization of Therapeutic Proteins, mAbs, 2009, 1(6), 580, DOI:10.4161/MABS.1.6.9773.
- A. Tosstorff, H. Svilenov, G. H. J. Peters, P. Harris and G. Winter, Structure-Based Discovery of a New Protein-Aggregation Breaking Excipient, Eur. J. Pharm. Biopharm., 2019, 144, 207–216, DOI:10.1016/J.EJPB.2019.09.010.
- S. Kang, M. Kim, J. Sun, M. Lee and K. Min, Prediction of Protein Aggregation Propensity via Data-Driven Approaches, ACS Biomater. Sci. Eng., 2023, 9(11), 6451–6463, DOI:10.1021/ACSBIOMATERIALS.3C01001/SUPPL_FILE/AB3C01001_SI_002.ZIP.
- E. N. Gasu, J. K. Mensah and L. S. Borquaye, Computer-Aided Design of Proline-Rich Antimicrobial Peptides Based on the Chemophysical Properties of a Peptide Isolated from Olivancillaria Hiatula, J. Biomol. Struct. Dyn., 2023, 41(17), 8254–8275, DOI:10.1080/07391102.2022.2131626.
- J. Schymkowitz, J. Borg, F. Stricher, R. Nys, F. Rousseau and L. Serrano, The FoldX Web Server: An Online Force Field, Nucleic Acids Res., 2005, 33(suppl_2), W382–W388, DOI:10.1093/NAR/GKI387.
- M. Jamroz, A. Kolinski and S. Kmiecik, CABS-Flex: Server for Fast Simulation of Protein Structure Fluctuations, Nucleic Acids Res., 2013, 41(W1), W427–W431, DOI:10.1093/NAR/GKT332.
- T. N. Kipf and M. Welling, Semi-Supervised Classification with Graph Convolutional Networks, 5th Int. Conf. Learn. Represent. ICLR 2017 - Conf. Track Proc., 2016 Search PubMed.
- M. Fey and J. E. Lenssen, Fast Graph Representation Learning with PyTorch Geometric, arXiv, 2019, preprint, arXiv:1903.02428, DOI:10.48550/arXiv.1903.02428.
- M. Chen, Z. Wei, Z. Huang, B. Ding and Y. Li, Simple and Deep Graph Convolutional Networks, Proceedings of the 37th International Conference on Machine Learning, PMLR, 2020, vol. 119, pp. 1725–1735, https://proceedings.mlr.press/v119/chen20v.html Search PubMed.
- Q. Li, Z. Han and X. M. Wu, Deeper Insights into Graph Convolutional Networks for Semi-Supervised Learning, 32nd AAAI Conf. Artif. Intell. AAAI 2018, 2018, pp. 3538–3545, DOI:10.1609/aaai.v32i1.11604.
- S. Ioffe and C. Szegedy, Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift, 32nd Int. Conf. Mach. Learn. ICML 2015, 2015, vol. 1, pp. 448–456 Search PubMed.
- A. M. Fred Agarap, Deep Learning Using Rectified Linear Units (ReLU), arXiv, 2018, preprint, arXiv:1803.08375, DOI:10.48550/arXiv.1803.08375.
- D. R. Jones, M. Schonlau and W. J. Welch, Efficient Global Optimization of Expensive Black-Box Functions, J. Global Optim., 1998, 13(4), 455–492, DOI:10.1023/A:1008306431147/METRICS.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, The Protein Data Bank, Nucleic Acids Res., 2000, 28(1), 235–242, DOI:10.1093/NAR/28.1.235.
- K. Leonhard, J. M. Prausnitz and C. J. Radke, Solvent–Amino Acid Interaction Energies in 3-D-Lattice MC Simulations of Model Proteins. Aggregation Thermodynamics and Kinetics, Phys. Chem. Chem. Phys., 2003, 5(23), 5291–5299, 10.1039/B305414D.
- Z. Szabó, B. K. Sriperumbudur, M. Learning and A. Gretton, Learning Theory for Distribution Regression, J. Mach. Learn. Res., 2016, 17, 1–40 Search PubMed.
- P. Hajibabaee, F. Pourkamali-Anaraki and M. A. Hariri-Ardebili, An Empirical Evaluation of the T-SNE Algorithm for Data Visualization in Structural Engineering, Proc. - 20th IEEE Int. Conf. Mach. Learn. Appl. ICMLA 2021, 2021, pp. 1674–1680, DOI:10.1109/ICMLA52953.2021.00267.
- N. Brandes, D. Ofer, Y. Peleg, N. Rappoport and M. Linial, ProteinBERT: A Universal Deep-Learning Model of Protein Sequence and Function, Bioinformatics, 2022, 38(8), 2102–2110, DOI:10.1093/BIOINFORMATICS/BTAC020.
- B. Strodel, Energy Landscapes of Protein Aggregation and Conformation Switching in Intrinsically Disordered Proteins, J. Mol. Biol., 2021, 433(20), 167182, DOI:10.1016/J.JMB.2021.167182.
- K. M. Ruff and R. V. Pappu, AlphaFold and Implications for Intrinsically Disordered Proteins, J. Mol. Biol., 2021, 433(20), 167208, DOI:10.1016/J.JMB.2021.167208.
- C. Kılıç and M. Tan, Positive Unlabeled Learning for Deriving Protein Interaction Networks, Netw. Model. Anal. Health Inform. Bioinform., 2012, 1(3), 87–102, DOI:10.1007/S13721-012-0012-8/TABLES/6.
Footnotes |
| † Electronic supplementary information (ESI) available: Hyperparameter tuning result of hAF2.0, Hyperparameter tuning result of PDB, Box plot of AA length for PDB_rev data and PDB_rev data, hyperparameter of top ten percent models, comparison of predicted versus calculated A3D score value and their accuracy, performance of different train size, A3D score distribution from PDB_rev and selected PDB for 0.1% datasets. See DOI: https://doi.org/10.1039/d4ra06285j |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |