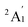Boron-doped scandium clusters B@Sc_n−1^−/0/+ with n = 2–13: uncovering the smallest endohedrally doped cages

Abstract

A comprehensive study using density functional theory with the PBE functional and the Def2-TZVP basis set investigates the pure Sc_n^+/0/− and doped Sc_n−1B^+/0/− clusters with n = 1–13 in three charged states. B@Sc₆^+/0/− clusters emerge as the smallest doped cages identified so far, distinguished by their near-perfect octahedral geometry, with a B atom centrally enclosed in the Sc₆^+/0/− cages. Structural analysis reveals size-dependent trends, with a critical size at n = 6, marking a transition from exohedral to endohedral configuration, and a shift in the substitution-addition pattern of the B atom within the pure Sc host. Incorporation of a B atom induces electron redistribution, stabilizes high spin states and reduces energetic degeneracy. B-doping enhances the stability of the initial Sc_n^+/0/− clusters, showing a consistent preference for cationic isomers. A molecular orbital (MO) analysis provides a detailed explanation for the observed energy degeneracy among various stable spin states by delving into their electronic configurations.

---

1. Introduction

There has been a remarkable surge of interest in small transition metal (TM) clusters, both in their pure form and when they are modified by other elements. This continuing enthusiasm is due not only to their well-known optical¹ and magnetic properties,^2,3 that are all size-dependent,^1,4 but also because of their versatility as catalysts in various chemical processes including the current challenges of renewable energy such as hydrogen storage^5–8 and CO₂ reduction.^9,10

However, identification of the global ground state of a TM cluster, even for a lighter element such as scandium, presents a considerable challenge for both theoretical and experimental approaches.^11,12 This difficulty arises from the presence of multiple quasi-degenerate isomers, each having a distinct spin magnetic moment, but which are closely matched in energy.

The scandium atom, despite its relatively simple electron configuration of [4s² 3d¹], where it features just one unpaired 3d electron, reveals unexpected complexity in the spin states of scandium clusters (Sc_n), even at very small sizes, such as the Sc₂ dimer,^11,13–21 and Sc₃ trimer.^14,22 This complexity becomes more pronounced as the number of flexible open-shell 3d electrons increases with the growing size of scandium clusters, leading to multiple high-spin states possessing different geometric structures but similar energy levels.¹⁸

In the field of atomic clusters, one effective strategy to potentially enhance or modify their properties, or to address inherent challenges, is the doping, wherein other elements are introduced into the cluster.^23,24 Doping can fundamentally influence the properties and behavior of nanoclusters, making it a valuable technique for customizing their characteristics to suit some specific applications or to overcome intrinsic limitations of the pure clusters.^23,25 For TM clusters, a doping can involve the incorporation of both metal and non-metal elements. Concerning the scandium clusters, as far as we know, only a limited number of studies, both experimental and theoretical, have been reported on pure and doped scandium clusters. Such a relative lack of investigation implies an insufficient understanding on this class of atomic clusters.

In previous studies, the potential applications of scandium-boron combinations have been explored, specifically in the form of scandium-doped boron clusters, with a particular emphasis on their possible use in hydrogen storage.^8,26 Furthermore, inclusion of scandium as a dopant induces a remarkable ability to stabilize the geometric configurations with high symmetry of boron cages. The structural arrangement of Sc-doped boron clusters Sc@B_n^0/− with n going from 10 to 20 undergoes a remarkable transition from a half-sandwich configuration to a drum-like shape, with a central location of the scandium atom.²⁷ These doped clusters usually adopt a cage-like topology. An intriguing discovery was the identification of the neutral Sc@B₁₃ cluster which was assigned as a magic cluster.²⁷ Additionally, a larger and nearly perfect boron box Sc₂@B₂₇⁺ was characterized by its distinctive triple-ring tubular shape featuring a high D_9h point group symmetry.²⁸ This tubular structure is formed through an antiprism interconnection of three B₉ strings, and the resulting box is capped by an Sc–Sc dimer, vertically placed at the center along the axis of the tubular box.²⁸

In this context, the concept of introducing an inverse doping by placing a boron atom inside a Sc_n cage constitutes a legitimate idea. This raises the questions as to whether the boron dopant could occupy the interior of the Sc_n cage preferentially, and whether such an endohedral arrangement can thermodynamically stabilize the Sc_n cage. Given the number of valent electrons [2s² 2p¹] in a boron atom is quite similar to that of [4s² 3d¹] in a scandium atom, some intriguing properties are expected to emerge, reminiscent of the cases of the isovalent B_x@Al_y (ref. 29–31) and Al_x@Sc_y clusters.^25,32,33

With the aim to delve deeper into this concept and identify the specific conditions under which boron atom would preferentially occupy a position inside a scandium cage, along with the necessary size criteria, we set out to carry out an extensive theoretical and computational study on the singly boron doped scandium clusters. Given that previous studies of Sajjad et al., Bhunia et al. and Li et al. only theoretically investigated the neutral Sc_n clusters using less accurate quantum chemical methods by combining DFT functional with small basis sets such as CEP-121 G, LANL2DZ, and LANL2MB,^19,20,34 except for the dimer Sc₂ and trimer Sc₃, we set out to provide in the present study a more comprehensive re-investigation. It focuses on scandium clusters Sc_n with n = 2–13 with across the cationic, neutral, and anionic charge states, utilizing a higher-level quantum chemical method. Subsequently, our study advances to determine the structures of singly boron-doped scandium clusters Sc_n−1B^+/0/− having the same size n = 2–13, also in three different charge states. This comprehensive investigation also takes the electronic and magnetic properties into account, as well as the growth patterns of both pure and boron-doped Sc clusters.

2. Computational methods

All standard electronic structure calculations are performed using the Gaussian 16 set of programs.³⁵ In previous investigations encompassing both pure scandium and boron systems, as well as mixed scandium-boron clusters, the utilization of the density functionals such as the PBE,^36,37 B3PW91,^38,39 BP86,^40,41 TPSSh⁴² and M05 ^43,44 has yielded consistent and appropriate results.^{8,11,19,20,28,34,45–50} To maintain a consistency to enable meaningful comparisons with previous results, we now consider these five functionals in conjunction with the Def2-TZVP basis set⁵¹ for the present study.

Preliminarily, we conduct a methods benchmark by re-evaluating the electronic and spin state of the Sc₃ trimer. We thus employ the five functionals considered including PBE, B3PW91, BP86, TPSSh and M05 along with the Def2-TZVP basis set, followed by a comparison with the available experimental data.¹⁴ Subsequently, we intend to undertake a comprehensive search for structures of a series of small Sc_n clusters and Sc_n−1B with n going from 2 to 13 across three charge states. For this extensive exploration, we use the PBE functional in conjunction with the Def2-TZVP basis set, as this functional has consistently demonstrated results in good agreement with experimental data as compared to the other functionals employed in this study (discussed in the next section “Some Benchmark Calculations on the Sc₃ Trimer”).

In our global search procedure for the global energy minima, we employ two distinct methodologies. Firstly, we utilize an upgraded stochastic algorithm, building upon the previously reported random kick procedure,⁵² to systematically generate diverse structures for both Sc_n^+/0/− and Sc_n−1B^+/0/− clusters. Simultaneously, we manually construct initial structures for the Sc_n−1B^+/0/− by strategically introducing a B atom into different positions within the local minimum structures of both neutral and charged states of the Sc_n−1^+/0/− species.^18,34,45 The process also involves a substitution of the B atoms with Sc atoms, taking inspiration from previous studies on the B_nSc^+/0/− counterparts²⁶ and incorporating replacement of B or Sc atoms into the patterns observed in the Al–Sc systems^25,32,33 as well as Al_nB systems^29,30,53,54 taking a similar number of valent electrons into account. This comprehensive and intensive search approach ensures a thorough exploration of the potential energy landscapes for the clusters considered in various charge states.

These initial structures generated are then subjected to geometry optimizations in different multiplicities using the PBE functional in conjunction with the small LANL2DZ basis set. Subsequently, the local energy minima identified from both search approaches, with relative energies of <5 eV with respect to the lowest-lying minimum of each size and charge, are subjected to a re-optimization using the same functional but with the larger Def2-TZVP basis set. Harmonic vibrational frequencies are then calculated at the same level to identify equilibrium geometries and evaluate their zero-point energy (ZPE) corrections. This process allows a reliable identification to be carried out for the structural and energetic characteristics of the lowest-lying isomers.

To further analyze the properties, the natural bond orbital (NBO) analysis is conducted using the NBO 5.0 program.⁵⁵ This aims to emphasize the electronic populations, and, consequently, the chemical bonding and magnetic properties, allowing for a detailed examination of the charge transfer and electron contribution. Besides, the relative stability of different geometries and spin states of the studied clusters are rationalized using the jellium shell model (JSM).⁵⁶ This popular model was successful in providing some simple but reasonable interpretations for stability patterns observed in other similar atomic clusters.^32,57

3. Results and discussion

3.1 Some benchmark calculations on the Sc₃ trimer

As mentioned above, debates have arisen, both experimentally and theoretically, concerning the most stable spin state of the neutral Sc₂ cluster. Calculated results disagree with each other on the ground state of the dimer. While CASPT2 computations carried out in 2008 ²¹ suggested that Sc₂ has a triplet ³Σ_u⁻ ground state, the following results using MRCI(Q) and multireference perturbation theory NEVPT3 methods reported in 2010 ^16,17 pointed out a quintet ⁵Σ_u⁻ ground state. Results obtained in 2017 ¹⁹ from coupled-cluster theory (U)CCSD(T) computations revealed a closed-shell ¹Σ_g⁺ ground state which was not seriously considered in previous theoretical studies. On the other hand, most DFT results obtained using several functionals converged to a quintet ⁵Σ_u⁻ ground state. Such a discrepancy is reflected by the inherent difficulty for treatment of transition metal dimers by quantum chemical methods. In fact, the debate over the ground state of the chromium dimer Cr₂ lasted several decades.⁵⁸ In this context the dimer is not suitable for a benchmarking of DFT functionals for Sc clusters. In this section, our objective is to present an overview and assessment of the benchmark calculations by considering the global energy, spin state, and vibrational frequencies of the neutral Sc₃ trimer. The calculations involve the use of several density functionals including the PBE, B3PW91, BP86, TPSSh, and M05, along with the Def2-TZVP basis set.

The experimental resonance Raman spectrum of Sc₃ trimer was well documented.¹⁴ The trimer is characterized as a near-equilateral triangle, demonstrating a symmetric stretching vibrational frequency of ∼248 cm⁻¹ and two vibrational frequencies of nearly degenerate asymmetric stretch-bends, both around 150 cm⁻¹. Furthermore, the ground state of the Sc₃ trimer has been assigned by a electron state based on a finding employed the electron paramagnetic resonance (ESR) spectroscopy's technique.⁵⁹

A previous theoretical study using CASSCF followed by contracted CI calculations reported the ground state of Sc₃ to be 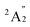.⁶⁰ However, this finding did not align with the ESR experiment results, and the symmetric stretching frequency (513 cm⁻¹) was significantly different from the Raman experimental data. Subsequent studies demonstrated that the BP86 functional, in conjunction with different basis sets, produced reasonable results, showing agreement with the 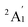ground state and providing vibrational frequencies close to the experimental values.^50,61,62

When combined with the Def2-TZVP basis set, all functionals used in this study yield results consistent with the experimental findings, confirming the ground state of the Sc₃ trimer as 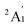. Additionally, across the different functionals, the Sc₃ trimer at its 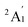state exhibits the same electron configuration, with an unpaired electron occupying the 2S molecular orbital (MO) (cf. Table S1†), indicating that the choice of a density functional induces little impact on the electronic structure. However, the results presented in Table 1 reveal that calculations employing the PBE functional provide better agreement with experiments compared to the other functionals used. For the calculated Sc₃ trimer, only the vibrations at the 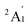electronic state employing the PBE functional yield signals closely resembling the experimental findings, with a pair of degenerate vibrations at ∼140 cm⁻¹ (∼140 and ∼145 cm⁻¹ when relaxing the symmetry) describing the nearly degenerate asymmetric signals at around 145 and 150 cm⁻¹, and a symmetric vibration at ∼260 cm⁻¹ (∼268 cm⁻¹ when relaxing the symmetry) corresponding to the ∼250 cm⁻¹ observed in the experiment.

Table 1 Relative energy (rE), electronic state (S), and Raman frequencies (Freq) of the Sc₃ trimer computed using the PBE, B3PW91, PB86, TPSSh and M05 functionals with the def2-TZVP basis set

Functional	PBE			B3PW91			PB86			TPSSh			M05
S^b		^4A′	^6A′		^4B2	^6A1		^4A1	^6A′		^4B2	^6A′		^4A2	^6A′
a Results are compared with the experimental Raman signals (Exp) of the Sc3 trimer reported in ref. 14.b Due to geometric distortions, several optimized structures do not have any symmetry; the others have low symmetry point group, but it is rather confusing to assign the symmetry of their electronic state. For the sake of simplicity, we consider the lowest-lying state in each multiplicity.
rE (kcal mol^−1)	0.0	5.3	6.4	0.0	2.5	3.5	0.0	13.6	6.5	0.0	3.0	5.2	0.0	16.2	24.8
Freq (cm^−1)	138	145	66	192	131	131	133	105	65.1	102	132	105	157	149	112
	138	181	185	192	142	146	133	232	186	102	141	136	157	250	190
	264	209	214	283	248	254	263	255	208	282	249	256	290	263	280
Expt^a (cm^−1)	145, 151, 248 (ref. 14)

---

Given the relatively accurate result in vibrational frequencies for the Sc₃ trimer, the PBE functional is thus further utilized in this study.

3.2 Structural evolution and the smallest size of exohedral–endohedral transition

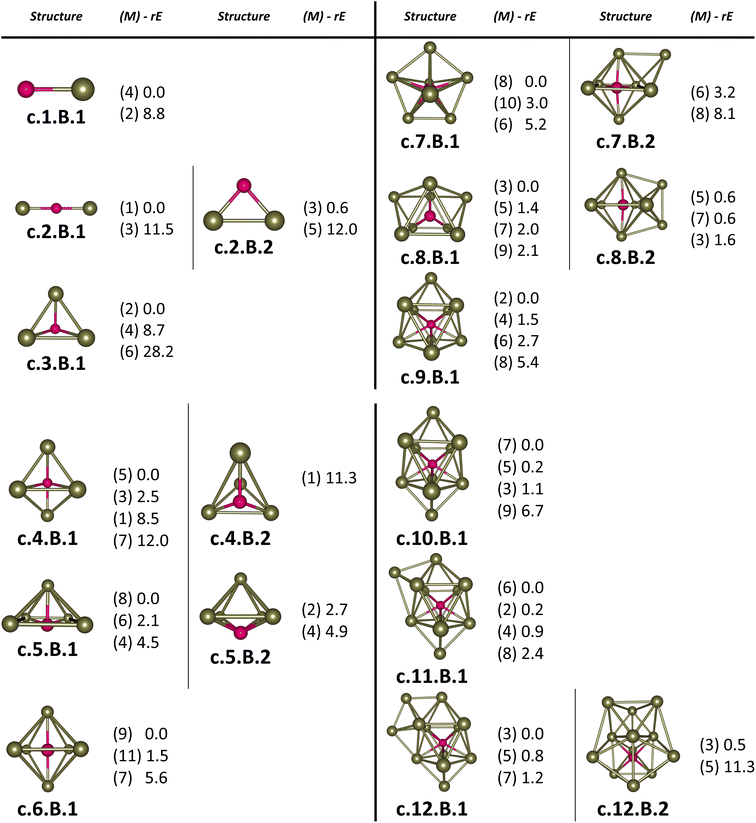
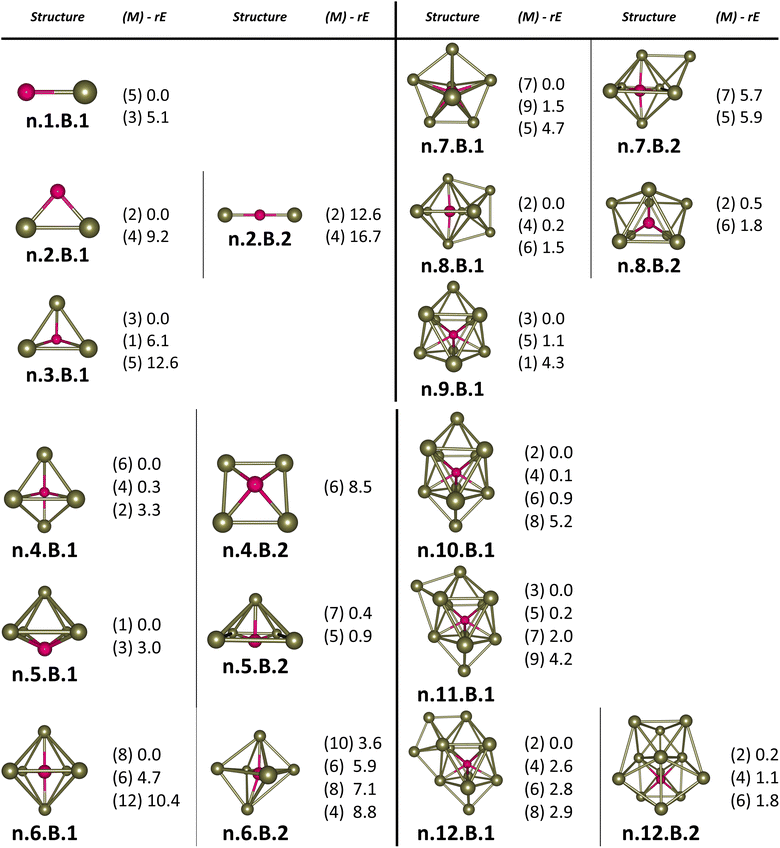
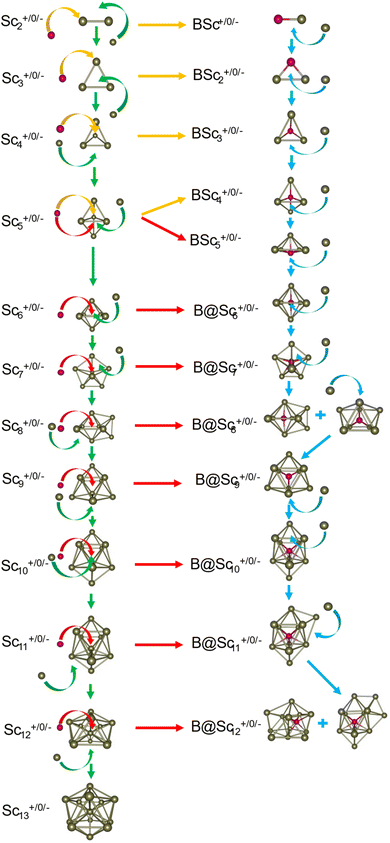
For the pure Sc_n^+/0/− and doped Sc_n−1B^+/0/− (n = 2–13) clusters, our selection process focuses on the lowest-lying isomers with relative energies closely aligned to the most stable structure with a difference of <∼12 kcal mol⁻¹ (∼0.5 eV) in relative energy. This approach is necessary due to the abundance of local minima on the potential energy surface, along with the presence of energetically degenerate isomers in both structures and spin states for each cluster size. The shapes, spin states, and relative energies of the pure Sc_n^+/0/− in three charge states are represented in Fig. S1 (S stands for the ESI file).† The shapes, spin states, and relative energies of the boron doped Sc_n−1B^+/0/− structures are depicted in Fig. 1–3, corresponding to the cationic, neutral and anionic charges, respectively.

Fig. 1 Structures, multiplicities (M, in bracket) and relative energies (rE, kcal mol⁻¹) of the lowest-lying cationic Sc_n−1B⁺ (n = 2–13) clusters calculated using the PBE functional with the def2-TZVP basis set.

Fig. 2 Structures, multiplicities (M, in bracket) and relative energies (rE, kcal mol⁻¹) of the lowest-lying neutral Sc_n−1B (n = 2–13) clusters calculated using the PBE functional with the def2-TZVP basis set.

Fig. 3 Structures, multiplicities (M, in bracket) and relative energies (rE, kcal mol⁻¹) of the lowest-lying anionic Sc_n−1B⁻ (n = 2–13) clusters calculated using the PBE functional with the def2-TZVP basis set.

In our labeling convention, the x.N.Z.y notation is employed for pure Sc_n^+/0/− isomers, where x = c, a, and n represent cationic, anionic and neutral isomers, respectively; N denotes the number of Sc atoms, and Z = A designates pure Sc_n^+/0/− clusters. The subscript y = 1, 2, 3, etc… indicates isomers with increasing relative energy. For example, c.5.A.1 consistently identifies the most stable isomer of the Sc₅⁺ cation.

Similarly, the x.M.Z.y label is utilized for doped Sc_n−1B^+/0/− isomers in which x = a, c and n indicate the anionic, cationic and neutral isomers, respectively. M = N−1 with N = 2–13 denotes the number of Sc atoms, and Z = B corresponds to the series of doped Sc_n−1B^+/0/− clusters. Again, the subscript y = 1, 2, 3, etc… stands for isomers with increasing relative energy. Accordingly, c.5.B.1 consistently denotes the most stable isomer of the Sc₅B⁺ cation.

The critical size of the Sc_n−1B^+/0/− clusters with n = 2–11 occurs at n = 6, marking the point at which an exohedral–endohedral rearrangement takes place, accompanied by a transition in the substitution-addition trend of the B atom. Across all three charge states considered, particularly for smaller sizes, those are characterized by very small number of Sc atoms having shapes such as a line, a triangle, a tetrahedron and a triangular bipyramid, respectively, corresponding to the doped Sc_n−1B^+/0/− clusters with n = 2–6. A distinct preference emerges for the exohedral trend of boron substitution into the corresponding original shapes of Sc_n^+/0/− (n = 2–6) clusters. This trend undergoes a notable shift, however, as the cluster size increases, accompanied with the expansion of Sc_n cage, favoring an endohedral trend of boron addition into the larger Sc_n^+/0/− (n = 6–10) clusters, as illustrated in Fig. 4. The trend of addition is initiated with a B atom attaching to the bottom face of a distorted triangular bipyramid composed of the Sc₅^+/0/− cages. This results in the formation of a nearly pyramidal structure in the B@Sc₅^+/0/− clusters in which the B atom is positioned at the center, slightly angled downward from the square bottom surface.

Fig. 4 Structural evolution of the pure Sc_n^+/0/− and doped Sc_n−1B^+/0/− clusters with n going from 2 to 13. Green and blue arrows illustrate the stepwise structural changes by adding one Sc atom in the Sc_n^+/0/− and Sc_n−1B^+/0/− clusters, respectively. Yellow and red arrows present trends in substitution and addition of B into pure Sc clusters, respectively.

Particularly striking is the stable and aesthetically pleasing lowest-lying structure of the B@Sc₆^+/0/− clusters, standing out as the smallest doped cage observed thus far.^53,57,63 Noteworthy for their nearly perfect octahedral shape, each of these clusters encapsulates a B atom at its centre within the confined space of a Sc₆^+/0/− cage. The specific size of the Sc₆^+/0/− cage provides snugly sufficient space, allowing a B atom to be centrally positioned, forming six B–Sc bonds, and enhancing the condensation of the initially loosely structured Sc₆^+/0/− cage (cf. Fig. 1–4 and S1 of the ESI file†). In fact, the doped B atom connects six Sc atoms together giving rise to six additional B–Sc bonds, thus stabilizing the initial Sc₆^+/0/− configurations and thereby solidifying the overall structure (cf. the next section “Thermodynamic stability”).

In line with the prevailing trend of additive design, the B@Sc₇^+/0/− enclosures also showcase a visually appealing structure, highlighting a central B atom positioned within the pentagonal bipyramidal Sc₇^+/0/− cage, revealing almost a C_2v symmetry. However, given their rather large size with respect to the modest atomic radius of B, the Sc₇^+/0/− crates are relatively spacious for accommodating the B atom, leading to their loosely distorted structures.

As the size of the crates increases, they progressively experience significant expansion, resulting in a loosening that prompts structural reorganization for enhanced condensation and effective bonding. For the next B@Sc₈^+/0/−, a notable energetic degeneracy is observed between the two most stable geometric configurations (cf. Fig. 1–4). In the first, the B atom occupies the central position of the octahedron belonging to the adjacently double face-capped octahedral Sc₈^+/0/− cages. In the second configuration, the B atom centrally resides in a Sc₈ rectangular antiprism. Such a rectangular antiprism B@Sc₈^+/0/−, in and of itself, serves as the basic building block for larger sizes, highlighting its own structural significance.

Building upon the structural block of the rectangular antiprism observed in B@Sc₈^+/0/−, the most stable configurations of B@Sc₉^+/0/− and B@Sc₁₀^+/0/− clusters integrate one and two additional Sc atoms onto the rectangular faces of the antiprism, respectively (cf. Fig. 4). The B atom consistently serves as a central point of connection, bringing the outer Sc atoms together. Such a cohesive effect results in the structures of B@Sc₉^+/0/− and B@Sc₁₀^+/0/− that are fixed and much more compact than the initially loosely distorted Sc₉^+/0/− and Sc₁₀^+/0/− cages.

It is noteworthy that the structures of B@Sc₁₀^+/0/− and Sc₁₁^+/0/− are quite similar to each other, featuring a quasi D_4d gyroelongated square bipyramid with a central connection point formed by a B and Sc atom, respectively.

However, in going beyond n = 11, the doping a B atom at a central point of the Sc cage to connect and shape the outer Sc cage is no longer effective. This is because the Sc_n^+/0/− cage has reached a sufficient size, and a Sc atom, with its larger radius, becomes more efficient in playing the central connecting role with other outer Sc atoms as compared to the smaller-radius B atom.

In contrast to boron-doped B@Al₁₂^0/− those preserve the icosahedral shape of the Al₁₃ cluster,^29,54 their isovalent B@Sc₁₂^+/0/− isomers cannot retain the icosahedron of the Sc₁₃ cluster. For larger sizes with n = 12 and 13, the Sc_n−1B^+/0/− clusters shift away from the earlier addition as well as substitution rules into the Sc_n^+/0/− host. Instead, a gradual addition of Sc atoms onto the outer faces of the B@Sc₁₀^+/0/− is observed. Meanwhile, Sc₁₂^+/0/− undergoes a rearrangement into a mono-capped pentagonal antiprism, followed by a well-known icosahedron of the Sc₁₃^+/0/− in which a Sc atom plays the role of an endohedral stabilizing center.

3.3 Energetic degeneracy and high magnetic moment

As the size expands, the intricacies of energetic degeneracy become more pronounced,¹⁸ that can be attributed to two primary factors. On the one hand, energetic degeneracy is triggered by a geometric competition for the global minimum, a consequence of the inherent flexibility and fluxionality within the clusters. With increasing size, numerous structural rearrangements and transformations occur, resulting in multiple energetic degeneracy.

On the other hand, the increasing number of unpaired electrons invariably induces energetic degeneracy among the high spin states. These electrons, closely packed in energy, particularly the 3d electrons, coupled with a strong Jahn–Teller effect, contribute to the small differences or even overlap in energy levels of the 1F, 2D, and even 2P shell orbitals, further complicating the energy landscape. In this complex scenario, the shapes of these shell orbitals become distorted due to the merging of different orbital types, disrupting molecular symmetry and making them difficult to be identified. Hereafter, we refer to the range encompassing these intricate energy levels as the “mixed band”. Within the mixed band, the HOMO–LUMO gap, or the HOMO–SOMO gap, is characterized with a very small energy, facilitating an easier traversal of electrons which continues until the mixed band becomes unoccupied. As a result, the HOMO level now shifts to the orbitals located at significantly lower energy levels, such as 2S, 1P, or 1D orbitals, ultimately establishing a notably large HOMO–LUMO (HOMO–SOMO) gap.

The energy degeneracy of the pure Sc_n^+/0/− tends to escalate as its size n increases and attains the pivotal magic number, namely n = 13. At this critical size, the Sc₁₃^+/0/− isomers enjoy a synergistic interplay between electronic and geometric structures within the cluster. This synergy culminates in the emergence of both an icosahedral structure and very high spin electronic states, with a ¹⁹A₁ state for the cationic, a ²⁰A state for the neutral, and a ¹⁹B_3u state for the anionic Sc₁₃ isomer. These isomers are characterized by their electron shells in cationic, neutral, and anionic states expressed as [1S²1P⁶2S²1D¹⁰SOMO¹⁸], [1S²1P⁶2S²1D¹⁰SOMO¹⁹] and [1S²1P⁶2S²1D¹⁰2F²SOMO¹⁸], respectively.

In Fig. 5, a uniform energy level pattern is depicted among these isomers, emphasizing three key regions: the core levels associated with the [1S²1P⁶2S²1D¹⁰] electron configuration, the [mixed band] comprising 19 closely spaced energy levels, and the “other” levels, which extend beyond the mixed band, exhibiting distinct orbital shapes and significantly higher energy levels—approximately 0.6 eV above those in the mixed band. On the beta side of these isomers, both cationic and neutral isomers exhibit a HOMO level of 1D_xy and a LUMO level corresponding to the first level of 1F in the mixed band, with a HOMO–LUMO gap of approximately 0.85 eV.

Fig. 5 Molecular orbital (MO) diagram on the beta side of (A) cationic Sc₁₃⁺, (B) neutral Sc₁₃, and (C) anionic Sc₁₃⁻ clusters, using the PBE/Def2-TZVP theory method.

However, the anionic Sc₁₃⁻ isomer, having 40 valence electrons, behaves differently. Here, the beta HOMO aligns with the first level of the [mixed band] rather than with the 1D level, while the LUMO aligns with the second level, creating a ¹⁹B_3u state with a nearly zero HOMO–LUMO gap, instead of maintaining the ²¹A_u state with an empty beta [mix band] seen in the neutral and cationic forms. This behavior is due to the added electron exceeding the capacity of the [mixed band], which destabilizes the cluster when attempting to occupy a significantly higher “other” level in the case of ²¹A_u electronic state. Consequently, this extra electron is more favorably placed in a beta 1F orbital within the [mixed band], resulting in an electron configuration of [1S²1P⁶2S²1D¹⁰2F²SOMO¹⁸] at the 19-electron spin state, which is consistent with previous findings,³² rather than the [1S²1P⁶2S²1D¹⁰SOMO²⁰] configuration seen in the 21-electron spin state.

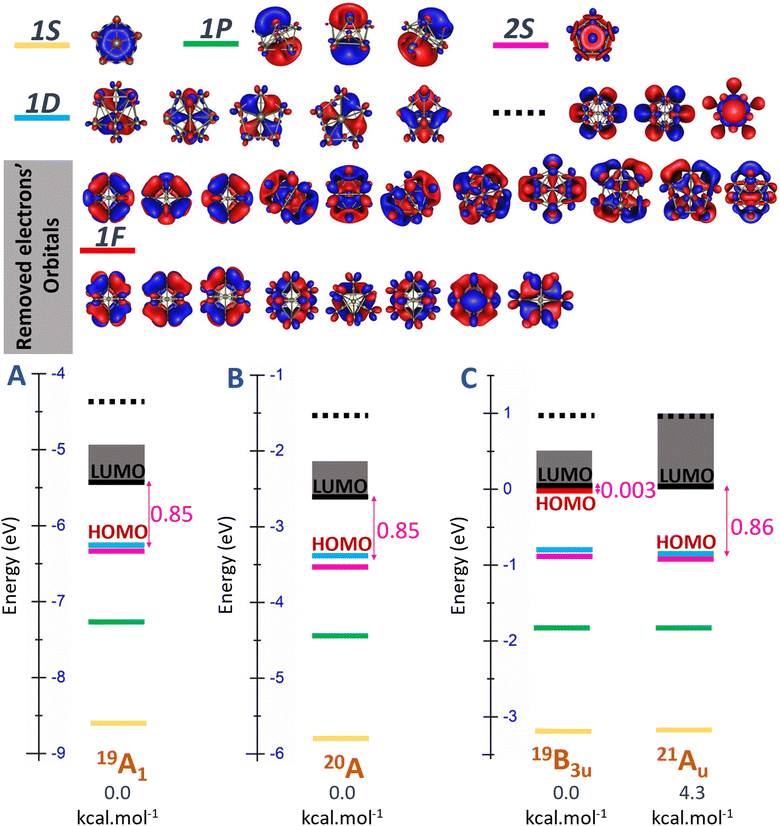
Another detailed examination of Fig. S2 (ESI file)† focusing on the Sc₁₁ species reveals a pronounced energy degeneracy in all three charge states, characterized by an energy degeneracy among several high spin states. Importantly, the energy differences between these states are mostly smaller than 0.1 eV that ranges within the error margin of ±0.2 eV of the DFT methods employed. This implies that their relative positions can be changed with respect to the methods employed. In the case of the cationic Sc₁₁⁺, spin states of energy degeneracy's isomers extend from triplet state and persist until reaching the 13-et spin state. At this point, electrons situated on the “mixed band” at beta side have already been removed, resulting in the electron shells of [1S²1P⁶1D¹⁰2S²SOMO¹²] as illustrated in Fig. S2A (ESI file).† Consequently, in the 13-et state of cationic Sc₁₁⁺, the beta HOMO is identified as the 2S-MO, contributing to a significant beta HOMO–LUMO gap specified by 0.7 eV. Similarly, in the case of the neutral Sc₁₁, the energetic degeneracy spans from the doublet to the 14-et spin states, where the HOMO on the beta side is also identified by 2S-MO, forming the electron shells of [1S²1P⁶1D¹⁰2S²SOMO¹³], with the beta HOMO–LUMO gap specified by 0.7 eV as well (cf. Fig. S2B, ESI file†).

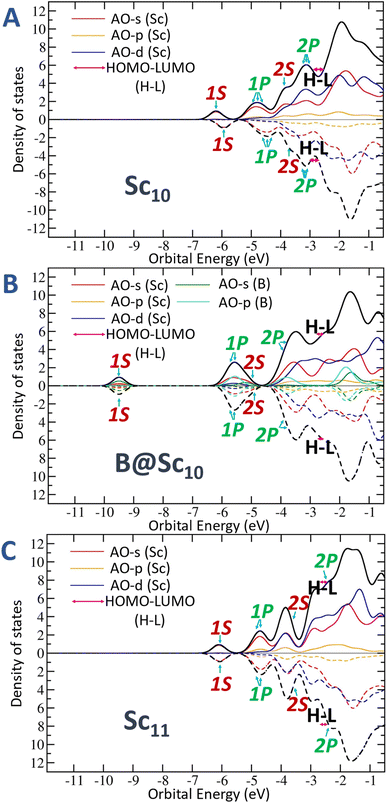
Additionally, Fig. 6 and S2 (ESI file)† offer a clearer illustration of the significant reduction in the number of energy-degenerate states following replacement of the central Sc atom of Sc₁₁^+/0/− by a B atom. The variation in electron levels leads to a modification of electron shells between the pure and doped B clusters (discussed in the next section “Electron contribution of boron dopant and its effect to scandium hosts”). Specifically, the electron shell undergoes a shift from [1S²1P⁶1D¹⁰2S²] + [mixed band] of the Sc₁₁^+/0/− to [1S²1P⁶2S²2P⁶1D¹⁰] + [mixed band] for B@Sc₁₀^+/0/−. This alteration is marked by an increase in the number of electrons at the “core” level and a corresponding decrease in the number of electrons in the [mixed band]. Consequently, this shift reduces the number of closely spaced energy levels in the [mixed band], resulting in a noteworthy reduction in the degeneracy of energy states.

Fig. 6 Molecular orbital (MO) diagram on the beta side of (A) cationic B@Sc₁₀⁺, (B) neutral B@Sc₁₀, and (C) anionic B@Sc₁₀⁻ clusters, using the PBE/Def2-TZVP method.

3.4 Electron contribution of boron dopant and its effect to scandium hosts

As mentioned above, the doping of boron atom not only influences the geometry but also triggers an electronic structure readjustment, significantly impacting on the spin state of the studied clusters, playing a crucial role in mitigating the energetic degeneracy among the extensive range of spin states in the initially pure Sc clusters.

To delve into a more profound understanding of the impact of boron doping on the scandium host, we now employ the NBO method⁵⁵ to scrutinize the natural electron configurations (NEC) and spin densities. On the one hand, the density of states (DOS) maps depicted in Fig. 7, S6 and S7 (ESI file)† reveals a difference in electron contributions when comparing scenarios with and without a B doping into the Sc host. Introduction of B into an Sc host involves its s and p electrons, contributing to the overall electron count, and consequently reducing the energy levels of the S and P molecular orbitals.

Fig. 7 Calculated density of states (DOS) for the lowest-lying neutral clusters of (A): Sc₁₀, (B): B@Sc₁₀, and (C): Sc₁₁. Positive and negative DOS represent spin-up and spin-down electrons, respectively.

On the other hand, an intriguing observation is emerged across nearly all Sc_n−1B clusters, that is, the number of valence electrons in boron dopant increases by an electron donation from Sc_n−1 host, approximately 1.5 times more (totaling around 4.5 electrons on 2s and 2p) as compared to the standard 3 electrons (2 electrons in 2s and 1 electron in 2p) of a typical boron atom. This augmented contribution significantly influences the electron configuration of the entire cluster by causing a downward shift in the 2P levels below the 1D levels.

This influence is prominently evident when examining the MO diagram of Sc₆^+/0/− clusters (Fig. S3–S5, respectively, ESI file†), where the 2P orbitals extend over the 1D orbitals' levels and beyond. Introducing boron into these clusters, as illustrated in the case of B@Sc₆^+/0/− (Fig. S6 and S7†), the 2P orbitals gradually shift below these 1D levels.

In a different context as mentioned in a paragraph above, examination of Sc₁₁^+/0/− (Fig. S2, ESI file†) reveals a general electronic structure of [1S²1P⁶1D¹⁰2S²] + [mixed band], where the 2P orbitals extend beyond the LUMO level. In contrast, the B@Sc₁₀^+/0/− scenario which mirrors the structure of the Sc₁₁^+/0/− but substitutes the central Sc atom with a B atom, showcases a distinct shell, namely, the 2P orbitals are lowered below the 1D levels, forming electron shells such as [1S²1P⁶2S²2P⁶1D¹⁰] + [mixed band] (Fig. 6).

Additionally, due to the smaller radius of B as compared to Sc, the bonds between the central atom and those at the vertices of the square antiprism in the B@Sc₁₀^+/0/− are shorter than those in the Sc₁₁^+/0/− (approximately 2.5 and 2.8 Å, respectively). This tends to elongate the B@Sc₁₀^+/0/− structure along the z-axis, passing through the B center and the two Sc apexes of equilateral square pyramids in the gyroelongated square bipyramidal structure. As a result, the energies of P_z and D_z² orbitals along the z-axis are significantly lower as compared to the similar P or D orbital types in other directions (cf. Fig. 6).

3.5 Thermodynamic stability

In this study, thermodynamic stability of the lowest-lying pure Sc_n^+/0/− and doped Sc_n−1B^+/0/− (n = 2–13) clusters in three charged states is evaluated by the average binding energies (E_b). The formulas used for calculating the average binding energies of these clusters are defined as follows (eqn (1)–(6)):

• For cationic pure clusters Sc_n⁺:

E_b(Sc_n⁺) = [(n − 1)E(Sc) + E(Sc⁺) − E(Sc_n⁺)]/n (1)

• For neutral pure clusters Sc_n:

E_b(Sc_n) = [nE(Sc) − E(Sc_n)]/n (2)

• For anionic pure clusters Sc_n⁻:

E_b(Sc_n⁻) = [(n − 1)E(Sc) + E(Sc⁻) − E(Sc_n⁻)]/n (3)

• For cationic doped clusters Sc_n−1B⁺:

E_b(Sc_n−1B⁺) = [(n−2)E(Sc) + E(Sc⁺) + E(B) − E(Sc_n−1B⁺)]/n (4)

• For neutral doped clusters Sc_n−1B:

E_b(Sc_n−1B) = [(n−1)E(Sc) + E(B) − E(Sc_n−1B)]/n (5)

• For anionic doped clusters Sc_n−1B⁻:

E_b(Sc_n−1B⁻) = [(n − 1)E(Sc) + E(B⁻) − E(Sc_n−1B⁻)]/n (6)

In these equations:

• E(Sc), E(Sc⁺) and E(Sc⁻) represent the total energies of a single scandium atom, scandium cation, and scandium anion, respectively.

• E(Sc_n⁺), E(Sc_n) and E(Sc_n⁻) represent the total energies of the lowest-lying cationic, neutral, and anionic Sc_n^+/0/−, respectively.

• E(B) and E(B⁻) denote the total energies of a single boron atom and boron anion, respectively.

• E(Sc_n−1B⁺), E(Sc_n−1B) and E(Sc_n−1B⁻) represent the total energies of the lowest-lying cationic, neutral and anionic Sc_n−1B^+/0/−, respectively.

For cationic clusters, because the ionization energy of the Sc atom (6.30 eV) is significantly lower that of the B atom (8.67 eV), we thus utilize only the total energies of the Sc⁺ cation E(Sc⁺) for calculating the average binding energy of cationic clusters, instead of the total energies of the B⁺ cation E(B⁺). For anionic cluster, since the electron affinity of the B atom (0.27 eV) is larger than that of the Sc atom (0.04 eV), the total energies of the B⁻ anion E(B⁻) is used for in the calculation of anionic cluster binding energies, instead of the total energies of the Sc⁻ anion E(Sc⁻).

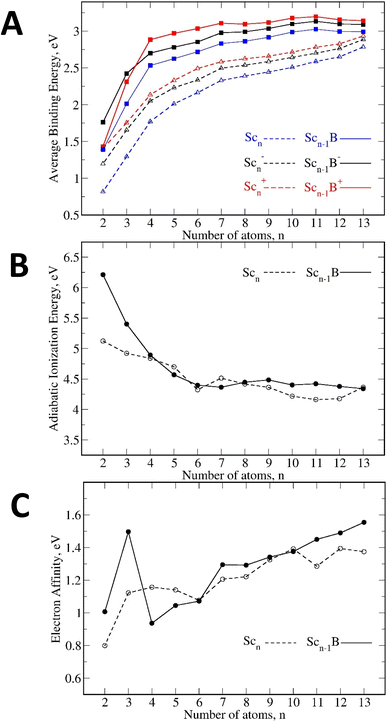
Fig. 8A clearly indicates that the binding energy values of the doped Sc_n−1B^+/0/− are stronger than those of the pure Sc_n^+/0/−, suggesting that introduction of a B atom into the Sc clusters enhances the thermodynamic stability of the initial Sc hosts. In addition, Fig. 8A highlights another noteworthy observation emphasizing the significant role of the charge state in the overall stability. In both pure and B-doped Sc clusters, the charged clusters exhibit greater stability with respect to their neutral counterparts, with the cationic states displaying the highest level of stability.

Fig. 8 (A): Average binding energy of Sc_n^+/0/− and Sc_n−1B^+/0/−, (B): adiabatic ionization energy and (C): adiabatic electron affinity C of the lowest-lying energy Sc_n and Sc_n−1B clusters including n = 2–13 using the PBE/def2-TZVP method.

Moreover, an analysis of the adiabatic ionization energies (IEa) and adiabatic electron affinities (EAa) for the lowest-lying neutral isomers in Fig. 8B and C, respectively, again shows a notable size dependence. The pattern of IEa exhibits its decrease with increasing size, as the clusters grow, detachment of an electron becomes more facile. Conversely, the trend of EAa rises along with size; as the clusters expand, reception of an electron also becomes more favorable. However, the EAa values are rather small (<1.6 eV) suggesting their instability with respect to electron addition. Hence, these observed trends suggest that the clusters considered predominantly exhibit a preference for the cationic states.

To enhance the assessment of thermodynamic stability, the dissociation energies (D_e) for diverse fragmentation channels (x) of the lowest-lying clusters are calculated. The results are presented in Tables 2 and 3, and the corresponding formulas are outlined below, where (x) represents the number order of the fragmentation channels, spanning from D_e(1)–D_e(15):

D_e(1): Sc_n → Sc_n−1 + Sc,

D_e(2): Sc_n⁻ → Sc_n−1⁻ + Sc,

D_e(3): Sc_n⁻ → Sc_n−1⁻ + Sc⁻,

D_e(4): Sc_n⁺ → Sc_n−1⁺ + Sc,

D_e(5): Sc_n⁺ → Sc_n−1 + Sc⁺,

D_e(6): Sc_n−1B → Sc_n−2B + Sc,

D_e(7): Sc_n−1B → Sc_n−1 + B,

D_e(8): Sc_n−1B⁻ → Sc_n−2B⁻ + Sc,

D_e(9): Sc_n−1B⁻ → Sc_n−2B + Sc⁻,

D_e(10): Sc_n−1B⁻ → Sc_n−1⁻ + B,

D_e(11): Sc_n−1B⁻ → Sc_n−1 + B⁻,

D_e(12): Sc_n−1B⁺ → Sc_n−2B⁺ + Sc,

D_e(13): Sc_n−1B⁺ → Sc_n−2B + Sc⁺,

D_e(14): Sc_n−1B⁺ → Sc_n−1⁺ + B,

D_e(15): Sc_n−1B⁺ → Sc_n−1 + B⁺.

Table 2 Dissociation energies (D_e, eV) obtained (PBE/Def2-TZVP + ZPE) for various fragmentation channels of Sc_n in neutral, cationic, and anionic states

n	Neutrals	Anion		Cation
	De(1)	De(2)	De(3)	De(4)	De(5)
2	1.63	2.39	2.39	2.81	2.81
3	2.25	2.57	3.33	2.45	3.63
4	3.2	3.23	4.32	3.28	4.66
5	2.97	2.96	4.07	3.11	4.57
6	2.92	2.86	3.96	3.3	4.9
7	3.32	3.45	4.49	3.13	5.11
8	2.81	2.83	3.99	2.91	4.69
9	2.88	2.99	4.17	2.94	4.82
10	3.08	3.14	4.43	3.22	5.16
11	3.39	3.28	4.64	3.45	5.52
12	3.34	3.45	4.69	3.32	5.46
13	4.41	4.39	5.74	4.22	6.34

---

Table 3 Dissociation energies (D_e, eV) obtained (PBE/Def2-TZVP + ZPE) for various fragmentation channels of Sc_n−1B in neutral, cationic, and anionic states

n	Neutrals		Anions				Cations
	De(6)	De(7)	De(8)	De(9)	De(10)	De(11)	De(12)	De(13)	De(14)	De(15)
2	2.78	2.78	3.52	3.75	3.75	3.48	5.24	2.86	2.86	5.24
3	3.26	4.41	3.75	4.72	5.10	4.84	4.21	4.30	4.27	7.82
4	4.09	6.25	3.53	4.99	6.07	5.80	4.46	5.50	6.28	10.03
5	2.99	6.04	3.10	4.00	5.93	5.67	3.32	4.72	6.31	10.14
6	3.19	6.26	3.21	4.22	6.19	5.92	3.36	5.09	6.56	10.53
7	3.51	6.84	3.73	4.76	7.06	6.79	3.54	5.44	6.80	11.15
8	3.09	6.60	3.08	4.34	6.69	6.42	3.00	4.93	6.67	10.83
9	3.34	7.13	3.39	4.64	7.25	6.98	3.30	5.15	7.06	11.32
10	3.63	7.87	3.66	4.96	7.92	7.66	3.71	5.52	7.83	12.14
11	3.42	8.22	3.50	4.83	8.28	8.01	3.40	5.30	8.01	12.47
12	2.64	7.47	2.68	4.09	7.68	7.41	2.69	4.56	7.26	11.76
13	2.96	7.09	3.02	4.47	7.25	6.99	3.00	4.91	6.93	11.42

---

Both pure and doped clusters display a tendency to favor the detachment of a neutral Sc atom over a charged Sc atom (Tables 2 and 3), indicating a consistent preference of charge retention within the clusters following dissociation. This preference aligns with the earlier discussion regarding a stability's tendency for the charged clusters over the neutral counterpart. Moreover, across all three charge states (Table 3), the dissociation energies for the Sc_n−1B^+0/− clusters in the B-dissociation channel D_e(7), D_e(10) and D_e(14) are greater than those of the Sc-detachment channel D_e(6), D_e(8) and D_e(12). This observation can be attributed to two main factors. Firstly, the B dopant has an intrinsic preference for reception of electrons from nearby Sc atoms (as the electron population in B is 1.5 times higher than normal), leading to formation of strong Sc–B bonds. Secondly, starting from n = 5 onwards, B is situated inside the Sc cages, making it more challenging to be extracted from the cage, as compared to the cutting of an outer Sc atom.

4. Concluding remarks

In the present theoretical study, a comprehensive investigation of pure Sc_n^+/0/− and doped Sc_n−1B^+/0/− clusters (n = 1–13) is conducted using DFT computations with the PBE/Def2-TZVP method, leading to several significant conclusions:

(i) A detailed structural analysis of the clusters in three charged states reveals a pronounced size dependency in their structures. However, the shape of a specific cluster size remains unchanged upon the removal or addition of an electron. The critical size for the Sc_n−1B^+/0/− clusters is determined to be n = 6, marking the point where an exohedral–endohedral transformation occurs. This transformation is also accompanied by a transition in the substitution-addition trend of the B atom into the pure Sc host. For doped Sc_n−1B^+/0/− clusters with n = 2–6, the boron atom prefers an exohedral substitution into the original shapes of the Sc_n^+/0/− clusters. Nevertheless, there is a shift towards a boron endohedral addition when the Sc_n−1B^+/0/− clusters reach a size of n = 6–11. In larger clusters, n = 12 and 13 of Sc_n−1B^+/0/−, a departure from the earlier trends is observed. Instead of direct addition or substitution into the Sc host, Sc atoms are gradually added onto the outer faces of Sc_n−1B^+/0/−. Meanwhile, Sc₁₂^+/0/− transforms into a mono-capped pentagonal antiprism, and Sc₁₃^+/0/− forms a well-known icosahedron.

(ii) The B@Sc₆^+/0/− clusters are identified as the smallest doped cages observed thus far. They are notable for their nearly perfect octahedral shape, with a B atom centrally enclosed within the Sc₆^+/0/− cages. The size of the Sc₆^+/0/− cages is optimal, allowing the B atom to fit snugly in the center. This enhances the condensation of the initially loosely structured Sc₆^+/0/− cages, resulting in a more compact overall structure and stabilizing their geometric configurations.

(iii) A molecular orbital (MO) analysis provides a suitable explanation for the observed energy degeneracy between various stable spin states, which arise from the closely packed 3d electrons influenced by the Jahn–Teller effect. This results in a mixed band with overlapping energy levels, where the small HOMO–LUMO gap facilitates easier electron traversal. The energy degeneracy is resolved when the HOMO level occupies distinct, lower-energy orbitals outside the mixed band, creating a noticeable HOMO–LUMO gap.

(iv) At the critical size of n = 13, Sc₁₃^+/0/− exhibits a synergetic interplay that results in both an icosahedral structure and a stable high-spin electronic state with a ¹⁹A₁ state for the cationic, a ²⁰A state for the neutral, and a ¹⁹B_3u state for the anionic Sc₁₃ isomer, all without any energetic degeneracy. The electron shells in these cationic, neutral, and anionic isomers are established as [1S²1P⁶2S²1D¹⁰SOMO¹⁸], [1S²1P⁶2S²1D¹⁰SOMO¹⁹] and [1S²1P⁶2S²1D¹⁰2F²SOMO¹⁸], respectively.

(v). The boron dopant unusually increases the number of valence electrons, approximately 1.5 times more than a regular boron atom due to electron donation from the Sc host. This heightened contribution significantly influences the electron configuration of the entire cluster, causing a downward shift in the 2P levels below the 1D levels. This adjustment in electron configuration plays a crucial role in stabilizing the spin state of the studied clusters, effectively mitigating the energetic degeneracy among the extensive range of spin states in the initially pure Sc clusters.

(vi). Overall, introduction of a B atom as dopant into the Sc clusters enhances the thermodynamic stability of the initial Sc hosts and displays a notable charge-dependent with a preference for stability in cationic isomers.

Data availability

The quantum chemical program Gaussian 16 has been used. Reference of this program is given in the list of references. The datasets supporting this article are uploaded as part of the ESI file† that includes the Cartesian coordinates of the optimized geometries, information on the electronic structures of the structures considered.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge Ho Chi Minh City University of Technology (HCMUT), Vietnam National University VNU-HCM for supporting this study.

References

1. M. V. Uwe Kreibig, Optical Properties of Metal Clusters, Springer, Berlin, Heidelberg 1995, p. 535.
2. A. Heimermann and C. van Wüllen, Magnetic moments of small cobalt clusters revisited: The contribution of 3d and 4s electrons, Int. J. Mass Spectrom., 2019, 438, 135–141.
3. L. N. Pham, C. N. van Dijk, A. Kirilyuk, L. Goerigk, M. T. Nguyen and E. Janssens, Structures and Magnetism of Cationic Chromium–Manganese Bimetallic Oxide Clusters, J. Phys. Chem. C, 2020, 124(4), 2598–2608.
4. M. Martins and W. Wurth, Magnetic properties of supported metal atoms and clusters, J. Phys.: Condens.Matter, 2016, 28(50), 503002.
5. Q. L. Lu, A. F. Jalbout, Q. Q. Luo, J. G. Wan and G. H. Wang, Theoretical study of hydrogenated Mg, Ca@Al₁₂ clusters, J. Chem. Phys., 2008, 128(22), 224707.
6. M. Maatallah, M. Guo, D. Cherqaoui, A. Jarid and J. F. Liebman, Aluminium clusters for molecular hydrogen storage and the corresponding alanes as fuel alternatives: A structural and energetic analysis, Int. J. Hydrogen Energy, 2013, 38(14), 5758–5767.
7. J. A. Alonso and M. J. López, Palladium clusters, free and supported on surfaces, and their applications in hydrogen storage, Phys. Chem. Chem. Phys., 2022, 24(5), 2729–2751.
8. S. S. Ray, S. R. Sahoo and S. Sahu, Hydrogen storage in scandium doped small boron clusters (B_nSc₂, n=3–10): A density functional study, Int. J. Hydrogen Energy, 2019, 44(12), 6019–6030.
9. M. Szalay, D. Buzsáki, J. Barabás, E. Faragó, E. Janssens, L. Nyulászi and T. Höltzl, Screening of transition metal doped copper clusters for CO₂ activation, Phys. Chem. Chem. Phys., 2021, 23(38), 21738–21747.
10. B. Barhács, E. Janssens and T. Höltzl, C₂ product formation in the CO₂ electroreduction on boron-doped graphene anchored copper clusters, Phys. Chem. Chem. Phys., 2022, 24(35), 21417–21426.
11. G. L. Gutsev, C. W. Weatherford, K. G. Belay, B. R. Ramachandran and P. Jena, An all-electron density functional theory study of the structure and properties of the neutral and singly charged M₁₂ and M₁₃ clusters: M = Sc–Zn, J. Chem. Phys., 2013, 138(16), 164303.
12. T. A. O'Brien, The Electronic Spectroscopy of Transition Metal Diatomic Molecules Modeled with Semiempirical Quantum Chemistry, Dissertation, University of Florida, 2000.
13. J. Harris and R. O. Jones, Density functional theory and molecular bonding. III. Iron-series dimers, J. Chem. Phys., 1979, 70(2), 830–841.
14. M. Moskovits, D. P. DiLella and W. Limm, Diatomic and triatomic scandium and diatomic manganese: A resonance Raman study, J. Chem. Phys., 1984, 80(2), 626–633.
15. L. B. Knight, R. J. Van Zee and W. Weltner, The ground state of the Sc₂ molecule, Chem. Phys. Lett., 1983, 94(3), 296–299.
16. C. Camacho, H. A. Witek and R. Cimiraglia, The low-lying states of the scandium dimer a), J. Chem. Phys., 2010, 132(24), 244306.
17. A. Kalemos, I. G. Kaplan and A. Mavridis, The Sc₂ dimer revisited, J. Chem. Phys., 2010, 132(2), 024309.
18. J. Wang, Structural, electronic, and magnetic properties of Sc_n (n =2-18) clusters from density functional calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(15), 155422.
19. S. Sajjad, Maria, T. Mahmood and K. Ayub, Benchmark study of structural and vibrational properties of scandium clusters, J. Mol. Struct., 2017, 1142, 139–147.
20. S. Bhunia, N. Vyas, C. Sahu and A. K. Ojha, Size dependent structural, electronic, and magnetic properties of Sc_N (N=2-14) clusters investigated by density functional theory, J. Mol. Model., 2014, 20(11), 2481.
21. J. M. Matxain, E. Rezabal, X. Lopez, J. M. Ugalde and L. Gagliardi, Quantum Monte Carlo study of the ground state and low-lying excited states of the scandium dimer, J. Chem. Phys., 2008, 128(19), 194315.
22. B. N. Papas and H. F. Schaefer III, Homonuclear transition-metal trimers, J. Chem. Phys., 2005, 123(7), 074321.
23. A. Ghosh, O. F. Mohammed and O. M. Bakr, Atomic-Level Doping of Metal Clusters, Acc. Chem. Res., 2018, 51(12), 3094–3103.
24. P. Ferrari, J. Vanbuel, E. Janssens and P. Lievens, Tuning the Reactivity of Small Metal Clusters by Heteroatom Doping, Acc. Chem. Res., 2018, 51(12), 3174–3182.
25. J. M. Guevara-Vela, A. S.-d. la Vega, M. Gallegos, Á. Martín Pendás and T. Rocha-Rinza, Wave function analyses of scandium-doped aluminium clusters, Al_nSc (n = 1–24), and their CO₂ fixation abilities, Phys. Chem. Chem. Phys., 2023, 25(28), 18854–18865.
26. H. Huang, B. Wu, Q. Gao, P. Li and X. Yang, Structural, electronic and spectral properties referring to hydrogen storage capacity in binary alloy ScB_n (n = 1–12) clusters, Int. J. Hydrogen Energy, 2017, 42(33), 21086–21095.
27. S. Jin, B. Chen, X. Kuang, C. Lu and G. L. Gutsev, Structural evolution and electronic properties of medium-sized boron clusters doped with scandium, J. Phys.: Condens.Matter, 2019, 31(48), 485302.
28. E. Shakerzadeh, L. Van Duong, E. Tahmasebi and M. T. Nguyen, The scandium doped boron cluster B₂₇Sc₂⁺: a fruit can-like structure, Phys. Chem. Chem. Phys., 2019, 21(17), 8933–8939.
29. M. Shibuta, T. Inoue, T. Kamoshida, T. Eguchi and A. Nakajima, Al₁₃⁻ and B@Al₁₂⁻ superatoms on a molecularly decorated substrate, Nat. Commun., 2022, 13(1), 1336.
30. J. C. Smith, A. C. Reber, S. N. Khanna and A. W. Castleman Jr, Boron Substitution in Aluminum Cluster Anions: Magic Clusters and Reactivity with Oxygen, J. Phys. Chem. A, 2014, 118(37), 8485–8492.
31. D. T. T. Mai, H. T. Pham, N. M. Tam and M. T. Nguyen, Geometry and bonding of small binary boron-aluminum clusters B_nAl_n (n = 1–7): Electron donation and interlocking aromaticity, Chem. Phys. Lett., 2019, 714, 87–93.
32. N. T. Cuong, N. T. Mai, N. T. Tung, N. T. Lan, L. V. Duong, M. T. Nguyen and N. M. Tam, The binary aluminum scandium clusters Al_xSc_y with x + y = 13: when is the icosahedron retained?, RSC Adv., 2021, 11(63), 40072–40084.
33. Y. Gao, J. Jiao, Y. Meng, Q. Liu and L. Cheng, Structural growth, stability and electronic characteristics of Al-Sc clusters, Comput. Theor. Chem., 2022, 1218, 113942.
34. X.-B. Li, H.-Y. Wang, J.-S. Luo, Y.-D. Guo, W.-D. Wu and Y.-J. Tang, Static dipole polarizabilities of Sc_n (n ≤ 15) clusters, Chin. Phys. B, 2009, 18(8), 3414.
35. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
36. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1997, 78(7), 1396.
38. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98(7), 5648–5652.
39. J. P. Perdew, P. Ziesche and H. Eschrig, Electronic Structure of Solids' 91, Akademie Verlag, Berlin, 1991.
40. A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38(6), 3098–3100.
41. J. P. Perdew, Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33(12), 8822–8824.
42. V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes, J. Chem. Phys., 2003, 119(23), 12129–12137.
43. Y. Zhao, N. E. Schultz and D. G. Truhlar, Exchange-correlation functional with broad accuracy for metallic and nonmetallic compounds, kinetics, and noncovalent interactions, J. Chem. Phys., 2005, 123(16), 161103.
44. C. J. Cramer and D. G. Truhlar, Density functional theory for transition metals and transition metal chemistry, Phys. Chem. Chem. Phys., 2009, 11(46), 10757–10816.
45. J. T. A. Gilmour and N. Gaston, 5-Fold symmetry in superatomic scandium clusters: exploiting favourable orbital overlap to sequester spin, Phys. Chem. Chem. Phys., 2020, 22(7), 4051–4058.
46. P. Saha, F. Buendía, L. Van Duong and M. T. Nguyen, A topological path to the formation of a quasi-planar B₇₀ boron cluster and its dianion, Phys. Chem. Chem. Phys., 2023, 26, 15369–15375.
47. H. T. Pham, L. V. Duong, B. Q. Pham and M. T. Nguyen, The 2D-to-3D geometry hopping in small boron clusters: The charge effect, Chem. Phys. Lett., 2013, 577, 32–37.
48. L. V. Duong, D. T. T. Mai, M. P. Pham-Ho and M. T. Nguyen, A theoretical approach to the role of different types of electrons in planar elongated boron clusters, Phys. Chem. Chem. Phys., 2019, 21(24), 13030–13039.
49. Z. J. Wu, H. J. Zhang, J. Meng, Z. W. Dai, B. Han and P. C. Jin, Structural stability and electronic state of transition metal trimers, J. Chem. Phys., 2004, 121(10), 4699–4704.
50. B. N. Papas and H. F. Schaefer III, Homonuclear transition-metal trimers, J. Chem. Phys., 2005, 123(7), 074321.
51. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305.
52. M. Saunders, Stochastic search for isomers on a quantum mechanical surface, J. Comput. Chem., 2004, 25(5), 621–626.
53. J. Zhao, Q. Du, S. Zhou and V. Kumar, Endohedrally Doped Cage Clusters, Chem. Rev., 2020, 120(17), 9021–9163.
54. T. Inoue, M. Hatanaka and A. Nakajima, Oxidative Activation of Small Aluminum Nanoclusters with Boron Atom Substitution prior to Completing the Endohedral B@Al₁₂⁻ Superatom, J. Am. Chem. Soc., 2023, 145(42), 23088–23097.
55. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales and F. Weinhold, Natural Bond Orbital, version 5.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2001.
56. M. Brack, The physics of simple metal clusters: self-consistent jellium model and semiclassical approaches, Rev. Mod. Phys., 1993, 65(3), 677–732.
57. N. M. Tam, T. B. Tai and M. T. Nguyen, Thermochemical Parameters and Growth Mechanism of the Boron-Doped Silicon Clusters, Si_nB_q with n = 1–10 and q = −1, 0, +1, J. Phys. Chem. C, 2012, 116(37), 20086–20098.
58. H. R. Larsson, H. Zhai, C. J. Umrigar and G. K.-L. Chan, The Chromium Dimer: Closing a Chapter of Quantum Chemistry, J. Am. Chem. Soc., 2022, 144(35), 15932–15937.
59. L. B. Knight Jr, R. W. Woodward, R. J. Van Zee and W. Weltner Jr, Properties of Sc₃, Y₃, and Sc₁₃ molecules at low temperatures, as determined by ESR, J. Chem. Phys., 1983, 79(12), 5820–5827.
60. S. P. Walch and C. W. Bauschlicher Jr, On 3d bonding in the transition metal trimers: The electronic structure of equilateral triangle Ca₃, Sc₃, Sc₃⁺, and Ti₃⁺, J. Chem. Phys., 1985, 83(11), 5735–5742.
61. I. Pápai and M. Castro, A density functional study of Sc₂ and Sc₃, Chem. Phys. Lett., 1997, 267(5), 551–556.
62. A. Bérces, The structures and vibrational frequencies of small clusters of transition metal and main group elements A gradient corrected density functional study, Spectrochim. Acta, Part A, 1997, 53(8), 1257–1272.
63. V. T. Ngan and M. T. Nguyen, The Aromatic 8-Electron Cubic Silicon Clusters Be@Si₈, B@Si₈⁺, and C@Si₈²⁺, J. Phys. Chem. A, 2010, 114(28), 7609–7615.

---

Footnote

† Electronic supplementary information (ESI) available: (i) The structures, multiplicities and relative energies (rE, kcal mol⁻¹) of the lowest-lying Sc_n^+/0/− (n = 2–13), (ii) the molecular orbital (MO) diagram of the Sc₆^+/0/−, B@Sc₆^+/0/− and Sc₁₁^+/0/− at different spin states, and (iii) calculated density of states (DOS) for the lowest-lying neutral clusters of the Sc₆, Sc₇, B@Sc₆ and B@Sc₇ isomers. (iv) Coordinates of the lowest-lying Sc_n^+/0/− and Sc_n−1B^+/0/− (n = 2–13) clusters. See DOI: https://doi.org/10.1039/d4ra06541g

---