DOI:
10.1039/D4RA07105K
(Paper)
RSC Adv., 2024,
14, 38615-38633
Enhanced magnetoresistance properties of K-site deficient La0.85K0.1□0.05MnO3 manganites synthesized via sol–gel, wet-mixing, and solid-state reaction methods
Received
3rd October 2024
, Accepted 18th November 2024
First published on 6th December 2024
Abstract
The effect of synthesis methods on the structural, magnetic, electrical transport, and magnetoresistance (MR) properties of K-deficient La0.85K0.1□0.05MnO3 (LKdMO) materials has been investigated. The compounds were synthesized via sol–gel (SG), wet-mixing (WM), and solid-state (SS) reaction. The resulting ceramics were characterized using X-ray diffraction (XRD), scanning electron microscopy (SEM), energy dispersive spectroscopy (EDS), X-ray photoelectron spectroscopy (XPS), and four point probe (FPP) techniques to evaluate their crystal structure, morphologies, elemental composition, electrical transport properties, and magnetoresistance (MR) behavior. This study reveals that the electrical- and magneto-transport properties of LKdMO ceramics are strongly influenced by their synthesis method. Among the samples, the WM method yielded ceramics with smaller grain sizes and more dispersed grain boundaries, leading to reduced resistivity. The MR values for LKdMO ceramics synthesized through SG, WM, and SS reached 17.05% at 287.74 K, 54.68% at 271.50 K, and 47.09% at 270.25 K, respectively. The WM-synthesized sample exhibited superior crystal quality and enhanced magnetic and electrical properties. These results indicate that LKdMO ceramics are promising candidates for application in magnetic sensors.
1. Introduction
Lanthanum manganite materials La1−xAExMnO3 (where AE represents alkaline earth ions) have been extensively studied because of their wide range of applications, including data storage, magnetic sensors, magnetic refrigeration, and spintronics.1–4 Doping with divalent or monovalent ions at the La site or doping Mn with 3d transition ions can lead to change from antiferromagnetic type-A to various states, such as ferromagnetic metals (FMMs), ferromagnetic insulators (FMIs), and antiferromagnetic insulators (AFMIs).5 Doped lanthanum manganites exhibit intriguing phenomena, such as magnetoresistance (MR) and the magnetocaloric effect (MCE), which depend on the ionic radii of the A-site ion6–10 and Mn3+/Mn4+.11 Substitution of divalent or monovalent ions at the La3+ site introduces mixed valence states of Mn (Mn3+ and Mn4+).12 Replacing divalent alkaline earth metals (such as Ba2+, Sr2+, and Ca2+) with monovalent ions (such as Na+, Ag+, and K+) results in significant changes in the mixed valence of manganese, leading to enhanced double exchange (DE) interactions and induction of colossal magnetoresistance (CMR).13,14 Doping with monovalent ions (K+) at the La3+ site, for each amount of K, twice the amount of Mn3+ ions is oxidized to Mn4+, resulting in an excess of Mn3+ regions around La3+ and excess Mn4+ regions around K+ ions. This indicates that even a small amount of dopant can generate a large number of charge carriers, thereby enhancing conductivity.15–17 Deficiencies at the A-site in the perovskite structure lead to an increased number of Mn4+ ions and changes in the ionic radii of the A-site 〈rA〉, which affect the Mn–O bond length and the Mn–O–Mn bond angle, thus increasing DE interaction and TC.18 Cation vacancies at the A-site also affect the physical properties of manganites, such as their magnetic and transport properties.19,20
Research on the colossal magnetoresistance (CMR) effect, particularly in perovskite manganite materials with mixed valence states, has garnered significant attention in recent years.21–23 The ferromagnetic properties of the material enhance the movement of conduction electrons and reduce the kinetic energy. CMR is associated with electron transport and is influenced by variations in magnetic structures induced by an external magnetic field.24 The CMR effect is influenced by the internal stress resulting from variations in the ionic radii of constituent ions,25 grain boundaries,26,27 grain size,28 crystallinity,29 and tunnel junctions resulting from doping.30 Oxides based on LaMnO3 exhibited high MR values under low field influence. Different synthesis preparation methods result in different properties of manganites.31–34 Experimental conditions can significantly influence various parameters that affect the physical properties of manganite materials.35–37 The most commonly used synthesis method for manganite materials is the solid-state reaction (SS) method. This method requires higher annealing temperatures and longer holding times to achieve a homogeneous composition and desired structure.38,39 Recently, chemical reaction methods requiring lower preparation temperatures and improved sample homogeneity have been developed,32 such as the sol–gel method.35–37 Additionally, the wet-mixing (WM) method is more efficient than the sol–gel (SG) method because it does not require additional precursors, such as citric acid for metal ion complexation, and results in less mass loss during heating. WM is a straightforward and promising method for low-cost material production.34 The properties of manganites continue to attract attention and development because of their excellent physical properties and potential applications in devices.40 Therefore, it is crucial to understand how synthesis methods affect various aspects of the physical properties of manganite.32 Lik et al. reported differences in properties such as TC and MR, which are highly influenced by the grain size and crystallinity affected by the synthesis method of the sample.41 In 2021, Jin et al. reported a maximum MR value of 46.39% at room temperature (293.03 K) for La1−xKxMnO3 with x = 0.15, attributed to the double exchange (DE) mechanism and tunneling effects.42 Additionally, the formation of vacancies in LaMnO3-based materials can lead to increased MR values. Dhahri et al. reported that La1−x□xMnO3 with x = 0.2 achieved an MR value of nearly 85% at 255 K.43 In 2021, Yu et al. investigated the influence of synthesis methods on the electrical transport properties of La0.67Ca0.33MnO3 material using the solid-state reaction and sol–gel methods. The MR value of LCMO ceramics was found to be 39.97% at a temperature of 246.78 K and 54.27% at a temperature of 263.80 K for the solid-state and sol–gel samples, respectively, with the application of a 1 T magnetic field.44 In Lik et al.'s research, they also compared the effect of synthesis methods on La0.7Sr0.3MnO3 ceramics synthesized using SG and SS methods, yielding maximum MR values of 22% and 18% at a temperature of 80 K, respectively.41 In 2013, Pan et al. successfully prepared La0.85K0.15MnO3 ceramics using variations of the solid-state (SS), sol–gel (SG), and co-precipitation (CP) methods and then compared the electron transport properties of the material. The MR values obtained were 6%, 3.5%, and 8%, respectively, at a temperature of 300 K under a 1 T applied magnetic field.45
Research on lanthanum manganites has attracted considerable interest due to their promising applications in fields such as magnetoresistance and energy technology. Although significant developments and progress have been made, challenges remain in optimizing magnetic and transport properties. Various solutions continue to be explored, such as doping effects and synthesis techniques. Based on the literature mentioned above, potassium-doped lanthanum manganites (LKMO) and doping in the form of vacancies have shown promising potential due to the possibility of enhanced magnetoresistance. Moreover, systematic studies comparing the effects of different synthesis methods on the transport properties of lanthanum manganites remain limited. Therefore, this study aims to address these gaps by investigating La0.85K0.1□0.05MnO3 (LKdMO) synthesized using several methods, such as sol–gel, wet-mixing, and solid-state reaction, to identify the most optimal synthetic method. By focusing on these aspects, this study fundamentally aims to answer unresolved questions about optimizing the magnetoresistance of lanthanum manganite-based materials and to tackle existing challenges in this field of materials science. Therefore, this study explores the effects of different synthesis routes on manganese oxide, focusing on the high magnetoresistance (MR) of ceramic K-deficient La0.85K0.1□0.05MnO3 (LKdMO). The crystal structure, morphology, electrical transport properties, and magnetic properties of LKdMO materials obtained using the SG, WM, and SS methods were compared and discussed.
2. Experimental
2.1 Sol–gel (SG) method
LKdMO samples were synthesized by SG using high purity La2O3, KNO3, and Mn(NO3)2·4H2O. All the raw materials were stirred and dissolved in deionized water, nitric acid, ethylene glycol, and citric acid. Citric acid was used as a catalyst in the synthesis process, whereas ethylene glycol acted as a chelating agent. Each dissolved base material was then mixed and stirred using a magnetic stirrer at a speed of 500 rpm, and the solution temperature was adjusted to the range of 75–80 °C for the nitric acid evaporation process. After the materials were mixed, the pH of the solution was adjusted by gradually adding an ammonia solution until the pH reached 7. Next, the process was continued with a heat treatment. The dehydration process was carried out at a temperature of 190 °C for 2 h to dry the sample and eliminate the water content within it. Subsequently, the process proceeded to calcination, wherein the sample was placed in a crucible and heated to 600 °C for 6 h in a furnace to remove any remaining organic substances. Next, the sample was ground and subjected to a pre-sintering process at 900 °C for 12 h. The powdered samples were compacted under a pressure of 10 t to form pellets. Finally, sintering was performed again with the sample in pellet form at 1200 °C for 24 h.
2.2 Wet-mixing (WM) method
LKdMO samples were synthesized via WM using high purity La2O3, KCO3, and MnCO3. All raw materials were mixed and dissolved using nitric acid (HNO3) in a beaker, which was stirred using a magnetic stirrer at a speed of 500 rpm within a temperature range of 75–80 °C until the solution formed a precipitate. The precipitate was then dehydrated in an oven at 190 °C for 2 h to remove the solvent. The dry sample was ground using a mortar and pestle to form a powder. The powder was then subjected to calcination at 600 °C for 6 h. After calcination, the sample was ground again and pre-sintered at 900 °C for 12 h. Following pre-sintering, the powder was compacted under a pressure of 10 t to form pellets. Finally, sintering was performed on the pellet-form sample at 1200 °C for 24 h.
2.3 Solid-state reaction (SS) method
LKdMO samples were synthesized via SS using high purity La2O3, KCO3, and MnCO3. All raw materials were ground using a mortar for 30 min. The resulting powder was then calcined at 600 °C for 6 h. After calcination, the powder was ground again and subjected to pre-sintering at 900 °C for 12 h. Following pre-sintering, the powder was compacted under 10 tons of load to form pellets. Finally, sintering was performed on the pellet samples at 1200 °C for 24 h. The synthesis process flow of the SG, WM, and SS methods is illustrated in Fig. 1.
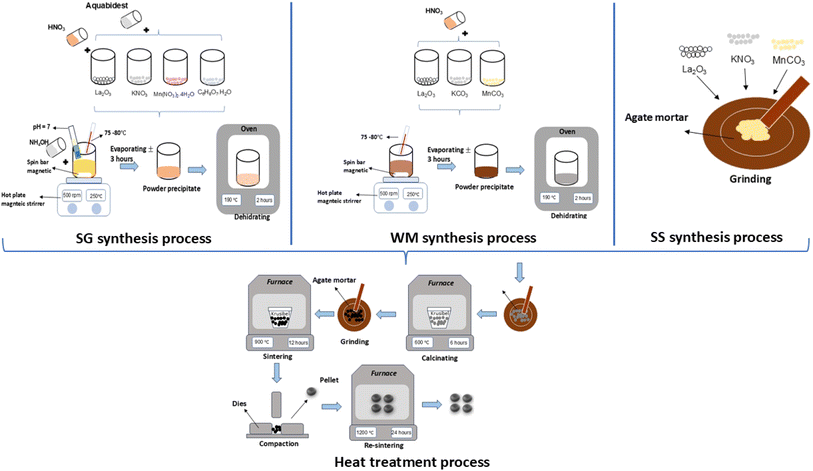 |
| | Fig. 1 Process flow of the SG, WM, and SS methods. | |
2.4 Characterization
The crystal structures and phases were identified using X-ray diffraction (Bruker AXS, D8) with Cu Kα (λ = 1.5406 Å) radiation in the 2θ range of 20°–90°. The surface morphology of LKdMO and elemental analysis were examined using scanning electron microscopy (SEM, Hitachi). The magnetic behavior was evaluated using a vibrating sample magnetometer (VSM, SQUID-VSM) with a magnetic field of 1 T at room temperature. The elemental compositions were identified using X-ray photoelectron spectroscopy (XPS) using an Axis Supra + Kratos Analytical system with photon energy radiation Al Kα (λ = 1486.6 eV). The resistivity was measured and evaluated by applying the four point probe (FPP) method using a Cryogenic Magnet (Oxford Teslatron instrument) in the temperature range of 50–300 K under 0 and 2 T applied magnetic fields.
3. Results and discussion
3.1 Crystal structure
The X-ray diffraction (XRD) patterns of LKdMO samples synthesized using the sol–gel (SG), wet-mixing (WM), and solid-state (SS) methods and compared with those of the parent compound (La0.85K0.15MnO3 (LKMO)) are shown in Fig. 1(a), and the FWHM shifts of the LKdMO and LKMO samples are illustrated in Fig. 2(b). As depicted in Fig. 2, it is confirmed that the substitution of vacancies at the K site, amounting to 0.05, did not alter the crystal structure of the parent compound. According to the XRD data, all the samples exhibited a rhombohedral crystal structure with R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group (no. 167). However, the SG sample also showed the presence of a secondary Mn2O3 phase with an orthorhombic crystal structure (Pbca). Figure 2 shows that the broadening and full width at half maximum (FWHM) in the LKdMO samples synthesized by the wet-mixing (WM) and solid-state (SS) methods are smaller, with higher intensity compared to the parental compound LKMO. This indicates that the growth of K-deficient formations promotes crystallinity and enhances crystal properties.46
c space group (no. 167). However, the SG sample also showed the presence of a secondary Mn2O3 phase with an orthorhombic crystal structure (Pbca). Figure 2 shows that the broadening and full width at half maximum (FWHM) in the LKdMO samples synthesized by the wet-mixing (WM) and solid-state (SS) methods are smaller, with higher intensity compared to the parental compound LKMO. This indicates that the growth of K-deficient formations promotes crystallinity and enhances crystal properties.46
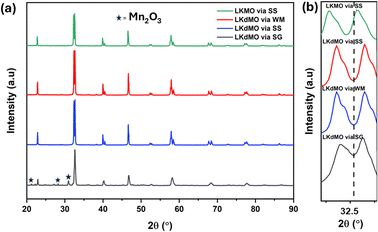 |
| | Fig. 2 (a) XRD patterns of the LKdMO compounds synthesized via SG, WM, and SS and parental compound (LKMO) via the SS method, (b) FWHM shift of the LKdMO and parental compound (LKMO) samples. | |
The unit cell volumes of each sample were not significantly different. The deficiency of La ions at the A site led to a reduction in the unit cell volume, which was attributed to the increased presence of Mn4+ ions in the compound. The ionic radius of Mn4+ (0.53 Å) is smaller than that of Mn3+ (0.645 Å).47 However, a deficiency of K+ ions results in an increase or decrease in the unit cell volume, which cannot be explained solely by the number of Mn4+ ions. This phenomenon is associated with the ionic radius of the vacancies at the A site, which may be larger or smaller than that of K+. Changes in the unit cell volume influence the Mn–O bond length, Mn–O–Mn bond angle, and electron movement between Mn3+ and Mn4+, which are significantly affected by the deficiency at the A site in manganite compounds.48 Substitution with K ions and vacancies results in the replacement of some lanthanum ions by K ions. Because K has a different ionic radius than La, combined with the formation of vacancies, this leads to lattice distortions in the crystal, resulting in deviations in the Mn–O–Mn bond angles and distances. These distortions cause an overlap between Mn and O, which plays an important role in electron mobility and magnetic interactions. Potassium doping and vacancy formation introduce strain due to changes in lattice symmetry, affecting electron hopping.49–51 In manganite materials, crystal strain affects changes in the electronic bandwidth, making the material more responsive to magnetic fields and potentially increasing the MR value.52 K ions have a lower valency than La, and vacancy formation also causes the A-site to lack the energy to stabilize, thus affecting the Mn3+/Mn4+ ratio. This can increase the number of charge carriers, facilitating electron hopping between Mn3+ and Mn4+. This increased electron hopping will improve conductivity, as charge carriers move more easily. The presence of Mn3+ and Mn4+ ions is necessary to strengthen electron transfer and magnetic coupling.52
The XRD characterization data were further analyzed using Rietveld refinement with FullProf software. The Rietveld refinement curves for the experimental data are shown in Fig. 3. The Rietveld refinement results confirmed that the samples had a rhombohedral structure with an R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group. The Goodness of fit (χ2) value indicated that the WM sample had a value close to 1, suggesting a better fit and good agreement with the XRD profile than the SG and SS samples. The use of the wet-mixing (WM) method is more efficient than the sol–gel (SG) method. The WM method does not require additional precursors or chelating agents to complex metal ions; thus, less mass is lost during the combustion process.34 Additionally, the amount of water used during WM synthesis was reduced, leading to a shorter mixing duration. The WM method, using nitric acid as a solvent, allows the use of a wide variety of carbonate precursors, including both soluble and insoluble carbonates. However, the SG method is limited to soluble precursors.53 It is possible that the wet-mixing method enables WM to produce crystals with better quality than the sol–gel (SG) and solid-state reaction (SS) methods. In the WM method, the use of nitric acid as a solvent and a simpler mixing process allows for a more uniform distribution of precursors, enabling the crystallization process to occur more optimally. Additionally, the minimal mass loss during combustion and shorter synthesis time may contribute to the formation of crystals with better quality compared with the SG and SS methods.
c space group. The Goodness of fit (χ2) value indicated that the WM sample had a value close to 1, suggesting a better fit and good agreement with the XRD profile than the SG and SS samples. The use of the wet-mixing (WM) method is more efficient than the sol–gel (SG) method. The WM method does not require additional precursors or chelating agents to complex metal ions; thus, less mass is lost during the combustion process.34 Additionally, the amount of water used during WM synthesis was reduced, leading to a shorter mixing duration. The WM method, using nitric acid as a solvent, allows the use of a wide variety of carbonate precursors, including both soluble and insoluble carbonates. However, the SG method is limited to soluble precursors.53 It is possible that the wet-mixing method enables WM to produce crystals with better quality than the sol–gel (SG) and solid-state reaction (SS) methods. In the WM method, the use of nitric acid as a solvent and a simpler mixing process allows for a more uniform distribution of precursors, enabling the crystallization process to occur more optimally. Additionally, the minimal mass loss during combustion and shorter synthesis time may contribute to the formation of crystals with better quality compared with the SG and SS methods.
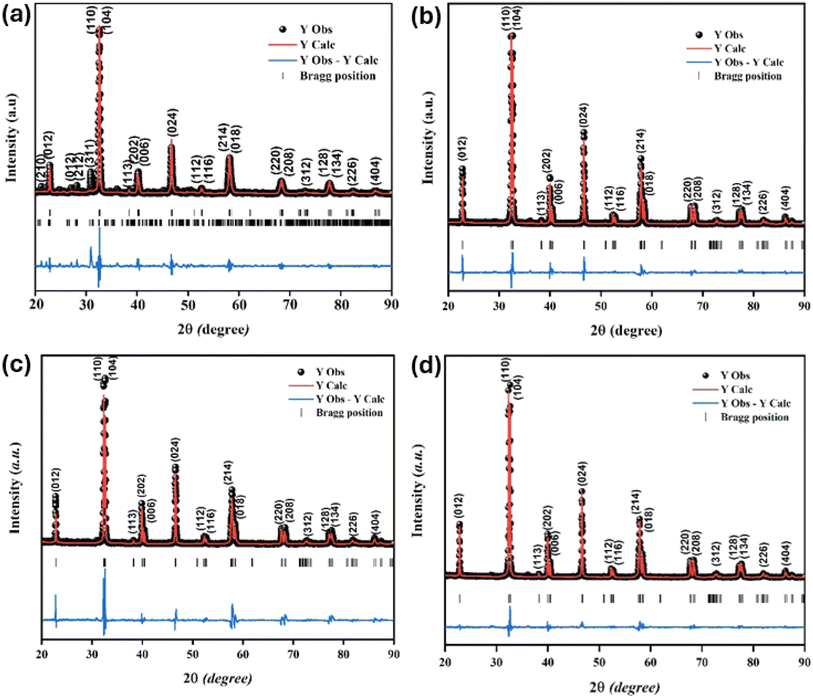 |
| | Fig. 3 Rietveld refinement diffraction patterns of the LKdMO compound synthesized using (a) SG, (b) WM, and (c) SS, and (d) the parental compound (LKMO). | |
Table 1 presents the lattice parameters for all samples, which did not exhibit significant differences. The differences in the lattice parameters and unit cell volumes among the samples may be attributed to the deficiencies in the constituent elements and variations in the Mn3+/Mn4+ ratio, which are influenced by different synthesis methods. The different synthesis methods for LdKMO material do not create significant differences in the crystal structure. The atomic positions of each element are as follows: La and K occupy position 6a (0, 0, ¼), Mn occupies position 6b (0, 0, 0), and O occupies position 18e (x, 0, ¼). The presence of a size disorder due to the influence of different methods affects lattice strain, causing oxygen ions to undergo random displacements. This leads to MnO6 octahedral distortion and electron localization.54 The c parameter shows a trend of varying values, with values ranging from 13.38850 to 13.96530 Å. This variation is associated with the presence of lattice strain during different synthesis treatments.55 From the XRD data, the theoretical density of the sample can also be calculated and determined using the equation 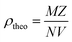 , where M is molecular mass, Z is the number of units per unit cell (Z = 6, for rhombohedral structure), N is Avogadro's number (N = 6.02 × 1023), and V is the unit cell volume.51 Based on the calculations, the density values for each sample do not show significant differences, as the only varying parameter is the unit cell volume, which does not differ greatly among the samples. The theoretical density of the LKdMO sample is 6.36 g cm−3 for all method variations, and 6.39 g cm−3 for parental compound (LKMO), a value within the density range of manganite-based materials, as previously reported.51
, where M is molecular mass, Z is the number of units per unit cell (Z = 6, for rhombohedral structure), N is Avogadro's number (N = 6.02 × 1023), and V is the unit cell volume.51 Based on the calculations, the density values for each sample do not show significant differences, as the only varying parameter is the unit cell volume, which does not differ greatly among the samples. The theoretical density of the LKdMO sample is 6.36 g cm−3 for all method variations, and 6.39 g cm−3 for parental compound (LKMO), a value within the density range of manganite-based materials, as previously reported.51
Table 1 Lattice parameters of the La0.85K0.1□0.05MnO3 sample using the SG, WM, and SS methods
| Parameter |
La0.85K0.1□0.05MnO3 |
La0.85K0.15MnO3 |
| SG |
WM |
SS |
SS |
| Space group |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
| a = b (Å) |
5.50309 |
5.52841 |
5.52974 |
5.53631 |
| c (Å) |
13.39260 |
13.96530 |
13.36940 |
13.38850 |
| Volume unit cell (Å3) |
353.9079 |
353.8879 |
354.0397 |
355.3885 |
| 〈DS〉 (nm) |
121.0237 |
79.8912 |
82.1216 |
65.6190 |
| 〈DW–H〉 (nm) |
180 |
151 |
166 |
138 |
| dMn–O (Å) |
1.9692 |
1.9653 |
1.9670 |
1.9663 |
| θMn–O–Mn (°) |
160.7 |
164.1 |
163.5 |
164.8 |
| Rprofile (%) |
36.6 |
19.9 |
15.4 |
34.3 |
| Rwp (%) |
39.4 |
22.3 |
17.8 |
33.0 |
| Goodness of fit (χ2) |
4.62 |
1.82 |
2.34 |
1.77 |
Notably, the unit cell volume of the SG sample was larger than those of the WM and SS samples. This is influenced by variations in the Mn–O bond length (dMn–O) and Mn–O–Mn angle (θMn–O–Mn) related to the Mn3+ and Mn4+ ratios and the A-site deficiency due to K+ ion substitution. The stability of the perovskite structure with the ABO3 formula in manganites was predicted using the Goldschmidt tolerance factor equation defined as 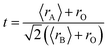 , where 〈rA〉 is the average ionic radius of the A-site, 〈rB〉 is the average ionic radius of the B-site, and 〈rO〉 is the ionic radii of oxygen. Ionic size mismatch in the crystal structure leads to a decrease in the symmetry. An ideal cubic structure was achieved when ‘t’ = 1. A tolerance factor in the range of ‘t’ = 1 within the range of 0.90 < t < 1 indicates that the crystal structure experiences rhombohedral distortion. This reduction was due to the rotation of the adjacent MnO6 octahedron in opposite directions along the cubic (111) axis. If ‘t’ = 1 within the range 0.75 < t < 0.90, the distortion increases, leading to an orthorhombic symmetry change caused by octahedron bending inconsistent with the MnO6 octahedron rotation around the (110) and (104) planes. For the LKdMO samples, a tolerance factor (t) value of 0.962 was obtained, indicating that the LKdMO ceramics had a rhombohedral crystal structure, which is consistent with the XRD analysis. The rhombohedral structure is evidenced by the presence of a doublet intensity in the 2θ range of 32.4 in the XRD pattern due to the (110) and (104) planes. Such peak splitting is characteristic of a rhombohedral crystal structure.17
, where 〈rA〉 is the average ionic radius of the A-site, 〈rB〉 is the average ionic radius of the B-site, and 〈rO〉 is the ionic radii of oxygen. Ionic size mismatch in the crystal structure leads to a decrease in the symmetry. An ideal cubic structure was achieved when ‘t’ = 1. A tolerance factor in the range of ‘t’ = 1 within the range of 0.90 < t < 1 indicates that the crystal structure experiences rhombohedral distortion. This reduction was due to the rotation of the adjacent MnO6 octahedron in opposite directions along the cubic (111) axis. If ‘t’ = 1 within the range 0.75 < t < 0.90, the distortion increases, leading to an orthorhombic symmetry change caused by octahedron bending inconsistent with the MnO6 octahedron rotation around the (110) and (104) planes. For the LKdMO samples, a tolerance factor (t) value of 0.962 was obtained, indicating that the LKdMO ceramics had a rhombohedral crystal structure, which is consistent with the XRD analysis. The rhombohedral structure is evidenced by the presence of a doublet intensity in the 2θ range of 32.4 in the XRD pattern due to the (110) and (104) planes. Such peak splitting is characteristic of a rhombohedral crystal structure.17
The average crystallite size from the XRD characterization results was calculated by applying the Scherrer method using the following equation:
| |
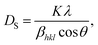 | (1) |
where
DS is the average crystallite size,
K is the shape factor constant (0.9),
λ is the X-ray wavelength of Cu Kα (
λ = 1.5406), and
βhkl is the full width at half maximum (FWHM) of the highest intensity peak in the XRD pattern, measured in radians. The crystallite sizes calculated using the Scherrer method are listed in
Table 1. The average crystallite sizes (
D) calculated using the Debye–Scherrer method (
DS) for the SG, WM, and SS samples were 121.02, 79.89, and 82.12 nm, respectively.
In addition to the Scherrer method, the crystallite size was calculated using the Williamson–Hall method (DW–H). This method assumes that the microstrain is uniform along the crystallographic direction, which makes it isotropic. The βhkl is the FWHM of the Bragg peak in radians and is calculated using the following equation:
| |
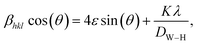 | (2) |
where
DW–H is the crystallite size and
ε is the microstrain of the sample, calculated from the slope and intercept of the plot of
β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos(
θ)
vs. 4
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
sin(
θ). The results of the W–H plot are shown in
Fig. 4. The
y-axis represents the value considered for each diffraction peak of the sample. A good linear fit across all values resulted in a straight line, where the crystallite size was obtained from the
y-intercept, and the microstrain was derived from the slope of the line. It should be noted that
βhkl (FWHM in radians) of each peak with intensity was measured using Gaussian function fitting.
56 The average crystallite sizes (
D) calculated using the Williamson–Hall method (
DW–H) for the SG, WM, and SS samples were 180, 161, and 166 nm, respectively. The SG sample exhibits a larger crystallite size, which was influenced by the FWHM values at higher (2
θ) angles, resulting in higher crystallinity compared to the WM and SS samples. Teixeira
et al. also noted that the SS method has a maximum crystallite size limitation of 100 nm.
57 The crystallite size calculated using the Williamson–Hall method (
DW–H) was larger than that obtained using the Scherrer method (
DS) because of the neglect of strain-induced broadening effects in the Scherrer method (
DS).
58
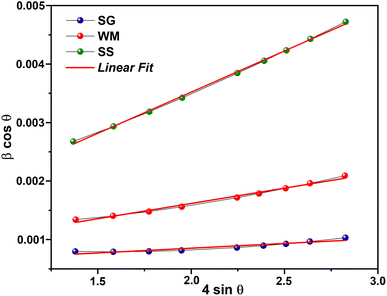 |
| | Fig. 4 W–H plot results. | |
3.2 Surface morphology
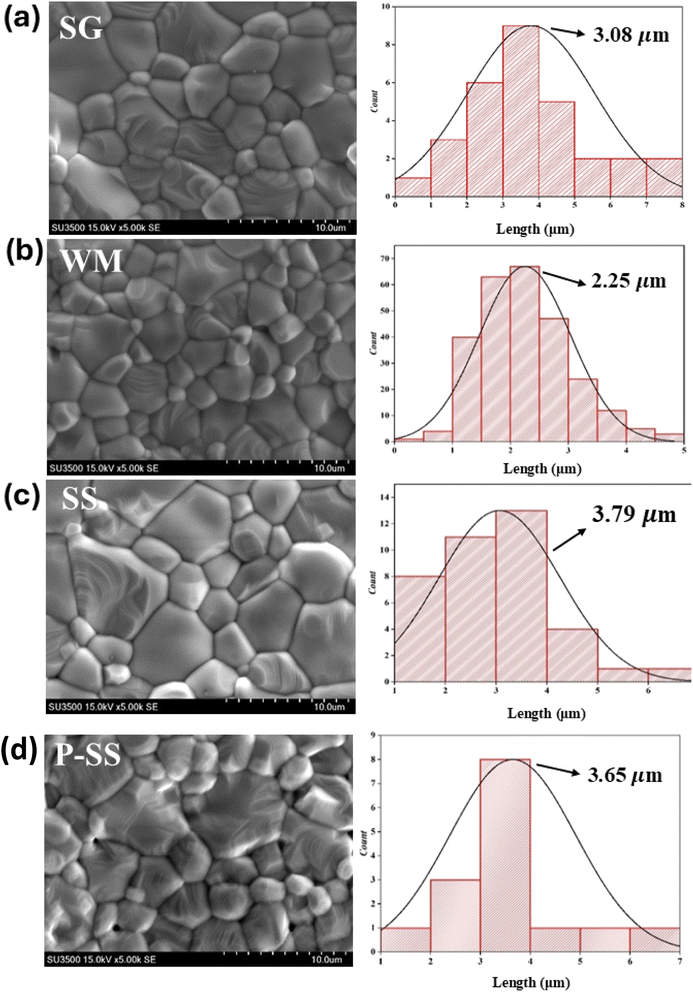
SEM images of the LKdMO sample synthesized by the SG, WM, and SS methods and the parental compound (LKMO) are shown in Fig. 5. The SEM images also indicate that the substitution of K deficiency in LKdMO does not alter the morphology of the parent compound's structure. All samples consisted of large and small grains ranging from spherical to truncated hexagonal shapes. The differences in the grain size of the LKdMO samples synthesized using different methods were investigated. The average grain sizes of the LKdMO by SG, WM, SS, and LKMO are 3.08 μm, 2.25 μm, 3.79 μm, and 3.65 μm, respectively. The grain size produced in each sample is found to be larger than the average crystal size. This indicates that each particle observed in the SEM measurements consists of several crystalline grains.59,60
 |
| | Fig. 5 SEM images of the La0.85K0.1□0.05MnO3 compound synthesized via (a) SG, (b) WM, and (c) SS, and (d) the parental compound via SS. | |
These results are within a reasonable range compared to previous experiments by Wei et al. and Shaikh et al., who reported grain sizes of 1–2 μm for La0.8−xK0.2Mn1+xO3 using the SG method61 and 2–3 μm for La1−xKxMnO3 (x = 0.1, 0.125, and 0.15) using the SS method.62 The SS sample had a larger average grain size than those of the SG and WM samples. Fig. 5 shows that the SS sample exhibits poor contraction, indicated by non-uniform grain sizes, while the SG sample shows significant differences in grain size, with more uniform grains. Therefore, the sol–gel method is effective in enhancing the uniformity of the grain size in LKdMO ceramic samples. This is because the SS sample had some grains that coagulated into larger grains.45 An increase in grain size can enhance electrostatic strength, which leads to a reduction in the lattice parameters a = b and affects the unit cell volume.63 Furthermore, lattice strain increases proportionally with grain size. The crystal lattice strain can directly impact the lattice parameters a = b as well as the unit cell volume, constricting the lattice.64
Furthermore, the WM sample showed smaller grain sizes than the SG sample. This was because the SG method was carried out under neutral pH conditions, while the WM method was carried out under acidic conditions because the precursor was dissolved using nitric acid. Therefore, the pH conditions and the addition of a chelating agent are parameters that affect the grain size differences of each sample.34 In the process of crystal and grain formation, the pH of the solution during the synthesis has a significant influence. A higher pH supports the growth of larger crystals and grains, which promotes the formation of higher porosity and reduces the density. Meanwhile, smaller and more compact grains are produced at lower or more acidic pH levels, thereby decreasing porosity and increasing density.65,66 This correlation is evident in this study, where the SG sample with a higher solution pH (pH = 7) exhibits larger crystal and grain sizes than the WM sample, which has a solution with a pH of less than 7. The SG sample may also produce greater porosity, reducing the quality of the grains formed. The grain size produced in each sample is found to be larger than the average crystal size. This indicates that each particle observed in the SEM measurements consists of several crystalline grains.59,60 An increase in grain size can enhance electrostatic strength, which leads to a reduction in the lattice parameters a = b and affects the unit cell volume.63 Furthermore, lattice strain increases proportionally with grain size. The crystal lattice strain can directly impact the lattice parameters a = b as well as the unit cell volume, constricting the lattice.64
The resistivity of a material is influenced by intra-grain and inter-grain electron transfers. The electron transport properties within the grains can be explained by the double-exchange (DE) mechanism and the Jahn–Teller effect. Following intra-grain electron transport, the grain boundary (GB) became the main factor affecting resistivity. Smaller grain sizes result in more GBs, which leads to increased scattering at GBs and domain boundaries, thus causing an increase in the resistivity of the materials.44
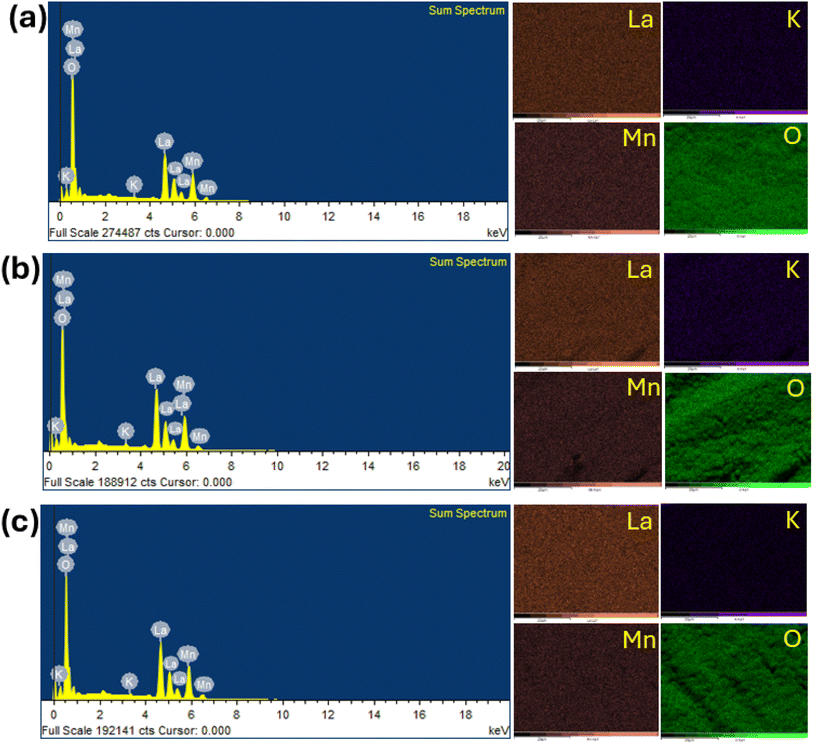
To confirm the elemental composition and surface distribution, energy dispersive X-ray spectroscopy (EDS) analysis was conducted, with the data collected, as shown in Fig. 6. Fig. 6 shows the EDS patterns and elemental distribution of the LKdMO samples synthesized by applying the SG, WM, and SS methods. The SG, WM, and SS samples exhibited a uniform distribution of La, K, Mn, and O in the LKdMO ceramics. From the EDS results, the atomic percentages of the elements La, K, Mn, and O were obtained. These percentages are compared with the XPS characterization and further stoichiometric calculations.
 |
| | Fig. 6 Elemental mapping image and EDS spectrum of LKdMO compounds synthesized by (a) SG, (b) WM, and (c) SS methods. | |
3.3 X-ray photoelectron spectroscopy (XPS)
The chemical valence states of the LKdMO ceramics were characterized by XPS, and the results are shown in Fig. 7. Peaks corresponding to La, K, Mn, and O appeared in the XPS spectra. A carbon peak (C 1s) was observed owing to a layer of carbon contamination. This could be because carbon often accumulates as a contaminant on the surface of samples, and XPS has a high surface detection efficiency. The XPS spectra were calibrated using a reference C 1s peak at a binding energy of 284.6 eV. Carbon often accumulates as a contaminant on sample surfaces, even in electron microscopy. Many previous studies also use the C 1s peak of carbon (typically around 284.8 eV) as a reference point for calibrating binding energy in XPS spectra because it is frequently present on surfaces exposed to air, making it a practical and easily accessible standard.67 This approach simplifies calibration, especially when there is no well-defined internal standard within the sample itself.
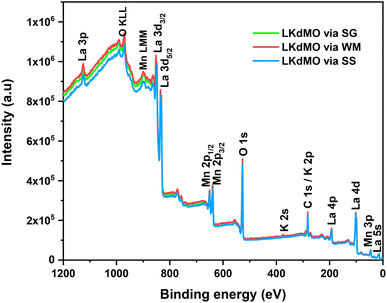 |
| | Fig. 7 XPS survey spectrum of LKdMO compounds. | |
The spectra also show Auger peaks at binding energies of 973 and 900 eV, which are associated with Mn (LMM) and O (KLL), respectively. The narrow-scan spectra for La 3d, K 2p, Mn 2p, and O 1s are presented in Fig. 8–11, respectively. The XPS spectra were analyzed using ESCape software, applying Gaussian–Lorentzian profiles, a Shirley background for the La and Mn spectra, and a linear background for the K and O spectra. The atomic ratios obtained from the XPS results are summarized in Table 2 and compared with the EDS results. Table 2 indicates that K-deficiency was successfully formed in the LKdMO sample for all the synthesis method variations. This is evidenced by the atomic percentages of La, K, Mn, and O, which closely matched the stoichiometric calculations for La0.85K0.1□0.05MnO3. The synthesis process for LKdMO used high-purity precursors (≥99.9%) and was conducted in a controlled atmosphere to minimize contaminants across all method variations. XRD analysis showed that the samples formed a single phase, except for the SG sample, which had a slight secondary phase (Mn2O3). Carbon contamination detected by XPS likely resulted from environmental exposure, but it had a minimal impact on MR and magnetic properties. The composition observed from XPS analysis aligned with theoretical values, confirming the successful formation of K-deficiency, which enhances magnetoresistance through modifications in Mn–O–Mn bonding and charge carrier density.
 |
| | Fig. 8 Narrow scan of La 3d XPS spectra of LKdMO samples synthesized using (a) SG, (b) WM, and (c) SS methods. | |
 |
| | Fig. 9 Narrow scan of K 2p and C 1s XPS spectra of LKdMO samples synthesized using (a) the SG, (b) WM, and (c) SS methods. | |
 |
| | Fig. 10 Narrow scan of Mn 2p XPS spectra of LKdMO samples synthesized via (a) the SG, (b) WM, and (c) SS methods. | |
 |
| | Fig. 11 Narrow scan of O 1s XPS spectra of LKdMO samples synthesized via (a) the SG, (b) WM, and (c) SS methods. | |
Table 2 EDS and XPS results of La0.85K0.1□0.05MnO3 synthesised using the SG, WM dan SS methods
| Samples |
Ratio |
Atomic % |
| La |
K |
Mn |
O |
| La0.85K0.1□0.05MnO3 (SG) |
EDS |
15.89 |
0.04 |
15.57 |
68.59 |
| XPS |
17.3 |
2.6 |
19.9 |
60.20 |
| La0.85K0.1□0.05MnO3 (WM) |
EDS |
17.58 |
0.36 |
17.16 |
64.90 |
| XPS |
17.0 |
2.4 |
19.9 |
60.70 |
| La0.85K0.1□0.05MnO3 (SS) |
EDS |
18.29 |
0.66 |
17.39 |
63.66 |
| XPS |
17.2 |
2.2 |
20.30 |
60.4 |
| La0.85K0.1□0.05MnO3 |
Stoichiometry |
17.17 |
2.03 |
20.20 |
60.60 |
| La0.85K0.15MnO3 (parental) |
Stoichiometry |
17 |
3 |
20 |
60 |
The properties of ceramics are significantly influenced by the grain boundaries (GB).68,69 The O2− ions in the Mn–O–Mn bonds at the GB tend to become unstable and prone to separation from the structure, creating oxygen vacancies. These oxygen vacancies were the main reason for the elemental distribution discrepancies observed in the EDS results. Although different synthesis methods were used, the peak positions of each constituent element in the XPS spectra remained constant.
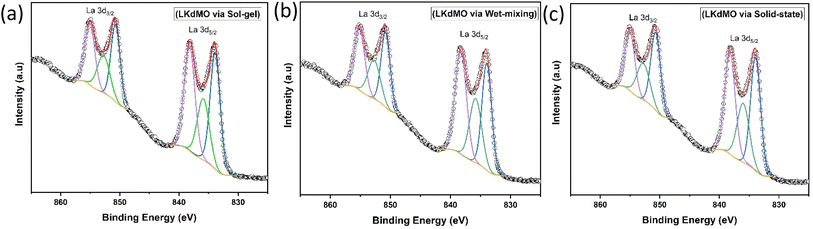
Fig. 8 shows the La 3d core level, which forms a doublet structure, specifically La 3d5/2 and La 3d3/2, at binding energies of approximately 833.8 eV and 850.7 eV, respectively. The separation between the La 3d peaks is 16.9 eV, which is similar to the value reported in the literature.58 After deconvolution of the La 3d spectrum, an energy separation of approximately 4.4 eV for La 3d5/2 and 4.3 eV for La 3d3/2, respectively, were observed. Weak peaks induced during charge transfer were identified as satellite peaks. These La 3d spectra are typical of the manganite oxide family.
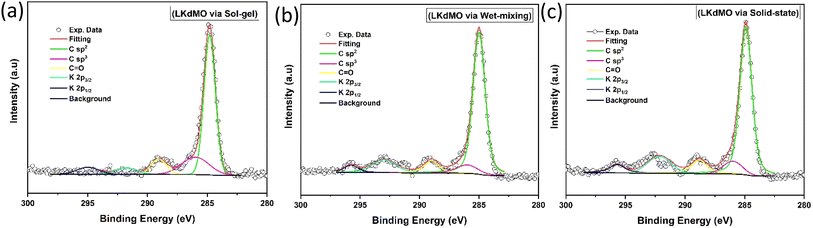
XPS is a method conducted on the surface that provides information about the outermost 10 nm layer, including the carbon surface content, metal content, metal distribution, and chemical state of elements. The binding energy range around carbon (284–289 eV) allows for the identification of various compounds. Deconvolution of the C 1s spectrum reveals components corresponding to C–C bonds at 284.9 eV, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds at 286–287 eV, and O
O bonds at 286–287 eV, and O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–O bonds in carbonates at 288–289 eV. Additionally, peaks at 292.2 eV and 295.0 eV represent K 2p3/2 and K 2p1/2, respectively (Fig. 9). The K 2p peaks cause a shift in the C 1s peak to lower binding energies due to the dipole formation caused by the electronegativity differences between K and C, which are 0.8 and 2.5, respectively.70
C–O bonds in carbonates at 288–289 eV. Additionally, peaks at 292.2 eV and 295.0 eV represent K 2p3/2 and K 2p1/2, respectively (Fig. 9). The K 2p peaks cause a shift in the C 1s peak to lower binding energies due to the dipole formation caused by the electronegativity differences between K and C, which are 0.8 and 2.5, respectively.70
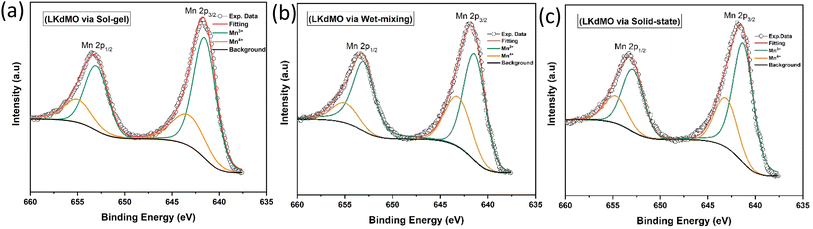
The curve fitting of the Mn 2p spectra for the LKdMO ceramics synthesized by the SG, WM, and SS methods is shown in Fig. 10, and the fitting data are summarized in Table 3. The Mn 2p3/2 peaks for the SG, WM, and SS samples are recorded at binding energies of 641.5 eV, 641.3 eV, and 641.2 eV, respectively, while the Mn 2p1/2 peaks are recorded at 643.2 eV, 643.1 eV, and 643.0 eV, respectively. The binding energies of Mn 2p should be close to those of Mn2O3 and MnO2.71,72 Therefore, the LKdMO ceramics consist of two valence states, Mn3+ and Mn4+. This finding is consistent with previous reports.48,73,74 The Mn 2p peaks for the SG, WM, and SS samples did not show significant changes and were close to the values observed for the studied perovskite materials. The Mn3+/Mn4+ ratios for the SG, WM, and SS samples are 2.41, 2.33, and 2.36, respectively. The WM sample shows a ratio value that is close to the theoretical value of 7/3 (2.33). The proportions of Mn3+ and Mn4+ valence states are influenced by the oxygen concentration, which affects the double-exchange mechanism.67,75
Table 3 XPS fitting results of Mn 2p spectra of LKdMO synthesised using the SG, WM, and SS methods
| Preparation method |
Valence |
Mn 2p3/2 |
Mn 2p1/2 |
Mn3+/Mn4+(7/3 = 2.33) |
| Peak position (eV) |
Area |
Peak position (eV) |
Area |
| SG |
Mn3+ |
641.57 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 786.05 786.05 |
652.82 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 171.98 171.98 |
2.41 |
| Mn4+ |
643.56 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 509.66 509.66 |
654.93 |
9648.849 |
| WM |
Mn3+ |
641.45 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 301.92 301.92 |
652.94 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 333.07 333.07 |
2.33 |
| Mn4+ |
643.21 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 333.07 333.07 |
654.93 |
7794.372 |
| SS |
Mn3+ |
641.22 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 081.18 081.18 |
652.98 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 018.79 018.79 |
2.36 |
| Mn4+ |
643.21 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 234.21 234.21 |
654.70 |
6029.096 |
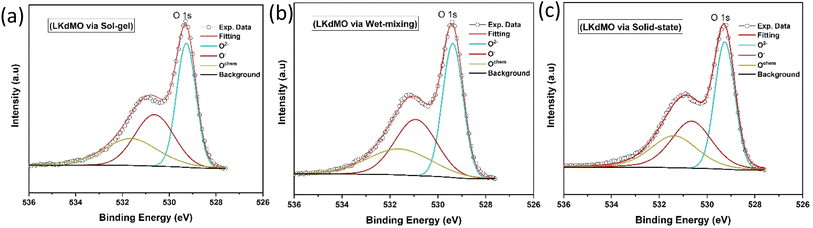
According to the literature, manganese oxides exhibit three valence states of oxygen: divalent oxygen ions (O2−), monovalent oxygen ions (O−), and chemically absorbed oxygen (Ochem) at binding energies of 529, 530, and 532 eV, respectively.44 O2− and O− represent lattice oxygen due to Mn–O and La/K–O bonds, respectively, while Ochem is likely attributed to oxygen vacancies associated with hydroxyl (OH) and carbon oxide (C–O) states.76,77 The O 1s ion at the lowest binding energy level (at 529 eV) is associated with the strong covalent Mn–O bond. Additionally, the O 1s spectrum peak at a binding energy of 530 eV is linked to the bond between La/K and O, or a combination of both, because the ionic La/K–O bond requires a higher binding energy compared to the covalent Mn–O bond.76 The highest binding energy peak, at 532 eV, may result from surface species, such as carbonyl groups or crystal lattice defects. It is said that elements on the outermost surface have higher binding energies. This indicates that surface sites often exhibit lower stability compared to bulk sites.78 Fig. 11 shows these as O2−, O−, and Ochem at binding energies close to 529, 530, and 532 eV, respectively. The ratio of O2− to (O2− + O− + Ochem) plays a crucial role in the double-exchange (DE) mechanism. The O2−/(O2− + O− + Ochem) ratios for the SG, WM, and SS samples were 0.3955, 0.3987, and 0.3983, respectively. The WM sample produces more O2− ions compared to the other samples, indicating an enhancement of the double exchange (DE) mechanism. O2− ions mediate the hopping of electrons between Mn3+ and Mn4+. The electron transfer from Mn3+ to Mn4+ involves the overlap of Mn 3d orbitals with the O 2p orbital, allowing an electron to hop from Mn3+ to Mn4+ through O2−. This hopping is spin-dependent and highly influenced by the relative alignment of the Mn spins, which directly affects the conductivity of the material. Because manganites are sintered under sufficient oxygen conditions, the concentration of Mn4+ can increase, and the substitutional ions can lead to lattice expansion (Table 4).79
Table 4 XPS fitting results of O 1s spectra of LKdMO synthesised using the SG, WM, and SS methods
| Preparation method |
Peak position (eV) |
Area |
O2−/(O2− + O− + Ochem) |
| O2− |
O− |
Ochem |
O2− |
O− |
Ochem |
| SG |
529.26 |
530.62 |
531.62 |
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 327.94 327.94 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 651.66 651.66 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 811.21 811.21 |
0.3955 |
| WM |
529.36 |
530.91 |
531.59 |
33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 897.84 897.84 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 819.7 819.7 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 285.11 285.11 |
0.3987 |
| SS |
529.25 |
530.64 |
531.37 |
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 981.99 981.99 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467.12 467.12 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 370.2 370.2 |
0.3983 |
3.4 Magnetic properties
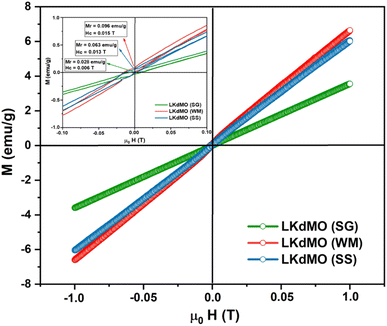
The magnetic properties were evaluated by measuring the magnetization as a function of the magnetic field (H) for the La0.85K0.1□0.05MnO3 material at room temperature under 1 T of the applied magnetic fields. The VSM results are shown in Fig. 12. The magnetization curve indicates that all samples show soft magnetic behavior, characterized by low remanent magnetization (Mr) and low coercivity (Hc). The maximum magnetization (Mmax) values for the SG, WM, and SS samples are 3.544, 6.619, and 6.071 emu g−1, respectively. The magnetization of the SS sample was higher than that of the SG sample. Pan et al. reported that an increase in the average grain size leads to an enhancement in the magnetization values.45 The magnetic properties of a material depend on the grain size. When the grain size decreases, it results in an increased number of grain boundaries, which leads to increased magnetic disorder and a weakening of ferromagnetic connectivity.33 Oumezzine et al. also reported that the formation of grain boundaries results in damaged bonds on the surface of the material, which decreases magnetization.40 The magnetization increased with the application of a higher magnetic field. The magnetic properties and electron transport related to the double-exchange (DE) interaction are controlled by the bandwidth (W), which is determined by the average radii of the cations at the site rA through the Mn–O–Mn angle (θMn–M–Mn) as described by the following equation:| |
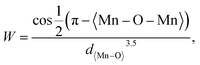 | (3) |
where 〈Mn–O–Mn〉 is the Mn–O–Mn bond angle and Mn–O–Mn, d〈Mn–O〉 is the Mn–O bond length.80 The results of the bandwidth (W) calculations are summarized in Table 5. Bandwidth (W) decreased with reduced electron mobility in the eg orbitals owing to a decrease in the Mn–O–Mn bond angle and an increase in the Mn–O bond length, which weakens the double-exchange (DE) interaction.81 K-site substitution can enhance the ferromagnetic exchange interaction by modifying the bond shape and the Mn3+/Mn4+ ratio. This improved interaction reduces resistance and greatly increases MR by improving electron spin alignment when a magnetic field is applied. Certain magnetic phases can also be stabilized by potassium doping, particularly when magnetic fields are applied. By reducing scattering effects and enabling a more transparent conduction channel, especially at lower temperatures, this stability aids MR.82 The bandwidth (W) calculations show that the WM sample has a higher W value than the SG and SS samples. Therefore, it is reasonable that based on the experimental results, the WM sample exhibits higher magnetization values compared to the SG and SS samples because the increase in bandwidth (W) leads to an increase in the DE mechanism. The higher magnetization value in the WM sample was also influenced by the greater number of O2− and Mn4+ ions present in the WM sample. O2− ions significantly influence the magnetization of manganite. They are integral to the Mn–O bond network, influencing the exchange interactions between Mn ions. The presence of O2− ions supports the stability of the magnetic order as they mediate the double exchange (DE) mechanism between Mn3+ and Mn4+ ions, which can enhance ferromagnetic behavior and improve magnetization values. Additionally, a higher concentration of O2− can contribute to a more robust magnetic structure, thereby positively affecting the overall magnetic properties of the material. Increased Mn4+ ion content in the WM samples also led to an increase in the DE mechanism.79,83
 |
| | Fig. 12 VSM results of the La0.85K0.1□0.05MnO3 compound synthesized using the SG, WM, and SS methods. | |
Table 5 Magnetization (M) and bandwidth (W) values of LKdMO synthesized through the SG, WM, and SS methods
| Parameter |
LKdMO |
| SG |
WM |
SS |
| Mmax (emu g−1) |
3.544 |
6.619 |
6.071 |
| Bandwidth (W) = eV |
0.091 |
0.093 |
0.092 |
| Mr (emu g−1) |
0.028 |
0.096 |
0.063 |
| Hc (T) |
0.006 |
0.015 |
0.013 |
3.5 Magnetoresistance and electrical transport properties
The larger radii of K+ (1.64 Å) compared to that of La3+ (1.36 Å) cause a mismatch in ionic radii, leading to distortion in the MnO6 octahedron lattice and reducing the geometric configuration of LKdMO for degeneracy. This phenomenon forms the basis of the Jahn–Teller (JT) effect. Substituting K+ for La3+ results in a mixed valence state of Mn3+ and Mn4+, maintaining charge neutrality. According to JT and Hund's rules, electrons in Mn3+ are divided into two states: (i) three electrons occupy the t2g orbitals, and (ii) one electron occupies the eg orbital. In the MnO6 octahedron, electron delocalization occurs from the eg orbital of Mn3+ to the eg orbital to the Mn4+. The electrons between the t2g and eg orbitals of Mn3+/Mn4+ exhibit parallel spins because of Hund's coupling effect. The delocalized eg electrons play a crucial role as a medium for electromagnetic interactions with localized t2g orbitals.44
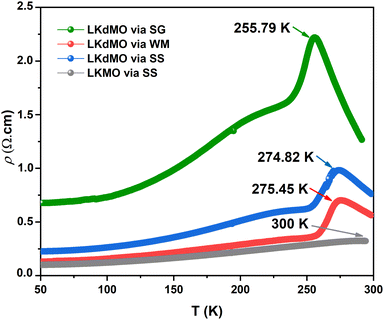
Fig. 13 shows the resistivity versus temperature graph in the range of 50–300 K for the LKdMO samples synthesized by applying the SG, WM, and SS methods, and the parental compound. The curve indicates that the samples with K deficiency had a higher resistivity than the parental compound in the measured temperature range. This is because the presence of vacancies increases the random distribution, leading to an increase in the resistance. Fig. 13 shows that the resistivity values of each sample strongly depend on the synthesis conditions. The resistivity increased from that of the WM sample to that of the SS sample, with the highest resistivity observed in the SG sample. The variation in the resistivity values among the samples was influenced by the electron bandwidth (W) in the conduction process. According to the double exchange (DE) mechanism, electronic transitions are identified by the strong interaction between the Mn3+ and Mn4+ spins, which enhances conductivity and reduces resistivity.44 From XPS results, the WM sample produces more O2− ions compared to the other samples. The increase in the number of O2− ions enhances the efficiency of electron transfer and strengthens the spin interactions between manganese ions, thereby improving the conductivity and reducing the resistivity. This explains why the WM sample exhibits better magneto-transport properties than other samples.83,84
 |
| | Fig. 13 ρ–T Curves of LKdMO samples prepared through the SS, WM, and SG methods, and LKMO through SS. | |
All samples exhibit transition behavior at the metal–insulator transition temperature (Tρ) from a metallic phase at low temperatures to an insulating phase at high temperatures. In the region where T < Tρ, the material exhibits a ferromagnetic (FM) phase, which can be explained by double-exchange (DE) interactions. Charge, spin, and magnetic ordering occur at low temperatures. The aligned electron spins at low temperatures cause the angle between Mn3+ and Mn4+ to align, maximizing electron hopping. Consequently, at low temperatures, LKdMO exhibited lower resistivity and ferromagnetic properties. Conversely, in the region where T > Tρ, the aligned electron spins are disrupted by strong thermal motion, leading to an increased resistivity and a paramagnetic (PM) phase. From Fig. 13, the Tρ peaks for the SG, WM, and SS samples were 255.79 K, 274.82 K, and 275.45 K, respectively. LKMO ceramics without K-deficiency showed a Tρ value of 289 K using the SG and SS methods.45 This is due to the smaller radius of vacancies compared to La3+, which affects the crystal cell volume. The mismatch in radii at the A-site leads to increased lattice strain, resulting in more distortion. This causes an overlap between the Mn 3d and O 2p orbitals, affecting the decrease in W and shifting Tρ to lower temperatures. The decrease in Tρ is also attributed to deviations related to the lower Mn4+ content compared to the theoretical value according to the XPS results. This mismatch weakens the DE interaction between Mn3+ and Mn4+. The presence of vacancies led to a random distribution, causing the Mn–O–Mn bond angle to deviate from 180°. The mismatch in cationic radii at the A-site, induced by vacancies, lowers the metal–insulator transition temperature in perovskite manganites. Magnetic interactions become more optimal in LKdMO material due to the combined effects of lattice distortion and increased charge carrier density. Manganites with K-deficient doping exhibit temperature-dependent MR behavior. At certain temperatures, electron hopping reaches an optimal level, where double-exchange interactions and maximum spin alignment occur, resulting in substantial MR.85
To determine the effect of the applied magnetic field on the resistivity of the material, the magnetoresistance (MR) was calculated. The MR value is defined by the following equation:
| |
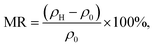 | (4) |
where
ρH is the resistivity of the material under an external magnetic field and
ρ0 is the resistivity without the influence of an external magnetic field.
86 The resistivity
versus temperature graphs with the application of magnetic fields of 0 T and 2 T for all the samples are shown in
Fig. 14. The application of a magnetic field increases the value of
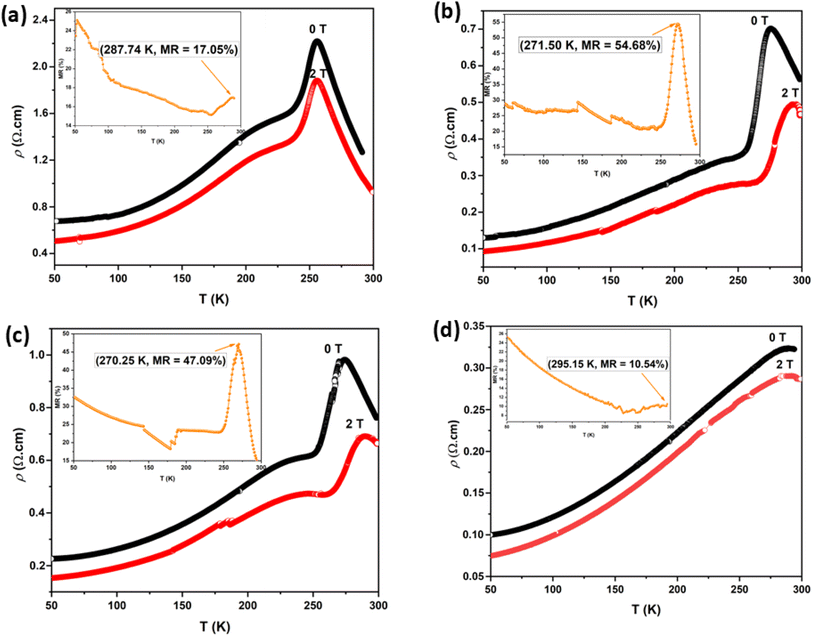
Tρ. This is because the applied magnetic field aligns the electron spin directions and drives a transition from a random to a parallel configuration, thereby reducing resistivity.
87–89 The MR values for the LK
dMO SG, WM, and SS samples are 17.05% at 287.74 K, 54.68% at 271.50 K, and 47.09% at 270.25 K, respectively, showing significant variation. The absolute value of the temperature-dependent MR reaches a maximum near the Curie temperatures (
TC). The K deficiency in the LK
dMO sample led to an increase in MR compared to the MR value of the parental sample (MR = 10.36% at 287 K). This enhancement occurs because the K deficiency disrupts the long-range magnetic order, leading to the formation of short-range ferromagnetic clusters. These clusters increase electrical resistance in the absence of an external magnetic field and exhibit significant changes in the magnetic cluster distribution when an external magnetic field is applied, resulting in an enhanced MR effect. The WM sample shows a substantial decrease in resistivity owing to the smaller grain size, which results in a higher number of grain boundaries acting as scattering centers. Consequently, the magnetic field enhances spin-polarized tunneling, thereby increasing the MR value.
45,90 Additionally, the increase in MR in the WM sample influenced by the Mn
3+/Mn
4+ ratio is closest to the theoretical value.
44 Mn
4+ ion plays a key role in magnetoresistance (MR), where the resistivity of the material decreases under the influence of an external magnetic field. As Mn
4+ promotes spin alignment through the double exchange (DE) mechanism, the applied magnetic field can enhance spin order and reduce resistivity, leading to a high MR effect.
79 Furthermore, the SS sample exhibited a higher MR value than the SG sample. This is contradictory, as the SG sample has a smaller grain size than the SS sample and should therefore have more grain boundaries. This may be because of the presence of clustered grains in the micron structure of the SS sample, where some layers of scattering might exist. When subjected to a magnetic field, these layers could enhance the spin-polarized tunneling. Additionally, the reduction in the MR value in the SG sample may be due to the presence of Mn
2O
3 impurities. Owing to the presence of Mn
2O
3 impurities, there was a deficiency of Mn-ions, which consequently resulted in a higher concentration of Mn
3+ than Mn
4+. This results in the super-exchange (SE) interaction between Mn
3+–O
2−–Mn
3+ and the formation of an antiferromagnetic (AFI) phase, which causes the MR value and
Tρ to decrease.
52,55
 |
| | Fig. 14 Resistivity dependence on temperature of LKdMO ceramics synthesized by employing (a) SG, (b) WM, (c) SS, and (d) the parental compound through SS under 0 and 2 T. Insets show MR dependence temperature plots for LKdMO and LKMO. | |
Fig. 15 shows the field dependence of the magnetoresistance (MR) curve at 150 K for all synthesized LKdMO samples. The applied magnetic field aligns the electron spins at the grain boundaries. The alignment was enhanced when the external field was increased. Thus, we can observe MR due to a decrease in resistivity for all samples as the applied field increases from 0 kOe to 20 kOe. None of the samples achieved MR saturation with a magnetic field of up to 20 kOe, which means that a higher field is required to align the spins fully. The MR values for all the samples at 150 K did not show significant differences. However, unlike the WM and SS samples, the SG sample did not exhibit an increase in MR within the temperature range of 250–275 K.
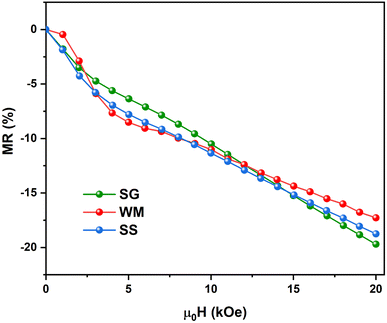 |
| | Fig. 15 Field dependence of the MR curve of LKdMO at 150 K. | |
The magnetic, electrical, and MR values obtained for the LKMO compounds are summarized in Table 6. Table 6 shows that the samples synthesized in this study have parameter values, such as resistivity, Tρ, and MR, which are similar to those obtained in previous experimental studies. The MR values for the WM and SS samples were relatively high at approximately 270 K. The samples produced under different experimental conditions exhibited significant MR values, demonstrating that different synthesis methods can significantly affect various parameters related to the MR effect. The experimental conditions, including the use of precursors and pH, resulted in varying grain sizes. These differences in grain size play a crucial role in transport processes within the LKdMO system.
Table 6 Magnetoresistance properties with parameters of electrical properties and MR of several LKMO manganites
| Sample |
Electrical properties |
MR |
Method |
Ref. |
| ρ(H) (Ω cm) |
Tρ (K) |
MR (%) |
TMR (K) |
(μ0H) B |
| La0.9K0.1MnO3 |
0.030 |
300 |
43.03 |
286.3 |
1 T |
SG |
42 |
| La0.85K0.15MnO3 |
0.028 |
>300 |
46.39 |
294.03 |
1 T |
SG |
42 |
| La0.8K0.2MnO3 |
0.025 |
>300 |
37.49 |
294.6 |
1 T |
SG |
42 |
| La0.75K0.25MnO3 |
0.020 |
>300 |
35.16 |
295.43 |
1 T |
SG |
42 |
| La0.7K0.3MnO3 |
0.017 |
>300 |
26.76 |
296.4 |
1 T |
SG |
42 |
| La0.85K0.1□0.05MnO3 |
2.2 |
255.79 |
17.05 |
287.74 |
2 T |
SG |
This work |
| La0.85K0.1□0.05MnO3 |
0.7 |
274.812 |
54.68 |
271.50 |
2 T |
WM |
This work |
| La0.85K0.1□0.05MnO3 |
1.0 |
275.45 |
47.09 |
270.25 |
2 T |
SS |
This work |
| La0.85K0.15MnO3 |
0.275 |
>300 |
10.36 |
287 |
2 T |
SS |
This work |
| La0.833K0.167MnO3 |
2.5 |
250 |
0.4 |
320 |
5.5 T |
SG |
91 |
| La0.67K0.33MnO3 |
22 |
290 |
40 |
300 |
6 T |
SG |
4 |
| La0.95K0.05MnO3 |
0.339 |
239.8 |
0.40 |
300 |
0.8 T |
Thermolysis of an aqueous |
15 |
| La0.90K0.10MnO3 |
0.281 |
261.9 |
2.82 |
300 |
0.8 T |
Thermolysis of an aqueous |
15 |
| La0.85K0.15MnO3 |
0.189 |
276.0 |
4.53 |
300 |
0.8 T |
Thermolysis of an aqueous |
15 |
| LaMnO3+δ |
5.00 |
150 |
0.07 |
175 |
0.6 T |
Precursor-based synthetic |
7 |
| La0.95 K0.05MnO3+δ |
1.2 |
230 |
0.08 |
225 |
0.6 T |
Precursor-based synthetic |
7 |
| La0.85K0.15MnO3 |
0.1 |
289 |
6 |
300 |
1 T |
SS |
45 |
| La0.85K0.15MnO3 |
1.1 |
289 |
3.5 |
300 |
1 T |
SG |
45 |
| La0.85K0.15MnO3 |
11 |
258 |
8 |
300 |
1 T |
Co-precipitation |
45 |
| La0.8□0.15MnO3 |
6.0 × 10−5 |
300 |
40 |
280 |
2 T |
SS |
92 |
| La0.8□0.15MnO3 |
9.0 × 10−5 |
290 |
60 |
290 |
5 T |
SS |
92 |
3.6 Conduction mechanism
In the low-temperature FM region (T < Tρ), the temperature-dependent resistivity ρ(T) was approximated using an expression that incorporated several scattering mechanisms, as analyzed based on the following equation:| | |
ρFM(T) = ρ0 + ρ2T2 + ρ4.5T4.5,
| (5) |
where ρ0 represents the temperature independent resistivity due to grain boundary scattering and plays a crucial role in the conduction process,93 ρ2 represents the electrical transport due to electron–electron scattering,94 and ρ4.5 represents the resistivity caused by electron–magnon scattering.95 In the high-temperature region (T > Tρ), within the PM insulating phase, the electrical resistivity is fitted using the thermally activated behavior, described by the following equation:| |
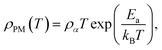 | (6) |
where ρα is the residual resistivity, Ea is the activation energy for hopping conduction, and kB is the Boltzmann constant. In this region, the charge carriers are small polarons, which facilitate conductivity by jumping to the nearest free state.40
The electrical transport mechanism across the entire temperature range, particularly around Tρ, was fitted using a new phenomenological model based on the percolation approach proposed by Li et al.96 The percolation model assumes that the resistivity of the material consists of FM and PM regions. Metallic transport properties are exhibited in the FM regions, whereas insulating properties are displayed in the PM regions. By employing this mechanism, the electrical resistivity across all temperature ranges can be determined using the volume fractions of the FM and PM regions. The resistivity over the entire temperature range can be defined by the following equation:
| | |
ρ(T) = ρFMf + ρPM(1 − f),
| (7) |
where
f and 1 −
f represent the volume fractions of the FM and PM regions, respectively. By following the Boltzmann distribution, the functions
f and 1 −
f can be determined through a mathematical combination as follows:
| |
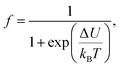 | (8) |
| |
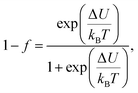 | (9) |
where Δ
U is defined as the energy difference between the FM and PM phases, and it is determined using the following equation:
| |
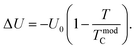 | (10) |
Thus, the temperature-dependent resistivity for the entire temperature range can be defined using
eqn (11):
| |
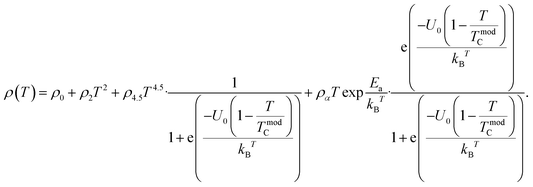 | (11) |
Eqn (11) is in good agreement with our experimental data in the temperature range of 50–300 K. The excellent match between the calculated data (solid red line) and experimental data (black dots) is clearly shown in
Fig. 16. The parameters obtained across the entire temperature range, namely
ρ0,
ρ2,
ρ4.5,
ρα,
Ea/
kB,
U0/
kB, and
TmodC, are summarized in
Table 7. The values of
ρ0,
ρ2, and
ρα for the LK
dMO SG, WM, SS, and parental compound samples showed some differences. The resistivity due to electron–electron scattering (
ρ2) was higher than the resistivity caused by electron–magnon scattering (
ρ4.5) for all samples (SG, WM, and SS). This indicates that electron–electron scattering is more dominant than electron–magnon scattering in the electron transport process in the FM metallic region (
T <
Tρ). The results from the percolation fitting indicate that the parameter
ρ0, which represents the resistivity due to grain/domain boundary scattering, increases from the SS to the SG sample. This is reasonable when considering the grain factor, as the SG sample has smaller grains, leading to more grain boundaries than the SS sample. Interestingly,
ρ0 for the WM sample showed the lowest value despite having the smallest grain size. This can be attributed to the higher spin-polarized tunneling at the grain boundaries in the WM sample. Parameter
ρ2, representing electrical transport due to electron–electron scattering, also shows an increase in resistivity across the WM, SS, and SG samples. WM sample has the lowest resistivity.
ρ2 can correlate with the Mn
4+ concentration from the XPS results, where the WM sample has the highest Mn
4+ concentration. Mn
4+ ions play a crucial role in electron transport and the double exchange (DE) mechanism. Additionally,
Ea, which represents activation energy for hopping conduction, can be related to the electron bandwidth (
W). The SG sample exhibited the highest
Ea value among all the samples, corresponding to its lowest
W value. A lower
W indicates that electrons find it more difficult to move, reducing conductivity and increasing the ability of charge localization. Consequently, electron hopping requires more energy in the SG sample. Furthermore, the value of
TmodC shows a slight variation from
Tρ, influenced by the existence of magnetic bi-phase states, including ferromagnetic and antiferromagnetic states, owing to strong s–d exchange.
97
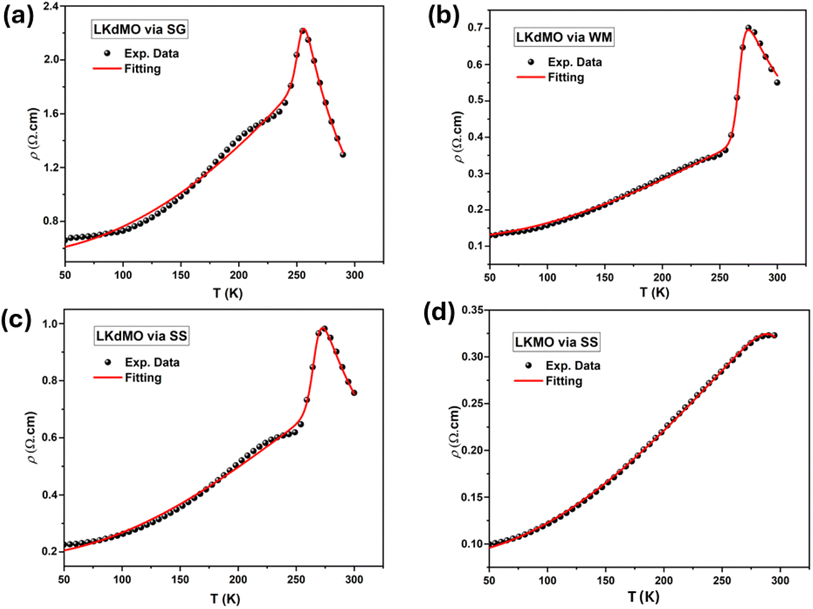 |
| | Fig. 16 Fitting curves of ρ–T data in the entire temperature range of the La0.85K0.1□0.05MnO3 samples by (a) SG, (b) WM, and (c) SS and (d) parental compound. Symbols are the experimental results and solid lines are the fitting using eqn (11). | |
Table 7 Fitting electrical resistivity parameters of LKdMO polycrystalline ceramics prepared by employing the SS, WM, and SS methods and LKMO by employing SS
| Region |
Parameter |
LKdMO |
LKMO |
| SG |
WM |
SS |
SS |
| Metallic region |
ρ0 (Ω m) |
0.56085 |
0.12050 |
0.18452 |
0.08688 |
| ρ2 (Ω m) |
2.01511 × 10−5 |
4.39968 × 10−6 |
8.43211 × 10−6 |
3.59854 × 10−6 |
| ρ4.5 (Ω m) |
−2.13622 × 10−13 |
−5.82457 × 10−13 |
−1.08629 × 10−12 |
−4.32522 × 10−13 |
| Insulator region |
ρα (Ω m) |
2.14489 × 10−5 |
5.91243 × 10−5 |
4.31794 × 10−5 |
8.98083 × 10−6 |
| Ea/kB |
1552.26062 |
1040.83009 |
1218.95178 |
1262.01042 |
| Supplement parameter |
U0/kB |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 933.9676 933.9676 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 748.72826 748.72826 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 568.02083 568.02083 |
7883.79956 |
| TmodC |
253.07 |
267.35 |
266.56 |
315.84 |
4. Conclusions
LKdMO ceramics were successfully synthesized using SG, WM, and SS methods, and the results were compared. The structure, magnetic properties, and electrical transport properties were studied using XRD, SEM, EDS, XPS, VSM, and FPP. No differences in the crystal phases and elements of the perovskite manganite materials were observed among the SG, WM, and SS samples. LKdMO ceramics produced using WM and SS exhibited a single phase belonging to the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group with a rhombohedral structure, while the SG sample showed the presence of a secondary Mn2O3 phase. The EDS and XPS results suggested that La, K, Mn, and O were uniformly distributed in the samples. The SEM results indicated that the WM sample had a smaller average grain size than the SG and SS samples. Consequently, the WM sample exhibited lower resistivity owing to the reduced scattering of the grain boundaries. However, the difference in grain size owing to the synthesis method affects the transport and magnetic performance. The highest MR values for the SG, WM, and SS samples were 17.05% at 287.74 K, 54.68% at 271.50 K, and 47.09% at 270.25 K, respectively. The K-site deficiency successfully enhanced the MR value in the LKdMO material compared to the parental compound (LKMO), achieving an MR value of 10.36% at 287 K. Compared with the SG and SS samples, the WM sample exhibited the highest MR, which was attributed to the enhancement of spin-polarized tunneling by the largest grain boundary contribution. Overall, the WM method is more effective for producing LKdMO polycrystalline ceramics with better crystal quality and electromagnetic properties. Our results show that K-deficient formation can improve MR by changing the manganite lattice, which probably changes the structure and makes it easier for electrons to move around. These findings contribute to resolving inconsistencies in this field and highlight the potential for simpler, scalable synthesis methods for practical applications. Future work will focus on optimizing synthesis conditions to precisely control defect densities and types, with the aim of achieving an optimal balance that maximizes MR.
c space group with a rhombohedral structure, while the SG sample showed the presence of a secondary Mn2O3 phase. The EDS and XPS results suggested that La, K, Mn, and O were uniformly distributed in the samples. The SEM results indicated that the WM sample had a smaller average grain size than the SG and SS samples. Consequently, the WM sample exhibited lower resistivity owing to the reduced scattering of the grain boundaries. However, the difference in grain size owing to the synthesis method affects the transport and magnetic performance. The highest MR values for the SG, WM, and SS samples were 17.05% at 287.74 K, 54.68% at 271.50 K, and 47.09% at 270.25 K, respectively. The K-site deficiency successfully enhanced the MR value in the LKdMO material compared to the parental compound (LKMO), achieving an MR value of 10.36% at 287 K. Compared with the SG and SS samples, the WM sample exhibited the highest MR, which was attributed to the enhancement of spin-polarized tunneling by the largest grain boundary contribution. Overall, the WM method is more effective for producing LKdMO polycrystalline ceramics with better crystal quality and electromagnetic properties. Our results show that K-deficient formation can improve MR by changing the manganite lattice, which probably changes the structure and makes it easier for electrons to move around. These findings contribute to resolving inconsistencies in this field and highlight the potential for simpler, scalable synthesis methods for practical applications. Future work will focus on optimizing synthesis conditions to precisely control defect densities and types, with the aim of achieving an optimal balance that maximizes MR.
Data availability
The data supporting our research are solely generated by us. The data that support the findings of this study are available from the corresponding author, upon reasonable request.
Conflicts of interest
The authors declare no conflict of interest.
Acknowledgements
The authors gratefully acknowledge the PMDSU Scholarship awarded to Okvarahireka Vitayaya and the financial support under grant “Hibah Publikasi Terindeks Internasional (PUTI) Q2 2024-2025” NKB-677/UN2.RST/HKP.05.00/2024.
References
- A. Ezaami, I. Sfifir, W. Cheikhrouhou-Koubaa, M. Koubaa and A. Cheikhrouhou, J. Alloys Compd., 2017, 693, 658–666 CrossRef CAS.
- J. M. D. Coey, M. Viret and S. Von Molnár, Adv. Phys., 1999, 48, 167–293 CrossRef CAS.
- S. Atalay, V. S. Kolat, H. Gencer and H. I. Adiguzel, J. Magn. Magn. Mater., 2006, 305, 452–456 CrossRef CAS.
- A. Goktas, I. H. Mutlu and A. Kawashi, Thin Solid Films, 2012, 520, 6138–6144 CrossRef CAS.
- A. Urushibara, Y. Moritomo, T. Arima, A. Asamitsu, G. Kido and Y. Tokura, Phys. Rev. B:Condens. Matter Mater. Phys., 1995, 51, 14103–14109 CrossRef CAS.
- T. Sun, F. Ji, Y. Liu, G. Dong, S. Zhang, Q. Chen and X. Liu, J. Eur. Ceram. Soc., 2019, 39, 352–357 CrossRef CAS.
- Y. Ng-Lee, F. Sapiña, E. Martinez-Tamayo, J. V. Folgado, R. Ibañez, D. Beltrán, F. Lloret and A. Segura, J. Mater. Chem., 1997, 7, 1905–1909 RSC.
- Y. Kalyana Lakshmi, G. Venkataiah, M. Vithal and P. Venugopal Reddy, Phys. B, 2008, 403, 3059–3066 CrossRef.
- N. Phahul Zhemas Zul, O. Vitayaya, D. Rezky Munazat, M. T. E. Manawan and D. Darminto, Phys. Chem. Chem. Phys., 2024, 26, 14476–14504 RSC.
- S. Joseph and K. V. Saban, Ceram. Int., 2019, 45, 6425–6439 CrossRef CAS.
- A. P. Ramirez, J. Phys.:Condens. Matter, 1997, 9, 8171–8199 CrossRef CAS.
- C. Zener, Phys. Rev., 1951, 82, 403–405 CrossRef CAS.
- M. Sahana, M. S. Hegde, C. Shivakumara, V. Prasad and S. V. Subramanyam, J. Solid State Chem., 1999, 148, 342–346 CrossRef CAS.
- B. Kurniawan, S. Winarsih, A. Imaduddin and A. Manaf, Phys. B, 2018, 532, 161–165 CrossRef CAS.
- S. Das and T. K. Dey, Solid State Commun., 2005, 134, 837–842 CrossRef CAS.
- G. Huo, Z. Gu, S. Liu, Y. Wang and Y. Wang, J. Alloys Compd., 2007, 433, 41–45 CrossRef CAS.
- A. G. Gamzatov, A. B. Batdalov, O. V. Melnikov and O. Y. Gorbenko, Low Temp. Phys., 2009, 35, 219–222 CrossRef CAS.
- W. Boujelben, A. Cheikh-Rouhou and J. C. Joubert, Eur. Phys. J. B, 2001, 24, 419–423 CrossRef CAS.
- M. Ellouze, W. Boujelben, A. Cheikhrouhou, H. Fuess and R. Madar, Solid State Commun., 2002, 124, 125–130 CrossRef CAS.
- W. Cheikh-Rouhou Koubaa, M. Koubaa, A. Cheikh-Rouhou, W. Boujelben and A. M. Haghiri-Gosnet, J. Alloys Compd., 2008, 455, 67–72 CrossRef CAS.
- S. K. Mandal, T. K. Nath and V. V. Rao, J. Phys.:Condens. Matter, 2008, 20, 385203 CrossRef CAS PubMed.
- T. Sarkar, B. Ghosh, A. K. Raychaudhuri and T. Chatterji, Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 77, 1–9 Search PubMed.
- S. V. Trukhanov, L. S. Lobanovski, M. V. Bushinsky, I. O. Troyanchuk and H. Szymczak, J. Phys.:Condens. Matter, 2003, 15, 1783–1795 CrossRef CAS.
- A. De Andrés, M. García-Hernández and J. L. Martínez, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 60, 7328–7334 CrossRef.
- H. Y. Hwang, S. W. Cheong, P. G. Radaelli, M. Marezio and B. Batlogg, Phys. Rev. Lett., 1995, 75, 914–917 CrossRef CAS.
- P. Lyu, D. Xing and J. Dong, Phys. Rev. B:Condens. Matter Mater. Phys., 1998, 58, 54–57 CrossRef CAS.
- M. Viret, M. Drouet, J. Nassar, J. P. Contour, C. Fermon and A. Fert, Europhys. Lett., 1997, 39, 545–549 CrossRef CAS.
- L. Balcells, J. Fontcuberta, B. Martínez and X. Obradors, Phys. Rev. B:Condens. Matter Mater. Phys., 1998, 58, R14697–R14700 CrossRef CAS.
- R. Shreekala, M. Rajeswari, K. Ghosh, A. Goyal, J. Y. Gu, C. Kwon, Z. Trajanovic, T. Boettcher, R. L. Greene, R. Ramesh and T. Venkatesan, Appl. Phys. Lett., 1997, 71, 282–284 Search PubMed.
- J. M. D. Coey, M. Viret and L. Ranno, Phys. Rev. Lett., 1995, 75, 3910–3913 CrossRef CAS.
- R. M'Nassri, N. Chniba Boudjada and A. Cheikhrouhou, J. Alloys Compd., 2015, 626, 20–28 CrossRef.
- S. Mahjoub, M. Baazaoui, E. K. Hlil and M. Oumezzine, Ceram. Int., 2015, 41, 12407–12416 CrossRef CAS.
- M. R. Laouyenne, M. Baazaoui, K. Farah, E. K. Hlil and M. Oumezzine, J. Magn. Magn. Mater., 2019, 474, 393–399 CrossRef CAS.
- D. R. Munazat, B. Kurniawan, D. S. Razaq, K. Watanabe and H. Tanaka, Phys. B, 2020, 592, 412227 CrossRef CAS.
- B. Vertruyen, A. Rulmont, R. Cloots, M. Ausloos, S. Dorbolo and P. Vanderbemden, Mater. Lett., 2002, 57, 598–603 CrossRef CAS.
- A. K. M. Akther Hossain, L. F. Cohen, F. Damay, A. Berenov, J. MacManus-Driscoll, N. M. Alford, N. D. Mathur, M. G. Blamire and J. E. Evetts, J. Magn. Magn. Mater., 1999, 192, 263–270 CrossRef CAS.
- C. Vázquez-Vázquez, M. Carmen Blanco, M. Arturo López-Quintela and R. D. Sánchez, J. Mater. Chem., 1998, 1998(8), 991–1000 RSC.
- A. Selmi, W. Cheikhrouhou-Koubaa, M. Koubaa and A. Cheikhrouhou, J. Supercond. Novel Magn., 2013, 26, 1421–1428 CrossRef CAS.
- R. M'nassri, W. Cheikhrouhou-Koubaa, M. Koubaa and A. Cheikhrouhou, IOP Conf. Ser.:Mater. Sci. Eng., 2012, 28, 0–8 Search PubMed.
- M. Oumezzine, S. Hcini, M. Baazaoui, H. B. Sales, I. M. G. Dos Santos and M. Oumezzine, J. Alloys Compd., 2013, 571, 79–84 CrossRef CAS.
- L. N. Lau, K. P. Lim, A. N. Ishak, M. M. Awang Kechik, S. K. Chen, N. B. Ibrahim, M. Miryala, M. Murakami and A. H. Shaari, Coatings, 2021, 11, 361 CrossRef CAS.
- S. Jin, X. Gu, X. Yu, X. Guan, Y. Yan, K. Wu, L. Zhao, Y. Zhu, S. Sun, J. Liu, J. Hu, J. Zhao, L. Kong, W. Yang, Q. Chen, P. Kameli and X. Liu, Appl. Surf. Sci., 2022, 589, 152905 CrossRef CAS.
- R. Dhahri and F. Halouni, J. Alloys Compd., 2004, 381, 21–25 CrossRef CAS.
- X. Yu, H. Li, K. Chu, X. Pu, X. Gu, S. Jin, X. Guan and X. Liu, Ceram. Int., 2021, 47, 13469–13479 CrossRef CAS.
- K. Y. Pan, S. A. Halim, K. P. Lim, W. M. W. Y. Daud, S. K. Chen and M. Navasery, J. Mater. Sci.:Mater. Electron., 2013, 24, 1869–1874 CrossRef CAS.
- B. Rajyaguru, K. Gadani, M. J. Keshvani, D. Dhruv, A. D. Joshi, K. Asokan, R. J. Choudhary, D. M. Phase, N. A. Shah and P. S. Solanki, Mater. Res. Bull., 2024, 170, 112548 CrossRef CAS.
- F. Elleuch, M. Triki, M. Bekri, E. Dhahri and E. K. Hlil, J. Alloys Compd., 2015, 620, 249–255 CrossRef CAS.
- B. Arun, V. R. Akshay and M. Vasundhara, Dalton Trans., 2018, 47, 15512–15522 RSC.
- S. Jin, S. Zhang, X. Yu, X. Guan, H. Li, K. Chu, X. Pu, X. Gu and X. Liu, Ceram. Int., 2021, 47, 24721–24731 CrossRef CAS.
- N. A. Liedienov, A. V. Pashchenko, V. P. Pashchenko, V. K. Prokopenko, D. D. Tatarchuk, Y. F. Revenko, V. A. Turchenko, V. V. Burchovetskii, V. Y. Sycheva, A. G. Sil'cheva, Y. V. Didenko and G. G. Levchenko, Low Temp. Phys., 2017, 43, 1076–1085 CrossRef CAS.
- C. Henchiri, R. Hamdi, T. Mnasri, M. A. Valente, P. R. Prezas and E. Dhahri, Appl. Phys. A:Mater. Sci. Process., 2019, 125, 1–19 CrossRef CAS.
- A. Zahrin, N. A. Azhar, N. Ibrahim and Z. Mohamed, Condens. Matter, 2022, 7, 51 CrossRef CAS.
- C. Luo, Y. Zheng, Y. Xu, N. Ding, Q. Shen and C. Zheng, Chem. Eng. J., 2015, 267, 111–116 CrossRef CAS.
- N. Soylu Koc, S. P. Altintas, N. Mahamdioua and C. Terzioglu, J. Alloys Compd., 2019, 797, 471–476 CrossRef CAS.
- M. A. I. Zainuddin, R. Rozilah, N. Ibrahim and Z. Mohamed, J. Alloys Compd., 2024, 976, 173225 CrossRef CAS.
- R. V. Lakshmi, P. Bera, M. Hiremath, V. Dubey, A. K. Kundu and H. C. Barshilia, Phys. Chem. Chem. Phys., 2022, 24, 5462–5478 RSC.
- S. S. Teixeira, F. Amaral, M. P. F. Graça and L. C. Costa, Mater. Sci. Eng., B, 2020, 255, 114529 CrossRef CAS.
- M. Khlifi, E. Dhahri and E. K. Hlil, J. Alloys Compd., 2014, 587, 771–777 CrossRef CAS.
- R. Atanasov, R. Bortnic, R. Hirian, E. Covaci, T. Frentiu, F. Popa and I. G. Deac, Materials, 2022, 15, 7645 CrossRef CAS PubMed.
- R. Tlili, M. Bejar, E. Dhahri, A. Zaoui, E. K. Hlil and L. Bessais, Polyhedron, 2017, 121, 19–24 CrossRef CAS.
- Z. Wei, N. A. Liedienov, Q. Li, A. V. Pashchenko, W. Xu, V. A. Turchenko, M. Yuan, I. V. Fesych and G. G. Levchenko, Ceram. Int., 2021, 47, 24553–24563 CrossRef CAS.
- M. W. Shaikh and D. Varshney, Mater. Chem. Phys., 2012, 134, 886–898 CrossRef CAS.
- G. Kimmel, A. Sahartov, Y. Sadia, Z. Porat, J. Zabicky and E. Dvir, J. Mater. Res. Technol., 2021, 12, 87–99 CAS.
- W. Qin, T. Nagase, Y. Umakoshi and J. A. Szpunar, Philos. Mag. Lett., 2008, 88, 169–179 CAS.
- Y. Zhang, Y. Zhang, B. Fu, M. Hong, M. Xiang, Z. Liu, H. Liu and S. Liu, J. Mater. Sci.:Mater. Electron., 2015, 26, 3179–3185 CrossRef CAS.
- A. White, A. Walpole, Y. Huang and D. L. Trimm, Appl. Catal., 1989, 56, 187–196 CrossRef CAS.
- D. R. Munazat, B. Kurniawan, N. Kurita, X. Wang, M. Manawan, T. Sudiro and H. Nojiri, Phys. Chem. Chem. Phys., 2024, 26, 18343–18367 RSC.
- R. Tripathi, A. Dogra, A. K. Srivastava, V. P. S. Awana, R. K. Kotnala, G. L. Bhalla and H. Kishan, J. Phys. D Appl. Phys., 2009, 42, 1–6 Search PubMed.
- A. Gupta and G. Gong, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, R15629–R15632 CrossRef CAS PubMed.
- X. Wang, Y. Chen, W. Quan, T. Masuzawa, Y. Okigawa, S. Ogawa and Y. Takakuwa, Nano Express, 2021, 2, 030004 CrossRef.
- J. J. Qian, W. H. Qi, Z. Z. Li, L. Ma, G. D. Tang, Y. N. Du, M. Y. Chen, G. H. Wu and F. X. Hu, RSC Adv., 2018, 8, 4417–4425 RSC.
- P. K. Siwach, P. Srivastava, H. K. Singh, A. Asthana, Y. Matsui, T. Shripathi and O. N. Srivastava, J. Magn. Magn. Mater., 2009, 321, 1814–1820 CrossRef CAS.
- B. Arun, V. R. Akshay and M. Vasundhara, RSC Adv., 2019, 9, 23598–23606 RSC.
- J. Van Elp, R. H. Potze, H. Eskes, R. Berger and G. A. Sawatzky, Phys. Rev. B:Condens. Matter Mater. Phys., 1991, 44, 1530–1537 CrossRef CAS.
- Y. Moualhi, M. Smari and H. Rahmouni, RSC Adv., 2023, 13, 30010–30021 RSC.
- P. R. Nadig, S. Murari and M. D. Daivajna, Phys. Chem. Chem. Phys., 2024, 26, 5237–5252 RSC.
- D. Kumar and A. K. Singh, J. Phys. Chem. Solids, 2023, 176, 111253 CrossRef CAS.
- G. Kozhina, V. Mitrofanov, O. Fedorova, A. Fetisov, A. Murzakaev and S. Estemirova, J. Alloys Compd., 2021, 864, 158816 CrossRef CAS.
- G. Dong, Y. Liu, S. Zhang, K. Chu, H. Li, X. Pu, T. Sun, F. Ji and X. Liu, Ceram. Int., 2019, 45, 21448–21456 CrossRef CAS.
- S. Othmani, M. Bejar, E. Dhahri and E. K. Hlil, J. Alloys Compd., 2009, 475, 46–50 CrossRef CAS.
- R. Rozilah, N. Ibrahim and A. K. Yahya, Solid State Sci., 2019, 87, 64–80 CrossRef CAS.
- Y. Kalyana Lakshmi, S. Manjunathrao and P. Venugopal Reddy, Mater. Chem. Phys., 2014, 143, 983–990 CrossRef CAS.
- R. Dhahri and F. Halouni, J. Alloys Compd., 2004, 385, 48–52 CrossRef CAS.
- S. V. Trukhanov, I. O. Troyanchuk, N. V. Pushkarev and H. Szymczak, J. Exp. Theor. Phys., 2002, 95, 308–315 CrossRef CAS.
- N. Zurauskiene, V. Stankevic, S. Kersulis, M. Vagner, J. Pietosa and A. Wisniewski, sensors, 2022, 22, 4004 CrossRef CAS.
- L. Yin, C. Wang and Q. Shen, Ceram. Int., 2023, 1–9 Search PubMed.
- O. Vitayaya, P. Z. Zul Nehan, D. R. Munazat, M. T. E. Manawan and B. Kurniawan, RSC Adv., 2024, 14, 18617–18645 RSC.
- R. Tripathi, V. P. S. Awana, H. Kishan, S. Balamurugan and G. L. Bhalla, J. Supercond. Novel Magn., 2008, 21, 151–159 CrossRef CAS.
- Y. Zhou, X. Zhu and S. Li, Ceram. Int., 2017, 43, 10026–10031 CrossRef CAS.
- U. Chand, K. Yadav, A. Gaur and G. D. Varma, J. Rare Earths, 2010, 28, 760–764 CrossRef CAS.
- W. Jian, J. Magn. Magn. Mater., 2012, 324, 2183–2187 CrossRef CAS.
- M. Wali, R. Skini, M. Khlifi, M. Bekri, E. Dhahri and E. K. Hlil, Ceram. Int., 2016, 42, 5699–5706 CrossRef CAS.
- A. Dhahri, M. Jemmali, E. Dhahri and E. K. Hlil, Dalton Trans., 2015, 44, 5620–5627 RSC.
- P. Schiffer, A. P. Ramirez, W. Bao and S. W. Cheong, Phys. Rev. Lett., 1995, 75, 3336–3339 CrossRef CAS PubMed.
- G. Venkataiah and P. V. Reddy, Solid State Commun., 2005, 136, 114–119 CrossRef CAS.
- G. Li, H. D. Zhou, S. J. Feng, X. J. Fan, X. G. Li and Z. D. Wang, J. Appl. Phys., 2002, 92, 1406–1410 CrossRef CAS.
- A. G. Gamzatov and I. K. Kamilov, J. Alloys Compd., 2012, 513, 334–338 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Phahul Zhemas Zul Nehana,
Dicky Rezky Munazata,
Toto Sudirob,
Agung Imaduddinb,
Heri Nugrahad,
Sigit Dwi Yudanto
*a,
Phahul Zhemas Zul Nehana,
Dicky Rezky Munazata,
Toto Sudirob,
Agung Imaduddinb,
Heri Nugrahad,
Sigit Dwi Yudanto e and
Maykel T. E. Manawanbc
e and
Maykel T. E. Manawanbc
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group (no. 167). However, the SG sample also showed the presence of a secondary Mn2O3 phase with an orthorhombic crystal structure (Pbca). Figure 2 shows that the broadening and full width at half maximum (FWHM) in the LKdMO samples synthesized by the wet-mixing (WM) and solid-state (SS) methods are smaller, with higher intensity compared to the parental compound LKMO. This indicates that the growth of K-deficient formations promotes crystallinity and enhances crystal properties.46
c space group (no. 167). However, the SG sample also showed the presence of a secondary Mn2O3 phase with an orthorhombic crystal structure (Pbca). Figure 2 shows that the broadening and full width at half maximum (FWHM) in the LKdMO samples synthesized by the wet-mixing (WM) and solid-state (SS) methods are smaller, with higher intensity compared to the parental compound LKMO. This indicates that the growth of K-deficient formations promotes crystallinity and enhances crystal properties.46

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group. The Goodness of fit (χ2) value indicated that the WM sample had a value close to 1, suggesting a better fit and good agreement with the XRD profile than the SG and SS samples. The use of the wet-mixing (WM) method is more efficient than the sol–gel (SG) method. The WM method does not require additional precursors or chelating agents to complex metal ions; thus, less mass is lost during the combustion process.34 Additionally, the amount of water used during WM synthesis was reduced, leading to a shorter mixing duration. The WM method, using nitric acid as a solvent, allows the use of a wide variety of carbonate precursors, including both soluble and insoluble carbonates. However, the SG method is limited to soluble precursors.53 It is possible that the wet-mixing method enables WM to produce crystals with better quality than the sol–gel (SG) and solid-state reaction (SS) methods. In the WM method, the use of nitric acid as a solvent and a simpler mixing process allows for a more uniform distribution of precursors, enabling the crystallization process to occur more optimally. Additionally, the minimal mass loss during combustion and shorter synthesis time may contribute to the formation of crystals with better quality compared with the SG and SS methods.
c space group. The Goodness of fit (χ2) value indicated that the WM sample had a value close to 1, suggesting a better fit and good agreement with the XRD profile than the SG and SS samples. The use of the wet-mixing (WM) method is more efficient than the sol–gel (SG) method. The WM method does not require additional precursors or chelating agents to complex metal ions; thus, less mass is lost during the combustion process.34 Additionally, the amount of water used during WM synthesis was reduced, leading to a shorter mixing duration. The WM method, using nitric acid as a solvent, allows the use of a wide variety of carbonate precursors, including both soluble and insoluble carbonates. However, the SG method is limited to soluble precursors.53 It is possible that the wet-mixing method enables WM to produce crystals with better quality than the sol–gel (SG) and solid-state reaction (SS) methods. In the WM method, the use of nitric acid as a solvent and a simpler mixing process allows for a more uniform distribution of precursors, enabling the crystallization process to occur more optimally. Additionally, the minimal mass loss during combustion and shorter synthesis time may contribute to the formation of crystals with better quality compared with the SG and SS methods.
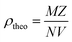 , where M is molecular mass, Z is the number of units per unit cell (Z = 6, for rhombohedral structure), N is Avogadro's number (N = 6.02 × 1023), and V is the unit cell volume.51 Based on the calculations, the density values for each sample do not show significant differences, as the only varying parameter is the unit cell volume, which does not differ greatly among the samples. The theoretical density of the LKdMO sample is 6.36 g cm−3 for all method variations, and 6.39 g cm−3 for parental compound (LKMO), a value within the density range of manganite-based materials, as previously reported.51
, where M is molecular mass, Z is the number of units per unit cell (Z = 6, for rhombohedral structure), N is Avogadro's number (N = 6.02 × 1023), and V is the unit cell volume.51 Based on the calculations, the density values for each sample do not show significant differences, as the only varying parameter is the unit cell volume, which does not differ greatly among the samples. The theoretical density of the LKdMO sample is 6.36 g cm−3 for all method variations, and 6.39 g cm−3 for parental compound (LKMO), a value within the density range of manganite-based materials, as previously reported.51![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c
c![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c
c![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c
c![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c
c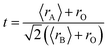 , where 〈rA〉 is the average ionic radius of the A-site, 〈rB〉 is the average ionic radius of the B-site, and 〈rO〉 is the ionic radii of oxygen. Ionic size mismatch in the crystal structure leads to a decrease in the symmetry. An ideal cubic structure was achieved when ‘t’ = 1. A tolerance factor in the range of ‘t’ = 1 within the range of 0.90 < t < 1 indicates that the crystal structure experiences rhombohedral distortion. This reduction was due to the rotation of the adjacent MnO6 octahedron in opposite directions along the cubic (111) axis. If ‘t’ = 1 within the range 0.75 < t < 0.90, the distortion increases, leading to an orthorhombic symmetry change caused by octahedron bending inconsistent with the MnO6 octahedron rotation around the (110) and (104) planes. For the LKdMO samples, a tolerance factor (t) value of 0.962 was obtained, indicating that the LKdMO ceramics had a rhombohedral crystal structure, which is consistent with the XRD analysis. The rhombohedral structure is evidenced by the presence of a doublet intensity in the 2θ range of 32.4 in the XRD pattern due to the (110) and (104) planes. Such peak splitting is characteristic of a rhombohedral crystal structure.17
, where 〈rA〉 is the average ionic radius of the A-site, 〈rB〉 is the average ionic radius of the B-site, and 〈rO〉 is the ionic radii of oxygen. Ionic size mismatch in the crystal structure leads to a decrease in the symmetry. An ideal cubic structure was achieved when ‘t’ = 1. A tolerance factor in the range of ‘t’ = 1 within the range of 0.90 < t < 1 indicates that the crystal structure experiences rhombohedral distortion. This reduction was due to the rotation of the adjacent MnO6 octahedron in opposite directions along the cubic (111) axis. If ‘t’ = 1 within the range 0.75 < t < 0.90, the distortion increases, leading to an orthorhombic symmetry change caused by octahedron bending inconsistent with the MnO6 octahedron rotation around the (110) and (104) planes. For the LKdMO samples, a tolerance factor (t) value of 0.962 was obtained, indicating that the LKdMO ceramics had a rhombohedral crystal structure, which is consistent with the XRD analysis. The rhombohedral structure is evidenced by the presence of a doublet intensity in the 2θ range of 32.4 in the XRD pattern due to the (110) and (104) planes. Such peak splitting is characteristic of a rhombohedral crystal structure.17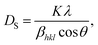
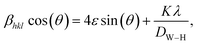
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ) vs. 4
cos(θ) vs. 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ). The results of the W–H plot are shown in Fig. 4. The y-axis represents the value considered for each diffraction peak of the sample. A good linear fit across all values resulted in a straight line, where the crystallite size was obtained from the y-intercept, and the microstrain was derived from the slope of the line. It should be noted that βhkl (FWHM in radians) of each peak with intensity was measured using Gaussian function fitting.56 The average crystallite sizes (D) calculated using the Williamson–Hall method (DW–H) for the SG, WM, and SS samples were 180, 161, and 166 nm, respectively. The SG sample exhibits a larger crystallite size, which was influenced by the FWHM values at higher (2θ) angles, resulting in higher crystallinity compared to the WM and SS samples. Teixeira et al. also noted that the SS method has a maximum crystallite size limitation of 100 nm.57 The crystallite size calculated using the Williamson–Hall method (DW–H) was larger than that obtained using the Scherrer method (DS) because of the neglect of strain-induced broadening effects in the Scherrer method (DS).58
sin(θ). The results of the W–H plot are shown in Fig. 4. The y-axis represents the value considered for each diffraction peak of the sample. A good linear fit across all values resulted in a straight line, where the crystallite size was obtained from the y-intercept, and the microstrain was derived from the slope of the line. It should be noted that βhkl (FWHM in radians) of each peak with intensity was measured using Gaussian function fitting.56 The average crystallite sizes (D) calculated using the Williamson–Hall method (DW–H) for the SG, WM, and SS samples were 180, 161, and 166 nm, respectively. The SG sample exhibits a larger crystallite size, which was influenced by the FWHM values at higher (2θ) angles, resulting in higher crystallinity compared to the WM and SS samples. Teixeira et al. also noted that the SS method has a maximum crystallite size limitation of 100 nm.57 The crystallite size calculated using the Williamson–Hall method (DW–H) was larger than that obtained using the Scherrer method (DS) because of the neglect of strain-induced broadening effects in the Scherrer method (DS).58






![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds at 286–287 eV, and O
O bonds at 286–287 eV, and O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–O bonds in carbonates at 288–289 eV. Additionally, peaks at 292.2 eV and 295.0 eV represent K 2p3/2 and K 2p1/2, respectively (Fig. 9). The K 2p peaks cause a shift in the C 1s peak to lower binding energies due to the dipole formation caused by the electronegativity differences between K and C, which are 0.8 and 2.5, respectively.70
C–O bonds in carbonates at 288–289 eV. Additionally, peaks at 292.2 eV and 295.0 eV represent K 2p3/2 and K 2p1/2, respectively (Fig. 9). The K 2p peaks cause a shift in the C 1s peak to lower binding energies due to the dipole formation caused by the electronegativity differences between K and C, which are 0.8 and 2.5, respectively.70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 786.05
786.05![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 171.98
171.98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 509.66
509.66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 301.92
301.92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 333.07
333.07![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 333.07
333.07![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 081.18
081.18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 018.79
018.79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 234.21
234.21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 327.94
327.94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 651.66
651.66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 811.21
811.21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 897.84
897.84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 819.7
819.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 285.11
285.11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 981.99
981.99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467.12
467.12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 370.2
370.2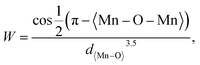


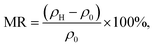
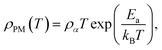
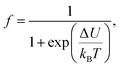
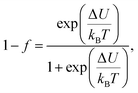
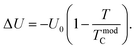


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 933.9676
933.9676![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 748.72826
748.72826![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 568.02083
568.02083![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group with a rhombohedral structure, while the SG sample showed the presence of a secondary Mn2O3 phase. The EDS and XPS results suggested that La, K, Mn, and O were uniformly distributed in the samples. The SEM results indicated that the WM sample had a smaller average grain size than the SG and SS samples. Consequently, the WM sample exhibited lower resistivity owing to the reduced scattering of the grain boundaries. However, the difference in grain size owing to the synthesis method affects the transport and magnetic performance. The highest MR values for the SG, WM, and SS samples were 17.05% at 287.74 K, 54.68% at 271.50 K, and 47.09% at 270.25 K, respectively. The K-site deficiency successfully enhanced the MR value in the LKdMO material compared to the parental compound (LKMO), achieving an MR value of 10.36% at 287 K. Compared with the SG and SS samples, the WM sample exhibited the highest MR, which was attributed to the enhancement of spin-polarized tunneling by the largest grain boundary contribution. Overall, the WM method is more effective for producing LKdMO polycrystalline ceramics with better crystal quality and electromagnetic properties. Our results show that K-deficient formation can improve MR by changing the manganite lattice, which probably changes the structure and makes it easier for electrons to move around. These findings contribute to resolving inconsistencies in this field and highlight the potential for simpler, scalable synthesis methods for practical applications. Future work will focus on optimizing synthesis conditions to precisely control defect densities and types, with the aim of achieving an optimal balance that maximizes MR.
c space group with a rhombohedral structure, while the SG sample showed the presence of a secondary Mn2O3 phase. The EDS and XPS results suggested that La, K, Mn, and O were uniformly distributed in the samples. The SEM results indicated that the WM sample had a smaller average grain size than the SG and SS samples. Consequently, the WM sample exhibited lower resistivity owing to the reduced scattering of the grain boundaries. However, the difference in grain size owing to the synthesis method affects the transport and magnetic performance. The highest MR values for the SG, WM, and SS samples were 17.05% at 287.74 K, 54.68% at 271.50 K, and 47.09% at 270.25 K, respectively. The K-site deficiency successfully enhanced the MR value in the LKdMO material compared to the parental compound (LKMO), achieving an MR value of 10.36% at 287 K. Compared with the SG and SS samples, the WM sample exhibited the highest MR, which was attributed to the enhancement of spin-polarized tunneling by the largest grain boundary contribution. Overall, the WM method is more effective for producing LKdMO polycrystalline ceramics with better crystal quality and electromagnetic properties. Our results show that K-deficient formation can improve MR by changing the manganite lattice, which probably changes the structure and makes it easier for electrons to move around. These findings contribute to resolving inconsistencies in this field and highlight the potential for simpler, scalable synthesis methods for practical applications. Future work will focus on optimizing synthesis conditions to precisely control defect densities and types, with the aim of achieving an optimal balance that maximizes MR.





