Calcium-atom-modified boron phosphide (BP) biphenylene as an efficient hydrogen storage material

Abstract

Porous nanosheets have attracted significant attention as viable options for energy storage materials because of their exceptionally large specific surface areas. A recent study (Int. J. Hydrogen Energy, 2024, 66, 33–39) has demonstrated that Li/Na-metalized inorganic BP-biphenylene (b-B₃P₃) and graphenylene (g-B₆P₆) analogues possess suitable functionalities for hydrogen (H₂) storage. Herein, we evaluate the H₂ storage performance of alkaline earth metal (AEM = Be, Mg, Ca)-decorated b-B₃P₃ and g-B₆P₆ structures based on first-principles density functional theory (DFT) calculations. Our investigations revealed that individual Be and Mg atoms are not stable on pure b-B₃P₃ and g-B₆P₆ sheets, and the formation of aggregates is favored due to their low binding energy to these surfaces. However, the binding energy improves for Ca-decorated b-B₃P₃ (b-B₃P₃(mCa)) and g-B₆P₆ (g-B₆P₆(nCa)) structures, forming stable and uniform mCa(nCa) (m and n stand for the numbers of Ca atom) coverages on both sides. Under maximum hydrogenation, the b-B₃P₃(8Ca) and g-B₆P₆(16Ca) structures exhibited the ability to adsorb up to 32H₂ and 48H₂ molecules with average adsorption energy (E_a) values of −0.23 eV per H₂ and −0.25 eV per H₂, respectively. Gravimetric H₂ uptakes of 7.28 wt% and 5.56 wt% were found for b-B₃P₃(8Ca)@32H₂ and g-B₆P₆(16Ca)@48H₂ systems, exceeding the target of 5.50 wt% set by the US Department of Energy (DOE) to be reached by 2025. Our findings indicate the importance of these b-B₃P₃ and g-B₆P₆ sheets for H₂ storage technologies.

---

1 Introduction

Growing concerns over environmental pollution and the limited supply of fossil fuels have driven the pursuit of clean energy sources.^1,2 Hydrogen (H₂) is regarded as a sustainable and alternative energy source capable of eradicating the use of fossil fuels, especially in transportation applications.^3–5 However, one of the main hindrances to the advancement of H₂ technology is creating small, light, safe, and affordable storage systems with large storage capacity under practical conditions.^3,6 Solid-state H₂ storage materials, which store H₂ via the physisorption or chemisorption method, have been extensively investigated as a promising approach to overcome the challenges associated with gas or liquid H₂ storage, which requires very high pressure (350–700 bar).^3,7,8 According to the US Department of Energy (DOE), by 2025 an ideal H₂ storage material should attain gravimetric and volumetric capacity greater than 5.5 wt% and 30 g L⁻¹, with adsorption energy (E_a) between 0.2 and 0.6 eV per H₂.^9–11 By meeting these minimum thresholds, an adsorbent material will allow suitable reversible H₂ storage under ambient conditions.

To date, a wide range of materials, including carbon-based materials,^12–14 MXenes,^15,16 metal–organic-frameworks (MOFs)^17–19 covalent organic frameworks (COFs)^20–22 and related low-dimensional materials^23–32 have attracted a significant number of studies in several research areas, including spintronics, batteries, optoelectronics and catalysis. Porous two-dimensional (2D) materials, in particular organic/inorganic-based biphenylene (BPN) or graphenylene (BPC) sheets, are ideally suited for H₂ storage applications.^33–44 However, the weak interaction between these surfaces and H₂ molecules (due to low E_a values) reduces their H₂ storage capacities. Extensive theoretical studies have shown that the metal-atom decoration technique^45–47 can be effective for improving the E_a, resulting in higher H₂ uptake. For instance, Denis et al.³³ studied the H₂ storage performance of BPN with adsorbed Li-adatoms, and obtained a H₂ uptake of 7.4 wt%, with an averaged E_a of 0.20 eV per H₂. In addition, ultrahigh H₂ storage capacity values of 11.9 wt% and 11.63% for K- and Ca-decorated BPN structures was predicted by Mahamiya et al.³⁴ Singh et al.⁴⁸ have found 11.07 wt% H₂ uptake near ambient temperature for a Sc-decorated BPN structure. Kaewmaraya et al.³⁵ reported 6.66 wt% and 6.76 wt% H₂ storage capacities for Li/Na-decorated divacancy BPN. Moreover, H₂ storage analysis was carried out on Li-decorated BPN and Li-decorated N-doped BPN by Zhang et al.³⁸ They reported H₂ uptakes of 9.581 wt% and 10.588 wt% for Li-decorated BPN and Li-decorated N-doped BPN, respectively. In another separate study, adsorption of H₂ on a Li-decorated B-doped BPN structure has been explored by Ma et al.⁴⁰ Their analysis indicated that the H₂ storage capacity value changed from 6.30 wt% to 19.22 wt% as a function of Li-ion concentration, which increased from 7.69% to 25.00%. On the other hand, Hussain et al.³⁶ used light metals to enhance the H₂ storage capacity value of BPC sheets. Their results revealed that the BPC can accommodate 20 H₂ molecules with storage capacity values between 4.90 wt% and 6.14 wt% under operating conditions. Additionally, Boezar et al.⁴⁹ evaluated the H₂ adsorption behavior of transition metal (Fe, Sc and Ti) decorated BPC structures. Their studies indicate that these structures can take up to 20 H₂ molecules with average E_a values higher than 0.2 eV per H₂. Structures with Li(Na)-atom-decorated inorganic graphenylene (IGP) based on SiC (Li(Na)@IGP-SiC) have been investigated by Martins et al.³⁷ for H₂ storage performance. Their calculations revealed that Li(Na)@IGP-SiC can take up to 48 H₂ molecules, yielding an enhanced H₂ storage capacity value of 8.27 wt% (6.78 wt%) for Li(Na)@IGP-SiC structures. Following this use of IGP sheets, Djebablia et al.³⁹ recently studied the H₂ performance of b-BP(Li, Na, K)/g-BP(Li, Na, K) structures. They found that each adatom binds strongly on the host b-BP/g-BP surfaces and adsorbs multiple H₂ molecules, resulting in uptakes of 9.05% and 6.99% for b-BP(Li) and g-BP(Li) structures, respectively, under practical conditions.

Motivated by the results mentioned above, we investigate the effect of alkaline earth metal (AEM = Be, Mg, Ca)-decorated b-B₃P₃ and g-B₆P₆ sheets for H₂ storage applications, using spin-polarized density functional theory (DFT). The obtained results reveal that Be and Mg atoms bind weakly to the b-B₃P₃ and g-B₆P₆ sheets. In contrast, Ca atoms exhibit a strong binding energy, making them suitable hosts for adsorbing a considerable number of H₂ molecules. Meanwhile, addition of H₂ molecules on the Ca-decorated b-B₃P₃ (b-B₃P₃(Ca)) and g-B₆P₆ (g-B₆P₆(Ca)) structures was analyzed to fully understand their H₂ storage performance. Moreover, the b-B₃P₃(Ca) and g-B₆P₆(Ca) structures reached storage capacities of 7.28 wt% and 5.56 wt%, respectively, exceeding the target of 5.50 wt% set by the US DOE to be attained by 2025. For the sake of convenience, b-B₃P₃(Ca) and g-B₆P₆(Ca) with adsorbed p(q)H₂ molecules are named b-B₃P₃(mCa)@pH₂ and g-B₆P₆(nCa)@qH₂, respectively (p/q and n/m correspond to the numbers of adsorbed H₂ molecules and Ca adatoms, respectively).

2 Computational details

The spin-polarized DFT⁵⁰ calculations on the ground-state properties of all studied structures have been implemented in the Vienna ab initio simulation package (VASP).⁵¹ The projector augmented-wave (PAW) approach⁵² was used to describe ion–electron interactions. The exchange–correlation functional was treated using the generalized gradient approximation (GGA) of the Perdew–Burke–Ernzerhof (PBE) functional.⁵² The van der Waals (vdW) interaction correction was added through the DFT-D2 approach.⁵³ It should be noted that the PBE-D2 vdW correction is prone to overestimating adsorption energy values in certain cases, which could have an impact on the conclusions drawn.⁵⁴ During the structural optimization calculations, the Brillouin zone (BZ) of all studied structures was sampled using the Monkhorst–Pack approach⁵⁵ with (6 × 6 × 1) and (12 × 12 × 1) grids for self-consistency and total density-of-state computations, respectively. We used a plane-wave basis set with a kinetic energy cut-off of 500 eV to expand the wave functions. We set a vacuum layer at least 18 Å thick perpendicularly to the cell dimension for all calculations. The convergence criteria for energy and force for all calculations were set at 0.001 eV Å⁻¹ and 10⁻⁵ eV, respectively. To assess the thermal stability of all studied b-B₃P₃(Ca) and g-B₆P₆(Ca) structures, ab initio molecular dynamics (AIMD) simulations have been performed at room temperature (300 K).⁵⁶ In the NVT ensemble, 1 fs for 5000 iterations and the Nosé thermostat were used for the MD simulation parameters. Bader analysis⁵⁷ was employed to study the charge transfer mechanism. With the aid of VESTA software,⁵⁸ the charge distribution and structural analysis were obtained.

Considering the b-B₃P₃(Ca) case, the average adsorption energy (E_a) is defined as:

E_a = (E_b-B3P3(mCa) − E_b-B3P3 − mE_Ca)/m (1)

where E_b-B3P3(mCa), E_b-B3P3 and E_Ca denote the total energy of b-B₃P₃ decorated with mCa adatoms, the pure b-B₃P₃ sheet and isolated Ca adatoms, respectively. We used the same E_a procedure for the g-B₆P₆(Ca) case.

The average E_a for the b-B₃P₃(mCa)@pH₂ structure is computed as:

E_a = (E_{b-B3P3(8Ca)@pH2)} − E_b-B3P3(8Ca) − pE_H2)/p (2)

where the E_{b-B3P3(8Ca)@pH2)} and E_H2 terms denote the total energy of the b-B₃P₃(8Ca)@pH₂) structure and isolated H₂ molecules, respectively. We used the same E_a procedure for the g-B₆P₆(nCa)@qH₂ case.

The H₂ molecule storage capacity (wt%) has been evaluated by employing the following expression:

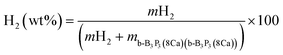Here, mH₂ and m_{b-B3P3(8Ca)(b-B3P3(8Ca))} stand for the mass of H₂ uptake and the mass of the b-B₃P₃(8Ca)(b-B₃P₃(8Ca)) structure, respectively.

The average desorption temperature (T_d) of the b-B₃P₃(8Ca)@pH₂ and g-B₆P₆(16Ca)@qH₂ systems has been estimated by employing the van't Hoff equation,⁵⁹ expressed as:

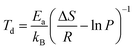where E_a is the averaged E_a (J per H₂) of H₂ molecules adsorbed on the b-B₃P₃(8Ca) and g-B₆P₆(16Ca) systems. The entropy change (ΔS), the Boltzmann constant (k_B), the universal gas constant (R) and the atmospheric pressure (P) are taken as 75.44 J K⁻¹ mol⁻¹, 1.380 × 10²³ J K⁻¹, 8.62 × 10⁻⁵ eV K⁻¹ and 1 atm, respectively.

3 Results and discussion

3.1 Adsorbent structures

This paper expands on the recently reported H₂ storage on b-B₃P₃(Li) and g-B₆P₆(Li) structures,³⁹ by investigating the H₂ storage performance of b-B₃P₃(Mg, Be, Ca) and g-B₆P₆(Mg, Be, Ca) structures. To begin with, we construct b-B₃P₃ and g-B₆P₆ supercells in (2 × 2 × 1) dimensions, as depicted in Fig. 1. Each (2 × 2 × 1) b-B₃P₃/g-B₆P₆ sheet consists of 24 B, 24 P, and 4 Ca atoms. Henceforth, we shall consider the (2 × 2 × 1) supercell of b-B₃P₃/g-B₆P₆ as b-B₁₂P₁₂X₄/g-B₂₄P₂₄X₄ sheets. The optimized lattice constants were evaluated to be a = 11.80 Å and b = 9.75 Å, and a = b = 17.61 Å, respectively, for b-B₃P₃ and g-B₆P₆ sheets, in good agreement with a recently reported paper.⁶⁰ It is well-known that pure 2D materials^{24,33–36,39,61–63} form weak interactions with H₂ molecules, which reduces their storage capacities. However, metalization of these b-B₃P₃ and g-B₆P₆ sheets with AEM (Be, Mg, Ca) adatoms is an efficient route to improve the H₂ chemical activity on their surfaces. We have examined eight distinct adsorption sites on the b-B₃P₃ and g-B₆P₆ sheets to determine the preferred location of single AEM atoms. Fig. 1 illustrates these adsorption sites, which are at the top of the boron (T_B) and phosphorus (T_P) atoms, the octagonal/decagonal cavity (A₁), the square (A₂) and hexagonal (A₃) rings, and the bridging sites (A₄, A₅ and A₆).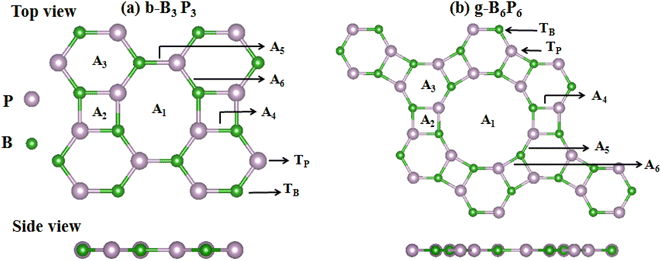

Fig. 1 Geometric structures of (a) b-B₃P₃ and (b) g-B₆P₆ sheets: top and side views with illustration of the available binding sites (A₁, A₂, A₃, A₄, A₅, A₆, T_B and T_P).

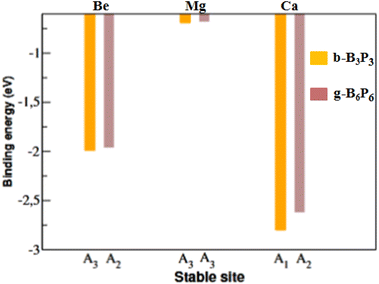
To achieve a uniform distribution, each AEM adatom must bind firmly to these b-B₃P₃ and g-B₆P₆ sheets. A negative E_a value signifies a stable configuration. Conversely, a positive E_a value suggests an unfavorable adsorption process. The calculated E_a values of single AEM adatoms at the most stable b-B₃P₃ and g-B₆P₆ sites are presented in Fig. 2. We have found that the Be and Mg adatoms bind on the b-B₃P₃ and g-B₆P₆ sheets with very small E_a values. Additionally, their cohesive energy (E_c) is notably greater than their E_a values on the these surfaces. Hence, these metals would rather form clusters than bind separately to the b-B₃P₃ and g-B₆P₆ sheets. Therefore, we have not considered b-B₃P₃(Be), b-B₃P₃(Mg), g-B₆P₆(Be) and g-B₆P₆(Mg) structures for the H₂ adsorption calculations (see Fig. 2). However, the E_a values of Ca-decorated b-B₃P₃ and g-B₆P₆ sheets are found to be −2.82 eV and −2.62 eV, respectively, larger than the E_c value of the bulk Ca atom (1.84 eV).⁶⁴ Bader charge (Q) analysis⁵⁷ confirms that there was a significant transfer of 1.40 e⁻ from the Ca⁺ ion to the b-B₃P₃/g-B₆P₆ monolayer, as compared with 1.32/1.02 e⁻ from Be⁺/Mg⁺ ions, respectively. This shows a favorable ionic bonding between Ca adatoms and the b-B₃P₃/g-B₆P₆ surfaces. The obtained E_a values correlate with the estimated electron transfer values. Hence, these stable b-B₃P₃(Ca) and g-B₆P₆(Ca) structures are considered for further studies. Because they have a large surface area, the b-B₃P₃ and g-B₆P₆ sheets are expected to possess the ability of binding multiple Ca adatoms. This could significantly improve their H₂ storage performance. Consequently, we introduced several Ca adatoms to investigate their binding properties. Our findings revealed that eight Ca adatoms can be adsorbed on the b-B₃P₃ sheet, with an E_a value of −2.46 eV per Ca. The g-B₆P₆ sheet can take up to 16Ca adatoms with E_a values of −2.47 eV per Ca. We have also carried out another analysis to illustrate the stability of dispersed Ca adatoms on b-B₃P₃ and g-B₆P₆ surfaces compared to Ca dimer formation or aggregation into clusters. This is done by comparing the single Ca atom and dimer E_a values for adsorption on these surfaces. As we know, if the Ca dimer binding on the surface becomes less stable compared to single-atom binding, cluster formation can be avoided. Hence, the clustering energy (E_cluster) was determined by comparing the E_a of the dimer to that of the single Ca adsorbed on the b-B₃P₃/g-B₆P₆ surfaces. If the E_cluster has a positive (negative) value, it means that the Ca atoms are susceptible to cluster formation (dispersion). The obtained E_cluster values are −0.23 and −0.79 eV for b-B₃P₃ and g-B₆P₆ monolayers, respectively. Clearly, all Ca atoms possess negative clustering energy values on these b-B₃P₃ and g-B₆P₆ surfaces. It can be inferred that the Ca atoms that are dispersed on the b/g-BP surfaces are generally stable and Ca cluster formation can be avoided. Additionally, Fig. S4 in the ESI File† confirms the dynamic stability of these b-B₃P₃ and g-B₆P₆ structures with adsorbed Ca adatoms.

Fig. 2 The E_a values of b-B₃P₃(Be, Mg, Ca) and g-B₆P₆(Be, Mg, Ca) structures.

Table 1 lists the calculated E_a values, the average heights of Ca adatoms from the b-B₃P₃(g-B₆P₆) sheets (bond lengths, d_{Ca–b-B3P3(g-B6P6)}) and the amounts of charge released by the Ca adatoms. The top and side views of the optimized b-B₃P₃(8Ca) and g-B₆P₆(16Ca) geometries are shown in Fig. S1.† For the b-B₃P₃(8Ca) and g-B₆P₆(16Ca) structures, there was an absence of any indication of structural reconstruction after optimization. Additionally, there is no tendency for Ca adatoms to cluster on the b-B₃P₃ and g-B₆P₆ surfaces.

Table 1 We provide the adsorption energies (E_a in eV per Ca), bond lengths (d_{Ca–b-B3P3(g-B6P6)}) and amounts of charge transfer (Q) (from Ca to b-B₃P₃ and g-B₆P₆ sheets) for the b-B₃P₃(mCa) and g-B₆P₆(nCa) structures. The d_{Ca–b-B3P3(g-B6P6)} is the averaged bond length along the z-axis between Ca adatoms and all the B/P atoms in the b-B₃P₃ and g-B₆P₆ structures. m/n represents the number of Ca adatoms

System	m/n	Ea	dCa–b-B3P3(g-B6P6) (Å)	Q (e^−)
b-B3P3(mCa)	1	−2.80	1.23	1.39
	4	−2.31	1.54	1.31
	8	−2.46	1.81	1.11
g-B6P6(nCa)	1	−2.62	1.79	1.39
	8	−2.35	2.28	1.15
	16	−2.47	1.98	1.09

---

We provide charge analysis calculations for the b-B₃P₃(mCa) and g-B₆P₆(nCa) structures to illustrate the charge transferred from the Ca adatoms to the b-B₃P₃(g-B₆P₆) sheets (see Table 1). There is a significant charge transfer from Ca⁺ ions to the b-B₃P₃ and g-B₆P₆ sheets for all structures. As a result, Ca adatoms and these surfaces form an ionic bond, as confirm by the ELF plots in Fig. S3.† It should be noted that the obtained E_a values agree with the obtained electron transfer values. The averaged bond length along the z-axis between Ca adatoms and all the B/P atoms in the b-B₃P₃ and g-B₆P₆ surfaces corresponds well with the E_a values listed in Table 1. It shows that the stronger the interaction, the lower the bond length, which affects the values of E_a. Also, the thermal stability of the b-B₃P₃(Ca) and g-B₆P₆(Ca)) structures was evaluated through AIMD at 300 K for a duration of 5 ps. In Fig. S4,† we have shown the oscillation range of total energy against time step at 300 K. According to the figure, the energy oscillations for each atom fluctuate within a fixed range on the order of meV. In addition, in Fig. S4† we give images of the side and top views of the b-B₃P₃(Ca) and g-B₆P₆(Ca)) structures. It is clear that these structures maintain their structural integrity at room temperature without any visible structural reconstructions. It is evident that these b-B₃P₃(Ca) and g-B₆P₆(Ca)) structures are suitable ones for H₂ storage applications under ambient conditions.

3.2 H₂ adsorption on b-B₃P₃(8Ca) and g-B₆P₆(16Ca) structures

Firstly, the H₂ molecule is introduced at a given height above the stable adsorption site of the b-B₃P₃(8Ca) and g-B₆P₆(16Ca) structures. Then, the b-B₃P₃(Ca)@H₂ and g-B₆P₆(Ca)@H₂ systems are fully relaxed without any geometry restriction. Subsequently, a number of H₂ molecules was incrementally added until the maximum adsorption limit was reached. According to the E_a values obtained for b-B₃P₃(8Ca) and g-B₆P₆(16Ca), there is strong physisorption and chemisorption of H₂ molecules. These structures provide a better binding of H₂ molecules than those obtained from the pristine b-B₃P₃@H₂ and g-B₆P₆@H₂ systems.³⁹ Fig. 4 displays all the remaining estimated E_a values. It is revealed that the b-B₃P₃(8Ca) structure can adsorb up to 32 H₂ molecules, with an average E_a value of −0.23 eV per H₂. On the other hand, the g-B₆P₆(16Ca) structure can retain 48H₂ molecules with an average E_a value of −0.25 eV per H₂. It should be noted that these estimated E_a values show the tendency to accommodate more H₂ molecules on the b-B₃P₃(8Ca) and g-B₆P₆(16Ca) structures. In comparison with the earlier results based on DFT calculations, our estimated moderate H₂ E_a values are better than or comparable with those reported for metallized boron monoxide, boron hydride and Me–C₈B₅ monolayers.^47,65,66 The significantly negative E_a value means a stronger interaction of H₂ molecules on b-B₃P₃(8Ca) and g-B₆P₆(16Ca) structures. The E_a value we obtained for the maximum of adsorbed H₂ molecules is within the above-mentioned acceptable range required for a H₂ storage material. This means that the H₂ molecule has been strongly physisorbed onto these b-B₃P₃(8Ca) and g-B₆P₆(16Ca) structures. Fig. 3 shows the relaxed structures of the b-B₃P₃(8Ca)@32H₂ and g-B₆P₆(16Ca)@48H₂ structures, whereas the remaining b-B₃P₃(8Ca)@pH₂ and g-B₆P₆(16Ca)@qH₂ structures are illustrated in Fig. S5 and S6.† We also provide, in Table 2, the numbers (p,q) of H₂ molecules adsorbed on the b-B₃P₃(8Ca) and g-B₆P₆(16Ca) structures, the E_a (eV per H₂), the average H–H bond length (d_H–H) and the corresponding H₂ capacity (wt%).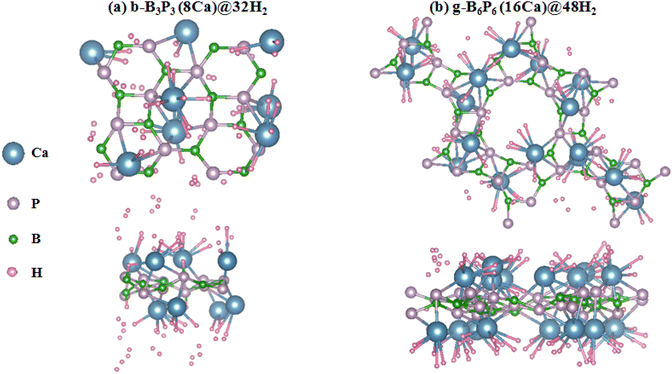

Fig. 3 The optimized structures with maximum adsorbed H₂ molecules: (a) b-B₃P₃(8Ca) and (b) g-B₆P₆(16Ca) structures.

Table 2 Number of H₂ molecules, adsorption energies E_a (eV per H₂), the corresponding average bond lengths for H₂ molecules d(H–H), H₂ storage capacity W (wt%), and desorption temperature T_D (K) for the b-B₃P₃(8Ca) and g-B₆P₆(16Ca) structures

System	Number of H2	Ea (eV per H2)	d(H–H)	TD (K)	W (wt%)
b-B3P3(8Ca)	1	−0.38	0.762	486.21	0.24
	4	−0.16	0.763	204.72	0.97
	8	−0.35	0.970	447.82	1.92
	12	−0.19	0.762	243.10	2.86
	16	−0.20	0.869	255.90	3.78
	32	−0.23	0.973	294.28	7.28
g-B6P6(16Ca)	1	−1.35	0.769	1727.32	0.12
	8	−0.34	0.770	435.03	0.97
	16	−0.51	1.081	652.54	1.92
	24	−0.35	0.947	447.82	2.86
	48	−0.25	0.840	319.87	5.56

---

It well-known that the interaction of an adsorbent surface with a H₂ molecule can be attributed to the electronic properties of the host material and the vdW forces between the H₂ and the surface. For weak vdW forces, the H₂ molecule can be physisorbed on the surface. Conversely, the H₂ molecule may dissociate into double H atoms and form a strong chemical bond with the surface atoms via a chemisorption mechanism, as previously reported.^47,63,67 It is noted from the optimized structures that 4 H₂ and 12 H₂ molecules are adsorbed through a physisorption process on the b-B₃P₃(8Ca) structure. However, we found that for adsorption of 8 H₂ and 16 H₂ molecules, one H₂ molecule is dissociated into 2H atoms, and four 4 H₂ molecules show a tendency to dissociate into 8 H atoms. In these cases, we found that the average H–H bond length is extended from 0.74 Å (gas-phase H–H distance) to 0.87 and 0.97 Å, showing that the adsorption of H₂ molecules on the b-B₃P₃(8Ca) structure arises through a strong physisorption process (see Fig. 4).

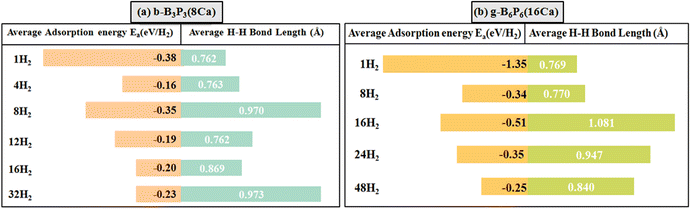Fig. 4 The average E_a values (eV per H₂) and average bond lengths (H–H) of H₂ molecules for (a) b-B₃P₃(8Ca) and (b) g-B₆P₆(16Ca). The lengths of the bars correspond to the E_a values.

On the other hand, for the g-B₆P₆(16Ca) structure, the adsorption of 8 H₂ molecules occurs through physisorption (molecular form). However, 3 H₂ molecules are dissociated into 6 H atoms in the case of 16 adsorbed H₂ molecules, while 2 H₂ molecules are dissociated into 4 H atoms in the cases of adsorption of 24 H₂ and 48 H₂ molecules. Their corresponding H–H bond lengths range between 0.84–1.08 Å. The tendency towards dissociation is attributed to the larger E_a values, which lead to an expanded d_H–H value for H₂ molecules (see Fig. 4). According to eqn (3), the estimated H₂ storage capacities are 7.28% and 5.56% for the b-B₃P₃(8Ca) and g-B₆P₆(16Ca) structures, respectively, exceeding the US DOE requirements. Within the limit of the theoretical method used in the current study, these obtained values are either similar to or higher than those of previously investigated metal-decorated 2D materials,^36,68,69 including the recently reported metallized boron monoxide, boron hydride and Me–C8B5 monolayers.^47,65,66 According to the PDOS plots, all the b-B₃P₃(8Ca)@32H₂ and g-B₆P₆(16Ca)@48H₂ structures exhibit metallic properties (see Fig. S4†). All the structures show evidence of asymmetric spin states around the Fermi level and beyond, which implies the existence of magnetic moments. The states are mainly from the p orbital of the Ca atom, while the s orbital of the H atom makes a small contribution in the vicinity of the Fermi level. Furthermore, there is a relative overlap between the Ca p orbital and the B p and P p orbitals beyond the Fermi level, except for H atoms. This emphasizes the nature of Ca’s interactions with the surroundings, specifically the s orbital of the H atom.

To achieve practical H₂ storage on these b-B₃P₃(8Ca) and g-B₆P₆(16Ca) surfaces, it is necessary to determine the average desorption temperature (T_D). Using eqn (4), the obtained T_D values for the b-B₃P₃(8Ca)@pH₂ and g-B₆P₆(16Ca)@qH₂ structures are summarised in Table 2. The obtained T_D values for the b-B₃P₃(8Ca)@pH₂ and g-B₆P₆(16Ca)@qH₂ structures are found to be in the range of 204–486 K and 319–1727 K, respectively. The T_D values decrease as the number of H₂ molecules increases, while the E_a value decreases. The T_D values for 32 H₂ and 48 H₂ molecules adsorbed on the b-B₃P₃(8Ca) and g-B₆P₆(16Ca) structures are estimated as 294 K and 319 K, respectively. The T_D value is over 9 times larger than the critical point of hydrogen (33 K). The obtained results clearly illustrate the correlation between bond lengths, E_a values, and T_D values. Table 2 reveals the T_D values that correspond to the average lengths of the H–H bonds. The higher T_D values suggest that some molecules are adsorbed through strong physisorption, and the greater H–H bond lengths may lead to dissociation at room temperature. It is worth mentioning that magnetic properties have been proven to be an effective way to regulate H₂'s desorption temperature.⁷⁰ It is expected that these studied b-B₃P₃(8Ca) and g-B₆P₆(16Ca) structures will enable the storage of H₂ under suitable conditions and have good reversibility.

4 Conclusions

In brief, spin-polarized DFT calculations are employed to investigate the performance of b-B₃P₃ and g-B₆P₆ sheets with adsorbed AEM (Be, Mg, Ca) adatoms for hydrogen storage. We find that Be and Mg adatoms are prone to cluster formation on b-B₃P₃ and g-B₆P₆ surfaces due to their low E_a values. However, the high E_a values for b-B₃P₃(Ca) and g-B₆P₆(Ca) structures show that the Ca adatom is stable and can prevent the segregation of Ca on the b-B₃P₃ and g-B₆P₆ surfaces, even at high concentrations. In addition, It has been demonstrated that the b-B₃P₃(Ca) and g-B₆P₆(Ca) structures are thermally stable at 300 K. Bader charge analysis reveals that Ca transfers an average of 1.11 (1.09) electrons to the b-B₃P₃(Ca) (g-B₆P₆(Ca)) sheets, making the b-B₃P₃(Ca) (g-B₆P₆(Ca)) surfaces suitable for enhanced H₂ molecule storage. In particular, the b-B₃P₃(8Ca) structure can store up to 32 H₂ molecules with an average E_a value of −0.23 eV per H₂. Meanwhile, the g-B₆P₆(16Ca) structure can take up 48 H₂ molecules with an average E_a value of −0.25 eV per H₂. The H₂ molecule storage capacities of the b-B₃P₃(8Ca)@32H₂ and g-B₆P₆(16Ca)@48H₂ structures are 7.28 wt% and 5.56 wt%, respectively. The calculated wt% values are higher than the 5.50 wt% target that needs to be reached by 2025. According to these findings, the b-B₃P₃(8Ca) and g-B₆P₆(16Ca) structures possess the potential to be reversible hydrogen storage media.

Data availability

Data will be made available on request.

Author contributions

Yusuf Zuntu Abdullahi: conceptualization, formal analysis, investigation, software, validation, writing – reviewing and editing, supervision, project administration. Ikram Djebablia: formal analysis, investigation, visualization, validation, writing – reviewing and editing. Tiem Leong Yoon: data curation, formal analysis, writing – reviewing. Lim Thong Leng: data curation, formal analysis, writing – reviewing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The calculations were performed at TUBITAK ULAKBIM, High Performance and Grid Computing Center (TR-Grid e-Infrastructure).

Notes and references

1. M. S. Dresselhaus and I. Thomas, Nature, 2001, 414, 332–337.
2. S. Chu and A. Majumdar, Nature, 2012, 488, 294–303.
3. L. Schlapbach and A. Züttel, Nature, 2001, 414, 353–358.
4. G. W. Crabtree, M. S. Dresselhaus and M. V. Buchanan, Phys. Today, 2004, 57, 39–44.
5. C.-J. Winter and J. Nitsch, Hydrogen as An Energy Carrier: Technologies, Systems, Economy, Springer Science & Business Media, 2012.
6. A. W. van den Berg and C. O. Areán, Chem. Commun., 2008, 668–681.
7. P. Jena, J. Phys. Chem. Lett., 2011, 2, 206–211.
8. C. Tarhan and M. A. Çil, J. Energy Storage, 2021, 40, 102676.
9. S. K. Bhatia and A. L. Myers, Langmuir, 2006, 22, 1688–1700.
10. Y.-H. Kim, Y. Zhao, A. Williamson, M. J. Heben and S. Zhang, Phys. Rev. Lett., 2006, 96, 016102.
11. R. C. Lochan and M. Head-Gordon, Phys. Chem. Chem. Phys., 2006, 8, 1357–1370.
12. T. Rimza, S. Saha, C. Dhand, N. Dwivedi, S. S. Patel, S. Singh and P. Kumar, ChemSusChem, 2022, 15, e202200281.
13. M. Mohan, V. K. Sharma, E. A. Kumar and V. Gayathri, Energy Storage, 2019, 1, e35.
14. X. Wu, Y. Chen, Z. Xing, C. W. K. Lam, S.-S. Pang, W. Zhang and Z. Ju, Adv. Energy Mater., 2019, 9, 1900343.
15. M. Hu, H. Zhang, T. Hu, B. Fan, X. Wang and Z. Li, Chem. Soc. Rev., 2020, 49, 6666–6693.
16. P. Kumar, S. Singh, S. Hashmi and K.-H. Kim, Nano Energy, 2021, 85, 105989.
17. D. Farrusseng, S. Aguado and C. Pinel, Angew. Chem., Int. Ed., 2009, 48, 7502–7513.
18. L. Zhu, X.-Q. Liu, H.-L. Jiang and L.-B. Sun, Chem. Rev., 2017, 117, 8129–8176.
19. S. Ma and H.-C. Zhou, Chem. Commun., 2010, 46, 44–53.
20. S.-Y. Ding and W. Wang, Chem. Soc. Rev., 2013, 42, 548–568.
21. J. Wang and S. Zhuang, Coord. Chem. Rev., 2019, 400, 213046.
22. X. Zhao, P. Pachfule and A. Thomas, Chem. Soc. Rev., 2021, 50, 6871–6913.
23. H. Jiang, W. Shyy, M. Liu, L. Wei, M. Wu and T. Zhao, J. Mater. Chem. A, 2017, 5, 672–679.
24. N. Khossossi, Y. Benhouria, S. R. Naqvi, P. K. Panda, I. Essaoudi, A. Ainane and R. Ahuja, Sustainable Energy Fuels, 2020, 4, 4538–4546.
25. T. Zhang, Y. Ma, B. Huang and Y. Dai, ACS Appl. Mater. Interfaces, 2019, 11, 6104–6110.
26. A. Kara, H. Enriquez, A. P. Seitsonen, L. L. Y. Voon, S. Vizzini, B. Aufray and H. Oughaddou, Surf. Sci. Rep., 2012, 67, 1–18.
27. V. Eswaraiah, Q. Zeng, Y. Long and Z. Liu, Small, 2016, 12, 3480–3502.
28. Y. Yong, H. Cui, Q. Zhou, X. Su, Y. Kuang and X. Li, Appl. Surf. Sci., 2019, 487, 488–495.
29. Y. Z. Abdullahi, F. Ersan, Z. D. Vatansever, E. Aktürk and O. Ü. Aktürk, J. Appl. Phys., 2020, 128, 113903.
30. T. Li, C. He and W. Zhang, J. Mater. Chem. A, 2019, 7, 4134–4144.
31. Y. Z. Abdullahi, A. Tigli and F. Ersan, Phys. Rev. Appl., 2023, 19, 014019.
32. R. Raccichini, A. Varzi, S. Passerini and B. Scrosati, Nat. Mater., 2015, 14, 271–279.
33. P. A. Denis and F. Iribarne, Comput. Theor. Chem., 2015, 1062, 30–35.
34. V. Mahamiya, A. Shukla and B. Chakraborty, Int. J. Hydrogen Energy, 2022, 47, 41833–41847.
35. T. Kaewmaraya, N. Thatsami, P. Tangpakonsab, R. Kinkla, K. Kotmool, C. Menendez, K. Aguey-Zinsou and T. Hussain, Appl. Surf. Sci., 2023, 629, 157391.
36. T. Hussain, M. Hankel and D. J. Searles, J. Phys. Chem. C, 2017, 121, 14393–14400.
37. N. F. Martins, A. S. Maia, J. A. Laranjeira, G. S. Fabris, A. R. Albuquerque and J. R. Sambrano, Int. J. Hydrogen Energy, 2024, 51, 98–107.
38. X. Zhang, F. Chen, B. Jia, Z. Guo, J. Hao, S. Gao, G. Wu, L. Gao and P. Lu, Int. J. Hydrogen Energy, 2023, 48, 17216–17229.
39. I. Djebablia, Y. Z. Abdullahi, K. Zanat and F. Ersan, Int. J. Hydrogen Energy, 2024, 66, 33–39.
40. L.-J. Ma, Y. Sun, J. Jia and H.-S. Wu, Fuel, 2024, 357, 129652.
41. Y. Fu, J. Xiang, Y. Xie, X. Gong, Y. Xu, Q. Zhao, Y. Liu, J. Xu and W. Liu, Comput. Mater. Sci., 2024, 238, 112951.
42. X. Gong, Y. Fu, Y. Xu, W. Liu and J. Xu, Mater. Today Commun., 2024, 40, 109626.
43. Y. Xie, L. Chen, J. Xu and W. Liu, RSC Adv., 2022, 12, 20088–20095.
44. Y. Xu, Y. Fu, X. Gong, J. Xu and W. Liu, Mater. Today Commun., 2024, 41, 110394.
45. P. Panigrahi, A. Kumar, A. Karton, R. Ahuja and T. Hussain, Int. J. Hydrogen Energy, 2020, 45, 3035–3045.
46. P. Panigrahi, M. Desai, M. K. Talari, H. Bae, H. Lee, R. Ahuja and T. Hussain, Int. J. Hydrogen Energy, 2021, 46, 7371–7380.
47. J. I. Jason, Y. Pal, P. Anees, H. Lee, T. Kaewmaraya, T. Hussain and P. Panigrahi, Int. J. Hydrogen Energy, 2024, 50, 455–463.
48. M. Singh, A. Shukla and B. Chakraborty, Sustainable Energy Fuels, 2023, 7, 996–1010.
49. K. Boezar, A. Reisi-Vanani and M. Dehkhodaei, Int. J. Hydrogen Energy, 2021, 46, 38370–38380.
50. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864.
51. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
52. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
53. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
54. D. Nazarian, P. Ganesh and D. S. Sholl, J. Mater. Chem. A, 2015, 3, 22432–22440.
55. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
56. G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643.
57. R. F. Bader, Acc. Chem. Res., 1985, 18, 9–15.
58. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
59. E. Durgun, S. Ciraci and T. Yildirim, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 085405.
60. Y. Z. Abdullahi and F. Ersan, Comput. Mater. Sci., 2024, 242, 113103.
61. K. Alhameedi, T. Hussain, H. Bae, D. Jayatilaka, H. Lee and A. Karton, Carbon, 2019, 152, 344–353.
62. A. Hashmi, M. U. Farooq, I. Khan, J. Son and J. Hong, J. Mater. Chem. A, 2017, 5, 2821–2828.
63. A. M. Satawara, G. A. Shaikh, S. K. Gupta, A. N. Andriotis, M. Menon and P. Gajjar, Int. J. Hydrogen Energy, 2023, 48, 25438–25449.
64. C. Kittel and P. McEuen, Introduction to Solid State Physics, John Wiley & Sons, 2018.
65. W. Othman, W. Alfalasi, T. Hussain and N. Tit, J. Energy Storage, 2024, 98, 113014.
66. Y. Gong, D. Chen, B. Guo, S. Chen, Z. Zhu and M. Cheng, Int. J. Hydrogen Energy, 2024, 82, 384–397.
67. S. Nachimuthu, P.-J. Lai, E. G. Leggesse and J.-C. Jiang, Sci. Rep., 2015, 5, 16797.
68. S. R. Naqvi, T. Hussain, P. Panigrahi, W. Luo and R. Ahuja, RSC Adv., 2017, 7, 8598–8605.
69. L. Yuan, L. Kang, Y. Chen, D. Wang, J. Gong, C. Wang, M. Zhang and X. Wu, Appl. Surf. Sci., 2018, 434, 843–849.
70. A. Yadav, B. Chakraborty, A. Gangan, N. Patel, M. Press and L. M. Ramaniah, J. Phys. Chem. C, 2017, 121, 16721–16730.

---

Footnote

† Electronic supplementary information (ESI) available: Snapshots of the molecular dynamics simulations, Electron Localization Function (ELF) and total density of states for optimized structures of b-B₃P₃(8Ca)@32H₂ and g-B₃P₃(8Ca)@48H₂ structures. See DOI: https://doi.org/10.1039/d4ra07271e

---