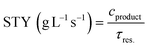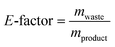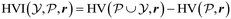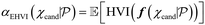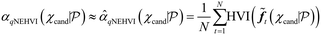Multi-objective Bayesian optimisation using q-noisy expected hypervolume improvement (qNEHVI) for the Schotten–Baumann reaction

Abstract

Amide bond formation is one of the most prevalent reactions in the pharmaceutical industry, among which the Schotten–Baumann reaction with a long history is useful as a potential green amide formation approach. However, the use of water in the reaction system often causes undesired hydrolysis and can generate a multiphase system. This makes the reaction space complex, making it challenging to find the optimal conditions. In this study, the Schotten–Baumann reaction was studied in a continuous flow and was optimised with two objectives using a Bayesian optimisation algorithm based on the q-noisy expected hypervolume improvement (qNEHVI) acquisition function. The algorithm guided the experiment design over a range of electrophiles, equivalents, solvents, and flow rates, and was able to identify the Pareto front of optimal solutions efficiently. Based on the optimisation results, reactions under a flow and batch conditions were compared; undesired hydrolysis was suppressed successfully using the flow conditions. Finally, the relationship between the solvent and flow rate was discussed to gain more insights into this reaction.

---

Introduction

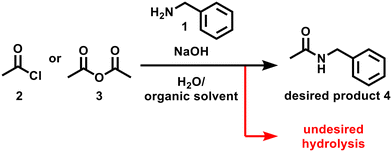
Amide bond formation is one of the most frequently used reactions in medicinal chemistry.¹ The demand for greener approaches for amide bond formation has been growing over the last decade.² Although amide bond formation with acid chloride or acid anhydride is particularly useful in large-scale synthesis,³ this approach usually requires organic bases (e.g. Et₃N: 101 g mol⁻¹) for trapping the generated acid. An alternative method, the Schotten–Baumann reaction,⁴ uses environmentally friendly solvents (e.g. water) and inorganic bases (e.g. NaOH) which are less wasteful and inexpensive. Water, which is necessary for dissolving inorganic bases, often causes undesired hydrolysis of electrophiles in the Schotten–Baumann reaction. In addition, the use of water sometimes makes scale-up of the reaction difficult due to inefficient mass transfer between aqueous and organic phases.⁵ Careful control of temperature is also required due to the highly exothermic nature of this reaction. These challenges make the practical use of the attractive amide bond formation reaction difficult.

To resolve the challenges of performing the Schotten–Baumann reaction as a robust protocol, we hypothesise that performing the reaction in a continuous flow may be an effective strategy. When well-designed, a continuous flow allows precise control of reaction time, temperature, and can achieve good mixing and heat transfer.⁶ Although the reaction itself is well-known, there are very few examples of performing the reaction in a flow,⁷ and there are no studies exploring process parameters to propose a robust experimental protocol.

To develop and optimise such a reaction system to achieve the best reaction outcomes is generally time-consuming and challenging, as the performance of the system is often nonlinear with respect to operating conditions and reaction. This usually requires good understanding of interactions between reaction parameters and conditions, which are sometimes difficult to predict; optimisation can easily get stuck in a local minimum.⁸ In addition, process optimisation needs to consider multiple competing objectives such as reaction yield, environmental impact, and economic factors, rather than one single objective.

In recent years, the idea of applying intelligent algorithms to guide reaction optimisation has shown to be an efficient way, which reduces the number of experiments and human intervention at the same time.⁹ Given a complex reaction space, an algorithm can search and design new experiments to move towards the optimal results with a reduced number of experiments.

One of the popular approaches to process development is Bayesian optimisation. It is a stochastic optimisation method suitable for nonlinear and expensive-to-evaluate objective functions.¹⁰ Previous studies have shown that reaction optimisation with multiple objectives can be performed using Bayesian optimisation. Schweidtmann et al. implemented Thompson sampling efficient multi-objective (TSEMO¹¹) for reaction optimisation in a flow reactor; both reactor productivity and environmental objectives were identified.^9a The trade-off between these objectives was found to form a Pareto front. Later, this algorithm was applied for multi-step reaction and separation,^9b biowaste conversion¹² and polymer synthesis.¹³ Müller et al. compared three different multi-objective Bayesian optimisation algorithms and found that TSEMO outperformed the other algorithms for their case study in terms of hypervolume improvement.¹⁴ However, when the reaction space contains a mix of continuous, discrete/categorical variables at the same time, implementing TSEMO to suggest the next experimental condition can be computationally expensive.¹⁵

More recently, a new multi-objective Bayesian optimisation algorithm based on the q-noisy expected hypervolume improvement (qNEHVI) acquisition function was proposed.¹⁶qNEHVI is an extension of expected hypervolume improvement acquisition function (qEHVI¹⁷) and is more robust to noise. The exact gradient of this acquisition function can be computed using auto-differentiation,¹⁸ therefore enabling efficient and effective optimisation using gradient-based optimisation methods. Recent studies implemented qEHVI and qNEHVI for butylpyridinium bromide synthesis,¹⁹ hexafluoroacetone heterogeneous synthesis,²⁰ cross-electrophile coupling²¹ and materials synthesis,²² mostly with multiple continuous variables.

In this study, the Schotten–Baumann reaction under continuous flow conditions is optimised over both categorical variables (electrophile and solvent choices) and continuous variables (equivalents and flow rates). Two Bayesian optimisation algorithms qNEHVI and TSEMO are compared using a benchmark. It is demonstrated that two objectives, space–time–yield and E-factor,²³ can be optimised simultaneously, and a set of optimal solutions can be identified. Based on the optimisation results, flow and batch conditions are compared, and the relationship between solvents and flow rates are examined to gain more insights into this reaction. The reaction scheme in this study is shown as follows (Scheme 1).

Scheme 1 The Schotten–Baumann reaction studied in this work.

Results and discussion

Multi-objective Bayesian optimisation algorithm comparison

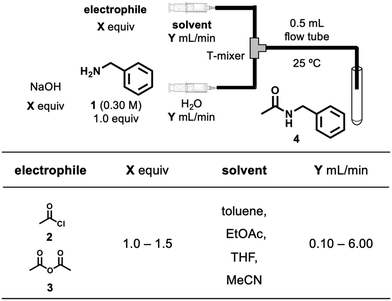
Fig. 1 summarises the experimental setup and reaction conditions for the desired N-benzylacetamide (4) from benzylamine (1) and acetyl chloride (2) or acetic anhydride (3). A PTFE T-shape mixer (0.5 mm ID) was connected to tubing (1 mm ID, 1.59 mm OD) and was immersed in a water bath maintained at 25 °C. A solution of electrophile 2 or 3 (X equiv.) in solvent and a solution of 1 (0.30 M, 1.0 equiv.) and NaOH (X equiv.) in water were injected independently into the T-shape mixer using TriContinent syringe pumps (controlled by lab automation software Flab²⁴). The resultant mixture was collected into an aqueous solution of 1 M HCl in a vial for quenching the reaction. After dilution of the reaction mixture, the yield of 4 was calculated using HPLC-UV analysis. To find environmentally and economically acceptable conditions for the synthesis of amide 4, we decided to maximize the space–time–yield (STY) and minimize the E-factor simultaneously. Experimental details can be found in the Experimental section.

where c_product (g L⁻¹) is the desired concentration of 4 × molecular weight of 4 × (yield of 4/100), τ_res (s) is the residence time, m_waste (g) is the total mass of the waste, and m_product (g) is the total mass of the product.

Fig. 1 The parameters in the reaction for the synthesis of 4.

In terms of reaction variables, we selected the electrophile choice, equivalents of the electrophile and NaOH, solvent choice, and flow rate. Equivalents and flow rates were used as continuous variables, and electrophile and solvent choices were categorical variables. The ranges of the reaction variables were selected based on previous experience in developing the flow process using highly active species.²⁵ The range of the flow rate for each pump in the study was 0.10–6.00 mL min⁻¹ and the corresponding residence time (defined as a ratio of the reactor volume to volumetric flow rate) was 2.5–150 s. To change the equivalents, solutions were prepared with different concentrations of electrophiles for each experiment.

To start the reaction optimisation, initial experimental results are required which are usually collected by a design of experiment method. In this case, both continuous and categorical variables were presented. We used a maximum projection design (MaxPro) which is a type of Latin hypercube design (LHD) based on a maximum projection criterion.²⁶ The MaxPro criterion was shown to have good space-filling properties in projections to all subsets of factors, which connects well with the Gaussian process (GP) model. Furthermore, MaxPro is one of the very few optimal design criteria in the literature that can consider both continuous and categorical factors. The initial design by MaxPro was implemented in R.²⁷

Based on the initial results, individual probabilistic surrogate models can be trained for each objective. In this case, we used Gaussian processes, which perform well in a low data limit.²⁸ For the categorical variables (namely solvent and electrophile choices), one-hot encoding was used and incorporated in the optimisation of the acquisition function using the rounding trick by Garrido-Merchán.²⁹

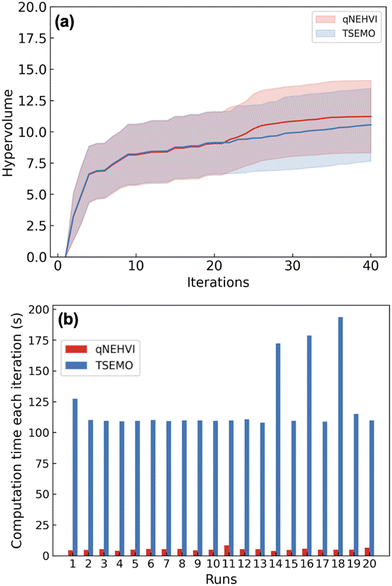
To test the performance of the new algorithm, we first benchmarked between qNEHVI¹⁷ and TSEMO¹¹in silico using the Python package Summit.¹⁵ A reaction simulator was generated based on 20 initial data to mimic the performance of Schotten–Baumann reaction systems (see the ESI† for more details). Both algorithms started with 20 initial experiments and optimised for another 20 experiments. Each algorithm was executed repeatedly 20 times, and the 95% confidence intervals were reported. The performance of the two algorithms was compared by calculating the hypervolumes after each iteration.

The hypervolume measures the volume dominated by the Pareto front and bound by a reference point. The value of the hypervolume can increase or stay equal as the Pareto front improves. As shown in Fig. 2, qNEHVI gave similar hypervolume performance compared to TSEMO (Fig. 2a) but a significant reduction in the computational time (average time per iteration of qNEHVI: 5.1 s vs. average time of TSEMO: 121.5 s) was achieved (Fig. 2b). The reason for the improvement of the calculation time is because TSEMO uses a multi-objective genetic algorithm (NSGA-II), while qNEHVI uses a second-order gradient algorithm (L-BFGS-B) with random restarts. The latter is generally significantly faster, especially with the categorical variables where we used the rounding trick. Therefore, we use qNEHVI to optimise the Schotten–Baumann reaction.

Fig. 2 Comparison between qNEHVI and TSEMO using a benchmark (noise level = 1%). (a) Average hypervolume improvement versus iterations averaged for 20 runs and the 95% confidence intervals. (b) Averaged computational time per iteration for 20 runs.

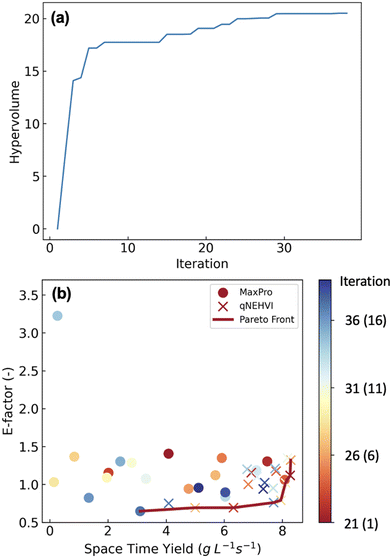
Reaction optimisation and Pareto front

We then carried out the optimisation for the Schotten–Baumann reaction based on 20 initial experiments generated by MaxPro (Fig. 3 and Table S1†). The optimisation was completed after 39 experiments as the hypervolume had not improved after the 29th iteration. The results show the trade-off between STY and E-factor: the optimal STY was 8.29 g L⁻¹ s⁻¹ with an E-factor of 1.32; on the other hand, the optimal E-factor was 0.65 with a STY of 3.11 g L⁻¹ s⁻¹. The Pareto front consisted of 8 points (Table S3†).

Fig. 3 Results of multi-objective optimisation of the Schotten–Baumann reaction. (a) Hypervolume improvement versus iteration number. (b) Optimisation results and the Pareto front (the colorbar represents the sequence of the iteration step from 1–20 for the initial design and 21–39 for the optimisation results).

To further verify the importance of flow conditions, batch reactions were examined under the same reaction conditions except for the reaction time (10 s) because it was difficult to perform batch reactions exactly within 2.5 s (Fig. S4†). The reaction conditions included in the Pareto front were used, and three independent experiments were carried out. Although the reaction mixture was vigorously stirred (1000 rpm) under the batch conditions, the yield decreased by ca. 35% compared to flow conditions. It is considered that efficient mixing was achieved in a flow, resulting in higher yields, while mixing under batch conditions was insufficient. In addition, generation of toxic gaseous hydrogen chloride was observed in batch. Therefore, the scale-up of this reaction under batch conditions could be problematic.

Influence of the flow rate and solvent

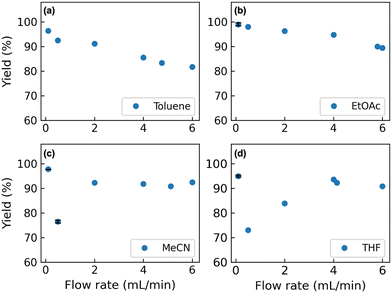
Based on the results of the 39 reaction runs performed (Tables S1 and S2†), some interesting trends were observed. The behaviours of the single-phase system and the two-phase systems are quite different. For the single-phase system (MeCN and THF), the higher flow rate led to an improvement in yield (e.g. entries 4 and 8 in Table S1†). In contrast, for the two-phase system, lower yield was observed at higher flow rates (e.g. entries 18 and 36 in Tables S1 and S2†).

We investigated this phenomenon further with four solvents at different flow rates using acetic anhydride (Fig. 4). In terms of the two-phase system (toluene or EtOAc), the yields of the desired amide 4 were decreased as flow rates were increased. When increasing the flow rates, the drop sizes were observed to be larger, and the flow became irregular.³⁰ We hypothesized that the decrease of the interfacial area of mass transfer between the two phases resulted in lower yields. Higher yields were observed when using EtOAc compared to toluene as the solvent. It is considered that the interfacial tension of the EtOAc–water system (6.8 mN m⁻¹) is smaller than that of the toluene–water system (35.4 mN m⁻¹); therefore, smaller drop sizes were generated, resulting in larger interfacial areas.

Fig. 4 The relationship between solvents and flow rates using acetic anhydride with solvents (a) toluene, (b) EtOAc, (c) MeCN and (d) THF. (acetic anhydride (0.39 M, 1.3 equiv.) in solvent, benzylamine (0.30 M, 1.0 equiv.) and NaOH (0.39 M, 1.3 equiv.) in water; flow rates: 0.10, 0.50, 2.00, 4.00, 6.00 mL min⁻¹, corresponding residence times: 150, 30, 7.5, 3.75, 2.5 s, and optimisation results are included).

In the case of using a single-phase system (MeCN or THF), both low (0.10 mL min⁻¹) and high flow rate (MeCN: 2.00 to 6.00 mL min⁻¹, THF: 4.00 to 6.00 mL min⁻¹) conditions gave 4 in excellent yields. However, when using relatively low flow rate (MeCN: 0.50 mL min⁻¹, THF: 0.50 to 2.00 mL min⁻¹) conditions, a decrease of the yields of 4 was observed.

These results show the complexity of the reaction system with respect to mixing conditions at different flow rates. The yield of the reaction not only depends on the reaction rates, but is also influenced by physical conditions such as mixing and physical properties of the system.³¹ It was shown in a previous study that when the flow rate is increased from low to high, the flow regime in a T-shape channel will change from segregated regime, vortex regime, engulfment regime and to unsteady regime, with mixing being improved significantly starting from the engulfment regime.³² In our case, when the flow rate was increased from 0.00 to 6.00 mL min⁻¹, the corresponding Reynolds number ranges from 0 to around 1200 for MeCN and around 1000 for THF (Table S5†).

At a low flow rate of 0.10 mL min⁻¹, the flow regime was expected to be segregated, where the two fluids are moving next to each other with a “moving interface”, similar to the two-phase system. This results in suppressed hydrolysis and the desired amidation reaction is dominating, giving the observed high yields. When increasing the flow rate to 0.50 mL min⁻¹, the two streams begin to mix with the onset of the so-called vortex regime and both the desired amidation and the undesired hydrolysis reactions proceed thus decreasing the yield.

A further increase in the flow rates to above 2.00 mL min⁻¹ results in an improved mixing. Under these conditions, we hypothesise that the observed high yields reflect the intrinsic reaction rates of the amidation (higher) and the hydrolysis (lower) reactions. Overall, partial mixing is not suitable for this reaction as hydrolysis will occur and the desired product cannot be afforded in high yields.

Conclusions

In this study, the Schotten–Baumann reaction was optimised in a flow using Bayesian optimisation based on qNEHVI acquisition function. The reaction was optimised for two competing objectives, space–time–yield and E-factor. The Pareto front and a set of optimal experimental conditions were identified with a small number of experiments (<40 experiments) and significantly shorter calculation time, when compared to a similar, state-of-the art optimisation methodology. Based on the optimisation results, batch and flow conditions were compared, and the undesired hydrolysis was successfully suppressed by using the flow conditions. The influence of the flow rate and solvent choice were further investigated to gain insights into the interactions between the reaction and mixing. Partial mixing was found to be unsuitable for this reaction due to hydrolysis, resulting in low yields of the desired product. This work would be useful for developing new chemical processes using organic and aqueous mixed solvent systems.

Methods

Bayesian optimisation using qNEHVI

In general, Bayesian optimisation relies on three key parts: a probabilistic model (typically a GP), an acquisition function and an optimisation algorithm. We first trained a GP using initial experimental data for each objective. The next point to evaluate was selected by maximising an acquisition function α(χ_cand). If gradients of α(χ_cand) are available, gradient-based optimisation algorithms can be utilized. If not, either gradients are approximated or gradient-free methods are used.

For multi-objective, a common acquisition function is the expected hypervolume improvement (EHVI). Given a Pareto set 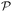and reference point r, the hypervolume improvement (HVI) of a set of points is defined as:

The acquisition function EHVI is the expectation of HVI over the posterior:
qNEHVI is an extension of EHVI and is formulated to deal with parallel settings (batch size q) and can handle noisy observations:¹⁷
where 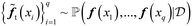, t = 1…N. In this study, we use q = 1. 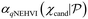can be approximated by the Monte Carlo (MC) integration 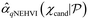based on a cached box decomposition method. The exact gradient of this MC estimator can be computed using auto-differentiation, which allows efficient gradient-based optimisation algorithm L-BFGS-B to be used. We used BoTorch for the implementation of GPs and qNEHVI.¹⁷

Experimental

General information

Benzylamine was purchased from Fluorochem Ltd. Acetic anhydride and acetyl chloride were purchased from Sigma Aldrich. All solvents were purchased from Fisher Scientific. NMR spectra were recorded on a 400 MHz Avance III HD (400 MHz for ¹H) instrument in the indicated solvent. Chemical shifts were reported in units of parts per million (ppm) relative to the signal of CDCl₃ (7.26 ppm) for ¹H NMR. Multiplicities are reported by using the following abbreviations: s; singlet, d; doublet, m; multiplet, br; broad, and J; coupling constants in Hertz (Hz). Analytical HPLC was carried out using a Shimadzu DGU-20A_5R degassing unit with a Shimadzu LC-20AD liquid chromatograph, a Shimadzu SIL-20A auto sampler, a Shimadzu CBM-20A communication bus module, a Shimadzu SPD-M20A diode array detector and a Shimadzu CTO-20AC column oven.

Procedure for reaction optimisation

A solution of benzylamine (1) (0.30 M, 1.0 equiv.) and NaOH (1.0–1.5 equiv.) in a solvent (flow rate 0.10–6.00 mL min⁻¹) and a solution of acetyl chloride or acetic anhydride (1.0–1.5 equiv.) in a solvent (flow rate 0.10–6.00 mL min⁻¹) were injected into a T-shape mixer at 25 °C using syringe pumps. The resultant mixture was passed through the reaction tube (volume: 0.50 mL, Vapourtec R-Series Tubing Kit) at the same temperature. The resultant mixture was added into 1 M aq. HCl at room temperature. Yields of N-benzylacetamide (4) were determined by HPLC-UV analysis (conditions: Agilent, Eclipse XDB-C18, 5 μm, 4.6 × 150 mm, MeCN/H₂O, 0–9 min: 0 to 60%, 9–15 min: 60 to 80%, 15–17 min: 80 to 0%, flow rate: 1.00 mL min⁻¹, detection wavelength: 254 nm, temperature: 30 °C, retention time: 4.1 min) using a calibration curve shown in Fig. S2† in order to allow rapid analysis of reaction results.

Procedure for the synthesis of 4 using a batch reactor (Fig. S4†)

To a vigorously stirred (magnetic stirrer, 1000 rpm) solution of acetyl chloride (2) (0.33 M, 1.1 equiv.) in EtOAc (2.50 mL), a solution of benzylamine (1) (0.30 M, 1.0 equiv.) and NaOH (0.33 M, 1.1 equiv.) in water (2.50 mL) was added in a round bottom flask at 25 °C. After being stirred for 10 s at the same temperature, 1 M aq. HCl was added at the same temperature. Under the flow conditions, the reaction time was 2.5 s. However, under the batch conditions, it was impossible to run the reaction within 2.5 s. Thus, the reaction time was extended to 10 s. Yields of N-benzylacetamide (4) were determined by HPLC-UV analysis using a calibration curve shown in Fig. S2.†

Procedure for the preparation of 4

Acetic anhydride (3) (1.2 equiv.) was added to a solution of benzylamine (1) (1.0 equiv.) and triethylamine (1.2 equiv.) in EtOAc (0.50 M) under ambient conditions. After the solution was stirred at the same temperature for 30 min, the resultant mixture was poured into a solution of EtOAc and 1 M aq. HCl at the same temperature. The organic layer was washed with 1 M aq. HCl, sat. aq. NaHCO₃, and brine, dried over MgSO₄, filtered and concentrated in vacuo at room temperature.

N-Benzylacetamide (4)

White solid, 716.0 mg, 95.9%. ¹H NMR (400 MHz, CDCl₃): δ 7.36–7.27 (m, 5H), 5.83 (brs, 1H), 4.42 (d, J = 5.7 Hz, 2H), 2.01 (s, 3H). Spectral data without the NH peak of ¹H NMR was well consistent with the previous report.³³

Author contributions

Jiyizhe Zhang: conceptualization, data curation, formal analysis, methodology, software, investigation and supervision. Naoto Sugisawa: conceptualization, data curation, formal analysis, methodology, software and investigation. Kobi C Felton: software. Shinichiro Fuse: supervision. Alexei A Lapkin: project administration and supervision. All authors: writing – review & editing.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was in part supported by EPSRC funded project EP/S019472/1 “Chembots: digital-chemical-robotics to convert code to molecules and complex systems”. The work was enabled by the Innovation Centre in Digital Molecular Technologies (iDMT), an ERDF co-funded project. The work was supported by the grant-in-aid for JSPS Fellows (22KJ1553 to N. Sugisawa). We would like to thank Dr. Keiichiro Hirai from Shionogi & Co., Ltd., Dr. Dasha Semochkina from the University of Southampton, Dr. Nicholas Jose from the University of Cambridge and Dr. Xiao Liang from Imperial College London for fruitful discussions.

References

1. D. G. Brown and J. Boström, J. Med. Chem., 2016, 59, 4443–4458.
2. D. J. Constable, P. J. Dunn, J. D. Hayler, G. R. Humphrey, J. L. Leazer, Jr, R. J. Linderman, K. Lorenz, J. Manley, B. A. Pearlman, A. Wells, A. Zaks and T. Y. Zhang, Green Chem., 2007, 9, 411–420.
3. J. Magano, Org. Process Res. Dev., 2022, 26, 1562–1689.
4. (a) C. Schotten, Ber. Dtsch. Chem. Ges., 1884, 17, 2544–2547; (b) E. Baumann, Ber. Dtsch. Chem. Ges., 1886, 19, 3218–3222Although the Schotten–Baumann reaction usually means amidation with acid chlorides, amidation with acid anhydrides was also referred to as the Schotten–Baumann reaction in this manuscript in accordance with the literature, see: Z. Wang, Schotten-Baumann Reaction, in Comprehensive Organic Name Reactions and Reagents, John Wiley & Sons, Inc., Hoboken, 2010, pp. 2536–2539.
5. K. J. Carpenter, Chem. Eng. Sci., 2001, 56, 305–322.
6. (a) J.-i. Yoshida, Flash Chemistry: Fast Organic Synthesis in Micro Systems, Wiley-VCH, Weinheim, 2008; (b) J.-i. Yoshida, A. Nagaki and T. Yamada, Chem. – Eur. J., 2008, 14, 7450–7459; (c) J.-i. Yoshida, Chem. Rec., 2010, 10, 332–341; (d) J.-i. Yoshida, Y. Takahashi and A. Nagaki, Chem. Commun., 2013, 49, 9896–9904.
7. (a) T. D. White, K. D. Berglund, J. M. Groh, M. D. Johnson, R. D. Miller and M. H. Yates, Org. Process Res. Dev., 2012, 16, 939–957; (b) L. S. de M. Miranda, R. O. M. A. de Souza, R. A. C. Leão, P. F. Carneiro, S. F. Pedraza, O. V. de Carvalho, S. P. de Souza and R. V. Neves, Org. Process Res. Dev., 2019, 23, 2516–2520; (c) S. Fuse, K. Masuda, Y. Otake and H. Nakamura, Chem. – Eur. J., 2019, 25, 15091–15097; (d) J. Salaklang, E. Mertens, V. Maes, R. Dams, W. Dermaut and T. Junkers, J. Flow Chem., 2020, 10, 673–679; (e) M. Magosso, M. van den Berg and J. van der Schaaf, React. Chem. Eng., 2021, 6, 1574–1590.
8. C. J. Taylor, A. Pomberger, K. C. Felton, R. Grainger, M. Barecka, T. W. Chamberlain, B. A. Bourne, C. N. Johnson and A. A. Lapkin, Chem. Rev., 2023, 123, 3089–3126.
9. (a) A. M. Schweidtmann, A. D. Clayton, N. Holmes, E. Bradford, R. A. Bourne and A. A. Lapkin, Chem. Eng. J., 2018, 352, 277–282; (b) A. D. Clayton, A. M. Schweidtmann, G. Clemens, J. A. Manson, C. J. Taylor, C. G. Niño, T. W. Chamberlain, N. Kapur, A. J. Blacker, A. A. Lapkin and R. A. Bourne, Chem. Eng. J., 2020, 384, 123340; (c) M. I. Jeraal, S. Sung and A. A. Lapkin, Chem. Methods, 2021, 1, 71–77; (d) P. Sagmeister, F. F. Ort, C. E. Jusner, D. Hebrault, T. Tampone, F. G. Buono, J. D. Williams and C. O. Kappe, Adv. Sci., 2022, 9, 2105547; (e) O. J. Kershaw, A. D. Clayton, J. A. Manson, A. Barthelme, J. Pavey, P. Peach, J. Mustakis, R. M. Howard, T. W. Chamberlain, N. J. Warren and R. A. Bourne, Chem. Eng. J., 2023, 451, 138443.
10. B. Shahriari, K. Swersky, Z. Wang, R. P. Adams and N. de Freitas, Proc. IEEE, 2016, 104, 148–175.
11. E. Bradford, A. M. Schweidtmann and A. A. Lapkin, J. Glob. Optim., 2018, 71, 407–438.
12. P. Jorayev, D. Russo, J. D. Tibbetts, A. M. Schweidtmann, P. Deutsch, S. D. Bull and A. A. Lapkin, Chem. Eng. Sci., 2022, 247, 116938.
13. S. T. Knox, S. J. Parkinson, C. Y. Wilding, R. A. Bourne and N. J. Warren, Polym. Chem., 2022, 13, 1576–1585.
14. P. Müller, A. D. Clayton, J. Manson, S. Riley, O. S. May, N. Govan, S. Notman, S. V. Ley, T. W. Chamberlain and R. A. Bourne, React. Chem. Eng., 2022, 7, 987–993.
15. K. C. Felton, J. G. Rittig and A. A. Lapkin, Chem.: Methods, 2021, 1, 116–122.
16. S. Daulton, M. Balandat and E. Bakshy, Adv. Neural Inf. Process., 2021, 34, 2187–2200.
17. S. Daulton, M. Balandat and E. Bakshy, Adv. Neural Inf. Process., 2020, 33, 9851–9864.
18. M. Balandat, B. Karrer, D. R. Jiang, S. Daulton, B. Letham, A. G. Wilson and E. Bakshy, Adv. Neural Inf. Process., 2020, 33, 21524–21538.
19. J. H. Dunlap, J. G. Ethier, A. A. Putnam-Neeb, S. Iyer, S.-X. L. Luo, H. Feng, J. A. G. Torres, A. G. Doyle, T. M. Swager, R. A. Vaia, P. Mirau, C. A. Crouse and L. A. Baldwin, Chem. Sci., 2023, 14, 8061–8069.
20. T. Qi, G. Luo, H. Xue, F. Su, J. Chen, W. Su, K.-J. Wu and A. Su, J. Flow Chem., 2023, 13, 337–346.
21. J. A. G. Torres, S. H. Lau, P. Anchuri, J. M. Stevens, J. E. Tabora, J. Li, A. Borovika, R. P. Adams and A. G. Doyle, J. Am. Chem. Soc., 2022, 144, 19999–20007.
22. B. P. MacLeod, F. G. Parlane, C. C. Rupnow, K. E. Dettelbach, M. S. Elliott, T. D. Morrissey, T. H. Haley, O. Proskurin, M. B. Rooney, N. Taherimakhsousi, D. J. Dvorak, H. N. Chiu, C. E. B. Waizenegger, K. Ocean, M. Mokhtari and C. P. Berlinguette, Nat. Commun., 2022, 13, 995.
23. R. A. Sheldon, Green Chem., 2017, 19, 18–43.
24. Flab 2.0.11, https://pypi.org/project/flab, (accessed July 2023).
25. (a) N. Sugisawa, H. Sugisawa, Y. Otake, R. V. Krems, H. Nakamura and S. Fuse, Chem. Methods, 2021, 1, 484–490; (b) N. Sugisawa, A. Ando and S. Fuse, Chem. Sci., 2023, 14, 6986–6991.
26. S. Ba and V. R. Joseph, MaxPro: maximum projection designs (Version 4.1-2), R package, 2018.
27. V. R. Joseph, E. Gul and S. Ba, Biometrika, 2015, 102, 371–380.
28. C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, MIT Press, Cambridge, 2006.
29. E. C. Garrido-Merchán and D. Hernández-Lobato, Neurocomputing, 2020, 380, 20–35.
30. P. Desir, T. Y. Chen, M. Bracconi, B. Saha, M. Maestri and D. G. Vlachos, React. Chem. Eng., 2020, 5, 39–50.
31. J. R. Bourne, Org. Process Res. Dev., 2003, 7, 471–508.
32. A. Mariotti, M. Antognoli, C. Galletti, R. Mauri, M. V. Salvetti and E. Brunazzi, Chem. Eng. J., 2020, 396, 125223.
33. S. Chakraborty, R. Nath, A. K. Ray, A. Paul and S. K. Mandal, Chem. – Eur. J., 2023, 29, e202202710.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3re00502j

---