Open Access Article
Open Access ArticleDesigning solvent systems using self-evolving solubility databases and graph neural networks†
Yeonjoon
Kim
 ab,
Hojin
Jung
ab,
Hojin
Jung
 a,
Sabari
Kumar
a,
Robert S.
Paton
a,
Sabari
Kumar
a,
Robert S.
Paton
 a and
Seonah
Kim
a and
Seonah
Kim
 *a
*a
aDepartment of Chemistry, Colorado State University, Fort Collins, CO 80523, USA. E-mail: seonah.kim@colostate.edu
bDepartment of Chemistry, Pukyong National University, Busan 48513, Republic of Korea
First published on 8th December 2023
Abstract
Designing solvent systems is key to achieving the facile synthesis and separation of desired products from chemical processes, so many machine learning models have been developed to predict solubilities. However, breakthroughs are needed to address deficiencies in the model's predictive accuracy and generalizability; this can be addressed by expanding and integrating experimental and computational solubility databases. To maximize predictive accuracy, these two databases should not be trained separately, and they should not be simply combined without reconciling the discrepancies from different magnitudes of errors and uncertainties. Here, we introduce self-evolving solubility databases and graph neural networks developed through semi-supervised self-training approaches. Solubilities from quantum-mechanical calculations are referred to during semi-supervised learning, but they are not directly added to the experimental database. Dataset augmentation is performed from 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 637 experimental solubilities to >900
637 experimental solubilities to >900![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 data points in the integrated database, while correcting for the discrepancies between experiment and computation. Our model was successfully applied to study solvent selection in organic reactions and separation processes. The accuracy (mean absolute error around 0.2 kcal mol−1 for the test set) is quantitatively useful in exploring Linear Free Energy Relationships between reaction rates and solvation free energies for 11 organic reactions. Our model also accurately predicted the partition coefficients of lignin-derived monomers and drug-like molecules. While there is room for expanding solubility predictions to transition states, radicals, charged species, and organometallic complexes, this approach will be attractive to predictive chemistry areas where experimental, computational, and other heterogeneous data should be combined.
000 data points in the integrated database, while correcting for the discrepancies between experiment and computation. Our model was successfully applied to study solvent selection in organic reactions and separation processes. The accuracy (mean absolute error around 0.2 kcal mol−1 for the test set) is quantitatively useful in exploring Linear Free Energy Relationships between reaction rates and solvation free energies for 11 organic reactions. Our model also accurately predicted the partition coefficients of lignin-derived monomers and drug-like molecules. While there is room for expanding solubility predictions to transition states, radicals, charged species, and organometallic complexes, this approach will be attractive to predictive chemistry areas where experimental, computational, and other heterogeneous data should be combined.
Introduction
Solubility is a key molecular property that controls reactivity, catalytic activity, separation ability, and other molecular properties. In chemical synthesis, solvent selection influences the solubilities of reactants, intermediates, and products and impacts catalytic activity and product selectivity. It is crucial in designing catalytic reactions pertinent to pharmaceutical synthesis in solutions, such as functionalization through C–H activation.1–6 In this regard, linear relationships have been elucidated between solvent properties (permittivity, polarity, etc.) and reaction rates for various organic reactions in different solvents.7–9 Such linear solvation energy relationships (LSERs) inform solvent selection, leading to the maximal yield of target products.In the pharmaceutical industry, solubilities in water and organic solvents are essential properties to consider during the screening and synthesis of drug candidates.10,11 Candidates having sufficient water solubility should be identified for high bioavailability in oral administration.12 Water solubility is also relevant to the toxicity of drugs and pesticides on human health and the environment.13–15 Solubilities in organic solvents matter as well, especially for assessing the in vivo efficacy and safety of intravenous drugs dissolved in non-toxic organic solvents.11,16,17 Specifically, solubilities of drug-like molecules in chloroform and diethyl ether have been investigated for the simplified modeling of the polar environment around proteins, and membranes.18,19 In addition, solubility plays a critical role in emerging research areas such as sustainable chemistry and renewable energy. For instance, solvent selection is conducted in biomass upgrading to biofuels and renewable polymers to maximize catalytic activity.20–23 The optimal water-organic solvent systems enhance not only the conversion to target products but also their extraction from separation processes.20,21 Meanwhile, developing organic redox flow batteries is another promising research area for renewable energy storage, and it is important to design electrolytes highly soluble in water or organic solvents for high charge densities.24–26
To date, solubilities of various solutes in water and organic solvents have been measured experimentally, and databases of experimental solubilities have been released. The available databases include AqSolDB,27 Open Notebook Scientific Challenge,28 Minnesota Solvation Database,29–31 FreeSolv,32 CompSol,33 and the Journal of Chemical Information and Modeling's solubility challenge database.12,34–36 Many computational methods have also been developed to predict solubilities in silico. Such methods include quantum mechanics (QM) or density functional theory (DFT) with implicit solvation models (e.g., Solvation Model based on Density – SMD),37 molecular dynamics (MD) simulations, or QM-based thermodynamic equilibrium methods, e.g., the Conductor-like Screening Model (COSMO).38–40 A modified version of the COSMO model, COSMO for real solvents (COSMO-RS), incorporates statistical thermodynamics to treat bulk properties such as solubility more accurately.41
For rapid and accurate solubility predictions, various predictive models have been developed by analyzing quantitative structure–property relationships (QSPRs)35,42–47 or via machine learning (ML) techniques.35,45,48–59 Current advanced ML models used graph neural networks (GNNs) combined with interaction layers,50,56,60 recurrent neural networks with attention layers,48 and Natural Language Processing (NLP)-based transformers.59 These models have achieved accuracies close to experimental uncertainties. Furthermore, the development of ML models has been expanded to predicting solubility limits at different temperatures,55 solvation enthalpy, LSERs, and solute parameters,54 and generative models for designing molecules having optimal aqueous solubility.57
The databases and models described above deal with either molar solubility (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S) or Gibbs solvation free energy (ΔGsolv). Log
S) or Gibbs solvation free energy (ΔGsolv). Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S is commonly used for solubility, but henceforth, this paper focuses on ΔGsolv, since ΔGsolv as well as log
S is commonly used for solubility, but henceforth, this paper focuses on ΔGsolv, since ΔGsolv as well as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S quantifies solubility:
S quantifies solubility:
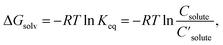 | (1) |
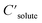 are the solute's concentration in the solvent and initial phase (before the solvation), respectively. ΔGsolv can also represent the solubility regardless of the solute's initial phase (solid, liquid, or gas):40
are the solute's concentration in the solvent and initial phase (before the solvation), respectively. ΔGsolv can also represent the solubility regardless of the solute's initial phase (solid, liquid, or gas):40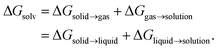 | (2) |
Moreover, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S and ΔGsolv are related to each other:29
S and ΔGsolv are related to each other:29
 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S directly quantifies the amount of solutes, the significance of ΔGsolv lies in its ability to represent the thermodynamic stability of a solute in a solvent.
S directly quantifies the amount of solutes, the significance of ΔGsolv lies in its ability to represent the thermodynamic stability of a solute in a solvent.
Further improvements are needed for accurate predictions of ΔGsolv for broad solvents and solutes. There are currently around 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 experimentally determined ΔGsolv in the most extensive database (e.g., CombiSolv-Exp in literature56), but more data points (around >100
000 experimentally determined ΔGsolv in the most extensive database (e.g., CombiSolv-Exp in literature56), but more data points (around >100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) are desirable for reliable GNNs, due to their data-hungry nature.56,61 Moreover, there is a tradeoff between the size and reliability of available solubility data. For example, a strictly curated dataset of reliable aqueous solubilities contains only hundreds of compounds.62 Due to the scarcity of reliable experimental data, there have been attempts to pre-train against huge computational databases, followed by re-training against the experimental data.56,63 Such transfer learning can lose the information gained from the computational database after the model is re-trained against the small experimental database. In addition, QM solubilities systematically deviate from experimental values. The absolute errors of ΔGsolv for neutral solutes and solvents are 0.0–3.0 kcal mol−1 or higher for COSMO-RS, SMD, and other implicit solvation models.37,64–70 Therefore, developing a database seamlessly integrating theoretical and experimental values is a challenging but essential step.
000) are desirable for reliable GNNs, due to their data-hungry nature.56,61 Moreover, there is a tradeoff between the size and reliability of available solubility data. For example, a strictly curated dataset of reliable aqueous solubilities contains only hundreds of compounds.62 Due to the scarcity of reliable experimental data, there have been attempts to pre-train against huge computational databases, followed by re-training against the experimental data.56,63 Such transfer learning can lose the information gained from the computational database after the model is re-trained against the small experimental database. In addition, QM solubilities systematically deviate from experimental values. The absolute errors of ΔGsolv for neutral solutes and solvents are 0.0–3.0 kcal mol−1 or higher for COSMO-RS, SMD, and other implicit solvation models.37,64–70 Therefore, developing a database seamlessly integrating theoretical and experimental values is a challenging but essential step.
Discrepancies between theoretical and experimental solubilities should be reconciled to build an integrated database. In other words, computational solubilities should have a fidelity as high as experimental ones despite the dependence of computational methods' accuracies on molecule size, constituent elements, functional groups, solvent properties, etc. Therefore, it is not feasible to merely combine experimental and computational databases. Each database has a different source and magnitude of errors and uncertainties,30,71–73 which would deteriorate the accuracy of predictive models. To overcome this limitation, a recent study added Gaussian-distributed random errors to the experimental datasets at different levels according to their uncertainties, leading to more accurate predictions than the models without Gaussian error distributions.74 Data augmentation and self-training techniques have also been employed, such as semi-supervised distillation (SSD)75–82 for the reliable integration of databases from heterogeneous sources. These techniques have been successfully applied to various ML predictive models for image classification,77,78 natural language processing,79 reaction classification,80 and protein structures.81
In this contribution, our own implementation of SSD was developed for our GNNs for solubilities. For reliable data integration, we refined the ΔGsolv values from COSMO-RS and SMD-DFT through the SSD, instead of directly adding values from these methods. Our approach dramatically amplified the database while correcting the discrepancies of different data sources. The resulting augmented database covers a much broader chemical space (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 213/1445/932
213/1445/932![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 509 solutes/solvents/data points) than that covered by experimental measurements (2275/1443/11
509 solutes/solvents/data points) than that covered by experimental measurements (2275/1443/11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 637 solutes/solvents/data points). Adopting the augmented database is powerful in enhancing GNNs' predictive accuracy, demonstrating the effectiveness of our approach. Moreover, we successfully applied our model to practical examples of solvent system design in reaction kinetics and separation. These examples demonstrate the potential of our ML approaches in enabling the chemistry-informed design of solvent systems.
637 solutes/solvents/data points). Adopting the augmented database is powerful in enhancing GNNs' predictive accuracy, demonstrating the effectiveness of our approach. Moreover, we successfully applied our model to practical examples of solvent system design in reaction kinetics and separation. These examples demonstrate the potential of our ML approaches in enabling the chemistry-informed design of solvent systems.
Results and discussion
Semi-supervised distillation scheme for developing solubility prediction models
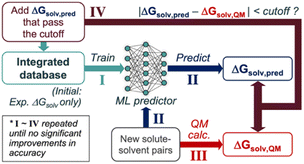
We propose the following SSD scheme for solubility (Scheme 1); first, the ‘Teacher’ ML model is trained against an experimental database of ΔGsolv (Step I). Second, ΔGsolv is predicted using the trained Teacher for the new solute–solvent pairs whose experimental ΔGsolv is unknown, resulting in ΔGsolv,pred (Step II). Meanwhile, QM-calculated ΔGsolv values are also obtained (ΔGsolv,QM) for these new solute–solvent pairs (Step III). ΔGsolv,QM is referenced to determine which ΔGsolv,pred are used for the data augmentation. If the absolute difference between these two (|ΔGsolv,pred − ΔGsolv,QM|) is below a certain cutoff, the corresponding ΔGsolv,pred are added to the database (Step IV). This cutoff is to avoid the introduction of unreliable prediction data points from the Teacher. Notably, ΔGsolv,pred is added instead of ΔGsolv,QM, enabling the data augmentation based on the inductive bias the ML model gained from the starting experimental database. Next, the ‘Student’ model is trained using the database combining the initial database and that from Teacher's predictions. This procedure is repeated to add reliable data points to the integrated database gradually.The SSD process described in Scheme 1 was applied to the GNNs for solubilities, constituting a one-of-a-kind approach in solubility predictions that consolidate deep learning and heterogeneous data sources from experiments and QM calculations. The following sections describe the databases, QM methods, and architecture of the GNNs in detail.
Evaluation of quantum-mechanical methods and solubility databases
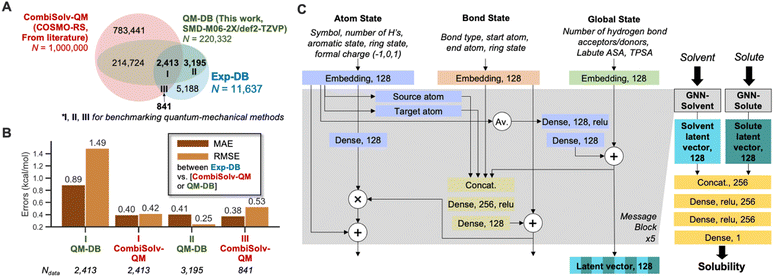
To accomplish data augmentation, first, we evaluated the QM methods used to provide reference ΔGsolv,QM during the SSD. 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 637 experimental ΔGsolv were collected and curated, resulting in Exp-DB (Fig. 1A). Most data points in Exp-DB overlap with those in CombiSolv-Exp,56 but our Exp-DB has additional 1419 data points with the identical solute and solvent.
637 experimental ΔGsolv were collected and curated, resulting in Exp-DB (Fig. 1A). Most data points in Exp-DB overlap with those in CombiSolv-Exp,56 but our Exp-DB has additional 1419 data points with the identical solute and solvent.
COSMO-RS and SMD-M06-2X/def2-TZVP were then benchmarked against Exp-DB. To assess COSMO-RS, we adopted CombiSolv-QM, the most extensive ΔGsolv database consisting of one million data points.56QM-DB (220![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 332 data points) was built to evaluate SMD-M06-2X/def2-TZVP which was elected among many SMD-DFT methods since it provided reliable results from calculating solubility-related properties (redox potentials of 174 organic molecules in water and acetonitrile).26 2413 ΔGsolv values are available for all three databases (Region I), and 3195 overlapped data points between Exp-DB and QM-DB (Region II). 841 solubilities in Exp-DB are available only in CombiSolv-QM (Region III) due to the unavailability of some solvents in SMD calculations.
332 data points) was built to evaluate SMD-M06-2X/def2-TZVP which was elected among many SMD-DFT methods since it provided reliable results from calculating solubility-related properties (redox potentials of 174 organic molecules in water and acetonitrile).26 2413 ΔGsolv values are available for all three databases (Region I), and 3195 overlapped data points between Exp-DB and QM-DB (Region II). 841 solubilities in Exp-DB are available only in CombiSolv-QM (Region III) due to the unavailability of some solvents in SMD calculations.
Accuracies of the two theoretical methods were analyzed for I–III. In Region I, COSMO-RS is more accurate than SMD-M06-2X. Nonetheless, SMD-M06-2X shows notably high accuracy for the 3195 data points in Region II, with an MAE and RMSE of 0.41 and 0.25 kcal mol−1, respectively. Meanwhile, COSMO-RS showed a decent accuracy in Region III. These results show that each theoretical method has strengths and weaknesses regarding the scope of molecules and accuracies, and do not necessarily indicate the superiority of one method. Although QM-DB is less extensive than CombiSolv-QM, SMD-M06-2X can be used as a complementary method to COSMO-RS for explaining the errors of QM methods and ML models after model development.
With regards to computational cost, COSMO-RS is typically a more cost-efficient option for high-throughput calculations than SMD-DFT because COSMO-RS needs DFT calculations of a charge density profile only once per one solute/solvent. In contrast, SMD-DFT methods (e.g., SMD-M06-2X/def2-TZVP) need multiple geometry optimizations and thermochemistry calculations for the same solute when a solvent changes. SMD parameters are tabulated for 179 solvents, limiting the molecular scope for estimating ΔGsolv. However, SMD-M06-2X/def2-TZVP can show higher accuracies than COSMO-RS for certain functional groups. These multiple theoretical methods would lead to more reliable evaluation of databases and predictive models than only one method.
Development of graph neural networks for solubility prediction
The GNNs for predicting solubility were constructed, as shown in Fig. 1C. The model takes 2D molecular structures (SMILES strings) of solvent and solute as inputs, and each undergoes separate message passing. The overall architecture of two GNNs (GNN-solvent and GNN-solute) is inspired and modified from our previously implemented GNNs for predicting bond dissociation enthalpy and cetane number (reactivity of fuel compounds).61,83 It consists of three blocks representing a molecule's atom, bond, and global state. Initial atom, bond, and global features are embedded as 128-dimensional vectors and pass through five message-passing layers. This work did not consider stereochemical information as the atom features since ΔGsolv values of stereoisomers are scarce in the existing experimental databases (114 out of 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 637). In each layer, mathematical operations among feature vectors lead to mutual updates, such that the model captures the influence of local atom/bond environments and global molecular structures on solubility. Each GNN outputs a 128-dimensional latent vector for solvent and solute, respectively. These two vectors are concatenated and undergo additional dense layers to account for solute–solvent interactions, and finally, ΔGsolv is predicted.
637). In each layer, mathematical operations among feature vectors lead to mutual updates, such that the model captures the influence of local atom/bond environments and global molecular structures on solubility. Each GNN outputs a 128-dimensional latent vector for solvent and solute, respectively. These two vectors are concatenated and undergo additional dense layers to account for solute–solvent interactions, and finally, ΔGsolv is predicted.
Our model is unique compared to other GNNs recently developed for solubilities.56 First, we minimized the number of atom features from 11 to five. Second, the dimensions of hidden layers were also minimized. Our model has hidden layers with 128 and 256 nodes before and after concatenation, respectively, whereas 200 and 500-dimensional hidden layers were used in the literature56 (See Methods for the details about the hyperparameter tuning). Third, a separate global state block of our model participates in feature updates during the message passing, whereas the literature concatenates global features after the message-passing layers.56 Both approaches show comparable accuracies (details in the Analysis of solubility model performance section), but the global updates within message-passing layers can incorporate the effects of long-range interactions on ΔGsolv into atom and bond features.84 This leads to the reliable chemical explanation of atom-wise contributions to ΔGsolv using the modified version of Shapley additive explanation (SHAP) analysis85 (vide infra). Meanwhile, other operations besides concatenation have also been reported in previous studies to consider molecular interactions, such as global convolution among molecules and graph-of-graphs neural networks.86,87 However, concatenating latent vectors was sufficient to achieve the accuracy close to experimental uncertainty (mean absolute error of the test set around 0.2 kcal mol−1, details in the next section).
We selected four global features after testing various molecular descriptors. Two are surface area descriptors: topological polar surface area (TPSA) and Labute accessible surface area (ASA). Each descriptor indicates different underlying chemistry of solutes/solvents. TPSA accounts for the molecule's viability to dipole–dipole interactions by quantifying the surface area of polar atoms, whereas Labute ASA is relevant to van der Waals radii of atoms and encodes long-range dispersion interactions.88 The Pearson correlation coefficients ρ between ΔGsolv in Exp-DB and the descriptors are −0.56 and −0.73 for solute's TPSA and Labute ASA, respectively (close to ±1 indicates stronger correlation). In contrast, ρ between TPSA and Labute ASA is only 0.28, indicating that these two descriptors can independently explain ΔGsolv well and it is necessary to consider both descriptors for global features. Two additional descriptors were adopted: number of hydrogen bond donors and acceptors. They were also used in our predictive model for cetane number,83 leading to the model with higher accuracy than that without these descriptors.
Semi-supervised distillation for self-evolving databases and graph neural networks
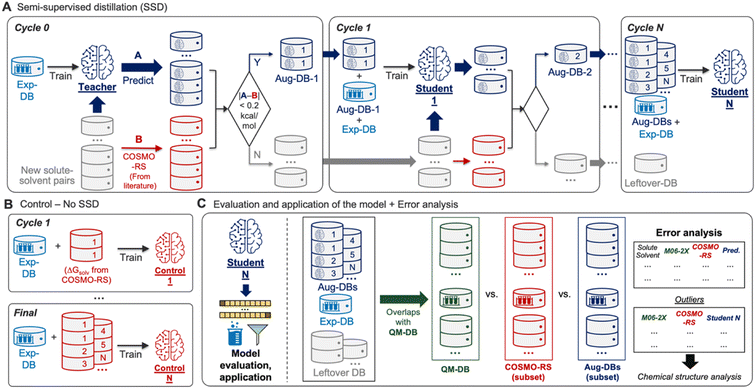
Building the GNN model and databases (Fig. 1) was followed by training the model based on SSD (Fig. 2A). The SSD was initiated by training the Teacher model using Exp-DB (Cycle 0). The trained model was then used for augmenting the database; new solute–solvent pairs were gathered from CombiSolv-QM, and their ΔGsolv was predicted using the Teacher model. The predicted values were compared with COSMO-RS solubilities stored in CombiSolv-QM. If the absolute difference between these two is below 0.2 kcal mol−1, the corresponding data points were held in the augmented database (Aug-DB-1) with Teacher-predicted solubility values. It should be emphasized that the ML-predicted values are saved instead of ΔGsolv from COSMO-RS. This is for refining data points based on the solubility trends learned from Exp-DB while maintaining the reliability gained via labeled QM solubility values. The threshold value was set to 0.2 as the uncertainty of experimental measurements of ΔGsolv is typically up to 0.2 kcal mol−1.30,71–73 If the deviation between ML and QM is below 0.2, it can be assumed that the difference is mainly from experimental uncertainty and the prediction from the Teacher is credible.Next, Student 1 was trained using the database combining Aug-DB-1 and Exp-DB (Cycle 1), and the same procedure was carried out for the solute–solvent pairs that remained after extracting Aug-DB-1. Student 1 predicted ΔGsolv for the remaining pairs, and the predicted values were subject to the 0.2 kcal mol−1 cutoff, resulting in Aug-DB-2. These cycles were repeated multiple times, enabling the self-training of ML models. The database is grown gradually, and subsequent student models learn larger databases that contain ΔGsolv values refined based on the guidance from previous Students and COSMO-RS solubilities. Such gradual integration leads to better accuracy than combining the whole CombiSolv-QM with Exp-DB and re-training simultaneously (details in the next section).
No trained weights of the GNN model are transferred from the previous cycle when training the Student model in the current cycle. Only the databases (Aug-DBs and Exp-DB) are carried over, and each Student is trained from scratch at each cycle. In other words, the current Student is totally blind to the training results of previous Students. Therefore, at each cycle, the model learns new relationships between chemical structure and solubility that are not biased by previous cycles but are comprehensively applicable to all molecules from the previous and current cycles. This SSD scheme ensures that the new Aug-DB-i at the i-th cycle is integrated well with the databases accumulated from earlier cycles, and it shows no significant discrepancies and anomalies during the training. Recent studies expanded the databases using computational methods, but the model was trained sequentially or independently for the experimental and computational databases due to the discrepancies from heterogeneous data sources.55,56,61,84 Meanwhile, a few studies attempted the ‘Δ-learning’ approach, where theory-experiment differences are trained and predicted.89,90 It should be emphasized that our approach is the first achievement of training the whole integrated database while carrying out the data augmentation and discrepancy corrections concurrently.
Ultimately, the Nth cycle yields the ‘Student N’ model and the integrated database containing Exp-DB and NAug-DBs. The cycle was terminated when the errors of the Exp-DB test set did not show any more significant improvement. This stopping criterion finds the cycle when the remaining data points in CombiSolv-QM no longer synchronize well with the large Aug-DBs cumulated during previous cycles. The solute–solvent pairs not included in Aug-DBs were stored in the so-called Leftover-DB. As a result, the Student 35 model obtained after 35 SSD cycles led to an optimal accuracy, with a total of 932![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 509 ΔGsolv in the integrated database (Details in Fig. 3, vide infra).
509 ΔGsolv in the integrated database (Details in Fig. 3, vide infra).
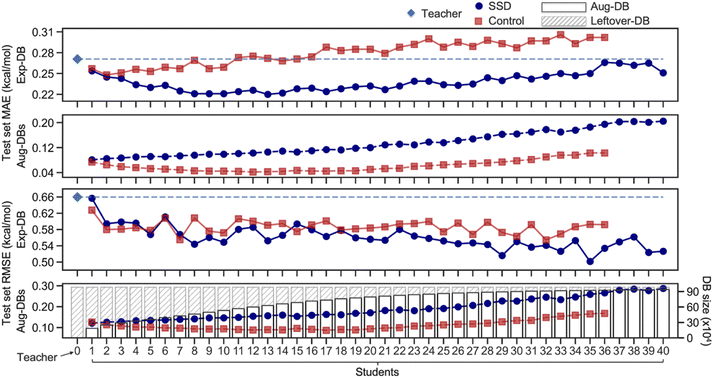 | ||
| Fig. 3 Mean absolute errors (MAEs) and root-mean-square errors (RMSEs) of test sets of Aug-DBs and Exp-DB during the SSD and the sizes of Aug-DBs. | ||
Analysis of solubility model performance
Accuracies of the Student models from SSD were compared with those trained by the databases simply combining ΔGsolv values from experiments and COSMO-RS (Control, Fig. 2B). The analysis on Control was performed at every SSD cycle to compare the increasing/decreasing trends of MAEs and RMSEs when the models are trained without/with SSD. All Control models are examined to demonstrate that the SSD approach in Fig. 2A is feasible for maximizing the database size while minimizing the discrepancy between experimental and computational ΔGsolv and achieving the best accuracy.The resulting model was then subject to subsequent evaluation, error analysis, and applications (Fig. 2C). To evaluate the model's accuracy, mean absolute errors (MAEs), root-mean-square errors (RMSEs), and distributions of errors were investigated. For additional error analysis, we obtained the solute–solvent pairs in QM-DB that overlap with those in other databases (Aug-DBs, Exp-DB, Leftover-DB). Next, we compared their ΔGsolv values acquired from four different sources: experiments (if available), predictions from Student N, SMD-M06-2X/def2-TZVP, and COSMO-RS calculations. Outliers were identified from this comparison, and their chemical structures were analyzed to assess the strengths and weaknesses of each QM method or ML model.
Fig. 3 illustrates the results from the SSD training (Fig. 2A) of the GNNs shown in Fig. 1C. The initial training to obtain the Teacher model resulted in the MAE of 0.27 kcal mol−1 for the test set of Exp-DB. As the SSD cycles proceeded, Aug-DBs gradually increased. Interestingly, the MAE for the Exp-DB test set reached a minimum at Student 13 (0.22 kcal mol−1), while the database grew from 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 637 to 639
637 to 639![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 925 data points. This indicates that the SSD scheme works appropriately in the data augmentation while the model still captures experimental solubility trends. On the contrary, the MAEs did not decrease in Control models (0.27 kcal mol−1 for both Teacher and Control-13), demonstrating that simply merging solubilities from experiments and COSMO-RS is not advantageous for accurate predictions of experimental solubilities. Moreover, Control at the 13th SSD cycle shows a discrepancy of 0.23 kcal mol−1 between test set MAEs of Exp-DB and Aug-DBs (0.27 vs. 0.04), whereas that from SSD is only 0.11 kcal mol−1 (0.22 vs. 0.11). In other words, more severe overfitting to Aug-DBs occurred in Control than in SSD.
925 data points. This indicates that the SSD scheme works appropriately in the data augmentation while the model still captures experimental solubility trends. On the contrary, the MAEs did not decrease in Control models (0.27 kcal mol−1 for both Teacher and Control-13), demonstrating that simply merging solubilities from experiments and COSMO-RS is not advantageous for accurate predictions of experimental solubilities. Moreover, Control at the 13th SSD cycle shows a discrepancy of 0.23 kcal mol−1 between test set MAEs of Exp-DB and Aug-DBs (0.27 vs. 0.04), whereas that from SSD is only 0.11 kcal mol−1 (0.22 vs. 0.11). In other words, more severe overfitting to Aug-DBs occurred in Control than in SSD.
It is hard to guarantee that 13 SSD cycles are sufficient to obtain the best model since the MAE is not the only metric for evaluating the accuracy. We analyzed RMSEs of Student models that show more irregular trends than MAEs. The initial Teacher training resulted in the RMSE of 0.66 kcal mol−1 for the test set of Exp-DB. As the SSD proceeds, the Exp-DB test set RMSE gradually decreases in general, while it fluctuates intermittently until Student 22. The accuracy of SSD models begins to surpass Control models in terms of RMSEs after Student 22. The best accuracy was achieved in Student 35 with an RMSE of 0.50 kcal mol−1, whereas the RMSE of the 35th Control model is 0.59 kcal mol−1. Although the MAE slightly increased from Student 13 to Student 35 (0.22–0.25 kcal mol−1), the RMSE reaches a minimum with the more extensive database (932![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 509 data points) compared to Student 13 (639
509 data points) compared to Student 13 (639![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 925 data points). The SSD cycles after Student 35 did not effectively improve the accuracy. RMSE is a good metric for penalizing large errors of outliers,91 indicating that Student 35 effectively alleviates prediction errors of Exp-DB outliers while maintaining reliable accuracy for other data points. It should be emphasized that MAE was used for the loss function (details in the Methods section), but RMSE was also minimized during the later stages of SSD. This result implies the importance of including a large amount of data to reduce high prediction errors of outliers by iterating the SSD loop multiple times. Moreover, the best accuracy was obtained in Student 35 when the prediction accuracy was assessed against the ‘external data set’ of 371 experimental partition coefficients (details in the Application 2 section).
925 data points). The SSD cycles after Student 35 did not effectively improve the accuracy. RMSE is a good metric for penalizing large errors of outliers,91 indicating that Student 35 effectively alleviates prediction errors of Exp-DB outliers while maintaining reliable accuracy for other data points. It should be emphasized that MAE was used for the loss function (details in the Methods section), but RMSE was also minimized during the later stages of SSD. This result implies the importance of including a large amount of data to reduce high prediction errors of outliers by iterating the SSD loop multiple times. Moreover, the best accuracy was obtained in Student 35 when the prediction accuracy was assessed against the ‘external data set’ of 371 experimental partition coefficients (details in the Application 2 section).
Aug-DBs grow slower as SSD cycles proceed (details in Section S1, ESI†). The leftover solute–solvent pairs in the late SSD cycles are mostly problematic cases (details in Error analysis of solubility prediction) whose true ΔGsolv are dubious; therefore, fewer solute–solvent pairs satisfy the cutoff. Different functional group distributions of Aug-DBs also influence the RMSE trends shown in Fig. 3; there is the tradeoff between ‘over-generalization’ to existing functional groups and newly introduced ones (details in Section S1, ESI†).92,93
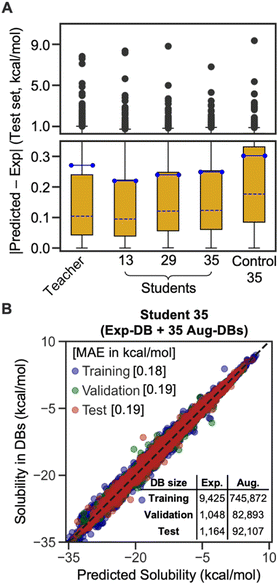
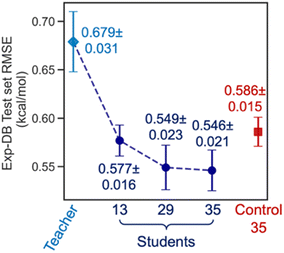
The box plot in Fig. 4A demonstrates that the SSD up to 35 cycles is beneficial to obtain an optimal model. We chose Students 13, 29, and 35, which resulted in the local minima of RMSEs during the SSD (Fig. 3), in addition to Teacher. For the test set of Exp-DB, Student 13 shows more significant outliers (gray dots) with higher errors than the Teacher. The error of the first outlier becomes even higher in Student 29 than in Student 13. However, such errors of outliers become lowest in Student 35, which indicates the mitigation of overfitting through SSD. The outlying behavior is remedied in Student 35 while maintaining a lower MAE and similar interquartile range (yellow box) compared to the Teacher. In contrast, the accuracy of Control 35 is even worse than Teacher, and their outliers also show higher errors. Fig. 4B illustrates the parity plot of the solubility values from the databases vs. those from the predictions of Student 35. For the whole integrated database (Exp-DB + 35 Aug-DBs), Student 35 achieved balanced accuracies among the training, validation, and test sets, with MAEs of 0.18, 0.19, and 0.19 kcal mol−1, respectively.
This model also showed comparable accuracies with the GNN models in the literature56 for the Exp-DB test set, and higher accuracies than computational methods. Table 1 summarizes the accuracies of GNNs from the literature,56 our GNNs (Student 35), COSMO-RS and SMD-M06-2X in predicting ΔGsolv values in Exp-DB. Student 35 showed comparable MAEs/RMSEs with the model in the literature (MAE: 0.20/0.22 kcal mol−1, RMSE: 0.44/0.50 kcal mol−1 for ours/literature) with 150 more data points in the test set. Although a fair comparison was not possible due to the different test sets, the MAE and RMSE differences of only 0.02 and 0.06 kcal mol−1 demonstrate the high reliability of our model and feasibility of SSD. In addition, Student 35 surpasses the accuracies of COSMO-RS and SMD-M06-2X. The MAEs and RMSEs of Student 35 are lower than those of COSMO-RS for the 3254 and 5608 data points in CombiSolv-QM and QM-DB overlapping with Exp-DB, respectively. Student 35 is still more accurate than COSMO-RS and SMD-M06-2X/def2-TZVP in all cases when these data points are categorized into training, validation, and test sets. It should be emphasized that our model predicts ΔGsolv more accurately while being computationally much less demanding (<1 second for GNNs vs. several hours or days for QM methods).
| Comparison with the GNNs in the literature (the best-case model)a,b | |||||
|---|---|---|---|---|---|
| GNNs in the literature | Student 35 | ||||
| # of data points (Exp-DB) | Test set MAE (kcal mol−1) | Test set RMSE (kcal mol−1) | # of data points (Exp-DB) | Test set MAE (kcal mol−1) | Test set RMSE (kcal mol−1) |
| a From the literature.56 b Of note, the experimental databases and test sets are not the same, and it is an indirect comparison. c Test set sizes. | |||||
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 145a [1014a,c] 145a [1014a,c] |
0.20a | 0.44a | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 637 [1164c] 637 [1164c] |
0.22 | 0.50 |
| Exp-DB overlapping with QM-DB | ||||||
|---|---|---|---|---|---|---|
| # of data points | SMD-M06-2X/def2-TZVP | Student 35 | ||||
| MAE (kcal mol−1) | RMSE (kcal mol−1) | Training/validation/test | # of data points | MAE (kcal mol−1) | RMSE (kcal mol−1) | |
| 5608 | 0.62 | 0.88 | Training | 4534 | 0.13 | 0.20 |
| Validation | 498 | 0.21 | 0.42 | |||
| Test | 576 | 0.22 | 0.39 | |||
| All | 5608 | 0.14 | 0.25 | |||
To verify that the model is not prone to overfitting, we carried out 10-fold cross-validation as depicted in Fig. 5. Fig. 5A shows how the databases (Exp-DB and Aug-DBs) are split into 11 data subsets (subsets A–K, each corresponding to either training/validation/held-out test set) to carry out the 10-fold cross-validation. This data set split was performed separately for Aug-DBs and Exp-DB to balance the ratio of the data points from data augmentation and experiments. The constituent solutes/solvents in each subset can vary depending on the sampling methods. The solute–solvent combinations can be sampled randomly, as shown in Fig. 5B. Meanwhile, solvent/solute-wise data splits are also possible with the stratified sampling (details in Section S2, ESI†).
 | ||
| Fig. 5 (A) Schematic illustration of the 10-fold cross-validation with data splits for Exp-DB and Aug-DBs. (B) Data subsets obtained from random solute–solvent sampling. | ||
Fig. 6 displays the Exp-DB test set RMSEs obtained from the 10-fold cross-validation of Teacher, three Students, and one Control model with the random solute–solvent sampling (Fig. 5B). Means and standard deviations of 10 RMSEs were evaluated for each model. The mean of RMSEs decreases significantly from 0.679 to 0.577 kcal mol−1 when SSD proceeds from Teacher to Student 13 and is reduced further at Student 29 (0.549 kcal mol−1). The accuracy of Student 35 (mean of RMSEs: 0.546 kcal mol−1) is slightly higher than that of Student 29, with a lower standard deviation among ten folds (0.023 and 0.021 kcal mol−1 for Student 29 and 35, respectively). The held-out test set from Aug-DBs was not considered for the evaluation since the sizes of Aug-DBs are different for all Student models. We also carried out the 10-fold cross-validation with the solvent-wise and solute-wise data splits. As a result, comparable accuracies were still obtained from these different methods of 10-fold cross-validation (details in Section S2, ESI†).
All the above results demonstrate the effectiveness of SSD in improving the accuracy of the ground-truth experimental solubilities while augmenting the database. Our empirical results are consistent with mathematical proofs that several rounds of SSD enhance the accuracy of the held-out data and reduce overfitting.92,93 It has been verified that self-distillation amplifies the regularization of the space of trainable parameters if the model architectures for Teacher and Students are identical (Fig. 1C).92 When Students are trained using an extensive distilled database with a limited parameter space, their variance is reduced without significantly increasing its bias. In other words, the models' trainable parameters are neither overly sensitive to different training set batches nor biased to specific batches, and therefore overfitting is reduced. Meanwhile, too many rounds of SSD may over-regularize the model, leading to underfitting. These mathematical findings align with our SSD results shown in Fig. 3. In addition, adding noises to the SSD model parameters showed minor output perturbations,93 and the ablation analysis with removing the augmented data significantly degraded the model performance.77 These previous studies further support the robustness of SSD with augmented datasets.
Other variants of SSD were also attempted using QM-DB, or both CombiSolv-QM and QM-DB (Section S3 in the ESI†), but the SSD shown in Fig. 2A showed the best accuracy. We also tested other variants of semi-supervised learning methods, such as noisy student self-distillation (NSSD); however, this led to higher prediction errors (see Section S4, ESI† for detailed discussion).
Next, we carried out a clustering analysis of t-distributed stochastic neighbor embeddings (t-SNEs) of latent vectors for 1447 solvents included in all the databases shown in Fig. 1A. This analysis is to further verify the chemical feasibility of Student 35. 2D t-SNE coordinates were obtained for these solvents. Each solvent was categorized according to the priority of categories listed in the legend of Fig. 7. For example, if a solvent contains both O and S, it is classified as ‘O,N-containing’ because O has higher priority than S. We identified certain clustering patterns among several categories: O,N-containing (upper side), halogen (X)-containing (mainly lower right), and hydrocarbon solvents (mainly lower left). O,N-Containing solvents exclusively occupy a specific region, possibly because they are solvents that can participate in hydrogen bonds and show characteristic solubility trends.
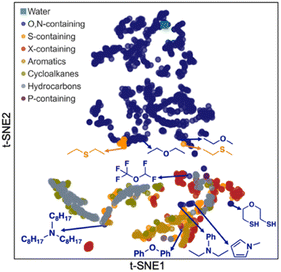 | ||
| Fig. 7 2D plot of t-distributed stochastic neighbor embeddings (t-SNEs) for the latent vectors of 1447 solvents obtained from Student 35 model. | ||
However, some O,N-containing solvents are located near other molecular groups, such as aromatics, hydrocarbons, and X-containing ones. These solvents contain oxygen or nitrogen, with the other atoms corresponding to the molecular groups they are close to. For instance, trioctylamine is in the cluster of hydrocarbons since it has three alkyl chains having eight carbons per each. Pentafluorodimethyl ether was found adjacent to the X-containing cluster. Ethers, amines, and pyrroles with aromatic rings are placed around the group of aromatic solvents. Meanwhile, an ether with two thiol groups (2-mercaptoethyl ether) was found near S-containing solvents rather than O,N-containing ones, indicating that their behavior as a solvent is close to S-containing solvents rather than O,N-containing ones. Conversely, some sulfides (diethyl sulfide, ethyl methyl sulfide) are near their ether analogs, implying that their chemical behavior could be analogous to ethers.
Error analysis of solubility prediction
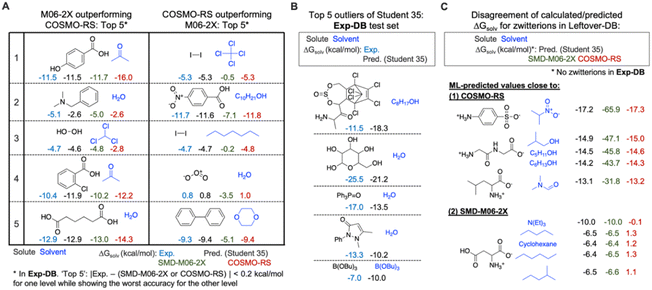
The error analysis was performed by comparing the QM-DB solubilities calculated in the SMD-M06-2X/def2-TZVP level of theory with those from COSMO-RS, experiments, and the Student 35 model. First, we analyzed Exp-DB solute–solvent pairs where SMD-M06-2X outperforms COSMO-RS and vice versa to identify the advantages and disadvantages of each theoretical method (Fig. 8A). The left side of Fig. 8A illustrates the five cases whose absolute error between ΔGsolv from experiment and SMD-M06-2X does not exceed 0.2 kcal mol−1, whereas COSMO-RS shows the worst performance. All these five cases correspond to polar solutes and solvents with halogen atoms, hydrogen bond donors and acceptors. SMD-M06-2X better reproduces the experimental solubilities of these molecules than COSMO-RS, which may be in part attributed to the halogenicity, hydrogen bond acidity, and basicity parameters used by SMD. For these five cases, the predictions of Student 35 are showing the values close to experimental values, although COSMO-RS ΔGsolv were referred during the SSD. 2 and 4 show the jeopardy of the predicted value biased to COSMO-RS. However, for 1, 3, and 5, Student 35's predictions are closer to the Exp-DB solubilities than those from COSMO-RS. Moreover, Student 35 showed the outliers with the lowest errors among other Students (Fig. 4A). This indicates that the distillation process (Fig. 2A) effectively corrected the discrepancy between experiment and theory.We also analyzed five different solute–solvent pairs for which COSMO-RS outperforms SMD-M06-2X (right side of Fig. 8A). They are solutes and solvents with low or no polarity or molecules with special moieties such as ozone. Investigating the two extreme cases shown in Fig. 8A demonstrates the importance of accounting for multiple theoretical methods in assessing the results from SSD.
The analysis on SMD-M06-2X and COSMO-RS was then followed by the outlier analysis of Student 35 (Fig. 8B). The outliers correspond to the gray dots in Fig. 4A; their extraordinary chemical structures indicate that they do not meaningfully deteriorate the model's accuracy. The top five outliers include solutes with multiple complex rings, five hydroxy groups, and heteroatoms (P and B) that rarely appear in the whole database (932![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 509 data points). For example, the solutes with a P
509 data points). For example, the solutes with a P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bond and aromatic substituents appear only in 808 data points, and only 69 data points have solutes/solvents with B–O single bonds. These outliers occurred not because of the overfitting to Aug-DBs but due to the chemical moieties rarely seen in the databases.
O double bond and aromatic substituents appear only in 808 data points, and only 69 data points have solutes/solvents with B–O single bonds. These outliers occurred not because of the overfitting to Aug-DBs but due to the chemical moieties rarely seen in the databases.
Further analysis was performed for Leftover-DB consisting of 57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 721 solute–solvent pairs in CombiSolv-QM that were not included in the Aug-DBs but remained after 35 SSD cycles. Since Leftover-DB does not have experimental values, we compared their ΔGsolv values from Student 35, SMD-M06-2X and COSMO-RS for 14
721 solute–solvent pairs in CombiSolv-QM that were not included in the Aug-DBs but remained after 35 SSD cycles. Since Leftover-DB does not have experimental values, we compared their ΔGsolv values from Student 35, SMD-M06-2X and COSMO-RS for 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 053 out of 57
053 out of 57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 721 data points whose ΔGsolv from all the three models or methods are available. As a result, significant discrepancies were observed for 1381 data points having zwitterionic solutes. Ten extreme cases are shown in Fig. 8C. SMD-M06-2X relatively overestimates ΔGsolv compared to the other two for the above five cases, whereas the ΔGsolv from COSMO-RS shows disagreement with Student 35 and SMD-M06-2X for the below five ones. It should be emphasized that no zwitterions are available in Exp-DB. However, 5446 zwitterions were already included in Aug-DBs during the SSD; these species have no experimental ground-truth ΔGsolv values. Such a lack of data availability for zwitterions necessitates experimental measurements for their solubility values or additional reliable theoretical methods, possibly leading to a more extensive database from SSD, including zwitterions.
721 data points whose ΔGsolv from all the three models or methods are available. As a result, significant discrepancies were observed for 1381 data points having zwitterionic solutes. Ten extreme cases are shown in Fig. 8C. SMD-M06-2X relatively overestimates ΔGsolv compared to the other two for the above five cases, whereas the ΔGsolv from COSMO-RS shows disagreement with Student 35 and SMD-M06-2X for the below five ones. It should be emphasized that no zwitterions are available in Exp-DB. However, 5446 zwitterions were already included in Aug-DBs during the SSD; these species have no experimental ground-truth ΔGsolv values. Such a lack of data availability for zwitterions necessitates experimental measurements for their solubility values or additional reliable theoretical methods, possibly leading to a more extensive database from SSD, including zwitterions.
Although the above error analysis suggests room for improving our model, it is sufficiently reliable to be utilized in the practical design of solvent systems in various chemical processes such as catalysis and separation. The following sections demonstrate the application of our model to practical examples.
Application 1 – linear solvation energy relationships (LSERs) between solvation free energy and reaction rates
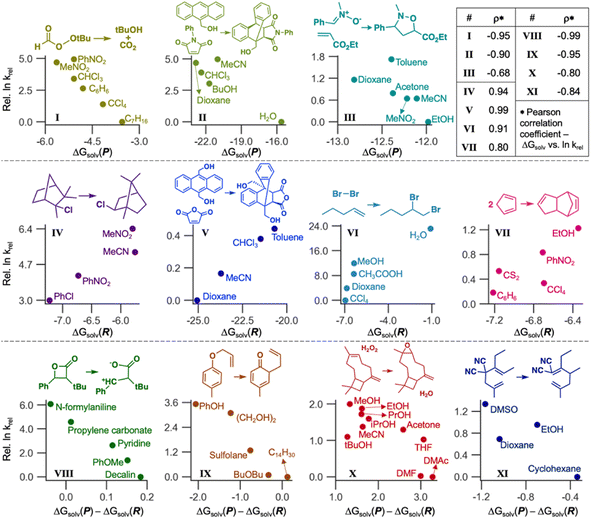
LSERs inform solvent selection to maximize the reaction rates in designing organic reactions.7–9 Here, we demonstrate the application of our ML model to discover LSERs in 11 organic reactions. Gibbs solvation free energies of the product(s) and reactant(s) (ΔGsolv(P) and ΔGsolv(R), respectively) were predicted using Student 35. If a reaction has two or more reactants or products, the sum of their ΔGsolv values was used as ΔGsolv(R) or ΔGsolv(P). These values and their differences [ΔGsolv(P) − ΔGsolv(R)] were used as the descriptors to find highly positive or negative Pearson correlation coefficients ρ (i.e., close to 1 or −1) with experimental reaction rates in different solvents. According to the Hammond postulate,94 at least one of these three descriptors should show a high correlation (details in Section S5, ESI†). The reaction rates were collected from the literature.2,95–97Fig. 9 depicts the correlation for 11 organic reactions with varying solvents. For each reaction, we chose one descriptor that shows the strongest correlation with experimental reaction rates. ΔGsolv(P) is the best descriptor for the reactions I, II, and III, with Pearson ρ values of −0.95, −0.90, and −0.68, respectively, whereas ΔGsolv(R) was chosen for IV–VII (ρ = 0.80–0.99). The rest four reactions (VIII–XI) can be explained by ΔGsolv(P) − ΔGsolv(R) as a descriptor (ρ from −0.99 to −0.80). Our ML model also showed reliable results (ρ = −0.80) in the complex reaction example, such as the epoxidation of β-caryophyllene investigated in 10 different solvents (X). These correlations are also chemically explainable (Section S5, ESI†). While Fig. 9 shows only the best-case descriptor, ρ values for all three descriptors are available for each reaction (Section S5, ESI†), with the reason for selecting a particular descriptor. Of note, some of the above 11 reactions were not performed at room temperature, whereas our GNN gives ΔGsolv at room temperature. Considering the temperature dependence of solubility would improve GNNs and LSERs, although the results in Fig. 9 already show decent correlations.
The ΔGsolv difference of only around 1 kcal mol−1 can significantly affect reactivity predictions (Fig. 9), demanding a fast and accurate ML model. Designing solvent systems using our GNN is advantageous because it is fast compared to expensive QM calculations while being accurate. Solvents that maximize reaction rates can be designed by predicting ΔGsolv(R) and ΔGsolv(P), finding LSERs, and extrapolating the relationship for the new solvents in which experiments have not been performed. Although ΔGsolv of transition states is not considered here, our model enables rapid solvent screening before investigating the transition states.
Application 2 – prediction of partition coefficients for lignin-derived monomers and drug-like molecules
As the second application example, we examined our GNN model by predicting 363 water-organic partition coefficients (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P) of depolymerized lignin derivatives and drug-like compounds (Sets A and B, Table 2). Their experimental log
P) of depolymerized lignin derivatives and drug-like compounds (Sets A and B, Table 2). Their experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values are available from the literature.98 Predicting log
P values are available from the literature.98 Predicting log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P would enable the design of solvents that effectively extract useful biomass-derived compounds and drug molecules with high yields. Here, we predicted the ΔGsolv values in water and organic solvents for Sets A and B and evaluated log
P would enable the design of solvents that effectively extract useful biomass-derived compounds and drug molecules with high yields. Here, we predicted the ΔGsolv values in water and organic solvents for Sets A and B and evaluated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values using the formula: log
P values using the formula: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = (ΔGsolv,water − ΔGsolv,org)/2.303RT. Two metrics were used to assess accuracies: RMSE and Kendall rank correlation coefficient (τ). A τ value closer to 1 indicates a stronger rank correlation (i.e., higher accuracy). These metrics were chosen because the literature98 used the same metrics in assessing COSMO-RS.
P = (ΔGsolv,water − ΔGsolv,org)/2.303RT. Two metrics were used to assess accuracies: RMSE and Kendall rank correlation coefficient (τ). A τ value closer to 1 indicates a stronger rank correlation (i.e., higher accuracy). These metrics were chosen because the literature98 used the same metrics in assessing COSMO-RS.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P) for COSMO-RS and GNN for two datasets with their description
P) for COSMO-RS and GNN for two datasets with their description
Description of the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P dataset P dataset |
Prediction methods | Kendall τ | RMSE | |
|---|---|---|---|---|
| Set A | 300 data points (30 depolymerized lignin derivatives, 10 organic solvents) | GNN (Student 35) | 0.87 | 0.51 |
| COSMO-RS | 0.77 | 0.50 | ||
| Set B | 63 data points (17 drug-like compounds, 4 organic solvents) | GNN (Student 35) | 0.70 | 1.15 |
| COSMO-RS | 0.77 | 1.00 |
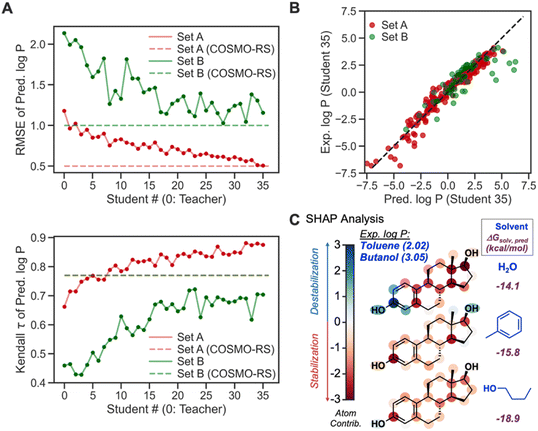
To further verify the feasibility of SSD, we compared the accuracies of our Teacher and Students from SSD with the COSMO-RS method (Fig. 10A). For both Sets, the latter Students show lower RMSEs than the earlier ones and Teacher, and their RMSEs become comparable to that of COSMO-RS, demonstrating the effectiveness of the SSD. Regarding Kendall τ of Set A, our GNN models even exceed the accuracy of COSMO-RS. For Set B, the τ values of Students are lower than that of COSMO-RS. However, it displays an increasing trend for latter Students, indicating the strength of SSD.
Table 2 compares τ and RMSEs for COSMO-RS and our final GNN model, Student 35. For Set A, our model showed a higher τ than COSMO-RS (0.87 vs. 0.77), whereas τ from Student 35 and COSMO-RS is 0.70 and 0.77, respectively, for Set B. Our GNN resulted in a better correlation for Set A than COSMO-RS, while COSMO-RS performed slightly better in Set B. In terms of RMSE, our model achieved an RMSE almost identical to that from COSMO-RS for Set A. COSMO-RS showed better accuracy in Set B. Notably, Set B has fewer data points (63) than Set A (300), so Set A can assess model accuracies better than Set B; we achieve better rank correlation than COSMO-RS in Set A. Fig. 10B depicts the parity plot of ML-predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P vs. experimental ones. Overall, the model shows predictions close to experimental ones. Log
P vs. experimental ones. Overall, the model shows predictions close to experimental ones. Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P of some cases in Set B is overestimated, but similar outliers were also found from the COSMO-RS results.98 Accuracies for these data points can be improved by considering ΔGsolv of ionic species for predicting distribution coefficients (log
P of some cases in Set B is overestimated, but similar outliers were also found from the COSMO-RS results.98 Accuracies for these data points can be improved by considering ΔGsolv of ionic species for predicting distribution coefficients (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D) for acidic/basic solute molecules.
D) for acidic/basic solute molecules.
Another merit of our GNNs is chemical interpretability, which is possible by quantifying and analyzing atom-wise contributions based on the procedure described in our recent work.83 This analysis was inspired by the Shapley additive explanation (SHAP) method.85 The summation of quantified atom-wise contribution values equals the predicted ΔGsolv. We examined our SHAP method for GNNs for estradiol (Fig. 10C) in two different organic solvents and water to explain a higher experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P value in butanol–water (3.05) than in toluene–water (2.02). The aromatic moiety decreases the solubility in water because it is a polar solvent. The same moiety shows solvation stabilization in toluene, presumably due to non-covalent interactions between toluene and estradiol, whereas the methyl and hydroxyl groups in the aliphatic ring display unfavorable interactions with toluene. Estradiol in 1-butanol shows overall stabilization since either alkyl or hydroxy group in 1-butanol can stabilize aliphatic, aromatic, and hydroxy groups through dispersion interaction and hydrogen bonds. Such difference in atom-wise contributions and chemical interactions leads to higher solvation stabilization in 1-butanol than in toluene, and thus a higher log
P value in butanol–water (3.05) than in toluene–water (2.02). The aromatic moiety decreases the solubility in water because it is a polar solvent. The same moiety shows solvation stabilization in toluene, presumably due to non-covalent interactions between toluene and estradiol, whereas the methyl and hydroxyl groups in the aliphatic ring display unfavorable interactions with toluene. Estradiol in 1-butanol shows overall stabilization since either alkyl or hydroxy group in 1-butanol can stabilize aliphatic, aromatic, and hydroxy groups through dispersion interaction and hydrogen bonds. Such difference in atom-wise contributions and chemical interactions leads to higher solvation stabilization in 1-butanol than in toluene, and thus a higher log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P. The quantified contribution values are consistent with chemical knowledge, enabling the chemistry-informed design of solvent systems.
P. The quantified contribution values are consistent with chemical knowledge, enabling the chemistry-informed design of solvent systems.
All these results indicate that our GNNs reliably capture solubility trends and accurately predict log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values in different organic solvents. It should be emphasized that GNN predictions of log
P values in different organic solvents. It should be emphasized that GNN predictions of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P take less than one second and are as accurate as COSMO-RS, whereas QM and COSMO-RS calculations are expensive (usually several hours or days per one molecule). Rapid and reliable log
P take less than one second and are as accurate as COSMO-RS, whereas QM and COSMO-RS calculations are expensive (usually several hours or days per one molecule). Rapid and reliable log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P predictions would lead to the computational solvent design for separation processes in organic, pharmaceutical synthesis, and renewable energy industries.
P predictions would lead to the computational solvent design for separation processes in organic, pharmaceutical synthesis, and renewable energy industries.
Conclusions
Solubility is a critical molecular property when designing chemical processes such as synthesis and separation in organic, pharmaceutical, and sustainable chemistry. Many ML models have been developed but lack reliable integrations of experimental and computational solubility databases to maximize the database size and, thus, prediction accuracy. To reduce the discrepancies among different data sources, semi-supervised self-training methodologies were adopted in solubility predictions, leading to self-evolving solubility databases and GNN predictive models. The resulting model showed reliable accuracy and was subsequently applied to practical examples of solvent selection in chemical reactions and separation processes. All these results demonstrate the practical applicability of the developed model to the design of solvent systems in chemical processes.Such approaches can be potentially improved by employing multiple QM methods during data augmentation. Additional QM calculations can be performed for transition states, radicals, ions, and other charged species in solution phase using reliable methods. Accuracies of predicting solubilities of zwitterions can also be improved. In terms of the molecular scope, the database adopted for model training can be expanded to organometallic complexes in addition to the organic molecules in the current database. Meanwhile, considering temperature effects on solubility in ML models should be pursued in the future to achieve the application of the model to a broader scope of chemistry. Lastly, predicting solubilities in multicomponent solvents is another challenge in developing future ML models, which would lead to the realistic modeling of mixtures utilized in various chemical reactions and separation processes.
Methods
Computational details for calculating ΔGsolv
The AQME Python package99 was used throughout the overall process for calculating ΔGsolv values of given solute–solvent pairs. First, the canonicalized SMILES strings of solutes were converted into 3D geometries, and conformational searches were carried out by employing the MMFF94s force field100 implemented in the RDKit cheminformatics library.101 The number of generated conformers was determined based on the number of rotatable bonds. The lowest-energy conformer was then chosen and subject to further geometry optimizations using DFT with the SMD implicit solvation model, per a recent study reporting that considering only the most stable conformer is sufficient to obtain energy values close to the Boltzmann-weighted ensemble average of multiple conformers for organic molecules.61 The subsequent geometry optimizations were performed using the M06-2X/def2-TZVP method with the SMD. Of note, only 3D structures of solutes were optimized, and solvents were specified by their name in the input file. While the SMD is available for any solvents whose descriptor values are available (dielectric constant, refractive index, surface tension, etc.), calculations were performed for only the solvents available in the Gaussian 16 package.102The optimized structures were confirmed as valid if no imaginary frequencies and no decomposition into disconnected molecules were observed. If the structure is not valid or the self-consistent field calculation does not converge, we assumed that the SMD-DFT could not correctly simulate the corresponding solute–solvent pair, and it was discarded. To calculate ΔGsolv from the optimized geometry, the external iteration method in Gaussian 16 was utilized, which considers the self-consistent solvent reaction field to calculate the solute's electrostatic potential. These calculations were carried out in the same level of theory, with specifying the keywords ‘Externaliteration’ and ‘1stVac’ in the Gaussian 16 input file.
COSMO-RS is another computational method adopted to obtain ΔGsolv. We used the database of COSMO-RS-calculated ΔGsolv values from the literature (CombiSolv-QM database). They were obtained using the DFT-calculated COSMO surfaces for each solute/solvent (BP/def2-TZVPD//BP/TZVPD level of theory103) with a FINE cavity for the surface segments.56 More details of COSMO-RS calculations are available in the literature.56
Development of graph neural networks with SSD
The GNN models were developed using Python 3.7 (ref. 104) with TensorFlow 2.4,105 Keras 2.9,106 and Neural Fingerprint (NFP)107 0.3.0 libraries. The NFP library provides the framework for deep learning using message-passing GNN108 with the atom, bond, and global features (Fig. 1C) generated through the RDKit cheminformatics package.101 The stochastic depth method was implemented by employing TensorFlow-Addons 0.14 to examine the effect of introducing noises to message-passing layers, although the SSD without added noise showed the best prediction accuracy. The optimal GNN structure shown in Fig. 1C was determined by hyperparameter tuning. We carried out an iterative grid search of possible combinations of different hyperparameters. These hyperparameters are the number of message-passing layers (3–6), dimension of hidden layer vectors (64, 128, and 256), learning rate (a·10−b; a = 1, 5, and b = 3–5), batch size (2n, n = 7–10), and activation functions (Rectified linear unit – ReLU, and LeakyReLU). We trained the models against Exp-DB with different hyperparameters and identified the one that shows the best compromise between accuracy and computational cost, resulting in the model shown in Fig. 1C. During the SSD process, all Teacher and Student models were trained for 1000 epochs with a learning rate of 1 × 10−4, followed by 200 epochs with a learning rate of 5 × 10−5, using a batch size of 1024. The ADAM optimizer with the MAE loss function was employed.MAE and RMSE loss functions have their own pros and cons. The RMSE loss function contains a quadratic L2 norm facilitates the minimization and convergence of prediction errors. However, using the MAE loss function in deep neural networks can also be advantageous in terms of generalizability to big data with a broad scope of molecules. MAE is reportedly Lipschitz continuous;109 the first derivative of MAE is a bounded function. Such boundedness prevents exploding gradients and thus outliers. In contrast, RMSE or MSE loss functions are not Lipschitz continuous. Moreover, it should be emphasized that RMSE was also minimized during the SSD (Fig. 3) although the MAE loss function was used, indicating the effectiveness of MAE in mitigating the overfitting. Mathematical proofs also showed that MAE as well as RMSE can minimize outlier errors, i.e., prevent overfitting, instead of maximizing the correctness of predictions that are already accurate.110
Exp-DB and all Aug-DBs were split into the training, validation, and test sets with a ratio of 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9. We adopted this ratio instead of the typical 8
9. We adopted this ratio instead of the typical 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio to perform 10-fold cross-validation with varying the training and validation sets. The training/validation set, and training/test set ratios are 9
1 ratio to perform 10-fold cross-validation with varying the training and validation sets. The training/validation set, and training/test set ratios are 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 8
1 and 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively, enabling the 10-fold partitioning while maintaining the held-out test set. The validation loss value was monitored at each epoch throughout the training to archive the best model with the lowest validation set error. It was sufficient to identify the best model when trained for 1200 epochs with two different learning rates mentioned above. Due to the high computational costs of cross-validation, only one of the 10 folds was utilized for the model training and data augmentation (Fig. 2A). However, the full 10-fold cross-validation was performed for Teacher, Students 13, 29, and 35 models (Fig. 5). This is to verify that the models are not prone to overfitting and the SSD scheme effectively reduces the deviation of prediction errors among different data splits. The model was trained using one GV100 GPU; the time taken for training ranges from 50 minutes (Exp-DB, 11
1, respectively, enabling the 10-fold partitioning while maintaining the held-out test set. The validation loss value was monitored at each epoch throughout the training to archive the best model with the lowest validation set error. It was sufficient to identify the best model when trained for 1200 epochs with two different learning rates mentioned above. Due to the high computational costs of cross-validation, only one of the 10 folds was utilized for the model training and data augmentation (Fig. 2A). However, the full 10-fold cross-validation was performed for Teacher, Students 13, 29, and 35 models (Fig. 5). This is to verify that the models are not prone to overfitting and the SSD scheme effectively reduces the deviation of prediction errors among different data splits. The model was trained using one GV100 GPU; the time taken for training ranges from 50 minutes (Exp-DB, 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 637 data points) to 1.7 days (Exp-DB + Aug-DBs, 932
637 data points) to 1.7 days (Exp-DB + Aug-DBs, 932![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 509 data points).
509 data points).
Data availability
The code, trained models, and databases are available via GitHub (https://github.com/BioE-KimLab/Solv_GNN_SSD). The CombiSolv-Exp and CombiSolv-QM datasets are available in ref. 56.Author contributions
Conceptualization, formal analysis, investigation, methodology, validation, visualization, writing – original draft: Y. K., formal analysis, investigation, writing – review & editing: H. J., conceptualization, methodology, writing – review & editing: Sabari Kumar, conceptualization, formal analysis, writing – review & editing: R. S. P., conceptualization, funding acquisition, project administration, supervision, writing – review & editing: Seonah Kim.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Colorado State University startup funds for PI (Seonah Kim) and the National Science Foundation under Grant No. CHE-2304658. The computer time was provided by the NSF Extreme Science and Engineering Discovery Environment (XSEDE), Grant No. TG-CHE210034. We acknowledge Alex Claiborne (CSU) for his help to collect some of solubility experimental data.Notes and references
- T. Dalton, T. Faber and F. Glorius, ACS Cent. Sci., 2021, 7, 245–261 CrossRef CAS PubMed.
- P. J. Dyson and P. G. Jessop, Catal. Sci. Technol., 2016, 6, 3302–3316 RSC.
- F. Huxoll, F. Jameel, J. Bianga, T. Seidensticker, M. Stein, G. Sadowski and D. Vogt, ACS Catal., 2021, 11, 590–594 CrossRef CAS.
- H. C. Hailes, Org. Process Res. Dev., 2007, 11, 114–120 CrossRef CAS.
- J. J. Varghese and S. H. Mushrif, React. Chem. Eng., 2019, 4, 165–206 RSC.
- J. D. Moseley and P. M. Murray, J. Chem. Technol. Biotechnol., 2014, 89, 623–632 CrossRef CAS.
- B. L. Slakman and R. H. West, J. Phys. Org. Chem., 2019, 32, e3904 CrossRef.
- J. Sherwood, H. L. Parker, K. Moonen, T. J. Farmer and A. J. Hunt, Green Chem., 2016, 18, 3990–3996 RSC.
- P. J. Dyson and P. G. Jessop, Catal. Sci. Technol., 2016, 6, 3302–3316 RSC.
- S. P. Pinho and E. A. Macedo, in Developments and Applications in Solubility, The Royal Society of Chemistry, 2007, pp. 305–322, 10.1039/9781847557681.
- A. Jouyban, J. Pharm. Pharm. Sci., 2008, 11, 32–58 CAS.
- A. Llinàs, R. C. Glen and J. M. Goodman, J. Chem. Inf. Model., 2008, 48, 1289–1303 CrossRef PubMed.
- C. A. S. Bergström, W. N. Charman and C. J. H. Porter, Adv. Drug Delivery Rev., 2016, 101, 6–21 CrossRef.
- C. A. S. Bergström and P. Larsson, Int. J. Pharm., 2018, 540, 185–193 CrossRef.
- S. E. Fioressi, D. E. Bacelo, C. Rojas, J. F. Aranda and P. R. Duchowicz, Ecotoxicol. Environ. Saf., 2019, 171, 47–53 CrossRef CAS PubMed.
- A. K. Nayak and P. P. Panigrahi, ISRN Phys. Chem., 2012, 2012, 820653 Search PubMed.
- N. Seedher and M. Kanojia, Pharm. Dev. Technol., 2009, 14, 185–192 CrossRef CAS PubMed.
- S. A. Newmister, S. Li, M. Garcia-Borràs, J. N. Sanders, S. Yang, A. N. Lowell, F. Yu, J. L. Smith, R. M. Williams, K. N. Houk and D. H. Sherman, Nat. Chem. Biol., 2018, 14, 345–351 CrossRef CAS.
- J. Kraml, F. Hofer, A. S. Kamenik, F. Waibl, U. Kahler, M. Schauperl and K. R. Liedl, J. Chem. Inf. Model., 2020, 60, 3843–3853 CrossRef CAS.
- J. Esteban, A. J. Vorholt and W. Leitner, Green Chem., 2020, 22, 2097–2128 RSC.
- G. W. Huber, J. N. Chheda, C. J. Barrett and J. A. Dumesic, Science, 2005, 308, 1446–1450 CrossRef CAS PubMed.
- Z. Shen and R. C. Van Lehn, Ind. Eng. Chem. Res., 2020, 59, 7755–7764 CrossRef CAS.
- Y. Kim, A. Mittal, D. J. Robichaud, H. M. Pilath, B. D. Etz, P. C. S. John, D. K. Johnson and S. Kim, ACS Catal., 2020, 10, 14707–14721 CrossRef CAS.
- A. Hollas, X. Wei, V. Murugesan, Z. Nie, B. Li, D. Reed, J. Liu, V. Sprenkle and W. Wang, Nat. Energy, 2018, 3, 508–514 CrossRef CAS.
- J. F. Kucharyson, L. Cheng, S. O. Tung, L. A. Curtiss and L. T. Thompson, J. Mater. Chem. A, 2017, 5, 13700–13709 RSC.
- S. S. Santhanalakkshmi Vejaykummar, J. N. Law, C. E. Tripp, D. Duplyakin, E. Skordilis, D. Biagioni, R. S. Paton and P. C. S. John, Nat. Mach. Intell., 2022, 4, 720–730 CrossRef.
- M. C. Sorkun, A. Khetan and S. Er, Sci. Data, 2019, 6, 143 CrossRef.
- J.-C. Bradley, C. Neylon, R. Guha, A. Williams, B. Hooker, A. Lang, B. Friesen, T. Bohinski, D. Bulger, M. Federici, J. Hale, J. Mancinelli, K. Mirza, M. Moritz, D. Rein, C. Tchakounte and H. Truong, Nat. Preced., 2010 DOI:10.1038/npre.2010.4243.3.
- A. V. Marenich, C. P. Kelly, J. D. Thompson, G. D. Hawkins, C. C. Chambers, D. J. Giesen, P. Winget, C. J. Cramer and D. G. Truhlar, Minnesota Solvation Database (MNSOL) version 2012, Retrieved from the Data Repository for the University of Minnesota, 2020, DOI:10.13020/3eks-j059.
- C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2005, 1, 1133–1152 CrossRef CAS.
- J. D. Thompson, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2004, 108, 6532–6542 CrossRef CAS.
- D. L. Mobley and J. P. Guthrie, J. Comput.-Aided Mol. Des., 2014, 28, 711–720 CrossRef CAS PubMed.
- E. Moine, R. Privat, B. Sirjean and J.-N. Jaubert, J. Phys. Chem. Ref. Data, 2017, 46, 033102 CrossRef.
- A. Llinas and A. Avdeef, J. Chem. Inf. Model., 2019, 59, 3036–3040 CrossRef CAS.
- A. Llinas, I. Oprisiu and A. Avdeef, J. Chem. Inf. Model., 2020, 60, 4791–4803 CrossRef CAS PubMed.
- J. G. M. Conn, J. W. Carter, J. J. A. Conn, V. Subramanian, A. Baxter, O. Engkvist, A. Llinas, E. L. Ratkova, S. D. Pickett, J. L. McDonagh and D. S. Palmer, J. Chem. Inf. Model., 2023, 63, 1099–1113 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS.
- S. Boothroyd, A. Kerridge, A. Broo, D. Buttar and J. Anwar, Phys. Chem. Chem. Phys., 2018, 20, 20981–20987 RSC.
- D. S. Palmer, J. L. McDonagh, J. B. O. Mitchell, T. van Mourik and M. V. Fedorov, J. Chem. Theory Comput., 2012, 8, 3322–3337 CrossRef CAS PubMed.
- R. E. Skyner, J. L. McDonagh, C. R. Groom, T. van Mourik and J. B. O. Mitchell, Phys. Chem. Chem. Phys., 2015, 17, 6174–6191 RSC.
- A. Klamt, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2011, 1, 699–709 CrossRef CAS.
- Y. Ran, Y. He, G. Yang, J. L. H. Johnson and S. H. Yalkowsky, Chemosphere, 2002, 48, 487–509 CrossRef CAS PubMed.
- D. S. Palmer and J. B. O. Mitchell, Mol. Pharm., 2014, 11, 2962–2972 CrossRef CAS.
- S. Boobier, D. R. J. Hose, A. J. Blacker and B. N. Nguyen, Nat. Commun., 2020, 11, 5753 CrossRef CAS.
- K. Yang, K. Swanson, W. Jin, C. Coley, P. Eiden, H. Gao, A. Guzman-Perez, T. Hopper, B. Kelley, M. Mathea, A. Palmer, V. Settels, T. Jaakkola, K. Jensen and R. Barzilay, J. Chem. Inf. Model., 2019, 59, 3370–3388 CrossRef CAS PubMed.
- J. Qiu, J. Albrecht and J. Janey, Org. Process Res. Dev., 2020, 24, 2702–2708 CrossRef CAS.
- M. Lovrić, K. Pavlović, P. Žuvela, A. Spataru, B. Lučić, R. Kern and M. W. Wong, J. Chemom., 2021, 35, e3349 CrossRef.
- H. Lim and Y. Jung, Chem. Sci., 2019, 10, 8306–8315 RSC.
- Q. Cui, S. Lu, B. Ni, X. Zeng, Y. Tan, Y. D. Chen and H. Zhao, Front. Oncol., 2020, 10, 121 CrossRef PubMed.
- Y. Pathak, S. Laghuvarapu, S. Mehta and U. D. Priyakumar, Proc. AAAI Conf. Artif. Intell., 2020, 34, 873–880 Search PubMed.
- M. C. Sorkun, J. M. V. A. Koelman and S. Er, iScience, 2020, 24, 101961 CrossRef PubMed.
- P. G. Francoeur and D. R. Koes, J. Chem. Inf. Model., 2021, 61, 2530–2536 CrossRef CAS PubMed.
- B. Tang, S. T. Kramer, M. Fang, Y. Qiu, Z. Wu and D. Xu, J. Cheminf., 2020, 12, 15 CAS.
- Y. Chung, F. H. Vermeire, H. Wu, P. J. Walker, M. H. Abraham and W. H. Green, J. Chem. Inf. Model., 2022, 62, 433–446 CrossRef CAS.
- F. H. Vermeire, Y. Chung and W. H. Green, J. Am. Chem. Soc., 2022, 144, 10785–10797 CrossRef CAS.
- F. H. Vermeire and W. H. Green, Chem. Eng. J., 2021, 418, 129307 CrossRef CAS.
- C. Bilodeau, W. Jin, H. Xu, J. A. Emerson, S. Mukhopadhyay, T. H. Kalantar, T. Jaakkola, R. Barzilay and K. F. Jensen, React. Chem. Eng., 2022, 7, 297–309 RSC.
- A. D. Vassileiou, M. N. Robertson, B. G. Wareham, M. Soundaranathan, S. Ottoboni, A. J. Florence, T. Hartwig and B. F. Johnston, Digital Discovery, 2023, 2, 356–367 RSC.
- J. Yu, C. Zhang, Y. Cheng, Y.-F. Yang, Y.-B. She, F. Liu, W. Su and A. Su, Digital Discovery, 2023, 2, 409–421 RSC.
- S. Lee, M. Lee, K.-W. Gyak, S. D. Kim, M.-J. Kim and K. Min, ACS Omega, 2022, 7, 12268–12277 CrossRef CAS PubMed.
- P. C. St. John, Y. Guan, Y. Kim, S. Kim and R. S. Paton, Nat. Commun., 2020, 11, 2328 CrossRef.
- A. Avdeef, ADMET DMPK, 2020, 8, 29–77 CrossRef.
- G. Panapitiya, M. Girard, A. Hollas, J. Sepulveda, V. Murugesan, W. Wang and E. Saldanha, ACS Omega, 2022, 7, 15695–15710 CrossRef CAS.
- J. Zhang, B. Tuguldur and D. van der Spoel, J. Chem. Inf. Model., 2015, 55, 1192–1201 CrossRef CAS.
- J. Zhang, H. Zhang, T. Wu, Q. Wang and D. van der Spoel, J. Chem. Theory Comput., 2017, 13, 1034–1043 CrossRef CAS PubMed.
- Y. Takano and K. N. Houk, J. Chem. Theory Comput., 2005, 1, 70–77 CrossRef.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS.
- A. Klamt, V. Jonas, T. Bürger and J. C. W. Lohrenz, J. Phys. Chem. A, 1998, 102, 5074–5085 CrossRef CAS.
- F. Eckert and A. Klamt, AIChE J., 2002, 48, 369–385 CrossRef CAS.
- M. A. Lovette, J. Albrecht, R. S. Ananthula, F. Ricci, R. Sangodkar, M. S. Shah and S. Tomasi, Cryst. Growth Des., 2022, 22, 5239–5263 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- A. Nicholls, D. L. Mobley, J. P. Guthrie, J. D. Chodera, C. I. Bayly, M. D. Cooper and V. S. Pande, J. Med. Chem., 2008, 51, 769–779 CrossRef CAS.
- M. T. Geballe, A. G. Skillman, A. Nicholls, J. P. Guthrie and P. J. Taylor, J. Comput.-Aided Mol. Des., 2010, 24, 259–279 CrossRef CAS PubMed.
- S. S. Kolmar and C. M. Grulke, J. Cheminf., 2021, 13, 92 Search PubMed.
- M. Orbes-Arteainst, J. Cardoso, L. Sørensen, C. Igel, S. Ourselin, M. Modat, M. Nielsen and A. Pai, Knowledge Distillation for Semi-supervised Domain Adaptation, OR 2.0 Context-Aware Operating Theaters and Machine Learning in Clinical Neuroimaging, OR 2.0 MLCN 2019 2019 , Lecture Notes in Computer Science" as book series, Springer, Cham, 2019, vol. 11796, DOI:10.1007/978-3-030-32695-1_8.
- M. Orbes-Arteaga, J. Cardoso, L. Sørensen, C. Igel, S. Ourselin, M. Modat, M. Nielsen and A. Pai, arXiv, 2019, preprint, arXiv:1908.07355.
- Q. Xie, M.-T. Luong, E. Hovy and Q. V. Le, Proc. IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., 2020, 10687–10698, DOI:10.48550/arXiv.1911.04252.
- K. Sohn, D. Berthelot, N. Carlini, Z. Zhang, H. Zhang, C. A. Raffel, E. D. Cubuk, A. Kurakin and C.-L. Li, Adv. Neural Inf. Process. Syst., 2020, 33, 596–608 Search PubMed.
- J. He, J. Gu, J. Shen and M. A. Ranzato, arXiv, 2019, preprint arXiv:1909.13788, DOI:10.48550/arXiv.1909.13788.
- M. Wen, S. M. Blau, X. Xie, S. Dwaraknath and K. A. Persson, Chem. Sci., 2022, 13, 1446–1458 RSC.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek, A. Potapenko, A. Bridgland, C. Meyer, S. A. A. Kohl, A. J. Ballard, A. Cowie, B. Romera-Paredes, S. Nikolov, R. Jain, J. Adler, T. Back, S. Petersen, D. Reiman, E. Clancy, M. Zielinski, M. Steinegger, M. Pacholska, T. Berghammer, S. Bodenstein, D. Silver, O. Vinyals, A. W. Senior, K. Kavukcuoglu, P. Kohli and D. Hassabis, Nature, 2021, 596, 583–589 CrossRef CAS PubMed.
- R. Magar, Y. Wang, C. Lorsung, C. Liang, H. Ramasubramanian, P. Li and A. B. Farimani, Mach. Learn.: Sci. Technol., 2022, 3, 045015 Search PubMed.
- Y. Kim, J. Cho, N. Naser, S. Kumar, K. Jeong, R. L. McCormick, P. St. John and S. Kim, Proc. Combust. Inst., 2023, 39, 4969–4978 CrossRef.
- M. Wen, S. M. Blau, E. W. C. Spotte-Smith, S. Dwaraknath and K. A. Persson, Chem. Sci., 2021, 12, 1858–1868 RSC.
- S. M. Lundberg and S.-I. Lee, in Advances in Neural Information Processing Systems 30, ed. I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan and R. Garnett, Curran Associates, Inc., 2017, pp. 4765–4774 Search PubMed.
- S. Qin, S. Jiang, J. Li, P. Balaprakash, R. Van Lehn and V. Zavala, Digital Discovery, 2023, 2, 138–151 RSC.
- H. Wang, D. Lian, Y. Zhang, L. Qin and X. Lin, arXiv, 2020, preprint, arXiv:2005.05537, DOI:10.48550/arXiv.2005.05537.
- P. Labute, J. Mol. Graphics Modell., 2000, 18, 464–477 CrossRef CAS.
- X. Chen, P. Li, E. Hruska and F. Liu, Phys. Chem. Chem. Phys., 2023, 25, 13417–13428 RSC.
- E. Hruska, A. Gale and F. Liu, J. Chem. Theory Comput., 2022, 18, 1096–1108 CrossRef CAS PubMed.
- H. Wang, Q. Tang and W. Zheng, IEEE Trans. Biomed. Eng., 2012, 59, 653–662 Search PubMed.
- H. Mobahi, M. Farajtabar and P. Bartlett, Adv. Neural Inf. Process. Syst., 2020, 33, 3351–3361 Search PubMed.
- L. Zhang, J. Song, A. Gao, J. Chen, C. Bao and K. Ma, Be your own teacher: Improve the performance of convolutional neural networks via self distillation, Proceedings of the IEEE/CVF International Conference on Computer Vision, 2019 Search PubMed.
- G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334–338 CrossRef CAS.
- T. Welton and C. Reichardt, Solvents and Solvent Effects in Organic Chemistry, John Wiley & Sons, 2011 Search PubMed.
- B. Steenackers, A. Neirinckx, L. De Cooman, I. Hermans and D. De Vos, ChemPhysChem, 2014, 15, 966–973 CrossRef CAS PubMed.
- V. D. Kiselev, D. A. Kornilov, I. A. Sedov and A. I. Konovalov, Int. J. Chem. Kinet., 2017, 49, 61–68 CrossRef CAS.
- S. Tshepelevitsh, K. Hernits and I. Leito, J. Comput.-Aided Mol. Des., 2018, 32, 711–722 CrossRef CAS.
- J. V. Alegre-Requena, S. S. V. Sowndarya, R. Pérez-Soto, T. M. Alturaifi and R. S. Paton, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2023, e1663, DOI:10.1002/wcms.1663.
- T. A. Halgren, J. Comput. Chem., 1996, 17, 490–519 CrossRef CAS.
- S. Riniker and G. A. Landrum, J. Chem. Inf. Model., 2015, 55, 2562–2574 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, 2016 Search PubMed.
- J. Reinisch, M. Diedenhofen, R. Wilcken, A. Udvarhelyi and A. Glöβ, J. Chem. Inf. Model., 2019, 59, 4806–4813 CrossRef CAS.
- G. Van Rossum, Python Programming Language, USENIX annual technical conference, 2007 Search PubMed.
- M. Abadi, P. Barham, J. Chen, Z. Chen, A. Davis, J. Dean, M. Devin, S. Ghemawat, G. Irving and M. Isard, Tensorflow: A System for Large-Scale Machine Learning, 2016 Search PubMed.
- A. Gulli and S. Pal, Deep Learning with Keras, Packt Publishing Ltd, 2017 Search PubMed.
- P. St John, NFP (Neural Fingerprint) 0.3.0, National Renewable Energy Lab (NREL), Golden, CO, United States, 2019, https://github.com/NREL/nfp Search PubMed.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, Proceedings of the 34th International Conference on Machine Learning, 2017, vol. 70, pp. 1263–1272 Search PubMed.
- J. Qi, J. Du, S. M. Siniscalchi, X. Ma and C. H. Lee, IEEE Signal Process. Lett., 2020, 27, 1485–1489 Search PubMed.
- K. Janocha and W. M. Czarnecki, arXiv, 2017, preprint, arXiv:1702.05659, DOI:10.48550/arXiv.1702.05659.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed information regarding the training results, analysis, and application of the graph neural network models trained via semi-supervised distillation. See DOI: https://doi.org/10.1039/d3sc03468b |
| This journal is © The Royal Society of Chemistry 2024 |