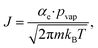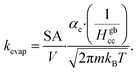Open Access Article
Open Access ArticleIodide oxidation by ozone at the surface of aqueous microdroplets†
Alexander M.
Prophet
ab,
Kritanjan
Polley
ab,
Gary J.
Van Berkel
 c,
David T.
Limmer
abde and
Kevin R.
Wilson
c,
David T.
Limmer
abde and
Kevin R.
Wilson
 *a
*a
aChemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA. E-mail: krwilson@lbl.gov
bDepartment of Chemistry, University of California, Berkeley, CA 94720, USA
cVan Berkel Ventures, LLC, Oak Ridge, TN 37830, USA
dMaterials Science Division, Lawrence Berkeley National Laboratory, Berkeley, California 94720, USA
eKavli Energy NanoScience Institute, Berkeley, California 94720, USA
First published on 4th December 2023
Abstract
The oxidation of iodide by ozone occurs at the sea-surface and within sea spray aerosol, influencing the overall ozone budget in the marine boundary layer and leading to the emission of reactive halogen gases. A detailed account of the surface mechanism has proven elusive, however, due to the difficulty in quantifying multiphase kinetics. To obtain a clearer understanding of this reaction mechanism at the air–water interface, we report pH-dependent oxidation kinetics of I− in single levitated microdroplets as a function of [O3] using a quadrupole electrodynamic trap and an open port sampling interface for mass spectrometry. A kinetic model, constrained by molecular simulations of O3 dynamics at the air–water interface, is used to understand the coupled diffusive, reactive, and evaporative pathways at the microdroplet surface, which exhibit a strong dependence on bulk solution pH. Under acidic conditions, the surface reaction is limited by O3 diffusion in the gas phase, whereas under basic conditions the reaction becomes rate limited on the surface. The pH dependence also suggests the existence of a reactive intermediate IOOO− as has previously been observed in the Br− + O3 reaction. Expressions for steady-state surface concentrations of reactants are derived and utilized to directly compute uptake coefficients for this system, allowing for an exploration of uptake dependence on reactant concentration. In the present experiments, reactive uptake coefficients of O3 scale weakly with bulk solution pH, increasing from 4 × 10−4 to 2 × 10−3 with decreasing solution pH from pH 13 to pH 3.
1. Introduction
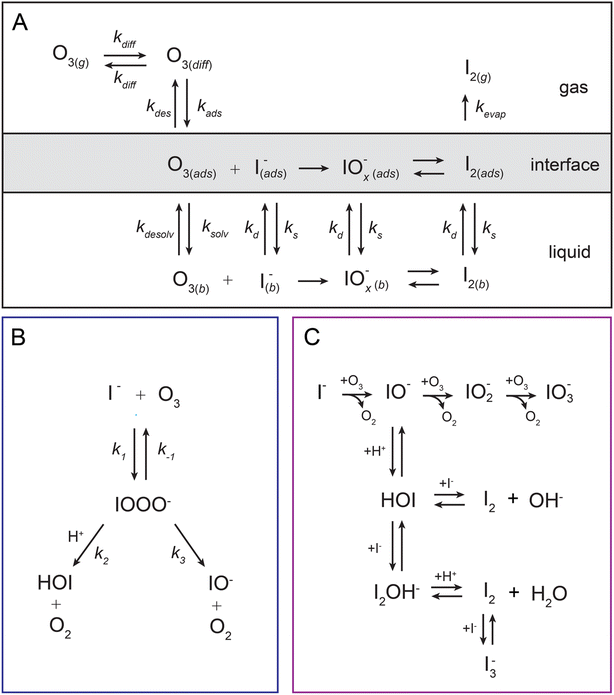
Oxidation reactions of iodine in the environment constitute a set of important pathways for mediating global atmospheric oxidant concentrations and reactive emissions.1,2 Iodine oxides, the primary products from such reactions, play a particularly significant role in catalytic destruction cycles of ozone in the troposphere, affect the overall atmospheric budget of HOx and NOx species, and serve as higher molecular-weight precursors for new particle formation.3–7 The iodide anion, I−, resides in seawater where oxidation at the sea-surface initiates the release of reactive iodine into the atmosphere. Furthermore, the I− + O3 reaction on the sea-surface makes up a major fraction of overall ozone deposition from the marine boundary layer.8 Since discovery of the environmental impact of iodine chemistry through field-based measurements, a host of laboratory-based experiments have aimed to understand the fundamentals underlying this multiphase reaction. Here we employ laboratory measurements on individual microdroplets together with molecular and continuum modeling to clarify the mechanism of iodide oxidation by ozone.The earliest laboratory measurements of the heterogenous I− + O3 reaction found evidence for a bimolecular rate coefficient that approaches the diffusion limit with krxn ∼1 × 109 M−1 s−1.9–11 This rate coefficient is similar in magnitude to what has been observed in both gas phase experiments12,13 and in the bulk aqueous phase using fast-mixing techniques.14 This chemistry has been investigated by a number of researchers studying the oxidation of bulk aqueous solutions,15–18 micron-scale aerosol,19–21 and single iodide-water clusters.22,23 Recent theoretical work has aimed to understand the kinetics and energetics of this reaction using a variety of modeling approaches ranging from numerical simulations to ab initio calculations of aqueous iodide oxidation by ozone.24–27 Although this system has been under investigation for decades, questions remain regarding the detailed reaction mechanism at the air–water interface, under what conditions surface reactions dominate over bulk, and how such processes are coupled to mass transport of reactants, emissions of volatile products, and the overall uptake of ozone from the gas phase. As such, novel experimental and modeling approaches are warranted. Willis & Wilson28 and Wilson et al.29 introduced a model framework for analyzing multiphase ozone oxidation reactions in aqueous microdroplets by describing ozone partitioning at the air–water interface and subsequent solvation of O3 into the droplet interior. This approach, implemented through stochastic reaction-diffusion simulations, allows for dynamic concentrations of reactants to be computed at the surface and bulk regions of the droplet using a set of detailed elementary steps describing adsorption, desorption, and solvation of O3. As we aim to show in this work by combining experiments, kinetic models, and molecular simulations—the dynamics of ozone at the air–water interface are critical for understanding the multiphase chemical mechanism driving surface reactions of I− and O3.
In the current study, we examine oxidation kinetics of iodide by ozone in individual microdroplets by trapping and reacting charged microdroplets in a quadrupole electrodynamic trap (QET). Reaction kinetics are obtained by measuring droplet composition using an open-port sampling interface for mass spectrometry (OPSI-MS) as recently demonstrated by Kaur Kohli et al.30 Iodide decay kinetics are monitored as a function of [O3] and pH. Using the framework of Willis & Wilson,28 a kinetic model is constructed to explain the observed kinetics. Key model constraints that include the desorption and solvation rates of O3 at the air–water interface are obtained directly from analysis of molecular simulations. Kinetic modeling results suggest the I− + O3 reaction occurs almost exclusively at the droplet surface under our experimental conditions where surficial O3 may become substantially depleted by the reaction due to diffusion limitations in the gas phase. Experimental kinetics also show a strong pH dependence, related in part to the different chemical mechanisms relevant for destruction of I− as a function of acidity. However, to fully explain the observed pH dependence, we postulate the existence of a relatively short-lived reaction intermediate IOOO−. This ozonide intermediate has been previously proposed to exist through both experiment and theory, and is analogous to the intermediate observed in Br− oxidation at the air–water interface.31 A steady-state analysis of the surface concentrations is also provided which, in conjunction with recently developed expressions for uptake, are used to compute uptake coefficients of O3 over a range of reactant concentrations.
2. Experimental
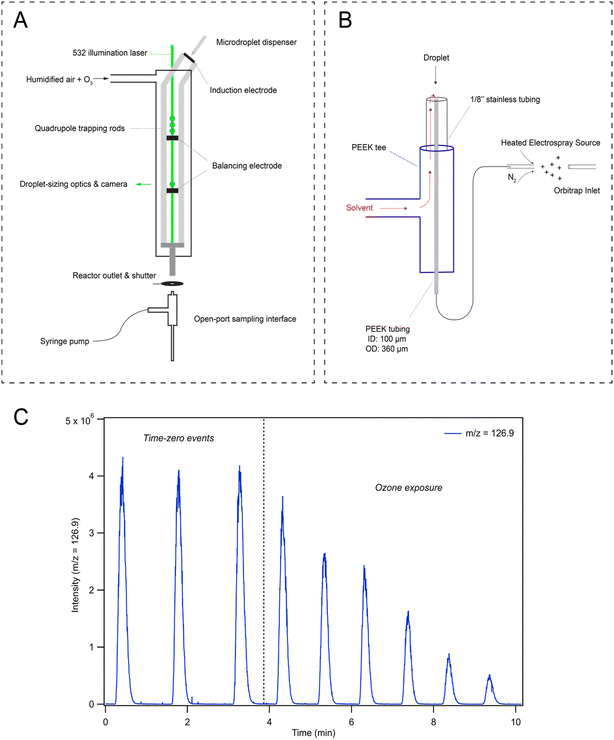
To investigate droplet reaction kinetics, a quadrupole electrodynamic trap (QET) is used to react arrays of individual microdroplets, which are then analyzed with mass spectrometry to monitor droplet composition as recently described by Willis & Wilson28 and elsewhere.32,33 As this technique has been previously described, we provide an overview with a particular focus on the features relevant to the current experiments, including the recently implemented open-port sampling interface (OPSI) for single droplet mass spectrometry.2.1. Quadrupole electrodynamic trap (QET)
The QET is used to charge and trap individual microdroplets under a controlled flow of humidified zero air (600 cm3 min−1 for all experiments) at room temperature (295 K). Microdroplets are generated by a piezo-electric dispenser (Microfab, MJ-ABP-01, 30 μm orifice) oriented co-axially with the QET trapping rods (Fig. 1A). Droplets are charged by applying ±200–500 V DC bias to an induction plate located directly below the dispensing region. An array of 10–100 droplets is trapped in an upper balancing region of the trap during a typical experiment. Single droplets can be individually transferred from the upper region to a lower trapping region. Microdroplets in the lower trapping region are sized by illuminating the droplet with a 532 nm laser focused axially across the QET interior. Mie scattered light from the microdroplet is then collected and analyzed as previously described by Davies34 to obtain a droplet radius. Once sized, single microdroplets are ejected from the QET and into the analysis region. Ozone is generated using a corona discharge ozone generator supplied with a low flow of oxygen (20–100 cm3 min−1), which is then diluted into 1.5–3 L min−1 of nitrogen. 50 cm3 min−1 of the resulting dilution flow is combined with the humidified airflow and directed through the QET. Ozone concentrations in the QET are monitored at the reactor outlet using a UV ozone analyzer (2B Technologies, model 106-M).2.2. Open-port sampling interface (OPSI) mass spectrometry
Droplets ejected into the analysis region are carried by the gas-flow and collide with the inlet of an open-port sampling interface (OPSI) for analysis by mass spectrometry (MS). A schematic of the OPSI is shown in Fig. 1B, outlining the major components of the assembly. A number of studies utilizing a similar design have been recently published for liquid droplet and particle capture,30,35–40 and thus, we briefly review the general construction of the OPSI and provide details on the specific components used. The OPSI design consists of a PEEK 3-way tee connected to a stainless 1/8′′ tube on the top port. A smaller (360 μm OD, 100 μm ID) PEEK tube runs axially inside the outer tube and tee, connecting the top of the assembly to a commercial heated-electrospray source (Thermo-Fischer HESI-II probe) separated by a length of ∼20 cm. An additional length of PEEK tubing delivers solvent (methanol in the current experiments) into the perpendicular tee port, allowing solvent to flow through the outer stainless 1/8′′ tubing and around the inner PEEK tubing. This solvent then flows to the top of the OPSI where it enters the inner tube given sufficient sheath gas flow is used in the HESI to generate a pressure differential between the top of the inner tube and the electrospray needle.By balancing the solvent delivery flow and sheath gas pressure, a stable flow of solvent through the inlet tube and into the ionization region is achieved. For the current experiments, the OPSI is operated in a slightly overfilled mode wherein the solvent delivery rate is marginally larger than the flowrate through the inner tube. A typical flow rate is ∼2.5 mL h−1. Contents of the microdroplets landing in the solvent pool on top of the OPSI are first diluted before traveling through the inner tube and analyzed using electrospray ionization mass spectrometry (MS, Q Exactive Orbitrap, Thermo Fischer Scientific, Inc.) Measuring the iodide signal as a function of analysis time provides a time-series showing single droplet detection events (Fig. 1C), with typical peak widths of ∼30 s. Peak areas from these single droplet events are then used to quantitatively determine concentrations of analytes in microdroplets. A calibration curve for droplet concentration response is provided in ESI Section SI-2,† demonstrating the linear response of the signal with droplet [NaI]. Fig. 1C shows that the observed [I−] decays when droplets are exposed to a gas phase flow of 1 ppm [O3] through the QET. After time-zero (marked with a dashed vertical line in Fig. 1C), the peak area of subsequent droplet events is observed to decay as I− is consumed by O3. Typical mass spectra observed in the experiment are provided in Fig. S2 in SI-2,† where an initial pre-reaction spectrum is provided along with a spectrum obtained from a droplet after undergoing ozone exposure.
During reaction, a shutter is placed between the QET outlet and the OPSI inlet to avoid the solvation and buildup of O3 in the ionization region of the mass spectrometer. During a typical measurement the shutter is opened for ∼0.5 s for each droplet detection event. Without this shutter, gas-phase chemistry (likely ion–molecule reactions) in the ESI source occurs even in the presence of trace O3. Using the shutter configuration outlined in Fig. 1A, gas-phase interference can be ruled out by shutting off the ozone flow midway through the experiment and analyzing droplet composition to ensure the iodide ion signal does not recover. No noticeable recovery of iodide signal is observed with the current approach, indicating all the chemistry observed originates from reactions occurring in the microdroplets and not gas-phase chemistry in the ionization region of the mass spectrometer.
2.3. Droplet composition
All reactions are performed using an initial [NaI] of 250 mM and [NaCl] between 500 mM and 700 mM. NaCl is used to decrease the water activity of solution to aw = 0.95, matching the gas phase relative humidity of 95 ± 1% in the QET. Maintaining the same water activity in both the dispenser solution and the gas phase prevents droplets from significantly changing size when equilibrating inside the QET. Using this approach, the 30 μm orifice dispenser reliably provides droplets of radius 24 ± 1 μm. The use of NaCl also ensures that the droplet size remains relatively stable during the reaction, with droplet radius changing only ∼1 μm during reaction as I− is consumed. pH 3 droplets are dispensed from a bulk aqueous solution containing 300 mM citric acid/sodium citrate, buffered at pH 3, and [NaCl] = 500 mM. Likewise, pH 8 droplets are dispensed from a bulk solution containing 300 mM Tris base (tris(hydroxymethyl)aminomethane), buffered at pH 8, and [NaCl] = 700 mM. The particular organic buffers used were chosen due to the presence of multiple hydroxyl groups in both buffer systems, which decreases the interfacial preference of the organics and therefore minimizes any interference with iodide surface chemistry. However, we anticipate that most buffers in this pH range would not have a strong surface propensity and therefore, our results would not be sensitive to the particular buffer used.Slightly different NaCl concentrations are used to compensate for the differences in the hygroscopicity of the citrate/citric acid and Tris base salt buffers. The [NaCl] is selected for each solution to give the same final droplet size of 24 μm, yielding a [NaI] concentration that is constant across pH given the same QET relative humidity. Unlike the pH 8 and pH 3 droplets, the pH 13 droplets are unbuffered due to the lack of viable buffers for this region and the constraint on the overall salt concentration to maintain stable droplet sizes. However, the consequence of an unbuffered solution in this case is minor as the reaction mechanism under basic conditions does not incorporate production or consumption of H+ or OH−. Fresh solutions were prepared daily using HPLC-grade water (Sigma-Aldrich), NaI (Sigma-Aldrich, ≥99.5%), NaCl (Sigma-Aldrich, ≥99.5%), citric acid (Sigma-Aldrich, ≥99.5%), sodium citrate monobasic (≥99.5%), tris(hydroxymethyl)aminomethane (Sigma-Aldrich, ≥99.8%) and NaOH (Sigma-Aldrich, ≥98%).
3. Experimental results & discussion
3.1. Iodide decay kinetics
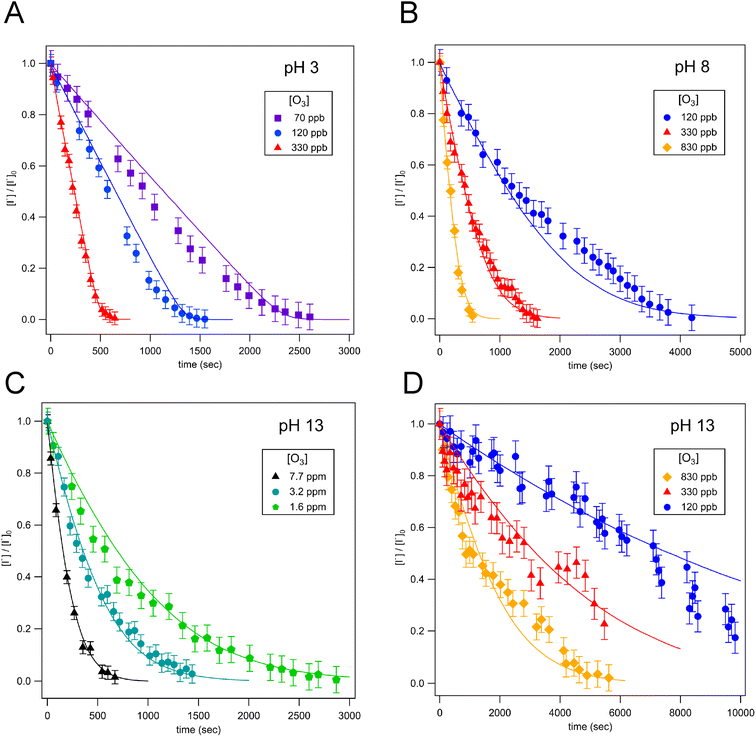
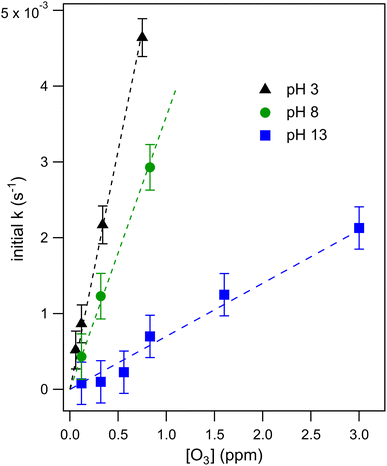
Droplet reaction kinetics for a series of pH and [O3] are shown in Fig. 2. Experimental results (shown as points) are compared with kinetic simulations (lines), described below in Sections 4 and 5. Error bars for individual data points are estimated using the standard deviation of droplet peak areas from a set of unreacted droplet events prior to each experiment (e.g., droplet events in the “time-zero” section in Fig. 1C). Fig. 2A and B show iodide decay in microdroplets dispensed from solutions buffered at pH 3 and pH 8, respectively. A number of qualitative features are observed as a function of pH and [O3]. For each droplet pH, the iodide consumption rate is first order in [O3]. This is summarized in Fig. 3, where initial rates of decay are shown to increase linearly with increasing ozone concentration. A strong dependence on dispensed-solution pH is also observed. The overall rate of the reaction increases significantly with decreasing pH. From the most basic to acidic conditions, the observed initial decay rate increases by almost an order of magnitude. As considered further in the model discussion Section 6.2 and as noted previously from product emission studies,15–17 a major contribution to the apparent reaction acceleration with decreasing pH originates from the reaction of I− with its primary oxidation product HOI to produce I2. However, an additional pH dependence of the reaction is proposed below to account for the complete set of pH dependent observations shown in Fig. 2 and 3.Beyond a difference in the overall rate, changes in the shape of the decay kinetics in Fig. 2 are also observed as a function of pH and even [O3] under strongly basic conditions. The decay of iodide in acidic solution appears mostly linear in time, with a small but significant tail as the iodide concentration approaches zero. Conversely, the decay of iodide under strongly basic conditions appears exponential for [O3] > 1 ppm but becomes increasingly bi-exponential or linear in time as [O3] decreases below 1 ppm. The origin of these functional forms for the decay kinetics appears to be driven by the complex interplay of reaction and surface adsorption of iodide, reaction intermediates, and products and will be examined in more detail below in Section 6.
3.2. Reaction product yields and kinetics
Utilizing droplet composition analysis with the OPSI-MS, products formed and remaining in the condensed phase of the droplet are detected in positive- or negative-mode electrospray ionization. For experiments done using pH 3 and 8, however, no condensed-phase products are observed as all I− in solution is quickly oxidized to I2, which evaporates into the continuous gas flow through the QET. However, under strongly basic conditions (notably, above the pKa of HOI of 10.8) IO3− is observed in the mass spectrometer at m/z = 174 as shown in SI-2 and Fig. S2.† Peak areas from time-traces of the ion signal at m/z 174 are monitored throughout the reaction under basic conditions and provided in Fig. S3† for three example ozone concentrations. As discussed further in SI-2,† the iodate yield appears to decrease with decreasing [O3]. While the origin of this shift in product yield is unknown, this may suggest a change in surface mechanism with decreasing availability of O3.4. Model description
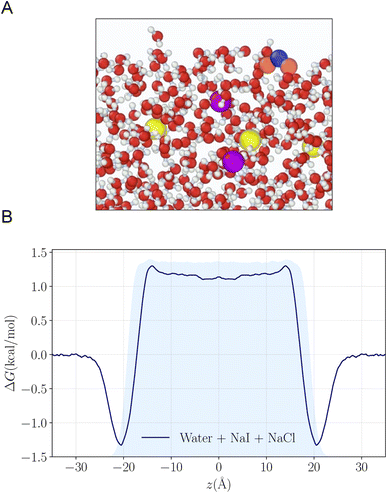
To understand the reactivity observed in the droplet experiments, a kinetic model is constructed. This model describes the partitioning and reaction of gas- and liquid-phase species at the droplet surface and within the bulk interior. The model framework is based on work from Willis & Wilson28 where a kinetic description of O3 adsorption and desorption at the microdroplet surface and subsequent solvation into the bulk liquid is presented and benchmarked using a set of ozone oxidation reactions. Further analysis of this approach in Wilson et al.29 provides closed-form expressions for predicting uptake and reaction of trace gases into microdroplets. In the current work, molecular dynamics (MD) simulations are used to study the solvation of ozone at the air–water interface and the kinetics of both the solvation and desorption processes. A water slab with 768 water molecules and sodium halide salts, modeled with a classical polarizable force field,41 was used to represent an aqueous droplet at 300 K. A snapshot from the simulation of O3 adsorption is shown in Fig. 4A. The free energy profile for transferring an ozone molecule through the air–water interface, with sodium halide salts (0.28 M NaI + 0.84 M NaCl) in the solution, is shown in Fig. 4B where the shaded blue region is the (scaled and shifted) water density profile. Results and details of the MD simulations and the procedures for obtaining the solvation and desorption rates are included in the ESI Section SI-3.† In the following modeling sections, we briefly outline the kinetic model and detail the specific novel components relevant for the application of this framework to the analysis of the I− + O3 reaction.The model developed in this section is implemented in Kinetiscope©,42 a software package previously used to simulate kinetics in a variety of systems such as organic aerosol, aqueous microdroplets, and emulsions.43–45 Droplet kinetics are simulated by conceptualizing the droplet bulk interior and surface as two separate compartments that have a rectangular prism geometry. Both compartments have the same 1 × 1 nm2 cross-sectional area but have different compartment lengths. The length of the bulk compartment is chosen to be r/3, in order to preserve the correct surface-to-volume ratio of a sphere with radius, r. The surface compartment length (δ) is 1 nm and represents the thickness of the air–water interface. This surface depth corresponds to the approximate length scale over which the water density changes across the air–water interface as observed by the MD results in Fig. 4B and previous simulations.46 Molecules move between the surface and bulk compartments in Kinetiscope by Fickian diffusion, which is governed by the relative concentrations in each compartment and the compartment lengths. Solutes that diffuse into the surface compartment from the bulk can then adsorb to the air–water interface through a kinetic description of solvation/desolvation to establish surface concentrations. Similarly, gas-phase species partition to the surface through a set of adsorption–desorption steps described in the following sections and summarized in the multiphase framework in Fig. 5A.
4.1. Ozone partitioning scheme
The ozone partitioning scheme is conceptualized as two parallel processes: one describing the kinetic adsorption process at the gas–liquid interface, and one describing diffusion of ozone through the gas phase to the droplet surface. As the kinetic partitioning description draws from the work of Willis & Wilson,28 we revisit the mechanics of this description before introducing the description of ozone diffusion.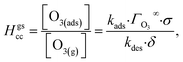 | (1) |
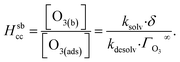 | (2) |
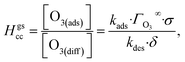 | (3) |
Simulating the adsorption and solvation steps for O3 within the kinetic model is done using a modified Langmuir adsorption framework49 where O3 adsorbs (from either the gas or liquid phase) to a surface site (steps (A1) and (A2), respectively):
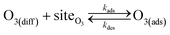 | (A1) |
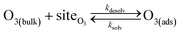 | (A2) |
Surface sites for ozone (not pictured in Fig. 5 for brevity), are conceptualized as available regions of the interface where ozone can adsorb. In this case, we assume the area of one surface site is equal to the molecular area of O3 (18.5 Å2) as computed by Vieceli et al.50 The maximum number of surface sites is ΓO3∞ and can be expressed in volumetric units using surface thickness ΓO3∞/δ. Throughout the simulation, the total number of surface sites is conserved and expressed as,
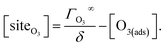 | (4) |
Eqn (1) includes a dependence on σ, the sticking coefficient (or the thermal accommodation coefficient) for a single O3 molecule onto a site. The sticking coefficient σ is distinct in the present model from the accommodation coefficient α, defined51 as the probability of solvation relative to desorption: α = ksolv/(kdes + ksolv). From the simulations presented in SI-3,†α = 0.0097. While Willis & Wilson28 could identify a lower bound for σ as >10−4, the conditions they analyzed were insensitive to values of σ above this value and the treatment of O3 gas-phase diffusion was not addressed. In the current work, a greater sensitivity is observed in the kinetic model, and a value σ = 0.93 is obtained from molecular simulations, in general agreement with measurements from direct scatting experiments.52–54 A value of σ ∼1 means that every O3 molecule that collides with the interface thermalizes before undergoing desorption, solvation, or reaction.
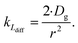 | (5) |
As the present model avoids explicitly simulating concentration gradients in preference for discretized spatial compartments, an additional characteristic length (the adsorption length Lads) is necessary for describing the local O3 concentrations near the interface. Originally introduced in the context of surfactant adsorption,57Lads denotes the length over which O3 is depleted in the gas-phase directly from the adsorption and desorption kinetics introduced above as step A1. Conceptually, as shown in Fig. S8,† a shell of width Lads surrounding the droplet contains the same number of O3 molecules as the droplet interface when the system comes to equilibrium. When the droplet surface reaches equilibrium, the number of O3 molecules on the interface can be calculated as nO3 = [O3(g)]·Hgscc·Vsurf where Vsurf is the simulated surface volume (1 × 1 × δ nm3 in current simulations). The rapid kinetic process at the surface draws nO3 molecules contained in a gas-adsorption volume Vads extending radially from the droplet surface. Maintaining the rectangular prism simulation geometry introduced above then necessitates Vads have length Hgscc·δ nm. This defines the simulation adsorption length Lads = Hgscc·δ nm (see SI-4 and Fig. S8† for summary illustration of characteristic diffusion and adsorption lengths). Since the volume defined by Lads is the relevant gas volume for O3 adsorption to the interface, the relevant rate for diffusion into the adsorption volume is found by multiplying eqn (5) by Ldiff/Lads
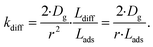 | (6) |
This definition of kdiff is used in the simulation to supply O3(diff) directly to the interface, providing an upper bound on diffusional transport of O3(g) to the surface. Diffusion is simulated in the kinetic model by including the following step directly in the surface compartment:
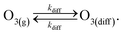 | (A3) |
4.2. Aqueous solute surface partitioning scheme
Surface-adsorption of solutes to the air–water interface is treated using a similar Langmuir description where species in solution, after diffusing into the surface compartment, may adsorb to the surface with a rate proportional to the bulk ion concentration and number of available surface sites. Equilibrium surface-adsorbed [I−] is expressed by a Langmuir isotherm: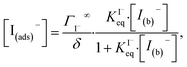 | (7) |
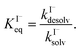 | (8) |
Previous investigations of I− at the air–water interface have repeatedly found a strong surface preference for iodide relative to other aqueous ions. Such determinations have been made through a variety of techniques including kinetic measurements,61,62 photoemission spectroscopy,19,63,64 and second-harmonic generation spectroscopy.65,66 Measurements of surface-affinity are quantified for iodide through a Gibbs free energy of adsorption to the air–water interface, 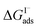 which can be directly related to a Langmuir equilibrium coefficient using a commonly employed Langmuir adsorption framework:65
which can be directly related to a Langmuir equilibrium coefficient using a commonly employed Langmuir adsorption framework:65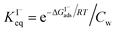 where Cw is the solvent concentration (assuming water with Cw ∼55 M). Values for
where Cw is the solvent concentration (assuming water with Cw ∼55 M). Values for 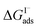 have also been computed from ion density profiles obtained by MD simulations of sodium iodide at the air–water interface.58,67 Reports of
have also been computed from ion density profiles obtained by MD simulations of sodium iodide at the air–water interface.58,67 Reports of 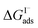 from experiment and simulations range from −0.8 kcal mol−1 to −6.2 kcal mol−1, demonstrating a strong dependence on solution composition and model framework employed for analysis.61–63,65,66,68 This range of
from experiment and simulations range from −0.8 kcal mol−1 to −6.2 kcal mol−1, demonstrating a strong dependence on solution composition and model framework employed for analysis.61–63,65,66,68 This range of 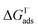 corresponds to a large uncertainty in
corresponds to a large uncertainty in 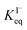 , ranging from 0.1 M−1 to 650 M−1. To determine the appropriate
, ranging from 0.1 M−1 to 650 M−1. To determine the appropriate 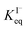 for the present model, we first performed MD simulations of the initial experimental solution composition and observe the initial surface concentration under these conditions to be [I(ads)−] = 780 mM (see Fig. S5 in SI-3†). Assuming a maximum surface concentration of ΓI−∞/δ = 10.5 M, the simulated [I(ads)−] constrains
for the present model, we first performed MD simulations of the initial experimental solution composition and observe the initial surface concentration under these conditions to be [I(ads)−] = 780 mM (see Fig. S5 in SI-3†). Assuming a maximum surface concentration of ΓI−∞/δ = 10.5 M, the simulated [I(ads)−] constrains 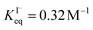 , a value on the lower side of the reported range in the literature.
, a value on the lower side of the reported range in the literature.
Although the surface concentrations in the kinetic model are constrained by the MD simulation results, a number of uncertainties persist due to the complex nature of the air–water interface. The surface selectivity of the halide ions depends strongly on the choice of water model and force field parameters in MD simulations.64,69–71 The prediction of our current model and force field is in agreement with recent observation from experiments and MD simulations.60,69,72 One clear deficiency of the current approach is the coarse-grain perspective of the surface, where a single kinetic volume is used to define the entire interface. In reality, small angstrom-scale features in the density profiles of the solutes and solvent at the interface are important for understanding the structure of the interface. Such features can be observed in the free energy and density profiles for aqueous iodide and ozone included in ESI Fig. S4 and S5 in Section SI-3.† Fine structural details of this aqueous system have also been observed using liquid microjet techniques combined with X-ray photoemission spectroscopy.71 From the perspective of reactivity, however, the interface may in fact be sufficiently represented without such fine details in some instances since the chemical loss of I− at the interface will be determined most strongly by the overlap region of the density profiles of I− and O3 at the interface, where concentrations will remain approximately constant (in the absence of diffusive limitations).
The surface affinities of the reaction products are known with less accuracy than iodide. However, some of the oxidation products in solution have been observed to be depleted from the interface and are suspected to be ∼10–100× less surface active than I−.73,74 Nevertheless, for the sake of simplicity we use the same 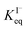 for all solutes in the simulation. Furthermore, we also assign the volatile, neutral products generated in solution (I2 and HOI) to possess the same partitioning behavior with
for all solutes in the simulation. Furthermore, we also assign the volatile, neutral products generated in solution (I2 and HOI) to possess the same partitioning behavior with 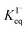 . Forward and reverse rates, kdesolv and ksolv, describing the kinetic components of
. Forward and reverse rates, kdesolv and ksolv, describing the kinetic components of 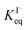 are included for each simulated species in ESI Table S1† and the sensitivity of these rates analyzed in Section SI-5.†
are included for each simulated species in ESI Table S1† and the sensitivity of these rates analyzed in Section SI-5.†
4.3. Product evaporation description
Volatile products generated by oxidation of iodide (e.g., I2 and HOI) evaporate from the simulated droplet surface through an irreversible step. As with ions in solution, the first step for a volatile species to partition out of the condensed phase is an adsorption step to the air–water interface. Once adsorbed, the species may evaporate from the surface described by a first-order rate. First-order evaporative rate coefficients for each volatile species are derived using the Hertz–Knudsen equation, where the flux of gas from the surface is calculated as,75where αe is the evaporation coefficient (assumed to be 1 for simplicity), m is the molecular weight of the volatile species, kB is the Boltzmann constant and T is the absolute temperature. The saturation vapor pressure of the species, pvap, is related to its Henry law coefficient and adsorbed surface concentration pvap = [I2(ads)]/Hgbcc. The surface flux is converted to a rate coefficient by scaling J with the surface area-to volume ratio (SA/V) to account for the overall surface accessibility from the bulk. Individual rate coefficients for volatile species are therefore calculated as,76
kevap for HOI and I2, computed from their associated Henry’s law constants77,78 are used to define evaporative rates for the following steps (E1) & (E2) (and simulation steps S21 and S22 in Table S1†).
| HOI(ads) → HOI(gas) + site | (E1) |
| I2(ads) → I2(gas) + site | (E2) |
4.4. Reaction steps
The chemical mechanism used in the present model relies on previous literature describing the I− + O3 reaction in both the gas and liquid phase. The complete set of reactive steps and associated rate coefficients are shown in Table S1.† A scheme showing each reaction step is shown in Fig. 5B and C. Below we first review the primary oxidation step of iodide outlined in Fig. 5B, followed by the subsequent reactions involving the primary oxidation products found in Fig. 5C.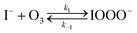 | (R1) |
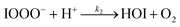 | (R2) |
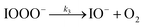 | (R3) |
The initiation reaction step (R1) involves a fast equilibrium for adduct formation between I− and O3. Once formed, the IOOO− adduct subsequently reacts with a proton or water to form HOI. The proton-assisted pathway is provided as step (R2) and the water-assisted pathway is defined as a unimolecular decay step (R3), assuming the droplet water content remains constant. While rate coefficients for these individual steps are unknown, we propose that previous measurements of the consumption rate of ozone in bulk solutions14,18 provide the rate of adduct formation, i.e., k1 = 1.2 × 109 M−1 s−1. For the sake of simplicity, and in the absence of evidence to the contrary, we assume steps (R1)–(R3) have the same rate at the surface and within the bulk. Given the measured gas- and liquid-phase rate coefficients for this reaction are nearly identical,12,14 we believe this is a reasonable assumption. We anticipate the validity of this assumption will be tested by measuring the iodide concentration dependence of the oxidation kinetics, and ideally through future experiments targeting the chemical lifetime of the ozonide intermediate in the bulk and at the surface. We also assume that the proton-assisted decay rate (R2) is diffusion limited, with a rate coefficient of k2 = 1011 M−1 s−1, an estimated upper bound for the ion recombination rate in solution as measured previously in the proton-hydroxide recombination reaction.79,80 While this assumption likely overestimates the rate of (R2), we similarly suggest that such details could be gathered from future experiments studying the ozonide intermediate directly, particularly in light of HOI and IO− formation kinetics in solution.
Using the aforementioned values of k1 and k2, coefficients k−1 and k3 are treated as adjustable parameters in the model. A single set of values for k−1 (3.6 × 104 s−1) and k3 (220 s−1) produce simulation results that agree with the observed droplet kinetics shown in Fig. 2. As presented by Liu et al.14 and shown below in eqn (9), the four rate coefficients k1, k−1, k2, and k3 combined with a steady-state approximation for reaction intermediate IOOO− yields an effective bimolecular rate coefficient (kobs) for the overall I− + O3 reaction,
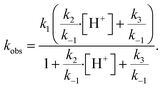 | (9) |
| IO− + O3 → IO2− + O2 | (R4) |
| IO2− + O3 → IO3− + O2 | (R5) |
Reactions (R4) and (R5) are included directly in the model at both the surface region and the bulk. Here we assume that (R4) and (R5) are irreversible given the relatively slow reverse rate of reaction.12 As suggested in previous literature, rate coefficients for (R4) and (R5) depend on the phase, where the rate in the gas-phase appears collision limited but the analogous liquid phase rate is ∼1000× slower. In the current model, we assume reactions (R4) and (R5) at the droplet surface resemble the gas-phase reactivity more than the liquid phase, and therefore use an approximate diffusion-limited reaction rate coefficient k ∼1010 M−1 s−1 for steps (R4) and (R5) at the surface. The slower liquid-phase reaction rates k ∼106 M−1 s−1 are used in the bulk phase and are based on past measurements in aqueous solution.81
For solutions below pH = 10.8, the primary oxidation product is HOI. Here, the proton-assisted decay of IOOO− to HOI contributes to the overall loss of the intermediate and quickly becomes the dominate pathway below pH 10. To fully capture the reaction mechanism under neutral to acidic conditions, it is important to account for HOI/IO− speciation and associated reactions with I−, OH−, and I2. The fate of the HOI/IO− conjugate pair and their reactivities with iodine in solution have long been studied using spectroscopic techniques in an attempt to unravel this complex mechanism relevant to oxidation processes in disinfection, nuclear chemistry, and halogen chemistry in biological systems.83–88 Here, we include the steps in the model that are most relevant for the fate of I− and the pH dependent reactivity in solution. This is summarized in the mechanistic overview in Fig. 5C. The most elementary of these reactions is simply the conjugate acid–base conversion
| H+ + IO− ⇄ HOI. | (R6) |
As introduced above for reaction (R2), we assume that recombination reactions occur at the proton neutralization rate79,80 in solution kneutral = 1011 M−1 s−1. This forward rate of (R6) then constrains the reverse dissociation rate of HOI using the pKa = 10.8. Solution pH is then simulated in the model using the fixed dissociation rate coefficient for HOI along with the pseudo-first order reaction rate (i.e., 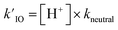 ).
).
Having defined solution pH through the speciation of HOI, subsequent chemistry with I− is addressed. We note that while the O3 + HOI reaction has been previously observed,81 this reaction is not included in the model since this reaction rate is 105 times slower than the O3 + I− reaction and is significantly slower than other sinks for HOI. In the presence of I−, HOI is quickly converted to I2 under acidic and neutral pH.86 Production of I2 has been reported to occur through two distinct mechanisms that dominate at different pH values, both included in the model as (R7)–(R9). The first pathway involves the formation of reactive intermediate I2OH−(R7) which dissociates to I2 through the proton-assisted reaction in (R8). The second formation pathways shown in (R9) involves the direct elimination of OH− from HOI by I−.89,90
| HOI + I− ⇄ I2OH− | (R7) |
| I2OH− + H+ ⇄ I2 + H2O | (R8) |
| HOI + I− ⇄ I2 + OH− | (R9) |
The forward and reverse rate coefficients for (R7)–(R9) with literature ref. 82, 89 and 90 are included in Table S1.† While step (R7) is independent of solution pH, reactions (R8) and (R9) both depend directly on pH explicitly through [H+] and [OH−]. As in the association between IO− and H+, pseudo-first order rate coefficients are calculated using [H+] and [OH−], as to avoid the computational cost of simulating these species directly. Lastly, once I2 is produced in solution, the triiodide anion91 is formed by,
| I2 + I− ⇄ I3−. | (R10) |
Simulation results, however, predict I3− concentrations under all pH conditions are negligible due to the rapid evaporative loss of I2, which is a dominant sink for iodine in small volumes (i.e., droplets).
The complete set of reactions ((R1)–(R10)) as shown in Fig. 5B and C, is included in both the surface and bulk compartments of the kinetic model. As mentioned above, since surface partitioning behaviors of most species involved are unknown, we generally assume the surface partitioning of all solutes match the iodide anion, likely an overestimation of surface activity for most species due to the high surface propensity of I−. Model sensitivity to absolute kdesolv and ksolv values is revisited in ESI Section SI-5† for the iodide ion only. We note that the sensitivity of these rates for other solutes is negligible due to the large proportion of bulk chemistry that drives the observed pH sensitivity. All rate coefficients for (R1)–(R10) are also assumed to be equal between the surface and bulk compartments, except for the difference in IO− and IO2− reactivity mentioned above and noted in Table S1.†
5. Model results
The simulation results are compared to experiments in Fig. 2–4 (Section 2). Overall, the simulations capture the observed trends in the iodide-decay kinetics and how they depend upon [O3] and pH. As discussed further below, the initial rate scaling with [O3] can be understood from transport limitations and surface concentrations, while the pH dependence arises from a surface-rate pH dependence (i.e., (R1)–(R3)) and the bulk reaction mechanism (i.e., (R6)–(R9)). Although the simulations generally recreate the shape of iodide decay kinetics, the observed experimental decay shapes are not fully replicated. Under basic conditions where [O3] < 1 ppm, simulations predict kinetics that appear more exponential in time, with experiments trending closer to a bi-exponential or linear time-dependence, albeit with larger experimental uncertainty. Although we cannot fully rationalize the origin of these deviations, the differences are relatively small, and the simulated trends generally agree with experiment. Some factors contributing to the shape of time-dependent kinetics will be examined in Section 6, with some potential reasons identified for the disagreement between model and experiment.6. Analysis and discussion
Here we analyze the major features observed in the experimental and simulated kinetics to provide greater insight into the underlying chemical and physical processes governing this heterogenous reaction. First, in Section 6.1, the pH dependence of the reaction is examined in more detail, with attention given to identifying which chemical steps appear to determine the overall reaction rate and products observed. Section 6.2 examines how adsorbed ozone concentrations evolve during the reaction, where an approximate kinetic derivation is used to predict steady-state surface concentrations of ozone during reaction. Results from this derivation are then used in Section 6.3 to understand the behavior of the overall uptake coefficient for O3 across a range of reactant concentrations. Results from experiment, simulation, and closed form expressions are compared with past measurements of this system to provide broader context to the current findings.6.1. pH Dependent reaction kinetics and product distributions
As shown in Fig. 4, the experimental and simulated kinetics exhibit a strong pH dependence. In the model, this pH dependence has two distinct origins; the first is the pH rate dependence in the primary oxidation step ((R1)–(R3)) and the second is the network of secondary iodide loss channels involving H+ and OH− ((R6)–(R9)). Model results shown in Section SI-6† demonstrate that the secondary chemistry of iodide alone cannot achieve the model/experiment agreement shown in Fig. 2–4. As summarized in Fig. S10,† this suggests an additional mechanism is responsible for the kinetics observed when varying pH. We propose this additional pH dependence results from the proton-assisted decay of an ozonide intermediate IOOO− as was first proposed (and later observed) for the analogous Br− system.14,31 To the best of our knowledge, no direct evidence of the IOOO− intermediate has been reported, likely due to a short chemical lifetime. However, according to the parameterization of steps (R1)–(R3) introduced above, such an intermediate may be relatively long lived under strongly basic solutions (with lifetimes on the order of 10–100 μs). On the other hand, as the surface lifetime of IOOO− and any degree of surface-stabilization is unknown, the overall lifetime may be significantly smaller if bulk solvation occurs on a timescale much faster than chemical decomposition. We also acknowledge that the bulk mechanism for the primary oxidation step may deviate significantly from the surface mechanism, and the kinetics of any intermediates involved may result in a different overall pH dependence. Recent theoretical work investigating the energetics of possible ozonide intermediates for aqueous iodide oxidation suggests a series of possible conformations of the intermediate.26 The evolution of such conformations and the kinetics involved may again depend greatly on the presence of the interface and local pH.Across the range of pH studied, a clear difference is observed in the overall product distribution predicted through the kinetic model. While the soluble, terminal product IO3− can be observed directly (Fig. S3†), volatile products such as I2 and HOI go undetected in the experiments. ESI Section SI-7† provides the modeled product distribution across the pH range analyzed for an example ozone concentration of [O3(g)] = 820 ppb. As expected, for simulations below the pKa of HOI, the dominant product is I2, with a small fraction of HOI emitted. For strongly basic solution, IO3− dominates the product distribution. As observed in the iodate formation kinetics shown in SI-2,† the overall fraction of IO3− appears to decrease with decreasing [O3] below 1 ppm. This trend is not observed in the simulations (Fig. S3†), and the origin of the changing mechanism is currently unknown.
6.2. Surface-adsorbed ozone concentrations
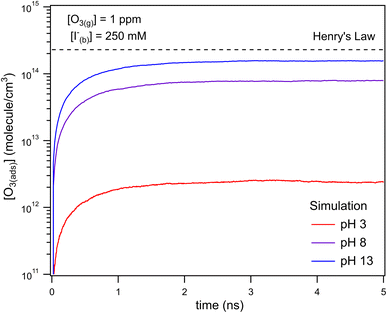
The kinetic simulations indicate that surface-adsorbed ozone concentrations fall below the concentration predicted by Henry's law for a range of solution pH. Fig. 7 shows surface-adsorbed [O3(ads)] for three solution pH values at early times in the simulation. For the simulation at pH 13, [O3(ads)] rapidly approaches its Henry's law concentration at the surface, achieving a steady-state concentration that is ∼50% of the expected Henry's law concentration. In the pH 8 simulation, however, [O3(ads)] finds its steady-state value that is ∼8× smaller. In the acidic extreme at pH 3, [O3(ads)] is ∼100× depleted from the Henry's law concentration, indicating that the primary oxidation step for I− + O3 is substantially limited by O3 transport to the air–water interface. This transport limitation results from the diffusive rate to the surface being slower than the reactive loss of O3(ads), ultimately depleting both O3(ads) and O3(diff) in the model results. We expect more generally that surface reactions will be limited by ozone diffusion for cases when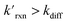 where the pseudo-first order reaction rate is
where the pseudo-first order reaction rate is 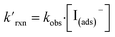 . This concept can be concisely expressed using the second Damköhler number, defined in this system as the ratio of the surface reaction rate to the characteristic gas-phase diffusion rate:
. This concept can be concisely expressed using the second Damköhler number, defined in this system as the ratio of the surface reaction rate to the characteristic gas-phase diffusion rate: 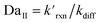 . Using this notation, the oxidation reaction under conditions with DaII < 1 will be limited by the surface reaction itself, whereas DaII > 1 denotes the rate will be limited by gas-phase diffusion and will display surface depletion of O3. As expressed in eqn (6), kdiff depends on both the droplet radius and the equilibrium partitioning of O3 which is captured in the model by use of Lads. While we reserve a more thorough investigation of the droplet-size and molecular specificity of kdiff to future work, the MD results in SI-3 Section B† show that the characteristic rate of surface equilibration (∼kdes) is faster than kdiff for the particular droplet radius studied—indicating that transport limits of O3 do not result from kinetic limitations. However, this is not generally the case for smaller droplet sizes, where kinetic limitations at the interface may become dominant.
. Using this notation, the oxidation reaction under conditions with DaII < 1 will be limited by the surface reaction itself, whereas DaII > 1 denotes the rate will be limited by gas-phase diffusion and will display surface depletion of O3. As expressed in eqn (6), kdiff depends on both the droplet radius and the equilibrium partitioning of O3 which is captured in the model by use of Lads. While we reserve a more thorough investigation of the droplet-size and molecular specificity of kdiff to future work, the MD results in SI-3 Section B† show that the characteristic rate of surface equilibration (∼kdes) is faster than kdiff for the particular droplet radius studied—indicating that transport limits of O3 do not result from kinetic limitations. However, this is not generally the case for smaller droplet sizes, where kinetic limitations at the interface may become dominant.
Fig. 8 shows that the degree of ozone depletion at the interface is also dependent on the bulk [I(b)−]. Simulations in this case are initialized for each given [I(b)−] by first computing the corresponding equilibrium [I(ads)−] as dictated by the Langmuir isotherm (eqn (7)). The simulation is then run until a steady state [O3(ads)] is observed. The inflection point noted as a vertical line in Fig. 8 indicates the point at which 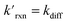 , when the reactive loss rate of O3 on the surface equals the rate of O3 diffusion into the adsorption length. For ease of example, the pH dependent mechanism and adduct formation is not considered in Fig. 8 and a simple second order rate coefficient of krxn = 1.2 × 109 M−1 s−1 is used for the I− + O3 reaction. As all experiments performed in the present work utilize [I−] = 250 mM, Fig. 8 suggests for kobs ∼109 M−1 s−1, [O3(ads)] is greatly depleted from its Henry's Law concentration. Since the reaction under this condition is limited by O3 transport, the kinetics scale as first-order in [O3] as demonstrated through the high linearity of initial rates vs. [O3] reported in Fig. 3.
, when the reactive loss rate of O3 on the surface equals the rate of O3 diffusion into the adsorption length. For ease of example, the pH dependent mechanism and adduct formation is not considered in Fig. 8 and a simple second order rate coefficient of krxn = 1.2 × 109 M−1 s−1 is used for the I− + O3 reaction. As all experiments performed in the present work utilize [I−] = 250 mM, Fig. 8 suggests for kobs ∼109 M−1 s−1, [O3(ads)] is greatly depleted from its Henry's Law concentration. Since the reaction under this condition is limited by O3 transport, the kinetics scale as first-order in [O3] as demonstrated through the high linearity of initial rates vs. [O3] reported in Fig. 3.
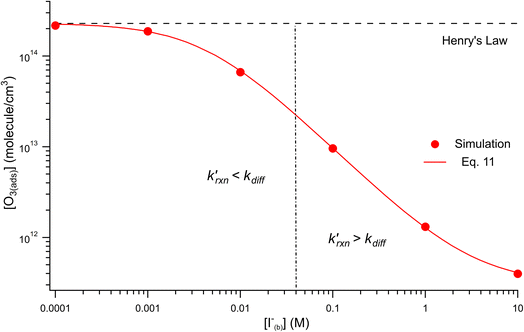 | ||
Fig. 8 Steady state [O3(ads)] dependence on [I(b)−] from μM to M concentrations for [O3(g)] = 1 ppm. Points denote simulation results from early steady-state analysis of ozone. The red curve shows steady-state expression from eqn (11). Results are compared to the Henry's Law concentration of [O3(ads)]. The dashed vertical line indicates the [I(b)−] where the chemical loss rate of O3 at the surface 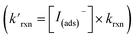 is equal to the simulated diffusion rate of O3 (i.e., kdiff). is equal to the simulated diffusion rate of O3 (i.e., kdiff). | ||
The surface depletion of O3 can also be computed analytically using a simple steady-state analysis of [O3(ads)] and [O(diff)] at early reaction times. As shown in Fig. 7, [O3(ads)] approaches steady state after approximately 1 ns. Assuming that [I(ads)−] is equal to the Langmuir equilibrium concentration, the steady-state expressions for [O3(ads)] and [O(diff)] are
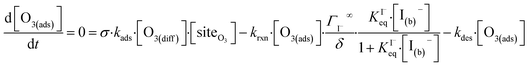 | (10a) |
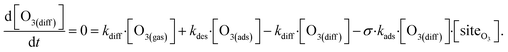 | (10b) |
Rearranging eqn (10a) and (10b) while substituting for [O3(diff)] produces an expression for [O3(ads)] as a function of [I(b)−]:
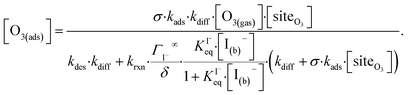 | (11) |
Eqn (11) accounts for the surface depletion of O3 by the surface reaction only and does not include solvation dynamics of O3, which quickly become insignificant when surface O3 becomes depleted by reaction. Furthermore, we highlight that eqn (11) assumes adsorbed I− equilibrates on a timescale much faster than the O3 depletion dynamics such that [I(ads)−] is equal to the Langmuir equilibrium value calculated from eqn (7). Relaxing this assumption leads to a case where both surface reactants may be depleted. Results from eqn (11) as a function of bulk iodide concentration [I(b)−] are compared with simulation results in Fig. 8 for [O3(g)] = 1 ppm. For simplicity, the results from eqn (11) in Fig. 8 utilize a simple bimolecular I− + O3 reaction rate of krxn = 1.2 × 109 M−1 s−1. Output from eqn (11) and the simulation predict the same surface behavior for adsorbed O3, where reaction depletion becomes significant for bulk [I(b)−] > 1 mM. Only for [I(b)−] < 1 mM does adsorbed ozone remain at its Henry's Law value. At these lower iodide concentrations, the multiphase kinetics are driven by bulk-reaction dynamics and should be accurately predicted using the closed formed analytical expressions derived in Wilson et al.29
6.3. Uptake coefficients
In this section we compute uptake coefficients from the experimental kinetics shown in Fig. 3 and introduce an expression for computing uptake while accounting for surface depletion of O3. This approach builds on the recent work by Wilson et al.28,29 where uptake expressions were derived to describe reaction conditions when O3 is depleted from the bulk solution, but not depleted from the microdroplet surface.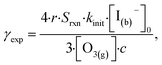 | (12) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
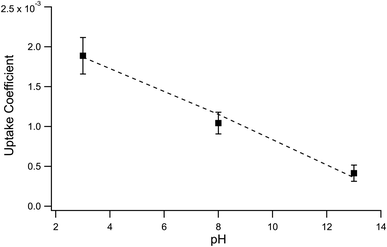
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ozone-to-iodide reaction equivalence is accounted for when calculating γexp by simply using Srxn = 0.5. At pH 13, however, the only relevant loss channel for I− is O3 and as such, Srxn = 1. We note that only conditions where [O3(g)] > 1 ppm were used in calculating uptake for pH 13 conditions given the apparent mechanistic complexity for sub-ppm concentrations of O3. Fig. 9 shows average γexp as a function of pH resulting from eqn (12), where a modest increase in γexp from ∼4 × 10−4 at pH 13 to 2 × 10−3 at pH 3 is observed. Experimental results in Fig. 9 are compared to the values obtained from the analytical expression introduced in the following section.
2 ozone-to-iodide reaction equivalence is accounted for when calculating γexp by simply using Srxn = 0.5. At pH 13, however, the only relevant loss channel for I− is O3 and as such, Srxn = 1. We note that only conditions where [O3(g)] > 1 ppm were used in calculating uptake for pH 13 conditions given the apparent mechanistic complexity for sub-ppm concentrations of O3. Fig. 9 shows average γexp as a function of pH resulting from eqn (12), where a modest increase in γexp from ∼4 × 10−4 at pH 13 to 2 × 10−3 at pH 3 is observed. Experimental results in Fig. 9 are compared to the values obtained from the analytical expression introduced in the following section.
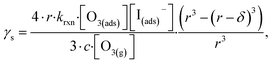 | (13) |
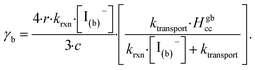 | (14) |
The radial term in eqn (13) accounts for the relative scaling of surface to bulk volume with changing radius r and surface thickness δ. In eqn (14), ktransport is a term introduced by Wilson et al.29 that describes an overall ozone equilibration rate into the bulk solution that includes liquid diffusion and kinetic contributions. While previous work utilized the equilibrium assumption [O3(ads)] = Hgbcc × [O3(g)], the current investigation with iodide has shown [O3(ads)] resides far below this equilibrium value. Therefore, eqn (11) which accounts for reactive depletion of [O3(ads)] is used in eqn (13) rather than assuming the Henry's Law concentration.
The surface uptake coefficient calculated from eqn (13) is compared to experimental uptake coefficients in Fig. 9. The pH dependence of γs is captured by using the pH-scaling of kobs discussed in Section 4.4 above and provided in eqn (9). As shown in Fig. 9, agreement is observed between experiment and the uptake expression in eqn (13), reinforcing the conclusion that the surface reaction dominates iodide loss under our experimental conditions. The agreement between experiment and uptake expressions further motivates the use of eqn (13) and (14) to predict uptake across a much larger concentration range. Fig. 10 shows uptake predictions from eqn (13) and (14) as well as the sum total γtotal = γs + γb for a constant [O3(g)] = 1 ppm and droplet radius r = 24 μm. Average uptake from the experiments at [I(b)−] = 250 mM and pH 3 are included for comparison in Fig. 10, as well as two limiting cases from resistor-based models discussed in more detail below.
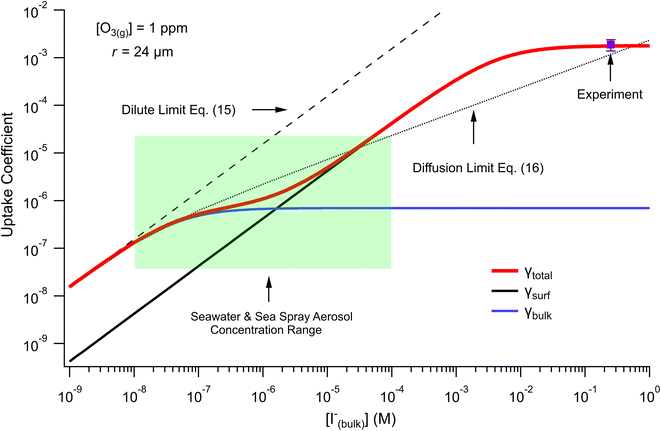 | ||
| Fig. 10 Uptake coefficients computed from eqn (13) and (14) using [O3(g)] = 1 ppm and droplet radius r = 24 μm. Total uptake is the sum of surface and bulk components. Results from the analytical approach are compared with two limiting cases from resistor-based uptake modeling shown as dashed and dotted lines. Experimental uptake at pH 8 is compared with the models. | ||
For very low iodide concentrations shown in Fig. 10, below 100 nM, the uptake coefficient is dominated by the bulk reaction and is limited by the oxidation reaction rate in the bulk. At approximately [I(b)−] = 100 nM, uptake of O3 by a bulk reaction starts becoming limited due to depletion of O3 in the droplet interior and the surface reaction starts to dominate the reactive uptake. For increasing iodide concentrations, the surface reaction totally governs the uptake of O3. When iodide concentrations increase above 1 mM, results from Fig. 8 suggest [O3(ads)] becomes greatly depleted due to gas-phase diffusion limitations. This depletion effect is similarly observed in Fig. 10 in the limiting of surface uptake to values ∼10−3.
Fig. 10 also compares the uptake coefficient expressions with commonly used resistor model limits shown with dashed lines. For very low [I(b)−], computed γtotal values agree with the dilute limit or “phase-mixed” case introduced by Schwartz et al.93
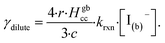 | (15) |
As bulk iodide concentrations increase and γs dominates γtotal, results approach the “uptake controlled by fast reaction” case from Worsnop et al.51 or the “diffusion limit” case by Schwartz et al.93
 | (16) |
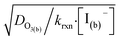 . Deviation from the diffusion limit becomes pronounced for intermediate [I(b)−] as the surface first becomes enriched with [I(ads)−] relative to the bulk concentration, followed by the depletion of [O3(ads)] for [I(b)−] > 1 mM.
. Deviation from the diffusion limit becomes pronounced for intermediate [I(b)−] as the surface first becomes enriched with [I(ads)−] relative to the bulk concentration, followed by the depletion of [O3(ads)] for [I(b)−] > 1 mM.
6.4. Atmospheric implications & literature comparison
Here, we comment on the relevance of our findings to uptake of O3 by seawater concentrations of I− in droplets, and subsequently discuss our findings in context of previous literature results. The expressions for uptake in eqn (13) and (14) allow for the prediction of uptake in systems such as seawater and sea spray aerosol (SSA) interacting with the marine boundary layer, where near-surface seawater iodide concentrations range from ∼10–200 nM (ref. 94) and typical ozone concentrations in the marine boundary layer are ∼20 ppb.95–98 For these concentrations, uptake of O3 by a droplet with radius r = 24 μm is on the order of 5 × 10−7 with bulk chemistry dominating the overall uptake. As previously reported, salt concentrations in SSA can increase dramatically upon emission from the sea surface, with I− becoming potentially enhanced by factors up to ∼1000 (ref. 99–101) and, in some measurements, making up a third of the total soluble iodine content of aerosol with particle radius r < 500 nm.102 Additionally, rapid acidification of SSA103 may contribute to an apparent acceleration of iodide oxidation by ozone relative to the pH of seawater (∼pH 8). Under these concentrated and acidic conditions where iodide concentrations could approach ∼100 μM, the expression obtained for γtotal predicts the uptake of ozone is driven almost exclusively by the surface reaction. However, we acknowledge that the current model construction employs a coarse-grain depiction of the droplet surface and bulk regions and therefore potentially overlooks important “sub-surface” dynamics which would affect the predicted transition in bulk vs. surface uptake. For reference we include the range of iodide concentrations encountered in seawater and SSA in the highlighted box in Fig. 10, where the transition from bulk to surface chemistry is observed.While the model predictions presented in Fig. 10 suggest both surface and bulk contributions to the uptake of O3 under relevant salt concentrations, we emphasize that results in Fig. 10 have resulted from evaluating eqn (13) and (14) for the droplet radius r = 24 μm investigated in the experiments. For SSA and marine aerosol a broad range of sizes are encountered, where typical aerosols have radii r < 10 μm and submicron particles make up the vast majority of aerosol by total number. For such small sizes, we expect the surface contribution to the overall uptake of O3 by I− to become even more significant due to the inverse radial scaling of the surface to volume ratio. On the other hand, eqn (13) and (14) predict the uptake of ozone by a macro-scale system such as the sea surface would be dominated by bulk chemistry using the same radial scaling argument. However, correctly calculating uptake for macro-scale systems utilizing the current model would require detailed knowledge of the system dimensions and the governing gas-phase mass transport steps for O3 across large systems such as the marine boundary layer. As such, we reserve a more complete discussion of the size-dependence of γtotal under relevant concentrations to future work.
Uptake coefficients calculated from the analysis above and observed in experiments can also be compared to previous laboratory measurements of uptake of O3 on aqueous iodide solutions and aerosol. One of the most comparable previous reports by Magi et al.10 measures uptake of O3 using a droplet-train apparatus, with droplet sizes ∼100 μm and NaI concentrations ranging from 0.5 to 3 M. The reported uptake coefficient from this work under conditions 293 K and [I−] = 0.5 M is γ = 5 × 10−3, only about 2–3 times greater than the maximum uptake measured in this work. However, as the droplet-train apparatus operates at reduced pressure (10–30 torr), deviations from uptake measured at ambient pressure may be expected. Additional relevant experiments performed by Ammann and coworkers20,21 use submicron sodium iodide aerosol to measure the uptake of ozone. The main difference between the conditions of these experiments and ours is particle size, as the present experiments all utilize much larger microdroplets. Nevertheless, measurements on submicron aerosol composed of iodide/chloride mixtures by Rouvière et al.20 yield uptake coefficients of γ ∼4.4 × 10−3, which differ by a factor of ∼2 from the largest uptake coefficients observed in our experiments. This reference also reports a relatively weak concentration dependence, where increasing [I−] from 0.9 M to 7.3 M increases the ozone reactive uptake coefficient by ∼2.5. This may point to a similar surface ozone depletion effect observed for sub-micron aerosol, although a more in-depth analysis of the experimental conditions used is needed to draw any specific conclusions from this past work.
Lastly, we note that while the conditions studied and modeled in the current work generally do not accurately represent conditions found in real-world systems, our current approach aims to identify and analyze the molecular-scale processes governing reactivity in simple multiphase systems. A deep understanding of these simple systems, in turn, builds the foundation for investigating the complex systems encountered in the environment.
7. Conclusion
Kinetics of iodide oxidation by ozone in single microdroplets are reported and analyzed with a recently developed multiphase model that describes individual surface and bulk processes occurring during the course of reaction. A kinetic model is constructed using literature references, basic assumptions about rate coefficients, and is further constrained using molecular simulations of O3 and iodide at the air–water interface. Use of the model provides insight into important surface mechanisms that govern the overall reactivity in microdroplets and provide a benchmark for developing more general expressions for O3 uptake in aerosol. Experimental results in conjunction with modeling work suggest the I− + O3 reaction under the conditions studied occurs exclusively at the air–water interface. Nevertheless, we note that since the model employed discretizes the entire droplet into two compartments, a detailed account of sub-surface diffusion and reaction processes may be lacking which could be important for a clear accounting of surface vs. bulk reactivity. We anticipate future work will clarify these subsurface processes to fully understand the transition between surface and bulk reactivity.A strong dependence on the consumption rate of I− with bulk solution pH is observed, as previously reported for bulk solution. However, the modeled pH-dependent chemistry involving I− in solution cannot fully explain the observed kinetics. To explain the observed pH dependence of the I− + O3 reaction we invoke an IOOO− intermediate, which is analogous to reaction intermediates found in the mechanism governing bromide oxidation by ozone at the air–water interface. A kinetic analysis also demonstrates a first-order dependence on [O3(gas)] for all pH conditions. Simulation and analytical results suggest this reaction order originates from the depletion of ozone at the droplet surface during reaction for neutral to acidic conditions, and the linear scaling of surface adsorbed O3 for mild to extremely basic conditions. Surface depletion of reagents appears to be a general feature of fast surface-reactions and may be relevant across scales for many systems involving uptake of trace gases. A kinetic expression for steady-state ozone concentrations on the droplet surface, eqn (11), is derived and subsequently used in a recently developed set of expressions, eqn (13) and (14), for predicting uptake coefficients in droplets due to both surface and bulk reactions. Surface uptake coefficients calculated using eqn (11) for surface-adsorbed O3 indicate a large sensitivity to reactive depletion of species at the air–water interface, warranting the further study of the conditions under which reactants become depleted at interfaces.
Total uptake coefficients predicted by the analytical expressions obtained are analyzed across a range of concentrations and compared to the experimental uptake values of γ ∼10−3 and previous aerosol uptake experiments from the literature. The applicability of the present findings to reaction in seawater and sea spray aerosol is considered, with a brief discussion of the major findings and limitations of the modeling approach. Future work aims to expand the current approach to understand mass transport limitations in heterogeneous chemistry more broadly while investigating which key parameters control uptake coefficients and how these processes are related to reaction mechanisms at the droplet surface, where a number of factors such as partial solvation, pH, and reaction depletion may significantly alter expected uptake.
Data availability
Data are available from the corresponding author upon request.Author contributions
A. M. P. and K. R. W. conceived of experiments and the kinetic model. A. M. P. performed experiments, analyzed data, and executed kinetic simulations. G. V. B. advised in construction of open-port sampling interface. K. P. and D. T. L. performed molecular simulations, and wrote description and analysis of results. A. M. P. and K. R. W. wrote manuscript with contributions from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Condensed Phase and Interfacial Molecular Science Program (CPIMS), in the Chemical Sciences Geosciences and Biosciences Division of the Office of Basic Energy Sciences of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. We thank Prof. Megan Willis (Colorado State University), Prof. Phill Geissler (1974–2022, UC Berkeley), Dr Amr Dodin (UC Berkeley), Liron Cohen (UC Berkeley/LBNL), Dr Shane Devlin (UNLV/LBNL), and Prof. Rich Saykally (UC Berkeley/LBNL) for helpful discussions.References
- A. Saiz-Lopez, J. M. C. Plane, A. R. Baker, L. J. Carpenter, R. von Glasow, J. C. Gómez Martín, G. McFiggans and R. W. Saunders, Atmospheric Chemistry of Iodine, Chem. Rev., 2012, 112(3), 1773–1804, DOI:10.1021/cr200029u.
- L. J. Carpenter, Iodine in the Marine Boundary Layer, Chem. Rev., 2003, 103(12), 4953–4962, DOI:10.1021/cr0206465.
- L. J. Carpenter, S. M. MacDonald, M. D. Shaw, R. Kumar, R. W. Saunders, R. Parthipan, J. Wilson and J. M. C. Plane, Atmospheric Iodine Levels Influenced by Sea Surface Emissions of Inorganic Iodine, Nat. Geosci., 2013, 6(2), 108–111, DOI:10.1038/ngeo1687.
- L. J. Carpenter, R. J. Chance, T. Sherwen, T. J. Adams, S. M. Ball, M. J. Evans, H. Hepach, L. D. J. Hollis, C. Hughes, T. D. Jickells, A. Mahajan, D. P. Stevens, L. Tinel and M. R. Wadley, Marine Iodine Emissions in a Changing World, Proc. R. Soc. A, 2021, 477(2247), 20200824, DOI:10.1098/RSPA.2020.0824.
- J. C. Gómez Martín, T. R. Lewis, M. A. Blitz, J. M. C. Plane, M. Kumar, J. S. Francisco and A. Saiz-Lopez, A Gas-to-Particle Conversion Mechanism Helps to Explain Atmospheric Particle Formation through Clustering of Iodine Oxides, Nat. Commun., 2020, 11(1), 4521, DOI:10.1038/s41467-020-18252-8.
- Y. J. Tham, X.-C. He, Q. Li, C. A. Cuevas, J. Shen, J. Kalliokoski, C. Yan, S. Iyer, T. Lehmusjärvi, S. Jang, R. C. Thakur, L. Beck, D. Kemppainen, M. Olin, N. Sarnela, J. Mikkilä, J. Hakala, M. Marbouti, L. Yao, H. Li, W. Huang, Y. Wang, D. Wimmer, Q. Zha, J. Virkanen, T. G. Spain, S. O'Doherty, T. Jokinen, F. Bianchi, T. Petäjä, D. R. Worsnop, R. L. Mauldin, J. Ovadnevaite, D. Ceburnis, N. M. Maier, M. Kulmala, C. O'Dowd, M. D. Maso, A. Saiz-Lopez and M. Sipilä, Direct Field Evidence of Autocatalytic Iodine Release from Atmospheric Aerosol, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(4), 2021, DOI:10.1073/PNAS.2009951118.
- J. C. Gómez Martín, T. R. Lewis, A. D. James, A. Saiz-Lopez and J. M. C. Plane, Insights into the Chemistry of Iodine New Particle Formation: The Role of Iodine Oxides and the Source of Iodic Acid, J. Am. Chem. Soc., 2022, 144(21), 9240–9253, DOI:10.1021/jacs.1c12957.
- L. Ganzeveld, D. Helmig, C. W. Fairall, J. Hare and A. Pozzer, Atmosphere-Ocean Ozone Exchange: A Global Modeling Study of Biogeochemical, Atmospheric, and Waterside Turbulence Dependencies, Global Biogeochem. Cycles, 2009, 23(4), GB4021, DOI:10.1029/2008GB003301.
- J. A. Garland, A. W. Elzerman and S. A. Penkett, The Mechanism for Dry Deposition of Ozone to Seawater Surfaces, J. Geophys. Res.: Oceans, 1980, 85(C12), 7488–7492, DOI:10.1029/JC085IC12P07488.
- L. Magi, F. Schweitzer, C. Pallares, S. Cherif, P. Mirabel and C. George, Investigation of the Uptake Rate of Ozone and Methyl Hydroperoxide by Water Surfaces, J. Phys. Chem. A, 1997, 101(27), 4943–4949, DOI:10.1021/jp970646m.
- J. H. Hu, Q. Shi, P. Davidovits, D. R. Worsnop, M. S. Zahniser and C. E. Kolb, Reactive Uptake of Cl2(g) and Br2(g) by Aqueous Surfaces as a Function of Br- and I- Ion Concentration: The Effect of Chemical Reaction at the Interface, J. Phys. Chem., 1995, 99(21), 8768–8776, DOI:10.1021/j100021a050.
- M. Bhujel, D. L. Marshall, T. A. Maccarone, I. B. McKinnon, J. A. Trevitt, G. d Silva, J. S. Blanksby and J. B. L. Poad, Gas Phase Reactions of Iodide and Bromide Anions with Ozone: Evidence for Stepwise and Reversible Reactions, Phys. Chem. Chem. Phys., 2020, 22(18), 9982–9989, 10.1039/D0CP01498B.
- R. Teiwes, J. Elm, K. Handrup, E. P. Jensen, M. Bilde and H. B. Pedersen, Atmospheric Chemistry of Iodine Anions: Elementary Reactions of I−, IO−, and IO2− with Ozone Studied in the Gas-Phase at 300 K Using an Ion Trap, Phys. Chem. Chem. Phys., 2018, 20(45), 28606–28615, 10.1039/C8CP05721D.
- Q. Liu, L. M. Schurter, C. E. Muller, S. Aloisio, J. S. Francisco and D. W. Margerum, Kinetics and Mechanisms of Aqueous Ozone Reactions with Bromide, Sulfite, Hydrogen Sulfite, Iodide, and Nitrite Ions, Inorg. Chem., 2001, 40(17), 4436–4442, DOI:10.1021/ic000919j.
- S. R. Schneider, P. S. J. Lakey, M. Shiraiwa and J. P. D. Abbatt, Reactive Uptake of Ozone to Simulated Seawater: Evidence for Iodide Depletion, J. Phys. Chem. A, 2020, 124(47), 9844–9853, DOI:10.1021/acs.jpca.0c08917.
- S. R. Schneider, P. S. J. Lakey, M. Shiraiwa and J. P. D. Abbatt, Iodine Emission from the Reactive Uptake of Ozone to Simulated Seawater, Environ. Sci.: Processes Impacts, 2023, 25(2), 254–263, 10.1039/D2EM00111J.
- Y. Sakamoto, A. Yabushita, M. Kawasaki and S. Enami, Direct Emission of I2 Molecule and IO Radical from the Heterogeneous Reactions of Gaseous Ozone with Aqueous Potassium Iodide Solution, J. Phys. Chem. A, 2009, 113(27), 7707–7713, DOI:10.1021/jp903486u.
- J. Hoigné, H. Bader, W. R. Haag and J. Staehelin, Rate Constants of Reactions of Ozone with Organic and Inorganic Compounds in Water—III. Inorganic Compounds and Radicals, Water Res., 1985, 19(8), 993–1004, DOI:10.1016/0043-1354(85)90368-9.
- E. Woods, C. A. Konys and S. R. Rossi, Photoemission of Iodide from Aqueous Aerosol Particle Surfaces, J. Phys. Chem. A, 2019, 123(13), 2901–2907, DOI:10.1021/acs.jpca.8b12323.
- A. Rouvière, Y. Sosedova and M. Ammann, Uptake of Ozone to Deliquesced KI and Mixed KI/NaCl Aerosol Particles, J. Phys. Chem. A, 2010, 114(26), 7085–7093, DOI:10.1021/JP103257D.
- A. Rouvière and M. Ammann, The Effect of Fatty Acid Surfactants on the Uptake of Ozone to Aqueous Halogenide Particles, Atmos. Chem. Phys., 2010, 10(23), 11489–11500, DOI:10.5194/acp-10-11489-2010.
- R. Teiwes, J. Elm, M. Bilde and H. B. Pedersen, The Reaction of Hydrated Iodide I(H2O)− with Ozone: A New Route to IO2− Products, Phys. Chem. Chem. Phys., 2019, 21(32), 17546–17554, 10.1039/C9CP01734H.
- H. B. Pedersen, J. Elm, C. H. Frederiksen, S. P. S. Jessen, R. Teiwes and M. Bilde, The Reaction of Isotope-Substituted Hydrated Iodide I(H182O)− with Ozone: The Reactive Influence of the Solvent Water Molecule, Phys. Chem. Chem. Phys., 2020, 22(34), 19080–19088, 10.1039/D0CP03219K.
- G. C. Moreno, O. Gálvez, V. L.-A. Moreno, E. María Espildora-García and M. Teresa Baeza-Romero, A Revisit of the Interaction of Gaseous Ozone with Aqueous Iodide. Estimating the Contributions of the Surface and Bulk Reactions, Phys. Chem. Chem. Phys., 2018, 20(43), 27571–27584, 10.1039/C8CP04394A.
- C. Moreno, M.-T. Baeza-Romero, M. Sanz, Ó. Gálvez, V. L. Arza, C. J. Ianni and E. Espíldora, Iodide Conversion to Iodate in Aqueous and Solid Aerosols Exposed to Ozone, Phys. Chem. Chem. Phys., 2020, 22(10), 5625–5637, 10.1039/C9CP05601G.
- Ó. Gálvez, M. T. Baeza-Romero, M. Sanz and L. F. Pacios, A Theoretical Study on the Reaction of Ozone with Aqueous Iodide, Phys. Chem. Chem. Phys., 2016, 18(11), 7651–7660, 10.1039/C5CP06440F.
- C. Moreno and M. T. Baeza-Romero, A Kinetic Model for Ozone Uptake by Solutions and Aqueous Particles Containing I− and Br−, Including Seawater and Sea-Salt Aerosol, Phys. Chem. Chem. Phys., 2019, 21(36), 19835–19856, 10.1039/C9CP03430G.
- M. D. Willis and K. R. Wilson, Coupled Interfacial and Bulk Kinetics Govern the Timescales of Multiphase Ozonolysis Reactions, J. Phys. Chem. A, 2022, 126(30), 4991–5010, DOI:10.1021/acs.jpca.2c03059.
- K. R. Wilson, A. M. Prophet and M. D. Willis, A Kinetic Model for Predicting Trace Gas Uptake and Reaction, J. Phys. Chem. A, 2022, 126(40), 7291–7308, DOI:10.1021/acs.jpca.2c03559.
- R. Kaur Kohli, G. J. Van Berkel and J. F. Davies, An Open Port Sampling Interface for the Chemical Characterization of Levitated Microparticles, Anal. Chem., 2022, 94(8), 3441–3445, DOI:10.1021/acs.analchem.1c05550.
- L. Artiglia, J. Edebeli, F. Orlando, S. Chen, M.-T. Lee, P. Corral Arroyo, A. Gilgen, T. Bartels-Rausch, A. Kleibert, M. Vazdar, M. Andres Carignano, J. S. Francisco, P. B. Shepson, I. Gladich and M. Ammann, A Surface-Stabilized Ozonide Triggers Bromide Oxidation at the Aqueous Solution-Vapour Interface, Nat. Commun., 2017, 8(1), 700, DOI:10.1038/s41467-017-00823-x.
- M. D. Willis, G. Rovelli and K. R. Wilson, Combining Mass Spectrometry of Picoliter Samples with a Multicompartment Electrodynamic Trap for Probing the Chemistry of Droplet Arrays, Anal. Chem., 2020, 92(17), 11943–11952, DOI:10.1021/ACS.ANALCHEM.0C02343/SUPPL_FILE/AC0C02343_SI_001.PDF.
- M. I. Jacobs, J. F. Davies, L. Lee, R. D. Davis, F. Houle and K. R. Wilson, Exploring Chemistry in Microcompartments Using Guided Droplet Collisions in a Branched Quadrupole Trap Coupled to a Single Droplet, Paper Spray Mass Spectrometer, Anal. Chem., 2017, 89(22), 12511–12519, DOI:10.1021/acs.analchem.7b03704.
- J. F. Davies, Mass, Charge, and Radius of Droplets in a Linear Quadrupole Electrodynamic Balance, Aerosol Sci. Technol., 2019, 53(3), 309–320, DOI:10.1080/02786826.2018.1559921.
- G. J. Van Berkel and V. Kertesz, An Open Port Sampling Interface for Liquid Introduction Atmospheric Pressure Ionization Mass Spectrometry, Rapid Commun. Mass Spectrom., 2015, 29(19), 1749–1756, DOI:10.1002/rcm.7274.
- C. Liu, G. J. Van Berkel, P. Kovarik, J. B. Perot, V. Inguva and T. R. Covey, Fluid Dynamics of the Open Port Interface for High-Speed Nanoliter Volume Sampling Mass Spectrometry, Anal. Chem., 2021, 93(24), 8559–8567, DOI:10.1021/acs.analchem.1c01312.
- O. S. Ovchinnikova, D. Bhandari, M. Lorenz and G. J. Van Berkel, Transmission Geometry Laser Ablation into a Non-Contact Liquid Vortex Capture Probe for Mass Spectrometry Imaging, Rapid Commun. Mass Spectrom., 2014, 28(15), 1665–1673, DOI:10.1002/rcm.6946.
- G. J. Van Berkel, V. Kertesz and H. Boeltz, Immediate Drop on Demand Technology (I-DOT) Coupled with Mass Spectrometry via an Open Port Sampling Interface, Bioanalysis, 2017, 9(21), 1667–1679, DOI:10.4155/bio-2017-0104.
- J. F. Cahill, J. Riba and V. Kertesz, Rapid, Untargeted Chemical Profiling of Single Cells in Their Native Environment, Anal. Chem., 2019, 91(9), 6118–6126, DOI:10.1021/acs.analchem.9b00680.
- R. Kaur Kohli, R. S. Reynolds, K. R. Wilson and J. F. Davies, Exploring the Influence of Particle Phase in the Ozonolysis of Oleic and Elaidic Acid, Aerosol Sci. Technol., 2023, 1–18, DOI:10.1080/02786826.2023.2226183.
- G. Lamoureux, E. Harder, I. V. Vorobyov, B. Roux and A. D. MacKerell Jr, A Polarizable Model of Water for Molecular Dynamics Simulations of Biomolecules, Chem. Phys. Lett., 2006, 418(1–3), 245–249 CrossRef CAS.
- W. D. Hinsberg and F. A. Houle, Kinetiscope, https://hinsberg.net/kinetiscope/, accessed 2022-02-15 Search PubMed.
- N. Heine, F. A. Houle and K. R. Wilson, Connecting the Elementary Reaction Pathways of Criegee Intermediates to the Chemical Erosion of Squalene Interfaces during Ozonolysis, Environ. Sci. Technol., 2017, 51(23), 13740–13748, DOI:10.1021/acs.est.7b04197.
- F. A. Houle, A. A. Wiegel and K. R. Wilson, Predicting Aerosol Reactivity Across Scales: From the Laboratory to the Atmosphere, Environ. Sci. Technol., 2018, 52(23), 13774–13781, DOI:10.1021/acs.est.8b04688.
- K. R. Wilson, A. M. Prophet, G. Rovelli, M. D. Willis, R. J. Rapf and M. I. Jacobs, A Kinetic Description of How Interfaces Accelerate Reactions in Micro-Compartments, Chem. Sci., 2020, 11(32), 8533–8545, 10.1039/D0SC03189E.
- R. Vácha, P. Slavíček, M. Mucha, B. J. Finlayson-Pitts and P. Jungwirth, Adsorption of Atmospherically Relevant Gases at the Air/Water Interface: Free Energy Profiles of Aqueous Solvation of N2, O2, O3, OH, H2O, HO2, and H2O2, J. Phys. Chem. A, 2004, 108(52), 11573–11579, DOI:10.1021/jp046268k.
- R. Sander, Compilation of Henry's Law Constants (Version 4.0) for Water as Solvent, Atmos. Chem. Phys., 2015, 15(8), 4399–4981, DOI:10.5194/acp-15-4399-2015.
- N. M. Panich, B. G. Ershov, A. F. Seliverstov and A. G. Basiev, Ozone Solubility in Concentrated Aqueous Solutions of Salts, Russ. J. Appl. Chem., 2007, 80(11), 1812–1815, DOI:10.1134/S1070427207110067.
- I. Langmuir, The Adsorption of Gases on Plane Surfaces of Glass, Mica and Platinum, J. Am. Chem. Soc., 1918, 40(9), 1361–1403, DOI:10.1021/ja02242a004.
- J. Vieceli, M. Roeselová, N. Potter, L. X. Dang, B. C. Garrett and D. J. Tobias, Molecular Dynamics Simulations of Atmospheric Oxidants at the Air–Water Interface: Solvation and Accommodation of OH and O3, J. Phys. Chem. B, 2005, 109(33), 15876–15892, DOI:10.1021/jp051361+.
- D. R. Worsnop, J. W. Morris, Q. Shi, P. Davidovits and C. E. Kolb, A Chemical Kinetic Model for Reactive Transformations of Aerosol Particles, Geophys. Res. Lett., 2002, 29(20), 57, DOI:10.1029/2002GL015542.
- G. M. Nathanson, P. Davidovits, D. R. Worsnop and C. E. Kolb, Dynamics and Kinetics at the Gas–Liquid Interface, J. Phys. Chem., 1996, 100(31), 13007–13020, DOI:10.1021/jp953548e.
- M. E. Saecker and G. M. Nathanson, Collisions of Protic and Aprotic Gases with Hydrogen Bonding and Hydrocarbon Liquids, J. Chem. Phys., 1993, 99(9), 7056–7075, DOI:10.1063/1.465425.
- C. F. Clement, M. Kulmala and T. Vesala, Theoretical Consideration on Sticking Probabilities, J. Aerosol Sci., 1996, 27(6), 869–882, DOI:10.1016/0021-8502(96)00032-8.
- S. E. Schwartz and J. E. Freiberg, Mass-Transport Limitation to the Rate of Reaction of Gases in Liquid Droplets: Application to Oxidation of SO2 in Aqueous Solutions, Atmos. Environ., 1981, 15(7), 1129–1144, DOI:10.1016/0004-6981(81)90303-6.
- J. H. Seinfeld and S. N. Pandis, Mass Transfer Aspects of Atmospheric Chemistry, in Atmospheric Chemistry and Physics: From Air Polution to Climate Change, John Wiley & Sons, Inc., 1998 Search PubMed.
- F. Jin, R. Balasubramaniam and K. J. Stebe, Surfactant Adsorption to Spherical Particles: The Intrinsic Length Scale Governing the Shift from Diffusion to Kinetic-Controlled Mass Transfer, J. Adhes., 2004, 80(9), 773–796, DOI:10.1080/00218460490480770.
- P. Jungwirth and D. J. Tobias, Ions at the Air/Water Interface, J. Phys. Chem. B, 2002, 106(25), 6361–6373, DOI:10.1021/jp020242g.
- A. C. Stern, M. D. Baer, C. J. Mundy and D. J. Tobias, Thermodynamics of Iodide Adsorption at the Instantaneous Air-Water Interface, J. Chem. Phys., 2013, 138(11), 114709, DOI:10.1063/1.4794688.
- L. Piatkowski, Z. Zhang, E. H. G. Backus, H. J. Bakker and M. Bonn, Extreme Surface Propensity of Halide Ions in Water, Nat. Commun., 2014, 5(1), 4083, DOI:10.1038/ncomms5083.
- D. I. Reeser and D. J. Donaldson, Influence of Water Surface Properties on the Heterogeneous Reaction between O3(g) and I(Aq)−, Atmos. Environ., 2011, 45(34), 6116–6120, DOI:10.1016/J.ATMOSENV.2011.08.042.
- S. N. Wren and D. J. Donaldson, Glancing-Angle Raman Spectroscopic Probe for Reaction Kinetics at Water Surfaces, Phys. Chem. Chem. Phys., 2010, 12(11), 2648–2654, 10.1039/B922254E.
- R. Weber, B. Winter, P. M. Schmidt, W. Widdra, I. V. Hertel, M. Dittmar and M. Faubel, Photoemission from Aqueous Alkali-Metal–Iodide Salt Solutions Using EUV Synchrotron Radiation, J. Phys. Chem. B, 2004, 108(15), 4729–4736, DOI:10.1021/jp030776x.
- B. Credidio, M. Pugini, S. Malerz, F. Trinter, U. Hergenhahn, I. Wilkinson, S. Thürmer and B. Winter, Quantitative Electronic Structure and Work-Function Changes of Liquid Water Induced by Solute, Phys. Chem. Chem. Phys., 2022, 24(3), 1310–1325, 10.1039/D1CP03165A.
- P. B. Petersen and R. J. Saykally, Probing the Interfacial Structure of Aqueous Electrolytes with Femtosecond Second Harmonic Generation Spectroscopy, J. Phys. Chem. B, 2006, 110(29), 14060–14073, DOI:10.1021/jp0601825.
- P. B. Petersen, J. C. Johnson, K. P. Knutsen and R. J. Saykally, Direct Experimental Validation of the Jones–Ray Effect, Chem. Phys. Lett., 2004, 397(1–3), 46–50, DOI:10.1016/j.cplett.2004.08.048.
- L. X. Dang, Computational Study of Ion Binding to the Liquid Interface of Water, J. Phys. Chem. B, 2002, 106(40), 10388–10394, DOI:10.1021/jp021871t.
- Y. Liu, Is the Free Energy Change of Adsorption Correctly Calculated?, J. Chem. Eng. Data, 2009, 54(7), 1981–1985, DOI:10.1021/je800661q.
- G. Olivieri, K. M. Parry, R. D'Auria, D. J. Tobias and M. A. Brown, Specific Anion Effects on Na+ Adsorption at the Aqueous Solution–Air Interface: MD Simulations, SESSA Calculations, and Photoelectron Spectroscopy Experiments, J. Phys. Chem. B, 2018, 122(2), 910–918, DOI:10.1021/acs.jpcb.7b06981.
- R. D'Auria and D. J. Tobias, Relation between Surface Tension and Ion Adsorption at the Air–Water Interface: A Molecular Dynamics Simulation Study, J. Phys. Chem. A, 2009, 113(26), 7286–7293, DOI:10.1021/jp810488p.
- N. Ottosson, M. Faubel, S. E. Bradforth, P. Jungwirth and B. Winter, Photoelectron Spectroscopy of Liquid Water and Aqueous Solution: Electron Effective Attenuation Lengths and Emission-Angle Anisotropy, J. Electron Spectrosc. Relat. Phenom., 2010, 177(2), 60–70, DOI:10.1016/j.elspec.2009.08.007.
- S. Ou, Y. Hu, S. Patel and H. Wan, Spherical Monovalent Ions at Aqueous Liquid–Vapor Interfaces: Interfacial Stability and Induced Interface Fluctuations, J. Phys. Chem. B, 2013, 117(39), 11732–11742, DOI:10.1021/jp406001b.
- S. Saha, S. Roy, P. Mathi and J. A. Mondal, Polyatomic Iodine Species at the Air–Water Interface and Its Relevance to Atmospheric Iodine Chemistry: An HD-VSFG and Raman-MCR Study, J. Phys. Chem. A, 2019, 123(13), 2924–2934, DOI:10.1021/acs.jpca.9b00828.
- S. Roy and J. A. Mondal, “Breaking” and “Making” of Water Structure at the Air/Water–Electrolyte (NaXO3; X = Cl, Br, I) Interface, J. Phys. Chem. Lett., 2021, 12(7), 1955–1960, DOI:10.1021/acs.jpclett.0c03827.
- T. Huthwelker and T. Peter, Analytical Description of Gas Transport across an Interface with Coupled Diffusion in Two Phases, J. Chem. Phys., 1996, 105(4), 1661–1667, DOI:10.1063/1.472025.
- A. A. Wiegel, M. J. Liu, W. D. Hinsberg, K. R. Wilson and F. A. Houle, Diffusive Confinement of Free Radical Intermediates in the OH Radical Oxidation of Semisolid Aerosols, Phys. Chem. Chem. Phys., 2017, 19(9), 6814–6830, 10.1039/C7CP00696A.
- I. Sanemasa, T. Kobayashi, C. Y. Piao and T. Deguchi, Equilibrium Solubilities of Iodine Vapor in Water, Bull. Chem. Soc. Jpn., 1984, 57(5), 1352–1357, DOI:10.1246/bcsj.57.1352.
- C.-C. Lin, Volatility of Iodine in Dilute Aqueous Solutions, J. Inorg. Nucl. Chem., 1981, 43(12), 3229–3238, DOI:10.1016/0022-1902(81)80094-2.
- G. C. Barker and D. C. Sammon, Kinetics of Proton-Transfer Reactions, Nature, 1967, 213(5071), 65–66, DOI:10.1038/213065b0.
- M. Eigen and L. De Maeyer, Untersuchungen über die Kinetik der Neutralisation. I, Z. Elektrochem. Ber. Bunsenges. Phys. Chem., 1955, 59(10), 986–993, DOI:10.1002/bbpc.19550591020.
- Y. Bichsel and U. von Gunten, Oxidation of Iodide and Hypoiodous Acid in the Disinfection of Natural Waters, Environ. Sci. Technol., 1999, 33(22), 4040–4045, DOI:10.1021/es990336c.
- Y. Bichsel, Behavior of Iodine Species in Oxidative Processes during Drinking Water Treatment. Doctoral thesis, ETH Zurich, 2000, DOI:10.3929/ethz-a-003861380.
- T. L. Allen and R. M. Keefer, The Formation of Hypoiodous Acid and Hydrated Iodine Cation by the Hydrolysis of Iodine, J. Am. Chem. Soc., 1955, 77(11), 2957–2960, DOI:10.1021/ja01616a008.
- C. H. Li and C. F. White, Kinetics of Hypoiodite Decomposition, J. Am. Chem. Soc., 1943, 65(3), 335–339, DOI:10.1021/ja01243a011.
- G. V. Buxton and Q. G. Mulazzani, On the Hydrolysis of Iodine in Alkaline Solution: A Radiation Chemical Study, Radiat. Phys. Chem., 2007, 76(6), 932–940, DOI:10.1016/j.radphyschem.2006.06.009.
- M. Eigen and K. Kustin, The Kinetics of Halogen Hydrolysis, J. Am. Chem. Soc., 1962, 84(8), 1355–1361, DOI:10.1021/ja00867a005.
- J. C. Wren, J. Paquette, S. Sunder and B. L. Ford, Iodine Chemistry in the +1 Oxidation State. II. A Raman and Uv–Visible Spectroscopic Study of the Disproportionation of Hypoiodite in Basic Solutions, Can. J. Chem., 1986, 64(12), 2284–2296, DOI:10.1139/v86-375.
- J. Paquette, J. C. Wren, S. Sunder and B. L. Ford, The Disproportionation of Iodine (I), United Kingdom, 1986, pp. 29–45, 0-7058-1073–9 Search PubMed.
- K. Sebők-Nagy and T. Körtvélyesi, Kinetics and Mechanism of the Hydrolytic Disproportionation of Iodine, Int. J. Chem. Kinet., 2004, 36(11), 596–602, DOI:10.1002/kin.20033.
- I. Lengyel, I. R. Epstein and K. Kustin, Kinetics of Iodine Hydrolysis, Inorg. Chem., 1993, 32(25), 5880–5882, DOI:10.1021/ic00077a036.
- D. A. Palmer, R. W. Ramette and R. E. Mesmer, Triiodide Ion Formation Equilibrium and Activity Coefficients in Aqueous Solution, J. Solution Chem., 1984, 13(9), 673–683, DOI:10.1007/BF00650374.
- J. D. Smith, J. H. Kroll, C. D. Cappa, D. L. Che, C. L. Liu, M. Ahmed, S. R. Leone, D. R. Worsnop and K. R. Wilson, The Heterogeneous Reaction of Hydroxyl Radicals with Sub-Micron Squalane Particles: A Model System for Understanding the Oxidative Aging of Ambient Aerosols, Atmos. Chem. Phys., 2009, 9(9), 3209–3222, DOI:10.5194/acp-9-3209-2009.
- S. E. Schwartz, Mass-Transport Considerations Pertinent to Aqueous Phase Reactions of Gases in Liquid–Water Clouds, Springer Berlin Heidelberg, Berlin, Heidelberg, 1986, pp. 415–471 Search PubMed.
- R. Chance, A. R. Baker, L. Carpenter and T. D. Jickells, The Distribution of Iodide at the Sea Surface, Environ. Sci.: Processes Impacts, 2014, 16(8), 1841–1859, 10.1039/C4EM00139G.
- J. E. Johnson, R. H. Gammon, J. Larsen, T. S. Bates, S. J. Oltmans and J. C. Farmer, Ozone in the Marine Boundary Layer over the Pacific and Indian Oceans: Latitudinal Gradients and Diurnal Cycles, J. Geophys. Res.: Atmos., 1990, 95(D8), 11847–11856, DOI:10.1029/JD095iD08p11847.
- H. B. Singh, G. L. Gregory, B. Anderson, E. Browell, G. W. Sachse, D. D. Davis, J. Crawford, J. D. Bradshaw, R. Talbot, D. R. Blake, D. Thornton, R. Newell and J. Merrill, Low Ozone in the Marine Boundary Layer of the Tropical Pacific Ocean: Photochemical Loss, Chlorine Atoms, and Entrainment, J. Geophys. Res.: Atmos., 1996, 101(D1), 1907–1917, DOI:10.1029/95JD01028.
- R. R. Dickerson, K. P. Rhoads, T. P. Carsey, S. J. Oltmans, J. P. Burrows and P. J. Crutzen, Ozone in the Remote Marine Boundary Layer: A Possible Role for Halogens, J. Geophys. Res.: Atmos., 1999, 104(D17), 21385–21395, DOI:10.1029/1999JD900023.
- K. Watanabe, Y. Nojiri and S. Kariya, Measurements of Ozone Concentrations on a Commercial Vessel in the Marine Boundary Layer over the Northern North Pacific Ocean, J. Geophys. Res.: Atmos., 2005, 110, D11310, DOI:10.1029/2004JD005514.
- F. Y. B. Seto and R. A. Duce, A Laboratory Study of Iodine Enrichment on Atmospheric Sea-Salt Particles Produced by Bubbles, J. Geophys. Res., 1972, 77(27), 5339–5349, DOI:10.1029/JC077i027p05339.
- R. A. Duce and E. J. Hoffman, Chemical Fractionation at the Air/Sea Interface, Annu. Rev. Earth Planet. Sci., 1976, 4(1), 187–228, DOI:10.1146/annurev.ea.04.050176.001155.
- B. S. Gilfedder, S. C. Lai, M. Petri, H. Biester and T. Hoffmann, Iodine Speciation in Rain, Snow and Aerosols, Atmos. Chem. Phys., 2008, 8(20), 6069–6084, DOI:10.5194/acp-8-6069-2008.
- J. C. Gómez Martín, A. Saiz-Lopez, C. A. Cuevas, A. R. Baker and R. P. Fernández, On the Speciation of Iodine in Marine Aerosol, J. Geophys. Res.: Atmos., 2022, 127(4), e2021JD036081, DOI:10.1029/2021JD036081.
- K. J. Angle, D. R. Crocker, R. M. C. Simpson, K. J. Mayer, L. A. Garofalo, A. N. Moore, S. L. Mora Garcia, V. W. Or, S. Srinivasan, M. Farhan, J. S. Sauer, C. Lee, M. A. Pothier, D. K. Farmer, T. R. Martz, T. H. Bertram, C. D. Cappa, K. A. Prather and V. H. Grassian, Acidity across the Interface from the Ocean Surface to Sea Spray Aerosol, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(2), e2018397118, DOI:10.1073/pnas.2018397118.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc04254e |
| This journal is © The Royal Society of Chemistry 2024 |