Open Access Article
Open Access ArticleThe enhancement of nonlinear optical properties of azulene-based nanographene by N atoms: a finishing touch†
Ya Qing
Zhang‡
a,
Cui-Cui
Yang‡
 ab,
Jia-Ying
Ma
a and
Wei Quan
Tian
ab,
Jia-Ying
Ma
a and
Wei Quan
Tian
 *a
*a
aChongqing Key Laboratory of Theoretical and Computational Chemistry, College of Chemistry and Chemical Engineering, Chongqing University, Huxi Campus, Chongqing 401331, P. R. China. E-mail: tianwq@cqu.edu.cn
bCollege of Science, Chongqing University of Technology, Huaxi Campus, Chongqing, 400054, P. R. China
First published on 11th December 2023
Abstract
Nonlinear optical (NLO) materials play an increasingly important role in optoelectronic devices, biomedicine, micro–nano processing, and other fields. The development of organic materials with strong second or (and) third NLO properties and a high stability is still challenging due to the unknown strategies for obtaining enhanced high order NLO properties. In the present work, π-conjugated systems are constructed by doping boron or (and) nitrogen atoms in the azulene moiety of azulene-based nanographenes (formed with an azulene chain with two bridging HCCHs at the two sides of the connecting CC bonds between azulenes, A1A2A3), and the NLO properties are predicted with time-dependent density functional theory based methods and a sum-over-states model. The doping of heteroatoms induces charge redistribution, tunes the frontier molecular orbital energy gap, changes the composition of some frontier molecular orbitals, and affects the NLO properties of those nanographenes. Among the designed nanographenes, the azulene-based nanographene with two nitrogen atoms at the two ends has the largest static first hyperpolarizability (91.30 × 10−30 esu per heavy atom), and the further introduction of two N atoms at the two ends of the central azulene moiety of this nanographene results in a large static second hyperpolarizability while keeping the large static first hyperpolarizability.
Introduction
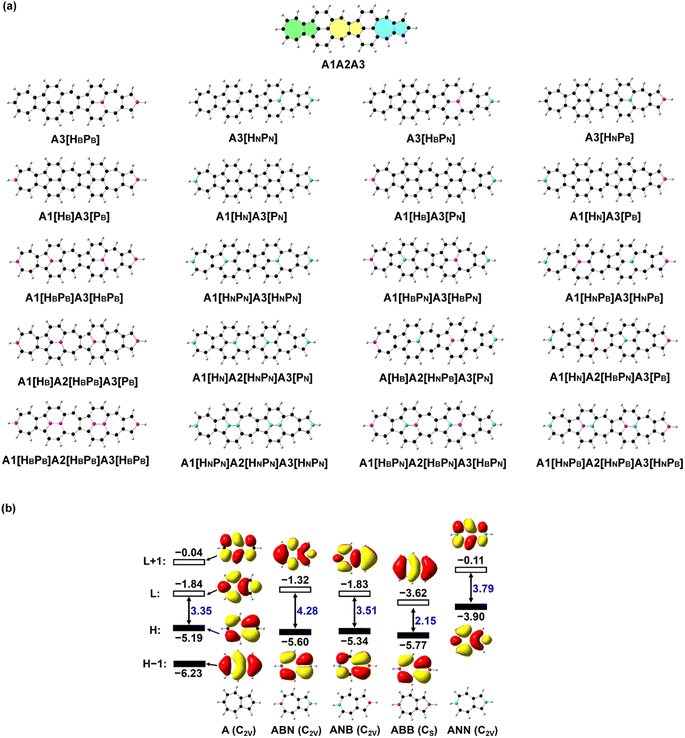
Novel nonlinear optical (NLO) materials with strong second or third order NLO properties, e.g., sum frequency generation, third harmonic generation, and two-photon absorption, continue to attract strong scientific interest due to their potential applications, for example, optical limiting,1,2 optical switch,3,4 photodynamic therapy,5,6 and nanophotonics devices.7Organic π-conjugated systems exhibit adjustable electronic properties, good π-conjugation, and structural flexibility and diversity, which render them attractive for applications in nonlinear optics.8–10 Azulene has an electron-deficient heptagon and an electron-rich pentagon, and its good polar π-conjugation and anti-Kasha behavior make it possible to be a promising functional group inducing rich optical and electronic properties.11–14 The introduction of polar azulene15 into carbon-based nanomaterials changes the electronic structure16 and mechanical properties17 of those nanomaterials, and azulene derivatives have been applied as nonlinear optical materials.18–20 The recently reported azulene-based nanographene with a fusion of azulenes and naphthalene (A1A2A3 in Fig. 1a corresponding to S6-3 in a previous work21) has a strong second order NLO response. To further improve the NLO properties of A1A2A3, it is essential to tune its electronic structure. The electronic structure of a system can be obtained through the Schrödinger equation ĤΨ = EΨ with Ĥ = ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) +
+ ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) . The potential (including nuclear–nuclear–VNN, nuclear–electron–VNe, and electron–electron–Vee interactions) determines the energy and space distribution of electrons and thus the electronic properties of the system. The doping of heteroatoms modifies the terms VNN and VNe and the electron occupation modulation modifies the terms VNe and Vee. Strategies to enhance NLO properties include the increase of π-conjugation length22 and the introduction of donor and acceptor groups.23 Moreover, the introduction of heteroatoms, such as boron and nitrogen, into the π-system can change the delocalization of the π-system, and modify the electronic structure of the materials to obtain new electronic properties and functions.24–29 The nonlinear optical properties of graphene-based nanomaterials can be improved by BN doping.30–32 The subtle changes in molecular structures, e.g., the two ends of azulene substituted by B or (and) N atoms, confer these heteroazulenes with different electronic properties while keeping the geometric structures essentially unmodified (Fig. 1b). The replacement of carbon atoms at the two ends of azulene by B and N (i.e., ABN or ANB in Fig. 1b) or two N atoms (i.e., ANN in Fig. 1b) results in an enlarged energy gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), while it brings about a narrowed HOMO–LUMO energy gap in the B-doped azulene (i.e., ABB in Fig. 1b). The HOMO distributions of ABN, ANB, and ABB are extremely similar to that of an isolated azulene (A), while the LUMO distribution of these three molecules exhibits π conjugation of the B atoms with C atoms, with low-lying LUMO energy. Remarkably, two fewer electrons in ABB with respect to azulene result in a significant lowering of the LUMO energy, and such a LUMO is similar to the HOMO − 1 of an isolated azulene; thus, the doping of B atoms modifies the electronic structure of the system. On the other hand, two more electrons in ANN lead to the conspicuous elevating of the HOMO and LUMO energies, and induce charge redistribution. The HOMO and LUMO of ANN correspond to the LUMO and LUMO + 1 of azulene (Fig. 1b), respectively, in terms of molecular orbital distribution. In the present work, B and N atoms are introduced into the azulene moiety of A1A2A3 (Fig. 1) for optimal NLO properties, and the correlation between the NLO properties and structure is investigated with quantum chemical calculations. The study finds that N doping provides an effective means to enhance the NLO responses of these azulene-based nanomaterials. N doping in the azulene moiety of A1A2A3 enhances both the second and third order NLO responses of these N-doped molecules. Functionalization of graphene-based nanomaterials through proper heteroatom doping is applicable to other carbon-based nanomaterials for desirable optoelectronic properties.
. The potential (including nuclear–nuclear–VNN, nuclear–electron–VNe, and electron–electron–Vee interactions) determines the energy and space distribution of electrons and thus the electronic properties of the system. The doping of heteroatoms modifies the terms VNN and VNe and the electron occupation modulation modifies the terms VNe and Vee. Strategies to enhance NLO properties include the increase of π-conjugation length22 and the introduction of donor and acceptor groups.23 Moreover, the introduction of heteroatoms, such as boron and nitrogen, into the π-system can change the delocalization of the π-system, and modify the electronic structure of the materials to obtain new electronic properties and functions.24–29 The nonlinear optical properties of graphene-based nanomaterials can be improved by BN doping.30–32 The subtle changes in molecular structures, e.g., the two ends of azulene substituted by B or (and) N atoms, confer these heteroazulenes with different electronic properties while keeping the geometric structures essentially unmodified (Fig. 1b). The replacement of carbon atoms at the two ends of azulene by B and N (i.e., ABN or ANB in Fig. 1b) or two N atoms (i.e., ANN in Fig. 1b) results in an enlarged energy gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), while it brings about a narrowed HOMO–LUMO energy gap in the B-doped azulene (i.e., ABB in Fig. 1b). The HOMO distributions of ABN, ANB, and ABB are extremely similar to that of an isolated azulene (A), while the LUMO distribution of these three molecules exhibits π conjugation of the B atoms with C atoms, with low-lying LUMO energy. Remarkably, two fewer electrons in ABB with respect to azulene result in a significant lowering of the LUMO energy, and such a LUMO is similar to the HOMO − 1 of an isolated azulene; thus, the doping of B atoms modifies the electronic structure of the system. On the other hand, two more electrons in ANN lead to the conspicuous elevating of the HOMO and LUMO energies, and induce charge redistribution. The HOMO and LUMO of ANN correspond to the LUMO and LUMO + 1 of azulene (Fig. 1b), respectively, in terms of molecular orbital distribution. In the present work, B and N atoms are introduced into the azulene moiety of A1A2A3 (Fig. 1) for optimal NLO properties, and the correlation between the NLO properties and structure is investigated with quantum chemical calculations. The study finds that N doping provides an effective means to enhance the NLO responses of these azulene-based nanomaterials. N doping in the azulene moiety of A1A2A3 enhances both the second and third order NLO responses of these N-doped molecules. Functionalization of graphene-based nanomaterials through proper heteroatom doping is applicable to other carbon-based nanomaterials for desirable optoelectronic properties.
Models and computational details
Since the relative position of B and N atoms in the B(N)-doped azulenes induces charge redistribution and has significant effects on the electronic structure, and doping along the dipole moment direction can change the polarization of those molecules to the greatest extent, the doping of heteroatoms is placed along the middle line of the three azulenes in A1A2A3. The carbon atoms at the end of a heptagon (H) or pentagon (P) in the three azulenes (denoted as A1, A2, and A3) of A1A2A3 are replaced by one to three pairs of BB/NN/BN or N/B atoms, respectively, resulting in thirty-six BN-doped A1A2A3 molecules. The stable structures with a large static first hyperpolarizability are selected (Fig. 1) for a detailed discussion here, and the rest of the structures are given in the ESI (Fig. S1 and Table S1†). The Kekulé structures of all the investigated molecules are provided in the ESI (Fig. S2†).Geometry optimizations of all these azulene-based nanographenes are carried out using a density functional theory (DFT)33,34 based method B3LYP35 and a 6-31G(d,p) basis set.36,37 Vibration frequency analyses confirm that each structure is a minimum on the potential energy surface with no imaginary vibrational frequency. The time-dependent (TD) DFT-based method CAM-B3LYP38 with 6-31++G(d,p) is employed to predict the electronic spectra under the Franck–Condon principle, generating electronic properties including dipole moments, transition energies, and transition dipole moments (extracted with Multiwfn39) for further NLO property calculations. The electronic parts of the second and third order NLO properties of all the systems are predicted by using the LinSOSProNLO program40 based on the sum-over-states (SOS) model41,42 with an improved computational efficiency.43
The orientation averaged second hyperpolarizability γ is defined as
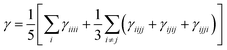 | (1) |
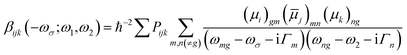 | (2) |
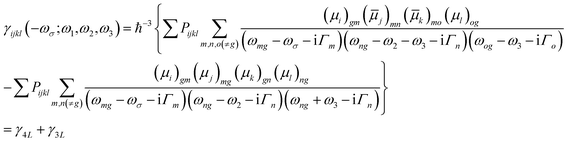 | (3) |
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) j)mn = 〈m|μj|n〉 − 〈g|μj|g〉δmn represents the dipole moment fluctuation. Γm (Γm = 0.01 × εm/ε2, in eV) defines the inverse radiative lifetime (or damping coefficients) of the electronic state m with εm (in eV) as the energy of the mth electronic state and ε2 (in eV) as the energy of the second electronic state. ∑Pijk or ∑Pijkl denotes the summations over the permutation of the set of distinct frequencies and Cartesian components. i, j, k, and l are Cartesian components.
j)mn = 〈m|μj|n〉 − 〈g|μj|g〉δmn represents the dipole moment fluctuation. Γm (Γm = 0.01 × εm/ε2, in eV) defines the inverse radiative lifetime (or damping coefficients) of the electronic state m with εm (in eV) as the energy of the mth electronic state and ε2 (in eV) as the energy of the second electronic state. ∑Pijk or ∑Pijkl denotes the summations over the permutation of the set of distinct frequencies and Cartesian components. i, j, k, and l are Cartesian components.
The third order NLO properties [eqn (3)] can be segmented into two terms, the first summation (i.e., γ4L, four-level) is two-photon processes, and the second one (i.e., γ3L, three-level) consists of two single-photon processes. The imaginary part of the second hyperpolarizability tensor is related to the coefficient of two-photon absorption. Two-photon absorption (TPA) efficiency is characterized by a TPA cross-section (δ) and is directly related to the imaginary part of 〈γ〉 in the degenerate four-wave mixing (DFWM) process through the following formula:
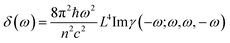 | (4) |
In this work, all π-electron molecular orbitals are included in predicting the electronic spectra. The predictions on the static first (〈β0〉) and second (〈γ0〉) hyperpolarizabilities of A1[HN]A3[PN] and A1[HN]A2[HNPN]A3[PN] find that 100 excited states are adequate to predict the converged 〈β0〉 and 〈γ0〉 (Fig. S3†), and the electronic spectra of all the investigated molecules are predicted with 300 excited states in the present work.
Only the electronic part of hyperpolarizability is predicted in the present work. The connection between the electronic and vibrational contributions to hyperpolarizability is “that electrons respond to changes in the nuclear Coulomb field (changes due to an infinitesimal shift in nuclear position) through the same nonlocal (hyper)polarizability densities that characterize their response to external electric fields”.45 The electronic hyperpolarizability could be used to estimate the molecular vibrational hyperpolarizability and vice versa.46
Results and discussion
Electronic properties tuned by B and N atoms
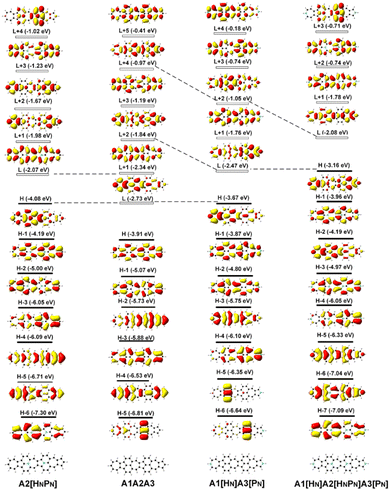
The deliberate incorporation of B and N atoms into A1A2A3 could alter the electronic structure (thus effectively tune the HOMO–LUMO energy gap of the structure) without compromising their planar geometries (all molecules in Fig. 1a have C2v symmetry), and the relevant electronic properties of B, N-doped A1A2A3 are listed in Tables 1 and S1.† The replacement of C by B and N in A1A2A3 alters both the LUMO and HOMO energies resulting in a change of the energy gap between the HOMO and LUMO (Table 1). To study the effect of B, N doping on the electronic structure of these nanographenes, the frontier molecular orbitals of A1A2A3, A2[HBPB], A2[HBPN], and A2[HNPN] are plotted in Fig. 2, as A2[HBPB], A2[HBPN], and A2[HNPN] have the same doping pattern. The different numbers of electrons and nuclear potential of B and N are the cause of the change of electronic structure resulting in charge redistribution in these nanographenes. The LUMO and HOMO of A2[HBPB] match the HOMO and HOMO − 2 of A1A2A3, respectively, and the LUMO and HOMO of A2[HBPN] are similar to the LUMO and HOMO of A1A2A3, whereas the LUMO and HOMO of A2[HNPN] find their counterparts as the LUMO and LOMO + 1 of A1A2A3. The molecular orbital distribution and energy of these frontier molecular orbitals (FMO), thus the HOMO–LUMO energy gap, vary with the doping of B and N. A similar phenomenon also exists in the other systems (Fig. S4†), i.e., the substitution of C by B and N atoms leads to a charge redistribution and different electronic structures. Those molecules are based on the same topological frame A1A2A3 with the same available electronic space (the space for the motion of electrons in terms of molecular orbitals); however, the different nuclear potentials of B, C, and N lead to different charge distributions and thus different electronic structures (molecular orbital energy re-ordering and redistribution of the molecular orbitals) in these A1A2A3 based molecules. In other words, the different nuclear potentials from B, C, and N bring about different electronic structures and this is the reason for using heteroatom doping to tune the electronic structure of graphene for novel electronic and optical properties.| Compounds | ΔE | LVF | ΔEOS–CS | ΔET–CS | 〈S2〉 | E H | E L | E gap | D g | 〈β0〉/(〈β0〉/N) | 〈γ0〉/(〈γ0〉/N) | 〈γ0〉3L/〈γ0〉4L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1A2A3 | — | 16.98 | 0.00 | 6.03 | 0.00 | −3.91 | −2.73 | 1.18 | 6.48 | 1808.94/47.60 | −21.74/−0.57 | −34.77/13.03 |
| A3[HBPB] (C2v) | 1.10 | 15.85 | 0.00 | −4.69 | 0.00 | −4.17 | −3.33 | 0.84 | 20.28 | — | — | — |
| A3[HNPN] (C2v) | 0.49 | 16.32 | 0.00 | 12.91 | 0.00 | −3.82 | −2.30 | 1.51 | 1.27 | −3002.80/−79.02 | −15.88/−0.42 | −23.65/7.77 |
| A3[HBPN] (C2v) | 0.00 | 16.27 | 0.00 | 9.24 | 0.00 | −3.81 | −2.46 | 1.35 | 1.56 | −923.09/−24.29 | −14.51/−0.38 | −26.60/12.09 |
| A3[HNPB] (C2v) | 1.38 | 17.00 | 0.00 | 8.36 | 0.00 | −4.11 | −2.83 | 1.29 | 11.73 | 2081.26/54.77 | −18.10/−0.47 | −31.05/12.95 |
| A1[HB]A3[PB] (C2v) | 0.00 | 17.45 | 0.00 | 21.32 | 0.00 | −5.25 | −3.41 | 1.84 | 2.05 | −88.26/−2.32 | −0.99/−0.03 | −17.84/16.85 |
| A1[HN]A3[PN] (C2v) | 0.18 | 16.94 | 0.00 | 11.06 | 0.00 | −3.67 | −2.47 | 1.20 | 6.08 | 3469.37/91.30 | −9.57/−0.25 | −29.28/19.71 |
| A1[HB]A3[PN] (C2v) | 0.15 | 17.14 | −2.55 | −0.98 | 0.72 | −4.03 | −2.91 | 1.12 | 17.98 | — | — | — |
| A1[HN]A3[PB] (C2v) | 1.07 | 16.46 | −0.99 | 4.04 | 0.38 | −4.28 | −3.17 | 1.11 | 11.02 | — | — | — |
| A1[HBPB]A3[HBPB] (C2v) | 0.19 | 14.80 | 0.00 | −0.53 | 0.00 | −4.80 | −4.15 | 0.65 | 7.76 | — | — | — |
| A1[HNPN]A3[HNPN] (C2v) | 0.00 | 16.23 | 0.00 | 18.43 | 0.00 | −3.65 | −1.82 | 1.83 | 0.92 | 881.79/23.21 | −7.29/−0.19 | −15.47/8.17 |
| A1[HBPN]A3[HBPN] (C2v) | 1.38 | 15.82 | 0.00 | 16.07 | 0.00 | −4.04 | −2.34 | 1.70 | 8.56 | −59.07/−1.55 | −9.13/−0.24 | −18.34/9.21 |
| A1[HNPB]A3[HNPB] (C2v) | 4.04 | 16.58 | 0.00 | 3.88 | 0.00 | −4.08 | −2.93 | 1.15 | 15.80 | 1850.73/48.7 | −5.37/−0.14 | −25.97/20.60 |
| A1[HB]A2[HBPB]A3[PB] (C2v) | 0.00 | 13.74 | −2.06 | −0.62 | 0.85 | −5.23 | −4.24 | 0.99 | 3.65 | — | — | — |
| A1[HN]A2[HNPN]A3[PN] (C2v) | 0.79 | 15.79 | 0.00 | 7.82 | 0.00 | −3.16 | −2.08 | 1.07 | 2.92 | 2106.08/55.42 | −52.44/−1.38 | −59.80/7.37 |
| A1[HB]A2[HNPB]A3[PN] (Cs) | 3.38 | 14.52 | −0.78 | 1.26 | 0.43 | −3.92 | −2.95 | 0.97 | 15.13 | — | — | — |
| A1[HN]A2[HBPN]A3[PB] (Cs) | 3.33 | 16.56 | 0.00 | −9.14 | 0.00 | −4.02 | −3.45 | 0.58 | 5.36 | — | — | — |
| A1[HNPB]A2[HNPB]A3[HNPB] (C2v) | 4.27 | 16.17 | −5.25 | −1.49 | 1.38 | −4.12 | −3.14 | 0.98 | 10.83 | — | — | — |
| A1[HBPN]A2[HBPN]A3[HBPN] (C2v) | 0.00 | 16.66 | 0.00 | 14.62 | 0.00 | −4.17 | −2.41 | 1.76 | 14.09 | 214.78/5.65 | 2.19/0.06 | −14.31/16.50 |
| A1[HBPB]A2[HBPB]A3[HBPB] (Cs) | — | 16.03 | 0.00 | 3.77 | 0.00 | −4.94 | −3.81 | 1.13 | 1.24 | — | — | — |
| A1[HNPN]A2[HNPN]A3[HNPN] (C2v) | — | 9.43 | 0.00 | 19.65 | 0.00 | −3.66 | −1.65 | 2.01 | 1.22 | 54.97/1.45 | 1.86/0.05 | −23.66/16.94 |
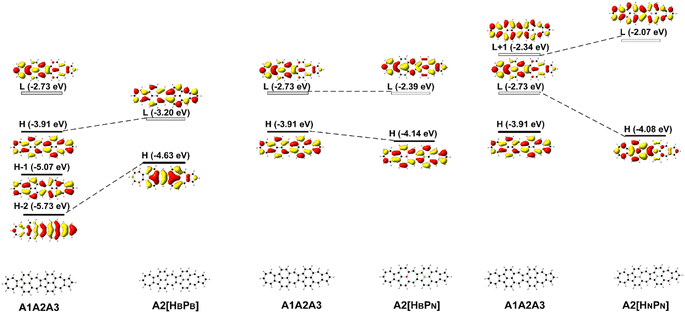 | ||
| Fig. 2 The frontier molecular orbital (H: HOMO; L: LUMO) correlation and energy diagrams of A1A2A3, A2[HBPB], A2[HBPN], and A2[HNPN] predicted with B3LYP/6-31G(d,p). | ||
Since FMOs play an important role in the optical and electronic properties of materials, the substitution of B and N atoms could affect the nonlinear optical properties of the materials. To understand the effect of different heteroatom doping patterns on the nonlinear optical properties of B, N-doped nanographenes, the frontier molecular orbitals of the B, N-doped nanographenes with strong second-order nonlinear optical responses are plotted for comparison (Fig. 3 and S5†). Pπ–π conjugation between boron and the adjacent carbon atoms effectively occurs in the B-doped series of azulene-based nanographenes (Fig. 1), which can be ascribed to the vacant p-orbital of the boron atom. However, such conjugation does not improve the stability of B-doped carbon nanographenes much (Table S1†). The N-atom substituted structure (A1[HN]A3[PN]) has a much stronger static first hyperpolarizability than that of other substituted structures (Table 1). The replacement of C atoms in A1A2A3 by two N atoms causes the occupation of the LUMO in A1A2A3 by two extra electrons from the two N atoms. Such occupation of the LUMO in A1A2A3 leads to the redistribution of molecular orbitals and energy reordering in A1[HNPN], A2[HNPN], A3[HNPN] or A1[HN]A3[PN] (Fig. 3). The HOMO distribution of A1[HNPN] is essentially delocalized, and the HOMO of A3[HNPN] mainly distributes around the N-doped azulene ring, while the HOMO of A2[HNPN] and A1[HN]A3[PN] mainly distributes on the two azulene rings of A1 and A2, respectively. On the other hand, the LUMO of A1[HNPN] mainly distributes on the un-doped A2 and A3, while the LUMO of A3[HNPN] mainly distributes on the un-doped A1 and A2. The LUMO of A2[HNPN] essentially distributes over the entire structure, and this is similar in the case of the LUMO of A1[HN]A3[PN]. The molecular orbital distribution and energy order have conspicuous changes in some FMOs of A1[HNPN] and A3[HNPN] with respect to those of A1A2A3 (Fig. 3). The HOMO–LUMO energy gap changes accordingly in those N-doped A1A2A3s. By further replacing the C atoms at the two ends of the central azulene in A1[HN]A3[PN] with two N atoms, the HOMO and LUMO of A1[HN]A2[HNPN]A3[PN] (A1[HN]A3[PN] and A1[HN]A2[HNPN]A3[PN] have strong second or third NLO responses with respect to those of A1A2A3) can find their counterparts as the LUMO and LUMO + 2 of A1[HN]A3[PN] (Fig. 4). To further check the effect of N-doping on the electronic structure of A1A2A3 based molecules, the frontier molecular orbital correlation diagrams of A1A2A3 and three representative N-doped A1A2A3 molecules (i.e., A2[HNPN], A1[HN]A3[PN], and A1[HN]A2[HNPN]A3[PN] with an extra two N atoms doped at the two ends of the middle azulene in A1[HN]A3[PN]) are plotted in Fig. 4. A1[HN]A2[HNPN]A3[PN] has a high-lying HOMO and LUMO with the smallest HOMO–LUMO energy gap among the three structures, and it is feasibly polarized by an external field. The occupation of the unoccupied FMOs of A1A2A3 upon N-doping leads to the orbital redistribution in FMOs and thus the energy re-ordering of those FMOs as well as the change of the HOMO–LUMO energy gap (Fig. 3 and 4). Such an occupation of the unoccupied FMOs of A1A2A3 upon N-doping also changes the nature of the electron excitations resulting in new electronic and optical properties of these N-doped A1A2A3 molecules. Since the weak stability or high chemical reactivity of an open-shell singlet or triplet as the ground state of the investigated nanographenes possibly hampers their syntheses, isolation, and practical applications, only the second and third order NLO properties of the nanographenes with a closed-shell singlet ground state are predicted (Tables 1 and S1†).
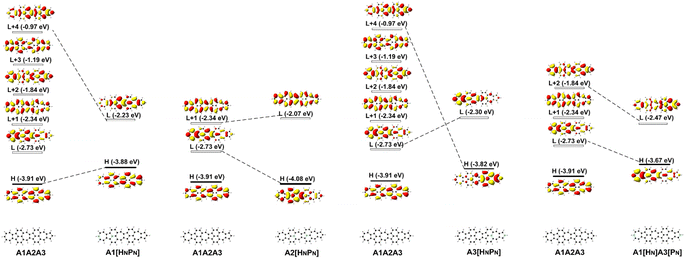 | ||
| Fig. 3 The frontier molecular orbital (H: HOMO; L: LUMO) correlation and energy diagrams of A1A2A3, A1[HNPN], A2[HNPN], A3[HNPN], and A1[HN]A3[PN] predicted with B3LYP/6-31G(d,p). | ||
 | ||
| Fig. 4 The frontier molecular orbital (H: HOMO; L: LUMO) correlation and energy diagrams of A1A2A3, A2[HNPN], A1[HN]A3[PN], and A1[HN]A2[HNPN]A3[PN] predicted with B3LYP/6-31G(d,p). | ||
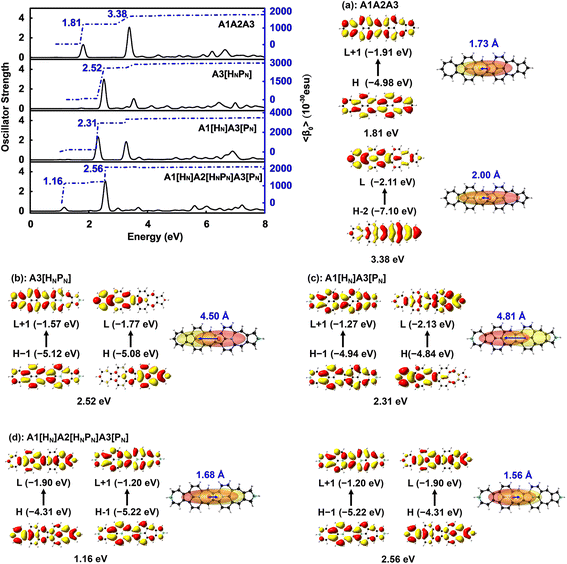
The electronic spectra and the static first hyperpolarizability 〈β0〉 of A3[HNPN], A1[HN]A3[PN], and A1[HN]A2[HNPN]A3[PN]
〈β0〉 of these N-doped A1A2A3s is significantly affected by the doping numbers and positions of N atoms and three molecules, i.e., A3[HNPN], A1[HN]A3[PN], and A1[HN]A2[HNPN]A3[PN] have strong second order NLO responses with respect to that of A1A2A3 (Table 1). The evolution of 〈β0〉 with the electron excitations of these four molecules is plotted (Fig. 5 and Table S2†) to study the correlation of the strong second order NLO properties with structure. In A1A2A3, there are two strong absorption peaks at 1.81 eV (686.5 nm; 1205.73 × 10−30 esu) and 3.38 eV (367.0 nm; 470.66 × 10−30 esu), and these two electron excitations with conspicuous contributions to 〈β0〉 are essentially local excitation (both MOs involved in these excitations locate at the same region) (Fig. 5a), mainly arising from the HOMO → LUMO + 1 (1.81 eV) and HOMO − 2 → LUMO + 1 (3.38 eV) electron transitions.21 The introduction of two N atoms in A1A2A3 results in an obvious blue-shift of electron excitation from 1.81 eV in A1A2A3 to 2.31 eV in A1[HN]A3[PN] and 2.52 eV in A3[HNPN], and these two strong electron excitations (with the strongest oscillator strength) at 2.31 eV (2706.72 × 10−30 esu) in A1[HN]A3[PN] and 2.52 eV (2498.26 × 10−30 esu) in A3[HNPN] contribute predominantly to the 〈β0〉 of A1[HN]A3[PN] and A3[HNPN], respectively. The HOMO − 1 → LUMO + 1 and HOMO → LUMO electron transitions of A3[HNPN] and A1[HN]A3[PN] are intramolecular charge transfer (ICT) based excitations with a large electron transition moment (Fig. 5 and Table S3†), and significantly contribute to the strong second order NLO responses. To quantify the relative degree of local excitation or ICT-based excitation, the real space representation of hole and electron distributions of electron transitions from the ground state to the excited states with major contributions to the 〈β0〉 of these molecules is plotted with Multiwfn.39 The index D (the distance between the center of mass of the hole and the center of mass of the electron) is closely related to the hole–electron Coulomb attraction energy and electron excitation, and is used to quantify the charge transfer associated with electron excitation. The relatively lower electron excitation energy and slightly larger D result in the larger 〈β0〉/N of A1[HN]A3[PN] (91.30 × 10−30 esu) than that of A3[HNPN] (−79.02 × 10−30 esu) (Table 1). The electronic spectra of A1[HN]A2[HNPN]A3[PN] have a weak peak at 1.16 eV (1067.7 nm) in the near-infrared region and a strong peak in the visible light region at 2.56 eV (483.9 nm), respectively. Compared with A1A2A3, the relatively large 〈β0〉/N of A1[HN]A2[HNPN]A3[PN] is primarily attributed to the low electron excitation energies. The replacement of carbon atoms by nitrogen atoms in the azulene-based all-carbon structure further polarizes the system and induces charge redistribution, thus enhancing the second order nonlinear optical properties of A1[HN]A2[HNPN]A3[PN].Two-dimensional second order NLO spectra
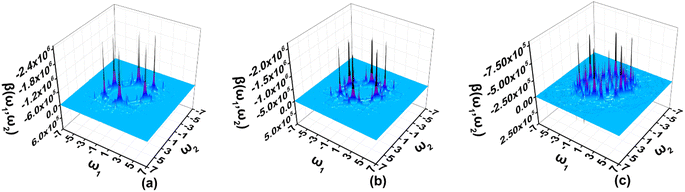
The two-dimensional (2D) second order NLO spectra include second-order NLO properties of the system with all possible combinations of external fields that can be obtained, for example, optical rectification (OR), electro-optical Pockels effect (EOPE), sum frequency generation (SFG), and difference frequency generation (DFG).47–49 In the present work, the 2D second order NLO spectra of A3, A1[HN]A3[PN], and A1[HN]A2[HNPN]A3[PN] are studied under external fields scanned up to 7.00 eV with a step size of 0.05 eV (Fig. 6).In the 2D second order NLO spectra of A3, the strong resonant response (2.44 × 10−24 esu) occurs at the external fields (2.55 eV, –0.05 eV) and (2.55 eV, –2.50 eV) (Fig. 6a), and a fine scan with a step size of 0.005 eV finds the strongest resonant NLO response (6.46 × 10−24 esu) locating at the external fields (2.515 eV, –2.515 eV) (OR) and (2.515 eV, 0.000 eV) (EOPE) (Fig. S6a†). For A1[HN]A3[PN], the strong NLO response (1.93 × 10−24 esu) shifts to the lower energy region (2.35 eV, –0.05 eV) and (2.35 eV, –2.30 eV) (Fig. 6b), and a smaller step size scan finds the OR and EOPE at external fields between 2.315 eV and 2.310 eV (Fig. S6b†). Another strong SFG (1.05 × 10−24 esu) with ω1 + ω2 = 2.310 eV (ω1, ω2 ∈ [0.000 eV, 2.310 eV]) occurs at the external field (1.295 eV, 1.015 eV) (Fig. S6c†). Similarly, a strong DFG response (1.00 × 10−24 esu) is also observed at the external fields (2.310 eV, –1.295 eV) and (2.310 eV, –1.015 eV), which may be caused by the resonance of external fields with the electron excitations at 1.29 eV and 2.31 eV (Fig. 6b and S6d†). In A1[HN]A2[HNPN]A3[PN], the strong second order NLO response (7.34 × 10−25 esu) is located at the external fields (2.55 eV, 0.00 eV) and (2.55 eV, –2.55 eV) (Fig. 6c). A fine scan with a step size of 0.01 eV finds such OR and EOPE (1.62 × 10−24 esu) at 2.56 eV (Fig. S6e†).
In summary, the introduction of N atoms in A1A2A3 makes the strong resonant NLO responses of these molecules move to a higher energy region with respect to that of A1A2A3.21 The strong resonant NLO responses in the visible and near-infrared regions endow these molecules with promising potential applications in light tuning, interface exploring,50,51 and nonlinear nanophotonic devices.7
Static and dynamic second hyperpolarizabilities
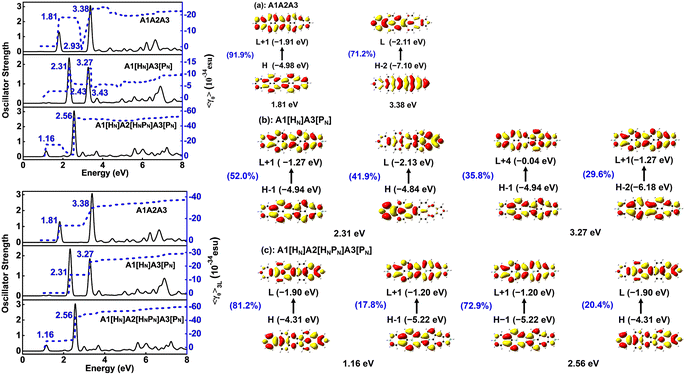
Materials with both strong second and third order NLO properties are vital in applications such as biomedical multimodal imaging,52 and thus it is highly desirable to predict the third order NLO responses of these molecules. Second order NLO responses are limited to non-centrosymmetric systems, while third order NLO responses can be observed in all systems. Both 〈β0〉 and 〈γ0〉 reflect the intrinsic properties of materials and the strength of the materials' NLO response to an external field. According to the decomposition of the total 〈γ0〉 into 〈γ0〉3L and 〈γ0〉4L [Eqn. (3)], 〈γ0〉3L and 〈γ0〉4L of all the studied nanographenes are of the same order of magnitude; however, 〈γ0〉3L has a determinant contribution to 〈γ0〉. The 〈γ0〉4L of these molecules essentially contributes unfavorably, resulting in a weakening of 〈γ0〉 (Table 1). Among these, A1[HN]A2[HNPN]A3[PN] has the largest 〈γ0〉 of –52.44 × 10−34 esu, and it is much larger than that of the other nanographenes with the same size, in which 〈γ0〉3L makes a predominant contribution to 〈γ0〉. The evolution of 〈γ0〉 and 〈γ0〉3L with the electron excitation of A1A2A3, A1[HN]A3[PN], and A1[HN]A2[HNPN]A3[PN] is depicted in Fig. 7 to investigate the influence of N-doping on the third order NLO properties. The 〈γ0〉 of A1A2A3, A1[HN]A3[PN], and A1[HN]A2[HNPN]A3[PN] is −21.74 × 10−34 esu, −9.57 × 10−34 esu, and −52.44 × 10−34 esu, respectively. In A1A2A3, three main electron excitations at 1.81 eV (–18.43 × 10−34 esu), 2.93 eV (2.26 × 10−34 esu), and 3.38 eV (–21.46 × 10−34 esu) have important contributions to 〈γ0〉. In A1[HN]A3[PN], the absorption peaks at 2.31 eV and 3.27 eV have significant contributions to 〈γ0〉, while the absorption peaks at 2.43 eV and 3.43 eV have opposite contributions to 〈γ0〉, thus resulting in a small 〈γ0〉. The absorption peaks at 1.16 eV and 2.56 eV in A1[HN]A2[HNPN]A3[PN] make significant contributions to 〈γ0〉, and the absorption peak at 2.37 eV makes a small opposite contribution to 〈γ0〉. The large contribution to 〈γ0〉 from the electron absorption at 2.56 eV leads to the large 〈γ0〉 of A1[HN]A2[HNPN]A3[PN]. The transition nature of the electron excitations at 1.16 eV and 2.56 eV are similar while with different weights of electrons transition from occupied MOs to virtual MOs (Fig. 7), and this explains that these two absorption peaks make joint contributions to 〈γ0〉 (Table S4†).Since the nanographenes lie along the z direction, the largest contribution to γ could come from the γz along the dipole direction z. The γ3L(zzzz) is invoked and can be written as,
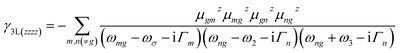 | (5) |
In A1A2A3, the electron excitations at 1.81 eV (–13.46 × 10−34 esu) and 3.38 eV (–16.09 × 10−34 esu) have dominant contributions to 〈γ0〉3L. In A1[HN]A3[PN], the absorption peaks at 2.31 eV and 3.27 eV have dominant contributions to 〈γ0〉3L. The transition nature of the electron excitations in A1A2A3 at 1.81 eV and 3.38 eV is similar to those at 2.31 eV and 3.27 eV in A1[HN]A3[PN], respectively, and such a similarity leads to a similar evolution of 〈γ0〉 with electron excitation in A1A2A3 and A1[HN]A3[PN]. On the one hand, the large 〈β0〉 of A1[HN]A3[PN] is dominantly contributed by the charge transfer based electron excitation at 2.31 eV (Fig. 5). In other words, different electron excitations are responsible for the second order and third order NLO properties in A1[HN]A3[PN]. In A1[HN]A2[HNPN]A3[PN], the electron excitations at 1.16 eV (–15.47 × 10−34 esu) and 2.56 eV (–50.55 × 10−34 esu) contribute dominantly to 〈γ0〉 with major contributions from 〈γ0〉3L, and these two electron excitations also make dominant contributions to 〈β0〉.
A1A2A3, A1[HN]A3[PN], and A1[HN]A2[HNPN]A3[PN] have similar evolution patterns to those of γ3L(zzzz) with electron excitations (Table S4†), and two strong absorption peaks have a positive contribution to γ3L(zzzz). With the doping of four N atoms, the 〈γ0〉 of A1[HN]A2[HNPN]A3[PN] is significantly larger than that of A1A2A3 and A1[HN]A3[PN]. The three-level term (S0 → S2 → S0 → S2 → S0), (S0 → S1 → S0 → S9 → S0), (S0 → S9 → S0 → S1 → S0), and (S0 → S9 → S0 → S9 → S0) processes in A1[HN]A2[HNPN]A3[PN] have major contributions to 〈γ0〉 (Table S4†). In the evolution of γ3L(zzzz) with electron excitations in A1[HN]A2[HNPN]A3[PN], the S0 → S9 electron transition at 2.56 eV related photon processes have the largest contribution to 〈γ0〉.
According to the evolution of the static first and second hyperpolarizabilities with the electron excitations of these nanographenes, charge transfer based electron excitations induced by N-doping enhance the second order NLO properties (〈β0〉) and the opposite contributions to the third order NLO properties from other electron excitations diminish the 〈γ0〉 of A1[HN]A3[PN]. While in A1[HN]A2[HNPN]A3[PN], the contributions from the electron excitations at 1.16 eV and 2.56 eV to 〈β0〉 and 〈γ0〉 enhance both the second and third order NLO properties, and such two electron excitations are induced by the doping of N atoms.
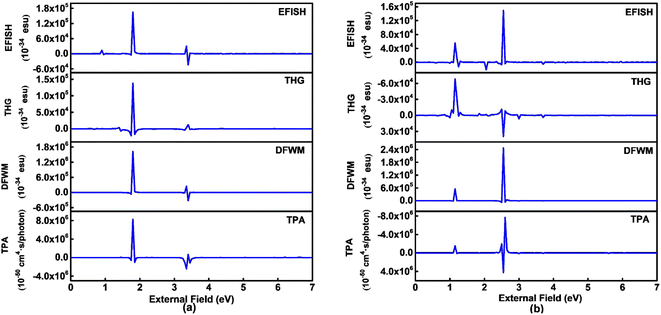
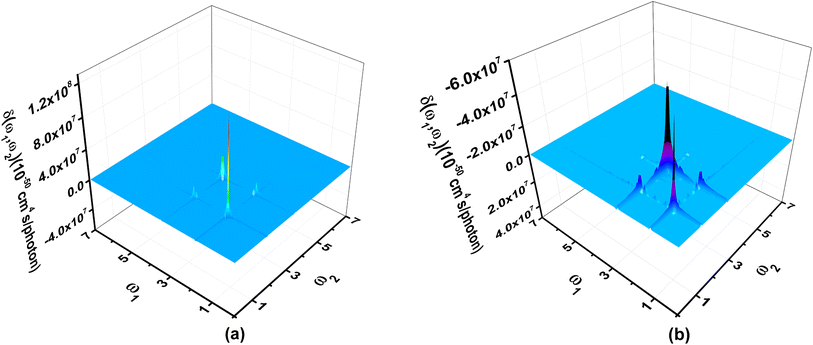
Third order NLO processes include EFISH (electric field induced second harmonic generation), THG (third harmonic generation), DFWM (degenerate four wave mixing), TPA, and others. The third order NLO responses of A1A2A3 and A1[HN]A2[HNPN]A3[PN] under external fields up to 7.00 eV with a step size of 0.05 eV are predicted by using the SOS model (Fig. 8). The strong responses of A1A2A3 in the third order NLO processes mainly occur in the regions of external fields 1.00–2.00 eV and 3.00–4.00 eV (Fig. 8a) ascribed to the strong electron excitations at 1.00 eV and 2.00 eV (Table S6 and Fig. S7†). EFISH has a strong response at 1.80 eV with a major contribution from the electron excitation at about 1.81 eV. The strongest THG response (1.38 × 10−29 esu) also occurs at the external field of 1.80 eV. In the DFWM process, there are two positive responses at 1.80 eV (1.62 × 10−28 esu) and 3.35 eV (2.49 × 10−29 esu), and a negative one (–3.24 × 10−29 esu) at 3.40 eV. These responses have prominent contributions from the electron excitations at 1.81 eV (685.1 nm) and 3.38 eV (366.9 nm), respectively. The TPA cross-section has a maximum at 1.80 eV (688.9 nm; 8.25 × 10−44 cm4 s per photon), and another strong one occurs at 3.35 eV (370.2 nm; –2.42 × 10−44 cm4 s per photon). Compared with the NLO responses of A1A2A3, the NLO responses of A1[HN]A2[HNPN]A3[PN] mainly occur at 1.00–2.00 eV and 2.00–3.00 eV (Fig. 7b). In the EFISH process of A1[HN]A2[HNPN]A3[PN], the response reaches a maximum of 1.49 × 10−29 esu at 2.55 eV (486.3 nm) and the contribution to such a response mainly comes from the electron excitation at 2.56 eV, similar to the case in the THG and DFWM (Fig. 8b and Table S7†) processes. There are three major TPA peaks in the near-infrared and ultraviolet-visible regions [i.e., 1.15 eV (1078.3 nm), 2.50 eV (496.0 nm), and 2.55 eV (486.3 nm)] with the strongest TPA peak at 2.55 eV (4.27 × 10−44 cm4 s per photon), which is caused by the resonance of external fields with the electron excitations at 2.56 eV (Table S7 and Fig. S8†). By and large, these strong third order NLO responses of A1A2A3 and A1[HN]A2[HNPN]A3[PN] mainly occur at visible or (and) near-infrared regions in resonance with electron excitations. The research of TPA cross-sections is crucial for understanding the correlation between the molecular structure and electronic and optical properties of novel organic materials.53 The large TPA cross-sections of A1A2A3 and A1[HN]A2[HNPN]A3[PN] in the visible or (and) near-infrared regions provide the possibility to design functional TPA materials. To simulate TPA responses under different external fields, the 2DTPA spectra54 of these two molecules under external fields up to 7.0 eV are predicted by using TD-CAM-B3LYP/6-31++G(d,p)-SOS (Fig. 9). 2DTPA can be divided into two parts: STPA (−ω; ω, ω, −ω)—TPA with one frequency (self-phase modulation) and CTPA (−ω1; ω1, ω2, −ω2)—TPA with two different frequencies (cross-phase modulation).55 These two molecules have similar 2DTPA spectra. In the 2DTPA spectra of A1A2A3, the strongest STPA response (1.26 × 10−42 cm4 s per photon) occurs at 1.80 eV (Fig. 9a), and fine scanning with a step size of 0.01 eV finds another strong resonant STPA response (1.45 × 10−43 cm4 s per photon) at 3.38 eV (Fig. S9a†). There are four strong CTPA responses (6.74 × 10−44 cm4 s per photon) and (3.09 × 10−44 cm4 s per photon) occurring at the external fields (1.85 eV, 3.35 eV), (3.35 eV, 1.85 eV) and (1.90 eV, 3.35 eV), (3.35 eV, 1.90 eV) (Fig. 9a). In A1[HN]A2[HNPN]A3[PN], the strongest STPA response moves to the low energy region at 1.15 eV (−5.71 × 10−43 cm4 s per photon) (Fig. 9b), further fine scanning locates the strongest STPA resonant response (1.00 × 10−42 cm4 s per photon) at 1.16 eV (Fig. S9b†), while another strong STPA response (−5.53 × 10−43 cm4 s per photon) occurs at 2.60 eV (Fig. 9b). Similar to A1A2A3, strong CTPA responses (−1.10 × 10−44 cm4 s per photon) and (−1.06 × 10−44 cm4 s per photon) are observed at the higher energy regions with external fields (1.10/2.55 eV, 2.55/1.10 eV) and (1.15/2.50 eV, 2.50/1.15 eV) (Fig. 9b). Such high S/CTPA cross-sections under external fields confer these carbon-based functional nanomaterials potential applications in optical power limiting56 and two-photon data storage,57 biophotonic two-photon fluorescence cell imaging58 and photodynamic therapy,5,59 and nano–micro fabrication.60,61
Conclusions
A series of N-doped azulene-based molecules has been systematically investigated by using quantum chemical calculations combined with the SOS model. A molecular design strategy to enhance the stability and the second or (and) third order nonlinear optical properties by replacing the carbon atoms at the two ends of the azulene moiety in azulene-based nanographene (A1A2A3) with nitrogen atoms is proposed. This proposed electronic structure modulation strategy through modifying the nuclear potential and electron occupation would enlighten the design, fabrication, and application of more advanced carbon-based functional nanomaterials and it is readily extendable to other functional materials design.Replacing C atoms at the two ends of A1A2A3 with electron-rich N atoms changes the low-lying frontier unoccupied molecular orbitals in A1A2A3 to occupied molecular orbitals in N-doped A1A2A3, which gives rise to an enlarged HOMO–LUMO energy gap, induces charge redistribution, modifies the nature of electron excitations, and thus brings about strong second order NLO responses. The static first hyperpolarizability (〈β0〉) of A1[HN]A3[PN] reaches 91.30 × 10−30 esu per heavy atom. Further introduction of N atoms into the two ends of the central azulene moiety of A1[HN]A3[PN] leads to an enhanced static second hyperpolarizability (〈γ0〉) (−52.44 × 10−34 esu) in A1[HN]A2[HNPN]A3[PN] ascribed to the two N-doping induced electron excitations with complementary contributions to the 〈γ0〉. Heteroatom doping is an important means to improve the NLO response of carbon-based nanographene with prospective broad applications. The strong second order and the large dynamic third order NLO responses render these azulene-based nanographenes as potential multifunction NLO materials. The present study is expected to provide insight into designing new azulene-based nanomaterials for optoelectronic applications.
Author contributions
Cui-Cui Yang wrote the manuscript with parts written by Ya Qing Zhang. Ya Qing Zhang conceived and designed the molecular structures, carried out all computations, summarized and analyzed the results with help from Cui-Cui Yang. Jia-Ying Ma conducted the preliminary exploration of similar structures. Wei Quan Tian supervised all the works and revised the manuscript. All the authors participated in the data analysis, discussion of results, and revision of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (21673025). The Open Projects of the State Key Laboratory of Supramolecular Structure and Materials (JLU) (SKLSSM2023022) and the Key Laboratory of Polyoxometalate and Reticular Material Chemistry of Ministry of Education (NENU) are also acknowledged.References
- J. Li, M. Chen, S. Hou, L. Zhao, T. Zhang, A. Jiang, H. Li and J. Hao, Carbon, 2022, 191, 555–562 CrossRef CAS.
- M. Zhang, X. Xu, J. Liu, Y. Jiang, J. Wang, N. Dong, C. Chen, B. Zhu, Y. Liang, T. Fan and J. Xu, ACS Appl. Mater. Interfaces, 2022, 14, 33787–33796 CrossRef CAS PubMed.
- S.-Y. Zhang, X. Shu, Y. Zeng, Q.-Y. Liu, Z.-Y. Du, C.-T. He, W.-X. Zhang and X.-M. Chen, Nat. Commun., 2020, 11, 2752 CrossRef CAS PubMed.
- X.-S. Xing, R.-J. Sa, P.-X. Li, N.-N. Zhang, Z.-Y. Zhou, B.-W. Liu, J. Liu, M.-S. Wang and G.-C. Guo, Chem. Sci., 2017, 8, 7751–7757 RSC.
- H. Liu, Y. Yang, A. Wang, M. Han, W. Cui and J. Li, Adv. Funct. Mater., 2016, 26, 2561–2570 CrossRef CAS.
- B. Sun, L. Wang, Q. Li, P. He, H. Liu, H. Wang, Y. Yang and J. Li, Biomacromolecules, 2017, 18, 3506–3513 CrossRef CAS PubMed.
- J. He, H. Chen, J. Hu, J. Zhou, Y. Zhang, A. Kovach, C. Sideris, M. C. Harrison, Y. Zhao and A. M. Armani, Nanophotonics, 2020, 9, 3781–3804 CrossRef.
- P. Karamanis, N. Otero and C. Pouchan, J. Am. Chem. Soc., 2014, 136, 7464–7473 CrossRef CAS PubMed.
- J. D. Cox and F. J. García de Abajo, ACS Photonics, 2015, 2, 306–312 CrossRef CAS.
- J. D. Cox, I. Silveiro and F. J. García de Abajo, ACS Nano, 2016, 10, 1995–2003 CrossRef CAS PubMed.
- C. Lambert, G. Noll, M. Zabel, F. Hampel, E. Schmalzlin, C. Brauchle and K. Meerholz, Chem.–Eur. J., 2003, 9, 4232–4239 CrossRef CAS PubMed.
- Y. Yamaguchi, K. Ogawa, K. I. Nakayama, Y. Ohba and H. Katagiri, J. Am. Chem. Soc., 2013, 135, 19095–19098 CrossRef CAS PubMed.
- J.-X. Dong and H.-L. Zhang, Chin. Chem. Lett., 2016, 27, 1097–1104 CrossRef CAS.
- D. Dunlop, L. Ludvíková, A. Banerjee, H. Ottosson and T. Slanina, J. Am. Chem. Soc., 2023, 145, 21569–21575 CrossRef CAS PubMed.
- G. W. Wheland and D. E. Mann, J. Chem. Phys., 1949, 17, 264–268 CrossRef CAS.
- O. V. Yazyev and S. G. Louie, Nat. Mater., 2010, 9, 806–809 CrossRef CAS PubMed.
- Y. Wei, J. Wu, H. Yin, X. Shi, R. Yang and M. Dresselhaus, Nat. Mater., 2012, 11, 759–763 CrossRef CAS PubMed.
- P. G. Lacroix, I. Malfant, G. Iftime, A. C. Razus, K. Nakatani and J. A. Delaire, Chem.–Eur. J., 2000, 6, 2599–2608 CrossRef CAS PubMed.
- L. Cristian, I. Sasaki, P. G. Lacroix, B. Donnadieu, I. Asselberghs, K. Clays and A. C. Razus, Chem. Mater., 2004, 16, 3543–3551 CrossRef CAS.
- A. Migalska-Zalas, Y. El kouari and S. Touhtouh, Opt. Mater., 2012, 34, 1639–1643 CrossRef CAS.
- C.-C. Yang, J.-Y. Ma, X. Su, X.-L. Zheng, J. Chen, Y.-Y. He, W. Q. Tian, W.-Q. Li and L. Yang, FlatChem, 2022, 33, 100362 CrossRef CAS.
- N. Hou, R. Feng and X.-H. Fang, ChemistrySelect, 2021, 6, 10806–10816 CrossRef CAS.
- H. Xu, D. L. Elder, L. E. Johnson, Y. de Coene, S. R. Hammond, W. Vander Ghinst, K. Clays, L. R. Dalton and B. H. Robinson, Adv. Mater., 2021, 33, 2104174 CrossRef CAS PubMed.
- X.-Y. Wang, F.-D. Zhuang, R.-B. Wang, X.-C. Wang, X.-Y. Cao, J.-Y. Wang and J. Pei, J. Am. Chem. Soc., 2014, 136, 3764–3767 CrossRef CAS PubMed.
- C. Dou, Z. Ding, Z. Zhang, Z. Xie, J. Liu and L. Wang, Angew. Chem., Int. Ed., 2015, 54, 3648–3652 CrossRef CAS PubMed.
- F.-D. Zhuang, Z.-H. Sun, Z.-F. Yao, Q.-R. Chen, Z. Huang, J.-H. Yang, J.-Y. Wang and J. Pei, Angew. Chem., Int. Ed., 2019, 58, 10708–10712 CrossRef CAS PubMed.
- J.-K. Li, X.-Y. Chen, Y.-L. Guo, X.-C. Wang, A. C. H. Sue, X.-Y. Cao and X.-Y. Wang, J. Am. Chem. Soc., 2021, 143, 17958–17963 CrossRef CAS PubMed.
- W. Li, C. Z. Du, X. Y. Chen, L. Fu, R. R. Gao, Z. F. Yao, J. Y. Wang, W. Hu, J. Pei and X. Y. Wang, Angew. Chem., Int. Ed., 2022, 134, e202201464 CrossRef.
- C. Chen, M. W. Wang, X. Y. Zhao, S. Yang, X. Y. Chen and X. Y. Wang, Angew. Chem., Int. Ed., 2022, 134, e202200779 CrossRef.
- M. Zhang, G. Li and L. Li, J. Mater. Chem. C, 2014, 2, 1482–1488 RSC.
- N. Otero, C. Pouchan and P. Karamanis, J. Mater. Chem. C, 2017, 5, 8273–8287 RSC.
- K. Chen, X. Zheng, C. Yang, W. Q. Tian, W. Li and L. Yang, Chem. Res. Chin. Univ., 2022, 38, 579–587 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- W. Q. Tian, V1.01. Linear Scaling of the Sum-Over-States Model in Nonlinear Optics; Registration No. 2017SR526488 and Classification No. 30219-7500, Copyright Protection Center of China, Beijing, China Search PubMed.
- B. J. Orr and J. F. Ward, Mol. Phys., 1971, 20, 513–526 CrossRef CAS.
- D. M. Bishop, J. Chem. Phys., 1994, 100, 6535–6542 CrossRef CAS.
- W. Q. Tian, J. Comput. Chem., 2012, 33, 466–470 CrossRef CAS PubMed.
- O. Roslyak, C. A. Marx and S. Mukamel, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 79, 063827 CrossRef PubMed.
- D. M. Bishop, Adv. Chem. Phys., 1998, 104, 1–40 CrossRef CAS.
- C. Castiglioni, M. Del Zoppo, P. Zuliani and G. Zerbi, Synth. Met., 1995, 74, 171–177 CrossRef CAS.
- L. Lepetit, G. Chériaux and M. Joffre, J. Nonlinear Opt. Phys. Mater., 1996, 5, 465–476 CrossRef CAS.
- L. Lepetit and M. Joffre, Opt. Lett., 1996, 21, 564–566 CrossRef CAS PubMed.
- J. Chen, M. Q. Wang, X. Zhou, L. Yang, W.-Q. Li and W. Q. Tian, Phys. Chem. Chem. Phys., 2017, 19, 29315–29320 RSC.
- S. Yamaguchi and T. Tahara, J. Phys. Chem. C, 2015, 119, 14815–14828 CrossRef CAS.
- G.-H. Deng, Y. Qian and Y. Rao, J. Chem. Phys., 2019, 150, 024708 CrossRef PubMed.
- S. Yue, M. N. Slipchenko and J. X. Cheng, Laser Photonics Rev., 2011, 5, 496–512 CrossRef PubMed.
- M. Pawlicki, H. A. Collins, R. G. Denning and H. L. Anderson, Angew. Chem., Int. Ed., 2009, 48, 3244–3266 CrossRef CAS PubMed.
- X.-L. Zheng, L. Yang, B. Shang, M.-Q. Wang, Y. Niu, W.-Q. Li and W. Q. Tian, Phys. Chem. Chem. Phys., 2020, 22, 14225–14235 RSC.
- U. Gubler and C. Bosshard, Adv. Polym. Sci., 2002, 158, 123–191 CrossRef CAS.
- C. Tang, Q. Zheng, H. Zhu, L. Wang, S.-C. Chen, E. Ma and X. Chen, J. Mater. Chem. C, 2013, 1, 1771–1780 RSC.
- J. Lott, C. Ryan, B. Valle, J. R. Johnson III, D. A. Schiraldi, J. Shan, K. D. Singer and C. Weder, Adv. Mater., 2011, 23, 2425–2429 CrossRef CAS PubMed.
- A. Parthasarathy, H.-Y. Ahn, K. D. Belfield and K. S. Schanze, ACS Appl. Mater. Interfaces, 2010, 2, 2744–2748 CrossRef CAS PubMed.
- L. T. Bergendahl and M. J. Paterson, J. Phys. Chem. B, 2012, 116, 11818–11828 CrossRef CAS PubMed.
- W. Zhou, S. M. Kuebler, K. L. Braun, T. Yu, J. K. Cammack, C. K. Ober, J. W. Perry and S. R. Marder, Science, 2002, 296, 1106–1109 CrossRef CAS PubMed.
- K. Liu, H. Ding, S. Li, Y. Niu, Y. Zeng, J. Zhang, X. Du and Z. Gu, Nat. Commun., 2022, 13, 4563 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc04443b |
| ‡ Y. Q. Zhang and C. C. Yang contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |