Open Access Article
Open Access ArticleWhat are the minimal folding seeds in proteins? Experimental and theoretical assessment of secondary structure propensities of small peptide fragments†
Zuzana
Osifová‡
 ab,
Tadeáš
Kalvoda‡
ab,
Tadeáš
Kalvoda‡
 *a,
Jakub
Galgonek
*a,
Jakub
Galgonek
 a,
Martin
Culka
a,
Martin
Culka
 a,
Jiří
Vondrášek
a,
Petr
Bouř
a,
Jiří
Vondrášek
a,
Petr
Bouř
 a,
Lucie
Bednárová
a,
Lucie
Bednárová
 *a,
Valery
Andrushchenko
*a,
Valery
Andrushchenko
 *a,
Martin
Dračínský
*a,
Martin
Dračínský
 *a and
Lubomír
Rulíšek
*a and
Lubomír
Rulíšek
 *a
*a
aInstitute of Organic Chemistry and Biochemistry of the Czech Academy of Sciences, Flemingovo náměstí 2, 160 00, Praha 6, Czech Republic. E-mail: tadeas.kalvoda@uochb.cas.cz; andrushchenko@uochb.cas.cz; dracinsky@uochb.cas.cz; rulisek@uochb.cas.cz
bDepartment of Organic Chemistry, Faculty of Science, Charles University, Hlavova 2030, Prague 128 00, Czech Republic
First published on 23rd November 2023
Abstract
Certain peptide sequences, some of them as short as amino acid triplets, are significantly overpopulated in specific secondary structure motifs in folded protein structures. For example, 74% of the EAM triplet is found in α-helices, and only 3% occurs in the extended parts of proteins (typically β-sheets). In contrast, other triplets (such as VIV and IYI) appear almost exclusively in extended parts (79% and 69%, respectively). In order to determine whether such preferences are structurally encoded in a particular peptide fragment or appear only at the level of a complex protein structure, NMR, VCD, and ECD experiments were carried out on selected tripeptides: EAM (denoted as pro-‘α-helical’ in proteins), KAM(α), ALA(α), DIC(α), EKF(α), IYI(pro-β-sheet or more generally, pro-extended), and VIV(β), and the reference α-helical CATWEAMEKCK undecapeptide. The experimental data were in very good agreement with extensive quantum mechanical conformational sampling. Altogether, we clearly showed that the pro-helical vs. pro-extended propensities start to emerge already at the level of tripeptides and can be fully developed at longer sequences. We postulate that certain short peptide sequences can be considered minimal “folding seeds”. Admittedly, the inherent secondary structure propensity can be overruled by the large intramolecular interaction energies within the folded and compact protein structures. Still, the correlation of experimental and computational data presented herein suggests that the secondary structure propensity should be considered as one of the key factors that may lead to understanding the underlying physico-chemical principles of protein structure and folding from the first principles.
1. Introduction
Understanding fully the relation between the amino acid sequence and the three-dimensional structure of proteins has been a subject of intense research over the last six decades.1–3 The recent unprecedented success of DeepMind's AlphaFold2 (AF2) algorithm at the 14th Critical Assessment of Structure Prediction (CASP14)4 contest is viewed as a major breakthrough in predicting protein 3-D structures.5 However, deep-learning neural networks used in AF2 do not reveal too many of the underlying physico-chemical/biophysical principles. In fact, the process by which AF2 and other state-of-the-art algorithms reach the final protein structure does not necessarily correspond to the steps of actual protein folding as described by experimental studies.6 Thus, there is still a need for a deeper understanding of the ‘Aufbau’ principle of protein 3-D structures and protein folding by an ab initio approach. This may allow us to fully grasp the beauty of one of nature's most fundamental processes.The traditional physical chemist's view of protein folding acknowledges a delicate interplay between several enthalpic and entropic terms, including interactions of the protein surface with the environment (solvent). On the protein side, the enthalpic contributions can be decomposed into an (unfavorable, destabilizing) local strain energy and mostly favorable (stabilizing) intramolecular (inter-residual) interaction energy. Strain energy appears because small fragments of the protein are not in their optimal geometry. We have shown that the strain energy may easily reach up to ∼5 kcal mol−1 per amino acid residue7 and is then expected to be compensated by the favorable intramolecular interactions. Interestingly, it seems that it is rather the favorable intramolecular interaction than low strain, which is conserved by evolution.7,8 Indeed, it has already been demonstrated that Flory isolated-pair hypothesis is invalid due to the significant interactions between neighboring amino acids.9–11 Since proteins exist in the condensed phase, the solvation (free) energy difference between the folded and unfolded states of a protein also plays a huge role in determining the final structure.12 Last but not least, the changes in the solvent entropy as well as the reduction of the conformational entropy of the protein are also considered to be major factors in its folding and stable conformations.13–16
One of the key questions – related to the above physico-chemical principles – that remains largely unsolved is whether the determinants of a secondary structure are “imprinted” in shorter protein building blocks, i.e. polypeptide chains of varying lengths.17–21 Do the polypeptide chains comprising proteins have variable ‘stiffness’ that predetermines them to be preferably used in one or the other secondary structure motif? Or is the protein structure a purely global phenomenon that only appears at the level of the full-length sequence of a protein?
To address this question, we recently presented a series of computational and bioinformatics studies providing a more rigorous theoretical framework to address protein folding from first principles (ab initio).7,8,22–24 First, for each of all 8000 possible canonical amino acid triplets (X1X2X3), we evaluated statistical probability of finding X1X2X3 in a particular secondary structure motif (mostly helical or extended) in any protein in a non-redundant subset of the Protein Data Bank (Top8000 database).23 This allowed us to identify the statistically most pro-helical (α-helix) and pro-extended (i.e., torsion angles corresponding to a single strand of the β-sheet) amino acid triplets (Fig. 1). Populations on both ends of the helical/extended ‘distribution’ were close to 80% which we consider statistically significant (e.g., EAM triplet is found 74% in α-helical, 3% in extended, and the rest mostly in unstructured parts of proteins, whereas VIV is found 79% in extended and 8% in α-helical).
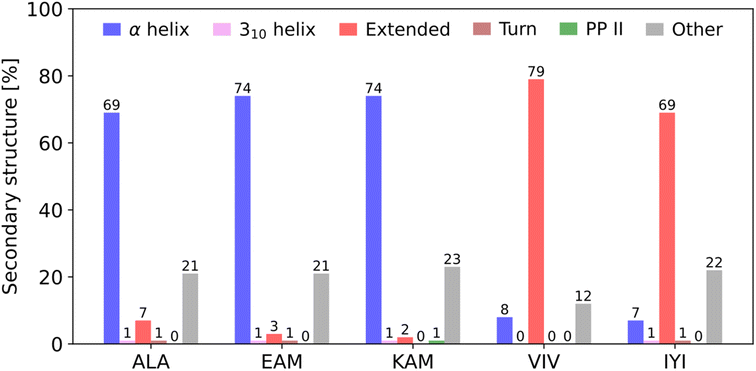 | ||
| Fig. 1 Secondary structure preferences of selected pro-α-helical and pro-extended (β-sheet) amino acid triplets in the Top8000 subset of the PDB. The original analysis23 was updated using the DSSP algorithm, version 4.3,25,26 which can also detect polyproline II helices. Only triplets where all three amino acids adopt the same secondary structure were considered, i.e., ααα for α-helix, βββ for β-sheet, etc. “Mixed” triplets, such as ααβ and unordered structures were included in the category “Other”. Bend, bridge, and π-helix secondary structures were detected in less than 1% of cases for all selected triplets. | ||
We correlated this statistically observed propensity with the results of a large-scale quantum mechanical conformational study on the corresponding N- and C-termini capped tripeptides.22 The computed free energy differences between the lowest-energy helical and extended conformers of the capped tripeptide, N-Ac-X1X2X3-NHCH3, ΔGHE = G(lowest helical) − G(lowest extended), showed that pro-helical tripeptides (such as EAM) tend to have lower ΔGHE values, by 1–2 kcal mol−1, than pro-extended ones (such as VIV).23 Thus, they might be considered more suitable building blocks for α-helices than their pro-extended counterparts (and vice versa), which is in line with their populations in protein secondary structures (vide supra). This suggested that the propensities for adopting a particular secondary structure might indeed be encoded in short peptide fragments. In addition, we showed on a limited set that the ‘pro-extended’ tripeptides/triplets benefit from the presence of an interacting partner to a significantly greater degree than the ‘pro-helical’ triplets.23
In this work, we materialized our theoretical findings and computational predictions by synthesizing selected (capped) tripeptides with expected extended or helical propensities. We do not expect that the short peptide sequences would adopt a single conformation or would form stable helices (though N-Ac-X1X2X3-NH2 species have exactly a minimal length for one α-helical turn) or purely extended forms. However, we may expect to find some tendencies (propensities) to one or the other type of secondary structures. For this aim, we probed their structural features experimentally, combining nuclear magnetic resonance (NMR) and circular dichroism (vibrational – VCD and electronic – ECD) spectroscopies. These are excellent, and to a certain degree complementary, tools for gaining valuable insights into the structure of biomolecules in solution.27–32
There are several NMR observables affected by the conformation of peptides: chemical shifts, indirect couplings (J-couplings), temperature dependence of chemical shifts of amide hydrogens or the nuclear Overhauser effect.33–35 Our investigation of the secondary structure with NMR is mostly based on the measurement of temperature dependence of the 3JNH,Hα coupling constants. Indirect coupling (J-coupling) has become an indispensable NMR parameter for structural analysis because it is closely related to molecular conformation according to the Karplus equations.36–41 The relation between amide NH and Hα hydrogen atoms 3JNH,Hα (in Hz) and the backbone torsion angle φ has been calibrated on known structures:42
3JNH,Hα = 6.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2(φ − 60°) − 1.4 cos2(φ − 60°) − 1.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(φ − 60°) + 1.9 cos(φ − 60°) + 1.9 | (1) |
As a rule of thumb, helices exhibit 3JNH,Hα lower than 6 Hz, β-sheet structures exhibit 3JNH,Hα higher than 8 Hz and random coil structures are in between.27 An advantage of J-couplings is that they are not significantly dependent on solvent43 or temperature,44,45i.e. any temperature dependence of J-couplings most probably reflects a conformational change. The temperature dependence of 3JNH,Hα was recently used in a study of short peptides and was interpreted in terms of conformational redistribution.46
A disadvantage of NMR is that only the φ angle of the Ramachandran plot could be measured (on non-labeled peptides) and thus the technique may not distinguish left-handed polyproline II (PPII) and right-handed (α-) helices. Information about the ψ angle (to distinguish between PPII and α-helix) can be obtained from NMR experiments with 13C and 15N-labeled peptides.47–49 However, PPII conformation is mostly found in unordered peptides, while it is rarer in proteins (c.f.Fig. 1 and also ref. 50). The helical chirality can be well distinguished by CD spectroscopy (VCD or ECD), which, however, does not provide residue-specific information, distinguishing (e.g.) αββ vs. ββα conformations. Instead, CD spectra reflect the average conformation.28,32
The experimental data for all studied peptides were complemented by accurate quantum chemical calculations including the solvation (DFT-D3//COSMO-RS), calibrated in the previous work.51 These followed exhaustive conformational sampling covering all three structural motives and provided unambiguous structure/energy mapping. The correlation of experimental and theoretical data allowed us to make several conclusions concerning the bottom-up approach in protein structure predictions ab initio.
2. Methods
2.1. Selected peptides
Based on our previous work,22–24 we selected five tripeptides with quite pronounced statistical preference for a particular secondary structure in proteins: EAM(α-helical), KAM(α), ALA(α), IYI(β-sheet/extended), and VIV(β), gauged by their respective secondary structure populations in the three-dimensional protein structures (Fig. 1).In addition, we analyzed the computational data from our previous work.22 Within the set of all 8000 tripeptides (200 conformers each, comprising the P-CONF_1.6M database), we ranked the tripeptides by the lowest computed ΔGHE (primary criterion) and ΔGH/PPII (secondary criterion) values. Thus, we searched for the potentially most pro-α-helical tripeptides (c.f. SI.xlsx Table (ESI†) with the ΔGHE and ΔGH/PPII values for all 8000 tripeptides). We excluded the tripeptides containing proline, as they are not expected to adopt extended conformations. Also, we preferred to avoid histidines due to their ambiguous protonation states. This resulted in addition of two tripeptides with potential α-helical propensity: DIC(α) and EKF(α). Thus, judged purely from quantum chemical computations, they should belong to the tripeptides with the highest tendencies/propensities for α-helical structures.
Throughout computations, all peptides were in their most frequent protonation state at pH 7 in water, i.e., K (Lys) and R (Arg) side chains are positively charged, and E (Glu) and D (Asp) side chains are charged negatively. In addition, EAM and IYI tripeptides were also used for the determination of the effect of solvent on their secondary structure (c.f. Fig. S10 in the ESI†).
For both computational and experimental analyses, we used a model of a peptide with an acetylated N-terminus and amidated C-terminus, shown in Fig. 2.
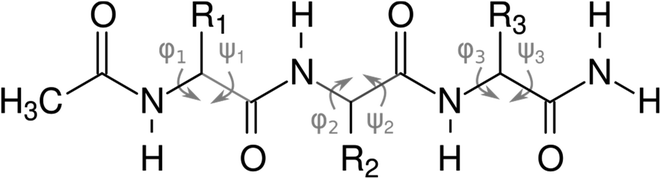 | ||
| Fig. 2 N-Acetylated tripeptides used for the calculations and experiments, with the main chain dihedral angles (φ and ψ) highlighted. | ||
Finally, a reference CATWEAMEKCK undecapeptide, in which the EAM triplet is in the core of the α-helix as found in the chain B of the 20-α-hydroxysteroid dehydrogenase (PDBID 1Q5M, Fig. S1 in the ESI†), was investigated.52 We presumed that it might also adopt a stable α-helical conformation in solution. As discussed below, this assumption was later confirmed in this study, by both NMR and VCD.
2.2. Experimental
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5
2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5) cleaving mixture. Each of the resins was washed with DCM, and the combined TFA filtrates were evaporated at room temperature. The precipitated residues were triturated with tert-butyl-methylether, collected by suction, and dried by lyophilization. The linear peptides were purified by HPLC using a Waters instrument with a Delta 600 pump, and a 2489 UV/VIS detector. The purity and identity of all peptides were determined by analytical HPLC and by the ESI MS technique.
2.5) cleaving mixture. Each of the resins was washed with DCM, and the combined TFA filtrates were evaporated at room temperature. The precipitated residues were triturated with tert-butyl-methylether, collected by suction, and dried by lyophilization. The linear peptides were purified by HPLC using a Waters instrument with a Delta 600 pump, and a 2489 UV/VIS detector. The purity and identity of all peptides were determined by analytical HPLC and by the ESI MS technique.
2.3. Theoretical
| G = ECOSMO + ΔE + μ | (2) |
3. Results
3.1. VCD and ECD spectra of the studied tripeptides in solution and comparison with those of the reference undecapeptide CATWEAMEKCK
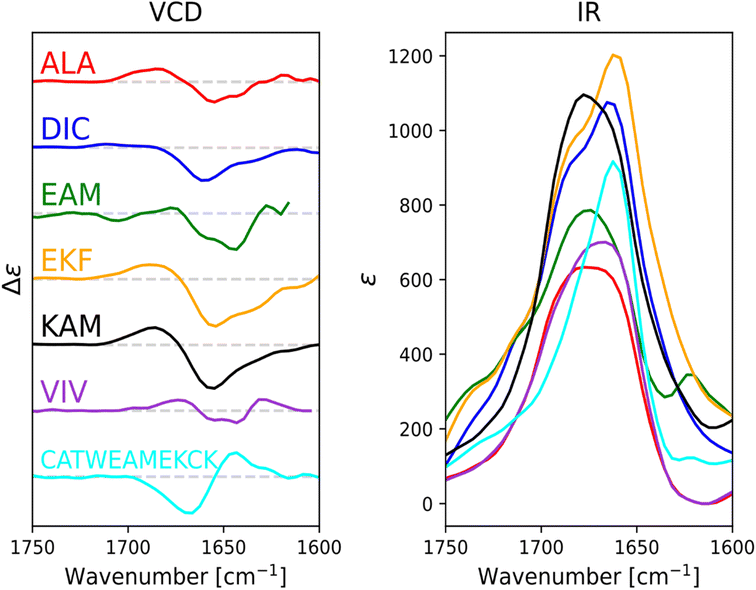
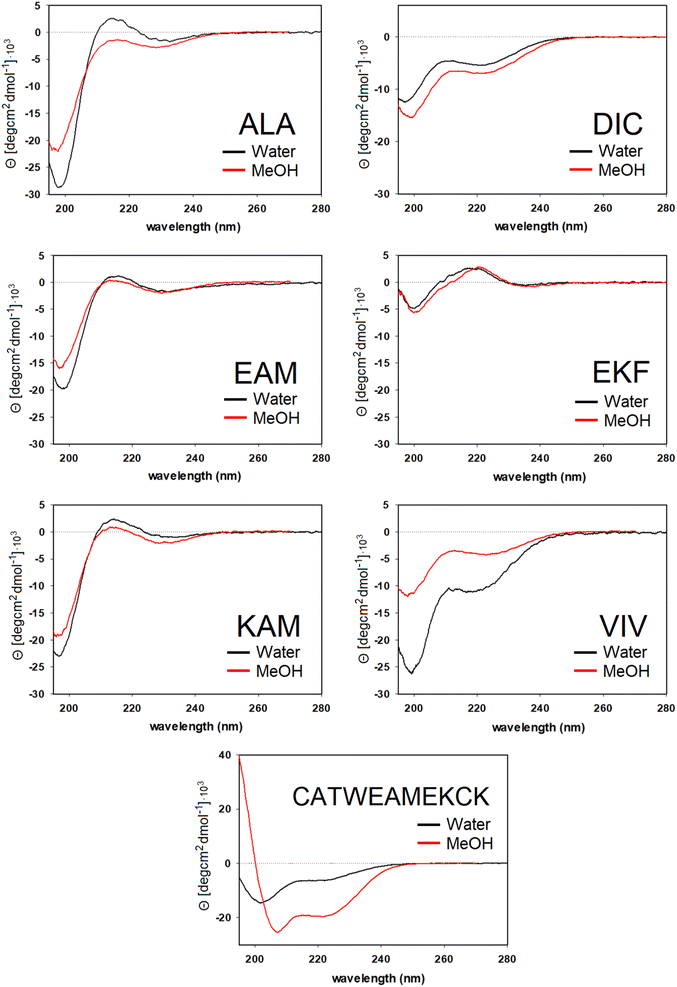
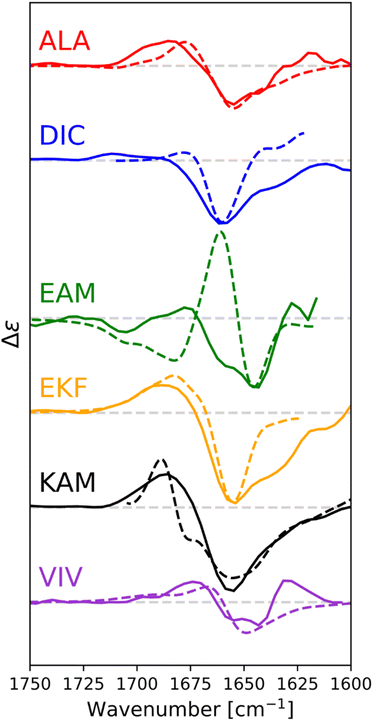
For ALA, DIC, EAM, EKF, KAM, and VIV, the VCD and IR spectra are depicted in Fig. 4, whereas ECD spectra can be found in Fig. 5. Due to its poor solubility, we were not able to measure any CD spectrum of the IYI tripeptide.VCD spectra of EAM and VIV show a predominantly negative band in the amide I region at around 1650 cm−1, with weak positive lobes at ∼1670 cm−1, and ∼1630 cm−1. It is significantly shifted to lower wavenumbers with respect to the IR absorption, which has a maximum at 1670–1675 cm−1 (see Fig. S3† for detailed comparison). Such a pattern implies significant content of β-sheets,82–84 which could include both extended β-strands and possibly a certain contribution of intermolecular β-sheets occurring due to potential peptide aggregation at high sample concentrations used in the VCD experiments. In particular, the IR band at ∼1622 cm−1 of EAM, typical for intermolecular β-sheets,85,86 could be connected to the presence of aggregated species in EAM (Fig. S3 in the ESI†). The absence of such a band for VIV implies that its VCD spectrum likely comes from its inherent propensity for extended β-strand conformation.
This is consistent with the ECD data obtained at lower sample concentrations minimizing the chance of aggregation. A distinct negative band at around ∼220 nm in ECD spectra of VIV (particularly in water) also suggested the presence of a β-sheet in addition to random coil/PPII indicated by the intense negative band at around 197 nm. Therefore, we can assume that the major conformation of VIV is indeed the extended β-strand. This is consistent with the published values for the similar VVV tripeptide: 68% of the β-strand secondary structure with the remaining contributions from PPII and the α-helix.87,88 In contrast, for EAM we may assume that β-type contribution in its VCD spectrum could come from the intermolecular β-sheet of the aggregated species, or from a combination of an intermolecular β-sheet in aggregated molecules and extended β-strand in non-aggregated ones. A more pronounced negative band at ∼1645 cm−1 and blue-shifted to ∼1677 cm−1 positive lobe common for PPII conformation suggest larger content of PPII structure in EAM, while a weaker negative shoulder at ∼1658 cm−1 might come from a smaller contribution of the α-helix.82,84 This assumption is generally corroborated by the ECD data for EAM in methanol, showing largely random coil/PPII conformation with some minor α-helical contribution (Fig. 5). Thus, PPII, α-helical and, possibly, extended β-strand secondary structures could be potentially accessible for the EAM tripeptide.
For DIC, which is a tripeptide with one of the lowest ΔGHE values (ca −2 kcal mol−1, c.f. SI.xlsx Table (ESI†) and ref. 23), VCD spectra are characterized by a large negative spectral band at ∼1660 cm−1 accompanied by a weak positive shoulder at ∼1711 cm−1 suggesting that it is a combination of α-helix and PPII, with significantly higher α-helix content compared to all other studied tripeptides. While the typical VCD spectrum of the α-helix is characterized by a positive (−/+) couplet (c.f. CATWEAMEKCK peptide in Fig. 4 featuring the distinctive 1668(−)/1644(+) couplet), we explain in detail the untypical shape of the DIC spectrum in the ESI (Fig. S4)† and discuss it also in Section 3.4 below (comparison of the calculated and experimental VCD). The remaining three tripeptides – KAM, ALA, and EKF – show the highest content of PPII (more visible in cases of ALA and EKF)82,89 in the VCD spectra characterized by a negative (∼1685 cm−1 (+)/∼1655 cm−1 (−)) couplet typical for this structure. This compares well with the published values87 suggesting 84% of the PPII secondary structure for AAA and other XXA tripeptides.
The ECD spectra of DIC, KAM and ALA are generally consistent with the VCD data. Similarly to VCD, ECD suggests the highest α-helical propensity for DIC (even in water) and mainly the PPII structure for KAM and ALA in methanol and water. Interestingly, the ECD spectra of EKF show high PPII content in combination with an extended structure and no contribution from the α-helix in water and methanol (see description in the ESI and Table S1† for details). It is worth mentioning that we did not experimentally observe the S–S bond formation between DIC tripeptides. In addition, we also measured the VCD and ECD spectra of the reference CATWEAMEKCK undecapeptide. CATWEAMEKCK is the longest α-helix which contains an EAM tripeptide in the middle, found in the Top8000 data set. The undecapeptide exhibits a clear character of α-helix in its VCD spectrum (negative/positive doublet at 1668 cm−1(−)/1644 cm−1(+)).82,84 ECD also indicates α-helix, with negative minima at 207 nm and 223 nm.32,54 Therefore, CATWEAMEKCK is an example of an α-helix stable in solution.
3.2. NMR spectra of the studied tripeptides in solution and comparison with that of the reference undecapeptide CATWEAMEKCK
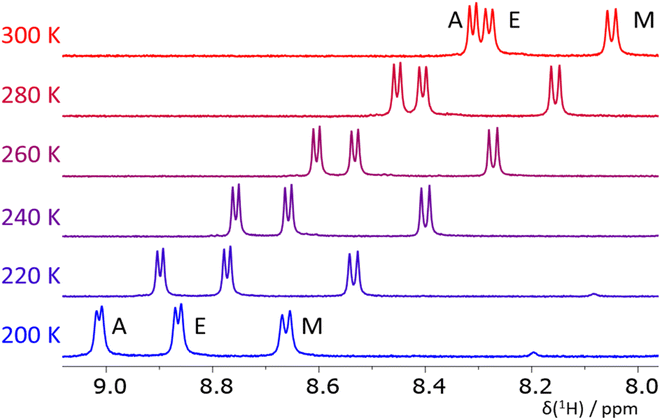
To obtain independent, somewhat complementary experimental information, we employed NMR spectroscopy to characterize the structure of the pro-helical ALA, DIC, EAM, EKF, and KAM, and pro-extended VIV and IYI tripeptides in solution (using DMF and methanol as solvents).Fig. 6 depicts the NH region of variable-temperature 1H NMR spectra of EAM in methanol whereas the spectra in DMF are shown in the ESI (Fig. S6).† For EAM in methanol at room temperature, the 3JNH,Hα coupling values of all three amino acids fall in the range typical for random-coil structures (Table 1) composed by a mixture of helical and extended conformers. However, variable-temperature experiments reveal that the couplings of all three amino acids decrease with decreasing temperature (Table 1), which indicates that the population of helical (α- or PPII) structures increases at lower temperatures. Similar conclusions can be made from the NMR data obtained in DMF which are deposited in the ESI (Table S3).†
| T/K | 300 | 280 | 260 | 240 | 220 | 200 | ΔJ200–300 |
|---|---|---|---|---|---|---|---|
| a Not determined because of a signal overlap, signal broadening or fast chemical exchange process. b The assignment of V1 and V3 in VIV and I1 and I3 in IYI may be interchanged. | |||||||
| ALA | |||||||
| A1 | 5.8 | 5.5 | 5.3 | 5.1 | 5.0 | ≤−0.8 | |
| L | 7.4 | 7.4 | 7.2 | 7.2 | 7.1 | ≤−0.3 | |
| A3 | 7.0 | 6.8 | 6.7 | 6.3 | 6.1 | ≤−0.9 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| DIC | |||||||
| D | 8.0 | 8.1 | 8.1 | 8.1 | 8.0 | 8.0 | 0.0 |
| I | 7.1 | 7.0 | 6.7 | 6.6 | 6.7 | 6.3 | −0.8 |
| C | 7.4 | 7.3 | 7.1 | 7.0 | 6.9 | 6.7 | −0.7 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| EAM | |||||||
| E | 6.6 | 6.3 | 6.3 | 6.1 | 6.0 | 5.7 | −0.9 |
| A | 6.2 | 6.1 | 6.0 | 5.7 | 5.5 | 5.2 | −1.0 |
| M | 7.9 | 7.9 | 7.8 | 7.7 | 7.6 | 7.5 | −0.4 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| EKF | |||||||
| E | 6.4 | 6.3 | 6.1 | 5.8 | 5.6 | ≤−0.8 | |
| K | 7.5 | 7.4 | 7.4 | 7.2 | 7.1 | ≤−0.4 | |
| F | 8.0 | 7.9 | 7.9 | 7.8 | 7.8 | 7.5 | ≤−0.5 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| KAM | |||||||
| K | 7.0 | 6.9 | 6.7 | 6.5 | 6.2 | −0.8 | |
| A | 6.2 | 6.1 | 5.9 | 5.7 | 5.5 | 5.2 | −1.0 |
| M | 7.8 | 7.7 | 7.7 | 7.6 | 7.2 | −0.6 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| VIV | |||||||
| V1b | 7.9 | 7.7 | 7.4 | 6.9 | −1.0 | ||
| I | 8.6 | 8.6 | 8.5 | ∼−0.1 | |||
| V3b | 8.7 | 8.5 | 8.3 | 8.3 | 8.1 | 8.0 | −0.7 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| IYI | |||||||
| I1b | 8.0 | 8.1 | 7.7 | ||||
| Y | 7.7 | 8.1 | 7.7 | 7.8 | ∼0 | ||
| I3b | 8.7 | 8.7 | |||||
The NMR measurements in less polar DMF (Tables S2–S8†) have a slightly different temperature window (360–240 K) but also cover more than a 100 K range. The value of 3JNH,Hα coupling in the glutamic acid (residue E) in EAM is, at 300 K, similar in both solvents, and the ΔJ value (the change of the coupling values induced by a 100 K decrease in temperature) is also similar. On the other hand, the 3JNH,Hα coupling in alanine (residue A) is higher in DMF (6.6 Hz vs. 6.2 Hz in methanol) and the ΔJ value is significantly lower (−0.6 Hz in DMF vs. −1.0 Hz in methanol). This observation indicates that the propensity of the EAM peptide to form some helical structures is higher in methanol than in DMF. The value of the 3JNH,Hα coupling in methionine is similar in both solvents, and the ΔJ value is close to zero in DMF, whereas it is −0.4 in methanol. VCD and ECD spectra suggest that the helical conformations observed in EAM by NMR at room temperature are rather of PPII character. Together with the fraction of extended conformations (in VCD mixed with the signal of aggregation), the EAM tripeptide is mostly a combination of all three secondary structure types.
Contrary to the EAM tripeptide, the magnitudes of all 3JNH,Hα couplings are significantly higher in the pro-extended IYI tripeptide (not measured by VCD) in both solvents (8–9 Hz, Table 1). Furthermore, the 3JNH,Hα coupling values are almost temperature independent. In DMF, the ΔJ values can be found between −0.2 and +0.2 Hz. Some of the coupling values in methanol at temperatures below 240 K and at 260 K could not be obtained because of a signal overlap. However, the coupling values that could be resolved are also almost temperature independent; only the coupling value of one of the isoleucine residues decreased slightly (−0.4 Hz). These characteristics are associated with extended structure motifs; therefore the IYI tripeptide is mostly extended.
Next, we measured the temperature dependence of 3JNH,Hα couplings in other peptides (ALA, KAM, and VIV) that were previously identified by bioinformatics to have a propensity for the α-helical (ALA and KAM) and extended (VIV) structures. Unfortunately, VIV is poorly soluble in DMF and methanol, and we were not able to obtain the full data set at all investigated temperatures. However, the data that could be obtained clearly show that the 3JNH,Hα coupling in the central isoleucine residue of VIV is high and almost temperature independent in methanol (Table 1), suggesting mainly an extended structure. The coupling in the valine residues V1 and V3 decreases with decreasing temperature in methanol, which is in line with conformational analysis (vide infra). These results are similar to the published results of the VVV tripeptide in water.49 Similarly, the 3JNH,Hα coupling of the central leucine residue in the ALA tripeptide is almost temperature independent. This is different from the statistics in proteins, where L in ALA is mostly in the α-helical conformation. However, the NMR data are in line with the conformational analysis (vide infra). The 3JNH,Hα couplings and their temperature dependence in the KAM tripeptide are similar to those in EAM. According to the VCD and ECD spectra, helical conformers of KAM are largely of the PPII type (left-handed helix) and not α-helical at room temperature.
We also measured the other two tripeptides with computationally predicted propensity towards α-helical conformation: DIC and EKF. For DIC, the 3JNH,Hα coupling in the asparagine residue (D) in methanol is almost temperature independent, while the couplings of the other two amino acid residues are significantly dependent on temperature. Values of these couplings at lower temperature (about 6.5 Hz) point to some form of helical structure (α- or PPII or combination). Similarly, the glutamine residue (E) of the EKF tripeptide shows stronger temperature dependence, as the 3JNH,Hα lowers by 1.0 Hz. The remaining two residues change much less with temperature. The DIC and EKF tripeptides were also measured in water (H2O–D2O mixture) at 280 and 300 K (Tables S4 and S5†) and the 3JNH,Hα coupling constants are similar to those obtained in methanol.
Lastly, we measured the NMR spectra for the reference CATWEAMEKCK undecapeptide and concluded that it indeed adopts an α-helix in its EAM core (Table 2, see also Chapter 7 in the ESI† for details), in perfect agreement with the VCD and ECD results presented above.
| T/K | 320 | 300 | 280 | 260 | ΔδNH/ΔT | δ(Hα) |
|---|---|---|---|---|---|---|
| a Not determined because of a signal overlap, signal broadening or fast chemical exchange process. | ||||||
| C1 | 5.2 | 5.0 | 4.9 | 4.7 | −6.5 | 4.30 |
| A2 | 4.5 | 4.6 | 4.5 | 4.2 | −5.6 | 4.27 |
| T | 4.00 | |||||
| W | 4.4 | 4.6 | 4.5 | −5.6 | 4.39 | |
| E5 | 4.4 (6.6) | 3.8 (6.3) | 3.4 (6.3) | −6.4 (−5.6) | 3.93 (4.28) | |
| A6 | 4.5 | 4.6 (6.2) | 4.4 (6.1) | 4.3 (6.0) | −3.5 (−6.7) | 4.03 (4.28) |
| M | 4.8 | 4.8 (7.9) | 4.7 (7.9) | 4.4 (7.8) | −3.7 (−6.2) | 4.13 (4.43) |
| E8 | 4.7 | 4.7 | 4.4 | −3.8 | 3.97 | |
| K9 | 5.4 | 5.1 | 4.9 | −4.2 | 4.08 | |
| C10 | 6.7 | 6.5 | 6.3 | 5.9 | −1.1 | 4.30 |
| K11 | 4.24 | |||||
In addition, we calculated the J-coupling values for ideal α-helical, extended, and PPII conformations of all seven tripeptides (see Table S9 in the ESI†), to show that the experimentally determined values fit in the range of the calculated results.
3.3. QM(DFT-D3)//COSMO-RS conformational sampling
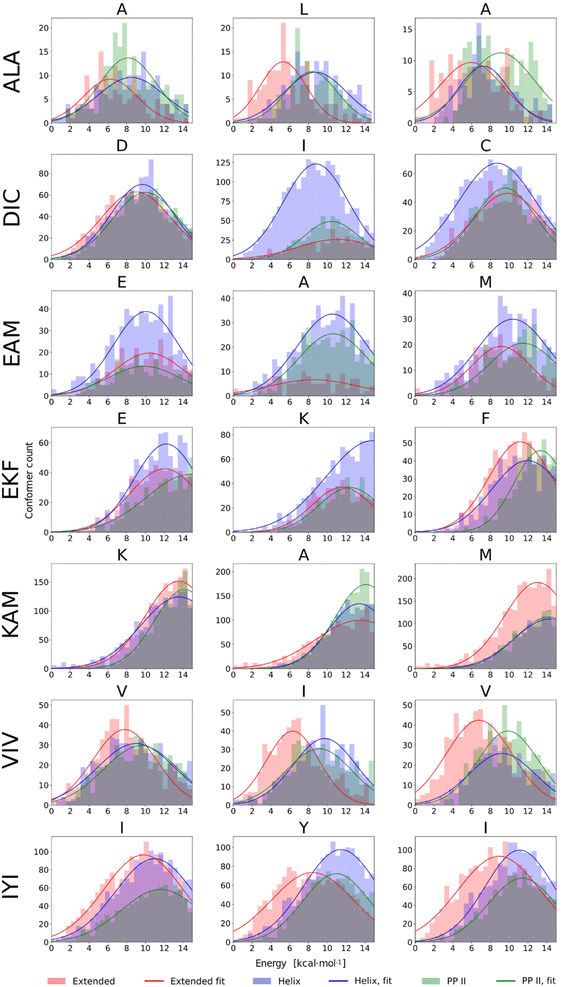
In our previous work, a limited sampling of all 8000 tripeptides was performed,22 employing the calibrated QM protocol.22,51,66. However, only 200 initial conformers were generated for each tripeptide, which covered a rather limited part of their vast conformational space. Therefore, we carried out extensive DFT-D3//COSMO-RS//GFN-2 conformational sampling, as described in Methods, of seven selected tripeptides: presumably pro-helical ALA, DIC, EKF, EAM, and KAM, and pro-extended VIV and IYI. This resulted in 608–5179 final conformers for each tripeptide. The results are summarized in Fig. 7, which compares the energetic distribution of α-helical, extended, and PPII conformers, separately for each amino acid. In this respect, QM calculations can be directly compared to the NMR data discussed above, reflecting the secondary structure of each residue.The histograms in Fig. 7 illustrate markedly different trends observed among the seven tripeptides. EAM has all three structural types (α-helix, extended, and PPII helix) energetically accessible, which is consistent with the spectroscopic results. DIC exhibits a stronger tendency to form α-helical structures (with respect to the other peptides studied herein). Moreover, by correlating NMR and computational data on a per-residue basis, we may observe almost perfect agreement between the two. From NMR, the tendency for helicity increases in the order D < C ≤ I, which is exactly the case in the DFT-D3//COSMO-RS histograms. The experiments indicated that VIV and IYI prefer extended conformations, and indeed, the VIV and IYI extended conformers are computed to be lower in energy. Furthermore, NMR predicts the tendency for the extended structure in the order V1/3 < I (c.f.Table 1), which is also seen from the computed histograms (Fig. 7). The same holds true for IYI.
Experimentally, EKF and KAM secondary structures seem to be mixtures of PPII helix with minor α-helix contribution, which is well reproduced by the calculations, both ‘globally’ and on a per-residue basis. For example, in KAM, the terminal methionine residue has quite a high propensity for extended conformations, which is observed both computationally as well as in NMR. In the case of ALA, NMR predicts that L is assumed to adopt preferably extended conformation, and this can also be seen in computed histograms. Terminal alanine residues behave somewhat differently with respect to each other in NMR (Table 1), which is also observed computationally, as A1 tends to adopt extended conformations less than the A3 residue. We also observed that conformational energy distribution is similar in other solvents, as illustrated in the ESI (Fig. S10)† for EAM and IYI.
In summary, we demonstrated that predictions provided by quantum chemical calculations are in agreement with the experimentally obtained 3JNH,Hα coupling constants, VCD and ECD spectral patterns. VCD and ECD spectroscopy nicely complements the NMR experimental data by distinguishing the left- (PPII) and right-(α) handed helix.
3.4. Theoretical calculations of VCD spectra
We calculated IR and VCD spectra of six tripeptides (ALA, DIC, EAM, EKF, KAM, and VIV; in MeOH). Fig. 8 depicts the amide I region of the six tripeptides. Note that the calculated frequencies in Fig. 8 were shifted down by about 50 cm−1 to match the experiment. This is a typical computational error arising mostly from limited accounting for the solvent and anharmonic contributions.70,90 It must also be considered that the experimental spectra represent a convolution of spectral patterns characteristic of different structures, as demonstrated in Section 3 of the ESI,† and thus cannot be directly assigned to classical spectral characteristic of a single structure. DIC shows the strongest α-helical character, evident from the negative band at 1660 cm−1 (scaled spectrum) and only a minor positive signal at higher wavenumbers. Both spectral features agree well with the experiment, where they appear at 1660 and 1711 cm−1, respectively. EAM exhibits a combination of PPII and α-helix (negative bands at 1645 cm−1 and at 1679 cm−1, with the strong positive band at 1661 cm−1 coming from the spectral overlap of both these structures; all in the scaled spectrum), pointing out their energetic accessibility. The experimental VCD spectrum of EAM is dominated by the intermolecular β-sheet contribution (coming from partially aggregated peptides in the experiment), with some contribution from PPII, α-helix and possibly an extended β-strand. The ALA tripeptide shows a nearly conservative negative couplet with the negative lobe calculated at 1655 cm−1 and the positive one at 1678 cm−1, which is a typical signature of the PPII structure. The computed spectrum agrees well with the experiment, suggesting a major PPII contribution to this peptide. The calculated spectrum of VIV could be associated with a contribution of PPII and possibly an extended structure (shown by the overall negative signal with a minimum calculated at 1650 cm−1 and a weaker positive lobe at a higher wavenumber).82,84 This is in general agreement with the experimental VCD spectrum, illustrating that in VCD, the PPII helix is generally more ‘visible’ than extended structures, which provide weaker signals.84 Peptides EKF and KAM are mostly a mix of PPII with other secondary structure types, without significant α-helical contribution. This also agrees quite well with the experimental spectra.4. Discussion
Experimental NMR, VCD, and ECD spectra, supported by large-scale calibrated66 DFT-D3//COSMO-RS calculations showed that there might indeed be some preference for a particular secondary structure encoded in the peptide fragments as small as tripeptides. These propensities are quite hard to decipher on a complex background given the high conformational flexibility of these small peptide fragments in solution. However, we tried to show that a careful correlation of the experimental (NMR, VCD, and ECD) and computational (DFT) data may represent a strategy to extract the secondary structure propensities. NMR and computations provide detailed local information, which can be decomposed on a per-residue basis, while VCD and ECD spectra are of a more global character. At the current technological level they do not distinguish subtle structural features of individual amino acids within the peptide chain without isotope labelling. In contrast, NMR spectra of (not isotopically labeled) peptides do not distinguish between α- and PPII helices, which is where VCD and ECD spectra provide an important insight. In addition to VCD, variable-temperature ECD experiments can also distinguish between PPII and random coil conformations (for details see the ESI†). We note that PPII is assumed to be more common helical arrangement in shorter peptides, mainly those containing alanine.49,50,91,92 Also, it has already been shown that for the trialanine residue this does not depend on pH.93Among the studied tripeptides, some were shown to prefer α-helical arrangement (e.g., DIC), while others, such as VIV and IYI, have inherent propensities for extended conformations. For EAM, the NMR data indicate that there are both extended and helical conformers present, in agreement with the CD spectra which further indicate a PPII helix rather than an α-helix. Large-scale DFT-D3//COSMO-RS conformational sampling of EAM shows almost equivalent populations of all three secondary structures (incl. PPII). There are also tripeptides with an inherent propensity for PPII, such as ALA, KAM, or EKF; however, they do not preserve this secondary structure in proteins (see Table 1). In fact, PPII conformations are quite rare for the selected triplets in proteins (see Fig. 1).
All of this illustrates that conformational behavior of protein constituents loosely correlates with their (over)populations in a particular secondary structure. This can be traced to fragments as short as tripeptides. For example, EAM and VIV (IYI) tripeptides show a sharp difference in secondary structure preference in proteins (α-helix/β-sheet, respectively). Our data consistently reproduce the preference of VIV (and IYI) for β-sheet conformation on the tripeptide level. Although EAM does not show a clear preference for α-helical conformers on the tripeptide level, it certainly has a larger tendency toward α-helical conformations than VIV. Thus, some amino acid triplets may “imprint” their accessible (preferred) conformations into the final protein folds. These are by no means “stable” secondary structures, as only some tripeptides exhibit these preferences, while the majority is rather flexible and could be viewed as a model for intrinsically disordered proteins.94 Very importantly, the calculations have shown that the equilibrium between the three (or more) conformational states of tripeptides is very subtle. Energetically, the lowest lying conformers corresponding to a particular secondary structure are typically within 1–2 kcal mol−1 (Fig. 7). At room temperature, they would correspond to populations not differing more than by one order of magnitude. These subtle equilibria can be easily overruled by strong intramolecular forces accompanying the “collapse” of the protein into the folded structures (as mentioned above, we have recently reported that strain energies within the folded protein structures can be, exceptionally, as high as 5 kcal mol−1 per amino acid residue).22 Thus, the conformers seen at experimental temperatures for the isolated tripeptides might not always be relevant for the behavior of the triplets in proteins. An example studied here is the KAM triplet/tripeptide that has a propensity for the PPII helix as an isolated tripeptide, while adopting α-helical conformation in ∼79% of its occurrence in proteins. DIC, with most α-helical propensity from all studied tripeptides has 48%/28% α-helix/extended populations in proteins.
Our results show that certain peptide multiplets, as short as tripeptides, exhibit the same propensities for the specific secondary structure in solution in which they are preferentially found in proteins (most pronounced for pro-β-sheet IYI and VIV). We hypothesize that these short peptides can be considered “seeds” that are important during protein folding. This compares well with our work on the WW domain7 showing that low-strain parts of the WW domain(s) are the initial folding seeds despite the fact that they are not the ones most conserved within the WW protein family. Like the spark at the beginning of fire, tripeptides with an inherent secondary structure propensity could be the initiators or early-stage ‘catalysts’ of the folding process.
5. Conclusions
The experimental, bioinformatics, and computational data presented herein show that certain tripeptides have an inherent preference for certain types of secondary structure. This statement can be deconvoluted from the complex experimental and computational background characterizing their conformational behavior. This has been indicated by VCD, ECD, and NMR spectroscopies and fully supported by the quantum chemical calculations. The theory provided an unambiguous structure/energy mapping to couple the computed data with NMR spectra and theoretically predicted VCD spectra to connect low-energy conformers to the VCD experimental data. Some of the studied tripeptides (notably DIC(α), VIV(β), and IYI(β)) could be considered “folding seeds”, initiating the complex and multidimensional process of protein folding. Somewhat surprisingly, only in some cases, the preference of a standalone tripeptide was the same as its behavior in proteins. This, again, suggests that the final conformation of a peptide fragment within a (folded) protein is an interplay of multiple subtle factors. In contrast, the reference CATWEAMEKCK undecapeptide has been unambiguously shown, by NMR, VCD, and ECD, to form a stable α-helix in solution. A less optimistic view of the presented results may lead to the statement that the secondary structure starts to appear somewhere between 3 and 11 amino acid long peptide sequences.Data availability
The primary computational data as well as additional experimental data were deposited in the ESI.†Author contributions
M. Culka and L. Rulíšek conceived the idea for this study, and carried out initial calculations. T. Kalvoda carried out all quantum chemical calculations presented in the work and compiled, analyzed, and correlated all theoretical and experimental data. Z. Osifová and M. Dračínský carried out and interpreted NMR measurements with respect to other experimental and theoretical data. V. Andrushchenko and L. Bednárová carried out VCD and ECD experiments, respectively, and interpreted the data. P. Bouř was involved in the discussions concerning experimental and (methodological aspects of) theoretical VCD data. J. Galgonek and J. Vondrášek provided bioinformatics support. L. Rulíšek, M. Dračínský, V. Andrushchenko and T. Kalvoda wrote major parts of the manuscript. All authors assisted with editing, analysis, and interpretation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Grant Agency of the Czech Republic (grants 23-05940S, 22-33060S). This work was supported by the Ministry of Education, Youth and Sports from the Large Infrastructures for Research, Experimental Development and Innovations (project “IT4Innovations National Supercomputing Center – e-INFRA CZ (ID:90254)”).References
- S. W. Englander and L. Mayne, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 15873–15880 CrossRef CAS.
- K. A. Dill and J. L. MacCallum, Science, 2012, 338, 1042–1046 CrossRef CAS PubMed.
- M. Dorn, M. B. e Silva, L. S. Buriol and L. C. Lamb, Comput. Biol. Chem., 2014, 53, 251–276 CrossRef CAS.
- Groups Analysis: Zscores – CASP14, https://predictioncenter.org/casp14/zscores_final.cgi Search PubMed.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek, A. Potapenko, A. Bridgland, C. Meyer, S. A. A. Kohl, A. J. Ballard, A. Cowie, B. Romera-Paredes, S. Nikolov, R. Jain, J. Adler, T. Back, S. Petersen, D. Reiman, E. Clancy, M. Zielinski, M. Steinegger, M. Pacholska, T. Berghammer, S. Bodenstein, D. Silver, O. Vinyals, A. W. Senior, K. Kavukcuoglu, P. Kohli and D. Hassabis, Nature, 2021, 596, 583–589 CrossRef CAS PubMed.
- C. Outeiral, D. A. Nissley and C. M. Deane, Bioinformatics, 2022, 38, 1881–1887 CrossRef CAS.
- M. Culka and L. Rulíšek, J. Phys. Chem. B, 2019, 123, 6453–6461 CrossRef CAS PubMed.
- M. Culka and L. Rulíšek, J. Phys. Chem. B, 2020, 124, 3252–3260 CrossRef CAS PubMed.
- P. J. Flory and M. Volkenstein, Biopolymers, 1969, 8, 699–700 CrossRef.
- S. Toal and R. Schweitzer-Stenner, Biomolecules, 2014, 4, 725–773 CrossRef PubMed.
- M. H. Zaman, M.-Y. Shen, R. S. Berry, K. F. Freed and T. R. Sosnick, J. Mol. Biol., 2003, 331, 693–711 CrossRef CAS PubMed.
- L.-Q. Yang, X.-L. Ji and S.-Q. Liu, J. Biomol. Struct. Dyn., 2013, 31, 982–992 CrossRef CAS.
- G. P. Brady and K. A. Sharp, Curr. Opin. Struct. Biol., 1997, 7, 215–221 CrossRef CAS.
- C.-L. Towse, M. Akke and V. Daggett, J. Phys. Chem. B, 2017, 121, 3933–3945 CrossRef CAS PubMed.
- O. V. Galzitskaya and S. O. Garbuzynskiy, Proteins: Struct., Funct., Bioinf., 2006, 63, 144–154 CrossRef CAS.
- N. V. Ilawe, A. E. Raeber, R. Schweitzer-Stenner, S. E. Toal and B. M. Wong, Phys. Chem. Chem. Phys., 2015, 17, 24917–24924 RSC.
- W. Yu, Z. Wu, H. Chen, X. Liu, A. D. MacKerell and Z. Lin, J. Phys. Chem. B, 2012, 116, 2269–2283 CrossRef CAS.
- L. Denarie, I. Al-Bluwi, M. Vaisset, T. Siméon and J. Cortés, Molecules, 2018, 23, 373 CrossRef.
- V. K. Prasad, A. Otero-de-la-Roza and G. A. DiLabio, Sci. Data, 2019, 6, 180–310 CrossRef.
- N. E. Shepherd, H. N. Hoang, G. Abbenante and D. P. Fairlie, J. Am. Chem. Soc., 2005, 127, 2974–2983 CrossRef CAS PubMed.
- J. L. Krstenansky, T. J. Owen, K. A. Hagaman and L. R. McLean, FEBS Lett., 1989, 242, 409–413 CrossRef CAS PubMed.
- M. Culka, T. Kalvoda, O. Gutten and L. Rulíšek, J. Phys. Chem. B, 2021, 125, 58–69 CrossRef CAS PubMed.
- M. Culka, J. Galgonek, J. Vymětal, J. Vondrášek and L. Rulíšek, J. Phys. Chem. B, 2019, 123, 1215–1227 CrossRef CAS PubMed.
- T. Kalvoda, M. Culka, L. Rulíšek and E. Andris, J. Phys. Chem. B, 2022, 126, 5949–5958 CrossRef CAS PubMed.
- W. Kabsch and C. Sander, Biopolymers, 1983, 22, 2577–2637 CrossRef CAS PubMed.
- R. P. Joosten, T. A. H. te Beek, E. Krieger, M. L. Hekkelman, R. W. W. Hooft, R. Schneider, C. Sander and G. Vriend, Nucleic Acids Res., 2011, 39, D411–D419 CrossRef CAS.
- J. N. S. Evans, Biomolecular NMR Spectroscopy, Oxford University Press Inc., 1995 Search PubMed.
- T. A. Keiderling, Curr. Opin. Chem. Biol., 2002, 6, 682–688 CrossRef CAS.
- J. Kessler, V. Andrushchenko, J. Kapitán and P. Bouř, Phys. Chem. Chem. Phys., 2018, 20, 4926–4935 RSC.
- Z. Shi, C. A. Olson, G. D. Rose, R. L. Baldwin and N. R. Kallenbach, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 9190–9195 CrossRef CAS.
- A. F. Drake, G. Siligardi and W. A. Gibbons, Biophys. Chem., 1988, 31, 143–146 CrossRef CAS PubMed.
- N. Koji and R. W. Woody, Circular Dichroism: Principles and Applications, ed. Nina Berova, Koji Nakanishi, and Robert W. Woody, Wiley-VCH, American Chemical Society, 2nd edn, 2002, vol. 124 Search PubMed.
- M. Billeter, W. Braun and K. Wüthrich, J. Mol. Biol., 1982, 155, 321–346 CrossRef CAS PubMed.
- M. Dračínský, Annu. Rep. NMR Spectrosc., 2017, 90, 1–40 CrossRef.
- A. C. Conibear, K. J. Rosengren, C. F. W. Becker and H. Kaehlig, J. Biomol. NMR, 2019, 73, 587–599 CrossRef CAS.
- M. Karplus, J. Am. Chem. Soc., 1963, 85, 2870–2871 CrossRef CAS.
- C. A. G. Haasnoot, F. A. A. M. D. Leeuw, H. P. M. D. Leeuw and C. Altona, Biopolymers, 1981, 20, 1211–1245 CrossRef CAS.
- A. Wu, D. Cremer, A. A. Auer and J. Gauss, J. Phys. Chem. A, 2002, 106, 657–667 CrossRef CAS.
- J. M. Schmidt, M. Blümel, F. Löhr and H. Rüterjans, J. Biomol. NMR, 1999, 14, 1–12 CrossRef CAS PubMed.
- S. A. Perera and R. J. Bartlett, Magn. Reson. Chem., 2001, 39, S183–S189 CrossRef CAS.
- P. Bouř, M. Buděšínský, V. Špirko, J. Kapitán, J. Šebestík and V. Sychrovský, J. Am. Chem. Soc., 2005, 127, 17079–17089 CrossRef.
- A. Pardi, M. Billeter and K. Wüthrich, J. Mol. Biol., 1984, 180, 741–751 CrossRef CAS.
- M. Dračínský and P. Bouř, J. Chem. Theory Comput., 2010, 6, 288–299 CrossRef PubMed.
- M. Dračínský and P. Hodgkinson, Chem. – Eur. J., 2014, 20, 2201–2207 CrossRef PubMed.
- M. Dračínský, J. Kaminský and P. Bouř, J. Chem. Phys., 2009, 130, 94–106 CrossRef.
- S. E. Toal, N. Kubatova, C. Richter, V. Linhard, H. Schwalbe and R. Schweitzer-Stenner, Chem. – Eur. J., 2017, 23, 18084–18087 CrossRef CAS PubMed.
- A. Hagarman, D. Mathieu, S. Toal, T. J. Measey, H. Schwalbe and R. Schweitzer-Stenner, Chem. – Eur. J., 2011, 17, 6789–6797 CrossRef CAS PubMed.
- A. Hagarman, T. J. Measey, D. Mathieu, H. Schwalbe and R. Schweitzer-Stenner, J. Am. Chem. Soc., 2010, 132, 540–551 CrossRef CAS PubMed.
- J. Graf, P. H. Nguyen, G. Stock and H. Schwalbe, J. Am. Chem. Soc., 2007, 129, 1179–1189 CrossRef CAS PubMed.
- R. Schweitzer-Stenner, Mol. Biosyst., 2011, 8, 122–133 RSC.
- J. Rezac, D. Bim, O. Gutten and L. Rulisek, J. Chem. Theory Comput., 2018, 14, 1254–1266 CrossRef CAS PubMed.
- J.-F. Couture, P. Legrand, L. Cantin, F. Labrie, V. Luu-The and R. Breton, J. Mol. Biol., 2004, 339, 89–102 CrossRef CAS PubMed.
- V. V. Andrushchenko, H. J. Vogel and E. J. Prenner, J. Pept. Sci., 2007, 13, 37–43 CrossRef CAS PubMed.
- N. Sreerama and R. W. Woody, Anal. Biochem., 2000, 287, 252–260 CrossRef CAS PubMed.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- S. Gnanakaran and A. E. García, Proteins: Struct., Funct., Bioinf., 2005, 59, 773–782 CrossRef CAS PubMed.
- P. S. Nerenberg and T. Head-Gordon, J. Chem. Theory Comput., 2011, 7, 1220–1230 CrossRef CAS.
- R. B. Best, N.-V. Buchete and G. Hummer, Biophys. J., 2008, 95, L07–L09 CrossRef CAS PubMed.
- S. Zhang, R. Schweitzer-Stenner and B. Urbanc, J. Chem. Theory Comput., 2020, 16, 510–527 CrossRef PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS.
- S. Ehlert, M. Stahn, S. Spicher and S. Grimme, J. Chem. Theory Comput., 2021, 17, 4250–4261 CrossRef CAS PubMed.
- TURBOMOLE V7.6 2021, A development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since, 2007, available from, http://www.turbomole.com Search PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS.
- N. Godbout, D. R. Salahub, J. Andzelm and E. Wimmer, Can. J. Chem., 1992, 70, 560–571 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- J. Hostaš and J. Řezáč, J. Chem. Theory Comput., 2017, 13, 3575–3585 CrossRef.
- A. Klamt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, 699–709 Search PubMed.
- A. Klamt, J. Volker, B. Thorsten and J. C. W. Lohrenz, J. Phys. Chem. A, 1998, 102, 5074–5085 CrossRef CAS.
- A. Klamt and M. Diedenhofen, J. Comput. Chem., 2018, 39, 1648–1655 CrossRef CAS.
- V. Andrushchenko, L. Benda, O. Páv, M. Dračínský and P. Bouř, J. Phys. Chem. B, 2015, 119, 10682–10692 CrossRef CAS PubMed.
- V. Andrushchenko, D. Tsankov, M. Krasteva, H. Wieser and P. Bouř, J. Am. Chem. Soc., 2011, 133, 15055–15064 CrossRef CAS.
- G. Lanza and M. A. Chiacchio, J. Phys. Chem. B, 2016, 120, 11705–11719 CrossRef CAS PubMed.
- P. J. A. Cock, T. Antao, J. T. Chang, B. A. Chapman, C. J. Cox, A. Dalke, I. Friedberg, T. Hamelryck, F. Kauff, B. Wilczynski and M. J. L. de Hoon, Bioinformatics, 2009, 25, 1422–1423 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Rev. A03, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, J. Phys. Chem. B, 1988, 37, 785–789 CAS.
- A. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- K. Scholten and C. Merten, Phys. Chem. Chem. Phys., 2022, 24, 3611–3617 RSC.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef.
- M. Krupová, P. Leszczenko, E. Sierka, S. E. Hamplová, R. Pelc and V. Andrushchenko, Chem. – Eur. J., 2022, 28, e202201922 CrossRef.
- P. Bouř and T. A. Keiderling, J. Am. Chem. Soc., 1993, 115, 9602–9607 CrossRef.
- A. M. Polyanichko, V. V. Andrushchenko, P. Bouř and H. Wieser, Vibrational Circular Dichroism Studies of Biological Macromolecules and their Complexes, in Circular Dichroism: Theory and Spectroscopy, ed. D. S. Rodgers, Nova Science Publishers, Inc., Hauppauge, NY, 2012, pp. 67–126 Search PubMed.
- T. A. Keiderling, Chem. Rev., 2020, 120, 3381–3419 CrossRef CAS.
- M. Jackson and H. H. Mantsch, Crit. Rev. Biochem. Mol. Biol., 1995, 30, 95–120 CrossRef CAS PubMed.
- S. A. Tatulian, Biochemistry, 2003, 42, 11898–11907 CrossRef CAS.
- R. Schweitzer-Stenner, J. Phys. Chem. B, 2009, 113, 2922–2932 CrossRef CAS PubMed.
- F. Eker, X. Cao, L. Nafie and R. Schweitzer-Stenner, J. Am. Chem. Soc., 2002, 124, 14330–14341 CrossRef CAS.
- R. K. Dukor and T. A. Keiderling, Biopolymers, 1991, 31, 1747–1761 CrossRef CAS PubMed.
- V. Andrushchenko, P. Matějka, D. T. Anderson, J. Kaminský, J. Horníček, L. O. Paulson and P. Bouř, J. Phys. Chem. A, 2009, 113, 9727–9736 CrossRef CAS.
- Z. Shi, K. Chen, Z. Liu and N. R. Kallenbach, Chem. Rev., 2006, 106, 1877–1897 CrossRef CAS.
- R. Schweitzer-Stenner, F. Eker, K. Griebenow, X. Cao and L. A. Nafie, J. Am. Chem. Soc., 2004, 126, 2768–2776 CrossRef CAS PubMed.
- S. Toal, D. Meral, D. Verbaro, B. Urbanc and R. Schweitzer-Stenner, J. Phys. Chem. B, 2013, 117, 3689–3706 CrossRef CAS.
- H. T. Tran, X. Wang and R. V. Pappu, Biochemistry, 2005, 44, 11369–11380 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Tables S1–S9 and Fig. S1–S26, including an in-depth discussion of various experimental details, primary computational data (SI_geoms_energies.zip file containing all the coordinates of the final QM-optimized peptide structures with their absolute DFT-D3//COSMO-RS energies in methanol), and the XLSX spreadsheet with ΔGHE and ΔGH/PPII values for all 8000 tripeptides extracted from ref. 22. See DOI: https://doi.org/10.1039/d3sc04960d |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |