Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Switching the proton-coupled electron transfer mechanism for non-canonical tyrosine residues in a de novo protein†
Astrid
Nilsen-Moe
a,
Clorice R.
Reinhardt
 b,
Ping
Huang
b,
Ping
Huang
 a,
Hemlata
Agarwala
c,
Rosana
Lopes
a,
Hemlata
Agarwala
c,
Rosana
Lopes
 d,
Mauricio
Lasagna
d,
Mauricio
Lasagna
 d,
Starla
Glover
a,
Sharon
Hammes-Schiffer
d,
Starla
Glover
a,
Sharon
Hammes-Schiffer
 e,
Cecilia
Tommos
e,
Cecilia
Tommos
 *d and
Leif
Hammarström
*d and
Leif
Hammarström
 *a
*a
aDepartment of Chemistry, Ångström Laboratory, Uppsala University, Box 523, 75120 Uppsala, Sweden. E-mail: leif.hammarstrom@kemi.uu.se
bDepartment of Molecular Biophysics and Biochemistry, Yale University, New Haven, CT 06520, USA
cTechnical University Munich, Campus Straubing for Biotechnology and Sustainability, Uferstraße 53, 94315 Straubing, Germany
dDepartment of Biochemistry and Biophysics, Texas A&M University, College Station, TX 77843, USA. E-mail: tommos@tamu.edu
eDepartment of Chemistry, Yale University, New Haven, CT 06520, USA
First published on 25th January 2024
Abstract
The proton-coupled electron transfer (PCET) reactions of tyrosine (Y) are instrumental to many redox reactions in nature. This study investigates how the local environment and the thermodynamic properties of Y influence its PCET characteristics. Herein, 2- and 4-mercaptophenol (MP) are placed in the well-folded α3C protein (forming 2MP-α3C and 4MP-α3C) and oxidized by external light-generated [Ru(L)3]3+ complexes. The resulting neutral radicals are long-lived (>100 s) with distinct optical and EPR spectra. Calculated spin-density distributions are similar to canonical Y˙ and display very little spin on the S–S bridge that ligates the MPs to C32 inside the protein. With 2MP-α3C and 4MP-α3C we probe how proton transfer (PT) affects the PCET rate constants and mechanisms by varying the degree of solvent exposure or the potential to form an internal hydrogen bond. Solution NMR ensemble structures confirmed our intended design by displaying a major difference in the phenol OH solvent accessible surface area (≤∼2% for 2MP and 30–40% for 4MP). Additionally, 2MP-C32 is within hydrogen bonding distance to a nearby glutamate (average O–O distance is 3.2 ± 0.5 Å), which is suggested also by quantum mechanical/molecular mechanical (QM/MM) molecular dynamics simulations. Neither increased exposure of the phenol OH to solvent (buffered water), nor the internal hydrogen bond, was found to significantly affect the PCET rates. However, the lower phenol pKa values associated with the MP-α3C proteins compared to α3Y provided a sufficient change in PT driving force to alter the PCET mechanism. The PCET mechanism for 2MP-α3C and 4MP-α3C with moderately strong oxidants was predominantly step-wise PTET for pH values, but changed to concerted PCET at neutral pH values and below when a stronger oxidant was used, as found previously for α3Y. This shows how the balance of ET and PT driving forces is critical for controlling PCET mechanisms. The presented results improve our general understanding of amino-acid based PCET in enzymes.
Introduction
Proton-coupled electron transfer (PCET) is a fundamental process that is ubiquitous in natural and synthetic redox chemistry and catalysis. Understanding how PCET functions in biochemical systems unlocks the potential to take advantage of the same basic principles in synthetic designs. PCET can proceed via a step-wise mechanism where electron transfer (ET) and proton transfer (PT) advance one after the other (PTET or ETPT), or via a concerted mechanism (CEPT) where both ET and PT proceed in one kinetic step. Theoretical and small-molecule experimental studies have shown that PCET rate constants and mechanisms depend on the driving forces for electron and proton transfer,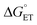 and
and 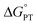 , electron and proton transfer (tunneling) distances, and the reorganization energy, λ.1–4 Systematic studies that examine how PCET is affected by changing
, electron and proton transfer (tunneling) distances, and the reorganization energy, λ.1–4 Systematic studies that examine how PCET is affected by changing 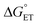 and
and 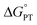 are important to advance our understanding of PCET in biology and chemistry.
are important to advance our understanding of PCET in biology and chemistry.
Some oxidoreductases use tyrosine (Y), tryptophan (W), glycine, and/or cysteine residues as 1e− redox (radical) cofactors.3,5 Amino-acid oxidation–reduction typically involves PCET, with the exception of W which participates in both 1e− and 1e−/1H+ reactions. In the context of PCET, 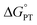 is determined by the pKa of the amino acid and the pKa of the primary proton acceptor. The latter may be a protein residue, a cofactor, buffer and/or water species. Modulating the
is determined by the pKa of the amino acid and the pKa of the primary proton acceptor. The latter may be a protein residue, a cofactor, buffer and/or water species. Modulating the 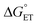 and/or
and/or 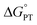 parameter(s) can change the mechanism between step-wise and concerted PCET.1 This has important consequences for the rate of radical generation and transfer. If PCET is a part of the rate-limiting step in a catalytic cycle, changes in the mechanism can consequently affect catalytic behavior and performance.
parameter(s) can change the mechanism between step-wise and concerted PCET.1 This has important consequences for the rate of radical generation and transfer. If PCET is a part of the rate-limiting step in a catalytic cycle, changes in the mechanism can consequently affect catalytic behavior and performance.
Here we use the α3X protein model system to alter the local environment of a Y redox site and investigate if, and in that case how, the structural changes alter the PCET properties. The α3X family of well-structured model proteins is based on a 65-residue, pH stable and redox inert three-helix bundle (α3).5,6 The α3 scaffold hosts a single redox-active Y or W residue at interior position 32 (X32). Oxidation-reduction of X32 is reversible, allowing accurate midpoint potentials, E°′, (i.e., [radical]/[reduced species] = 1) to be obtained.7,8 This represents a major advantage of using the α3X model system to characterize amino-acid based PCET reactions. Additionally, the broad pH stability of the α3X proteins allows PCET characterization as a function of pH. Tommos et al. introduced a series of noncanonical Y residues at site 32, including aminotyrosine (α3(NH2)Y), fluorotyrosines (α3(Fn)Y, n = 2, 3), and covalently bound mercaptophenols (2MP- and 4MP-α3C).8–11 With these Y analogs, the E°′(X32˙/X32) and the phenol pKa could be expanded across a range of 722 mV and 4.1 pKa units, respectively.5 In this study, we report the structural, spectroscopic, and radical (X32˙) formation and decay characteristics of 2MP-α3C and 4MP-α3C relative to those of α3Y. Previous studies using external [Ru(bpy)3]3+ (bpy = 2,2′-bipyridine) oxidants showed that the 1e−/1H+ oxidation of Y32 is pH-dependent with CEPT dominating at low pH and pre-equilibrium PTET dominating at high pH.12,13 Water (H2O) was assigned as the dominant primary proton acceptor for the CEPT mechanism. Y32˙ was shown to be long-lived (t1/2 = 2–10 s) and to decay via radical–radical dimerization.12
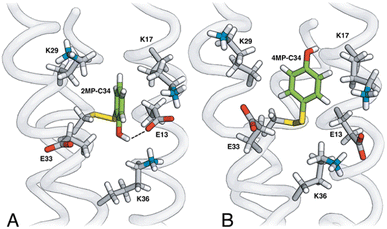
The MP-α3C proteins were designed to specifically modulate interactions at the phenol OH group. By ligating the different MPs to the buried C32 residue, the aim was to shift the phenol OH from the protein interior (2MP-α3C, Fig. 1A) towards the protein surface (4MP-α3C, Fig. 1C).9 The solution nuclear magnetic resonance (NMR) structure of 2MP-α3C confirmed the intended design for this protein.14 This structure also revealed that 2MP-C32 is involved in a weak, interhelical hydrogen bond (H-bond) with the sidechain oxygen(s) of E13. The solution NMR structure of 4MP-α3C, presented herein, solidifies the protein design further by showing that the solvent accessible surface area (SASA) of the phenol OH changes from ≤∼2% in 2MP-α3C to 30–40% in 4MP-α3C.
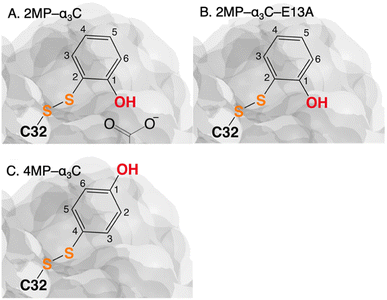 | ||
| Fig. 1 Schematic description illustrating the protein design and key differences between the MP-C32 site in (A) 2MP-α3C, (B) 2MP-α3C-E13A, and (C) 4MP-α3C. Modified with permission from ref. 14 Copyright © 2013 American Chemical Society. | ||
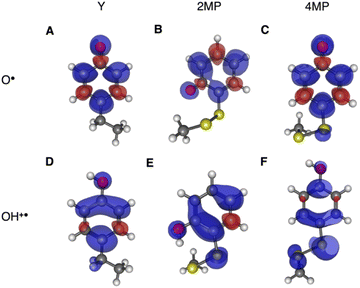
Using transient absorption (TA) spectroscopy, we show the light-induced formation of 2MP˙-C32 and 4MP˙-C32 radicals, which are long-lived (t1/2 > 100 s) and exhibit different optical and EPR spectra. Calculations show the alternate spin-density distribution patterns typical of neutral (deprotonated) phenol radicals with only minor spin densities on the sulfur atoms. We found that the rate and mechanism by which X32 is oxidized are not sensitive to a major change in the phenol OH SASA nor removing the 2MP-C32/E13 interaction. Instead, we observed that a 1.6 unit decrease in the phenol pKa compared to α3Y is sufficient to alter the oxidation reaction from a pH-dependent, mixed CEPT/PTET mechanism to mainly following a PTET pathway. Interestingly, this pKa driven change in the X32 oxidation mechanism can be reversed by increasing the 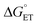 . Our results highlight the critical balance between ET and PT driving forces in controlling PCET mechanisms.
. Our results highlight the critical balance between ET and PT driving forces in controlling PCET mechanisms.
Materials and methods
Transient absorption sample preparation
2MP- and 4MP-α3C were prepared as described earlier14 and stored as lyophilized protein powder. Lyophilized protein was dissolved in 100 mM phosphate buffer KPi (KH2PO4 from Sigma Life Science ≥99% purity, K2HPO4 from ACROS Organics 99%+ purity), containing 40 mM KCl (Alfa Aesar 99.0–100.5% purity). In experiments where rate constants were measured as a function of buffer concentration, the following concentrations were used: [KPi], 20–400 mM; [2MP-α3C], 320–360 μM; [4MP-α3C], 240 μM; [Ru(bpy)3]Cl2, 20–30 μM; and [Co(NH3)5Cl]Cl2, 3–5 mM. In experiments where rate constants were measured as a function of pH, the following concentrations were used: [KPi], 100 mM; [2MP-α3C,] 240–390 μM; [4MP-α3C], 170–540 μM; [2MP-α3C-E13A], 330 μM; [Ru(bpy)3]Cl2, 20-30 μM; [Ru(dmb)3]Cl2, 20–30 μM; [Ru(deeb)3]Cl2, 20–30 μM; [Co(NH3)5Cl]Cl2, 4–6 mM; and [Na2S2O8], 5 mM. Protein, photosensitizer and quencher concentrations were determined spectrophotometrically using a Cary 50 UV-vis spectrometer and extinction coefficients: ε290(2MP-α3C) 3700 M−1 cm−1;9ε290(4MP-α3C) 2300 M−1 cm−1;9ε452([Ru(bpy)3]2+) 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 M−1 cm−1;15ε460([Ru(dmb)3]2+) 14
600 M−1 cm−1;15ε460([Ru(dmb)3]2+) 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 M−1 cm−1;15ε464([Ru(deeb)3]2+) 23
600 M−1 cm−1;15ε464([Ru(deeb)3]2+) 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 M−1 cm−1;15ε532([Co(NH3)5Cl]2+) 52 M−1 cm−1.12 Photosensitizer and quencher solutions were always prepared separately and mixed under dark conditions. For the α3X samples, the protein was added to the photosensitizer solution prior to mixing with the quencher solution. The solution pH was adjusted with 0.1–1 M NaOH and 0.01–1 M HCl and measured using a calibrated Metrohm LL Biotrode pH-electrode.
300 M−1 cm−1;15ε532([Co(NH3)5Cl]2+) 52 M−1 cm−1.12 Photosensitizer and quencher solutions were always prepared separately and mixed under dark conditions. For the α3X samples, the protein was added to the photosensitizer solution prior to mixing with the quencher solution. The solution pH was adjusted with 0.1–1 M NaOH and 0.01–1 M HCl and measured using a calibrated Metrohm LL Biotrode pH-electrode.
Transient absorption methods
The TA laser flash-photolysis setup has previously been described in detail.12,16,17 Briefly, the sample was excited using a Nd:YAG laser (Quantel, BrilliantB) with the laser light passed through an OPO tuned to 460 nm. Care was taken to avoid probe-light photochemistry during each experiment, and irreversible photoconversion of the sample by ambient, laser or probe light prior to the actual experiment. The probe light was first passed through a monochromator (Applied Photophysics, pbp Spectra Kinetic Monochromator 05-109 with slit widths set to 4 mm in and out) before hitting the sample at a 90° angle relative to the excitation light. After the sample, the probe light was passed through a 2nd monochromator (same model as listed above with slit widths set to 2 mm in and out) before reaching the PMT detector (Hamamatsu R928). The signal was digitized in a digital oscilloscope (Agilent Technologies Infiniium 600 MHz). TA traces were produced with the Applied Photophysics LKS software package. The laser power was 10–13 mJ per shot. TA spectra were recorded on a UV-vis spectrometer (Agilent 8453 diode array). The sample was excited using a 447.5 nm LED (Luxeion Star, Rebel premounted LED fitted with carlco 29.8/10 mm lens) controlled by an HP 8116A 50 MHz pulse/function generator to supply a reproducible pulse length of 500 ms.TA samples were contained in a 4 × 10 mm cuvette with an extra-long neck to avoid losing sample during deoxygenation. For the flash-photolysis measurements, the probe light was led through the 10 mm pathlength, and for the TA spectra, the probe light was led through the 4 mm pathlength. When [Co(NH3)5Cl]Cl2 was used as the quencher, oxygen was excluded from the sample by gently purging with high purity Ar gas for 10 minutes. When Na2S2O8 was used as the quencher, oxygen was not removed. All experiments were carried out at 23 (±1) °C.
Changes in pH of ca. 0.1–0.2 units were observed for flash-photolysis samples. The pH was therefore measured before and after TA, and the average values reported here.
Solution NMR spectroscopy
13C,15N-α3C expression and purification, MP labeling, and NMR sample preparations were conducted as described previously.14,18 Standard multidimensional NMR experiments were conducted at 30 °C using a 750 MHz Bruker Avance III spectrometer equipped with a cryoprobe. 1H, 13C, and 15N resonance assignments were made as described in ref. 14 and 18. NOE-based distance restraints were obtained as described in ref. 18. NMR data were processed with Felix95 (Accelrys Inc., San Diego, CA) and analyzed with SPARKY.19 Structural calculations were performed with the CNS software suite,20 as described in ref. 12. SASA analyses were perform with MOLMOL.21 Structural coordinates (RCSB Protein Data Bank ID 8VSW) and NMR chemical shifts (Biological Magnetic Resonance Data Bank, BMRB ID 31067) have been deposited for 4MP-α3C.X-band EPR spectroscopy
All electron paramagnetic resonance spectra were recorded on a Bruker EMX-micro spectrometer equipped with an EMX-Primium bridge and an ER4119HS resonator. Individual solutions were deoxygenated before mixing and the final sample concentrations were 230–250 μM protein, 20–30 μM [Ru(bpy)3]2+, and 4.5 mM [Co(NH3)5Cl]2+. Each sample was ∼100 μL and contained in a flat cell. A dark spectrum was recorded before the sample was exposed to in situ continuous illumination of a 447.5 nm LED (same setup as above) at ambient atmosphere. EPR settings: microwave frequency, 9.85 GHz; microwave power 6.3 mW; modulation frequency 100 kHz; modulation amplitude 0.1 mT. The Xepr software package (Bruker) was used for data acquisition and processing.Computational studies
Geometry optimizations were performed using density functional theory (DFT) with Gaussian 16.22 The DFT calculations used the B3LYP-D3(BJ),23,24 ωB97X-D,25 and M06-2X26 density functionals and various basis sets as specified. In addition, complete active space self-consistent field (CASSCF) calculations were performed with the aug-cc-pVTZ basis set27,28 using the PySCF program29,30 for geometries optimized at the DFT ωB97X-D/6-31+G** level. The active spaces were chosen with the automated π-orbital space (PiOS) method,31 which constructed a (9e, 8o) active space for the 4MP and 2MP models and a (7e,7o) active space for the Y model. Mulliken spin population analyses were conducted for the various radical systems.To investigate H-bonding interactions, classical molecular dynamics (MD) simulations of the 2MP-α3C and 4MP-α3C proteins were performed with Amber20 (ref. 32) using the ff14SB forcefield33 with TIP3P water.34 The simulation protocol was similar to our previous computational studies on α3Y proteins.13 Detailed H-bonding analyses were conducted for 1 microsecond trajectories. An additional 5 ps quantum mechanical/molecular mechanical (QM/MM) trajectory was also propagated. Complete computational details are provided in the ESI.†
Results and discussion
Site 32 in α3Y, 2MP-α3C and 4MP-α3C
The α3X system was designed to sequester X32 and thereby isolate and stabilize the X32˙ state. NMR spectroscopy has been used to obtain high-quality solution structures of α3X proteins, including α3Y (RCSB PDB ID 2MI7), 2MP-α3C (2LXY) and 4MP-α3C (this study, see ESI† page S9 for experimental restraints and structural statistics). Y32 displays effectively no SASA (0.2 ± 0.2%) and resides at an average depth of 7.7 ± 0.3 Å below the protein surface.12 The MP-α3C proteins were designed to modulate the exposure of the phenol OH while minimizing other structural changes, both globally to the α3 scaffold and locally to the radical site.9 As illustrated in Fig. 2, the MP-α3C structures confirm this very detailed design and show that the phenol OH SASAs for 2MP-α3C and 4MP-α3C differ by around one order of magnitude.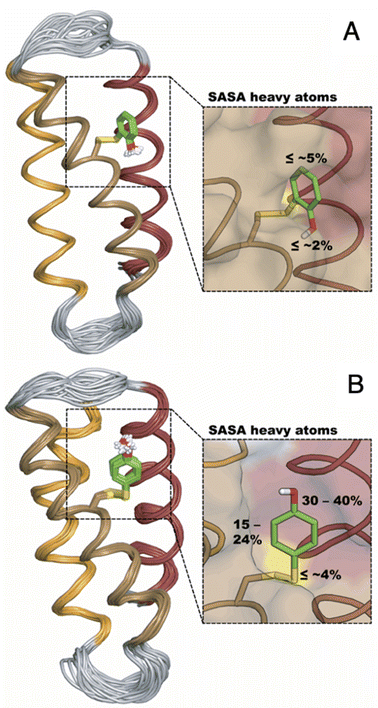 | ||
| Fig. 2 Ribbon diagram representations of the (A) 2MP-α3C (RCSB PDB ID 2LXY) and (B) 4MP-α3C (8VSW) solution NMR structures. The average SASA of 2MP-C32 and 4MP-C32 are 3.5 ± 0.7% and 8.7 ± 2.4%, respectively, across the 32-member structural ensembles that represent these proteins in solution. The zoom-in panels display the ensemble average SASA of the heavy atoms in the MP-C32 residues. Top panel, SASA of 2MP-C32: aromatic C1 carbon and phenol oxygen, ≤∼2%; all other heavy atoms, ≤∼5%. Bottom panel, SASA of 4MP-C32: aromatic C1 carbon and phenol oxygen, 30–40%; all remaining aromatic carbons, 15–24%; S–S bridge and C32 atoms, ≤∼4%. The percent SASA given for the heavy atoms are relative to the total area of each individual atom. | ||
Fig. 3 shows the five hydrophilic residues that form part of the MP-C32 radical sites. We observe no obvious protein residue that may serve as the primary proton acceptor upon 4MP-C32 oxidation. Water and/or buffer species appear more likely. In contrast, the 2MP-C32 phenol O and the E13 carboxylate group reside at an average distance consistent with a weak H-bond (O–O distance = 3.2 ± 0.5 Å). We hypothesized that the presence of a H-bond could facilitate PT to E13 upon 2MP-C32 oxidation. To investigate this further, PCET rate constants were determined for 4MP-α3C and 2MP-α3C ± E13 (vide infra).
Table 1 summarizes relevant thermodynamic properties of the MP-α3C proteins relative to the α3Y reference with protein. E°′(X32˙/X32) of 2MP-α3C and 4MP-α3C are 54 ± 3 and 175 ± 10 mV less oxidizing relative to α3Y between pH 5.0 and 10.5 The MP-C32 residues exhibit pKa values that are 1.6–2.1 units below the pKa of Y32. 2MP-α3C has a higher pKa value than the other MP-α3C proteins, likely because of stabilization from H-bonding to E13. In the absence of this interaction, the pKa of the phenol OH decreases by 0.5 units.
| Protein | E°′(X32˙/X32)/mV | E°(X32˙/X32−) mVb | pKa | |
|---|---|---|---|---|
| At pH 5.5 | At pH 8.5 | |||
| a Potentials (vs. NHE) and pKa values were obtained from ref. 5. b Determined from α3X Pourbaix diagrams5 at pH >> pKa of reduced X32. c Determined in the present work (Fig. S1 and S2). | ||||
| α3Y | 1065 (±2) | 904 (±3) | 749 (±4) | 11.3 (±0.1) |
| 2MP-α3C | 1011 (±3) | 847 (±2) | 780 (±4) | 9.7 (±0.2)c |
| 4MP-α3C | 890 (±10) | 715 (±10) | 654 (±10) | 9.5 (±0.1) |
| 2MP-α3C-E13A | — | — | 9.2 (±0.2)c | |
Radical formation and decay in MP-α3C
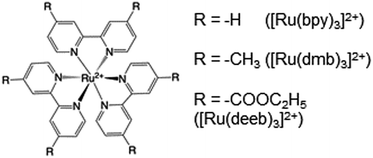
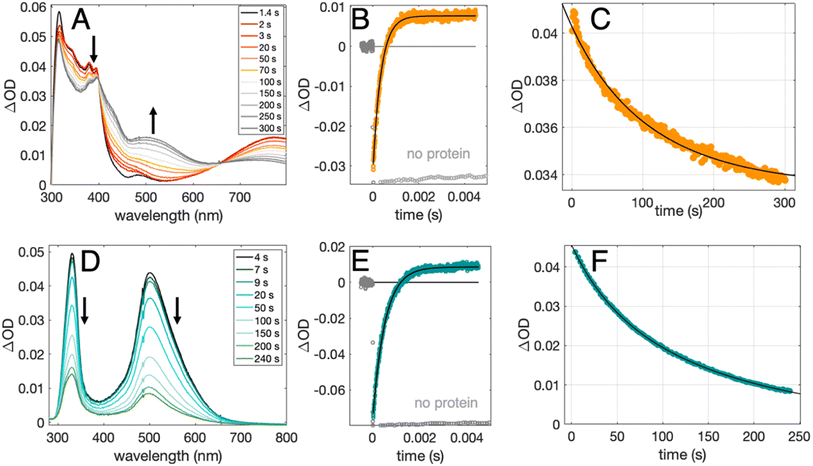
Radical formation and decay were followed by TA spectroscopy. The Ru3+ oxidant was formed in situ via the flash-quench method12,13,17,35 on samples containing MP-α3C protein, photosensitizer ([Ru(L)3]2+, L = 4,4′-R2-2,2′-bipyridine, R = –H [Ru(bpy)3]2+, –CH3 [Ru(dmb)3]2+, or –COOC2H5 [Ru(deeb)3]2+, Scheme 1), and quencher ([Co(NH3)5Cl]2+ or persulfate (Na2S2O8)). The photosensitizers used here span a ΔE° range of ca. 440 mV: E°([Ru(dmb)3]3+/2+) = 1100 mV, E°([Ru(bpy)3]3+/2+) = 1260 mV, and E°([Ru(deeb)3]3+/2+) = 1540 mV; all values reported vs. the NHE, see ESI† page S7 for details).15 The estimated error for each absolute E°(Ru3+/2+) value is ∼±30 mV. For radical formation kinetics, a 10 ns laser flash at 460 nm was used to excite the photosensitizer, which in turn was oxidatively quenched to form [Ru(L)3]3+. The PCET reaction leading to radical formation was followed at 410 and 450 nm, monitoring [Ru(L)3]2+ ground state bleach recovery concomitant with the growth of radical absorption (Fig. 4B and E). The 410 and 450 nm traces were well fitted with single-exponential functions, following a pseudo-first order dependence on the concentration of [Ru(L)3]3+, with MP-α3C in excess (vide infra). Note that without protein, the [Ru(L)3]2+ ground state bleach was stable on the time scale examined (grey data in Fig. 4B and E). For radical spectra and decay kinetics, a 500 ms LED pulse was instead used to excite the photosensitizer, which was quenched by [Co(NH3)5Cl]2+.Fig. 4 shows TA spectra and radical formation and decay kinetics for 2MP-α3C (top row) and 4MP-α3C (bottom row). We note that previous protein film voltammetry (PFV) and TA studies have shown that the α3 scaffold is unreactive, even at highly oxidizing conditions.7,8,12–14,17 PFV characterization of α3X proteins containing Y or Y analogs show fully reversible X32 ↔ X32˙ + H+(bulk) redox cycles.7,8,10,11,14 This is due to the large redox-induced pKa shifts of phenols, with the pKa of the cation radical typically <0.36 The TA spectra shown in Fig. 4A and D are thus assigned to the neutral 2MP˙-C32 and 4MP˙-C32 radicals, respectively. Consistent with this conclusion, the 2MP˙-C32 spectra are reminiscent of Y32˙ spectra recorded under similar conditions,12 while the 4MP˙-C32 spectra share spectral similarities with the neutral 4-hydroxythiophenoxyl radical.37
Radical decay kinetics were extracted by plotting the change in radical absorption (380 nm for 2MP-α3C and 500 nm for 4MP-α3C) as a function of time. A fit to second order kinetics was used to calculate the first half-life, t1/2, where t1/2 = 1/(k2Abs0(MP˙-C32)). This analysis provided t1/2(2MP˙-C32) = 100 s, t1/2(4MP˙-C32) = 130 s, and t1/2(2MP˙-C32 in 2MP-α3C-E13A) = 24 s (Fig. S10†). Extinction coefficients are not known for these radicals, but we estimated the initial concentrations, and thus calculated the rate constants. From the initial Ru2+ ground state bleach and final radical signal in Fig. 4B and E, and assuming ∼100% conversion to the radicals, the initial radical concentration is ∼13 μM in the experiments with pulsed diode excitation (Fig. 4A, C, D and F; see ESI† for details). This estimate gives rate constants for radical–radical decay of k2 ≈ 80, 60 and 300 M−1 s−1 for 2MP˙-C32, 4MP˙-C32, and 2MP˙-C32 in 2MP-α3C-E13A, respectively. Both 2MP˙-C32 and 4MP˙-C32 give rise to optical features that persisted for more than 200 s. This provided the opportunity to collect EPR spectra, as describe below.
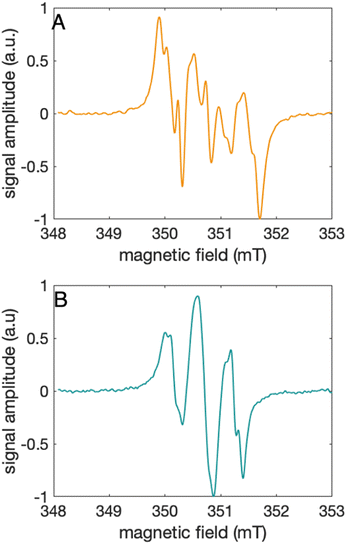
Characterization of the 2MP-α3C and 4MP-α3C radicals
The distinct UV-vis spectra shown in Fig. 4A and D suggest that 2MP˙-α3C and 4MP˙-α3C have significantly different electronic structures. To support the notion that each UV-vis spectrum represents a single major radical species, we used EPR spectroscopy to further characterize MP-α3C under photo-oxidizing conditions. EPR spectra were collected from MP-α3C dissolved in 100 mM KPi, 40 mM KCl pH 6.5 buffer, and using [Ru(bpy)3]2+ as the photosensitizer and [Co(NH3)5Cl]2+ as the quencher. The experiments were conducted at room temperature under constant illumination by a 447.4 nm LED lamp. A strong paramagnetic signal was observed to rise when the LED lamp was switched on and to subsequently decay when the LED lamp was switched off. No signal was observed prior to illumination. The EPR spectra representing the light-induced 2MP˙ and 4MP˙ species are shown in Fig. 5A and B, respectively. The spectra are consistent with the primary radicals 2MP˙ and 4MP˙. The former give rise to a hyperfine pattern due to hydrogen nuclear spin of four inequivalent protons, while the latter contains two equivalent proton pairs. As expected, the widths of the MP-α3C spectra are narrow relative to a typical protein Y˙ spectrum. The MP-C32 residues lack β-methylene protons (Fig. 1), which have a major geometry-dependent impact on the linewidth of a Y˙ spectrum.38The radical spin distribution was investigated using both DFT and multireference methods. The spin densities were calculated for optimized geometries of the 2MP-α3C, 4MP-α3C, and α3Y side chain analogs in their neutral and cationic radical states using unrestricted DFT and CASSCF calculations. Spin densities were visualized, and the Mulliken spin population39 values were computed. These are provided for the CASSCF/aug-cc-pVTZ computations in Fig. 6 and Table 2. Fig. 6 shows the expected alternating pattern of α and β spin density in the aromatic ring for neutral radicals, with cationic radicals having less spin density on the oxygen and being more delocalized over the aromatic ring. This behavior is quantified in Table 2 through Mulliken spin population analysis. These trends show that the neutral radical 4MP˙ has slightly more spin on the sulfur atoms than 2MP˙, but this effect is much more pronounced in the radical cation forms. Values for the spin populations computed for the Y neutral and cationic radicals are also provided as a reference. These trends were also observed for DFT calculations using three different functionals, namely B3LYP-D3(BJ),23,24,40 ωB97X-D,25 and M06-2X,26 with the 6-31G** and 6-31+G** basis sets for all three functionals and additionally the 6-31++G** basis set41–43 for the ωB97X-D functional (see ESI†). We conclude that for the neutral radicals there is very little spin density on the sulfur atoms that ligate the phenols to the α3 scaffold (we note that early calculations suggested a larger spin density on the sulphur).37 Our results strengthen the use of MPs as a model system for canonical protein Y redox sites.
 | ||
| Fig. 6 Spin densities computed with CASSCF/aug-cc-pVTZ for neutral radicals (A–C) and cationic radicals (D–F) with an isovalue of 0.002 Å−3. Analogous plots for DFT are provided in the ESI.† | ||
| System | Atoma | Total Sb | ||
|---|---|---|---|---|
| O | S | S2 | ||
| a O refers to the hydroxyl oxygen of the sidechain, S refers to the sulfur atom closest to the phenol ring, and S2 refers to the sulfur atom most distal to the phenol ring, i.e., closest to the backbone. b “Total S” refers to the total spin population on the sulfur atoms in the molecule. A full set of data is available in the ESI for all theoretical methods used in this study. | ||||
| Y–O˙ | 0.340 | — | — | — |
| 2MP-O˙ | 0.310 | 0.013 | 0.006 | 0.019 |
| 4MP-O˙ | 0.321 | 0.049 | 0.002 | 0.051 |
| Y–OH+˙ | 0.106 | — | — | — |
| 2MP-OH+˙ | 0.120 | 0.105 | 0.003 | 0.108 |
| 4MP-OH+˙ | 0.041 | 0.453 | 0.078 | 0.531 |
pH-dependent rate constants for radical formation
PCET rate constants (kPCET) reflecting MP-C32 oxidation by Ru(L)33+ were obtained as a function of buffer concentration (Fig. S5†), pH, and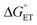 (Fig. 7 and 8; Table 3).
(Fig. 7 and 8; Table 3). 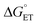 was modulated by using the three photosensitizers shown in Scheme 1 (ΔE°(Ru(3+/2+)) ca. 440 mV, vide supra). In all experiments, the protein concentration was much higher (200–600 μM) than the concentration of the in situ generated Ru3+ oxidant (1–6 μM), resulting in pseudo-first order kinetics for radical formation. To confirm that the reactions were first order with regards to [protein], rate constants were also determined as a function of [protein] at one or two pH values for each oxidant (Fig. S4, S7, and S9; see ESI† for details). The large excess of protein also resulted in complete consumption of [Ru(L)3]3+, with no significant remaining Ru2+ bleach. Thus, the reverse reaction could be ignored even for the reactions where ΔG° ≈ 0 and the observed rate constant can be identified as the forward rate constant for PCET, kPCET (see General discussion).
was modulated by using the three photosensitizers shown in Scheme 1 (ΔE°(Ru(3+/2+)) ca. 440 mV, vide supra). In all experiments, the protein concentration was much higher (200–600 μM) than the concentration of the in situ generated Ru3+ oxidant (1–6 μM), resulting in pseudo-first order kinetics for radical formation. To confirm that the reactions were first order with regards to [protein], rate constants were also determined as a function of [protein] at one or two pH values for each oxidant (Fig. S4, S7, and S9; see ESI† for details). The large excess of protein also resulted in complete consumption of [Ru(L)3]3+, with no significant remaining Ru2+ bleach. Thus, the reverse reaction could be ignored even for the reactions where ΔG° ≈ 0 and the observed rate constant can be identified as the forward rate constant for PCET, kPCET (see General discussion).
 | ||
| Fig. 7 Rate constants for radical formation vs. pH using [Ru(bpy)3]3+ as oxidant for 2MP-α3C (orange dots), 2MP-α3C-E13A (grey squares), and 4MP-α3C (green triangles), compared to previously published data for α3Y (black circles).13 Standard deviations are shown, but are often smaller than the size of the data symbols. Samples contained 60–620 μM protein, 30 μM [Ru(bpy)3]2+, and 4–6 mM [Co(NH3)5Cl]2+. Fits according to eqn (1) are shown as lines (see Table 4 for results). | ||
 | ||
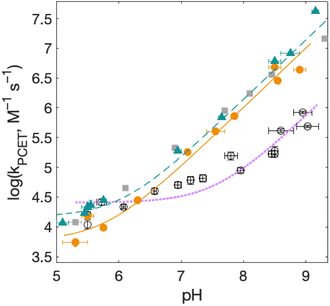
| Fig. 8 Rate constants for radical formation as a function of pH for 2MP-α3C (orange dots) and 4MP-α3C (green triangles), with [Ru(deeb)3]3+ as oxidant, and α3Y (black circles, fit with a purple dotted line curve) with [Ru(bpy)3]3+ as oxidant from ref. 13, other conditions as in Fig. 7. Standard deviations are shown, but are often smaller than the size of the data symbols. Fits according to eqn (1) are shown (see Table 4 for results). | ||
| Oxidant | pH | k PCET (M−1 s−1) | E°a (mV vs. NHE) |
|---|---|---|---|
| a Error bars are estimated to be ±30 mV. | |||
| 2MP-α 3 C | |||
| Ru(dmb)33+ | 5.5(±0.1) | 2.8 × 103 | +1100 |
| Ru(bpy)33+ | 5.5(±0.1) | 1.5 × 104 | +1260 |
| Ru(dmb)33+ | 8.5(±0.1) | 7.7 × 105 | +1100 |
| Ru(bpy)33+ | 8.5(±0.1) | 4.8 × 106 | +1260 |
| Ru(deeb)33+ | 8.5(±0.1) | 3.2 × 107 | +1540 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| 4MP-α 3 C | |||
| Ru(dmb)33+ | 5.5(±0.1) | 4.4 × 103 | +1100 |
| Ru(bpy)33+ | 5.5(±0.1) | 2.1 × 104 | +1260 |
| Ru(dmb)33+ | 8.5(±0.1) | 1.5 × 106 | +1100 |
| Ru(bpy)33+ | 8.5(±0.1) | 6.1 × 106 | +1260 |
| Ru(deeb)33+ | 8.5(±0.1) | 5.4 × 107 | +1540 |
There is no significant change in kPCET derived from 2MP-α3C and 4MP-α3C samples containing 20 to 400 mM KPi (Fig. S5†). This observation shows that a buffer species does not serve as the primary acceptor of the phenolic proton as 2MP-C32 or 4MP-C32 is oxidized. These results agree with results for α3Y, where buffer species were shown to not participate in the PCET reaction,13 but stand in stark contrast to results obtained for small molecule Y and W derivatives in solution, where common buffers may be the primary acceptor even at moderate concentrations (≳10 mM).44,45
Fig. 7 shows kPCET as a function of pH using [Ru(bpy)3]3+ as the oxidant for 2MP-α3C (orange), 2MP-α3C-E13A (grey), and 4MP-α3C (green) compared to previously published data on α3Y (black/purple). Kinetic data for all proteins are fit with eqn (1) (below), and the resulting kPCET values are given in Table 4.
| kPCET = kYOH + kYO− × 10(pH-pKa) | (1) |
| Oxidant | k YOH (M−1 s−1) | k YO− (M−1 s−1) |
|---|---|---|
| a From fits according to eqn (1). b Calculated from the pH 8.5 value multiplied by 10(pKa−8.5), see text. | ||
| 2MP-α 3 C | ||
| Ru(dmb)33+ | — | 1.2 × 107b |
| Ru(bpy)33+ | 5.8 × 103 | 5.1 × 107 |
| Ru(deeb)33+ | 8.4 × 105 | 2.7 × 108 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| 4MP-α 3 C | ||
| Ru(dmb)33+ | — | 1.5 × 107b |
| Ru(bpy)33+ | 1.5 × 104 | 4.4 × 107 |
| Ru(deeb)33+ | 2.3 × 106 | 4.0 × 108 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| α 3 Y | ||
| Ru(bpy)33+ | 2.6 × 104 | 1.4 × 108 |
For α3Y, the first, pH-independent term that dominates at low pH is assigned to a concerted CEPT reaction with water as the primary proton acceptor.13 The second term is assigned to pre-equilibrium PTET (PTETpre-eq) with the equilibrium fraction of the Y–O− species increasing ten-fold per pH unit. For MP-α3C, the contribution of the first term is very small and is only noticeable as a weak pH dependence for the lowest pH data points. As shown in the next section, the mechanisms can be assigned in complete analogy to the α3Y system: CEPT with H2O as proton acceptor at the lowest pH values, and PTET at the higher pH values.
Assigning the PCET mechanisms
The kinetic isotope effect (KIE) on PCET rates was determined at 2–3 different pL (L = H or D) values using [Ru(bpy)3]3+ as oxidant. The observed KIE values were significant: 2.9 (pL 6.0 ± 0.1) and 3.6 (pL 9.0 ± 0.1) for 2MP-α3C, and 6.2 (pL 5.3 ± 0.3), 11.2 (pL 6.3 ± 0.1), and 13.5 (pL 8.6 ± 0.1) for 4MP-α3C. The large KIE values confirm that PT is part of the rate-limiting step. From these KIEs, we can exclude an ET-limited ETPT reaction over the entire pH range examined. We can also exclude a pre-equilibrium ETPT because this mechanism requires that the pre-equilibrium is faster than the subsequent reaction, which is highly improbable given that the pKa's of phenols typically drop to values <0 upon oxidation.36A pH-independent PTET reaction at low pH can be excluded because deprotonation of weak acids to water (H2O) is slow: kPT ∼100 s−1 for pKa = 9,46 which is much slower than our observed first-order rate constants. Other potential proton acceptors (OH−, buffer) increase in concentration as the pH increases and would not have given a pH-independent rate constant. This analysis suggests that the pH-independent reaction is CEPT with H2O as the primary proton acceptor.
The pH-dependent rate constants (second term in eqn (1)) can have two origins. First, for a PTETpre-eq mechanism, the pre-equilibrium shifts with pH because at higher pH values there is a larger fraction of already deprotonated species, which leads to faster rate constants. Second, for an irreversible reaction step (CEPT or PT-limited PTET), the concentration of the proton-accepting species can depend on pH, which would be the case for e.g. OH− and base forms of the buffer. At high pH, CEPT with OH− as the primary proton acceptor can most likely be excluded because the observed (pseudo-first order) rate constants are too large to be explained by a diffusional reaction with the [OH−] present in the solution in the pH interval studied, see ESI page S12.† The PT-limited PTET could be excluded by comparing the rate constants with those obtained with a weaker oxidant, namely [Ru(dmb)3]3+ at pH 5.5 ± 0.1 and 8.5 ± 0.1 (Table 3). Both 2MP-α3C and 4MP-α3C showed slower rate constants with the weaker oxidant. This is inconsistent with a PT-limited reaction but is consistent with PTETpre-eq, for which the overall rate constant depends also on the rate constant for the second step. This analysis suggests that 2MP-α3C and 4MP-α3C oxidation by [Ru(bpy)3]3+ (Fig. 7) proceeds mainly via a PTETpre-eq mechanism, with CEPT dominating only at the lowest pH values. Note that we can exclude a significant contribution from the reverse PCET reaction for reactions at ΔG° ≈ 0, which could have given a pH-dependence of the net reaction,47 because we use great excess of protein, making the reaction go to completion in a single kinetic phase (ΔG < 0), and no remaining Ru2+ bleach is seen over a large variation of pH values and observed rate constants. Moreover, a parallel pH-dependence is observed also with the strong oxidant [Ru(deeb)3]3+, for which ΔG° ≪ 0.
Proton transfer is not facilitated by increased solvent exposure nor by a nearby internal proton acceptor
Rate constants determined for 4MP-α3C are slightly higher compared to those for 2MP-α3C. This is most likely due to the lower E°′(X32˙/X32) and pKa values of 4MP-α3C. As the rate constant difference is modest, it appears that the higher phenol OH SASA of 4MP-C32 does not further accelerate PCET. Specifically, it does not seem to facilitate PT to water, and it does not allow sufficient access of buffer for this to be the primary proton acceptor.The relatively close distance of 2MP and E13 in 2MP-α3C (Fig. 3A) did not lead to any clear increase of the PCET rate constant compared to 4MP-α3C. Glutamate is a stronger base than water, with pKa ∼4.5 vs. 0 for their respective conjugate acids, and glutamate as a proton acceptor would be expected to accelerate PCET. Moreover, the 2MP-α3C rate constant is even slightly higher for 2MP-α3C-E13A, which lacks this glutamate residue (Fig. 7). We can therefore exclude E13 as the primary proton acceptor and instead assign water as the likely proton acceptor for 2MP-α3C, just as for the other proteins.
MD simulations were performed on the MP-α3C solution NMR structures (Fig. 2) to better understand the H-bonding interaction between the 2MP-C32 or 4MP-C32 and water, E13, or E33 (Fig. 3 and Table S12†). The simulations show that 4MP-C32 H-bonds primarily with water and has negligible interaction with E13 and E33. 2MP-C32 H-bonds with water to a much lesser extent and interacts also with E33 but not significantly with E13. Note that the NMR structure does not indicate a H-bond between 2MP-C32 and E33 (Fig. S21†), within strict distance and angle criteria. Moreover, the H-bond between 2MP-C32 and E13 is retained in a QM/MM MD trajectory, where the 2MP-C32 and E13 sidechains are treated with DFT (Fig. S23†). Thus, the preference for H-bonding of 2MP-C32 to E33 over E13 may be due to limitations of the force field, and the QM/MM simulations suggest that 2MP-C32 can H-bond to E13. Nevertheless, analysis of the rate constants suggests that although E13 is within H-bonding distance to 2MP-C32, other factors such as insufficient proton vibrational wavefunction overlap inhibit PT.
Rate constants for PCET with various oxidation strengths
For solvated small-molecule Y compounds, a stronger oxidant has been shown to change the PCET mechanism from PTET to CEPT.2 To test whether an external oxidant could change the PCET mechanism in the α3X protein system, rate constants were determined as a function of pH using the stronger oxidant [Ru(deeb)3]3+ with persulfate as the quencher (Fig. 8; see ESI† for details). This gave much faster PCET rate constants, and a much more prominent contribution from the pH-independent CEPT reaction (first term in eqn (1)). The pH dependence is very similar to what was observed for α3Y using [Ru(bpy)3]3+ as the oxidant (black data with purple dotted fit in Fig. 8).13 Fitting the data to eqn (1) yielded rate constants for the protonated and deprotonated fractions of MP-C32 (Table 4).With [Ru(deeb)3]3+ as the oxidant, the rate constants at pH >7 increase with pH, analogous to the data with [Ru(bpy)3]3+. The mechanism can thus be assigned to PTETpre-eq also with the stronger oxidant; PT-limited PTET and CEPT with OH− as the proton acceptor can be excluded as for the experiments with [Ru(bpy)3]3+ above. The rate constant kYO− is higher with [Ru(deeb)3]3+, as expected from the driving force dependence of Y–O− oxidation (see General discussion below).
Fig. 8 shows PCET rate constants of 2MP-α3C and 4MP-α3C with the stronger oxidant [Ru(deeb)3]3+, in comparison to α3Y using [Ru(bpy)3]3+. The general trend in pH-dependence of PCET rate constants for 2MP-α3C and 4MP-α3C versus α3Y is similar, but the rate constants are significantly accelerated in the former. At low pH, the use of a stronger oxidant can favor the ETPT mechanism, and it is important to demonstrate that proton transfer is a part of the rate limiting step. Experiments were therefore repeated in D2O at pL 5.6(±0.1) with [Ru(deeb)3]3+ as the oxidant, and resulted in KIE ∼3 for both 2MP-α3C and 4MP-α3C. This large KIE excludes an ET-limited ETPT mechanism and suggests that PCET proceeds via CEPT with H2O as the primary proton acceptor, as was the case with the weaker oxidants. The rate constant is much larger, as can be expected with the much stronger oxidant (see next section). We note that the pH-independent rate constant cannot be explained by formation of an internal H-bond for 2MP-C32 since 4MP-C32 shows the same behavior without having a nearby protein proton acceptor.
General discussion
Changing the PCET mechanism by tuning the driving force
The recently introduced PCET zone diagrams1 can help to visualize which mechanism dominates a PCET reaction, depending on the driving force for initial ET or PT (represented by ΔE° and ΔpKa, respectively), see Fig. 9. The diagrams assume a Marcus-type free-energy dependence of the rate constant for each mechanistic step (ET, PT or CEPT; see eqn (2) below). The size and shape of each of the mechanistic regions are dictated by the relative pre-exponential factor and reorganization energies for each mechanism.1 The schematic zone diagram in Fig. 9 has a large CEPT region, which is a result of two factors. First, a large energetic interdependence of ET and PT, manifested by a large difference in E°(X32˙+/X32) vs. E°′(X32˙/X32−) and a correspondingly large difference in the phenol pKa of oxidized and reduced X32, favors a CEPT mechanism under a wide range of conditions. Secondly, a large vibronic coupling between the reactant and product state for CEPT allows for a high probability of electron and proton tunneling. With sufficient kinetic data as a function of ΔE° and ΔpKa for a system, the lines dividing the zones can be quantitatively estimated.48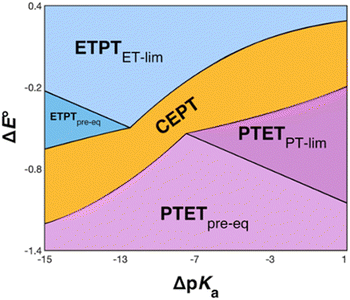 | ||
| Fig. 9 Schematic zone diagram for a PCET oxidation of a compound HA to A˙, where the reaction exhibits a sufficiently large vibronic coupling that CEPT can compete in this range of ΔE° and ΔpKa values. The axes are defined as ΔE° = E°(oxidant) − E°(HA˙+/HA) (in units of volts) and ΔpKa = pKa(H+ base) − pKa(HA), so that the overall driving force for PCET increases when moving upwards and to the right in the diagram. Adapted with permission from ref. 1. Copyright © 2021 American Chemical Society. | ||
For bimolecular PCET reactions, bases and oxidants of different strengths can be used to access different PCET regions. However, the protein shields the X32 pocket and excludes negatively charged buffer species. This is evidenced by our previous studies on α3Y12,13 as well as the independence of kPCET rate constants on the buffer concentration in the present data. Having shown that 2MP-α3C is similar to α3Y in that X32 exhibits a low SASA, comparison between the two proteins allows us to investigate the effect of altering the PT driving force. The pKa value is 1.6 lower for 2MP-α3C, giving an increase in PT driving force of 95 meV. A change in rate constant by one order of magnitude per pKa unit is expected for a PTETpre-eq reaction. Indeed, in the high pH region of Fig. 7, the difference in kPCET between 2MP-α3C and α3Y is between one and one and a half orders of magnitude, as expected.
E°(X32˙/X32−) is very similar for 2MP-α3C (780 ± 4 mV) and α3Y (749 ± 4 mV). Instead, the lower pKa value for 2MP-α3C changes the PT driving force and would mean moving to the right in Fig. 9 for 2MP-α3C compared to α3Y. This is consistent with moving from the CEPT region to the PTETpre-eq region. Indeed, this is what is experimentally observed, as CEPT dominates at low pH for α3Y, while PTETpre-eq dominates over almost the entire pH range for 2MP-α3C with the moderately strong oxidant [Ru(bpy)3]3+ (Fig. 7). When the ET driving force increases by ca. 280 meV by using the much stronger oxidant [Ru(deeb)3]3+, we move upwards in the diagram and re-enter the CEPT region, as is shown by the data in Fig. 8. 4MP-α3C shows an entirely parallel behavior as compared to 2MP-α3C; the ca. 125 mV lower E°(X32˙/X32−) value is not sufficient to favor CEPT with the weaker oxidants, whereas the much greater difference in ΔE° with [Ru(deeb)3]3+ has this effect.
From the more qualitative discussion of changing mechanisms (above), we continue by drawing quantitative comparisons of the rate constants between the different combinations of protein and oxidant with the aid of theories for ET and CEPT. A simplified expression for the free-energy dependence of the rate constant for ET or CEPT is given in eqn (2).49
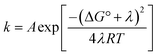 | (2) |
A CEPT reaction may have contributions to the rate constant from transitions to and from several proton vibrational states that can modify the free-energy prediction of eqn (2). For simplicity these effects will be neglected in the present analysis.50 The derivative in eqn (3) shows the predicted slope of a typical plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k vs. driving force, where ∂
k vs. driving force, where ∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(kCEPT)/∂(−ΔG°) = (50 meV)−1 when ΔG° = 0.
ln(kCEPT)/∂(−ΔG°) = (50 meV)−1 when ΔG° = 0.
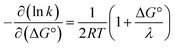 | (3) |
The driving force for CEPT is given by 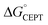 = −F(E°(RuIII/RuII) − E°′(X32˙/X32)) at pH = pKa of the conjugate acid of the proton acceptor; in these systems water is the proton acceptor, and pKa (H3O+) = 0. E°′(X32˙/X32)pH0 can be predicted from the Pourbaix diagrams of α3Y, 2MP-α3C, and 4MP-α3C5,9 and give
= −F(E°(RuIII/RuII) − E°′(X32˙/X32)) at pH = pKa of the conjugate acid of the proton acceptor; in these systems water is the proton acceptor, and pKa (H3O+) = 0. E°′(X32˙/X32)pH0 can be predicted from the Pourbaix diagrams of α3Y, 2MP-α3C, and 4MP-α3C5,9 and give 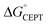 ≈ 110, 55 and −50 meV, respectively, when [Ru(bpy)3]3+ is the oxidant. The PCET reaction is observed even when
≈ 110, 55 and −50 meV, respectively, when [Ru(bpy)3]3+ is the oxidant. The PCET reaction is observed even when 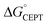 > 0 because the reaction is driven to completion by the more than 100-fold excess of protein vs. [Ru(bpy)3]3+ generated per laser flash (ca. 1–6 μM), Fig. 4B and E.
> 0 because the reaction is driven to completion by the more than 100-fold excess of protein vs. [Ru(bpy)3]3+ generated per laser flash (ca. 1–6 μM), Fig. 4B and E.
As described above, the PCET mechanism is consistent with CEPT when kPCET is pH-independent (at low pH-values, Fig. 7 and 8). The use of [Ru(deeb)3]3+in lieu of [Ru(bpy)3]3+ increases 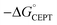 by 280 meV, and kYOH for 2MP-α3C and 4MP-α3C increase by ca. two orders of magnitude (Table 4). This corresponds to a slope according to eqn (3) of (60 meV)−1, consistent with CEPT in the normal region with a small driving force.
by 280 meV, and kYOH for 2MP-α3C and 4MP-α3C increase by ca. two orders of magnitude (Table 4). This corresponds to a slope according to eqn (3) of (60 meV)−1, consistent with CEPT in the normal region with a small driving force.
Shifting the oxidant strength in the CEPT region gives rise to predictable changes in kPCET for each protein individually. Comparing the trend in kPCET between the different proteins, however, does not consistently correlate with changes in 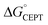 . Notably, α3Y has the least favorable
. Notably, α3Y has the least favorable 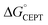 , and yet its CEPT rate constants are the largest (see Fig. 7, low pH region). 4MP-α3C, which exhibits the most favorable
, and yet its CEPT rate constants are the largest (see Fig. 7, low pH region). 4MP-α3C, which exhibits the most favorable 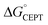 and which is predicted to have its phenol OH consistently in contact with water (Fig. 3, Table S12†), does not have the largest CEPT rate constants, though they are greater than rate constants for 2MP-α3C. From the study of CEPT in this homogeneous series of proteins, it is clear that factors outside of the driving force influence CEPT rate constants. One possibility is that the vibronic coupling varies significantly among the protein systems due to different proton donor–acceptor distances, which influence the overlap between the proton vibrational wavefunctions. As described above, water is assigned as the dominant primary proton acceptor for the α3X proteins investigated here. We have previously identified local side chain motions near the Y32 site that permit transient access of one to two water molecules to within H-bonding distance of the phenol OH.13 2MP-α3C and 4MP-α3C behave in a similar manner (Table S12†). The observed differences in the concerted PCET kinetics indicate that α3Y can access a state or states where the phenol OH and the water proton acceptor are more optimally oriented with respect to PT relative to the MP-α3C proteins.
and which is predicted to have its phenol OH consistently in contact with water (Fig. 3, Table S12†), does not have the largest CEPT rate constants, though they are greater than rate constants for 2MP-α3C. From the study of CEPT in this homogeneous series of proteins, it is clear that factors outside of the driving force influence CEPT rate constants. One possibility is that the vibronic coupling varies significantly among the protein systems due to different proton donor–acceptor distances, which influence the overlap between the proton vibrational wavefunctions. As described above, water is assigned as the dominant primary proton acceptor for the α3X proteins investigated here. We have previously identified local side chain motions near the Y32 site that permit transient access of one to two water molecules to within H-bonding distance of the phenol OH.13 2MP-α3C and 4MP-α3C behave in a similar manner (Table S12†). The observed differences in the concerted PCET kinetics indicate that α3Y can access a state or states where the phenol OH and the water proton acceptor are more optimally oriented with respect to PT relative to the MP-α3C proteins.
At high pH-values, all combinations of protein and oxidant reacted via PTETpre-eq. The observed rate constants are proportional to the ET rate constant from deprotonated Y32 or MP-C32 (kYO− in eq. (1)), and thus depend on the driving force for ET. The values of kYO− taken from the fits to eqn (1) in Fig. 7 and 8 are plotted vs. the driving force for ET from Y–O− to Ru(L)33+ (Fig. 10). The kYO− values for MP-α3C/[Ru(dmb)3]3+ are taken from the rate constants at pH 8.5 and multiplying with 10(pKa−8.5), i.e. assuming that only the second term of eqn (1) is important at pH ≥ 8.5. The data can be fitted with eqn (2), as shown in Fig. 10, with reasonable values of the reorganization energy and pre-exponential factor. kYO− is a second order rate constant that, below the diffusion-controlled limit, is equal to the product of the equilibrium constant for encounter complex formation with the oxidant (Kd) and the rate constant for unimolecular ET in the encounter complex. It is reasonable to assume that Kd is constant in the present series of reactions, and it is often assumed that Kd ∼1. This means that the second-order rate constant is also expected to follow the free-energy dependence of eq. (2).49 The good agreement of PTET data and predictions of eqn (2) in Fig. 10 shows that the series of proteins and oxidants form a homogeneous series, where factors that may affect the ET rate constant other than the reaction free energy – such as λ or Kd – remain comparatively constant. Thus, the differences of the PCET rate constants between the proteins discussed in the previous paragraph can be assigned to the PT part of the reaction.
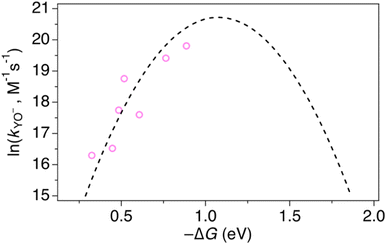 | ||
| Fig. 10 Natural logarithm (ln) of kYO− rate constants (pink circles) as a function of driving force for ET from YO− to the [Ru(L)3]3+ oxidant. The dashed line shows a fit according to eqn (2) assuming A = 1 × 109 M−1 s−1, which gave λ = 1.1 eV. | ||
To conclude this section, the free-energy dependencies of both the CEPT and PTET rate constants show that our mechanistic assignments are consistent with current theories. The dependence of the PCET mechanism on oxidant strength and phenolic pKa can be utilized to analyze and control the mechanism in a rational and predictable way.
Conclusions
2MP-α3C and 4MP-α3C were designed with the specific aim of studying the effect of different degrees of solvent exposure on X32 properties and PCET reactivity. Both proteins could be oxidized by a series of external [Ru(L)3]3+ complexes with different oxidant strengths (E° = +1100–1540 mV vs. NHE), and a long-lived neutral radical (t1/2 > 100 s) was observed. The much greater SASA for the phenol OH of 4MP-α3C (30–40% vs. ≤∼2% for 2MP-α3C) did not result in any detectable increase in the rate constant for radical formation, however, and did not allow for access of buffer species as primary proton acceptors. A glutamate (E13) was found nearby the phenol O of 2MP-C32 in the solution NMR structure (O–O distance 3.2 ± 0.5 Å) and also in QM/MM MD simulations, which led to the expectation of a facilitated PCET by H-bonding and PT to E13. No kinetic evidence for such an effect was detected, and a variant where E13 was replaced with alanine (2MP-α3C-E13A) showed very similar kinetics, with even slightly faster rates. This suggests that the distance and orientation of E13 relative to X32 are not sufficiently favorable to facilitate proton tunneling, leaving water as the primary proton acceptor for all MP-α3C proteins.Instead, we found that the differences in E°′ and pKa values of 2MP-C32, 4MP-C32, and Y32 induced important changes in the rate constants and mechanisms for PCET. With the two weakest [Ru(L)3]3+ oxidants, all three MP-α3C proteins reacted predominantly by PTETpre-eq at pH ≳ 6, with CEPT being important only at the lowest pH-values examined. This was different from α3Y, for which CEPT was prominent over a larger pH range and PTETpre-eq dominated only at pH ≳ 8. When the strongest oxidant was used, 2MP-α3C and 4MP-α3C showed a similar balance of the two PCET mechanisms as for α3Y with the weaker oxidant. This can be rationalized by the lower pKa values for the MP-α3C proteins, which favor PTET, but with a stronger oxidant the balance is again in favor of CEPT at neutral and acidic pH. Changing E°′ and pKa values alters 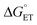 and
and 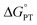 , and consequently controls which mechanism dominates the reaction, as is illustrated by the zone diagram reproduced in Fig. 9.
, and consequently controls which mechanism dominates the reaction, as is illustrated by the zone diagram reproduced in Fig. 9.
While the difference when changing the oxidant for a given protein can be explained by just changing the driving force (eqn (2)), the difference in kCEPT among the proteins clearly depends also on other factors. Y32 has the least favorable 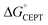 , and yet the CEPT rate constant with [Ru(bpy)3]3+ is the largest. Thus, while the three proteins appear to form a homogeneous series when comparing the oxidation rate constants for the deprotonated form (kYO−), the CEPT reactions differ by more than just their driving forces. MD simulations on the α3Y and MP-α3C solution NMR structures revealed fast side chain motions that allow water in and out of the X32 site. The observed difference in kCEPT suggests that α3Y can transiently line up the phenol OH/water H-bond more favorably with respect to PT relative to the two other proteins, giving rise to the somewhat faster kCEPT rate constant.
, and yet the CEPT rate constant with [Ru(bpy)3]3+ is the largest. Thus, while the three proteins appear to form a homogeneous series when comparing the oxidation rate constants for the deprotonated form (kYO−), the CEPT reactions differ by more than just their driving forces. MD simulations on the α3Y and MP-α3C solution NMR structures revealed fast side chain motions that allow water in and out of the X32 site. The observed difference in kCEPT suggests that α3Y can transiently line up the phenol OH/water H-bond more favorably with respect to PT relative to the two other proteins, giving rise to the somewhat faster kCEPT rate constant.
The present results demonstrate how the PCET mechanism for X32 oxidation depends on the driving forces for ET and PT. A sufficiently strong oxidant will favor ETPT and a sufficiently strong base will favor PTET, but if the driving forces for ET and PT are balanced, a concerted CEPT mechanism can dominate. This has implications for enzymes, where the pKa of residues and reduction potentials can be altered depending on the protein environment. The mechanism in turn determines the rate of the PCET reaction and its dependence on reaction conditions. Our results also show that water is a viable proton acceptor even for amino acids with minimal solvent exposure.
Data availability
Computational data have been deposited in the Open Science Framework Repository (DOI: https://doi.org/10.17605/OSF.IO/QPFSH).Author contributions
R. L. and M. L. generated purified MP-α3C material for the optical spectroscopy studies. A. N.-M. prepared samples, performed and analyzed all optical spectroscopy measurements. M. L. and C. T. deposited the 4MP-α3C NMR data and structural coordinates. C. T. developed the overall MP-α3C protein design strategy and performed protein structural analyses. C. R. R. performed and analyzed all computational work, under supervision of S. H.-S. P. H. performed and analyzed the EPR experiments. H. A. prepared the oxidant complexes. A. N.-M., S. D. G. S. H.-S., C. T. and L. H. conceived the study, and together with C. R. R. they prepared the manuscript draft and finalized the paper. All authors agreed on the final version of the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Swedish Research Council (grant no. 2020-05246 (L. H.) and grant no. 2017-04992 (S. D. G.)) and the National Institutes of Health grant R01 GM079190 (C. T.). The computational portion of this work was supported by NIH Grant R35 GM139449 (S. H.-S.). C. R. R. was supported by NSF Graduate Research Fellowship Program Grant DGE1752134. Computational resources were provided by the Yale Center of Research Computing. C. R. R. would like to thank Phillips Hutchison for technical assistance. The solution NMR structure of 4MP-α3C was initially described in the PhD thesis of Dr Melissa C. Martínez-Rivera, University of Pennsylvania, 2013.18References
- R. Tyburski, T. Liu, S. D. Glover and L. Hammarström, Proton-Coupled Electron Transfer Guidelines, Fair and Square, J. Am. Chem. Soc., 2021, 143, 560–576 CrossRef CAS PubMed.
- T. Irebo, M. T. Zhang, T. F. Markle, A. M. Scott and L. Hammarström, Spanning four mechanistic regions of intramolecular proton-coupled electron transfer in a Ru(bpy)3(2+)-tyrosine complex, J. Am. Chem. Soc., 2012, 134, 16247–16254 CrossRef CAS PubMed.
- A. Migliore, N. F. Polizzi, M. J. Therien and D. N. Beratan, Biochemistry and theory of proton-coupled electron transfer, Chem. Rev., 2014, 114, 3381–3465 CrossRef CAS PubMed.
- S. Hammes-Schiffer and A. A. Stuchebrukhov, Theory of coupled electron and proton transfer reactions, Chem. Rev., 2010, 110, 6939–6960 CrossRef CAS PubMed.
- C. Tommos, Insights into the Thermodynamics and Kinetics of Amino-Acid Radicals in Proteins, Annu. Rev. Biophys., 2022, 51, 453–471 CrossRef CAS PubMed.
- C. Tommos, J. J. Skalicky, D. L. Pilloud, A. J. Wand and P. L. Dutton, De novo proteins as models of radical enzymes, Biochem., 1999, 38, 9495–9507 CrossRef CAS PubMed.
- B. W. Berry, M. C. Martinez-Rivera and C. Tommos, Reversible voltammograms and a Pourbaix diagram for a protein tyrosine radical, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9739–9743 CrossRef CAS PubMed.
- K. R. Ravichandran, A. B. Zong, A. T. Taguchi, D. G. Nocera, J. Stubbe and C. Tommos, Formal reduction potentials of difluorotyrosine and trifluorotyrosine protein residues: Defining the thermodynamics of multistep radical transfer, J. Am. Chem. Soc., 2017, 139, 2994–3004 CrossRef CAS PubMed.
- S. Hay, K. Westerlund and C. Tommos, Moving a phenol hydroxyl group from the surface to the interior of a protein: effects on the phenol potential and pK(A), Biochem., 2005, 44, 11891–11902 CrossRef CAS PubMed.
- K. R. Ravichandran, L. Liang, J. Stubbe and C. Tommos, Formal reduction potential of 3,5-difluorotyrosine in a structured protein: insight into multistep radical transfer, Biochem., 2013, 52, 8907–8915 CrossRef CAS PubMed.
- W. Lee, M. Kasanmascheff, M. Huynh, A. Quartararo, C. Costentin, I. Bejenke, D. G. Nocera, M. Bennati, C. Tommos and J. Stubbe, Properties of Site-Specifically Incorporated 3-Aminotyrosine in Proteins To Study Redox-Active Tyrosines: Escherichia coli Ribonucleotide Reductase as a Paradigm, Biochem, 2018, 57, 3402–3415 CrossRef CAS PubMed.
- S. D. Glover, C. Jorge, L. Liang, K. G. Valentine, L. Hammarström and C. Tommos, Photochemical tyrosine oxidation in the structurally well-defined alpha3Y protein: proton-coupled electron transfer and a long-lived tyrosine radical, J. Am. Chem. Soc., 2014, 136, 14039–14051 CrossRef CAS PubMed.
- A. Nilsen-Moe, C. R. Reinhardt, S. D. Glover, L. Liang, S. Hammes-Schiffer, L. Hammarström and C. Tommos, Proton-Coupled Electron Transfer from Tyrosine in the Interior of a de novo Protein: Mechanisms and Primary Proton Acceptor, J. Am. Chem. Soc., 2020, 142, 11550–11559 CrossRef CAS PubMed.
- C. Tommos, K. G. Valentine, M. C. Martinez-Rivera, L. Liang and V. R. Moorman, Reversible phenol oxidation and reduction in the structurally well-defined 2-Mercaptophenol-α3C protein, Biochem, 2013, 52, 1409–1418 CrossRef CAS PubMed.
- A. Juris, V. Balzani, F. Barigelletti, S. Campagna, P. Belser and A. von Zelewsky, Ru(II) polypyridine complexes: photophysics, photochemistry, electrochemistry, and chemiluminescence, Coord. Chem. Rev., 1988, 84, 85–277 CrossRef CAS.
- A. Nilsen-Moe, A. Rosichini, S. D. Glover and L. Hammarström, Concerted and Stepwise Proton-Coupled Electron Transfer for Tryptophan-Derivative Oxidation with Water as the Primary Proton Acceptor: Clarifying a Controversy, J. Am. Chem. Soc., 2022, 144, 7308–7319 CrossRef CAS PubMed.
- S. D. Glover, R. Tyburski, L. Liang, C. Tommos and L. Hammarström, Pourbaix Diagram, Proton-Coupled Electron Transfer, and Decay Kinetics of a Protein Tryptophan Radical: Comparing the Redox Properties of W32˙ and Y32˙ Generated Inside the Structurally Characterized α3W and α3Y Proteins, J. Am. Chem. Soc., 2018, 140, 185–192 CrossRef CAS PubMed.
- M. C. Martínez-Rivera, Using Model Proteins to Study Tyrosine Oxidation-Reduction: Reversible Voltammograms, Long-Lived Radicals and Detailed Design of the Radical Site, PhD, University of Pennsylvania, 2013 Search PubMed.
- T. D. Goddard and D. G. Kneller, SPARKY 3, University of California, San Francisco, CA, 2008 Search PubMed.
- A. T. Brunger, P. D. Adams, G. M. Clore, W. L. DeLano, P. Gros, R. W. Grosse-Kunstleve, J. S. Jiang, J. Kuszewski, M. Nilges, N. S. Pannu, R. J. Read, L. M. Rice, T. Simonson and G. L. Warren, Crystallography & NMR system: A new software suite for macromolecular structure determination, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1998, 54, 905–921 CrossRef CAS PubMed.
- R. Koradi, M. Billeter and K. Wuthrich, MOLMOL: a program for display and analysis of macromolecular structures, J. Mol. Graph., 1996, 14(51–55), 29–32 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision D.01, Gaussian, Inc., 2016 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- T. H. Dunning Jr, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- D. E. Woon and T. H. Dunning Jr, Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova, S. Sharma, S. Wouters and G. K.-L. Chan, PySCF: the Python-based simulations of chemistry framework, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, 1–15 Search PubMed.
- Q. Sun, J. Yang and G. K.-L. Chan, A general second order complete active space self-consistent-field solver for large-scale systems, Chem. Phys. Lett., 2017, 683, 291–299 CrossRef CAS.
- E. R. Sayfutyarova and S. Hammes-Schiffer, Constructing Molecular π-Orbital Active Spaces for Multireference Calculations of Conjugated Systems, J. Chem. Theory Comput., 2019, 15, 1679–1689 CrossRef CAS PubMed.
- D. A. Case, K. Belfon, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, I. T. E. Cheatham, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, G. Giambasu, M. K. Gilson, H. Gohlke, A. W. Goetz, R. Harris, S. Izadi, S. A. Izmailov, K. Kasavajhala, A. Kovalenko, R. Krasny, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, V. Man, K. M. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, A. Onufriev, F. Pan, S. Pantano, R. Qi, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. L. Simmerling, N. R. Skrynnikov, J. Smith, J. Swails, R. C. Walker, J. Wang, L. Wilson, R. M. Wolf, X. Wu, Y. Xiong, Y. Xue, D. M. York and P. A. Kollman, AMBER 2020, University of California, San Francisco, 2020 Search PubMed.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- S. D. Glover, G. A. Parada, T. F. Markle, S. Ott and L. Hammarström, Isolating the Effects of the Proton Tunneling Distance on Proton-Coupled Electron Transfer in a Series of Homologous Tyrosine-Base Model Compounds, J. Am. Chem. Soc., 2017, 139, 2090–2101 CrossRef CAS PubMed.
- W. T. Dixon and D. Murphy, Determination of the acidity constants of some phenol radical cations by means of electron spin resonance, J. Chem. Soc., Faraday Trans. 2, 1976, 72 Search PubMed.
- G. Dey, R. Hermann, S. Naumov and O. Brede, Encounter geometry determines product characteristics of electron transfer from 4-hydroxythiophenol to n-butyl chloride radical cations, Chem. Phys. Lett., 1999, 310, 137–144 CrossRef CAS.
- C. Tommos, X.-S. Tang, K. Warncke, C. W. Hoganson, S. Styring, J. McCracken, B. A. Diner and G. T. Babcock, Spin-Density Distribution, Conformation, and Hydrogen Bonding of the Redox-Active Tyrosine YZ in Photosystem II from Multiple-Electron Magnetic-Resonance Spectroscopies: Implications for Photosynthetic Oxygen Evolution, J. Am. Chem. Soc., 1995, 117, 10325–10335 CrossRef CAS.
- R. S. Mulliken, Electronic Population Analysis on LCAO–MO Molecular Wave Functions. I, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- W. J. Hehre, R. Ditchfield and J. A. Pople, Self-consistent molecular orbital methods. XII. Further extensions of Gaussian—type basis sets for use in molecular orbital studies of organic molecules, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, The influence of polarization functions on molecular orbital hydrogenation energies, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+G basis set for first-row elements, Li–F, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- M. T. Zhang and L. Hammarström, Proton-coupled electron transfer from tryptophan: a concerted mechanism with water as proton acceptor, J. Am. Chem. Soc., 2011, 133, 8806–8809 CrossRef CAS PubMed.
- T. Irebo, S. Y. Reece, M. Sjodin, D. G. Nocera and L. Hammarström, Proton-coupled electron transfer of tyrosine oxidation: buffer dependence and parallel mechanisms, J. Am. Chem. Soc., 2007, 129, 15462–15464 CrossRef CAS PubMed.
- M. Eigen, Proton Transfer, Acid-Base Catalysis, and Enzymatic Hydrolysis. Part I: Elementary Processes, Angew. Chem., 1964, 3, 1–19 CrossRef.
- C. Costentin, M. Robert and J.-M. Savéant, Concerted Proton−Electron Transfer Reactions in Water. Are the Driving Force and Rate Constant Depending on pH When Water Acts as Proton Donor or Acceptor?, J. Am. Chem. Soc., 2007, 129, 5870–5879 CrossRef CAS PubMed.
- R. Tyburski and L. Hammarström, Strategies for switching the mechanism of proton-coupled electron transfer reactions illustrated by mechanistic zone diagrams, Chem. Sci., 2021, 13, 290–301 RSC.
- R. A. Marcus and N. Sutin, Electron transfers in chemistry and biology, Biochim. Biophys. Acta, Bioenerg., 1985, 811, 265–322 CrossRef CAS.
- S. Hammes-Schiffer and A. V. Soudackov, Proton-coupled electron transfer in solution, proteins, and electrochemistry, J. Phys. Chem. B, 2008, 112, 14108–14123 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc05450k |
| This journal is © The Royal Society of Chemistry 2024 |