Open Access Article
Open Access ArticleTriazenide-supported [Cu4S] structural mimics of CuZ that mediate N2O disproportionation rather than reduction†
Neal P.
Mankad
 *
*
Department of Chemistry, University of Illinois Chicago, Chicago, IL 60607, USA. E-mail: npm@uic.edu
First published on 26th December 2023
Abstract
As part of the nitrogen cycle, environmental nitrous oxide (N2O) undergoes the N2O reduction reaction (N2ORR) catalyzed by nitrous oxide reductase, a metalloenzyme whose catalytic active site is a tetranuclear copper–sulfide cluster (CuZ). On the other hand, heterogeneous Cu catalysts on oxide supports are known to mediate decomposition of N2O (deN2O) by disproportionation. In this study, a CuZ model system supported by triazenide ligands is characterized by X-ray crystallography, NMR and EPR spectroscopies, and electronic structure calculations. Although the triazenide-ligated Cu4(μ4-S) clusters are closely related to previous formamidinate derivatives, which differ only in replacement of a remote N atom for a CH group, divergent reactivity with N2O is observed. Whereas the formamidinate-ligated clusters were previously shown to mediate single-turnover N2ORR, the triazenide-ligated clusters are found to mediate deN2O, behavior that was previously unknown to natural or synthetic copper–sulfide clusters. The reaction pathway for deN2O by this model system, including previously unidentified transition state models for N2O activation in N–O cleavage and O–O coupling steps, are included. The divergent reactivity of these two related but subtly different systems point to key factors influencing behavior of Cu-based catalysts for N2ORR (i.e., CuZ) and deN2O (e.g., CuO/CeO2).
Introduction
Anthropogenic nitrous oxide (N2O) emissions have approximately 500 times the global warming potential of CO2 per molecule1 and represent the leading cause of ozone layer depletion.2 Therefore, it is critical to understand the mechanisms by which both natural and synthetic catalysts convert N2O to benign compounds.3–5 In nature, N2O is converted to N2 according to eqn (1) as part of the nitrogen cycle.6,7 This N2O reduction reaction (N2ORR) is catalyzed by nitrous oxide reductase (N2OR),8–10 a copper-dependent enzyme crucial to bacterial denitrification. The catalytic site of N2OR is a copper–sulfide cluster known as CuZ,11 which has consistently been found to contain a [Cu4(μ4-S)]n+ core in all its catalytically active forms.12–15 Alternatively, heterogeneous catalysts are known to mediate the decomposition of N2O (deN2O) according to eqn (2). Although this disproportionation reaction is catalyzed most efficiently by Rh,16 explorations of earth-abundant alternatives have identified Cu-doped zeolites and CuO/CeO2 as viable catalyst materials.17–19| N2O + 2H+ + 2e− → N2 + H2O | (1) |
| N2O → N2 + ½O2 | (2) |
Our group has reported previous synthetic studies on structural20–22 and functional23–25 mimics of CuZ involving [Cu4(μ4-S)] cores supported by bridging diphosphine or formamidinate ligands.11 One of these complexes, [Cu4(μ4-S)(NCN)4]− ([1C]−), not only possesses an electronic structure similar to CuZ according to XAS analysis24 but also was found to mediate a single turnover of N2ORR, producing N2 and O2− along with [Cu4(μ4-S)(NCN)4] (1C) quantitatively (NCN = [MesN = CH-NMes]−, see Scheme 1).23 In this reaction, it was proposed that one equivalent of [1C]− activates the N2O substrate (mimicking CuZ in N2OR) while another [1C]− equivalent acts as a sacrificial electron donor (mimicking the CuA electron transfer site in N2OR). Based on computational modeling, μ-1,3-N2O binding across a Cu–S edge of the cluster enabled by sulfide redox non-innocence was proposed,24 although details of the N–O bond breaking pathway (e.g., the transition state structure) were not elucidated. This manuscript details the synthesis, characterization, and N2O reactivity of an analogous [Cu4(μ4-S)(NNN)]n− system (NNN = [MesN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-NMes]−; n = 0, 1; see Scheme 1). Unlike its formamidinate analogue [1C]−, the triazenide derivative [1N]− reacts with N2O in a 1
N-NMes]−; n = 0, 1; see Scheme 1). Unlike its formamidinate analogue [1C]−, the triazenide derivative [1N]− reacts with N2O in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry upon reductive activation, mediating a single turnover of deN2O rather than N2ORR. Computational analysis of the deN2O process includes transition state models for N–O cleavage and O–O coupling steps that were not identified in previous studies. The divergent selectivity of N2ORR for [1C]−vs. deN2O for [1N]− points to key factors influencing behavior of Cu-based catalysts for N2ORR (i.e., CuZ) and deN2O (e.g., CuO/CeO2).
1 stoichiometry upon reductive activation, mediating a single turnover of deN2O rather than N2ORR. Computational analysis of the deN2O process includes transition state models for N–O cleavage and O–O coupling steps that were not identified in previous studies. The divergent selectivity of N2ORR for [1C]−vs. deN2O for [1N]− points to key factors influencing behavior of Cu-based catalysts for N2ORR (i.e., CuZ) and deN2O (e.g., CuO/CeO2).
Results and discussion
Synthesis and characterization of the 1N system somewhat parallel those of the 1C system21–24 but will be detailed here to facilitate important comparisons between complexes that are summarized in Table 1.| Property | Cu4S(NNN)4 (1N) | [Cu4S(NNN)4]− ([1N]−) | Cu4S(NCN)4 (1C)a | [Cu4S(NCN)4]− ([1C]−)b |
|---|---|---|---|---|
| a From Johnson et al.;22 b From Johnson et al.23 and Rathnayaka et al.;24 c Generated by crystallography symmetry. d Mulliken populations for the LUMO and SOMO, respectively. | ||||
| λ max (nm) | 602, 768 (sh) | 620, 934 | 470 (sh), 561 | 566 |
| ε (M−1 cm−1) | 1.2 × 104 | 4.1 × 103, 3.3 × 103 | 1.4 × 104 | 8.6 × 103 |
| d (Cu⋯Cu) (Å) | 2.405(3) | 2.5853(16) | 2.4226(6) | 2.502(1) |
| 2.965(3) | 2.6031(16) | 3.0353(6) | 2.809(1) | |
| 2.405(3)c | 2.5853(16)c | 2.4226(6)c | 2.532(1) | |
| 2.965(3)c | 2.6031(16)c | 3.0353(6)c | 2.831(2) | |
| E° (V vs. [FeCp2]+/0) | −0.85 | irreversible | −1.28 | irreversible |
| g tensors | n/a | 2.143, 2.066, 2.005 (rhombic) | n/a | 2.043, 2.090 (axial) |
| A(63,65Cu) tensors (MHz) | n/a | ≤122, 90, 100 (from H-strain) | n/a | 15, 100 |
| Redox-active MOd | S 3p, 25% | S 3p, 26% | S 3p, 21% | S 3p, 20% |
| Cu 3d, 11% each | Cu 3d, 12% each | Cu 3d, 13% each | Cu 3d, 14% each | |
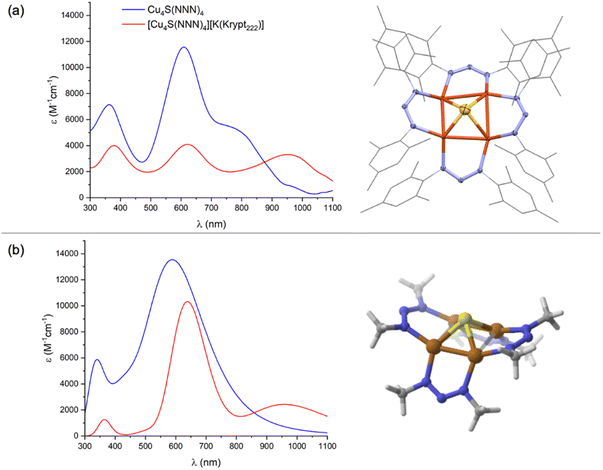
Addition of a toluene solution of elemental sulfur to a bright yellow THF solution of dicopper(I) precursor, Cu2(NNN)2, immediately produced an inky blue solution from which [Cu4(μ4-S)(NNN)4] (1N) began to spontaneously crystallize. Complex 1N is highly crystalline, showing only sparing solubility in THF, CH2Cl2, and CHCl3 and no measurable solubility in CH3CN, Et2O, and toluene. Notably, 1N is indefinitely stable on a benchtop in open air. The 1H NMR of 1N in CDCl3 (Fig. S1†) is consistent with two inequivalent NNN environments (syn and anti to the μ4-S ligand, respectively), each with restricted N–C bond rotation. A similar interpretation of the 1H NMR spectrum of 1C was attributed to intramolecular π-stacking interactions between neighboring mesityl groups evident by X-ray crystallography.23 The UV-Vis-NIR spectrum of 1N in CH2Cl2 (Fig. 1a) is dominated by an intense charge transfer transition at λmax = 602 nm (ε = 1.2 × 104 M−1 cm−1) with a shoulder at λmax ≈ 768 nm. Another feature at higher energy (λmax = 369 nm) is likely ligand-based, as it appears in all complexes examined, including previously reported Cu2(NNN)2.26 For comparison, the analogous charge transfer transitions for 1C, which is purple-colored, were observed at 561 (ε = 1.4 × 104 M−1 cm−1) and ∼470 nm (shoulder).22
Complex 1N crystallized with cubic symmetry in the R![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3n space group, with the molecule residing on a crystallographic special position. The asymmetric unit (Fig. S3†) contains a single NNN ligand, a single Cu atom disordered over two positions, and a single S atom. Applying crystallographic symmetry elements reveals a cluster with four well-ordered NNN ligands related by a molecular S4 axis, along with a disordered inorganic core with eight distinct Cu positions and two S positions (Fig. S3†). To assist with interpretation, a computational model of 1N was built and optimized by DFT. (Here and throughout the study, computational models use methyl groups in place of mesityls.) The resulting structure (Fig. 1b) features a rectangle-based pyramidal Cu4S core with Cu–Cu distances of 2.45 and 2.85 Å and Cu–S distances of 2.24 Å. The crystallographic model was then analyzed by grouping together four Cu atoms with one S position and the other four Cu atoms with the other S position to match the computational model as closely as possible. This analysis indicated a rectangular pyramidal Cu4S core disordered over two positions, with experimental Cu–Cu distances of 2.405(3) and 2.965(3) Å and Cu–S distances of 2.176(2) Å (Fig. 1a). Grouping together the Cu and S atoms in alternative ways provided geometries dissimilar to the computational model, e.g., with unreasonably long Cu–S bonds. Additionally, this interpretation of the crystallographic data provides a model that is isostructural to 1C, which was reported to have Cu–Cu distances of 2.4226(6) and 3.0353(6) Å within its rectangle-based pyramidal Cu4S core.22
3n space group, with the molecule residing on a crystallographic special position. The asymmetric unit (Fig. S3†) contains a single NNN ligand, a single Cu atom disordered over two positions, and a single S atom. Applying crystallographic symmetry elements reveals a cluster with four well-ordered NNN ligands related by a molecular S4 axis, along with a disordered inorganic core with eight distinct Cu positions and two S positions (Fig. S3†). To assist with interpretation, a computational model of 1N was built and optimized by DFT. (Here and throughout the study, computational models use methyl groups in place of mesityls.) The resulting structure (Fig. 1b) features a rectangle-based pyramidal Cu4S core with Cu–Cu distances of 2.45 and 2.85 Å and Cu–S distances of 2.24 Å. The crystallographic model was then analyzed by grouping together four Cu atoms with one S position and the other four Cu atoms with the other S position to match the computational model as closely as possible. This analysis indicated a rectangular pyramidal Cu4S core disordered over two positions, with experimental Cu–Cu distances of 2.405(3) and 2.965(3) Å and Cu–S distances of 2.176(2) Å (Fig. 1a). Grouping together the Cu and S atoms in alternative ways provided geometries dissimilar to the computational model, e.g., with unreasonably long Cu–S bonds. Additionally, this interpretation of the crystallographic data provides a model that is isostructural to 1C, which was reported to have Cu–Cu distances of 2.4226(6) and 3.0353(6) Å within its rectangle-based pyramidal Cu4S core.22
The cyclic voltammogram of 1N in nBu4NPF6/THF (Fig. S6†) showed a reversible reduction at −0.85 V vs. FeCp2+/0 to the [1N]− state, and an irreversible reduction at lower potentials to the [1N]2− state that is unstable on this timescale. The redox behavior mirrors that of 1C, which possesses a reversible reduction at −1.28 V and an irreversible reduction at lower potentials.22 Thus, the substitution of four formamidinate ligands for four triazenides shifts the redox potentials positively by approximately 0.4 V.
Chemical reduction of 1N was carried out with either CoCp2 (E°′ = −1.33 V vs. FeCp2+/0) or K[FeCp(CO)2] (E°′ = −1.8 V vs. FeCp2+/0) in THF or CH2Cl2.27 In each case, a subtle color change from inky blue to a duller blue was observed. While the [1N][CoCp2] salt was too insoluble for solution analysis, use of Kryptofix-222 to form [1N][K(Krypt222)] provided material suitable for characterization. As expected, only resonances for the cationic portion were observed by 1H NMR (Fig. S7†) due to the S = 1/2 ground state of the [1N]− anion. The [1N][K(Krypt222)] salt is air-sensitive in solution, gradually converting to neutral 1N when left on the benchtop. The UV-Vis-NIR spectrum of [1N][K(Krypt222)] in THF (Fig. 1a) has three main features, all of which have lower molar extinction coefficients than for corresponding peaks for 1N. Charge transfer transitions at λmax = 382 nm and λmax = 620 nm (ε = 4.1 × 103 M−1 cm−1) are minimally shifted in wavelength compared to 1N. However, the feature for 1N at λmax = 768 nm shifts significantly to λmax = 934 nm (ε = 3.3 × 103 M−1 cm−1) for [1N]−. For comparison, purple-colored [1C]− was reported to have a charge transfer band at λmax = 566 nm (ε = 8.6 × 103 M−1 cm−1), and no NIR data was reported in the previous study.23 Generally, both 1N and [1N]− have their optical transitions shifted to longer wavelengths by 40–50 nm compared to 1C and [1C]−.
Crystallization of [1N][K(Krypt222)] invariably gave thin plates with very weak X-ray diffraction, and X-ray quality crystals of other salts of [1N]− (e.g., [1N][CoCp2], [1N][K(18-crown-6)]) were not obtained after repeated attempts. Compound [1N][K(Krypt222)] crystallizes with orthorhombic symmetry in the C2221 space group, with both cation and anion portions residing on crystallographic special positions (Fig. S9†). The [K(Krypt222)]+ unit exhibited severe disorder. Furthermore, within the [1N]− unit, the S atom was disordered over two positions and the NNN ligands exhibited significant disorder, too. Fortunately, the four Cu positions were well ordered. The crystallographic data indicates that, upon reduction from 1N to [1N]−, the Cu4S core converts from a rectangular towards a square-based pyramid shape, with experimental Cu–Cu distances of 2.5853(16) and 2.6031(16) Å. A DFT model of [1N]− (Fig. S10†) was found to have computed Cu–Cu distances of 2.54 and 2.74 Å, which are also shifted from rectangular towards square shaped compared to the DFT model of 1N (vide supra). The change from rectangular to square shape in the Cu4 base was also observed previously upon reduction of 1C to [1C]−, the latter of which has experimental Cu–Cu distances of 2.502(1) and 2.809(1) Å.23
Having optimized computational models for 1N and [1N]−, next we conducted TD-DFT calculations to better understand the electronic transitions evident by UV-Vis-NIR. As shown in Fig. 1b, the salient features of the experimental UV-Vis-NIR spectra are well captured in the computed spectra, especially when considering that the computational models used a truncated [MeN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–NMe]− ligand in place of the [MesN
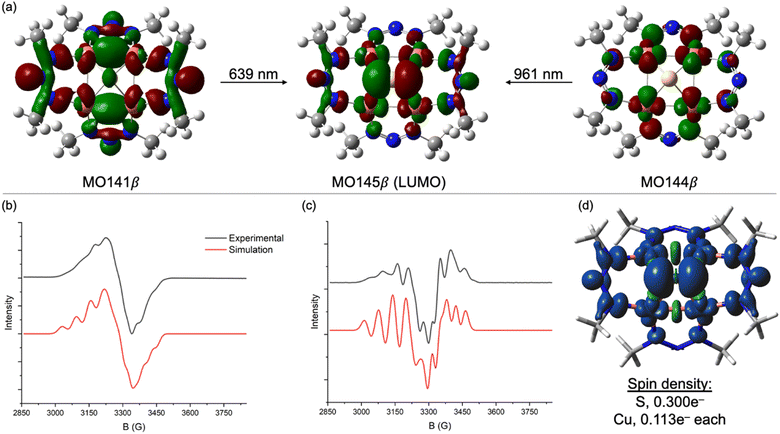
N–NMe]− ligand in place of the [MesN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-NMes]− ligand used experimentally. For [1N]−, excitations calculated at 639 nm (experimental: 620 nm) and 961 nm (experimental: 934 nm) are both charge transfers into the LUMO (MO145β), which is a highly delocalized MO with 26% S 3p character, 48% Cu 3d character (12% per Cu), and significant contribution from the two NNN ligands syn to the μ4-S atom (Fig. 2a). The transition calculated at 639 nm involves excitation of an electron from MO144β, which has 74% Cu 3d character. Thus, this transition can be viewed as a combination of Cu→S and Cu→NNN MLCT. The transition calculated at 961 nm involves excitation of an electron from MO141β, which is exclusively based on the four NNN ligands (<5% Cu 3d, <5% S 3p). Thus, this transition can be viewed as NNN→[Cu4S] CT. The corresponding transitions for neutral 1N are qualitatively similar but less readily interpreted because of some admixture of states via configuration interactions at each excitation wavelength (Fig. S4†).
N-NMes]− ligand used experimentally. For [1N]−, excitations calculated at 639 nm (experimental: 620 nm) and 961 nm (experimental: 934 nm) are both charge transfers into the LUMO (MO145β), which is a highly delocalized MO with 26% S 3p character, 48% Cu 3d character (12% per Cu), and significant contribution from the two NNN ligands syn to the μ4-S atom (Fig. 2a). The transition calculated at 639 nm involves excitation of an electron from MO144β, which has 74% Cu 3d character. Thus, this transition can be viewed as a combination of Cu→S and Cu→NNN MLCT. The transition calculated at 961 nm involves excitation of an electron from MO141β, which is exclusively based on the four NNN ligands (<5% Cu 3d, <5% S 3p). Thus, this transition can be viewed as NNN→[Cu4S] CT. The corresponding transitions for neutral 1N are qualitatively similar but less readily interpreted because of some admixture of states via configuration interactions at each excitation wavelength (Fig. S4†).
The X-band EPR spectrum of [1N][K(Krypt222)] at 77 K in a frozen CH3CN/CH2Cl2 glass is shown in Fig. 2b. Fine structure was not well resolved in the first-derivative spectrum but was emphasized by plotting the second derivative (Fig. 2c). Surprisingly, hyperfine splitting due to the four 63,65Cu nuclei (ICu = 3/2) was not evident. Instead, the spectra were best simulated with hyperfine splitting from two equivalent 14N nuclei. The simulation also required inclusion of significant “H-strain”, i.e., unresolved hyperfine coupling that can be assigned to a combination of the four 63,65Cu centers and remaining 14N nuclei. This pattern can be rationalized by analyzing the spin density from the DFT model of [1N]−, which is plotted in Fig. 2d. Of the total 1e− spin, only 0.113e− resides on each Cu center (0.452e− total), meaning that most of the unpaired spin is ligand-centered. The largest contributor is the μ4-S atom, which carries 0.300e−. Of the remaining 0.248e− of NNN-centered spin, nearly all resides on the two NNN ligands syn to the μ4-S ligand, with effectively none on the two anti-NNN ligands. Thus, the A(14N) coupling observed by EPR spectroscopy can be assigned to the central N-atoms of the two syn-NNN ligands. The small and apparently unresolved A(63,65Cu) coupling is consistent with the high degree of covalency (i.e., μ4-S and NNN redox non-innocence) apparent from calculations. Although the EPR spectroscopy of [1C]− differs in that it is an axial signal dominated by A(63,65Cu) coupling,23 nonetheless the redox-active MOs for both the 1N and 1C systems are similar to each other (Table 1).24
No reaction was observed when [1N][K(Krypt222)] was exposed to N2O (1 atm) in CH2Cl2. This behavior contrasts that of [1C][K(18-crown-6)], which converts quantitatively to 1C under the same conditions.23 In the latter case, it was proposed that reversible N2O binding to [1C][K(18-crown-6)] to transiently form [1C·N2O][K(18-crown-6)] shifts the reduction potential such that a second equivalent of [1C][K(18-crown-6)] can act as an electron donor, producing [1C·N2O][K(18-crown-6)]2 and 1C (i.e., N2O-induced disproportionation of the copper cluster). The shift of the 1N/[1N]− potential to more positive values apparently prevents such N2O-induced disproportionation from occurring spontaneously for the triazenide derivative. Therefore, the reaction was repeated with a stronger sacrificial electron donor, CoCp2, to reduce a transiently-formed [1N·N2O][K(Krypt222)]. A 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of [1N][K(Krypt222)] and CoCp2 in CH2Cl2 solution was observed to darken slightly upon exposure to N2O (1 atm). Over 24 h, the major species in solution remained [1N]− according to UV-Vis-NIR spectroscopy. However, analysis of the reaction mixture by 1H NMR spectroscopy indicated small conversion (∼10%) of CoCp2 to [CoCp2]+ along with formation of a new, diamagnetic product (2) containing the NNN ligand. The same product 2 was generated when exposing a 1
1 mixture of [1N][K(Krypt222)] and CoCp2 in CH2Cl2 solution was observed to darken slightly upon exposure to N2O (1 atm). Over 24 h, the major species in solution remained [1N]− according to UV-Vis-NIR spectroscopy. However, analysis of the reaction mixture by 1H NMR spectroscopy indicated small conversion (∼10%) of CoCp2 to [CoCp2]+ along with formation of a new, diamagnetic product (2) containing the NNN ligand. The same product 2 was generated when exposing a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
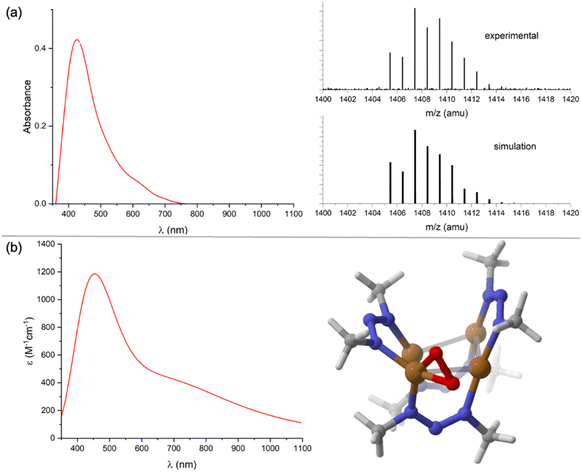
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture of 1N and CoCp2 to N2O (1 atm) or when replacing N2O with excess Me3NO under N2. Compound 2 could be extracted into toluene or Et2O, which served to separate it from [CoCp2]+, [1N]−, and/or 1N. Washing 2 with pentane served to separate it from CoCp2 (and excess Me3NO where relevant, see Fig. S12†). At this point, compound 2 was found to have a brown color, with a UV-Vis-NIR spectrum in CH2Cl2 (Fig. 3a) showing a single distinct feature at λmax = 420 nm but lacking any well-defined charge transfer transitions in the 600–1000 nm region as observed for 1N and [1N]−. From these collected observations, it can be concluded that (1) the reaction involves O-atom transfer from N2O since Me3NO can replace it, (2) the resulting product 2 is diamagnetic and neutral in charge based on NMR characterization and solubility properties, and (3) compound 2 likely lacks the μ4-S atom that would produce low-energy CT electronic transitions.
2 mixture of 1N and CoCp2 to N2O (1 atm) or when replacing N2O with excess Me3NO under N2. Compound 2 could be extracted into toluene or Et2O, which served to separate it from [CoCp2]+, [1N]−, and/or 1N. Washing 2 with pentane served to separate it from CoCp2 (and excess Me3NO where relevant, see Fig. S12†). At this point, compound 2 was found to have a brown color, with a UV-Vis-NIR spectrum in CH2Cl2 (Fig. 3a) showing a single distinct feature at λmax = 420 nm but lacking any well-defined charge transfer transitions in the 600–1000 nm region as observed for 1N and [1N]−. From these collected observations, it can be concluded that (1) the reaction involves O-atom transfer from N2O since Me3NO can replace it, (2) the resulting product 2 is diamagnetic and neutral in charge based on NMR characterization and solubility properties, and (3) compound 2 likely lacks the μ4-S atom that would produce low-energy CT electronic transitions.
Unfortunately, all reaction conditions explored consistently provided only low conversion (<15%) to 2, with the remaining mass balance being predominantly [1N]−. Furthermore, repeated attempts at obtaining X-ray quality crystals of 2 failed. The identity of 2 was made clear by analyzing it using EI-HRMS. The parent ion mass and isotope distribution (Fig. 3a) indicate the empirical formula, Cu4(O2)(NNN)4. To investigate this possibility further, the structure of 2 assuming that formula was modeled computationally. Two energy minima were located: one with μ2:η2 binding of an O2 unit to one Cu from the periphery of the Cu4 core, and another with μ3:η2,η1,η1 binding of the O2 unit to three Cu atoms in the capping position typically occupied by sulfide (Fig. S13†). The former isomer (Fig. 3b) was calculated to be lower in Gibbs free energy by −13.6 kcal mol−1. The predicted UV-Vis-NIR spectrum (Fig. 3b) of this structure reproduces key features of the experimental spectrum, with a prominent absorbance at λmax = 448 nm (experimental: 420 nm) that tails into the lower energy region of the spectrum without well-defined absorbance features in the 600–1000 nm region. The local structure within 2 of the Cu(O2) unit in a nitrogen-rich environment resembles 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Cu
1 Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O2 species that have been long studied since seminal works of Kitajima, Tolman, and others.28,29 Notably, the presence of an absorbance at ∼400 nm is characteristic of such compounds and is typically assigned to the π → π* transition of the bound O2.30 The calculated O–O distance of 1.37 Å in 2 and the short calculated Cu–O distances of 1.85 and 1.86 Å are all indicative of a highly reduced O2 unit.31,32 Curiously, the 1H NMR spectrum for 2 shown only one set of NNN peaks, rather than the three sets expected based on the calculated structure. This is likely indicative of fluxionality due to the O2 ligand rapidly hopping from Cu site to Cu site.
O2 species that have been long studied since seminal works of Kitajima, Tolman, and others.28,29 Notably, the presence of an absorbance at ∼400 nm is characteristic of such compounds and is typically assigned to the π → π* transition of the bound O2.30 The calculated O–O distance of 1.37 Å in 2 and the short calculated Cu–O distances of 1.85 and 1.86 Å are all indicative of a highly reduced O2 unit.31,32 Curiously, the 1H NMR spectrum for 2 shown only one set of NNN peaks, rather than the three sets expected based on the calculated structure. This is likely indicative of fluxionality due to the O2 ligand rapidly hopping from Cu site to Cu site.
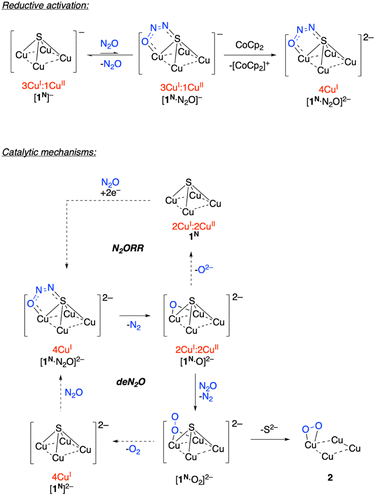
Based on these observations, a plausible mechanism for a hypothetical deN2O reaction for is presented in Scheme 2. Reversible binding of N2O to [1N]− would generate a small equilibrium concentration of [1N·N2O]−. Despite CoCp2 not being a strong enough reductant to spontaneously reduce [1N]−, reduction of [1N·N2O]− could be spontaneous due to the π-accepting nature of N2O raising the reduction potential of the Cu4S core. The resulting [1N·N2O]2− intermediate would, then, be the active catalyst in the “fully reduced” 4CuI redox state.33 Based on previous computational modeling with [1C·N2O]−,24 a μ-1,3-N2O binding mode spanning a Cu–S cluster edge is proposed. Low conversion to 2 observed experimentally is likely due to inefficiency of this reductive activation process, i.e., most of the dissolved complex remains unactivated as [1N]−.
On the active cycle, loss of N2 from [1N·N2O]2− would generate [1N·O]2−, which is proposed to feature μ2-O2− binding based on previous modeling for [1C·O]2−.23 For N2ORR chemistry associated with the 1C system, dissociation of O2− from [1C·O]2− generates 1C, which can hypothetically undergo 2e− reduction under N2O to regenerate [1C·N2O]2−. In the 1N system, N2ORR chemistry is not observed. Instead, a second N2O molecule presumably intercepts [1N·O]2− to generate [1N·O2]2− with loss of N2. To complete the hypothetical deN2O cycle, O2 loss would form [1N]2−, which would regenerate [1N·N2O]2− upon N2O coordination. On the other hand, if S2− dissociation outcompetes O2 dissociation, then off-cycle species 2 is formed. (Other pathways to 2 cannot be ruled out, vide infra.) Experimentally, examination of the headspace gas above the N2O reaction revealed only trace quantities of N2 and O2, consistent with the off-cycle decomposition to 2 outcompeting on-cycle N2O-for-O2 substitution.
To gain further insight, the deN2O cycle was modeled computationally. The reaction energy profile is shown in Fig. 4, which features models for the four key intermediates as well as the two transition states associated with N–O cleavage of N2O. The computed intermediate [1N·N2O]2− (A) is isostructural to [1C·N2O]2− calculated previously,24 with μ-1,3-N2O binding across a Cu–S edge of the cluster and significant N2O activation according to the bent O–N–N angle of 126°. Loss of N2 from A to form [1N·O]2− (B) is exergonic by ΔG = −28.2 kcal mol−1 and proceeds via transition state TS1 with a barrier height of ΔG‡ = 12.9 kcal mol−1. The structure of TS1 differs from that of reactant A in that the N2O ligand occupies a μ-1,1-O binding mode spanning a Cu–Cu cluster edge in TS1. This binding mode has been previously proposed for a synthetic model complex34 and for N2O activation by Cu-ZSM-5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 but differs from that proposed for CuZ itself.12 At TS1, the N2O molecule has undergone further activation as evidenced by the elongated N–O bond distance (1.57 Å) and contracted N–N bond distance (1.14 Å) relative to those in A (1.297 and 1.233 Å, respectively). The Cu–Cu edge of the cluster with the N2O bound is short (2.54 Å) to accommodate the bridging ligand and is compensated by a long Cu–Cu distance of 3.35 Å along the edge opposite the N2O ligand. The structure of B following N2 loss features a μ-oxo ligand with a Cu–O–Cu angle of 87° and a Cu–Cu distance (2.56 Å) similar to that in TS1.
35 but differs from that proposed for CuZ itself.12 At TS1, the N2O molecule has undergone further activation as evidenced by the elongated N–O bond distance (1.57 Å) and contracted N–N bond distance (1.14 Å) relative to those in A (1.297 and 1.233 Å, respectively). The Cu–Cu edge of the cluster with the N2O bound is short (2.54 Å) to accommodate the bridging ligand and is compensated by a long Cu–Cu distance of 3.35 Å along the edge opposite the N2O ligand. The structure of B following N2 loss features a μ-oxo ligand with a Cu–O–Cu angle of 87° and a Cu–Cu distance (2.56 Å) similar to that in TS1.
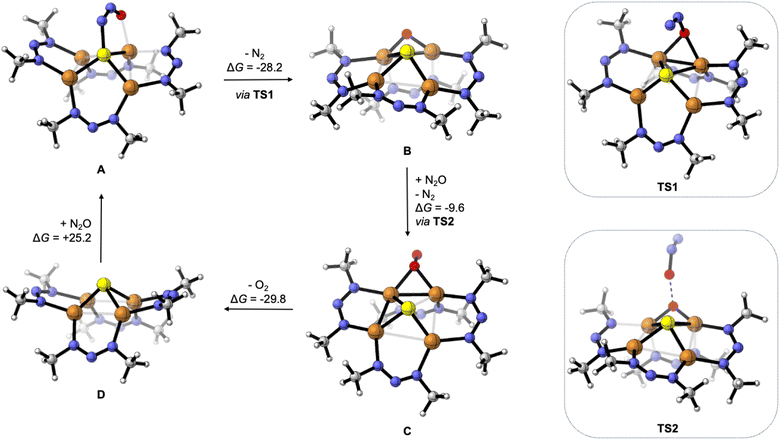 | ||
| Fig. 4 Reaction intermediates and transition states for deN2O calculated by DFT, with Gibbs free energy values given in units of kcal mol−1. Computations were done at the B3LYP/def2TZVPP level of DFT using the CPCM implicit solvation model (CH2Cl2) except for TS2 (see ESI†). | ||
Oxygenation of B by N2O to form [1N·O2]2− (C) was calculated to be exergonic by ΔG = −9.6 kcal mol−1 and proceeds via transition state TS2. The structure of TS2 features the N2O substrate approaching the Cu–O–Cu unit with an O⋯O distance of 1.84 Å. The N2O unit is significantly activated in TS2, with a bent O–N–N angle of 143°, a long O–N distance of 1.50 Å, and a short N–N distance of 1.13 Å. Unlike compound 2 formed from S2− loss, the structure of C features a μ2:η1-O2 ligand. The calculated O–O distance of 1.35 Å in C is indicative of significant O2 reduction,31 though the Cu–O distances in C (2.02 and 2.06 Å) are longer than those calculated for 2.
Loss of O2 from C to form [1N]2− (D) was calculated to be exergonic by ΔG = −29.8 kcal mol−1. Unlike intermediates B and C and transition states TS1 and TS2 that all involve bridging O-ligands along one cluster edge, the structure of D features a nearly square-shaped tetracopper core, with all calculated Cu–Cu distances between 2.66 and 2.78 Å. To complete the hypothetical catalytic deN2O cycle, coordination of N2O to D to regenerate A was calculated to be endergonic by ΔG = +25.2 kcal mol−1. Thus, although the net deN2O reaction is calculated to be favorable (ΔGrxn = −42.4 kcal mol−1), the rate-determining N2O binding step prevents efficient catalysis under the experimental conditions examined, allowing for off-cycle conversion of C to inactive 2. At this time, the path from C to 2 is ambiguous: it could involve simple S2− dissociation from C to form 2 directly but could also involve exergonic O2 dissociation from C to form D followed by O2-promoted conversion of D to 2.
Oxygenation of B to form C presumably involves nucleophilic addition of the N2O oxygen to the electrophilic μ-oxo ligand of B (see TS2). In accord with that hypothesis, analysis of the frontier molecular orbitals of B indicated that the LUMO has significant (24%) oxygen 2p character (Fig. 5). One reason that the 1N system is more likely than 1C to do deN2O chemistry might be the stabilization of this LUMO due to the electronegative nature of the NNN− ligands relative to less electronegative NCN−, thus favoring O–O coupling by N2O nucleophilic addition in the NNN− case. A second contributing reason could be that the relatively electron-withdrawing NNN− ligands make the tetracopper core more Lewis acidic than for the NCN− analogues, thus causing O2− loss required for N2ORR to be less facile for B and instead shunting the 1N system into the deN2O pathway.
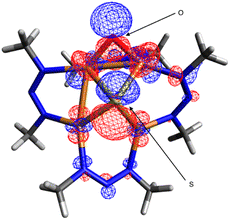 | ||
| Fig. 5 Lowest unoccupied molecular orbital (0.03 isosurface) calculated for [1N·O]2− (B) by DFT at the B3LYP/def2TZVPP level using the CPCM implicit solvation model (CH2Cl2). | ||
Conclusions
A redox pair of Cu4(μ4-S) clusters supported by triazenide ligands was synthesized and thoroughly characterized. While much of the characterization data mirrored those of the related formamidinate-supported system studied previously,21–24 divergent reactivity behavior with N2O was observed. While the formamidinate-ligated system was found to promote single-turnover N2ORR akin to the biological CuZ cluster it mimics, the triazenide system was found to promote (inefficient) deN2O reactivity that is a typical hallmark of heterogeneous catalysts like CuO/CeO2. Computational modeling of the deN2O pathway allowed for comparisons to be made with previously studied N2ORR chemistry, enabling deeper understanding of factors influencing selectivity. A simple working model is as follows. The formamidinate system is relatively electron-rich, providing a “soft” tetracopper core that behaves like CuZ (that features a soft sulfide ligand) by readily dissociating O2− upon N2O deoxygenation to favor N2ORR. On the other hand, the triazenide system is relatively electron-poor, providing a “hard” tetracopper core that behaves like CuO/CeO2 (that features hard oxide ligation) by forming a tightly-bound and electrophilic μ-oxo intermediate upon N2O deoxygenation to favor deN2O. These insights stand to inform future N2O-fixing catalyst designs.Data availability
Spectral data is reproduced in ESI,† and raw data are available from the author upon request. Computational output coordinates have been uploaded as ESI.† X-ray crystallography data is available upon request from the CCDC under deposition numbers 2299540 and 2299541.Author contributions
N. P. M. carried out experiments, conducted computational modeling, and wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funding was provided by NIH/NIGMS under grant R35 GM140850. Computational resources and services were provided by the Advanced Cyberinfrastructure for Education and Research (ACER) group at UIC. Dr Daniel McElheny (UIC) and Dr Samantha MacMillan (Cornell) assisted with collection of EPR and X-ray diffraction data, respectively.Notes and references
- J. Hansen and M. Sato, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 16109–16114 CrossRef CAS PubMed.
- A. R. Ravishankara, J. S. Daniel and R. W. Portmann, Science, 2009, 326, 123–125 CrossRef CAS PubMed.
- H. Tian, R. Xu, J. G. Canadell, R. L. Thompson, W. Winiwarter, P. Suntharalingam, E. A. Davidson, P. Ciais, R. B. Jackson, G. Janssens-Maenhout, M. J. Prather, P. Regnier, N. Pan, S. Pan, G. P. Peters, H. Shi, F. N. Tubiello, S. Zaehle, F. Zhou, A. Arneth, G. Battaglia, S. Berthet, L. Bopp, A. F. Bouwman, E. T. Buitenhuis, J. Chang, M. P. Chipperfield, S. R. S. Dangal, E. Dlugokencky, J. W. Elkins, B. D. Eyre, B. Fu, B. Hall, A. Ito, F. Joos, P. B. Krummel, A. Landolfi, G. G. Laruelle, R. Lauerwald, W. Li, S. Lienert, T. Maavara, M. MacLeod, D. B. Millet, S. Olin, P. K. Patra, R. G. Prinn, P. A. Raymond, D. J. Ruiz, G. R. van der Werf, N. Vuichard, J. Wang, R. F. Weiss, K. C. Wells, C. Wilson, J. Yang and Y. Yao, Nature, 2020, 586, 248–256 CrossRef CAS PubMed.
- S. R. Pauleta, M. S. P. Carepo and I. Moura, Coord. Chem. Rev., 2019, 387, 436–449 CrossRef CAS.
- W. C. Trogler, Coord. Chem. Rev., 1999, 187, 303–327 CrossRef CAS.
- N. Lehnert, B. W. Musselman and L. C. Seefeldt, Chem. Soc. Rev., 2021, 50, 3640–3646 RSC.
- C. Ferousi, S. H. Majer, I. M. Dimucci and K. M. Lancaster, Chem. Rev., 2020, 120, 5252–5307 CrossRef CAS.
- S. R. Pauleta, S. Dell'Acqua and I. Moura, Coord. Chem. Rev., 2013, 257, 332–349 CrossRef CAS.
- S. R. Pauleta, C. Carreira and I. Moura, in Metalloenzymes in Denitrification: Applications and Environmental Impacts, ed. I. Moura, L. B. Maia, S. R. Pauleta and J. J. G. Moura, Royal Society of Chemistry, 2017, pp. 141–169 Search PubMed.
- C. Carreira, S. R. Pauleta and I. Moura, J. Inorg. Biochem., 2017, 177, 423–434 CrossRef CAS PubMed.
- S. C. Rathnayaka and N. P. Mankad, Coord. Chem. Rev., 2021, 429, 213718 CrossRef CAS PubMed.
- E. M. Johnston, C. Carreira, S. Dell'Acqua, S. G. Dey, S. R. Pauleta, I. Moura and E. I. Solomon, J. Am. Chem. Soc., 2017, 139, 4462–4476 CrossRef CAS PubMed.
- E. M. Johnston, S. Dell'Acqua, S. Ramos, S. R. Pauleta, I. Moura and E. I. Solomon, J. Am. Chem. Soc., 2014, 136, 614–617 CrossRef CAS PubMed.
- A. Pomowski, W. G. Zumft, P. M. H. Kroneck and O. Einsle, Nature, 2011, 477, 234–237 CrossRef CAS PubMed.
- A. Wüst, L. Schneider, A. Pomowski, W. G. Zumft, P. M. H. Kroneck and O. Einsle, Biol. Chem., 2012, 393, 1067–1077 CrossRef PubMed.
- M. Konsolakis, ACS Catal., 2015, 5, 6397–6421 CrossRef CAS.
- M. H. Groothaert, K. Lievens, H. Leeman, B. M. Weckhuysen and R. A. Schoonheydt, J. Catal., 2003, 220, 500–512 CrossRef CAS.
- P. J. Smeets, M. H. Groothaert, R. M. van Teeffelen, H. Leeman, E. J. M. Hensen and R. A. Schoonheydt, J. Catal., 2007, 245, 358–368 CrossRef CAS.
- M. Zabilskiy, P. Djinović, B. Erjavec, G. Dražić and A. Pintar, Appl. Catal., B, 2015, 163, 113–122 CrossRef CAS.
- B. J. Johnson, S. V. Lindeman and N. P. Mankad, Inorg. Chem., 2014, 53, 10611–10619 CrossRef CAS PubMed.
- S. C. Rathnayaka, C. W. Hsu, B. J. Johnson, S. J. Iniguez and N. P. Mankad, Inorg. Chem., 2020, 59, 6496–6507 CrossRef CAS PubMed.
- B. J. Johnson, W. E. Antholine, S. V. Lindeman and N. P. Mankad, Chem. Commun., 2015, 51, 11860–11863 RSC.
- B. J. Johnson, W. E. Antholine, S. V. Lindeman, M. J. Graham and N. P. Mankad, J. Am. Chem. Soc., 2016, 138, 13107–13110 CrossRef CAS PubMed.
- S. C. Rathnayaka, S. M. Islam, I. M. Dimucci, S. N. MacMillan, K. M. Lancaster and N. P. Mankad, Chem. Sci., 2020, 11, 3441–3447 RSC.
- C.-W. W. Hsu, S. C. Rathnayaka, S. M. Islam, S. N. MacMillan and N. P. Mankad, Angew. Chem., Int. Ed., 2020, 59, 627–631 CrossRef CAS PubMed.
- P. Alayoglu, T. Chang, M. V. Lorenzo Ocampo, L. J. Murray, Y.-S. Chen and N. P. Mankad, Inorg. Chem., 2023, 62, 15267–15276 CrossRef CAS PubMed.
- N. G. Connelly and W. E. Geiger, Chem. Rev., 1996, 96, 877–910 CrossRef CAS PubMed.
- K. Fujisawa, M. Tanaka, Y. Moro-oka and N. Kitajima, J. Am. Chem. Soc., 1994, 116, 12079–12080 CrossRef CAS.
- D. J. E. Spencer, N. W. Aboelella, A. M. Reynolds, P. L. Holland and W. B. Tolman, J. Am. Chem. Soc., 2002, 124, 2108–2109 CrossRef CAS PubMed.
- N. W. Aboelella, S. V. Kryatov, B. F. Gherman, W. W. Brennessel, V. G. Young, R. Sarangi, E. V. Rybak-Akimova, K. O. Hodgson, B. Hedman, E. I. Solomon, C. J. Cramer and W. B. Tolman, J. Am. Chem. Soc., 2004, 126, 16896–16911 CrossRef CAS PubMed.
- D. A. Iovan, A. T. Wrobel, A. A. McClelland, A. B. Scharf, G. A. Edouard and T. A. Betley, Chem. Commun., 2017, 53, 10306–10309 RSC.
- N. C. Tomson, K. D. Williams, X. Dai, S. Sproules, S. DeBeer, T. H. Warren and K. Wieghardt, Chem. Sci., 2015, 6, 2474–2487 RSC.
- S. Ghosh, S. I. Gorelsky, P. Chen, I. Cabrito, J. J. G. Moura, I. Moura and E. I. Solomon, J. Am. Chem. Soc., 2003, 125, 15708–15709 CrossRef CAS PubMed.
- I. Bar-Nahum, A. K. Gupta, S. M. Huber, M. Z. Ertem, C. J. Cramer and W. B. Tolman, J. Am. Chem. Soc., 2009, 131, 2812–2814 CrossRef CAS PubMed.
- M.-L. L. Tsai, R. G. Hadt, P. Vanelderen, B. F. Sels, R. A. Schoonheydt and E. I. Solomon, J. Am. Chem. Soc., 2014, 136, 3522–3529 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental section and spectra data, crystallographic data, computational output. CCDC 22995402299541. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc05451a |
| This journal is © The Royal Society of Chemistry 2024 |