Open Access Article
Open Access ArticleDetermining the key vibrations for spin relaxation in ruffled Cu(II) porphyrins via resonance Raman spectroscopy†
Nathanael P.
Kazmierczak
 ,
Nathan E.
Lopez
,
Nathan E.
Lopez
 ,
Kaitlin M.
Luedecke
,
Kaitlin M.
Luedecke
 and
Ryan G.
Hadt
and
Ryan G.
Hadt
 *
*
Division of Chemistry and Chemical Engineering, Arthur Amos Noyes Laboratory of Chemical Physics, California Institute of Technology, Pasadena, California 91125, USA. E-mail: rghadt@caltech.edu
First published on 12th January 2024
Abstract
Pinpointing vibrational mode contributions to electron spin relaxation (T1) constitutes a key goal for developing molecular quantum bits (qubits) with long room-temperature coherence times. However, there remains no consensus to date as to the energy and symmetry of the relevant modes that drive relaxation. Here, we analyze a series of three geometrically-tunable S = ½ Cu(II) porphyrins with varying degrees of ruffling distortion in the ground state. Theoretical calculations predict that increased distortion should activate low-energy ruffling modes (∼50 cm−1) for spin–phonon coupling, thereby causing faster spin relaxation in distorted porphyrins. However, experimental T1 times do not follow the degree of ruffling, with the highly distorted copper tetraisopropylporphyrin (CuTiPP) even displaying room-temperature coherence. Local mode fitting indicates that the true vibrations dominating T1 lie in the energy regime of bond stretches (∼200–300 cm−1), which are comparatively insensitive to the degree of ruffling. We employ resonance Raman (rR) spectroscopy to determine vibrational modes possessing both the correct energy and symmetry to drive spin–phonon coupling. The rR spectra uncover a set of mixed symmetric stretch vibrations from 200–250 cm−1 that explain the trends in temperature-dependent T1. These results indicate that molecular spin–phonon coupling models systematically overestimate the contribution of ultra-low-energy distortion modes to T1, pointing out a key deficiency of existing theory. Furthermore, this work highlights the untapped power of rR spectroscopy as a tool for building spin dynamics structure–property relationships in molecular quantum information science.
1. Introduction
The rise of molecular quantum information science has placed new importance on developing molecules with long-lasting electron spin coherence times (T2), a parameter which sets the maximum length of time quantum information can be stored and processed.1 At elevated temperatures, vibration-mediated spin relaxation (T1) limits the maximum attainable value of T2,2 implying that vibrations effectively leak quantum information into the environment. While room-temperature electron spin coherence has been measured in a handful of S = ½ systems,3–8 other key classes of molecular qubits, such as the Cr(IV) optically addressable qubits, remain limited to sub-liquid nitrogen temperatures owing to T1-limited T2.9–12 Thus, understanding the relationship between molecular geometric/electronic structure and spin relaxation rates remains a key mechanistic goal of molecular quantum information science. The number of thermally-accessible vibrational modes that could potentially contribute to spin relaxation renders such investigations theoretically and spectroscopically challenging.One approach to build T1 mechanistic understanding is to employ theoretical models of the spin-relaxation process. Several models based on the easily-handled spin Hamiltonian have been proposed, but crucially, multiple expressions have been used for the spin–phonon coupling coefficient (Fig. 1A). One can use derivatives of either the g-tensor2,13–17 or the hyperfine tensor,15,16 pick different elements of the tensor (on-diagonal only2,5,13,14vs. including off-diagonal15–17), and employ first13–15vs. second16,18 derivatives. Depending on the theoretical choices made, different vibrational modes are predicted to dominate spin relaxation, ranging from ultra-low-energy eg rotational modes (<50 cm−1)19 to totally symmetric metal–ligand stretching modes (>200 cm−1).2,13,14 None of these spin Hamiltonian models can be considered mechanistically definitive due to two key issues: (1) derivatives of a spin Hamiltonian tensor do not constitute true matrix elements between spin states,20 no matter how sophisticated the quantum master equation21 used to handle the rate calculations, and (2) no spin Hamiltonian model successfully accounts for T1 anisotropy, which instead requires analysis of spin–orbit wavefunctions.20 At best, spin Hamiltonian models can predict the average temperature-dependent T1 over all molecular orientations, functioning as a proxy for the true spin–orbit mechanism.20 Further discrepancies arise when comparing the theoretically predicted temperature scaling of T1 to experiment. On the basis of ultra-low-energy modes, contemporary ab initio models commonly predict flat, single-exponent power law behavior19 for temperature-dependent T1. However, experimental log–log plots of 1/T1vs. temperature display marked curvature for most S = ½ molecular qubits, which has been interpreted by local mode fitting to indicate the contribution of molecular vibrational modes >100 cm−1 that give rise to a nonconstant power law exponent.14,22,23 Experimentally-parameterized T1 models have successfully reproduced this curvature for high-symmetry Cu(II) and V(IV) complexes,14 but the curvature is not successfully predicted by ab initio models that emphasize ultra-low-energy modes.19 We conclude that ab initio prediction of T1 in S = ½ molecular qubits has not yet achieved satisfactory agreement with experimental data.
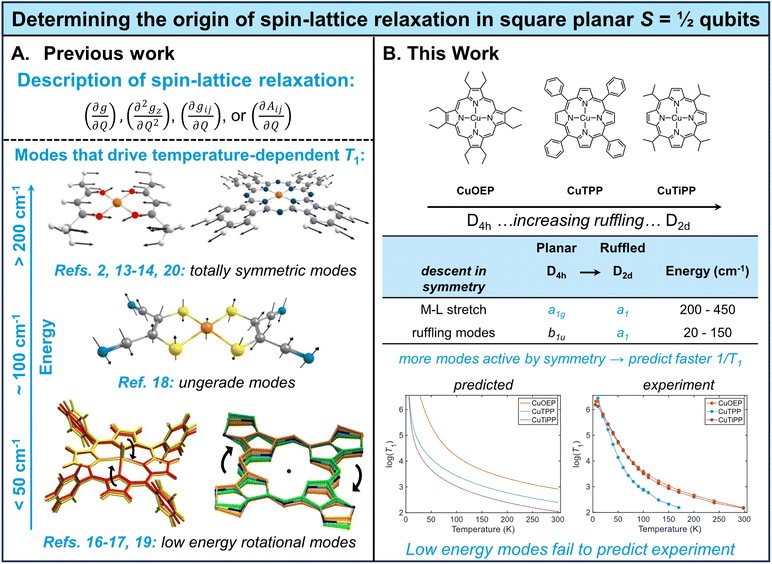 | ||
| Fig. 1 Mechanistic studies of spin–lattice relaxation in S = ½ qubits. (A) Previous theoretical studies have employed a variety of models for molecular spin–phonon coupling, leading to disparate predictions of modes with different energies and symmetries driving spin relaxation. Figures adapted with permission from ref. 17–20. (B) This work systematically probes the effect of the b1u ruffling distortion on spin relaxation in a series of copper porphyrins, finding that existing theory systematically overestimates the contribution of low-energy ruffling modes. | ||
Alternatively, mechanistic understanding may be developed from experimentally-determined T1 structure–property relationships. While relatively few such relationships have been explored in detail, one of the best-established connections has been demonstrated between the degree of first coordination sphere planarity and T1 in four-coordinate Cu(II) S = ½ molecular qubits.2 Two limiting geometries are possible: square planar (D4h), in which the opposing L–M–L bond angle is 180°, and tetrahedral (Td), in which the opposing L–M–L bond angle is 109.5°. From the D4h geometry, ligated atoms can undergo distortion along the b2u bending mode, which lowers the point group to D2d and systematically decreases the L–M–L angle from 180° towards 109.5°. It has been experimentally demonstrated that planar structures have longer spin lifetimes (long T1) than b2u-distorted structures.5,23 This result can be understood via application of group theory selection rules to the spin–phonon coupling problem.13,14 In order for a vibrational mode to cause spin relaxation by altering the g value, it must transform as either a totally symmetric vibrational mode (a1 or a1g) or an excited-state Jahn-Teller mode. In the D4h geometry, the b2u bending mode does not satisfy these symmetry requirements. However, once the equilibrium structure has been distorted along the bending motion in the D2d point group, the bending mode now transforms as a1 and can induce spin relaxation, as confirmed by calculation of dg/dQ spin–phonon coupling coefficients.13 This specific relationship illustrates a general principle: when a high-symmetry equilibrium structure is distorted along a non-totally-symmetric vibrational mode, that mode transforms as the totally symmetric representation in the new point group (Fig. 1B, ESI Section 4C†) and can cause spin relaxation.14
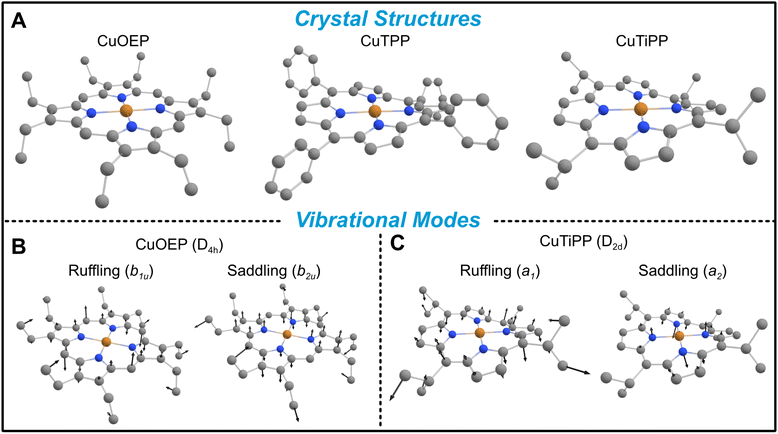
Metalloporphyrins offer an attractive platform for extending T1 structure–property relationships to new types of molecular geometries. Depending on the steric hindrance and substitutional pattern of peripheral moieties, porphyrins may adopt equilibrium geometries with saddled (b2u), ruffled (b1u), domed (a2u), or waved (eg) distortions, where the labels indicate the symmetry of the distorting vibrational mode in the D4h point group.24 The saddling distortion is equivalent to the same first coordination sphere bending distortion to D2d described above (Fig. 2B and C). By contrast, the b1u ruffling distortion (Fig. 2B and C) also results in a D2d equilibrium geometry, but the first coordination sphere remains completely unaltered (Fig. 2A). Instead, the porphyrin meso carbons are distorted above and below the plane of the first coordination sphere, rendering ruffling a secondary-sphere structural distortion. By analogy to the b2u bending mode argument, the b1u ruffling mode will transform as a1 in the D2d distorted point group, opening up the possibility of contributions to spin relaxation (ESI Section 4C†). Ruffling modes in porphyrins exist in the ultra-low-energy range (∼50 cm−1), indicating that ruffled S = ½ porphyrins may show a decisive, unique contribution of low-energy modes to T1.
In this study, we measure temperature-dependent T1via pulse electron paramagnetic resonance (EPR) on a series of three Cu(II) metalloporphyrins (CuP) (Fig. 1B and 2A): copper octaethylporphyrin (CuOEP), copper tetraphenylporphyrin (CuTPP), and copper tetraisopropylporphyrin (CuTiPP). CuOEP possesses a planar crystal structure, while CuTPP and CuTiPP exhibit increasing degrees of the ruffling distortion (Fig. 2A). Computational modeling via density functional theory (DFT) suggests that T1 times should decrease with increasing ruffling distortion. However, experimental T1 measurements do not trend with ruffling: the planar CuOEP and highly ruffled CuTiPP display robust room-temperature coherence while the moderately ruffled CuTPP does not. The breakdown of the computational analysis can be attributed to an over-emphasis of the lowest-energy ruffling mode. We then employ resonance Raman (rR) spectroscopy to detect the vibrational modes driving spin relaxation across this series and find a set of symmetric stretching vibrations in the 200–300 cm−1 region that trend with the experimentally observed T1. Our results demonstrate that ultra-low-energy modes do not drive spin relaxation in copper porphyrins, thereby distinguishing between conflicting theoretical models of spin relaxation (Fig. 1A).
2. Results
To quantify the amount of distortion in a given metalloporphyrin crystal structure, we applied the normal coordinate structural decomposition (NSD) developed by Shelnutt25 and implemented in the program by Kingsbury and Senge.24 CuOEP was chosen as the undistorted control compound, as it displays no tendency towards ruffling and only slight amounts of waving (Table 1). The distorted ruffled structures were chosen according to two criteria: (a) ruffling should be by far the largest distortion of the porphyrin, and (b) there must exist a diamagnetic host matrix of comparable distortions for preparation of EPR solid-state dilution samples. CuTPP and CuTiPP satisfy criterion (a), with CuTPP having only a small secondary saddling distortion and CuTiPP having a very small secondary waving distortion. Regarding criterion (b), the corresponding Ni(II) porphyrins both display dominant ruffling distortions. The NiTPP matrix is closely matched to the CuTPP structure in both the primary magnitude of ruffling and the secondary saddling, while the NiTiPP matrix displays somewhat increased ruffling over the Cu structure (2.03 vs. 1.35) and an additional saddling distortion (0.46 vs. 0.00). These metrics indicate that the ruffling distortion increases in the series CuOEP < CuTPP < CuTiPP. Note that metalloporphyrins can crystallize in multiple phases: while the ruffled structure for CuTPP is the more common polymorph in the Cambridge Structure Database,†26–28 there also exist two planar polymorphs.29,30 Additionally, we obtained a new ruffled solvate crystal phase for CuTiPP through single crystal X-ray diffraction (ESI Section 2C†). We confirmed that all EPR sample preparations in this work adhered to the ruffled (or, for CuOEP and ZnOEP, planar) geometries via powder X-ray diffraction (PXRD) and Rietveld refinement for comparison to the single crystal structures (ESI Section 2B, 4B†). Good EPR sample agreement with the polymorphs used for the NSD analysis in Table 1 was found in all cases.| Distortion mode | Ruffling (b1u) | Sadding (b2u) | Doming (a2u) | Waving (eg(x)) | Waving (eg(y)) |
|---|---|---|---|---|---|
| CuOEP | 0.00 | 0.00 | 0.00 | 0.11 | 0.05 |
| CuTPP | 1.18 | 0.22 | 0.00 | 0.00 | 0.00 |
| CuTiPP | 1.35 | 0.00 | 0.00 | 0.00 | 0.11 |
| ZnOEP | 0.00 | 0.00 | 0.00 | 0.16 | 0.06 |
| NiTPP | 1.27 | 0.27 | 0.00 | 0.00 | 0.00 |
| NiTiPP | 2.03 | 0.46 | 0.03 | 0.09 | 0.10 |
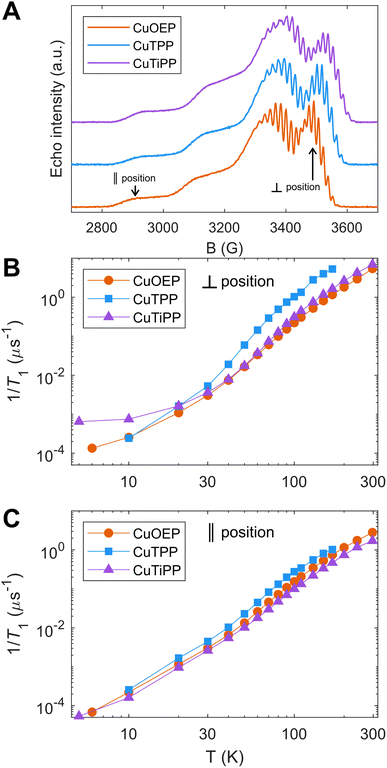
Temperature-dependent T1 measurements were acquired for all three CuP species (Fig. 3), prepared as 1% solid-state powder dilutions in the corresponding isostructural diamagnetic host (Table 1). Inversion recovery traces were acquired at field positions corresponding to both perpendicular (Fig. 3B) and parallel (Fig. 3C) orientations.20 CuTPP exhibits the fastest spin relaxation of all CuP species at both field positions, with a particularly distinct relaxation trend at the perpendicular position. The comparatively fast spin relaxation is consistent with previous studies on Ti(III)/CuTPP bimetallic and monometallic congeners in solution,31 as well as CuTPP embedded in a metal–organic framework (MOF),32,33 which did not observe room-temperature coherence for CuTPP. CuOEP exhibits the slowest relaxation (i.e., longest T1 time) at the perpendicular position, while CuTiPP exhibits the slowest relaxation at the parallel position; the orientation-averaged 1/T1 values are very similar for CuOEP and CuTiPP (Fig. S36†). Observer position differences in spin relaxation point to the presence of T1 anisotropy for the three CuP species. T1 anisotropy arises from the presence of anisotropic minority spin contributions in the ground state spin–orbit wavefunction and how they are modulated by totally symmetric vibrations.20 Note that the T1 values for all three porphyrins are quite similar at 20 K but diverge as temperature increases, indicating that higher-energy molecular vibrational modes are responsible for the differences between the compounds. Note also that CuOEP and CuTiPP display room-temperature (297 K) coherence, with T1 and Tm (the phase memory time2) of 185 ns and 87 ns for CuOEP and 145 ns and 50 ns for CuTiPP at perpendicular orientations. To the best of our knowledge, room-temperature electron spin coherence has only been demonstrated in one previous CuN4 molecular qubit, Cu(tmtaa),5 and is not observed for copper phthalocyanine (CuPc).22 CuTPP displays an extremely weak spin echo at room temperature, with T1 and Tm of 60 and 49 ns at the perpendicular position. No echo was detectable at the CuTPP parallel position, and a room-temperature echo-detected field sweep could not be acquired. As such, we do not consider this signal robust enough for designation of CuTPP as a room-temperature coherent molecular qubit.
Since 1/T1 increases in the order CuOEP = CuTiPP ≪ CuTPP, while ruffling increases in the order CuOEP < CuTPP < CuTiPP, the results of Fig. 3 do not support the hypothesis that increased ruffling distortion activates new channels for spin relaxation. To examine the theoretical underpinnings of this notion, we performed molecular spin–phonon coupling calculations according to a previously published procedure to predict 1/T1 traces (eqn (1)).14 The normal-mode derivatives of the principal values of the g-tensor, dg/dQ, were averaged to obtain the spin–phonon coupling coefficients, thereby modeling the average 1/T1 relaxation across all orientations. Thermal weighting was applied via a two-phonon Green's function to model the temperature dependence of the Raman spin relaxation process.16 An experimentally-calibrated proportionality constant of A = 1.01 × 105 μs−1 was used to convert the 1/T1 simulations into absolute rates.14 This model has been shown to correctly predict the T1 log–log slope of the molecular qubits CuPc and VOPc, as well as correctly ordering the relative T1 for a series of four Cu(II) and V(IV) sulfur and selenium-ligated qubits.14
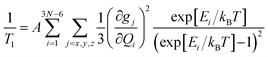 | (1) |
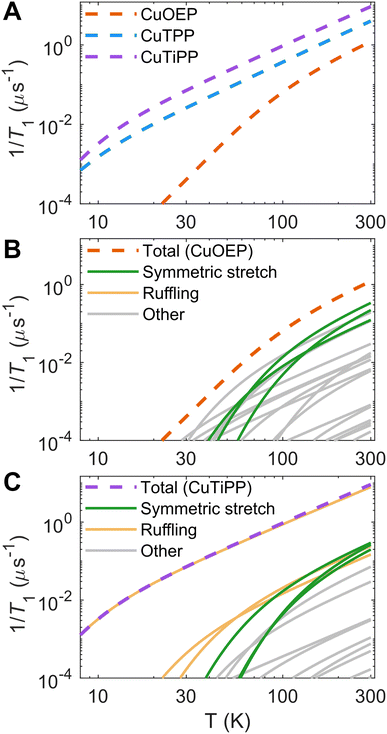
Theoretical calculations predict that 1/T1 should increase in the order CuOEP < CuTPP < CuTiPP (Fig. 4A; see Fig. S51† for an overlay of theory and experiment). This trend agrees with the order of increasing ruffling, but it does not agree with the experimental T1 ordering. To understand the origin of the trend in the calculations, the individual vibrational mode contributions to 1/T1 are plotted for CuOEP (Fig. 4B) and CuTiPP (Fig. 4C); ruffled CuTPP follows similar behavior to ruffled CuTiPP (Fig. S52†). The contributions from each normal mode are additive towards the total rate of spin relaxation. All mode contributions have the same functional shape in accordance with the thermal weighting function, with two degrees of freedom: (1) a larger energy of the vibrational mode translates the 1/T1 contribution to the right, since the mode will not be thermally populated until higher temperatures, and (2) a larger dgi/dQ value shifts the 1/T1 contribution up on the plot, indicating that it mediates faster spin relaxation. For CuOEP, the calculated relaxation rate from ∼30–70 K is set by low-energy vibrational modes, mostly of an eg rotational character with small amounts of symmetric stretch mixed in due to the waving distortion in CuOEP (Table 1). However, at 100 K and above, totally symmetric stretch modes take over the dominant contribution to spin relaxation (green lines, Fig. 4B and S38–S40, S54A†). By contrast, spin relaxation for CuTiPP is predicted to be dominated by a single low-energy ruffling mode at 26 cm−1 (Fig. S46†) over the entire temperature range studied (yellow lines, Fig. 4C), which almost exactly matches the total 1/T1 calculated trace. The contribution from other modes, including the totally symmetric stretch, is predicted to be <15% (Fig. S54C†). Therefore, molecular spin–phonon coupling calculations predict that the low-energy ruffling modes should dominate the 1/T1 for the ruffled porphyrins, and the absence of these distortion-activated modes in CuOEP should lead to a longer calculated spin lifetime. The room-temperature coherence of CuTiPP contradicts this prediction.
To determine the source of this discrepancy, we analyzed the temperature-dependent log–log slope of 1/T1. For a single power law process, such as those predicted by the Debye model for acoustic phonon spin relaxation,34 the log–log slope should be constant. This behavior is often observed in experimental T1 for inorganic lattices where the acoustic phonon branches drive T1 over the entire Raman process temperature range.34,35 However, variation in the log–log slope with temperature is common for molecular complexes. This behavior can originate from either (1) a crossover between two different spin relaxation processes (such as acoustic phonon relaxation vs. molecular vibration/local mode relaxation), or (2) the thermal population of higher-energy molecular vibrations, for which the innate spin relaxation contribution does not follow a power law form (eqn (1)).14 In the first case, a sharp increase occurs in the log–log slope with increasing temperature, as a process that scales weakly with temperature gives way to a process that scales more strongly with temperature. In the second case, a smooth decrease occurs in the log–log slope with increasing temperature due to the thermal weighting functional form. The curvature of the log–log 1/T1 can then be used to pinpoint the energy of the contributing molecular vibration. Higher-energy molecular vibrations display a larger and temperature-dependent log–log slope even at elevated temperatures. In contrast, the log–log slope of a low-energy molecular vibration flattens out towards a constant value of 2 in the high temperature limit (kbT ≫ Evib), owing to the asymptotic behavior of the two-phonon Green's function.
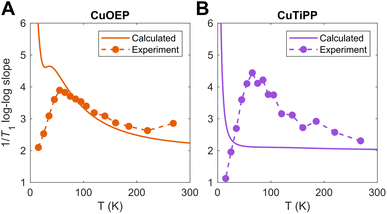
Both CuOEP and CuTiPP display a temperature-dependent log–log slope (Fig. 5A and B), which starts at a minimum below 10 K for the one-phonon direct process, peaks sharply at a value of ∼4 at ∼60 K, and then diminishes gradually towards ∼2.5 at room temperature. The sharp increase from 10–60 K experimentally indicates a change in the relaxation process (case 1), wherein two-phonon scattering from a higher-energy molecular vibration (>60 K) takes over from acoustic/pseudoacoustic phonons (<30 K). The gradual decrease from 60 K towards room temperature indicates that one or more molecular vibrational modes controls spin relaxation over this region (case 2). By comparing these slopes to those of the theoretical calculations (Fig. 4), the origin of the discrepancies with experiment can be ascertained. The calculated T1 log–log slope for CuOEP matches the experimental behavior, which can be attributed in the calculation to the population of totally symmetric stretch modes above 60 K (Fig. 4B and 5A). Note that the calculations do not include acoustic phonons, so the divergence of the calculated log–log slope below 20 K is expected. However, the calculated T1 for CuTiPP displays a qualitatively incorrect log–log slope of 2 throughout the entire temperature range, while the experimental log–log slope peaks at a value of ∼4.5 at 60 K. The calculated log–log slope of 2 arises from the 26 cm−1 ruffling mode (Fig. 5B), which is predicted to dominate spin relaxation across all temperatures. A similar disagreement arises for CuTPP due to the same ruffling mode phenomenon (Fig. S53 and S55†). We conclude that the calculated spin relaxation for CuOEP is in agreement with experiment, but the calculated spin relaxation for CuTiPP and CuTPP is incorrect due to overemphasis on the low-energy ruffling modes. Evidently, the ultra-low-energy modes do not dominate spin relaxation in experiment.
To experimentally ascertain the energy range of the vibrational modes driving spin relaxation, local mode fits22 to the 1/T1 data (Fig. 6A–C) were carried out according to eqn (2). The least-squares fit was performed on the log–log data for equivalent residuals weighting across the entire temperature range.
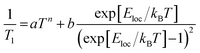 | (2) |
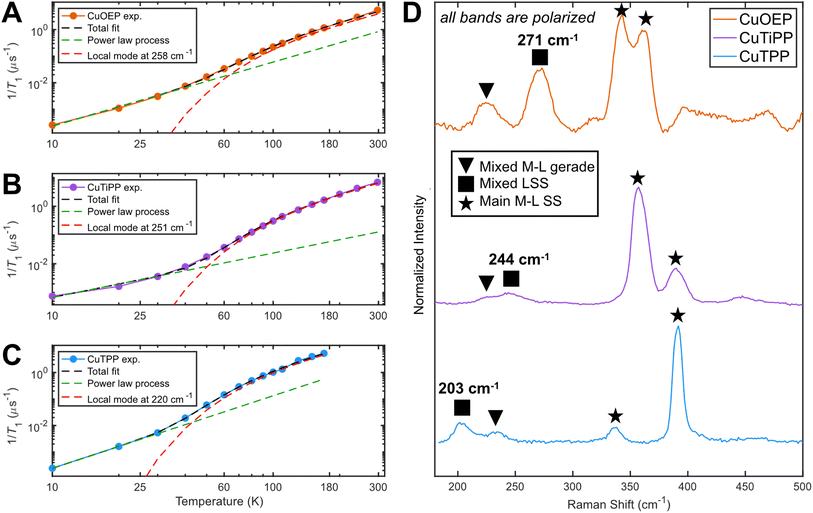 | ||
| Fig. 6 Determination of the dominant vibrational mode energy for spin relaxation. Local mode fitting at the perpendicular observer position according to eqn (1) for (A) CuOEP, (B) CuTiPP, and (C) CuTPP. (D) Resonance Raman spectroscopy obtained via 457.9 nm excitation (Soret preresonance enhancement). CuOEP collected in CS2 at room temperature, while CuTiPP and CuTPP collected in C6H6 at room temperature; all samples are at a concentration of 2 mM. All peak positions are accurate to within 5 cm−1. | ||
The power law term accounts for a combination of the one-phonon direct process plus two-phonon Raman relaxation operating on low-energy phonons; combining these reduces the number of free parameters to avoid overfitting. Lower temperature measurements (<10 K) would likely be needed to isolate the direct process contribution. It is well established that the Raman process in molecular solids need not follow the Debye model T9 scaling,36 so a variable exponent n is included. The second term has the same functional form as the two-phonon Green's function used for thermal weighting of molecular vibrational modes. In effect, this fitting postulates a single molecular vibration of energy Eloc capable of explaining the high-temperature T1 values, while allowing for an unresolved collection of weakly-coupled low-energy modes to determine the low-temperature T1 values. All fits yield a local mode energy between 200–270 cm−1, which fall in the energetic range of bond stretching vibrational modes. This analysis indicates that a similar type of vibrational mode likely determines T1 in all three porphyrins. The fitted energy for CuTPP is lower than the fitted energies for CuOEP or CuTiPP, matching the room-temperature coherence observation for CuOEP and CuTiPP but not CuTPP. Local mode fitting on T1 values collected at the parallel field position reinforces that the local mode energy for CuTPP is distinct from, and lower than, the mode energies for CuOEP and CuTiPP (Table S7†). The local mode energies Eloc correlate better with the observed T1 values than the coupling prefactor b, suggesting that vibrational mode energy shifts are principally responsible for the different T1 values across the compound series (Table S8†).
rR spectroscopy was employed to identify vibrational modes in this energy range that could participate in spin–phonon coupling. Owing to selection rules of Raman scattering, only gerade modes are visible in centrosymmetric complexes. Furthermore, the A-term mechanism of Soret-band rR intensity enhancement selectively excites totally symmetric a1/a1g modes,37,38 which are precisely those modes predicted by group theory to have the correct symmetry for driving spin relaxation.14 rR spectra for all three compounds display four main bands in the 200–400 cm−1 region, including two bands between 200–300 cm−1 (Fig. 6D). Crucially, these latter bands appear lower in energy for CuTPP than for CuOEP or CuTiPP, in agreement with the relative rates of spin relaxation. All bands display a depolarization ratio less than 0.75 (Fig. S22–S24†), indicating at least some component of totally symmetric motion is present. The band positions in the solution-phase data are consistent within 8 cm−1 of rR spectra acquired in the solid state and display similar relative resonance enhancement (Table S2 and Fig. S25†), indicating these reflect the vibrational structure present in the EPR samples as well. DFT frequency calculations of vibrations with Raman intensity display very good agreement with the experimental spectra and enable the assignment of the 300–400 cm−1 bands to totally symmetric metal–ligand stretching modes (ESI Section 3C†). The 200–300 cm−1 bands contain one instance of a mixed ligand symmetric stretch (LSS) and one instance of a mixed metal–ligand gerade mode with a principal contribution from non-totally symmetric motion. At least some symmetric motion must be admixed to account for the observation that all bands are polarized. Note the ordering of these latter two modes changes between the three CuP species.
Owing to the spin–phonon coupling group theory selection rule for totally symmetric vibrations, the mixed LSS mode energies were extracted from the rR spectra and compared with the local mode fits. Good agreement is found (Table 2), showing a >40 cm−1 distinction between the low-energy CuTPP LSS mode (203 cm−1) and those of CuOEP (271 cm−1) and CuTiPP (244 cm−1). This trend indicates that the energetic positioning of the LSS mode can explain the temperature-dependent T1 results for the three CuP systems. In addition, the presence of a minor saddling distortion for CuTPP but not CuOEP or CuTiPP (Table 1) may lead to enhanced spin–phonon coupling, as saddling motions are known to be activated for spin relaxation via a first coordination sphere distortion. Porphyrin saddling contributions to T1 will be analyzed in more detail in a future study. We conclude that high-energy totally symmetric stretch modes, and not low-energy ruffling modes, control the relative T1 ordering for CuOEP, CuTiPP, and CuTPP above 60 K.
| Compound | Perpendicular orientation local mode (cm−1) | Raman mixed LSS mode (cm−1) |
|---|---|---|
| CuOEP | 258 | 271 |
| CuTiPP | 251 | 244 |
| CuTPP | 220 | 203 |
3. Discussion
The failure of computational spin relaxation models to predict the correct high-energy stretching vibrational modes is not a unique feature of ruffled porphyrins. In several cases, molecular spin–phonon coupling models seem to have a bias toward over-emphasizing low-energy modes, leading to predictions of ultra-low-energy vibrations dominating T1. However, such assignments often fail to account for the temperature-dependent T1 curvature and log–log slope changes, such as in the case of ab initio modeling of vanadyl tetraphenylporphyrin (VOTPP).19 Thus, such theoretical claims of low-energy phonon dominance should be treated with significant caution.The origins of this computational low-energy bias are unclear, but likely relate to some of the approximations used to build the models. One possibility is that gas-phase DFT overestimates the amplitudes of low-energy vibrational modes, which should be more constrained in the solid-state. However, condensed-phase phonon calculations retain the same bias toward low-energy modes.19 Additionally, the use of full-g-tensor dgij/dQ values for spin Hamiltonian matrix elements may overestimate the coupling of certain types of low-energy modes, such as eg rotations of the first coordination sphere, that do not dynamically change the total amount of minority spin mixing through the magnitude of spin–orbit coupling. Incorporation of spin–orbit coupling spin-flip matrix elements into ab initio T1 modeling with quantum master equations may remedy this difficulty.
Experimentally, this work shows that rR spectroscopy is a powerful tool for building spin dynamics structure–property relationships by leveraging the selectivity for totally symmetric mode energies. Previous works have attempted to empirically correlate vibrations to features of spin relaxation through terahertz spectroscopy39–42 or computation of the vibrational density of states.5,32 However, terahertz or IR absorption spectroscopies rely on electric dipole selection rules that select for ungerade modes in centrosymmetric complexes. Group theory analysis has established a selection rule for spin–phonon coupling, which indicates that only gerade vibrations (predominately a1g modes) are able to couple to the spins in centrosymmetric complexes.14,17 Thus, IR or far-IR absorption spectroscopies do not probe the modes of relevance for spin–phonon coupling for square-planar complexes. Furthermore, the full vibrational density of states, or even atom-specific partial density of states, becomes very complicated in macrocyclic qubits like porphyrins, rendering statements about specific vibrational modes challenging. A-term enhanced rR spectra, however, have the key virtue of selectivity for the a1/a1g modes most relevant to spin relaxation, making spectral correlations much more straightforward.
In addition, the magnitude of A-term resonance enhancement provided by excitation into a strongly dipole-allowed electronic absorption band is determined by the amount of excited-state distortion through the electronuclear coupling integral.37 This same term arises in the ligand field theory of spin–phonon coupling, where excited-state distortion is required to observe nonzero dgi/dQ.14 Thus, there may be a connection between the magnitude of resonance enhancement and the magnitude of spin–phonon coupling itself. The caveat is that the electronic excited state of relevance is different for g-tensor contributions (d–d transition) vs. rR spectroscopy (charge transfer). In general, one cannot reliably acquire rR spectra for d–d bands, and many molecular qubits feature intense electronic transitions that obscure these transitions in electronic absorption spectra. The excited-state distortions need not be the same between the two types of electronic excited states. Further work will investigate whether reliable information on spin relaxation can be extracted from the magnitude of A-term enhancement in rR spectra of molecular qubits.
4. Conclusions
This work probes the effect of the ruffling distortion on spin relaxation in a series of three copper porphyrins. Two of the three members of the series (CuOEP and CuTiPP) display room-temperature coherence, indicating the suitability of copper porphyrins as a new class of molecules for room-temperature molecular quantum information science applications. Unlike in the well-studied case of b2u bending/saddling vibrations, increasing b1u ruffling distortion does not correlate to decreased T1 times, despite the mode transforming as a1 in D2d. This unexpected result may indicate that primary coordination sphere distortions are required to materially activate new vibrational modes for spin relaxation, and secondary sphere effects such as ruffling have too weak an influence on angular momentum and spin–orbit coupling to induce spin flips. Computational spin relaxation models fail to account for the insensitivity of T1 to the ruffling distortion, indicating a direction for future theoretical efforts. rR spectroscopy successfully identifies a specific vibrational mode with totally symmetric character that correctly trends with the experimental T1 local mode fits. Thus, this study indicates the primary vibrational modes responsible for S = ½ CuP spin relaxation above ∼60 K correspond to bond stretches with totally symmetric character, not ultra-low-energy modes of rotational character.Data availability
Crystallographic information can be found in the CCDC, deposition number 2303071. The data supporting this study may be obtained from the authors upon reasonable request.Author contributions
Conceptualization: N. P. K. and R. G. H; investigation and formal analysis: N. P. K., N. E. L., and K. M. L; visualization: N. P. K., N. E. L., and K. M. L.; supervision: R. G. H.; all authors contributed to writing the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors wish to thank Dr Paul H. Oyala for assistance with EPR spectroscopy, Dr Jay R. Winkler for assistance with resonance Raman spectroscopy, Dr Mike Takase for performing the CuTiPP crystallography, and Prof. Brendon J. McNicholas for assistance with porphyrin synthesis. X-ray diffraction and powder X-ray diffraction data were collected in the X-Ray Crystallography Facility (XRCF) in the Beckman Institute at Caltech. Resonance Raman data were collected in the Beckman Institute Laser Resource Center (BILRC) at Caltech, a facility supported by the Arnold and Mabel Beckman Foundation. N. P. K. acknowledges support by the Hertz Fellowship. N. P. K. and K. M. L. both acknowledge support by the National Science Foundation Graduate Research Fellowship Program under Grant No. DGE-1745301. N. E. L. acknowledges support by a John Stauffer SURF Fellowship. Financial support from the Research Corporation for Science Advancement (RCSA) through a Cottrell Award (Award ID: 28165) is gratefully acknowledged.References
- M. Atzori and R. Sessoli, The Second Quantum Revolution: Role and Challenges of Molecular Chemistry, J. Am. Chem. Soc., 2019, 141(29), 11339–11352, DOI:10.1021/jacs.9b00984.
- R. Mirzoyan, N. P. Kazmierczak and R. G. Hadt, Deconvolving Contributions to Decoherence in Molecular Electron Spin Qubits: A Dynamic Ligand Field Approach, Chem.–Eur. J., 2021, 27, 9482–9494, DOI:10.1002/chem.202100845.
- K. Bader, D. Dengler, S. Lenz, B. Endeward, S.-D. Jiang, P. Neugebauer and J. van Slageren, Room Temperature Quantum Coherence in a Potential Molecular Qubit, Nat. Commun., 2014, 5(1), 5304, DOI:10.1038/ncomms6304.
- M. S. Fataftah, M. D. Krzyaniak, B. Vlaisavljevich, M. R. Wasielewski, J. M. Zadrozny and D. E. Freedman, Metal–Ligand Covalency Enables Room Temperature Molecular Qubit Candidates, Chem. Sci., 2019, 10(27), 6707–6714, 10.1039/C9SC00074G.
- M. J. Amdur, K. R. Mullin, M. J. Waters, D. Puggioni, M. K. Wojnar, M. Gu, L. Sun, P. H. Oyala, J. M. Rondinelli and D. E. Freedman, Chemical Control of Spin–Lattice Relaxation to Discover a Room Temperature Molecular Qubit, Chem. Sci., 2022, 13, 7034–7045, 10.1039/D1SC06130E.
- M. Atzori, L. Tesi, E. Morra, M. Chiesa, L. Sorace and R. Sessoli, Room-Temperature Quantum Coherence and Rabi Oscillations in Vanadyl Phthalocyanine: Toward Multifunctional Molecular Spin Qubits, J. Am. Chem. Soc., 2016, 138(7), 2154–2157, DOI:10.1021/jacs.5b13408.
- M. Atzori, E. Morra, L. Tesi, A. Albino, M. Chiesa, L. Sorace and R. Sessoli, Quantum Coherence Times Enhancement in Vanadium(IV)-Based Potential Molecular Qubits: The Key Role of the Vanadyl Moiety, J. Am. Chem. Soc., 2016, 138, 11234–11244 CrossRef CAS PubMed.
- A.-M. Ariciu, D. H. Woen, D. N. Huh, L. E. Nodaraki, A. K. Kostopoulos, C. A. P. Goodwin, N. F. Chilton, E. J. L. McInnes, R. E. P. Winpenny, W. J. Evans and F. Tuna, Engineering Electronic Structure to Prolong Relaxation Times in Molecular Qubits by Minimising Orbital Angular Momentum, Nat. Commun., 2019, 10(1), 3330, DOI:10.1038/s41467-019-11309-3.
- D. W. Laorenza, A. Kairalapova, S. L. Bayliss, T. Goldzak, S. M. Greene, L. R. Weiss, P. Deb, P. J. Mintun, K. A. Collins, D. D. Awschalom, T. C. Berkelbach and D. E. Freedman, Tunable Cr4+ Molecular Color Centers, J. Am. Chem. Soc., 2021, 143, 21350–21363, DOI:10.1021/jacs.1c10145.
- S. L. Bayliss, D. W. Laorenza, P. J. Mintun, B. D. Kovos, D. E. Freedman and D. D. Awschalom, Optically Addressable Molecular Spins for Quantum Information Processing, Science, 2020, 370(6522), 1309–1312, DOI:10.1126/science.abb9352.
- S. L. Bayliss, P. Deb, D. W. Laorenza, M. Onizhuk, G. Galli, D. E. Freedman and D. D. Awschalom, Enhancing Spin Coherence in Optically Addressable Molecular Qubits through Host-Matrix Control, Phys. Rev. X, 2022, 12(3), 031028, DOI:10.1103/PhysRevX.12.031028.
- N. P. Kazmierczak, K. M. Luedecke, E. T. Gallmeier and R. G. Hadt, T 1 Anisotropy Elucidates Spin Relaxation Mechanisms in an S = 1 Cr(IV) Optically Addressable Molecular Qubit, J. Phys. Chem. Lett., 2023, 7658–7664, DOI:10.1021/acs.jpclett.3c01964.
- R. Mirzoyan and R. G. Hadt, The Dynamic Ligand Field of a Molecular Qubit: Decoherence through Spin–Phonon Coupling, Phys. Chem. Chem. Phys., 2020, 22(20), 11249–11265, 10.1039/D0CP00852D.
- N. P. Kazmierczak, R. Mirzoyan and R. G. Hadt, The Impact of Ligand Field Symmetry on Molecular Qubit Coherence, J. Am. Chem. Soc., 2021, 143(42), 17305–17315, DOI:10.1021/jacs.1c04605.
- A. Lunghi and S. Sanvito, How Do Phonons Relax Molecular Spins?, Sci. Adv., 2019, 5(9), eaax7163, DOI:10.1126/sciadv.aax7163.
- A. Lunghi and S. Sanvito, The Limit of Spin Lifetime in Solid-State Electronic Spins, J. Phys. Chem. Lett., 2020, 11(15), 6273–6278, DOI:10.1021/acs.jpclett.0c01681.
- F. Santanni, A. Albino, M. Atzori, D. Ranieri, E. Salvadori, M. Chiesa, A. Lunghi, A. Bencini, L. Sorace, F. Totti and R. Sessoli, Probing Vibrational Symmetry Effects and Nuclear Spin Economy Principles in Molecular Spin Qubits, Inorg. Chem., 2021, 60(1), 140–151, DOI:10.1021/acs.inorgchem.0c02573.
- L. Escalera-Moreno, N. Suaud, A. Gaita-Ariño and E. Coronado, Determining Key Local Vibrations in the Relaxation of Molecular Spin Qubits and Single-Molecule Magnets, J. Phys. Chem. Lett., 2017, 8(7), 1695–1700, DOI:10.1021/acs.jpclett.7b00479.
- E. Garlatti, A. Albino, S. Chicco, V. H. A. Nguyen, F. Santanni, L. Paolasini, C. Mazzoli, R. Caciuffo, F. Totti, P. Santini, R. Sessoli, A. Lunghi and S. Carretta, The Critical Role of Ultra-Low-Energy Vibrations in the Relaxation Dynamics of Molecular Qubits, Nat. Commun., 2023, 14(1), 1653, DOI:10.1038/s41467-023-36852-y.
- N. P. Kazmierczak and R. G. Hadt, Illuminating Ligand Field Contributions to Molecular Qubit Spin Relaxation via T1 Anisotropy, J. Am. Chem. Soc., 2022, 144(45), 20804–20814, DOI:10.1021/jacs.2c08729.
- A. Lunghi, Toward Exact Predictions of Spin-Phonon Relaxation Times: An Ab Initio Implementation of Open Quantum Systems Theory, Sci. Adv., 2022, 8(31), eabn7880, DOI:10.1126/sciadv.abn7880.
- A. H. Follmer, R. D. Ribson, P. H. Oyala, G. Y. Chen and R. G. Hadt, Understanding Covalent versus Spin–Orbit Coupling Contributions to Temperature-Dependent Electron Spin Relaxation in Cupric and Vanadyl Phthalocyanines, J. Phys. Chem. A, 2020, 124(44), 9252–9260, DOI:10.1021/acs.jpca.0c07860.
- A. J. Fielding, S. Fox, G. L. Millhauser, M. Chattopadhyay, P. M. H. Kroneck, G. Fritz, G. R. Eaton and S. S. Eaton, Electron Spin Relaxation of Copper(II) Complexes in Glassy Solution between 10 and 120K, J. Magn. Reson., 2006, 179(1), 92–104, DOI:10.1016/j.jmr.2005.11.011.
- C. J. Kingsbury and M. O. Senge, The Shape of Porphyrins, Coord. Chem. Rev., 2021, 431, 213760, DOI:10.1016/j.ccr.2020.213760.
- W. Jentzen, X.-Z. Song and J. A. Shelnutt, Structural Characterization of Synthetic and Protein-Bound Porphyrins in Terms of the Lowest-Frequency Normal Coordinates of the Macrocycle, J. Phys. Chem. B, 1997, 101(9), 1684–1699, DOI:10.1021/jp963142h.
- E. B. Fleischer, C. K. Miller and L. E. Webb, Crystal and Molecular Structures of Some Metal Tetraphenylporphines, J. Am. Chem. Soc., 1964, 86(12), 2342–2347, DOI:10.1021/ja01066a009.
- M. Zeller, S. J. DiMuzio, R. J. Wilcox and A. D. Hunter, CCDC 252379: Experimental Crystal Structure Determination, CSD Commun, 2005, DOI:10.5517/cc8gm8l.
- C. Chen, X.-T. He, D.-L. Hong, J.-W. Wang, Y.-H. Luo and B.-W. Sun, Tuning the Crystal Structures of Metal-Tetraphenylporphines via a Magnetic Field, New J. Chem., 2018, 42(15), 12570–12575, 10.1039/C8NJ01882K.
- H.-S. He, A Second Polymorph of (5,10,15,20-Tetra-phenyl-porphyrinato)Copper(II), Acta Crystallogr., Sect. E: Struct. Rep. Online, 2007, 63(4), m976–m977, DOI:10.1107/S1600536807008574.
- L. Aparici Plaza and J. Chojnacki, Influence of Chloro-form on Crystalline Products Yielded in Reactions of 5,10,15,20-Tetra-phenyl-porphyrin with HCl and Copper(II) Salts, Acta Crystallogr. C, 2012, 68(1), m24–m28, DOI:10.1107/S0108270111054102.
- S. von Kugelgen, M. D. Krzyaniak, M. Gu, D. Puggioni, J. M. Rondinelli, M. R. Wasielewski and D. E. Freedman, Spectral Addressability in a Modular Two Qubit System, J. Am. Chem. Soc., 2021, 143(21), 8069–8077, DOI:10.1021/jacs.1c02417.
- C.-J. Yu, S. von Kugelgen, M. D. Krzyaniak, W. Ji, W. R. Dichtel, M. R. Wasielewski and D. E. Freedman, Spin and Phonon Design in Modular Arrays of Molecular Qubits, Chem. Mater., 2020, 32(23), 10200–10206, DOI:10.1021/acs.chemmater.0c03718.
- C.-J. Yu, M. D. Krzyaniak, M. S. Fataftah, M. R. Wasielewski and D. E. Freedman, A Concentrated Array of Copper Porphyrin Candidate Qubits, Chem. Sci., 2019, 10(6), 1702–1708, 10.1039/C8SC04435J.
- K. J. Standley and R. A. Vaughan, Electron Spin Relaxation Phenomena in Solids, Springer US, Boston, MA, 1969, DOI:10.1007/978-1-4899-6539-4.
- E. S. Sabisky and C. H. Anderson, Spin-Lattice Relaxation of Tm2+ in CaF2, SrF2, and BaF2, Phys. Rev. B: Condens. Matter Mater. Phys., 1970, 1(5), 2028–2040, DOI:10.1103/PhysRevB.1.2028.
- L. Gu and R. Wu, Origin of the Anomalously Low Raman Exponents in Single Molecule Magnets, Phys. Rev. B, 2021, 103(1), 014401, DOI:10.1103/PhysRevB.103.014401.
- A. C. Albrecht, On the Theory of Raman Intensities, J. Chem. Phys., 1961, 34(5), 1476–1484, DOI:10.1063/1.1701032.
- J. G. Rankin and R. S. Czernuszewicz, Fingerprinting Petroporphyrin Structures with Vibrational Spectroscopy: Resonance Raman Spectra of Nickel and Vanadyl Etioporphyrins I and III, Org. Geochem., 1993, 20(5), 521–538, DOI:10.1016/0146-6380(93)90021-3.
- M. Atzori, S. Benci, E. Morra, L. Tesi, M. Chiesa, R. Torre, L. Sorace and R. Sessoli, Structural Effects on the Spin Dynamics of Potential Molecular Qubits, Inorg. Chem., 2018, 57(2), 731–740, DOI:10.1021/acs.inorgchem.7b02616.
- A. Albino, S. Benci, L. Tesi, M. Atzori, R. Torre, S. Sanvito, R. Sessoli and A. Lunghi, First-Principles Investigation of Spin–Phonon Coupling in Vanadium-Based Molecular Spin Quantum Bits, Inorg. Chem., 2019, 58(15), 10260–10268, DOI:10.1021/acs.inorgchem.9b01407.
- A. Albino, S. Benci, M. Atzori, L. Chelazzi, S. Ciattini, A. Taschin, P. Bartolini, A. Lunghi, R. Righini, R. Torre, F. Totti and R. Sessoli, Temperature Dependence of Spin–Phonon Coupling in [VO(Acac)2]: A Computational and Spectroscopic Study, J. Phys. Chem. C, 2021, 125(40), 22100–22110, DOI:10.1021/acs.jpcc.1c06916.
- L. C. d. Camargo, M. Briganti, F. S. Santana, D. Stinghen, R. R. Ribeiro, G. G. Nunes, J. F. Soares, E. Salvadori, M. Chiesa, S. Benci, R. Torre, L. Sorace, F. Totti and R. Sessoli, Exploring the Organometallic Route to Molecular Spin Qubits: The [CpTi(Cot)] Case, Angew. Chem., 2021, 133(5), 2620–2625, DOI:10.1002/ange.202009634.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2303071. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc05774g |
| This journal is © The Royal Society of Chemistry 2024 |