Excitonic cuprophilic interactions in one-dimensional hybrid organic–inorganic crystals

Abstract

The everlasting pursuit of hybrid organic–inorganic lead-free semiconductors has directed the focus towards eco-friendly copper-based systems, perhaps because of the diversity in chemistry, controlling the structure–property relationship. In this work, we report single crystals of a Cu(I) halide-based perovskite-like organic–inorganic hybrid, (TMA)Cu₂Br₃, (TMA = tetramethylammonium), consisting of unusual one-dimensional inorganic anionic chains of –(Cu₂Br₃)–, electrostatically stabilized by organic cations, and the Cu(I)–Cu(I) distance of 2.775 Å indicates the possibility of cuprophilic interactions. X-ray photoelectron spectroscopy measurements further confirmed the presence of exclusive Cu(I) in (TMA)Cu₂Br₃ and electronic structure calculations based on density functional theory suggested a direct bandgap value of 2.50 eV. The crystal device demonstrated an impressive bulk photovoltaic effect due to the emergence of excitonic Cu(I)–Cu(I) interactions, as was clearly visualized in the charge-density plot as well as in the Raman spectroscopic analysis. The single crystals of a silver analogue, (TMA)Ag₂Br₃, have also been synthesized revealing a Ag(I)–Ag(I) distance of 3.048 Å (signature of an argentophilic interaction). Unlike (TMA)Cu₂Br₃, where more density of states from Cu compared to Br near the Fermi level was observed, (TMA)Ag₂Br₃ exhibited the opposite trend, possibly due to variation in the ionic potential influencing the overall bonding scenario.

---

Introduction

The chemistry of hybrid organic–inorganic lead (Pb) halide perovskites (ABX₃; A = organic-based cations, B=Pb(II), and X = halides) and related structures have seen a tremendous surge over the past two decades.^1–3 It is the unusual chemical bonding scenarios in various combinations of A, B and X, leading to distinctive optoelectronic properties in the systems and opening the door towards a plethora of application possibilities such as solar cells, light-emitting diodes, photodetectors, fluorescence-based sensing, second and third harmonic generations, thermoelectrics, piezoelectrics, and catalysis.^4–13 Owing to the ease of controllability over the photoelectric performance, improved stability and carrier mobility, and broadband absorption, ABX₃ and similar materials present an enormous opportunity for implementation in optoelectronics.^14–17 However, in view of the toxicity of Pb(II),¹⁸ various lead-free systems with elements such as germanium, tin, antimony, bismuth, and even the first–row transition metals were also explored.^19–22 Indeed, such lead-free structures are emerging as attractive alternatives; specifically, Cu(II) and Cu(I)-based hybrid organic–inorganic perovskite-like systems where the redox chemistry offers a great opportunity for structural flexibility vis-a-vis tuning of the optoelectronic properties.^23–27 However, one aspect that still remains elusive among such transition-metal based systems is the role of metallophilic interactions in regulating photoresponsivity and similar attributes.

An intriguing aspect of the chemistry of coinage metals, consisting of Cu, Ag and Au is the respective cuprophilicity (3d¹⁰–3d¹⁰), argentophilicity (4d¹⁰–4d¹⁰) and aurophilicity (5d¹⁰–5d¹⁰) – so called chemistry beyond valence electrons. In light of the relativistic effect in Au, aurophilicity is well-established,²⁸ followed by the exploration of argentophilicity²⁹ and also cuprophilicity to some extent.^30,31 The Cu(I)–Cu(I) interactions have been observed to play a pivotal role in achieving superconductivity, photoluminescence, mechanochromism, mechanical flexibility, and catalysis.^32–37 Therefore, cuprophilicity can certainly have far reaching implications for imparting multi-functionality in hybrid organic–inorganic perovskite-based systems. Herein, we report a facile one-step synthesis of a thermally stable one-dimensional Cu(I)-based hybrid organic–inorganic perovskite-like single-crystal, (TMA)Cu₂Br₃, (TMA = tetramethylammonium cation), [(CH₃)₄N⁺], where the anionic inorganic polymeric chain [Cu₂Br₃]_nⁿ⁻ exhibits an unusual and rare 1D ladder-like structure of Cu(I) ions arranged in a distorted tetrahedral fashion. The TMA cations stabilize the anionic polymer unit predominantly through electrostatic interactions. The Cu(I)–Cu(I) distance has been observed to be 2.775 Å (which is shorter than the sum of the van der Waals radii of two Cu atoms) thereby providing a signature of cuprophilic interactions. Interestingly, photoresponsivity on the single-crystal device of (TMA)Cu₂Br₃ was realized to be remarkable. To unravel the mechanistic insights, electronic structure calculations based on density functional theory (DFT) were performed and the unusual photoconduction is assigned to be due to the emergence of excitonic cuprophilic interactions in the (TMA)Cu₂Br₃ system, also visualized experimentally from Raman spectral signatures which is indeed exceptionally noteworthy. Additionally, we have synthesized (TMA)Ag₂Br₃ and indeed, the Ag(I)–Ag(I) distance of 3.048 Å suggested the presence of argentophilic interaction. The DFT calculations for the (TMA)Ag₂Br₃ system also revealed distinctive electronic structures.

Results

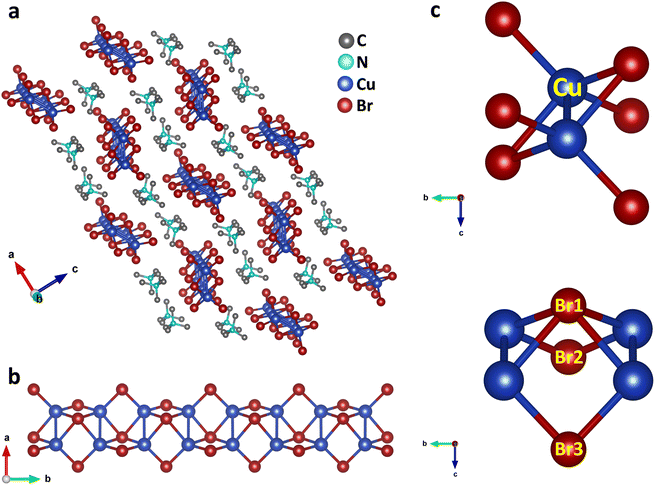
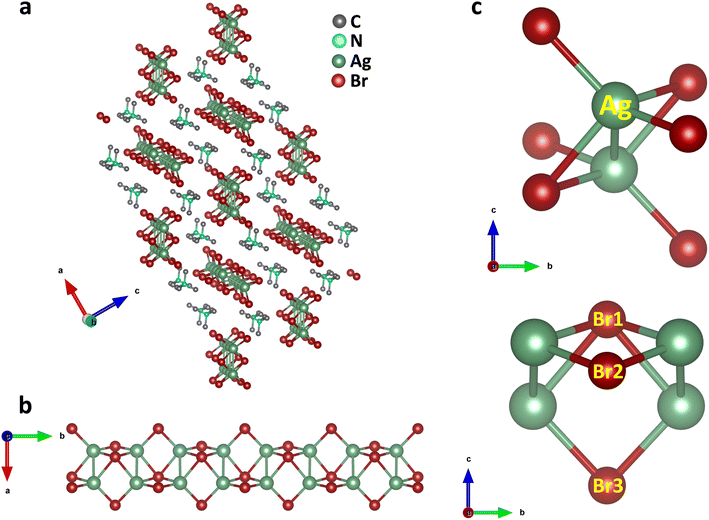
Single crystals of (TMA)Cu₂Br₃ were synthesized via a slow-cooling method in a Teflon lined autoclave (Fig. S1†). The crystal structure of (TMA)Cu₂Br₃ was determined through single-crystal X-ray diffraction (SCXRD) measurements at 296 K, and the details of crystallographic refinement parameters are listed in Tables S1–S4.† The crystal of (TMA)Cu₂Br₃ belongs to the orthorhombic space group Pnma with the unit cell parameters as follows: a = 16.3590(3) Å, b = 6.5479(11) Å, c = 9.5918(17) Å, and V = 1027.45 ų. The structure consists of polymeric chains of (Cu₂Br₃)_nⁿ⁻ anions and TMA⁺ monomeric cations (Fig. 1a and S2a–c†). Each Cu(I) ion in the chain is tetrahedrally coordinated to four Br⁻ ions, whereas an additional fifth bond is coordinated to another Cu(I) ion (Fig. 1b and c). The Cu(I) ions form a 1D ladder along the crystallographic b axis, and the structure can be best described as two parallel interconnected chains of a distorted tetrahedron (Fig. 1b, S3a and b†).³⁸ The Cu–Cu distance was 2.775 Å in the direction perpendicular to the propagation of the ladder. This distance falls under the regime of cuprophilic interactions between the two Cu atoms in this particular direction, whereas the Cu–Cu distance along the direction of propagation of the ladder is found to have alternate values of 3.258 Å and 3.290 Å, respectively.

Fig. 1 Crystal structure of (TMA)Cu₂Br₃. (a) Arrangements of cations (TMA) and anionic chains as viewed along the crystallographic b-axis (slightly tilted, H atoms are omitted for clarity). (Cu₂Br₃)_nⁿ⁻ polymeric ladders are isolated from one another, and each ladder is surrounded by six stacks of TMA cations which run along the b axis. (b) Zoomed-in view of the inorganic (Cu₂Br₃)_nⁿ⁻ chain along the crystallographic c-axis. (c) Coordination environment around Cu depicting the distorted tetrahedral geometry as well as the Cu–Cu bond (top panel) and distinctive bonding scenario of three Br (Br1, Br2 and Br3) around Cu (bottom panel), as viewed from the crystallographic a-axis.

The structure also consists of a total of three different types of Br atoms: one central Br atom and two different terminal Br atoms (Fig. 1c). The central Br1 atoms coordinate to four Cu atoms and reside alternatively above and below the plane of the Cu atoms. The four Cu–Br1 bonds have two distinct Cu–Br1 distances, two of them having a distance of 2.573 Å, whereas the other two have a distance of 2.587 Å. Both of these are somewhat longer than the Cu–Br distance in CuBr,³⁸ as expected, because of the four coordination of these Br atoms. Besides, these Br atoms form a Br1–Cu–Br1 angle of 114.92° around the Cu atoms. Also, around the Br1 atoms we can have as many as three different Cu–Br1–Cu angles. Along the ladder the Cu–Br1–Cu angle is 65.08°, whereas two different Cu–Br1–Cu angles of 78.06° and 79.49° are seen perpendicular to the ladder. Interestingly, all of these are smaller than most of the reported Cu–Br–Cu angles. The second type of Br atoms (Br2 and Br3) are located on both the sides of the ladder and reside on the opposite side of the plane of the ladder compared to the central Br atoms. These Br atoms coordinate to only two Cu atoms and have two different Cu–Br bond distances. Cu–Br3 has a distance of 2.411 Å, whereas the Cu–Br2 bond shows a distance of 2.446 Å, both having a shorter Cu–Br distance than that in CuBr. These Br atoms have a Br2–Cu–Br3 angle of 122.42° around the Cu atoms. Also, they have a Cu–Br2–Cu angle of 84.54° around Br2 and Cu–Br3–Cu angle of 85.03° around Br3 respectively. Moreover, the Cu atoms have four different Br–Cu–Br bond angles resulting in a distorted tetrahedral environment.

(Cu₂Br₃)_nⁿ⁻ polymeric ladders are isolated from each other, and one single ladder is surrounded by six stacks of TMA⁺ cations which run along the b axis (Fig. 1a and S3c†). This leads to a typical 1D structure in the crystal. TMA⁺ cations are held together with the ladder mainly by electrostatic interactions. The shortest distance between the N atom of a TMA⁺ cation and Br atom is found to be 4.275 Å. Also, the methyl carbons and the bromine atoms have a shortest contact of 3.595 Å which is even less than the sum of their van der Waal's radii of 3.95 Å.³⁹ The closest distance between cations is 4.003 Å found between C3 atoms in two adjacent stacks. Furthermore, the distance between the N atoms of successive cations in each stack is 6.548 Å, same as the length of the b axis.

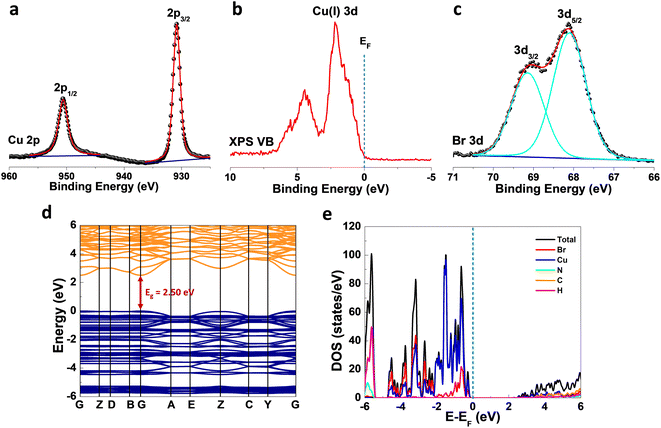
X-ray photoelectron spectroscopy (XPS) analysis of (TMA)Cu₂Br₃ was carried out to get further insight into the valence state of the elements. The Cu 2p photoemission showed clear peaks at binding energy values of ∼950.6 eV and ∼930.8 eV corresponding to Cu 2p_1/2 and Cu 2p_3/2, respectively, which indicates the exclusive presence of Cu(I) in (TMA)Cu₂Br₃ (Fig. 2a).⁴⁰ Moreover, the absence of any satellite features excluded the possibility of any trace of Cu(II) in (TMA)Cu₂Br₃. Furthermore, the valence-band (VB) photoemission signal was also collected to get the 3d features of Cu, and the spectrum indeed showed a prominent peak at ∼2.1 eV which is a characteristic photoemission signature from Cu 3d states of Cu(I) species, while the peak at ∼5.0 eV is primarily contributed by Br 4p with minor contributions from Cu 3d states, complementing the density of states (DOS) plot discussed below (Fig. 2b).^41,42 Br 3d photoemission showed two prominent peaks at ∼69.1 eV and ∼68.1 eV corresponding to Br 3d_3/2 and Br 3d_5/2, respectively, indicative of the presence of bromide ions in the sample (Fig. 2c).⁴⁰ Also, as expected from the chemical formula, the elemental stoichiometric ratio of Cu : Br was estimated to be 2 : 3 from the XPS data.

Fig. 2 Electronic structure of (TMA)Cu₂Br₃. (a) Cu2p XPS spectrum featuring spin–orbit coupled (∼19.8 eV) doublet signals (2p_3/2 and 2p_1/2). Raw spectral data points (black spheres) were duly fitted (red lines). (b) Valence band (VB) spectra showing a signal at ∼2.1 eV corresponding to the Cu(I) 3d state. The dotted vertical line represents the Fermi level (E_F). (c) Br3d XPS spectrum featuring spin–orbit coupled (∼1.0 eV) doublet signals (3d_5/2 and 3d_3/2). Raw spectral data points (black spheres) were duly fitted (cyan lines). (d) Electronic band structure calculated from DFT showing a direct bandgap (E_g) value of 2.50 eV at the gamma (G) point. (e) Density of states (DOS) plots exhibiting the total as well as atomic contributions. The dotted vertical line represents the Fermi level (E_F).

X-band electron paramagnetic resonance (EPR) spectra of the sample were collected in the temperature range of 100–300 K, and the data revealed no observable peak at any temperature (Fig. S4†), which further confirms the absence of any Cu(II) species in (TMA)Cu₂Br₃, thereby complementing the XPS investigations. To understand the electronic properties of (TMA)Cu₂Br₃, density functional theory (DFT) calculations were performed, and band structures (Fig. 2d) along with the density of states (DOS) plots (Fig. 2e) were extracted. (TMA)Cu₂Br₃ possessed a direct bandgap (E_g) of 2.50 eV with both the valence band maximum (VBM) and conduction band minimum (CBM) located at the gamma (G) point. This bandgap is comparable with those of other Cu(I) halide-based hybrid organic–inorganic perovskite-like systems such as (MA)₄Cu₂Br₆ (3.87 eV), [N(CH3)₄]₃[Cu₂Br₅] (3.08 eV), [N(C₂H₅)₄]₂[Cu₂Br₄] (3.09 eV), and [N(C₃H₇)₄]₂[Cu₄Br₆] (3.01 eV).^24,43 We performed the diffuse reflectance spectroscopy (DRS) measurements to get insight about the optical absorption properties of the (TMA)Cu₂Br₃ system. The spectrum shows the majority of its absorption in the UV region (200–350 nm) with the absorption maxima centered at around ∼275 nm and an absorption tail with very small intensity extending up to ∼460 nm (Fig. S5a†). Absorption in this lower energy region is so weak that practically it does not contribute to the color, and thus, (TMA)Cu₂Br₃ appears to be colorless under visible light; similar observations have already been reported in the literature.⁴⁴ Furthermore, the optical band gap of the material is calculated experimentally from the Tauc plot and is found to have an onset of absorption at 3.6 eV; however, upon closer inspection into the lower energy region, another absorption onset can be found at 2.65 eV corresponding to the weakly absorbing tail (Fig. S5b†). This value reasonably matches with the band gap predicted from the DFT calculations and the slight disagreement is a very common realization.⁴⁵

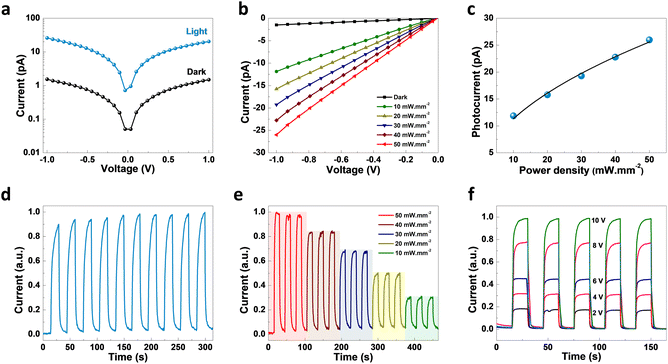
As revealed by the DOS plot, the VBM is predominantly composed of Cu 3d and Br 4p orbitals, while the CBM is mainly composed of Cu 4s and Br 4p orbitals (Fig. S6–S8†). Interestingly, little contribution from the organic part is realized in the VBM and CBM of (TMA)Cu₂Br₃. Notably, a relatively narrow band gap in the (TMA)Cu₂Br₃ system could facilitate efficient photon harvesting. Accordingly, a single crystal device was fabricated where two eutectic-gallium–indium (EGaIn) alloy spheres were used as contact electrodes and placed on two opposite edges of the crystal (Fig. S9†). The probes were then connected to the contact electrodes and electrical transport measurements were performed in a conventional two-probe set-up in the GaIn/(TMA)Cu₂Br₃/GaIn configuration under ambient conditions. The current–voltage (I–V) profiles were recorded in the dark and at three different wavelengths of laser irradiation (450 nm, 532 nm, and 808 nm) as well as with varied light intensity at each wavelength (Fig. 3, S10, and S11†). The dark current (I_dark) was measured to be I_dark ≈ 1.5 pA (V_bias = 1 V) and the best photoresponse was seen with the 450 nm laser, where I_light was measured to be as high as ∼26 pA, giving rise to the highest on/off ratio of ∼17.5 (Fig. 3a). A low I_dark is desirable for efficient photodetection and our extremely low I_dark value is indicative of the sensitivity of the device. Also, the good linearity and symmetric nature of all the I–V curves in the dark and under light illumination imply that an ohmic contact was consistently established between the crystal and the contact electrodes. In addition to this, an open-circuit voltage (V_oc) of −4.7 mV and a short-circuit current (I_sc) of 0.18 pA were recorded for the 450 nm laser irradiation. This V_oc indicates the offset of a built-in electric potential across the device, suggestive of a self-powered photodetector. A systematic variation of light power with the 450 nm laser was carried out and the corresponding I–V profiles were recorded (Fig. 3b). With increasing light intensity from 10 mW mm⁻² to 50 mW mm⁻², a gradual yet significant increment in the photocurrent was observed ranging from ∼12 pA to ∼26 pA, which is a direct consequence of the proportional relationship between the photogenerated charge-carriers and photon flux absorption. This dependency can be fitted using the power law, I_p = α × P^β, where I_p represents the photocurrent, α denotes a proportionality constant, P stands for incident light excitation power and β signifies the recombination of the photoexcited carriers.⁴⁶ The fitted curve suggests a sublinear relationship and the value of β was calculated to be 0.51 from the fit (Fig. 3c). It is noteworthy that such a fractional value of power dependence (0.5 < β < 1.0) arises probably due to the complexity of the processes of carrier generation, recombination, and trapping within the system. A similar finding was consistently obtained for the irradiation with 532 nm and 808 nm laser sources (Fig. S10a–c and S11a–c†).

Fig. 3 Photo-responsivity on the (TMA)Cu₂Br₃ crystal device. (a), Current–voltage (I–V) profiles in the dark and under light illumination (light wavelength of 450 nm and intensity of 50 mW.mm⁻²). (b), I–V curves at varying light intensities ranging from 10 mW.mm⁻² to 50 mW.mm⁻². (c), Plot of photocurrent variation with incident light intensity. Data points are fitted using the power law (black line). (d), Time-dependent photocurrent response at 50 mW.mm⁻² light intensity at 0 V bias (normalized plots). (e), Current as a function of time at different light irradiation intensities (0 V bias) (normalized plots). (f), Current as a function of time at different bias voltages (light intensity 50 mW.mm⁻²) (normalized plots).

To study the time response, current–time (I–t) plots were generated in self-powered mode (V_bias = 0 V, bulk photovoltaic) with a pulse bandwidth of 30 s per cycle. A reversible switching between the high and low conducting states was observed for both the laser irradiation sources, with the 450 nm laser having the best on/off ratio (Fig. 3d). Furthermore, the temporal response was recorded as a function of power, where the I–t plot depicts the gradual increment in photocurrent with increasing light intensity due to the increased population of photogenerated carriers (Fig. 3e). Similar behavior for the other laser sources was also noted (Fig. S10d, e, S11d and e†). The I–t plots were also recorded at different bias voltages, starting from 2 V to 10 V with similar pulse bandwidth (Fig. 3f, S10f, and S11f†), showing a continuous increase in I_light with increasing voltage, including the self-powered mode (0 V) (Fig. S12†). We calculated the responsivity (R) of (TMA)Cu₂Br₃ as a function of light irradiation intensity at 1 V bias voltage, and the dataset is presented in Table S9.† The cycling stability of the crystal device was tested upon turning on and off the 450 nm laser irradiation for 200 continuous cycles in self-powered mode (0 V bias). The photocurrent exhibits no significant change between the high and low conducting states, thus indicating excellent stability and reversibility (Fig. S13†). Also, the photocurrent measurements were carried out under the same testing conditions after storage in open air for 3 months without any encapsulation to validate its long-term environmental stability; the crystal device continued to work efficiently, maintaining nearly the same photocurrent response (Fig. S14†). Furthermore, the thermal stability of the (TMA)Cu₂Br₃ system was investigated by thermogravimetric analysis (TGA) and the crystal showed excellent stability up to 550 K (Fig. S15†).

Discussion

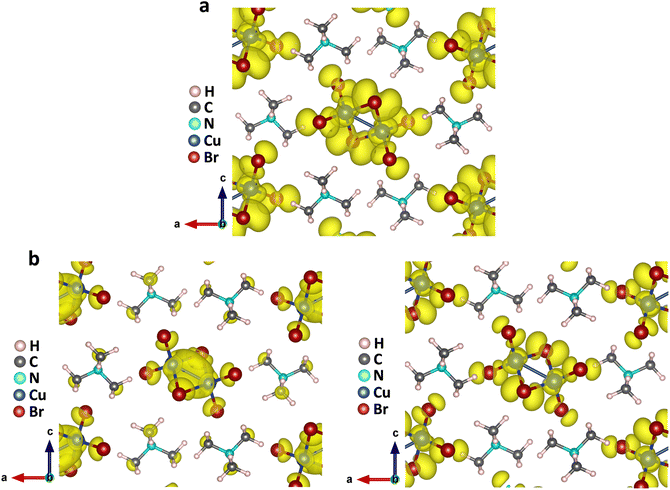
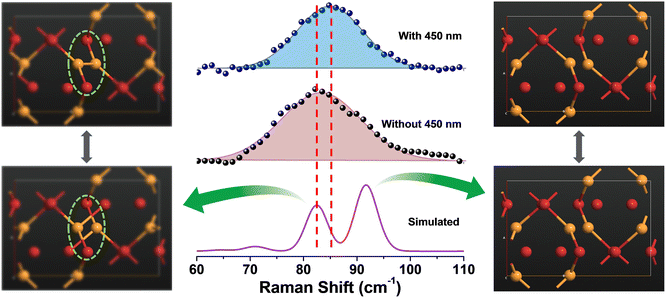
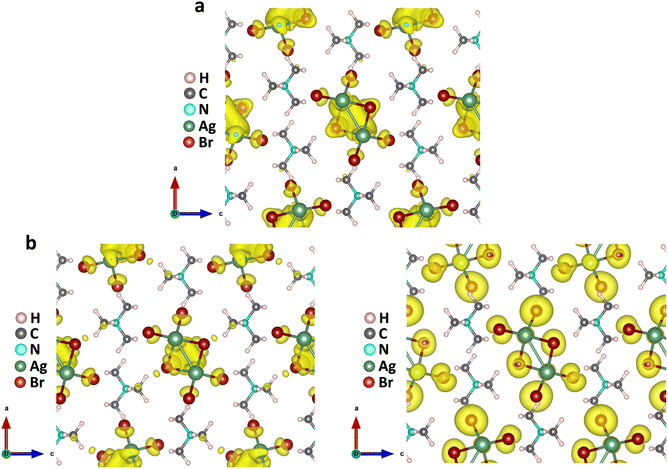
The above findings on the photoresponsive characteristics are really exciting for such a Cu(I)-based hybrid perovskite-like material, certainly rendering our (TMA)Cu₂Br₃ promising for photodetector applications. The question remains: what drives the photoconduction in (TMA)Cu₂Br₃? From the DOS plots, it is clear that the VBM and CBM were primarily composed of Cu 3d and Cu 4s states and, therefore, can be assigned to an implication of the presence of cuprophilic interactions as was suggested by the single-crystal X-ray diffraction (SCXRD) analysis. To understand the mechanistic insights, we have estimated exciton binding energy and reorganization energy in the (TMA)Cu₂Br₃ system using DFT calculations. We found an exciton binding energy of ∼600 meV and reorganization energy values due to addition and removal of one electron per unit cell in the system that were estimated to be −0.087 eV and −0.575 eV, respectively. Such a distinctive energy difference in the reorganization energy along with a large exciton binding energy suggest that the electron–hole recombination in (TMA)Cu₂Br₃ is apparently a slow process. Addition of electrons and holes in the (TMA)Cu₂Br₃ system changed the respective DOS plots as well as the band structures, though the VBM and CBM were primarily composed of Cu and Br states (Fig. S16 and S17†). Looking at the charge-density plot after electronic excitation, (and comparing it with the same before electronic excitation), the hole density near the VBM was mainly found to be distributed over the Cu and Br atoms and so was the distribution of electrons near the CBM (Fig. 4 and S18†). More importantly, direct visualization of the Cu–Cu interaction is seen in the charge-density plot viz. orbital overlap which is remarkable in the sense that without excitation no direct orbital overlap was evidenced. Therefore, we would like to attribute the efficient photoconduction by the (TMA)Cu₂Br₃ system to a novel phenomenon – excitonic cuprophilic interactions.

Fig. 4 Visualizing the excitonic cuprophilic interactions in (TMA)Cu₂Br₃. (a) Charge density plot depicting the distribution of electron charge before electronic excitation (electron accumulation is represented by the yellow isosurface). (b) Charge density plot depicting the distribution of electron charge at the CBM, upon addition of one electron in the system (electron accumulation is represented by the yellow isosurface) (left panel). The charge density plot depicting the distribution of hole charge at the VBM, upon removal of one electron (addition of one hole) from the system (hole accumulation is represented by the yellow isosurface) (right panel) is shown.

In order to experimentally probe the excitonic cuprophilic interactions in (TMA)Cu₂Br₃, Raman spectroscopic measurements were performed and compared with the simulated Raman spectrum for tracking the behavioral changes of the Cu(I)–Cu(I) environment within the inorganic chain under additional photon excitation. The experimental Raman spectra (λ_exc = 632.8 nm) exhibited a broad signal at ∼82.5 cm⁻¹, with a shoulder at ∼90.3 cm⁻¹ (Fig. 5). The simulated Raman spectrum suggested that the former phonon mode was centered around Cu(I)–Cu(I) bonds within an inorganic chain (Fig. 5 and Movies S1–S2†). Interestingly, when an additional laser excitation of 450 nm (which has energy greater than the estimated band-gap of the material of ∼2.50 eV) was incident along with λ_exc, this phonon mode underwent a significant spectral blue shift by ∼2.6 cm⁻¹ (Fig. 5), while the rest of the phonon signatures remained unperturbed (Fig. S19†). This blue shift is in agreement with the theoretical calculations, corroborating the increased electronic charge density around the Cu(I)–Cu(I) region after electron excitation. Therefore, the above observations present direct evidence of photon irradiation influencing cuprophilic interactions within our (TMA)Cu₂Br₃ system, hence implying a causality towards the origin of its photoresponsive behavior.

Fig. 5 Experimental validation using Raman spectroscopy. Comparison between the simulated Raman spectrum and the experimental spectra without and with additional 450 nm laser irradiation with a ∼632.8 nm laser being the excitation source (λ_exc). The additional irradiation resulted in a ∼2.6 cm⁻¹ spectral blue shift (middle panel). The simulated peak at ∼82.53 cm⁻¹ represents the phonon mode exhibiting continuous breaking and making of the Cu–Cu bond, rendering it ideal to monitor the cuprophilic interactions (left panel). Visualization of the phonon mode at ∼91.68 cm⁻¹ (right panel). Copper and bromine atoms are represented by yellow and red coloured spheres.

It is important to find out the influencing factors that modulate the extent of metallophilicity. In that regard, a systematic comparison was investigated, wherein, the single crystals of the silver analogue of (TMA)Cu₂Br₃, formulated as (TMA)Ag₂Br₃, have also been synthesized following a similar reaction protocol. The crystal structure was determined using single crystal X-ray diffraction (SCXRD) at 150 K and the crystal parameters are listed in Tables S5–S8.† The crystal is solved in orthorhombic space group Pnma, having the following unit cell parameters: a = 16.535(2) Å, b = 7.0771(9) Å, c = 9.6517(11) Å, and V = 1129.4(2) ų. Structurally, (TMA)Ag₂Br₃ is composed of inorganic polymeric chains of (Ag₂Br₃)_nⁿ⁻ anions and organic TMA⁺ cations, where both are electrostatically bound together giving stability to the system (Fig. 6a and S20a–c†). This is quite similar to the previously synthesized (TMA)Cu₂Br₃. The chains are separated from each other and a single chain is surrounded by six stacks of TMA⁺ cations along the b-axis. This relative orientation manifested into a typical 1D structure of the crystal (Fig. 6b and S21a†). Furthermore, each Ag(I) in a chain is coordinated to four Br⁻ anions in a tetrahedral manner. It also consists of three different Br atoms, one central tetra-coordinated and two different terminal bi-coordinated bromines to be specific (Fig. 6c, S21b and c†). The smallest Ag–Ag distance in the crystal is found to be 3.048 Å which falls under the conventional definition of argentophilic interaction between neighboring Ag atoms.

Fig. 6 Crystal structure of (TMA)Ag₂Br₃. (a) Arrangements of cations (TMA) and anionic chains as viewed along the crystallographic b-axis (slightly tilted, H atoms are omitted for clarity). (Ag₂Br₃)_nⁿ⁻ polymeric ladders are isolated from one another, and each ladder is surrounded by six stacks of TMA cations which run along the b axis. (b) Zoomed-in view of the inorganic (Ag₂Br₃)_nⁿ⁻ chain along the crystallographic c-axis. (c) Coordination environment around Ag depicting the distorted tetrahedral geometry as well as the Ag–Ag bond (top panel) and distinctive bonding scenario of three Br (Br1, Br2 and Br3) around Ag (bottom panel), as viewed from the crystallographic a-axis.

To dive into the electronic properties of (TMA)Ag₂Br₃, similar density functional theory (DFT) calculations were executed to shed light on the band structure along with partial charge density plots. (TMA)Ag₂Br₃ is shown to have a direct band gap (E_g) value of 2.98 eV at the crystallographic gamma (G) point (Fig. S22a†). Furthermore, density of states (DOS) plots were generated and they showed that both the VBM and CBM primarily consist of Ag 4d and Br 4p orbitals (Fig. S22b†). Here, it is noteworthy to mention that, contrary to (TMA)Cu₂Br₃, where the VBM has a greater contribution from Cu compared to Br, (TMA)Ag₂Br₃ shows the opposite trend (more contribution from Br than Ag). Also, there is a nominal contribution of the organic part towards the VBM and CBM. The charge density plot in the ground state of (TMA)Ag₂Br₃ depicted accumulation of electronic charge mainly on Ag and Br atoms (Fig. 7a and S23a†). Interestingly, unlike (TMA)Cu₂Br₃, there is already electron accumulation in the Ag–Ag region (orbital overlap) in (TMA)Ag₂Br₃, indicative of strong argentophilic interaction in the ground state itself. After electronic excitation, both electronic density near the CBM and hole density near the VBM remained distributed mainly over Ag and Br atoms (Fig. 7b and S23b†). Moreover, electron density accumulation is mostly unaltered in the Ag–Ag region showing retention of argentophilicity within the system. Keeping our DFT results from the perspective of molecular orbital theory (MOT), it can be rationalized that during electron excitation, electrons from the antibonding orbitals of the Cu–Cu bond are expected to be removed resulting in an increase in the bond order viz. stronger orbital overlap, whereas considering the strong orbital overlap in the ground state itself, electrons are expected to come out of the bonding orbitals of the Ag–Ag bond.

Fig. 7 Visualizing the argentophilic interactions in (TMA)Ag₂Br₃. (a) Charge density plot depicting the distribution of electron charge before electronic excitation (electron accumulation is represented by the yellow isosurface). (b) Distribution of additional electronic charge density (at the CBM) due to addition of an extra electron (left panel). Distribution of hole density (at the VBM) due to removal of an electron (right panel). Hydrogen, carbon, nitrogen, silver, and bromine atoms are represented by pink, grey, cyan, green, and red coloured spheres.

Photocurrent measurements were also performed for the (TMA)Ag₂Br₃ system in both the dark and under 450 nm of laser irradiation. From current–voltage (I–V) plots, dark current (I_dark) was measured to be I_dark ≈ 4.4 pA (V_bias = 1 V), whereas, interestingly, under 450 nm light irradiation no significant modulation in the current (I_light) is observed (Fig. S25a†). This demonstrates the lack of responsivity of this particular material towards light irradiation. Furthermore, for systematic comparison, I–V measurements were carried out at variable light intensities, and the compound remains non-responsive at all of the above light intensities (Fig. S25b†). To support these findings, current–time (I–t) experiments were also designed under 450 nm light (50 mW mm⁻²), where no reversible switching between any high-conducting and low-conducting states was observed, confirming the absence of photoresponse in (TMA)Ag₂Br₃ (Fig. S25c†). In (TMA)Ag₂Br₃, since there is already strong electronic charge accumulation in the Ag–Ag region in the ground state (argentophilic interaction), this system differs electronically from the Cu analogue (TMA)Cu₂Br₃, and is, therefore, unable to show current modulation upon irradiation of light – clearly endorsing our claim on the excitonic cuprophilic interactions.

Conclusions

In summary, we present a lead-free Cu(I)-based organic–inorganic hybrid semiconductor, (TMA)Cu₂Br₃, consisting of a rare structural arrangement of the inorganic chain, wherein the Cu(I)–Cu(I) distance was observed to be unusually short. Our electrical conductivity measurements under light irradiation on the single-crystal device clearly present a prospect of using (TMA)Cu₂Br₃ as a favorable candidate for the fabrication of highly stable and environment-friendly photodetectors. DFT calculations revealed a direct band gap electronic structure for the (TMA)Cu₂Br₃ system and unraveled features of excitonic cuprophilic interactions which were further confirmed by combined experimental-simulated Raman spectral analysis. In contrast, the (TMA)Ag₂Br₃ system revealed orbital overlap between the Ag atoms, both in the ground state as well as upon electron excitation. Identification of an excitonic cuprophilicity is an impressive observation which certainly encourages gaining further insights on this still elusive concept. Such an excitonic effect on metal–metal bonding offers great potential for developing structure–property relationships in similar hybrid organic–inorganic systems for various other optoelectronic applications.

Experimental

Materials

Copper(I) bromide (CuBr; ≥98%), silver(I) bromide (AgBr; 99%), tetramethylammonium bromide (TMAB; ≥98%) and hydrobromic acid (48 wt% in H₂O; ≥99.99%) were purchased from Sigma-Aldrich. Acetone (HPLC grade), DMF (HPLC grade), DMSO (HPLC grade) and hypophosphorous acid (H₃PO₂; 50 wt% in H₂O) were purchased from RANKEM (India). All chemicals were used without any further purification.

Synthesis of (TMA)Cu₂Br₃ single crystals

A mixture of CuBr (143.45 mg, 1 mmol) and TMAB (154.05 mg, 1 mmol) was taken in a 15 mL teflon-lined vessel and dissolved in 3 mL acetone. This was followed by the addition of 500 μL of H₃PO₂ to prevent the oxidation of Cu(I) to Cu(II). Subsequently, 1 mL of HBr was added to the reaction mixture and the vessel was sealed in a stainless-steel autoclave. Thereafter, it was heated at 60 °C for 1 h in an oven and finally, the reaction mixture was allowed to cool down slowly to room-temperature for 24 h. Colourless needle-like single crystals of (TMA)Cu₂Br₃ were obtained, collected through filtration and washed with acetone, followed by drying at 100 °C for 12 h.

Synthesis of (TMA)Ag₂Br₃ single crystals

(TMA)Ag₂Br₃ was synthesized following a slightly different reaction protocol. A mixture of AgBr (187.77 mg, 1 mmol) and TMAB (462.15 mg, 3 mmol) was taken in a 30 mL glass vessel and dissolved in a solvent mixture of 12 mL DMF, 4 mL DMSO and 4 mL acetone. This was followed by the addition of 100 μL of H₃PO₂ to prevent areal oxidation. Subsequently, it was heated at 60 °C for 6 h in an oil bath and then the solution was filtered through a ∼0.22μ syringe filter. Finally, the reaction mixture was allowed to cool down slowly to room-temperature for 24 h. Colourless needle-like single crystals of (TMA)Ag₂Br₃ were obtained, filtered and washed with acetone, followed by drying at 100 °C for 12 h.

Characterization

Crystal data for the single crystals were collected on a Bruker Smart Apex Duo diffractometer at 296 K for (TMA)Cu₂Br₃ and at 150 K for (TMA)Ag₂Br₃ using Mo Kα radiation (λ = 0.71073 Å). Absorption corrections were performed using the APEX3 software. The crystal structure was solved by the direct method and refined by full-matrix least-squares on F2(SHELXL-2014/6) and Olex2 with a ShelXT2 structure solution program.^47–49 Details of the structural refinement are presented in the ESI.† XPS spectra were recorded by using a Thermo Fisher Scientific ESCALAB Xi+. EPR was recorded using an EMX micro X BRUKER EPR spectrophotometer with an X-band on solid samples. TGA profiles were recorded using a PerkinElmer thermal analyzer STA 6000 model. Electrical transport measurements on crystals were carried out using a Keithley 4200 SCS parameter analyzer system assembled with an Everbeing probe station using eutectic gallium indium (EGaIn) alloys as contact electrodes. Light irradiation experiments were carried out under ambient conditions, using 450 nm, 532 nm and 808 nm 1 W fiber coupled diode lasers supplied by Specialise Instruments Intelligent Solutions (India). Raman spectra (λ_exc = 632.8 nm) were recorded on a Raman microscope (LabRAM HR, HoribaJobinYvon) using a 50× objective lens (spectral resolution of the system is ∼1 cm⁻¹).

Computational studies

A detailed computational study was performed using first principles electronic structure calculations based on density functional theory (DFT) as implemented in the Vienna Ab initio Simulation Package (VASP).⁵⁰ The unit cell structure was modelled from the experimentally produced crystal structure information and subsequently relaxed to obtain the ground state geometric configuration. The generalized gradient approximation (GGA) exchange–correlation potential with Perdew, Burke and Ernzerhof (PBE) parametrization⁵¹ was used to optimize the structure. The on-site Coulomb interaction for 3d electrons has been considered using the DFT + U method as introduced by Liechtenstein.⁵² Our calculation uses an effective U = 4 eV for Cu 3d states. The electronic properties are calculated from the converged optimized geometry. The self-consistent energy convergence criteria were set to be 10⁻⁵ eV, and the accuracy of force convergence on all atoms was set to 0.01 eV A⁻¹. The Brillouin zone sampling was performed using the gamma-centered k-point grid with a k-point mesh of 5 × 3 × 2. A Gaussian smearing of 0.01 eV is used to optimize the orbitals, calculate the band structure and extracting the atom projected as well as the total density of states of the system. To estimate the electron and hole density states during the photo-excitation process, we further studied the charged system by increasing (electron) and decreasing (hole) one electron from the total number of valence electrons. The partial (band decomposed) charge density method was used to separate and plot the electron/hole density. The ionization potential (IP) and electron affinity (EA) were calculated using the Koopmans theorem, from which the exciton binding energy (EBE) was estimated using the following formula: EBE = IP − EA − E_g, where E_g represents the electronic band gap of the system. Finally, the electron and hole reorganization energy was calculated from the optimized energy of the charged systems. To calculate the Raman spectrum, we utilized the QuantumATK⁵³ atomic-scale modelling software and computed all phonon modes by determining the dynamical matrix and susceptibility derivatives.⁵⁴ This is accomplished using the central finite difference method with an atomic displacement of 0.01 Angstrom in a repeated cell, also known as the frozen-phonon or super-cell method. We evaluate all vibrational phonon modes at the gamma point (0 0 0) only as a fractional q-point.

Data availability

The datasets supporting this article have been uploaded as part of the ESI.†

Author contributions

N. H. prepared the samples, carried out the experiments, and performed electrical transport measurements along with S. S., under the guidance of N. B. S. N. performed DFT calculations under the supervision of K. T. N. B. conceived and supervised the research project and wrote the manuscript with input from the co-authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support from SERB (India, Project No. CRG/2020/001804) and IISER Pune, India is gratefully acknowledged. K. T. acknowledges VGST (GRD No. 536) for financial support. K. T. and S. N. acknowledge C-DAC for providing the computational facility in PARAMUtkarsh. N. H. and S. S. thank IISER Pune for providing research fellowships. The authors acknowledge the DST-FIST grant (SR/FST/CS-II/2019/105) for the EPR facility. N. H. acknowledges Mr Jabed Hossain and Mr Radha Krishna Kashyap for help in solving crystal structures and light irradiation experiments.

Notes and references

1. Y. Zhao and K. Zhu, Organic–inorganic hybrid lead halide perovskites for optoelectronic and electronic applications, Chem. Soc. Rev., 2016, 45, 655–689.
2. B. Saparov and D. B. Mitzi, Organic–inorganic perovskites: structural versatility for functional materials design, Chem. Rev., 2016, 116, 4558–4596.
3. C. C. Stoumpos, C. M. M. Soe, H. Tsai, W. Nie, J.-C. Blancon, D. H. Cao, F. Liu, B. Traoré, C. Katan, J. Even, A. D. Mohite and M. G. Kanatzidis, High members of the 2D ruddlesden-popper halide perovskites: synthesis, optical properties, and solar cells of (CH₃(CH₂)₃NH₃)₂(CH₃NH₃)₄Pb₅I₁₆, Chem, 2017, 2, 427–440.
4. S. Hu, Z. Ren, A. B. Djurišić and A. L. Rogach, Metal halide perovskites as emerging thermoelectric materials, ACS Energy Lett., 2021, 6, 3882–3905.
5. Z.-X. Zhang, H.-Y. Zhang, W. Zhang, X.-G. Chen, H. Wang and R.-G. Xiong, Organometallic-based hybrid perovskite piezoelectrics with a narrow band gap, J. Am. Chem. Soc., 2020, 142, 17787–17794.
6. S. Wang, L. Li, W. Weng, C. Ji, X. Liu, Z. Sun, W. Lin, M. Hong and J. Luo, Trilayered lead chloride perovskite ferroelectric affording self-powered visible-blind ultraviolet photodetection with large zero-bias photocurrent, J. Am. Chem. Soc., 2020, 142, 55–59.
7. J. Liu, F. Xia, D. Xiao, F. J. García de Abajo and D. Sun, Semimetals for high-performance photodetection, Nat. Mater., 2020, 19, 830–837.
8. X. Zhu, Y. Lin, Y. Sun, M. C. Beard and Y. Yan, Lead-halide perovskites for photocatalytic α-alkylation of aldehydes, J. Am. Chem. Soc., 2019, 141, 733–738.
9. X.-N. Hua, W.-Q. Liao, Y.-Y. Tang, P.-F. Li, P.-P. Shi, D. Zhao and R.-G. Xiong, A room-temperature hybrid lead iodide perovskite ferroelectric, J. Am. Chem. Soc., 2018, 140, 12296–12302.
10. I. Abdelwahab, G. Grinblat, K. Leng, Y. Li, X. Chi, A. Rusydi, S. A. Maier and K. P. Loh, Highly enhanced third-harmonic generation in 2D perovskites at excitonic resonances, ACS Nano, 2018, 12, 644–650.
11. T. Wu, R. Mukherjee, O. S. Ovchinnikova, L. Collins, M. Ahmadi, W. Lu, N.-G. Kang, J. W. Mays, S. Jesse, D. Mandrus and B. Hu, Metal/ion interactions induced p–i–n junction in methylammonium lead triiodide perovskite single crystals, J. Am. Chem. Soc., 2017, 139, 17285–17288.
12. S. Yakunin, D. N. Dirin, Y. Shynkarenko, V. Morad, I. Cherniukh, O. Nazarenko, D. Kreil, T. Nauser and M. V. Kovalenko, Detection of gamma photons using solution-grown single crystals of hybrid lead halide perovskites, Nat. Photon., 2016, 10, 585–589.
13. H. Zhu, Y. Fu, F. Meng, X. Wu, Z. Gong, Q. Ding, M. V. Gustafsson, M. T. Trinh, S. Jin and X. Y. Zhu, Lead halide perovskite nanowire lasers with low lasing thresholds and high quality factors, Nat. Mater., 2015, 14, 636–642.
14. H. Cho, S.-H. Jeong, M.-H. Park, Y.-H. Kim, C. Wolf, C.-L. Lee, J. H. Heo, A. Sadhanala, N. Myoung, S. Yoo, S. H. Im, R. H. Friend and T.-W. Lee, Overcoming the electroluminescence efficiency limitations of perovskite light-emitting diodes, Science, 2015, 350, 1222–1225.
15. Z. Jin, Y. Peng, Y. Fang, Z. Ye, Z. Fan, Z. Liu, X. Bao, H. Gao, W. Ren, J. Wu, G. Ma, Q. Chen, C. Zhang, A. V. Balakin, A. P. Shkurinov, Y. Zhu and S. Zhuang, Photoinduced large polaron transport and dynamics in organic–inorganic hybrid lead halide perovskite with terahertz probes, Light: Sci. Appl., 2022, 11, 209.
16. Z. Fang, L. Wang, X. Mu, B. Chen, Q. Xiong, W. D. Wang, J. Ding, P. Gao, Y. Wu and J. Cao, Grain boundary engineering with self-assembled porphyrin supramolecules for highly efficient large-area perovskite photovoltaics, J. Am. Chem. Soc., 2021, 143, 18989–18996.
17. T. Leijtens, A. R. Srimath Kandada, G. E. Eperon, G. Grancini, V. D'Innocenzo, J. M. Ball, S. D. Stranks, H. J. Snaith and A. Petrozza, Modulating the electron–hole interaction in a hybrid lead halide perovskite with an electric field, J. Am. Chem. Soc., 2015, 137, 15451–15459.
18. A. Babayigit, A. Ethirajan, M. Muller and B. Conings, Toxicity of organometal halide perovskite solar cells, Nat. Mater., 2016, 15, 247–251.
19. J. Luo, X. Wang, S. Li, J. Liu, Y. Guo, G. Niu, L. Yao, Y. Fu, L. Gao, Q. Dong, C. Zhao, M. Leng, F. Ma, W. Liang, L. Wang, S. Jin, J. Han, L. Zhang, J. Etheridge, J. Wang, Y. Yan, E. H. Sargent and J. Tang, Efficient and stable emission of warm-white light from lead-free halide double perovskites, Nature, 2018, 563, 541–545.
20. X.-G. Zhao, D. Yang, J.-C. Ren, Y. Sun, Z. Xiao and L. Zhang, Rational design of halide double perovskites for optoelectronic applications, Joule, 2018, 2, 1662–1673.
21. W. Ke and M. G. Kanatzidis, Prospects for low-toxicity lead-free perovskite solar cells, Nat. Commun., 2019, 10, 965.
22. H. Zhu, J. Ma, P. Li, S. Zang, Y. Zhang and Y. Song, Low-dimensional Sn-based perovskites: evolution and future prospects of solar cells, Chem, 2022, 8, 2939–2960.
23. W. Liu, Y. Fang, G. Z. Wei, S. J. Teat, K. Xiong, Z. Hu, W. P. Lustig and J. Li, A family of highly efficient Cu(I)-based lighting phosphors prepared by a systematic, bottom-up synthetic approach, J. Am. Chem. Soc., 2015, 137, 9400–9408.
24. S. Chen, J. Gao, J. Chang, Y. Li, C. Huangfu, H. Meng, Y. Wang, G. Xia and L. Feng, Family of highly luminescent pure ionic copper(I) bromide based hybrid materials, ACS Appl. Mater. Interfaces, 2019, 11, 17513–17520.
25. K. Zhu, Z. Cheng, S. Rangan, M. Cotlet, J. Du, L. Kasaei, S. J. Teat, W. Liu, Y. Chen, L. C. Feldman, D. M. O'Carroll and J. Li, A new type of hybrid copper iodide as nontoxic and ultrastable LED emissive layer material, ACS Energy Lett., 2021, 6, 2565–2574.
26. X. Zhan, X. Jiang, P. Lv, J. Xu, F. Li, Z. Chen and X. Liu, Enhanced structural stability and pressure-induced photoconductivity in two-dimensional hybrid perovskite (C₆H₅CH₂NH₃)₂CuBr₄, Angew. Chem., Int. Ed., 2022, 61, e202205491.
27. Z. Ma, X. Ji, S. Lin, X. Chen, D. Wu, X. Li, Y. Zhang, C. Shan, Z. Shi and X. Fang, Recent advances and opportunities of eco-friendly ternary copper halides: a new superstar in optoelectronic applications, Adv. Mater., 2023, 2300731.
28. N. Mirzadeh, S. H. Privér, A. J. Blake, H. Schmidbaur and S. K. Bhargava, Innovative molecular design strategies in materials science following the aurophilicity concept, Chem. Rev., 2020, 120, 7551–7591.
29. H. Schmidbaur and A. Schier, Argentophilic interactions, Angew. Chem., Int. Ed., 2015, 54, 746–784.
30. J.-M. Poblet and M. Bénard, Cuprophilicity, a still elusive concept: a theoretical analysis of the ligand-unsupported CuI–CuI interaction in two recently reported complexes, Chem. Commun., 1998, 1179–1180.
31. N. V. S. Harisomayajula, S. Makovetskyi and Y.-C. Tsai, Cuprophilic interactions in and between molecular entities, Chem.–Eur. J., 2019, 25, 8936–8954.
32. M. T. Buckner and D. R. McMillin, Photoluminescence from copper(I) complexes with low-lying metal-to-ligand charge transfer excited states, J. Chem. Soc.: Chem. Commun., 1978, 759–761.
33. J. M. Zuo, M. Kim, M. O'Keeffe and J. C. H. Spence, Direct observation of d-orbital holes and Cu–Cu bonding in Cu₂O, Nature, 1999, 401, 49–52.
34. Q. Benito, X. F. Le Goff, S. Maron, A. Fargues, A. Garcia, C. Martineau, F. Taulelle, S. Kahlal, T. Gacoin, J.-P. Boilot and S. Perruchas, Polymorphic copper iodide clusters: insights into the mechanochromic luminescence properties, J. Am. Chem. Soc., 2014, 136, 11311–11320.
35. J. Nitsch, F. Lacemon, A. Lorbach, A. Eichhorn, F. Cisnetti and A. Steffen, Cuprophilic interactions in highly luminescent dicopper(i)–NHC–picolyl complexes – fast phosphorescence or TADF?, Chem. Commun., 2016, 52, 2932–2935.
36. L. Zhang, X.-X. Li, Z.-L. Lang, Y. Liu, J. Liu, L. Yuan, W.-Y. Lu, Y.-S. Xia, L.-Z. Dong, D.-Q. Yuan and Y.-Q. Lan, Enhanced cuprophilic interactions in crystalline catalysts facilitate the highly selective electroreduction of CO₂ to CH₄, J. Am. Chem. Soc., 2021, 143, 3808–3816.
37. L.-C. An, X. Li, Z.-G. Li, Q. Li, P. J. Beldon, F.-F. Gao, Z.-Y. Li, S. Zhu, L. Di, S. Zhao, J. Zhu, D. Comboni, I. Kupenko, W. Li, U. Ramamurty and X.-H. Bu, Plastic bending in a semiconducting coordination polymer crystal enabled by delamination, Nat. Commun., 2022, 13, 6645.
38. J. R. Boehm, A. L. Balch, K. F. Bizot and J. H. Enemark, Oxidation of 1,1-dimethylhydrazine by cupric halides. Isolation of a complex of 1,1-dimethyldiazene and a salt containing the 1,1,5,5-tetramethylformazanium ion, J. Am. Chem. Soc., 1975, 97, 501–508.
39. L. Pauling, The Nature of the Chemical Bond, and the Structure of Molecules and Crystals: An Introduction to Modern Structural Chemistry, Cornell University Press, 1940.
40. R. P. Vasquez, CuBr by XPS, Surf. Sci. Spectra, 1993, 2, 144–148.
41. R. Matzdorf, J. Skonieczny, J. Westhof, H. Engelhard and A. Goldmann, Band structure and optical properties of CuBr: new photoemission results, J. Phys.: Cond. Matter, 1993, 5, 3827.
42. S. Hüfner, Photoelectron Spectroscopy: Principles and Applications, Springer Science & Business Media, 2013.
43. H. Peng, S. Yao, Y. Guo, R. Zhi, X. Wang, F. Ge, Y. Tian, J. Wang and B. Zou, Highly efficient Self-Trapped Exciton Emission of a (MA)₄Cu₂Br₆ Single Crystal, J. Phys. Chem. Lett., 2020, 11, 4703–4710.
44. D. A. Popy, T. D. Creason, Z. Zhang, D. J. Singh and B. Saparov, Electronic structures and optical properties of (Ph₄P)MX₂ (M = Cu, Ag; X = Cl, Br), J. Solid State Chem., 2022, 316, 123626.
45. J. P. Perdew and M. Levy, Physical content of the exact kohn-sham orbital energies: band gaps and derivative discontinuities, Phys. Rev. Lett., 1983, 51, 1884–1887.
46. A. Rose, Concepts in Photoconductivity and Allied Problems, Interscience publishers, 1963.
47. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, OLEX2: a complete structure solution, refinement and analysis program, J. Appl. Cryst., 2009, 42, 339–341.
48. G. Sheldrick, Crystal structure refinement with SHELXL, Acta Cryst. Sec. C, 2015, 71, 3–8.
49. A. Spek, Single-crystal structure validation with the program PLATON, J. Appl. Cryst., 2003, 36, 7–13.
50. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
51. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
52. A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467–R5470.
53. S. Smidstrup, T. Markussen, P. Vancraeyveld, J. Wellendorff, J. Schneider, T. Gunst, B. Verstichel, D. Stradi, P. A. Khomyakov, U. G. Vej-Hansen, M.-E. Lee, S. T. Chill, F. Rasmussen, G. Penazzi, F. Corsetti, A. Ojanperä, K. Jensen, M. L. N. Palsgaard, U. Martinez, A. Blom, M. Brandbyge and K. Stokbro, QuantumATK: an integrated platform of electronic and atomic-scale modelling tools, J. Phys. Condens. Matter., 2020, 32, 015901.
54. D. Porezag and M. R. Pederson, Infrared intensities and Raman-scattering activities within density-functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 7830–7836.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2253455 and 2309331. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc06255d

---