Open Access Article
Open Access ArticleIn-depth theoretical analysis of the influence of an external electric field on charge transport parameters†
Gui-Ya
Qin
a,
Xiao-Qi
Sun
b,
Rui
Wang
a,
Jing-Fu
Guo
 b,
Jian-Xun
Fan
c,
Hui
Li
b,
Jian-Xun
Fan
c,
Hui
Li
 a,
Lu-Yi
Zou
a,
Lu-Yi
Zou
 a and
Ai-Min
Ren
a and
Ai-Min
Ren
 *a
*a
aCollege of Chemistry, Jilin University, Changchun 130023, China. E-mail: renam@jlu.edu.cn
bSchool of Physics, Northeast Normal University, Changchun 130024, China
cCollege of Chemistry and Materials Science, Weinan Normal University, Weinan 714000, China
First published on 2nd February 2024
Abstract
It is important to develop materials with environmental stability and long device shelf life for use in organic field-effect transistors (OFETs). The microscopic, molecular-level nature of the organic layer in OFETs is not yet well understood. The stability of geometric and electronic structures and the regulation of the external electric field (EEF) on the charge transport properties of four typical homogeneous organic semiconductors (OSCs) were investigated by density functional theory (DFT). The results showed that under the EEF, the structural changes in single-bond linked oligomers were more sensitive and complex than those of condensed molecules, and there were non-monotonic changes in their reorganization energy (λ) during charge transport under an EEF consisting of decreases and then increases (Series D). The change in λ under an EEF can be preliminarily and qualitatively determined by the change in the frontier molecular orbitals (FMOs) – the number of C-atoms with nonbonding characteristics. For single-bonded molecules, the transfer integral is basically unchanged under a low EEF, but it will greatly change at a high EEF. Because the structure and properties of the molecule will greatly change under different EEFs, the effect of an EEF should be fully considered when determining the intrinsic mobility of OSCs, which could cause a deviation 0.3–20 times in mobility. According to detailed calculations, one heterogeneous oligomer, TH-BTz, was designed. Its λ can be greatly reduced under an EEF, and the change in the energy level of FMOs can be adjusted to different degrees. This study provides a reasonable idea for verification of the experimental mobility value and also provides guidance for the directional design of stable high-mobility OSCs.
1 Introduction
Compared with inorganic materials, organic materials such as small molecules and polymers are inexpensive with satisfactory solubility, strong mechanical flexibility, and excellent film-forming capability.1–6 Organic semiconductors (OSCs) have been greatly developed over the past few decades to harness these advantages. With the rapid development of high-performance OSC devices, organic materials are widely used in organic field-effect transistors (OFETs),7,8 organic thin-film transistors (OTFTs),9,10 organic light-emitting transistors (OLETs),11,12 sensors,13 flexible displays,14 and wearable electronic devices.4,15,16OFETs are quite important as active components in circuits and sensors, and also exhibit considerable application potential in artificial intelligence, deep learning algorithms, and artificial skin sensors. The rapid development of material design and synthesis, and the continuous expansion of basic knowledge has established the applications of OFETs. One limiting factor of OFETs is that there is insufficient carrier mobility (μ) of organic small molecules in the active layer of OSC devices, and small molecules and polymers with a charge carrier mobility greater than 1 cm2 V−1 s−1 are desired for practical applications. The charge carrier mobility in OFETs has exceeded 10 cm2 V−1 s−1, which outperforms the commercial amorphous Si FETs and is sufficient for the electric performance required for practical device applications.17,18 However, these achievements are lackluster when compared to inorganic materials, as there are few organic materials with mobility above 1 cm2 V−1 s−1. The low mobility and high power consumption, such as huge contact resistance, remain a hindrance limiting the development of OFETs.
Transistors are variable current switches that function by adjusting the carriers of active organic material with the assistance of an external electric field (EEF).19,20 For some OFET devices, chemical instabilities result when active organic materials are exposed to atmospheric species and light. Hence, there is an urgent need to develop materials with environmental stability and long device shelf life. According to the structure of FETs, common OSCs are often perpendicularly grown on the substrate in edge-on style, such as pentacene,21,22 2,6-diphenylanthracene,23,24 C8-BTBT,25 and others.26–29 Because the insulating layer is thicker than the organic molecular layer (in general, there are 1–2 organic molecular layers), especially in the OTFT, and the distance between the source and drain electrodes is much larger than the insulating layer thickness, the charge carriers generally possess a strong EEF perpendicular to the drift direction within the channels and transport along the perpendicular direction to the long axes of oligomers. However, in many systems, the significant degradation experimentally observed results from the shift in the threshold voltage after the prolonged gate bias stress in the ON and/or OFF state.
This phenomenon is mainly caused by trapping of the charge carriers in localized states in organic semiconductors, in dielectric gates, or at the interface between the two layers. Vertical organic field-effect transistors (VOFETs) were first proposed by Ma et al. in 2004.30,31 The purpose of VOFETs is to provide an in-between semiconductor layer with charge transport vertically occurring in the bulk of the organic semiconductor rather than at the semiconductor/dielectric interface, and this has provided potential solutions to address the bias-stability problem mentioned above. However, the microscopic, molecular-level nature of these defects and whether they are related to intrinsic structural defects is not well understood. To explore the origin of high performance of OSC devices, it is necessary to deeply understand the regulation mechanism used by an EEF to affect molecules in devices, especially the effect of the gate voltage, which can directly regulate the carrier injection barrier and then regulate the mobility.32,33
Theoretical calculations can clearly describe the changes in the internal molecular structure of organic semiconductors under an EEF at microscopic atomic and molecular scales, and thus, this part of the research is essential. The effect of the EEF on the molecules in an organic material layer has been noted in several systems over the last 20 years.34,35 Acenes and other oligomers, such as oligothiophene, are typical OSC structures, and they are the well-known two of ‘star’ examples for investigation. In 2003, Brédas used semi-empirical quantum-chemical calculations to investigate the variation of two important parameters for charge transfer (reorganization and transfer integral) of pentacene and sexithienyl molecules under an EEF.32 The electric fields along the long axis of the pentacene and sexithienyl molecules can lead to significant geometric distortions and charge redistribution. Thus, the parameters related to charge transport property, such as reorganization energy, carrier injection ability, carrier mobility, and the design of new molecules, have been continuously explored.36–39
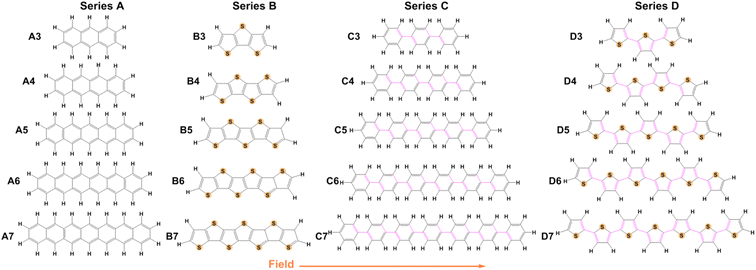
There has been considerable research conducted over the past 20 years regarding the influence of EEFs on charge transport parameters, and relevant theoretical and experimental research has also been conducted in this area.40–44 However, knowledge regarding the mechanisms and characteristics of the EEF effect on organic molecules remains inadequate, and additional theoretical calculation work is needed to explore the relationship between structure and properties under an EEF. Uncovering materials whose charge transport parameters are sensitive to the strength or direction of an EEF may also assist in rationalizing some theoretical-experimental discrepancies and guide the fabrication of high-performance devices. Therefore, we chose an EEF that is parallel to the long axis of the molecular skeleton, and focused on the influence of EEFs on the charge transport parameters of typical organic semiconductor systems, including different lengths of acene (Series A),45–47 oligothienoacenes (Series B),48–50 oligobenzene (Series C)51 and oligothiophenes (Series D),52–55 as shown in Fig. 1.
The effect of the EEF on the geometric structure and charge transfer parameters (reorganization energy and transfer integral) were further analyzed in depth. The change in the frontier molecular orbital (FMO) energy level under an EEF is a non-negligible parameter that severely affects the efficiency (contact resistance) and service life of charge carrier transport, and the relationships between the variation in mobility for different molecular lengths under an EEF are discussed in detail. To extend the type of device, in addition to the organic molecule with a single extended structure mentioned above, a small molecule with a heterogeneous structure (D–A–D–A) was also designed for oligomer semiconductors. The results show that it can maintain greater stability and efficient charge transport ability under a strong EEF. Through this study, a clearer regulation mechanism is expected to be ascertained that will reveal how an EEF affects the properties of OFET material, and provide guidance for the design of high-performance devices.
2 Theory and model
The charge carrier transport in OSCs occurs mainly via an incoherent hopping regime between neighboring molecules at room temperature, caused by small electronic couplings and large electron–phonon couplings.56 Every hopping event is regarded as a self-exchange electron–transfer reaction:57A + A± = A± + A, where A is the molecule undergoing the charge transfer. What we expect to see here is a regular trend in charge transport properties, and therefore, the Marcus model was chosen, which is relatively simple for evaluating charge transport rates.58 The rate formula for charge transfer k can be expressed as: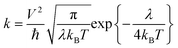 | (1) |
λ is a very important parameter for charge transport, and it consists of two parts: internal reorganization energy (λint) and external reorganization energy (λext).59 The total λ is their sum: λ = λint + λext. Generally, λext is much smaller than λint in pure organic condensed phases.60 Hence, the latter is neglected in this study, and all the λ mentioned henceforth refers to internal reorganization energy. The Normal Mode (NM) analysis61 can be used to calculate the λ, and the contributions of every vibrational mode to λ can be obtained as follows:
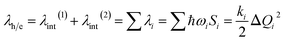 | (2) |
The transfer integrals62 (V) for the nearest neighboring dimers along the transfer pathways in the crystals can be directly calculated by the site energy overlap correction method:63
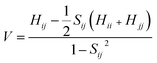 | (3) |
The charge mobilities (μ) can be determined by employing the Einstein equation,64 which is expressed as follows:
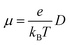 | (4) |
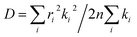 denotes the diffusion coefficient (r denotes the centroid distance between molecules, and is set as 4 Å for the model; n denotes the dimensionality of the charge transport, and here, it is set as 1D (that is, n = 1)).
denotes the diffusion coefficient (r denotes the centroid distance between molecules, and is set as 4 Å for the model; n denotes the dimensionality of the charge transport, and here, it is set as 1D (that is, n = 1)).
3 Results and discussion
3.1 Molecular structures
As is well-known, the properties of molecules are closely related to their structure. Due to the low dielectric constant of the organic semiconductor,65 the range of the EEF was set to 0–0.02 a.u. (approximately 0–1 V Å−1). For an EEF located at the center of mass of a molecule, the direction is parallel to the long axis of the molecule. The structural changes of four series of molecules under different EEFs were investigated in detail, and the molecular structures were optimized at the B3LYP/6-31G (d,p) level by the Gaussian16 program.66 The changes in bond lengths for Series A–D for their two structures in different EEFs and in the absence of an EEF were analyzed.Because the change in bond lengths in each series of molecules basically follows the same trend under the EEF, the molecules with 5 aromatic rings in each series were selected as examples for illustration. The molecular structures of Series A–D at EEF = 0, 0.01, and 0.02 a.u. are shown in Fig. S1,† and the change in bond length under the EEF is shown in Fig. 2 (the bond lengths of other molecules are shown in Fig. S2–S5†). For Series A, the bond length changes are attractive. According to the range of change in bond length, when under an EEF, the greater the number of aromatic benzene rings, the more drastic the change in bond length of acene molecules. For the most drastic change of the C–C bond length, the range is from 0.012 Å for anthracene to 0.06 Å for A7.
The C–C bonds appear at the junction between the two benzene rings, such as the label 6, 11, 16, and 21 for A5. For Series A with the benzene ring number of 3–5, the change in the C–C bond at the connection of benzene rings was the most drastic, but for A6 and A7, the change in bond length was chaotic, especially under a high EEF. When the EEF > 0.01 a.u., the C–C bond length for A7 dramatically changed so that large and condensed aromatic hydrocarbons were very susceptible to the effect of EEF, resulting in structural instability.
For the molecules of the thiophene series (Series B), there are three types of bond length variations, C–C, C–S, and C–H. The greater thiophene number, the more drastic the changes under the EEF. This characteristic is the same as that in Series A, but the C–C bond changes are more intense (ΔLC–C > 0.02 Å) than that of Series A, as shown in Fig. 2(b). The largest change in bond length occurs in the thiophene ring on the right side of the molecules. The C–C bond length presents an ‘extension–shortening alternating’ phenomenon, and is the largest change in bond length, followed by the C–S bond at low EEF. However, when the EEF = 0.02 a.u., the change in C–S bond length is greater than that of the C–C bond.
The C–H bond on the right thiophene (label d) gradually deviates from the thiophene plane (shown in Fig. S5†), which indicates that the molecule become less stable when a high EEF is applied. In reality, the molecular structure of B7 is dispersed and the C–S bond has been broken, and thus, the molecule is broken down at EEF = 0.02 a.u. When the EEF is set as 0.016 a.u. for B7, the C–H bond on the right thiophene (label d) begins to gradually deviates from the thiophene plane in a manner similar to that of B5. It was also proven that for molecules composed of the same structural units, the longer the skeleton, the smaller the strength of the EEF that can be withstood.
For the structures in Series C, the C–C single bond mainly presents a shortening phenomenon, and the four C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds connected to each single bond are extended. For C5, under a high EEF, EEF = 0.02 a.u, and the length of the C–C bond labeled 33 suddenly increases and extends to approximately 0.08 Å, which corresponds to the molecular structure, as when the C–H bond at the right end has broken, as shown in Fig. S1.† For C6, this phenomenon can be found at EEF = 0.016 a.u. and at EEF = 0.012 a.u. for C7. As for Series D, the C–C bond lengths also are of the ‘extension–shortening alternating’ type similar to that of Series B. However, only the C–S bond labeled 1 is shortened under the action of an EEF, while other C–S bonds were extended, and the stronger the EEF intensity, the larger the range of bond length shortening/extension intensity.
C bonds connected to each single bond are extended. For C5, under a high EEF, EEF = 0.02 a.u, and the length of the C–C bond labeled 33 suddenly increases and extends to approximately 0.08 Å, which corresponds to the molecular structure, as when the C–H bond at the right end has broken, as shown in Fig. S1.† For C6, this phenomenon can be found at EEF = 0.016 a.u. and at EEF = 0.012 a.u. for C7. As for Series D, the C–C bond lengths also are of the ‘extension–shortening alternating’ type similar to that of Series B. However, only the C–S bond labeled 1 is shortened under the action of an EEF, while other C–S bonds were extended, and the stronger the EEF intensity, the larger the range of bond length shortening/extension intensity.
For D5 in Fig. 2, the right C–H bond deviated from the planar structure of thiophene under the high EEF, and this trend also gradually moved to the lower field with the increase in the thiophene ring. For D7, the deviation begins at an EEF of 0.01 a.u., and at EEF = 0.016 a.u., there is the C–S and C–H broken bond. The structural characteristics of single-bonded benzene and thiophene series molecules (Series C and D) include not only the change in bond length, but also the change in the dihedral angle between two aromatic rings under the EEF. The dihedral angles are labeled 1, 2, 3…, from the left end of the molecule to the right end. To show the contrast, the dihedral angles between aromatic rings under an EEF for C3vs.D3 and C5vs.D5 with and without an EEF are listed in Tables S1 and S2.†
The torsional angles for Series C and D decreased with increasing EEF, and the aromatic rings tended to be flat. Because the steric hindrance of C–H between thiophene rings is less than that between benzene rings, the dihedral angle gradually approaches 180° with increasing EEF, e.g., for D7 at EEF = 0.004 a.u., the dihedral angle reached 180°. However, at higher EEFs, this flatness is broken again, and there will be more obvious thiophene ring torsion on the far right, such as ∠D5-4 = 175.04° at EEF = 0.02 a.u. By comparing the relationship between the structure of each series of molecules and the intensity of EEF, it was found that under an EEF, almost all bond lengths parallel to the EEF tended to become shorter, no matter whether they were organic small molecules with condensed aromatic rings or connected by a single bond. The greater the number of aromatic rings in system, the greater the sensitivity to an EEF. Excessive EEF will lead to damage to the molecular structure, and eventually, damage to the device.
3.2 Frontier molecular orbitals (FMO) and charge distribution
The contact resistance for OFETs is related to the injection barrier between the electrode and the semiconductor layer.35 The hole and electron injection capacity depend on the degree of matching between the metal electrode (such as Au: −5.1 eV) and highest occupied molecular orbital/the lowest unoccupied molecular orbital (HOMO/LUMO) levels of an OSC molecule. Hence, the response of FMO energy level to EEF change is a problem worth considering, and the results are shown in Fig. 3 and Tables S3–S6,† with Table S7† displaying the spatial distributions of HOMO for Series A, B, C and D under an EEF.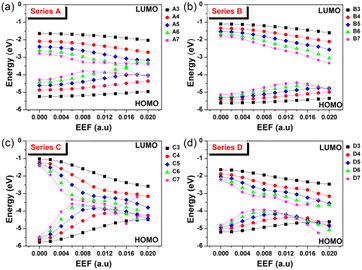 | ||
| Fig. 3 The change in the HOMO/LUMO levels for (a) Series A, (b) Series B, (c) Series C, and (d) Series D within the EEF range of 0–0.02 a.u. | ||
Fig. 3 shows that for the four series of molecular structures, the FMOs generally show a trend of HOMO increasing and LUMO decreasing, with an increase in the aromatic nucleus (EEF = 0.0 a.u.). When low EEFs are applied, their HOMO and LUMO increase and decrease, respectively, which also leads to a decrease in the energy gap with increasing EEF. However, under a high EEF, the HOMO/LUMO of molecules with a long conjugated structure irregularly change due to structural deformation and bond breaking. Compared with acenes (Series A) and oligothienoacenes (Series B), the change gradient (slope) of FMOs with a change in EEF intensity for oligobenzene (Series C) and oligothiophenes (Series D) is larger.
In particular, the longer the benzene chain, the greater the change in the energy level of the FMO under the influence of a low EEF, such as for Series C. The energy gap of C7 changed to nearly 0, which denotes a breakdown in the semiconductor material. The four series of molecules have one thing in common: the values of the increase in the HOMO and the decrease in LUMO are basically the same when choosing a low EEF range (0–0.004 a.u.), as shown in Tables S3–S6.† As a traditional OSC charge transport material, the regulation range of HOMO/LUMO (up or down) for such homogenously structured molecules by EEF is consistent. In addition, with a longer structure or a higher EEF, the FMO energy level greatly changes under the electric field, which indicates that the molecular redox instability and the carrier injection barrier greatly change, which is unfavorable to the charge transport properties.
3.3 Reorganization energy
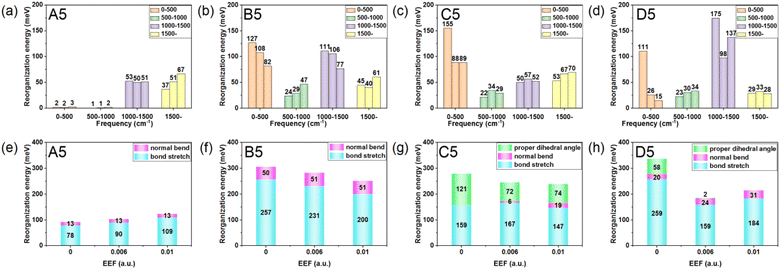
As one important parameter for charge transport process, the EEF dependence of reorganization energy (λ) was studied by NM analysis. First, the range of EEF was set as 0–0.02 a.u.32 for Series A and B, but the structural fracture and the twist of single bond at strong EEF for Series C and D (shown in Fig. S1†) is difficult to obtain, as is a stable optimal neutral/ionic structure without an imaginary frequency, and therefore, a portion of the data is missing. Hence, for the λ, the setting range of the EEF was finally determined to be 0–0.01 a.u., which is sufficiently high for an OSC.39 The λ values are shown in Fig. 4, and the exact values are listed in Table S8.†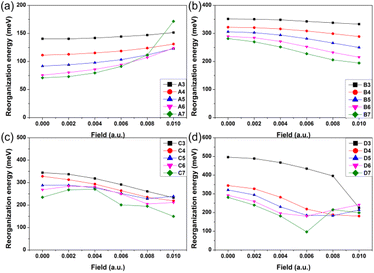 | ||
| Fig. 4 Reorganization energy of the molecules for (a) Series A, (b) Series B, (c) Series C, and (d) Series D within the EEF range of 0–0.01 a.u. | ||
Fig. 4 shows that at a weak EEF (0–0.01 a.u.), the λs of molecules in Series A increase with increasing EEF. With the extension of the conjugate structure, there is a more obvious increase in the λ value. For the A3 molecule, when no EEF is applied, the reorganization energy can be 140.42 meV, and when the EEF is 0.01 a.u., the λ slightly increases to 151.52 meV. However, for the A7 molecule, if there is no EEF applied, the λ is 70.96 meV, and the λ can be changed to 171.56 meV when the EEF = 0.01 a.u., which is approximately 2.5 times greater than the original. This is not conducive to the charge transfer of an OSC. However, with regard to the molecules in the other three series, their λs all show a decreasing trend as the EEF increases, and the longer the conjugated structure, the faster the λ can be reduced.
For Series B, the λ gradually decreases with the increase in the EEF, and there is a more rapid decrease in λ with the extension of the skeleton. For B3, the λ linearly varies with the EEF from 0 to 0.01 a.u. The λ decreased by 18.27 meV, but for B7, the curve exponentially decreased, and from 0 to 0.01 a.u., the λ can be reduced by 87.22 meV. For Series C and D, the dependence between the λ and the EEF is as follows: for a molecule with a shorter molecular chain (N = 3/4), the λ decreases with the increase in the EEF. However, when the molecular chain continues to increase, it was found that the λ is not monotonic with the change in the EEF.
To explore the origin of changes in the λ of the four series of molecules in the presence of EEF, the λs were calculated to project onto their respective vibrational normal modes (NMs). The molecular structures (N = 5) from the four series were used as examples for detailed analysis under the conditions of EEF = 0, 0.006, and 0.01 a.u. Their λs were decomposed into the contribution of each vibration mode by NM analysis, and the results are depicted in Fig. S6.† The contributions of different vibrational frequency ranges (Fig. 5(a–d)) and different bond lengths, bond angles, and dihedral angles (Fig. 5(e–h)) to the λ were classified. The λ values caused by a change in bond lengths, bond angles, and dihedral angles are listed in Table S9.† For A5, the contribution of λ is primarily derived from the change in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibration in the high-frequency region (1200–1700 cm−1). The greater the EEF intensity, the greater the significant increase in the contribution of the stretching vibration between C
C stretching vibration in the high-frequency region (1200–1700 cm−1). The greater the EEF intensity, the greater the significant increase in the contribution of the stretching vibration between C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds (labeled 1, 2, and 3) on the left side of the molecule to λ, and hence the total λ.
C bonds (labeled 1, 2, and 3) on the left side of the molecule to λ, and hence the total λ.
With regard to B5, when there is no EEF, the main contributions to λ are the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibration and the out-of-plane bending vibration of a molecular skeleton. The contribution of the C
C stretching vibration and the out-of-plane bending vibration of a molecular skeleton. The contribution of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibration is the largest in the middle position (labeled 5, 6, and 7), as shown in Fig. 6(b), and then it gradually decreases at both ends. With the increase in the EEF, the contribution to λ by the C
C stretching vibration is the largest in the middle position (labeled 5, 6, and 7), as shown in Fig. 6(b), and then it gradually decreases at both ends. With the increase in the EEF, the contribution to λ by the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibration on the left side of the molecule increases, which is the same as for A5, but the contribution of the C
C stretching vibration on the left side of the molecule increases, which is the same as for A5, but the contribution of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibration to the λ at the right end of the molecule sharply decreases. Additionally, the value of the decreasing contributions is greater than the increasing contribution of the left side, which eventually leads to a reduction in the λ with the increase in the EEF.
C stretching vibration to the λ at the right end of the molecule sharply decreases. Additionally, the value of the decreasing contributions is greater than the increasing contribution of the left side, which eventually leads to a reduction in the λ with the increase in the EEF.
For C5 and D5, the origin of λ is complex, because there are torsion angles between the molecular units. For EEF = 0 a.u., the λ is mainly derived from two parts of the C–C(S)/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibration and torsional vibration between molecular units. The vibration that contributes most to λ is the stretching vibration of C–C in the middle position of the molecular skeleton. When a weak EEF is applied (≤0.006 a.u.), the molecular units on the right side tend to be planar, and the contributions of the C–C stretching vibration and torsional vibration between molecular units on the right side of the λ sharply decrease, especially with D5, as shown in Fig. 6(d). With the EEF range increasing from 0 to 0.006 a.u., there is a decreasing contribution to λ from the torsional vibration of the unit on the left side of the molecule, which is consistent with the change in the torsional angle of the molecular unit of a monomolecular structure under a weak EEF (Table S9†). However, for C5, if the range of the EEF is 0.01 a.u., the λ increases compared with an EEF = 0.006 a.u.
C stretching vibration and torsional vibration between molecular units. The vibration that contributes most to λ is the stretching vibration of C–C in the middle position of the molecular skeleton. When a weak EEF is applied (≤0.006 a.u.), the molecular units on the right side tend to be planar, and the contributions of the C–C stretching vibration and torsional vibration between molecular units on the right side of the λ sharply decrease, especially with D5, as shown in Fig. 6(d). With the EEF range increasing from 0 to 0.006 a.u., there is a decreasing contribution to λ from the torsional vibration of the unit on the left side of the molecule, which is consistent with the change in the torsional angle of the molecular unit of a monomolecular structure under a weak EEF (Table S9†). However, for C5, if the range of the EEF is 0.01 a.u., the λ increases compared with an EEF = 0.006 a.u.
Through analysis, it was found that the contribution of the C–C/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibration between two benzene ring units on the left side of λ was slightly strengthened. However, at a high EEF = 0.01 a.u., there is a greater decrease in the contribution to λ from the torsion between molecular units, and therefore, the total λ decreases. When the EEF is strong, the torsional contribution of molecules has reached the limit under the action of the EEF. At this time, due to the steric hindrance and repulsion of H atoms between benzene rings in C5 molecules, additional C–H out-of-plane bending vibrations will be generated that will increase the λ. Actually, when the EEF of D5 is 0.01 a.u., the λ also increases compared to the EEF = 0.006 a.u., which is mainly due to the increased contribution of the stretching vibration of C–C between five-membered rings (labeled 8, 12, and 16) to the λ. After combining the HOMO distribution of C5 and D5 under EEF = 0.01 a.u. in Table 1, the single bond connecting the two units exhibits bonding characteristics, and the contribution to λ will increase.
C stretching vibration between two benzene ring units on the left side of λ was slightly strengthened. However, at a high EEF = 0.01 a.u., there is a greater decrease in the contribution to λ from the torsion between molecular units, and therefore, the total λ decreases. When the EEF is strong, the torsional contribution of molecules has reached the limit under the action of the EEF. At this time, due to the steric hindrance and repulsion of H atoms between benzene rings in C5 molecules, additional C–H out-of-plane bending vibrations will be generated that will increase the λ. Actually, when the EEF of D5 is 0.01 a.u., the λ also increases compared to the EEF = 0.006 a.u., which is mainly due to the increased contribution of the stretching vibration of C–C between five-membered rings (labeled 8, 12, and 16) to the λ. After combining the HOMO distribution of C5 and D5 under EEF = 0.01 a.u. in Table 1, the single bond connecting the two units exhibits bonding characteristics, and the contribution to λ will increase.
Through the above analysis, it was determined that for the condensed oligomer (Series A and B) and non-condensed oligomer (Series C and D), when the EEF = 0.00 a.u., the contribution of the C–C/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibration at the center of the molecule is the largest, and it symmetrically decreases at the two ends. When there is an EEF, for Series A and B, the contribution of the C
C stretching vibration at the center of the molecule is the largest, and it symmetrically decreases at the two ends. When there is an EEF, for Series A and B, the contribution of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C vibration on the left side of the molecules increases, but there is a different change in the contribution of the right side of the molecule to the λ. Fig. 5(e and f) show that the contribution of the EEF to the out-of-plane bending vibration (pink column) on the molecular skeleton remains unchanged under the action of no EEF. However, for the molecule in Series A, there continues to be an increase in the contribution of the right side of the molecule to the λ. The greater the EEF, the greater the contribution to the λ.
C vibration on the left side of the molecules increases, but there is a different change in the contribution of the right side of the molecule to the λ. Fig. 5(e and f) show that the contribution of the EEF to the out-of-plane bending vibration (pink column) on the molecular skeleton remains unchanged under the action of no EEF. However, for the molecule in Series A, there continues to be an increase in the contribution of the right side of the molecule to the λ. The greater the EEF, the greater the contribution to the λ.
For Series B, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibration on the right thiophene ring contributes less to the λ. For molecules with torsion in Series C and D, the molecular units tend to be flat due to the EEF, which reduces the contribution of the dihedral angle to the λ. However, due to the influence of steric hindrance, the contribution of the C–H plane bending vibration to the λ will be further introduced. In addition, under different EEFs, the C–C stretching vibration on the left molecular unit will also significantly impact the λ. Hence, the size of λ depends upon these three competitions. For the oligomer (N < 6), there is an overall decrease in λ under the action of the EEF.
C stretching vibration on the right thiophene ring contributes less to the λ. For molecules with torsion in Series C and D, the molecular units tend to be flat due to the EEF, which reduces the contribution of the dihedral angle to the λ. However, due to the influence of steric hindrance, the contribution of the C–H plane bending vibration to the λ will be further introduced. In addition, under different EEFs, the C–C stretching vibration on the left molecular unit will also significantly impact the λ. Hence, the size of λ depends upon these three competitions. For the oligomer (N < 6), there is an overall decrease in λ under the action of the EEF.
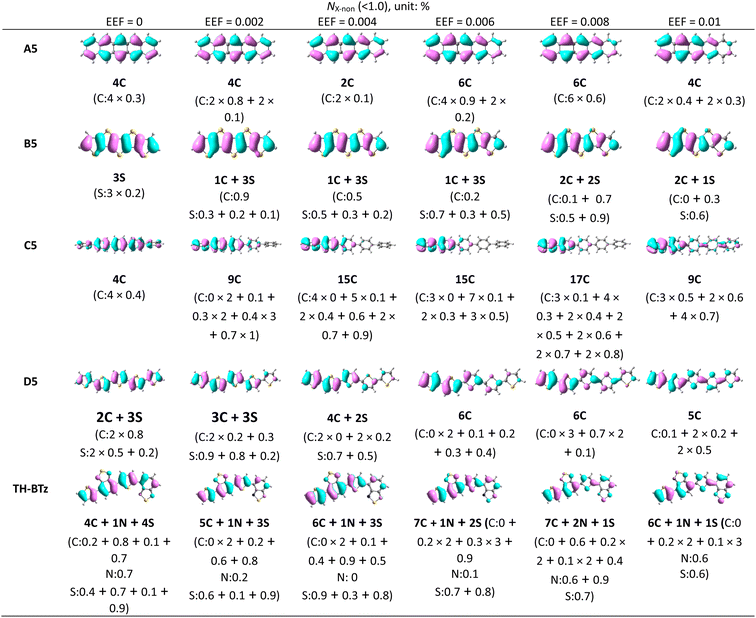
According to previous studies, the λ is closely related to the FMO.59,67 With increasing EEF, the electron density shifts to different degrees of HOMO, and nonbonding characteristics appear in the migration process. To determine whether the change trend for λ can be simply judged by the electron density, the molecules with condensed rings of 5 were once again used as examples, and each atom's contribution to the FMO was calculated. We considered atoms that contributed less than 1% of their orbitals to possess nonbonding characteristics and spatial distributions of HOMO (isoval = 0.025), and the numbers of atoms with nonbonding characteristics are listed in Table 1.
For A5, when the EEF = 0, the number of carbon atoms with nonbonding characteristics (NC-non) is 4, and each atom contributes 0.3% to the molecular orbital, which is a fairly small contribution. The nonbonding characteristic is also the reason for its small λ. With increasing EEF, the NC-non is changed to 2, which denotes that the nonbonding characteristics are weakening. Under a higher EEF, the NC-non is 6 or 4, but there are no significant reductions to the contributions to the HOMO by these atoms. Additionally, the relationship between the number of atoms with non-bonding properties and the size of the λ is well represented in B5, C5, and D5.
B5 and D5 illustrate that the value of λ is mainly related to the nonbonding characteristics of the C atom. For example, in B5, when the EEF = 0, the nonbonding characteristics are mainly derived from the S atoms, and at this time, the contribution of other C atoms to HOMO is greater than 1.0%. With the increase in the EEF, the electron density of one C atom (Table 1) is gradually decreased. When the electric field strength is in the range of 0.002–0.006 a.u., there is a gradual decrease in the contribution of the atom to the HOMO, with an increase in nonbonding characteristics. The contribution to the HOMO increases from 0.9%, to 0.5%, and to 0.2% (as shown in Table 1), which results in a decrease in λ. At a higher EEF, another C atom is added to show nonbonding characteristics. Although the number of S atoms with nonbonding characteristics (NS-non) is reduced, the λ remains reduced. This is also evident on D5 molecules, which further proves that the nonbonding characteristics on C atoms mainly affect the λ, but not on S heteroatoms.
The change in λ for C5 and D5 is not monotonic under the EEF. However, it can be seen that the change trend for λ is consistent with the number of carbon atoms with nonbonding characteristics, such as the λ decreasing from EEF = 0 to 0.008 a.u. when the NC-non increases from 4 to 17, and then λ increases, and the NC-non changes to 9. This condition is not suitable for C5 under the condition of EEF = 0.002 a.u., although when the NC-non in C5 increases, the λ also increases. According to the electron density distribution, this may be due to the reduction in the delocalization length of the electron density as a whole. In addition, under other EEF conditions, the change in λ continues to be negatively correlated with NC-non. Hence, the change trend for λ under an EEF can be judged simply by NC-non, and this conclusion may also apply to other conditions that can cause changes in electron density.
3.4 Transfer integrals
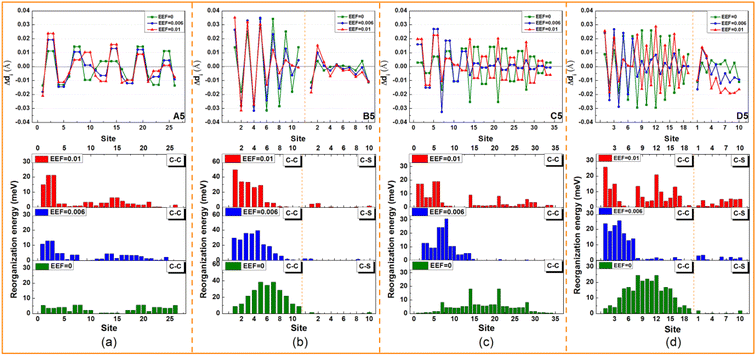
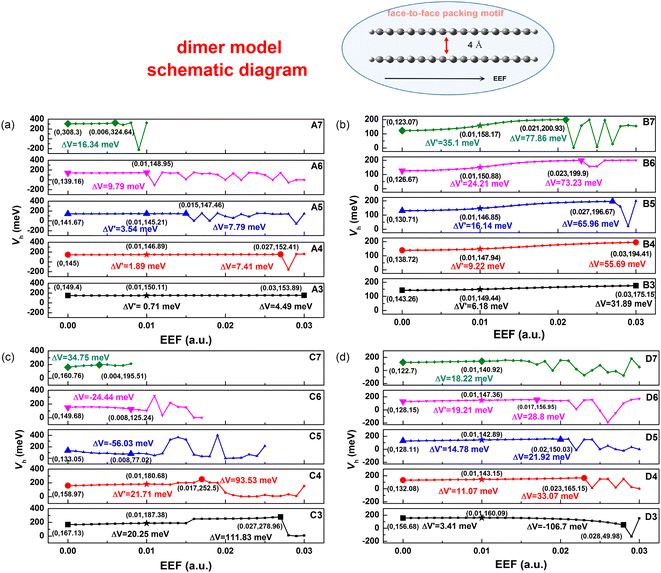
The transfer integral (V) is another important parameter for the charge transport property of OSCs, which is defined as the electron coupling between HOMO–HOMO/LUMO–LUMO. To prove the sensitivity of intermolecular Vs with respect to EEF, we adopted a dimer model of a face-to-face packing motif to understand the relationship in greater detail, and the distance between two molecules was set as 4 Å (as shown in Fig. 7). To compare the sensitivity of the V to the EEF between dimers of molecules with different lengths, the Vs over a wide range of EEF strengths (0–0.03 a.u.) were calculated through the ADF package, and the results are depicted in Fig. 7. The range of EEFs between the same symbols in each molecule in Fig. 7 is the region where the electron structure is stable, and when this range of the EEF is exceeded, the electrons in the molecular orbital are excited to higher orbitals.The range of EEFs that each molecule can withstand corresponds well to the FMO energy levels discussed earlier in Fig. 2 and Tables S3–S6.† For the A7 molecule, as shown in Fig. 3, there was extreme narrowing of the energy gap when the EEF exceeded 0.006 a.u., and the electrons were easily excited, which also implies structural instability. The comparison between the stable range of the transfer integral electric field and the energy gap shows that when the energy gap is less than 1 eV, the electronic structure of the molecule is extremely unstable, and the electrons are excited in the EEF.
According to the results, at low EEFs (<0.004 a.u.), there is little change in the Vs of Series A and B as shown in Table S10,† which is consistent with recent research.32 However, where there were strong changes in the EEF (0.004 < EEF < 0.01 a.u.), the hole Vs of Series B increased. The longer the conjugated skeleton, the more obvious the trend of increasing hole Vs under the EEF. Additionally, the change in the hole V for Series B was more obvious than that for Series A. This indicates that the electron-rich thiophene ring is more conducive to increasing the electron coupling between molecules and enhancing the charge transport stability under the action of the EEF.
For single-bonded molecules, the Vs of Series C and D were calculated using the same method. However, due to the large torsion between the various units of the molecules in Series C, the phenomenon of too close proximity of the atoms between the molecules will occur when the model is established, and the final calculation results will be markedly increased or decreased, which may result in a margin of error. Fig. 7 shows that there is clearly an increasing trend with the V of Series D as the EEF increased, and with the increase in structural units, the V significantly increased. Although there was less of an increase in the V of D3, ΔV′ = 3.41 meV from non-EEF to EEF = 0.01 a.u., and the overall trend was that of an increase at a low EEF range.
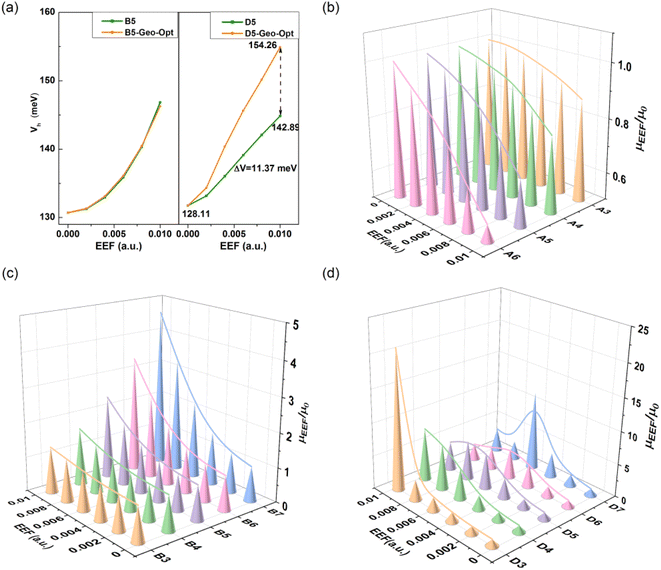
Considering that the geometric structure of the series greatly changes under the action of an EEF, the V will be further affected. Hence, the V of B5 and D5 was recalculated with the same model as above using the geometric structure optimized under different EEFs, and the calculation results are shown in Fig. 8(a). For B5 molecules with a planar structure, there was little change in the magnitude of the V after considering the geometric structure. However, for single-bonded D5 molecules, the ΔV gradually increased as the EEF increased. When the EEF was set as 0.01 a.u., the ΔV1 was 14.78 meV, and the ΔV2 = 26.16 meV when the geometric structure was considered (ΔV = ΔV2 − ΔV1 = 11.37 meV in Fig. 8(a)), which indicates that the structural deformation under the EEF also has an important effect on the V of single-bonded molecules. Therefore, if the microscopic process of charge transport is to be more comprehensively considered, it is very important to examine the effect of the EEF on the geometry and the V.
3.5 Mobility
It is important to understand the relationship between experimental and intrinsic mobility, and hence, the mobility for these models can be calculated by the Marcus theory, which is based on the reorganization energy (λ) and transfer integral (V). The calculated results are shown in Table S11.† For the mobility of Series A and B with condensed rings, due to the regulated change of λ and V, the change in mobility under an EEF is monotonic. For the molecules of Series A, the mobility decreased with the increase in EEF (the λ decreased), while the mobility increased with the increase in EEF (the λ decreased and the V increased) for the molecules of Series B. For Series C and D, the mobility initially increased and then decreased, which resulted in by the λ. For N = 3/4, the mobility increased with the increase in the EEF, but for polythiophenes with larger lengths, the migration first increased and then decreased, and with the increase in the number of rings, the lower EEF caused the mobility to begin to decrease. However, the overall mobility under the EEF remained higher than the intrinsic mobility.For Series A and B, in the EEF range of 0–0.01 a.u., the rate of change in mobility is related to the number of condensed rings, as shown in Fig. 8(b). There is a negative correlation for Series A between the mobility trend and the number of condensed rings at 0–0.01 a.u., but a positive correlation between that of Series B. This indicates that the greater the number of benzene rings, the lower the actual mobility under the EEF as compared to its intrinsic mobility, and the greater the number of thiophene rings, the higher the actual mobility. For Series D, from Fig. 8(d), there is optimal mobility in the range of EEF = 0–0.01 a.u. For D3 and D4, the maximum mobility is the mobility when the EEF = 0.01 a.u., but the longer the repeating unit, the greater the shift in the optimal value to the direction of the lower field, such as the optimal mobility when D5 is at EEF = 0.08 a.u., and when D6 and D7 are at EEF = 0.06 a.u. For the longer building units of Series D, the presence of an optimal EEF can result in greater mobility, and the longer the chain, the stronger the required EEF.
3.6 Designed molecule, TH-BTz
Except for the oligomers of homogenous units, there has been considerable research on semiconducting polymers with heterogeneous units, due to their promising utilization as building blocks for electronic circuits in the cost-effective and flexible manufacturing of large-area OFETs.68 The donor–acceptor (D–A) strategy has been extensively used for constructing semiconducting polymers with tailored optoelectronic properties, where thiophene-containing units are the most widely used electron donors. As an electron-deficient building block, it has been demonstrated that benzothiadiazole (BTz) is efficient for high-performance ambipolar or n-type polymers.68,69Inspired by the above studies and the above calculation results, a single-bonded thiophene structure was selected, and one electron-withdrawing group, BTz, was introduced to regulate the FMO energy level and λ. An extended ‘D–A–D–A’ structure (TH-BTz) was designed to investigate the charge transport property under an EEF. A schematic diagram of the molecular structure is shown in Fig. 9(a), and the change in the HOMO/LUMO levels is shown in Fig. 9(b). Compared with that of Series A–D under an EEF, although there is little change in the delocalization of the charge density distribution of the HOMO, the nonbonding characteristics also appear when the EEF increases. The HOMO value of TH-BTz gradually approaches the potential of a gold electrode and is maintained at approximately −5.1 eV, which indicates that it can stably transport holes over a wide range of EEFs due to its small hole injection barrier (contact resistance) and carrier stability.
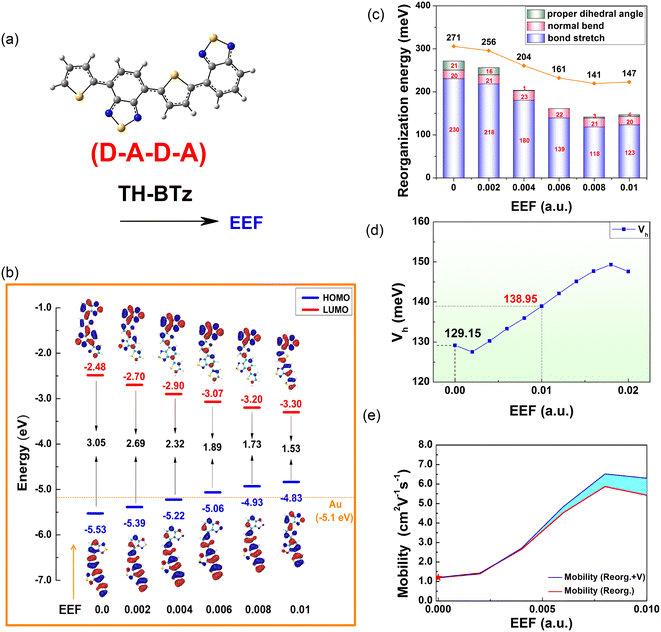 | ||
| Fig. 9 A schematic diagram of (a) TH-BTz molecular structures, (b) HOMO/LUMO level energy, (c) reorganization energy, (d) transfer integrals, and (e) 1D mobility under the EEF. | ||
The electron cloud distribution for TH-BTz on the LUMO level gradually becomes delocalized, which results in a gradual decrease in the LUMO energy level with a subsequent decrease in the electron injection barrier. The change in value for FMOs is 0.31 eV for HOMO and −0.42 eV for LUMO in the range of 0–0.004 a.u., indicating that the EEF can adjust the FMO level change to varying degrees through molecular design, and this change in value is much smaller than that for C6 or D6, which denotes greater injection stability.
The hole λ and V were calculated, and the results are shown in Fig. 9(c and d). According to the electron cloud distribution of the HOMO, it can be preliminarily concluded that the λ should decrease with the increasing EEF, and this is exactly what the calculations show. Based on the analysis of λ, the change in the λ is the same as that of Series C and D, and the contribution of bond length to the λ is shown in Fig. S7.† With the increase in the EEF, the molecule tends to be planarized (the dihedral angles are shown in Table S12†), and the contribution of the dihedral vibration to the λ decreases, reaching 0 at EEF = 0.006 a.u. The stretching vibration between atoms on the right side of the molecule is inhibited, resulting in a reduced λ, and the out-of-plane vibration of the molecule is not disturbed by the EEF parallel to the major axis of the molecule.
According to the value of λ under an EEF in the range of 0–0.01 a.u., for TH-BTz with D–A–D–A structural characteristics, the λ is reduced by 52%, which is greater than that for the other series (Series B and D are reduced by a maximum of 26% for B6 and 38% for D6 at 0–0.01 a.u., respectively) and indicates that the EEF plays a very favorable role in the charge transport properties of such molecules. Fig. 9(d and e) show that the hole Vs of TH-BTz at the EEF range of 0–0.01 a.u. also increase as the EEF increases. These two parameters can greatly increase the charge transfer rate. To confirm this, the charge transfer rate was tested by the Marcus formula, and the results are listed in Table S13.†
Furthermore, the 1D hole mobilities under the EEF were calculated, and the results are shown in Fig. 9(e). The blue line represents the change curve of the mobility after considering the effect of a varied EEF on the λ and the V, and the red line represents the mobility of the λ during the change in the EEF. The sky blue area between the two color curves represents the influence of multiple mobility of the V when the EEF changes. According to Fig. 9(d), the intrinsic mobility of the material can be increased by more than 5 times in the presence of an EEF, which indicates that there is a very important influence of the EEF on the mobility. In addition, the mobility is mainly dominated by the size of the λ, but with increasing EEF, the influence of the V on the mobility gradually increases.
4 Conclusions
In summary, the effect of regulation of an EEF on the charge transport properties of four typical OSC materials was investigated by means of density functional theory. The variation in FMO parameters, which affect the molecular stability, carrier injection ability, and mobility in the presence of an EEF, is discussed in detail. The longer the molecular skeleton, the greater its sensitivity to an EEF. The geometry and electronic structures of single-bonded molecules are more easily affected than condensed aromatic conjugated oligomers under an EEF.For Series A and B, an EEF will only affect the change in reorganization energy by affecting the bond length, while the effect of an EEF on reorganization energy is more complicated for Series C and D molecules connected by single bonds. With an increasing EEF, the molecular structure gradually tends to flatten with increased rigidity. Compared to Series C with benzene units, the decreased steric hindrance between the thiophene units in Series D causes a flatter molecular geometry under an EEF. The contribution of the dihedral angle to the reorganization energy decreases, even to 0, with a further decrease in the reorganization energy, which could be more conducive to charge transfer under the same conditions.
Furthermore, for single-bonded oligomers, the influence of not only the EEF, but also of geometric deformation on the transfer integral should be fully considered, especially when subjected to a high EEF. Hence, when calculating the intrinsic mobility of organic semiconductors, the effect of the EEF should be fully considered because the EEF could cause a deviation 0.3–20 times in mobility. The mobility's change ratio for common organic semiconductor molecules under an EEF is given, which provides a theoretical reference for the actual mobility measured in experiments. The change ratio for intrinsic mobility under an EEF is negatively/positively related to the number of condensed rings for acene (Series A) and thiophene (Series B). For oligothiophenes (Series D), there is an optimal mobility in the EEF range of 0–0.01 a.u., especially for the molecules with a long structure. According to detailed calculations, one heterogeneous oligomer, TH-BTz, was designed.
Like Series D, the λ of TH-BTz can be greatly reduced under an EEF, and the change in the energy level of the FMO can be adjusted to different degrees while maintaining satisfactory stability. It is worth mentioning that according to the change in FMOs under an EEF (nonbonding characteristics), the change in reorganization energy under an EEF can be preliminarily and qualitatively determined. However, if quantitative results are required, a detailed normal mode analysis would be needed. We also explain in detail that the increase in the reorganization energy of Series A under an EEF is mainly due to the weakening of its non-bonding characteristics.
These results theoretically reveal in detail the effect of EEF regulation on the stability of molecular structures and on the charge transport property, and provide important theoretical guidance for the use of EEFs to regulate and predict the performance of organic semiconductors. We hope the new ideas in this study will contribute to the experimental and theoretical development of organic semiconductors with high mobility.
Data availability
Data are available in the ESI† and from the authors on request.Author contributions
Gui-Ya Qin, Prof. Jing-Fu Guo and Prof. Ai-Min Ren conceived and supervised the research. Gui-Ya Qin performed DFT calculations and wrote the manuscript under the guidance of Ai-Min Ren. All authors discussed, commented and approved the final manuscript. In addition, we are very grateful to Prof. Jing-Fu Guo for providing software technical support.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the 2020-0Q project (GFQ2126-007), the National Natural Science Foundation of China (No. 21473071, 21173099, and 20973078), and the Scientific Research Planning Project of the Jilin Provincial Education Department (No. JJKH20241249KJ).References
- X. Li, F. Pan, C. Sun, M. Zhang, Z. Wang, J. Du, J. Wang, M. Xiao, L. Xue, Z.-G. Zhang, C. Zhang, F. Liu and Y. Li, Nat. Commun., 2019, 10, 519 CrossRef CAS PubMed.
- X. Zhou, Y. Cai, M. Xu, J. Li, C. Sheng, Q. Zhang, X. Qiu, W. Wang, S. Xiong, C. Cong, Z.-J. Qiu, R. Liu and L. Hu, Small Methods, 2022, 6, 2101509 CrossRef CAS PubMed.
- R. Samanta, S. Das, S. Mondal, T. Alkhidir, S. Mohamed, S. P. Senanayak and C. M. Reddy, Chem. Sci., 2023, 14, 1363–1371 RSC.
- X. Xu, Y. Zhao and Y. Liu, Small, 2023, 19, 2206309 CrossRef CAS PubMed.
- J. Duan, G. Zhu, J. Chen, C. Zhang, X. Zhu, H. Liao, Z. Li, H. Hu, I. McCulloch, C. B. Nielsen and W. Yue, Adv. Mater., 2023, 35, 2300252 CrossRef CAS PubMed.
- H. Zhang, Y. Hu, X. Chen, L. Yu, Y. Huang, Z. Wang, S. Wang, Y. Lou, X. Ma, Y. Sun, J. Li, D. Ji, L. Li and W. Hu, Adv. Funct. Mater., 2022, 32, 2111705 CrossRef CAS.
- M. Li, J. Zheng, X. Wang, R. Yu, Y. Wang, Y. Qiu, X. Cheng, G. Wang, G. Chen, K. Xie and J. Tang, Nat. Commun., 2022, 13, 4912 CrossRef CAS PubMed.
- X. Chen, Z. Wang, J. Qi, Y. Hu, Y. Huang, S. Sun, Y. Sun, W. Gong, L. Luo, L. Zhang, H. Du, X. Hu, C. Han, J. Li, D. Ji, L. Li and W. Hu, Nat. Commun., 2022, 13, 1480 CrossRef CAS PubMed.
- D. Kim, S. Im, D. Kim, H. Lee, C. Choi, J. H. Cho, H. Ju and J. A. Lim, Adv. Funct. Mater., 2023, 33, 2210367 CrossRef CAS.
- Y. Shi, W. Li, X. Wang, L. Tu, M. Li, Y. Zhao, Y. Wang and Y. Liu, Chem. Mater., 2022, 34, 1403–1413 CrossRef CAS.
- Z. Qin, H. Gao, H. Dong and W. Hu, Adv. Mater., 2021, 33, 2007149 CrossRef CAS PubMed.
- Q. Li, Y. Zhang, J. Lin, Y. Zou, P. Wang, Z. Qin, Y. Wang, Y. Li, Y. Zhang, C. Gao, Y. Zang, W. Hu and H. Dong, Angew. Chem., Int. Ed., 2023, 62, e202308146 CrossRef CAS PubMed.
- C.-M. Yang, Y.-C. Yang, B.-H. Jiang, J.-H. Yen, X.-M. Su and C.-P. Chen, Sens. Actuators, B, 2023, 381, 133449 CrossRef CAS.
- Z. Zhao, K. Liu, Y. Liu, Y. Guo and Y. Liu, Natl. Sci. Rev., 2022, 9, nwac090 CrossRef CAS PubMed.
- D. Lv, Q. Jiang, Y. Shang and D. Liu, npj Flexible Electron., 2022, 6, 38 CrossRef CAS.
- Q. Li, T. Wang, Y. Fang, X. Hu, C. Tang, X. Wu, H. Zhu, L. Ji, Q.-Q. Sun, D. W. Zhang and L. Chen, Nano Lett., 2022, 22, 6435–6443 CrossRef CAS PubMed.
- P. Hu, X. He and H. Jiang, InfoMat, 2021, 3, 613–630 CrossRef CAS.
- T. Okamoto, C. P. Yu, C. Mitsui, M. Yamagishi, H. Ishii and J. Takeya, J. Am. Chem. Soc., 2020, 142, 9083–9096 CrossRef CAS PubMed.
- J. Veres, S. Ogier, G. Lloyd and D. de Leeuw, Chem. Mater., 2004, 16, 4543–4555 CrossRef CAS.
- K. Zeng, X. Shi, C. Tang, T. Liu and H. Peng, Nat. Rev. Mater., 2023, 8, 552–561 CrossRef.
- D. W. Kim, S.-Y. Min, Y. Lee and U. Jeong, ACS Nano, 2020, 14, 907–918 CrossRef CAS PubMed.
- K. S. Lee, T. J. Smith, K. C. Dickey, J. E. Yoo, K. J. Stevenson and Y. L. Loo, Adv. Funct. Mater., 2006, 16, 2409–2414 CrossRef CAS.
- J. Liu, H. Zhang, H. Dong, L. Meng, L. Jiang, L. Jiang, Y. Wang, J. Yu, Y. Sun, W. Hu and A. J. Heeger, Nat. Commun., 2015, 6, 10032 CrossRef CAS PubMed.
- X. Fang, J. Shi, X. Zhang, X. Ren, B. Lu, W. Deng, J. Jie and X. Zhang, Adv. Funct. Mater., 2021, 31, 2100237 CrossRef CAS.
- W. Deng, H. Lei, X. Zhang, F. Sheng, J. Shi, X. Zhang, X. Liu, S. Grigorian, X. Zhang and J. Jie, Adv. Mater., 2022, 34, 2109818 CrossRef CAS PubMed.
- K. He, S. Zhou, W. Li, H. Tian, Q. Tang, J. Zhang, D. Yan, Y. Geng and F. Wang, J. Mater. Chem. C, 2019, 7, 3656–3664 RSC.
- B. Fu, F. Yang, L. Sun, Q. Zhao, D. Ji, Y. Sun, X. Zhang and W. Hu, Adv. Mater., 2022, 34, 2203330 CrossRef CAS PubMed.
- T. Kubo, R. Häusermann, J. Tsurumi, J. Soeda, Y. Okada, Y. Yamashita, N. Akamatsu, A. Shishido, C. Mitsui, T. Okamoto, S. Yanagisawa, H. Matsui and J. Takeya, Nat. Commun., 2016, 7, 11156 CrossRef CAS PubMed.
- Z. Chen, S. Duan, X. Zhang and W. Hu, Appl. Phys. Lett., 2021, 119, 210501 CrossRef CAS.
- L. Ma and Y. Yang, Appl. Phys. Lett., 2004, 85, 5084–5086 CrossRef CAS.
- X. Qiu, J. Guo, P.-A. Chen, K. Chen, Y. Liu, C. Ma, H. Chen and Y. Hu, Small, 2021, 17, 2101325 CrossRef CAS PubMed.
- J. C. Sancho-Garía, G. Horowitz, J. L. Brédas and J. Cornil, J. Chem. Phys., 2003, 119, 12563–12568 CrossRef.
- C. Wang, X. Zhang, H. Dong, X. Chen and W. Hu, Adv. Energy Mater., 2020, 10, 2000955 CrossRef CAS.
- F. Molina-Lopez, H. Yan, X. Gu, Y. Kim, M. F. Toney and Z. Bao, Adv. Funct. Mater., 2017, 27, 1605503 CrossRef.
- S. Mandal, A. Mandal, G. Jana, S. Mallik, S. Roy, A. Ghosh, P. K. Chattaraj and D. K. Goswami, ACS Appl. Mater. Interfaces, 2020, 12, 19727–19736 CrossRef CAS PubMed.
- A. Förster, F. Günther, S. Gemming and G. Seifert, J. Phys. Chem. C, 2017, 121, 3714–3723 CrossRef.
- G. Simone, M. J. Dyson, C. H. L. Weijtens, S. C. J. Meskers, R. Coehoorn, R. A. J. Janssen and G. H. Gelinck, Adv. Opt. Mater., 2020, 8, 1901568 CrossRef CAS.
- Y. Zhang, Y. Ye, Y. Li, X. Yin, H. Liu and J. Zhao, J. Mol. Struct.: THEOCHEM, 2007, 802, 53–58 CrossRef CAS.
- X. Lu, Y. Sun and W. Hu, J. Mater. Chem. A, 2021, 9, 21044–21050 RSC.
- X. Wu, C. Gao, Q. Chen, Y. Yan, G. Zhang, T. Guo and H. Chen, Nat. Commun., 2023, 14, 1579 CrossRef CAS PubMed.
- X. Zhan, H. Shi, H. Liu and J. Y. Lee, J. Comput. Chem., 2017, 38, 304–311 CrossRef CAS PubMed.
- T. Lu and Q. Chen, ChemPhysChem, 2021, 22, 386–395 CrossRef CAS PubMed.
- H. Liu, S. Kang and J. Y. Lee, J. Phys. Chem. B, 2011, 115, 5113–5120 CrossRef CAS PubMed.
- H. Hu, X. Mu, B. Li, R. Gui, R. Shi, T. Chen, J. Liu, J. Yuan, J. Ma, K. Gao, X. Hao and H. Yin, Adv. Sci., 2023, 10, 2205040 CrossRef CAS PubMed.
- A. N. Aleshin, J. Y. Lee, S. W. Chu, J. S. Kim and Y. W. Park, Appl. Phys. Lett., 2004, 84, 5383–5385 CrossRef CAS.
- O. D. Jurchescu, M. Popinciuc, B. J. van Wees and T. T. M. Palstra, Adv. Mater., 2007, 19, 688–692 CrossRef CAS.
- Y. Takeyama, S. Ono and Y. Matsumoto, Appl. Phys. Lett., 2012, 101, 083303 CrossRef.
- Y. Liu, Y. Wang, W. Wu, Y. Liu, H. Xi, L. Wang, W. Qiu, K. Lu, C. Du and G. Yu, Adv. Funct. Mater., 2009, 19, 772–778 CrossRef CAS.
- Y. Liu, X. Sun, C.-a. Di, Y. Liu, C. Du, K. Lu, S. Ye and G. Yu, Chem.–Asian J., 2010, 5, 1550–1554 CrossRef CAS PubMed.
- X. Zhang, A. P. Côté and A. J. Matzger, J. Am. Chem. Soc., 2005, 127, 10502–10503 CrossRef CAS PubMed.
- D. J. Gundlach, Y.-Y. Lin, T. N. Jackson and D. G. Schlom, Appl. Phys. Lett., 1997, 71, 3853–3855 CrossRef CAS.
- S. Nagamatsu, K. Kaneto, R. Azumi, M. Matsumoto, Y. Yoshida and K. Yase, J. Phys. Chem. B, 2005, 109, 9374–9378 CrossRef CAS PubMed.
- G. Horowitz, D. Fichou, X. Peng, Z. Xu and F. Garnier, Solid State Commun., 1989, 72, 381–384 CrossRef CAS.
- A. Facchetti, M.-H. Yoon, C. L. Stern, G. R. Hutchison, M. A. Ratner and T. J. Marks, J. Am. Chem. Soc., 2004, 126, 13480–13501 CrossRef CAS PubMed.
- A. Dodabalapur, L. Torsi and H. E. Katz, Science, 1995, 268, 270–271 CrossRef CAS PubMed.
- V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J.-L. Brédas, Chem. Rev., 2007, 107, 926–952 CrossRef CAS PubMed.
- G.-Y. Qin, L.-F. Ji, J.-X. Fan, N.-X. Zhang, P.-P. Lin, S.-F. Zhang, L.-Y. Zou and A.-M. Ren, J. Phys. Chem. A, 2019, 123, 3300–3314 CrossRef CAS PubMed.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–610 CrossRef CAS.
- Y.-C. Chang and I. Chao, J. Phys. Chem. Lett., 2010, 1, 116–121 CrossRef CAS.
- W. Senevirathna, C. M. Daddario and G. Sauvé, J. Phys. Chem. Lett., 2014, 5, 935–941 CrossRef CAS PubMed.
- M. C. R. Delgado, K. R. Pigg, D. A. da Silva Filho, N. E. Gruhn, Y. Sakamoto, T. Suzuki, R. M. Osuna, J. Casado, V. Hernández, J. T. L. Navarrete, N. G. Martinelli, J. Cornil, R. S. Sánchez-Carrera, V. Coropceanu and J.-L. Brédas, J. Am. Chem. Soc., 2009, 131, 1502–1512 CrossRef CAS PubMed.
- H. Li, J.-L. Brédas and C. Lennartz, J. Chem. Phys., 2007, 126, 164704 CrossRef PubMed.
- G. Qin, P. Lin, X. Sun, J. Guo, J. Fan, L. Ji, H. Li and A. Ren, Phys. Chem. Chem. Phys., 2023, 25, 540–554 RSC.
- L. B. Schein and A. R. McGhie, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 20, 1631–1639 CrossRef CAS.
- J. Brebels, J. V. Manca, L. Lutsen, D. Vanderzande and W. Maes, J. Mater. Chem. A, 2017, 5, 24037–24050 RSC.
- M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, Gaussian 09, Revision a. 02, 200, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- W.-C. Chen and I. Chao, J. Phys. Chem. C, 2014, 118, 20176–20183 CrossRef CAS.
- H. Liang, C. Liu, Z. Zhang, X. Liu, Q. Zhou, G. Zheng, X. Gong, L. Xie, C. Yang, L. Zhang, B. He, J. Chen and Y. Liu, Adv. Funct. Mater., 2022, 32, 2201903 CrossRef CAS.
- J. Chen, Y. Jiang, J. Yang, Y. Sun, L. Shi, Y. Ran, Q. Zhang, Y. Yi, S. Wang, Y. Guo and Y. Liu, ACS Appl. Mater. Interfaces, 2018, 10, 25858–25865 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc06728a |
| This journal is © The Royal Society of Chemistry 2024 |