Open Access Article
Open Access ArticleRobust vibrational coherence protected by a core–shell structure in silver nanoclusters†
Jie
Kong‡
 a,
Zhuoran
Kuang‡
a,
Zhuoran
Kuang‡
 b,
Wei
Zhang‡
b,
Wei
Zhang‡
 a,
Yongbo
Song
a,
Yongbo
Song
 *c,
Guo
Yao
d,
Chunfeng
Zhang
d,
He
Wang
*c,
Guo
Yao
d,
Chunfeng
Zhang
d,
He
Wang
 e,
Yi
Luo
e,
Yi
Luo
 *a and
Meng
Zhou
*a and
Meng
Zhou
 *a
*a
aHefei National Research Center for Physical Sciences at the Microscale, University of Science and Technology of China, Hefei, Anhui 230026, P. R. China. E-mail: yiluo@ustc.edu.cn; mzhou88@ustc.edu.cn
bState Key Laboratory of Information Photonic and Optical Communications, School of Science Beijing University of Posts and Telecommunications (BUPT), Beijing 100876, P. R. China
cSchool of Biomedical Engineering, Research and Engineering Center of Biomedical Materials, Anhui Medical University, Hefei, Anhui 230032, P. R. China. E-mail: ybsong860@ahmu.edu.cn
dNational Laboratory of Solid State Microstructures, School of Physics, Collaborative Innovation Center for 5Advanced Microstructures, Nanjing University, Nanjing 210093, P. R. China
eDepartment of Physics, University of Miami, Coral Gables, Florida 33146, USA
First published on 1st April 2024
Abstract
Vibrational coherence has attracted considerable research interests because of its potential functions in light harvesting systems. Although positive signs of vibrational coherence in metal nanoclusters have been observed, the underlying mechanism remains to be verified. Here, we demonstrate that robust vibrational coherence with a lifetime of 1 ps can be clearly identified in Ag44(SR)30 core–shell nanoclusters, in which an icosahedral Ag12 core is well protected by a dodecahedral Ag20 cage. Ultrafast spectroscopy reveals that two vibrational modes at around 2.4 THz and 1.6 THz, corresponding to the breathing mode and quadrupolar-like mode of the icosahedral Ag12 core, respectively, are responsible for the generation of vibrational coherence. In addition, the vibrational coherence of Ag44 has an additional high frequency mode (2.4 THz) when compared with that of Ag29, in which there is only one low frequency vibration mode (1.6 THz), and the relatively faster dephasing in two-layer Ag29 relative to that in Ag44 further supports the fact that the robust vibrational coherence in Ag44 is ascribed to its unique matryoshka-like core–shell structure. Our findings not only present unambiguous experimental evidence for a multi-layer core–shell structure protected vibrational coherence under ambient conditions but also offers a practical strategy for the design of highly efficient quantum optoelectronic devices.
Introduction
Coherence refers to the oscillatory behavior that is the superposition on the excited state, which is widely observed in many different systems, such as isolated molecules, semiconductors, as well as metal nanoparticles (NPs).1–7 For isolated molecules, coherences arise from the wave packet moving on the potential energy surface of the excited- or ground-state which leads to the enhancement or depletion in intensity.8–11 It was also observed that the vibrational coherence can transfer from one excited state potential energy surface to another, and this can be used to drive the intersystem crossing (singlet–triplet conversion) process, track the electron transfer, and analyze the structural variables,12–16 while the coherent oscillations of the metal NPs are due to the lattice expansions from the laser heating effect, which can be modulated by the size and shape.6,17 Metal nanoclusters (NCs) are sub-2 nm nanoparticles that possess a discrete energy level because of the quantum confinement effect.18–20 Because coherence is an important property in other systems, and widely applied, the coherence of the metal NCs that are newly observed using broadband transient absorption (TA) spectroscopy have attracted great attention in recent years.21–33It is known that in organic molecules, the soft structure can accelerate the dephasing of the coherence because of the fast energy transfer to the environment, whereas in solid-state systems including inorganic semiconductors and metals, phonons and surface defects can cause significant decoherence.1 Conversely, the vibrational coherence can be easily perturbed by the solvent fluctuation and environmental heat, which will significantly accelerate the damping of the coherent oscillations.22 In this context, metal NCs have attracted considerable research interest, and they can serve as an intermediate state between metallic nanoparticles and isolated metal atoms.34–36 For instance, gold and silver NCs exhibit discrete energy levels and multiple absorption bands that arise from single exciton transitions, making them potential candidates for light harvesting nanomaterials.37–39 Ligand-protected metal NCs show well-defined structures, and it is possible to correlate the optical properties with their atomic structures.37 Many of these thiolate-protected gold and silver NCs are made of a metal core protected by a shell structure that consists of metal atoms, such as surface sulfur atoms and carbon tails.36,37,40 Using an ultrafast laser to selectively excite the vibrations of the metal core, signs of vibrational coherence have been observed in the excited state dynamics of metal NCs.25,26,41,42 However, the underlying mechanism needs to be further verified as coherent vibrational modes involved are difficult to identify, and the fast decoherence has complicated the entire analysis. A previous study assigned coherent vibrations in several gold NCs to mechanical vibrations similar to those in large metallic gold nanoparticles, which are typically induced by ultrafast laser heating.24 Further experimental research and theoretical work are needed to assign the vibration modes and design metal NCs with slow decoherence.
Here, we chose [Ag44(SR)30]4− (SR = SPhF2, Ag44 for short) as a model system to understand the vibrational coherence in silver NCs. Femtosecond transient absorption measurements indicate that the excited state absorption and ground state bleaching of Ag44 exhibit mirror-image dynamics, suggesting similar excited state and ground state electronic structures. Significant vibrational coherences with frequencies around 2.4 THz and 1.6 THz can be observed in TA spectra, and the decay time of the coherent oscillations is around 1 ps. Theoretical calculation results indicate that these two modes arise from the breathing and quadra-polar like modes of the metal core in Ag44, respectively. The analysis of the damping of the coherent oscillations indicates that the robust coherence is protected by the three-layer core–shell structure in Ag44 during the excited state relaxation.
Results and discussion
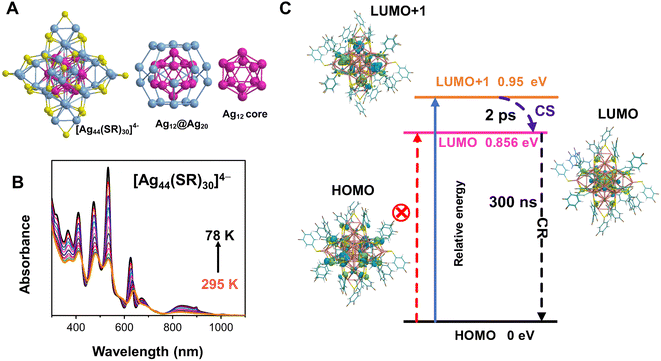
The structure of the Ag44 NCs consists of an Ag32 core, which can be described as a three layer matryoshka-like core–shell structure (Fig. 1A).36 The first layer is a hollow icosahedral cage of Ag12, and the second layer is a dodecahedral Ag20 cage. The two-layer Ag32 core is protected by six Au2(SR)5 motifs (third layer) to form the Ag44(SR)30 structure. To characterize electron-vibration interactions in the Ag44 NCs, we first measured the temperature-dependent electronic absorption spectrum. As shown in Fig. 1B, six excitonic peaks dominated the electronic absorption spectrum between 300 nm and 1100 nm at room temperature (295 K), which agrees with those found in a previous work.36 Upon decreasing the temperature from 295 K to 78 K, it was observed that: (1) all those six absorption peaks become sharper and stronger; (2) the positions of five absorption peaks between 300 nm and 800 nm are apparently blue shifted (Fig. S1†), whereas the position of the absorption band at around 850 nm remains unchanged (Fig. 1B). A similar trend in the absorption spectra at cryogenic temperatures has been reported for several Au nanoclusters, which was explained as electron-vibration coupling within the metal core and on surface motifs.43,44 The strong temperature dependence of the electronic absorption spectrum suggests that significant electron-vibrational coupling occurs in Ag44. Further, the temperature dependent full width at half maximum (FWHM) at ∼610 nm was extracted and is presented in Fig. S2,†45–49 which gives a strength of γLO = 17 meV for the coupling between an optical phonon with an electron.Unlike [Au25(SR)18]− (Au25 for short) which shows splitting in the lowest absorption band at cryogenic temperatures,43,44 the lowest energy absorption band in Ag44 remains as a single peak at 78 K. Previous theoretical calculations on Ag44 reported that the lowest energy absorption band around 1.5 eV arose from HOMO to LUMO+1, whereas the HOMO → LUMO transition is dipole-forbidden.36 The optical energy gap at room temperature estimated from the absorption spectrum is around 1.2 eV (see Fig. S1†), and the photoluminescence was reported to be centered around 1400 nm (0.88 eV),50 which gives a large Stokes shift of 0.32 eV.
To understand the nature of the transition of the lowest-energy absorption band and property of the excited state, quantum chemical calculations were performed using density functional theory (DFT) and time-dependent density functional theory (TDDFT) methods.51,52 Before calculating the electronic transition, the structure was completely relaxed. Fig. S3† displays the isosurface of frontier orbitals of the Ag44 nanocluster. The HOMO and HOMO-1 of Ag44 show a delocalized distribution on the second shell of the cluster (Ag20 cage). The LUMO+1 is symmetrically distributed on the four vertices of the Ag20 cage, whereas the LUMO is concentrated on the Ag12 core (see Fig. 1C). It was found that S0 → S1 is mainly contributed by the HOMO to LUMO transition (98%), and the oscillator strength is very weak (f = 0). S0 → S2 comes from the HOMO-1 to LUMO transition (98%) with an oscillator strength of 0, and S0 → S3 which stems from the HOMO to LUMO+1 transition with an oscillator strength of f = 0.0054 (see Table S1†). The results indicate that the HOMO → LUMO transition is dipole-forbidden, and the lowest-energy optical transition is HOMO → LUMO+1, which agrees with the previous work on all-thiol-stabilized Ag44.21
The analysis of hole–electron distributions is performed to reveal the features of S1−3 states.53 The charge density differences (CDDs) between S1/S3 and S0 states at optimized S0 geometries of Ag44 were calculated by using Δρ(r) = ρele(r) − ρhole(r), and obtained CDDs are displayed in Fig. S4.† The TDDFT calculation results display the charge transefer (CT) feature in the S0 → S3 transition, the CT excited state further deactivation to fully charge transfer (Ag20 → Ag12, CS) state (S1), and then charge recombination. The photoluminescence was previously reported to be 1400 nm (0.88 eV),50 which is consistent with the energy of the CS state (0.899 eV) as shown in Table S1†.
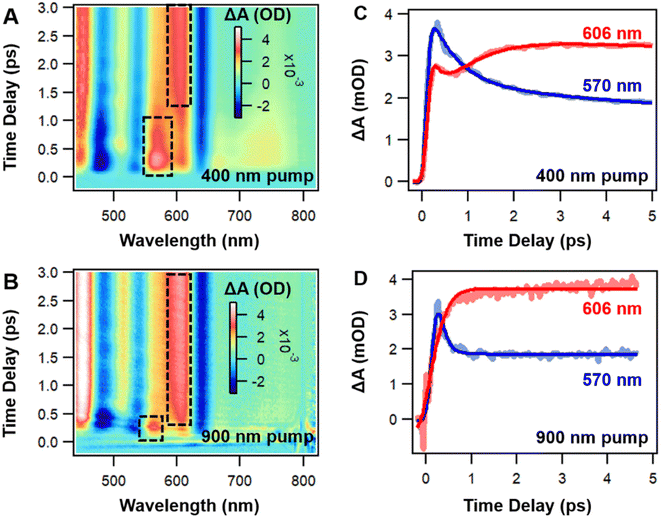
Before examining the coherence dynamics of Ag44, we first used femto-nanosecond transient absorption (TA) spectroscopy to analyze the population dynamics. We chose to pump at 400 nm (3.1 eV) and 900 nm (1.38 eV) to selectively excite the NCs to higher and lower excited states to obtain complete relaxation dynamics. In the TA spectra of Ag44, excited state absorption (ESA, positive signal) and ground state bleaching (GSB, negative signal) are sharp and less overlapped (Fig. 2A, B and S5†). In the initial 3 ps, with 400 nm and 900 nm excitations, significant spectral evolution was observed between 550 nm and 620 nm. The ESA probe at 570 nm decays, and the ESA probe at 606 nm increases at the same time (Fig. 2C and D), which indicates a two-state relaxation model. It should be noted that relative to the excitation under 900 nm, there is an additional ESA band located at the 680–720 nm (Fig. 1A) under 400 nm during the initial delay time, which is ascribed to high-energy populated excited states. The decay of this ESA can be ascribed to the internal conversion (IC) from a higher excited state to a lower excited state. Meanwhile, the excited state dynamics of Ag44 are totally independent of pump fluences (Fig. S6†), ruling out auger recombination as a possible relaxation pathway. From 10 ps to 10 ns, the TA spectra remains unchanged, and there is no spectral evolution (Fig. S5†), and the lifetime of the final excited state is around 300 ns. In a previous work, a long-lived charge separation state has been proposed as the final excited state of the Ag44 NCs.54 Considering the large Stokes shift and two-state relaxation process under both excitation conditions, our results indicate that the final long-lived state at around 0.88 eV should be a CS state, which agrees with DFT calculation results in Fig. 1C.
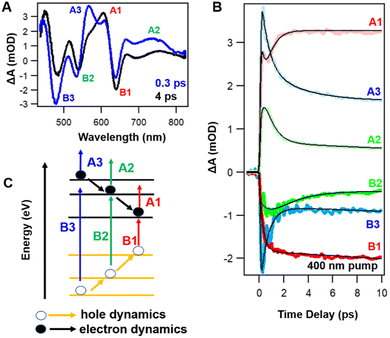
Because ESA and GSB peaks in Ag44 are well separated, it allows us to analyze the electron and hole dynamics, respectively. As shown in Fig. 3A, the GSB peaks around 480, 535 and 640 nm are marked as B3, B2 and B1, respectively, whereas the ESA peaks around 570, 603 and 780 nm are marked as A3, A1 and A2, respectively, (Fig. 3A). It is interesting to see that these three pairs of ESA and GSB peaks show mirror image dynamics, that is, A1 and B1, A2 and B2, A3 and B3 exhibit similar dynamics, respectively, (Fig. 3B). For the three GSB peaks, B3 decays to give rise to B2, and B2 decays give rise to B1. Similarly, A3 decays give rise to A2, and A2 decays to give rise to A1.
All these ESA and GSB decays can be well fitted by a two-step sequential model (see Fig. S7†). Based on the data analysis, the relaxation pathway of Ag44 pumped at 400 nm is summarized in Fig. 3C. The relaxation of electrons and holes involve three steps: (1) a fast decay from a higher excited state to a lower excited state (IC process) in 0.5 ps, (2) a slow decay from a lower excited state to a charge separated state in 2 ps, and (3) a slow charge recombination from the CS state to the ground state in 300 ns. With 900 nm excitation, the mirror image dynamics of ESA and GSB still persist, and the relaxation only involves two steps: fast relaxation to a charge-separated state in 0.2 ps (see Fig. S8†) and the recombination of the CS state in 300 ns. The mirror image dynamics of ESA and GSB indicate that the excited states and ground states of Ag44 share very similar electronic structures. Such an observation could be explained by the highly symmetrical structure in the metal core of the Ag44 NCs.
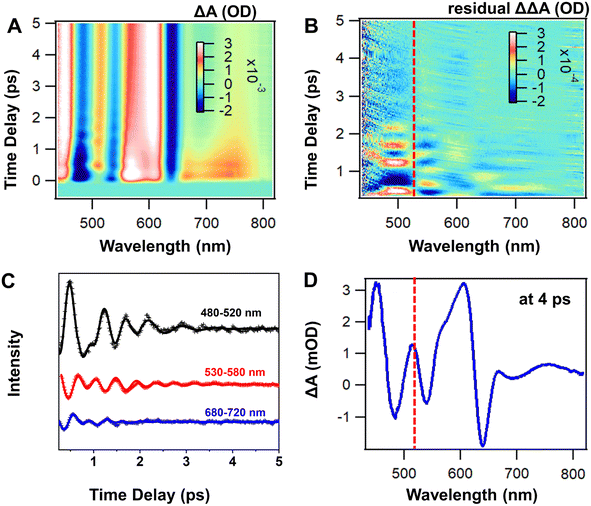
In the initial 5 ps, significant ripples can be observed from the TA data map at almost all of the probe wavelengths under 400 nm and 900 nm excitations (Fig. 4A and S9A†), which indicated significant vibrational coherence. To obtain a clear picture of the coherence signal, we performed global fitting on the TA data of the Ag44 NCs to remove the population dynamics. The residual data as a function of time delay and probe wavelengths represent the distribution of the coherent oscillations (Fig. 4B and S9B†), which indicates wave packet motions. From the residual data map with 400 nm excitation, it was observed that: (1) oscillations probed between 420 nm and 620 nm showed slower damping, whereas those probed between 620 nm and 820 nm were damped more rapidly (see Fig. 4B); (2) the phase flip (node) can be observed around the ESA maximum of around 520 nm (Fig. 4B and D). Because the phase shift and amplitude node were observed in the residual data map, the coherence oscillations in Ag44 should arise from the modulation of the excited state absorption frequency.
Based on oscillation behaviors, we can divide the probe wavelength of the TA spectra into three regions: 480–520 nm, 525–580 nm, and 680–720 nm. The residual kinetics (oscillations) probed in each region are very similar so that we can average the TA kinetics in each region (Fig. 4C). We fit the residual kinetics in these three regions using a damped cosinusoidal function (see eqn S2–S6, ESI†) and obtained the phase and damping information of the oscillations (see Fig. 4C and S10†). The residual kinetics probed over the entire wavelength range exhibited two major vibration modes with periods of ∼0.4 ps and ∼0.6 ps. Moreover, the coherent oscillations probed between 680–720 nm had a damping time of ∼0.25–0.5 ps, two–four times faster than the damping times of those probed in the other two regions (1.0 ps). Fig. S9C, D and Table S2† show the fitting results of the oscillations with 900 nm excitation. The periods and damping times of the oscillations are similar with those obtained with 400 nm excitation (Table 1).
| Probe range (nm) | Period (ps) | Frequency (THz) | t damp (ps) |
|---|---|---|---|
| 480–520 | 0.41 | 2.43 | 1.04 |
| 0.60 | 1.66 | 1.06 | |
| 525–580 | 0.41 | 2.43 | 1.02 |
| 0.61 | 1.64 | 1.04 | |
| 680–750 | 0.37 | 2.69 | 0.23 |
| 0.61 | 1.63 | 0.58 |
The dephasing of vibrational coherence indicates the disappearance of the coherence between two states, while the disappearance of the oscillation can be ascribed to the depopulation of the excited state. The damping of the oscillations measures the decay time of the vibrations in the Ag44 NCs. The decay of the oscillations may arise from pure dephasing or population relaxation.55 With 400 nm excitation, the fast damping (0.25–0.5 ps) of the oscillations probed between 680 nm and 720 nm is consistent with the fast decay of the ESA band probed at the same region (see Fig. 3). In addition, it could be observed that no oscillations in 680–720 nm as well as in the IC process were obtained under 900 nm excitation. Therefore, the rapid disappearance of the oscillations with 400 nm excitation in this region should be related to the fast depopulation relative to other spectral region, and when the populations evolve from a higher to a lower excited state, the wave packet motion of the higher excited state should disappear quickly. This also explains the disappearance of the oscillations probed between 620 nm and 820 nm with 900 nm excitation, because the ESA band in this region remains unchanged during the probing time window. The relatively long-lived vibrational coherence (>1 ps) in Ag44 probed at other wavelengths indicated that the damping should arise from the pure dephasing from the energy disorder or fluctuations.55
The phase of the oscillations provides information on the starting time of the coherence.8 According to a previous study of the coherence of organic molecules, the position of the phase flip can help identify the origin of the wave packet motions.56 The phase flip at the GSB maximum indicates a ground state coherence, while the phase flip occurring at the maximum of the ESA or the stimulated emission (SE) indicates an excited state coherence.8,57 Here, phase shift and zero amplitude are located at around 520 nm (Fig. 4B and D), which is around the ESA peak position. Therefore, excited state coherence is more likely to be responsible for these coherent oscillations.
To further obtain the frequency and amplitude distribution of the coherence, we performed fast Fourier transform (FFT) on the oscillations of each probe wavelength (residual data map) and from this obtained the FFT data map of Ag44 at 400 nm and 900 nm excitations (Fig. 5A and B). Two vibration modes with frequencies of 1.6 THz and 2.4 THz can be identified from the FFT data map, which agrees with the frequency obtained from the fitting results of the oscillations (Table 1). It is worth noting that the 2.4 THz mode agrees with the results in a previous work on Ag44 NCs.38
From the FFT amplitude distribution (Fig. 5C and D) under both excitation conditions, it was found that 1.6 THz and 2.4 THz modes can be observed in the GSB and ESA between 470 nm and 520 nm, while the GSB peak at around 550 nm mainly shows the 2.4 THz mode. With the 900 nm excitation, the 2.4 THz mode disappears together with the ESA band at 700 nm, which agrees with the results in Fig. 3 and S7.† The observation of the two modes with 400 nm and 900 nm excitation indicates that the vibrational coherence in Ag44 (probed between 480 nm and 580 nm) can be generated regardless of the initial state prepared by the pump laser.
To reveal the nature of the low frequency vibration bands associated with Ag44, theoretical computations of Raman spectra were performed. The calculated Raman spectrum (see Fig. S11†) shows three distinct and strong bands (1.8, 2.7 and 3.9 THz, i.e. 61.7, 92.7 and 130.0 cm−1) in the low frequency region (<4.5 THz, 150 cm−1) that are associated with the vibrations involving the Ag metal atom of the cores. These results are in good agreement with the experimental Raman spectrum (1.6, 3.0, 4.0 THz, i.e. 53, 103, 133 cm−1) of Ag44 reported previously.58 In the metal NCs, those vibrations with a frequency below 3 THz (100 cm−1) were previously assigned to the acoustic vibration of the metal core. In Au25(SR)18 and Au144(SR)60 NCs, two vibration modes (2.4 THz and 1.2 THz for Au25 and 2 THz and 1.5 THz for Au144) have been reported, and they were assigned to the breathing mode and quadrupolar-like mode that was dominated by icosahedral cores in Au25 and Au144, respectively.22,24,59 Similarly, the 2.4 THz mode observed in Ag44 should be assigned to the breathing vibration mode of the icosahedral Ag12 core, while the 1.6 THz mode should be assigned to the quadrupolar-like mode of icosahedral Ag12. These two modes agree with the calculation results of the Raman modes of the Ag12 kernel (see Fig. S11 and 12†) at around 2.7 THz (61.7 cm−1) and 1.8 THz (92.7 cm−1).
To further understand the structural effect of the vibrational coherence in metal NCs, we chose Ag29BDT12TPP4 (BDT: 1,3-benzenedithiol; TPP: triphenylphosphine) (Ag29 for short) NCs60 and compared its vibrational coherence with that of Ag44. Ag29 contains an icosahedral Ag13 core protected by a one layer silver shell (Fig. 6A), and it is an ideal model to probe the effect of surface layers on the vibrational coherence. Fig. 6B and C show the TA data map and fitting residual map of Ag29 with photo-excitation of 400 nm. Significant coherent oscillations can also be observed in the TA kinetics in the first 5 ps probed between 450 and 650 nm. The FFT data map of TA residuals shows a significant peak at around 1.6 THz (Fig. 6D, S13 and S14†), which is comparable to the quadrupolar-like mode (see Fig. 5) of icosahedral Ag12 in Ag44. Therefore, in Ag44 and Ag29, we observed the 1.6 THz mode from the icosahedral silver core. After fitting the TA residual kinetics, we found that the dephasing time of the vibrational coherence in Ag29 is shorter when compared to that of Ag44 (see Fig. 6E and S13†). The absence of the 2.4 THz mode in the Ag29 NCs should indicate an even faster decoherence, which is not resolved in our experiments. The fitting parameters of the oscillations of Ag29 are shown in Table 2. The relatively faster dephasing of vibrational coherence and fewer vibration modes in the two-layer Ag29 further supports the fact that the multi-layer core–shell structure can protect the vibrational coherence in the metal NCs. We further analysed the GSB position (∼540 nm) of Ag44 at different time delays, and it was observed that the peak position shows a periodic shift with a period of ∼0.4 ps (Fig. S16A†), corresponding to frequency modulated oscillations (Fig. S16B†).7 However, the TA spectral peak positions of Ag29 almost remained the same during the oscillation, and only the peak intensity shows a periodic change (Fig. S16C†), thus it can be assigned to amplitude modulated oscillations (Fig. S16D†).7
| Probe range (nm) | Period (ps) | Frequency (THz) | t damp (ps) |
|---|---|---|---|
| 476 | 0.61 | 1.64 | 0.53 |
| 523 | 0.63 | 1.59 | 0.91 |
| 562 | 0.64 | 1.57 | 0.51 |
In a previous work on metal NCs, the strong vibrational coherence arises from the low frequency vibration of the inner metal core layer, while the role of the surface layers has not been well understood. It was also reported that icosahedral [Au13(dppe)5Cl2]3+ [dppe: 1,2-bis(diphenylphosphino)ethane)] NCs, with no core–shell structure, did not show significant coherent vibrations in time-resolved experiments.42 However, strong coherent vibrations can be observed in [Au25(SR)18]− NC which contains an icosahedral Au13 core and a one layer shell consisting of four Au3(SR)4 motifs.59 Recently, significant coherent vibrations were reported in Au144(SR)60 (ref. 61) (Au144 for short) NCs with an icosahedral Au12 core protected by two layer gold shells (Au42 and Au60).22 Au144 exhibits similar vibration frequencies as those of [Au25(SR)18]−, while the damping was relatively slower.22,59 After comparing the vibrational coherence results of Au144 and Ag44 in this work, we found that both of NCs consisted of three layers, which should prevent the vibrational coherence of the innermost core from rapid dephasing. Based on a previous study and results reported here, the robust vibrational coherence observed in the Ag44 NCs should be ascribed to their matryoshka-like core–shell structure, which slows the damping of wavepackets by collision with the surrounding environment. The slow dephasing of the vibrational coherence in multi-layer silver NCs should be of importance to their future functions in light harvesting and energy transfer.
Conclusion
In this work, we reported that robust vibrational coherence in the Ag44 NCs can be generated via ultrafast laser excitation. Significant vibrational coherence with frequencies of 2.4 THz and 1.6 THz can be observed. The coherence in Ag44 has a dephasing time of 1 ps at room temperature, which is independent on the excited state relaxation process. Conversely, Ag29 shows a relative faster dephasing time, indicating that the robust vibrational coherence in Ag44 is ascribed to its unique matryoshka-like core–shell structure, which protects the coherence from dephasing. These results not only provide evidence for the vibrational coherence under ambient conditions but also offer new strategies to prepare long-lived vibrational coherence in metal NCs for use in future applications.Methods
Sample preparations
The preparation of [Ag44(SR)30]4+ (SR = SPhF2) and Ag29BDT12TPP4 (BDT = 1,3-benzenedithiolate) NCs follows the method reported in previous work.36,60Temperature dependent UV-vis-NIR absorption spectra
The steady state absorption spectra were measured using a UV-vis-NIR absorption spectrometer (UV-3600 Plus, Shimadzu). The temperature dependent absorption spectra were obtained using a homemade system comprising the UV-3600Plus absorption spectrometer, a cryostat (OptistatCF2, Oxford Instruments), an electronic temperature controller (MercuryiTC, Oxford Instruments) and a vacuum pump. The temperature was adjusted between 295 K and 78 K, and the sample was dissolved in 2-methyltetrahydrofuran (99%, Alfa Aesar), which can form a clear glass at low temperatures.Femtosecond and nanosecond transient absorption spectra
Femtosecond TA measurements were performed on a commercial Ti:Sapphire laser (Astrella, Coherent Instruments, Australia, 800 nm, 35 fs, 1.2 mJ, 5 kHz). The pump pulse was generated using a commercial optical parametric amplifier (TOPAS-prime, Light Converison, Lithuania). The probe pulse was produced by focusing a small portion of the 800 nm femtosecond laser into a sapphire plate. The femtosecond pump-probe measurements were performed on a commercial spectrometer (Helios Fire, Ultrafast Systems, USA). The white light and pump beam were overlapped onto the sample, and linear polarizations were set at the magic angle (54.7°) to record the isotropic response. The instrument response function of the whole device was around 100 fs. The pump energy at the sample was about 40 nJ (spot size diameter was about 100 μm). The concentration of samples in different solvents was adjusted to an absorbance of around 0.3 OD at the excitation wavelength in a 1 mm quartz cuvette. No degradation was observed throughout the experiment, and this was confirmed by the steady absorption spectra. The nanosecond TA measurements were conducted using the same pump pulse and an electronically delayed supercontinuum light (EOS, Ultrafast Systems). The low temperature TA measurements were performed in a cryostat (Janis Research), and the sample was dissolved in polystyrene and drop-casted onto the glass to form a uniform thin film.Quantum chemical calculations
All theoretical calculations were performed using the Gaussian 16 software package. The geometry optimization of the ground state (S0) of Ag44 was calculated using DFT within the D3 dispersion correction at the PBEPBE functional and 6-311G(d,p) basis set (LanL2TZ for Ag).33,62–67 In addition, the stable geometry of S0 was verified by vibrational analysis without imaginary frequencies. The single point energy and vertical excitation energy were calculated using time-dependent density functional theory (TDDFT) based on the optimized S0 geometry.68–70 To extensively study the excited state properties of Ag44, hole–electron distribution analysis for the S0 → S1/3 excitation was further performed using the Multiwfn 3.6 (dev) program.Data availability
The authors declare that the data supporting the findings of this study are available within the paper and its ESI files.† All relevant data are available from the corresponding author on request.Author contributions
J. K., W. Z., and Z. K. contributed equally. J. K., Z. K. and W. Z. planned and performed the experiments, analyzed the data, and wrote the manuscript. G. Y. planned and performed the experiments. C. Z., Y. S., H. W. and Y. L assisted with the experimental design and assisted with the data interpretation. M. Z. planned and performed the experiments, acquired funding, analyzed the data, and wrote the manuscript.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
M. Z. acknowledges the financial support from the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB0450202), National Natural Science Foundation of China (22273095), and Chinese Academy of Sciences (YSBR-007). Y. S. acknowledges the financial support from the Natural Science Foundation of China (22171007). Z. K. acknowledges the financial support from the Natural Science Foundation of China (22303008) and Beijing Natural Science Foundation (2232012).References
- G. D. Scholes, G. R. Fleming and L. X. Chen, et al. , Nature, 2017, 543, 647–656 CrossRef CAS PubMed.
- J. D. Schultz, J. Y. Shin, M. Chen, J. P. O'Connor, R. M. Young, M. A. Ratner and M. R. Wasielewski, J. Am. Chem. Soc., 2021, 143, 2049–2058 CrossRef CAS PubMed.
- J. C. Dean and G. D. Scholes, Acc. Chem. Res., 2017, 50, 2746–2755 CrossRef CAS PubMed.
- S. M. Falke, C. A. Rozzi, D. Brida, M. Maiuri, M. Amato, E. Sommer, A. De Sio, A. Rubio, G. Cerullo, E. Molinari and C. Lienau, Science, 2014, 344, 1001–1005 CrossRef CAS PubMed.
- S. Rafiq and G. D. Scholes, J. Am. Chem. Soc., 2019, 141, 708–722 CrossRef PubMed.
- G. V. Hartland, Chem. Rev., 2011, 111, 3858–3887 CrossRef CAS PubMed.
- D. M. Sagar, R. R. Cooney, S. L. Sewall, E. A. Dias, M. M. Barsan, I. S. Butler and P. Kambhampati, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235321 CrossRef.
- C. Fitzpatrick, J. H. Odhner and R. J. Levis, J. Phys. Chem. A, 2020, 124, 6856–6866 CrossRef CAS PubMed.
- C. J. Bardeen, Q. Wang and C. V. Shank, Phys. Rev. Lett., 1995, 75, 3410–3413 CrossRef CAS PubMed.
- D. M. Jonas, S. E. Bradforth, S. A. Passino and G. R. Fleming, J. Phys. Chem., 1995, 99, 2594–2608 CrossRef CAS.
- S. Rafiq, B. Fu, B. Kudisch and G. D. Scholes, Nat. Chem., 2021, 13, 70–76 CrossRef CAS PubMed.
- Y. Song, S. N. Clafton, R. D. Pensack, T. W. Kee and G. D. Scholes, Nat. Commun., 2014, 5, 4933 CrossRef PubMed.
- J. D. Gaynor, J. Sandwisch and M. Khalil, Nat. Commun., 2019, 10, 5621 CrossRef CAS PubMed.
- S. R. Rather, N. P. Weingartz, S. Kromer, F. N. Castellano and L. X. Chen, Nature, 2023, 620, 776–781 CrossRef PubMed.
- M. Khalil, N. Demirdöven and A. Tokmakoff, J. Chem. Phys., 2004, 121, 362–373 CrossRef CAS PubMed.
- R. Monni, G. Capano, G. Auböck, H. B. Gray, A. Vlček, I. Tavernelli and M. Chergui, Proc. Natl. Acad. Sci. U.S.A., 2018, 115, E6396–E6403 CrossRef CAS PubMed.
- M. Pelton, J. E. Sader, J. Burgin, M. Liu, P. Guyot-Sionnest and D. Gosztola, Nat. Nanotechnol., 2009, 4, 492–495 CrossRef CAS PubMed.
- R. Jin, C. Zeng, M. Zhou and Y. Chen, Chem. Rev., 2016, 116, 10346–10413 CrossRef CAS PubMed.
- M. Zhou, X. Du, H. Wang and R. Jin, ACS Nano, 2021, 15, 13980–13992 CrossRef CAS PubMed.
- M. Zhou and R. Jin, Annu. Rev. Phys. Chem., 2021, 72, 121–142 CrossRef CAS PubMed.
- J. Kong, W. Zhang, Y. Wu and M. Zhou, Aggregate, 2022, 3, e207 CrossRef CAS.
- W. Zhang, J. Kong, Y. Li, Z. Kuang, H. Wang and M. Zhou, Chem. Sci., 2022, 13, 8124–8130 RSC.
- J. Koivisto, S. Malola, C. Kumara, A. Dass, H. Häkkinen and M. Pettersson, J. Phys. Chem. Lett., 2012, 3, 3076–3080 CrossRef CAS PubMed.
- P. Maioli, T. Stoll, H. E. Sauceda, I. Valencia, A. Demessence, F. Bertorelle, A. Crut, F. Vallée, I. L. Garzón, G. Cerullo and N. Del Fatti, Nano Lett., 2018, 18, 6842–6849 CrossRef CAS PubMed.
- M. Y. Sfeir, H. Qian, K. Nobusada and R. Jin, J. Phys. Chem. C, 2011, 115, 6200–6207 CrossRef CAS.
- M. Zhou, T. Higaki, G. Hu, M. Y. Sfeir, Y. Chen, D.-e. Jiang and R. Jin, Science, 2019, 364, 279–282 CrossRef CAS PubMed.
- H. Qian, M. Y. Sfeir and R. Jin, J. Phys. Chem. C, 2010, 114, 19935–19940 CrossRef CAS.
- M. Zhou, S. Tian, C. Zeng, M. Y. Sfeir, Z. Wu and R. Jin, J. Phys. Chem. C, 2017, 121, 10686–10693 CrossRef CAS.
- E. Thyrhaug, S. A. Bogh, M. R. Carro-Temboury, C. S. Madsen, T. Vosch and D. Zigmantas, Nat. Commun., 2017, 8, 15577 CrossRef CAS PubMed.
- Y.-z. Wu, J. Kong, W. Zhang, S. Wang and M. Zhou, J. Phys. Chem. C, 2023, 127, 13723–13730 CrossRef CAS.
- W. Zhang, J. Kong, W. Xu, X. Niu, D. Song, W. Liu and A. Xia, Chin. J. Chem. Phys., 2022, 35, 69–76 CrossRef CAS.
- X. Yu, W. Pei, W.-w. Xu, Y. Zhao, Y. Su and J. Zhao, Inorg. Chem., 2023, 62, 20450–20457 CrossRef CAS PubMed.
- Y. Zhong, J. Zhang, T. Li, W. Xu, Q. Yao, M. Lu, X. Bai, Z. Wu, J. Xie and Y. Zhang, Nat. Commun., 2023, 14, 658 CrossRef CAS PubMed.
- R. Jin, C. Zeng, M. Zhou and Y. Chen, Chem. Rev., 2016, 116, 10346–10413 CrossRef CAS PubMed.
- Y. Negishi, T. Nakazaki, S. Malola, S. Takano, Y. Niihori, W. Kurashige, S. Yamazoe, T. Tsukuda and H. Häkkinen, J. Am. Chem. Soc., 2015, 137, 1206–1212 CrossRef CAS PubMed.
- H. Yang, Y. Wang, H. Huang, L. Gell, L. Lehtovaara, S. Malola, H. Häkkinen and N. Zheng, Nat. Commun., 2013, 4, 2422 CrossRef PubMed.
- M. Zhu, C. M. Aikens, F. J. Hollander, G. C. Schatz and R. Jin, J. Am. Chem. Soc., 2008, 130, 5883–5885 CrossRef CAS PubMed.
- Y. Wang, X.-H. Liu, Q. Wang, M. Quick, S. A. Kovalenko, Q.-Y. Chen, N. Koch and N. Pinna, Angew. Chem., Int. Ed., 2020, 59, 7748–7754 CrossRef CAS PubMed.
- M. A. Abbas, P. V. Kamat and J. H. Bang, ACS Energy Lett., 2018, 3, 840–854 CrossRef CAS.
- H. Yang, J. Lei, B. Wu, Y. Wang, M. Zhou, A. Xia, L. Zheng and N. Zheng, Chem. Commun., 2013, 49, 300–302 RSC.
- O. Varnavski, G. Ramakrishna, J. Kim, D. Lee and T. Goodson III, ACS Nano, 2010, 4, 3406–3412 CrossRef CAS PubMed.
- M. Zhou, R. Jin, M. Y. Sfeir, Y. Chen, Y. Song and R. Jin, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E4697–E4705 CrossRef CAS PubMed.
- M. S. Devadas, S. Bairu, H. Qian, E. Sinn, R. Jin and G. Ramakrishna, J. Phys. Chem. Lett., 2011, 2, 2752–2758 CrossRef CAS.
- Z. Liu, Y. Li, W. Shin and R. Jin, J. Phys. Chem. Lett., 2021, 12, 1690–1695 CrossRef CAS PubMed.
- J. Mooney, M. M. Krause and P. Kambhampati, J. Phys. Chem. C, 2014, 118, 7730–7739 CrossRef CAS.
- T. G. Mack, L. Jethi and P. Kambhampati, J. Phys. Chem. C, 2017, 121, 28537–28545 CrossRef CAS.
- D. P. Strandell and P. Kambhampati, J. Phys. Chem. C, 2021, 125, 27504–27508 CrossRef CAS.
- Z. Liu, M. Zhou, L. Luo, Y. Wang, E. Kahng and R. Jin, J. Am. Chem. Soc., 2023, 145, 19969–19981 CrossRef CAS PubMed.
- Y. Wang, Z. Liu, A. Mazumder, C. G. Gianopoulos, K. Kirschbaum, L. A. Peteanu and R. Jin, J. Am. Chem. Soc., 2023, 145, 26328–26338 CrossRef CAS PubMed.
- O. M. Bakr, V. Amendola, C. M. Aikens, W. Wenseleers, R. Li, L. Dal Negro, G. C. Schatz and F. Stellacci, Angew. Chem., Int. Ed., 2009, 48, 5921–5926 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks and H. B. Schlegel, et al., Gaussian, Vol. 16, Revision C.02, Gaussian, Inc., Wallingford CT, 2019 Search PubMed.
- M. Bursch, J.-M. Mewes, A. Hansen and S. Grimme, Angew. Chem., Int. Ed., 2022, 61, e202205735 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- M. Pelton, Y. Tang, O. M. Bakr and F. Stellacci, J. Am. Chem. Soc., 2012, 134, 11856–11859 CrossRef CAS PubMed.
- Y. Yoneda, B. Kudisch, S. Rafiq, M. Maiuri, Y. Nagasawa, G. D. Scholes and H. Miyasaka, J. Am. Chem. Soc., 2021, 143, 14511–14522 CrossRef CAS PubMed.
- S. Rafiq and G. D. Scholes, J. Phys. Chem. A, 2016, 120, 6792–6799 CrossRef PubMed.
- I. H. M. v. Stokkum, C. C. Jumper, J. J. Snellenburg, G. D. Scholes, R. v. Grondelle and P. Malý, J. Chem. Phys., 2016, 145, 174201 CrossRef PubMed.
- K. K. Ramankutty, H. Yang, A. Baghdasaryan, J. Teyssier, V. P. Nicu and T. Buergi, Phys. Chem. Chem. Phys., 2022, 24, 13848–13859 RSC.
- H. Qian, M. Y. Sfeir and R. Jin, J. Phys. Chem. C, 2010, 114, 19935–19940 CrossRef CAS.
- L. G. AbdulHalim, M. S. Bootharaju, Q. Tang, S. Del Gobbo, R. G. AbdulHalim, M. Eddaoudi, D.-e. Jiang and O. M. Bakr, J. Am. Chem. Soc., 2015, 137, 11970–11975 CrossRef CAS.
- W. R. Jeffries, S. Malola, M. A. Tofanelli, C. J. Ackerson, H. Häkkinen and K. L. Knappenberger Jr, J. Phys. Chem. Lett., 2023, 14, 6679–6685 CrossRef CAS.
- W.-D. Si, C. Zhang, M. Zhou, W.-D. Tian, Z. Wang, Q. Hu, K.-P. Song, L. Feng, X.-Q. Huang, Z.-Y. Gao, C.-H. Tung and D. Sun, Sci. Adv., 2023, 9, eadg3587 CrossRef CAS PubMed.
- D. Arima and M. Mitsui, J. Am. Chem. Soc., 2023, 145, 6994–7004 CrossRef CAS PubMed.
- J. Li, P. Wang and Y. Pei, J. Phys. Chem. Lett., 2022, 13, 3718–3725 CrossRef CAS PubMed.
- P. Luo, X.-J. Zhai, S. Bai, Y.-B. Si, X.-Y. Dong, Y.-F. Han and S.-Q. Zang, Angew. Chem., Int. Ed., 2023, e202219017 CAS.
- Z.-J. Guan, R.-L. He, S.-F. Yuan, J.-J. Li, F. Hu, C.-Y. Liu and Q.-M. Wang, Angew. Chem., Int. Ed., 2022, 61, e202116965 CrossRef CAS PubMed.
- X.-L. Pei, Z.-J. Guan, Z.-A. Nan and Q.-M. Wang, Angew. Chem., Int. Ed., 2021, 60, 14381–14384 CrossRef CAS PubMed.
- D. Lin, M. Zheng and W. W. Xu, Phys. Chem. Chem. Phys., 2020, 22, 16624–16629 RSC.
- X.-Y. Xie, P. Xiao, X. Cao, W.-H. Fang, G. Cui and M. Dolg, Angew. Chem., Int. Ed., 2018, 57, 9965–9969 CrossRef CAS PubMed.
- L.-M. Wang, S. Bulusu, H.-J. Zhai, X.-C. Zeng and L.-S. Wang, Angew. Chem., Int. Ed., 2007, 46, 2915–2918 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc00009a |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |