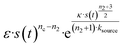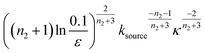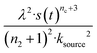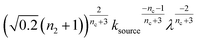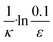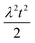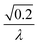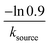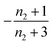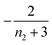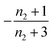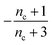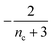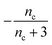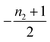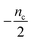Open Access Article
Open Access ArticleKinetic models reveal the interplay of protein production and aggregation†
Jiapeng
Wei
 a,
Georg
Meisl
a,
Georg
Meisl
 a,
Alexander
Dear
ab,
Matthijs
Oosterhuis‡
c,
Ronald
Melki
d,
Cecilia
Emanuelsson
c,
Sara
Linse
a,
Alexander
Dear
ab,
Matthijs
Oosterhuis‡
c,
Ronald
Melki
d,
Cecilia
Emanuelsson
c,
Sara
Linse
 e and
Tuomas P. J.
Knowles
e and
Tuomas P. J.
Knowles
 *af
*af
aCentre for Misfolding Diseases, Yusuf Hamied Department of Chemistry, University of Cambridge, Lensfield Road, Cambridge CB2 1EW, UK. E-mail: tpjk2@cm.ac.uk
bDepartment of Biochemistry and Structural Biology, Lund University, SE22100, Lund, Sweden
cDepartment of Biochemistry and Structural Biology, Center for Molecular Protein Science, Lund University, Sweden
dInstitut Francois Jacob (MIRCen), CEA and Laboratory of Neurodegenerative Diseases, CNRS, 18 Route du Panorama, Fontenay-Aux-Roses cedex, 92265, France
eDepartment of Biochemistry and Structural Biology, Lund University, Lund, Sweden
fCavendish Laboratory, University of Cambridge, J J Thomson Avenue, CB3 0HE, UK
First published on 10th May 2024
Abstract
Protein aggregation is a key process in the development of many neurodegenerative disorders, including dementias such as Alzheimer's disease. Significant progress has been made in understanding the molecular mechanisms of aggregate formation in pure buffer systems, much of which was enabled by the development of integrated rate laws that allowed for mechanistic analysis of aggregation kinetics. However, in order to translate these findings into disease-relevant conclusions and to make predictions about the effect of potential alterations to the aggregation reactions by the addition of putative inhibitors, the current models need to be extended to account for the altered situation encountered in living systems. In particular, in vivo, the total protein concentrations typically do not remain constant and aggregation-prone monomers are constantly being produced but also degraded by cells. Here, we build a theoretical model that explicitly takes into account monomer production, derive integrated rate laws and discuss the resulting scaling laws and limiting behaviours. We demonstrate that our models are suited for the aggregation-prone Huntington's disease-associated peptide HttQ45 utilizing a system for continuous in situ monomer production and the aggregation of the tumour suppressor protein P53. The aggregation-prone HttQ45 monomer was produced through enzymatic cleavage of a larger construct in which a fused protein domain served as an internal inhibitor. For P53, only the unfolded monomers form aggregates, making the unfolding a rate-limiting step which constitutes a source of aggregation-prone monomers. The new model opens up possibilities for a quantitative description of aggregation in living systems, allowing for example the modelling of inhibitors of aggregation in a dynamic environment of continuous protein synthesis.
Introduction
The self-assembly of proteins into amyloid fibrils is an important process in the development of a range of neurodegenerative diseases such as Alzheimer's, Parkinson's and Huntington's disease.1–5 Motivated by this biological importance, the aggregation of many the associated proteins has been studied in detail under controlled in vitro conditions.1,6,7 The analysis of these data using chemical kinetics has provided a wealth of mechanistic insights,8,9 from elucidating the differences between disease associated mutations,10–12 over determining the mode of action of inhibitory compounds,13–18 to unravelling global trends across different proteins.19 A key advance that enabled these discoveries was the development of integrated rate laws to describe time-evolution of the measured quantities and link them to the underlying reaction mechanisms.20–24 These rate laws not only made feasible the fitting of experimental data to extract mechanistic information,25 they also provide intuitive understanding of how changes in the different molecular processes influence the observable time evolution of aggregate numbers and sizes. In this work we derive new integrated rate laws that account for a range of different reactions that produce aggregation-prone monomer, forming the basis for the analysis of aggregation in living systems.Protein aggregation is the result of the combined action of several microscopic-level processes that operate together in a complex reaction network. The aggregation process is initiated by primary nucleation, which is the spontaneous formation of an elongation-competent fibril from free monomers.26–28 After the formation of fibrils, free monomers can further add onto either end of the fibril in the process of elongation. In many protein systems, there are also secondary processes, autocatalytic fibril multiplication events, which lead to the formation of new aggregates from existing aggregates.29–31 Fibril fragmentation and surface-catalyzed secondary nucleation are typical examples of such secondary processes.20,32
Explicit description of primary nucleation, elongation and secondary processes covers all the main processes that are commonly driving the aggregation kinetics of proteins in pure buffer systems. However, the condition that all monomer that will eventually aggregate is present at the beginning of the reaction is not always satisfied. For instance, for some protein aggregation reactions, there is an additional step before the aggregation to change a non-aggregating precursor into the aggregation-prone monomer, for example by unfolding a natively folded protein monomer or dissociation of either an oligomeric form of a protein or a complex this protein forms with partners.33–39 In an in vivo situation, monomers are created and degraded constantly by the organism. They further partition between aggregation prone and incompetent forms depending on their partners. In other words, in these systems protein aggregation has already started before all free monomers that will aggregate during the aggregation reaction are present, which breaks the conservation law between free monomers and aggregates. We summarize this process of creating or adding new free monomers during the aggregation as the monomer source-term.
In this work, we generate new integrated rate laws which describe protein aggregation with a source-term. We demonstrate the utility of our model by applying it to the analysis of the in vitro experimental data of HTTExon1Q45 (HTTQ45) aggregation (HTTExon1Q45 is encoded by the exon 1 of HTT gene bearing 45 glutamine residues) and the in vitro experimental data of P53 aggregation, showcasing how adding a source-term can fundamentally alter aggregation behaviour in practice. To provide an intuitive understanding of the effect of monomer production we also derive analytical solutions for the scaling of key experimental observables, such as the timescale of the reaction, with monomer concentration and monomer production rate. We also analytically solve a simplified in vivo aggregation model which contains constant monomer production rate and monomer clearance process proportional to the monomer concentration. Finally, we discuss a range of different monomer production processes and present a general approach to deriving analytical solutions for new source-terms not explicitly treated in this work.
Results
The fundamentals of aggregation with a source-term
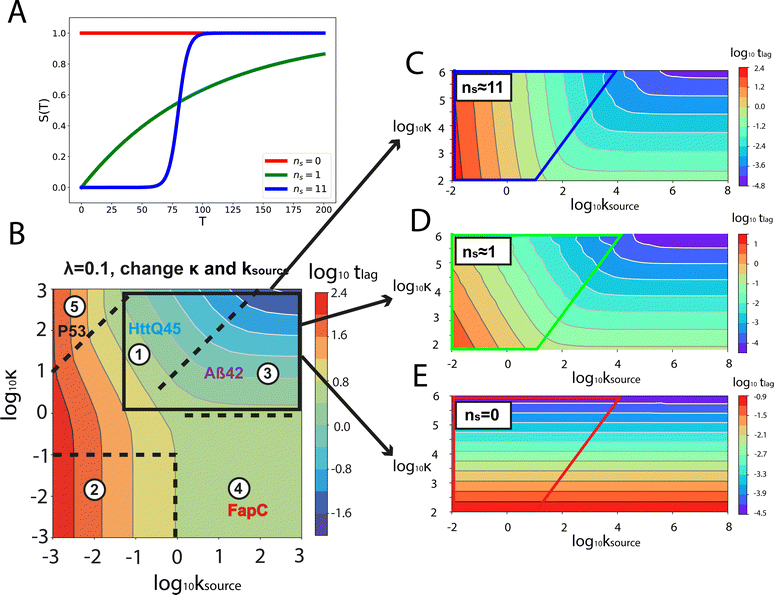
Fig. 1A shows the reaction network of aggregation with a monomer source: primary nucleation, elongation, secondary nucleation and the monomer source. | ||
| Fig. 1 Elementary steps of protein aggregation with a source-term and schematic representation of a typical kinetic curve for amyloid growth, with and without a source-term. (A) Non-aggregating precursor (red circles) is converted to aggregation-prone monomer (blue circles). This in turn can form new aggregates (blue squares) by primary nucleation, which then grow by elongation and self-replicate, for example by secondary nucleation. (B) Comparison of the aggregation curve without a source-term (blue curve) and with the source-term S(T) = 1 − e−KT (red curve), which are numerical solutions of eqn (2). Parameters of the red curve are K = 1010, ε = 10−10, nc = n2 = 2. Parameters of the blue curve are K = 10−2.25, ε = 10−10, nc = n2 = 2. | ||
Adding a source-term breaks the conservation law between the aggregation-prone monomer concentration m(t) and the aggregate mass concentration M(t). The kinetic equations and boundary conditions therefore need to be altered from their usual forms (see eqn (S3c)†).20,25 The reaction network in Fig. 1 is described by:
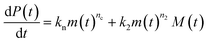 | (1a) |
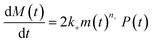 | (1b) |
| m(t) + M(t) = s(t, ksource) | (1c) |
| M(0) = P(0) = 0, M(∞) = mtot, m(0) = s(0, ksource) | (1d) |
To facilitate an exploration of possible behaviours of this system, we can non-dimensionalize eqn (1) by introducing a series of dimensionless parameters: a dimensionless time variable T = κ·t, where 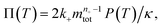 a dimensionless source-term rate constant K = ksource/κ, a dimensionless free monomer concentration μ(T) = m(T)/mtot, a dimensionless aggregate mass ν(T) = M(T)/mtot, a dimensionless aggregate number
a dimensionless source-term rate constant K = ksource/κ, a dimensionless free monomer concentration μ(T) = m(T)/mtot, a dimensionless aggregate mass ν(T) = M(T)/mtot, a dimensionless aggregate number 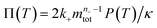 and a dimensionless parameter ε = λ2/(2κ2), where
and a dimensionless parameter ε = λ2/(2κ2), where 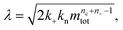 which describes the relative importance of primary nucleation compared to the secondary process. The dimensionless source-term function is S(T, K) = s(t, ksource)/mtot. In this manner, eqn (1) become:
which describes the relative importance of primary nucleation compared to the secondary process. The dimensionless source-term function is S(T, K) = s(t, ksource)/mtot. In this manner, eqn (1) become:
| Π′(T) = 2εμ(T)nc + ν(T)μ(T)n2 | (2a) |
| ν′(T) = μ(T)n+Π(T) | (2b) |
| S(T, K) = μ(T) + ν(T) | (2c) |
| ν(0) = Π(0) = 0, ν(∞) = 1, μ(0) = S(0, K). | (2d) |
To illustrate the effect of a monomer source, we now choose a specific source-term function. A number of different types of monomer sources, such as enzyme cleavage (in excess of enzyme),40 unfolding34 or dissociation (when the reverse reaction is slow enough to be neglected, at first glance this is counter-intuitive as a complex at equilibrium will have equal dissociation and association rates, but this condition may be met if the dissociated monomer is consumed more rapidly in amyloid formation than in the reverse reaction),33 can be approximated as first order reactions. In other words, the reaction rate is approximately proportional to the concentration of non-aggregating precursor and it is not affected by the concentration of free monomers and the aggregated fibrils. Under such assumptions, the source-term function can be easily obtained from the solution of a first order reaction:
| S(T, K) = 1 − e−KT. | (3) |
An example numerical solution of ν(T) in eqn (2) for representative parameters is shown as the blue curve in Fig. 2B. In the absence of a source-term the curve plateaus immediately after the growth phase. By contrast, in a system with a source-term, the growth phase is followed not by a flat plateau phase but by a gradually increasing phase dominated by the source-term function S(T). We refer to this as the source phase since the aggregation rate in this regime is determined by the source-term. Its presence is a key distinguishing feature between aggregation reactions with and without a source.
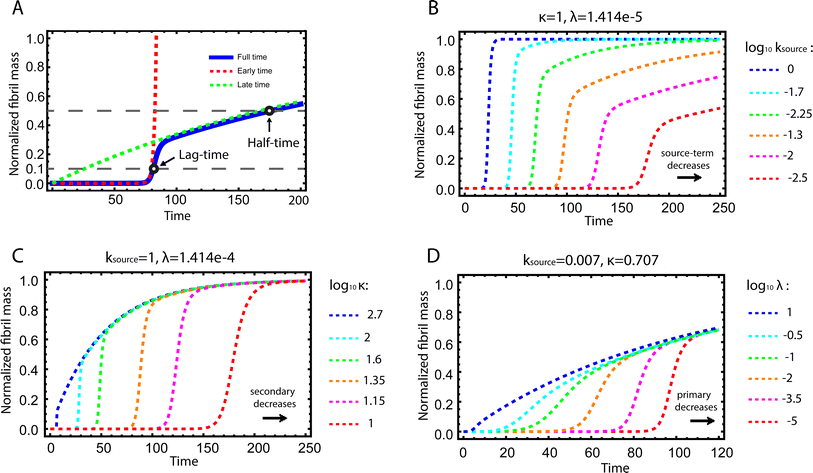 | ||
| Fig. 2 Kinetics of source-term aggregation. (A) The exact, numerical solution of eqn (2) is the blue solid line. The early time solution, eqn (5), is the red dashed line. The late time solution, eqn (3), is the green dashed line. ε = 10−10 and K = 10−3. (B) Aggregation curves at fixed aggregation rates, κ and λ, and decreasing monomer production rate constant ksource from left to right. (C) The monomer production rate ksource and the primary nucleation rate λ are fixed, the secondary nucleation rate κ, decreases from left to right. (D) The monomer production rate ksource and the secondary nucleation rate κ are fixed, the primary nucleation rate λ, decreases from left to right. nc = n2 = 2 and n+ = 1 for all panels. | ||
Fig. 2B–D are the numerical solutions of eqn (1) for different values of ksource, λ and κ, which show how the shape of the aggregation curve is affected in different ways by the monomer production rate constant, ksource, the rate of aggregate formation via primary nucleation, λ, and the rate of aggregate formation via secondary nucleation, κ. In Fig. 2B the monomer production rate ksource decreases from left to right, which not only increases the length of the lag phase but also change the shape of the source phase. Clearly, the lower the rate of monomer production from the source, the more does the curve shape deviate from a regular curve with a flat plateau phase. In Fig. 2C and Dksource is instead fixed and κ (Fig. 2C) or λ (Fig. 2D) decrease from left to right. This increases the length of the lag phase and decreases the slope during the growth phase, while the source phases of these curves are collapsed. This highlights that only ksource can affect shape of the source phase whereas all three parameters affect the length of the lag phase.
Deriving an approximate analytical expression for the integrated rate law
Next we set out to obtain an approximate analytical solution to the rate equations to yield an equation that can easily be fitted to experimental data. Our strategy to derive an integrated rate law includes two steps. First, constructing a perturbative solution for μ(T) as this will turn out to be singular and valid only at early times. The second step is to regularize it and convert it into a global solution valid for all times, which can be applied to complete aggregation curves.We derive the perturbation equations in ESI Section 6;† they turn out to be identical to the early-time limit of the full equations. This limit can be taken as follows. At early times, it is reasonable to approximate the free monomer concentration by the total converted precursor concentration: μ(T) ≈ μ(T) + ν(T) = S(T) since the mass concentration of aggregates, ν(T), is still small enough to be ignored. Thus, the kinetic equations simplify to:
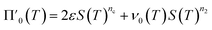 | (4a) |
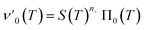 | (4b) |
Eqn (4) can be analytically solved only when all steps have the same reaction order, i.e. nc = n2 = n+. For general reaction orders, we therefore seek an approximate solution, using as a starting point the exact analytical solution of the special case nc = n2 = n+ (for details see ESI Section 4†).
This ultimately yields the following approximate early time solution:
 | (5) |
The second task is to obtain a global solution, ν(t). This is done by regularizing the perturbative solution ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) 0 = μ0/S = 1 − ν0/S using the recently-developed method of asymptotic Lie symmetries (ESI Section 6†):22,41–44
0 = μ0/S = 1 − ν0/S using the recently-developed method of asymptotic Lie symmetries (ESI Section 6†):22,41–44
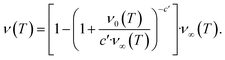 | (6) |
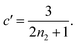
Substituting the early time solution eqn (5) into the unified equation eqn (6), we obtain the approximate full timescale solution for aggregation with a source-term. This approximate analytical solution converges on the exact numerical solution of the aggregation kinetics almost precisely, as shown in Fig. S2 in the ESI Section 6.†
Experimental data confirm the importance of source-terms in different systems
A central motivation for the development of source-term models is the fact that in an in vivo situation, monomers are constantly being created during an on-going aggregation reaction. To demonstrate that our strategy is able to model such systems, we show its application to a simplified in vivo aggregation model which includes a constant monomer production rate and a monomer clearance process proportional to the monomer concentration in a later section. For the comparison with experimental data, we will instead focus on well-controlled in vitro systems where the source-term is a well-characterised process that converts a finite pool of non-aggregating precursor.To evaluate the performance of our models, we use an in vitro system producing aggregation-prone monomer via cleaving a large, non-aggregating construct in a closed system with constant total protein mass. We have developed such a system for the aggregation of HttQ45, as an in vitro model of Huntington's disease.45 In this system, aggregation is initiated by enzymatic cleavage of an MBP–HttQ45 fusion protein by the TEV enzyme40 and subsequent aggregation of HttQ45, as shown in Fig. 3B. While this differs from the way in which HttQ45 is produced in vivo, it provides a useful system for evaluating the performance of our models as the monomer production rate can easily be tuned.
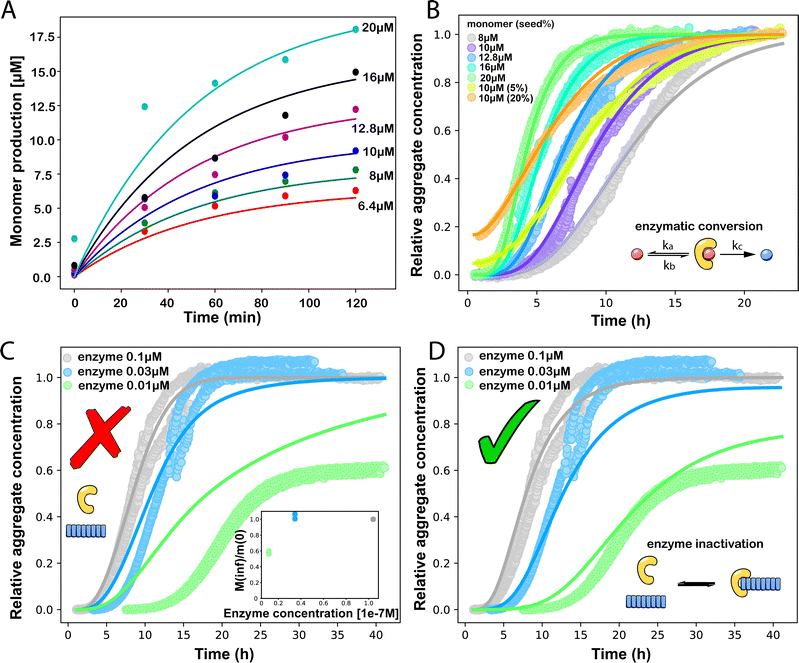 | ||
Fig. 3 (A) Monomer production due to enzymatic cleavage (points) as estimated using SDS PAGE together with the best fit using s(t) = mtot(1 − e−ksourcet), resulting in a value of ksource/e0 = 2.22 h−1 μM−1. The values of mtot were set at 6.4 μM, 8 μM, 10 μM, 12.8 μM, 16 μM, 20 μM for various curves. The gel electrophoresis images of A are shown in ESI Section 7 Fig. S3.† It's important to note that e0 remained constant at 0.54 μM for different curves and across all curves. (B) Numerical global fit to the aggregate curves of HttQ45 aggregation with the source-term s(t) = mtot(1 − e−ksourcet). mtot = 8 μM, 10 μM, 12.8 μM, 16 μM, 20 μM. e0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mtot = 1 mtot = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50. Two curves among them are aggregations with 5% and 20% seed fibrils (from the plateau phase of a reaction under the same conditions) with mtot = 10 μM. (Inset) Schematic of the enzymatic cleavage of MBP–HttQ45 as an aggregation source-term. B is kinetic data from Månsson et al.40 (C and D) Numerical global fit to the aggregate curves of HttQ45 aggregation with different concentration of enzyme. mtot = 11 μM and enzyme concentrations are: 0.1 μM, 0.03 μM, 0.01 μM. (C) Fitted with the model without enzyme binding. Fitted parameters are: kn = 64.6 M1−nc s−1, nc = 0.00133, k2 = 7.6 × 10−8 M−n2 s−1, n2 = 0.001, k+ = 2.54 × 10−4 M−1 s−1 and kc = 4.04 × 106 M−1 s−1. (Inset) The relation between the final aggregate percentage M(∞)/mtot and enzyme concentration. (D) Fitted with the model with enzyme binding. Fitted parameters are: kn = 412 M1−nc s−1, nc = 2.38, k2 = 3.39 × 10−8 M−n2 s−1, n2 = 0.0003, k+ = 6 × 107 M−1 s−1, kc = 5.13 × 106 M−1 s−1, KD = 2.9 × 10−12, kf = 5.22 × 104 M−1 s−1, and α = 0.0569. (Inset) Cartoon illustrating the enzyme binding on fibril ends which may interfere with the microscopic step elongation. 50. Two curves among them are aggregations with 5% and 20% seed fibrils (from the plateau phase of a reaction under the same conditions) with mtot = 10 μM. (Inset) Schematic of the enzymatic cleavage of MBP–HttQ45 as an aggregation source-term. B is kinetic data from Månsson et al.40 (C and D) Numerical global fit to the aggregate curves of HttQ45 aggregation with different concentration of enzyme. mtot = 11 μM and enzyme concentrations are: 0.1 μM, 0.03 μM, 0.01 μM. (C) Fitted with the model without enzyme binding. Fitted parameters are: kn = 64.6 M1−nc s−1, nc = 0.00133, k2 = 7.6 × 10−8 M−n2 s−1, n2 = 0.001, k+ = 2.54 × 10−4 M−1 s−1 and kc = 4.04 × 106 M−1 s−1. (Inset) The relation between the final aggregate percentage M(∞)/mtot and enzyme concentration. (D) Fitted with the model with enzyme binding. Fitted parameters are: kn = 412 M1−nc s−1, nc = 2.38, k2 = 3.39 × 10−8 M−n2 s−1, n2 = 0.0003, k+ = 6 × 107 M−1 s−1, kc = 5.13 × 106 M−1 s−1, KD = 2.9 × 10−12, kf = 5.22 × 104 M−1 s−1, and α = 0.0569. (Inset) Cartoon illustrating the enzyme binding on fibril ends which may interfere with the microscopic step elongation. | ||
The source-term, i.e. the enzymatic cleavage reaction, can be measured directly by monitoring the precursor and products by gel electrophoresis (see ESI Section 7 Fig. S3†). Since the enzyme concentration used in this experiment is e0 = 0.54 μM ≪ mtot, we can use the steady state approximation to write the source-term s(t):
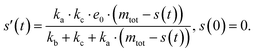 | (7) |
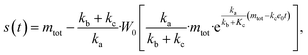 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) min−1 = 1.2 h−1 where ka = ksource/e0.
min−1 = 1.2 h−1 where ka = ksource/e0.
We then use this rate constant when fitting the aggregation kinetics of HttQ45. Experiments under two conditions are shown, the first at a range of monomer and seed concentrations, at a constant enzyme to protein ratio of e0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mtot = 1
mtot = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50, Fig. 3B, the second at a constant monomer concentration with increasing inhibitor concentration, Fig. 3C and D. The aggregation kinetics are monitored by ThT fluorescence intensity.
50, Fig. 3B, the second at a constant monomer concentration with increasing inhibitor concentration, Fig. 3C and D. The aggregation kinetics are monitored by ThT fluorescence intensity.
We use a customised version of Amylofit25 to fit the kinetic data to the model in eqn (1) with the source-term s(t) = 1 − e−ksourcet. For the data in Fig. 3B the fitting parameters are: ksource = ka × mtot/50, kn = 2 × 104 M1−nc s−1, nc = 2.7, k2 = 3.7 × 10−5 M−n2 s−1, n2 = 0, k+ = 6.3 × 107 M−1 s−1, from which we calculate that λ = 0.28 and κ = 0.14. The source-term rate constant ksource ≈ 0.44 h−1 ≈ λ ≈ κ, which implies that the system lies close to the boundary where the source-term starts affecting the kinetics, but is still mainly dominated by the aggregation reaction, rather than the source.
In order to push the system into a regime where the source-term becomes more dominant, we then further decreased the enzyme concentration. In this experiment, the aggregation kinetics are measured at constant concentration, 11 μM, of MBP-HttQ45 with different enzyme concentrations: 0.1 μM, 0.03 μM and 0.01 μM.
Using the same model as in the high enzyme limit performs acceptably at the higher enzyme concentrations, but fails to match the data at the lower enzyme concentrations, Fig. 3C. We also find that for the lower enzyme concentrations, the aggregation curves do not reach the same fluorescence level at the plateau as the high enzyme concentrations, indicating that not all precursor has been cleaved by the enzyme, Fig. 3C inset. Inactivation of the enzyme could explain both the fact that the aggregation at low enzyme concentrations proceeds slower than predicted and that the plateau fluorescence levels decrease with decreasing enzyme. To test this hypothesis, we designed a kinetic experiment in which a low concentration of enzyme was present initially, but further enzyme was added after 24 hours. As expected, we observe that, upon addition of further enzyme, the fluorescence again increases, reaching the same plateau level as in the high enzyme case (see ESI Section 9†). While these data show both that our models accurately describe the source-term when the enzyme cleavage reaction is well behaved, and that enzyme is indeed being inactivated when our models no longer fit, we decided to further test the capability of our approach by extending the models to include one possible mechanism of enzyme inactivation. We do note that, surprisingly, the larger the protein concentration, the more pronounced the inactivation effect is, despite the faster aggregation reaction at higher protein concentrations (see ESI Section 10†). This observation is in disagreement with a mechanism of deactivation that is aggregation independent, such as for example oxidation. It leads us to propose the following mechanism: the enzyme cleaves the precursor to form aggregation-prone monomer, but can be inactivated by binding to fibrils (for example, small amounts of uncleaved monomer may incorporate into the fibril, and then sequester the enzyme, leading to enzyme inactivation). The differential equations describing this mechanism are:
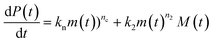 | (9a) |
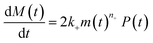 | (9b) |
| m(t) + M(t) = mtot × [1 − e−kc·E(t)·t] | (9c) |
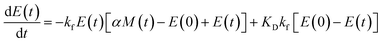 | (9d) |
| M(0) = P(0) = 0 = m(0) = 0 | (9e) |
In summary, at lower enzyme concentrations, additional effects of enzyme inactivation complicate the situation, but our minimal source-term model describes well the experimentally measured aggregation kinetics, correctly reproducing both monomer and enzyme concentration dependence.
Another in vitro example of such a situation is the aggregation of the P53 protein, whose aggregation is implicated in cancer.33,35 Monomeric P53 unfolding drives its aggregation. Thus, the rate-limiting P53 unfolding can be considered a source-term within our description. This unfolding process can be captured by the source-term s(t) = mtot(1 − e−ksourcet). To investigate in more detail the rate-limiting step of this process with our models, we use P53 aggregation kinetics data from Wilcken et al.35 We find that aggregation curves normalised by mtot collapse onto a single curve, which implies that the kinetics are dominated by a first order reaction in m(t), consistent with a source-term dominated system where M(t) = s(t). We use the model in eqn (1) to globally fit the P53 aggregation data at different mtot.25 The fitting result shows that ksource = 0.0572 M−1 s−1 ≪ ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) mon ∼ 108 M−1 s−1 (
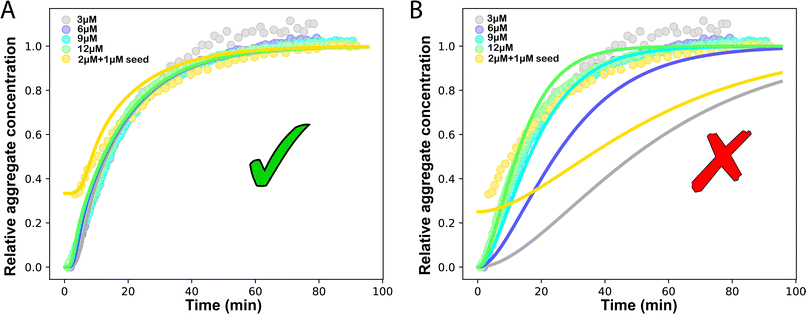
mon ∼ 108 M−1 s−1 (![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) mon is the critical monomer production rate, which is defined in eqn (11)). Fitting result is shown in Fig. 4A, which implies that for P53 aggregation, unfolding source-term is the rate determining step and P53 source-term aggregation lies in region 5 of Fig. 5. Fig. 4B is fitted with the aggregation model without a source-term, which clearly shows that it is not possible to describe P53 aggregation kinetic without a source-term.
mon is the critical monomer production rate, which is defined in eqn (11)). Fitting result is shown in Fig. 4A, which implies that for P53 aggregation, unfolding source-term is the rate determining step and P53 source-term aggregation lies in region 5 of Fig. 5. Fig. 4B is fitted with the aggregation model without a source-term, which clearly shows that it is not possible to describe P53 aggregation kinetic without a source-term.
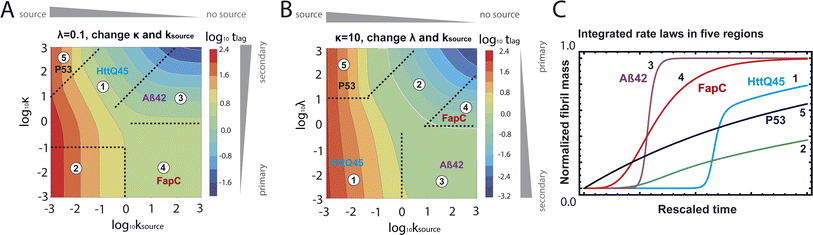 | ||
| Fig. 5 Lag time contour plots. (A) Is the numerical lag time contour plot for nc = n2 = 2 and λ = 0.1. (B) Is the numerical lag time contour plot for nc = n2 = 2 and κ = 10. The color indicates the value of lag time. Colder color represents smaller lag time. Grey triangles imply the dominant microscopic step in each regime. Dashed black lines in (A) and (B) are theoretical predictions (Table S2†) of the boundaries between different regimes. (C) Shows the shape of the integrated rate laws in these five regimes. The plotting parameters are: K = 10−2, 10−2, 10, 10, 10−7, and ε = 10−10, 1, 10−10, 102, 10−6, and κ = 1.25, 4, 2.5, 286, 2 × 10−5 for regimes 1–5. nc = n2 = 2 for all curves. | ||
Characteristic time points and scaling exponents
The half-time of aggregation (when half of the maximal aggregate concentration is reached, i.e. ν(thalf) = 1/2) is a commonly used measure for the overall aggregation rate. It is easily determined from experimental data and its scaling with monomer concentration contains information about the mechanism of aggregation.46 The grey dashed horizontal line marks the half-time in Fig. 1B. For aggregation without a source-term, the half-time falls into the growth phase, whereas it may appear in the source phase for the source-term aggregation. Thus it reports on two related distinct properties depending on which phase it falls into. This property renders the half time less suitable as an easily interpretable characteristic time point when the monomer source is kinetically relevant. In order to easily and accurately describe the shape of the aggregation curves, we therefore need to find a new characteristic time point instead. The lag time, loosely defined as the end of the lag phase, can achieve this and contains much the same information as the half time.21Fig. 2A shows the lag time, which is defined here as the time when 10% of the final aggregate concentration is formed, ν(tlag) = 0.1. This threshold of 10% was chosen to balance the need for a threshold that is on the one hand feasible to determine from experimental data (lower thresholds may be difficult to distinguish from noise) and on the other hand low enough to only fall into the growth phase in extreme cases.The lag time not only depends on monomer production rate constant ksource but also depends on aggregation rates κ and λ. While tlag generally increases with decreasing rates ksource, κ and λ, the degree to which it is affected by each process differs in different regimes, as detailed below.
When solving for the lag time in Fig. 2A, we can use different approximations to obtain the solutions in different extreme limits. First, we consider the rate constant of monomer production ksource, compared to the rate of aggregation κ (or λ). When the monomer production rate is much higher than the aggregation rate, the source-term s(t)/mtot = 1 − e−ksourcet ≈ 1, which we refer to as the fast monomer production regime. When the monomer production rate is much lower than the aggregation rate, the source-term s(t)/mtot = 1 − e−ksourcet ≈ ksourcet, which we refer to as the slow monomer production regime. We also compare the rate of primary nucleation with the rate of the secondary nucleation, giving the primary or secondary nucleation dominant regimes. Considering the possible combinations of these limits, we have thus separated parameter space into four regimes. The different early time solutions and the corresponding lag time solutions for these regimes are approximately calculated from the early time solution eqn (5) (we can approximate that ν(t) ≈ ν0(t) at tlag, which implies that tlag can be obtained by ν0(tlag) = 0.1), which are listed in Table 1. The approximation process from eqn (5) to the ν0(t) column in Table 1 is shown in ESI Section 5.† We substitute the early time solutions into eqn (6) to get the full time solutions M(t) for all regimes (ESI Section 12 Table S1†).
Table 1 clearly shows that the lag time can be expressed as a power law function of ksource, κ and λ. The scaling exponents of ksource, κ, λ, mtot that emerge in the different regimes are shown in the last four columns of Table 2, which can be directly read from the tlag column of Table 1. In order to evaluate the performance of our solutions across the space of possible behaviours, we computed the lag time by numerically integrating eqn (2) and determining the time at which 10% aggregation is reached. Since it is difficult to show lag time contour lines in the 4D scatter plot (tlag is plotted according to ksource, κ and λ), we make two cuts at a fixed value of λ = 0.1 or a fixed value of κ = 10 in Fig. 5A and B respectively. In regime 1 and 2, monomer production is much slower than the aggregation, thus the lag time not only depends on the monomer production rate constant ksource but also depends on the aggregation rates λ or κ. In regime 1, secondary nucleation dominates the aggregation, therefore the lag time depends on κ rather than λ. By contrast, in regime 2, primary nucleation dominates the aggregation, thus the lag time depends on λ rather than κ. Finally, in regimes 3 and 4, the monomer production process is much faster than the aggregation process, and therefore the system behaves like an aggregation reaction without a source-term. The lag time in these two regimes only depends on λ and κ and we recover the previously established scaling exponents.21
Our approximate analytical solutions also allow us to determine whether the source-term or the aggregation dominates the reaction depending on the values of the rate constant of monomer production ksource and the rate of the aggregation κ (or λ). For instance, the boundary between regimes 1 and 3 can be approximated as log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) κ ≈ log10
κ ≈ log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ksource + 1 (ESI Section 13 Table S2†).
ksource + 1 (ESI Section 13 Table S2†).
Comparing the scaling exponents in Tables 2 and S2† with the slopes of the lag time contour lines (solid lines) and boundary lines (dashed lines) in Fig. 5A and B, we find that our analytical solutions match the numerically computed scaling exponents of the lag time very well. Fig. 5C shows the shape of integrated rate laws in five different regimes.
In addition to the lag time, one also needs to consider the relative magnitude of the lag phase tlag and the source phase tsource when describing the full time-course of the aggregation reaction. In particular, when tlag ≪ tsource, i.e. when the lag phase is much shorter than the source phase, the lag phase can generally be neglected since it has negligible influence on the overall kinetics. The aggregation curve is effectively the same as the source-term alone, aggregation is not rate-limiting. This gives rise to the idea of a critical monomer production rate, ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) mon, defined as the value of ksource that solves tlag = tsource. When the monomer production rate ksource is much smaller than this critical monomer production rate ksource ≪
mon, defined as the value of ksource that solves tlag = tsource. When the monomer production rate ksource is much smaller than this critical monomer production rate ksource ≪ ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) mon, the lag phase is much shorter than the source phase tlag ≪ tsource, and the lag phase can be neglected and the lag time only depends on the monomer production rate constant ksource. We can directly express the early time solution as well as the late time solution as the source-term. This source-term dominated regime is named as regime 5.
mon, the lag phase is much shorter than the source phase tlag ≪ tsource, and the lag phase can be neglected and the lag time only depends on the monomer production rate constant ksource. We can directly express the early time solution as well as the late time solution as the source-term. This source-term dominated regime is named as regime 5.
For aggregation with a source-term s(t) = 1 − e−ksourcet, the characteristic timescale of the source phase is given by tsource ≈ ksource−1. When primary nucleation is much slower than secondary nucleation, comparing tlag of regime 1 in Table 1 with the tsource, we obtain the critical monomer production speed:
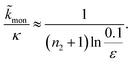 | (10) |
When instead primary nucleation is much faster than the secondary nucleation, comparing tlag of regime 2 in Table 1 with the tsource, we obtain the critical monomer production speed:
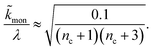 | (11) |
Different protein aggregation reactions are in different regimes in Fig. 5. HttQ45 aggregation with enzyme cleavage47,48 can lie in regime 1, Aβ42 aggregation23 lies in regime 3, FapC aggregation29 lies in regime 4 and P53 aggregation35 lies in regime 5.
A simple source-term model for in vivo protein expression and clearance
While the source-term discussed above assumed there was a finite pool of non-aggregating precursor, in vivo protein expression happens continuously and the precursor pool is not depleted. In this section we show that the same approach to discovering an analytical solution still applies also under those conditions. We assume aggregation-prone monomers are generated with a constant production rate, with rate constant kp. Simultaneously, there are also monomer clearance processes that remove aggregation-prone monomer with a rate proportional to the monomer concentration and rate constant kr. Our analytical solutions are able to match the numerical integrated rate laws also in this scenario, see Fig. 6. The detailed derivation and analytical solution are given in the ESI Section 11.† As can be seen in Fig. 6, two regimes emerge in this scenario. In the first, early time regime, monomer production and clearance rates dominate over the rates of aggregate formation. In this regime the growth of aggregate mass closely resembles that of the source-term discussed above. In the second, late time regime, the aggregate mass is so high that any new monomer, as soon as it is produced, is immediately incorporated into fibrils. The free monomer concentration approaches the peptide solubility and the rate of aggregate increase is purely controlled by the rate of monomer production kp. The expression for the lag time in the early time regime corresponds to the scenarios discussed above. However, as the reaction never reaches completion the half time and lag time in this situation are not defined.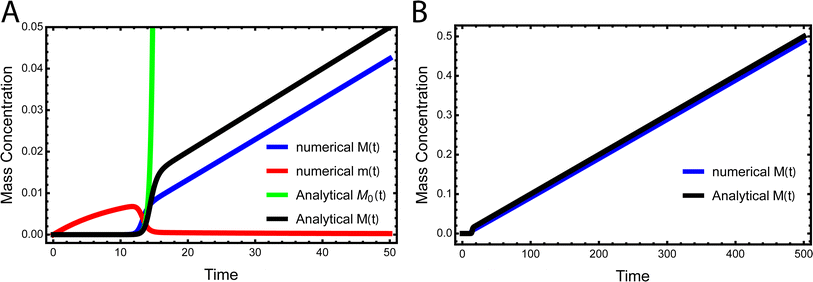 | ||
| Fig. 6 Kinetics of aggregation for a simple in vivo model. In (A), the exact, numerical solution of M(t) and m(t) of eqn (S28)† are the blue curve and the red curve, respectively. The approximate analytical early time solution M0(t) is the green curve and the approximate analytical full time solution M(t) is the black curve. kn = 10−5, k2 = 105, k+ = 102, kp = 10−3, kr = 10−1, nc = n2 = 2. (B) Shows the numerical M(t) and analytical M(t) at a larger timescale. | ||
Generalising to other source-term functions
We have derived the analytical solutions when the source-term can be approximated as s(t) = 1 − e−ksourcet, which includes all simple types of monomer sources such as unfolding, dissociation and enzymatic cleavage. In this section we generalise the conclusions to additional types of source-terms, as might be encountered for more complex monomer production reactions as may occur for example in living systems. We use the same approximation method to extend our analytical solutions to these cases.In order to render this task tractable, we put some restrictions on the source-terms: for t > 0, the source-term is bound, i.e. 0 ≤ S(t) ≤ 1 and the boundary condition is m(0) = 0. Since we are neglecting fibril dissociation, all monomers will aggregate to fibrils eventually. Thus, for an unseeded reaction the source-term satisfies S(0) = 0, S(∞) = 1. Furthermore, we impose the condition that S(t) increases monotonously with time (i.e. aggregation-prone monomer and fibril are not removed).
To proceed, we first derive the analytical solution of aggregation with a monomial source-term, then we will show how a variety of source-term can be approximated as a monomial function.
We express a general monomial source-term as S(T) = a·(KT)ns·β during the early time, the power with respect to time is ns·β, where ns ≥ 0 is the order of the source-term function and a > 0. To allow us to find approximate analytical solutions by the above approach, we require the source-term function to become constant when monomer production is much faster than aggregation. While the exponential source-term S(T) = 1 − e−KT naturally approaches a constant one S(T) = 1 = (KT)0 for a fast source-term (K ≫ 1), the monomial source-term needs an additional parameter β to tune it between a power law function and a constant when K changes. To achieve this, we define β = 1/((10K)2 + 1). When the monomer production is very fast (monomer production rate is much larger than the aggregation rate), K ≫ 1 and β → 0. When the monomer production is very slow (monomer production rate is much lower than the aggregation rate), K ≪ 1 and β → 1. The switch in behaviour occurs at β = 1/2 when K = 0.1, which agrees well with the boundary between region 1 and region 3 in the lag time contour plot (see ESI Section 13 Fig. S7†). The scaling exponent of ‘10K’ in β is 2, which makes the analytical lag time contour plot agrees well with numerical simulations. Using the same approximation method as above, with a time-dependent effective parameter, we derive the lag time for aggregation with the source-term S(T) = a·(KT)ns·β:
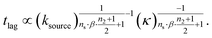 | (12) |
The approximate lag time expression in eqn (12) shows that the parameters β and ns define the scaling exponent of the lag time. Four different regimes emerge: fast or slow monomer production and high or low order of the source-term, as shown in Fig. 7.
Fig. 7C–E shows the lag time contour plots from numerical integration of the moment equations under the early time approximation for different orders of the source-term functions.
In the left-hand regimes of the contour plots, outlined in blue, green and red, the monomer production speed is low compared to the aggregation speed log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K < −2. In this regime the order of the source-term significantly affects the kinetics.
K < −2. In this regime the order of the source-term significantly affects the kinetics.
In the limit of a high order source-term, the regime outlined in blue in Fig. 7C, the lag time is dominated almost exclusively by the source-term: substituting ns ≫ 1, K ≪ 1, β = 1 into eqn (12), we obtain tlag ∝ ksource−1. The contour plot for ns = 11 also shows that the lag time essentially only depends on monomer production rate constant ksource. Physically, the reason for this is as follows: the concentration of aggregation prone monomer increases very suddenly, from close to 0 to its maximum value. Before the sudden increase only negligible aggregation can take place, after the sudden increase, the sample can aggregate fully. Now because we are in the slow monomer production regime, the time until this sudden switch from negligible to complete availability of aggregation-prone monomer dominates the lag time.
At intermediate reaction orders, the regime outlined in green in Fig. 7D both monomer source and aggregation contribute to the lag time. Substituting ns = 1, K ≪ 1, β = 1 into eqn (12), we obtain 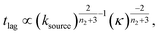 recovering the behaviour from our earlier detailed discussion of the S(T) = 1 − e−KT source-term.
recovering the behaviour from our earlier detailed discussion of the S(T) = 1 − e−KT source-term.
Finally, when the reaction order is ns = 0, i.e. all monomer is available from the start of the reaction, the regime outlined in red in Fig. 7E, we again recover the no source-term behaviour. Substituting ns = 0, K ≪ 1, β = 1 into eqn (12), we obtain tlag ∝ κ−1 as expected.
What remains to be done is to present a strategy to find a monomial source-term S(T) = a·(KT)nsβ, which approximates the real source-term for 0 ≤ S(T) ≤ α, where 0 < α ≤ 1 is chosen to ensure that the approximate source-term describes the real one well before the lag time. Eqn (12) can then be used to derive the approximate analytical lag time. Since the tuning parameter β only depends on K, we only need to find the source-term order ns for a general source-term when K ≪ 1, i.e. β = 1.
The general method of finding the approximate monomial source-term is as follows: the original source-term is S(T) and the approximate monomial source-term is Smon(T, a, ns) = a·(KT)ns, where a, ns are the parameters to be determined. We can define the error between the S and Smon until the lag time as:
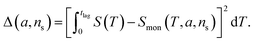 | (13) |
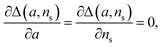 we find the approximate ns and a for the general source-term. For example, for the blue curve in Fig. 7A: S(T) = 1/(1 + e−KT+15), we can use eqn (13) to derive the order of which is ns = 11. The lag time contour plot of which, shown in Fig. 7B, fit well with the analytical prediction in eqn (12). For the green curve in Fig. 7A: S(T) = 1 − e−KT, we can use eqn (13) to derive the order of which is ns = 1. The lag time contour plot of which, shown in Fig. 7C, also fit well with the analytical prediction in eqn (12).
we find the approximate ns and a for the general source-term. For example, for the blue curve in Fig. 7A: S(T) = 1/(1 + e−KT+15), we can use eqn (13) to derive the order of which is ns = 11. The lag time contour plot of which, shown in Fig. 7B, fit well with the analytical prediction in eqn (12). For the green curve in Fig. 7A: S(T) = 1 − e−KT, we can use eqn (13) to derive the order of which is ns = 1. The lag time contour plot of which, shown in Fig. 7C, also fit well with the analytical prediction in eqn (12).
Conclusions
Protein aggregation systems in which all monomers are not available from start require an expanded analytical framework. The presence of a source-term introduces a new parameter, the monomer production rate ksource, which modifies the shape of the aggregation curves significantly. In particular, at some point during the reaction, the kinetics transition from being determined by both aggregation and monomer production, to being dominated only by the kinetics of the monomer production reaction. Similarly, the monomer concentration-dependence of the reaction, which is tracked by the scaling exponent, can be altered significantly by the presence of a source-term.We have developed a novel theoretical framework to derive analytical rate laws for a general class of protein aggregation reactions with a monomer production process (source-term). The central idea is to introduce time-dependent effective kinetic parameters which adjust the reaction orders of the fundamental processes of aggregation and thereby turn a set of unsolvable moment equations into solvable ones. Using this strategy, we derived analytical solutions for the aggregation curve shapes as well as the scaling exponent for a wide range of source-terms, including unfolding, dissociation, clearance and reversible monomer production reactions, as well as any other more complex source-term that can be approximated as a monomial function.
We successfully applied this model to fit the kinetics of HttQ45 and P53 aggregation, at a range of monomer concentrations and source rates, and highlight how our model ties together observations across a range of systems from the cancer-associated P53 protein, to the Alzheimer-associated Aβ42 peptide. Our work thus provides a comprehensive study of aggregation behaviours to be expected when the total protein concentration is not conserved and monomer is produced during the aggregation reaction. As such it will be key in taking detailed mechanistic descriptions of aggregation to increasingly complex systems, such as the cellular environment.
Data availability
The additional data and derivations can be found in ESI.†Author contributions
JW, GM, AD, SL and TPJK conceived the study. MO, CE performed experiments. RM provided materials. JW, GM, AD analysed the data. JW, GM, AD wrote the original draft of the paper. All author contributed to the final manuscript.Conflicts of interest
GM and AD are employees and SL and TPJK are founders of Wavebreak therapeutics. The work reported here was not influenced by this connection.Acknowledgements
We wish to acknowledge the support from the ERC grant DiProPhys (agreement ID 10100161, T. P. J. K), the Nidus studentship scheme (J. W.), Fondation pour la Recherche Médicale (RM ALZ201912009776) and the Swedish Research Council (VR 2015-00143 to S. L.).References
- F. Chiti and C. M. Dobson, Annu. Rev. Biochem., 2006, 75, 333–366 CrossRef PubMed.
- D. J. Selkoe, Nature, 2003, 426, 900–904 CrossRef CAS PubMed.
- C. M. Dobson, Trends Biochem. Sci., 1999, 24, 329–332 CrossRef CAS PubMed.
- D. Eisenberg and M. Jucker, Cell, 2012, 148, 1188–1203 CrossRef CAS PubMed.
- T. P. J. Knowles, M. Vendruscolo and C. M. Dobson, Nat. Rev. Mol. Cell Biol., 2014, 15, 384–396 CrossRef CAS PubMed.
- P. T. Lansbury and H. A. Lashuel, Nature, 2006, 443, 774–779 CrossRef CAS PubMed.
- S. I. Cohen, M. Vendruscolo, C. M. Dobson and T. P. Knowles, J. Mol. Biol., 2012, 421, 160–171 CrossRef CAS PubMed.
- G. Meisl, T. Kurt, I. Condado-Morales, C. Bett, S. Sorce, M. Nuvolone, T. C. T. Michaels, D. Heinzer, M. Avar, S. I. A. Cohen, S. Hornemann, A. Aguzzi, C. M. Dobson, C. J. Sigurdson and T. P. J. Knowles, Nat. Struct. Mol. Biol., 2021, 28, 365–372 CrossRef CAS PubMed.
- T. C. T. Michaels, A. J. Dear and T. P. J. Knowles, New J. Phys., 2018, 20, 055007 CrossRef.
- G. Meisl, L. Rajah, S. A. I. Cohen, M. Pfammatter, A. Šarić, E. Hellstrand, A. K. Buell, A. Aguzzi, S. Linse, M. Vendruscolo, C. M. Dobson and T. P. J. Knowles, Chem. Sci., 2017, 8, 7087–7097 RSC.
- G. Meisl, X. Yang, B. Frohm, T. P. J. Knowles and S. Linse, Sci. Rep., 2016, 6, 18728 CrossRef CAS PubMed.
- P. K. Auluck, G. Caraveo and S. Lindquist, Annu. Rev. Cell Dev. Biol., 2010, 26, 211–233 CrossRef CAS PubMed.
- T. C. T. Michaels, A. Šarić, G. Meisl, G. T. Heller, S. Curk, P. Arosio, S. Linse, C. M. Dobson, M. Vendruscolo and T. P. J. Knowles, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 24251–24257 CrossRef CAS PubMed.
- P. Arosio, M. Vendruscolo, C. M. Dobson and T. P. Knowles, Trends Pharmacol. Sci., 2014, 35, 127–135 CrossRef CAS PubMed.
- S. Linse, T. Scheidt, K. Bernfur, M. Vendruscolo, C. M. Dobson, S. I. A. Cohen, E. Sileikis, M. Lundqvist, F. Qian, T. O'Malley, T. Bussiere, P. H. Weinreb, C. K. Xu, G. Meisl, S. R. A. Devenish, T. P. J. Knowles and O. Hansson, Nat. Struct. Mol. Biol., 2020, 27, 1125–1133 CrossRef CAS PubMed.
- T. Härd and C. Lendel, J. Mol. Biol., 2012, 421, 441–465 CrossRef PubMed.
- H. Amijee and D. I. Scopes, J. Alzheimer's Dis., 2009, 17, 33–47 CAS.
- J. Habchi, P. Arosio, M. Perni, A. R. Costa, M. Yagi-Utsumi, P. Joshi, S. Chia, S. I. A. Cohen, M. B. D. Müller, S. Linse, E. A. A. Nollen, C. M. Dobson, T. P. J. Knowles and M. Vendruscolo, Sci. Adv., 2016, 2, e1501244 CrossRef PubMed.
- G. Meisl, C. K. Xu, J. D. Taylor, T. C. T. Michaels, A. Levin, D. Otzen, D. Klenerman, S. Matthews, S. Linse, M. Andreasen and T. P. J. Knowles, Sci. Adv., 2022, 8, eabn6831 CrossRef CAS PubMed.
- T. P. J. Knowles, C. A. Waudby, G. L. Devlin, S. I. A. Cohen, A. Aguzzi, M. Vendruscolo, E. M. Terentjev, M. E. Welland and C. M. Dobson, Science, 2009, 326, 1533–1537 CrossRef CAS PubMed.
- S. I. A. Cohen, M. Vendruscolo, M. E. Welland, C. M. Dobson, E. M. Terentjev and T. P. J. Knowles, J. Chem. Phys., 2011, 135, 065105 CrossRef PubMed.
- A. J. Dear, G. Meisl, S. Linse and L. Mahadevan, arXiv, 2023, preprint, arXiv:2309.05038, DOI:10.48550/arXiv.2309.05038.
- S. I. A. Cohen, S. Linse, L. M. Luheshi, E. Hellstrand, D. A. White, L. Rajah, D. E. Otzen, M. Vendruscolo, C. M. Dobson and T. P. J. Knowles, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9758–9763 CrossRef CAS PubMed.
- P. Arosio, T. P. J. Knowles and S. Linse, Phys. Chem. Chem. Phys., 2015, 17, 7606–7618 RSC.
- G. Meisl, J. B. Kirkegaard, P. Arosio, T. C. T. Michaels, M. Vendruscolo, C. M. Dobson, S. Linse and T. P. J. Knowles, Nat. Protoc., 2016, 11, 252–272 CrossRef CAS PubMed.
- A. J. Dear, T. C. T. Michaels, G. Meisl, D. Klenerman, S. Wu, S. Perrett, S. Linse, C. M. Dobson and T. P. J. Knowles, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 12087–12094 CrossRef CAS PubMed.
- W.-F. Xue, S. W. Homans and S. E. Radford, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 8926–8931 CrossRef CAS PubMed.
- T. C. T. Michaels, A. Šarić, S. Curk, K. Bernfur, P. Arosio, G. Meisl, A. J. Dear, S. I. A. Cohen, C. M. Dobson, M. Vendruscolo, S. Linse and T. P. J. Knowles, Nat. Chem., 2020, 12, 445–451 CrossRef CAS PubMed.
- G. Meisl, C. K. Xu, J. D. Taylor, T. C. T. Michaels, A. Levin, D. Otzen, D. Klenerman, S. Matthews, S. Linse, M. Andreasen and T. P. J. Knowles, Sci. Adv., 2022, 8, eabn6831 CrossRef CAS PubMed.
- S. I. A. Cohen, M. Vendruscolo, C. M. Dobson and T. P. J. Knowles, J. Chem. Phys., 2011, 135, 065106 CrossRef PubMed.
- A. M. Ruschak and A. D. Miranker, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 12341–12346 CrossRef CAS PubMed.
- G. Meisl, T. C. T. Michaels, P. Arosio, M. Vendruscolo, C. M. Dobson and T. P. J. Knowles, in Biological and Bio-inspired Nanomaterials: Properties and Assembly Mechanisms, ed. S. Perrett, A. K. Buell and T. P. Knowles, Springer Singapore, Singapore, 2019, pp. 1–33 Search PubMed.
- P. Hammarström, R. L. Wiseman, E. T. Powers and J. W. Kelly, Science, 2003, 299, 713–716 CrossRef PubMed.
- B. A. Vernaglia, J. Huang and E. D. Clark, Biomacromolecules, 2004, 5, 1362–1370 CrossRef CAS PubMed.
- R. Wilcken, G. Wang, F. M. Boeckler and A. R. Fersht, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 13584–13589 CrossRef CAS PubMed.
- G. Wang and A. R. Fersht, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 13590–13595 CrossRef CAS PubMed.
- O. Szczepankiewicz, C. Cabaleiro-Lago, G. G. Tartaglia, M. Vendruscolo, T. Hunter, G. J. Hunter, H. Nilsson, E. Thulin and S. Linse, Mol. BioSyst., 2011, 7, 521–532 RSC.
- L. A. Morozova-Roche, J. Zurdo, A. Spencer, W. Noppe, V. Receveur, D. B. Archer, M. Joniau and C. M. Dobson, J. Struct. Biol., 2000, 130, 339–351 CrossRef CAS PubMed.
- X. Sun, H. J. Dyson and P. E. Wright, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E6201–E6208 CrossRef PubMed.
- C. Månsson, V. Kakkar, E. Monsellier, Y. Sourigues, J. Härmark, H. H. Kampinga, R. Melki and C. Emanuelsson, Cell Stress Chaperones, 2013, 19, 227–239 CrossRef PubMed.
- L. Y. Chen, N. Goldenfeld and Y. Oono, Phys. Rev. Lett., 1994, 73, 1311–1315 CrossRef PubMed.
- L.-Y. Chen, N. Goldenfeld and Y. Oono, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 376–394 CrossRef CAS PubMed.
- T. C. T. Michaels, A. J. Dear and T. P. J. Knowles, Phys. Rev. E, 2019, 99, 062415 CrossRef CAS PubMed.
- A. J. Dear, G. Meisl, T. C. T. Michaels, M. R. Zimmermann, S. Linse and T. P. J. Knowles, J. Chem. Phys., 2020, 152, 045101 CrossRef CAS PubMed.
- T. Ratovitski, M. Gucek, H. Jiang, E. Chighladze, E. Waldron, J. D'Ambola, Z. Hou, Y. Liang, M. A. Poirier, R. R. Hirschhorn, R. Graham, M. R. Hayden, R. N. Cole and C. A. Ross, J. Biol. Chem., 2009, 284, 10855–10867 CrossRef CAS PubMed.
- G. Meisl, X. Yang, C. M. Dobson, S. Linse and T. P. J. Knowles, Chem. Sci., 2017, 8, 4352–4362 RSC.
- C. Månsson, P. Arosio, R. Hussein, H. H. Kampinga, R. M. Hashem, W. C. Boelens, C. M. Dobson, T. P. Knowles, S. Linse and C. Emanuelsson, J. Biol. Chem., 2014, 289, 31066–31076 CrossRef PubMed.
- V. Kakkar, C. Månsson, E. P. de Mattos, S. Bergink, M. van der Zwaag, M. A. van Waarde, N. J. Kloosterhuis, R. Melki, R. T. van Cruchten, S. Al-Karadaghi, P. Arosio, C. M. Dobson, T. P. Knowles, G. P. Bates, J. M. van Deursen, S. Linse, B. van de Sluis, C. Emanuelsson and H. H. Kampinga, Mol. Cell, 2016, 62, 272–283 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc00088a |
| ‡ Current address: Patheon Biologics, Zuiderweg 72/2, 9727 DL Groningen, Netherlands. |
| This journal is © The Royal Society of Chemistry 2024 |