Open Access Article
Open Access ArticleDeciphering the chemical bonding of the trivalent oxygen atom in oxygen doped graphene†
Andoni
Ugartemendia
 ab,
Irene
Casademont-Reig
ab,
Irene
Casademont-Reig
 c,
Lili
Zhao
c,
Lili
Zhao
 d,
Zuxian
Zhang
d,
Gernot
Frenking
d,
Zuxian
Zhang
d,
Gernot
Frenking
 bde,
Jesus M.
Ugalde
ab,
Aran
Garcia-Lekue
*df and
Elisa
Jimenez-Izal
bde,
Jesus M.
Ugalde
ab,
Aran
Garcia-Lekue
*df and
Elisa
Jimenez-Izal
 *ab
*ab
aPolimero eta Material Aurreratuak: Fisika, Kimika eta Teknologia Saila, Kimika Fakultatea, Euskal Herriko Unibertsitatea (UPV/EHU), M. de Lardizabal Pasealekua 3, Donostia, Euskadi, Spain. E-mail: elisa.jimenez@ehu.es
bDonostia International Physics Center (DIPC), Manuel de Lardizabal Pasealekua 3, Donostia, Euskadi, Spain. E-mail: wmbgalea@ehu.eus
cDepartment of General Chemistry (ALGC), Vrije Universiteit Brussel (VUB), Pleinlaan 2, 1050 Brussels, Belgium
dInstitute of Advanced Synthesis, School of Chemistry and Molecular Engineering, Jiangsu National Synergetic Innovation Center for Advanced Materials, Nanjing Tech University, Nanjing 211816, China
eFachbereich Chemie, Philipps-Universität Marburg, Hans-Meerwein-Strasse, D-35043 Marburg, Germany
fIKERBASQUE, Basque Foundation for Science, Euskadi, Bilbao, Spain
First published on 26th March 2024
Abstract
Recently, planar and neutral tricoordinated oxygen embedded in graphene has been imaged experimentally (Nat. Commun., 2019, 10, 4570–4577). In this work, this unusual chemical species is studied utilizing a variety of state-of-the-art methods and combining periodic calculations with a fragmental approach. Several factors influencing the stability of trivalent oxygen are identified. A σ-donation and a π-backdonation mechanism between graphite and oxygen is established. π-Local aromaticity, with a delocalized 4c–2e bond involving the oxygen atom and the three nearest carbon atoms aids in the stabilization of this system. In addition, the framework in which the oxygen is embedded is crucial too to the stabilization, helping to delocalize the “extra” electron pair in the virtual orbitals. Based on the understanding gathered in this work, a set of organic molecules containing planar and neutral trivalent oxygen is theoretically proposed for the first time.
1. Introduction
Oxygen is one of the most abundant chemical elements on Earth and it is essential for life. It forms a rich variety of functional groups in organic compounds which are involved in many biochemical processes, such as the Krebs cycle and photosynthesis. As a general rule, oxygen behaves as a divalent atom; either forming one double bond as in the case of O2 and carbonyls, or two single bonds as in H2O, hydroxyls and ethers. Nonetheless, there are a number of remarkable exceptions to this rule: molecules containing oxonium ions, i.e., positively charged trivalent oxygen. The best known and simplest case is the hydronium molecule (H3O+), where oxygen is coordinated to three hydrogen atoms. Oxonium ions are generally highly unstable and reactive, being relevant as reaction intermediates or synthetic reagents. Although these species can be isolated in the form of oxonium salts (Meerwein salts) using non-nucleophilic counterions such as BF4− and PF6−, they still possess very high reactivity. However, Mascal et al. reported the synthesis and characterization of a new type of oxonium ion, i.e., oxatriquinane and oxatriquinacene, which are surprisingly stable. In these molecules the O+ ion is stabilized by fusing it inside a tricyclic condensed ring.2–4 The lack of reactivity of these species against nucleophilic attack is associated with the ring strain, revealing the potential of embedding oxonium ions in ring frameworks for their stability. Subsequently, an oxatriquinane with a hydroxyl group in the α-position to oxygen was found to possess the longest C–O bond length reported to date (1.658 Å).5 Steric repulsion and strong donation from oxygen non-bonding orbitals to adjacent σ*(C–O+) were argued to be the reasons for such C–O bond lengthening. These findings have encouraged the exploration of a plethora of new analogous oxonium ions.6–13 However, it should be emphasized that, to the best of our knowledge, in all the molecules containing trivalent oxygen, O is positively charged and tetrahedral due to the sp3 hybridization. There are only three exceptions to this rule: Al3O, Tl3O and Ga3O.14–16 These three inorganic molecules were theoretically hypothesized to adopt a T-shape configuration with a planar tricoordinated oxygen (Al3O can also adopt a Y-shape configuration).14Oxygen functionalization in graphene has also been subject of numerous studies, due to the relevance for the processing of graphene oxide (GO) and its influence in the performance of supercapacitors, batteries, and electrocatalysts.17–28 Functionalization of graphene with oxygen leads to an effective way of binding cations, which can either be part of the electrochemical reactions or serve as anchors for metals.29 Recently, Hofer et al. explored the possible binding configurations of oxygen in GO. Individual oxygen atoms were directly visualized using aberration-corrected scanning transmission electron microscopy (STEM) and single-atom electron energy loss spectroscopy (EELS).1 In most cases oxygen was bound to two neighboring carbon atoms, as usual. Unexpectedly, however, in some cases oxygen was bonded to three carbons forming three equivalent bonds, a finding of great importance due to the rarity of this species. The electronic and transport properties of this system were later investigated. It was found that the tricoordinated oxygen acts as a n-type dopant, which is in contrast to the usual p-type oxygen bonded to the basal plane of graphene.30
However, it is unclear how oxygen binds to graphene in this configuration. Unlike molecular oxonium ions, the oxygen atom is not positively charged; it displays planar or quasi-planar coordination, and it is integrated into an extended system. These features make the chemical arrangement of oxygen unique. The present work aims at unveiling the chemical bonding of this atypical species. We believe such understanding will open the door to the development of new chemical species that can be integrated into different extended systems, to modulate at will their physico-chemical properties.
2. Methods
Periodic density functional theory (DFT) calculations were carried out with the PBE exchange–correlation functional31,32 and projector augmented wave (PAW) pseudopotentials,33 as implemented in the VASP code.34–37 The planewave kinetic energy cutoff was set to 450 eV, and the convergence criteria for geometry (SCF) relaxation was set to 10−5 (10−6) eV. The Brillouin zone was sampled with a 5 × 5 × 1 Monkhorst–Pack k-grid. The DFT-D3 scheme was used to account for the dispersion interactions.38 The system was modeled using a 6 × 6 oxygen monodoped graphene supercell of 72 atoms. In this cell, a single oxygen atom equates to a concentration of 1.4%. A vacuum separation of at least 15 Å was added in the z direction to avoid self-interaction with repeating images. To study the electronic structure in greater detail, projected crystal orbital Hamilton population (pCOHP) analysis was performed by means of the LOBSTER program.39–42 The pCOHP is a very useful tool to discern the bonding/antibonding character of the interaction between specific pairs of atoms. For these calculations, the sigma value was reduced to 0.05 eV and a finer k-grid of 36 × 36 × 1 was used.Considered molecules were modeled with the Gaussian 16 package43 using the CAM-B3LYP44 functional. Geometry optimizations were carried out with the 6-31G45 basis set whereas delocalization indices and Bader charges were computed using the 6-311G(d,p) basis set.46 The bonding analysis was done with the Adaptive Natural Density Partitioning (AdNDP) method.47 AdNDP partitions the electron density matrix into n centers and 2 electrons (nc–2e) bonds. Furthermore, AdNDP was shown to be nearly basis-set independent, and hence the CAM-B3LYP functional was used together with a smaller 6-31G basis set.
The calculation of the delocalization indices (DIs) employs the atomic partitions from the quantum theory of atoms in molecules (QTAIM),48 as obatained with the AIMAll software.49 The delocalization index (DI)50–52 between two different atoms (A and B) is defined as:
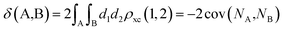 | (1) |
NBO53 and EDA-NOCV54–56 calculations were carried out at the BP86-D3(BJ)/def2-TZ2P level of theory.57,58 This method combines the energy decomposition analysis with the natural orbitals for chemical valence and decomposes the interaction energy (ΔEint) between two fragments into four energy components, namely, the electrostatic interaction (ΔEelstat), Pauli repulsion (ΔEPauli), attractive orbital interactions (ΔEorb), and the dispersion interaction (ΔEdisp) :
| ΔEint = ΔEelstat + ΔEPauli + ΔEorb + ΔEdisp | (2) |
3. Results
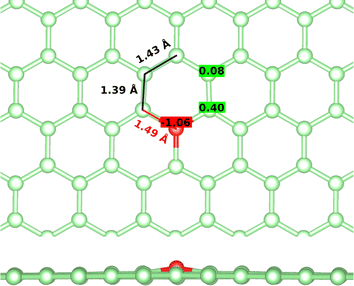
First, the tricoordinated oxygen embedded in graphene, the so-called graphitic oxygen, was characterized using a slab model and plane-waves DFT (PW-DFT). This configuration can be considered as a substitutional doping of oxygen in pristine graphene. As shown in Fig. 1, oxygen is located 0.20 Å above the plane, in agreement with the work by Hofer et al.1 It forms three symmetrical bonds with the nearest carbon atoms, with bond lengths of 1.49 Å. These bond lengths are larger than the C–O bonds in ordinary ethers, ∼1.43 Å, a feature found in molecules containing tricoordinated oxygen.4 The lengthening of the bond has previously been ascribed to the filling of the σ*(C–O) antibonding molecular orbital (MO).4 In addition, the carbon atoms directly bonded to oxygen form a shrunken bond with their adjacent carbon atoms of ca. 1.39 Å, whereas the latter carbon atoms form slightly larger C–C bonds (1.43 Å vs. 1.42 Å in pristine graphene). The relaxed scan in Fig. S1† shows that the out-of-plane structure is a minimum in the potential energy surface of the system, whereas the completely planar structure is not. The computed Bader charges show that oxygen withdraws 1.06 |e|, mostly from the three closest carbon atoms. In this line, local charge depletion areas can also be observed between the C and O atoms and in the closest C atoms, as indicated by the charge density distribution (CDD) in Fig. S2.†The electronic structure is then studied in detail. The calculations reveal a nonmagnetic structure for the ground state. In order to analyze the chemical bonding in the graphitic oxygen, first a pCOHP analysis was performed, which partitions the band-structure in terms of orbital-pair contributions, discerning between bonding/antibonding contributions. This analysis suggests that the oxygen–graphene bonding can be divided into three components. On the one hand, Fig. 2b shows a σ contribution to the pCOHP between O and one of the closest C arising from their s, px and py atomic orbitals (AOs). A bonding overlap (–pCOHP > 0) was observed throughout the −16 to −10 eV energy range, corresponding to this C–O σ bond. This interaction, together with the quasi-planar geometry of the system, pinpoints to a sp2 hybridization on oxygen. Additionally, the COHP was projected into the pz AOs to analyze the π interactions. In Fig. 2c) the π contribution to the C–O1 interaction is shown, along with the pCOHP between pairs of the C atoms in the O-containing ring (see Fig. 2a)). Two localized peaks appear at around −8.9 and −0.02 eV, indicating the presence of O pz and C pz AOs hybridization. The peak at −8.9 eV corresponds to a π bonding state (–pCOHP > 0) with contribution from O–C1, as well as C1–C2 and C2–C3 pairs. Contrary to the previous case, in the π state at −0.02 eV the O and C pz AOs overlap in an antibonding manner (–pCOHP < 0). At the same energy, the pCOHP of C1–C2 is bonding while that of C2–C3 becomes antibonding again. It can be concluded that the latter state presents alternating nodal planes between O and C1 and C2 and C3 perpendicular to the basal plane. This antibonding π state is filled leading to the n-type behavior of oxygen, which is in agreement with previous work carried out on the same system.30
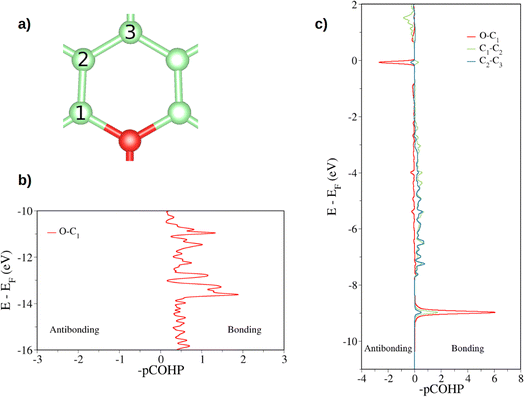 | ||
| Fig. 2 Projected crystal orbital Hamilton population (pCOHP) plot between the different pairs of atoms is indicated (a). In (b) the COHP is projected onto the sum of s, px, py atomic orbitals of O and C while in (c) the total COHP is projected onto the atomic pz orbitals (a pCOHP plot between C1–C2 pz AOs can be seen in Fig. S3†). Positive –pCOHP values correspond to bonding interactions, while negative –pCOHP to antibonding interactions, respectively. The energy is given with respect to the Fermi energy (EF). | ||
In order to gain a deeper understanding of the chemical bonding of the graphitic oxygen, a fragmental approach was used, which has been successfully applied in previous studies on graphene and boron α-sheets.59,60 In our approach we studied five molecules, with the tricoordinated oxygen located in the center, adding one coordination sphere from the smallest molecule containing O. The set of molecules studied were: [OC12H9]7+, [OC36H15]13+, [OC72H21]19+, [OC120H27]25+ and [OC180H33]31+. These molecules were built starting from the optimized periodic graphitic oxygen and freezing their geometry. As mentioned above, oxygen is slightly out of plane in graphitic oxygen, and it remains in this position in the fragment molecules (although as we will show, it has no effect on the chemical bonding). Hydrogen atoms were added to saturate the σ bonds of the peripheral carbon atoms. In the infinite graphene lattice, each carbon atom shares its π electrons with three adjacent hexagons, contributing with only 1/3 of its π electrons to each hexagonal ring. Thus, in order to mimic the infinite graphene lattice, positive charges were added so that the number of π electrons in the periodic system were preserved.
First of all, Bader charges and delocalization indexes were computed in order to determine at which molecular size these electronic properties converge around oxygen. As shown in Fig. S4–S8,† the DIs of the atoms in the first coordination sphere converge at the intermediate [OC72H21]19+ size. In this molecule the Bader charges also converged. Therefore, [OC72H21]19+ was chosen as a model molecule to study how oxygen is bonded and stabilized in graphitic oxygen. It should be mentioned that the Electron Localization Function (ELF) was additionally plotted for both the extended surface and the [OC72H21]19+ molecule and we concluded that this property is also converged at this molecular size. Further details can be found in the ESI (Section 5 and Fig. S9).†
The DI is a quantitative measure of the number of electron pairs that are delocalized or shared between two atoms. A value close to 1 is expected for an electron pair shared between two atoms, a 2-center 2-electron bond (2c–2e).61 In benzene the DIs between pairs of C atoms is 1.40. In Fig. 3 the DIs of [OC72H21]19+ are shown and compared with the analogous molecule made of all carbon atoms, [C73H21]19+ (see Fig. S4–S8† for further details). The most significant difference between the two molecules was found at the DI between C–O vs. C–C (0.74 vs. 1.16). Such a low value in the C–O bond shows that the delocalization is lower in the hexagons containing oxygen. Moreover, a DI value smaller than 1.0 is indicative either of a strongly polarized bond or the population of antibonding orbitals.
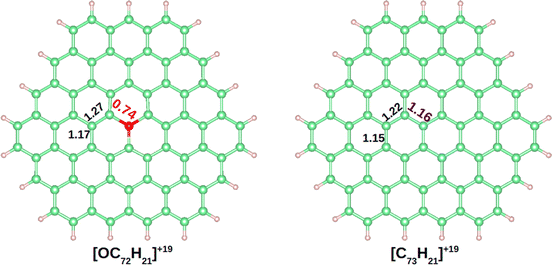 | ||
| Fig. 3 Delocalization indexes on [OC72H21]19+ and [C73H21]19+. Carbon, hydrogen, and oxygen atoms are depicted in green, white and red, respectively. | ||
The computed Bader charges on [OC72H21]19+ are very similar to those obtained for the periodic system: −0.93 |e| on oxygen, 0.33 |e| on the three closest carbon atoms, and 0.14 |e| on the second nearest carbon atoms. We then performed a chemical bonding analysis on the [OC72H21]19+ model fragment using the AdNDP tool,47 which provides a description of localized and delocalized bonds by localizing the valence electrons in 1-center 2-electron bonds (1c–2e), 2-center 2-electron bonds (2c–2e), and n-center 2-electron bonds (nc–2e). As shown in Fig. 4, in our model molecule AdNDP localizes 96 2c–2e bonds between each adjacent C–C atoms (occupation numbers, ON = 1.99–1.97 |e|) and 21 2c–2e bonds between C and H atoms at the edges (ON = 1.98–1.97 |e|). In addition, oxygen forms three σ 2c–2e with the nearest carbon atoms (ON = 1.99 |e|). Due to the difference in electronegativity between carbon and oxygen (2.55 vs. 3.44), such C–O bonds will be polarized towards oxygen, explaining the negative charge on oxygen gained from these three closest carbon atoms.
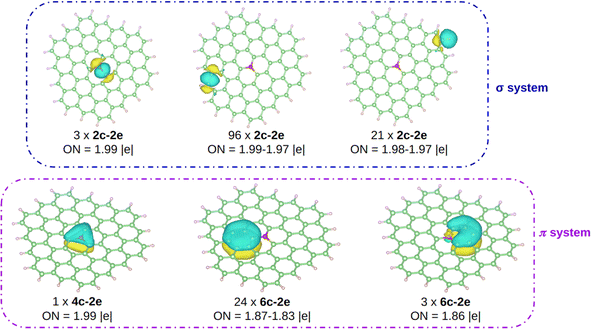 | ||
| Fig. 4 AdNDP analysis on [OC72H21]19+. Carbon, hydrogen, and oxygen atoms are depicted in green, white, and red, respectively. | ||
Moreover, AdNDP shows that the additional two electrons contributed by oxygen are delocalized over a completely bonding 4c–2e bond, that involves the oxygen atom and the three nearest carbon atoms (ON = 1.99 |e|). With two delocalized electrons populating this bond, the system obeys the Hückel rule for aromaticity (4n + 2), with n = 0, making the system locally π aromatic. Aromaticity confers an enhanced stability on chemical systems and could explain, at least in part, the reason why, unlike other species in which oxygen is tricoordinated, in this case O has a sp2 hybridization being almost planar. Indeed, this geometrical arrangement allows for the orbital overlap between oxygen and the three closest carbon atoms. We should highlight that the AdNDP analysis was also carried out on an analogous molecule, which is completely planar, and the results are identical.
The remaining electrons are delocalized over the hexagonal rings forming the π system. On the one hand, on each ring composed of only carbon atoms there is a 6c–2e bond (ON = 1.87–1.83 |e|), in agreement with previous works.60 On the other hand, a 6c–2e bond is located (ON = 1.86 |e|) on each of the three hexagons containing oxygen. Note however, that unlike in the all-C rings where the bond is clearly fully bonding, in the O-containing rings the delocalized bond has an antibonding character, since oxygen is in antiphase with the rest of the electronic π cloud. This filling of the bonds with antibonding character is consistent with the fact that the DI value for the C–O bond is smaller than 1 as well as with the pCOHP analysis near the Fermi energy.
Overall the bonding picture given by AdNDP on the fragment molecules can be easily reconciled with the pCOHP results obtained for the graphitic oxygen. According to both models, oxygen is bonded to the three nearest carbon atoms through C–O σ bonds, and π bonds with both bonding and antibonding character.
In order to tackle the influence of the π-conjugated system in the planarity of the trivalent oxygen, the previously built fragment molecules were relaxed at the CAM-B3LYP/6-31G level of theory, but in their neutral form (charge = 0). When they are neutral, these molecules have a doublet ground spin state. The smallest molecule, OC12H9, is unstable when it is planar and neutral. In other words, it is not a minimum on the potential energy surface. However, the remaining molecules, OC36H15, OC72H21, OC120H27, and OC180H33, are stable in the D3h symmetry. The vibrational analysis confirmed that the resulting molecular geometries have no imaginary frequencies. The fact that trivalent oxygen cannot be stabilized in the planar and neutral form in OC12H9 suggests that a π-conjugated system is required to accept the “extra” electron pair brought by the O atom. According to our calculations OC36H15 is the smallest organic molecule, and the only molecule in which oxygen forms three equivalent bonds reported so far, that could accommodate a planar neutral trivalent oxygen.
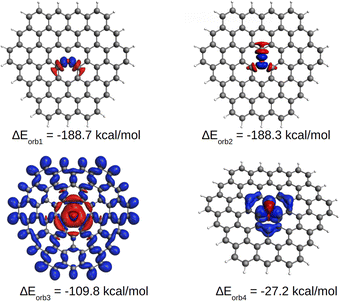
Finally, the energy decomposition analysis with the combination of natural orbital for chemical valence (EDA-NOCV) calculations was carried out to complement the previous investigation. This method provides the most appropriate model to represent the bonding situation in the equilibrium geometry. The [OC72H21]19+ cationic molecule was first optimized and it was found that the Cs and C3v structures are nearly degenerate, while the D3h form of the cation is 5.3 kcal mol−1 higher in energy. Nevertheless, as depicted in Tables S1 and S2† the EDA-NOCV calculations are nearly unchanged regardless of the symmetry of the molecule, as the bond lengths do not change and the core of the molecule remains planar.
EDA-NOCV results for the [OC72H21]19+ molecule are shown in Table 1. The best bonding description emerges from the interaction between neutral O and the charged ligand, both in their triplet state. The energy decomposition analysis reveals that approximately 25% of the contribution to the total interaction energy comes from electrostatic forces and ca. 75% from the orbital interaction. Similarly, most of the orbital interaction is contributed by stabilizing σ interactions (ΔEorb1, ΔEorb2 and ΔEorb3 in Table 1) between oxygen and the graphitic ligand. As shown in Fig. 5, S10 and S11,† the two nearly degenerate interactions, ΔEorb1 and ΔEorb2, arise from the electron-sharing σ interaction of the singly occupied 2p AOs of O, while ΔEorb3 originates from a dative interaction of the doubly occupied 2s AO of O. Moreover, the deformation density suggests that the associated σ charge-donation mainly goes from the three directly bonded carbon atoms to the oxygen atom [C72H21]+19 → O, indicating that the highly charged ligand is a σ donor and the neutral oxygen atom is a σ acceptor. This scenario correlates well with the previously proposed C–O σ bonds which are polarized, leading to a negative charge on O. This seemingly paradoxical charge migration becomes understandable when one realizes that the positive charge on the ligand is localized at the outermost atoms, revealing that the graphite ligand behaves like a Faraday cage. In addition to such a strong σ bonding associated with the ligand to oxygen donation, a comparatively weak π interaction is found in the opposite direction, i.e., from oxygen to the ligand. ΔEorb4 comes from the π donation [C72H21]19+ ← O. The shape of the deformation density indicates that the π donation from O to C essentially only affects the carbon atoms located in the three rings with a common oxygen atom in the center, as observed in the AdNDP analysis.
| Fragments | O(T) + [C72H21]19+(T) | O(S) + [C72H21]19+(S) |
|---|---|---|
| a The values in parentheses give the percentage contribution to the total attractive interactions ΔEelstat + ΔEorb + ΔEdisp. b The values in parentheses give the percentage contribution to the total orbital interactions ΔEorb. | ||
| ΔEint | −316.6 | −954.5 |
| ΔEPauli | 475.0 | 286.5 |
| ΔEelstata | −233.0 (29.4%) | −348.0 (28.0%) |
| ΔEdispa | −2.8 (0.4%) | −2.8 (0.2%) |
| ΔEorba | −555.9 (70.2%) | −890.2 (71.7%) |
| ΔEorb1b | −188.7 (33.9%) | |
| ΔEorb2b | −188.3 (33.9%) | |
| ΔEorb3b | −109.8 (19.8%) | |
| ΔEorb4b | −27.2 (4.9%) | |
| ΔEorb(rest)b | −41.9 (7.5%) | |
It is noteworthy that the [OC36H15]+13 molecule was additionally tested in both the cationic and anionic forms. The EDA-NOCV results are shown in Fig. S12, S13, Tables S3 and S4.† The analysis reveals the same trends as in the larger molecule. Moreover, the bonding between oxygen and the graphitic ligand in the highly charged cation is very similar, in terms of total interaction as well as the type of interaction, to the neutral system. In fact, the interaction energies and the energy components are very similar. These results suggest that the effect of the charge is confined to the outer sphere, with a minor effect on the bonding in the center of the molecule, supporting the use of the fragmental approach to study the graphitic oxygen.
4. Conclusions
Oxygen is usually divalent, forming two chemical bonds, although there are a few exceptions to this rule among the known organic compounds: the hydronium molecule, H3O+, and oxonium salts. However, in the recent experimental finding by Hofer et al.1 the tricoordinated oxygen embedded in graphene is so striking because, unlike molecular oxonium ions, the oxygen atom is not positively charged, it displays planar or quasi-planar coordination and it is integrated into an extended system. These features make the chemical arrangement of oxygen unique. In this theoretical work, using a variety of state-of-the-art methods and combining periodic calculations with a fragmental approach we tried to unravel the factors influencing the stability of this exotic species. A σ-donation from the graphitic ligand to oxygen and a π-backdonation in the opposite direction are identified. Importantly, the electronic structure indicates aromatic stabilization for at least part of the regions of delocalized bonding. In fact, the system is found to have local π aromaticity, with a delocalized 4c–2e bond that involves the oxygen atom and the three nearest carbon atoms. Finally, the framework in which oxygen is embedded plays a pivotal role on the stabilization. In fact, the π-conjugated system helps to delocalize the “extra” electron pair in the virtual orbitals. In this way, a set of organic molecules containing planar and neutral trivalent oxygen is theoretically proposed for the first time.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request. The corresponding author, on behalf of all authors of the paper, is responsible for submitting a competing interests statement.Author contributions
A. U. performed the calculations in the extended system and analyzed the results. I. C.-R. performed and analyzed the Bader charges and performed DI calculations, L. Z. and Z. Z. performed the EDA-NOCV calculations and analyzed the results, G. F. analyzed the EDA-NOCV results, J. M. U. supervised the work, A. G.-L. brought the inspiration and supervised the work, E. J.-I. performed and analyzed the AdNDP calculations and supervised the work. All the authors contributed to the writing of the work. All authors reviewed the manuscript.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was supported by funding provided by Gobierno Vasco-Eusko Jaurlaritza (IT1584-22). This work was also supported by grant PID2019-107338RB-C66 and PID2020-114754GA-I00, funded by MCIN/AEI/10.13039/501100011033, and PID2022-140845OB-C66, funded by MCIN/AEI/10.13039/501100011033 and FEDER. In addition, the work was supported by the Spanish Research Agency and the European Union NextGenerationEU/PRTR under Contract No. TED2021-132388B-C44, and the European Union (EU) H2020 program through the FET Open project SPRING (Grant Agreement No. 863098). A. G.-L. also acknowledges the financial support received from the IKUR Strategy under the collaboration agreement between Ikerbasque Foundation and DIPC on behalf of the Department of Education of the Basque Government. A. U. gratefully thanks Eusko Jaurlaritza for his predoctoral grant. I. C. R. acknowledges co-funding from the European Union's Horizon 2020 Research and Innovation Maria Skłodowska-Curie Actions, under grant agreement number 945380. We also thank DIPC and SGI-IZO-SGIker (UPV/EHU) for the generous allocation of computational resources. The authors thankfully acknowledge also the computer resources at MareNostrum and the technical support provided by Barcelona Supercomputing Center (QHS-2022-2-002 and QHS-2022-3-0015).References
- C. Hofer, V. Skákalová, T. Görlich, M. Tripathi, A. Mittelberger, C. Mangler, M. R. A. Monazam, T. Susi, J. Kotakosk and J. C. Meyer, Direct imaging of light-element impurities in graphene reveals triple-coordinated oxygen, Nat. Commun., 2019, 10, 4570–4577 CrossRef CAS PubMed.
- M. Mascal, N. Hafezi, N. K. Meher and J. C. Fettinger, Oxatriquinane and Oxatriquinacene: Extraordinary Oxonium Ions, J. Am. Chem. Soc., 2008, 130, 13532–13533 CrossRef CAS PubMed.
- M. Haley, Taming the Highly Reactive Oxonium Ion, Angew. Chem., Int. Ed., 2009, 48, 1544–1545 Search PubMed.
- G. Gunbas, N. Hafezi, W. L. Sheppard, M. M. Olmstead, I. V. Stoyanova, F. S. Tham, M. P. Meyer and M. Mascal, Extreme oxatriquinanes and a record C-O bond length, Nat. Chem., 2012, 4, 1018–1023 CrossRef CAS PubMed.
- G. Gunbas, W. L. Sheppard, J. C. Fettinger, M. M. Olmstead and M. Mascal, Extreme Oxatriquinanes: Structural Characterization of α-Oxyoxonium Species with Extraordinarily Long Carbon−Oxygen Bonds, J. Am. Chem. Soc., 2013, 135, 8173–8176 Search PubMed.
- H. Suzuki and H. Muratake, Functionalized oxatriquinanes and their structural equilibrium in protic solvent, Chem. Pharm. Bull., 2014, 62(9), 921–926 CrossRef CAS PubMed.
- E. S. Stoyanov, G. Gunbas, N. Hafezi, M. Mascal, I. V. Stoyanova, F. S. Tham and C. A. Reed, The R3O+···H+ Hydrogen Bond: Toward a Tetracoordinate Oxadionium(2+) Ion, J. Am. Chem. Soc., 2012, 134, 707–714 CrossRef CAS PubMed.
- H. Suzuki and H. Muratake, Functionalized oxatriquinanes and their structural equilibrium in protic solvent, Chem. Pharm. Bull., 2014, 62, 921–926 CrossRef CAS PubMed.
- H. S. S. Chan, Q. N. N. Nguyen, R. S. Paton and J. W. Burton, Synthesis, characterization and reactivity of complex tricyclic oxonium ions, proposed intermediates in natural product biosynthesis, J. Am. Chem. Soc., 2019, 141(40), 15951–15962 CrossRef PubMed.
- I. Novak, Computational thermochemistry of oxatriquinane and its analogues, Comput. Theor. Chem., 2019, 1147, 35–39 CrossRef CAS.
- O. Smith, M. V. Popescu, M. J. Hindson, R. Paton, J. W. Burton and M. D. Smith, Control of stereogenic oxygen in a helically chiral oxonium ion, Nature, 2023, 615, 430–435 CrossRef CAS PubMed.
- N. Hafezi and M. Mascal, Chemistry of the Heterotriquinanes and Heterotriquinacenes, Synlett, 2022, 33, 231–246 CrossRef CAS.
- S. J. Grabowski, E. Formoso, D. Casanova and J. M. Ugalde, Tetravalent Oxygen and Sulphur Centres Mediated by Carborane Superacid: Theoretical Analysis, ChemPhysChem, 2019, 20, 2443–2450 CrossRef CAS PubMed.
- A. I. Boldyrev and P. v. R. Schleyer, Ab Initio Prediction of the Structures and Stabilities of the Hyperaluminum Molecules: Al3O and Square-Planar Al4O, J. Am. Chem., 1991, 113, 9045–90544 CrossRef CAS.
- K. Zhou, S. K. Roy and C. B. Zhao, GaxO (x = 2–4) Contain Novel Linear Dicoordinate, T-shape Tricoordinate and Planar Tetracoordinate Oxygen, Russ. J. Inorg. Chem., 2019, 64, 303–307 CrossRef CAS.
- K. Zhou, S. Roy and C.-B. Zhao, TlxO (x = 2–4) contain novel linear di-coordinated, T-shaped tri-coordinated and square-planar tetra-coordinated oxygen, Comput. Theor. Chem., 2017, 1110, 35–39 CrossRef CAS.
- X. Lu, W.-L. Yim, B. H. R. Suryanto and C. Zhao, Electrocatalytic Oxygen Evolution at Surface-Oxidized Multiwall Carbon Nanotubes, J. Am. Chem. Soc., 2015, 137(8), 2901–2907 CrossRef CAS PubMed.
- Z. Lu, G. Chen, S. Siahrostami, Z. Chen, K. Liu, J. Xie, L. Liao, T. Wu, D. Lin, Y. Liu, T. F. Jaramillo, J. K. Nørskov and Y. Cui, High-efficiency oxygen reduction to hydrogen peroxide catalysed by oxidized carbon materials, Nat. Catal., 2018, 1(2), 156–162 CrossRef CAS.
- F. Yang, X. Ma, W.-B. Cai, P. Song and W. Xu, Nature of Oxygen-Containing Groups on Carbon for High-Efficiency Electrocatalytic CO2 Reduction Reaction, J. Am. Chem. Soc., 2019, 141(51), 20451–20459 CrossRef CAS PubMed.
- Z. Liu, Z. Zhao, Y. Wang, S. Dou, D. Yan, D. Liu, Z. Xia and S. Wang, In Situ Exfoliated, Edge-Rich, Oxygen-Functionalized Graphene from Carbon Fibers for Oxygen Electrocatalysis, Adv. Mater., 2017, 29(18), 1606207 CrossRef PubMed.
- J. Yan, Q. Wang, T. Wei, L. Jiang, M. Zhang, X. Jing and Z. Fan, Template-Assisted Low Temperature Synthesis of Functionalized Graphene for Ultrahigh Volumetric Performance Supercapacitors, ACS Nano, 2014, 8(5), 4720–4729 CrossRef CAS PubMed.
- B. Liu, B. Y. Liu, H. Chen, M. Yang and H. Li, Oxygen and nitrogen co-doped porous carbon nanosheets derived from Perilla frutescens for high volumetric performance supercapacitors, J. Power Sources, 2017, 341, 309–317 CrossRef CAS.
- P. Cai, K. Zou, G. Zou, H. Hou and X. Ji, Quinone/ester-based oxygen functional group-incorporated full carbon Li-ion capacitor for enhanced performance, Nanoscale, 2020, 12(6), 3677–3685 RSC.
- I. K. Ilic, K. Leus, J. Schmidt, J. Hwang, M. Maranska, S. Eigler and C. Liedel, Polymerization in Carbone: A Novel Method for the Synthesis of More Sustainable Electrodes and Their Application as Cathodes for Lithium−Organic Energy Storage Materials Based On Vanillin, ACS Sustainable Chem. Eng., 2020, 8(8), 3055–3064 CrossRef CAS.
- C. Matei Ghimbeu, J. Górka, V. Simone, L. Simonin, S. Martinet and C. Vix-Guterl, Insights on the Na+ ion storage mechanism in hard carbon: Discrimination between the porosity, surface functional groups and defects, Nano Energy, 2018, 44, 327–335 CrossRef CAS.
- X. Chen, X.-R. Chen, T.-Z. Hou, B.-Q. Li, X.-B. Cheng, R. Zhang and Q. Zhang, Lithiophilicity chemistry of heteroatom-doped carbon to guide uniform lithium nucleation in lithium metal anodes, Sci. Adv., 2019, 5(2), eaau7728 CrossRef CAS PubMed.
- X. Zhu, K. Liu, Z. Lu, Y. Xu, S. Qi and G. Zhang, Effect of oxygen atoms on graphene: Adsorption and doping, Phys. E, 2020, 117, 113827 CrossRef CAS.
- A. F. Jiménez-González, J. M. Ramírez-de-Arellano and L. F. Magaña, Substantial Variations in the Optical Absorption and Reflectivity of Graphene When the Concentrations of Vacancies and Doping with Fluorine, Nitrogen, and Oxygen Change, Int. J. Mol. Sci., 2021, 22, 6832–6848 CrossRef PubMed.
- M. Jerigová, M. Odziomek and N. López-Salas, “We Are Here!” Oxygen Functional Groups in Carbons for Electrochemical Applications, ACS Omega, 2022, 7, 11544–11554 CrossRef PubMed.
- D. M. A. Mackenzie, M. Galbiati, X. D. de Cerio, I. Y. Sahalianov, T. M. Radchenko, J. Sun, D. Peña, L. Gammelgaard, B. S. Jessen, J. D. Thomsen, P. Bøggild, A. Garcia-Lekue, L. Camilli and J. M. Caridad, Unraveling the electronic properties of graphene with substitutional oxygen, 2D Mater., 2021, 8, 045035–045043 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Perdew, Burke, and Ernzerhof reply, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 Search PubMed.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104–154122 CrossRef PubMed.
- R. Dronskowski and P. E. Blöchl, Crystal orbital Hamilton populations (COHP): energy-resolved visualization of chemical bonding in solids based on density-functional calculations, J. Phys. Chem., 1993, 97, 8617–8624 CrossRef CAS.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, LOBSTER: A tool to extract chemical bonding from plane-wave based DFT, J. Comput. Chem., 2016, 37, 1030–1035 CrossRef CAS PubMed.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, Analytic projection from plane-wave and PAW wavefunctions and application to chemical-bonding analysis in solids, J. Comput. Chem., 2013, 34, 2557–2567 CrossRef CAS PubMed.
- V. L. Deringer, A. L. Tchougreeff and R. Dronskowski, Crystal Orbital Hamilton Population (COHP) Analysis As Projected from Plane-Wave Basis Sets, J. Phys. Chem. A, 2011, 115, 5461–5466 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsujiet al., Gaussian 16 Revision C.01, Gaussian Inc., Wallingford, CT, USA, 2016 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- R. Ditchfield, W. J. Hehre and J. A. Pople, Self-Consistent Molecular Orbital Methods. 9. Extended Gaussian-type basis for molecular-orbital studies of organic molecules, J. Chem. Phys., 1971, 54, 724 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS; W. J. Hehre, L. Radom, P. V. R. Schleyer and J. A. Pople, Ab Initio Molecular Orbital Theory, Wiley, New York, 1986 Search PubMed.
- D. Y. Zubarev and A. I. Boldyrev, Developing paradigms of chemical bonding: Adaptive natural density partitioning, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217 RSC.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
- T. A. Keith, AIMAll (Version 14.11.23), 2014, tK Gristmill Software, Overland Park KS, USA, https://aim.tkgristmill.com/ Search PubMed.
- X. Fradera, M. A. Austen and R. F. W. Bader, The Lewis model and beyond, J. Phys. Chem. A, 1999, 103, 304–314 CrossRef CAS.
- X. Fradera, J. Poater, S. Simon, M. Duran and M. Solà, Electron-pairing analysis from localization and delocalization indices in the framework of the atoms-in-molecules theory, Theor. Chem. Acc., 2002, 108, 214–224 Search PubMed.
- J. Poater, X. Fradera, M. Solà, M. Duran and S. Simon, On the electron-pair nature of the hydrogen bond in the framework of the atoms in molecules theory, Chem. Phys. Lett., 2003, 369, 248–255 CrossRef CAS.
- (a) C. R. Landis and F. Weinhold, The NBO View of Chemical Bonding, in The Chemical Bond: Fundamental Aspects of Chemical Bonding, ed. G. Frenking and S. Shaik, Wiley-VCH, Weinheim, 2014, pp. 91–120 Search PubMed; (b) F. Weinhold and C. R. Landis, Discovering Chemistry With Natural Bond Orbitals. Wiley, New Jersey, 2012 CrossRef; (c) C. R. Landis and F. Weinhold, Valency and Bonding: A Natural Bond Orbital Donor-Acceptor Perspective, Cambridge University Press, Cambridge, 2005 Search PubMed.
- F. M. Bickelhaupt and E. J. Baerends, Kohn-Sham Density Functional Theory: Predicting and Understanding Chemistry, Rev. Comput. Chem., 2000, 15, 1 CrossRef CAS.
- M. Mitoraj and A. Michalak, Donor–Acceptor Properties of Ligands from the Natural Orbitals for Chemical Valence, Organometallics, 2007, 26, 6576 CrossRef CAS.
- P. Jerabek, P. Schwerdtfeger and G. Frenking, Dative and Electron-Sharing Bonding in Transition Metal Compounds, J. Comput. Chem., 2019, 40, 247 CrossRef CAS PubMed.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Energy-adjusted ab initio pseudopotentials for the second and third row transition elements, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- I. A. Popov, T. R. Galeev, Q. Chen, J. C. Guo, H. Bai, C. Q. Miao, H. G. Lu, A. P. Sergeeva, S. D. Li and A. I. Boldyrev, Deciphering the mystery of hexagon holes in an all-boron graphene α-sheet, Phys. Chem. Chem. Phys., 2011, 13, 11575–11578 RSC.
- I. A. Popov and K. V. Bozhenko, A. I. BoldyrevIs Graphene Aromatic?, Nano Res., 2012, 5(2), 117–123 CrossRef CAS.
- E. Matito and M. Sol, The role of electronic delocalization in transition metal complexes from the electron localization function and the quantum theory of atoms in molecules viewpoints, Coord. Chem. Rev., 2009, 253, 647–665 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc00142g |
| This journal is © The Royal Society of Chemistry 2024 |