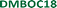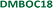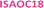Open Access Article
Open Access ArticleOn the origin of cooperativity effects in the formation of self-assembled molecular networks at the liquid/solid interface†
Tamara
Rinkovec
 a,
Demian
Kalebic
a,
Demian
Kalebic
 a,
Wim
Dehaen
a,
Wim
Dehaen
 a,
Stephen
Whitelam
a,
Stephen
Whitelam
 b,
Jeremy N.
Harvey
b,
Jeremy N.
Harvey
 *a and
Steven
De Feyter
*a and
Steven
De Feyter
 *a
*a
aDepartment of Chemistry, KU Leuven, Celestijnenlaan 200F, B-3001 Leuven, Belgium. E-mail: jeremy.harvey@kuleuven.be; steven.defeyter@kuleuven.be
bMolecular Foundry, Lawrence Berkeley National Laboratory, 1 Cyclotron Road, Berkeley, CA 94720, USA
First published on 14th March 2024
Abstract
In this work we investigate the behaviour of molecules at the nanoscale using scanning tunnelling microscopy in order to explore the origin of the cooperativity in the formation of self-assembled molecular networks (SAMNs) at the liquid/solid interface. By studying concentration dependence of alkoxylated dimethylbenzene, a molecular analogue to 5-alkoxylated isophthalic derivatives, but without hydrogen bonding moieties, we show that the cooperativity effect can be experimentally evaluated even for low-interacting systems and that the cooperativity in SAMN formation is its fundamental trait. We conclude that cooperativity must be a local effect and use the nearest-neighbor Ising model to reproduce the coverage vs. concentration curves. The Ising model offers a direct link between statistical thermodynamics and experimental parameters, making it a valuable tool for assessing the thermodynamics of SAMN formation.
Introduction
Cooperativity is a fundamental concept that plays an important role in many biological and physical processes, central to understanding molecular recognition and supramolecular self-assembly.1–4 Cooperativity arises from the collective behaviour of a group of molecules or atoms interacting with one another. If the interplay of interactions favours the binding of a subsequent molecule, the process is positively cooperative. If further interactions are disfavored, negative cooperativity results. In self-assembly at the solution/solid interface, the building blocks (molecules, monomers) from the solution phase can cooperatively adsorb on the surface and interact with each other in order to form a stable two-dimensional (2D) structure.5–7 This positive cooperativity is another example of the important all-or-nothing3,8 type of behaviour commonly observable in nature and can be driven by various interactions such as chemical bonding, electrostatic interactions, hydrogen bonding or van der Waals forces. Other examples of such behaviour include protein folding, oxygen binding to haemoglobin and DNA melting.3,9–11However, cooperative binding is not fully understood.4 By gaining a better understanding of the cooperative behaviour of molecules and atoms, more effective strategies for self-assembly can be developed and potentially unlock new avenues for the creation of functional materials with tailored properties.12–15
Cooperativity in the formation of supramolecular structures in the solution phase has been extensively studied.16–20 In particular, thermodynamic investigation of supramolecular polymerisation has attracted great attention to understand the mechanisms driving assembly in solution as well as to correlate molecular structure and intermolecular interactions to properties of formed aggregates. To that end, different thermodynamic models have been developed including thermally activated equilibrium polymerization model and the mass-balance (MB) model.16,20 The MB model introduces cooperativity through a parameter, σ, and the value of this parameter is used to distinguish between processes of different cooperativity.
In the context of self-assembly at the solution/solid interface, cooperativity in the formation of self-assembled molecular networks (SAMN) has been qualitatively observed at the nanoscale by scanning tunnelling microscopy (STM).9,10 Despite its early recognition, there have been few attempts to quantitatively measure and understand the cooperativity effect due to the experimental complexity and stochasticity inherent to the systems under investigation. Notable progress has nevertheless been made in recent years towards achieving a better understanding of cooperativity at the solution/solid interface and in the following, we will briefly highlight some of the most valuable attempts.
In the work of Matsuda et al., cooperativity was integrated into the development of the analytical thermodynamic model and used to explain a sharp change in the concentration-dependent surface coverage observed for different diarylethene self-assembled monolayers.21–23 The origin of this model stems from the elaborate work and thermodynamic models previously developed for the processes in solution.20
More recently, the work of Hipps et al. has shown that there is a small degree of cooperativity in the binding of small ligands such as methoxypyridine, 1-phenylimidazole or 3-phenylthiophene to a self-assembled network of cobalt(II) octaethyl-porphyrin (CoOEP) at the 1-phenyloctane/HOPG interface,24–26 While adsorption overall appears to follow a Langmuir isotherm, which would suggest no cooperativity, comparing the fraction of adjacent bound CoOEP molecules with the fraction that would be obtained from a random distribution indicates that cooperativity is present. Additionally, the same group has presented a computational study to determine position-dependent desorption energies for coronene on Au(111) and HOPG as substrates by utilizing the nearest neighbour interaction energy model and showed that it performs well for systems showing weak adsorbate-substrate cooperativity.27 In our recent publication, a systematic study of the concentration-dependent formation of SAMNs at the heptanoic acid/HOPG interface using a model system of 5-alkoxylated isophthalic acids (ISA) was presented.28 The formation of the SAMN was shown to be highly cooperative, and the role of graphitic terraces was emphasized as important in determining surface structures, particularly in conditions leading to the average partial surface coverage.
In parallel, mechanisms of molecular self-assembly on surfaces have been also studied using a computational, coarse-grained Monte Carlo approach.29–35 These theoretical investigations examine the structural features of the 2D self-assembly for different systems ranging from simpler model tripodal molecules31,33 to more complex chiral systems, and co-assembly in metal–organic networks.34 In parallel to quantifying thermodynamic factors, the development of computational methods studying morphology of 2D systems is also of great importance to establish predictive power over self-assembly at the liquid/solid interface.
Thus, while the concept of cooperativity has been observed as important in determining the type of network observed on the surface36,37 and evaluated for several examples,21,24,26–28,38 a deeper quantitative understanding and thermodynamic investigation of the effect of cooperativity in the formation of SAMNs is still missing.
In the presented work, we focus on evaluating the cooperative behaviour in SAMN formation and investigate its origin. To that end, the cooperativity effect was studied with a combination of experimental and theoretical approaches. To quantitatively study the influence of hydrogen bonding on the overall behaviour of SAMN formation, we synthesized a molecular analogue of ISA that cannot form hydrogen bonds with its neighbors and evaluated its concentration-dependent behaviour at the nanoscale using STM. Additionally, we have adapted the problem of cooperativity and concentration-dependent surface coverage onto a lattice system and have developed an 2D Ising-type model for the description of SAMN formation. Using a Monte Carlo approach, we have simulated coverage vs. concentration curves under different conditions and have fitted the experimental results to the Ising-type model. This has allowed us to connect classical and statistical thermodynamics and explain the experimental results in terms of molecular behaviour using the nearest-neighbour model approach, thus revealing the free energy contributions to the total free energy of the SAMN formation arising from the molecule–molecule and molecule–surface interactions.
Results
Scanning tunnelling microscopy
The cooperativity effect in the study of concentration-dependent SAMN formation at the solid/liquid interface can be evaluated through a correlation between the physical chemistry of the self-assembly (the concentration-dependent behaviour) and the molecular structure (the supramolecular interactions).1,5,7 Studying structurally similar molecules with a slight variation in supramolecular architecture allows for investigating the influence of molecular features on the SAMN structure that can be observed by STM. Most often, the changes are reflected in the structural parameters of the networks (unit-cell parameters), type of the networks formed (porous vs. dense) or in concentration-dependent surface coverage. This is a well-known and quite often employed method, particularly for studying the effect of the length of the alkyl chain on the on-surface structure.23,28,39–43As a principle this was also applied in the work presented here to study the influence of hydrogen bonding on the overall behaviour of SAMN formation. We prepared a structural analogue 1-(octadecyloxy)-3,5-dimethylbenzene (DMBOC18, Scheme 1) of previously studied derivatives of 5-alkoxy isophthalic acids, ISAs (Scheme 1). DMBOC18 differs structurally from ISAs in that the carboxylic acid functional groups of the latter molecules are replaced by methyl groups, thus removing the capacity to form intermolecular hydrogen bonds.
In this way, by performing a concentration-dependent surface coverage study of DMBOC18, we aim to observe and quantify the differences in molecular patterns observed for DMBOC18 and ISAOC18 (1), the effect such a change of molecular structure has on the critical concentration for the SAMN formation (2) and note any differences in the cooperativity effect (3). Finally, the main goal of this work is to provide experimental evidence concerning the origin of cooperativity in the SAMNs formation.
Scanning tunnelling microscopy of DMBOC18
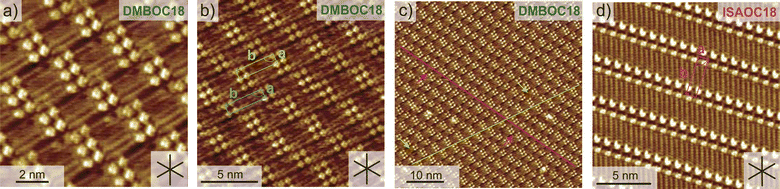
Changing the molecular structure from ISAOC18, bearing carboxylic acid moieties, to DMBOC18, having methyl groups in their place (Scheme 1), changes the scope of supramolecular architecture and possibilities of the molecular organization within the SAMN. It limits the chemical nature of interactions available and places constraints on the range of intermolecular arrangements between DMBOC18 molecules that are favourable enough to form a stable monolayer. Due to this, it is expected that the SAMN of DMBOC18 at the heptanoic acid/HOPG interface forms, to an extent, a structurally different assembly.The observed molecular ordering for DMBOC18 at the nanoscale using STM is presented in Fig. 1. The assembly is particularly interesting as it consists of alternating six- and four-membered sub-assemblies (Fig. 1a) stabilized via interdigitation of the alkyl chains (dark, striped features), which is the dominant intermolecular interaction that holds the network together. The inability to form hydrogen bonds has caused the loss of formation of distinct lamellae due to loss of stronger interactions of the head-groups in the growth of the monolayer, observed by the offset in the aromatic headgroup interactions between subassemblies (Fig. 1b). The columnar shift between the six- and four-membered sub-assemblies shows that with less directional head-group interactions, the van der Waals interactions achieved through the interdigitation become important for stabilizing the network through the extending assembly.
Additionally, in the large-scale STM image, the extent of periodicity for the SAMN of DMBOC18 appears to be low, as the alternation of six- and four-membered assemblies occasionally shows a discontinuity. Following the magenta line in Fig. 1c, this alteration is occasionally disrupted by a repeat of two six-membered assemblies and as an abrupt change within one row from six-membered sub-assemblies to a four-membered sub-assembly (green indicators, Fig. 1c). These observed breaks in the larger scale STM images could be attributed to the mismatch of periodicity between the molecular lattice and the graphite lattice.
We note that a self-assembled network containing alternating hexamers and tetramers was previously observed and studied for a series of 1,3-dibromo-5-alkoxybenzene derivatives.44 That study concluded that when competing weak interactions are at play (halogen bonding compared to packing density), the minor effects (in that case, the small differences in molecule–substrate interactions) can become structure-determining. In the absence of strong, structure-directing interactions such as hydrogen bonds, as observed in ISA systems, the same rationale seems to hold for DMBOC18.
To ensure a fair thermodynamic comparison between DMBOC18 and ISAOC18, we conducted a series of high-resolution STM experiments to determine the structural details of the formed networks, focusing on the unit-cell parameters. Fig. 1b illustrates the unit-cell vectors for DMBOC18, and Table 1 presents the average magnitudes of the vectors. The determination of the unit-cell parameters for DMBOC18 is a non-trivial issue due to the quasi-periodicity of the assembly. However, since packing density is the most important parameter relevant for a thermodynamic comparison, we report several unit-cell parameters in Table S1 of the ESI.† We separately determined unit-cell vectors for a four- and six-membered sub-assembly based on the smallest molecular repeat (distance between two bright features in an STM image in x and y direction). The values are presented in Table S1,† and the average of those is taken as an average unit-cell for the assembly in Table 1.
The magnitude of vector a represents the head-to-head distance between molecules in the close-packed network, and excellent agreement is observed for both molecules (Table 1). Additionally, the magnitude of vector b, which extends along the direction of the alkyl chain in the assembly, depends on the length of the alkyl chain within the molecular structure. Since both molecules have equal chain lengths, the interrow distance in the lamellar structure remains the same. Furthermore, the close similarity between the packing of the two molecules is supported by the similar angle (γ) between the vectors. Therefore, based on the structural parameters obtained from high-resolution STM images, we can conclude that the packing density (ρ, Table 1) of the SAMN formed by ISAOC18 and DMBOC18 is comparable.
Concentration-dependent STM study
A starting point of this study at the nanoscale level is evaluating the effect of DMBOC18 solution concentration on the adsorption behaviour, focusing on the surface coverage using scanning tunnelling microscopy. For this, a series of STM experiments was conducted where the solution concentration of the studied molecule was varied. The solution concentrations studied ranged from 1.00 × 10−3 mol dm−3 to 8.09 × 10−3 mol dm−3. Initially, 40–50 μL of the solution was added to an STM solution cell28,40,45 holding the HOPG substrate. With this volume and the lowest concentrations of 1.00 × 10−3 mol dm−3, the amount of DMBOC18 molecules in solution (>5 × 10−8 mol) is more than sufficient for allowing a complete surface coverage (<3 × 10−11 mol) under these conditions.Representative STM images for a concentration series for the case of DMBOC18 are shown in Fig. 2. One image that corresponds to the average value of surface coverage was chosen at a given concentration from the complete data set that was obtained in a statistical manner, as described in the methods section (see ESI†).
For DMBOC18, no 2D ordering was observed (or at least could not be detected by STM) when the concentration was less than 1.42 × 10−3 mol dm−3, while complete surface coverage was never observed (Fig. 2). At concentrations higher than 8.09 × 10−3 mol dm−3 (Fig. 2), the surface coverage exceeds a value of 80%, but increasing the concentration further with the aim of achieving full coverage leads to a plateau in terms of coverage. Full coverage is hence not observed, perhaps because of the limited range of concentrations available given the solubility of the compound in heptanoic acid. In the concentration range from 1.42 × 10−3 to 8.09 × 10−3 mol dm−3, the observed surface coverage increases, but not rapidly. Additionally, the surface coverage analysis of acquired STM images shows that surface defects (graphitic terraces) have a prominent role in SAMN formation. Specifically, graphitic terraces exist as areas where molecular orderings are most likely to be stable enough to be observed and stable throughout the STM measurement (Fig. S2†). The role of the terraces appears to be creating patches of reduced surface area, stabilizing smaller SAMN domains, and therefore enabling their visualization by STM.
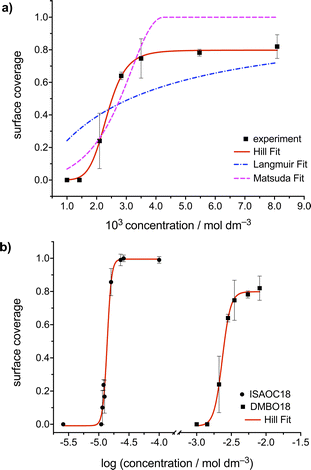
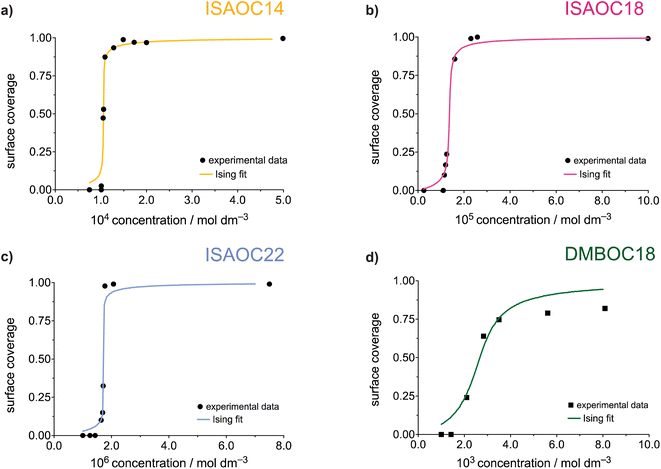
The concentration dependence of the surface coverage of DMBOC18 studied at the heptanoic acid/HOPG interface is presented in Fig. 3 and shows a sigmoidal trend which is distinctive for positive cooperativity.4 The critical concentration for the formation of self-assembled molecular networks on surfaces is defined as the concentration at which the surface coverage is 0.5. In the case of DMBOC18, the rough estimate of the value of this threshold, as determined by a numerical derivation of the experimental dataset, amounts to c1/2 = 2.50 × 10−3 mol dm−3.28
Moreover, the dataset of the concentration dependence of the surface coverage of DMBOC18 was subjected to non-linear regression analysis with different phenomenological thermodynamic models. The models included the Langmuir, the Hill, and the Matsuda model, as reported for the case of ISAs, and the corresponding fits are presented as lines in Fig. 3.4,21,46 The main difference between the stated adsorption isotherms is the introduction of molecule–molecule interactions in the Hill and Matsuda models as opposed to the Langmuir model which is developed under the assumption of non-interacting molecules.4,46,47 By the introduction of intermolecular interactions, a new parameter is added to the models that accounts for these interactions and is known as a cooperativity factor. For additional details of each of the models and their comparison, we direct the reader to relevant literature.2–4,46
In the case of DMBOC18, the effect of modification of solution concentration on the surface coverage is not very rapid. Upon an increase in solution concentration, there is an increase in the average value of surface coverage, but interestingly this increase does not appear to follow the hyperbolic shape of the saturation curve that the Langmuir model would predict. The curve of best fit for the Langmuir model is plotted as a blue dashed line in Fig. 3a, and as can be seen, there is a considerable discrepancy between the line of best fit and experimental data points. On the other hand, both the Hill and the Matsuda models account better for the experimental data points, which is also reflected in the goodness of fit for each of the isotherms (see ESI†). Of the two cooperative models, for DMBOC18 the Hill isotherm gives the better fit and the values of estimated adsorption parameters from the regression analysis for DMBOC18 and ISAOC18 are presented in Table 2. The value of equilibrium constant K represents the solution concentration that produces half saturation, and n is the Hill constant, an empirical coefficient accounting for the mismatch to the hyperbolic behaviour characteristic of adsorption with no interactions. Additionally, it has been shown that for systems showing positive cooperativity, the Hill coefficient sets the lower limit for the number of interacting adsorption sites.4,46 Although determined by data analysis methods with different error margins, the values of parameter K ((2.34 ± 0.03) × 10−3 mol dm−3) from the Hill isotherm and the critical concentration threshold c1/2 (2.50 × 10−3 mol dm−3), which both correspond to a solution concentration that produces half coverage, are in very good agreement.
Discussion
DMBOC18 and ISAOC18 comparison
In this section, we will examine and contrast the structural characteristics of the two molecules based on their assemblies observed in STM, along with their concentration behaviour, in an attempt to draw meaningful conclusions regarding the cooperativity effect.The SAMN structure for alkoxylated isophthalic acid derivatives at the heptanoic acid/HOPG interface has been extensively reported previously.28,41–43,48 It is characterized by the formation of lamellar double rows, within which the aromatic ISA headgroups (which show up as bright features in STM images) arrange in a head-to-head orientation and the alkyl chains (dark striped features in STM images) of the molecules in adjacent lamellae interdigitate and lie flat along one of the major symmetry axes of the graphite lattice. Together, this closed-packed assembly is hence stabilised by van der Waals interactions between the interdigitated alkyl chains and the four-fold hydrogen bonding between the ISA head groups. In comparison, instead of observing continuous double rows for DMBOC18, which are prominent in the case of ISA derivatives, the assembly is characterised by formation of smaller assemblies consisting of groups of four or six molecules, slightly offset between each other. While for ISA, the hydrogen bonding between molecular head-groups causes the growth of the assembly in the long rows, for DMBOC18, no long-range directionality is observed that would propagate the interaction of the DMBOC18 headgroups throughout the network.
Additionally, the difference between the assemblies can also be observed in size and the quality of the monolayer on a larger scale. For DMBOC18, the domains formed are not defect-free and are generally smaller in size than the domains formed by ISAOC18. Domains formed by DMBOC18 appear as less defined and sharp and hence, as less crystalline due to the presence of many domain edges, which also adds to the difficulty of visualization. In contrast to large domains and continuous double-rows observed for ISAOC18, what is observed for DMBOC18 is the formation of relatively stable, smaller, island-type domains (Fig. S1 of the ESI†). Together, these observations can be attributed to the lack of directional interactions between the headgroups of DMBOC18, which consequently allows for the easier formation of domain edges and breaks within the domains.
The comparison between the concentration-dependent surface coverage behaviour between ISAOC18 and DMBOC18 is presented in Fig. 3b using a logarithmic scale. In comparison to ISAOC18, there are two main differences between the systems. Firstly, the curve for DMBOC18 is shifted to much larger values of solution concentrations due to a much higher value of the critical concentration for SAMN formation. The estimated value of this parameter increased roughly 150-fold, from c1/2 = 1.60 × 10−5 mol dm−3 for ISAOC18 to c1/2 = 2.50 × 10−3 mol dm−3 for DMBOC18. Using the values of the equilibrium constant K as determined by the Hill isotherm, the Gibbs free energy of monolayer formation was calculated at 25 °C for both molecules and is presented in Table 2. The difference in free energy gain associated with the SAMN formation from DMBOC18 to ISAOC18 amounts to approximately 12.7 kJ mol−1. Considering the differences in molecular structure, this shows that exchanging a single methyl with a carboxylic acid group brings additional stabilisation of about 6.35 kJ mol−1.
Evidently, the hydrogen bonding within the SAMN is an extremely important factor in the stability of the SAMN. This is a much stronger effect than the previously reported structural modifications which showed that increasing the length of the hydrophobic alkyl chain by a single methylene unit provides additional free energy gain of 1.27 kJ mol−1.23,28,42 Since assembling DMBOC18 molecules gain less in terms of stability from the intermolecular interactions, and as the HOPG surface is weakly interacting, the system requires a high chemical potential to be able to form a thermodynamically stable supramolecular network.
A second aspect of comparing the two systems is the way they respond to a change in solution concentration. Our previous study of concentration-dependent self-assembly of ISA derivatives has shown extremely high positive cooperativity, as observed from a sharp transition from an empty to a full surface upon a small change in solution concentration. The overall concentration-dependent study for DMBOC18 shows less prominent steepness of the transition which contrasts with all the ISA derivatives studied previously. Even though the effect of modification of solution concentration on the surface coverage in the case of DMBOC18 shows a much less steep transition, as discussed previously, it is still better described using a cooperative model (Hill or Matsuda model) than a non-cooperative model (Langmuir).
This finding is significant because it highlights that cooperativity in SAMN formation is a fundamental trait of the self-assembly process at the interface that does not really depend on the molecular architecture. Therefore, as a fundamental trait, the cooperativity effect must stem from local, nearest-neighbour interactions and not necessarily from the chemistry of those interactions. The extent of the cooperativity effect is modulated by the number and type of supramolecular interactions achievable, which is evident from the value of the critical concentration threshold. The stronger and more directional the interactions are, the network will be able to stabilise at lower solution concentrations.
Theoretical evaluation
The thermodynamic models we have used in the study of SAMN behaviour have so far been limited to phenomenological analysis of experimental results. Such analysis does not provide a molecular understanding of the cause of cooperativity in our experiments. We therefore developed an approach based on statistical thermodynamics in order to provide a molecular understanding of our experiments.The Ising model is the prototypical description of collective behaviour in terms of local interactions.49–52 The model was originally formulated to describe ferromagnetism, but has since been broadly used in the molecular sciences, for example, in protein folding,53–55 and chiral selection at the vacuum/solid interface56,57 as well as in biology,58 economy and psychology.59
We can consider the classical Ising model, eqn (1), to be a coarse-grained representation of our system to represent a reasonable model for self-assembly and adsorption.56,57,60–62 Instead of considering spins and placing them onto a lattice, the idea is to convert to a tiling problem where a rectangular 2D lattice represents the surface that is filled with molecules and characterised by isotropic nearest-neighbour interactions. Upon adsorption of a molecule to a lattice position, its occupation changes from ‘empty’ (O = 0) to ‘occupied’ (O = 1) and vice versa upon desorption. The total energy of the system has two contributions. The first term is the adsorption energy term where μ represents the free energy of binding of a monomer from solution to a site with no neighbours. The second contribution accounts for the free energy gain associated with nearest-neighbour interactions, with 〈i, j〉 a sum limited only to the nearest neighbours and shows that those interactions lower the overall energy of the system (for J > 0).
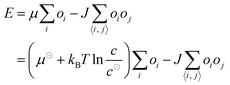 | (1) |
The approximation of an ideal solution is expected to be valid for the systems studied within the scope of this work. This expectation stems from the fact that the systems under consideration are very dilute, with concentrations spanning from 10−6 to 10−4 mol dm−3. Furthermore, there is no discernible experimental indication of solution-phase dimerization or multimerization of the solute molecules occurring in the solution, which would otherwise significantly influence the concentration and cause occurrence of non-ideal behaviour.
2D Ising model for molecular self-assembly on surfaces
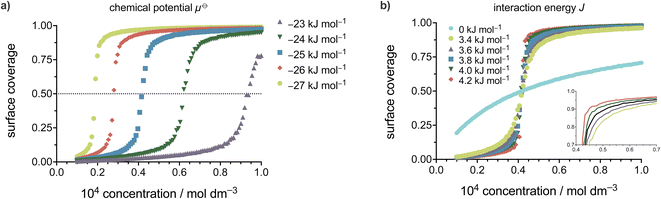
The fact that the total energy of the system explicitly depends on the solution concentration is very important, as it allows a direct connection and comparison between experimental variables and the statistical model. The solution to the lattice gas problem in 2D as defined by eqn (1) is a non-trivial issue and is commonly solved by the Monte Carlo (MC) approach.31,33,63,64 To that end, we developed an MC code to simulate coverage vs. concentration curves and to perform non-linear regression analysis of experimental data. The MC algorithm comprises several steps, where a 2D square lattice (dimensions d × d, under periodic boundary conditions) is first generated and the occupation at each site is assigned. Adsorption or desorption events are then considered based on the occupation of the chosen site, followed by application of the Metropolis algorithm51,59,65–68 to determine whether the event is accepted or not based on the value of the energy change implied and the temperature. Note that the dependence of the adsorption energy on the solution concentration removes the numerical convergence issues near the critical point, and we indeed find that the simulations converge well irrespective of the initial coverage used when starting the simulation.Fig. 4 illustrates coverage versus concentration curves simulated with the MC code developed for the 2D Ising model utilized in self-assembly on surfaces. Panels a and b of Fig. 4 demonstrate the effects of varying the previously described parameters of the Ising model on the shape, curvature, and location of the critical concentration threshold in each curve. These simulations provide valuable insights into the interplay between the different parameters of the Ising model and the resulting self-assembly behaviour.
Modifying the standard chemical potential for the adsorption of the molecule from the solution to the surface has a profound effect on the coverage vs. concentration curves as seen from Fig. 4a.
Upon increasing the standard chemical potential for adsorption, μ⊖, from −23 kJ mol−1 to −27 kJ mol−1 the curves shift to the left, i.e. the transition from empty to full surface happens at lower concentrations values, effectively shifting the critical concentration threshold to lower concentrations. Thus, the stronger the molecule–surface interactions (higher μ⊖) the lower the critical concentration value for a given molecule. Consequently, increasing the molecule–surface interactions by modifying the molecular structure is expected to cause the SAMN formation at lower critical concentration.
The intermolecular interaction parameter J has a considerable effect on the coverage vs. concentration curve (Fig. 4b) which is reflected in the curvature of the sigmoid. It is convenient to express the value of J as a multiple of kBT, which represents the thermal energy available at a given temperature (approximately 2.5 kJ mol−1 at room temperature). Values of J greater than kBT significantly affect the thermodynamics of the studied processes.56,57,69 Here, the higher the value of J the steeper the sigmoid becomes and vice versa. In Fig. 4b this was highlighted by changing the value of J between 3.4 and 4.2 kJ mol−1 where all the simulated curves in that energy range show sigmoidal behaviour but with a change in their steepness, as additionally highlighted by the inset.
An additional curve (shown in cyan) was simulated to show what happens when there are no intermolecular interactions (J = 0). As can be seen from Fig. 4b the curve in this case changes from a sigmoid to a hyperbola showing steady saturation with the increase in concentration, corresponding to the behaviour expected with a Langmuir isotherm. Therefore, the nonzero value of J makes a phase transition possible and directly relates the cooperativity of the process (steepness of the curve) to the intermolecular interactions.
The experimental datasets obtained by the STM for the ISA derivatives and DMBOC18 were subjected to a non-linear regression fitting of μ⊖ and J using the 2D Ising code and are presented in Fig. 5 (the code minimises the squared sum of residuals between the experimental and Ising model surface coverages). In all cases, the grid size used involved 20 × 20 sites, at a temperature of 298.15 K, with 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 equilibration Monte Carlo sweeps at each concentration, and 8000 production sweeps.
000 equilibration Monte Carlo sweeps at each concentration, and 8000 production sweeps.
Our model assumes a homogeneous surface characterised by identical adsorption sites. It is important to note here that, as discussed in our previous work,28 the inhomogeneities in the potential energy of the surface appear to play a role in the thermodynamic analysis. At a certain ‘local’ scale, SAMN formation can be considered to occur as a very sharp step function in coverage vs. concentration curves, represented by a (single) critical concentration. The overall smoother change in coverage with concentration can then be attributed to contributions from multiple different ‘local’ environments, each corresponding to a graphitic terrace, with each of them having a slightly different critical concentration. These slight changes in affinity on different terraces would most likely be due to interactions with step edges at the boundary of the terrace. Partial coverage within such terraces has not been observed experimentally. In the present modelling we neglect these boundary molecule–edge interaction effects and instead treat the shape of the sigmoidal surface coverage curve as resulting entirely from molecule–molecule interaction as modelled by a single intermolecular parameter J. Interpretation of the value of J obtained therefore needs to take into account the fact that it describes both molecule–molecule and molecule–edge effects.
The parameters of the data fitting for all molecules are presented in Table 3. As explained and reported previously, the experimentally observed datasets show a difference in their concentration dependence. Firstly, in the series of ISAs it was observed that increasing the length of the alkyl chain from 14 to 22 shows a linear increase in the Gibbs free energy of the SAMN. Upon analysing the datasets using the Ising model, this trend is still present and is noticeable in the value of free energy of binding of a molecule to the surface, μ⊖.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, Nprod = 8000)
000, Nprod = 8000)
Additionally, in this case, the free energy of adsorption (μ⊖) shows a linear dependence on the length of the alkyl chain (Fig. S8†) with an additional stabilisation of 1.28 kJ mol−1 upon adding a single methylene unit, which is in excellent agreement with previously reported experimental studies.23,28 Thus, the process of SAMN formation will to a large degree be determined by the molecule–surface interactions as the strength of these interactions shows to be most relevant for the experimental conditions where the monolayer forms and is observable by STM. Comparing the intermolecular interaction parameter J amongst the ISA derivatives shows that in order to accurately model the SAMN formation, the molecule–molecule interactions need to be included in the model. However, the changes in the interaction energy are relatively small within the series and, due to the scattering of the experimental data, the nature of the experiment, and the uncertainty mentioned above about the relative role of molecule–molecule and molecule–edge effects, should be treated as having a larger error margin.
From the Ising analysis of ISAs we can conclude that the change in molecular structure significantly affects the free energy of molecule–surface interactions, thereby influencing the stability of the network. The cooperativity effect across the ISA series varies slightly as reflected from the value of intermolecular interaction energy J, and for a series of these isostructural molecules, the increase in the alkyl chain length makes the process of SAMN formation more cooperative. Even though the differences in parameter J are not as obvious as for μ⊖ it should be highlighted that for a single molecule, the free energy of a molecule binding to the growing SAMN comes from its binding free energy (μ⊖) and, in this primitive model, from four possible nearest-neighbour interactions each of a strength equal to the value of free energy of molecule–molecule interaction J (maximal stabilisation is equivalent to 4 J).
Comparing the Ising parameters for ISAOC18 to DMBOC18, it can be observed that the values of both the intermolecular interaction term and the free energy of monomer adsorption decrease. In the isotropic view of the simplest 2D Ising model, the supramolecular interactions that form are averaged out to be equal in all four directions (each molecule has four nearest neighbours). However, the differences in the values of J (Table 3) still highlight that DMBOC18 has a lower gain in free energy due to weaker interactions between the molecules, by about 1.1 kJ mol−1 per neighbour in this averaged representation. As observed experimentally, the removal of the hydrogen bonding weakens the interactions of the aromatic headgroups, which is also paralleled by a significant decrease in value of the parameter J, considering that the expectation values of J are of the order of several kJ mol−1.
Fitting the experimental STM datasets to the Ising model has revealed a large difference in the value of the free energy of monomer binding μ⊖. The free energy difference is lower by approximately 13.1 kJ mol−1 in the formation of the DMBOC18 monolayer. The free energy of monomer binding μ⊖ is a free energy “umbrella” term which encompasses the enthalpic and entropic contributions for a process in which a free, solvated molecule binds to the surface. This process must be accompanied by an enthalpic gain due to favourable molecule–surface interactions, and an unfavourable entropic contribution caused by the loss of translational and rotational degrees of freedom. Moreover, solvent effects can also play a role. For example, if the solvent interacts more favourably with the free molecules than with the growing monolayer, solvation effects will make SAMN formation less favourable in enthalpic terms but more favourable in entropic terms. All these effects contribute to the fitted values of μ⊖. The molecule–substrate interactions that are achievable by ISAOC18 and DMBOC18 are quite similar, as both molecules have an aromatic core and a long alkyl chain, and the carboxylic acid function is not expected to provide a much stronger interaction with the HOPG substrate than a methyl group. The intrinsic entropic term associated with surface adsorption is also expected to be similar. The large difference in μ⊖, as observed from the non-linear fits to the Ising model, is thereby likely to be due to solvation effects. The solvent in both systems is heptanoic acid, a carboxylic acid that can partake in hydrogen bonding with the ISA headgroups in solution and on the surface. Experimentally it was not observed that the solvent molecule co-adsorbs on the surface, but the difference in solvation of the molecules could lead to increased stability of the ISAOC18 monolayer. Investigation and quantification of solvent effects in the formation of SAMNs is crucial for a complete evaluation of the thermodynamics of monolayer formation, and therefore deserves to be further investigated.
Drawbacks of the 2D Ising model
Despite providing quite valuable and novel insights into the different contributions to the free energy of the SAMN formation, the application of the Ising model based on the approach presented here has some limitations.Firstly, the model does not consider the chemistry of the substrate. Thus, the effect of changing the substrate, for example comparing Au(111) to HOPG, is expected to lead to changes in both parameters of the Ising model, μ⊖ and J, but does not allow predictions of how they change. As the lattice used is rectangular, it also does not accurately portray the hexagonal symmetry of the HOPG substrate that was used in the experiments. If needed, this aspect of the monolayers could also be treated with the present type of model, using six nearest neighbours for each site. Another limitation caused by the choice of the parameters of the model is that each adsorbing molecule on the rectangular grid interacts in the same way with each of its neighbours, i.e. the free energy increments are the same for each of the four neighbouring sites. This provides a mean value of the interaction energy and could be refined by implementing a form of anisotropy (possibly with a hexagonal grid), that could reflect the different supramolecular architectures and functionalities within the molecular structure. Additionally, in this way the 2D Ising model could be applied to a broader scope of systems, including studying systems that show on-surface polymorphism.
Finally, the 2D Ising model works well for systems where the solvent was shown not to co-adsorb and influence the network formation. However, for more complicated systems the role of the solvent should be evaluated thoroughly. Apart from co-adsorbing, the solvent affects the solubility of the solute. In this work, the solvent used was heptanoic acid. This is a carboxylic acid and due to the possibility for hydrogen bonding it better solubilises the ISA derivatives than DMBOC18. The thermodynamics of solvation could play a very important role in the SAMN formation and therefore it is important to further develop the theoretical models to account for the solvent effect to improve the understanding of its role.
At this point, parameters of the developed Ising code are free energy terms. Work is underway in expanding the model by the introduction of entropic and enthalpic contributions to both parameters. In this way, instead of limiting the evaluation to overall free energy contributions from molecule–molecule interaction term (J) and molecular adsorption (μ⊖), one could understand both factors through their separate enthalpic (JH and μ⊖H) and entropic (JS and μ⊖S) contributions, as well as study the temperature dependence of the system.
Conclusions
In this study, we present an experimental investigation of the cooperativity effect in the formation of self-assembled monolayers at the liquid/solid interface. To achieve this, we conducted a comparative analysis between previously reported derivatives of isophthalic acid (ISA) and a modified molecular analogue known as alkoxy dimethylbenzene (DMB), which lacks hydrogen bonding architecture. The concentration dependence was explored at the nanoscale using scanning tunnelling microscopy (STM), and the resulting surface coverage curve was analysed employing analytical thermodynamic models, namely Langmuir, Hill, and Matsuda models. The formation of the DMB monolayer exhibited a positive cooperativity effect, although less pronounced than observed with ISA. The Hill model provided the best description for this phenomenon. Although the qualitative observation of positive cooperativity in self-assembled monolayer formation has been reported previously,9,10 we demonstrate its experimental quantification even for molecules with weak interactions, highlighting cooperativity as an inherent characteristic of self-assembled monolayer formation. Furthermore, our findings indicate that the presence of additional supramolecular moieties in the molecular structure strengthens intermolecular interactions, leading to a decrease in the critical concentration threshold.The cooperativity effect is further investigated by incorporating nearest-neighbour interactions through the development of a Monte Carlo lattice gas or Ising model, fitted so as to accurately reproduce the coverage versus concentration curves. While previous attempts have explored this approach to some extent,56,57,60–62 to the best of our knowledge, our study represents a novel use of the Ising model for data fitting and analysis of cooperativity in terms of both molecule–surface and molecule–molecule interactions. Moreover, we have successfully established a direct correlation between statistical modelling and experimental parameters, specifically concentration, thereby providing a valuable tool for a wider audience to assess the thermodynamics of the SAMN formation. Our findings, derived from using the Ising model, reveal that both molecule–surface and molecule–molecule interactions contribute to the formation of a more stable monolayer. While the evaluation of the molecule–molecule interaction term is relatively straightforward and can be linked to molecular structure, the assessment of the molecule–surface interaction term is more intricate. Our next objective is to refine the Ising model to disentangle the individual effects of this term.
This study represents a significant step forward and serves as a benchmark for further developments. Future modifications of the model could account for surface symmetry, molecular anisotropy, and solvent effects, making it even more robust and versatile. Additionally, these modifications would open the possibilities for a temperature-dependent study and the assessment of the delicate balance of enthalpy vs. entropy in the SAMN formation.
Data availability
The experimental data underlying this study are openly available in KU Leuven Research Data Repository at https://doi.org/10.48804/Y4ASXA.Author contributions
T. R. conceptualized the idea, performed STM investigation and data analysis, wrote MC software and participated in writing – original draft, review and editing. D. K. synthesised the chemicals needed to perform the study and participated in writing – original draft, review and editing. W. D. provided resources, supervised and partook in writing – review and editing. S. W. contributed to the design of the lattice-gas model, and reviewed and edited the text. J. N. H. conceptualized the idea, supervised the work and software development, provided resources and participated in writing – original draft, review and editing. S. D. F. conceptualized the idea, supervised the work, participated in writing – original draft, review and editing, provided resources and funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funding from KU Leuven – internal funds (C14/23/090) and Research Foundation Flanders (FWO) (G0H2122N via EOS 40007495) is acknowledged. T. R. also acknowledges FWO for a PhD fellowship for fundamental research (fellowship number: 11F2422N). We acknowledge Sven Bernaerts for recording IR spectra.References
- A. S. Mahadevi and G. N. Sastry, Chem. Rev., 2016, 116, 2775–2825 CrossRef CAS PubMed.
- L. K. S. von Krbek, C. A. Schalley and P. Thordarson, Chem. Soc. Rev., 2017, 46, 2622–2637 RSC.
- C. A. Hunter and H. L. Anderson, Angew. Chem., Int. Ed., 2009, 48, 7488–7499 CrossRef CAS PubMed.
- D. I. Cattoni, O. Chara, S. B. Kaufman and F. L. González Flecha, PLoS One, 2015, 10, e0146043 CrossRef PubMed.
- Y. Li, Y. Wang, G. Huang and J. Gao, Chem. Rev., 2018, 118, 5359–5391 CrossRef CAS PubMed.
- R. Ye, M. Zhao, X. Mao, Z. Wang, D. A. Garzón, H. Pu, Z. Zhao and P. Chen, Nat. Commun., 2021, 12, 4287 CrossRef CAS PubMed.
- S. Liu, J. Colloid Interface Sci., 2015, 450, 224–238 CrossRef CAS PubMed.
- E. Lopez-Fontal, L. Milanesi and S. Tomas, Chem. Sci., 2016, 7, 4468–4475 RSC.
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421 CrossRef CAS PubMed.
- G. M. Whitesides, J. P. Mathias and C. T. Seto, Science, 1991, 254, 1312–1319 CrossRef CAS PubMed.
- J. M. Lehn, Chem. Soc. Rev., 2007, 36, 151–160 RSC.
- D. Cui, J. M. Macleod and F. Rosei, Chem. Commun., 2018, 54, 10527–10539 RSC.
- D. B. Amabilino and S. L. Tait, Faraday Discuss., 2017, 204, 487–502 RSC.
- U. Mazur and K. W. Hipps, Chem. Commun., 2015, 51, 4737–4749 RSC.
- R. Gutzler, L. Cardenas and F. Rosei, Chem. Sci., 2011, 2, 2290–2300 RSC.
- C. Kulkarni, E. W. Meijer and A. R. A. Palmans, Acc. Chem. Res., 2017, 50, 1928–1936 CrossRef CAS PubMed.
- M. L. Ślęczkowski, E. W. Meijer and A. R. A. Palmans, Macromol. Rapid Commun., 2017, 38, 1700566 CrossRef PubMed.
- P. Jonkheijm, P. van der Schoot, A. P. H. J. Schenning and E. W. Meijer, Science, 2006, 313, 80–83 CrossRef CAS PubMed.
- G. Vantomme, G. M. ter Huurne, C. Kulkarni, H. M. M. ten Eikelder, A. J. Markvoort, A. R. A. Palmans and E. W. Meijer, J. Am. Chem. Soc., 2019, 141, 18278–18285 CrossRef CAS.
- D. Zhao and J. S. Moore, Org. Biomol. Chem., 2003, 1, 3471–3491 RSC.
- S. Yokoyama, T. Hirose and K. Matsuda, Chem. Commun., 2014, 50, 5964–5966 RSC.
- N. Nishitani, T. Hirose and K. Matsuda, Chem.–Asian J., 2015, 10, 1926–1931 CrossRef CAS PubMed.
- S. Yokoyama, T. Hirose and K. Matsuda, Chem.–Eur. J., 2015, 21, 13569–13576 CrossRef CAS PubMed.
- K. V. Korpany, B. Chilukuri, K. W. Hipps and U. Mazur, J. Phys. Chem. C, 2020, 124, 18639–18649 CrossRef CAS.
- K. N. Johnson, K. W. Hipps and U. Mazur, Phys. Chem. Chem. Phys., 2020, 22, 24226–24235 RSC.
- K. N. Johnson, S. Rana, B. Chilukuri, K. W. Hipps and U. Mazur, J. Phys. Chem. C, 2022, 126, 19188–19199 CrossRef CAS.
- B. Chilukuri, U. Mazur and K. W. Hipps, Phys. Chem. Chem. Phys., 2019, 21, 10505–10513 RSC.
- T. Rinkovec, D. Kalebic, M. Van der Auweraer, W. Dehaen, J. N. Harvey and S. De Feyter, J. Phys. Chem. C, 2023, 127, 2025–2034 CrossRef CAS.
- J. Lisiecki and P. Szabelski, Phys. Chem. Chem. Phys., 2021, 23, 5780–5796 RSC.
- D. Nieckarz and P. Szabelski, ChemPhysChem, 2020, 21, 643–650 CrossRef CAS PubMed.
- P. Szabelski, W. Rżysko and D. Nieckarz, J. Phys. Chem. C, 2016, 120, 13139–13147 CrossRef CAS.
- Ł. Baran, D. Nieckarz, P. Szabelski and W. Rżysko, J. Phys. Chem. C, 2019, 123, 19549–19556 CrossRef.
- A. Ciesielski, P. J. Szabelski, W. Rżysko, A. Cadeddu, T. R. Cook, P. J. Stang and P. Samorì, J. Am. Chem. Soc., 2013, 135, 6942–6950 CrossRef CAS PubMed.
- K. Nieckarz, P. Szabelski and D. Nieckarz, Surf. Sci., 2022, 719, 122041 CrossRef CAS.
- T. K. Piskorz, C. Gobbo, S. J. Marrink, S. De Feyter, A. H. de Vries and J. H. van Esch, J. Phys. Chem. C, 2019, 123, 17510–17520 CrossRef CAS.
- K. G. Nath, O. Ivasenko, J. M. MacLeod, J. A. Miwa, J. D. Wuest, A. Nanci, D. F. Perepichka and F. Rosei, J. Phys. Chem. C, 2007, 111, 16996–17007 CrossRef CAS.
- S. Yasuda, A. Furuya and K. Murakoshi, RSC Adv., 2014, 4, 58567–58572 RSC.
- K. N. Johnson, S. Rana, B. Chilukuri, K. W. Hipps and U. Mazur, J. Phys. Chem. C, 2022, 126, 19188–19199 CrossRef CAS.
- L. Verstraete, T. Rinkovec, H. Cao, H. I. Reeves, J. N. Harvey and S. De Feyter, J. Phys. Chem. C, 2021, 125, 1557–1563 CrossRef CAS.
- M. O. Blunt, J. Adisoejoso, K. Tahara, K. Katayama, M. Van der Auweraer, Y. Tobe and S. De Feyter, J. Am. Chem. Soc., 2013, 135, 12068–12075 CrossRef CAS PubMed.
- S. De Feyter, A. Gesquière, M. Klapper, K. Müllen and F. C. De Schryver, Nano Lett., 2003, 3, 1485–1488 CrossRef CAS.
- P. N. Dickerson, A. M. Hibberd, N. Oncel and S. L. Bernasek, Langmuir, 2010, 26, 18155–18161 CrossRef CAS PubMed.
- K.-W. Park, J. Adisoejoso, J. Plas, J. Hong, K. Müllen and S. De Feyter, Langmuir, 2014, 30, 15206–15211 CrossRef CAS PubMed.
- A. Mukherjee, A. Sanz-Matias, G. Velpula, D. Waghray, O. Ivasenko, N. Bilbao, J. N. Harvey, K. S. Mali and S. De Feyter, Chem. Sci., 2019, 10, 3881–3891 RSC.
- O. Ochs, N. Martsinovich, W. M. Heckl and M. Lackinger, J. Phys. Chem. Lett., 2020, 11, 7320–7326 CrossRef CAS PubMed.
- H. Swenson and N. P. Stadie, Langmuir, 2019, 35, 5409–5426 CrossRef CAS PubMed.
- Y. Ben Torkia, M. Khalfaoui and A. Ben Lamine, IOSR Journal of Applied Physics, 2014, 6, 62–73 CrossRef.
- A. M. Bragança, A. Minoia, R. Steeno, J. Seibel, B. E. Hirsch, L. Verstraete, O. Ivasenko, K. Müllen, K. S. Mali, R. Lazzaroni and S. De Feyter, J. Am. Chem. Soc., 2021, 143, 11080–11087 CrossRef PubMed.
- E. M. Schwen, I. Mazilu and D. A. Mazilu, Eur. J. Phys., 2015, 36, 025003 CrossRef.
- S. Whitelam and R. L. Jack, Annu. Rev. Phys. Chem., 2015, 66, 143–163 CrossRef CAS PubMed.
- K. A. Dawson and Z. Kurtović, J. Chem. Phys., 1990, 92, 5473–5485 CrossRef CAS.
- S. Whitelam, L. O. Hedges and J. D. Schmit, Phys. Rev. Lett., 2014, 112, 155504 CrossRef PubMed.
- C. Millership, J. J. Phillips and E. R. G. Main, J. Mol. Biol., 2016, 428, 1804–1817 CrossRef CAS PubMed.
- E. R. Henry, R. B. Best and W. A. Eaton, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 17880–17885 CrossRef CAS PubMed.
- A. Bakk and J. S. Høye, Phys. A, 2003, 323, 504–518 CrossRef CAS.
- S. Dutta and A. J. Gellman, Entropy, 2022, 24, 565 CrossRef CAS PubMed.
- S. Dutta, Y. Yun, M. Widom and A. J. Gellman, ChemPhysChem, 2021, 22, 197–203 CrossRef CAS PubMed.
- K. Blom and A. Godec, Phys. Rev. X, 2021, 11, 031067 CAS.
- K. A. Dill and S. Bromberg, Molecular driving forces: statistical thermodynamics in biology, chemistry, physics, and nanoscience, Garland Science, 2011 Search PubMed.
- Y. Makoudi, J. Jeannoutot, F. Palmino, F. Chérioux, G. Copie, C. Krzeminski, F. Cleri and B. Grandidier, Surf. Sci. Rep., 2017, 72, 316–349 CrossRef CAS.
- Y. Wei, W. Tong and M. B. Zimmt, J. Am. Chem. Soc., 2008, 130, 3399–3405 CrossRef CAS PubMed.
- C. Schiel, M. Vogtland, R. Bechstein, A. Kühnle and P. Maass, J. Phys. Chem. C, 2020, 124, 21583–21590 CrossRef CAS.
- C. A. Palma, M. Cecchini and P. Samorí, Chem. Soc. Rev., 2012, 41, 3713–3730 RSC.
- D. Nieckarz and P. Szabelski, ChemPhysChem, 2020, 21, 643–650 CrossRef CAS PubMed.
- S. Greenberg and D. Randall, Theoretical Computer Science, 2009, 410, 1417–1427 CrossRef.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press, 1989 Search PubMed.
- A. Shekaari and M. Jafari, Theory and Simulation of the Ising Model, arXiv, 2021, preprint, arXiv:2105.00841, DOI:10.48550/arXiv.2105.00841.
- J. Kotze, Introduction to Monte Carlo methods for an using Model of a Ferromagnet, arXiv, 2008, preprint, arXiv:0803.0217, DOI:10.48550/arXiv.0803.0217.
- L. G. López and A. J. Ramirez-Pastor, Langmuir, 2012, 28, 14917–14924 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental methods, NMR spectra, additional STM images, STM image analysis, details of error analysis, additional Ising modelling results. See DOI: https://doi.org/10.1039/d4sc00284a |
| This journal is © The Royal Society of Chemistry 2024 |