Open Access Article
Open Access ArticleMetal-free platforms for molecular thin films as high-performance supercapacitors†
Ritu
Gupta
a,
Ankur
Malik
a,
Kusum
Kumari
b,
Saurabh Kumar
Singh
 b,
Vincent
Vivier
*c and
Prakash Chandra
Mondal
b,
Vincent
Vivier
*c and
Prakash Chandra
Mondal
 *a
*a
aDepartment of Chemistry, Indian Institute of Technology Kanpur, Uttar Pradesh 208016, India. E-mail: pcmondal@iitk.ac.in
bDepartment of Chemistry, Indian Institute of Technology Hyderabad, Telangana 502285, India
cCNRS, Laboratoire de Réactivité de Surface, Sorbonne Université, 4 place Jussieu, Paris 75005 Cedex 05, France. E-mail: vincent.vivier@sorbonne-universite.fr
First published on 25th April 2024
Abstract
Controlling chemical functionalization and achieving stable electrode–molecule interfaces for high-performance electrochemical energy storage applications remain challenging tasks. Herein, we present a simple, controllable, scalable, and versatile electrochemical modification approach of graphite rods (GRs) extracted from low-cost Eveready cells that were covalently modified with anthracene oligomers. The anthracene oligomers with a total layer thickness of ∼24 nm on the GR electrode yield a remarkable specific capacitance of ∼670 F g−1 with good galvanostatic charge–discharge cycling stability (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) recorded in 1 M H2SO4 electrolyte. Such a boost in capacitance is attributed mainly to two contributions: (i) an electrical double-layer at the anthracene oligomer/GR/electrolyte interfaces, and (ii) the proton-coupled electron transfer (PCET) reaction, which ensures a substantial faradaic contribution to the total capacitance. Due to the higher conductivity of the anthracene films, it possesses more azo groups (–N
000) recorded in 1 M H2SO4 electrolyte. Such a boost in capacitance is attributed mainly to two contributions: (i) an electrical double-layer at the anthracene oligomer/GR/electrolyte interfaces, and (ii) the proton-coupled electron transfer (PCET) reaction, which ensures a substantial faradaic contribution to the total capacitance. Due to the higher conductivity of the anthracene films, it possesses more azo groups (–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–) during the electrochemical growth of the oligomer films compared to pyrene and naphthalene oligomers, which is key to PCET reactions. AC-based electrical studies unravel the in-depth charge interfacial electrical behavior of anthracene-grafted electrodes. Asymmetrical solid-state supercapacitor devices were made using anthracene-modified biomass-derived porous carbon, which showed improved performance with a specific capacitance of ∼155 F g−1 at 2 A g−1 with an energy density of 5.8 W h kg−1 at a high-power density of 2010 W kg−1 and powered LED lighting for a longer period. The present work provides a promising metal-free approach in developing organic thin-film hybrid capacitors.
N–) during the electrochemical growth of the oligomer films compared to pyrene and naphthalene oligomers, which is key to PCET reactions. AC-based electrical studies unravel the in-depth charge interfacial electrical behavior of anthracene-grafted electrodes. Asymmetrical solid-state supercapacitor devices were made using anthracene-modified biomass-derived porous carbon, which showed improved performance with a specific capacitance of ∼155 F g−1 at 2 A g−1 with an energy density of 5.8 W h kg−1 at a high-power density of 2010 W kg−1 and powered LED lighting for a longer period. The present work provides a promising metal-free approach in developing organic thin-film hybrid capacitors.
Introduction
The increasing global population and depletion of fossil fuels have raised significant demands for technological gear, especially portable and lightweight energy storage systems.1–6 To meet ever-expanding energy storage requirements, the number of organic supercapacitor (OSC) devices has been expanding, but it is vital to elevate the energy density and power density.7–12 Excellent synthetic flexibility, light weight, low production cost, tunable electrical conductivity, porosity, sustainable organic electrodes, and easy fabrication under ambient conditions make organic supercapacitors suitable for advanced technological solutions for storing electrical energy in different forms.13–17 Heteroatoms (N, P, O, S), due to their relatively larger electronegativity than carbon, increase surface wettability, alter the Fermi energy (EF), and enhance capacitive performance upon functionalization on carbon electrodes.18–21 Generally, the energy density of an OSC can be improved either by broadening the operational voltage window (which also depends on the nature of the electrolyte) or by increasing the specific capacitance of the electrode materials by combining electrical double-layer capacitance (EDLC) and pseudocapacitance.22–25 Over the last decades, both organic and inorganic “nanomaterials” have played significant roles in electrical energy storage applications.26–28 In addition to the advantages of high surface area, the critical size of energy-storing materials shrinks to a nanoscale dimension (∼1–100 nm in length); thus, the diffusion length for ions is reduced compared to the bulk, which quickens the charging–discharging process, increases the cycle life, and lowers the operational bias, hence enhancing overall supercapacitor performance.29 Among the promising candidates, graphite rods (GRs) have been extensively exploited in dry cells and electrochemical supercapacitors due to their high double-layer capacitance and lower cost; however, they suffer from low energy density and lower cyclic stability.30In conjunction with the emergence of these nanostructured carbon materials, there has been a surge of interest in controlling physical and chemical properties through covalent surface modification.31–34 Such covalent surface functionalization is a challenging task, and sometimes relies on high-energy reagents and harsh reaction conditions that make uncontrollable and un-reproduceable nanostructures.35,36 To address this issue, the electrochemical reduction of aryl diazonium is the most efficient approach as it can create strong, stable, robust covalent bonds between the molecule and the working electrode that may be suitable for multi-purpose usage.37–41 Though surface modification of carbon materials by spontaneous reduction of diazonium has already been studied in energy storage,42,43 the technique does not provide a controlled, homogeneous nanoscale multilayer film and requires a longer time.
We have opted here for a simple, fast-film-forming bottom-up approach to modify graphite rods (GRs) with high surface area and nitrogen-rich graphene structures formed via electrochemical reduction of diazonium salts of three different amine compounds, 1-amino anthracene (ANT), naphthalene (NAPH), and pyrene (PYR), and their electrochemical capacitance performances are compared with each molecular layer. The ANT-modified GR oligomer films show high charge storage due to two major contributions: non-faradaic (electrochemical double-layer) and faradaic (interfacial proton-coupled electron transfer). We also reused the used graphite rods extracted from commercially available low-cost Eveready cells (US$1.5 for 10 cells of 1.5 V) for electrochemical supercapacitor studies upon growing nanoscale molecular films, which also reveal excellent charge storage compared to the unmodified ones. In addition, we fabricated asymmetric supercapacitor devices using ANT-grafted porous carbon as a positive electrode and porous carbon as a negative electrode, showing a capacitance value of 155 F g−1 at 2 A g−1, illustrating the excellent potential of a covalently bonded anthracene oligomer in charge storage. The present study comprises low-cost materials that can be easily scaled up to fabricate high-capacity energy systems for practical applications in molecular energy storage at the nanoscale, so the concept of “waste to energy” could be viable.
Results and discussion
The synthesis and characterization of respective diazonium salts are discussed in ESI (Fig. S1–S3†), and they were used for the growth of molecular layers on graphite rods (GRs) by the electrochemical (E-Chem) reduction method. Fig. 1a shows the potentiostatic cyclic voltammogram (CV) scans (1–20 cycles) of electrochemical grafting of a GR substrate performed in 5 mM of anthracene diazonium salts in acetonitrile recorded at a 100 mV s−1 scan rate using 0.1 M n-tetrabutyl ammonium perchlorate (TBAP) as a supporting electrolyte. The CV shows the two reduction peaks: a broad irreversible reduction peak at −0.22 V (vs. Ag/AgNO3) observed during the first scan, indicating the reduction of anthracene diazonium salts (D-ANT); and a higher cathodic peak indicating the formation of ANT layers on the different planes of the GR. Being highly reactive, aryl radicals (generated at the working electrode surface) covalently bonded to the graphite rod and were extended with a repeated number of CV scans, keeping the potential window unchanged (Fig. S4 and S5, Table S1†). Continuous binding of (for instance, ANT) radicals maintains the growth of anthracene molecular layers along with azo groups (–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–) as bridges. However, though there have been previous studies on E-Chem-grafted molecular layers utilized for hybrid supercapacitors, none of the work highlighted such unexpected azo formation during E-Chem grafting.39 Non-radical formation of azo bridges between layers is one of the main assumptions to explain layer growth other than radical polymerization. A proposed schematic structure of an ANT thin film with different types of nitrogen on the GR electrode is shown in Fig. 1b with a digital image of a GR. Atomic force microscopy (AFM) measurements were used to evaluate the thickness of the molecular films by scratching the ANT films with a sharp needle, and it was found to be 23 ± 0.8 nm using depth analysis (Fig. S6 and S7†). The baseline-corrected UV-vis spectra of the thin film are shown in Fig. S8.† The obtained spectra for NAPH and PYR thin films show strong peaks at λ = 344 nm and λ = 365 nm due to a π to π* transition. However, the ANT oligomer film shows a broad signal in the visible region, which is red-shifted (n to π* transition) due to the formation of extended conjugation in the ANT film, offering a lower band gap of 1.7 eV compared to NAPH and PYR thin films (Tables S2 and S3†).
N–) as bridges. However, though there have been previous studies on E-Chem-grafted molecular layers utilized for hybrid supercapacitors, none of the work highlighted such unexpected azo formation during E-Chem grafting.39 Non-radical formation of azo bridges between layers is one of the main assumptions to explain layer growth other than radical polymerization. A proposed schematic structure of an ANT thin film with different types of nitrogen on the GR electrode is shown in Fig. 1b with a digital image of a GR. Atomic force microscopy (AFM) measurements were used to evaluate the thickness of the molecular films by scratching the ANT films with a sharp needle, and it was found to be 23 ± 0.8 nm using depth analysis (Fig. S6 and S7†). The baseline-corrected UV-vis spectra of the thin film are shown in Fig. S8.† The obtained spectra for NAPH and PYR thin films show strong peaks at λ = 344 nm and λ = 365 nm due to a π to π* transition. However, the ANT oligomer film shows a broad signal in the visible region, which is red-shifted (n to π* transition) due to the formation of extended conjugation in the ANT film, offering a lower band gap of 1.7 eV compared to NAPH and PYR thin films (Tables S2 and S3†).
The amorphous nature of the ANT films grown on GR was confirmed by X-ray diffraction (XRD) studies (Fig. S9 and S10†). The diffraction peaks at 2θ values of 26.5°, 42.4°, 44.5°, 54.5°, 77.5°, and 83.6° correspond to the (002), (100), (101), (004), (103), and (110) planes of hexagonal graphite with P63/mmc space group (JCPDS 00-008-0415) for all the films, including bare GR. However, no significant change was observed after grafting, possibly due to the lower surface coverage of ANT layers on the GR surface. In addition, the field-emission scanning electron microscopy (FE-SEM) image of bare GR shows micrometer-sized flake-like structures (Fig. S11a†), whereas, after grafting with ANT, the FE-SEM image reveals globular structures with an increase in roughness, suggesting the growth of ANT layers and filling of voids on the graphite surface (Fig. S11b†). The Raman spectra of bare GR and ANT/GR show a strong D-band at 1351 cm−1, a G-band at around 1583 cm−1, and a strong 2D-band around 2705 cm−1 (Fig. 1c and S12†). The D-band is observed due to the breathing mode of k-point phonons of A1g symmetry of the porous carbon, which also reveals the presence of defect sites, impurities, and disorder in the structure.44 The ID/IG ratios were 0.12 and 0.36 for bare GR and ANT/GR, respectively, indicating increased disorder with the ANT oligomer films, as is apparent in the FE-SEM image. The G-band represents the E2g phonon of sp2 carbon atoms and corresponds to the ordered sp2-hybridized graphene network.45 The 2D peak was observed at about 2700 cm−1, caused by the second-order vibration of two phonons with opposite wavevectors. The X-ray photoelectron spectra (XPS) of the C1s in bare GR were deconvoluted into three peaks at binding energies of 284.5 eV, 284.9 eV, and 285.9 eV corresponding to sp2-hybridized C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, sp3-hybridized C–C, and C–O components, respectively46–48 (Fig. S13 and S14†). In contrast, the expanded and deconvoluted XPS spectra of C1s of ANT/GR show four contributions at 284.4 eV, 284.7 eV, 285.5 eV, and 286.1 eV for C
C, sp3-hybridized C–C, and C–O components, respectively46–48 (Fig. S13 and S14†). In contrast, the expanded and deconvoluted XPS spectra of C1s of ANT/GR show four contributions at 284.4 eV, 284.7 eV, 285.5 eV, and 286.1 eV for C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, C–C, C–N, and C–O, respectively (Fig. 1d), which are well correlated with previous reports.49–51 Interestingly, in ANT/GR, two broad peaks in the range of 398 eV to 402 eV were obtained, which were further deconvoluted into four peaks at 399.5 eV, 400.5 eV, 402.2 eV, and 402.8 eV, suggesting the presence of four types of N (as illustrated in Fig. 1b), pyridinic N, pyrolytic N, graphitic N, and N–N, respectively, but they were absent in bare GR, supporting the presence of nitrogen-comprising ANT layers on the GR surface (Fig. 1e and S15†).46,52 The binding energies of elements in both bare GR and ANT/GR electrodes are given in Table S4.† The presence of hydrophilic nitrogen elements was further supported by static water-contact angle studies. The ANT/GR surface shows a hydrophilic surface with a reduced water contact angle of 63.5° ± 0.77° compared to bare GR with a water contact angle of 127° ± 0.02° (Fig. S16, Table S5†). This observation unequivocally suggests the formation of oligomer films on GR surfaces.
C, C–C, C–N, and C–O, respectively (Fig. 1d), which are well correlated with previous reports.49–51 Interestingly, in ANT/GR, two broad peaks in the range of 398 eV to 402 eV were obtained, which were further deconvoluted into four peaks at 399.5 eV, 400.5 eV, 402.2 eV, and 402.8 eV, suggesting the presence of four types of N (as illustrated in Fig. 1b), pyridinic N, pyrolytic N, graphitic N, and N–N, respectively, but they were absent in bare GR, supporting the presence of nitrogen-comprising ANT layers on the GR surface (Fig. 1e and S15†).46,52 The binding energies of elements in both bare GR and ANT/GR electrodes are given in Table S4.† The presence of hydrophilic nitrogen elements was further supported by static water-contact angle studies. The ANT/GR surface shows a hydrophilic surface with a reduced water contact angle of 63.5° ± 0.77° compared to bare GR with a water contact angle of 127° ± 0.02° (Fig. S16, Table S5†). This observation unequivocally suggests the formation of oligomer films on GR surfaces.
The BET surface area was evaluated by measuring the N2 adsorption–desorption isotherm, and the pore volume was calculated using the DFT simulation. The isotherms were of Type III, indicating multilayer formation where the mesopores and macropores were not filled completely. The adsorption–desorption hysteresis was H3-type, suggesting a plate-like structure of bare GR and ANT/GR, which is also visible from the FE-SEM microscopic images, where we can see the existence of inkbottle and slit-shaped pores (Fig. S17†). The bare GR shows a relatively low specific surface area of 2.05 m2 g−1 and a pore volume of 0.004 cm3 g−1, whereas after grafting ANT films, both surface area and pore volume increased to 2.41 m2 g−1 and 0.006 cm3 g−1. A 20% increase in surface area and pore volume is potentially due to the disordered growth of ANT layers on GR, as evidenced in the FE-SEM images and Raman spectra. Fig. S18† presents mesopores, as most of the pore size distribution lies in the 10–50 nm range, with a slight contribution from macropores.
Based on the experimental observations, we considered four different structural possibilities of ANT films, where azo-functionalized ANT was separately grafted on GR/N-GR via chemisorption through C–C or C–N coupling (Fig. S19–S21†). Geometric optimization was carried out using the density functional theory (DFT) framework with VASP code,53,54 where the azo-functionalized anthracene oligomeric molecules were optimized on an 8 × 8 supercell of hexagonal 2D monolayered graphene. The DFT computed geometry shows that the azo-functionalized anthracene oligomeric structures are intact on the GR/N-GR sheet (Fig. S22†). Upon grafting, the hybridization of the C/N of the GR/N-GR sheet changes from sp2 to sp3, which pushes the C/N atoms out of the plane of the sheet. The charge difference density plots show an electron-rich C/N atom of the GR/N-GR sheet with a charge accumulation on the C–C and C–N bonds (Fig. 2a and b). To gain better insight into the nature of the interaction, we undertook energy decomposition analysis55 using a cluster model comprised of 245 atoms where terminal carbon atoms were saturated with hydrogens. For both the studied cluster models, we observed that the C–C and C–N bond formations stabilize with intermolecular interaction energies of ∼54 kcal mol−1 and ∼72 kcal mol−1 for 1@N-GR and 1@GR, respectively. The orbital and electrostatic interactions are the major contributors to the total intermolecular interaction energy, with the former being relatively dominant. The sizeable electrostatic interaction in 1@N-GR arises from the large negative Mulliken charge on the N atom of N-GR compared to the C atom of GR. Electron deformation density analysis55 shows electron flow from the GR/N-GR sheet to the 2pz antibonding orbital of the C–C and C–N bonds, which agrees with the CDD analysis of the periodic structure (Fig. 2c and d, S23 and S24, Table S6†). Our computational results demonstrate that azo-functionalized anthracene oligomeric structures are stabilized on graphene/N-doped graphene, which agrees with experimental observations where ANT films are created via covalent bond formation.
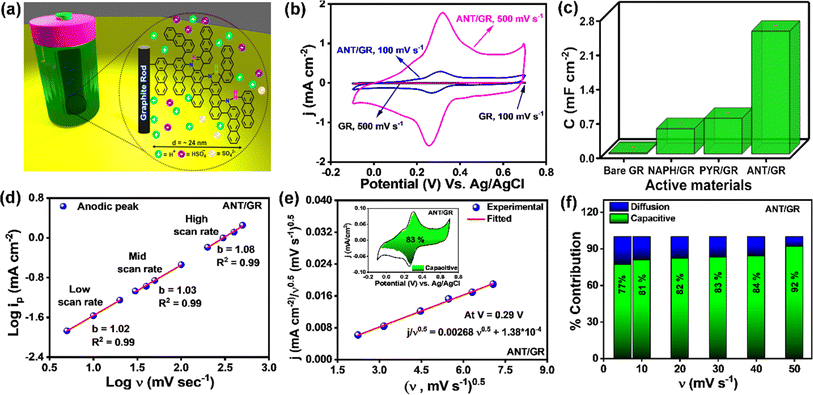
Next, the ANT/GR electrode was examined for electrochemical supercapacitor applications (a set-up is shown in Fig. 3a). Fig. 3b shows the cyclic voltammograms (CVs) of bare GR and ANT-modified GR recorded in 1 M H2SO4 (three-electrode set-up) at 100 mV s−1 and 500 mV s−1 scan rates (CVs at other scan rates are shown in Fig. S25a and b†). In contrast to bare GR, the ANT/GR electrodes exhibited a well-defined faradaic feature at about +0.31 V (vs. Ag/AgCl) which can be ascribed to interfacial proton-coupled electron transfer (PCET). An increase in the peak-to-peak separation (ΔEp) was observed as a function of the scan rate, which was used to determine the apparent rate constant, kapp, using the Laviron formalism.56 At slower scan rates (≤100 mV s−1), ΔEp remains constant in the 50–53 mV range but increases at higher scan rates. Fig. S26† shows the trumpet plot for ANT/GR in 1 M H2SO4 solution, allowing the charge transfer coefficient, α, and 1 − α to be calculated at 0.35 and 0.36, respectively. The kapp of the anodic reaction and the cathodic reaction were calculated as 14.9 ± 0.8 and 14.0 ± 0.6 s−1, respectively, indicative of a fast charge transfer process (see ESI† for detailed calculations) and nearly 10 times higher than those of the self-assembled organic redox-active species.57,58 Moreover, the reversible redox behavior of bare GR and ANT/GR electrodes was observed in the presence of ferrocene, a well-known redox marker59 (Fig. S27†). The diffusion coefficient, D, related to the electrochemical nature of the charge transfer process, was deduced using the well-known Randles–Ševčík eqn (i).60
| ip = 2.695 × 105AD1/2n3/2ν1/2C | (i) |
The anodic and cathodic currents were plotted as a function of the square root of the scan rate (iavs. ν1/2) (Fig. S28†). From the slope of the plot, the diffusion coefficients (D) of ferrocene were calculated to be 4.2 ± 0.18 × 10−5 cm2 s−1 for bare GR and 5.6 ± 0.44 × 10−5 cm2 s−1 for ANT/GR electrodes, ensuring the facile formation of ferrocene–ferricinium species at the electrode surfaces.59 The CVs of ANT-modified GR were recorded with varying electrolyte temperatures, and the activation energy (Ea) was calculated to be 10.5 (±0.4) kJ mol−1 (Fig. S29†). The ANT-grafted GR electrode showed excellent thermal stability when heated at 75 °C for 12 h (Fig. S30†). The total capacitance was further determined and compared for both systems by integrating the surface area obtained from the CVs in 1 M H2SO4 electrolyte and compared with naphthalene (NAPH) and pyrene (PYR) films (Fig. S31–S34†). Bare GR shows an electrochemical double-layer capacitance (EDLC) of 24 ± 1.36 μF cm−2 measured at a scan rate of 500 mV s−1, which agrees well with that of typical carbon materials.61 However, the ANT/GR electrode exhibits higher total areal capacitance with a well-defined faradaic feature at ∼0.31 V (vs. Ag/AgCl), illustrating the pseudocapacitive behavior of the interface. As confirmed by the XPS spectra, nitrogen from azo groups creates several electroactive sites for pseudocapacitive reactions and PCET in response to electrochemical bias. A bar diagram is also shown in Fig. 3c to compare the total areal capacitance of all modified active electrodes at a 500 mV s−1 scan rate, showing the huge increase in the capacitance for the ANT/GR electrode in comparison to pyrene and naphthalene oligomeric films. The capacitance in the common metric of F g−1 was also evaluated for the ANT/GR electrode using the theoretical mass loading of the ANT film. Since it is challenging to accurately weigh the mass of the nanoscale-grown film on the GR surface experimentally, we considered the theoretical mass loading for the specific capacitance calculations (see ESI section 16† for detailed estimation). A specific capacitance of 687 ± 37 F g−1 was calculated from the integrated area between −0.1 V and 0.7 V for the ANT/GR electrode at 500 mV s−1 scan rate; here, gfilm indicates the theoretical mass of the ANT film (see ESI section 16†). So far, commercially available carbon-based supercapacitors are in the range of 60–100 F g−1, thus a capacitance of ∼687 F g−1 for such a nanoscale-grown molecular film is quite notable. Generally, the total capacitance can be divided into two regimes: (i) EDLC and (ii) the faradaic reaction of the active material. However, not all faradaic reactions are pseudocapacitive in nature. A few are controlled by ion diffusion in the active electrode material, including in the electrolytes.62 Hence, it is necessary to evaluate the dominant faradaic capacitive and non-capacitive contributions to provide an adequate explanation of the working performance of the active electrode. As shown in eqn (ii), a power–law relationship can be used to distinguish the dominant charge storage process, where i is current at a particular voltage, ν is scan rate, and a and b are constants.63 The measured current is fitted linearly with the log(i) vs. log(ν) plot, providing the b value from the slope. A value of b = 0.5 suggests a direct relation between the current and the square root of the scan rate and follows the traditional diffusion-controlled approach. In contrast, b = 1 implies a direct relation between the current and the scan rate, which is the hallmark of capacitor-like charge storage behavior.63 CVs from low to high scan rates were used to calculate b values at the maxima in anodic (Fig. 3d) and cathodic regimes (Fig. S35†). The linear fit in all three regions displayed a and b values close to 1, indicating that the dominant charge transport mechanism in the ANT/GR electrode is capacitor-like.
| i(ν) = aϑb | (ii) |
The capacitive contribution to the total current was further evaluated using the Dunn equation, shown below in eqn (iii), where i is the current at a fixed potential, and k1ν and k2ν0.5 relate to capacitive and diffusion contributions to the total current.63,64
| i(v) = k1ν + k2ν0.5 | (iii) |
The value of k1 was calculated using the above equation at slow scan rates (5 mV s−1 to 50 mV s−1), and an 83% capacitive contribution was obtained at a 30 mV s−1 scan rate, as shown in Fig. 3e. The capacitive contribution was also calculated at different scan rates. With increasing scan rate, the percentage of capacitive contribution also increases due to the slow diffusion of ions (Fig. 3f). The high capacitive contribution further claimed the fast redox reaction of ANT/GR electrodes, which is highly desirable for pseudocapacitive materials.
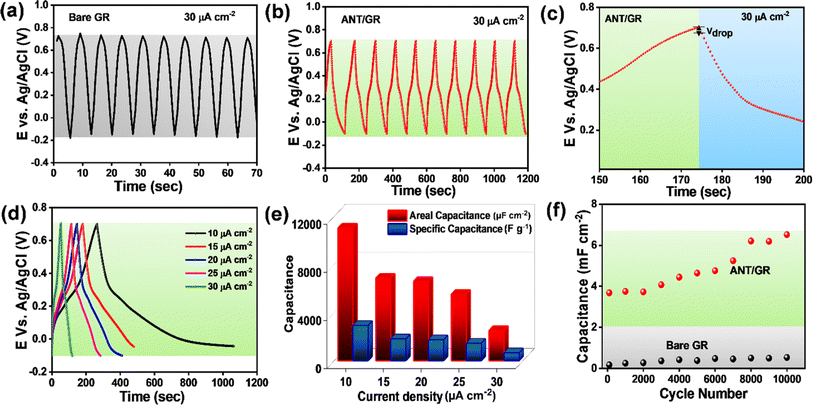
Moreover, the capacitance performances were also evaluated by galvanostatic charge/discharge (GCD) cycling over potential ranges of −0.1 V (vs. Ag/AgCl) to +0.7 V (vs. Ag/AgCl) at 30 μA cm−2 for 10 cycles. Bare GR demonstrated a symmetrical and nearly triangular-shaped charge/discharge cycle, clearly indicating the EDLC feature (Fig. 4a). In contrast, a significant change in shape with a negligible potential drop, Vdrop (equivalent series resistance/ESR of 0.98 ± 0.02 mΩ cm2 (Fig. 4b and c)), was observed in ANT/GR, which is the combined EDLC and faradaic contribution (PCET to nitrogen) in the capacitance, as depicted in Fig. 3b. The duration of charging/discharging also increased after ANT grafting, attributed to the faradaic process. A single charge/discharge cycle is shown in ESI,† illustrating different charge/discharge timescales before and after modification (Fig. S36†). The ANT/GR electrode showed the highest areal capacitance of ∼11 mF cm−2 and specific capacitance of ∼2900 F g−1 at a lower current density of 10 μA cm−2, which decreased with increasing applied current density (Fig. 4d and e). However, this value differs from the CV measurements, because the charging/discharging current in the CVs was much higher than in the GCD measurements. The cycle life of ANT/GR was determined by performing 104 GCD cycles at an applied current density of 1 mA cm−2 (Fig. S37†). It is noteworthy that ANT/GR exhibited excellent cycling performance up to 104 GCD cycles and could hold larger charges for a longer time (Fig. 4f). ANT/GR shows increased areal capacitance with the number of GCD cycles, while the coulombic efficiency remains unchanged (∼99–97%) (Fig. S38†).
A gradual increase in capacitance value was observed with increasing GCD cycling. A similar increment in the enclosed area in CV further supports an increment in capacitance (Fig. S39a†). To understand this gradual increase in capacitance value, we performed various studies after 104 GCD cycles. The FE-SEM image after 104 GCD cycles shows a sponge-like morphology, illustrating the creation of additional active sites for ion adsorption/desorption; hence, a higher EDLC contribution can be anticipated (Fig. S39b†). Also, BET analysis revealed a 179% increase in surface area after 104 GCD cycles (Fig. S39c and d†). With an increase in the number of GCD cycles, we observed surface opening in the graphite surfaces taking place, which provides an additional surface area in the electrode and assists in the gradual increase in capacitance with EDLC the dominant contribution. We did not observe any significant change in the XRD peak intensity, and no new peak after GCD cycling was observed; hence, the possibility of forming another carbon-based structure like graphene or graphene oxide can be ruled out (Fig. S39e†). The ID/IG ratio in the Raman spectrum after GCD cycling was 0.34, slightly lower than that of ANT/GR (ID/IG = 0.36). A slight decrease in the ID/IG ratio may be due to an increased graphite surface area due to surface opening during charging/discharging (Fig. S39f†). Also, the N1s XPS spectra after 104 GCD cycles revealed the presence of four types of N: pyridinic N (399.5 eV), pyrolytic N (400.0 eV), graphitic N (401.1 eV), and N–N (402.2 eV), with a slight shift in binding energy from pristine ANT/GR. The results confirmed the integrity and stability of ANT films on the GR surface even after 104 GCD cycles, which is certainly due to the strong covalent bonding of ANT to the GR surface (Fig. S40†).
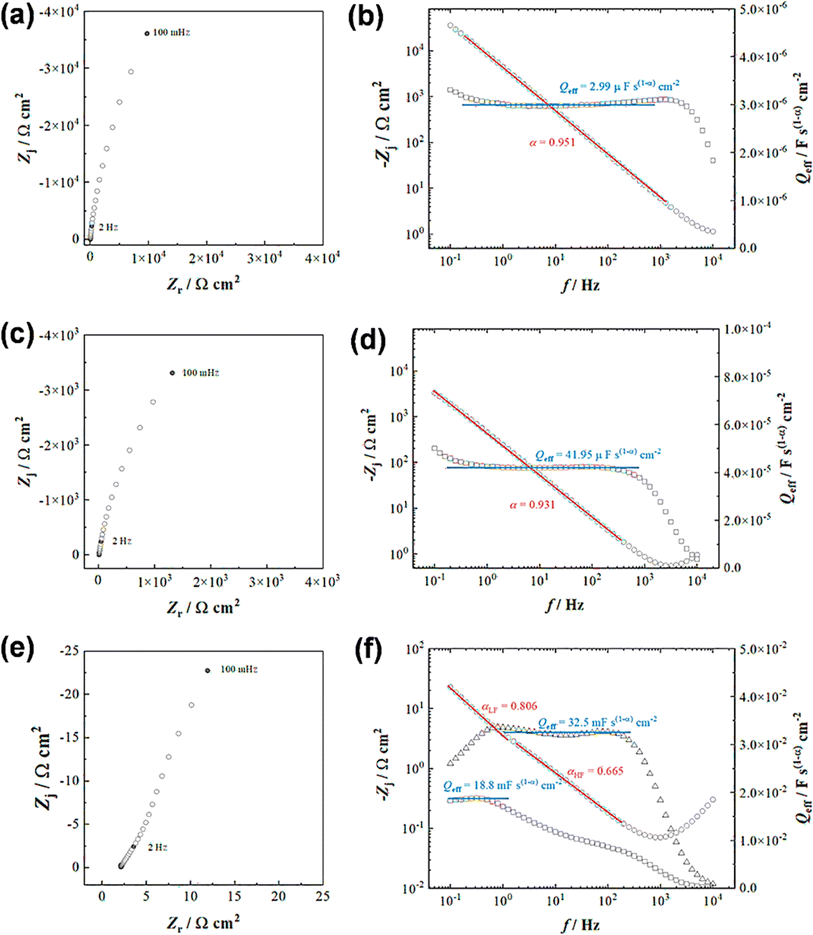
Both the CV and GCD techniques are based on DC-based measurements producing either total current or charges in the system, but they do not forecast frequency response, which is crucial for understanding capacitance performance.65 Electrochemical impedance spectra obtained in frequency ranges of 10−1 to 104 Hz for a bare GR electrode and ANT-modified GR electrode before and after 104 GCD cycles are presented in Fig. 5. As expected, the bare electrode shows a constant phase element (CPE) (Fig. 5a) that can be better evidenced by the variation in the imaginary part of the impedance as a function of frequency (Fig. 5b).66,67 The slope of the curve is the opposite of the coefficient α of the CPE, whereas the determination of Q is possible from eqn (iv):
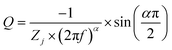 | (iv) |
Then, using the Brug formula,68,69C = Q1/αR(1−α)/αe in which Re is the electrolyte resistance, a capacitance of about 1.5 μF cm−2 can be obtained. Such a value is consistent with a double layer formed at a graphite/electrolyte interface.70 On the ANT-modified electrode (Fig. 5c), the shape of the impedance diagram remains unchanged, but the modulus is 10 times smaller, corresponding to an increase in the active surface area. Graphical analysis of this diagram is also consistent with capacitive behavior (Fig. 5d). After 104 GCD cycles, the shape of the impedance diagram clearly shows two linear domains corresponding to two types of CPE behavior, whereas the modulus is about 100 times smaller than that measured on the as-prepared electrode (Fig. 5e). This can be explained by a rearrangement of the layer upon cycling and the formation of small pores in the thin film. This is confirmed by the graphical analysis presented in Fig. 5f, which distinctly exhibits two different linear domains for the determination of α, one in the high frequencies with a value close to 0.66 and a second one in the lowest frequency domain with a value close to 0.81. Such a value in high frequency is consistent with a porous system. However, it is not possible to go further in the determination of the size, depth, and diameter of the pores because all these parameters are linked.71 Moreover, analysis of the graphically determined value of the Q parameter (Fig. 5f) shows that the capacitance value is in the range of a few mF cm−2, in agreement with the CV and GCD results, but the change in the active surface during cycling does not allow better quantitative analysis. Finally, these diagrams were obtained at the faradaic process at +0.3 V (vs. Ag/AgCl), which is superimposed on the capacitive response. Extrapolation of the diagram presented in Fig. 5e allows us to determine a charge transfer resistance of about 200 Ω. This value can only be obtained at very low frequencies because of the parallel behavior of resistance with a double-layer capacitance of an electrode of a very high value. Furthermore, if we relate this value to a unit area, the analysis of impedance diagrams shows that there is an increase of a factor of 100 to 1000 between a bare electrode and an electrode after cycling. We deduce that the charge transfer resistance is small, which is characteristic of a Nernstian system, again in agreement with the cyclic voltammetry results. The fitted electrochemical parameters are shown in Fig. S41 and Table S7.†
Additionally, we have directly isolated graphited rods from a discharged Eveready dry cell (EV-GR, AA, 1.5 V) in order to recycle and increase the charge-storing efficiency of discharged graphite electrodes. We modified EV-GR via electrochemical grafting using anthracene diazonium salts (Fig. S42 and S43a†). Compared to unmodified EV-GR, ANT-modified EV-GR shows a faradaic redox feature at ∼+0.36 V (vs. Ag/AgCl in 1 M H2SO4) and exhibits a seven-fold increase in total areal capacitance. A large increase in capacitance was observed with covalent ANT modifications calculated from GCD in −0.1 V to +0.7 V (vs. Ag/AgCl) at an applied current density of 30 μA cm−2 for nine cycles from 615 ± 7.5 μF cm−2 to 9761 ± 44 μF cm−2 (Fig. S43b–d†). The electrical conductivity of bare and modified GRs was also tested using two probe contact methods, showing excellent conductivity even after modification with organic molecules (Fig. S44 and S45†). In addition, we fabricated an asymmetrical supercapacitor (ASC) solid-state device using ANT-grafted porous carbon (ANT/PC) as a positive electrode, porous carbon (PC) as a negative electrode, and a Whatman filter paper soaked with 1 M H2SO4 as a separator. The ASC device demonstrated a specific capacitance of 155 F g−1 at 2 A g−1 with an energy density of 5.8 W h kg−1 at a high-power density of 2010 W kg−1 (Fig. S46†), calculated using methods in the literature.72–75 Four ASC devices were connected in series, showcasing excellent performance with an LED light-up time of 5 ± 0.8 minutes after charging with a 6 V battery for 2 minutes (Fig. S47†).
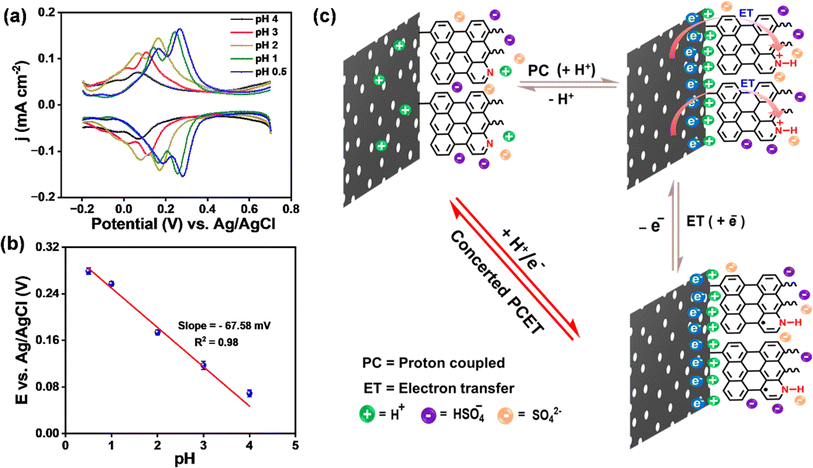
To understand the origin of pseudocapacitance in metal-free ANT thin films, we performed pH-dependent electrochemical studies to examine whether the faradaic process follows the interfacial proton-coupled electron transfer (PCET) pathway.76–80 The differential pulse voltammogram (DPV) of the ANT/GR electrode with varied pH was recorded in H2SO4 solution using 0.1 M KCl as an electrolyte (Fig. 6a). The plot clearly shows the shift in anodic and cathodic potential with respect to pH, illustrating the dependence of the faradaic process on the pH of the solution, a hallmark of PCET reactions.81 Next, the reduction potential as a function of pH was observed from the Pourbaix diagram to understand the interfacial proton-coupled electron transfer (PCET) reactions (Fig. 6b). The plot shows a slope of 67.6 ± 3.0 mV per pH (close to 59 mV), suggesting that the process involves concerted 1 H+/1 e− transfer events. The overall interfacial PCET pathway is illustrated in Fig. 6c. For simplicity, we have considered only a few molecular layers for depiction of the mechanism. The electrochemical charge storage performance of carbon materials functionalized by a few organic molecules using diazonium chemistry is studied by a few groups, and our results are compared in Table S9.†
Conclusions
The electrochemical grafting method performed on a metal-free platform demonstrates promising potential to further extend the scope of functionalization on a variety of carbon electrodes, including flexible carbon materials and carbon clothes, and can be employed for microfabricated flexible supercapacitor devices. To enhance the young family of organic supercapacitors, we validated low-cost graphite rod modification in nanoscale dimension via a versatile electrochemical grafting approach, showing promising opportunities for reusing waste carbon rods for large amounts of energy storage applications. However, the capacitance value of the present work does not meet the demand for practical application, but considering the molecular film thickness, which is ∼24 nm, and low surface coverage, this value cannot be neglected. Upon increasing the surface coverage and attaching more molecular layers, capacitance can be enhanced. The present work opens new horizons in the field of nanoscale hybrid supercapacitors (rigid to flexible) with baselines for future energy metrics to advance toward commercial implementation.Data availability
Data is available upon request from the corresponding author.Author contributions
R. G. and A. M. designed, conducted the experiments, and wrote the manuscript. K. K. and S. K. S. performed computational studies. V. V. performed impedance spectra analysis. P. C. M. conceived the idea, supervised the work, and edited the manuscript. All authors contributed to the discussion and editing of the manuscript.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. RG, AM, and PCM have filed a provisional Indian patent application (Application No. 202211060927) lodged with the IIT Kanpur based on the work reported here.Acknowledgements
R. G. and A. M. thank IIT Kanpur for the senior research fellowship and Institute post-doctoral fellowship (No. PDF-254), respectively. P. C. M. acknowledges the Council of Scientific & Industrial Research (CSIR), New Delhi, for partial financial support, Sanctioned No. 01(3049)/21/EMR-II, Science and Engineering Research Board, New Delhi (Grant No. CRG/2022/005325), IIT Kanpur. S. K. S. acknowledges financial support from CRG/2023/002936. The authors acknowledge IIT Kanpur for its infrastructure and instrumentation facility.References
- M. Yu, Y. Peng, X. Wang and F. Ran, Adv. Funct. Mater., 2023, 33, 2301877 CrossRef CAS.
- M. Salanne, B. Rotenberg, K. Naoi, K. Kaneko, P.-L. Taberna, C. P. Grey, B. Dunn and P. Simon, Nat. Energy, 2016, 1, 16070 CrossRef CAS.
- P. Yang and W. Mai, Nano Energy, 2014, 8, 274–290 CrossRef CAS.
- D. Rawlings, D. Lee, J. Kim, I. B. Magdǎu, G. Pace, P. M. Richardson, E. M. Thomas, S. P. O. Danielsen, S. H. Tolbert, T. F. Miller, R. Seshadri and R. A. Segalman, Chem. Mater., 2021, 33, 6464–6474 CrossRef CAS.
- X. Pu and Z. L. Wang, Chem. Sci., 2021, 12, 34–49 RSC.
- P. Iamprasertkun, A. Ejigu and R. A. W. Dryfe, Chem. Sci., 2020, 11, 6978–6989 RSC.
- J. Huang, Y. Xie, Y. You, J. Yuan, Q. Xu, H. Xie and Y. Chen, Adv. Funct. Mater., 2023, 33, 2213095 CrossRef CAS.
- Y. Zhang, L. Li, X. Li, R. Feng, T. Zhao, M. Pan and L. Dong, Adv. Funct. Mater., 2023, 33, 2300555 CrossRef CAS.
- Q. Meng, K. Cai, Y. Chen and L. Chen, Nano Energy, 2017, 36, 268–285 CrossRef CAS.
- H. Hu, F. Zhang, S. Luo, W. Chang, J. Yue and C. H. Wang, Nano Energy, 2020, 74, 104844 CrossRef CAS.
- K. E. Wyckoff, D. D. Robertson, M. B. Preefer, S. M. L. Teicher, J. Bienz, L. Kautzsch, T. E. Mates, J. A. Cooley, S. H. Tolbert and R. Seshadri, Chem. Mater., 2020, 32, 9415–9424 CrossRef CAS.
- S. Mukhopadhyay, A. R. Kottaichamy, M. C. Devendrachari, R. M. Mendhe, H. M. Nimbegondi Kotresh, C. P. Vinod and M. Ottakam Thotiyl, Chem. Sci., 2024, 15, 1726–1735 RSC.
- G. Nikiforidis, S. Wustoni, D. Ohayon, V. Druet and S. Inal, ACS Appl. Energy Mater., 2020, 3, 7896–7907 CrossRef CAS.
- S. Eigler and A. Hirsch, Angew. Chem., Int. Ed., 2014, 53, 7720–7738 CrossRef CAS PubMed.
- A. K. Farquhar, S. R. Smith, C. Van Dyck and R. L. McCreery, ACS Appl. Mater. Interfaces, 2020, 12, 10211–10223 CrossRef CAS PubMed.
- R. Gupta, J. A. Fereiro, A. Bayat, A. Pritam, M. Zharnikov and P. C. Mondal, Nat. Rev. Chem., 2023, 7, 106–122 CrossRef CAS PubMed.
- W. Liu, M. Ulaganathan, I. Abdelwahab, X. Luo, Z. Chen, S. J. Rong Tan, X. Wang, Y. Liu, D. Geng, Y. Bao, J. Chen and K. P. Loh, ACS Nano, 2018, 12, 852–860 CrossRef CAS PubMed.
- C. Cui, Y. Gao, J. Li, C. Yang, M. Liu, H. Jin, Z. Xia, L. Dai, Y. Lei, J. Wang and S. Wang, Angew. Chem., Int. Ed., 2020, 59, 7928–7933 CrossRef CAS PubMed.
- H. Jin, X. Feng, J. Li, M. Li, Y. Xia, Y. Yuan, C. Yang, B. Dai, Z. Lin, J. Wang, J. Lu and S. Wang, Angew. Chem., Int. Ed., 2019, 59, 2397–2401 CrossRef.
- Y. Lu, J. Liang, S. Deng, Q. He, S. Deng, Y. Hu and D. Wang, Nano Energy, 2019, 65, 103993 CrossRef CAS.
- R. Kushwaha, C. Jain, P. Shekhar, D. Rase, R. Illathvalappil, D. Mekan, A. Camellus, C. P. Vinod and R. Vaidhyanathan, Adv. Energy Mater., 2023, 13, 2301049 CrossRef CAS.
- G. Jeanmairet, B. Rotenberg and M. Salanne, Chem. Rev., 2022, 122, 10860–10898 CrossRef CAS PubMed.
- J. S. M. Lee, M. E. Briggs, C. C. Hu and A. I. Cooper, Nano Energy, 2018, 46, 277–289 CrossRef CAS.
- S. Haldar, D. Rase, P. Shekhar, C. Jain, C. P. Vinod, E. Zhang, L. Shupletsov, S. Kaskel and R. Vaidhyanathan, Adv. Energy Mater., 2022, 12, 2200754 CrossRef CAS.
- X. C. Li, Y. Zhang, C. Y. Wang, Y. Wan, W. Y. Lai, H. Pang and W. Huang, Chem. Sci., 2017, 8, 2959–2965 RSC.
- L. Wu, X. Shi and Z. Wu, Adv. Funct. Mater., 2023, 33, 2211454 CrossRef CAS.
- M. Yu and X. Feng, Joule, 2019, 3, 338–360 CrossRef CAS.
- F. Fusalba, H. A. Ho, L. Breau and D. Bélanger, Chem. Mater., 2000, 12, 2581–2589 CrossRef CAS.
- Y. Gogotsi, ACS Nano, 2014, 8, 5369–5371 CrossRef CAS PubMed.
- R. L. McCreery, Chem. Rev., 2008, 108, 2646–2687 CrossRef CAS PubMed.
- G. Bottari, M. Ángeles Herranz, L. Wibmer, M. Volland, L. Rodríguez-Pérez, D. M. Guldi, A. Hirsch, N. Martín, F. D'Souza and T. Torres, Chem. Soc. Rev., 2017, 46, 4464–4500 RSC.
- J. Bai, X. Zhong, S. Jiang, Y. Huang and X. Duan, Nat. Nanotechnol., 2010, 5, 190–194 CrossRef CAS PubMed.
- P. C. Mondal, V. Singh and M. Zharnikov, Acc. Chem. Res., 2017, 50, 2128–2138 CrossRef CAS PubMed.
- V. Singh, P. C. Mondal, A. K. Singh and M. Zharnikov, Coord. Chem. Rev., 2017, 330, 144–163 CrossRef CAS.
- J. J. Navarro, F. Calleja, R. Miranda, E. M. Pérez and A. L. Vázquez De Parga, Chem. Commun., 2017, 53, 10418–10421 RSC.
- R. L. McCreery, Acc. Chem. Res., 2022, 55, 2766–2779 CrossRef CAS PubMed.
- R. Gupta, J. Pradhan, A. Haldar, C. Murapaka and P. C. Mondal, Angew. Chem., Int. Ed., 2023, 62, e202307458 CrossRef CAS PubMed.
- P. Sachan and P. C. Mondal, Analyst, 2020, 145, 1563–1582 RSC.
- A. K. Farquhar, M. Supur, S. R. Smith, C. Dyck and R. L. McCreery, Adv. Energy Mater., 2018, 8, 1802439 CrossRef.
- R. Gupta, P. Jash, P. Sachan, A. Bayat, V. Singh and P. C. Mondal, Angew. Chem., Int. Ed., 2021, 60, 26904–26921 CrossRef CAS PubMed.
- R. Gupta, S. Bhandari, S. Kaya, K. P. Katin and P. C. Mondal, Nano Lett., 2023, 23, 10998–11005 CrossRef CAS PubMed.
- A. Le Comte, D. Chhin, A. Gagnon, R. Retoux, T. Brousse and D. Bélanger, J. Mater. Chem. A, 2015, 3, 6146–6156 RSC.
- D. Malka, O. Hanna, T. Hauser, S. Hayne, S. Luski, Y. Elias, R. Attias, T. Brousse and D. Aurbach, J. Electrochem. Soc., 2018, 165, A3342–A3349 CrossRef CAS.
- P. Makkar, A. Malik and N. N. Ghosh, ACS Appl. Energy Mater., 2021, 4, 6015–6024 CrossRef CAS.
- B. Song, C. Sizemore, L. Li, X. Huang, Z. Lin, K. S. Moon and C. P. Wong, J. Mater. Chem. A, 2015, 3, 21789–21796 RSC.
- C. Xia, S. Surendran, S. Ji, D. Kim, Y. Chae, J. Kim, M. Je, M. Han, W. Choe, C. H. Choi, H. Choi, J. K. Kim and U. Sim, Carbon Energy, 2022, 4, 491–505 CrossRef CAS.
- J. Zhao, Y. Wu, Y. Chen, H. Jin, S. Pan, S. Zhao, X. Feng, Y. Wang, Q. Zhang and S. Wang, Mater. Chem. Front., 2021, 5, 4700–4711 RSC.
- J. Wu, J. Zhao, B. Vaidhyanathan, H. Zhang, A. Anshuman, A. Nare and S. Saremi-Yarahmadi, Materialia, 2020, 13, 100833 CrossRef CAS.
- X. Sun, Y. Kong, Y. Liu, L. Zhou, A. K. Nanjundan, X. Huang and C. Yu, Front. Chem., 2020, 8, 1–10 CrossRef PubMed.
- Q. Zhang, C. Deng, Z. Huang, Q. Zhang, X. Chai, D. Yi, Y. Fang, M. Wu, X. Wang, Y. Tang and Y. Wang, Small, 2023, 19, 2205725 CrossRef CAS PubMed.
- H. Zhang, L. Xu and G. Liu, Appl. Sci., 2020, 10, 422 CrossRef CAS.
- M. F. Genisel, M. N. Uddin, Z. Say, M. Kulakci, R. Turan, O. Gulseren and E. Bengu, J. Appl. Phys., 2011, 110, 074906 CrossRef.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975 CrossRef CAS PubMed.
- E. Laviron, J. Electroanal. Chem., 1979, 101, 19–28 CrossRef CAS.
- M. A. Ghanem, J. M. Chrétien, A. Pinczewska, J. D. Kilburn and P. N. Bartlett, J. Mater. Chem., 2008, 18, 4917–4927 RSC.
- X. Yan, C. U. Jansen, F. Diao, K. Qvortrup, D. Tanner, J. Ulstrup and X. Xiao, Electrochem. Commun., 2021, 124, 106962 CrossRef CAS.
- G. Roy, R. Gupta, S. Ranjan Sahoo, S. Saha, D. Asthana and P. C. Mondal, Coord. Chem. Rev., 2022, 473, 214816 CrossRef CAS.
- L. R. Faulkner and A. J. Bard, Electrochemical Methods: Fundamentals and Applications, 2nd edn, 2020 Search PubMed.
- C. Merlet, B. Rotenberg, P. A. Madden, P.-L. Taberna, P. Simon, Y. Gogotsi and M. Salanne, Nat. Mater., 2012, 11, 306–310 CrossRef CAS PubMed.
- L. Guan, L. Yu and G. Z. Chen, Electrochim. Acta, 2016, 206, 464–478 CrossRef CAS.
- J. Wang, J. Polleux, J. Lim and B. Dunn, J. Phys. Chem. C, 2007, 111, 14925–14931 CrossRef CAS.
- T. -C. Liu, W. G. Pell, B. E. Conway and S. L. Roberson, J. Electrochem. Soc., 1998, 145, 1882 CrossRef CAS.
- P. Jash, R. K. Parashar, C. Fontanesi and P. C. Mondal, Adv. Funct. Mater., 2022, 32, 2109956 CrossRef CAS.
- M. E. Orazem, N. Pebere and B. Tribollet, Electrochim. Acta, 2006, 51, 1473–1479 CrossRef.
- V. Vivier and M. E. Orazem, Chem. Rev., 2022, 122, 11131–11168 CrossRef CAS PubMed.
- G. J. Brug, A. L. G. van den Eeden, M. Sluyters-Rehbach and J. H. Sluyters, J. Electroanal. Chem. Interfacial Electrochem., 1984, 176, 275–295 CrossRef CAS.
- B. Hirschorn, M. E. Orazem, B. Tribollet, V. Vivier, I. Frateur and M. Musiani, Electrochim. Acta, 2010, 55, 6218–6227 CrossRef CAS.
- B. E. Conway, Electrochemical Supercapacitors – Scientific Fundamentals and Technological Applications, Kluwer Academic/Plenum Publishers, New York, New York, 1999 Search PubMed.
- O. E. Barcia, E. D'Elia, I. Frateur, O. R. Mattos, N. Pébère and B. Tribollet, Electrochim. Acta, 2002, 47, 2109–2116 CrossRef CAS.
- K. Chhetri, A. P. Tiwari, B. Dahal, G. P. Ojha, T. Mukhiya, M. Lee, T. Kim, S. H. Chae, A. Muthurasu and H. Y. Kim, J. Electroanal. Chem., 2020, 856, 113670 CrossRef CAS.
- J. Kunwar, D. Acharya, K. Chhetri, B. Karki, B. Deo, R. M. Bhattarai, S. Neupane, M. P. Adhikari and A. P. Yadav, J. Electroanal. Chem., 2023, 950, 117915 CrossRef CAS.
- K. Chhetri, A. Adhikari, J. Kunwar, D. Acharya, R. M. Bhattarai, Y. S. Mok, A. Adhikari, A. P. Yadav and H. Y. Kim, Int. J. Energy Res., 2023, 2023, 1–46 CrossRef.
- D. Acharya, A. Muthurasu, T. H. Ko, R. M. Bhattarai, T. Kim, S. H. Chae, S. Saidin, K. Chhetri and H. Y. Kim, ACS Appl. Energy Mater., 2023, 6, 9196–9206 CrossRef CAS.
- R. E. Warburton, P. Hutchison, M. N. Jackson, M. L. Pegis, Y. Surendranath and S. Hammes-Schiffer, J. Am. Chem. Soc., 2020, 142, 20855–20864 CrossRef CAS PubMed.
- A. Ge, G. Kastlunger, J. Meng, P. Lindgren, J. Song, Q. Liu, A. Zaslavsky, T. Lian and A. A. Peterson, J. Am. Chem. Soc., 2020, 142, 11829–11834 CrossRef CAS PubMed.
- S. Hammes-Schiffer, J. Am. Chem. Soc., 2015, 137, 8860–8871 CrossRef CAS PubMed.
- D. G. Nocera, J. Am. Chem. Soc., 2022, 144, 1069–1081 CrossRef CAS PubMed.
- D. R. Weinberg, C. J. Gagliardi, J. F. Hull, C. F. Murphy, C. A. Kent, B. C. Westlake, A. Paul, D. H. Ess, D. G. McCafferty and T. J. Meyer, Chem. Rev., 2012, 112, 4016–4093 CrossRef CAS PubMed.
- A. N. Oldacre and E. R. Young, RSC Adv., 2020, 10, 14804–14811 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis, and characterization of aryl diazoniums, voltammograms of electrochemical reduction, thin film characterization, and additional data on asymmetric supercapacitor devices (PDF). See DOI: https://doi.org/10.1039/d4sc00611a |
| This journal is © The Royal Society of Chemistry 2024 |