The photoactivated dynamics of dGpdC and dCpdG sequences in DNA: a comprehensive quantum mechanical study

Abstract

Study of alternating DNA GC sequences by different time-resolved spectroscopies has provided fundamental information on the interaction between UV light and DNA, a process of great biological importance. Multiple decay paths have been identified, but their interplay is still poorly understood. Here, we characterize the photophysics of GC-DNA by integrating different computational approaches, to study molecular models including up to 6 bases described at a full quantum mechanical level. Quantum dynamical simulations, exploiting a nonadiabatic linear vibronic coupling (LVC) model, coupled with molecular dynamics sampling of the initial structures of a (GC)₅ DNA duplex, provide new insights into the photophysics in the sub-picosecond time-regime. They indicate a substantial population transfer, within 50 fs, from the spectroscopic states towards G → C charge transfer states involving two stacked bases (CT^intra), thus explaining the ultrafast disappearance of fluorescence. This picture is consistent with that provided by quantum mechanical geometry optimizations, using time dependent-density functional theory and a polarizable continuum model, which we use to parametrize the LVC model and to map the main excited state deactivation pathways. For the first time, the infrared and excited state absorption signatures of the various states along these pathways are comprehensively mapped. The computational models suggest that the main deactivation pathways, which, according to experiment, lead to ground state recovery on the 10–50 ps time scale, involve CT^intra followed by interstrand proton transfer from the neutral G to C⁻. Our calculations indicate that CT^intra is populated to a larger extent and more rapidly in GC than in CG steps and suggest the likely involvement of monomer-like and interstrand charge transfer decay routes for isolated and less stacked CG steps. These findings underscore the importance of the DNA sequence and thermal fluctuations for the dynamics. They will also aid the interpretation of experimental results on other sequences.

---

Introduction

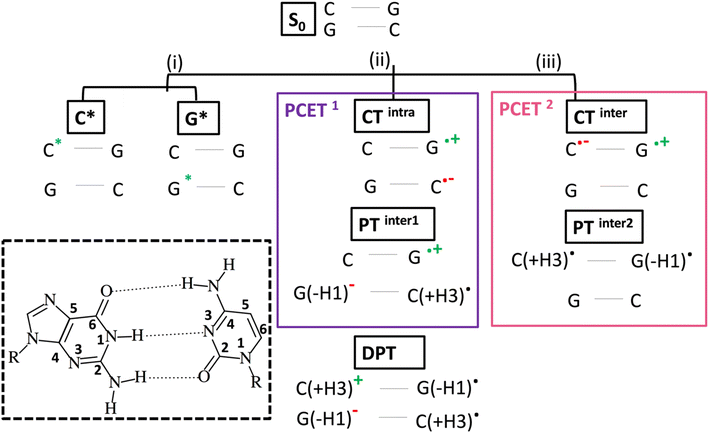
Absorption of UV light by DNA is a major source of oxidative damage for cells, triggering a cascade of molecular events with potentially very harmful outcomes for living organisms (DNA mutations, apoptosis, and cancer).^1–3 As a consequence, huge efforts have been devoted to characterizing the photoactivated dynamics of polynucleotides. Thanks to the developments in time-resolved (TR) spectroscopy techniques^4–6 and the contribution of quantum mechanical (QM) calculations,^7–10 important advances have been made, especially in the study of model polynucleotide sequences.^{7–9,11–13} Their photoactivated dynamics is extremely complex, combining ultrafast processes, characterized by time constants in the sub-picoseconds (ps) up to a few ps, with others occurring on a much-slower time scale, up to nanoseconds (ns) and beyond. The fastest processes are usually associated with monomer-like decay processes, i.e. ones similar to those occurring in the isolated bases, whereas the assignment of the slower ones has been debated. There is now general agreement that many different decay pathways, involving excimers with different degree of (de-)localization, states with significant Charge Transfer (CT) character and Proton Coupled Electron Transfer (PCET) processes can coexist.^14–19 However, the precise interplay between these different decay paths is still poorly understood, and our comprehension of the underlying photochemical processes is fragmented.

A good example of the advances made until now and, at the same time, of the challenges ahead is provided by the results obtained on the guanine (G)-cytosine (C) sequence (GC)_n (hereafter GC-DNA). The signals of the TR spectra are multiphasic, with decay components of ≤5 ps (fast dynamics), 30–40 ps, and a component of several ns, which is near the long lifetime limit of what can be measured with a typical femtosecond (fs) transient absorption (TA) spectrometer.^17,19–24 Fluorescence upconversion (FU) experiments on the same sequence reveal a fluorescence lifetime of 0.2 ps, shorter than those of its components dGMP (∼0.6 ps)²⁵ and dCMP (∼0.4 ps).^26,27 After 1 ps, the duplex signal has lost 95% of its amplitude, and after 1.5 ps the emission at 330 nm is almost zero.²⁶ Ground state (GS) recovery signals observed in TA experiments decay more slowly, suggesting that most of the initial excited state population decays to non-emissive states.²⁰ However, correctly interpreting the FU and TA spectra is not easy because the former experiments may sample only the small fraction of excited states that are emissive, while the latter experiments can suffer from broad and overlapped bands that are difficult to assign. The application of TR infrared spectroscopy (TR-IR) has thus been extremely informative because vibrational bands are typically much better resolved than electronic bands, and the frequency and intensity of the vibrational resonances are exquisitely sensitive to non-covalent interactions (e.g., hydrogen-bonding and π-stacking) experienced by IR-active functional groups of the nucleobases.^{14–21,28–30} Depletion of the GS population following light absorption is monitored by negative bleaching signals in the differential IR (DIR) spectrum, the dynamics of which provide key information on the excited state decay. Positive features are instead mainly associated with absorption by transient species generated by the excitation laser. This has made it possible to identify the vibrational markers of cationic and anionic nucleobases in several sequences, proving the involvement of CT states in the photodynamics.¹⁷ Moreover, the analysis of the slow (i.e. >10 ps) component of the TR-IR spectra of (GC)₉, as well as other duplexes, indicates that PCET processes are operative.^17,30

As depicted in Scheme 1, intrastrand electron transfer (ET) between stacked bases can create a radical ion pair (G⁺ and C⁻) that can trigger interstrand proton transfer (PT), resulting, overall, in a PCET process (PCET¹). For closely stacked bases in DNA, the electron transfer is not complete and we simply observe a state with strong intrastrand CT character, we label CT^intra (and, therefore, in Scheme 1, PCET¹ = CT^intra + PT^inter1). The driving force for the PT depends on the involved bases and, therefore, PCET¹ is sequence dependent. It occurs in the (GC)_n duplex and in adenine (A)-thymine (T) homoduplexes (A)_n(T)_n, but not in alternating (AT)_n duplexes. In the latter duplex, intrastrand CT is observed, but it is not followed by interstrand PT.¹³ It is also possible that, starting from PT^inter1, G⁺ radical cation transfers the N1–H proton to the its hydrogen bonded partner C, resulting in a Double Proton Transfer (DPT) process (see Scheme 1).

Scheme 1 Schematic illustration of the excited states of two base pairs (2CG or 2GC) in alternating GC-DNA studied computationally. Atom numbering is shown in the inset (dashed black). As G* or C*, we label a generic bright state localized on G or C.

Although these studies advanced understanding of the photoactivated dynamics of DNA, key questions remain about the ‘fast’ part of the excited state dynamics (i.e. <5 ps) and about its relationship to the slower dynamics. It is still uncertain how the initially photoexcited bright ππ* excited states (ES) reach the dark CT states. Additionally, dark ¹nπ* states exist on the individual bases, which are close in energy to the ¹ππ* states,⁷ and multiple (both intra and interstand) CT processes can occur in a duplex. Processes in which both ET and PT reactions occur between different strands, (PCET² = CT^inter + PT^inter2, i.e., excited state hydrogen atom transfer from G to C in a single base pair), labelled as (iii) in Scheme 1, are particularly interesting. This reaction has been documented in a GC hydrogen-bonded pair in the Watson and Crick (WC) arrangement, both in the gas phase and in chloroform solution,^{23,24,31–33} but its involvement in a DNA duplex containing multiple base pairs is still a matter of debate.^9,33–39 In an isolated GC base pair, this decay pathway leads to GS recovery within a few ps,²³ and, in principle, this could also be the case within DNA.

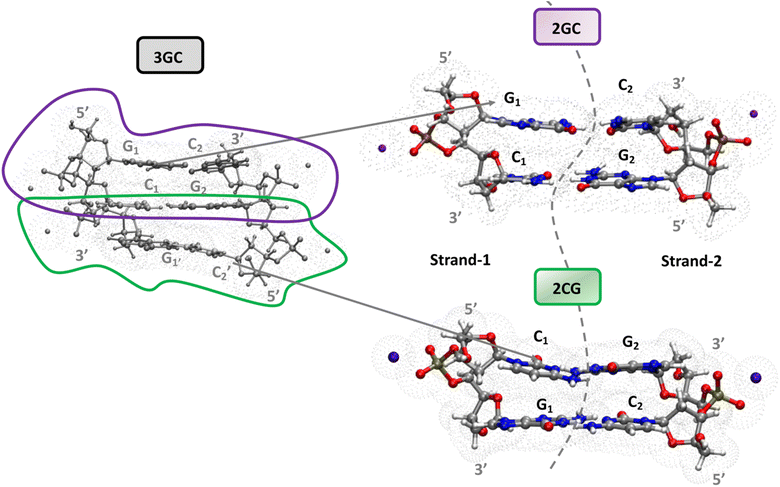
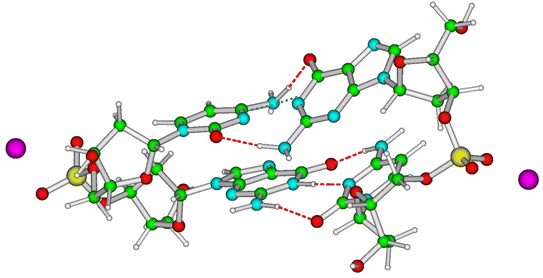
A complete and detailed picture, at the molecular level, of the first ps of the photoactivated dynamics of GC DNA is therefore still lacking. In this study, we take steps to resolve these issues by integrating various computational approaches, from classical to quantum, and static to dynamic, on the computational models depicted in Fig. 1. In detail, using static DFT computations, we map the potential energy surface (PES) of the lowest energy excited states, a tetramer made up of two stacked G·C base pairs, the minimal model needed to account for the observed excited states of the GC double helix (Fig. 1). These systems are labelled as 2GC when G is at the 5′ end, and 2CG when C is at the 5′ end. Test calculations have also been performed on the nucleobase hexamer (hereafter 3GC) containing both GC and CG sequences (Fig. 1). In parallel, dynamical computations are performed both in the GS and ES. In the GS, we run classical molecular dynamics (MD) simulations for 2 µs on a d(GC)₅ B-DNA duplex in water to ascertain how thermal fluctuations affect the base stacking that dictates the subsequent photoactivated dynamics. Concerning the latter processes, we focus on nonadiabatic transitions occurring in the 100 fs timescale after photoexcitation. In order to describe them properly, we adopt a full nonadiabatic quantum dynamical (QD) methodology, i.e. we propagate vibronic wave packets on the coupled surfaces of the relevant electronic states, and we exploit the fact that on this short time scale they can be approximated with a linear vibronic coupling (LVC) model.^40,41 Specifically, we perform these QD simulations starting at 18 different 2GC and 2CG structures extracted from the MD simulations, as well as from the QM minima structures, considering any possible excitation to the two lowest energy bright states localized on each G base (G-L_a and G-L_b) and on the lowest energy bright state localized on each C base (C*). The main goal of the MD/QD simulations, which does not consider PT processes, is to assess the population transfer from the bright to the CT states (intrastrand and interstrand), and how it is affected by the thermal fluctuation of the backbone. Finally, we computed the IR and the absorption spectra of the excited state minima that, based on the joint static and dynamical analysis, are the most populated ones. In this way we can identify the spectral signatures of the main decay pathways, interpreting the available experimental results. On this ground, we shall propose a global picture of the excited state dynamics of GC and CG sequence in DNA, highlighting which are the features that can be considered well assessed and those that need additional efforts, and laying the ground to extend the conclusion of our study to other DNA sequences.

Fig. 1 Computational models for 3GC, 2GC and 2CG DNA used in this study and the cavity used in the PCM calculations. When computing the IR spectra, all labile hydrogens have been substituted with deuterium atoms to facilitate comparison with experiments performed in D₂O. In the dimer, strand 1 is defined as the strand with the larger overlap between G and C on the same strand. In the following we label the bases in strand 1 as G₁C₁, and those in strand 2 G₂C₂.

Results and discussion

Mapping the excited states PES of GC and CG sequences

Magnifying a trend already present in the starting crystallographic structures, the optimized minima of 2CG and 2GC exhibit quite different base stacking. In 2CG, there is one strand (hereafter, strand 1, see Fig. 1), where the G and C rings have a large overlap and a close stacking distance (Scheme 1, C5 atoms of G and C at 3.6 Å), whereas in the other, strand 2 (Fig. 1), the bases are much more distant (C5 atoms of G and C at 5.9 Å). In 2GC the differences are less extreme: the distance between the C5 atoms of G and C is 3.8 Å in strand 1 and 4.7 Å in strand 2. Interestingly, in 2GC the G bases on opposite strands (G₁ and G₂ in Fig. 1) are much closer (C5–C5 distance equals 6.2 Å) than the two C bases (C₁ and C₂ in Fig. 1, C5–C5 distance equals 9.7 Å). Moreover, in strand 2 of 2GC the two bases are slightly twisted, thanks to the combination of shifts from the ideal value of the propeller and roll coordinate (see also ESI†),⁴² with respect to the plane of the WC base pair to maximize an intrastrand HB between the amino group of G₂ and the C=O group of C₂.

Despite these differences, the computed IR spectra of 2GC and 2CG (Fig. 2) are similar and agree well with the experimental FTIR spectrum of d(GC)₉.¹⁷ A detailed description can be found in the ESI.†

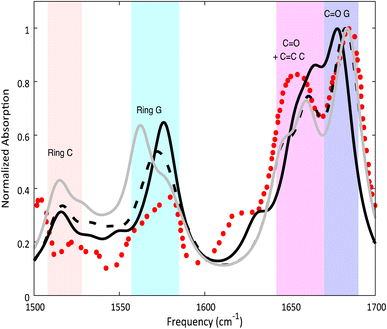Fig. 2 Calculated ground state spectra for 2GC (solid black line), 2CG (solid grey line), 3GC (dashed black line) and experimental spectrum¹⁷ of d(GC)₉ (red dots) in D₂O. PCM/M052X/6-31G(d) calculations. Computed IR frequencies scaled by 0.955.

As already discussed,³³ the lowest energy excited states of 2GC, up to 6 eV, derive from the mixing of the ππ* bright excited states of G (L_a and L_b) and C, with G → C CT states. Due to the close stacking between the bases, the different excited states are strongly mixed. Nonetheless, it is possible to qualitatively recognize their predominant diabatic character as detailed in Table S2.† The two lowest energy excited states (S₁ and S₂), despite their non-zero oscillator strength, have a strong intrastrand CT character (CT^intra) (S₁ within strand 1, CT^intra-1) and S₂ (within strand 2, CT^intra-2). S₃ corresponds mainly to a ππ* excited state localized on G₁. It is similar to the lowest energy bright excited state of ‘free’ guanine, usually labeled as L_a, hereafter denoted as G₁-L_a. S₄, S₅ and S₆ derive from the mixing of the lowest energy bright states of C₂ (mainly S₄, in the following we label this excited state as 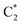), C₁ (mainly S₅, labelled as 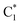), and G₂ (mainly S₆, a La-like transition, hereafter G₂-L_a). S₄ and S₅ are similar to the lowest energy ππ* state on an isolated C base, described by a HOMO → LUMO transition, which is bonding/antibonding with respect to the C5=C6 double bond. S₇ is the first excited state with substantial interstrand G₁ → C₂ CT character (CT^inter), 0.6–0.7 eV less stable than the CT^intra states. Finally, S₈ corresponds to the first L_b ππ* excited state of G and is 0.4 eV above the L_a state.

In 2CG (Table S2 and Fig. S1†) S₁ has a predominant strong intrastrand CT character and is localized on strand 1 (CT^intra-1). S₂ and S₃ can be described as Frenkel excitons deriving from the interaction of and , though in the latter a small G1 → C1 CT component is present. In S₄ and S₅, G₂-L_a, G₁-L_a and G₂ → C₂ CT excited states are mixed. S₆, S₇, and S₈ derive from the interactions of G-L_b and G₂ → C₂ CT (S₇). The first excited state with predominant interstrand CT character is S₁₁, 0.7 eV less stable than the CT^intra states, and to which both G₂ → C₁ and G₁ → C₂ CT states contribute. The qualitative picture of the FC region obtained for 3GC is similar to that described for 2GC (see Table S3, Fig. S2 and Section 3.2 in the ESI†).

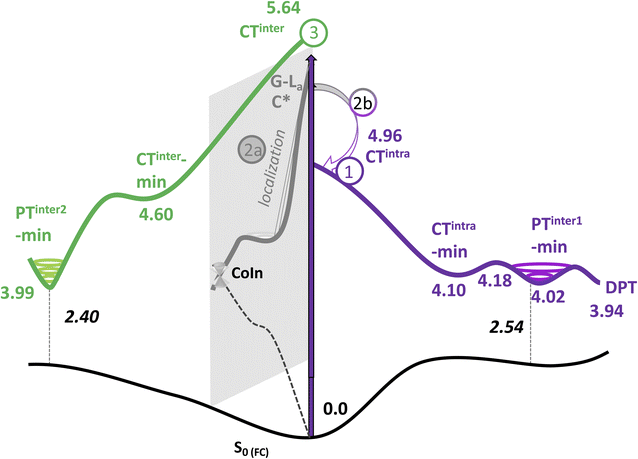
As a next step, we have mapped the PES of 2GC and 2CG, locating the different minima. A detailed description of the PES is provided in Section 3.5 of the ESI,† whereas the main outcome of our analysis (the nature of the main minima and the energy barrier associated to these paths) is summarized in Table 1 and Fig. 3.

Table 1 Schematic description of the outcome of the excited state geometry optimizations of 2GC and 2CG, reporting in bold the minima whose IR and ESA spectra have been characterized. PCM/TD-M052X/6-31G(d) calculations

Excited adiabatic state	Outcome of the optimization	Possible interstrand PT reaction	Notes
S1/S2	Decay to CT^intra-min (localized on strand 1 or 2)	G (H1) → C^− leads to PT-inter^1-min	Path 1 in Fig. 3
		From PT-inter^1-min G^+ (H1) → C leads to DPT-min
S3/S4/S5/S6	Localization on G-La or C*, decay to G-La-min and C*-min		Path 2 in Fig. 3
			2a. Monomer-decay, very small energy barrier towards a CI with S0 for both minima
			2b. Crossing to CT^intra that is close in energy to G-La-min and C*-min
S7	Decay to CT^inter-min	G^+(H1) → C^− leads to PT^inter2-min	Path 3 in Fig. 3. PT reaction strongly exoergonic. PT^inter2-min close to a crossing with S0

---

Fig. 3 Schematic description of the PES associated to the main decay pathways in 2GC: (1) CT^intra route, (2a) monomer-like route, (2b) coupling of the bright states with CT^intra and (3) CT^inter route. The LR-PCM/TD-M052X adiabatic energies (eV) respect to the ground state minimum are reported. Vertical emission energies (eV) in black.

Nonadiabatic quantum dynamical simulations of the excited state population

In order to get insights into the mixing of the bright and CT states in the ultrafast timescale, we turn to quantum dynamics calculations with a model LVC Hamiltonian, parameterized via a fragment based diabatization (FrD).⁴⁰ In this Hamiltonian, by construction the local excitations are fully localized on a monomer and, analogously, the CT states involve the transfer of one electron between the two bases (see Methods for further details, with parameters reported in Tables S4 and S6 in the ESI†). The results of our 250-fs long FrD-LVC QD simulations with a Hamiltonian parameterized at the minimum structure of 2GC are reported in Fig. 4 (solid lines), following excitation to each of the 3 lowest bright states on each strand (G-L_a and G-L_b, and C*). For 2GC, a very fast and effective population transfer to the intrastrand CT states is predicted (Fig. 4). When exciting the bright states on the bases of strand 1, within 50 fs ∼50% of the population has been transferred to CT^intra-1 and the same happens for strand 2, where the population transfer to CT^intra-2 is even faster and more effective. In this latter strand, after 100 fs ∼80% of the population is on CT^intra-2. Interestingly, despite the bases in strand 2 being slightly further away from each other, resulting in the CT^intra-2 diabatic energy being ∼0.1 eV larger than CT^intra-1, the coupling of the bright states to the CT is larger for strand 2 than strand 1. This indicates that the relative stacking orientation, and not simply the distance, is an important factor due to orbital overlap effects. On a longer timescale, for both strands, some population transfer to the CT^intra state localized on the opposite strand is predicted. As a consequence, after 200 fs the large majority of the photoexcited population is on CT^intra states.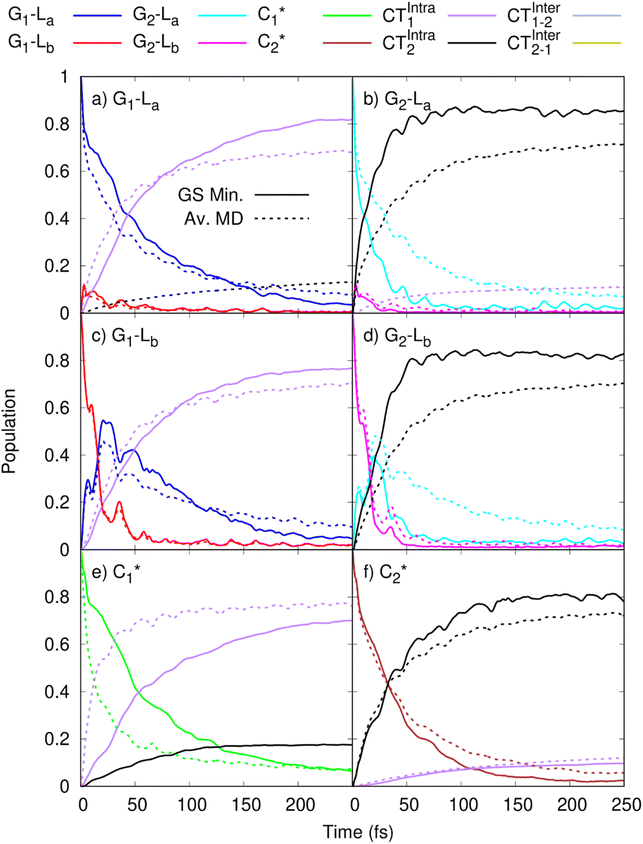

Fig. 4 Population dynamics following initial excitation to (a) G₁-L_a (b) G₂-L_a (c) G₁-L_b (d) G₂-L_b (e) and (f) for 2GC (according to labelling of Fig. 1). Calculations on a FrD-LVC model using 124 in-plane vibrational modes of each base parameterized by M052X/PCM calculations at the GS minimum in solid lines, and averaged MD snapshot results in dashed lines. Only states which reach population >0.1 are illustrated for clarity. Full figure in the ESI, Fig. S3.†

QD simulations of 2CG, with a Hamiltonian parameterized at its ground state minimum structure, provide (Fig. 5, solid lines) a less substantial population of CT^intra states, especially for strand 2, which is less closely stacked. Indeed, when exciting G₂-L_a after 50 fs only 10% of the excited population is transferred to CT^intra-2, and most of the excited population is still on G₂-L_a. Interestingly, some excitation energy transfer to is instead predicted. Excitation to this latter state leads, instead, to a more substantial population of CT (40% after 50 fs). The stronger coupling between bright and CT states in strand 1 is mirrored by a quite effective population of CT^intra-1, especially for an initial excitation of G₁-L_a, which leads to 80% of the population on CT^intra-1 in 50 fs. Starting from , we instead observe a steady population of CT^intra-1, reaching 40% after 150 fs. Both for 2GC and 2CG, no significant population of the interstrand CT state is predicted (Fig. 4 and 5).

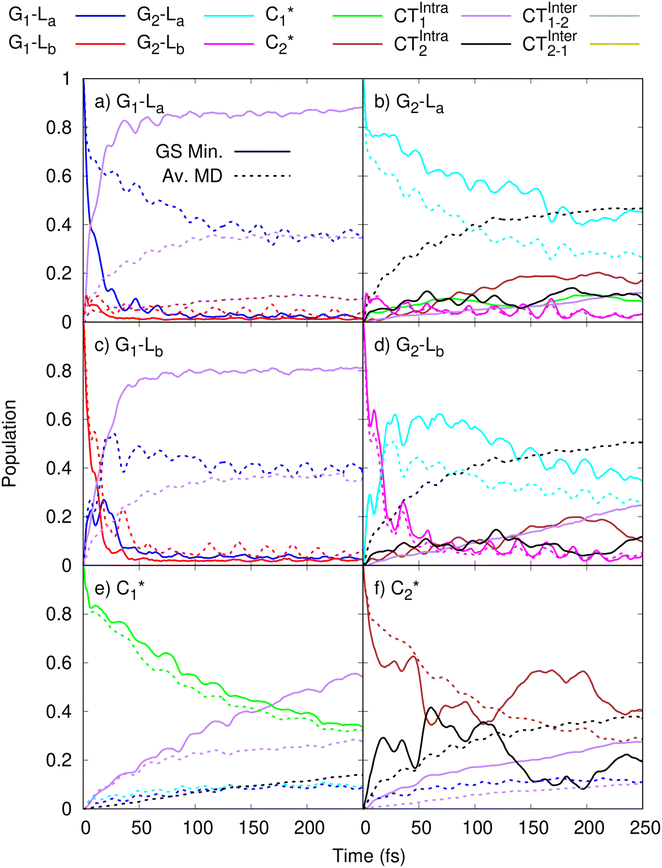Fig. 5 Population dynamics following initial excitation to (a) G₁-L_a (b) G₂-L_a (c) G₁-L_b (d) G₂-L_b (e) and (f) for 2CG (according to labelling of Fig. 1). Calculations on a FrD-LVC model using 124 in-plane vibrational modes of each base parameterised by M052X/PCM calculations at the GS minimum in solid lines, and averaged MD snapshot results in dashed lines. Only states which reach population >0.1 are illustrated for clarity. Full figure in the ESI, Fig. S10.†

As a next step, we studied the effect of thermal fluctuations on the ultrafast dynamics of GC and CG sequences, performing QD simulations of the photoinduced dynamics starting from a fairly representative sample of the structures of GC and CG steps extracted every 400 ns from the (GC)₅ MD simulations (see Computational details and section in the ESI†). The assumption behind these computations is that the inter-molecular distortions are slower than the fast intra-molecular vibrations (described by the LVC Hamiltonian). Although they are considered frozen for the ultrafast photo-excited dynamics investigated by QD, their fluctuations before photoexcitation do affect such dynamics, by modulating the stacking geometry and, therefore, the electronic couplings between the different bases. This effect is introduced by the fact that the LVC Hamiltonian is re-parameterized for each (GC)₅ configuration sampled by the MD, and we then analyse the average of the excited-state populations obtained for each snapshot. We also note that the thermal effects are only partially taken into account by our approach, as it is only the classical molecular dynamics simulations that directly include thermal effects on the DNA backbone. Thermal effects of the low frequency vibrational modes of the GC and CG tetrads are not considered in the quantum dynamics simulations, as these are conducted at 0 K. Thermalisation of these modes could be introduced through a stochastic mean field⁴³ or thermofield dynamics approach,⁴⁴ at the cost of a much more computationally expensive calculation. Due to the large size of our system, and the fact that we were most interested in the disruption of stacking via backbone fluctuations, we chose not to do this. The corresponding MD trajectory is analysed in the ESI (Tables S5, S7 and Fig. S3–S16).† For 2GC, these QD simulations (Fig. 4, dashed lines) confirm the picture obtained with LVC models parametrized at the absolute QM minima, at least when looking at the average populations. For excitation to the bright states on either strand, the transfer to the CT^intra states is effective, with >50% population achieved after 50 fs. However, interestingly, for some structures the population transfer is smaller. They are characterized by a smaller overlap between the stacked bases and/or a larger interbase distance (see Table S1 in the ESI†).

The average behavior of the photoexcited population in 2CG (Fig. 5, dashed lines) is similar to that described for 2GC, with population transfer from the bright states to the intrastrand CT states, albeit the transfer is somewhat slower and less complete due to the CG structures typically being less well stacked than GC. Moreover, the two strands exhibit a rather similar behavior, in contrast to what is predicted based on the single ground state minimum structure. The reason for this is that the stacking asymmetry of the two strands is strongly reduced by the conformational averaging performed by MD simulations. When exciting G-L_a or G-L_b, after 100 fs 40% of the population has been transferred to CT^intra, while the population transfer following excitation of C* is smaller (20%). However, there is a non-zero probability that excitation on one strand decays to the CT^intra state on the opposite strand. As detailed in the ESI,† in some structures partial excitation energy transfer processes are operative between the bright states of bases on the opposite strands. Only for one structure we do instead observe some population transfer (10–20% after 50 fs) to an interstrand CT state.

Finally, it should be reminded that PT processes cannot be described by our QD approach based on LVC models.

Computing the IR and difference IR spectra of the relevant excited state minima

We use the IR spectra associated with the most relevant minima and their difference IR spectra (see Fig. 6) to interpret the experimental TR-IR spectra (Fig. 7). Our main reference will be the experimental spectra obtained on d(GC)₉, but we shall also analyze some experimental results on the d(CG)₂ miniduplex reported in ref. 19.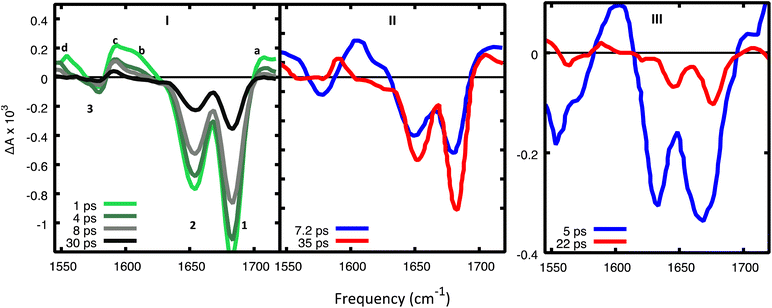

Fig. 6 Excited state IR spectra (colored shaded curves) and difference spectra with respect to the Ground state (solid lines) computed in 2GC for (I) G* (black) and CT^intra-1 (purple), (II) PT^inter1 (pink) and DPT (blue), (III) CT^inter (green) and PT^inter2 (ochre) and in 2CG (IV) G* (black) and CT^intra-1 (purple), (V) PT^inter1 (pink) and DPT (blue) and (VI) CT^inter (green) and PT^inter2 (ochre). The inverted GS spectrum is reported in all the panels by the light grey shaded curve. Computations performed substituting all exchangeable Hs with Ds.

Fig. 7 (I) Experimental TR-IR spectra¹⁷ in d(GC)₉ in D₂O after excitation at 265 nm for selected decay times and (II) DADS. Reprinted with permission from J. Am. Chem. Soc., 2015, 137, 7059–7062. Copyright 2015 American Chemical Society. (III) DADS from TR-IR spectra of a cCG/CG miniduplex excited at 265 nm. Reprinted with permission from J. Am. Chem. Soc., 2016, 138, 7395–7401. Copyright 2016 American Chemical Society. Amplitudes in panels I and III cannot be meaningfully compared since they were recorded under different experimental conditions.

The C=O stretch of G⁺ in CT^intra-min (Fig. 6I) blue shifts to ∼1715 cm⁻¹ compared to the GS spectrum, in good agreement with the 1703 cm⁻¹ feature assigned to G⁺ from experiments on the guanosine monophosphate monomer and poly(dGdC).^29,45 The two vibrational frequencies associated with G⁺ ring stretching modes blue shift by 25–40 cm⁻¹, leading to the appearance of a band around ∼1600 cm⁻¹. This band is consistent with a positive peak observed in the experiment just above 1600 cm⁻¹ after photoionization of dG.⁴⁶ In comparison, the C=O stretching mode of C˙⁻ (∼1580 cm⁻¹) red shifts by ∼70 cm⁻¹ compared to C in the GS, whereas several vibrational modes in the range 1400–1600 cm⁻¹ have contributions from stretching of the C5=C6 double bond of C˙⁻. Importantly, the vibrational modes of the G and C that are not involved in the CT state decrease noticeably in intensity compared to the GS as a result of base pairing and stacking with the radical ions. Additionally, the frequency of the C=O stretching mode of the C base paired with G⁺ is predicted to red shift by 10–30 cm⁻¹. The latter finding highlights the importance of including non-covalent interactions when calculating the vibrational frequencies of nucleobases in DNA.

In 2GC the computed spectrum of PT^inter1-min (Fig. 6II) shares some features with that of CT^intra-min, such as (i) the ‘blue-shifted’ peaks associated to G⁺, at 1725 cm⁻¹ (C=O stretching) and at 1600/1625 cm⁻¹ (ring stretching). Additionally, at (ii) 1660 cm⁻¹ we find a strong peak associated to the C=O stretching mode of the (C + H) radical, and (iii) two close lying peaks at 1590 cm⁻¹, which can be assigned to ring stretching modes of G(−H)⁻ radical. Actually, the FTIR spectrum of G(−H)⁻ in water shows two close-lying peaks at ∼1590 cm⁻¹.¹⁷ Another, (iv) less intense peak at 1590 cm⁻¹ can be assigned to the C=C stretching of (C + H) radical. Finally, at 1520 cm⁻¹ we find an intense transition associated to the C base on strand 1 (v) clearly, the region around 1670 cm⁻¹ absorbs much less than in the ground state and also than in CT-intra, since the contribution from C=O group of the ‘neutral’ G is lost.

The spectrum of DPT-min (Fig. 6II), as expected, exhibits some of the peaks just described for PT^inter1-min, such as (i) the peaks at 1590 cm⁻¹ associated to G(−H)⁻ radical. We also find, on the blue-wing, (ii) two vibrational peaks at 1704 cm⁻¹ and 1665 cm⁻¹ associated to [C + H]⁺ moiety (see the light blue shaded curves).

The spectra computed for CT^inter-min in 2GC (Fig. 6III) and 2CG (Fig. 6VI), which share many features with CT^intra-min (Fig. 6I and IV) (one G⁺ and one C⁻ base are present), are not exactly the same, due to some differences in the HB distances. Indeed, although the PT has not taken place, the HB distance between the C and H–N1 of G decreases to ∼1.6 Å (in 2GC) and ∼1.7 Å (in 2CG) with respect to the GS (∼1.9 Å). The HB distances involving the G⁺–NH₂ with the C=O group of C⁻ are also very short, i.e. ∼1.65 Å in 2GC and ∼1.5 Å in 2CG. The N–D vibrations of the G⁺ and C⁻ bases are strongly coupled, as expected, with the C=O stretching modes. In 2GC, we find just above 2000 cm⁻¹ (not shown in the figure) a feature associated with G⁺ ND₂ stretching, and at 1715 cm⁻¹, a peak due to the coupling between the G⁺ C=O and N–1D stretching modes. In 2CG, the two peaks are closer in energy at 1750 and at 1700 cm⁻¹ and can be described as the symmetric and anti-symmetric combinations of the G⁺ N1-D and one of the G⁺ ND₂ stretching modes, coupled with G⁺ C=O stretching.

The most significant vibrational features of PT^inter2-min are the disappearance of the absorption peaks above 1700 cm⁻¹ and in the 1600 cm⁻¹ region (see Fig. 6, panels III and VI).

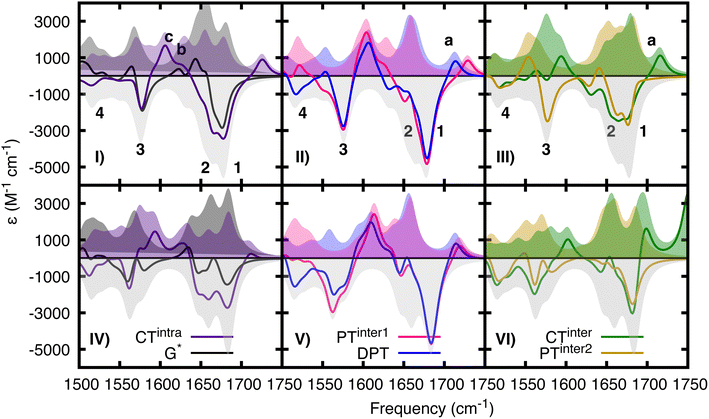
In the experimental TR-IR spectra (Fig. 7), the negative peaks are due to the bleaching of the GS vibrations (GSB) (labelled as 1, 2, 3 in panels 7.I) while the positive ones (labelled as a, b, c, d) are due to vibrations of the excited electronic states (see ESI†) because the experimental TR-IR spectra lack the distinctive signature of vibrationally hot GS species (a rise of a positive band on the low-frequency side of the GSB, followed by a blue-shift of the maximum and subsequent decay).¹⁸ The TR-IR spectrum at 1 ps (Fig. 7I) exhibits (i) a positive feature above 1700 cm⁻¹ (peak a), (ii) two negative GSB signals 1 and 2, where the former is more intense than the latter, (iii) a composite positive band at 1600–1620 cm⁻¹ (peaks b and c), (iv) bleach 3 which is much weaker than 1. A key feature of the experimental TR-IR spectrum is the presence, even at <1 ps, of a weak positive signal above 1700 cm⁻¹. This feature is also present in both DADS (Fig. 7II). According to our calculations, this peak is best assigned to G⁺ with its blue-shifted C=O stretching frequency. Thus, an excited state that generates G⁺, i.e. CT^intra, PT^inter1 or CT^inter, must have formed in less than 1 ps after excitation. Alternatively, DPT could have taken place because deuterated dCMP has a peak near 1700 cm⁻¹ (see Fig. S3 in ref. 47) (see Fig. 6, panels II and V).

Considering the large number of excited states which could be involved and the conformational heterogeneity of d(GC)_9, the experimental spectrum is relatively simple, and its shape does not change between 1 and 30 ps, except for a moderate decrease of the relative intensity of bands b and d with respect to the other bands in the first few ps. Interestingly, no significant rises in the ESA are observed in the investigated frequency window. Additionally, the shape of the DADS associated with the fast and the slow components of the spectrum are fairly similar (Fig. 7II), the most significant difference is the large decrease of the positive peak above 1600 cm⁻¹.

The calculated DIR spectra of CT^intra, PT^inter1, and DPT (see Fig. 6, panels I,II, IV, V) are qualitatively similar to the experimental TR-IR traces of d(GC)₉ (see Fig. 7, panel I). In detail, we note in the calculations a positive peak above 1700 cm⁻¹, two bleaching bands at 1680 cm⁻¹ and 1650 cm⁻¹, the former slightly more intense, and one large positive feature at 1600 cm⁻¹, preceding the bleaching band at 1560 cm⁻¹. The positive band above 1600 cm⁻¹ is, on average, more intense and slightly blue-shifted for PT^inter1 and DPT with respect to CT^intra. The most significant discrepancy concerns the relative intensity of the bleaching bands 1 (at 1680 cm⁻¹) and 2 (at 1650 cm⁻¹). The former is underestimated in the computed DIR spectrum of CT^intra, while the latter is underestimated in PT^inter1 and DPT. The spectra computed for 2CG are qualitatively similar to those calculated for 2GC.

Comparing the computed DIR and experimental TR-IR spectra does not provide a firm indication on the possible involvement of the CT^inter/PCET² route in the GC DNA excited state dynamics. The DIR associated with CT^inter is indeed fairly similar to that of CT^intra. However, an interesting difference arises at the high frequency edge of the investigated energy window. According to our calculations, the N–D stretch mode of CT^inter can red-shift below 2000 cm⁻¹ and is predicted to occur at 1750 cm⁻¹ for CG. In the TR-IR spectrum of the CG miniduplex,¹⁹ there is a very broad and intense positive feature at ∼1730 cm⁻¹ that decays on a few ps time-scale. No significant positive feature is predicted for the computed DIR of PCET,² the largest one falling at ∼1550 cm⁻¹. The absence of absorption above 1700 cm⁻¹ by the PCET² excited state indicates that it cannot be the only deactivation route as the positive feature above 1700 cm⁻¹ persists in the experimental spectra for longer than 40 ps.

The comparison between computed and experimental spectra does not provide evidence of major participation by monomer-like decay paths in (GC)₉. Actually, the positive DIR features associated with these paths are predicted to be rather low in intensity and therefore are not very informative. We include the spectrum of G*, which is more intense than that of C*, in Fig. 6, whereas that of C*, which is extremely weak, is plotted in Fig. S19 and S20 of the ESI.† However, compared to the excited states involving CT, their bleaching bands are relatively less intense and, on the average, slightly red-shifted. Disappearance of C* or G* would thus be mirrored by a blue-shift of the bleaching bands 1 and 2, which is not observed in the experiments. On the contrary, in the TR-IR spectra of the CG miniduplex, which is much less stiff than a long sequence, the bleaching bands 1 and 2 noticeably blue-shift after a few ps, suggesting the involvement of monomer-like decay routes.

Computing the excited state absorption spectra of the relevant minima

We have also computed the electronic excited-state absorption spectra from the most relevant excited-state minima in 2GC. They are shown in Fig. 8, together with the experimental decay-associated difference spectra (DADS) in D₂O.²⁰ Transient absorption spectra should be computed by subtracting ground state absorption and stimulated emission from the excited state absorption. However, DNA has negligible GS absorption at λ > 300 nm, and at the considered excited-state geometries the transition dipole with the ground state is almost zero. As a consequence, the experimental transient absorption spectra (and the derived DADS) can be compared directly with the computed ESA spectra for the different minima.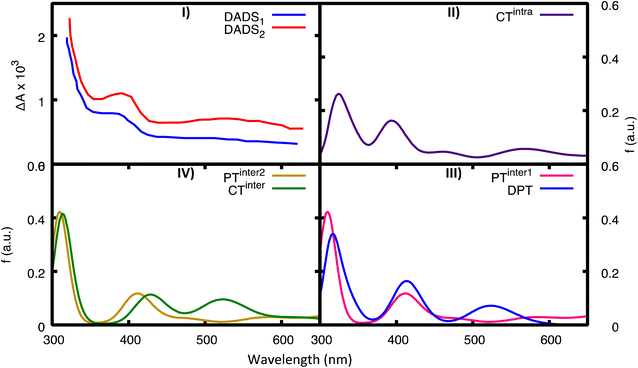

Fig. 8 Computed ESA from the most important minima for 2GC. For comparison in panel (I) we report the experimental TAS in D₂0 (blue, fast component, DADS1, red, slow component, DADS2), see ref. 20. (II) CT^intra-1, (III) PT^inter1 (pink) and DPT (blue), (IV) CT^inter (green) and PT^inter2 (ochre).

Global fits to the experimental broadband data provide, in addition to a decay component of less than 1 ps, a fast component (DADS₁ ∼5 ps) and a slow component (DADS₂ ∼22 ps in H₂O and ∼28 ps in D₂O). As discussed in detail in ref. 20, their shape is very similar in the two solvents, but their amplitudes differ. Both DADS₁ and DADS₂ exhibit a strong peak below 350 nm, another one at 400 nm and a broad absorption in the 500–600 nm region. These spectral features resemble the pulse radiolysis spectra of G˙⁺ and G(−H)˙, which are very similar. The spectra computed for CT^intra, PT^inter1, DPT, and PT^inter2, which provide evidence for the presence of G˙⁺ and G(−H)˙, are consistent with the experimental transient absorption spectra. However, the approximations in our computational approach do not allow us to discriminate between these possible species because of their similar spectra. The ESA spectra of the monomers (Fig. S27†) instead have very different features with respect to the experimental DADS of d(GC)₉.

A global picture of the photoactivated dynamics of GC and CG sequences in DNA

A complete disentanglement of the excited state dynamics of a system as (GC)₉, from the sub-ps to the ∼30 ps time scale is a very challenging task. Dozens of chromophores are present in a flexible system, which has well-stacked bases that co-exist with more loosely interacting ones. The number of possible deactivation paths is large, especially considering that interstrand proton transfer routes may be operative. From the computational point of view, it is not possible to characterize all possible minima and state crossings. Moreover, the size of the systems makes only TD-DFT calculations feasible and imposes several approximations such as not considering anharmonic vibrational effects. On the other hand, although these limitations make a perfect agreement between experimental and simulated spectra impossible, the picture provided by static QM calculations and QD simulations appears fully consistent with the experimental indications, enabling a coherent description of the main deactivation routes, namely, those associated with the most prominent TR experimental features.

Our computations indicate that the most significant decay channel involves the intrastrand G → C CT state. According to TD-DFT, the lowest-energy excited states in the FC region have a strong intrastrand G → C CT character. Moreover, QD simulations predict that the intrastrand CT states are populated very effectively from all bright excited states. For both CG and GC sequences, ≥50% of the photoexcited population has decayed to CT^intra-1 or CT^intra-2 in less than 100 fs after photo-excitation. These indications are robust with respect to increasing the number of structures considered in the simulations and are confirmed also when GC/CG sequences are included in an AT rich sequence.⁴⁸ Finally, whereas the LVC potentials adopted for QD are more approximate, arising from a local expansion at the FC point, accurate geometry optimizations on the real TD-DFT surfaces confirm that the most stable excited state minimum is associated with CT^intra. We have also documented the existence, in the proximity of the FC region, of effective crossings between CT^intra and the spectroscopic bright states localized on G and C. On these grounds, we predict a substantial and extremely fast sub-ps disappearance of all bright/emissive states and the concomitant population of the CT^intra state. This picture accounts for the experimental TR fluorescence, which reveals that emission associated with the bright G and C states disappears much faster than in the isolated monomers.²⁶ It also explains the TR-IR spectra, which show that the spectral signature of CT^intra states, i.e. the positive feature at >1700 cm⁻¹ associated with the G⁺ base, appears on the sub-ps time-scale.¹⁷

The computed IR spectra also confirm the very fast disappearance of the monomer-like excited states. Indeed, according to our calculations, if G-L_a or C* decay after ∼1 ps, a shift in the position of the bleaching bands 1 and 2 would be expected (see Fig. S19 and S20 in the ESI†). However, the position of these bleaching bands does not show any significant change in the experiments in the investigated time-window. Obviously, it is clear that some poorly stacked bases (like ones found in the miniduplex) can undergo monomer-like decay.

Though our QD simulations cannot describe PT (and therefore PCET) processes, they indicate that CT^inter states are not significantly populated in (GC)₉. Though their minima are close in energy to those of the CT^intra states, the latter are much more stable in the FC region and more strongly coupled with the bright excited states. Calculations and TR experiments, thus, provide strong and convergent evidence for the substantial and fast population of CT^intra states in d(GC)₉.

What happens next? The excited state decay in d(GC)₉ shows a significant isotope effect and is faster in H₂O than in D₂O,²⁰ suggesting the involvement of a PT reaction. Moreover, our calculations, in agreement with the experimental pK_a of the bases (and of their deprotonated/protonated counterparts), indicate that the PT^inter1 minimum, which is reached by G → C⁻ PT, is more stable than CT^intra-min. Population of PT^inter1 thus seems likely. At the same time, as discussed in detail in the SI, a complete disappearance of CT^intra population on the sub-ps time scale seems unlikely due to the energy barrier that separates CT^intra-min and PT^inter1-min. It is not easy to predict the extent of CT^intra → PT^inter1 (or even DPT) transfer and its time scale. A QD study of the possible PT reactions could shed light on this issue but is outside of the scope of the present paper. The main features of the CT^intra and PT^inter1 (and DPT) DIR spectra are indeed fairly similar, the main difference concerns the relative intensity of the negative-going bands 1 and 2 in the calculated DIR spectra (Fig. 6). The normalized kinetic signals that describe the recovery of these two bands agree within experimental uncertainty. This suggests that either just a single transient state (CT^intra or PT^inter1) is present during the observed dynamics, or, if multiple states are present (CT^intra and PT^inter1) then these must interconvert more rapidly (i.e., in less than 100 fs) than can be observed in our measurements such that their populations change in lockstep throughout the decay. The bleaching bands 1 and 2 associated with the minima of CT^intra and PT^inter1 are, however, different (Fig. 6IV and V). On this ground, keeping in mind that the difference between the bleaching bands 1 and 2 in CT^intra and PT^inter1 is close to the expected accuracy of the calculations, this experimental result suggests that no significant CT^intra → PT^inter population transfer occurs after a few hundred fs.

On these premises, the scenario most consistent with the available experimental results provides two parallel decay routes. In one of them the system is trapped in CT^intra, while in the other one we observe an ultrafast population of PT^inter1/DPT. The minima of DPT and PT^inter1 exhibit energy and IR spectra too similar to allow a clear discrimination between these two decay paths. We expect that this PT reaction is modulated by the isotope effect and by the conformation adopted by the duplex at the moment of the excitation, which could enable an ultrafast CT^intra → PT^inter population transfer in the hot CT^intra state before it can thermalize. Because the CT^intra → PT^inter reaction involves the shift of a charge between the two strands, it should be sensitive to the location of the charged moieties (phosphate groups, counter-ions etc.). According to the analysis reported in the ESI,† another significant parameter is the ‘propeller’ twist in the WC pairing. The molecular structure corresponding to the maximum of the PES associated with the PT^inter1 reaction (pseudo transition state, Fig. 9) exhibits indeed a very twisted arrangement, which enables the approach of the nitrogen atoms involved in the PT reaction and avoids a steric clash of the NH₂ and C=O groups of G and C, respectively. When the propeller twist motion is not possible (for example in strongly stacked structures), our calculations indicate that the PT energy barrier is two times larger than for ‘twisted’ structures.

Fig. 9 Schematic drawing of the pseudo transition state for the PT reaction leading from CT^intra to PT^inter. The propeller twist deformation in the involved GC pair, the upper one, is clearly visible.

It is not possible to fully elucidate the kinetics of GS recovery from CT^intra-min or PT^inter1-min. We can hypothesize that the decay from PT^inter1 is faster because it is more stable than CT^intra-min and the charge recombination (CR) process occurs in the inverted region of Marcus theory.^30,49 Moreover, the energy gap with the GS of PT^inter1-min and, even more, DPT-min is rather small, suggesting that a crossing region with GS, and therefore, an effective ground state recovery route could be rather close. On the other hand, in the CpG dinucleotide a time constant of 8 ps was assigned to CR.⁴⁹ The decrease in the solvent exposed surface is expected to lead to an increase of the excited state lifetime because charge recombination is in the Marcus inverted region.^16,49 Because in AT DNA the excited state lifetime of the intrastrand CT state is 3 times larger in the duplex with respect to the single strand, a lifetime of ∼30 ps is, in principle, possible for CT^intra in (GC)₉. This framework also rationalizes the faster decay observed in H₂O, because the PT processes should be easier for the lighter H, decreasing the population trapped in CT^intra. Interestingly, it has been suggested²⁰ that the DADS associated with the fast component (DADS₁ in Fig. 8) is more similar to that of a G(-H) species (present in PT^inter1 or DPT), whereas that of DADS₂ resembles the G⁺ spectrum. Finally, the disappearance of the PT^inter1/DPT population would be mirrored by a strong decrease of the positive DIR above 1600 cm⁻¹, which is indeed observed in the TR-IR experiments in the first ps (see Fig. 7).

Dependence of the photoactivated dynamics on the nucleobase sequence

On balance, the pictures provided by QM geometry optimizations and QD simulations on the photoactivated dynamics of CG and GC sequences are similar. However, the CT^intra state is predicted to be populated less effectively for CG sequences, where one of the two strands is relatively less stacked (see ESI†). Actually, the results we obtain on 2CG are not very relevant for interpreting the data on (GC)₉, where the bases belonging to strand 2, the less stacked one, are closely stacked with another base in the ‘adjacent’ GC step (see, for example the G1 and C2 bases in the 3GC model in Fig. 1). In other words, each base always belongs to a GC and CG step and, consequently, it has, at least, one closely stacked partner. However, the results are particularly interesting for an ‘isolated’ CG sequence in DNA (i.e. not included in a repetitive GC tract), where C and G could be stacked to bases for which the intrastrand CT route is less effective, as in the GA, GG, or TC sequences.³⁸ On the other hand, a complete analysis of all possible tetramers is well beyond the scope of the present study.

The system that can be more directly compared to our 2CG is the CG miniduplex, where a CG tetramer is held together by two chemical bridges. Though the large conformational flexibility of the miniduplex suggest cautions against translating the results obtained on B-DNA computational models, many experimental features can be nicely accommodated in our picture. First, the majority of the excited state population decays on the <5 ps time scale, suggesting that the fastest ‘monomer-like’ decay channels are operative. Moreover, we observe a blue-shift of the bleaching bands 1 and 2 during the time monitored in the experiments, clearly revealed by the DADS associated with the short and long-lived components (compare the blue and red traces in Fig. 7III). As discussed above, this feature can be associated with the loss of G-L_a or C* population. Concerning the strong positive peak above 1600 cm⁻¹ in the TR-IR spectrum of the miniduplex, which decays in a few ps, it is mainly due to the ‘monomer’-like minima (especially G-L_a). Our calculations indeed show that a positive feature at ∼1600 cm⁻¹ is associated with the G-L_a minimum in the duplex. Moreover, the TR-IR spectra of dGMP show positive features at 1590–1632 cm⁻¹ (stronger) and 1546 cm⁻¹. They are usually assigned to hot GS absorption, decaying on a few ps time scale.^50,51 For dCMP a very weak positive feature at 1630 cm⁻¹ is found, which is also assigned to hot GS absorption.

Another interesting feature emerging from our calculations on CG is a strong positive feature above 1750 cm⁻¹ associated with the CT^inter minimum (see Fig. 6, panel VI). Interestingly, there are indications that the positive band seen above 1700 cm⁻¹ is broader and extends to higher frequencies in the TR-IR spectra measured miniduplexes containing CG base pairs than in the corresponding spectra of d(GC)₉·d(GC)₉ (compare panels a and b of Fig. 1 in ref. 19). Although features appearing near the edge of the IR detection window can be distorted by systematic errors arising from the low amplitude of the probe pulse in this region, there does appear to be a difference in bandshapes. We suggest that a higher fraction of the hydrogen-bonded base pairs in the miniduplex are poorly stacked with neighbors, favoring the CT^inter/PCET² pathway.

Conclusions

In this work, we characterized the main deactivation routes of GC-DNA by integrating different strategies. Only considering a dimer sequence (the minimum model accounting for both base stacking and base pairing), there are ∼20 excited states falling within 1 eV in the lowest energy absorption band of GC-DNA. In addition, many of these excited states have significant CT character and can trigger interstrand PT. As a consequence, the number of different excited state processes potentially activated by UV absorption in DNA is extremely high. We coupled quantum dynamical calculations with an extended characterization of the excited-state potential energy surfaces, identifying and characterizing the main minima. By computing the difference IR and excited state absorption spectra associated with the different minima we can interpret the available time-resolved experiments. Moreover, by exploiting the results of the structural characterization at the MD level, we verified how our picture is affected by thermal fluctuations in the structure. Finally, we repeated this analysis for GC and CG steps, getting interesting new insights on the dependence of the photoactivated dynamics of DNA on the base sequence, laying the ground for extending the current methodology to other DNA sequences.

The QD simulations (in line with the results of the geometry optimizations) indicate that a significant part (>60%) of the photoexcited population decays in less than 100 fs to an intrastrand G → C CT state. This conclusion is fully consistent with the ultrafast appearance of the IR signature of the G⁺ radical cation in the TA spectra, and with the disappearance of the fluorescence signal from G and C bright states. Though the amount of CT population is affected by thermal fluctuations (and therefore from the instantaneous DNA structure when photoexcitation takes place), it is always substantial, independently of the location of the GC step within the sequence. We show that the transfer to the CT^intra, though not small (i.e. 30–40%), is less effective for the less stacked CG sequence. This result does not alter the picture for alternating GC DNA, but it could be significant for CG sequences in other sequences, or in less stacked GC base pairs like the ones in the CG miniduplex. For this latter system, we propose the involvement of monomer-like as well as interstrand CT/PCET decay routes. Unfortunately, with the calculations we performed it is not yet possible to fully characterize the dynamics of the interstrand PT processes triggered by intrastrand CT. The energetics of the PT reaction from the neutral G to C⁻ (PT^inter1 process) indicate that this decay route is the most important one, and this conclusion is consistent with the TR-IR and TA spectra, but the similar spectra of PT-inter¹ and CT^intra do not allow us at the present time to discriminate between these two decay routes. A critical comparison between our computational results and the available experimental spectra suggests that both decay routes are active. Bifurcation likely occurs very early in the FC region and will be modulated by the structure of the duplex at the moment of the excitation and by the isotope (H/D) present. On the other hand, this study sets the stage for a full dynamical characterization of all PT processes in DNA, which is surely one of the challenges ahead in this field.

Methods

Quantum mechanical calculations

As a starting structure for the geometry optimizations of 2GC, 2CG and 3GC we have considered a duplex extracted from the crystal structure of a CG rich duplex (1CGC.pdb).⁵² We used calculations rooted in density functional theory (DFT) and its time-dependent extension (TD-DFT) to optimize the geometries and the vibrational frequencies of the ground and the excited electronic states, respectively. The M052X^53,54 functional has been adopted throughout our study. It provides a reliable description of dispersion interactions (critical to study a system governed by weak non-bonding interactions such as DNA) and CT transitions.^53,55 This functional has been already profitably used to study the photochemistry and photophysics of oligonucleotides. In particular, it has shown good performance in the calculation of vibrational spectra, both in the ground and in the excited electronic states.^16,27,33 The cost-effective 6-31G(d) basis set has been employed in all calculations. Interestingly, this basis set has been recently applied to the study of the ground state vibrational spectrum of a GC Watson–Crick (WC) pair in chloroform, providing remarkably accurate anharmonic IR spectra.⁵⁶

Solvent effects have been included via the Polarizable Continuum Model (PCM),^57,58 which has already provided a reliable description of bulk solvent effects on the DNA photoactivated dynamics. The main limitation of this approach is the lack of explicit solute–solvent interactions, but this is expected to play a minor role in the study of GC base pairs since the bases are already engaged in many strong interstrand hydrogen bonds (HB). Geometry optimizations have been performed using TD-M052X with Linear Response PCM both at the non-equilibrium and equilibrium level, the two computational schemes providing similar minima. Energy barriers in the reaction paths have been obtained through relaxed scans along the specific N–H distance.

The CT character of each singlet transition S_N in the GS minimum, in the following also referred as Franck–Condon (FC) geometry, has been qualitatively estimated by computing the charge difference, δq, between the S_N and the GS, S₀, (δq = q(S_N) − q(S₀)) for each nucleobase (i.e. not considering any sugar atom) using Mulliken charges.

IR and TA analysis. Harmonic vibrational frequencies are known to be, on average, blue-shifted with respect to those that include anharmonic corrections and, therefore, also with respect to the experimental ones. As a consequence, and to allow an easier comparison with experiments, we report and discuss in the main text only scaled frequencies, which are obtained by multiplying harmonic frequencies by 0.955, following the procedure frequently adopted in the literature.^59,60 This value, which is consistent with those suggested on the basis of extensive comparison between experimental and computed harmonic spectra, considering the functional and the basis set adopted,^59,60 has been already profitably adopted in previous studies of oligonucleotides.^16,21,61,62 Each stick transition has been broadened with a Lorentzian with half width at half maximum of 10 cm⁻¹. Difference IR spectra associated with the different excited states are then computed by subtracting the GS IR spectrum to the IR spectrum of each ES. The unscaled spectra are reported in the ESI.† The spectra have been computed at the solvent equilibrium level. Since the reference experiments were performed in D₂O, all of the exchangeable hydrogen atoms (those bonded to nitrogen and oxygen atoms) have been substituted by deuterium atoms in our IR calculations. Furthermore, at each excited minimum the electronic excited-state absorption spectra have been simulated by (linear response) non-equilibrium TD-DFT calculations, exploiting the multiwfn program⁶³ to obtain the transition dipole moments between excited states. Each stick transition has been broadened with a Gaussian with half width at half maximum of 0.15 eV.

All the calculations have been done using the Gaussian16 program.⁶⁴

LVC quantum dynamical simulations

We parameterized an LVC model using the recently developed Fragment Diabatisation (FrD) technique with the freely available Overdia code,⁶⁵ and TD-DFT computations. In practice a set of diabatic states comprising local excitations and CT states is built on the grounds of computations on fragments. For a tetramer, 4 fragments are defined which correspond to the four nucleobases. Local excitations are taken identical to the TD-DFT response vectors for computation on each fragment, whereas CT states are defined as mono-electronic orbital transitions from the HOMO to the LUMO of two different fragments. The effect of the three remaining nucleobases on the nature of the diabatic states is introduced by computing molecular orbitals and the reference excited states of the fragments embedded in the electrostatic field of the RESP charges of the other three fragments in their ground electronic state. Once diabatic states are defined, their energies and couplings are obtained by projecting them on a set of adiabatic states of the whole tetramer large enough to ensure full projection of all diabatic states (notice that the overlap matrix between diabatic and adiabatic states is computed considering the full transition densities). Linear couplings in the LVC Hamiltonian were obtained by displacing the tetramer structure along each single normal mode, repeating the diabatization and taking the numerical derivatives of the Hamiltonian matrix. Further details are given in ref. 40 and the same procedure was also followed in ref. 48. Once the projection is completed, the accuracy of the LVC parameters is comparable to the accuracy of the TD-DFT computations adopted for its parameterization. For dynamics, the LVC model treats the diabatic potentials as harmonic (the resulting adiabatic potentials can on the contrary be anharmonic and properly describe conical intersections between excited states),⁴¹ and is therefore expected to be accurate for the motion of stiff coordinates on ultrafast-time scale (100 fs). The possible occurrence of PT processes is not considered in our QD simulations, since their proper description would require more complex shapes of the potentials than those predicted by our LVC models. We used TD-M052X/PCM (water) to provide the reference data for the diabatization, and included 12 diabatic electronic states, namely the two lowest bright states on each base (G-L_a and G-L_b, and C*1 and C*2),^27,66–69 as well as the two intra and two interstrand G → C CT states. In order to reduce the computational burden of the QD calculations, we replaced the sugar ring on each of the bases with a methyl group, considered each of the bases to have C_s symmetry, and included only the in-plane vibrational modes. This 124 mode LVC model was fully parameterized with computations at the QM minimum structures of 2GC and 2CG, whilst for each of the MD snapshots, only the zero order terms (i.e. diabatic excited state energies and excitonic/CT-like couplings) of the LVC model were updated. These zero order terms are those expected to change most significantly from snapshot to snapshot, and hence will rule the dynamics. This approximation also allows a dramatic computational speedup; see ref. 70 and the ESI† for further details. The QD propagations using these FrD-LVC models were performed using the Multilayer Multiconfiguration Time-Dependent Hartree (ML-MCTDH) method,^71–73 and the Quantics package.^74,75

MD simulations

A 2 microsecond (µs) MD simulation was carried out for the 10-mer sequence d(GC)₅ using the CUDA version of AMBER18 (ref. 76–79) and the OL15 DNA force field.^80,81 The starting model was derived by using the w3DNA 2.0 (web interface) building routine for B-DNA fiber models.⁸² The structure was immersed in a truncated octahedral box with a 10 Å solvation shell around the model. Sodium ions were added to achieve electroneutrality. Some water molecules were then replaced with Na⁺ and Cl⁻ ions to set an ionic strength of approximately 150 mM excess salt (equivalent to 13 Na⁺ and 13 Cl⁻ ions). The simulation was performed with periodic boundary conditions and the SPC/E water model.⁸³ The equilibration step was carried out following previously used protocol.⁴⁸ Additional details on the MD analysis are reported in the ESI (Scheme S1 and Table S1).†

After initial equilibration, for the analysis we considered the starting structure of the production run (t = 0 ns) as well as structures extracted every 400 ns along the trajectory, i.e., a total of six structures. In each snapshot, we analyzed three consecutive CG and GC steps (i.e. 18 CG and 18 GC structures in total) by excluding three nucleotides at the terminal strand positions (see Scheme S1 in the ESI†) which show rather high fluctuations along the simulation. The stacking interactions between nucleobases were analyzed in terms of the overlap area of planar projections of the ring and exocyclic atoms in consecutive bases. In addition, the interbase distance was calculated as the distance between the centers of mass of ring atoms of consecutive bases along each strand.

Time resolved spectra

Transient absorption spectra were acquired at room temperature for d(GC)₉ and cCG/CG miniduplex after exciting the duplexes with 265-nm laser pulses in buffered D₂O solution,^17,19,20 while their global analysis was performed using the Glotaran software package.^84,85 A detailed description of the experimental set up and procedure can be found in the original works.^17,19,20

Data availability

The data that support the findings of this study are available in the ESI† of this article and are available on request from the corresponding authors.

Author contributions

Conceptualization, R. I. and L. M. F.; methodology, J. A. G, F. S., L. M. F. and R. I.; formal analysis, all authors; investigation, L. M. F., L. E., J. A. G., M. Y. J, and R. I.; software, F. S. and J. A. G.; writing – original draft, L. M. F., B. K., and R. I.; writing – review and editing, all authors; supervision, F. S., J. A. G., B. K., and R. I.; funding acquisition F. S., B. K. and R. I. All authors have read and agreed to the published version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

RI, LE and FS thank the CNR program “Progetti di Ricerca @cnr'', project UCATG4. RI, LE also thank NUTRAGE funded by FOE-2021 DBA.AD005.225, and RI CN3, National Center for GeneTherapy and Drugs based on RNA technology, funded by the European Union-NextGenerationEU-PNRR for financial support.

References

1. J. S. Taylor, Unraveling the Molecular Pathway from Sunlight to Skin Cancer, Acc. Chem. Res., 1994, 27, 76–82.
2. J. Cadet and P. Vigny, The Photochemistry of Nucleic Acids, In Bioorganic Photochemistry, ed. H. Morrison, Wiley, New York, 1990, vol. 1, pp. 1–272.
3. R. Improta and T. Douki, DNA Photodamage, The Royal Society of Chemistry. 2022.
4. C. T. Middleton, K. de La Harpe, C. Su, Y. K. Law, C. E. Crespo-Hernández and B. Kohler, DNA Excited-State Dynamics: From Single Bases to the Double Helix, Annu. Rev. Phys. Chem., 2009, 60, 217–239.
5. W. J. Schreier, P. Gilch and W. Zinth, Early Events of DNA Photodamage, Annu. Rev. Phys. Chem., 2015, 66, 497–519.
6. T. Gustavsson and D. Markovitsi, Fundamentals of the Intrinsic DNA Fluorescence, Acc. Chem. Res., 2021, 54, 1226–1235.
7. R. Improta, F. Santoro and L. Blancafort, Quantum Mechanical Studies on the Photophysics and the Photochemistry of Nucleic Acids and Nucleobases, Chem. Rev., 2016, 116, 3540–3593.
8. M. Barbatti, A. C. Borin and S. Ullrich, in Photoinduced Phenomena in Nucleic Acids I: Nucleobases in the Gas Phase and in Solvents, ed. M. Barbatti, C. A. Borin and S. Ullrich, Springer International Publishing, Cham, 2015,  DOI:10.1007/128_2014_569, pp. 1–32.
9. L. Martínez Fernández, F. Santoro and R. Improta, Nucleic Acids as a Playground for the Computational Study of the Photophysics and Photochemistry of Multichromophore Assemblies, Acc. Chem. Res., 2022, 55, 2077–2087.
10. S. Matsika, Electronic Structure Methods for the Description of Nonadiabatic Effects and Conical Intersections, Chem. Rev., 2021, 121, 9407–9449.
11. S. Mai, P. Marquetand and L. González, in Photoinduced Phenomena in Nucleic Acids I: Nucleobases in the Gas Phase and in Solvents, ed. M. Barbatti, A. C. Borin and S. Ullrich, Springer International Publishing, Cham, 2015, pp. 99–153.
12. P. Marquetand, J. J. Nogueira, S. Mai, F. Plasser and L. González, Challenges in Simulating Light-Induced Processes in DNA, Molecules, 2016, 22, 49.
13. F. Segatta, L. Cupellini, M. Garavelli and B. Mennucci, Quantum Chemical Modeling of the Photoinduced Activity of Multichromophoric Biosystems, Chem. Rev., 2019, 119, 9361–9380.
14. G. W. Doorley, M. Wojdyla, G. W. Watson, M. Towrie, A. W. Parker, J. M. Kelly and S. J. Quinn, Tracking DNA excited states by picosecond-time-resolved infrared spectroscopy: signature band for a charge-transfer excited state in stacked adenine-thymine systems, J. Phys. Chem. Lett., 2013, 4, 2739–2744.
15. B. M. Pilles, D. B. Bucher, L. Z. Liu, P. Gilch, W. Zinth and W. J. Schreier, Identification of charge separated states in thymine single strands, Chem. Commun., 2014, 50, 15623–15626.
16. L. Martinez-Fernandez, Y. Zhang, K. de La Harpe, A. A. Beckstead, B. Kohler and R. Improta, Photoinduced long-lived charge transfer excited states in AT-DNA strands, Phys. Chem. Chem. Phys., 2016, 18, 21241–21245.
17. Y. Zhang, K. de La Harpe, A. A. Beckstead, R. Improta and B. Kohler, UV-Induced Proton Transfer between DNA Strands, J. Am. Chem. Soc., 2015, 137, 7059–7062.
18. P. M. Keane, M. Wojdyla, G. W. Doorley, J. M. Kelly, A. W. Parker, I. P. Clark, G. M. Greetham, M. Towrie, L. M. Magno and S. J. Quinn, Long-lived excited states in i-motif DNA studied by picosecond time-resolved IR spectroscopy, Chem. Commun., 2014, 50, 2990–2992.
19. Y. Zhang, X.-B. Li, A. M. Fleming, J. Dood, A. A. Beckstead, A. M. Orendt, C. J. Burrows and B. Kohler, UV-Induced Proton-Coupled Electron Transfer in Cyclic DNA Miniduplexes, J. Am. Chem. Soc., 2016, 138, 7395–7401.
20. Y. Zhang, K. de La Harpe, F. R. Kohl and B. Kohler, Isotopic substitution affects excited state branching in a DNA duplex in aqueous solution, Chem. Commun., 2019, 55, 4174–4177.
21. Y. Zhang, K. de La Harpe, A. A. Beckstead, L. Martínez-Fernández, R. Improta and B. Kohler, Excited-State Dynamics of DNA Duplexes with Different H-Bonding Motifs, J. Phys. Chem. Lett., 2016, 7, 950–954.
22. I. Vayá, F.-A. Miannay, T. Gustavsson and D. Markovitsi, High-Energy Long-Lived Excited States in DNA Double Strands, ChemPhysChem, 2010, 11, 987–989.
23. K. Röttger, H. J. B. Marroux, M. P. Grubb, P. M. Coulter, H. Böhnke, A. S. Henderson, M. C. Galan, F. Temps, A. J. Orr-Ewing and G. M. Roberts, Ultraviolet Absorption Induces Hydrogen-Atom Transfer in G·C Watson–Crick DNA Base Pairs in Solution, Angew. Chem., Int. Ed., 2015, 54, 14719–14722.
24. T. Schultz, E. Samoylova, W. Radloff, I. V. Hertel, A. L. Sobolewski and W. Domcke, Efficient deactivation of a model base pair via excited-state hydrogen transfer, Science, 2004, 306, 1765–1768.
25. F.-A. Miannay, T. Gustavsson, A. Banyasz and D. Markovitsi, Excited-State Dynamics of dGMP Measured by Steady-State and Femtosecond Fluorescence Spectroscopy, J. Phys. Chem. A, 2010, 114, 3256–3263.
26. F.-A. Miannay, Á. Bányász, T. Gustavsson and D. Markovitsi, Ultrafast Excited-State Deactivation and Energy Transfer in Guanine−Cytosine DNA Double Helices, J. Am. Chem. Soc., 2007, 129, 14574–14575.
27. L. Martinez-Fernandez, A. J. Pepino, J. Segarra-Martí, J. Jovaisaite, I. Vayá, A. Nenov, D. Markovitsi, T. Gustavsson, A. Banyasz, M. Garavelli and R. Improta, The Photophysics of Deoxycytidine and 5-methyl-deoxycytidine in Solution: a comprehensive picture by Quantum Mechanical Calculations and Femtosecond Fluorescence Spectroscopy, J. Am. Chem. Soc., 2017, 139, 7780–7791.
28. J. P. Hall, F. E. Poynton, P. M. Keane, S. P. Gurung, J. A. Brazier, D. J. Cardin, G. Winter, T. Gunnlaugsson, I. V. Sazanovich, M. Towrie, C. J. Cardin, J. M. Kelly and S. J. Quinn, Monitoring one-electron photo-oxidation of guanine in DNA crystals using ultrafast infrared spectroscopy, Nat. Chem., 2015, 7, 961–967.
29. D. B. Bucher, B. M. Pilles, T. Carell and W. Zinth, Charge separation and charge delocalization identified in long-living states of photoexcited DNA, Proc. Natl. Acad. Sci. U.S.A., 2014, 111, 4369–4374.
30. Y. Zhang, J. Dood, A. A. Beckstead, X. B. Li, K. V. Nguyen, C. J. Burrows, R. Improta and B. Kohler, Photoinduced Electron Transfer in DNA: Charge Shift Dynamics Between 8-Oxo-Guanine Anion and Adenine, J. Phys. Chem. B, 2015, 119, 7491–7502.
31. A. L. Sobolewski, W. Domcke and C. Hättig, Tautomeric selectivity of the excited-state lifetime of guanine/cytosine base pairs: The role of electron-driven proton-transfer processes, Proc. Natl. Acad. Sci. U.S.A., 2005, 102, 17903–17906.
32. V. Sauri, J. P. Gobbo, J. J. Serrano-Pérez, M. Lundberg, P. B. Coto, L. Serrano-Andrés, A. C. Borin, R. Lindh, M. Merchán and D. Roca-Sanjuán, Proton/Hydrogen Transfer Mechanisms in the Guanine–Cytosine Base Pair: Photostability and Tautomerism, J. Chem. Theory Comput., 2013, 9, 481–496.
33. L. Martinez-Fernandez and R. Improta, Photoactivated proton coupled electron transfer in DNA: insights from quantum mechanical calculations, Faraday Discuss., 2018, 207, 199–216.
34. G. Groenhof, L. V. Schäfer, M. Boggio-Pasqua, M. Goette, H. Grubmüller and M. A. Robb, Ultrafast Deactivation of an Excited Cytosine−Guanine Base Pair in DNA, J. Am. Chem. Soc., 2007, 129, 6812–6819.
35. N. K. Schwalb and F. Temps, Base sequence and higher-order structure induce the complex excited-state dynamics in DNA, Science, 2008, 322, 243–245.
36. D. B. Bucher, A. Schlueter, T. Carell and W. Zinth, Watson-Crick base pairing controls excited-state decay in natural DNA, Angew. Chem., Int. Ed., 2014, 53, 11366–11369.
37. D. Soler-Polo, J. I. Mendieta-Moreno, D. G. Trabada, J. Mendieta and J. Ortega, Proton Transfer in Guanine-Cytosine Base Pairs in B-DNA, J. Chem. Theory Comput., 2019, 15, 6984–6991.
38. A. Francés-Monerris, H. Gattuso, D. Roca-Sanjuán, I. Tuñón, M. Marazzi, E. Dumont and A. Monari, Dynamics of the excited-state hydrogen transfer in a (dG)·(dC) homopolymer: intrinsic photostability of DNA, Chem. Sci., 2018, 9, 7902–7911.
39. G. W. Doorley, D. A. McGovern, M. W. George, M. Towrie, A. W. Parker, J. M. Kelly and S. J. Quinn, Picosecond Transient Infrared Study of the Ultrafast Deactivation Processes of Electronically Excited B-DNA and Z-DNA Forms of [poly(dG-dC)]2, Angew. Chem., Int. Ed., 2009, 48, 123–127.
40. J. A. Green, M. Yaghoubi Jouybari, H. Asha, F. Santoro and R. Improta, Fragment Diabatization Linear Vibronic Coupling Model for Quantum Dynamics of Multichromophoric Systems: Population of the Charge-Transfer State in the Photoexcited Guanine–Cytosine Pair, J. Chem. Theory Comput., 2021, 17, 4660–4674.
41. H. Köppel, W. Domcke and L. S. Cederbaum, in Advances in Chemical Physics, 1984, pp. 59–246,  DOI:10.1002/9780470142813.ch2.
42. R. E. Dickerson, Definitions and nomenclature of nucleic acid structure components, Nucleic Acids Res., 1989, 17, 1797–1803.
43. R. Binder and I. Burghardt, First-principles quantum simulations of exciton diffusion on a minimal oligothiophene chain at finite temperature, Faraday Discuss., 2020, 221, 406–427.
44. Y. Takahashi and H. Umezawa, THERMO FIELD DYNAMICS, Int. J. Mod. Phys. B, 1996, 10, 1755–1805.
45. M. K. Kuimova, A. J. Cowan, P. Matousek, A. W. Parker, X. Z. Sun, M. Towrie and M. W. George, Monitoring the direct and indirect damage of DNA bases and polynucleotides by using time-resolved infrared spectroscopy, Proc. Natl. Acad. Sci. U.S.A., 2006, 103, 2150–2153.
46. A. W. Parker, C. Y. Lin, M. W. George, M. Towrie and M. K. Kuimova, Infrared Characterization of the Guanine Radical Cation: Finger Printing DNA Damage, J. Phys. Chem. B, 2010, 114, 3660–3667.
47. Q. Dai, P. J. Sanstead, C. S. Peng, D. Han, C. He and A. Tokmakoff, Weakened N3 Hydrogen Bonding by 5-Formylcytosine and 5-Carboxylcytosine Reduces Their Base-Pairing Stability, ACS Chem. Biol., 2016, 11, 470–477.
48. H. Asha, J. A. Green, L. Esposito, L. Martinez-Fernandez, F. Santoro and R. Improta, Effect of the Thermal Fluctuations of the Photophysics of GC and CG DNA Steps: A Computational Dynamical Study, J. Phys. Chem. B, 2022, 126, 10608–10621.
49. T. Takaya, C. Su, K. de La Harpe, C. E. Crespo-Hernández and B. Kohler, UV excitation of single DNA and RNA strands produces high yields of exciplex states between two stacked bases, Proc. Natl. Acad. Sci. U.S.A., 2008, 105, 10285–10290.
50. Y. Zhang, R. Improta and B. Kohler, Mode-specific vibrational relaxation of photoexcited guanosine 5’-monophosphate and its acid form: A femtosecond broadband mid-IR transient absorption and theoretical study, Phys. Chem. Chem. Phys., 2014, 16, 1487–1499.
51. M. K. Kuimova, J. Dyer, M. W. George, D. C. Grills, J. M. Kelly, P. Matousek, A. W. Parker, X. Z. Sun, M. Towrie and A. M. Whelan, Monitoring the effect of ultrafast deactivation of the electronic excited states of DNA bases and polynucleotides following 267 nm laser excitation using picosecond time-resolved infrared spectroscopy, Chem. Commun., 2005, 1182–1184,  10.1039/B414450c.
52. U. Heinemann, C. Alings and M. Bansal, Double helix conformation, groove dimensions and ligand binding potential of a G/C stretch in B-DNA, EMBO J., 1992, 11, 1931–1939.
53. Y. Zhao and D. G. Truhlar, Density Functionals With Broad Applicability in Chemistry, Acc. Chem. Res., 2008, 41, 157–167.
54. Y. Zhao, N. E. Schultz and D. G. Truhlar, Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions, J. Chem. Theory Comput., 2006, 2, 364–382.
55. C. Zuluaga, V. A. Spata and S. Matsika, Benchmarking Quantum Mechanical Methods for the Description of Charge-Transfer States in π-Stacked Nucleobases, J. Chem. Theory Comput., 2021, 17, 376–387.
56. J. A. Green and R. Improta, Vibrations of the guanine–cytosine pair in chloroform: an anharmonic computational study, Phys. Chem. Chem. Phys., 2020, 22, 5509–5522.
57. S. Miertuš, E. Scrocco and J. Tomasi, Electrostatic interaction of a solute with a continuum. A direct utilizaion of AB initio molecular potentials for the prevision of solvent effects, Chem. Phys., 1981, 55, 117–129.
58. J. Tomasi, B. Mennucci and R. Cammi, Quantum Mechanical Continuum Solvation Models, Chem. Rev., 2005, 105, 2999–3093.
59. K. K. Irikura, R. D. Johnson and R. N. Kacker, Uncertainties in Scaling Factors for ab Initio Vibrational Frequencies, J. Phys. Chem. A, 2005, 109, 8430–8437.
60. D. O. Kashinski, G. M. Chase, R. G. Nelson, O. E. Di Nallo, A. N. Scales, D. L. VanderLey and E. F. C. Byrd, Harmonic Vibrational Frequencies: Approximate Global Scaling Factors for TPSS, M06, and M11 Functional Families Using Several Common Basis Sets, J. Phys. Chem. A, 2017, 121, 2265–2273.
61. X. Wang, L. Martínez-Fernández, Y. Zhang, P. Wu, B. Kohler, R. Improta and J. Chen, Ultrafast Formation of a Delocalized Triplet-Excited State in an Epigenetically Modified DNA Duplex under Direct UV Excitation, J. Am. Chem. Soc., 2024, 146, 1839–1848.
62. L. Martínez-Fernández, F. R. Kohl, Y. Zhang, S. Ghosh, A. J. Saks and B. Kohler, Triplet Excimer Formation in a DNA Duplex with Silver Ion-Mediated Base Pairs, J. Am. Chem. Soc., 2024, 146, 1914–1925.
63. T. Lu and F. Chen, Multiwfn: A Multifunctional Wavefunction Analyzer, J. Comput. Chem., 2012, 33, 580–592.
64. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox., Gaussian 16, Wallingford, CT. 2016.
65. F. Santoro and J. A. Green, Overdia 1.0, a Fortran 90 code for parametrization of model Hamiltonians based on a maximum-overlap diabatisation, available free of charge at http://www.iccom.cnr.it/overdia-en.
66. N. Ismail, L. Blancafort, M. Olivucci, B. Kohler and M. A. Robb, Ultrafast Decay of Electronically Excited Singlet Cytosine via a π,π* to nO,π* State Switch, J. Am. Chem. Soc., 2002, 124, 6818–6819.
67. V. Karunakaran, K. Kleinermanns, R. Improta and S. A. Kovalenko, Photoinduced Dynamics of Guanosine Monophosphate in Water from Broad-Band Transient Absorption Spectroscopy and Quantum-Chemical Calculations, J. Am. Chem. Soc., 2009, 131, 5839–5850.
68. J. Ortín-Fernández, J. González-Vázquez, L. Martínez-Fernández and I. Corral, Molecular Identification of the Transient Species Mediating the Deactivation Dynamics of Solvated Guanosine and Deazaguanosine, Molecules, 2022, 27, 989.
69. L. Blancafort, M. J. Bearpark and M. A. Robb, in Radiation Induced Molecular Phenomena in Nucleic Acids: A Comprehensive Theoretical and Experimental Analysis, ed. M. K. Shukla and J. Leszczynski, Springer Netherlands, Dordrecht, 2008, pp. 473–492,  DOI:10.1007/978-1-4020-8184-2_17.
70. A. Segalina, D. Aranda, J. A. Green, V. Cristino, S. Caramori, G. Prampolini, M. Pastore and F. Santoro, How the Interplay among Conformational Disorder, Solvation, Local, and Charge-Transfer Excitations Affects the Absorption Spectrum and Photoinduced Dynamics of Perylene Diimide Dimers: A Molecular Dynamics/Quantum Vibronic Approach, J. Chem. Theory Comput., 2022, 18, 3718–3736.
71. H. Wang, Multilayer Multiconfiguration Time-Dependent Hartree Theory, J. Phys. Chem. A, 2015, 119, 7951–7965.
72. M. H. Beck, A. Jäckle, G. A. Worth and H. D. Meyer, The multiconfiguration time-dependent Hartree (MCTDH) method: a highly efficient algorithm for propagating wavepackets, Phys. Rep., 2000, 324, 1–105.
73. H. Wang and M. Thoss, Multilayer formulation of the multiconfiguration time-dependent Hartree theory, J. Chem. Phys., 2003, 119, 1289–1299.
74. G. A. Worth, Quantics: A general purpose package for Quantum molecular dynamics simulations, Comput. Phys. Commun., 2020, 248, 107040.
75. G. A. Worth, K. Giri, G. W. Richings, I. Burghardt, M. H. Beck, A. Jäckle, and H.-D. Meyer, The QUANTICS Package, Version 1.1, University of Birmingham, Birmingham, U.K, 2015.
76. R. Salomon-Ferrer, A. W. Götz, D. Poole, S. Le Grand and R. C. Walker, Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 2. Explicit Solvent Particle Mesh Ewald, J. Chem. Theory Comput., 2013, 9, 3878–3888.
77. A. W. Götz, M. J. Williamson, D. Xu, D. Poole, S. Le Grand and R. C. Walker, Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 1. Generalized Born, J. Chem. Theory Comput., 2012, 8, 1542–1555.
78. S. Le Grand, A. W. Götz and R. C. Walker, SPFP: Speed without compromise—A mixed precision model for GPU accelerated molecular dynamics simulations, Comput. Phys. Commun., 2013, 184, 374–380.
79. D. A. Case, T. E. Cheatham Iii, T. Darden, H. Gohlke, R. Luo, K. M. Merz Jr, A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, The Amber biomolecular simulation programs, J. Comput. Chem., 2005, 26, 1668–1688.
80. M. Zgarbová, J. Šponer, M. Otyepka, T. E. Cheatham III, R. Galindo-Murillo and P. Jurečka, Refinement of the Sugar–Phosphate Backbone Torsion Beta for AMBER Force Fields Improves the Description of Z- and B-DNA, J. Chem. Theory Comput., 2015, 11, 5723–5736.
81. R. Galindo-Murillo, J. C. Robertson, M. Zgarbová, J. Šponer, M. Otyepka, P. Jurečka and T. E. Cheatham III, Assessing the Current State of Amber Force Field Modifications for DNA, J. Chem. Theory Comput., 2016, 12, 4114–4127.
82. S. Li, W. K. Olson and X.-J. Lu, Web 3DNA 2.0 for the analysis, visualization, and modeling of 3D nucleic acid structures, Nucleic Acids Res., 2019, 47, W26–W34.
83. H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, The missing term in effective pair potentials, J. Phys. Chem., 1987, 91, 6269–6271.
84. I. H. M. van Stokkum, D. S. Larsen and R. van Grondelle, Global and Target Analysis of Time-Resolved Spectra, Biochim. Biophys. Acta, Bioenerg., 2004, 1657, 82–104.
85. J. J. Snellenburg, S. P. Laptenok, R. Seger, K. M. Mullen and I. H. M. van Stokkum, Glotaran: A Java-Based Graphical User Interface for the R Package TIMP, J. Stat. Software, 2012, 49, 1–22.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc00910j

---