Open Access Article
Open Access ArticleA physics-aware neural network for protein–ligand interactions with quantum chemical accuracy†
Zachary L.
Glick
 a,
Derek P.
Metcalf
a,
Derek P.
Metcalf
 a,
Caroline S.
Glick
a,
Caroline S.
Glick
 a,
Steven A.
Spronk
a,
Steven A.
Spronk
 b,
Alexios
Koutsoukas
b,
Daniel L.
Cheney
b,
Alexios
Koutsoukas
b,
Daniel L.
Cheney
 b and
C. David
Sherrill
b and
C. David
Sherrill
 *a
*a
aSchool of Chemistry and Biochemistry, School of Computational Science and Engineering, Georgia Institute of Technology, Atlanta, Georgia 30332-0400, USA. E-mail: sherrill@gatech.edu
bMolecular Structure and Design, Bristol Myers Squibb Company, P.O. Box 5400, Princeton, New Jersey 08543, USA
First published on 24th July 2024
Abstract
Quantifying intermolecular interactions with quantum chemistry (QC) is useful for many chemical problems, including understanding the nature of protein–ligand interactions. Unfortunately, QC computations on protein–ligand systems are too computationally expensive for most use cases. The flourishing field of machine-learned (ML) potentials is a promising solution, but it is limited by an inability to easily capture long range, non-local interactions. In this work we develop an atomic-pairwise neural network (AP-Net) specialized for modeling intermolecular interactions. This model benefits from a number of physical constraints, including a two-component equivariant message passing neural network architecture that predicts interaction energies via an intermediate prediction of monomer electron densities. The AP-Net model is trained on a comprehensive dataset composed of paired ligand and protein fragments. This model accurately predicts QC-quality interaction energies of protein–ligand systems at a computational cost reduced by orders of magnitude. Applications of the AP-Net model to molecular crystal structure prediction are explored, as well as limitations in modeling highly polarizable systems.
1 Introduction
Non-covalent interactions (NCIs) play a key role in the chemical sciences. Although they are weaker than covalent bonds, the presence (or absence) of NCIs can have profound effects on chemical and biomolecular systems. For example, NCIs drive DNA intercalation—the insertion of a molecule between consecutive DNA base pairs—which is the mechanism of action in anti-cancer drugs such as doxorubicin.1,2 Not only can an understanding of NCIs provide mechanistic insights into intercalation and other small molecule binding modes, careful consideration of NCIs allows one to control the selectivity of reaction catalysts,3 enhance electrochemical reaction kinetics,4 or optimize the properties of nanostructures.5NCIs play a particularly important role in small molecule drug design. The efficacy of a drug depends in part on the presence of strong interactions with the target protein. Often, preliminary drug design efforts produce a promising but sub-optimal “lead” compound. This lead compound is then iteratively revised in an attempt to enhance desired properties. Maximizing favorable intermolecular contacts is a critical aspect of the lead optimization process, and can be aided by in silico models of NCIs.
The strength of a protein–ligand interaction can be rigorously quantified by using the tools of quantum chemistry to compute an interaction energy. Quantum chemistry methods, which seek to solve the many-body Schrödinger equation, are subject to a well-established trade-off between computational cost and accuracy. Highly accurate interaction energies can be obtained from wavefunction-based methods such as coupled cluster (CC) theory, but such calculations are often too expensive for all but the smallest systems. Less expensive methods like density functional theory (DFT) yield slightly less robust interaction energies. Simple, transferable force fields like GAFF are orders of magnitude faster than any quantum chemistry method, but force field interaction energies are only semi-quantitatively accurate.
One quantum chemistry method of particular interest for studying protein–ligand interactions is symmetry-adapted perturbation theory (SAPT), which yields not only an interaction energy, but also its physically meaningful components: electrostatics, exchange-repulsion, induction/polarization, and London dispersion.6–8 These components provide additional insight to help understand non-covalent interactions.9 The fragment-based partitioning of SAPT10 was used to understand substituent effects in protein–ligand interactions in factor Xa inhibitors.11 However, models of the protein including only nearby residues (∼200 atoms) still required many hours of CPU time for the SAPT computations.
Recently, advances in machine learning (ML) have led to the re-evaluation of this classic cost-accuracy trade-off. Models like neural networks (NNs) are capable of expressing arbitrarily complicated non-linear functions such as molecular potential energy surfaces.12–16 Large datasets of quantum chemical computations17–20 make it possible to parameterize general atomistic NN potentials to quantum chemical accuracy,21–23 and these potentials can be evaluated at near force field computational cost. NN potentials can be used to improve the accuracy of costly alchemical free energy predictions24 or to perform reactive molecular dynamics simulations.25
The emergence of NN potentials has also benefited from a number of architectural developments. The “message passing” NN (MPNN) framework is tailored to the graph-like structure of molecular geometries.26 Directional MPNNs additionally account for the relative orientation between neighboring atoms in a molecule. The most data-efficient architectures achieve this by employing locally equivariant representations of atoms in molecules.27–33 In these equivariant models, atomic environments are represented as tensorial quantities which rotate with the local coordinate frame.
The locality of atomic environments used in NN potentials allows these models to easily describe local interactions, which include distortions of bonds, angles, and dihedrals, as well as short-range non-covalent interactions. Unfortunately, a consequence of this locality is that NN potentials are either indirectly or explicitly unable to model the long-range interactions that are essential to protein–ligand interactions.34 The lack of these long-range effects has been demonstrated to affect the quality of simulated properties of bulk water and small peptides,35 and many ML methods have been developed to capture these long-range interactions.36–38 In a recent work, we proposed an atomic-pairwise NN framework for modeling NCIs, which we called AP-Net.34 Extending this basic proof-of-concept, we now develop a robust, chemically accurate AP-Net model for quantifying arbitrary protein–ligand interactions. This is accomplished by constraining the AP-Net architecture to respect the known physics of intermolecular interactions.
2 Results
2.1 A physics-aware intermolecular architecture
In this work, we develop a physics-aware neural network architecture specialized for modeling intermolecular interactions. This architecture adheres to four physical principles:1. Intermolecular interactions are fundamentally a function of molecular properties, some of which, such as the electron density, can be partitioned into atomic properties.
2. For the most part, intermolecular interactions are atomic-pairwise additive.
3. Intermolecular interactions are decomposable into different types of interactions (electrostatics, exchange-repulsion, induction/polarization, and dispersion).
4. In the dissociative limit, intermolecular interactions obey simple functional forms of molecular and atomic properties and smoothly decay to zero.
In reference to the second principle, this physics-aware architecture is designated AP-Net, short for atomic-pairwise neural network. The AP-Net name was first used in a previous proof-of-concept study that differs significantly from the current work in applicability and complexity.34 The previous AP-Net architecture shares the general paradigm of predicting interaction energies in an atomic-pairwise framework, but the previous model was limited by simple, ad hoc atomic feature vectors whereas the model described in this work featurizes atom pairs with an equivariant MPNN (Section 2.1.2). The current AP-Net model is additionally differentiated by the inclusion of an electrostatic force field, a related atomic property module (Section 2.1.1), and a much larger, more diverse training set (Section 2.2).
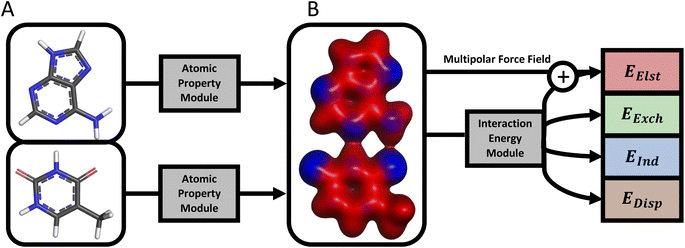
A schematic of the current AP-Net architecture is provided in Fig. 1. AP-Net enforces the four physical principles above via a pair of independently trained NNs, which are respectively referred to as the atomic property module and the interaction energy module. These two NNs are used to predict protein–ligand interaction energies through an intermediate prediction of the electron density of both molecules via an atom-centered multipole expansion. This physically motivated functional form yields accurate, generalizable interaction energy predictions for protein–ligand systems.
Most notably, instead of operating on only the dimer geometry, the interaction energy module operates on the output of the atomic property module—atom-centered multipoles through second order and hidden-state vectors encoding atomic environments—evaluated separately for each monomer. The output of the atomic property module is used by the interaction energy module in two ways. First, the learned representation of each atomic environment from the atomic property module is incorporated into the corresponding atomic environment in the interaction energy module. This shared representation allows the interaction energy module to indirectly utilize the monomer data used to train the atomic property module. Second, the predicted atomic multipoles of the atomic property module are used to evaluate a multipolar electrostatic energy. The interaction energy module is then trained to predict the interaction energy as a correction on top of the multipolar electrostatic energy. Because the multipolar electrostatic energy captures the leading long-range behavior of intermolecular interactions, the interaction energy module is effectively limited to predicting a much more local, medium- and short-range quantity.
This strategy of combining two different methods is similar to the correction-based concept of Δ-learning, in which one reformulates a regression task as a small predicted correction on top of a computationally affordable baseline result.41 However, unlike conventional Δ-learning use cases in quantum chemistry, the baseline model, multipole electrostatics via predicted multipoles, is as computationally affordable as the machine learning correction.
2.2 Systematically-generated protein–ligand interactions
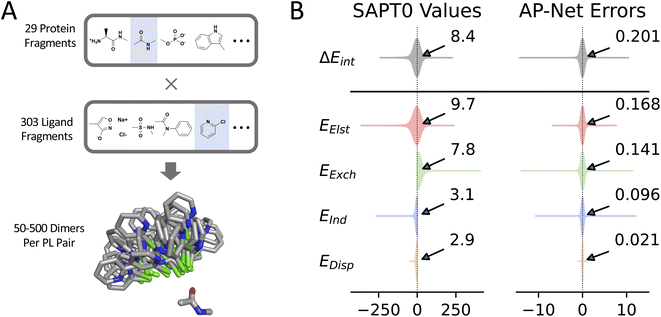
The Splinter dataset42 is a collection of approximately 1.7 million systematically generated protein–ligand fragment dimers and interaction energies computed using many-body SAPT based on a Hartree–Fock (HF) representation of monomers (i.e. SAPT0). These and all other SAPT computations carried out in this work are performed in an aug-cc-pV(D+d)Z basis set (abbreviated aDZ), which yields good error cancellation.43 The construction of this dataset is illustrated in Fig. 2A. The Splinter dimers are not only chemically diverse, they also were intentionally generated in variety of repulsive, optimized, and dissociated configurations. Consequently, the interaction energies associated with the Splinter dimers span a range of over 500 kcal mol−1.A large fraction of the Splinter dataset was used to train the interaction energy module of the AP-Net model. The performance of AP-Net on 150K held-out validation dimers, which were not used to fit the model, is shown in Fig. 2B. AP-Net predicts the SAPT interaction energies with a mean absolute error (MAE) of only 0.20 kcal mol−1 and a maximum error of less than 15 kcal mol−1. The interaction energy of over 97% of the validation dimers is predicted within 1 kcal mol−1, a metric commonly referred to as chemical accuracy.44 The individual SAPT components of the interaction energy are predicted with even greater accuracy than the total interaction energy. As observed in previous efforts to predict the SAPT decomposition with ML models, errors in electrostatics and exchange are largest, followed by induction, and then dispersion.34,45 Dispersion is predicted particularly accurately, with a MAE of only 0.02 kcal mol−1. It should be noted that the error in this prediction is much smaller than errors inherent in the SAPT0 approximation or even the choice of finite basis set.
2.3 Crystallographic protein–ligand interactions
The ultimate goal of the AP-Net intermolecular potential is to accurately predict interaction energies of realistic models of protein–ligand systems. Therefore, it would not be sufficient to only evaluate the model on dimers sampled from Splinter, which are procedurally generated and come from the same chemical space as the training data. For this reason, we developed a more diverse, realistic dataset of dimers, referred to as SAPT-PDB-13K. The 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 216 dimers in SAPT-PDB-13K consist of an entire ligand interacting with one or two capped amino acids. The protein and ligand geometries are taken from crystallographic Protein Data Bank (PDB) entries, making them meaningful and practical test cases. An illustrative dimer from the SAPT-PDB-13K dataset is shown in Fig. 3.
216 dimers in SAPT-PDB-13K consist of an entire ligand interacting with one or two capped amino acids. The protein and ligand geometries are taken from crystallographic Protein Data Bank (PDB) entries, making them meaningful and practical test cases. An illustrative dimer from the SAPT-PDB-13K dataset is shown in Fig. 3.
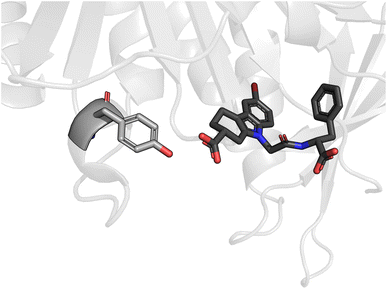 | ||
| Fig. 3 An example dimer from the SAPT-PDB-13K dataset. A small molecule inhibitor interacts with the nearest amino acid, a tyrosine, of an Escherichia coli sliding clamp protein. This dimer was extracted from PDB entry 4PNU. | ||
The diversity of the SAPT-PDB-13K dataset makes it a useful test of AP-Net's generalization ability. Compared to the Splinter dataset, SAPT-PDB-13K contains different, larger ligands that span more charge states. Regardless, Fig. 4 shows that AP-Net still accurately predicts the SAPT0 interaction energy decomposition with a MAE of 0.74 kcal mol−1. In many ways, the prediction errors on the SAPT-PDB-13K dimers resemble the prediction errors on the held-out Splinter dimers. One notable difference is in the prediction of the SAPT induction term. Interestingly, the induction MAE is larger relative to the other three SAPT components. It is also apparent from Fig. 4 that the predicted induction energies have a slight positive bias for dimers with large, negative induction energies. This observation is in line with the fact that induction is an inherently many-body phenomenon, in contrast to the atomic-pairwise additivity of AP-Net.46 The many-body nature of induction—which can be thought of as mutual polarization between three or more atoms combined with charge transfer—becomes apparent in a few SAPT-PDB-13K dimers that contain strongly interacting di- and tri-anions.
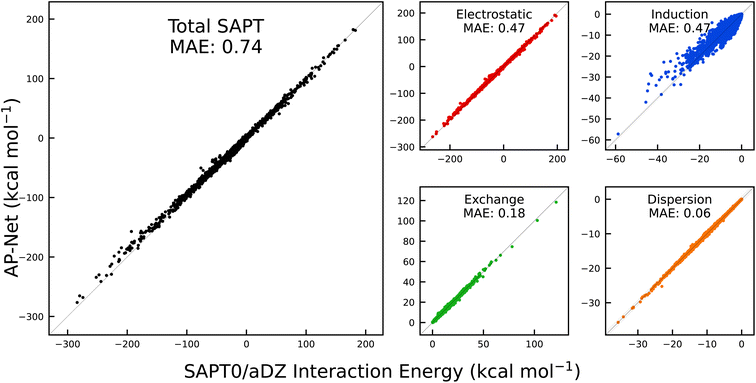 | ||
Fig. 4 Correlation between AP-Net predicted interaction energies and computed SAPT0/aDZ interaction energies on the 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 216 dimers in the SAPT-PDB-13K dataset. 216 dimers in the SAPT-PDB-13K dataset. | ||
2.4 Relative interaction energies
AP-Net's performance on the Splinter and SAPT-PDB-13K datasets demonstrates the model's ability to accurately predict interaction energies (ΔEint) of protein–ligand systems. A derived quantity of interest is the relative interaction energy (ΔΔEint), defined as the difference in interaction energies between two related dimers, such as those that differ by a change in a single functional group. An example experiment is illustrated in Fig. 5. Such single-point alchemical computations may be used to guide the drug design process.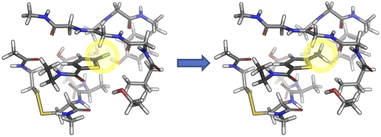 | ||
| Fig. 5 Example of an alchemical ΔΔEint experiment. The chlorine group of the P1 substructure of the Factor Xa inhibitor, BAY 59-7939, is mutated to a methyl. The structure is extracted from PDB entry 2W26. | ||
The results of nine ΔΔEint experiments are listed in Table 1, and a breakdown by SAPT component is included in the ESI.† In each experiment, the ΔΔEint of two related protein–ligand dimers is calculated using both SAPT and AP-Net. Each pair of dimers is constructed from an initial protein–ligand complex, taking a portion of the ligand and its surrounding protein environment.47 The second dimer of each pair is characterized by a change in a ligand functional group. In seven of the nine pairs, a chlorine is replaced with a methyl group, and in 2O7N, a cyano group is replaced with a bromine. The ligands of the 2Y5G/2Y5H matched pair differ by a heterocycle rotation rather than an atomic substitution. In all nine computational experiments, the sign of the AP-Net ΔΔEint matches the sign of the SAPT-computed ΔΔEint, meaning the AP-Net interaction energies are accurate enough to predict whether each functional group substitution stabilized or destabilized the protein–ligand interaction. SAPT0 computations on some of these complexes (∼200 atoms) required as much as 1.5 days or more, running on 12 cores, while the AP-Net computations ran in a few seconds each. This makes in silico ligand design experiments of this type (with quantum-mechanical accuracy) now feasible for routine and easy use.
2.5 Transfer learning to gold standard quantum chemistry
The SAPT0/aDZ level of theory used in the Splinter dataset has been extensively benchmarked and strikes a good balance between computational cost and accuracy.43 A more accurate level of theory is coupled cluster with singles, doubles, and perturbative triples [CCSD(T)]48 in the complete basis set (CBS) limit. CCSD(T)/CBS is often referred to as the “gold standard” in quantum chemistry because of its reliability. Ideally, the AP-Net model would be trained on CCSD(T)/CBS interaction energies for the Splinter dimers, but the steep scaling of this method makes obtaining many such high-quality interaction energies prohibitively expensive. An appealing solution from the field of machine learning is the process of transfer learning, in which one leverages data associated with one task (predicting SAPT0/aDZ interaction energies) to improve performance at some other similar, usually data-limited task (predicting CCSD(T)/CBS interaction energies).49 Generally, transfer learning is realized by initially training some NN model on the first large dataset, and then re-training the same model on the smaller, relevant dataset. This approach has been successfully used in the development of atomic potentials.50
scaling of this method makes obtaining many such high-quality interaction energies prohibitively expensive. An appealing solution from the field of machine learning is the process of transfer learning, in which one leverages data associated with one task (predicting SAPT0/aDZ interaction energies) to improve performance at some other similar, usually data-limited task (predicting CCSD(T)/CBS interaction energies).49 Generally, transfer learning is realized by initially training some NN model on the first large dataset, and then re-training the same model on the smaller, relevant dataset. This approach has been successfully used in the development of atomic potentials.50
A transfer learning experiment was performed to assess the practicality and data requirements of training a CCSD(T) quality AP-Net intermolecular potential. This experiment was performed with the DES370K dimer dataset.20 DES370K is similar to the Splinter dataset in that it contains many small molecule dimers. Unlike Splinter, DES370K contains interaction energies computed at the CCSD(T)/CBS level of theory. Two separate “AP-Net-CC” models were trained on the DES370K dataset to predict CCSD(T)/CBS interaction energies. These models are referred to as AP-Net-CC to differentiate them from the standard AP-Net model, which is fit to the SAPT decomposition. Because AP-Net is constructed to separately predict the four SAPT interaction energy components, all AP-Net-CC models are trained so that the sum of the four predicted components matches the CCSD(T)/CBS interaction energy. Therefore, any AP-Net-CC model lacks the interpretability of an AP-Net model trained to predict the SAPT decomposition. As a baseline, the first AP-Net-CC model was constructed with randomly initialized weights in the interaction energy module. The second “pre-trained” AP-Net-CC model was constructed with interaction energy module weights taken from the original AP-Net model. Both AP-Net-CC models used the same frozen atomic property module as the original AP-Net model.
The accuracy of the two AP-Net-CC models as a function of the amount of DES370K training data is shown in Table 2. The pre-trained AP-Net-CC model outperforms the baseline AP-Net-CC model, particularly in the low data regime. At 100 training data points, transfer learning results in a nearly four-fold error reduction (from 1.91 kcal mol−1 to 0.48 kcal mol−1). The accuracy of a pre-trained AP-Net-CC model with only 100 training data points is similar to that of a baseline AP-Net-CC trained on a few thousand data points. Transfer learning provides diminishing returns when more CCSD(T)/CBS data is available. The pre-trained model is nearly equivalent to the baseline model when 50K training points are used. These results demonstrate that transfer learning is an economical approach for leveraging the original AP-Net model, which was trained on the SAPT decomposition of over 1.5 M dimers, to predict interaction energies at more computationally expensive levels of theory. A minimal amount of expensive, high accuracy CCSD(T)/CBS data is required to fine-tune AP-Net from SAPT to this gold standard quantum chemistry method.
| Training dimers | Baseline | Pre-trained |
|---|---|---|
| 100 | 1.91 | 0.48 |
| 200 | 1.64 | 0.47 |
| 500 | 1.22 | 0.40 |
| 1000 | 0.80 | 0.37 |
| 2000 | 0.56 | 0.33 |
| 5000 | 0.35 | 0.29 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.26 | 0.23 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.20 | 0.18 |
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.14 | 0.12 |
2.6 Predicting interaction energy surfaces
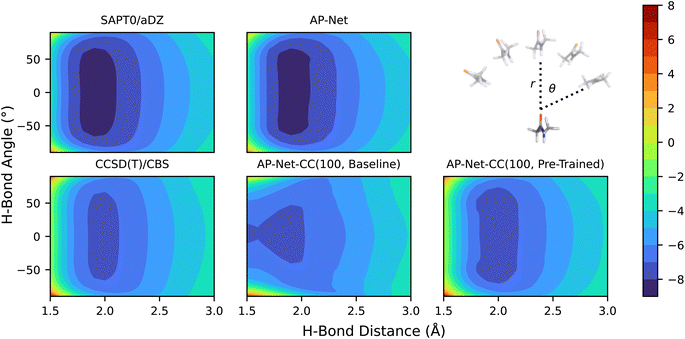
The transfer learning approach applies not just between different levels of quantum chemical theory, but also between different regions of chemical space. In particular, one might want to repurpose the AP-Net potential, which is parameterized to model protein–ligand interactions in general, into an interaction energy model specialized for a particular dimer, which may not even be a protein–ligand system. To explore the usefulness of such a model, we examined the performance of the previously described AP-Net-CC models on the interaction energy surface of the hydrogen-bonded N-methylacetamide (NMA) dimer. This dimer is a model system for peptide bonding. SAPT0/aDZ and CCSD(T)/CBS interaction energies were computed along a two-dimensional scan of the intermolecular hydrogen bond length and angle of this dimer. The intermolecular O⋯H bond length was varied from 1.5 Å to 3.0 Å in 0.1 Å increments and the intermolecular O⋯ HN bond angle from −90° to +90° in 1.5° increments. Fig. 6 shows these reference interaction energy surfaces compared to predictions of the AP-Net and two AP-Net-CC models. An additional one-dimensional visualization of this surface is available in the ESI.† The computed SAPT0/aDZ and CCSD(T)/CBS surfaces differ by a small amount: the SAPT0/aDZ surface is overall lower in energy than the gold standard reference method, with a minimum energy of −8.43 kcal mol−1 at a hydrogen bond length of 2.0 Å. The CCSD(T)/CBS surface has a minimum energy of −7.28 kcal mol−1 at 2.0 Å.The AP-Net predicted surface agrees with with the reference SAPT surface. This is expected given the quantity and diversity of data used to train the model. The baseline AP-Net-CC model trained on only 100 data points poorly predicts the CCSD(T)/CBS surface. This predicted interaction energy surface lacks both a repulsive wall and a reasonable minimum. However, using the same 100 points to repurpose the AP-Net model to the CCSD(T)/CBS theory with transfer learning results in an excellent prediction of the interaction energy surface. It's particularly notable that these 100 dimers are randomly selected from the DES370K dataset, and do not include NMA.
2.7 Ranking molecular crystal polymorphs
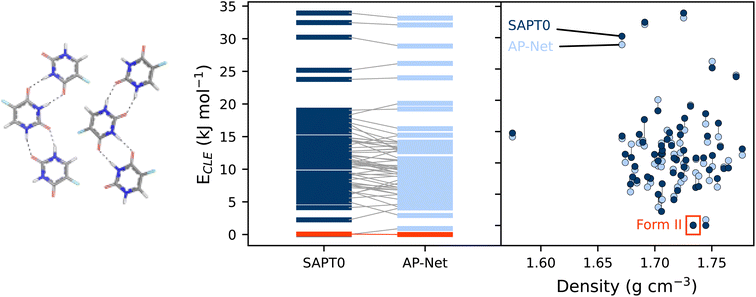
Intermolecular interactions largely govern the structure of molecular crystals and other clusters, making these systems a promising application of AP-Net outside of protein–ligand interactions. A vast majority of molecular crystals are polymorphic, meaning that they can exist in multiple stable crystalline forms, with potentially different physical properties like density, solubility, hygroscopicity, melting point, etc.51 In drug development, thoroughly determining all polymorphs of a drug candidate is a necessary procedure that is routinely guided by computation. A common crystal structure prediction (CSP) task is to screen and rank the most energetically stable putative polymorphs of a target molecule.52 Using the many body expansion (MBE), the energy of a crystal lattice can be recast as approximately a sum of many dimer interaction energies.53 This two-body contribution to the crystal lattice energy, hereafter referred to as the crystal lattice energy, can therefore be computed with any quantum chemistry method used for interaction energies or predicted with AP-Net. Note that polymorph ranking must also account for monomer strain, zero-point vibrational energy, and finite temperature and pressure.54We performed a preliminary experiment to assess AP-Net at ranking polymorphs of the 5-fluorouracil crystal. 61 low-lying 5-fluorouracil crystal structures, one of which is the experimentally observed form II, were taken from the work of Price.55 The CrystaLattE program53 was used to reduce each crystal structure into a set of unique dimers, from which the crystal lattice energies were computed at the SAPT0/aDZ level of theory and predicted with AP-Net. An intermolecular closest contact cutoff of 15 Å was used to generate the dimers. The computed and predicted crystal lattice energies are compared in Fig. 7. Importantly, AP-Net reproduces the approximate ranking of the polymorphs. Form II is correctly predicted to be among the lowest energy structures. The AP-Net ranking of form II happens to be slightly better than that of SAPT0/aDZ due to fortuitous errors in the interaction energies. The MAE of the AP-Net predicted crystal lattice energies relative to SAPT0 is 1.18 kJ mol−1, which is smaller than the disagreement between many quantum chemistry methods.56 Note that this result is in spite of the fact that AP-Net was trained specifically on protein–ligand data, not 5-fluorouracil homodimers or even ligand–ligand dimers.
The 61 AP-Net crystal lattice energy predictions required less than two CPU minutes, a nearly 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-fold savings over the corresponding SAPT0/aDZ cost of 980 CPU hours. Because the cost of quantum chemistry computations scales poorly with system size, AP-Net predicted crystal lattice energies of a larger drug-like molecule would result in even more pronounced savings relative to SAPT0/aDZ.
000-fold savings over the corresponding SAPT0/aDZ cost of 980 CPU hours. Because the cost of quantum chemistry computations scales poorly with system size, AP-Net predicted crystal lattice energies of a larger drug-like molecule would result in even more pronounced savings relative to SAPT0/aDZ.
3 Materials and methods
3.1 Implementation
The AP-Net model was implemented using version 2.3 of the TensorFlow Python package.57 The implementation and architectural details of the two constituent modules of the AP-Net model are described below.![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) ,
, ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) ,
, ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) ) respectively.
) respectively.
The initial environment of atom i in the MPNN is a simple mapping or embedding of the integer nuclear charge (Zi) to a vector (h0i) as was proposed in SchNet.22 The mappings are generated at uniform random for all Z corresponding to atomic elements of interest: H, C, N, O, F, Na, P, S, Cl, and Br. An edge between atoms i and j exists if the distance between the atoms is less than a cutoff distance, rc, which is set to 5.0 Å. The edge feature vector eij, is a simple encoding of the scalar distance |rij| using a set of Bessel functions as described in the work of Gasteiger, et al.:32
| eij = [eij,1,…,eij,N], | (1) |
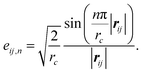 | (2) |
| mijt = (h0i, hit, h0j, hjt) × (1, eij). | (3) |
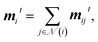 | (4) |
| hit+1 = Ut(mit), | (5) |
![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) i is determined from the hidden states through all T time steps and a set of dense, feed-forward neural networks:
i is determined from the hidden states through all T time steps and a set of dense, feed-forward neural networks: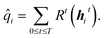 | (6) |
The displacement vector and displacement unit vector between atoms i and j are simply:
| rij = rj − ri, | (7) |
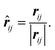 | (8) |
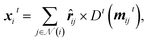 | (9) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij, which is then used to predict a rotationally equivariant dipole vector:
ij, which is then used to predict a rotationally equivariant dipole vector: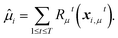 | (10) |
Lastly, the network architecture enforces conservation of total molecular charge, Q:
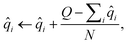 | (11) |
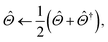 | (12) |
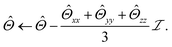 | (13) |
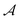 and
and 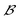 , respectively. The interaction energy components are predicted through learned, intermolecular, atomic-pairwise partition:
, respectively. The interaction energy components are predicted through learned, intermolecular, atomic-pairwise partition: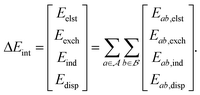 | (14) |
The interaction energy module uses an MPNN architecture similar to that of the atomic property module. Specifically, the message and update functions in this module are identical, but have different weights.
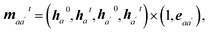 | (15) |
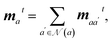 | (16) |
| hat+1 = Ut(mat). | (17) |
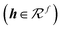 , a directional, rotationally equivariant hidden state vector
, a directional, rotationally equivariant hidden state vector 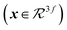 is also updated throughout the message passing:
is also updated throughout the message passing: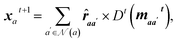 | (18) |
| ha = (h0a,…,haT), | (19) |
| xa=(x0a,…,xTa), | (20) |
pab = (![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) a, a, ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) b, ha, hb, b, ha, hb, ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ab·xa, ab·xa, ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ba·xb). ba·xb). | (21) |
| Eab,comp = |rab|−p[Rcomp(pab) + Rcomp(pba)], | (22) |
| Eab,elst ← Eab,elst + Eab,mtp. | (23) |
The predicted interaction energy, though defined as a sum of atom-pair interaction energies, is still a many-body quantity (where “body” refers to atoms). This is a consequence of using a MPNN to featurize each atom with its local atomic environment. In contrast, AP-Net produces a strictly two-body dimer interaction energy (where “body” refers to molecules).
3.2 Training data and procedure
The AP-Net model is trained in a two step procedure. All code used to train this model is present in the AP-Net GitHub repository.58 First, the atomic property module is trained on a dataset of molecular monomers and computed atomic multipoles. This was done with our previous dataset of 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 623 mostly drug-like fragments and corresponding atomic multipoles computed from HF/cc-pVDZ wavefunctions and partitioned with the minimal basis iterative stockholder (MBIS) scheme.59 Because the dataset lacks non-neutral monomers and monomers representing protein systems, it was further expanded to include monomers present in the Splinter dataset. 6550 additional computations were performed on randomly selected monomers from the Splinter dataset, totaling 53
623 mostly drug-like fragments and corresponding atomic multipoles computed from HF/cc-pVDZ wavefunctions and partitioned with the minimal basis iterative stockholder (MBIS) scheme.59 Because the dataset lacks non-neutral monomers and monomers representing protein systems, it was further expanded to include monomers present in the Splinter dataset. 6550 additional computations were performed on randomly selected monomers from the Splinter dataset, totaling 53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 173 monomers. The 53
173 monomers. The 53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 173 monomers were then randomly split into training and validation subsets of 47
173 monomers were then randomly split into training and validation subsets of 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 855 and 5318 monomers.
855 and 5318 monomers.
The atomic property module was constructed with three message passing iterations. Each dense feed-forward neural network in the module is composed of three hidden layers with 256, 128, and 64 neurons. The ReLU activation function is applied after each hidden layer, followed by an appropriately sized linear operation after the last hidden layer. The edge feature vectors are constructed from 8 Bessel functions and a radial cutoff of 5 Å. Training was performed to minimize the sum of the mean squared errors of the atomic charges, dipoles, and quadrupoles:
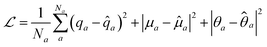 | (24) |
In the second step of training, the interaction energy module is trained on the Splinter dimer dataset to predict SAPT decomposed interaction energies. The interaction energy module requires atomic multipoles as an input, which were obtained from the atomic property module. The architecture of the MPNN in this module is identical to that of the atomic property module. Intermolecular atom pair readouts are performed with an 8 Å cutoff. This means that the interaction energy of atom pairs within this cutoff is predicted with a full neural network inference; the interaction energy of atom pairs outside of this cutoff is only accounted for by multipolar electrostatics. The asymptotic decay coefficient (p) was set to three. Random training and validation subsets of 1.5M and 150K dimers are taken from the 1.66M dimers in the Splinter dataset. The module is optimized to minimize the MSE of the individual SAPT components:
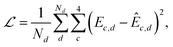 | (25) |
3.3 SAPT-PDB-13K dataset preparation
The SAPT-PDB-13K test set of 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 216 dimers was prepared to consist of diverse, drug-like molecules paired with mono- and dipeptides extracted from crystallographic structures deposited in the PDB. The following procedure was followed to ensure that ligands were structurally diverse and drug-like: ligand molecules were extracted from the PDBbind 2019 refined set of 4852 complexes,60,61 imported into Maestro 2021-3,62 assigned charges and bond orders with LigPrep63 and clustered using the spectral clustering utility with default settings, which provided 133 representative ligands. An additional 600 ligands were visually selected which further added structural diversity and represented the full range of elements compatible with the AP-Net model (H, C, N, O, F, Na, P, S, Cl, and Br). The corresponding 733 PDB protein/ligand complexes were subjected to refinement using the Schrodinger Protein Prep64 tool with default settings. Dimers consisting of ligands and proximal mono- and dipeptides were created, wherein the N- and C-termini were capped with acetyl and N–Me groups, respectively. Visual inspection led to removal of erroneous structures (e.g., presence of hypervalent carbons or otherwise non-physical geometries) and duplicates. SAPT0/aug-cc-pV(D+d)Z interaction energies of the 13
216 dimers was prepared to consist of diverse, drug-like molecules paired with mono- and dipeptides extracted from crystallographic structures deposited in the PDB. The following procedure was followed to ensure that ligands were structurally diverse and drug-like: ligand molecules were extracted from the PDBbind 2019 refined set of 4852 complexes,60,61 imported into Maestro 2021-3,62 assigned charges and bond orders with LigPrep63 and clustered using the spectral clustering utility with default settings, which provided 133 representative ligands. An additional 600 ligands were visually selected which further added structural diversity and represented the full range of elements compatible with the AP-Net model (H, C, N, O, F, Na, P, S, Cl, and Br). The corresponding 733 PDB protein/ligand complexes were subjected to refinement using the Schrodinger Protein Prep64 tool with default settings. Dimers consisting of ligands and proximal mono- and dipeptides were created, wherein the N- and C-termini were capped with acetyl and N–Me groups, respectively. Visual inspection led to removal of erroneous structures (e.g., presence of hypervalent carbons or otherwise non-physical geometries) and duplicates. SAPT0/aug-cc-pV(D+d)Z interaction energies of the 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 216 dimers were computed with Psi4 and made available in the ESI.†
216 dimers were computed with Psi4 and made available in the ESI.†
4 Discussion
The AP-Net potential developed in this work is a robust, physically-motivated NN intermolecular interaction model. In contrast to the many general purpose ML potentials which predict a total energy, the AP-Net potential predicts interaction energies. As a consequence of this specialization, AP-Net is constructed to adhere to known physical priors of intermolecular interactions, such as their approximate atomic pairwise nature and distance decay. An additional physical prior is captured by AP-Net's unique two-component architecture. Rather than simply predict atom-pair contributions to the interaction energy, AP-Net is constructed to predict monomer electron densities (in the form of atom-centered multipoles), evaluate a long-range electrostatic interaction energy from the predicted multipoles, and then predict atom-pair corrections to this evaluated energy.This two-component architecture confers a number of advantages to the AP-Net model. Because of the multipolar electrostatic force field, the AP-Net model produces electrostatic interaction energies that are asymptotically exact at the target level of theory using a relatively small amount of multipole training data. An analogous pure-NN model would need to be trained on an intractable number of dimer interaction energies to reach the same level of accuracy. This case of long-range electrostatics illustrates a weakness of NN models, which is that unnecessary flexibility can be a detriment to data efficiency. AP-Net's architecture effectively limits the flexibility of the functional form at long-range where the physics is known, allowing the modeling capacity to be applied to the more difficult short-range interactions. In addition to improving the data efficiency of the model, concentrating on short-range intermolecular interactions improves the computational efficiency of the AP-Net model. Neural network inferences, which are more expensive than force field evaluations, are only required for pairs of interaction atoms within a relatively short distance threshold (8 Å).
This physically-motivated AP-Net is applied to the challenging and consequential problem of modeling protein–ligand interaction energies. A useful AP-Net model is made possible by the Splinter dataset: a comprehensive and diverse collection of 1.66M protein–ligand dimers and SAPT0 interaction energies. The trained AP-Net accurately reproduces the SAPT decomposition of interaction energies well within chemical accuracy in the great majority of cases. More importantly, generalizability to larger models of protein–ligand dimers is observed, with good agreement between AP-Net and SAPT0 for substituent effects for ∼200-atom model systems where SAPT0 results can still be obtained. While the SAPT0 computations require many hours, the AP-Net results run in seconds. These findings suggest that the AP-Net model is an immediately practical tool for drug design research when quantum-level accuracy is desired for protein–ligand interaction energies, as was helpful in previous studies by our group on factor Xa inhibitors.11
This AP-Net model is not without shortcomings. One apparent deficiency is the underestimation of strong induction interactions, which occurs for a few select realistic protein–ligand dimers of the SAPT-PDB-13K dataset. These dimers represent an edge case where the non-local, many-body nature is poorly captured by the atomic-pairwise architecture of AP-Net. Efficiently modeling this non-pairwise additivity likely requires a model architecture with an appropriate inductive bias. In the same way that the current AP-Net model fuses classical long-range multipole electrostatics with a NN-predicted short-range correction, a future AP-Net model might benefit from incorporating a classical Thole-type induction model as is done in polarizable ab initio force fields like AMOEBA.65,66 This could be incorporated by training the atomic property module to predict atomic polarizability tensors. Another potential limitation arises from using a framework of interacting monomers to predict intermolecular interaction energies. This framework is largely incompatible with reactive chemistry, where the formation or dissolution of bonds changes the definition of monomers. Modeling reactive chemistry with an intermolecular potential can be done with the empirical valence bond (EVB) approach,25,67 but it might be easier to simply train a NN potential to the total system energy.
Because of the high accuracy of AP-Net relative to SAPT0, the development of future models will likely target training data computed at a higher level of quantum chemistry theory. Additional AP-Net model development, whether targeting new levels of theory or new types of dimers, can benefit from transfer learning from the current, general, protein–ligand model. This approach greatly reduces training data requirements. Surprisingly, the protein–ligand AP-Net model can be used for modeling ligand–ligand interaction energies accurately enough to rank polymorphs of the 5-fluorouracil crystal, an application far outside of the original intention of the AP-Net model. This result illustrates one of many potential future AP-Net use cases, and it also points towards the possibility of a universal interaction energy potential.
Data availability
The AP-Net model has been trained on the Splinter Dataset (ref. 42). The remaining data supporting this article have been included as part of the ESI.† The code for AP-Net can be found at https://github.com/zachglick/apnet with DOI https://doi.org/10.5281/zenodo.11493604. The version of the code employed for this study is version 0.1.1.Author contributions
Conceptualization: ZLG, DPM, SAS, AK, DLC, CDS. Methodology: ZLG, DPM, CSG, SAS, AK, CDS. Investigation: ZLG. Visualization: ZLG. Supervision: CDS and DLC. Writing – original draft: ZLG. Writing – review & editing: CDS, DLC, ZLG, DPM.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge financial support from the Department of Research and Early Development Information Technology, Bristol Myers Squibb, and the U. S. National Science Foundation through a grant to CDS (CHE-1955940) and an NSF Graduate Research Fellowship to CSG (DGE-2039655). Any opinion, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation. The authors thank S. Price for for providing computationally predicted 5-fluorouracil crystal structures. The authors also thank Andrea Bortolato for his assistance in constructing the SAPT-PDB-13K test set.Notes and references
- L. Strekowski and B. Wilson, Mutat. Res., 2007, 623, 3–13 CrossRef CAS PubMed.
- A. Bodley, L. F. Liu, M. Israel, R. Seshadri, Y. Koseki, F. C. Giuliani, S. Kirschenbaum, R. Silber and M. Potmesil, Cancer Res., 1989, 49, 5969–5978 CAS.
- H. J. Davis and R. J. Phipps, Chem. Sci., 2017, 8, 864–877 RSC.
- B. Huang, S. Muy, S. Feng, Y. Katayama, Y.-C. Lu, G. Chen and Y. Shao-Horn, Phys. Chem. Chem. Phys., 2018, 20, 15680–15686 RSC.
- B. Rybtchinski, ACS Nano, 2011, 5, 6791–6818 CrossRef CAS PubMed.
- B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930 CrossRef CAS.
- K. Szalewicz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 2, 254–272 Search PubMed.
- K. Patkowski, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1452 CAS.
- C. D. Sherrill, Acc. Chem. Res., 2012, 46, 1020–1028 CrossRef PubMed.
- R. M. Parrish, T. M. Parker and C. D. Sherrill, J. Chem. Theory Comput., 2014, 10, 4417–4431 CrossRef CAS PubMed.
- R. M. Parrish, D. F. Sitkoff, D. L. Cheney and C. D. Sherrill, Chem.–Eur. J., 2017, 23, 7887–7890 CrossRef CAS PubMed.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- C. M. Handley and P. L. A. Popelier, J. Phys. Chem. A, 2010, 114, 3371–3383 CrossRef CAS PubMed.
- J. Behler, Chem. Rev., 2021, 121, 10037–10072 CrossRef CAS PubMed.
- O. T. Unke, S. Chmiela, M. Gastegger, K. T. Schütt, H. E. Sauceda and K.-R. Müller, Nat. Commun., 2021, 12, 7273 CrossRef CAS PubMed.
- J. Wang, S. Olsson, C. Wehmeyer, A. Pérez, N. E. Charron, G. De Fabritiis, F. Noé and C. Clementi, ACS Cent. Sci., 2019, 5, 755–767 CrossRef CAS PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. v. Lilienfeld, Sci. Data, 2014, 1, 140022 CrossRef CAS PubMed.
- S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schütt and K.-R. Müller, Sci. Adv., 2017, 3, e1603015 CrossRef PubMed.
- J. S. Smith, R. Zubatyuk, B. Nebgen, N. Lubbers, K. Barros, A. E. Roitberg, O. Isayev and S. Tretiak, Sci. Data, 2020, 7, 134 CrossRef CAS PubMed.
- A. G. Donchev, A. G. Taube, E. Decolvenaere, C. Hargus, R. T. McGibbon, K.-H. Law, B. A. Gregersen, J.-L. Li, K. Palmo, K. Siva, M. Bergdorf, J. L. Klepeis and D. E. Shaw, Sci. Data, 2021, 8, 55 CrossRef CAS PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 RSC.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148, 241722 CrossRef PubMed.
- K. Yao, J. E. Herr, D. Toth, R. Mckintyre and J. Parkhill, Chem. Sci., 2018, 9, 2261–2269 RSC.
- D. A. Rufa, H. E. B. Macdonald, J. Fass, M. Wieder, P. B. Grinaway, A. E. Roitberg, O. Isayev and J. D. Chodera, bioRxiv, 2020 DOI:10.1101/2020.07.29.227959.
- J. P. Stoppelman and J. G. McDaniel, J. Chem. Phys., 2021, 155, 104112 CrossRef CAS PubMed.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, Proceedings of the 34th International Conference on Machine Learning, Sydney, NSW, Australia, 2017, pp. 1263–1272 Search PubMed.
- V. G. Satorras, E. Hoogeboom and M. Welling, Proceedings of the 38th International Conference on Machine Learning, 2021, pp. 9323–9332 Search PubMed.
- T. E. Smidt, Trends Chem., 2021, 3, 82–85 CrossRef CAS.
- M. Geiger and T. Smidt, arXiv, preprint, arXiv:2207.09453, 2022, DOI:10.48550/arxiv.2207.09453.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, Nat. Commun., 2022, 13, 2453 CrossRef CAS PubMed.
- I. Batatia, D. P. Kovacs, G. Simm, C. Ortner and G. Csanyi, Adv. Neural Inf. Process. Syst., 2022, 11423–11436 Search PubMed.
- J. Gasteiger, J. Groaa and S. Günnemann, International Conference on Learning Representations, 2020 Search PubMed.
- S. Takamoto, S. Izumi and J. Li, Comput. Mater. Sci., 2022, 207, 111280 CrossRef CAS.
- Z. L. Glick, D. P. Metcalf, A. Koutsoukas, S. A. Spronk, D. L. Cheney and C. D. Sherrill, J. Chem. Phys., 2020, 153, 044112 CrossRef CAS PubMed.
- D. Rosenberger, J. S. Smith and A. E. Garcia, J. Phys. Chem. B, 2021, 125, 3598–3612 CrossRef CAS PubMed.
- K. K. Huguenin-Dumittan, P. Loche, N. Haoran and M. Ceriotti, J. Phys. Chem. Lett., 2023, 14, 9612–9618 CrossRef CAS PubMed.
- M. Konrad and W. Wenzel, J. Chem. Theory Comput., 2021, 17, 4996–5006 CrossRef CAS PubMed.
- I.-B. Magdău, D. J. Arismendi-Arrieta, H. E. Smith, C. P. Grey, K. Hermansson and G. Csányi, npj Comput. Mater., 2023, 9, 146 CrossRef.
- Z. L. Glick, A. Koutsoukas, D. L. Cheney and C. D. Sherrill, J. Chem. Phys., 2021, 154, 224103 CrossRef CAS PubMed.
- D. P. Metcalf, A. Jiang, S. A. Spronk, D. L. Cheney and C. D. Sherrill, J. Chem. Inf. Model., 2021, 61, 115–122 CrossRef CAS PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. v. Lilienfeld, J. Chem. Theory Comput., 2015, 11, 2087–2096 CrossRef CAS PubMed.
- S. A. Spronk, Z. L. Glick, D. P. Metcalf, C. D. Sherrill and D. L. Cheney, Sci. Data, 2023, 10, 619 CrossRef CAS PubMed.
- T. M. Parker, L. A. Burns, R. M. Parrish, A. G. Ryno and C. D. Sherrill, J. Chem. Phys., 2014, 140, 094106 CrossRef PubMed.
- T. Helgaker, T. A. Ruden, P. Jørgensen, J. Olsen and W. Klopper, J. Phys. Org. Chem., 2004, 17, 913–933 CrossRef CAS.
- D. P. Metcalf, A. Koutsoukas, S. A. Spronk, B. L. Claus, D. A. Loughney, S. R. Johnson, D. L. Cheney and C. D. Sherrill, J. Chem. Phys., 2020, 152, 074103 CrossRef CAS PubMed.
- A. Stone, The Theory of Intermolecular Forces, Oxford University Press, 2013 Search PubMed.
- J. B. Schriber, D. R. Nascimento, A. Koutsoukas, S. A. Spronk, D. L. Cheney and C. D. Sherrill, J. Chem. Phys., 2021, 154, 184110 CrossRef CAS PubMed.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- K. Weiss, T. M. Khoshgoftaar and D. Wang, J. Big Data, 2016, 3, 9 CrossRef.
- J. S. Smith, B. T. Nebgen, R. Zubatyuk, N. Lubbers, C. Devereux, K. Barros, S. Tretiak, O. Isayev and A. E. Roitberg, Nat. Commun., 2019, 10, 2903 CrossRef PubMed.
- G. P. Stahly, Cryst. Growth Des., 2007, 7, 1007–1026 CrossRef CAS.
- A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, A. D. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell and R. Car, et al. , Acta Crystallogr., Sect. B, 2016, 72, 439–459 CrossRef CAS PubMed.
- C. H. Borca, B. W. Bakr, L. A. Burns and C. D. Sherrill, J. Chem. Phys., 2019, 151, 144103 CrossRef PubMed.
- G. J. O. Beran, Chem. Rev., 2016, 116, 5567–5613 CrossRef CAS PubMed.
- A. T. Hulme, S. L. Price and D. A. Tocher, J. Am. Chem. Soc., 2005, 127, 1116–1117 CrossRef CAS PubMed.
- J. Brandenburg and S. Grimme, Acta Crystallogr., Sect. B, 2016, 72, 502–513 CrossRef CAS PubMed.
- M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, Y. Jia, R. Jozefowicz, L. Kaiser, M. Kudlur, J. Levenberg, D. Mane, R. Monga, S. Moore, D. Murray, C. Olah, M. Schuster, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viegas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems, 2016 Search PubMed.
- Z. L. Glick, zachglick/apnet: v0.1.1, 2022, DOI:10.5281/zenodo.11493604.
- T. Verstraelen, S. Vandenbrande, F. Heidar-Zadeh, L. Vanduyfhuys, V. V. Speybroeck, M. Waroquier and P. W. Ayers, J. Chem. Theory Comput., 2016, 12, 3894–3912 CrossRef CAS PubMed.
- Z. Liu, M. Su, L. Han, J. Liu, Q. Yang, Y. Li and R. Wang, Acc. Chem. Res., 2017, 50, 302–309 CrossRef CAS PubMed.
- Y. Li, Z. Liu, J. Li, L. Han, J. Liu, Z. Zhao and R. Wang, J. Chem. Inf. Model., 2014, 54, 1700–1716 CrossRef CAS PubMed.
- Schrödinger Release 2021-1, Maestro, Schrödinger, LLC, New York, NY, 2021 Search PubMed.
- Schrödinger Release 2021-1, LigPrep, Schrödinger, LLC, New York, NY, 2021 Search PubMed.
- Schrödinger Release 2021-1: Protein Preparation Wizard, Epik, Schrödinger, LLC, New York, NY, 2021; Impact, Schrödinger, LLC, New York, NY; Prime, Schrödinger, LLC, New York, NY, 2021 Search PubMed.
- B. T. Thole, Chem. Phys., 1981, 59, 341–350 CrossRef CAS.
- J. W. Ponder, C. Wu, P. Ren, V. S. Pande, J. D. Chodera, M. J. Schnieders, I. Haque, D. L. Mobley, D. S. Lambrecht and R. A. DiStasio Jr, et al. , J. Phys. Chem. B, 2010, 114, 2549–2564 CrossRef CAS PubMed.
- S. C. Kamerlin and A. Warshel, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 30–45 CAS.
Footnote |
† Electronic supplementary information (ESI) available: Table S1 describing the SAPT0 decomposition of the ΔΔE results. Fig. S1 showing one-dimensional slices of Fig. 6. SAPT0 interaction energies and Cartesian coordinates of the 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 216 validation set dimers and nine protein–ligand matched pairs. See DOI: https://doi.org/10.1039/d4sc01029a 216 validation set dimers and nine protein–ligand matched pairs. See DOI: https://doi.org/10.1039/d4sc01029a |
| This journal is © The Royal Society of Chemistry 2024 |