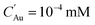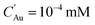Open Access Article
Open Access ArticleMechanisms of controlled stabilizer-free synthesis of gold nanoparticles in liquid aerosol containing plasma†
Jae Hyun
Nam
 a,
Gaurav
Nayak
a,
Stephen
Exarhos
a,
Chelsea M.
Mueller
b,
Dongxuan
Xu
a,
George C.
Schatz
a,
Gaurav
Nayak
a,
Stephen
Exarhos
a,
Chelsea M.
Mueller
b,
Dongxuan
Xu
a,
George C.
Schatz
 b and
Peter J.
Bruggeman
b and
Peter J.
Bruggeman
 *a
*a
aDepartment of Mechanical Engineering, University of Minnesota, Minneapolis, MN-55455, USA
bDepartment of Chemistry, Northwestern University, Evanston, IL-60208, USA. E-mail: pbruggem@umn.edu
First published on 19th June 2024
Abstract
The interaction between low-temperature plasma and liquid enables highly reactive solution phase chemistry and fast reaction kinetics. In this work, we demonstrate the rapid synthesis of stabilizer-free, spherical and crystalline gold nanoparticles (AuNP). More than 70% of gold ion complex (AuCl−4) conversion is achieved within a droplet residence time in the plasma of ∼10 ms. The average size of the AuNPs increases with an increase in the droplet residence time and the particle synthesis showed a power threshold effect suggesting the applicability of the classical nucleation theory. Leveraging UV-vis absorption and emission spectroscopy, and nanoparticle size distributions obtained from TEM measurements, we showed that the AuCl−4 conversion exceeded by 250 times the maximum faradaic efficiency. We identified important roles of both short-lived reducing species including solvated electrons and possibly vacuum ultraviolet (VUV) photons, and long-lived species, H2O2, in the reduction of AuCl−4. A quantitative investigation was performed by a 1-D reaction-diffusion model which includes transport, plasma-enabled interfacial reduction of AuCl−4, classical nucleation, monomer absorption and autocatalytic surface growth enabled by H2O2. The model shows good agreement with the experimental results. The timescale analysis of the simulation revealed that nucleation is enabled by fast reduction of gold ions, and autocatalytic growth mainly determines the particle size and is responsible for the majority of the ion precursor conversion while also explaining the excessively large faradaic efficiency found experimentally.
Introduction
Gold nanoparticles (AuNPs) exhibit unique optical, electrical, and thermal properties, which are beneficial for a wide range of applications, including efficient drug delivery,1,2 disinfection,3 photovoltaics,4 catalysis,5 biological and chemical sensing,6 and cell imaging and detection.7 The performance of AuNPs in these applications can be enhanced by the precise control of size, shape, and the surface properties of NPs.The first synthesis of AuNP was reported by Michael Faraday,8 where colloidal gold was synthesized by reducing chloroauric acid using phosphorus. Since then, many synthesis approaches were developed. One of the most popular synthesis approaches was developed by Turkevich et al.,9 in the 1950s. This approach uses chloroauric acid as a precursor and trisodium citrate as a reducing agent. This method is referred to as the “Turkevich method” and has been further developed and improved in many studies.10,11 Such chemical synthetic studies have evolved until today using different reducing agents such as sodium borohydride (NaBH4)12 or tetraoctylammonium bromide (TOAB).13 The synthesis procedures typically involve the mixing of a reducing agent with a metal salt precursor to which a stabilizer or surfactant is added, preventing aggregation/coalescence of the formed NPs. The reducing agent can in some cases also act as a stabilizer such as in the case of the Turkevich method where AuNPs are stabilized by the citrate layers formed on AuNP surfaces.14 While these chemical synthesis approaches can provide excellent control on particle size, they have significant limitations. Firstly, NPs synthesis is very slow, typically on timescales from hours to days. Secondly, impurities caused by used chemicals (reducing agents or surfactants) could remain at the NPs surface and cause modifications of optical and chemical properties and have potentially even harmful effects on the human body when used for biological and medical applications. Thirdly, many reducing agents are highly toxic and lead to significant waste.
To overcome these limitations, several alternative techniques to chemical synthesis have been investigated including photolysis and electron beam based approaches15,16 which enable electron-induced reduction of metal ions17–19 and do not require the use of the addition of potentially harmful reducing agents. Especially, liquid cell transmission electron microscopy (TEM), has enabled in situ studies of NPs growth facilitated by electron beams.
Plasma synthesis of NPs in the liquid phase is such an alternative approach to wet chemistry and has been extensively studied in particular for Au and Ag NPs.20–29 Plasmas can reduce the metal ions in a solution to produce metal NPs on timescale of milliseconds to minutes without the use of chemical reducing agents or stabilizers, and without producing harmful byproducts.27,30,31 Most of the plasma-enabled NP synthesis in solution has been achieved using DC glow discharges in contact with a solution, where the metal ion precursor is reduced at the plasma–liquid interface.21,30,32 Since the interfacial reduction of metallic ions by plasma is exceedingly fast, the ions at the interface are depleted within a short timescale.33 The resulting gradients in reduced metal precursor constantly leads to a wide range of nucleation and particle growth conditions causing an increased dispersion in NP properties, and thus, provides less control of the critical parameters, such as size, shape, or crystallinity of the NPs.
A recent approach to mitigate these challenges involves NP synthesis on timescales ranging from micro- to milliseconds using the surface–bound interactions between plasma and liquid precursor droplets with picoliter volumes.34,35 The liquid droplets are completely immersed in the plasma, hence the influx of the plasma-generated chemical species including electrons into the droplet can be very effective, and the large surface to volume ratio enables faster diffusion of the metal precursor towards the droplet surface. This provides opportunities for controlled synthesis in a small solution volume with a well-defined plasma treatment time equal to the droplet residence time in the plasma and a continuous delivery of high purity, uncoated, as-synthesized and surfactant-free NPs to the target, circumventing the challenge of particle agglomeration and growth mediation.
Maguire et al. reported unprecedented gold nanoparticle synthesis rates (>1024 atoms per L per s) in such liquid droplets treated by an RF plasma.34 Such high rates were attributed to a high electron flux and large surface-to-volume ratio of the droplets with an estimated average dose of 0.8–800 electrons per gold ion.34 Other studies have reported the reduction of gold ions by H2O2 and H radicals.15,20,24,30,36–40 The reduction of gold ions in bulk liquid likely involves the following reactions:
| [AuClx(OH)4−x]− + 3eaq− → Au0 + xCl− + (4 − x)OH− | (R1) |
| [AuClx(OH)4−x]− + 3Haq → Au0 + xCl− + (4 − x)OH− + 3H+ | (R2) |
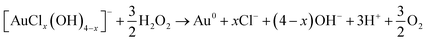 | (R3) |
 | (R4) |
While NPs synthesis has been studied for several decades, the underpinning mechanisms, particularly nucleation processes even for the Turkevich synthesis, are still being debated to date. Classical nucleation theory was first developed by Becker and Doring43 to describe the condensation of liquid from the gas phase vapor. The driving force for this phase transition is to minimize the Gibbs free energy of the particles. The theoretical work done by LaMer et al.44,45 extended classical nucleation theory to explain NPs formation by separating particle synthesis into a two-step process, burst nucleation followed by particle growth. In the first step, burst nucleation, the concentration of monomers increases and eventually exceeds the critical solubility limit. Monomers with higher kinetic energy than the critical Gibbs free energy starts to nucleate, and the concentration of monomer decreases below the critical concentration due to the fast conversion of monomers by nucleation, followed by the termination of nucleation. As a second step, the particle size grows by the diffusion driven monomer attachment to the surface of existing nuclei.46 During the growth process, the concentration of particles remains rather constant. Turkevich et al.9,47 analyzed the process of AuNPs synthesis by applying nucleation and growth steps, which is referred to as LaMer's mechanism. LaMer's burst nucleation and diffusional growth theory has been generally recognized as a fundamental model in chemical synthesis studies.
In contrast to the two-step mechanism of LaMer, Watzky and Finke41 proposed a new mechanism by studying the reduction of transition metals by hydrogen, where slow nucleation and autocatalytic surface growth occur simultaneously. Although this mechanism is conceptually different from the two steps in LaMer's mechanism, the slow nucleation process in the Finke–Watzky mechanism still follows classical nucleation theory. As Watzky and Finke did in their study, the photochemical reduction study of gold ions was carried by Meader et al.16 by fitting the gold ion concentration with an equation describing the reaction mechanism to estimate rate constants for reduction and autocatalytic surface growth. They found that the rate constant of autocatalytic surface growth is dependent on the concentration of hydrogen peroxide as shown in reaction R4.
Despite the well-established mechanisms of LaMer and Finke–Watzky, the commonly believed mechanisms of NP formation have been challenged by other explanations.48 Similarly, although extensive research has been performed to understand the role of plasma-generated reactive species and solvated electrons in bulk phase interactions, detailed quantitative studies are still missing. In addition, little is known about the plasma activation of liquid droplets for NP synthesis, for conditions with supposedly far superior synthesis rates and yields.34
In this manuscript, we aim to provide quantitative insights on plasma produced reactive species fluxes to droplets and the underpinning mechanism of the resulting AuNPs synthesis. We focus our investigation on the in-flight synthesis of AuNPs in the precursor-loaded (HAuCl4·3H2O) picoliter volume droplets treated by an RF glow discharge (He/Ar and He/Ar/H2O) at atmospheric pressure on millisecond timescales. The characterization of plasma, liquid droplets (H2O2), and resulting AuNPs is performed by optical emission spectroscopy, UV/vis absorption spectroscopy, and TEM analysis. The plasma–microdroplet reactor used in this study provides a controlled environment, and has previously been used for the investigation of plasma conversion of organic and fluorinated compounds in water droplets.49–51 We not only show that we can produce stabilizer-free AuNPs with a narrow size distribution, but we also investigate the effect of plasma-produced short-lived species (electrons and VUV photolysis) and H2O2 by proposing a reaction-diffusion model consisting of fast reduction processes and particle growth mechanism that is able to describe the experiment. The model analysis provides a picture of overall process of AuNPs formation consisting of steps with different timescales. For the detailed experimental methods, see ESI.†
Results and discussions
Plasma and droplet characterization
The RF glow plasma was operated in two different working gas mixtures, He + 17% Ar and He + 17% Ar + 0.2% H2O. In the case with added water vapor to the gas flow, it was reported earlier that the decomposition of formate in the water droplets was dominated by OH radical induced chemistry.50 In addition to OH radicals, He/Ar/H2O plasma also produces a large amount of H2O2. In the case of He/Ar plasma, a smaller OH and H2O2 flux to the droplet will be present, leading to potentially an important role of VUV radiation as shown in Nayak et al.51 We operated at gas flow rates ranging from 1 to 3 slm, which correspond to gas residence times in the inter-electrode gap ranging from 22 ms (1 slm) to 7 ms (3 slm). The emission from the He/Ar and He/Ar/H2O plasma did not fill the inter-electrode volume completely at 6 W. However at 14 W in He/Ar/H2O, the ionizing plasma zone was larger and filled ∼90% of the inter-electrode volume.52 The steady-state gas temperature in these plasmas has been measured previously for similar operating conditions, and was found to be 335 ± 9 K for He/Ar plasma at 12.4 W53 and 450 ± 20 K for He/Ar/H2O plasma at ∼14 W,50 at a total gas flow rate of 1 slm.The droplet dynamics were investigated previously for the plasma conditions studied in this work using a fast framing camera.50 The droplet diameter, when it enters the plasma, was fixed at 41 ± 2 μm for all conditions. In both the plasma cases, the reduction in the droplet size is enhanced with increasing droplet residence time in the plasma or decreasing gas flow rate. A maximum reduction in droplet size of 1.8% was observed in He/Ar plasma at 6 W, while a size reduction of 2.6% occurred in He/Ar/H2O plasma at 14 W and 1 slm, despite a much higher gas temperature. While solvent evaporation can in first approximation be neglected for the liquid phase, the impact on the gas composition near the droplet caused by this evaporation can be important and will be discussed below. With a total gas flow rate of 1 to 3 slm, the average gas velocity varied from 0.5 to 1.4 m s−1, corresponding to droplet residence times of 5.6–10.9 ms and 4.9–10.2 ms measured in He/Ar and He/Ar/H2O plasmas, respectively.51,52
The electron properties determined from continuum radiation as a function of total gas flow rate and plasma power are shown in Fig. S2 in ESI.† Using these absolute local gas-phase plasma densities near the droplet, the total electron current (Γe) equal to ion current (Γi) to the droplet can be estimated by the following equation:51
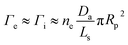 | (1) |
As already motivated elsewhere, the contribution of gas phase H can be neglected because of its much lower Henry's law solubility constant.49,55 However, the VUV photons from Ar excimer radiation predominantly produce Haq and OHaq radicals at the liquid interface via H2O dissociation at 124 nm56 as
| H2O + hν → Haq + OHaq | (R5) |
| eaq− + H+aq → Haq | (R6) |
Plasma–droplet nanoparticle synthesis
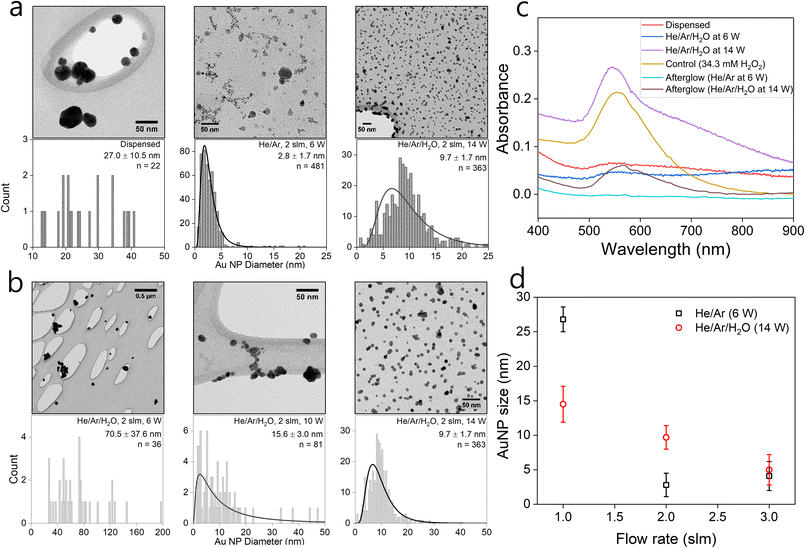
In the following, we assess the impact of varying plasma conditions on the AuNP synthesis. Measurements were performed with droplets containing 1 mM HAuCl4·3H2O precursor solution dispensed without any plasma as well as in the presence of He/Ar and He/Ar/H2O plasmas. The TEM images and the corresponding particle size distributions are shown in Fig. 1(a). The TEM images show that spherical crystalline AuNPs are produced in both dispensed and plasma-treated conditions. Dispensing the precursor-loaded droplets leads to the formation of a small number of NPs, which tend to aggregate and are much larger than the plasma-processed particles with all observed particles having a diameter in excess of 10 nm. This is consistent with the observations of the group of Zare that previously reported enhanced NP synthesis rates in microdroplets compared to bulk solutions.59 Nonetheless TEM images suggest that the plasma synthesized AuNPs are significantly more abundant than from droplet dispensing only. In the He/Ar plasma case, a narrow particle size distribution was observed with a mean AuNP diameter of 2.8 ± 1.7 nm as compared to the larger mean AuNP diameter of 9.7 ± 1.7 nm in the He/Ar/H2O plasma case. Interestingly, the He/Ar plasma yields smaller AuNP sizes than the He/Ar/H2O plasma which will be discussed in detail later.The effect of plasma power on the NP synthesis was investigated by treating precursor-loaded droplets at different plasma powers. Fig. 1(b) shows the TEM images and the corresponding particle size distributions of AuNPs as a function of power. The average AuNP size decreases with increasing plasma power. Intuitively, one would expect that larger power might produce larger particles, with larger agglomerates leading to crystallinity, however, Fig. 1(b) shows a reverse trend. He/Ar/H2O plasma at 6 W shows a wide and sparse size distribution which seems similar to the precursor dispensing case without plasma shown in Fig. 1(a). It is reasonable to infer that there might have been limited additional plasma-driven nucleation in this case but likely the existing particles from dispensing just grew by reaction mechanism R3 with H2O2 produced from plasma or diffusion driven monomer attachment, like seed-mediated growth. This can be qualitatively confirmed by UV/vis absorbance profiles. Indeed, Fig. 1(c) shows absorbance curves of just dispensed and plasma treated by He/Ar/H2O at 6 W, which are similar to each other, non-zero, and broadened profiles, which are attributed to the sparse and big AuNPs produced from dispensing only. On the other hand, a clear log-normal size distribution was observed in Fig. 1(b) treated by He/Ar/H2O plasma at 10 W. This result suggests a threshold power required for significant AuNP production between 6 W and 10 W in He/Ar/H2O plasma despite the larger H2O2 concentration (see H2O2 measurement in ESI†) in all cases as compared to He/Ar plasma treated solution. In Fig. 1(c), as power increases from 6 W to 14 W, a more prominent absorbance peak is seen. As electron/ion flux increases with increasing discharge power as shown in Fig. 1(b), a threshold power requirement might indicate a requirement for a threshold reducing species flux, which is consistent with classical nucleation theory since the classical nucleation theory requires supersaturation of monomers (Au0 in this case) above a critical concentration.
Effect of flow rate and humidity of gas flow
A much smaller particle size (μ = 2.8 nm) produced by He/Ar plasma compared to all He/Ar/H2O cases for different discharge power (6 W to 14 W) with the same flowrate (2 slm) is not explainable by the relation between electron flux and particle size, since the electron density of He/Ar 6 W plasma is similar or even smaller than the electron densities of He/Ar/H2O plasmas (see Fig. S2 in ESI†). This finding has two possible explanations. Firstly, He/Ar plasma produces higher VUV photon flux compared to He/Ar/H2O plasma which enhances the reduction due to its lower gas phase H2O concentration responsible for quenching the formed excimers. Nayak et al.,51 reported a suppressed decomposition rate of organic compounds (formate and PFOA) throughout their study upon the addition of water vapor to the feed gas consistent with such an explanation. The increased reduction rate induces enhanced nucleation resulting in a larger number of nuclei. The second explanation is that the NP size is determined by autocatalytic surface growth (R4) which is less pronounced in the He/Ar plasma case, compared to the He/Ar/H2O case due to the significantly lower H2O2 concentration (see H2O2 measurement in ESI†). The model reported later in this work will include both processes and allow a more in-depth discussion on the dominant processes.To experimentally assess the impact of the precursor reduction rate in more detail, droplets containing 1 mM solution of HAuCl4·3H2O were treated with He/Ar/H2O plasma at 14 W for 5 minutes at different gas flow rates from 1 to 3 slm. Fig. 1(d) shows the mean particle size or diameter of the AuNPs synthesized in plasma-treated droplets as a function of different gas flow rates in both He/Ar (6 W) and He/Ar/H2O (14 W) plasmas. In both cases, the mean NP size decreases with increasing gas flow rate or decreasing droplet residence time in the plasma.
In the He/Ar/H2O plasma case, the total estimated electron current to the droplet increased by a factor 3 from 1 to 3 slm (see Fig. S2 in ESI†). This is because the humidity around the droplet reduces the plasma density, which is more pronounced at lower gas flow rates or larger droplet residence times (see Nayak et al.51 for more details). This result is consistent with the observation that the particle size decreases with increasing plasma power. The resulting higher reducing current results in a larger number of nuclei for the 3 slm case compared to the 1 slm case. The measured H2O2 concentrations in the collected droplets increase by a factor 2 (see Fig. S3 in ESI†). However, the total number of gold ions reduced by autocatalytic reduction (R3) will be similar for the 1 slm and 3 slm cases as the gold precursor ion concentration is the growth limiting factor (its concentration is much smaller than the H2O2 concentration). In conclusion, “resource competition” occurs with elevated reducing current, either by increased power or gas flow rate leading to smaller nanoparticles. This will be analysed quantitatively in the modelling section in detail.
Total conversion estimates
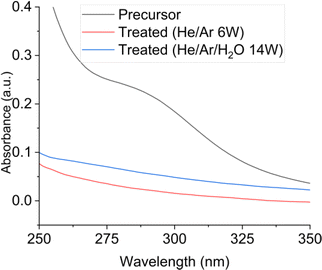
Fig. 2 shows the averaged UV/vis absorbance profiles of samples treated by He/Ar and He/Ar/H2O plasmas for the estimation of the precursor ion conversion. The final percentage precursor ion conversions can be determined from the ratio of the untreated and treated samples and are 89(±5)% and 72(±8)% for the He/Ar and He/Ar/H2O plasma cases, respectively. More details are provided in the ESI (Conversion of precursor ions).† The percentage conversion obtained here shows good correspondence with the estimation reported by Maguire et al.34 (>50%), and allows us to deduce important findings. Firstly, the total number of precursor ions converted and incorporated in AuNPs in a droplet is estimated to be more than 1.4 × 1010 (obtained by the multiplication of precursor concentration with the volume of a droplet and conversion percentage). The total number of electrons injected by the gas phase plasma during 10 ms (droplet residence time in plasma) is not larger than 108. Considering the reaction stoichiometry, three electrons are required to reduce a gold ion (R1). Therefore, if the reduction of AuCl−4 is only enabled by electrons, the number of electrons required is 250 times larger than the available electrons.As for conventional electrochemistry, we can define faradaic efficiency for plasma–liquid interaction as the number of electrochemical conversions per transferred electron from the plasma into the liquid. A floating liquid droplet in an RF plasma has no net current through the interface as the average electron and positive ion current are equal in steady-state. Nonetheless, we determined the electron flux to the droplet and measured the conversion of the gold ion precursor which allows us to define a faradaic efficiency. As plasma also injects ions and neutral species that are not accounted for in this efficiency, in the case of plasmas non-faradaic reactions can significantly contribute to the overall conversion and hence lead to faradaic efficiencies in excess of 100%. In this work, the observed faradaic efficiency exceeds the maximal faradaic efficiency by a factor 250. We would however like to stress that even for non-faradaic reactions initiated by neutral plasma-produced reactive species, these neutral reactive species are produced through electron-induced reactions in the gas phase or secondary reactions involving radicals or ions produced in electron-induced gas phase reactions.
The above suggests that other species are needed to achieve the observed high conversion of AuCl−4, possibly H radicals from photolysis (R5 and R2) or plasma-produced H2O2 (R3 or R4). Secondly, reduction at the plasma–liquid interface, as in the case for short-lived plasma-produced species such as solvated electrons, is limited by the diffusion of AuCl−4 to the interface. The maximum percentage conversion during the droplet residence time in the plasma (10 ms) obtained from a simple diffusion-limited model (see 1-D Diffusion Model in ESI†) is 27%, which means that the reduction process involves not only short-lived species at the plasma–liquid interface but also long-lived species which can penetrate into the droplet and likely reactions in the afterglow. This could imply that slow reduction processes by H2O2 will be important.
H2O2 positive control and afterglow measurements
To assess the role of H2O2 in AuNP synthesis in our system, we performed a series of control experiments. The average H2O2 concentration in the collected Au precursor-loaded droplets treated by He/Ar/H2O plasma at 2 slm and 14 W was measured to be 34.3 ± 5.3 mM. For positive control experiment, 34.3 mM H2O2 solution was added to 1 mM HAuCl4·3H2O solution and allowed to react for 5 minutes (the same duration as used for droplet collection for absorbance measurements). To then isolate the effect of plasma generated long-lived H2O2 from short-lived and locally produced species including e−aq on the AuNP synthesis, a 10 μl droplet of 1 mM HAuCl4·3H2O was treated with the He/Ar/H2O plasma afterglow at 2 slm and 14 W for a period of 5 minutes without freezing the droplet. A similar afterglow experiment was performed with He/Ar plasma at 2 slm and 6 W for a period of 3.75 minutes. The TEM images of the AuNPs produced in these positive control and afterglow experiments are shown in Fig. 3. Fig. 3(a), (b) and (c) show that, regardless of its origin, H2O2 has the ability to reduce gold ions supported by the observed significant absorbance at 555 nm (corresponding UV-vis absorbance spectra are shown in Fig. 1(c)) due to the plasmonic resonance of the produced AuNPs. The measured H2O2 concentrations at the end of the control experiments dropped from 34.3 ± 5.3 mM to 20.6 ± 2.1 mM (see values at H2O2 measurement in ESI†), suggesting that ∼10 mM of H2O2 was consumed during the experiments, where reaction R1 and R3 could account for at most ∼1.5 mM H2O2 for 1 mM precursor concentration. While the afterglow treated precursor solution by the He/Ar/H2O plasma had an average H2O2 concentration of 46.6 ± 2.5 mM, He/Ar afterglow treated precursor solution had only an average H2O2 concentration of 0.5 ± 0.8 mM. While this low concentration is still sufficient to convert 1/3 of the AuCl−4 to Au0, negligible absorbance corresponding to AuNPs was observed, in Fig. 1(c), for droplets treated in the He/Ar afterglow, suggesting AuNPs were hardly formed. By comparing the control experiment (34.3 mM of H2O2) and afterglow treatment by He/Ar/H2O plasma (46.6 mM of H2O2), the absorbance curve of the control experiment shows a more prominent absorption peak than the absorbance curve of an afterglow treatment. This is probably due to the linear increase of the H2O2 concentration in the afterglow treatment (see also H2O2 measurement in ESI†), resulting in ∼24 mM as an average, whereas the H2O2 concentration remains relatively high (decrease from 34.3 mM to 20.6 mM). The AuNPs produced from afterglow treatments (Fig. 3(b) and (c)) are much larger than the plasma-processed AuNPs (Fig. 3(d)), which is also consistent with the red-shifted peaks in Fig. 1(c). Furthermore, the AuNPs treated by afterglow in Fig. 3(c) tend to show non-spherical and loosened (or dendritic) morphology, while well-separated and compact individual AuNPs are produced in the droplets treated by the RF plasma. The small-sized and well-separated AuNPs from the plasma treatment suggests an important contribution of short-lived species fluxes to the reduction.In conclusion, the experiments strongly support the idea that a significant part of the precursor ions can be reduced by H2O2 produced by the gas-phase plasma. It seems that reducing reactions by short-lived species such as solvated electrons and VUV photolysis from the plasma are also critical with the aid of H2O2 for AuNP formation and for the growth with a narrow size distribution and sizes of a few nm. Plasma-produced AuNPs show relatively compact and well-separated AuNPs while H2O2 enabled AuNP growth showed a more loosened and non-spherical shape.
Modeling
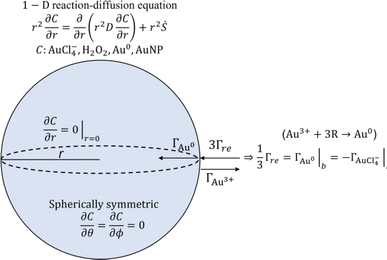
In addition to the above-described experiments, a 1-dimensional model was developed to describe the observed AuNP growth in the experiment and to assess the applicability of the existing AuNP growth models to plasma-enabled AuNP synthesis. The scheme of the model is presented in Fig. 4 including the governing equation and boundary conditions. To model AuNP growth, we consider three processes: reduction of gold ions (AuCl−4), nucleation from reduced monomers (Au0), and particle growth. The model is detailed in the 1-D reaction-diffusion model section of the ESI.†The formation of nuclei (or small clusters) can be explained by either nucleation or coalescence driven by colloidal stability. From Polte's explanation of the Turkevich method as a model of the four-step process,48 instead of nucleation, monomers aggregate and coalesce to form small clusters due to the colloidal instability in the early stage of reduction, explained by DLVO theory60,61(named after Derjaguin, Landau, Verwey and Overbeek), and these particles grow by diffusion driven monomer attachment and the reduction of surface attached ions, referred to as autocatalytic surface growth. However, we could not find proof of applicability of DLVO theory to explain initial Au clusters for our experimental conditions and therefore use classical nucleation theory to describe the formation of initial Au cluster (nuclei). The minimum power (more than 6 W in the He/Ar/H2O plasma as shown in Fig. 1(b)) required to produce a significant number of nanoparticles suggests a threshold effect which is consistent with the concept of an “activation barrier” of classical nucleation theory. Furthermore, we did not observe a minimum size of AuNPs, which could be the evidence of “deactivation barrier” of DLVO theory in our experiments, although this might be obscured by the finite resolution (0.34 nm) of the TEM measurements for the experimental conditions. For the NP growth process, we follow the approach of Meader et al.16 While the nucleation process was assumed to be slow in the study of Meader and occurs simultaneously with surface growth through the Finke-Watzky mechanism, we conjecture the supersaturation of gold monomer concentration at the center of the cuvette in their setup was hardly achieved due to isotropic diffusion, thus leading to the synthesis timescales of 10–100 s, as observed in their work. By contrast, for our conditions, it was shown that plasma-produced short-lived species are critical for the formation of nanoparticles and hence significant nucleation occurs likely during the flight time of droplets in the plasma on a timescale of ∼10 ms. This timescale is even shorter than the fastest chemical synthesis rate reported by Polte et al.62 where reduction and nucleation are completed within 100 ms, achieved under rapid mixing of gold precursor with NaBH4 inside micro-mixer. We anticipate that supersaturation of reduced monomers is expected to reach its critical concentration due to the limited-diffusion and high reducing flux on these timescales. Therefore, LaMer's explanation of burst nucleation is consistent with the milliseconds timescale of plasma treatment and resulting particle formation in our experiments.
Although LaMer stated that the growth of thermodynamically stable particles might be driven by diffusion of monomers, the exact growth mechanism was unspecified. As we showed in the previous section of this manuscript, a significant amount of H2O2 was produced from the gas phase plasma and was also consumed in the presence of the gold precursor. This observation strongly suggests the applicability of autocatalytic surface growth as expressed in mechanism R4.
The characteristic time (τD) for mass diffusion of AuCl−4 from the bulk of the droplet to the surface can be estimated by
| τD = Λ2/D | (2) |
While it is known that OH radicals have a strong capability to oxidize organic/inorganic molecules, direct evidence or quantitative measurements of gold monomer oxidation by OH radicals have not been reported, to the best of our knowledge. Nonetheless, OH radicals were reported to be able to oxidize gold on a macroscopic scale. Nowicka et al.64 firstly discovered that small asperities on a gold surface could be oxidized and dissolved by OH radicals. Furthermore, in the field of catalysis, gold nanoparticles have been studied for facilitating oxidation reactions such as CO to alcohols which is proposed to involve OH-driven chemistry.65 This implies that OH radicals might be able to induce oxidation at the monomer scale as well particularly as the plasma–liquid interface is an OH-rich environment. Oinuma et al.49 reported OH radicals concentrations of ∼10−4 mM at the interface layer of a droplet for similar plasma conditions as studied in this manuscript. However, the time scale of gold surface oxidation reported from Nowicka et al.64 is of the order of ∼10 min. Therefore, while recognizing the knowledge gap on OH-driven reactions, it is likely that reoxidation of the gold monomer occurs on a much longer time scale as reduction at the plasma–liquid interface. This suggests that OH has a minimal impact on nanoparticle synthesis and we have not considered OH-driven chemistry in this work.
Total reducing current estimation
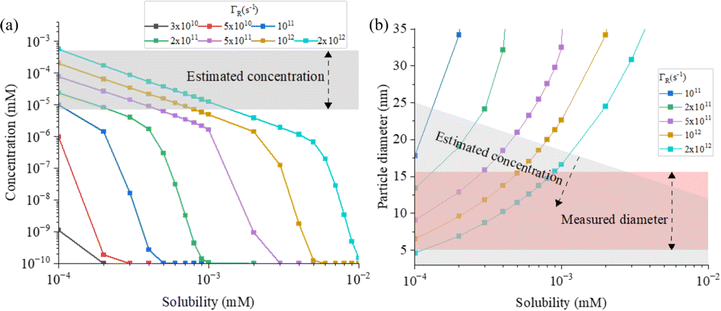
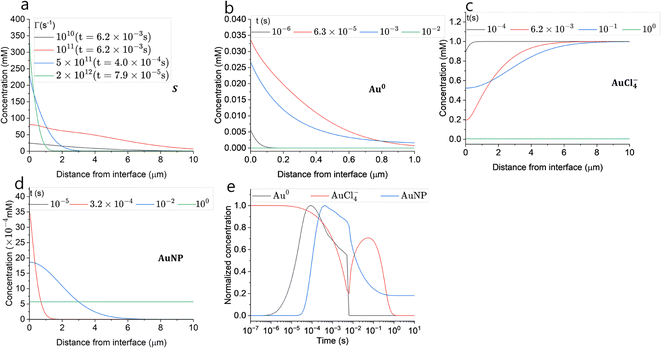
Although the maximum electron current is estimated above (see Plasma and droplet characterization), the total reducing current including VUV photons is unknown. Based on the experimentally determined upper limit of the electron current (Γe < 2 × 1010 s−1), parametric simulations were carried out by varying the reducing current with a fixed plasma droplet residence time of 6.2 ms (corresponding to 2 slm in the experiment).50Fig. 5 shows the results of parametric simulations for different reducing fluxes and solubilities of gold monomers. Fig. 5(a) and (b) indicate that the obtained concentration and diameter of the synthesized gold nanoparticles are sensitive to the solubility of gold monomers. In our model, particle concentration is determined by the rate of nucleation, which is proportional to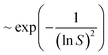 , where S represents the degree of supersaturation. Higher solubility leads to a slower nucleation rate, resulting in a lower concentration of nuclei. Consequently, the reduced monomers after nucleation are distributed among fewer particles, as previously discussed, causing resource competition and leading to larger particle sizes. In Fig. 5(a), the possible range of reducing current can be estimated as 1011 s−1–2 × 1012 s−1 based on the known solubility range and the measured AuNPs concentration range (grey area, 7 × 10−6 mM–5 × 10−4 mM) calculated from our experiments (see Estimation of AuNP concentration in ESI†). In the case of ΓR = 2 × 1012 s−1, the concentration of gold ions was depleted at the interface when t ≅ 6.2 ms. The reduction rate at the interface will be limited (or controlled) by the diffusion of AuCl−4 in this case. Hence, we expect that the concentration of AuNPs made by larger reducing species currents will not deviate much from the concentration of ΓR = 2 × 1012 s−1 case and we took this value as the upper limit in this study. In Fig. 5(b), the estimated particle concentration and the measured diameter are shown with colored ranges at the same time. The experimentally observed overlapping area (grey and red) implies the reducing current could vary from 2 × 1011 s−1 to 2 × 1012 s−1 and the solubility could vary from 10−4 mM to 10−3 mM. However, at the high end of the solubility range, 10−3 mM, the resulting particle diameter does not vary much. On the other hand, if the solubility is around 10−4 mM, the smaller particle size along with higher reducing current is achievable, a trend shown in Fig. 1(d), although the sensitivity to the reducing current in the experiment is somewhat higher than the model. The reducing current of the experiments could vary between 2 × 1011 s−1 and 2 × 1012 s−1 with a solubility of around 10−4 mM which is close to the value obtained by Chen et al.66 (4 × 10−4 mM). Interestingly, the estimated lower limit of reducing current is at least 10 times higher than the electron current to the droplet, suggesting the inevitable participation of other processes, likely to be VUV photolysis, in the reduction process. The quantitative estimation of the VUV photon flux inside the RF plasma has been rarely reported, however, we can use values of VUV irradiance measured by Brandenburg et al.67 to estimate a VUV photon flux. They acquired 8.3 mW cm−2 at a distance of 5 mm with similar operating conditions as in our experiments. Considering photons at 125 nm (Ar excimer radiation) have an energy of 9.9 eV, and the surface area of a droplet (ϕ = 41 μm) is 5.3 × 10−9 m2, the VUV photon flux into the droplets in our experimental setup can be of the order of 3 × 1011 s−1, a value which is more than an order of magnitude higher than the electron current (1.7 × 1010 s−1) and is within the range of the total reducing current identified by the model. Although this remains an estimation, it is reasonable to conclude that VUV-induced photolysis has likely the capability to enhance fast reduction of gold ions compared to the reduction by electrons only.
, where S represents the degree of supersaturation. Higher solubility leads to a slower nucleation rate, resulting in a lower concentration of nuclei. Consequently, the reduced monomers after nucleation are distributed among fewer particles, as previously discussed, causing resource competition and leading to larger particle sizes. In Fig. 5(a), the possible range of reducing current can be estimated as 1011 s−1–2 × 1012 s−1 based on the known solubility range and the measured AuNPs concentration range (grey area, 7 × 10−6 mM–5 × 10−4 mM) calculated from our experiments (see Estimation of AuNP concentration in ESI†). In the case of ΓR = 2 × 1012 s−1, the concentration of gold ions was depleted at the interface when t ≅ 6.2 ms. The reduction rate at the interface will be limited (or controlled) by the diffusion of AuCl−4 in this case. Hence, we expect that the concentration of AuNPs made by larger reducing species currents will not deviate much from the concentration of ΓR = 2 × 1012 s−1 case and we took this value as the upper limit in this study. In Fig. 5(b), the estimated particle concentration and the measured diameter are shown with colored ranges at the same time. The experimentally observed overlapping area (grey and red) implies the reducing current could vary from 2 × 1011 s−1 to 2 × 1012 s−1 and the solubility could vary from 10−4 mM to 10−3 mM. However, at the high end of the solubility range, 10−3 mM, the resulting particle diameter does not vary much. On the other hand, if the solubility is around 10−4 mM, the smaller particle size along with higher reducing current is achievable, a trend shown in Fig. 1(d), although the sensitivity to the reducing current in the experiment is somewhat higher than the model. The reducing current of the experiments could vary between 2 × 1011 s−1 and 2 × 1012 s−1 with a solubility of around 10−4 mM which is close to the value obtained by Chen et al.66 (4 × 10−4 mM). Interestingly, the estimated lower limit of reducing current is at least 10 times higher than the electron current to the droplet, suggesting the inevitable participation of other processes, likely to be VUV photolysis, in the reduction process. The quantitative estimation of the VUV photon flux inside the RF plasma has been rarely reported, however, we can use values of VUV irradiance measured by Brandenburg et al.67 to estimate a VUV photon flux. They acquired 8.3 mW cm−2 at a distance of 5 mm with similar operating conditions as in our experiments. Considering photons at 125 nm (Ar excimer radiation) have an energy of 9.9 eV, and the surface area of a droplet (ϕ = 41 μm) is 5.3 × 10−9 m2, the VUV photon flux into the droplets in our experimental setup can be of the order of 3 × 1011 s−1, a value which is more than an order of magnitude higher than the electron current (1.7 × 1010 s−1) and is within the range of the total reducing current identified by the model. Although this remains an estimation, it is reasonable to conclude that VUV-induced photolysis has likely the capability to enhance fast reduction of gold ions compared to the reduction by electrons only.
The simulation results can also explain the experiment of Maguire et al.34 where they estimated nanoparticle synthesis rates, mean particle diameters, and the maximum particle concentrations. From their estimation, the nanoparticle synthesis rate of 1024 atoms per L per s suggests that their reducing current should be larger than ∼2 × 1012 s−1 which is likely to be diffusion-limited as shown by our simulation. If we assume the solubility as ∼10−4 mM, their reducing current should result in a particle diameter of <5 nm which is close to the reported mean diameter of 4.4 nm from their experiment.
Dominant reduction pathways and particle size contributions
Since the model results depend on the value of solubility which still has an order of magnitude of uncertainty, we explore several reference cases. The two extreme cases of reducing currents (2 × 1011 and 2 × 1012 s−1) and two solubilities (10−4 and 10−3 mM) were chosen. In these representative cases, we investigate the contribution of each process (see Fig. 6) to the consumption of species including AuCl−4 and Au0 as shown in Table 1. Note that the total conversion of the precursor ions for every case was ∼100%. In the low reducing current case, most of the precursor ions were reduced by autocatalytic reaction, however, in the higher reducing current cases, a relatively large portion of precursor ions was reduced by reduction at the plasma–droplet interface. Among the high current cases, more monomers are consumed by nucleation in the lower solubility case, leading to larger particle concentration which results in smaller particle diameter.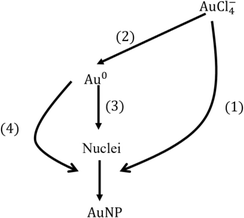 | ||
| Fig. 6 Consumption pathways of gold precursor ions and monomers by different mechanisms. Each number denotes the percentage contribution of each process for the consumption species: (1) autocatalytic surface reaction (reaction R4), (2) reduction at the plasma–droplet interface, (3) nucleation, and (4) diffusion-driven monomer absorption. Note that the percentage conversion of gold ions is the summation of (1) and (2), and the summation of (1), (3) and (4) is 100%. See also Table 1. | ||
| Case | Process | ||||
|---|---|---|---|---|---|
| (1) Autocatalytic surface growth (%) | (2) Reduction (%) | Particle diameter (nm) | |||
| (3) Nucleation (%) | (4) Monomer absorption (%) | ||||
| Low current (2 × 1011 s−1) | 98.3 | 1.7 | 13.4 | ||
| <0.1 | 1.7 | ||||
| High current (2 × 1012 s−1) | Low solubility (10−4 mM) | 82.4 | 17.6 | 4.6 | |
| 0.7 | 16.8 | ||||
| High solubility (10−3 mM) | 82.5 | 17.5 | 16.6 | ||
| <0.1 | 17.1 | ||||
Overall, the contribution of each process for the particle size determination is as follows: autocatalytic surface growth (>80%), monomer absorption (<20%), and nucleation (<1%).
Since the contribution of autocatalytic surface growth is significant, one can expect He/Ar/H2O plasma will produce much larger AuNPs than He/Ar plasma. However, in our preliminary inspection (see Effect of H2O2 concentration to the particle size in ESI†), where we lowered the concentration of H2O2 from 34.3 mM to 3.6 mM (the H2O2 concentration from He/Ar/H2O at 14 W and He/Ar at 6 W afterglow treatment, respectively), there was no significant reduction in particle size. This is because the simulation time scale is of order of 102 s which is much longer than the timescale of autocatalytic reduction (10 ms–1 s, see further) and the total conversion is determined by the initial precursor concentration of 1 mM. In other words, the particle size is not determined by the H2O2 concentration.
Therefore, among the two possible explanations of why He/Ar plasma resulted in a smaller particle size (2.8 nm), the lower H2O2 concentration explanation is eliminated. If we capitulate, as identified above, that the VUV photon dominates total reducing current, the VUV photon flux provides convincing explanation of the different particle size by He/Ar and He/Ar/H2O plasmas. The higher VUV photon flux in He/Ar plasma compared to He/Ar/H2O, due to the quenching of excimers by the presence of H2O, likely results in a larger reducing current and more particle nucleation, and hence, smaller particle sizes.
Key species concentration
Fig. 7(a) shows the maximum supersaturation from the simulation results with different reducing species current (ΓR) at a gas flow rate of 2 slm. When the reducing species current is less than 1011 s−1 supersaturation was reached at the end of the droplet residence time (6.2 ms). Hence, the supersaturation is limited by droplet residence time, however, the level of supersaturation was not enough to induce sufficient nucleation and resulting particle concentration, as shown in Fig. 5(a). With the reducing species current of 1011 s−1, the maximum supersaturation is reached also at the end of the droplet residence time in the plasma, and this reducing current could enhance nucleation resulting in a AuNP concentration of 10−5 mM, as shown in Fig. 5(a). With the reducing species currents ΓR ≥ 5 × 1011 s−1, the supersaturation near the interface reached its local maximum (>100) within a very short time of <400 μs. Overall, the higher current enables higher and faster supersaturation of monomers, which explains the fast synthesis and narrow size distribution, through “burst nucleation”, of our experiment and the result reported by Maguire et al.34To investigate the concentration changes of the involved species and particles, Au0, AuCl−4, and AuNPs, we chose a high reducing current and low solubility case as the reference case (ΓR = 2 × 1012 s−1 and 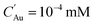 ) and the results are shown in Fig. 7(b)–(d). Fig. 7(b) shows that the gold monomer, Au0, concentration reaches its maximum of ∼0.03 mM (S ∼ 300) within 1 μm from the plasma–droplet interface. After reaching its maximum, Au0 was rapidly consumed by burst nucleation and diffusion-limited monomer absorption to NPs. Within a timescale of 10 ms, most of the Au0 was consumed, leading to the termination of nucleation and particle growth by diffusion-limited monomer absorption. Fig. 7(c) shows the precursor ion concentration. During the plasma treatment (<6 ms), within 1 μm from the interface, 80% of the precursor was rapidly consumed by reduction, and after the droplet exits the plasma, depleted ions are restored by diffusion from the bulk. Between 100 ms and 1 s, most of the ions are consumed by autocatalytic surface growth (R4). The rate of autocatalytic surface growth reaches its maximum around 100 ms (Fig. 8(a)). The local concentration of AuNP within 100 nm from the interface reaches its maximum during the plasma treatment (Fig. 7(d)), and it is flattened by the diffusion from the interface to the bulk with the timescale of 1 s, resulting in the final AuNPs concentration of ∼5 × 10−4 mM. The normalized temporal changes of the species concentration at a distance of 0.1 μm from the droplet interface are shown in Fig. 7(e). The ion concentration starts to be depleted at ∼10−5 s and increases again at 6 ms (at the end of the plasma exposure) due to the replenishment of the ions from the bulk by diffusion. The concentration of Au0 reaches its peak at ∼10−4 s. The AuNP concentration increases with a time scale roughly 10 times slower than that of Au0 consistent with the nucleation initiation rate requiring 13 atoms to form one nucleus. Note that the Au0 concentration decrease is caused by the consumption (nucleation and monomer absorption), whereas the decrease of AuNP concentration is caused by the diffusion of the AuNPs towards the bulk of the droplet which occurs due to its larger size on time scales larger than for monomer consumption, as shown also in Fig. 7(d).
) and the results are shown in Fig. 7(b)–(d). Fig. 7(b) shows that the gold monomer, Au0, concentration reaches its maximum of ∼0.03 mM (S ∼ 300) within 1 μm from the plasma–droplet interface. After reaching its maximum, Au0 was rapidly consumed by burst nucleation and diffusion-limited monomer absorption to NPs. Within a timescale of 10 ms, most of the Au0 was consumed, leading to the termination of nucleation and particle growth by diffusion-limited monomer absorption. Fig. 7(c) shows the precursor ion concentration. During the plasma treatment (<6 ms), within 1 μm from the interface, 80% of the precursor was rapidly consumed by reduction, and after the droplet exits the plasma, depleted ions are restored by diffusion from the bulk. Between 100 ms and 1 s, most of the ions are consumed by autocatalytic surface growth (R4). The rate of autocatalytic surface growth reaches its maximum around 100 ms (Fig. 8(a)). The local concentration of AuNP within 100 nm from the interface reaches its maximum during the plasma treatment (Fig. 7(d)), and it is flattened by the diffusion from the interface to the bulk with the timescale of 1 s, resulting in the final AuNPs concentration of ∼5 × 10−4 mM. The normalized temporal changes of the species concentration at a distance of 0.1 μm from the droplet interface are shown in Fig. 7(e). The ion concentration starts to be depleted at ∼10−5 s and increases again at 6 ms (at the end of the plasma exposure) due to the replenishment of the ions from the bulk by diffusion. The concentration of Au0 reaches its peak at ∼10−4 s. The AuNP concentration increases with a time scale roughly 10 times slower than that of Au0 consistent with the nucleation initiation rate requiring 13 atoms to form one nucleus. Note that the Au0 concentration decrease is caused by the consumption (nucleation and monomer absorption), whereas the decrease of AuNP concentration is caused by the diffusion of the AuNPs towards the bulk of the droplet which occurs due to its larger size on time scales larger than for monomer consumption, as shown also in Fig. 7(d).
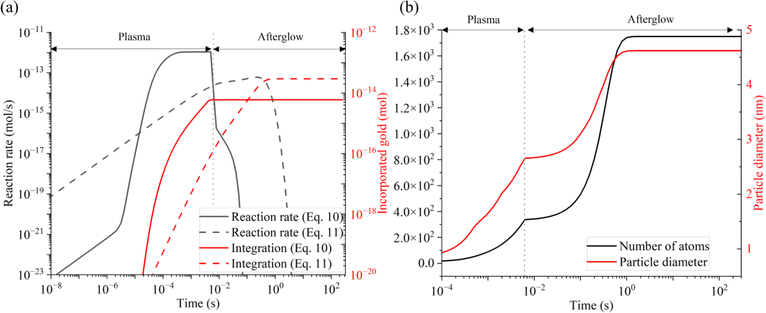 | ||
| Fig. 8 Temporal evolution of (a) reaction rates of each growth processes (black) and cumulative amount of incorporated gold atoms in AuNP (red) from diffusion limited absorption of Au (eqn 10 in ESI†) and autocatalytic growth (eqn 11 in ESI†) and (b) number of Au atoms per AuNP (black) and diameter of AuNP (red). | ||
Timescales of key processes
The timescale of the growth mechanisms and incorporated gold atoms by these mechanisms are shown in Fig. 8(a), and resulting particle diameter evolution is presented in Fig. 8(b). The diffusion-driven monomer absorption was completed immediately after the droplet exits the plasma. The autocatalytic surface growth subsequently occurs and is completed within approximately 1 s due to the complete consumption of gold precursor ions as shown from Fig. 7(c) and (e). A significant portion of gold atoms in AuNPs was obtained by the autocatalytic surface growth, which was already confirmed by Table 1.Informed by the above experimental and simulation results, the proposed AuNP growth mechanism in our plasma–droplet system is summarized schematically in Fig. 9. At first, gold ions are quickly reduced to gold monomers during the plasma treatment, and the reduction is diffusion limited if the reducing current is higher than 2 × 1012 s−1. The monomer concentration increases and reaches supersaturation. The degree of supersaturation builds up (S ∼ 102) during the droplet residence time in the plasma or even on faster timescales. Burst nucleation immediately follows and terminates within 10 ms due to the depletion of monomers. The diffusion-driven monomer absorption is the driving mechanism for the particle growth during the droplet residence time in the plasma which accounts for less than 20% of the NP size. After the droplet leaves the plasma the autocatalytic surface reaction drives particle growth, enabling significant increases in the AuNP size.
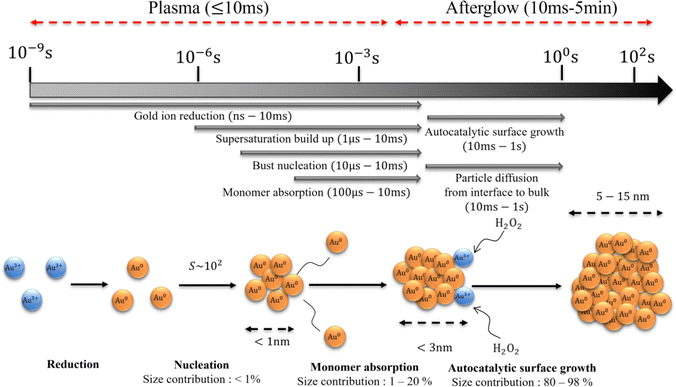 | ||
| Fig. 9 The schematic of the proposed particle growth mechanism including timescales, relative contributions, and particle sizes in each of the steps. | ||
Conclusion
In this work, we demonstrated the synthesis of ligand-free, spherical Au nanoparticles without the use of stabilizer(s) via the interaction of in-flight liquid micro-droplets with a capacitively coupled RF glow discharge in He + 17% Ar and He + 17% Ar + 0.2% H2O plasmas. These nanoparticles were produced within a droplet residence time of ∼10 ms used in this study. The particles and precursor conversion were characterized with UV-vis absorption spectroscopy complemented with TEM imaging to obtain particle size distributions. The average size of the AuNPs increases with an increase in the droplet residence time and the particle synthesis showed a power threshold effect. We showed that the ion precursor conversion exceeded by 250 times the maximum faradaic efficiency and were experimentally able to identify through a series of control measurements a dominant role of both short-lived reducing species and H2O2 in the reduction of AuCl−4.We reported on a 1-D reaction-diffusion model which includes transport, plasma-enabled interfacial reduction of AuCl−4, classical nucleation, monomer absorption and autocatalytic surface growth enabled by H2O2. The modelling results reported in this work show excellent agreement with the experiment. With the aid of a model, we identified that the estimated reducing current in our experiment is 10 times higher than the electron current, which is attributed to the VUV photolysis, and this value is consistent with the estimation of VUV flux in our system based on the literature. The model suggests that the nucleation process occurring within 10 ms is enabled by fast reduction, by electrons and VUV photons, while the particle growth is mainly led by autocatalytic growth mediated by plasma produced H2O2 that continues after the droplet exits the ionizing plasma region. This autocatalytic growth process that has a timescale of 1 s significantly contributes to the enhancement of plasma-enabled reduction compared to the reduction by solvated electrons only. These insights will be helpful in the development of general plasma-enabled nanoparticle synthesis processes.
Data availability
All the additional experimental, characterization, and simulation data are available in ESI.†Author contributions
Jae Hyun Nam: conceptualization, methodology, software, validation, investigation, writing – original draft, review & editing, visualization. Gaurav Nayak: conceptualization, methodology, investigation, writing – original draft, review & editing, visualization. Stephen Exarhos: investigation, writing – review & editing, visualization. Chelsea M. Mueller: investigation, writing – review & editing. Dongxuan Xu: investigation, writing – review & editing. George Schatz: supervision, writing – review & editing, funding acquisition, conceptualization. Peter J Bruggeman: writing – review & editing, resources, supervision, project administration, conceptualization, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Research was sponsored by the Army Research Office and was accomplished under Grant No. W911NF 20-1-0105. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Office or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein. GN and PJB acknowledge funding from the National Science Foundation under Grant No. PHYS 1903151 and from the United States Department of Energy, Office of Science, Fusion Energy Sciences under award number DE-SC-0020232. Parts of this work were carried out in the Characterization Facility, University of Minnesota, which receives partial support from the U.S. National Science Foundation (NSF) through the MRSEC program. The authors acknowledge the Minnesota Supercomputing Institute (MSI) at the University of Minnesota for providing resources that contributed to the results reported in this paper.References
- E. Boisselier and D. Astruc, Chem. Soc. Rev., 2009, 38, 1759–1782 RSC.
- S. Wilhelm, A. J. Tavares, Q. Dai, S. Ohta, J. Audet, H. F. Dvorak and W. C. W. Chan, Nat. Rev. Mater., 2016, 1, 1–12 Search PubMed.
- Y. Zhang, T. P. Shareena Dasari, H. Deng and H. Yu, J. Environ. Sci. Health, Part C: Environ. Carcinog. Ecotoxicol. Rev., 2015, 33, 286–327 CrossRef CAS PubMed.
- M. Notarianni, K. Vernon, A. Chou, M. Aljada, J. Liu and N. Motta, Sol. Energy, 2014, 106, 23–37 CrossRef CAS.
- M. Turner, V. B. Golovko, O. P. H. Vaughan, P. Abdulkin, A. Berenguer-Murcia, M. S. Tikhov, B. F. G. Johnson and R. M. Lambert, Nature, 2008, 454, 981–983 CrossRef CAS PubMed.
- M.-C. Daniel and D. Astruc, Chem. Rev., 2004, 104, 293–346 CrossRef CAS PubMed.
- A. B. Chinen, C. M. Guan, J. R. Ferrer, S. N. Barnaby, T. J. Merkel and C. A. Mirkin, Chem. Rev., 2015, 115, 10530–10574 CrossRef CAS PubMed.
- M. Faraday, Philos. Trans. R. Soc. London, 1857, 14, 145–181 Search PubMed.
- J. Turkevich, P. C. Stevenson and J. Hillier, Discuss. Faraday Soc., 1951, 11, 55 RSC.
- G. Frens, Nat. Phys. Sci., 1973, 241, 20–22 CrossRef CAS.
- T. Yonezawa and T. Kunitake, Colloids Surf., A, 1999, 149, 193–199 CrossRef CAS.
- M. Iqbal, G. Usanase, K. Oulmi, F. Aberkane, T. Bendaikha, H. Fessi, N. Zine, G. Agusti, E.-S. Errachid and A. Elaissari, Mater. Res. Bull., 2016, 79, 97–104 CrossRef CAS.
- M. Brust, M. Walker, D. Bethell, D. J. Schiffrin and R. Whyman, J. Chem. Soc., Chem. Commun., 1994, 801–802 RSC.
- J.-W. Park and J. S. Shumaker-Parry, J. Am. Chem. Soc., 2014, 136, 1907–1921 CrossRef CAS PubMed.
- K. M. Tibbetts, B. Tangeysh, J. H. Odhner and R. J. Levis, J. Phys. Chem. A, 2016, 120, 3562–3569 CrossRef PubMed.
- V. K. Meader, M. G. John, C. J. Rodrigues and K. M. Tibbetts, J. Phys. Chem. A, 2017, 121, 6742–6754 CrossRef CAS PubMed.
- T. J. Woehl, J. E. Evans, I. Arslan, W. D. Ristenpart and N. D. Browning, ACS Nano, 2012, 6, 8599–8610 CrossRef CAS PubMed.
- I. G. Gonzalez-Martinez, A. Bachmatiuk, V. Bezugly, J. Kunstmann, T. Gemming, Z. Liu, G. Cuniberti and M. H. Rümmeli, Nanoscale, 2016, 8, 11340–11362 RSC.
- Y. Zhang, D. Keller, M. D. Rossell and R. Erni, Chem. Mater., 2017, 29, 10518–10525 Search PubMed.
- Q. Chen, J. Li and Y. Li, J. Phys. D: Appl. Phys., 2015, 48, 424005 CrossRef.
- C. Richmonds and R. M. Sankaran, Appl. Phys. Lett., 2008, 93, 131501 CrossRef.
- T. Kaneko, K. Baba, T. Harada and R. Hatakeyama, Plasma Processes Polym., 2009, 6, 713–718 CrossRef CAS.
- Q. Chen, T. Kaneko and R. Hatakeyama, Chem. Phys. Lett., 2012, 521, 113–117 CrossRef CAS.
- J. Patel, L. Němcová, P. Maguire, W. G. Graham and D. Mariotti, Nanotechnology, 2013, 24, 245604 Search PubMed.
- H. Furusho, K. Kitano, S. Hamaguchi and Y. Nagasaki, Chem. Mater., 2009, 21, 3526–3535 Search PubMed.
- W. H. Chiang, C. Richmonds and R. M. Sankaran, Plasma Sources Sci. Technol., 2010, 19, 034011 CrossRef.
- X. Z. Huang, X. X. Zhong, Y. Lu, Y. S. Li, A. E. Rider, S. A. Furman and K. Ostrikov, Nanotechnology, 2013, 24, 95604 Search PubMed.
- R. Wang, S. Zuo, W. Zhu, S. Wu, W. Nian, J. Zhang and J. Fang, Plasma Processes Polym., 2014, 11, 44–51 Search PubMed.
- N. Shirai, S. Uchida and F. Tochikubo, Jpn. J. Appl. Phys., 2014, 53, 46202 Search PubMed.
- D. Mariotti, J. Patel, V. Švrček and P. Maguire, Plasma Processes Polym., 2012, 9, 1074–1085 Search PubMed.
- H. Lee, S. H. Park, S.-C. Jung, J.-J. Yun, S.-J. Kim and D.-H. Kim, J. Mater. Res., 2013, 28, 1105 CrossRef CAS.
- C. Richmonds, M. Witzke, B. Bartling, S. W. Lee, J. Wainright, C.-C. Liu and R. M. Sankaran, J. Am. Chem. Soc., 2011, 133, 17582–17585 Search PubMed.
- Y. Zheng, L. Wang and P. Bruggeman, J. Vac. Sci. Technol., A, 2020, 38, 063005 Search PubMed.
- P. Maguire, D. Rutherford, M. Macias-Montero, C. Mahony, C. Kelsey, M. Tweedie, F. Pérez-Martin, H. McQuaid, D. Diver and D. Mariotti, Nano Lett., 2017, 17, 1336–1343 CrossRef CAS PubMed.
- K. Nitta, Y. Shimizu, K. Terashima and T. Ito, J. Phys. D: Appl. Phys., 2021, 54, 33LT01 CrossRef CAS.
- B. R. Panda and A. Chattopadhyay, J. Nanosci. Nanotechnol., 2007, 7, 1911–1915 CrossRef CAS PubMed.
- K. Pacławski and K. Fitzner, Metall. Mater. Trans. B, 2006, 37, 703–714 CrossRef.
- T. K. Sarma, D. Chowdhury, A. Paul and A. Chattopadhyay, Chem. Commun., 2002, 1048–1049 Search PubMed.
- Q. Li, B. Lu, L. Zhang and C. Lu, J. Mater. Chem., 2012, 22, 13564–13570 Search PubMed.
- X. Liu, H. Xu, H. Xia and D. Wang, Langmuir, 2012, 28, 13720–13726 Search PubMed.
- M. A. Watzky and R. G. Finke, J. Am. Chem. Soc., 1997, 119, 10382–10400 Search PubMed.
- R. Burlica and B. R. Locke, IEEE Trans. Ind. Appl., 2008, 44, 482–489 Search PubMed.
- R. Becker and W. Döring, Kinetic Treatment of the Nucleation in Supersaturated Vapors, National Advisory Commitee for Aeronautics, 1954 Search PubMed.
- V. K. LaMer, Ind. Eng. Chem. Res., 1952, 44, 1270–1277 Search PubMed.
- V. K. LaMer and R. H. Dinegar, J. Am. Chem. Soc., 1950, 72, 4847–4854 Search PubMed.
- H. Reiss, J. Chem. Phys., 1951, 19, 482–487 Search PubMed.
- J. Turkevich, P. C. Stevenson and J. Hillier, J. Phys. Chem., 1953, 57, 670–673 CrossRef CAS.
- J. Polte, CrystEngComm, 2015, 17, 6809–6830 RSC.
- G. Oinuma, G. Nayak, Y. Du and P. J. Bruggeman, Plasma Sources Sci. Technol., 2020, 29, 095002 CrossRef CAS.
- G. Nayak, G. Oinuma, Y. Yue, J. S. Sousa and P. Bruggeman, Plasma Sources Sci. Technol., 2021, 30, 115003 CrossRef CAS.
- G. Nayak, J. Wang, R. Li, D. Aranzales, S. M. Thagard and P. J. Bruggeman, Plasma Processes Polym., 2023, 20, e2200222 CrossRef.
- G. Nayak, M. Meyer, G. Oinuma, M. J. Kushner and P. Bruggeman, Plasma Sources Sci. Technol., 2023, 32, 045005 Search PubMed.
- G. Nayak, N. Sadeghi and P. J. Bruggeman, Plasma Sources Sci. Technol., 2019, 28, 125006 CrossRef.
- I. Dotan, W. Lindinger and D. L. Albritton, J. Chem. Phys., 1977, 67, 5968–5969 CrossRef CAS.
- R. Sander, Atmos. Chem. Phys., 2015, 15, 4399–4981 CrossRef CAS.
- P. J. Bruggeman, M. J. Kushner, B. R. Locke, J. G. E. Gardeniers, W. G. Graham, D. B. Graves, R. C. H. M. Hofman-Caris, D. Maric, J. P. Reid, E. Ceriani, D. F. Rivas, J. E. Foster, S. C. Garrick, Y. Gorbanev, S. Hamaguchi, F. Iza, H. Jablonowski, E. Klimova, J. Kolb, F. Krcma, P. Lukes, Z. Machala, I. Marinov, D. Mariotti, S. M. Thagard, D. Minakata, E. C. Neyts, J. Pawlat, Z. L. Petrovic, R. Pflieger, S. Reuter, D. C. Schram, S. Schröter, M. Shiraiwa, B. Tarabová, P. A. Tsai, J. R. R. Verlet, T. von Woedtke, K. R. Wilson, K. Yasui and G. Zvereva, Plasma Sources Sci. Technol., 2016, 25, 053002 Search PubMed.
- H. Shiraishi, G. R. Sunaryo and K. Ishigure, J. Phys. Chem., 1994, 98, 5164–5173 CrossRef CAS.
- J. Ma, U. Schmidhammer and M. Mostafavi, J. Phys. Chem. Lett., 2014, 5, 2219–2223 Search PubMed.
- J. K. Lee, D. Samanta, H. G. Nam and R. N. Zare, Nat. Commun., 2018, 9, 1562 Search PubMed.
- B. Derjaguin and L. Landau, Prog. Surf. Sci., 1993, 43, 30–59 CrossRef.
- E. J. W. Verwey, J. Th and G. Overbeek, J. Phys. Chem., 1947, 51, 631–636 CrossRef CAS PubMed.
- J. Polte, R. Erler, A. F. Thünemann, S. Sokolov, T. T. Ahner, K. Rademann, F. Emmerling and R. Kraehnert, ACS Nano, 2010, 4, 1076–1082 Search PubMed.
- M. B. Hariri, A. Dolati and R. S. Moakhar, J. Electrochem. Soc., 2013, 160, D279 Search PubMed.
- A. M. Nowicka, U. Hasse, M. Hermes and F. Scholz, Angew. Chem., Int. Ed., 2010, 49, 1061–1063 Search PubMed.
- M. S. Ide and R. J. Davis, Acc. Chem. Res., 2014, 47, 825–833 Search PubMed.
- X. Chen, J. Schröder, S. Hauschild, S. Rosenfeldt, M. Dulle and S. Förster, Langmuir, 2015, 31, 11678–11691 Search PubMed.
- R. Brandenburg, H. Lange, T. von Woedtke, M. Stieber, E. Kindel, J. ö. Ehlbeck and K.-D. Weltmann, IEEE Trans. Plasma Sci., 2009, 37, 877–883 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc01192a |
| This journal is © The Royal Society of Chemistry 2024 |