Open Access Article
Open Access ArticleSurface proton hopping conduction mechanism dominant polymer electrolytes created by self-assembly of bicontinuous cubic liquid crystals†
Takahiro
Ichikawa
 *a,
Takeshi
Yamada
*a,
Takeshi
Yamada
 *b,
Nanami
Aoki
a,
Yuki
Maehara
a,
Kaori
Suda
a and
Tsubasa
Kobayashi
*b,
Nanami
Aoki
a,
Yuki
Maehara
a,
Kaori
Suda
a and
Tsubasa
Kobayashi
 a
a
aDepartment of Biotechnology and Life Science, Tokyo University of Agriculture and Technology, Naka-cho, Koganei, Tokyo 184-8588, Japan. E-mail: t-ichi@cc.tuat.ac.jp
bNeutron Science and Technology Center, Comprehensive Research Organization for Science and Society, Tokai, Ibaraki, 319-1106, Japan
First published on 10th April 2024
Abstract
For the development of the next generation of fuel cells, it is essential to create an innovative design principle of polymer electrolytes that is beyond extension of the existing strategy. In the present study, we focused on the surface hopping proton conduction mechanism where an activation energy for proton conduction is greatly reduced by decreasing the distance between SO3− groups. Our gyroid nanostructured polymer film (Film-G), with a hydrophilic surface where the SO3− groups are aligned densely and precisely, shows high proton conductivity of the order of 10−2 S cm−1 when the water content is about 15 wt%. We reveal that the high proton conductivity of Film-G is attributed to the exhibition of an extremely-fast surface hopping conduction mechanism due to the reduced activation energy barrier along the gyroid minimal surface. This finding should introduce a game-changing novel opportunity in polymer electrolyte design.
Introduction
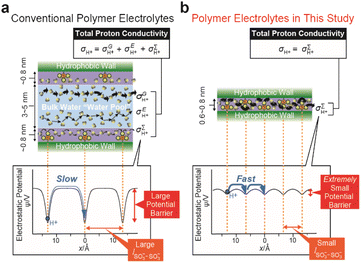
Nafion, which was developed in the late 1960s by DuPont, is surely the most successful polymer electrolyte because of its advanced proton conductivity and high mechanical stability.1–3 Significant efforts have been made for several decades to develop proton conductive polymer electrolytes beyond Nafion;4 however, Nafion still reigns as the most commonly used polymer electrolyte membrane for fuel cells and some other applications.3 Proton conduction in Nafion can be understood using a simple 2D nanochannel model composed of a water nanochannel sandwiched between hydrophobic walls (Fig. 1a).5,6 There are three proton conduction mechanisms in the nanochannel. One is the Grotthuss mechanism,7 which is a mechanism to transport protons via the formation/cleavage of hydrogen-bonding networks of water molecules in the bulk water region, namely a water pool, in the center of the nanochannel. The second is the en masse diffusion mechanism, which is the mechanism whereby hydrated oxonium ions migrate in the water pool. The third one is the surface proton hopping conduction (SPHC) mechanism where there are proton hops (PHs) from an SO3− site on the surface of the hydrophobic wall to the neighboring SO3− site via bridging water molecules between them. The proton conductivities in each mechanism are represented by σG, σE, and σ∑, respectively. The total proton conductivity of the polymer electrolyte membranes is σG + σE + σ∑. Because of the significantly high proton conductivity in the Grotthuss mechanism, it has been common sense that the construction of macroscopically-continuous water pools, to enhance the contribution of σG, is the most important design principle for creating advanced proton conductive polymer electrolytes.Here, we propose a totally new design principle departing from the common sense idea for the creation of proton conductive polymer electrolytes showing high proton conductivity. We focused on the theoretical foresight on the SPHC mechanism. In 2001, Eikerling et al. revealed that distances between the neighboring SO3− groups (lSO3−–SO3−) on a hydrophobic wall surface strongly influence the electrostatic potential barrier in a direction parallel to the hydrophobic wall surface, ψ (Fig. 1a).5 According to their estimates, when lSO3−–SO3− = 15 Å, ψ is about 30 kJ mol−1 while it reduces exponentially to 2–3 kJ mol−1 as lSO3−–SO3− decreases to 5 Å. Since lSO3−–SO3− values in Nafion are relatively large at approximately 12 to 20 Å,3,5 the ψ in Nafion is considered to be very large and consequently the σ∑ of Nafion appears as a very small value. These insights have led many researchers to consider the SPHC mechanism to be trivial; however, we envision that the dense and highly periodic alignment of SO3− sites on a continuous surface should enable an ultrafast SPHC mechanism with an extremely small electrostatic potential barrier, resulting in the exhibition of a high proton conductivity on the order of 10−2 to 10−1 S cm−1, that is, comparable to σG in Nafion and/or bulk water (Fig. 1b). Recently, the number of studies on the design of advanced proton conductive materials focusing on the alignment of the SO3− groups has been increasing.8–15 Moreover, there are some studies that focus on the importance of the SPHC mechanism.16,17 There are also some studies that have employed the potential utility of zwitterions as ion conductive materials.18–20 Even bearing these previous studies in mind, the present work is the first study in which high proton conductivity is induced solely by the SPHC mechanism with an extremely-small activation energy.
Results and discussion
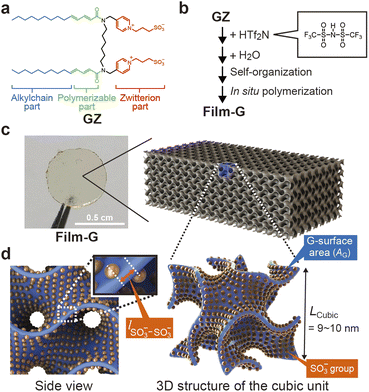
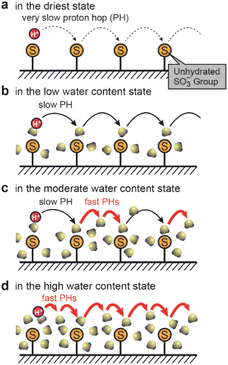
Aiming for the construction of polymer electrolytes with a dense and highly periodic alignment of SO3− sites for the SPHC mechanism, we focused on our previously-designed liquid-crystalline (LC) amphiphile GZ (Fig. 2a).21GZ has an ability to co-organize into bicontinuous cubic (Cubbi) phases with some acids, such as bis(trifluoromethane)sulfonimide (HTf2N) (Fig. 2b) and a small amount of water. In the Cubbi phase, all of the SO3− groups of GZ are aligned on a 3D gyroid minimal surface (G-surface) in a cubic cell with a lattice parameter (LCubic) of approximately 9–10 nm. A significant point is that it is possible to preserve its unique molecularly assembled nanostructure by in situ polymerization, which yields a self-standing polymer film, Film-G, with gyroid nanostructures (Fig. 2c). We roughly calculated lSO3−–SO3− in Film-G containing X wt% of water (Film-G(X)) based on structural analysis and its physicochemical properties (Fig. S2†). lSO3−–SO3− in Film-G(16.4) was estimated to be roughly 5.9 Å (Fig. 2d and S3†), which is predominantly shorter than that in Nafion. This is a value for which one can expect the exhibition of an ultrafast SPHC mechanism with a very small electrostatic potential barrier, ψ.We expect that SPHC mechanisms in Film-G with lSO3−–SO3− = 5.9 Å can be roughly classified into four types depending on the degree of hydration of the SO3− groups (Fig. 3a–d). In the driest state, SPHC is composed only of very slow PHs due to the strong electrostatic interaction between the SO3− anion and a proton (Fig. 3a). In the low-water-content state, these PHs are slightly accelerated due to the hydration of the SO3− groups that largely weakens SO3−–proton interactions, while the PH speed is still slow because lSO3−–SO3− = 5.9 Å is a large value for a proton to hop directly (Fig. 3b). A further increase in water content leads to the situation where two hydrated SO3− groups are connected via bound water molecules. PHs via these hydrated SO3− groups are greatly accelerated, while PHs via those with fewer bound water molecules are still slow (Fig. 3c). When the water content reaches a situation where all the SO3− groups are connected by bound water molecules (Fig. 3d), all PHs are highly activated and an effective SPHC mechanism is enabled at a macroscopic scale. This expectation is consistent with the dependence of proton conductivity (σH+) of Film-G on water content that was reported in our previous study.21
When the SPHC is dominant in proton conductivity, its σH+ can be described by
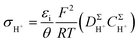 | (1) |
According to the view of random walk diffusion, DH+Σ is given by the Einstein–Smoluchowski equation22,23
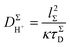 | (2) |
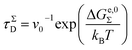 | (3) |
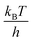 , where h is Planck's constant. The main component of ΔGe,0Σ is the potential barrier in the SPHC mechanism.5 Assuming that the proton conduction in Film-G(X) is solely based on the SPHC mechanism, ΔGe,0Σ was estimated to be 13.3 kJ mol−1 for Film-G(15.2) using the experimental value of σH+ = 8.5 × 10−3 S cm−1 (Tables S4 and S5†). To confirm the validity of ΔGe,0Σ = 13.3 kJ mol−1, we examined the activation energy (Ea) of Film-G(X). The temperature dependences of σH+ of Film-G(15.2), Film-G(9.9), and Film-G(6.0) are shown in Fig. 4 using an Arrhenius plot. The measurements were performed in a narrow temperature range of 30 to 40 °C under a constant relative humidity of 90% with the aim of reducing the change in water content during the measurements. Ea was found to be 17.2 kJ mol−1 for Film-G(15.2), which was close enough to ΔGe,0Σ = 13.3 kJ mol−1. Since there is a small increase in the water content in Film-G(15.2) upon heating from 30 to 40 °C when the sample is kept under RH = 90% due to the increase in the absolute humidity, Ea = 17.2 kJ mol−1 is expected to be an overestimate. The exact value of Ea should be slightly smaller than 17.2 kJ mol−1, meaning that our estimate of ΔGe,0Σ = 13.3 kJ mol−1 is very reasonable. These results strongly support the validity of our assumption that the SPHC mechanism is solely-dominant for the proton conduction mechanism in Film-G(15.2). Conversely, larger values of Ea = 26.8 and 35.3 kJ mol−1 were found for Film-G(9.9) and Film-G(6.0), respectively, with lower water contents. This can be explained by the situation, where the SO3− groups are partially bridged with bound water molecules, as shown in Fig. 3c, and some PHs with slower speed exist along the G-surface. This indicates that a suitable amount of water molecules is required to exclude slow PHs and yield only fast PHs, leading to the exhibition of high proton conductivity at a macroscopic scale.
, where h is Planck's constant. The main component of ΔGe,0Σ is the potential barrier in the SPHC mechanism.5 Assuming that the proton conduction in Film-G(X) is solely based on the SPHC mechanism, ΔGe,0Σ was estimated to be 13.3 kJ mol−1 for Film-G(15.2) using the experimental value of σH+ = 8.5 × 10−3 S cm−1 (Tables S4 and S5†). To confirm the validity of ΔGe,0Σ = 13.3 kJ mol−1, we examined the activation energy (Ea) of Film-G(X). The temperature dependences of σH+ of Film-G(15.2), Film-G(9.9), and Film-G(6.0) are shown in Fig. 4 using an Arrhenius plot. The measurements were performed in a narrow temperature range of 30 to 40 °C under a constant relative humidity of 90% with the aim of reducing the change in water content during the measurements. Ea was found to be 17.2 kJ mol−1 for Film-G(15.2), which was close enough to ΔGe,0Σ = 13.3 kJ mol−1. Since there is a small increase in the water content in Film-G(15.2) upon heating from 30 to 40 °C when the sample is kept under RH = 90% due to the increase in the absolute humidity, Ea = 17.2 kJ mol−1 is expected to be an overestimate. The exact value of Ea should be slightly smaller than 17.2 kJ mol−1, meaning that our estimate of ΔGe,0Σ = 13.3 kJ mol−1 is very reasonable. These results strongly support the validity of our assumption that the SPHC mechanism is solely-dominant for the proton conduction mechanism in Film-G(15.2). Conversely, larger values of Ea = 26.8 and 35.3 kJ mol−1 were found for Film-G(9.9) and Film-G(6.0), respectively, with lower water contents. This can be explained by the situation, where the SO3− groups are partially bridged with bound water molecules, as shown in Fig. 3c, and some PHs with slower speed exist along the G-surface. This indicates that a suitable amount of water molecules is required to exclude slow PHs and yield only fast PHs, leading to the exhibition of high proton conductivity at a macroscopic scale.
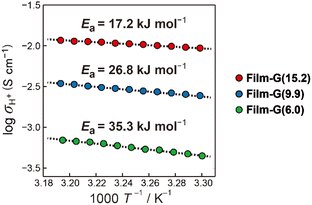 | ||
| Fig. 4 Experimentally-obtained σH+ values of Film-G(15.2), Film-G(9.9), and Film-G(6.0) plotted against the reciprocal of absolute temperature. | ||
Here, we compare the estimated physical property values of Film-G with those of Nafion. Using the value of ΔGe,0Σ = 13.3 kJ mol−1, the DH+Σ of Film-G(15.2) is calculated to be 6.99 × 10−6 cm2 s−1, which is 70 times larger than that in Nafion.6 The ultrafast SPHC in Film-G(15.2) is ascribed to the formation of a considerably reduced electrostatic potential barrier on the G-surface by the correlated barrier hopping model24 that was realized for the first time by creating a unique situation, where the SO3− groups are placed on a continuous surface in a dense and highly-periodic manner.
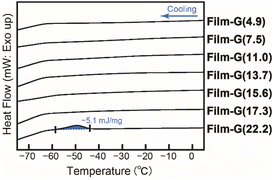
The experimental results on the water composition dependence of the σH+ of Film-G indicated that it is necessary to introduce a suitable amount of water molecules on the SO3−-aligned surface to enable the SPHC mechanism with a reduced ψ. We expected that the elucidation of the water state, dynamics and their composition dependence should be a significant way to understand the proton conduction mechanism in Film-G(X). The state of water in Film-G(X) was examined by DSC measurements (Fig. 5 and S11†). The DSC thermograms on cooling are shown in Fig. 5. There is no exothermic peak corresponding to the crystallization of water when the water content X is 17.3 wt% or less, while a small exothermic peak is observed when X = 22.2 wt%. These results clearly suggest that the water molecules in Film-G(X) exist as non-freezing bound water at least when X ≤ 17.3, suggesting that the ultrafast SPHC mechanism in Film-G(15.2) is assisted only by non-freezing bound water.
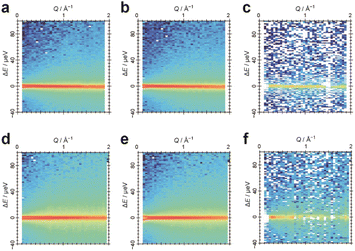
With the aim of further investigating the dynamics of water in Film-G(X), we focused on quasi-elastic neutron scattering (QENS) measurements. QENS is a powerful technique for investigating the dynamics of water molecules in the picosecond to nanosecond timeframe and Ångstrom length-scale due to the large incoherent scattering cross-section of hydrogen. It has been employed for various materials including Nafion to reveal the dynamics of water molecules in it.25,26 Unlike Nafion that is mainly composed of C, O, S, and F elements, Film-G contains many hydrogen atoms. Thus, to obtain information on the dynamics of the water molecules in Film-G, we planned to examine the difference between the QENS spectra of Film-G containing normal water (H2O) and those of Film-G containing heavy water (D2O). Two types of Film-G samples with moderate water content (9.0 wt% (Film-G(9.0))) and high water content (16.4 wt% (Film-G(16.4))) were prepared by putting them under controlled relative humidity conditions. Resultant polymer films contain 3.0 and 6.0 water molecules per SO3− group, respectively. Below they are described as Film-G/mH2O (m = 3 and 6). Using D2O, Film-G/mD2O (m = 3 and 6) were also prepared.
QENS experiments were carried out for these four samples at 300, 280, 260, and 240 K. The same experiment was performed at 10 K for resolution. Contour maps of QENS data of Film-G/3H2O and Film-G/3D2O at 300 K are shown in Fig. 6a and b. X- and Y-axes are momentum transfer (Q) and energy transfer (ΔE), respectively. ΔE reflects the quantity of energy exchange between an incident neutron and the sample. If a sample shows a relaxation phenomenon, a broad peak is observed as QENS around the elastic position (ΔE = 0). The width of the QENS broadening is inversely proportional to the relaxation time.27 There is a strong sharp scattering intensity at ΔE = 0, and a moderate broad scattering intensity centered at ΔE = 0, indicating that elastic and quasi-elastic components exist in the films. To extract the information on water molecules in Film-G, a differential contour map between the two was created using a scaling factor derived from the weight ratio of the two samples in the dry state (Fig. 6c). In the differential contour map, a significant difference is found mostly only in the ΔE = 0 region, indicating that the dynamics of the water molecules in Film-G/3H2O have almost stopped or are slower than the timescale represented by the instrumental energy resolution. Conversely, completely different results were obtained when m = 6. The contour maps of the QENS data of Film-G/6H2O and Film-G/6D2O and their differential data are shown in Fig. 6d–f. It is noteworthy that a broad scattering intensity was found in Fig. 6f, indicating that there is a certain amount of mobile water molecules in Film-G/6H2O.
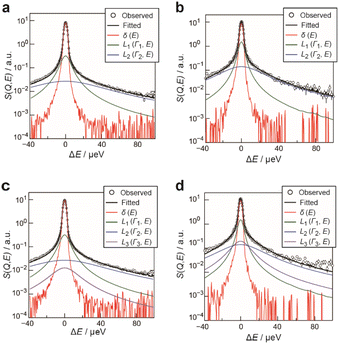
To evaluate the dynamics of the water molecules in Film-G more quantitatively, we analyzed the QENS profiles of Film-G/mD2O and Film-G/mH2O (m = 3 and 6). The QENS profiles of m = 3 were integrated in the Q direction due to the small contribution from hydrated water. The obtained results were fitted by the following phenomenological equation
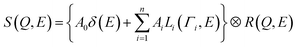 | (4) |
In the case of m = 3, the number of immobile and mobile hydrogen atoms (NH(immob) and NH(mob)) in Film-G/3H2O was estimated as follows,
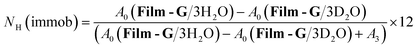 | (5) |
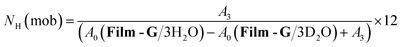 | (6) |
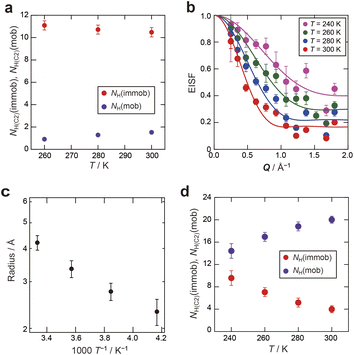 | ||
| Fig. 8 (a) Number of immobile and mobile hydrogen atoms (NH(immob) and NH(mob)) in 3H2O. (b) Q dependence of EISF of 6H2O in Film-G/6H2O. The solid lines are results fitted with eqn (8). (c) Temperature dependence of the radius of the confined sphere obtained from the fitted results of the EISF (b). (d) Number of immobile and mobile hydrogen atoms (NH(immob) and NH(mob)) in 6H2O. | ||
In contrast, in the case of m = 6, since it was revealed that a certain amount of the water molecules are in the mobile state, the Q dependence of the parameter L3 was examined to extract spatial information about the observed dynamics. The Q dependence of Γ3 at 300 K did not approach zero at Q = 0 Å−1 (Fig. S20†). Although obtained data was scattered, Γ3 was found to be almost constant with respect to Q. These results suggest that the observed dynamics corresponding to L3 is a local mode, such as rotation and/or local jumps of the water molecules. A similar trend was also observed at other temperatures. This means the scale of the localized mode is within a scale of several Ångstroms. For further consideration, the Q dependence of the elastic incoherent scattering factor (EISF) was calculated as follows,
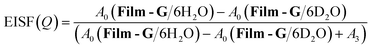 | (7) |
The Q dependence of EISF, as plotted in Fig. 8b, was well reproduced by a diffusion model in the confined sphere,28 as follows,
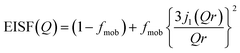 | (8) |
The relaxation time of these mobile water molecules (τQENS) was evaluated using the following formula,
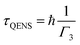 | (9) |
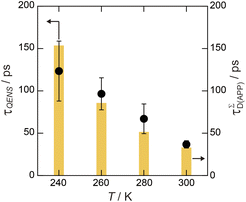 | ||
| Fig. 9 Relaxation time of mobile water molecules (τQENS) estimated from the HWHM of L3 in 6H2O. τΣD values of Film-G(15.2) at various temperatures are also shown in the yellow bar graph. | ||
Conclusions
We have succeeded in demonstrating the potential utility of the surface proton hopping conduction (SPHC) mechanism for the development of advanced proton conductive polymer electrolytes. These findings will contribute to the development of advanced fuel cells, such as anhydrous-drive-type and/or low-temperature-drive-type ones. From a comprehensive viewpoint, present findings suggest that control over self-organization should be a key strategy for creating new functional materials that support next-generation technologies.Data availability
The datasets supporting this article have been uploaded as part of the ESI.†Author contributions
T. I. supervised this project. T. I. and T. K. designed materials. T. I., N. A., Y. M., K. S., T. K., and T. Y. performed the experiments and analyzed the data. T. I. and T. Y. wrote the manuscript. All authors discussed the results and commented on the manuscript. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Japan Science and Technology Agency (JST) FOREST (JPMJFR223C). This work was also supported by JSPS KAKENHI numbers JP21H02010, JP22H04526, and JP23K17937 from the Japan Society for the Promotion of Science. This work was partially supported by Nippon Sheet Glass Foundation for Materials Science and Engineering. The QENS experiments at the Materials and Life Science Experimental Facility of the J-PARC was performed under a user program (Proposal No. 2022A0005 and 2023A0072).Notes and references
- K.-D. Kreuer, Chem. Mater., 1996, 8, 610–641 CrossRef CAS.
- K. A. Mauritz and R. B. Moore, Chem. Rev., 2004, 104, 4535–4586 CrossRef CAS PubMed.
- A. Kusoglu and A. Z. Weber, Chem. Rev., 2017, 117, 987–1104 CrossRef CAS PubMed.
- T. J. Peckham and S. Holdcroft, Adv. Mater., 2010, 22, 4667–4690 CrossRef CAS PubMed.
- M. Eikerling and A. A. Kornyshev, J. Electroanal. Chem., 2001, 502, 1–14 CrossRef CAS.
- P. Choi, N. H. Jalani and R. Datta, J. Electrochem. Soc., 2005, 152, E123–E130 CrossRef CAS.
- N. Agmon, Chem. Phys. Lett., 1995, 244, 456–462 CrossRef CAS.
- T. Kato, M. Yoshio, T. Ichikawa, B. Soberats, H. Ohno and M. Funahashi, Nat. Rev. Mater., 2017, 2, 17001 CrossRef.
- S. Ueda, J. Kagimoto, T. Ichikawa, T. Kato and H. Ohno, Adv. Mater., 2011, 23, 3071–3074 CrossRef CAS PubMed.
- T. Ichikawa, T. Kato and H. Ohno, J. Am. Chem. Soc., 2012, 134, 11354–11357 CrossRef CAS PubMed.
- Y. Chen, M. Thorn, S. Christensen, C. Versek, A. Poe, R. C. Hayward, M. T. Tuominen and S. Thayumanavan, Nat. Chem., 2010, 2, 503–508 CrossRef CAS PubMed.
- G. L. Jackson, D. V. Perroni and M. K. Mahanthappa, J. Phys. Chem. B, 2017, 121, 9429–9436 CrossRef CAS PubMed.
- Y. Nagao, Langmuir, 2017, 33, 12547–12558 CrossRef CAS PubMed.
- E. B. Trigg, T. W. Gaines, M. Maréchal, D. E. Moed, P. Rannou, K. B. Wagener, M. J. Stevens and K. I. Winey, Nat. Mater., 2018, 17, 725–731 CrossRef CAS PubMed.
- D.-W. Lim and H. Kitagawa, Chem. Soc. Rev., 2021, 50, 6349–6368 RSC.
- C. Yin, J. Li, Y. Zhou, H. Zhang, P. Fang and C. He, ACS Appl. Mater. Interfaces, 2018, 10, 14026–14035 CrossRef CAS PubMed.
- M. Tanaka, Polym. J., 2016, 48, 51–58 CrossRef CAS.
- M. Yoshizawa, M. Hirao, K. I. Akita and H. Ohno, J. Mater. Chem., 2001, 11, 1057–1062 RSC.
- C. Tiyapiboonchaiya, et al. , Nat. Mater., 2004, 3, 29–32 CrossRef CAS PubMed.
- O. Kim, K. Kim, U. H. Choi and M. J. Park, Nat. Commun., 2018, 9, 5029 CrossRef PubMed.
- T. Kobayashi, Y. Li, A. Ono, X.-b. Zeng and T. Ichikawa, Chem. Sci., 2019, 10, 6245–6253 RSC.
- P. W. Atkins, Physical Chemistry, W. H. Freeman and Company, New York, 3rd edn, 1986 Search PubMed.
- J. Philibert, Atom Movements Diffusion and Mass Transport in Solids, Les Editions de Physique, Les Ulis, 1991 Search PubMed.
- Y. Ben Taher, et al. , Appl. Phys. A, 2015, 120, 1537–1543 CrossRef CAS.
- J.-C. Perrin, S. Lyonnard and F. Volino, J. Phys. Chem. C, 2007, 111, 3393–3404 CrossRef CAS.
- Q. Berrod, S. Hanot, A. Guillermo, S. Mossa and S. Lyonnard, Sci. Rep., 2017, 7, 8326 CrossRef PubMed.
- M. Bée, Quasielastic Neutron Scattering: Principles and Applications in Solid State Chemistry, Biology, and Materials Science, Adam Hilger, Bristol, England, Philadelphia, 1988 Search PubMed.
- F. Volino and A. J. Dianoux, Mol. Phys., 1980, 41, 271 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc01211a |
| This journal is © The Royal Society of Chemistry 2024 |