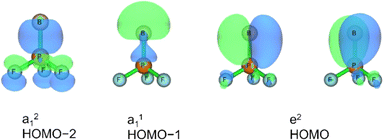Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h2_char_e001.gif) P double bonds relieved from steric encumbrance: matrix-isolation infrared spectroscopy of the phosphaborene F2B–P
P double bonds relieved from steric encumbrance: matrix-isolation infrared spectroscopy of the phosphaborene F2B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h2_char_e001.gif) BF and the triradical B
BF and the triradical B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h2_char_e001.gif) PF3†
PF3†
Mei
Wen
 ,
Robert
Medel
,
Robert
Medel
 ,
Pavel V.
Zasimov
,
Pavel V.
Zasimov
 ,
Carsten
Müller
,
Carsten
Müller
 and
Sebastian
Riedel
and
Sebastian
Riedel
 *
*
Freie Universität Berlin, Institut für Chemie und Biochemie – Anorganische Chemie, Fabeckstraße 34/36, 14195 Berlin, Germany. E-mail: s.riedel@fu-berlin.de
First published on 30th April 2024
Abstract
Free phosphaborenes have a labile boron–phosphorus double bond and therefore require extensive steric shielding by bulky substituents to prevent isomerisation and oligomerisation. In the present work, the small free phosphaborene F2B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BF was isolated by matrix-isolation techniques and was characterised by infrared spectroscopy in conjunction with quantum-chemical methods. In contrast to its sterically hindered relatives, this small phosphaborene exhibits an acute BPB angle of 83° at the CCSD(T) level. An alternative orbital structure for the B
BF was isolated by matrix-isolation techniques and was characterised by infrared spectroscopy in conjunction with quantum-chemical methods. In contrast to its sterically hindered relatives, this small phosphaborene exhibits an acute BPB angle of 83° at the CCSD(T) level. An alternative orbital structure for the B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P double bond is found in the triradical B
P double bond is found in the triradical B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF3, the direct adduct of laser-ablated atomic B and PF3. The single-bonded isomer F2B–PF and the dimer F3P–B
PF3, the direct adduct of laser-ablated atomic B and PF3. The single-bonded isomer F2B–PF and the dimer F3P–B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B–PF3 are also tentatively assigned.
B–PF3 are also tentatively assigned.
Introduction
Linear iminoboranes RB![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) NR′ are isoelectronic to alkynes RC
NR′ are isoelectronic to alkynes RC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR′ and subject of a maturing field or research.1 In contrast, reports on phosphaborenes RB
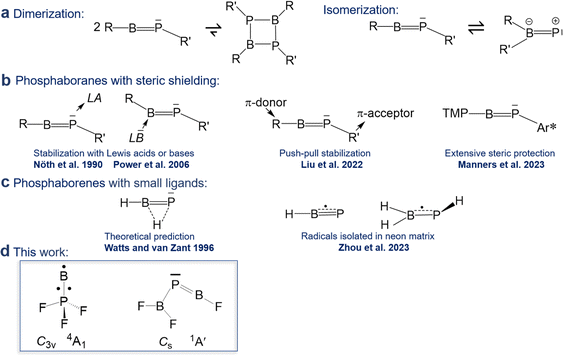
CR′ and subject of a maturing field or research.1 In contrast, reports on phosphaborenes RB![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PR′ (also called boraphosphenes or phosphinidene boranes) were very rare for a longer period of time and only recently became more frequently. This backlog is due to the challenge of overcoming the very strong tendency of phosphaborenes to oligo- and isomerize (Scheme 1a), as they have a double bond rather than a triple bond, with a free electron pair on the phosphorus atom and a vacant p-orbital on the boron atom. This bonding situation is reflected in bent structures with a BPR′ angle that is strongly dependent on the substituents R and R′ in a range of at least 52–123°.2,3
PR′ (also called boraphosphenes or phosphinidene boranes) were very rare for a longer period of time and only recently became more frequently. This backlog is due to the challenge of overcoming the very strong tendency of phosphaborenes to oligo- and isomerize (Scheme 1a), as they have a double bond rather than a triple bond, with a free electron pair on the phosphorus atom and a vacant p-orbital on the boron atom. This bonding situation is reflected in bent structures with a BPR′ angle that is strongly dependent on the substituents R and R′ in a range of at least 52–123°.2,3
 | ||
| Scheme 1 Overview of previous work on phosphaborenes. TMP = 2,2,6,6-tetramethyl piperidine, Ar* = 2,6-bis(triisopropylphenyl)-3,5-diisopropylphenyl. | ||
The first free phosphaborene was observed in 1986 by mass spectrometry after thermolysis of its sterically encumbered dimer.4 The first room temperature stable phosphaborene was reported in 1990, obtained by ring cleavage, facilitated by additional coordination of a Lewis acid to the phosphorus atom for further steric shielding.5 As a counter-strategy, it was later shown that protecting the boron atom by coordinating a bulky Lewis base was also viable.6–9 Free phosphaborenes without further coordination could be isolated only very recently by utilizing substituents R and R′ that are either even more sterically demanding10 or combine π-acceptor and π-donor capabilities in a kind of push–pull cooperation, in addition to their bulkiness (Scheme 1b).9 However, extensive steric shielding also limits a possible application of phosphaborenes as further reagents.10,11 The design of substituents that balance stability and reactivity is therefore a current challenge.
Free phosphaborenes with sterically undemanding ligands were theoretically predicted to be thermodynamically and kinetically unstable, not only with respect to oligomerization, but also to 1,2-rearrangement to the RR′B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P isomer. Their experimental detection was therefore concluded to be unlikely.3 This also holds true for another theoretical investigation which considered further substitution patterns.12 However, a closer look at the calculations reveals that the picture is not as bleak as it was painted. For R = R′ = F, Cl or SiH3 the isomerization from RB
P isomer. Their experimental detection was therefore concluded to be unlikely.3 This also holds true for another theoretical investigation which considered further substitution patterns.12 However, a closer look at the calculations reveals that the picture is not as bleak as it was painted. For R = R′ = F, Cl or SiH3 the isomerization from RB![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PR′ to RR′B
PR′ to RR′B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P was indeed calculated to be exergonic, but endergonic for R = R′ = H, OH or CH3.3,12 Despite this prediction, the parent phosphaborene HB
P was indeed calculated to be exergonic, but endergonic for R = R′ = H, OH or CH3.3,12 Despite this prediction, the parent phosphaborene HB![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PH eluded experimental detection in recent work, but so did its isomers. Instead the radical species HBP and H2BPH were observed with formal B–P bond orders of 2.5 and 1.5, respectively (Scheme 1c).13 Furthermore, only homosubstituted (R = R′) small phosphaborenes have been considered in the above mentioned theoretical investigations, with the single exception of the ClB
PH eluded experimental detection in recent work, but so did its isomers. Instead the radical species HBP and H2BPH were observed with formal B–P bond orders of 2.5 and 1.5, respectively (Scheme 1c).13 Furthermore, only homosubstituted (R = R′) small phosphaborenes have been considered in the above mentioned theoretical investigations, with the single exception of the ClB![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF species.3,12 On the contrary, it has recently been proposed that dissimilar ligands with opposite electronic properties (π-donor and π-acceptor abilities for R and R′, respectively) can be used to stabilize the RB
PF species.3,12 On the contrary, it has recently been proposed that dissimilar ligands with opposite electronic properties (π-donor and π-acceptor abilities for R and R′, respectively) can be used to stabilize the RB![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PR′ moiety.9
PR′ moiety.9
Indeed, in the present article we report the detection of by far the smallest free phosphaborene to date, F2B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BF (Scheme 1d), which exhibits this type of push–pull stabilisation (π-acceptor R′ = F2B and π-donor R = F). Other species with varying degrees of B
BF (Scheme 1d), which exhibits this type of push–pull stabilisation (π-acceptor R′ = F2B and π-donor R = F). Other species with varying degrees of B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P double bonds have been assigned as well: the triradical B
P double bonds have been assigned as well: the triradical B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF3 and tentatively its isomer F2B–PF as well as its dimer F3P–B
PF3 and tentatively its isomer F2B–PF as well as its dimer F3P–B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B–PF. These molecules have been prepared via the reaction of laser-ablated B atoms with PF3, isolated in solid neon matrices and characterized by FTIR spectroscopy and theoretical methods.
B–PF. These molecules have been prepared via the reaction of laser-ablated B atoms with PF3, isolated in solid neon matrices and characterized by FTIR spectroscopy and theoretical methods.
Results and discussion
Vibrational assignment
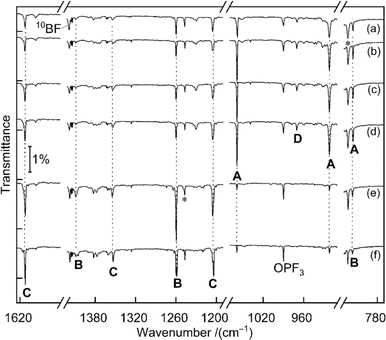
Fig. 1 displays matrix-isolation FTIR spectra obtained after codeposition of laser-ablated 10B-enriched boron atoms with 0.05% PF3 in neon at 5 K. In addition to known absorptions from BF, BF2, BF3, PF3−, PF5 and OPF3,14 new product bands were observed.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e001.gif) PF3.
A set of absorptions at 1058.9, 921.5 and 816.0 cm−1 (labeled as A) increased during sample annealing to 9 K and almost vanished upon subsequent irradiation (λ > 220 nm). This set is assigned to B
PF3.
A set of absorptions at 1058.9, 921.5 and 816.0 cm−1 (labeled as A) increased during sample annealing to 9 K and almost vanished upon subsequent irradiation (λ > 220 nm). This set is assigned to B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF3, the direct addition product of the two reactants atomic B and PF3. Analogous experiments were performed with a boron target with isotopes in natural abundance (10B
PF3, the direct addition product of the two reactants atomic B and PF3. Analogous experiments were performed with a boron target with isotopes in natural abundance (10B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11B ≈ 1
11B ≈ 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) (Fig. S1†). The 1058.9 cm−1 band exhibited a 19.8 cm−1 10B/11B isotopic shift and is assigned to the B
4) (Fig. S1†). The 1058.9 cm−1 band exhibited a 19.8 cm−1 10B/11B isotopic shift and is assigned to the B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P stretching mode. The 921.5 cm−1 band experienced no detectable isotopic shift, indicative of the antisymmetric P–F stretching mode without boron participation. The weak band at 816.0 cm−1 showed a 13.4 cm−1 isotopic shift and is attributed to the breathing mode for the in-phase change of all four bond lengths. This assignment of B
P stretching mode. The 921.5 cm−1 band experienced no detectable isotopic shift, indicative of the antisymmetric P–F stretching mode without boron participation. The weak band at 816.0 cm−1 showed a 13.4 cm−1 isotopic shift and is attributed to the breathing mode for the in-phase change of all four bond lengths. This assignment of B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF3 is supported by the agreement with the calculated vibrational wavenumbers and their 10B/11B isotopic shifts at CCSD(T) and B3LYP levels of theory (Tables 1 and S1†).
PF3 is supported by the agreement with the calculated vibrational wavenumbers and their 10B/11B isotopic shifts at CCSD(T) and B3LYP levels of theory (Tables 1 and S1†).
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF3 (A), F2B–PF (B) and F2B–P
PF3 (A), F2B–PF (B) and F2B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BF (C). IR intensities (in km mol−1) in parentheses were calculated at the B3LYP/aug-cc-pVTZ level
BF (C). IR intensities (in km mol−1) in parentheses were calculated at the B3LYP/aug-cc-pVTZ level
| Obs. ν(10B) | Cal. ν(10B) | Obs. Δν (11B) | Cal. Δν (11B) | Stretching mode | |
|---|---|---|---|---|---|
B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF3 (C3v, 4A1) PF3 (C3v, 4A1) |
816.0 | 813.9 (84) | 13.4 | 14.1 | Breathing |
| 921.5 | 921.7 (160 × 2) | 0.0 | 0.0 | Antis. PF3 | |
| 1058.9 | 1060.6 (219) | 19.8 | 20.4 | B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P P |
|
| F2B–PF (Cs, 2A′′) | — | 637.3 (8) | — | 5.2 | B–P |
| 816.0 | 819.6 (114) | 0.0 | 0.0 | PF | |
| 1260.0 | 1277.4 (323) | 40.7 | 41.2 | Sym. BF2 | |
| 1409.3 | 1454.8 (295) | 45.3 | 50.5 | Antis. BF2 | |
F2B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BF (Cs, 1A′) BF (Cs, 1A′) |
— | 628.6 (33) | — | 5.3 | B–P |
| — | 660.1 (2) | — | 2.5 | In-phase P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BF BF |
|
| 1205.4 | 1217.2 (569) | 39.5 | 39.4 | Sym. BF2 | |
| 1354.3 | 1384.5 (217) | 45.6 | 47.4 | Antis. BF2 | |
| 1613.1 | 1633.6 (548) | 53.2–58.7 (resonance) | 58.0 | Out-of-phase P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BF BF |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF3. Two bands at 1260.0 and 1409.3 cm−1 are strongly shifted upon boron isotope substitution by 40.7 and 45.3 cm−1, they are attributed to the symmetric and the antisymmetric BF2 vibration modes, respectively. An expected weak band for the P–F stretching mode likely coincides with the 816.0 cm−1 band of set A that did not decline as sharply as expected from the change of the isotope ratio. This could be explained by the fact that only the breathing mode of B
PF3. Two bands at 1260.0 and 1409.3 cm−1 are strongly shifted upon boron isotope substitution by 40.7 and 45.3 cm−1, they are attributed to the symmetric and the antisymmetric BF2 vibration modes, respectively. An expected weak band for the P–F stretching mode likely coincides with the 816.0 cm−1 band of set A that did not decline as sharply as expected from the change of the isotope ratio. This could be explained by the fact that only the breathing mode of B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF3 is shifted by the change of boron mass while the pure P–F stretching mode of F2B–PF is not. Compared to the B
PF3 is shifted by the change of boron mass while the pure P–F stretching mode of F2B–PF is not. Compared to the B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P stretching of B
P stretching of B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF3, the B–P stretching mode of F2B–PF is calculated to be substantially lower in wavenumber (1060.6 vs. 637.3 cm−1 at CCSD(T) level for 10B) and in IR intensity (219 vs. 9 km mol−1, calculated at B3LYP level), it is thus not observed. Because of the suspected overlap in the 816.0 cm−1 band and some deviation between the observed and calculated boron isotopic shift of the 1409.3 cm−1 band [50.5 vs. 45.3 cm−1, the latter value being consistent across different theoretical methods (Tables 1 and S1†)], we consider the assignment of F2B–PF as tentative.
PF3, the B–P stretching mode of F2B–PF is calculated to be substantially lower in wavenumber (1060.6 vs. 637.3 cm−1 at CCSD(T) level for 10B) and in IR intensity (219 vs. 9 km mol−1, calculated at B3LYP level), it is thus not observed. Because of the suspected overlap in the 816.0 cm−1 band and some deviation between the observed and calculated boron isotopic shift of the 1409.3 cm−1 band [50.5 vs. 45.3 cm−1, the latter value being consistent across different theoretical methods (Tables 1 and S1†)], we consider the assignment of F2B–PF as tentative.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e001.gif) BF.
A third set of absorptions (C) also growths on irradiation but differently than set B, as apparent in the difference spectra upon selective 470 nm irradiation shown in Fig. S2.† Three bands at 1205.4, 1354.3 and 1613.1 cm−1 are assigned to F2B–P
BF.
A third set of absorptions (C) also growths on irradiation but differently than set B, as apparent in the difference spectra upon selective 470 nm irradiation shown in Fig. S2.† Three bands at 1205.4, 1354.3 and 1613.1 cm−1 are assigned to F2B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BF, at least formally an insertion product of a second boron atom into the P–F bond of F2B–PF. The bands at 1205.4 and 1354.3 cm−1 of C show large 11B isotopic shifts of 39.5 and 45.6 cm−1 and are attributed to the symmetric and antisymmetric BF2 vibration modes of F2B–P
BF, at least formally an insertion product of a second boron atom into the P–F bond of F2B–PF. The bands at 1205.4 and 1354.3 cm−1 of C show large 11B isotopic shifts of 39.5 and 45.6 cm−1 and are attributed to the symmetric and antisymmetric BF2 vibration modes of F2B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BF, respectively. The high wavenumber of the 1613.1 cm−1 band can be attributed to a strong out-of-phase coupling between the two bond stretches in the P
BF, respectively. The high wavenumber of the 1613.1 cm−1 band can be attributed to a strong out-of-phase coupling between the two bond stretches in the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) B–F moiety, amplified by its linear structure and the lightweight central boron atom. The corresponding in-phase combination is calculated as low as about 660 cm−1 but not observed due to negligible infrared activity. Isotopic substitution of boron leads to a large shift of the 1613.1 cm−1 band by 53.2–58.7 cm−1. A more accurate value cannot be determined because for the F210/11B–P
B–F moiety, amplified by its linear structure and the lightweight central boron atom. The corresponding in-phase combination is calculated as low as about 660 cm−1 but not observed due to negligible infrared activity. Isotopic substitution of boron leads to a large shift of the 1613.1 cm−1 band by 53.2–58.7 cm−1. A more accurate value cannot be determined because for the F210/11B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) 11BF isotopologs the band is split into two components (1559.9 and 1554.4 cm−1) with similar intensities. A possible explanation might be a resonance between the out-of-phase P
11BF isotopologs the band is split into two components (1559.9 and 1554.4 cm−1) with similar intensities. A possible explanation might be a resonance between the out-of-phase P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) 11B–F stretching fundamental (calculated in the harmonic approximation at 1575.6 cm−1 for F211B–P
11B–F stretching fundamental (calculated in the harmonic approximation at 1575.6 cm−1 for F211B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) 11BF) and the combination mode (estimated at 1567.2 cm−1) of two quanta of P
11BF) and the combination mode (estimated at 1567.2 cm−1) of two quanta of P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) 11B–F bending (2 × 454.8 cm−1) and one quantum of in-phase P
11B–F bending (2 × 454.8 cm−1) and one quantum of in-phase P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) 11B–F stretching (657.6 cm−1) with matching symmetry (a′) and spatial location. For F210B–P
11B–F stretching (657.6 cm−1) with matching symmetry (a′) and spatial location. For F210B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) 10BF the calculated difference (1633.6 vs. 1601.1 cm−1) is larger, explaining the absence of the suspected resonance. Because all modes are largely localized at either side of the phosphorous atom, the vibrational wavenumbers of the two mixed 10/11B isotopologs are calculated to coincide within 1 cm−1 with the corresponding ones of the isotopically pure species (Table S2†), in line with the absence of any further resolved spectral splitting.
10BF the calculated difference (1633.6 vs. 1601.1 cm−1) is larger, explaining the absence of the suspected resonance. Because all modes are largely localized at either side of the phosphorous atom, the vibrational wavenumbers of the two mixed 10/11B isotopologs are calculated to coincide within 1 cm−1 with the corresponding ones of the isotopically pure species (Table S2†), in line with the absence of any further resolved spectral splitting.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e002.gif) B–PF3.
The band at 970.0 cm−1 in the 10B-enriched experiment (labeled as D in Fig. 1) increased during sample annealing to 9 K and almost vanished upon irradiation with λ > 220 nm.
B–PF3.
The band at 970.0 cm−1 in the 10B-enriched experiment (labeled as D in Fig. 1) increased during sample annealing to 9 K and almost vanished upon irradiation with λ > 220 nm.
In the natural abundance boron experiments the band splits into three absorptions at 970.0, 960.4 and 952.5 cm−1 with approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 relative intensities (Fig. S3†), which indicates that the observed species features two equivalent boron atoms. Based on the comparison with calculated band positions and isotopic shifts (Table S3†) this band is tentatively assigned to the antisymmetric B–P stretching mode of F3P–B
16 relative intensities (Fig. S3†), which indicates that the observed species features two equivalent boron atoms. Based on the comparison with calculated band positions and isotopic shifts (Table S3†) this band is tentatively assigned to the antisymmetric B–P stretching mode of F3P–B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B–PF3. This species is likely be formed by the dimerization of the triradical B
B–PF3. This species is likely be formed by the dimerization of the triradical B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF3, analogous to OC–B
PF3, analogous to OC–B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B–CO from B
B–CO from B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CO.15 However, B(PF3)2 was not observed, in contrast to its analogue B(CO)2. For F3P–B
CO.15 However, B(PF3)2 was not observed, in contrast to its analogue B(CO)2. For F3P–B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B–PF3 only one other band with significant IR activity is predicted (Table S4†) in the detector range (>450 cm−1). However, it could not be identified, potentially due a combination of its expected weak intensity and spectral overlap. We therefore suggest to consider the assignment of F3P–B
B–PF3 only one other band with significant IR activity is predicted (Table S4†) in the detector range (>450 cm−1). However, it could not be identified, potentially due a combination of its expected weak intensity and spectral overlap. We therefore suggest to consider the assignment of F3P–B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B–PF3 as tentative.
B–PF3 as tentative.
Theoretical characterizations
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e001.gif) PF3.
For B
PF3.
For B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF3 two electronic states, 4A1 with C3v symmetry and 2A′ with Cs symmetry, are calculated to be very similar in energy, the former higher at CCSD(T)/aug-cc-pVTZ level by 1.6 kcal mol−1. Curiously, the observed band positions agree only with the higher energy 4A1 state. However, this energy difference almost vanishes with aug-cc-pVQZ single-point correction and reverses in sign with aug-cc-pV5Z (Table S5†). The calculated properties and optimised structures of the unobserved 2A′ state are shown in the ESI in Table S6 and Fig. S7,† respectively. CCSD(T) calculations predict a B–P bond length of 1.762 Å for the assigned 4A1 state (Fig. 2). This value is significantly shorter than reported B–P single bond lengths (1.92–2.00 Å) and at the lower end of B
PF3 two electronic states, 4A1 with C3v symmetry and 2A′ with Cs symmetry, are calculated to be very similar in energy, the former higher at CCSD(T)/aug-cc-pVTZ level by 1.6 kcal mol−1. Curiously, the observed band positions agree only with the higher energy 4A1 state. However, this energy difference almost vanishes with aug-cc-pVQZ single-point correction and reverses in sign with aug-cc-pV5Z (Table S5†). The calculated properties and optimised structures of the unobserved 2A′ state are shown in the ESI in Table S6 and Fig. S7,† respectively. CCSD(T) calculations predict a B–P bond length of 1.762 Å for the assigned 4A1 state (Fig. 2). This value is significantly shorter than reported B–P single bond lengths (1.92–2.00 Å) and at the lower end of B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P double bond lengths (1.763–1.853 Å).6,7,16 The Wiberg bond index (WBI) of 1.472 (calculated at B3LYP level) as well indicates at least a partial double bond character.
P double bond lengths (1.763–1.853 Å).6,7,16 The Wiberg bond index (WBI) of 1.472 (calculated at B3LYP level) as well indicates at least a partial double bond character.
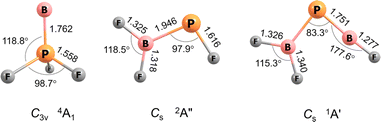 | ||
| Fig. 2 Optimized structures at the CCSD(T)/aug-cc-pVTZ level of theory. Bond lengths (Å), bond angles (°) and molecular symmetries are also shown. | ||
Three unpaired electrons are distributed over a doubly degenerate B–P π-bonding HOMO with largely boron p character and a non-bonding HOMO–1 of largely boron sp character, see Fig. 3. In addition, there is a doubly occupied σ-bonding HOMO–2 for an overall B–P formal bond order of two. The total spin density is predominantly located at the boron atom (Fig. S5†). In order to further understand the interaction between B and PF3, the charge flow upon combination of the B and PF3 fragments were visualized with ETS-NOCV (Extended Transition State-Natural Orbital for Chemical Valence) calculations,17 deformation maps are shown in Fig. S4.† Dative character of the PF3→B σ-bonding and π-backdonation is indicated. This bonding situation of B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF3 is analogous to the known 4Σ− B
PF3 is analogous to the known 4Σ− B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CO.18
CO.18
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e002.gif) B–PF3.
The tentatively assigned F3P–B
B–PF3.
The tentatively assigned F3P–B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B–PF3 is predicted to show a 1A1g ground state in D3d symmetry at B3LYP/aug-cc-pVTZ level. The optimized structure (Fig. S6†) shows a very short B–B bond (1.430 Å, WBI = 2.37), even shorter than the one in O
B–PF3 is predicted to show a 1A1g ground state in D3d symmetry at B3LYP/aug-cc-pVTZ level. The optimized structure (Fig. S6†) shows a very short B–B bond (1.430 Å, WBI = 2.37), even shorter than the one in O![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–B
C–B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B–C
B–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O (1.444 Å, WBI = 1.97 calculated at the same level of theory).15 The formal B
O (1.444 Å, WBI = 1.97 calculated at the same level of theory).15 The formal B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B triple bond is derived from a σ-bonding orbital (HOMO–1) and a doubly degenerate π-bonding orbital (HOMO) (Fig. S12†). Based on the strong π-acceptor properties of PF3, the HOMO is substantially delocalized over the B–P bonds, so that F3P–B
B triple bond is derived from a σ-bonding orbital (HOMO–1) and a doubly degenerate π-bonding orbital (HOMO) (Fig. S12†). Based on the strong π-acceptor properties of PF3, the HOMO is substantially delocalized over the B–P bonds, so that F3P–B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B–PF3 retains some of the B
B–PF3 retains some of the B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P double-bond character (1.768 Å, WBI = 1.19) of its monomer B
P double-bond character (1.768 Å, WBI = 1.19) of its monomer B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF3 (1.757 Å, WBI = 1.55 at the same level of theory). This is also reflected in the natural resonance theory (NRT) analysis, where, besides structures with the leading F3P–B
PF3 (1.757 Å, WBI = 1.55 at the same level of theory). This is also reflected in the natural resonance theory (NRT) analysis, where, besides structures with the leading F3P–B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B–PF3 motif (48%), also resonance forms that show one or two B
B–PF3 motif (48%), also resonance forms that show one or two B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P double bonds have significant combined weights of 14% and 20%, respectively (Fig. S13†). The spin-allowed dimerization energy of 2 B
P double bonds have significant combined weights of 14% and 20%, respectively (Fig. S13†). The spin-allowed dimerization energy of 2 B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF3 (4A1) → F3P–B
PF3 (4A1) → F3P–B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B–PF3 (1A1g) is computed to be −152.6 kcal mol−1.
B–PF3 (1A1g) is computed to be −152.6 kcal mol−1.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF3 compound. As shown in Fig. S5,† the unpaired electron is located in a HOMO with dominant phosphorus pz character with only very minor contribution from the boron atom. The B–P bond order is therefore only very slightly higher than one, which is reflected in a WBI of 1.122. This is in contrast to the trifluorovinyl radical F2C
PF3 compound. As shown in Fig. S5,† the unpaired electron is located in a HOMO with dominant phosphorus pz character with only very minor contribution from the boron atom. The B–P bond order is therefore only very slightly higher than one, which is reflected in a WBI of 1.122. This is in contrast to the trifluorovinyl radical F2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CF which is instead a σ radical with a double bond,19 further emphasizing the differences between carbon–carbon and boron–phosphorus compounds.
CF which is instead a σ radical with a double bond,19 further emphasizing the differences between carbon–carbon and boron–phosphorus compounds.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e001.gif) BF.
F2B–P
BF.
F2B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BF can be characterized as a free phosphaborene RB
BF can be characterized as a free phosphaborene RB![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PR′ with small substituents (R = F and R′ = BF2). The observation of a member of this class of molecules is somewhat unexpected, as it was thought to be thermodynamically and kinetically unstable with respect to spontaneous unimolecular rearrangement in 1,2-shift reaction.3 Yet, F2B–P
PR′ with small substituents (R = F and R′ = BF2). The observation of a member of this class of molecules is somewhat unexpected, as it was thought to be thermodynamically and kinetically unstable with respect to spontaneous unimolecular rearrangement in 1,2-shift reaction.3 Yet, F2B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BF is calculated to be the most stable isomer, 31.0 kcal mol−1 lower in energy than the second lowest isomer (F2B)FB
BF is calculated to be the most stable isomer, 31.0 kcal mol−1 lower in energy than the second lowest isomer (F2B)FB![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P at B3LYP/aug-cc-pVTZ level. This might be explained by the recently proposed push–pull stabilization of the B
P at B3LYP/aug-cc-pVTZ level. This might be explained by the recently proposed push–pull stabilization of the B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P double bond by a π-donor (–F) and a π-acceptor (–BF2) which diminish the Lewis acidity and basicity of boron and phosphorous atoms, respectively.9 The optimized structures and relative energies of all obtained isomers of the formula B2PF3 are provided in Fig. S11.† However, in the absence of bulky ligands, the dimerization of F2B–P
P double bond by a π-donor (–F) and a π-acceptor (–BF2) which diminish the Lewis acidity and basicity of boron and phosphorous atoms, respectively.9 The optimized structures and relative energies of all obtained isomers of the formula B2PF3 are provided in Fig. S11.† However, in the absence of bulky ligands, the dimerization of F2B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BF is still computed to be considerably exothermic by −49.3 kcal mol−1 at B3LYP level. However, its dimerization is prevented under matrix-isolation conditions.
BF is still computed to be considerably exothermic by −49.3 kcal mol−1 at B3LYP level. However, its dimerization is prevented under matrix-isolation conditions.
The B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P and P–B bond distances are computed to be 1.751 and 1.925 Å (Fig. 2) with WBIs of 1.866 and 1.073, respectively. Bond orders of two and one are also present in the dominant resonance structures from the NRT analysis (Fig. 4). Other NRT structures with lower weights are shown in Fig. S8.† NRT resonance structures with a B
P and P–B bond distances are computed to be 1.751 and 1.925 Å (Fig. 2) with WBIs of 1.866 and 1.073, respectively. Bond orders of two and one are also present in the dominant resonance structures from the NRT analysis (Fig. 4). Other NRT structures with lower weights are shown in Fig. S8.† NRT resonance structures with a B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P triple bond have a combined weight of 21%, those with a double bond of 55% and those with a single bond of 22%. The B–F bond length to the singular fluorine ligand is very short (1.277 A) at CCSD(T) level, if comparable with the diatomic BF molecule (calculated 1.275 Å, experimental 1.263 Å (ref. 20)) which can be explained by boron sp-hybridization and two B ← F π-donation interactions, both in and orthogonal to the molecular plane. In contrast, the B–F bonds in the BF2 moiety are slightly elongated (1.326 and 1.340 Å) when compared to both F2B–PF (1.325 and 1.318 Å) and BF3 (calculated 1.315 Å, experimental 1.311 Å (ref. 21)), which is likely due to competition between B ← F and B ← P π-donation. In line with an increase in B ← P π-donation, the P–B bond length in F2B–P
P triple bond have a combined weight of 21%, those with a double bond of 55% and those with a single bond of 22%. The B–F bond length to the singular fluorine ligand is very short (1.277 A) at CCSD(T) level, if comparable with the diatomic BF molecule (calculated 1.275 Å, experimental 1.263 Å (ref. 20)) which can be explained by boron sp-hybridization and two B ← F π-donation interactions, both in and orthogonal to the molecular plane. In contrast, the B–F bonds in the BF2 moiety are slightly elongated (1.326 and 1.340 Å) when compared to both F2B–PF (1.325 and 1.318 Å) and BF3 (calculated 1.315 Å, experimental 1.311 Å (ref. 21)), which is likely due to competition between B ← F and B ← P π-donation. In line with an increase in B ← P π-donation, the P–B bond length in F2B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BF (1.925 Å) is slightly shorter than in F2B–PF (1.946 Å).
BF (1.925 Å) is slightly shorter than in F2B–PF (1.946 Å).
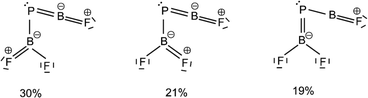 | ||
Fig. 4 Leading resonance structures for F2B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BF from natural resonance theory (NRT). Further structures with weights of less than 8% are available in Fig. S8.† BF from natural resonance theory (NRT). Further structures with weights of less than 8% are available in Fig. S8.† | ||
The HOMO of this compound is a polarized π-bonding orbital with leading contributions from the phosphorus atom (64% according to Hirshfeld partition), the two-coordinated boron atom (22%) and the tri-coordinated boron atom (9%). Despite this moderate 3-center-2-electron bonding character, as previously reported for a similar free phosphaborene BPB moiety,9 the B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P and P–B interactions clearly have very different overall bond orders. The HOMO–1 resembles mostly an in-plane lone pair orbital of P (71% contribution) which contributes little to B
P and P–B interactions clearly have very different overall bond orders. The HOMO–1 resembles mostly an in-plane lone pair orbital of P (71% contribution) which contributes little to B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P and P–B bonding according to Mulliken and Mayer bond order decomposition (Tables S8–S11†).22 This is more consistent with the lone pair interpretation for previously isolated free phosphaborenes,10 but less consistent with the bonding picture presented by Su et al. who propose a second in-plane π-bond for an overall triple bond.3 Nevertheless, the HOMO–1 shows a boron contributions [12% B(F2), 10% B(F)] that seem to be of some significance for the structure of the molecule. A striking feature of F2B–P
P and P–B bonding according to Mulliken and Mayer bond order decomposition (Tables S8–S11†).22 This is more consistent with the lone pair interpretation for previously isolated free phosphaborenes,10 but less consistent with the bonding picture presented by Su et al. who propose a second in-plane π-bond for an overall triple bond.3 Nevertheless, the HOMO–1 shows a boron contributions [12% B(F2), 10% B(F)] that seem to be of some significance for the structure of the molecule. A striking feature of F2B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BF is the acute BPB bond angle of 83°, which cannot be explained by VSEPR or hybridisation considerations alone. In contrast, the BPR′ bond angles of previously experimentally detected free phosphaborenes are obtuse and amount to 115.5(1)10 and 106.00(6),9 which are most likely broadened by steric repulsion between the bulky substituents. Conversely, the acute angle in F2B–P
BF is the acute BPB bond angle of 83°, which cannot be explained by VSEPR or hybridisation considerations alone. In contrast, the BPR′ bond angles of previously experimentally detected free phosphaborenes are obtuse and amount to 115.5(1)10 and 106.00(6),9 which are most likely broadened by steric repulsion between the bulky substituents. Conversely, the acute angle in F2B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BF might suggest an attractive interaction. Indeed, the WBI of 0.156 for the B⋯B interaction at 2.45 Å is small but not negligible, as are other evaluated bond order measures (Table S7†). A small minority of NRT structures even feature a covalent B–B single bond with a low combined weight of 2% (Fig. S8†). It is tempting to link this attraction to the three-center character of the π-type HOMO, but Mulliken and Mayer bond order decomposition instead suggests leading contributions from in-plane orbitals, such as HOMO–1 and HOMO–12 (Tables S12 and S13†). While one orbital lobe of HOMO–1 resembles a phosphorus lone pair, the other connects the two boron nuclei (Fig. 5). This interpretation is further supported by decomposition of the B⋯B Wiberg bond index in NAO basis, with about 2/3 being contributed by interactions involving the in-plane px and py-orbitals and 1/3 by those involving the out-of-plane pz-orbitals of the boron atoms (Table S14†). There is no (3, −1) critical point located between the boron nuclei according to the quantum theory of atoms in molecules (QTAIM). An overall BPB multi-center bond order in NAO basis of 0.16 is calculated, somewhat lower than the values for the textbook examples of the allyl cation (0.22) and diborane (0.25) calculated at the same level of theory.
BF might suggest an attractive interaction. Indeed, the WBI of 0.156 for the B⋯B interaction at 2.45 Å is small but not negligible, as are other evaluated bond order measures (Table S7†). A small minority of NRT structures even feature a covalent B–B single bond with a low combined weight of 2% (Fig. S8†). It is tempting to link this attraction to the three-center character of the π-type HOMO, but Mulliken and Mayer bond order decomposition instead suggests leading contributions from in-plane orbitals, such as HOMO–1 and HOMO–12 (Tables S12 and S13†). While one orbital lobe of HOMO–1 resembles a phosphorus lone pair, the other connects the two boron nuclei (Fig. 5). This interpretation is further supported by decomposition of the B⋯B Wiberg bond index in NAO basis, with about 2/3 being contributed by interactions involving the in-plane px and py-orbitals and 1/3 by those involving the out-of-plane pz-orbitals of the boron atoms (Table S14†). There is no (3, −1) critical point located between the boron nuclei according to the quantum theory of atoms in molecules (QTAIM). An overall BPB multi-center bond order in NAO basis of 0.16 is calculated, somewhat lower than the values for the textbook examples of the allyl cation (0.22) and diborane (0.25) calculated at the same level of theory.
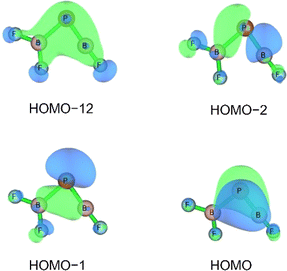 | ||
Fig. 5 Selected bonding molecular orbitals of F2B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BF calculated at HF/aug-cc-pVTZ//CCSD(T)/aug-cc-pVTZ level. BF calculated at HF/aug-cc-pVTZ//CCSD(T)/aug-cc-pVTZ level. | ||
To explore whether this feature is inherent to F2B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BF or more widespread, we optimized at CCSD(T) level the structure of a number of other small phosphaborenes. The isomer with swapped substituents, F2B–B
BF or more widespread, we optimized at CCSD(T) level the structure of a number of other small phosphaborenes. The isomer with swapped substituents, F2B–B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF, is computed to be less stable by 50.9 kcal mol−1 and its BPF angle amounts to 102°. Similar obtuse BPR′ angles are obtained for FB
PF, is computed to be less stable by 50.9 kcal mol−1 and its BPF angle amounts to 102°. Similar obtuse BPR′ angles are obtained for FB![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF (99°) and FB
PF (99°) and FB![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PCH3 (97°). In contrast, acute angles are found for FB
PCH3 (97°). In contrast, acute angles are found for FB![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PH (80°) and FB
PH (80°) and FB![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PSiH3 (79°). Small angles correlate with higher B⋯R′ WBIs and BPR′ multi-center bond orders (Fig. S9†), although there are clearly other contributing factors, such as the size of the ligand R′. Extreme cases are the non-classical structures of the parent phosphaborene HB
PSiH3 (79°). Small angles correlate with higher B⋯R′ WBIs and BPR′ multi-center bond orders (Fig. S9†), although there are clearly other contributing factors, such as the size of the ligand R′. Extreme cases are the non-classical structures of the parent phosphaborene HB![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PH,2 in which one hydrogen atom effectively bridges the B
PH,2 in which one hydrogen atom effectively bridges the B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P bond (53°), and the hydrogen homolog of F2B–P
P bond (53°), and the hydrogen homolog of F2B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BF: B2PH3 (56°). The latter converges to a structure with C2v symmetry, with one hydrogen atom and the phosphorus atom bridging either side of the B–B bond with a distance of 1.70 Å (Fig. S10†). Clearly, a more systematic study of substitution effects on the unusual bonding situations and stability of small phosphaborenes is required.
BF: B2PH3 (56°). The latter converges to a structure with C2v symmetry, with one hydrogen atom and the phosphorus atom bridging either side of the B–B bond with a distance of 1.70 Å (Fig. S10†). Clearly, a more systematic study of substitution effects on the unusual bonding situations and stability of small phosphaborenes is required.
Formation pathways
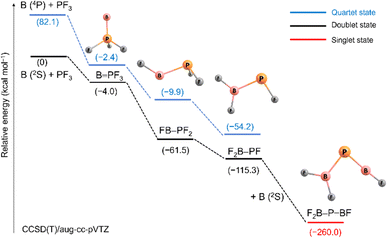
Scheme 2 outlines relative energies and possible pathways for the formation of the observed species. Because overall spin multiplicity is conserved, a plausible route for the formation of the observed quartet B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF3 is the reaction of singlet PF3 with a laser-ablated boron atom in an excited 4P (2s12p2) state23 (2s → 2p promotion, 82.1 kcal mol−1 excitation energy). However, the apparent growth of B
PF3 is the reaction of singlet PF3 with a laser-ablated boron atom in an excited 4P (2s12p2) state23 (2s → 2p promotion, 82.1 kcal mol−1 excitation energy). However, the apparent growth of B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF3 on annealing suggests that it can be formed as well in cryogenic matrices without activation energy. Indeed, the formation of B
PF3 on annealing suggests that it can be formed as well in cryogenic matrices without activation energy. Indeed, the formation of B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF3 in its excited doublet state by reaction of PF3 with a ground state 2P (2s22p1) boron atom is calculated to be slightly exothermic (−4.0 kcal mol−1). The subsequent fast intersystem crossing (ISC) to the quartet state could explain the non-observation of the doublet state. Triggered by irradiation, exothermic stepwise 1,2-rearrangement would then lead first to the unobserved intermediate FB–PF2 (−59.1 kcal mol−1), quickly followed by further isomerization to the most stable isomer F2B–PF (−53.8 kcal mol−1). Transition states and barriers are reported at B3LYP level in the ESI.† Finally, the phosphaborene F2B–P
PF3 in its excited doublet state by reaction of PF3 with a ground state 2P (2s22p1) boron atom is calculated to be slightly exothermic (−4.0 kcal mol−1). The subsequent fast intersystem crossing (ISC) to the quartet state could explain the non-observation of the doublet state. Triggered by irradiation, exothermic stepwise 1,2-rearrangement would then lead first to the unobserved intermediate FB–PF2 (−59.1 kcal mol−1), quickly followed by further isomerization to the most stable isomer F2B–PF (−53.8 kcal mol−1). Transition states and barriers are reported at B3LYP level in the ESI.† Finally, the phosphaborene F2B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BF could be produced by irradiation-induced insertion of a second boron atom in the remaining P–F bond of F2B–PF. This step is calculated to be exothermic by −144.7 kcal mol−1 which is by far more exothermic than the insertion of a B atom into one of the P–F bonds of PF3 (−61.5 kcal mol−1). This sequence of initial barrier-free B atom adduction, light-induced isomerisation and second B atom insertion appears to be the most plausible pathway. The formation of F2B–P
BF could be produced by irradiation-induced insertion of a second boron atom in the remaining P–F bond of F2B–PF. This step is calculated to be exothermic by −144.7 kcal mol−1 which is by far more exothermic than the insertion of a B atom into one of the P–F bonds of PF3 (−61.5 kcal mol−1). This sequence of initial barrier-free B atom adduction, light-induced isomerisation and second B atom insertion appears to be the most plausible pathway. The formation of F2B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BF by reaction of B2 with PF3 was also considered but none of the expected intermediates (Scheme S2†) were observed.
BF by reaction of B2 with PF3 was also considered but none of the expected intermediates (Scheme S2†) were observed.
Conclusions
In summary, the reaction of laser-ablated atomic boron and phosphorus trifluoride produced a variety of previously unreported boron–phosphorus compounds that were characterized by matrix-isolation infrared spectroscopy and quantum-chemical methods. B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PF3 and F2B–P
PF3 and F2B–P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) BF both feature a boron–phosphorus double bond but with different orbital structures. The latter molecule is a phosphaborene without protection from sterically demanding substituents, a class of molecules previously thought to be too unstable to be observed experimentally.
BF both feature a boron–phosphorus double bond but with different orbital structures. The latter molecule is a phosphaborene without protection from sterically demanding substituents, a class of molecules previously thought to be too unstable to be observed experimentally.
Furthermore, we tentatively assign two new species, the single bonded F2B–PF and the dimer F3P–B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B–PF3 with a delocalised π-system. We hope that these findings will contribute to molecular design in the emerging field of multiple-bonded boron–phosphorus compounds.
B–PF3 with a delocalised π-system. We hope that these findings will contribute to molecular design in the emerging field of multiple-bonded boron–phosphorus compounds.
Author contributions
M. W. planed and performed the experiments, carried out the quantum-chemical calculations and wrote the first draft of the manuscript. R. M. performed some theoretical calculations and bonding analysis, and revised the manuscript. P. Z. analyzed the experiment result. C. M. revised the manuscript. S. R. guided and advised the project and proofread the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the Zentraleinrichtung für Datenverarbeitung (ZEDAT)24 of the Freie Universität Berlin for the allocation of computing resources. We also thank the ERC Project HighPotOx (Grant agreement ID: 818862) as well as the CRC 1349 (SFB 1349) Fluorine-Specific Interactions-Project-ID 387284271 for continuous support. M. W. thanks the China Scholarship Council (PhD Program) for financial support.Notes and references
- Y. Fan, J. Cui and L. Kong, Eur. J. Org Chem., 2022, e202201086 CrossRef.
- J. D. Watts and L. C. van Zant, Chem. Phys. Lett., 1996, 251, 119 CrossRef CAS.
- J.-S. Lu, M.-C. Yang and M.-D. Su, ACS Omega, 2018, 3, 76 CrossRef CAS PubMed.
- A. M. Arif, J. E. Boggs, A. H. Cowley, J. G. Lee, M. Pakulski and J. M. Power, J. Am. Chem. Soc., 1986, 108, 6083 CrossRef CAS PubMed.
- (a) G. Linti, H. Nöth, K. Polborn and R. T. Paine, Angew Chem. Int. Ed. Engl., 1990, 29, 682 CrossRef; (b) K. Knabel, T. M. Klapötke, H. Nöth, R. T. Paine and I. Schwab, Eur. J. Inorg. Chem., 2005, 2005, 1099 CrossRef.
- E. Rivard, W. A. Merrill, J. C. Fettinger and P. P. Power, Chem. Commun., 2006, 3800 RSC.
- A. N. Price and M. J. Cowley, Chem.–Eur. J., 2016, 22, 6248 CrossRef CAS PubMed.
- (a) A. N. Price, G. S. Nichol and M. J. Cowley, Angew Chem. Int. Ed. Engl., 2017, 56, 9953 CrossRef CAS PubMed; (b) W. Yang, K. E. Krantz, D. A. Dickie, A. Molino, D. J. D. Wilson and R. J. Gilliard, Angew Chem. Int. Ed. Engl., 2020, 59, 3971 CrossRef CAS PubMed; (c) J. Li, Y. Mei and L. L. Liu, Eur. J. Inorg. Chem., 2022, e202200368 CrossRef CAS.
- J. Li, Z. Lu and L. L. Liu, J. Am. Chem. Soc., 2022, 144, 23691 CrossRef CAS PubMed.
- E. A. LaPierre, B. O. Patrick and I. Manners, J. Am. Chem. Soc., 2023, 145, 7107 CrossRef CAS PubMed.
- A. Koner, B. Morgenstern and D. M. Andrada, Angew Chem. Int. Ed. Engl., 2022, 61, e202203345 CrossRef CAS PubMed.
- L. Junxi, D. Yu, B. Jun, L. Zhenhua, W. Xiaoe and S. Qiong, Comput. Theor. Chem., 2020, 1185, 112873 CrossRef CAS.
- L. Wang, X. Jiang, G. Wang, X. Zeng and M. Zhou, Chem.–Eur. J., 2023, 29, e202203704 CrossRef CAS PubMed.
- (a) M. E. Jacox and W. E. Thompson, J. Chem. Phys., 1995, 102, 4747 CrossRef CAS; (b) X.-F. Wang and L. Andrews, J. Am. Chem. Soc., 2011, 133, 3768 CrossRef CAS PubMed; (c) C. L. Lugez, K. K. Irikura and M. E. Jacox, J. Chem. Phys., 1998, 108, 8381 CrossRef CAS.
- M. Zhou, N. Tsumori, Z. Li, K. Fan, L. Andrews and Q. Xu, J. Am. Chem. Soc., 2002, 124, 12936 CrossRef CAS PubMed.
- (a) R. A. Bartlett, X. Feng and P. P. Power, J. Am. Chem. Soc., 1986, 108, 6817 CrossRef CAS; (b) X. Feng, M. M. Olmstead and P. P. Power, Inorg. Chem., 1986, 25, 4615 CrossRef CAS; (c) R. A. Bartlett, H. V. R. Dias, X. Feng and P. P. Power, J. Am. Chem. Soc., 1989, 111, 1306 CrossRef CAS; (d) S. J. Geier, T. M. Gilbert and D. W. Stephan, Inorg. Chem., 2011, 50, 336 CrossRef CAS PubMed.
- M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962 CrossRef CAS PubMed.
- M. Zhou, N. Tsumori, L. Andrews and Q. Xu, J. Phys. Chem. A, 2003, 107, 2458 CrossRef CAS.
- B. E. Wurfel, N. Pugliano, S. E. Bradforth, R. J. Saykally and G. C. Pimentel, J. Phys. Chem., 1991, 95, 2932 CrossRef CAS.
- G. Cazzoli, L. Cludi, C. Degli Esposti and L. Dore, J. Mol. Spectrosc., 1989, 134, 159 CrossRef CAS.
- V. P. Spiridonov and A. G. Gershikov, J. Mol. Struct., 1986, 140, 173 CrossRef CAS.
- S. I. Gorelsky, J. Chem. Theory Comput., 2012, 8, 908 CrossRef CAS PubMed.
- B. Xu, H. Beckers, H. Ye, Y. Lu, J. Cheng, X. Wang and S. Riedel, Angew Chem. Int. Ed. Engl., 2021, 60, 17205 CrossRef CAS PubMed.
- L. Bennett, B. Melchers and B. Proppe, Curta: A General-purpose High-Performance Computer at ZEDAT, Freie Universität Berlin, 2020 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc01913j |
| This journal is © The Royal Society of Chemistry 2024 |