Band engineering of layered oxyhalide photocatalysts for visible-light water splitting

Abstract

The band structure offers fundamental information on electronic properties of solid state materials, and hence it is crucial for solid state chemists to understand and predict the relationship between the band structure and electronic structure to design chemical and physical properties. Here, we review layered oxyhalide photocatalysts for water splitting with a particular emphasis on band structure control. The unique feature of these materials including Sillén and Sillén–Aurivillius oxyhalides lies in their band structure including a remarkably high oxygen band, allowing them to exhibit both visible light responsiveness and photocatalytic stability unlike conventional mixed anion compounds, which show good light absorption, but frequently encounter stability issues. For band structure control, simple strategies effective in mixed-anion compounds, such as anion substitution forming high energy p orbitals in accordance with its electronegativity, is not effective for oxyhalides with high oxygen bands. We overview key concepts for band structure control of oxyhalide photocatalysts such as lone-pair interactions and electrostatic interactions. The control of the band structure of inorganic solid materials is a crucial challenge across a wide range of materials chemistry fields, and the insights obtained by the development of oxyhalide photocatalysts are expected to provide knowledge for diverse materials chemistry.

---

Daichi Kato

Daichi Kato is an assistant professor of the Department of Energy & Hydrocarbon Chemistry in the Graduate School of Engineering at Kyoto University. He received his PhD in 2020 from Kyoto University supervised by Prof. Hiroshi Kageyama. His recent research focuses on synthesizing novel solid-state materials, particularly those with multiple anions (mixed anion compounds), aimed at developing new functional materials like photocatalysts and solid electrolytes.

Hajime Suzuki

Hajime Suzuki received his BS (2013), MS (2015), and PhD (2018) degrees from Kyoto University. He then worked as a postdoctoral fellow (2018–2019) at Osaka University. He is currently an assistant professor at the Department of Energy and Hydrocarbon Chemistry, Graduate School of Engineering, Kyoto University. His current research focuses on the development of novel visible-light-responsive photocatalysts and catalysts for water splitting.

Ryu Abe

Ryu Abe received his BS (1996), MS (1998), and PhD (2001) degrees from the Tokyo Institute of Technology. After working at the National Institute of Advanced Science and Technology (AIST) Japan, he became an associate professor at the Catalysis Research Center, Hokkaido University, Japan, in 2005. In 2012, he was appointed as a full professor at the Department of Energy and Hydrocarbon Chemistry, Graduate School of Engineering, Kyoto University. His research mainly focuses on the development of highly efficient photocatalyst materials and systems for water splitting under visible light toward artificial photosynthesis.

Hiroshi Kageyama

Hiroshi Kageyama received his PhD (1998) from Kyoto University under the supervision of Professor Koji Kosuge. Afterwards he worked as a research associate under Professor Yutaka Ueda at the Institute for Solid State Physics, University of Tokyo. In 2003, he became an associate professor at the Graduate School of Science, Kyoto University, collaborating with Prof. Kazuyoshi Yoshimura. In 2010, he was appointed as a professor at the Graduate School of Engineering, Kyoto University. His specialization is solid state chemistry, with a focus on the discovery of new crystalline solids, particularly mixed-anion compounds, which exhibit novel chemical and physical properties, and the development of new design principles.

---

1. Introduction

Solid-state materials continue to be essential for a wide range of electronic applications due to their functional properties such as ferroelectricity, magnetism, superconductivity, catalysis and the photovoltaic effect. While the electronic states of molecules are characterized by the discrete energy levels, those of extended solids with translational symmetry are described by continuous energy levels (i.e., bands) with energy dispersions against the reciprocal lattice space. The band structure offers fundamental information on electronic properties such as electronic conductivity, band gap and effective masses of electrons, and so on and so forth. It is therefore crucial for solid state chemists to extract chemical bonding (e.g., covalency and ionicity) and structural stability from the band structure of the material, as well as to understand and ultimately predict the chemical and physical properties, in order to design ideal materials with optimized properties.¹

Although recent advances in computational chemistry have enabled the quick access of the band structure of solid state materials even with complicated structures, predicting physical properties such as those involving strongly correlated electrons and the structures involving solid solution, defects, and superlattices remains difficult, if not impossible, and requires a large computational expense and may lead to artefacts.^2–4 Therefore, comprehensive studies within a specific family of materials are crucial for gaining insights into the design of band structures and the resulting properties, as beautifully demonstrated by research on copper oxide and iron pnictide superconductors.^5,6

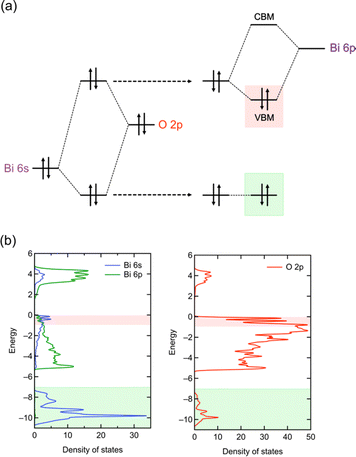
Photocatalytic overall water splitting has attracted great attention as a method for producing hydrogen by harvesting solar energy,^8–17 since the initial study in the early 1970s with a titanium dioxide photoanode under ultraviolet (UV) light irradiation.¹⁸ Transition metal oxide semiconductors have been the major focus of research due to their abundance and excellent stability,^12,19,20 with an Al-doped SrTiO₃ photocatalyst achieving nearly 100% apparent quantum efficiency.²⁰ However, most oxide photocatalysts have too large a band gap to harvest visible light because the valence band maximum (VBM) of oxide materials lies more negative in energy (approximately +3.0 V vs. SHE) as shown in Fig. 1a.²¹ Thus, achieving efficient solar energy to hydrogen conversion by overall water splitting requires the design of suitable band structures of semiconducting materials other than oxides.

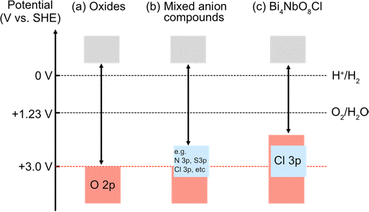Fig. 1 Schematic band structures of (a) oxides, (b) conventional mixed-anion compounds, and (c) Bi₄NbO₈Cl.⁷ To achieve overall water splitting, electrons and holes in photocatalysts need to have enough potential, respectively, for reduction and oxidation of water; i.e., the conduction band maximum (CBM) must be more negative than the water reduction potential (0 V vs. SHE) and valence band maximum (VBM) must be more positive than the water oxidation potential (1.23 V vs. SHE), which are shown as dotted black lines. The VBM of oxides is formed by O 2p bands located at around 3.0 V (red dotted line), and hence oxide photocatalysts typically have too wide a band gap to harvest visible light.

Mixed-anion compounds are compounds that consist of multiple anion species, such as oxide (O²⁻), nitride (N³⁻), sulfide (S²⁻), and halide (F⁻, Cl⁻, Br⁻, and I⁻) anions.²² Among them, oxynitrides and oxysulfides have been extensively studied as visible-light responsive photocatalysts since non-oxide anions form their valence bands at higher energy than oxide anions due to their smaller electronegativities (3.04 for N and 2.58 for S vs. 3.44 for O), leading to a narrower band gap than that of the corresponding oxides, as shown in Fig. 1b. For example, perovskite LaMg_1/3Ta_2/3O₂N²³ and wurtzite (Ga_1−xZn_x)(N_1−xO_x)^24,25 with bandgaps of 2.1 eV and 2.6 eV, respectively, function as efficient photocatalysts under visible light irradiation.²⁶ However, mixed-anion compounds are generally prone to self-oxidative decomposition because non-oxide anions could easily be oxidized by photogenerated holes, and hence surface modifications such as cocatalyst loading are crucial to avoid such unfavourable decomposition reactions;^27–30 the photocurrent of a photoanode made from pristine oxynitride BaTaO₂N shows an immediate decrease within 5 min due to the oxidation of nitride anions (i.e., 2N³⁻ + 6h⁺ → N₂) while the BaTaO₂N photoanode loaded with CoO_x and RhO_x exhibits a steady photocurrent even after 1 hour.³⁰

In 2016, our research demonstrated that layered oxyhalides Bi₄NbO₈X (X = Cl, Br) are efficient and stable photocatalysts for water splitting, notably without any surface modifications.⁷ Unlike conventional mixed-anion compounds, the VBM of Bi₄NbO₈X primarily consists of remarkably high oxygen bands rather than halide bands (Fig. 1c), ensuring both stability and visible light responsivity.⁷ Since the discovery of Bi₄NbO₈X photocatalysts, various members of the layered oxyhalide family have undergone systematic investigation,^31–36 providing invaluable insights into the design of band structures. In this invited review article, we overview the development of layered oxyhalides as a novel class of photocatalysts, with a special emphasis on valence band (VB) and conduction band (CB) engineering. These discoveries will be crucial not only as a foundation for the future advancement of oxyhalide photocatalysts but also for the manipulation of the chemical and physical properties of a wide range of functional materials, especially layered and/or lone-pair cation containing compounds.

Here, we briefly outline the essential concepts of band engineering in oxyhalides (Fig. 2) to provide a better overall perspective. For conventional mixed-anion compounds, the VBM can be extensively and finely tuned via substitution of non-oxide anions (Fig. 2a), forming higher energy bands according to electronegativity. This strategy proves effective for some Sillén phases such as BiOX (X = Cl, Br, I), where the VBM comprises halogen bands, as expected for conventional mixed-anion compounds. On the other hand, this approach is not applicable to Sillén(–Aurivillius) oxyhalides such as Bi₄NbO₈Cl with the VBM formed by high oxygen bands (Fig. 1c). Systematic studies on double fluorite layered compounds have revealed that lone pair interactions (Fig. 2b) and Madelung site potentials (Fig. 2c) play crucial roles in controlling the unusual valence band structure. In contrast to the VBM, it is not straightforward to control the conduction band maximum (CBM) for Sillén and Sillén–Aurivillius oxychloride and oxybromide phases based on double fluorite layers. Studies on Bi₂MO₄Cl with triple fluorite layers have demonstrated that local symmetry breaking around Bi in the fluorite layer enables the extensive tuning of the CBM (Fig. 2f), although this symmetry breaking sacrifices photoconductivity and photocatalytic activity. More recent studies have broadened to include oxyiodides, which establish the key to designing the VBM and CBM via the softness and the size of the iodide anion (Fig. 2d and e) without decreasing photocatalytic activities.

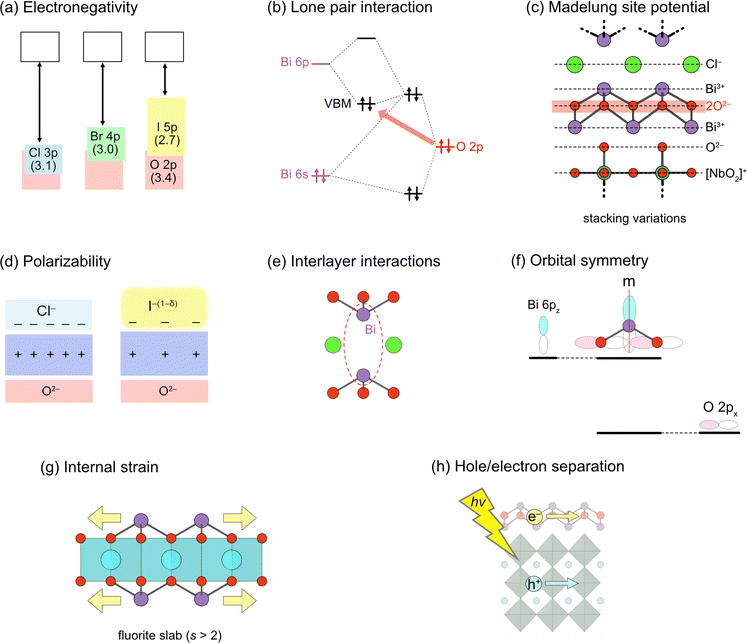Fig. 2 Design principles for band engineering of Sillén and Sillén–Aurivillius oxyhalide photocatalysts. (a) Replacing halogens forming the VBM. Pauling's electronegativity is shown in parentheses. (b) Lone pair interaction between Bi 6s, 6p and O 2p orbitals, elevating O 2p bands in the VBM. (c) Madelung site potential at the oxygen site, explaining the electrostatic destabilization of the oxygen sublayer, e.g., in Bi₄NbO₈X. Layer-by-layer Madelung analysis is useful for extracting the electrostatic contribution of each layer. (d) Polarizability of halogens. The use of soft and polarizable iodide anions results in a higher VBM due to the smaller electrostatic stabilization of oxygen next to the fluorite layer. (e) Interlayer interaction between Bi 6p_z orbitals across the single halogen layer. The CBM becomes lower due to the formation of anti-bonding orbitals, which varies with the interlayer distance. (f) (Broken) mirror symmetry at the Bi site. In Bi₂YO₄Cl, the mirror symmetry at Bi prohibits interactions between Bi 6p_z and O 2p_x, leading to the non-bonding Bi 6p_z. In Bi₂MO₄Cl (M = La, Bi), however, the mirror symmetry is broken, allowing Bi 6p_z and O 2p_x anti-bonding interactions and elevating the CBM. (g) Tensile strain acting on the outer sublayer within a triple (and thicker) fluorite slab, leading to bond breaking to form, e.g., zigzag chains in Bi₂LaO₄Cl.³⁷ (h) Spatial separation of the CBM and VBM. Given that electrons and holes flow in the CBM and VBM, respectively, charge recombination may be suppressed by placing the CBM and VBM in different layers.³⁸

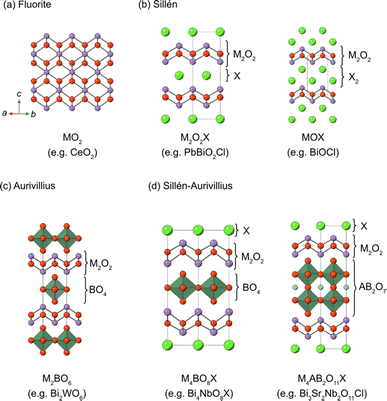
2. Crystal structures of Sillén and Sillén–Aurivillius oxyhalides

Sillén structures refer to a class of layered oxyhalides composed of alternating metal oxide layers and halogen layers.^39,40 The metal oxide layer of the Sillén compounds represents a segment of the cubic fluorite structure (Fig. 3a) sliced in the 001 plane. The best representative compound is BiOCl (or [Bi₂O₂][Cl₂]), consisting of fluorite layers ([Bi₂O₂]²⁺) separated by a double halogen layer ([Cl₂]²⁻), as shown in Fig. 3b (right).^41,42 When the cationic charge is adjusted to separate the fluorite layers with a single halogen layer (Fig. 3b, left), the stacking can be expressed as [M₂O₂][Cl], as exemplified by PbBiO₂Cl (or [PbBiO₂][Cl]).⁴³ The cation (M) site can be occupied with relatively large cations, including post-transition metals, such as Bi³⁺ and Pb²⁺ or alkali earth metals such as Ba²⁺ and Sr²⁺. In most cases, the M site adjacent to the halogen layers is occupied by lone pair cations because of its high asymmetry. The general formula for Sillén compounds can be given by [M_sO_2s−2][X]_m, where s (s = 2, 3,…) and m (m = 1 or 2) represent the thickness of the fluorite layer and the number of halogen (X = Cl, Br, I) layers, respectively. Most Sillén structures consist of double (s = 2) fluorite layers, as seen in BiOCl, and are the focus of research, whereas compounds with a thicker fluorite layer (s ≥ 3) are quite rare but important, as discussed later.

Fig. 3 Schematic views of (a) fluorite, (b) Sillén, (c) Aurivillius and (d) Sillén–Aurivillius structures. The general formula of Sillén, Aurivillius and Sillén–Aurivillius phases can be written as [M_sO_2s−2][X]_m, [M₂O₂][A _n−1B_nO_3n+1] and [M₄O₄X][A_n−1B_nO_3n+1], where s (s = 2, 3, …), m (m = 1 or 2) and n (n = 1, 2, 3, ….) represent the thickness of the fluorite layer, the number of halogen layers, and the number of perovskite layers, respectively. Here, M, A, B and X indicate cations in fluorite layers, A-site cations in perovskite layers, B-site cations in perovskite layers, and halogens, respectively. Examples of compounds are shown at the bottom of each panel.

The Aurivillius phase (Fig. 3c) is a representative example of layered perovskites, where perovskite A_n−1B_nO_3n+1 layers (n is the number of perovskite layers) are sandwiched by a double fluorite Bi₂O₂ layer. The Sillén–Aurivillius phase M₄A_n−1B_nO_3n+5X (Fig. 3d) can be viewed as an intergrowth structure combining Sillén and Aurivillius phases, with a stacking sequence of [M₂O₂][A_n−1B_nO_3n+1][M₂O₂][X]. The M site is predominantly occupied by Bi³⁺, but can be partially substituted by cations like Pb²⁺, alkali earth metals, and lanthanoides.^40,44,45 The options for cations at the B sites of perovskite layers are relatively restricted compared to simple perovskite oxides due to charge and size constraints. High valence cations (Ti⁴⁺, Nb⁵⁺, Ta⁵⁺, W⁶⁺, and Sb⁵⁺) can occupy these sites, while cations with smaller charge (Cr³⁺, Ga³⁺, and Fe³⁺) can only partially occupy these positions.^{40,44,46–49} The A site can accommodate a variety of divalent and trivalent cations with radii ranging from 1.1 to 1.5 Å, such as Bi³⁺, Pb²⁺, lanthanoids (or lanthanide), and alkali earth metals.

Even predating the identification of the photocatalytic properties in Bi₄NbO₈X, the Sillén–Aurivillius phases have been recognized as a promising platform for lead-free ferroelectric materials due to their polar crystal structures.⁵⁰ The polar structures have been considered to be potentially advantageous for photocatalytic properties because photo-generated electrons and holes can be separated by spontaneous polarizations.^51–57 It has been claimed that the photocatalytic activity of Bi₄NbO₈Cl can be altered by changing in-plane and out-of-plane spontaneous polarization.⁵³ There is also a report claiming that coupling piezoelectric and photocatalytic effects increases activity such as the generation of reactive oxygen species including H₂O₂ from Bi₄NbO₈Br under simultaneous light and ultrasound irradiation.^58–61

In this context, precise information about crystal structures is crucial not only for ferroelectric investigations but also for photocatalytic studies. However, accurately determining the complicated structure of Sillén–Aurivillius phases involving octahedral rotations through powder structure analysis is difficult. For example, Bi₄NbO₈Br was initially reported to adopt the space group of orthorhombic P2₁cn, with intralayer polarization along the a-axis. Yet, a comprehensive structural analysis using transmission electron microscopy (TEM) and neutron powder diffraction for Bi₄NbO₈Br unveiled that it adopts the monoclinic Ic space group, indicating spontaneous polarization in both inter- and intra-layer directions, a fact which may facilitate charge separation not only along the in-plane direction but also in the out-of-plane direction.⁶² In addition, out-of-plane polarization is quite rare in layered materials in general, despite the importance for technological application as thin-film ferroelectric devices, making this finding valuable.^63,64

To understand charge separation by spontaneous polarization, information about the (average) crystal structure may not be sufficient. This is because ferroelectric compounds generally form domain structures, i.e., nanoregions to micro regions with the same polarization directions within a single crystalline grain.^51,65 For Sillén–Aurivillius phases, Bi₄NbO₈Br presents a unique domain configuration with nanoscale ferroelastic 90° domains in the ab-plane and ferroelectric 180° domains within these domains.⁶⁶ Moreover, although reported as centrosymmetric structures without distortion in powder diffraction measurements, Sillén–Aurivillius phases may have polar nano-regions, as in the pseudo-tetragonal Bi₃Pb₂Nb₂O₁₁Cl (n = 2), which shows relaxor behavior, possibly due to cation disorder in (Bi_1.5Pb_0.5)O₂ fluorite layers.⁶⁷ It should be noted that most Sillén–Aurivillius phases exhibiting cationic disorder are reported to be tetragonal.^44,45,67,68 Therefore, it is crucial to carefully consider the local structure when studying the impact of spontaneous polarization in these materials.

3. Anomalous valence band structure of Bi₄NbO₈Cl

3.1. Band structures of BiOX and Bi₄NbO₈X

As previously mentioned, mixed-anion semiconductors exhibit narrower bandgaps than oxides due to the p orbitals of non-oxide anions (e.g., N³⁻, S²⁻, Br⁻, or I⁻) forming bands at higher energy levels (Fig. 1b). Sillén-type BiOX oxyhalides (X = Cl, Br, I) showcase such bandgap manipulation with non-oxide anions (Fig. 2a);³² the bandgap of BiOX decreases from 3.48 eV in BiOCl, to 2.93 eV in BiOBr, and further to 1.91 eV in BiOI because of the upshift of the VBM, composed of halogen bands, in accordance with the reduced electronegativity sequence (Cl > Br > I).⁶⁹

In 2016, we demonstrated the stable photocatalysis of Bi₄NbO₈Cl for the O₂ evolution half-reaction under visible light.⁷ Bi₄NbO₈Cl belongs to the n = 1 member of the Sillén–Aurivillius family, consisting of perovskite [NbO₄] layers sandwiched by [(Bi₂O₂)₂Cl]³⁺ blocks (Fig. 3d). We observed several unusual behaviours in Bi₄NbO₈X (X= Cl, Br). Firstly, Bi₄NbO₈Cl powder exhibits a bright yellow color, contrasting with the white color of BiOCl powder. Experimental studies revealed that Bi₄NbO₈Cl possesses suitable band positions for both water reduction and oxidation processes (Fig. 1c), with a much narrower bandgap (2.43 eV) compared to BiOCl (3.48 eV), allowing efficient absorption of visible light. Secondly, the Br counterpart of Bi₄NbO₈Br has almost the same bandgap (2.48 eV) as Bi₄NbO₈Cl,³² unlike the trend observed in BiOX (Fig. 2a). Furthermore, the pristine Bi₄NbO₈X materials function as stable O₂ evolution photocatalysts, contrasting with conventional mixed-anion compounds (e.g., LaTiO₂N and TaON) that require surface modifications.^27–30

Surprisingly, density functional theory (DFT) calculations revealed that the electronic structure of Bi₄NbO₈X deviates from what is expected in conventional mixed-anion compounds (Fig. 1c and 2a). The VBM of Bi₄NbO₈Cl consists mainly of O 2p orbitals, rather than Cl 3p orbitals (as in BiOCl), and is substantially more negative than that available for conventional oxides and oxychlorides. This unusual occupation of the VBM with the O 2p band contributes to the exceptional stability of Bi₄NbO₈Cl during photocatalytic reactions, as the photogenerated holes are presumed to be populated near the VBM, preventing oxidative decomposition of Bi₄NbO₈Cl.

3.2. The origin of distinct band structures of Bi₄NbO₈Cl

3.2.1 Lone pair interactions. One of the factors contributing to the elevation of the oxygen 2p band in Bi₄NbO₈Cl is the lone pair interaction described by the revised lone pair (RLP) model.^70–73 This model was originally proposed to elucidate the origin of an asymmetric coordination environment in cations with lone pair electrons (LPEs), such as Pb²⁺ in PbO, with a d¹⁰s²p⁰ electronic configuration.⁷⁰ In the classical model, the stereochemically active lone pair is explained in terms of the on-site mixing of the cation s and p orbitals, forming an asymmetric nonbonding lobe of electron density that repels surrounding ions. However, this model does not account for why oxyhalides display a stronger preference for structural distortions compared to chalcogenides. The revised model emphasizes lone pair interactions, where anion p states mediate the interaction between s and p states of the lone pair cation, providing stereochemical activity while affecting electronic structures. Fig. 4a schematically illustrates the lone pair interaction between Bi and O. Initially, the Bi 6s LPEs strongly interact with the O 2p states in the valence band (Fig. 4a, left), yielding bonding and anti-bonding states, which are inherently unstable. Subsequently, unoccupied cation Pb 6p states hybridize with the anti-bonding (Bi 6s + O 2p)* states, stabilizing the occupied electronic states (Fig. 4a, right). The resulting VBM from the lone pair interaction becomes higher than that without it (i.e., the original O 2p state). As shown in Fig. 4b, the presence of the lone pair interaction in Bi₄NbO₈X is evident from two aspects of density of states (DOS) in the valence band: (1) a substantial contribution of Bi 6s (and Bi 6p) to the DOS near the VBM, in conjunction with O 2p in the energy region of 0 to −1 eV (highlighted in red), and (2) the DOS overlap between Bi 6s and O 2p orbitals in a much lower energy region ranging from −7 to −11 eV (highlighted in green). In this way, the presence and extent of lone pair interaction can be inferred for other materials through similar considerations.

Fig. 4 (a) Schematic illustration of the lone pair interactions of Bi based on the RLP model.³² The left and right parts, respectively, show the Bi 6s–O 2p interaction and the interaction between the resultant anti-bonding and Bi 6p orbitals. Note that the understanding of the structural distortion based on a RLP is essentially the same as that based on the second-order Jahn–Teller (SOJT) effects, which is often used to describe the structural distortion of compounds with d⁰ cations. However, in the case of a RLP, the interaction involves filled cation s orbitals. (b) DOS of Bi₄NbO₈Cl. The red and green highlights represent the VBM and Bi 6s–O 2p bonding states, where characteristics of lone pair interactions are seen, corresponding to the orbitals highlighted in the same colour in (a).

An example highlighting the importance of lone pair interactions is found in the Sillén phase PbBiO₂X (X = Cl, Br, I), with the structure shown in Fig. 3b (left), composed of double fluorite ([PbBiO₂]⁺) layers separated by a single halogen layer (s = 2 and m = 1).³³ PbBiO₂X (X = Cl, Br) has a narrower band gap of about 2.4 eV than that for SrBiO₂X and BaBiO₂X (3.5–3.6 eV).³³ DFT calculations show that the VBM of all MBiO₂X compounds (M = Sr, Ba, Pb; X = Cl, Br) is predominantly occupied by oxygen bands, akin to Bi₄NbO₈Cl. However, due to the higher positioning of Pb 6s orbitals compared to Bi 6s,⁷⁰ the lone pair interaction of Pb 6s gives rise to higher bands than those without Pb. In the case of PbBiO₂I, the VBM is mainly occupied with iodine bands, accounting for its narrower band gap than that of PbBiO₂X (X = Cl, Br). The lone pair orbitals of lead contribute to a more extensive band dispersion than that in SrBiO₂Cl, resulting in a smaller effective mass for both (photogenerated) electrons and holes in PbBiO₂Cl, hence enhancing its photocatalytic activity.³⁵

3.2.2 Madelung site potential. With respect to understanding the striking difference in electronic structures between Bi₄NbO₈X from BiOX, the covalent interactions based on the RLP scenario described above fail. This is because the coordination environment around Bi in the common fluorite block is nearly identical in both phases, implicating a longer-range interaction at play. A systematic examination of a series of Sillén and Sillén–Aurivillius compounds including Bi₄NbO₈X (X = Cl, Br) and BiOX (X = Cl, Br, I) unveiled the pivotal role of the Madelung site potential in destabilizing oxygen 2p orbitals in the fluorite layers.³¹Fig. 6 displays a generalized model of the band formation of ionic solids, adapted from a textbook of P. A. Cox⁷⁴ and modified for oxyhalides. The energy position of the VBM in ionic compounds is primarily determined by the Madelung potential and the electron affinity of the anions for ionic solids, although other parameters such as bandwidth could also significantly impact the energy position. Indeed, the energy levels calculated by using the summation of Madelung site potentials of anions and electron affinity capture essential features of the valence band structures of these compounds (Fig. 7a). In particular, oxide anions in the fluorite layer are found to be destabilized in Bi₄NbO₈X and Bi₂GdO₄X (Fig. 7a).

Moreover, the relationship with layer stacking is elucidated by analysing the contribution of each sublayer adjacent to the oxide sublayer in the fluorite blocks (layer-by-layer Madelung analysis).^31,75Fig. 7b compares the sublayer stacking and electrostatic potentials of Bi₄NbO₈Cl and BiOCl. Bi₄NbO₈Cl exhibits greater electrostatic destabilization from the downside of the 2nd nearest neighbor sublayer (2NNL_d), while no significant differences are observed in the closer sublayer (Fig. 7b). This suggests that the electrostatic destabilization of oxide anions in Bi₄NbO₈Cl results from a more negative O²⁻ sublayer compared to the Cl⁻ sublayer of BiOCl in 2NNL_d, reflecting the long-range nature of electrostatic interactions.

The Madelung analysis proves to be a powerful tool for roughly predicting valence band structures of oxyhalide compounds, even when the crystal structure is too complicated to be calculated, as in the case of Sillén–Aurivillius-type Bi₃Sr₂Nb₂O₁₁X involving Bi/Sr disorder.^31,76 Furthermore, the low computational cost of Madelung potential calculation is advantageous in exploring candidate photocatalysts from databases.⁷⁶ By employing Madelung potential calculations to screen databases, a Sillén-type Bi₄BaO₆Cl₂ with double and triple fluorite layers separated by a chloride layer was identified to have more destabilized oxygen sites than Bi₄NbO₈Cl, indicating its potential as a stable photocatalyst possessing a high VBM composed of oxygen bands. This finding led to the experimental confirmation of stable photocatalysis of this material, as well as the improvement of photocatalytic properties through the synthesis of new materials Bi₄AO₆Cl₂ (A = Sr, Ca).⁷⁶

The structural diversity of oxyhalides arising from various layer and stacking combinations is not only comparable to that of copper oxide and iron pnictide superconductors but also has a significant impact on their electronic structures. Madelung potential analysis holds promise in predicting novel oxyhalides with band structures favorable for water splitting and other photocatalysis reactions. Specifically, the layer-by-layer analysis is a unique concept established through the study of oxyhalide photocatalysts, which may allow the prediction and design of properties in a wide range of layered materials, combining recently developed material informatics. From a broader perspective, recent progress in thin-film technology has significantly enhanced the flexibility in stacking layers of two-dimensional (2D) materials, including the twisting of stacking layers and the artificial stacking of different types of 2D materials.^77–80 The concept of layer-by-layer analysis could provide new opportunities for the design and prediction of materials by combining such recent technology of thin-film growth.

4. Fluorite layer manipulation

4.1. Cation substitution

The double fluorite layer (s = 2), M₂O₂, is the common building block of the Sillén and Sillén–Aurivillius phases and plays a dominant role in determining their band structures in most cases. The cation site in these fluorite blocks is primarily composed of Bi³⁺. Other cations, such as Pb²⁺, La³⁺, and Sr²⁺, can substitute these sites, though the occupation is partial in most cases. For Sillén–Aurivillius phases, such as La_2.1Bi_2.9Ti₂O₁₁Cl,⁸¹ the alkali earth metal and lanthanide cations tend to prefer the M site on the perovskite layer side, probably due to the stereoactive LPEs of Bi³⁺ favoring an asymmetric environment coordinated to opposite halide ligands to form MO₄X₄ (vs. MO₈).^31,45,68,81 Lone pair cations (e.g., Bi³⁺ and Pb²⁺) in the fluorite layer determine the VBM position via lone pair interactions; in MBiO₂X (M = Sr, Ba, Pb), and the VBM position can be tuned with M (Fig. 2c and 5c). In contrast, the 6p orbitals of Bi³⁺ occupy the CBM in most Sillén(–Aurivillius) phases. Because it is difficult to fully replace Bi³⁺, the CBM is hardly changed by simple cation substitutions.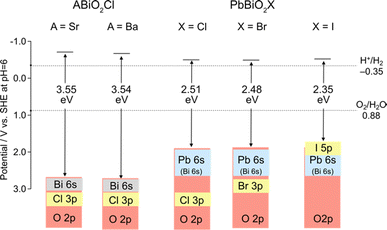

Fig. 5 Band alignments and band structures of Sillén-type MBiO₂X (M = Sr, Ba, Pb; X = Cl, Br, I).³³

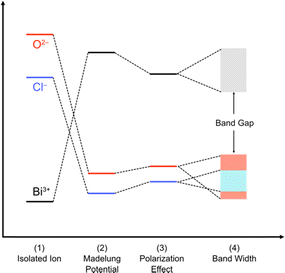Fig. 6 Band formation in solids from an isolated atom adopted and modified from ref. 73 for oxychlorides. The atoms constituting the ionic solids are first ionized (1). The energy levels of the isolated cations and anions are described by using the ionization potential and electronegativity. Then, the cations and anions are aligned periodically to from a crystal, providing the electrostatic interaction between charges. The electrostatic potential generated at a particular ion from all the surrounding ions in a crystalline material is referred to as the Madelung site potential (2). In purely ionic solids, the energy levels are expected to be dominated by this electrostatic interaction. However, in a realistic system, it should be noted that the energy levels of ions are also affected by polarization of electron clouds (3) and the bandwidth derived from covalent interactions (4).

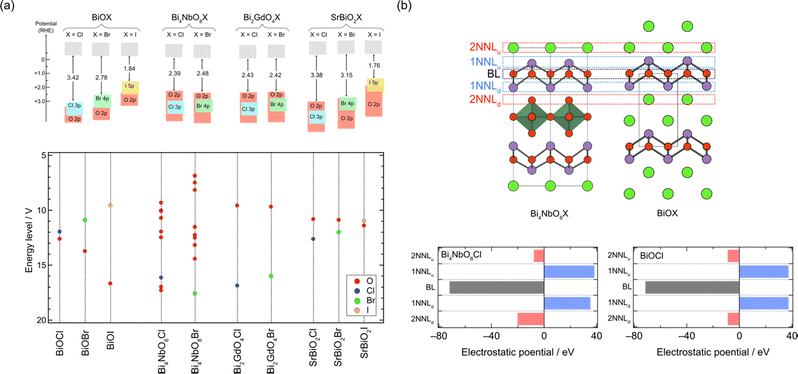Fig. 7 (a) Schematic band structures obtained by DFT calculations and experiments (top) and energy levels of anions obtained by Madelung site potential calculations (bottom). (b) Sublayer stacking of Bi₄NbO₈Cl and BiOCl (top) and the electrostatic potential generated at the oxygen site in the fluorite block from adjacent sublayers (bottom).^31,75 The oxygen sublayer in the fluorite layer, its adjacent layers, and 2nd adjacent layers are denoted as the basal layer (BL), 1st nearest neighbour layers (1NNL), and 2nd nearest neighbour layers (2NNL). The subscript of NNL_u and NNL_d indicates the upper or down side layer, respectively. Surrounding ions within 4 Å are considered in the calculations.

Cation substitution into the fluorite layer not only affects the location of the VBM but also the carrier dynamics of Sillén phases. This is because photo-generated electrons and holes are expected to flow in the fluorite layer, which dominates the CBM and VBM.³⁵ In the Sillén phase PbBiO₂Cl, the overlapped orbitals of Pb/Bi and O account for both the CBM and VBM. Therefore, partial substitution of Pb with Sr disrupts the orbital connection, resulting in a reduction in band dispersion (i.e. an increase in effective mass m*). The impact of this Sr substitution on carrier dynamics can be evaluated by time-resolved microwave conductivity (TRMC) measurements. This method allows the observation of transient changes in microwave reflectivity by carriers in a sample generated by the laser pulse, and provides an electrode-less approach for determining the generation yield, mobility, and lifetime of charge carriers in powder photocatalysts (Fig. 8a).^34,35 The photoconductivity signal (φΣμ), determined by TRMC, which is the product of the quantum yield (φ) and the sum of charge carrier mobilities Σμ (=μ₊ + μ₋), decreased with increasing Sr substitution x in Sr_xPb_1−xBiO₂Cl, corresponding to the change in m* (Fig. 8b and c). Furthermore, the photocatalytic activity of Sr_xPb_1−xBiO₂Cl also decreased with increasing x, consistent with the change in TRMC and m*. These results highlight the critical requirement to account for the band dispersion (effective mass) for obtaining optimal photocatalytic performance.

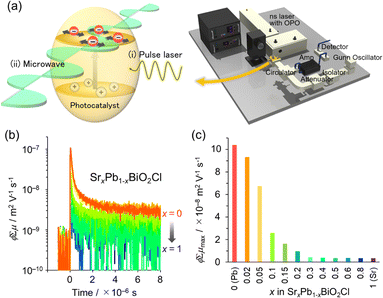Fig. 8 (a) Schematic image of TRMC measurement. (b) TRMC transients of Sr_xPb_1−xBiO₂Cl (orange for x = 0 to blue for x = 1). (c) φΣμ maximum (φΣμ_max) values with respect to x for λ_ex = 266 nm and I₀ = 6.8 × 10¹⁵ photons cm⁻² per pulse. (b and c) Adapted with permission from ref. 35 Copyright 2020, American Chemical Society.

4.2. Triple fluorite layers (s = 3)

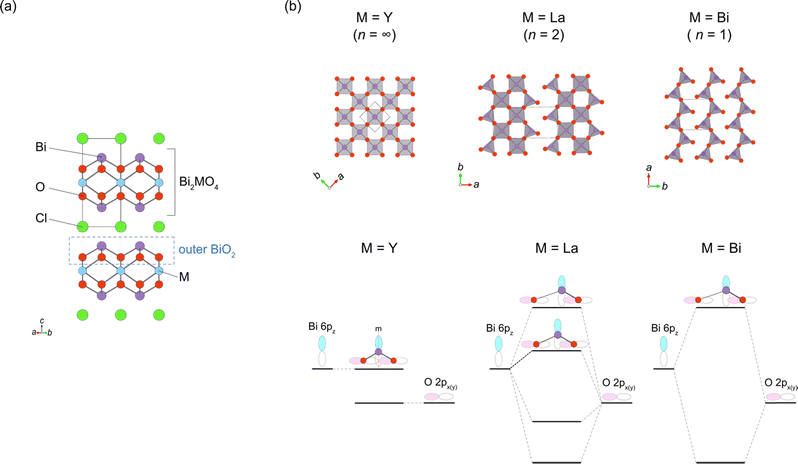
While the majority of reported Sillén-type compounds are based on the double fluorite layer (s = 2), represented by the Bi₂O₂ layer, varying the thickness of fluorite slabs, if possible, could enrich the structural and compositional diversity and improve photocatalytic properties. As shown in Fig. 9a, Bi₂MO₄Cl (M = Y, La, Bi) has triple fluorite layers (s = 3), with the M cation selectively occupying the inner cation site, while two Bi cations occupy the outer cation site in the triple fluorite block. Although the electronic structure is governed by Bi–O bonds (shown later), the M cation in the inner sublayer has a significant influence on the outer sublayers, drastically modifying the CBM.

Fig. 9 (a) Crystal structure of Bi₂YO₄Cl (space group: P4/mmm) with a triple fluorite layer. The outer BiO₂ sublayer in the triple fluorite layer is shown by the dotted black line. (b) The outer BiO₂ sublayer in Bi₂MO₄Cl with M = Y (n = ∞; left), M = La (n = 2; middle) and M = Bi (n = 1; right) projected along the c-axis (top) and the interaction between Bi 6p_z and O 2p_x orbitals at the Γ point (bottom), which accounts for the upshift of the CBM with decreasing n. While the M = Y phase (Bi₂YO₄Cl) has the ideal structure with edge-sharing BiO₄ square pyramids forming a 2D network, one of the Bi–O bonds is substantially elongated in the M = Bi phase (Bi₃O₄Cl; space group: I2/a), leading to the single zigzag chains formed by BiO₃ units along the a axis (corresponding to the [110] direction with respect to the Bi₂YO₄Cl lattice). In the M = La phase (Bi₂LaO₄Cl; space group: P2₁/a), half of the Bi cations are three-coordinated and the other half are four-coordinated, leading to the double zigzag chains along the b-axis. For M = Y, mirror symmetry at the Bi site prohibits any interaction between Bi 6p_z and O 2p_x orbitals, resulting in a low-lying nonbonding state at the CBM. For M = La and Bi, the mirror symmetry is broken due to the formation of double/single zigzag chains, leading to the upshift of the CBM via the anti-bonding interaction. The ‘residual’ four-coordinate Bi site for M = La places the CBM between M = Y and Bi.

When the M site is occupied with Y, which has an ionic radius of 1.02 Å, no distortion is observed in the crystal structure (space group: P4/mmm), with edge-sharing BiO₄ square pyramids (Fig. 9b, left). On the other hand, for M = Bi(2) with a larger ionic radius of 1.16 Å, edge-sharing Bi(1)O₄ square pyramids are substantially elongated (Bi(1)–O2 = 3.33 Å), resulting in the monoclinic distortion (space group: I2/a), where one-dimensional (1D) zigzag chains of BiO₃ units run along the [100] direction (Fig. 9b, right). Thus, the ‘inserted’ Bi(2) layer is regarded as applying an tensile strain to the outer Bi(1)O₂ network (Fig. 2g), similar to a widely used strategy in thin film materials, i.e., compressive or tensile strain applied from a substrate.^82–86 Namely, with respect to the ideal Bi₂YO₄Cl, the bond breaking occurs in the outer Bi(1)O₂ sublayer of Bi₃O₄Cl (Fig. 9b). The stereochemical activity of Bi³⁺ LPEs may be also at play for this structural distortion, in addition to the size of Bi³⁺. A similar phenomenon occurs for M = La with an ionic radius of 1.17 Å, but only half of the Bi atoms experience bond cleavage to form BiO₃ coordination, leading to the formation of double zigzag chains running along [100] (Fig. 9b, right). Bi₂LaO₄Cl adopts the space group of P2₁/a, with a doubled b axis compared with Bi₃O₄Cl. Consequently, the Bi₂MO₄Cl structure can be conceptualized as a series of n-zigzag chains (n = 1 for Bi, n = 2 for La and n = ∞ for Y). In this context, Bi₂MO₄Cl is reminiscent of n-legged spin ladders that connect the 2D square lattice with the 1D chain,⁸⁷ as realized in S = 1/2 Sr_n−1Cu_nO_2n−1 (ref. 88) and S = 2 Sr_n+1Fe_nO_2n+1.^89–91 Thus, the triple fluorite layer system has rich chemistry based on bond cleavage, with the potential to be further extended in intermediate dimensions between 1D and 2D by, e.g., M-site substitution and external pressure.

The concept of strain engineering with the triple fluorite block (Fig. 2g) was not mentioned in ref. 37, but was first proposed in the Bi_2−xSb_xYO₄Cl solid solution study, along with the bond breaking process.⁹² Here, Sb₂YO₄Cl exhibits a distinct distortion, as shown in Fig. 8a.^93,94 The substitution by smaller Sb³⁺ (0.76 Å (VI)) for Bi³⁺ (1.03 Å (VI)) means that, relative to Bi₂YO₄Cl, the ‘fixed’ inner Y layer in Bi_2−xSb_xYO₄Cl provides “effectively” a tensile strain to the outer SbO₂ layer. As a consequence, a structural phase transition involving bond breaking occurs at x = 1.5, leading to the Sb₂YO₄Cl-type structure. Sb₂YO₄Cl has zero-dimensional (0D) Sb₄O₈ rings formed by four corner-sharing SbO₃ (Fig. 10a). In addition, Sb₂MO₄Br (M = Y, Eu–Tb) has a single zigzag chain, as in Bi₃O₄Cl, but running along the 100_p direction relative to the primitive Bi₂YO₄Cl lattice, while the zigzag chains in Bi₂MO₄Cl (M = La, Bi) are running along 110_p (Fig. 10b).

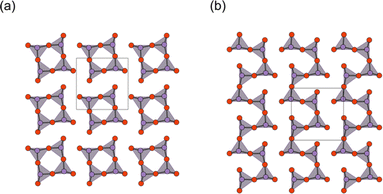Fig. 10 The outer SbO₂ sublayer of a triple fluorite block in (a) Sb₂YO₄Cl and (b) Sb₂MO₄Br (M = Y, Eu–Tb). Bi₂MO₄Cl possesses 1D chains of corner-sharing BiO₃ (see Fig. 9 for comparison), while in Sb₂YO₄Cl, 0D Sb₄O₈ (0D) rings are formed. Purple and red balls represent Sb and O, respectively.

The breaking of Bi–O bonds in Bi₂MO₄Cl significantly impacts the CBM position, a feature not seen in compounds with double fluorite layers. The CBM decreases from −0.36 V (M = Y; n = ∞) to −0.57 V (M = La; n = 2), and further to −0.94 V (M = Bi; n = 1). This systematic shift can be understood in terms of the local symmetry between the Bi 6p and O 2p orbitals, taking into account the presence or absence of mirror symmetry at the Bi site of the outer BiO₂ sublayer of the tripe fluorite slab (Fig. 2f and 9b). In the ideal Bi₂YO₄Cl, the Bi site in the outer BiO₂ sublayer has a 4 mm site symmetry with four equidistant Bi–O bonds. However, the presence of two perpendicular mirror symmetries prohibits any Bi 6p_z–O 2p_x,y interaction at the Γ point, resulting in a low-lying nonbonding state at the CBM, as illustrated in Fig. 9b (left). On the other hand, in Bi₃O₄Cl, the deformation of the BiO₂ network into single zigzag chains removes mirror symmetries at the three-coordinate Bi(1) site with a site symmetry of 1. This permits the mixing of Bi 6p_z and O 2p_x,y orbitals, strongly antibonding at the Γ point, thereby raising the CBM (Fig. 9, right). In Bi₂LaO₄Cl, the absence of mirror symmetry for both Bi sites (site symmetry of 1) indicates a finite antibonding interaction between Bi 6p_z and O 2p_x,y orbitals for both sites, as in Bi₃O₄Cl. However, half of the Bi cations (Bi(2) site) retain four-fold coordination as in Bi₂YO₄Cl, forming Bi 6p_z bands that are higher in energy than those in Bi₂YO₄Cl but lower than those in Bi₃O₄Cl (Fig. 9b, middle).

The modifications in crystal and band structures of Bi₂MO₄Cl also exert a notable influence on the carrier dynamics and photocatalytic activity. The non-bonding nature at the CBM of Bi₂YO₄Cl provides a highly dispersive conduction band, resulting in elevated photoconductivity and enhanced photocatalytic activity.³⁷ In contrast, both the photoconductivity and photocatalytic activity are considerably reduced for Bi₂MO₄Cl (M = La, Bi) due to their small band dispersion. Thus, the search for compounds with wider zigzag chains (n > 2) is essential to improve photoconductivity and achieve finer control over the CBM tuning.

The symmetry of the middle cation in the triple fluorite layer is important for tuning the VBM of Bi₂MO₄Cl when it is occupied by Bi with lone pair electrons.⁹⁵ While the middle Bi in Bi₃O₄Cl is significantly displaced from the center of the cube formed by oxygen, the solid solution Bi₂(Bi_xY_1−x)O₄Cl (x ≤ 0.5), retaining high tetragonal symmetry, has Bi in a centrosymmetric environment. The high symmetry suppressed the “secondary” lone pair interaction of the middle Bi (the right of Fig. 4a) between Bi 6p and the anti-bonding (Bi 6s + O 2p)* states, which elevates the VBM by keeping the anti-bonding (Bi 6s + O 2p)* states at higher energy levels. This observation highlights the importance of considering the symmetry of lone pair cations for designing band structures (Fig. 2b and f).

4.3. Bi₁₂O₁₇Cl₂ with sextuple layers (s = 6)

Layered oxyhalides with a fluorite layer thickness greater than s = 3 are exceptionally rare. An example of such a compound is Ce_1.3Nd_0.7O₃Cl, which presents a Sillén-type oxyhalide with quadruple (s = 4) fluorite layers of [Ce_2.6Nd_1.4O₆] separated by double chloride layers.⁹⁶ In 2022, it was found that Bi₁₂O₁₇Cl₂ comprises a sextuple (s = 6) fluorite-like block of Bi₆O_8.5 separated by a single chloride layer.⁹⁷ It is noteworthy that, prior to this study, Bi₁₂O₁₇Cl₂ had been extensively investigated as a photocatalyst for various reactions, such as degradation of organic pollutants and CO₂ reduction.^98–105 Despite its applications, the structure remained unresolved until 2022. In the resolved crystal structure of Bi₁₂O₁₇Cl₂, the oxygen in the central part of the sextuple Bi₆O_8.5 block does not occupy tetrahedral sites, as in the fluorite structure, but instead occupies octahedral sites, resembling the rock-salt structure. This arrangement forms a 1D rock-salt block running along the b-axis (Fig. 11a). Periodically inserted 1D rock-salt units induce an in-plane corrugation of the Bi₆O_8.5 fluorite layer along the a-axis, leading to a commensurately modulated superstructure with a 4√2a × √2b × c supercell based on the ideal layered fluorite structure with a = b ∼ 3.85 Å and c ∼ 35.2 Å. It would be possible to assume that the inclusion of the rock-salt units eliminates the mismatch between inner and outer sublayers (see Fig. 2g), which is inherent in a compound with s ≥ 3 ‘pure’ fluorite layers (but not in layered perovskites).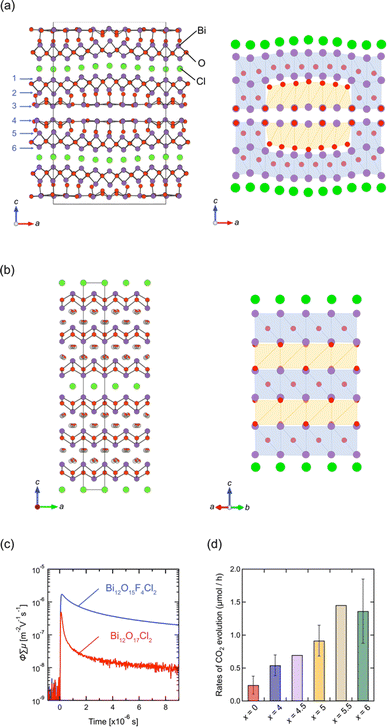

Fig. 11 Crystal structures of (a) Bi₁₂O₁₇Cl₂ and (b) Bi₁₂O_17−0.5xF_xCl₂ (x = 4.5).⁹⁷ Purple, green, and red balls represent Bi, Cl, and O atoms, respectively. The anions in the rock-salt block in (b) are mainly occupied with fluorine and randomly shifted from the ideal octahedral site. In the right panel, the sextuple fluorite Bi-(O, F) layers are illustrated, where blue and orange represent a fluorite-like block with anions at the tetrahedral site and the rock-salt-like block with anions at the octahedral site. (c) TRMC transients of Bi₁₂O_17−0.5xF_xCl₂ (x = 0, 4) upon 355 nm laser excitation. (d) The rates of CO₂ evolution for the initial 10 hours from the photocatalytic decomposition of acetic acid over Bi₁₂O_17−0.5xF_xCl₂ (x = 0, 4, 4.5, 5, 5.5, 6). (c and d) Reprinted with permission from ref. 97 Copyright 2022, John Wiley and Sons.

Previous studies on Bi₁₂O₁₇Cl₂ have predominantly focused on synthesizing nanoparticles and constructing phase junctions to improve its photocatalytic activity.^98–105 However, the understanding of the crystal structure opens new avenues for improving its properties. In terms of photocatalysts, the corrugation in the Bi₆O_8.5 block, coupled with increased thickness, may significantly impact the dynamics of photo-excited carriers and, consequently, the photocatalytic activity. Thus, we conducted a topotactic anion-exchange (2F⁻/O²⁻) reaction using NH₄F, suitable for redox-free fluorination.¹⁰⁶ This process succeeded in eliminating the structural modulation, yielding Bi₁₂O_17−0.5xF_xCl₂ (x ≤ 6).⁹⁷ Interestingly, an in-depth structural analysis revealed that Bi₁₂O_17−0.5xF_xCl₂ is composed of alternate fluorite and rock-salt blocks along the c axis (Fig. 11b), where fluoride anions selectively occupy the rock-salt block. The loss of corrugation leads to high photo-carrier conductivity (Fig. 11c) and photocatalytic activity against oxidative decomposition of acetic acid (Fig. 11d).

5. Halogen layer

5.1. Monolayer vs. bilayer

Whether the halogen layer is a monolayer or bilayer plays a critical role in the location of the halogen bands, which can be largely explained by using the Madelung potential (Fig. 2c). Monolayer halogen arrangement is electrostatically stabilized by being sandwiched between adjacent cation sublayers, whereas bilayer configurations encounter greater electrostatic destabilization. This distinction explains why the VBM of Sillén phases with a bilayer halogen structure (Fig. 3b, left), such as BiOX, is predominantly characterized by halogen bands. In contrast, the VBM of most Sillén and Sillén–Aurivillius phases with a monolayer halogen structure, such as Bi₄NbO₈Cl (Fig. 3d, left) and PbBiO₂Cl (Fig. 3b, left), is typically occupied by oxygen bands.

The introduction of a combination of single and double halogen layers brings a new degree of freedom. MBi₃O₄X₃ (M = Sr, Pb; X = Cl, Br) consists of both single and double halogen layers, sandwiching a double fluorite layer (Fig. 12a).^107,108 For M = Pb, PbBi₃O₄Br₃ exhibits a slightly smaller bandgap compared to PbBi₃O₄Cl₃, which is ascribed to the contribution of electrostatically destabilized Br bilayers surpassing that of O 2p. Another important effect of combining these two types of halogen layers is the asymmetry of the fluorite layer along the out-of-plane direction introduced by sandwiching with the single and double halogen layers. In the Sr counterpart (SrBi₃O₄Cl₃), the asymmetry around the fluorite [Sr_0.5Bi_1.5O₂] layer leads to the preferential occupation of Bi at the site adjacent to the chloride monolayer.¹⁰⁷ This is in contrast to the equally distributed Sr and Bi in the fluorite layer of SrBiO₂Cl, which comprises only a halogen monolayer. The narrower bandgap of SrBi₃O₄Cl results from a higher VBM and lower CBM compared with those of BiOCl and SrBiO₂Cl (Fig. 12b), which respectively have only double (Fig. 3b, right) and single halogen layers (Fig. 3b, left). The higher VBM can be rationalized by the electrostatic destabilization of Cl in the halogen bilayer due to the selective coordination of low-valent Sr²⁺, leading to higher Cl 3p bands. Moreover, the exclusive occupation of Bi on the side of the halogen monolayer allows for Bi–Bi interaction (Fig. 2e), leading to a lower CBM compared with those of SrBiO₂Cl and BiOCl. Further discussion on interlayer Bi–Bi interaction will be provided in the subsequent section (Section 5.2 and Fig. 14).

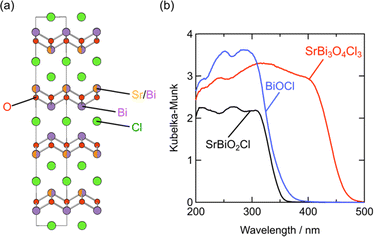Fig. 12 (a) Crystal structure of SrBi₃O₄Cl₃ and (b) UV-vis absorption spectra of BiOCl, SrBiO₂Cl, and SrBi₃O₄Cl₃.¹⁰⁷ The cation site on the side of the halogen monolayer in SrBi₃O₄Cl₃ is exclusively occupied by Bi³⁺, which allows interlayer Bi 6p_z interactions, while Sr and Bi face across the Cl layer in SrBiO₂Cl. Reproduced from ref. 107 with permission of The Royal Society of Chemistry.

5.2. Iodide layer

Iodide anions possess distinct characteristics compared to bromide and chloride anions, including low electronegativity, high polarizability, and a large ionic radius. Based on the concept in Fig. 2a, iodine can form the highest bands among the halogens (as observed in BiOI) due to its lowest electronegativity (2.66) compared to chlorine (3.16) and bromine (2.96). In contrast, as we have seen in Section 3.1, when the VBM is occupied with oxygen bands due to the electrostatic destabilization, replacing Cl with Br hardly changes the bandgap. Even in such a case, introducing iodine narrows the bandgap of some Sillén phases since the iodine 5p band is located even higher than the oxygen 2p band as seen in PbBiO₂I (Fig. 5).³³ However, the occupation of iodide anions at the VBM is problematic because of self-oxidation by photo-generated holes.

Recently, we found that in Sillén–Aurivillius Ba₂Bi₃Nb₂O₁₁I with a double perovskite block (Fig. 13a), the oxygen band dominates the VBM, with a bandgap smaller than that of its chloride and bromide counterparts due to the higher VBM.¹⁰⁹ Importantly, unlike PbBiO₂I described above, the VBM of Ba₂Bi₃Nb₂O₁₁I is mainly formed by oxygen bands, which not only allows for stable photocatalysis but also access to a wider visible light range. Among oxygen sites, the central (bridging) oxygen (O1 site) in the perovskite block, rather than the oxygen (O4 site) in the fluorite block, dominates the VBM of Ba₂Bi₃Nb₂O₁₁I. The usual Madelung analysis (Fig. 13c) based on formal valence states (i.e. fully ionic picture) cannot reproduce this behavior because the oxygen band is more stabilized due to lattice expansion. The origin of the elevated oxygen (O1) band in the perovskite layer is attributed to the high polarizability of iodide (Fig. 2d), which reduces the effective charge of itself and of the adjacent Bi(2) ion with moderate electronegativity (2.02), that is, I^−1+δ and Bi(2)^+3−δ/2 (Fig. 13a). This is rationalized by the DFT calculations for BiOX, which show that the effective charges of F, Cl, Br and I in Sillén BiOX are −0.7, −0.5, −0.4 and −0.3, respectively.¹¹⁰ Thus, the [BaNb₂O₇]^2– perovskite layer sandwiched by the [Ba_0.5Bi_1.5O₂]^1.5−δ/2 fluorite layers is electrostatically destabilized. This is supported by a modified Madelung potential calculation that takes into account the reduced effective charge (Fig. 13d). Moreover, the benefits of using iodine also appear in the carrier (especially hole) mobility; the introduction of iodide anions enhances the photocatalytic activities of a wide range of Sillén–Aurivillius related phases such as Bi₄NbO₈X, Ba₂Bi₃Nb₂O₁₁X and Bi₆NbWO₁₄X due to improved charge transport properties.^109,111 This comes from the high polarizability of the iodide, which shields the Coulomb potential and reduces the effective mass, as discussed for halide perovskite and other materials.^112–114

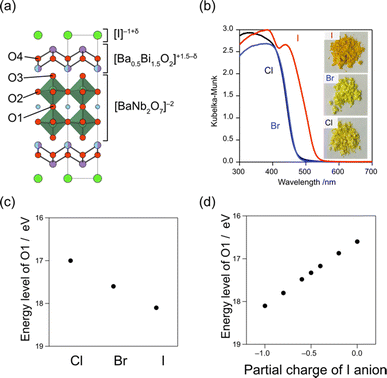Fig. 13 (a) Crystal structure of Bi₃Ba₂Nb₂O₁₁I, showing the effective charges of I and Bi(2). (b) Diffuse reflectance spectra and sample color of Bi₃Ba₂Nb₂O₁₁X (X = Cl, Br, I). (c) Ionic energy levels of O²⁻ at the O1 site in Ba₂Bi₃Nb₂O₁₁I, which contributes to the VBM obtained by using the Madelung potential calculated using formal charges. (d) Ionic energy levels at the O1 site, calculated under different assumptions of the effective charge of the iodide anion considering its softness. (b–d) Adapted with permission from ref. 109 Copyright 2021, American Chemical Society.

Moreover, the large size of the iodide anion modifies the CBM (Fig. 2e), where bonding and antibonding orbitals are formed in the CBM, primarily composed of Bi 6p_z orbitals between face-to-face Bi across the single halide layer (Fig. 2e and 14).¹¹¹ With iodide anions, the Bi–Bi distance increases and Bi 6p_z interactions are suppressed (Fig. 2e), resulting in a smaller bandwidth and higher CBM.

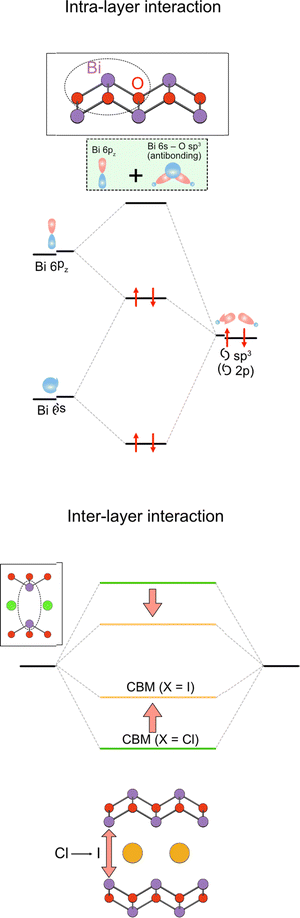Fig. 14 Formation of the conduction band in the Sillén–Aurivillius compounds via the intra- and interlayer interactions. (left) The intralayer interaction involves lone pair interactions, where the antibonding Bi 6s/O 2p state interacts with Bi 6p_z to produce occupied bonding (antibonding + p_z) and unoccupied antibonding (antibonding + p_z)* levels (see also Fig. 4 and Section 3.2.1). (right) The latter (highlighted in green) further interacts with another (antibonding + p_z)* via interlayer interaction to form the conduction band. The resulting CBM is modified by the halogens present between the Bi layers, which changes the interlayer Bi–Bi distance.¹¹¹

6. Perovskite layer manipulation

6.1. Octahedral cation

For conventional (layered) perovskite oxide/oxynitride semiconductors such as NaTaO₃ and BaNbO₂N, changing the transition metal at the octahedral site drastically affects the position of the CBM because their CBM is mainly formed by the d orbitals of transition metals at the octahedral (B) site.¹¹⁵ For example, replacing M = Nb in NaMO₃ with Ta increases the bandgap from 3.4 eV to 4.0 eV due to the difference in electronegativity.^12,115 In contrast, for Sillén–Aurivillius phases, the bandgap of Bi₄MO₈Cl remains almost the same between M = Nb (2.43 eV) and M = Ta (2.50 eV) because the CBM of most Sillén–Aurivillius phases is dominated by Bi 6p orbitals rather than d orbitals of transition metals.³² However, Bi₄SbO₈Cl, the first Sillén–Aurivillius phase with the B site exclusively occupied with p block elements,⁴⁶ shows much better hydrogen evolution performance compared to the Nb counterpart due to a slightly higher CBM.

6.2. Thickness of perovskite layers

Although the n = 1 Sillén–Aurivillius phase is the most widely studied of the Sillén–Aurivillius family, its compositional variation is relatively limited. This is due to the absence of a cuboctahedral (A) site and the limitation in the valence of the octahedral (B) site (Nb⁵⁺, Sb⁵⁺, W⁶⁺, etc.). Increasing the perovskite layer n of Sillén–Aurivillius phases (M₄A_n−1B_nO_3n+5X) provides broad compositional and structural variations and changes optical and electrochemical properties.^{36,38,67,81,116–122} For example, of the fourteen bilayer (n = 2) M₄AB₂O₁₁Cl (M = Bi, Pb, Ba, Sr; B = Ta, Nb, Ti), ten were discovered in 2019.⁶⁸

The synthesis of a series of n-layer perovskite compounds is of importance because it could allow systematic investigations on the role of the number of perovskite layers, as for cuprate superconductors.¹²³ However, in general, the synthesis of pure layered perovskite phases with large n is difficult via conventional solid state synthesis, because it competes with the formation of other n phases.¹²⁴ This can sometimes be solved with longer heating times or higher temperatures, but Sillén–Aurivillius phases suffer from volatilization of halogen species during a high-temperature treatment.^125,126 An effective strategy to address these difficulties is a multi-step (“bricklaying”) synthesis using compounds with common structural units as starting materials,³⁸e.g., Dion–Jacobson perovskite KCa₂Na₂Nb₅O₁₆ (n = 5) is obtained by the reaction of pre-synthesized KCa₂NaNb₄O₁₃ (n = 4) and NaNbO₃.¹²⁷ This approach was proven effective for acquiring Sillén–Aurivillius phases with n ≥ 3 (Fig. 15). For example, a phase-pure n = 4 Ba₂Bi₅Ti₄O₁₇Cl can be obtained by reacting Sillén BaBiO₂Cl and n = 4 Aurivillius Bi₄Ti₃O₁₂, the latter of which is pre-synthesized from n = 3 Aurivillius Bi₄Ti₃O₁₂ and BaTiO₃ (Fig. 15).³⁸ With the “bricklaying” synthesis, a series of Ti-based Sillén–Aurivillius phases such as BaBi₅Ti₃O₁₄Cl (n = 3), Ba₂Bi₅Ti₄O₁₇Cl (n = 4) and Ba₃Bi₅Ti₅O₂₀Cl (n = 5) can be obtained.³⁸

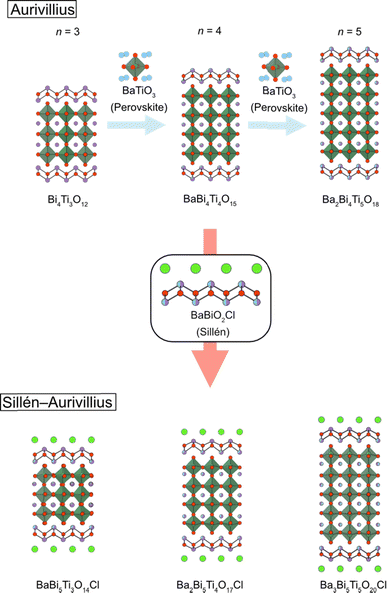Fig. 15 An illustration of the bricklaying synthesis for multi-layered Sillén–Aurivillius phases BaBi₅Ti₃O₁₄Cl (n = 3), Ba₂Bi₅Ti₄O₁₇Cl (n = 4) and Ba₃Bi₅Ti₅O₂₀Cl (n = 5).³⁸

Normally, the separation of electrons and holes in photocatalysts has been achieved by, e.g., modifying the surface or phase boundaries by co-catalyst loading, constructing phase junctions, and facet engineering,^128–132 as has been performed in Sillén–Aurivillius phases. On the other hand, the systematic study of a series of Ti-based Sillén–Aurivillius phases has shown that in compounds with larger n, the pathways through which electrons and holes flow could be well separated, leading to suppression of charge recombination.³⁸ From the DFT calculations of Ti-based Sillén–Aurivillius phases (n = 3 and 5), the fluorite layer is responsible for the CBM and the middle of the perovskite layer for the VBM. Therefore, the excited holes flowing in the middle of the perovskite slab are spatially well separated from the excited electrons in the fluorite layer. This could explain the improved photocatalytic activity for the O₂ evolution half reaction with increasing n (Fig. 2h).³⁸

6.3. Other intergrowth compounds

The Sillén–Aurivillius phase consists of –[X]–[Bi₂O₂]–[A_n−1M_nO_3n+1]–[Bi₂O₂]–[X]– stacking, but other combinations are possible. One example is Bi₆NbWO₁₄Cl (Fig. 16a), which has an intergrowth structure between a Sillén–Aurivillius block (–[Cl]–[Bi₂O₂]–[(Nb, W)O₄]–[Bi₂O₂]–[Cl]–) and a Aurivillius block (–[Bi₂O₂]–[(Nb, W)O₄]–[Bi₂O₂]–).¹³³ Another example is (A_0.6X)Bi₄(Nb_0.6W_0.4)O₈X (A = K, Rb, Cs), where the A_0.6X layer is inserted between the halide bilayers of the Sillén–Aurivillius phase (Fig. 16b).¹³⁴ While the bandgap of Bi₆NbWO₁₄X (2.49 eV) is similar to that of Bi₄NbO₈X (2.39 eV), (A_0.6Cl)Bi₄(Nb_0.6W_0.4)O₈Cl has a much larger bandgap of 3.1 eV.¹³⁴ There are other potential building blocks such as anti-fluorite and rock-salt layers.^135–137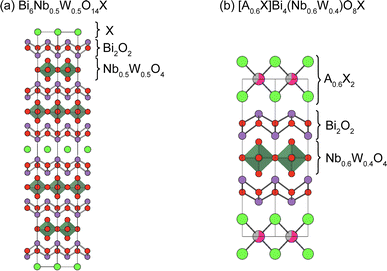

Fig. 16 Crystal structures of (a) Bi₆Nb_0.5W_0.4O₁₄X¹³³ and (b) [A_0.6X]Bi₄(Nb_0.6W_0.4)O₈X (A = K, Rb, Cs).¹³⁴ Note that non-distorted ideal structures are shown for clarity.

There are a variety of layered compounds structurally related to Sillén phases, in which the fluorite layers are separated by negatively charged layers other than halides (e.g., chalcogen). For example, Bi₂O₂S, which consists of fluorite bilayers that are separated by a sulfide layer, is isostructural with Sillén PbBiO₂Cl and has a smaller bandgap (1.1 eV) than the relevant oxyhalide compounds due to the higher S 3p orbitals.^138,139 BiOCuSe (or [Bi₂O₂][Cu₂Se₂]) and Bi₂YO₄Cu₂Se₂ have double and triple fluorite layers, separated by anti-fluorite Cu₂Se₂ layers, and have been studied in the field of thermoelectricity.^140,141

Moreover, molecular anions can occupy interlayer spaces between fluorite layers. For example, BiOIO₃ (or [Bi₂O₂][IO₃]), Bi₂O₂CO₃, and Bi₂O₂(NCN) have double fluorite layers separated by 2IO₃⁻, CO₃²⁻ and NCN²⁻ anions, respectively.^142–144 While compounds with oxoacid anions have a large bandgap (e.g., 3.1 eV for Bi₂O₂CO₃),¹⁴² Bi₂O₂(NCN) has a smaller bandgap (1.8 eV) because nitrogen in NCN²⁻ can form a high VBM, likely due to the difference in electronegativity between oxygen and nitrogen (Fig. 2a).¹⁴⁴ Therefore, the use of non-oxoacid anions in the interlayer site between the fluorite layer may be a useful approach to elevate the VBM, though stability against photo-generated holes could be an issue. Furthermore, blending molecular anions with single anions could lead to a unique structural modulation, as seen in [Bi₂O₂]₂I(BO₃).¹⁴⁵ where the single interlayer anion site is occupied with both I⁻ and BO₃²⁻ anions. BO₃²⁻ has a roughly comparable thermochemical radius (191 Å)¹⁴⁶ with Br⁻ (1.96 Å) and I⁻ (2.2 Å).²² The half occupation of borate anions leads to the complex ordering of I⁻ and BO₃²⁻ anions in the interlayer site with in-plane incommensurate modulations. The introduction of other anions including chalcogenide and other molecular anions has the potential to broaden the material diversity of photocatalysts and provide new aspects to band engineering.

7. Other issues

The photocatalytic activities depend on various complicated factors such as the particle shape, surface area, crystallinity and defect state as well as the electronic structure of materials.¹⁴⁷ Since the discovery of stable photocatalysis of Bi₄NbO₈Cl, Sillén and Sillén–Aurivillius phases have been studied from various aspects to improve their activities. However, as the scope of this review is band structure control, we will only give a brief overview of these efforts here. Common methods, which have been used to enhance photocatalyst activity, such as loading cocatalysts and constructing phase junctions, are effective for oxyhalide photocatalysts for Sillén–Aurivillius phases.^130,148,149 Furthermore, certain unique characteristics of oxyhalide photocatalysts have been elucidated. Optimal synthesis conditions require the suppression of halogen volatility to achieve high crystallinity and enhanced photoconductivity.^{125,126,150,151} Strategies such as alkali halide flux methods^150,151 and multi-step synthesis^36,38,68 have proven effective by reducing reaction temperatures or compensating for halogen volatility. Another distinctive characteristic is its layered structure, which favors platelet particle shapes and facilitates carrier flow primarily along the in-plane direction. By utilizing these features, the reaction site of reduction and oxidation can be separated in different planes, by modifying the synthesis and the way of loading cocatalysts.^152–154

8. Conclusion and outlook

From the first discovery of stable photocatalysis of Bi₄NbO₈Cl, various new Sillén and Sillén–Aurivillius photocatalysts have been discovered including the finding of new materials and structures such as Bi₄NbO₈I and Bi₁₂O₁₇Cl₂. These studies have unveiled the distinctive features of their electronic structures compared with those of conventional oxides and mixed-anion compounds and have established several key concepts for understanding and designing their band structures, summarized in Fig. 2. In particular, it is remarkable that the variation of layer stacking not only allows rational design of new materials like cuprate superconductors, but also significantly affects the electronic structure, which is understood by using the Madelung potential and interlayer interactions. Moreover, recent progress in increasing the thickness of fluorite and perovskite layers, along with the utilization of soft and easily polarizable iodide anions, opens a new avenue for the material design of Sillén(–Aurivillius) photocatalysts, showing great promise for future advancements of oxyhalide photocatalysts.

There are still challenges for the development of oxyhalide photocatalysts for water splitting. One important challenge is to achieve overall water splitting using these oxyhalide families. So far, oxyhalides exhibit remarkable activity in water oxidation, but the efficiency in water reduction is comparatively limited. This imbalance poses a challenge for achieving overall water splitting. Therefore, elevating the CBM to increase the driving force for water reduction as well as optimizing the synthetic method and surface modification is important for achieving overall water splitting. Another important thing is to decrease the band gap more for efficient solar-energy conversion. Considering the distribution of the solar spectrum, a material that can harvest light with a wavelength longer than 600 nm (corresponding to a band gap smaller than 2.0 eV) is highly desirable. However, no oxyhalides have achieved such a small band gap and stability. Considering the available compositional and structural variation, there is still much room for designing band structures through developing new compounds.

It is also noteworthy that the layered compounds related to Sillén and Sillén–Aurivillius phases have been recently investigated in a wide range area of material chemistry. For example, Sillén–Aurivillius Bi₄NbO₈Cl¹⁵⁵ and Sillén Bi₂LaO₄Cl¹⁵⁶ based compounds were recently demonstrated to show high oxide ion conductivity. Incorporation of chalcogenides expands the composition and layer stacking of materials as seen in Bi₄O₄SeX₂ with double fluorite layers separated by single and double halide/selenide layers, which have attracted attention as thermoelectric materials.^157–159 The insight into crystal and electronic structure engineering obtained via oxyhalide photocatalyst development will be of importance for a wide range of functional properties of related layered materials.

Author contributions

All authors contributed to writing this review.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by JSPS Core-to-Core Program (A) Advanced Research Networks (JPJSCCA20200004), the Grant-in-Aid for Scientific Research on Innovative Areas “Mixed Anion” project (16H06438 and 16H06439), JSPS KAKENHI (JP21K2055, JP20H00398, JP22H04914, and 23H0206), JST CREST (JPMJCR1421) and JST PRESTO (JPMJPR21A5).

Notes and references

1. R. Hoffmann, Angew. Chem., Int. Ed., 1987, 26, 846–878.
2. A. Walsh and K. T. Butler, Acc. Chem. Res., 2014, 47, 364–372.
3. A. Gruneis, G. Kresse, Y. Hinuma and F. Oba, Phys. Rev. Lett., 2014, 112, 096401.
4. D. O. Scanlon, C. W. Dunnill, J. Buckeridge, S. A. Shevlin, A. J. Logsdail, S. M. Woodley, C. R. Catlow, M. J. Powell, R. G. Palgrave, I. P. Parkin, G. W. Watson, T. W. Keal, P. Sherwood, A. Walsh and A. A. Sokol, Nat. Mater., 2013, 12, 798–801.
5. Y. Tokura and T. Arima, Jpn. J. Appl. Phys., 1990, 29, 2388–2402.
6. J. Paglione and R. L. Greene, Nat. Phys., 2010, 6, 645–658.
7. H. Fujito, H. Kunioku, D. Kato, H. Suzuki, M. Higashi, H. Kageyama and R. Abe, J. Am. Chem. Soc., 2016, 138, 2082–2085.
8. A. J. Bard, J. Photochem., 1979, 10, 59–75.
9. K. Domen, J. N. Kondo, M. Hara and T. Takata, Bull. Chem. Soc. Jpn., 2000, 73, 1307–1331.
10. F. E. Osterloh, Chem. Mater., 2008, 20, 35–54.
11. Y. Inoue, Energy Environ. Sci., 2009, 2, 364–386.
12. A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278.
13. R. Abe, J. Photochem. Photobiol., C, 2010, 11, 179–209.
14. M. Kitano and M. Hara, J. Mater. Chem., 2010, 20, 627–641.
15. K. Maeda, J. Photochem. Photobiol., C, 2011, 12, 237–268.
16. F. E. Osterloh, Chem. Soc. Rev., 2013, 42, 2294–2320.
17. T. Takata, C. S. Pan and K. Domen, Sci. Technol. Adv. Mater., 2015, 16, 033506.
18. A. Fujishima and K. Honda, Nature, 1972, 238, 37–38.
19. H. Kato, K. Asakura and A. Kudo, J. Am. Chem. Soc., 2003, 125, 3082–3089.
20. T. Takata, J. Jiang, Y. Sakata, M. Nakabayashi, N. Shibata, V. Nandal, K. Seki, T. Hisatomi and K. Domen, Nature, 2020, 581, 411–414.
21. D. E. Scaife, Sol. Energy, 1980, 25, 41–54.
22. H. Kageyama, K. Hayashi, K. Maeda, J. P. Attfield, Z. Hiroi, J. M. Rondinelli and K. R. Poeppelmeier, Nat. Commun., 2018, 9, 772.
23. C. S. Pan, T. Takata, M. Nakabayashi, T. Matsumoto, N. Shibata, Y. Ikuhara and K. Domen, Angew. Chem., Int. Ed., 2015, 54, 2955–2959.
24. K. Maeda, K. Teramura, D. Lu, T. Takata, N. Saito, Y. Inoue and K. Domen, Nature, 2006, 440, 295.
25. K. Maeda, T. Takata, M. Hara, N. Saito, Y. Inoue, H. Kobayashi and K. Domen, J. Am. Chem. Soc., 2005, 127, 8286–8287.
26. K. Maeda, Phys. Chem. Chem. Phys., 2013, 15, 10537–10548.
27. R. Abe, M. Higashi and K. Domen, J. Am. Chem. Soc., 2010, 132, 11828–11829.
28. M. Higashi, K. Domen and R. Abe, J. Am. Chem. Soc., 2012, 134, 6968–6971.
29. A. Kasahara, K. Nukumizu, G. Hitoki, T. Takata, J. N. Kondo, M. Hara, H. Kobayashi and K. Domen, J. Phys. Chem. A, 2002, 106, 6750–6753.
30. M. Higashi, K. Domen and R. Abe, J. Am. Chem. Soc., 2013, 135, 10238–10241.
31. D. Kato, K. Hongo, R. Maezono, M. Higashi, H. Kunioku, M. Yabuuchi, H. Suzuki, H. Okajima, C. Zhong, K. Nakano, R. Abe and H. Kageyama, J. Am. Chem. Soc., 2017, 139, 18725–18731.
32. H. Kunioku, M. Higashi, O. Tomita, M. Yabuuchi, D. Kato, H. Fujito, H. Kageyama and R. Abe, J. Mater. Chem. A, 2018, 6, 3100–3107.
33. H. Suzuki, H. Kunioku, M. Higashi, O. Tomita, D. Kato, H. Kageyama and R. Abe, Chem. Mater., 2018, 30, 5862–5869.
34. H. Suzuki, M. Higashi, H. Kunioku, R. Abe and A. Saeki, ACS Energy Lett., 2019, 4, 1572–1578.
35. H. Suzuki, S. Kanno, M. Hada, R. Abe and A. Saeki, Chem. Mater., 2020, 32, 4166–4173.
36. M. Ogawa, H. Suzuki, K. Ogawa, O. Tomita and R. Abe, Solid State Sci., 2023, 141, 107221.
37. A. Nakada, D. Kato, R. Nelson, H. Takahira, M. Yabuuchi, M. Higashi, H. Suzuki, M. Kirsanova, N. Kakudou, C. Tassel, T. Yamamoto, C. M. Brown, R. Dronskowski, A. Saeki, A. Abakumov, H. Kageyama and R. Abe, J. Am. Chem. Soc., 2021, 143, 2491–2499.
38. D. Ozaki, H. Suzuki, K. Ogawa, R. Sakamoto, Y. Inaguma, K. Nakashima, O. Tomita, H. Kageyama and R. Abe, J. Mater. Chem. A, 2021, 9, 8332–8340.
39. V. A. Dolgikh and L. N. Kholodkovskaya, Zh. Neorg. Khim., 1992, 37, 970–985.
40. D. O. Charkin, Russ. J. Inorg. Chem., 2008, 53, 1977–1996.
41. K. G. Keramidas, G. P. Voutsas and P. I. Rentzeperis, Z. Kristallogr.–Cryst. Mater., 1993, 205, 35–40.
42. L. G. Sillén, Svensk Kem. Tidsk, 1941, 53, 39.
43. D. O. Charkin, P. S. Berdonosov, V. A. Dolgikh and P. Lightfoot, J. Solid State Chem., 2003, 175, 316–321.
44. J. F. Ackerman, J. Solid State Chem., 1986, 62, 92–104.
45. D. Charkin, S. Kazakov and D. Lebedev, Russ. J. Inorg. Chem., 2010, 55, 1248–1256.
46. W. Fang, Y. Mi, Y. Yang, Y. Jiang, Y. Liu and W. Shangguan, Mater. Today Chem., 2022, 26, 101175.
47. S. Liu, W. Miiller, Y. Liu, M. Avdeev and C. D. Ling, Chem. Mater., 2012, 24, 3932–3942.
48. D. Ávila-Brande, L. C. Otero-Díaz, Á. R. Landa-Cánovas, S. Bals and G. Van Tendeloo, Eur. J. Inorg. Chem., 2006, 2006, 1853–1858.
49. D. O. Charkin, I. V. Plokhikh, S. M. Kazakov, S. N. Kalmykov, V. S. Akinfiev, A. V. Gorbachev, M. Batuk, A. M. Abakumov, Y. A. Teterin, K. I. Maslakov, A. Y. Teterin and K. E. Ivanov, Solid State Sci., 2018, 75, 27–33.
50. A. M. Kusainova, S. Y. Stefanovich, V. A. Dolgikh, A. V. Mosunov, C. H. Hervoches and P. Lightfoot, J. Mater. Chem., 2001, 11, 1141–1145.
51. W. Song, P. A. Salvador and G. S. Rohrer, ACS Appl. Mater. Interfaces, 2018, 10, 41450–41457.
52. G. Wan, L. Yin, X. Chen, X. Xu, J. Huang, C. Zhen, H. Zhu, B. Huang, W. Hu, Z. Ren, H. Tian, L. Wang, G. Liu and H. M. Cheng, J. Am. Chem. Soc., 2022, 144, 20342–20350.
53. C. Hu, F. Chen and H. Huang, Angew. Chem., Int. Ed., 2023, 62, e202312895.
54. F. Chen, H. Huang, L. Guo, Y. Zhang and T. Ma, Angew. Chem., Int. Ed., 2019, 58, 10061–10073.
55. S. Assavachin and F. E. Osterloh, J. Am. Chem. Soc., 2023, 145, 18825–18833.
56. S. Xu, Y. Zhang, Y. Wang, J. Chen, C. Zhou, Z. Mu, Z. Zhang, J. Zhang, J. Wang and Q. Zhang, J. Alloys Compd., 2023, 952, 169932.
57. Z. Chen, R. Xu, S. Ma, Y. Ma, Y. Hu, L. Zhang, Y. Guo, Z. Huang, B. Wang, Y. Y. Sun, J. Jiang, R. Hawks, R. Jia, Y. Xiang, G. C. Wang, E. A. Wertz, J. Tian, D. Gall, X. Chen, V. Wang, L. Gao, H. Zhu and J. Shi, Adv. Funct. Mater., 2022, 32, 2206343.
58. C. Hu, H. Huang, F. Chen, Y. Zhang, H. Yu and T. Ma, Adv. Funct. Mater., 2019, 30, 1908168.
59. M. Banoo, J. Kaur, A. K. Sah, R. S. Roy, M. Bhakar, B. Kommula, G. Sheet and U. K. Gautam, ACS Appl. Mater. Interfaces, 2023, 15, 32425–32435.
60. M. Banoo, R. S. Roy, M. Bhakar, J. Kaur, A. Jaiswal, G. Sheet and U. K. Gautam, Nano Lett., 2022, 22, 8867–8874.
61. H. Zheng, Y. Wang, J. Liu, J. wang, K. Yan and K. Zhu, Appl. Catal., B, 2024, 341, 123335.
62. C. C. Zhong, Y. Ishii, C. Tassel, T. Zhu, D. Kato, K. Kurushima, Y. Fujibayashi, T. Saito, T. Ogawa, A. Kuwabara, S. Mori and H. Kageyama, Inorg. Chem., 2022, 61, 9816–9822.
63. M. S. Senn and A. L. Goodwin, Nat. Mater., 2022, 21, 1100–1101.
64. X. Z. Lu, H. M. Zhang, Y. Zhou, T. Zhu, H. Xiang, S. Dong, H. Kageyama and J. M. Rondinelli, Sci. Adv., 2023, 9, eadi0138.
65. A. Pramanick, A. D. Prewitt, J. S. Forrester and J. L. Jones, Crit. Rev. Solid State Mater. Sci., 2012, 37, 243–275.
66. C. Zhong, D. Mizushima, K. Hirata, Y. Ishii, K. Kurushima, D. Kato, H. Nakajima, S. Mori, H. Suzuki, K. Ogawa, R. Abe, T. Fukuma and H. Kageyama, Appl. Phys. Express, 2020, 13, 091004.
67. A. M. Kusainova, P. Lightfoot, W. Zhou, S. Y. Stefanovich, A. V. Mosunov and V. A. Dolgikh, Chem. Mater., 2001, 13, 4731–4737.
68. A. Nakada, M. Higashi, T. Kimura, H. Suzuki, D. Kato, H. Okajima, T. Yamamoto, A. Saeki, H. Kageyama and R. Abe, Chem. Mater., 2019, 31, 3419–3429.
69. X. Xiao, C. Liu, R. Hu, X. Zuo, J. Nan, L. Li and L. Wang, J. Mater. Chem., 2012, 22, 22840.
70. A. Walsh, D. J. Payne, R. G. Egdell and G. W. Watson, Chem. Soc. Rev., 2011, 40, 4455–4463.
71. M. W. Stoltzfus, P. M. Woodward, R. Seshadri, J.-H. Klepeis and B. Bursten, Inorg. Chem., 2007, 46, 3839–3850.
72. P. S. Halasyamani, Chem. Mater., 2004, 16, 3586–3592.
73. G. Laurita and R. Seshadri, Acc. Chem. Res., 2022, 55, 1004–1014.
74. P. A. Cox, The electronic structure and chemistry of solids, Oxford University Press, Oxford, United Kingdom, 1986, p. 146.
75. D. Kato, R. Abe and H. Kageyama, J. Mater. Chem. A, 2019, 7, 19846–19851.
76. C. Zhong, D. Kato, K. Ogawa, C. Tassel, F. Izumi, H. Suzuki, S. Kawaguchi, T. Saito, A. Saeki, R. Abe and H. Kageyama, Inorg. Chem., 2021, 60, 15667–15674.
77. Y. H. Chu, npj Quantum Mater., 2017, 2, 67.
78. A. K. Geim and I. V. Grigorieva, Nature, 2013, 499, 419–425.
79. F. Xing, G. Ji, Z. Li, W. Zhong, F. Wang, Z. Liu, W. Xin and J. Tian, Mater. Horiz., 2023, 10, 722–744.
80. H. Ago, S. Okada, Y. Miyata, K. Matsuda, M. Koshino, K. Ueno and K. Nagashio, Sci. Technol. Adv. Mater., 2022, 23, 275–299.
81. V. Werner, U. Aschauer, G. J. Redhammer, J. Schoiber, G. A. Zickler and S. Pokrant, Inorg. Chem., 2023, 62, 6649–6660.
82. Y. Konishi, Z. Fang, M. Izumi, T. Manako, M. Kasai, H. Kuwahara, M. Kawasaki, K. Terakura and Y. Tokura, J. Phys. Soc. Jpn., 1999, 68, 3790–3793.
83. K. J. Choi, M. Biegalski, Y. L. Li, A. Sharan, J. Schubert, R. Uecker, P. Reiche, Y. B. Chen, X. Q. Pan, V. Gopalan, L. Q. Chen, D. G. Schlom and C. B. Eom, Science, 2004, 306, 1005–1009.
84. J. H. Lee, L. Fang, E. Vlahos, X. L. Ke, Y. W. Jung, L. F. Kourkoutis, J. W. Kim, P. J. Ryan, T. Heeg, M. Roeckerath, V. Goian, M. Bernhagen, R. Uecker, P. C. Hammel, K. M. Rabe, S. Kamba, J. Schubert, J. W. Freeland, D. A. Muller, C. J. Fennie, P. Schiffer, V. Gopalan, E. Johnston-Halperin and D. G. Schlom, Nature, 2010, 466, 954–958.
85. J. P. Locquet, J. Perret, J. Fompeyrine, E. Mächler, J. W. Seo and G. Van Tendeloo, Nature, 1998, 394, 453–456.
86. T. Yamamoto, A. Chikamatsu, S. Kitagawa, N. Izumo, S. Yamashita, H. Takatsu, M. Ochi, T. Maruyama, M. Namba, W. Sun, T. Nakashima, F. Takeiri, K. Fujii, M. Yashima, Y. Sugisawa, M. Sano, Y. Hirose, D. Sekiba, C. M. Brown, T. Honda, K. Ikeda, T. Otomo, K. Kuroki, K. Ishida, T. Mori, K. Kimoto, T. Hasegawa and H. Kageyama, Nat. Commun., 2020, 11, 5923.
87. E. Dagotto and T. M. Rice, Science, 1996, 271, 618–623.
88. M. Azuma, Z. Hiroi, M. Takano, K. Ishida and Y. Kitaoka, Phys. Rev. Lett., 1994, 73, 3463–3466.
89. Y. Tsujimoto, C. Tassel, N. Hayashi, T. Watanabe, H. Kageyama, K. Yoshimura, M. Takano, M. Ceretti, C. Ritter and W. Paulus, Nature, 2007, 450, 1062–1065.
90. C. Tassel, L. Seinberg, N. Hayashi, S. Ganesanpotti, Y. Ajiro, Y. Kobayashi and H. Kageyama, Inorg. Chem., 2013, 52, 6096–6102.
91. H. Kageyama, T. Watanabe, Y. Tsujimoto, A. Kitada, Y. Sumida, K. Kanamori, K. Yoshimura, N. Hayashi, S. Muranaka, M. Takano, M. Ceretti, W. Paulus, C. Ritter and G. Andre, Angew. Chem., Int. Ed., 2008, 47, 5824–5829.
92. A. Gabov, D. Kato, H. Ubukata, R. Aso, N. Kakudou, K. Fujita, H. Suzuki, O. Tomita, A. Saeki, R. Abe, S. Z. Karazhanov and H. Kageyama, Chem. Sci., 2024 10.1039/D4SC02092H.
93. F. C. Goerigk, V. Paterlini, K. V. Dorn, A.-V. Mudring and T. Schleid, Crystals, 2020, 10, 1089.
94. R. J. C. Locke, F. C. Goerigk, M. J. Schafer, H. A. Hoppe and T. Schleid, RSC Adv., 2021, 12, 640–647.
95. K. Ogawa, R. Abe and A. Walsh, J. Am. Chem. Soc., 2024, 146, 5806–5810.
96. J.-F. Vigier, C. Renard, N. Henry, A. Laplace and F. Abraham, Inorg. Chem., 2012, 51, 4352–4358.
97. D. Kato, O. Tomita, R. Nelson, M. A. Kirsanova, R. Dronskowski, H. Suzuki, C. C. Zhong, C. Tassel, K. Ishida, Y. Matsuzaki, C. M. Brown, K. Fujita, K. Fujii, M. Yashima, Y. Kobayashi, A. Saeki, I. Oikawa, H. Takamura, R. Abe, H. Kageyama, T. E. Gorelik and A. M. Abakumov, Adv. Funct. Mater., 2022, 32, 2204112.
98. M. Zhao, L. F. Dong, Q. Zhang, H. Z. Dong, C. D. Li and H. Y. Tang, Powder Diffr., 2016, 31, 2–7.
99. Z. Zhang, Y. Zhao, J. Shen, Z. Pan, Y. Guo, P. K. Wong and H. Yu, Appl. Catal., B, 2020, 269, 118774.
100. E. Jiang, N. Song, X. Zhang, L. Yang, C. Liu and H. Dong, Chem. Eng. J., 2020, 388, 123483.
101. C. Zhou, C. Lai, P. Xu, G. Zeng, D. Huang, C. Zhang, M. Cheng, L. Hu, J. Wan, Y. Liu, W. Xiong, Y. Deng and M. Wen, ACS Sustain. Chem. Eng., 2018, 6, 4174–4184.
102. Y. Wang, X. Huang, K. Wang, L. Zhang, B. Wang, Z. Fang, Y. Zhao, F. Gao, P. Liu and W. Feng, J. Mater. Chem. A, 2018, 6, 9200–9208.
103. J. Di, C. Zhu, M. Ji, M. Duan, R. Long, C. Yan, K. Gu, J. Xiong, Y. She, J. Xia, H. Li and Z. Liu, Angew. Chem., Int. Ed., 2018, 57, 14847–14851.
104. X. Xiao, J. Jiang and L. Zhang, Appl. Catal., B, 2013, 142–143, 487–493.
105. J. Li, G. M. Zhan, Y. Yu and L. Z. Zhang, Nat. Commun., 2016, 7, 1–9.
106. O. Clemens and P. R. Slater, Rev. Inorg. Chem., 2013, 33, 105–117.
107. H. Suzuki, D. Ozaki, Y. Ishii, O. Tomita, D. Kato, S. Nozawa, K. Nakashima, A. Saeki, H. Kageyama and R. Abe, J. Mater. Chem. A, 2023, 11, 15159–15167.
108. H. Suzuki, M. Higashi, O. Tomita, Y. Ishii, T. Yamamoto, D. Kato, T. Kotani, D. Ozaki, S. Nozawa, K. Nakashima, K. Fujita, A. Saeki, H. Kageyama and R. Abe, Chem. Mater., 2021, 33, 9580–9587.
109. K. Ogawa, H. Suzuki, C. Zhong, R. Sakamoto, O. Tomita, A. Saeki, H. Kageyama and R. Abe, J. Am. Chem. Soc., 2021, 143, 8446–8453.
110. W. L. Huang, J. Comput. Chem., 2009, 30, 1882–1891.
111. K. Ogawa, H. Suzuki, A. Walsh and R. Abe, Chem. Mater., 2023, 35, 5532–5540.
112. K. Miyata, D. Meggiolaro, M. T. Trinh, P. P. Joshi, E. Mosconi, S. C. Jones, F. D. Angelis and X.-Y. Zhu, Sci. Adv., 2017, 3, e1701217.
113. H. Zhu, M. T. Trinh, J. Wang, Y. Fu, P. P. Joshi, K. Miyata, S. Jin and X. Y. Zhu, Adv. Mater., 2017, 29, 1603072.
114. F. Bechstedt and J. Furthmüller, Appl. Phys. Lett., 2019, 114, 122101.
115. H. W. Eng, P. W. Barnes, B. M. Auer and P. M. Woodward, J. Solid State Chem., 2003, 175, 94–109.
116. D. Avila-Brande, A. R. Landa-Canovas and L. C. Otero-Diaz, Chem. Mater., 2007, 19, 323–328.
117. A. Pandey, G. Naresh and T. K. Mandal, Sol. Energy Mater. Sol. Cells, 2017, 161, 197–205.
118. A. M. Kusainova, S. Y. Stefanovich, J. T. S. Irvine and P. Lightfoot, J. Mater. Chem., 2002, 12, 3413–3418.
119. A. Nakada, A. Saeki, M. Higashi, H. Kageyama and R. Abe, J. Mater. Chem. A, 2018, 6, 10909–10917.
120. D. Ozaki, H. Suzuki, O. Tomita, Y. Inaguma, K. Nakashima, H. Kageyama and R. Abe, J. Photochem. Photobiol., A, 2021, 408, 113095.
121. D. Ozaki, H. Suzuki, A. Nakada, M. Higashi, O. Tomita, H. Kageyama and R. Abe, Chem. Lett., 2020, 49, 978–981.
122. D. O. Charkin, V. S. Akinfiev, A. M. Alekseeva, M. Batuk, A. M. Abakumov and S. M. Kazakov, Dalton Trans., 2015, 44, 20568–20576.
123. C. W. Chu, L. Z. Deng and B. Lv, Physica C, 2015, 514, 290–313.
124. A. J. Jacobson, Synthesis and Reaction Chemistry of Layered Oxides with Perovskite Related Structures, Springer, New York, NY, 1993, pp. 117–139.
125. H. Kunioku, A. Nakada, M. Higashi, O. Tomita, H. Kageyama and R. Abe, Sustainable Energy Fuels, 2018, 2, 1474–1480.
126. C. Zhong, D. Kato, F. Takeiri, K. Fujii, M. Yashima, E. Nishiwaki, Y. Fujii, A. Koreeda, C. Tassel, R. Abe and H. Kageyama, Inorganics, 2018, 6, 41.
127. A. J. Jacobson, J. W. Johnson and J. T. Lewandowski, Inorg. Chem., 1985, 24, 3727–3729.
128. X. Tao, Y. Gao, S. Wang, X. Wang, Y. Liu, Y. Zhao, F. Fan, M. Dupuis, R. Li and C. Li, Adv. Energy Mater., 2019, 9, 1803951.
129. T. Kotani, K. Ogawa, H. Suzuki, K. Kato, O. Tomita, A. Yamakata and R. Abe, EES Catal., 2023, 1, 255–262.
130. A. Nakada, H. Suzuki, J. J. M. Vequizo, K. Ogawa, M. Higashi, A. Saeki, A. Yamakata, H. Kageyama and R. Abe, ACS Appl. Mater. Interfaces, 2019, 11, 45606–45611.
131. J. Yu, S. Chang, L. Shi and X. Xu, ACS Catal., 2023, 13, 3854–3863.
132. J. Li, G. Zhan, Y. Yu and L. Zhang, Nat. Commun., 2016, 7, 11480.
133. H. Kunioku, M. Higashi, C. Tassel, D. Kato, O. Tomita, H. Kageyama and R. Abe, Chem. Lett., 2017, 46, 583–586.
134. D. Kato, C. Herve, T. Yamamoto, H. Kunioku, M. Higashi, R. Abe and H. Kageyama, Chem. Lett., 2017, 46, 1083–1085.
135. D. O. Charkin, D. N. Moskvin, P. S. Berdonosov, V. A. Dolgikh and P. Lightfoot, J. Alloys Compd., 2006, 413, 40–45.
136. Y. Mizuguchi, J. Phys. Soc. Jpn., 2019, 88, 041001.
137. Y. Yang, X. Fan, J. Liu, C. Cao, Z. Liu, J. Deng, T. Lin, Q. Zhang, K. Liao, X. Dong, G. Wang and X. Chen, Adv. Sci., 2023, 10, e2303569.
138. X. Zhang, Y. Liu, G. Zhang, Y. Wang, H. Zhang and F. Huang, ACS Appl. Mater. Interfaces, 2015, 7, 4442–4448.
139. A. L. Pacquette, H. Hagiwara, T. Ishihara and A. A. Gewirth, J. Photochem. Photobiol., A, 2014, 277, 27–36.
140. S. Tippireddy, P. K. D S, S. Das and R. C. Mallik, ACS Appl. Energy Mater., 2021, 4, 2022–2040.
141. A. Parida, S. Senapati and R. Naik, Mater. Today Chem., 2022, 26, 101149.
142. Y. Zheng, F. Duan, M. Chen and Y. Xie, J. Mol. Catal. A: Chem., 2010, 317, 34–40.
143. S. D. Nguyen, J. Yeon, S.-H. Kim and P. S. Halasyamani, J. Am. Chem. Soc., 2011, 133, 12422–12425.
144. A. J. Corkett, Z. Chen, D. Bogdanovski, A. Slabon and R. Dronskowski, Inorg. Chem., 2019, 58, 6467–6473.
145. S. Volkov, R. Bubnova, M. Krzhizhanovskaya and L. Galafutnik, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2020, 76, 992–1000.
146. H. D. B. Jenkins and K. P. Thakur, J. Chem. Educ., 1979, 56, 576–577.
147. K. Takanabe, Acs Catal., 2017, 7, 8006–8022.
148. H. Suzuki, T. Takashima, O. Tomita, T. Kanazawa, S. Nozawa, K. Kato, A. Yamakata, K. Nakashima, A. Saeki and R. Abe, J. Phys. Chem. C, 2023, 127, 7965–7973.
149. V. Andrei, R. A. Jagt, M. Rahaman, L. Lari, V. K. Lazarov, J. L. MacManus-Driscoll, R. L. Z. Hoye and E. Reisner, Nat. Mater., 2022, 21, 864–868.
150. K. Ogawa, Y. Wakisaka, H. Suzuki, O. Tomita and R. Abe, ACS Appl. Mater. Interfaces, 2021, 13, 5176–5183.
151. Y. Ishii, H. Suzuki, K. Ogawa, O. Tomita, A. Saeki and R. Abe, Sustainable Energy Fuels, 2022, 6, 3263–3270.
152. Z. Luo, X. Ye, S. Zhang, S. Xue, C. Yang, Y. Hou, W. Xing, R. Yu, J. Sun, Z. Yu and X. Wang, Nat. Commun., 2022, 13, 2230.
153. A. Adenle, M. Shi, W. Jiang, B. Zeng, C. Li and R. Li, J. Mater. Chem. A, 2022, 10, 14293–14299.
154. K. Ogawa, R. Sakamoto, C. C. Zhong, H. Suzuki, K. Kato, O. Tomita, K. Nakashima, A. Yamakata, T. Tachikawa, A. Saeki, H. Kageyama and R. Abe, Chem. Sci., 2022, 13, 3118–3128.
155. M. Kluczny, J. T. Song, T. Akbay, E. Niwa, A. Takagaki and T. Ishihara, J. Mater. Chem. A, 2022, 10, 2550–2558.
156. H. Yaguchi, D. Morikawa, T. Saito, K. Tsuda and M. Yashima, Adv. Funct. Mater., 2023, 33, 2214082.
157. Q. D. Gibson, M. S. Dyer, C. Robertson, C. Delacotte, T. D. Manning, M. J. Pitcher, L. M. Daniels, M. Zanella, J. Alaria, J. B. Claridge and M. J. Rosseinsky, Inorg. Chem., 2018, 57, 12489–12500.
158. Q. D. Gibson, T. D. Manning, M. Zanella, T. Zhao, P. A. E. Murgatroyd, C. M. Robertson, L. A. H. Jones, F. McBride, R. Raval, F. Cora, B. Slater, J. B. Claridge, V. R. Dhanak, M. S. Dyer, J. Alaria and M. J. Rosseinsky, J. Am. Chem. Soc., 2020, 142, 847–856.
159. Q. D. Gibson, J. A. Newnham, M. S. Dyer, C. M. Robertson, M. Zanella, T. W. Surta, L. M. Daniels, J. Alaria, J. B. Claridge and M. J. Rosseinsky, J. Solid State Chem., 2022, 312, 123246.

---