Open Access Article
Open Access ArticleThe interplay of covalency, cooperativity, and coupling strength in governing C–H bond activation in Ni2E2 (E = O, S, Se, Te) complexes†‡
Sunita
Sharma
,
Bhawana
Pandey
and
Gopalan
Rajaraman
 *
*
Department of Chemistry, Indian Institute of Technology Bombay, Mumbai, 400076, India. E-mail: rajaraman@chem.iitb.ac.in
First published on 3rd June 2024
Abstract
Dinickel dichalcogenide complexes hold vital multifaceted significance across catalysis, electron transfer, magnetism, materials science, and energy conversion. Understanding their structure, bonding, and reactivity is crucial for all aforementioned applications. These complexes are classified as dichalcogenide, subchalcogenide, or chalcogenide based on metal oxidation and coordinated chalcogen, and due to the associated complex electronic structure, ambiguity often lingers about their classification. In this work, using DFT, CASSCF/NEVPT2, and DLPNO-CCSD(T) methods, we have studied in detail [(NiL)2(E2)] (L = 1,4,7,10-tetramethyl-1,4,7,10-tetraazacyclododecane; E = O, S, Se and Te) complexes and explored their reactivity towards C–H bond activation for the first time. Through a comprehensive analysis of the structure, bonding, and reactivity of a series of [(NiL)2(E2)] complexes with E = O, S, Se, and Te, our computational findings suggest that {Ni2O2} and {Ni2S2} are best categorised as dichalcogenide-type complexes. In contrast, {Ni2Se2} and {Ni2Te2} display tendencies consistent with the subchalcogenide classification, and this aligns with the earlier structural correlation proposed (Berry and co-workers, J. Am. Chem. Soc. 2015, 137, 4993) reports on the importance of the E–E bond strength. Our study suggests the reactivity order of {Ni2O2} > {Ni2S2} > {Ni2Se2} > {Ni2Te2} for C–H bond activation, and the origin of the difference in reactivity was attributed to the difference in the Ni–E bond covalency, and electronic cooperativity between two Ni centres that switch among the classification during the reaction. Further non-adiabatic analysis at the C–H bond activation step demonstrates a decrease in coupling strength as we progress down the group, indicating a correlation with metal–ligand covalency. Notably, the reactivity trend is found to be correlated to the strength of the antiferromagnetic exchange coupling constant J via developing a magneto-structural-barrier map – offering a hitherto unknown route to fine-tune the reactivity of this important class of compound.
Introduction
Transition metal ions are integral to oxidation and electron transfer processes in nature, as well as in the realms of industrial and academic chemistry.1–4 The high valent metal-oxo or hydroxo functional groups participate in a series of electron transfer processes in biological and chemical events. Because of their wide significance in biological and chemical sciences, an immediate issue is determining the reactivity differences among these related active transition metal ion species and understanding their roles in various oxidation processes. Iron,5–7 manganese,8,9 and copper10,11 ion-containing metalloenzymes are very popular, but other metal ions also play an important role in biological chemistry. The study of these complexes helps us better understand the detailed mechanism of the reaction catalysed by metalloenzymes and gives an idea for developing a biomimetic catalyst.12Apart from the aforementioned metal ions, the studies on nickel complexes are also essential in metalloenzyme chemistry13 due to their involvement in various biological reactions and homogenous catalysis.14,15 Nickel enzymes play important roles in the global biological carbon, nitrogen, and oxygen cycle. Some examples, including hydrogenases,16,17 Ni-SOD,18–20 urease,21,22 glyoxalase,23 CO dehydrogenase,24etc., are a few examples of metalloenzymes containing nickel ions in the active sites. In comparison to NiII chemistry, dealing with the NiIII oxidation state poses a greater challenge in nickel chemistry, primarily due to the complexity involved in synthesizing and characterizing NiIII complexes.24,25 Many homo- and hetero-metallic oxo-bridged Ni complexes have been reported, but only a few high-valent metal oxo species have been characterised well so far.26 Moro-oka and co-workers have studied the synthesis and characterisation of the thermally unstable dinuclear bis(μ-oxo)NiIII-complex [TpMe3Ni(μ-O)2NiTpMe3].27 Although five coordinated NiIII complexes were reported, later they synthesised a new doubly oxo bridged six coordinated bis(μ-oxo)nickel(III) complex, [Ni2(μ-O)2(Me3-tpa)2]2+.28 Mitra and co-workers29 have reported a thermally stable mono-oxo bridged dinuclear NiIII complex, [Ni(salen)2O], and crystallographic studies on that complex show distorted square pyramidal geometry around the metal ion. These high-valent bis-μ-oxo dimers having an {M2(μ-O)2} core, i.e., a diamond core structure, have tremendous applications in oxidation catalysts.28,30,31 Monomeric nickel-oxo is very rare because of the tendency of the oxo and hydroxo ligands to form a bridge.32 Metal complexes with terminal oxo7,33 or hydroxo ligands have been implicated in various oxidative transformations, such as C–H bond functionalisation and oxo–transfer reactions.34–36 Several bio-inspired catalysts have been probed as a catalyst for hydroxylation, sulfoxidation, and epoxidation.37–40 It is assumed that this species has high relevance to the (μ-η2:-η2peroxo)Cu2 complex.30
Metals containing not only oxygen but other chalcogen ligands, such as S, Se, and Te have fascinated researchers because of their unique structural properties, bonding, catalytic reactivity, and synthetic applications.41,42 These complexes have biological significance as well.43,44 In the case of sulfur-containing complexes, metalloproteins usually consist of metal sulfur bonds. Several metalloproteins contain nickel in the active site, ligated with sulfur such as acetyl-CoA synthase/carbon monoxide dehydrogenase (ACS/CODH),45,46 [NiFe] hydrogenase,47 nickel superoxide dismutase,48 and methyl-CoM reductase.49 In 2010, Brunold and co-workers studied [{(PhTttBu)NiII}2(μ-η2:η2-S2)] (PhTttBu = phenyltris[(tert-butylthio)methyl]borate) complex of nickel-containing thioether chelating ligand with a tridentate monoanionic PhTttBu ligand.50,51
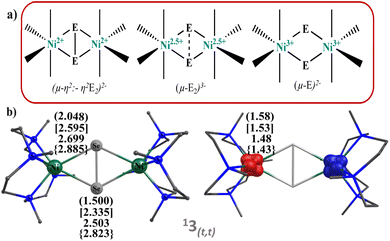
Notably, nickel oxygen and nickel sulfur complexes have been synthesised and structurally characterised. But corresponding chemistry of the heavier dichalcogenides viz. Se2, Te2 is substantially unexplored. In 2001, Sitzmann and co-workers, reported the formation of the dimers [{(C5HR4)NiE}2] (E = S, Se, Te) by the reaction of dimeric cyclopentadienylnickel bromide derivative [{(C5HR4)Ni(i-Br)}2] with sodium dichalcogenides Na2E2.52 The structure predicts unusual E⋯E distance giving rise to ambiguities in the description of their electronic structure and chemical reactivity. Three bonding modes are proposed for the Ni2E2 core (E = O, S, Se, and Te; see Fig. 1), and the bonding modes are directly correlated to their oxidation states and hence their reactivity.53–56 In 2012, Berry and co-workers studied a [(Cp′Ni)2(μ2-Se2)] (Cp′ = 1,2,3,4 tetraisopropylcyclopentadiene) complex by means of X-ray absorption spectroscopy, X-ray, and theoretical methods and predicted bonding mode in Ni2E2 as “subselenide” Se23− ligand.54 Although rare, Ni–Se bonding also has biological implications wherein [NiFeSe] hydrogenases were found to be more reactive compared to [NiFe] hydrogenases containing cysteine sulphur group and terminal side-on {Se–S} bonding with Ni atom likely to cause greater reactivity.57 The reactivity of NiSe dichalcogenide complexes has been of interest since then, and in this regard, a report by Riordan and co-workers on a rare C–H bond activation by a dinickel dichalcogenide complex [(NiL)2(Se2)] (PF6)2 (here, L = 1,4,7,10-tetramethyl-1,4,7,10-tetraazacyclododecane) having planar Ni2(μ-η2:-η2Se2) core structure gains attention. Particularly, this compound was found to oxidise the C–H bonds of DHA and CHD, yielding aromatic product and hydroselenide, demonstrating a scarce C–H bond activation by {Ni2Se2} compound.58
Although there are several reports on the structure and bonding of Ni2E2 species, comparative analysis across the periodic table from O, S, Se, to Te is lacking and is important given the recent trend of greater reactivity shown by the later dichalcogenide complexes. Further, the reactivity of these species with respect to their bonding has not been studied as all the reports were restricted to the ground state energy of the structure where the E⋯E distances are constant. If we consider the C–H bond activation of these species, the E⋯E distance is expected to vary. Hence, various forms of the structure described in Fig. 1 are expected to play a role in enhancing/diminishing the reactivity. More importantly, even if a Ni2E2 complex has a well-characterised dichalcogenide E23− diamond core structure, it may not be preserved during the course of the reaction, and it may be interconverted to other forms prior to the reaction. To assess and understand these intriguing aspects, in this work, we have explored dinickel dichalcogenides (Ni2E2) complexes {[Ni(L)]2(E2)}2+ (E = O(1), S(2), Se(3) and Te(4)) with all four chalcogen atoms to understand the electronic structure, bonding and its implication in activating the C–H bonds of dihydroanthracene using DFT and ab initio calculations (CASSCF, DLPNO-CCSD(T)) methods. Using this theoretical method, we aim to answer the following intriguing questions (i) Is the nature of E (E = O, S, Se, Te) crucial in dictating the formation of specific isomers among di-, sub-, and chalcogenides in {Ni2E2} complexes? (ii) how do the covalency and the corresponding electronic structure evolve as we move down the group from O to Te? and (iii) are these compounds capable of performing C–H bond activation? If so, what dictates their reactivity?
Computational details
All the geometry optimizations calculations were carried out using the Gaussian 09 suite of programs.59 The optimisations have been performed with B3LYP functional.60–62 The B3LYP has a proven track record of predicting the structures and the energetics accurately for such metal-mediated catalytic reactions. LACVP basis set comprising LanL2DZ – Los Alamos effective core potential for Ni63–65 and a 6-31G* basis set for the C, H, N, O, and S66,67 atoms has been employed for geometry optimisation, and the optimised geometries were then used to perform single-point energy calculations using a B3LYP-D3/SDD68 (S, Se, Te); TZVP (all) level. The solvation energies have been computed using the PCM solvation model,68,69 employing dichloromethane as the solvent. Frequency calculations were performed on the optimised structures to verify that they are minima on the potential-energy surface (PES) and also to obtain free energy corrections. The quoted DFT energies are B3LYP-D3 solvation free energies incorporating zero-point, enthalpy, and entropic corrections at 298.15 K unless otherwise mentioned. The fragment approach available in Gaussian 09 is employed to aid smooth convergence in the case of radical intermediates. As the ligands chosen for this study favours {NiII2(μ-η2:η2-E2)} geometry, to obtain the other extreme structure i.e. {NiIII2(μ-E2)} the Ni–Ni and E–E bonds are fixed to the reported X-ray structures.27,31,51,53,58,70–73 The natural bonding orbital (NBO)74 and the spin-natural orbital (SNO)75,76 analysis have been performed using the Gaussian 09 suite of programs. In the molecular orbital diagram n represents the orbital's number.The strain energy (ΔEstrain) has been calculated to obtain the destabilising steric energy associated with the transition states. The transition states are divided into two fragments, A (catalyst part) and B (substrate part) and solvent phase single-point calculations were performed on this geometries. We have estimated the energy using the following equation
| ΔEstrain = TS(A + B)(Esolvation+Gibbs) − A(Esolvation+Gibbs) − B(Esolvation+Gibbs) |
The ORCA 4.2 package77 was used to calculate the absorption spectra and to perform SA-CASSCF calculations, DLPNO-CCSD(T) calculations and for calculating non adiabatic coupling of the transition state. Time-dependent density functional theory (TDDFT) implemented in the ORCA program was used for the calculation of excitation energies. To obtain these electronic transitions for all the four complexes 11–4(t,t), the time-dependent (TD) DFT method has been used. For complexes 1–3, TDDFT calculations have been performed by using B3LYP functional along with the def2-TZVP basis78 set for all atoms and def2TZVPP basis set for complex 4 considering the presence of heavier Te atoms.79 The RIJCOSX approximation with def2/J auxiliary basis set has been employed. Further, the domain-based local pair natural orbital approximation to coupled-cluster theory with single, double, and perturbative triple excitations, DLPNO-CCSD(T)/cc-PVTZ method has been employed to gain confidence on the spin-state energetics.80–83 The zero-field splitting (ZFS) parameters were estimated by utilising state-average complete active space self-consistent field (SA-CASSCF) theory84,85 along with the incorporation of N-Electron Valence State Perturbation Theory (NEVPT2).86,87 The CASSCF/NEVPT2 calculations use a combination of basis set DKH-def2-TZVP88 for Ni, O, S, and Se,89 Sapporo-TZP-2012 for Te.90 The CASSCF calculations have been performed with active space CAS(16,10) and CAS(20,12), including 10 orbitals of two nickels for the former and two orbitals of chalcogenides in the later one active space and performed calculations only considering five singlets, triplets, and quintets states (CASCI calculation conducted to assess low-lying multiplets and have chosen all the states which like within the energy window of ∼4000 cm−1. This has been consistently kept for all complexes. Other excited states were found to lie much higher in energy, and hence, we have chosen to include five singlets, 5 triplets and 5 quintets). We employed a time-dependent response approach to calculate the non-adiabatic coupling (NAC) parameters of the transition state. For this analysis, we have used the def2-TZVP basis set for O, S, and Se atoms along with Ni metal center, and the Sapporo-TZP-2012 basis set for the Te atom.
The J values were computed from the energy differences between the high spin (EHS) state and the low spin (EBS) state determined using the broken symmetry (BS) approach developed by Noodleman.91,92 Negative and positive values for J correspond to antiferromagnetic and ferromagnetic interactions, respectively. The following notation MX(sNi1,sNi2) where superscript ‘M’ denotes the total multiplicities of the spin-coupled dimer and subscript ‘(sNi1, sNi2)’ denotes the spin multiplicity on Ni(1) and Ni(2) atoms are employed throughout the report. MO diagram were generated using the G09 suite.
Results and discussion
Electronic structure and bonding of complex 1–4
We have performed DFT calculations on all the four dinickel dichalcogenide (Ni2E2) complexes (where E = O, S, Se, Te) supported by 1,4,7,10-tetramethyl-1,4,7,10-tetraazacyclododecane ligand, considering all possible spin states arising due to d8 electronic configuration for both the nickel–metal centre, i.e. Ni centres can possess S = 0 and S = 1 state and could be coupled ferro/antiferromagnetically in the latter. In all four complexes, the ST = 0 state that arises from the antiferromagnetic coupling between two NiII centres S = 1 state is found to be the ground state (11–4(t,t)). This is followed by the corresponding ferromagnetically coupled state (51–4(t,t)) at 12.3 kJ mol−1, 16.1 kJ mol−1, 12.4 kJ mol−1, and 71.5 kJ mol−1, for 1–4, respectively. The singlet state, on the other hand, is found to be at 336.5 kJ mol−1, 156.4 kJ mol−1, 159.8 kJ mol−1, and 152.3 kJ mol−1 for complexes 1–4. The states with S = 0 spin on either one of the NiII centres (31–4(t,s)) or both the NiII centres (11–4(s,s)) were found to lie much higher in energy. The singlet-quintet gap (ΔE(11(t,t)–51(t,t))) is found to be the smallest for 1, followed by 3, 2, and 4, which has a very large gap (≈72.0 kJ mol−1) (see Fig. S1–S17‡). A close analysis reveals that while the geometry is maintained as [NiII2(μ-η2:η2-E2)(L)2]2+ both at the singlet and quintet state for all complexes with the exception of quintet state at 4. The singlet state is the ground state for complex 4, whereas the quintet excited state adopts a trans-endon E2 geometry, leading to a substantially larger energy gap compared to other states. Our AIM analysis further confirms that the quintet state of complex 4 features only one Ni–Te bond (see ESI, Fig. S15‡ for details). Further, to obtain confidence in this spin-state ordering, we have also performed DLPNO-CCSD(T)81–83 calculations on the DFT optimised geometries, and this method also predicts the ST = 0 as the ground state (see Tables S1 and S2‡), though the ground state-excited state gap is lower compared to DFT methods.The optimised structures of all possible states and the spin density plots are given in Fig. 1 (see ESI Fig. S1–S17‡ for optimised geometries and spin density plots). The ground-state structure of all four complexes has a centre of symmetry maintained with all four Ni–E bond lengths being nearly equal (E = O 2.048 Å, S = 2.595 Å, Se = 2.699 Å, and Te = 2.885 Å). The E–E bond distances in 11(t,t) and 12(t,t) are found to be shorter than that observed in earlier reported {Ni2IIIE2}/{Ni2II(μ-η2:η2-E2)} complexes (E = O 1.500 Å; S = 2.335 Å) but in case of complex 13(t,t) and 14(t,t), it is larger than the reported complexes (E = Se = 2.503 Å and Te = 2.823 Å). At the same time, the Ni–Ni bond distance is found to be longer than the previously reported complexes.43 However, the Ni–E–Ni and E–Ni–E bond angles for 12–4(t,t) match well with the previous literature reports (see Table S3‡). The energies computed for two isomeric bis(μ-oxo) {Ni2IIIE2} and side-on μ-η2:η2-peroxo[NiII2(μ-η2:η2-E2)(L)2]2+ forms reveals that the side-on isomer is more stable for all four species 1–4 with the energy margin of 60–144 kJ mol−1 (see Table S2, Fig. 2, and S18‡). The WB index (Wiberg Bond Index) computed reveals an increase in the Ni–E bond index and a decrease in the E–E bond index as we move from 1 to 4 (see Tables 1 and S4‡). As these two parameters are correlated to the nature of the two isomeric forms, it is clear that as we move from 1 to 4, the geometries tend to have a stronger side-on μ-η2:η2-peroxo character. So based on the data of previously reported dichalcogenide complexes, it can be seen that chalcogenide complexes 11–4(t,t), 11(t,t), and 12(t,t) fall into the dichalcogenide category. While complex 13(t,t) falls between the selenide and subselenide categories, which confers E2 exists as E22− (μ-η2:-η2peroxo) dinickel(II) complex.
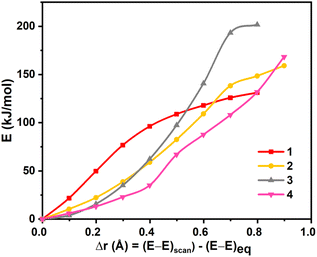 | ||
| Fig. 2 Rigid scan performed by varying the E⋯E distance in complexes 1–4. The x-axis represents variation in the E⋯E distance with respect to the equilibrium geometry. | ||
| Complexes | J (in cm−1) | WBI | λ max (nm) | |V(r)/G(r)| | ν(E–E) (cm−1) | ΔG(C–H) (kJ mol−1) | ||
|---|---|---|---|---|---|---|---|---|
| Ni1–E1 | Ni2–E1 | E1–E2 | ||||||
| 1 1 (t,t) | S = 0 (AF, −303) | 0.261 | 0.261 | 1.032 | 288, 315, 377, 560 (386, 450) | 0.91 | 829.7 | 58.5 |
| 1 2 (t,t) | S = 0 (AF, −344) | 0.363 | 0.363 | 1.013 | 286, 327, 411, 580 (320, 394, 464) | 1.05 | 421.2 | 68.2 |
| 1 3 (t,t) | S = 0 (AF, −354) | 0.376 | 0.376 | 0.922 | 281, 380, 449, 580 (390, 410, 690) | 1.10 | 268.4 | 89.3 |
| 1 4 (t,t) | S = 0 (AF, −422) | 0.478 | 0.478 | 0.932 | 299, 333, 413, 506 (314, 420, 487) | 1.20 | 173.1 | 95.4 |
The computed spin state for the ground state reveals strong delocalisation of spin density to the coordinated atoms, and at the antiferromagnetic state, the bridging atoms E has a net spin density of zero, and this is due to equal spin delocalisation of positive and negative spin densities (∼0.07) from Ni(1) and Ni(2) centers. The spin density on the metal center decreases as we move from 1 to 4, suggesting strong delocalisation of spin density to the coordinated atoms. This indicates a stronger covalency for the Ni–E bond as we move down the group. To further validate this point, atoms-in-molecule (AIM) calculations were performed. These calculations reveal |V(r)/G(r)| ratio of 0.91, 1.05, 1.10 and 1.20 for 1–4, respectively (see Table 1 and Fig. S19–S22‡). This reveals that the Ni–O bond is strongly ionic while Ni–S, Ni–Se, and Ni–Te fall in the borderline cases with increasing per cent of covalency as we move down the group. The NBO analysis also affirms this point (see Fig. S23–S27‡). Further, NBO second-order perturbation theory donor–acceptor interactions also reveal an increase in donation from E to Ni orbitals as we move down from O to Te with the stabilisation energy of 13.8, 19.4, 22.4, and 23.0 kJ mol−1, respectively. The reason for greater stabilisation is routed back to the enhanced p-character of the sp hybrid orbital of the Ni involved in the interaction as we go down in the series. This is also accompanied by a concomitant reduction of p-character (or increase in s-character for alpha spin-up orbitals see Fig. S27 and Table S5‡) of the donor orbital of E as we move down the group.
The Eigen-value plot corresponding to the d-orbitals of 1–4 is shown in Fig. S28–S31.‡ As expected, the NiII centre has (dxy)2(dyz)2(dxz)2(dz2)1(dx2−y2)1 electronic configuration. However, the order of the d-orbitals is drastically different if we compare 1 with 2–4. Particularly a very strong πNi(dyz)–O(py) overlap can be seen in the case of complex 1, and a strong σNi(dxy)–E(px) can be seen in complexes 2–4, and these two different interactions are leading to the stabilisation of dyz and dxy as the lowest-lying orbitals for 1 and 2–4 complexes, respectively. The SA-CASSCF(16,10) and SA-CASSCF(20,12) calculations were performed to ascertain the nature of the ground state electronic configuration. The first set includes the NiII orbitals of both metal centres, and the second set includes two orbitals of the E2 moiety, and both calculations reveal the ground state with multiplicity 1 configuration shows very little mixing of the excited states (see Table S6 and Fig. S32–S39‡). The calculations suggest that all four complexes, from O to Te, exhibit a ground state predominantly characterized by one configuration (dxz2dyz2dxy2dyz2dxz2dxy2dx2−y21dz21dz21dx2−y21), with a contribution of 88.9%–94.3%, and minor mixing with the first excited state, contributing 3.3–7.1%, alongside very little contributions from other higher excited states. The magnetic coupling is estimated using the ground state structure, employing the standard protocol, and this yields the J value is −303.0 cm−1, −343.7 cm−1, −354.2 cm−1, and −422.0 cm−1 for complexes 1–4, respectively. These values suggest a strong antiferromagnetic coupling between two nickel(II) centres (see Table 1), with the magnitude of coupling increasing as we move down the group. The antiferromagnetic coupling results from the strong overlap between the dx2−y2 orbitals on the NiII centres (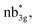 where n = 4 for complex 1, n = 2 for complex 2 and 3, and n = 3 for complex 4), and this overlap tend to get stronger as we go down from O to Te. This strong antiferromagnetic nature is important during the electron transfer process from the substrate to the oxygen centric Ni–E π* orbital. This is reflected in the nature of computed SOMO (see Tables 1 and S7‡). As we move down the group, the enhancement in antiferromagnetic coupling was noticed earlier in several other examples reported.93 Although direct experimental evidence for the antiferromagnetic coupling is absent, room temperature effective magnetic moment measured for 3 is found to be 2.71 μB. This value is significantly smaller than the expected value for the ST = 2 ferromagnetically coupled state and suggests that the ground state is ST = 0 with some per cent of the S = 2 population at room temperature, placing the exchange coupling in the range of ∼200–300 cm−1.58
where n = 4 for complex 1, n = 2 for complex 2 and 3, and n = 3 for complex 4), and this overlap tend to get stronger as we go down from O to Te. This strong antiferromagnetic nature is important during the electron transfer process from the substrate to the oxygen centric Ni–E π* orbital. This is reflected in the nature of computed SOMO (see Tables 1 and S7‡). As we move down the group, the enhancement in antiferromagnetic coupling was noticed earlier in several other examples reported.93 Although direct experimental evidence for the antiferromagnetic coupling is absent, room temperature effective magnetic moment measured for 3 is found to be 2.71 μB. This value is significantly smaller than the expected value for the ST = 2 ferromagnetically coupled state and suggests that the ground state is ST = 0 with some per cent of the S = 2 population at room temperature, placing the exchange coupling in the range of ∼200–300 cm−1.58
To further understand the nature of bonding, qualitative MO diagrams based on the computed ground state are constructed for complexes 1–4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 53 (see Fig. 3 for complex 3 and Fig. S40–S43‡ for complexes 1, 2, and 4, respectively). These were constructed assuming a pseudo D2h symmetry for the {Ni2E2N8} core and quantification of the deviation reveal that except in case of complex 1 where the deviations are relatively larger, it lies in the range of 0.11 to 0.22 (Fig. S40‡). For all four complexes, nb1g (where n = 1 for complex 1, and n = 2 for complex 2–4), which is a combination of π*(E1(py) − E2(py)) and δ(Ni1(dyz) − Ni2(dyz)) orbitals, is found to be the highest occupied molecular orbital (HOMO). For dichalcogenide complexes, the b1g is expected to have a significant δ(Ni1(dyz) − Ni2(dyz)) contribution and very little/no π*(E1(py) − E2(py)) contribution. For subchalcogenide complexes, the contribution is expected to be significant in π*(E1(py) − E2(py)) orbital with a sizeable δ(Ni1(dyz) − Ni2(dyz)) orbital contribution. For chalcogenide, on the other hand, as one more electron from the Ni centre is lost, both π*(E1(py) − E2(py)) and σ*(E1(pz) − E2(pz)) will be occupied with very little/no contributions from Ni centres. From the qualitative MO diagram, it is clear that complex 1 falls in the dichalcogenide category while complexes 2–4 have a strong subchalcogenide character, which is found to be increasing as we move down the group. Further, the lowest unoccupied orbitals (LUMO) in complexes 2–4 were found to have a strong Ni(dx2−y2) character along with the E2 character suggesting loss of one electron as expected for subchalcogenide. As this orbital is important for its reactivity towards C–H bond activation, a strong metallic character detected for 2–4 is likely to help reduce the kinetic barrier (vide infra).
53 (see Fig. 3 for complex 3 and Fig. S40–S43‡ for complexes 1, 2, and 4, respectively). These were constructed assuming a pseudo D2h symmetry for the {Ni2E2N8} core and quantification of the deviation reveal that except in case of complex 1 where the deviations are relatively larger, it lies in the range of 0.11 to 0.22 (Fig. S40‡). For all four complexes, nb1g (where n = 1 for complex 1, and n = 2 for complex 2–4), which is a combination of π*(E1(py) − E2(py)) and δ(Ni1(dyz) − Ni2(dyz)) orbitals, is found to be the highest occupied molecular orbital (HOMO). For dichalcogenide complexes, the b1g is expected to have a significant δ(Ni1(dyz) − Ni2(dyz)) contribution and very little/no π*(E1(py) − E2(py)) contribution. For subchalcogenide complexes, the contribution is expected to be significant in π*(E1(py) − E2(py)) orbital with a sizeable δ(Ni1(dyz) − Ni2(dyz)) orbital contribution. For chalcogenide, on the other hand, as one more electron from the Ni centre is lost, both π*(E1(py) − E2(py)) and σ*(E1(pz) − E2(pz)) will be occupied with very little/no contributions from Ni centres. From the qualitative MO diagram, it is clear that complex 1 falls in the dichalcogenide category while complexes 2–4 have a strong subchalcogenide character, which is found to be increasing as we move down the group. Further, the lowest unoccupied orbitals (LUMO) in complexes 2–4 were found to have a strong Ni(dx2−y2) character along with the E2 character suggesting loss of one electron as expected for subchalcogenide. As this orbital is important for its reactivity towards C–H bond activation, a strong metallic character detected for 2–4 is likely to help reduce the kinetic barrier (vide infra).
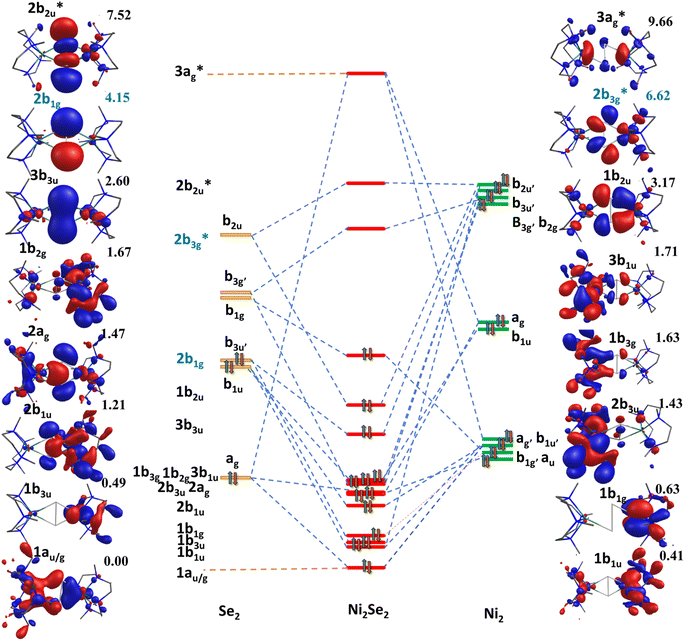 | ||
| Fig. 3 Qualitative molecular orbital diagram for complex 3 (energy in eV). Here HOMO–LUMO energy written in blue color code. | ||
As the qualitative MO diagram developed53 can be correlated directly to the experimental absorption features, we used time-dependent density functional theory (TD-DFT) to compute absorption features of 1–4 (see Table 1 and Fig. S44‡) for the ground state geometries. The major absorption features observed in experiments for complex 3 are reproduced in our calculations, particularly a peak at 281 nm observed corresponds to metal-to-ligand charge transfer (1b3g to 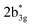 in Fig. 3), while the peaks at 380 nm (1b2u to
in Fig. 3), while the peaks at 380 nm (1b2u to 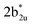 in Fig. 3) and 449 nm (1b2u to
in Fig. 3) and 449 nm (1b2u to 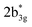 in Fig. 3) are considered as bonding orbitals of Ni2Se2 to pure antibonding orbitals of Se22−. The peak at 580 nm (ag to 3b1u in Fig. 3) shows ligand-to-metal charge transfer. The 1b2u to
in Fig. 3) are considered as bonding orbitals of Ni2Se2 to pure antibonding orbitals of Se22−. The peak at 580 nm (ag to 3b1u in Fig. 3) shows ligand-to-metal charge transfer. The 1b2u to 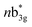 (where n = 4 for complex 1, n = 2 for complex 2 and 3, and n = 3 for complex 4) transition is observed in all four complexes, with the energy gap decreasing, we move from oxygen to Te (315 nm, 411 nm, 449 nm, and 506 nm for 1–4, respectively). This is consistent with the decrease in the E–E bond order observed as we move from 1–4. Further, the computed spectra for complexes 2 and 4 also qualitatively agree with earlier reported complexes having different terminal ligands.53 The calculations performed reproduce the experimental observables offering confidence in the methodology employed.
(where n = 4 for complex 1, n = 2 for complex 2 and 3, and n = 3 for complex 4) transition is observed in all four complexes, with the energy gap decreasing, we move from oxygen to Te (315 nm, 411 nm, 449 nm, and 506 nm for 1–4, respectively). This is consistent with the decrease in the E–E bond order observed as we move from 1–4. Further, the computed spectra for complexes 2 and 4 also qualitatively agree with earlier reported complexes having different terminal ligands.53 The calculations performed reproduce the experimental observables offering confidence in the methodology employed.
Reactivity of complexes 1–4 towards C–H activation
Riordan and co-workers reported that diselenide dinickel complex exhibited reactivity towards 9,10-dihydroanthracene (DHA) and cyclohexadiene (CHD) molecules.58 The mechanism adapted for the C–H bond activation (Scheme S1‡) reveals that the chalcogenide atom (viats1) activates the C–H bond, leading the Ni–E1–H intermediate (Int1) with the second hydrogen atom abstraction viats2 by chalcogenide atom E2 leading to two hydrochalcogenide NiII product (PC) that was detected by experiments and characterised using X-ray and spectral methods.58The computed potential energy surface for 1–4 is shown in Fig. 4 and S45.‡ For complexes 1, 3 and 4, the triplet state (51,3-4ts1(t,t)) has the lowest barrier of 58.5, 89.3 and 95.4 kJ mol−1, respectively. For complex 2, on the other hand, the singlet state (12ts1(t,t)) was found to have the lowest barrier of 68.2 kJ mol−1. The 11,3-4ts1(t,t) and 52ts1(t,t) transition states were found to lie at 78.5, 99.8, 97.7 and 82.0 kJ mol higher. For complex 3, the computed barrier height of 89.3 kJ mol−1 is slightly higher than expected for an otherwise facile C–H bond activation pathway, and this larger barrier, however consistent with the experimental finding that the reaction does not proceed at ambient temperature and temperature as high as 55 °C is required to effect this transformation.94 We have also estimated the barrier height at the singlet surface for complex 3 (13ts1(s,s)) to assess and analyse, if the closed-shell singlet participate at all in the reactivity. This set of calculations resulted in a prohibitively high barrier height of 302.0 kJ mol−1, thereby ruling out the possibility of this state contributing to the reactivity, as depicted in Fig. 4c.
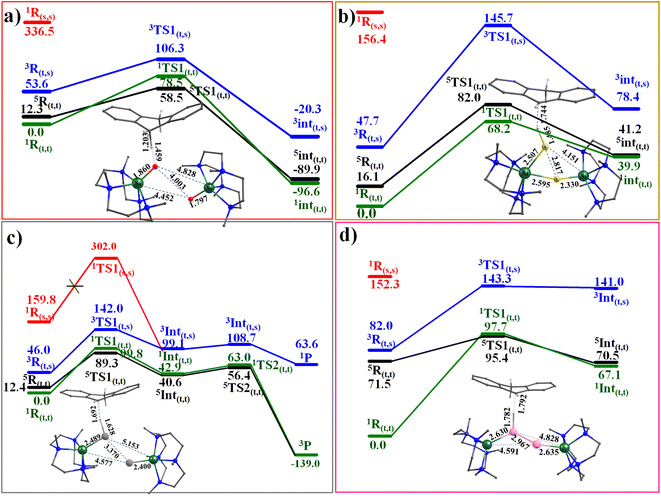 | ||
| Fig. 4 Computed potential energy surface energy surface for the C–H activation by complexes (a) 1, (b) 2, (c) 3, and (d) 4. | ||
In all the transition state computed, hydrogen atom abstraction is detected, leading to a carbon-centred radical, as also evidenced by IRC analysis (See Fig. S46 and S47 in ESI‡). In all the transition states computed, the ∠E–H–C bond angle was found to be lying in the range of 154°–172° suggesting σ-pathway for the H atom abstraction. This is also attributed to the nature of the LUMO orbitals at the reactant, which has significant px/py orbitals of the E atom contribution along with dx2−y2 orbital of the NiII, promoting the σ-pathway. At the transition state, electron transfer is nearly complete, with the early transition state for 1 and the late transition state for 2–4, reflecting the difference in the electronic structure described earlier (dichalcogenide vs. subchalcogenide). As dichalcogenide complexes are expected to have lower pKa than subchalcogenide complexes, the variation in the transition state observed correlates well with the established electronic structure. Further, the HAT abstraction is accompanied by the electron transfer due to which the E1–E2 bond is fully broken in all the complexes 1–4 with a significant radical character generated on E2˙. This radical character, in turn, leads to partial Ni = E2 character and the formation of a weakly interacting monomeric Ni hydrochalcogenide product (see Fig. S2‡). This also suggests significant electronic cooperativity between two Ni centres, rationalising the reason for the higher reactivity of dinickel dichalcogenide complexes compared to their monomeric analogues (see Table S8‡).
The computed barrier height reveals the following order of reactivity 1 > 2 > 3 > 4, suggesting higher reactivity of O, which has a dichalcogenide character (also very high basicity of –O center) and lower reactivity for subchalcogenide complexes. As the degree of subchalcogenide increases, as we move from 2 to 4, the barrier height also increases proportionately, suggesting much lower reactivity for subchalcogenide complexes (see Fig. 4 and 5). To understand the trend in the estimated barrier height, the strain energy analysis of the transition state was performed, which reveals that the catalyst strain is significant, and this is compensated to some extent by a favourable strain energy for the substrate for all four complexes. A larger strain in the catalysts was reflected as we moved from 1 to 4, which is directly related to the computed barrier height. The interaction energy computed reveals a favourable overlap of the frontier orbitals as expected, and this interaction energy was found to diminish as we move from 1 to 4 leading to a larger barrier height. Thus increase in the barrier height observed as we move from 1 to 4 originates from both larger strain and smaller interaction energy (see Table S9‡).
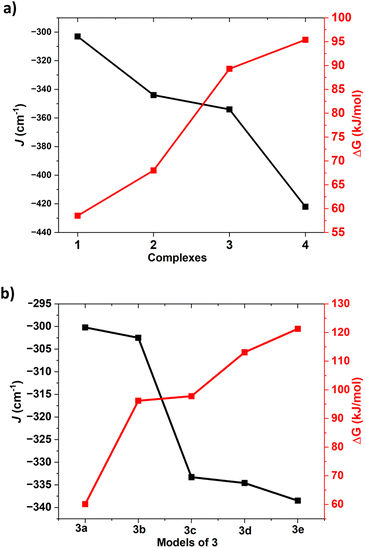 | ||
| Fig. 5 (a) First hydrogen abstraction barrier height correlation with J value of complexes 1–4 (b) magneto–structural correlation for the substituted geometries of the complex 3 (3a–3e). | ||
In the next step, we would like to extend the HAT event further and quantify it in detail by exploring the non-adiabaticity of the first hydrogen abstraction transition state (ts1) for all four complexes (1–4). In this connection, it is important to highlight the seminal work performed by Hammes-Schiffer and co-workers that describes the vibronic nonadiabaticity between the electron–proton quantum subsystem and the classical nuclei, along with the electron–proton nonadiabaticity within the electrons and proton(s) of the quantum subsystem for an enzyme that supported the use of Golden rule rate constant expression.95–101 While this approach is the best suited to analyse our transition state, the gap computed between different multiplets at the transition state in our case was too small to develop the full potential energy surface (>2 kJ mol−1 for 1). We then turn to calculate the non-adiabatic coupling (NAC) of the first hydrogen abstraction using a time-dependent response approach, which avoids the explicit computation of excited-state wave functions.102 These calculations were performed using the ORCA suite (see Computational details). These calculations reveal that as we move from 1 to 4, there is a decrease in the maximum non-adiabatic coupling strength (see Table S10‡). This observation suggests that complexes 1 and 2 possess larger non-adiabatic coupling, and 3 and 4 have relatively smaller values, clubbing the Se and Te together in this context (see Table S10‡). To further understand the nature of the hydrogen atom transfer (HAT) reaction, we have further expanded our analysis and performed spin-natural orbital analysis for all four complexes 1–4. For 1, the carbon atom of the substrate exhibits a small spin density of approximately −0.19. This, combined with the SNO analysis, indicates that the dominant proton transfer pathway is likely operational. Conversely, in complex 2, only a dominant HAT nature is evident, with the occupation value of 0.69e of the spin natural orbital, as supported by the spin density plot displaying a significant electron density of −0.46 at the carbon radical centre of the DHA molecule. In the cases of complexes 3 and 4, a pronounced radical nature is also observed at the carbon center, with values of −0.48 and 0.44, respectively, and the SNO analysis reveals that complex 3 exhibits a strong PCET character (1.00e) with a slight HAT character (0.84e), while in complex 4, a strong HAT character (1.00e) is predominant in the transition state, albeit with a slight PCET character. The computed data indicate a trend: as we progress from complex 2 to 4, the HAT nature of the transition state becomes increasingly prominent, and this is also in line with the increase in the metal–ligand covalency that is expected to promote HAT pathway (see Fig. S48–S52 and S53–S56‡ for EVP).103 After the hydrogen atom abstraction, the formation of radical intermediate (Int1) is exothermic for 1 and endothermic for the rest (−96.6, 39.9, 40.6 and 67.1 kJ mol−1, for 1–4, respectively) with ST = 0 ground state arising from antiferromagnetic for all with the exception of 3 (here ST = 2). In all cases, the corresponding exchange coupled excited state was found to lie close within an energy margin of 1.3–6.6 kJ mol−1, with the triplet states lying much higher in energy (38–71 kJ mol−1). At this species, the E–E bond is found to be broken in all cases with a concomitant strengthing of the Ni–E bonds. The chalcogenide that abstracts the H atom also creates a Ni–E bond shorter than that of the reactant.
In 3, the Ni–Se bond distance is found to be 2.395 Å, and this is in excellent agreement with the value reported from the X-ray structure (2.389 Å), offering further confidence in the chosen methodology.58 Encouraged by the direct experimental evidence that is available for the intermediate computed with species 3, we also extended our mechanism to probe the barrier for the second hydrogen atom abstraction. This is presumed to route through the transition state (ts2; see Fig. 4) with a barrier for 15.8 kJ mol−1 from the intermediate, suggesting a facile abstraction of the second hydrogen atom leading to the formation of anthracene by −139.0 kJ mol−1 gain in energy.
The results obtained from DFT calculations exhibit a noteworthy trend in the structural and bonding analysis of complexes 1–4. In all four complexes, the high spin antiferromagnetic state 11–4(t,t) is identified as the ground state, and this is due to the strong overlap of dx2−y2 orbitals of two Ni centres. The nature of the ground state is further affirmed by the SA-CASSCF and DLPNO-CCSD(T) methods. Further AIM analysis reveals an increase in Ni–E bond covalency as we move down the group by 15.0%, 20.9% 31.9% for Ni–S, Ni–Se and Ni–Te, respectively, compared to the Ni–O bond. This is attributed to a stronger donation from E to Ni as we move down the group (40.5%, 62.3% and 66.7% for Ni–S, Ni–Se and Ni–Te, respectively, compared to the Ni–O bond). The increase in the Ni–E bond covalency was also found to enhance the multiconfigurational mixing of states in SA-CASSCF calculations suggesting multistate reactivity for higher analogues.41
The singlet state arising from the S = 0 state (11–4(s,s)) at each Ni centres is too high in energy with respect to the transition state computed at the singlet and triplet surfaces and hence rules out the possibility of these states involvement in the HAT reaction. Further, the triplet state 31–4(t,s) is also found to be higher in energy compared to a quintet and singlet state arising from antiferromagnetic coupling and hence is unlikely to participate in the HAT reaction invoking two-state reactivity or TSR scenario for the HAT reactions. The C–H bond activation for all four species was found to be either routed via S = 2 states (for 1, 2, and 4) or via close-lying S = 0 states facilitating two-state reactivity (in case of 3). In all four cases, partially closed-shell triplet states (i.e., a triplet on one Ni center and a singlet state on the other) and fully closed-shell singlets (S = 0 on both Ni centers) were found to be high in energy, with transition states prohibitively high to participate in the reaction. This suggests that only the spin-coupled triplet states of the Ni centers contribute to the reactivity.
All these calculations suggests that the quintet-singlet gap that is correlated to the exchange interaction between two Ni centres is key to the reactivity. As this parameter is correlated to the exchange interaction, we have plotted the computed J values for these complexes along with the rate-determining step barrier height corresponding to the C–H bond activation (Fig. 5).
This suggests that there is a clear correlation as the J value is found to increase in the order 1 < 2 < 3 < 4 with the increase in the quintet-singlet gap while the reactivity follows the reverse trend (1 > 2 > 3 > 4), suggesting greater reactivity when the antiferromagnetic coupling between the two centres are weak/small.104,105 Deeper orbital analysis and overlap integral computed suggest strong antiferromagnetic coupling is found to associated with the greater dx2−y2|px|dx2−y2 overlap, which is important during the electron transfer process from the substrate to the chalcogenide centric Ni–E(π*) orbital. The quintet state of complex 1 having strong Ni-centric HOMO and LUMO due to its dichalcogenide and stronger Ni(II) character enable the facile transfer of α-electron from the C–H bond maximising the exchange-enhanced reactivity,106 stabilising the corresponding transition state. Further, as the α-electron, which is getting transferred from the substrate, triggers Ni–E bond cleavage, the transferred electron is found to be located on the E(2) centre, resulting in the formation of Ni(II)–E˙ species at the transition state. As the coupling between Ni(II) and E˙ has to be ferromagnetic due to orbital orthogonality (see Table S11 in ESI‡ for computed Js), this quintet state is the preferred transition state. In the singlet state, as shown in the orbital evolution diagram, the Ni(II)–E(2)˙ forced to be in antiferromagnetic state (See Fig. S57 and also corresponding spin density plots in Fig. S2 and S5, S8, S11 and S16‡).
Also the careful analysis of all optimized ground state transition state geometries suggested that in the case of complex 2, the {Ni2S2} core does not break completely during the transition state formation. This observation suggests that the overlapping of sulphur 3p orbitals with the metal 3d orbitals (specifically dx2−y2|px|dx2−y2 overlap) persists, thereby stabilizing the antiferromagnetic state. Also, the comparison of Ni–E bond lengths was observed in complexes 1, 3, and 4 (ranging from 4.450 to 4.560 Å), while in the case of complex 2, the Ni–E bond seemed significantly shorter by 2.595 Å. This shorter bond length favours antiferromagnetic coupling state as the ground state of complex 2, in contrast to other complexes.
As we move down in the group, increased covalency and transition to subchalcogenide offer a strongly delocalised LUMO that is less electrophilic, enhancing the overall kinetic barrier. For complex 4, a β-electron transfer from the C–H bond is noticed, enhancing the barrier height further. The pronounced electronic cooperativity at play during the C–H bond activation step is clearly discernible across complexes 1–4. This is evidenced by the electron transfer from the C–H bond, which ultimately resides on E2, a participant not directly engaged in the reaction. Overall, our study suggests that a ferromagnetic Ni2E2 would be more reactive, and if the antiferromagnetic interaction is diminished, this would also be expected to enhance the reactivity. As the antiferromagnetic interaction between the two Ni(II) centres is correlated to the Ni–E–Ni angle,107 this offers a viable route to enhance the reactivity of higher analogues that are generally unreactive.
To further probe the correlation between the antiferromagnetic coupling and the barrier height, we have now expanded the calculations on complex 3 with various substitutes at the ligand moiety and carved out five additional models (the –NCH3 group was replaced by a –NH groups, see Fig. S58 in ESI‡ for models developed; models 3a–3e) to develop magneto–structural correlation (see Fig. 5 and S58‡). Using these models, we have computed the J and also computed the corresponding barrier height for these models. For these models, the computed exchange coupling is found to be antiferromagnetic, but the magnitude of the J was found to vary from 300.2 cm−1 to 338.5 cm−1. The barrier height corresponding to the HAT reaction for models 3a–3e was found to vary from 60.1 to 121.3 kJ mol−1 (see Table S12 in ESI‡). We have now plotted this magneto–structural correlation that connects J with the barrier height within this model series (see Fig. 5). The computed values revealed a correlation: as the antiferromagnetic coupling exchange J value increases, so does the barrier height. This supports the observed trend among complexes 1–4, where an increase in antiferromagnetic coupling corresponds to higher barrier heights. This explains why complex 1 exhibited the highest reactivity with the lowest antiferromagnetic exchange value. This finding aligns with the observed trend of all four complexes 1–4, where higher J values correspond to lower reactivity of the reaction (see Fig. S58 and Table S12,‡ also see Tables S13–S27‡ for detailed structural parameters).
Conclusions
Dinickel dichalcogenide complexes are important due to their diverse applications, including catalysis, electron transfer processes, magnetic properties, materials science contributions, theoretical insights, and energy conversion potential. In this study, we employed an array of theoretical tools to study in detail the structure, bonding and reactivity of a series of {[Ni(L)]2(E2)}(PF6)2 (E = O, S, Se and Te) complexes. The following conclusions are derived from our work (i) by studying the geometry, bonding and spectral features of the four dinickel dichalcogenide complexes, our calculations unambiguously suggest {Ni2O2} and {Ni2S2} fall under the category of dichalcogenide type complexes, while complexes {Ni2Se2} and {Ni2Te2} exhibits tendencies towards the subchalcogenide category. None of the complexes were found to have pure chalcogenide characters at their ground state. The geometry and spectral features are broadly in agreement with the experimental findings. (ii) The bonding Ni–E (E = O, S, Se and Te) bond is found to be ionic for O with a significant increase in covalency as we move down the group. This is associated with the greater overlap of Ni-3d orbitals with the diffused 3p/4p/5p orbitals compared to the oxygen 2p orbitals. A strong covalency also enhances the multiconfigurational character of the heavier analogues, completing the simple picture often derived from DFT. The observed covalency correlates with reactivity, as stronger covalent compounds exhibit slower reaction rates, while non-adiabatic coupling diminishes along this route, favoring hydrogen atom transfer as we progress down the series. (iii) All complexes studied have singlet ground states resulting from the antiferromagnetic coupling between two Ni centres. The C–H bond activation studies on these complexes reveal that the following order of decreasing reactivity {Ni2O2} > {Ni2S2} > {Ni2Se2} > {Ni2Te2}. The transition state is characterised in all cases to be a chalcogenide category, suggesting how subtle different classifications are when it comes to reactivity. Particularly during the C–H bond activation, strong electronic cooperativity between the metal centres is noticed along with variation in their classification as the E–H bond formation takes place. Investigating the multi-state reactivity of all complexes reveals that only the spin-coupled triplet states, which yield overall singlet and triplet states, dictate the overall reactivity, while the closed-shell singlets are too high in energy and do not participate in the reaction. This highlights the importance of maintaining a weak/moderate ligand field around the Ni center to achieve greater reactivity. (iv) Further, a strong correlation between the J values and the C–H bond activation step is detected with a lower gap yielding higher reactivity. As quintet state, in general, found to have lower barriers, efforts to obtain a ferromagnetic coupling in Se or Te analogues would be fruitful in enhancing their reactivity.Data availability
All relevant computational data associated with our study, including Cartesian coordinates, geometry, spin density plots, and detailed structural information, are available in the ESI† provided with our submission.Author contributions
Sunita Sharma: conducted the majority of the computational studies, analysed data, and contributed significantly to the writing of the manuscript. Bhawana Pandey: assisted with computational work, data analysis, and contributed to the interpretation of the results and preparation of the manuscript. Gopalan Rajaraman: conceived and supervised the project, provided guidance on computational methodologies, analysed data, and contributed to the writing and editing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank SERB (SB/SJF/2019-20/12; CRG/2022/001697) for funding. SS/BP thanks UGC for the fellowship and HPC for the computational facility.References
-
P. A. Frey and A. D. Hegeman, Enzymatic Reaction Mechanisms, Oxford University Press, 2007 Search PubMed
.
- R. H. Holm and E. I. Solomon, Chem. Rev., 1996, 96, 2237 CrossRef PubMed
.
-
B. Meunier, G. Brudvig, J. L. Mclain, S.-i. Murahashi, V. Pecoraro, D. Riley, A. Robert, J. Rodriguez, R. Sheldon and J. Valentine, Biomimetic Oxidations Catalyzed by Transition Metal Complexes, World Scientific, 2000 Search PubMed
.
-
H. Sigel and A. Sigel, Metal Ions in Biological Systems: Electron Transfer Reactions in Metalloproteins, CRC Press, vol. 27, 1991 Search PubMed
.
- J. T. Groves, J. Inorg. Biochem., 2006, 100, 434–447 CrossRef CAS PubMed
.
-
P. R. O. De Montellano, Cytochrome P450: Structure, Mechanism, and Biochemistry, Springer, 2005 Search PubMed
.
- J. Hohenberger, K. Ray and K. Meyer, Nat. Commun., 2012, 3, 1–13 Search PubMed
.
-
D. F. Leto, Biomimetic Peroxo- and Oxo-manganese Complexes: Insights into Structure and Reactivity through Kinetic, Spectroscopic, and Computational Studie, 2014 Search PubMed
.
- R. H. Holm, Chem. Rev., 1987, 87, 1401–1449 CrossRef CAS
.
- J. P. Klinman, Chem. Rev., 1996, 96, 2541–2562 CrossRef CAS PubMed
.
- E. I. Solomon, U. M. Sundaram and T. E. Machonkin, Chem. Rev., 1996, 96, 2563–2606 CrossRef CAS PubMed
.
- D. Wilson, M. Fataftah, Z. Mathe, B. Mercado, S. DeBeer and P. Holland, J. Am. Chem. Soc., 2024, 146(6), 4013–4025 CrossRef CAS PubMed
.
- S. W. Ragsdale, J. Biol. Chem., 2009, 284, 18571–18575 CrossRef CAS PubMed
.
-
A. Parkins, Activation of Unreactive Bonds and Organic Synthesis Topics in Organometallic Chemistry, Wiley Online Library, 2000 Search PubMed
.
- W. Keim, Angew. Chem., Int. Ed. Engl., 1990, 29, 235–244 CrossRef
.
- P. M. Vignais and B. Billoud, Chem. Rev., 2007, 107, 4206–4272 CrossRef CAS PubMed
.
- J. C. Fontecilla-Camps, A. Volbeda, C. Cavazza and Y. Nicolet, Chem. Rev., 2007, 107, 4273–4303 CrossRef CAS PubMed
.
- B. Palenik, B. Brahamsha, F. Larimer, M. Land, L. Hauser, P. Chain, J. Lamerdin, W. Regala, E. Allen and J. McCarren, Nature, 2003, 424, 1037–1042 CrossRef CAS PubMed
.
- J. Wuerges, J.-W. Lee, Y.-I. Yim, H.-S. Yim, S.-O. Kang and K. D. Carugo, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 8569–8574 CrossRef CAS PubMed
.
- H.-D. Youn, E.-J. Kim, J.-H. Roe, Y. C. Hah and S.-O. Kang, Biochem. J., 1996, 318, 889–896 CrossRef CAS PubMed
.
-
A. Messerschmidt, R. Huber, T. Poulos and K. Wieghardt, Handbook of Metalloproteins, John Wiley & Sons, Chichester, 2001 Search PubMed
.
-
R. P. Hausinger, Biochemistry of Nickel, Springer Science & Business Media, 2013 Search PubMed
.
- S. W. Ragsdale and E. Pierce, Biochim. Biophys. Acta – Proteins Proteom., 2008, 1784, 1873–1898 CrossRef CAS PubMed
.
- W. Martin and M. J. Russell, Philos. Trans. R. Soc. Lond., B, Biol. Sci., 2007, 362, 1887–1926 CrossRef CAS PubMed
.
- D. M. Grove, G. Van Koten, R. Zoet, N. W. Murrall and A. J. Welch, J. Am. Chem. Soc., 1983, 105, 1379–1380 CrossRef CAS
.
- J. Cho, R. Sarangi, J. Annaraj, S. Y. Kim, M. Kubo, T. Ogura, E. I. Solomon and W. Nam, Nat. Chem., 2009, 1, 568–572 CrossRef CAS PubMed
.
- S. Hikichi, M. Yoshizawa, Y. Sasakura, M. Akita and Y. Moro-oka, J. Am. Chem. Soc., 1998, 120, 10567–10568 CrossRef CAS
.
- K. Shiren, S. Ogo, S. Fujinami, H. Hayashi, M. Suzuki, A. Uehara, Y. Watanabe and Y. Moro-oka, J. Am. Chem. Soc., 2000, 122, 254–262 CrossRef CAS
.
- B. Bag, N. Mondal, G. Rosair and S. Mitra, Chem. Commun., 2000, 1729–1730 RSC
.
- S. Itoh, H. Bandoh, M. Nakagawa, S. Nagatomo, T. Kitagawa, K. D. Karlin and S. Fukuzumi, J. Am. Chem. Soc., 2001, 123, 11168–11178 CrossRef CAS PubMed
.
- R. Schenker, B. S. Mandimutsira, C. G. Riordan and T. C. Brunold, J. Am. Chem. Soc., 2002, 124, 13842–13855 CrossRef CAS PubMed
.
- L. Que Jr and W. B. Tolman, Angew. Chem., Int. Ed., 2002, 114, 1160–1185 CrossRef
.
- K. Ray, F. Heims and F. F. Pfaff, Eur. J. Inorg. Chem., 2013, 2013, 3784–3807 CrossRef CAS
.
- C. Krebs, D. Galonic Fujimori, C. T. Walsh and J. M. Bollinger Jr, Acc. Chem. Res., 2007, 40, 484–492 CrossRef CAS PubMed
.
- L. Que Jr, Acc. Chem. Res., 2007, 40, 493–500 CrossRef PubMed
.
- W. Nam, Acc. Chem. Res., 2007, 40, 522–531 CrossRef CAS PubMed
.
- G. Xue, R. De Hont, E. Münck and L. Que, Nat. Chem., 2010, 2, 400–405 CrossRef CAS PubMed
.
- W. J. Song, Y. O. Ryu, R. Song and W. Nam, J. Biol. Inorg. Chem., 2005, 10, 294–304 CrossRef CAS PubMed
.
- K. Chen and L. Que, J. Am. Chem. Soc., 2001, 123, 6327–6337 CrossRef CAS PubMed
.
- Y. Mekmouche, S. Ménage, C. Toia-Duboc, M. Fontecave, J. B. Galey, C. Lebrun and J. Pécaut, Angew. Chem., Int. Ed., 2001, 40, 949–952 CrossRef CAS PubMed
.
- E. Zars, L. Gravogl, M. R. Gau, P. J. Carroll, K. Meyer and D. J. Mindiola, Chem. Sci., 2023, 14, 6770–6779 RSC
.
- O. P. Lam, F. W. Heinemann and K. Meyer, Chem. Sci., 2011, 2, 1538–1547 RSC
.
- K. Kalantar-zadeh, J. Z. Ou, T. Daeneke, M. S. Strano, M. Pumera and S. L. Gras, Adv. Funct. Mater., 2015, 25, 5086–5099 CrossRef CAS
.
- B. Krebs and G. Henkel, Angew. Chem., Int. Ed. Engl., 1991, 30, 769–788 CrossRef
.
- T. C. Brunold, J. Biol. Inorg. Chem., 2004, 9, 533–541 CrossRef CAS PubMed
.
- J. L. Craft, B. S. Mandimutsira, K. Fujita, C. G. Riordan and T. C. Brunold, Inorg. Chem., 2003, 42, 859–867 CrossRef CAS PubMed
.
- A. Volbeda, M.-H. Charon, C. Piras, E. C. Hatchikian, M. Frey and J. C. Fontecilla-Camps, Nature, 1995, 373, 580–587 CrossRef CAS PubMed
.
- A. T. Fiedler, P. A. Bryngelson, M. J. Maroney and T. C. Brunold, J. Am. Chem. Soc., 2005, 127, 5449–5462 CrossRef CAS PubMed
.
- U. Ermler, W. Grabarse, S. Shima, M. Goubeaud and R. K. Thauer, Science, 1997, 278, 1457–1462 CrossRef CAS PubMed
.
- K. M. Van Heuvelen, J. Cho, C. G. Riordan and T. C. Brunold, Inorg. Chem., 2010, 49, 3113–3120 CrossRef CAS PubMed
.
- J. Cho, K. M. Van Heuvelen, G. P. Yap, T. C. Brunold and C. G. Riordan, Inorg. Chem., 2008, 47, 3931–3933 CrossRef CAS PubMed
.
- H. Sitzmann, D. Saurenz, G. Wolmershäuser, A. Klein and R. Boese, Organometallics, 2001, 20, 700–705 CrossRef CAS
.
- S. A. Yao, V. Martin-Diaconescu, I. Infante, K. M. Lancaster, A. W. Götz, S. DeBeer and J. F. Berry, J. Am. Chem. Soc., 2015, 137, 4993–5011 CrossRef CAS PubMed
.
- S. A. Yao, K. M. Lancaster, A. W. Götz, S. DeBeer and J. F. Berry, Chem.–Eur. J., 2012, 18, 9179–9183 CrossRef CAS PubMed
.
- R. Sarangi, S. DeBeer George, D. J. Rudd, R. K. Szilagyi, X. Ribas, C. Rovira, M. Almeida, K. O. Hodgson, B. Hedman and E. I. Solomon, J. Am. Chem. Soc., 2007, 129, 2316–2326 CrossRef CAS PubMed
.
- J. T. Henthorn, G. E. Cutsail III, T. Weyhermüller and S. DeBeer, Nat. Chem., 2022, 14, 328–333 CrossRef CAS PubMed
.
- M. C. Marques, C. Tapia, O. Gutiérrez-Sanz, A. R. Ramos, K. L. Keller, J. D. Wall, A. L. De Lacey, P. M. Matias and I. A. Pereira, Nat. Chem. Biol., 2017, 13, 544–550 CrossRef CAS PubMed
.
- J. Wallick, C. G. Riordan and G. P. Yap, J. Am. Chem. Soc., 2013, 135, 14972–14974 CrossRef CAS PubMed
.
-
M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, Gaussian Inc, Wallingford, 2009
.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed
.
- M. P. Andersson and P. Uvdal, J. Phys. Chem. A, 2005, 109, 2937–2941 CrossRef CAS PubMed
.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS
.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS
.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS
.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298 CrossRef CAS
.
- A. Savin, O. Jepsen, J. Flad, O. K. Andersen, H. Preuss and H. G. von Schnering, Angew. Chem., Int. Ed. Engl., 1992, 31, 187–188 CrossRef
.
- W. J. Hehre, Acc. Chem. Res., 1976, 9, 399–406 CrossRef CAS
.
- D. Andrae, U. Haeussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS
.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed
.
- M. T. Kieber-Emmons and C. G. Riordan, Acc. Chem. Res., 2007, 40, 618–625 CrossRef CAS PubMed
.
- C. Mealli and S. Midollini, Inorg. Chem., 1983, 22, 2785–2786 CrossRef CAS
.
- S. Yao, Y. Xiong, X. Zhang, M. Schlangen, H. Schwarz, C. Milsmann and M. Driess, Angew. Chem., Int. Ed., 2009, 121, 4621–4624 CrossRef
.
- M. Di Vaira, M. Peruzzini and P. Stoppioni, J. Chem. Soc., Chem. Commun., 1986, 374–375 RSC
.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437 CrossRef CAS PubMed
.
- S. Ye, C.-Y. Geng, S. Shaik and F. Neese, Phys. Chem. Chem. Phys., 2013, 15, 8017–8030 RSC
.
- D. Janardanan, D. Usharani, H. Chen and S. Shaik, J. Phys. Chem. Lett., 2011, 2, 2610–2617 CrossRef CAS
.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
.
- F. Weigend, J. Comput. Chem., 2008, 29, 167–175 CrossRef CAS PubMed
.
- P. Verma, Z. Varga, J. E. Klein, C. J. Cramer, L. Que and D. G. Truhlar, Phys. Chem. Chem. Phys., 2017, 19, 13049–13069 RSC
.
- P. Comba, D. Faltermeier, S. Krieg, B. Martin and G. Rajaraman, Dalton Trans., 2020, 49, 2888–2894 RSC
.
- J. Rezac and P. Hobza, J. Chem. Theory Comput., 2013, 9, 2151–2155 CrossRef CAS PubMed
.
- K. Pierloot, Q. M. Phung and A. Domingo, J. Chem. Theory Comput., 2017, 13, 537–553 CrossRef CAS PubMed
.
- K. Andersson, P. Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS
.
- P. Å. Malmqvist, A. Rendell and B. O. Roos, J. Phys. Chem., 1990, 94, 5477–5482 CrossRef CAS
.
- C. Angeli, B. Bories, A. Cavallini and R. Cimiraglia, J. Chem. Phys., 2006, 124, 054108 CrossRef PubMed
.
- E. v. Lenthe, E.-J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef
.
- S. K. Singh, M. Atanasov and F. Neese, J. Chem. Theory Comput., 2018, 14, 4662–4677 CrossRef CAS PubMed
.
- E. A. Pritchina, N. P. Gritsan, O. A. Rakitin and A. V. Zibarev, Targets Heterocycl. Syst., 2019, 23, 143–154 CAS
.
- P. Pollak and F. Weigend, J. Chem. Theory Comput., 2017, 13, 3696–3705 CrossRef CAS PubMed
.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743 CrossRef CAS
.
- L. Noodleman and E. R. Davidson, Chem. Phys., 1986, 109, 131–143 CrossRef
.
- L. Fohlmeister, K. R. Vignesh, F. Winter, B. Moubaraki, G. Rajaraman, R. Pöttgen, K. S. Murray and C. Jones, Dalton Trans., 2015, 44, 1700–1708 RSC
.
- F. Bordwell, J. Cheng, G. Z. Ji, A. Satish and X. Zhang, J. Am. Chem. Soc., 1991, 113, 9790–9795 CrossRef CAS
.
- A. V. Soudackov and S. Hammes-Schiffer, J. Phys. Chem. Lett., 2014, 5, 3274–3278 CrossRef CAS PubMed
.
- S. Hammes-Schiffer and A. A. Stuchebrukhov, Chem. Rev., 2010, 110, 6939–6960 CrossRef CAS PubMed
.
- A. Sirjoosingh and S. Hammes-Schiffer, J. Phys. Chem. A, 2011, 115, 2367–2377 CrossRef CAS PubMed
.
- A. Sirjoosingh and S. Hammes-Schiffer, J. Chem. Theory Comput., 2011, 7, 2831–2841 CrossRef CAS PubMed
.
- S. Hu, S. C. Sharma, A. D. Scouras, A. V. Soudackov, C. A. M. Carr, S. Hammes-Schiffer, T. Alber and J. P. Klinman, J. Am. Chem. Soc., 2014, 136, 8157–8160 CrossRef CAS PubMed
.
- E. Hatcher, A. V. Soudackov and S. Hammes-Schiffer, J. Am. Chem. Soc., 2007, 129, 187–196 CrossRef CAS PubMed
.
- E. Hatcher, A. V. Soudackov and S. Hammes-Schiffer, J. Am. Chem. Soc., 2004, 126, 5763–5775 CrossRef CAS PubMed
.
- R. Send and F. Furche, J. Chem. Phys., 2010, 132 Search PubMed
.
- A. Sen, A. Ansari, A. Swain, B. Pandey and G. Rajaraman, Inorg. Chem., 2023, 62, 14931–14941 CrossRef CAS PubMed
.
- M. Ansari, D. Senthilnathan and G. Rajaraman, Chem. Sci., 2020, 11, 10669 RSC
.
- G. Xue, R. De Hont, E. Münck and L. Que Jr, Nat. Chem., 2010, 2, 400 CrossRef CAS PubMed
.
- S. Shaik, H. Chen and D. Janardanan, Nat. Chem., 2011, 3, 19–27 CrossRef CAS PubMed
.
- S. K. Gupta, A. A. Dar, T. Rajeshkumar, S. Kuppuswamy, S. K. Langley, K. S. Murray, G. Rajaraman and R. Murugavel, Dalton Trans., 2015, 44, 5961–5965 RSC
.
Footnotes |
| † Dedicated to the 65th birthday of Prof. M. S. Balakrishna, IIT Bombay, India. |
| ‡ Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc02882a |
| This journal is © The Royal Society of Chemistry 2024 |