Open Access Article
Open Access ArticleRelationship between spatially heterogeneous reaction dynamics and photochemical kinetics in single crystals of anthracene derivatives†
Sogo
Kataoka
a,
Daichi
Kitagawa
 *a,
Hikaru
Sotome
*a,
Hikaru
Sotome
 b,
Syoji
Ito
b,
Syoji
Ito
 b,
Hiroshi
Miyasaka
b,
Hiroshi
Miyasaka
 b,
Christopher J.
Bardeen
b,
Christopher J.
Bardeen
 *c and
Seiya
Kobatake
*c and
Seiya
Kobatake
 *a
*a
aDepartment of Chemistry and Bioengineering, Graduate School of Engineering, Osaka Metropolitan University, 3-3-138 Sugimoto, Sumiyoshi-ku, Osaka, 558-8585, Japan. E-mail: kitagawa@omu.ac.jp; kobatake@omu.ac.jp
bDivision of Frontier Materials Science and Center for Promotion of Advanced Interdisciplinary Research, Graduate School of Engineering Science, Osaka University, 1-3 Machikaneyama-cho, Toyonaka, Osaka 560-8531, Japan
cDepartment of Chemistry, University of California, Riverside, 501 Big Springs Road, Riverside, CA 92521, USA. E-mail: christob@ucr.edu
First published on 26th July 2024
Abstract
Understanding physicochemical property changes based on reaction kinetics is required to design materials exhibiting desired functions at arbitrary timings. In this work, we investigated the photodimerization of anthracene derivatives in single crystals. Single crystals of 9-cyanoanthracene (9CA) and 9-anthraldehyde (9AA) exhibited reaction front propagation on the optical length scale, while 9-methylanthracene and 9-acetylanthracene crystals underwent spatially homogeneous conversion. Moreover, the sigmoidal behavior in the absorbance change associated with the reaction was much pronounced in the case of 9CA and 9AA and correlated with the observation of heterogeneous reaction progress. A kinetic analysis based on the Finke–Watzky model showed that the effective quantum yield of the photochemical reaction changes by more than an order of magnitude during the course of the reaction in 9CA and 9AA. Both the reaction front propagation and nonlinear kinetic behavior could be rationalized in terms of the difference in the cooperativity of the reactions. We propose a plausible mechanism for the heterogeneous reaction progress in single crystals that depends on the magnitude of the conformational change required for reaction. Our results provide useful information to understand the connection between photochemical reaction progress in the crystalline phase and the dynamic changes in the physicochemical properties.
Introduction
In recent years, stimuli-responsive organic crystals that exhibit functions such as fluorescence color change,1,2 superelasticity,3,4 self-healing,5–8 and gas adsorption/desorption9 in response to external stimuli have been attracting attention as next-generation functional materials.10,11 Changes in the physical properties of stimuli-responsive crystalline materials are generally brought about by changes in the molecular structure or crystal packing.12,13 These structural changes can be accurately determined by single-crystal X-ray diffraction (SCXRD) measurements, which provide molecular-level insight into why changes in physicochemical property occur.14–17 However, this method only captures the “static” state before and after the structural change and it is generally difficult to capture the “dynamic” changes. In order to design stimuli-responsive organic crystals that exhibit desired functions at arbitrary timings, it is necessary to understand how reaction dynamics in crystals give rise to changes in physical properties.Reactions in the crystalline state often show different behavior from those in solution.18–21 This is because the molecule in the crystalline state is surrounded by many other molecules and intermolecular interactions with its neighbors exert a strong influence on its dynamics. This situation is significantly different from the solution state where molecules evolve independently. For the purposes of this paper, a cooperative process is one in which the reactant–product interactions are strong enough to give rise to a measurable deviation from the exponential behavior observed for molecules reacting independently in dilute solution.22 As an example, in the case of the [2 + 2] photodimerization reaction of cinnamic acid crystals, the reaction does not progress much immediately after the start of photoirradiation, but once the reaction starts, the reaction progresses rapidly.23 This is due to the cooperative effects that cause reactant molecules around the products to become more reactive. In these cases, the plot of the conversion ratio from the reactant to the product relative to the irradiation time shows a sigmoidal curve.23 To correctly analyze changes in solid-state properties, kinetic analysis of reactions using theoretical models incorporating cooperative reaction processes is essential.
We recently investigated the photochemical reaction kinetics of 9-methylanthracene (9MA) in the crystalline phase where it undergoes photodimerization.24 Interestingly, the photochemical kinetics of 9MA in single crystals were close to exponential while those for polycrystalline samples had a pronounced sigmoidal behavior, which is presumably due to the difference in crystal defects. The extended Finke–Watzky (FW) model that we have developed reproduced both regimes in terms of an effective quantum yield that depends on reaction progress. This approach provides a way to quantify the cooperativity of the photochemical reactions in the crystalline state. Furthermore, in the course of study on the photochemical reaction dynamics in organic molecular single crystals, we found that the photochemical reaction of 2,5-distyrylpyrazine (DSP) in single crystals proceeds from the edge to the center of the crystal.25 Namely, the photochemical reaction of DSP proceeds heterogeneously on length scales that can be resolved by optical microscopy, typically on the order of 1 micron, in contrast to photochemical reactions in single crystals that proceed homogeneously on such optical length scales. Heterogeneous reaction dynamics have been observed in the context of thermal polymorphic transitions,26–29 but have only recently been demonstrated for photochemical reactions. However, it remains unclear what factors cause a photochemical reaction to be heterogeneous on the optical length scale.
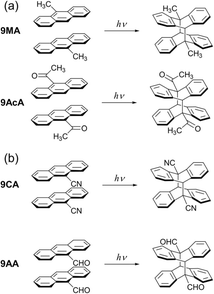
The observation of cooperative reaction kinetics (in the form of sigmoidal time behavior) and spatial reaction front propagation raises the question of whether these two phenomena are related. To address this issue, in this work we measure both the photochemical kinetics on the molecular scale and the progress of the photochemical reaction on the optical length scale for single crystals composed of anthracene derivatives. 9MA, 9-acetylanthracene (9AcA), 9-cyanoanthracene (9CA), and 9-anthraldehyde (9AA) are selected as the candidates (Fig. 1). The spatial progress of the photochemical reaction, observed under crossed Nicols using a polarized optical microscope, shows different behaviors depending on the compounds. The photochemical kinetic analysis for the change in the absorbance using the extended FW model reveals that the cooperative effect also depends greatly on the compounds. We find that the magnitude of the molecular conformational change associated with the photochemical reaction in crystals strongly correlates with both cooperative reaction kinetics and the observation of heterogeneous reaction dynamics on the optical length scale. The observation that different crystal packing motifs can give rise to very different kinetic behaviors provides a dramatic example of a novel solid-state structure–function relationship.
Experimental
Materials
9MA and 9AA were purchased from TCI and used as received. 9AcA and 9CA were purchased from Sigma-Aldrich and used as received.Preparation of single crystals
The single crystals of 9MA, 9AcA, 9CA, and 9AA were prepared as follows. As for 9MA and 9AcA, the compounds were dissolved in tetrahydrofuran (THF). Then, the solution was dropped onto water on a slide glass. After evaporation of THF and water in the dark, single crystals were obtained. In the case of 9CA and 9AA, the compounds were dissolved in THF. Then, the solution was mixed with water in a Petri dish. Then, it was left undisturbed in the dark, resulting in the crystallization due to the evaporation of THF. The face indices of the samples were determined by powder X-ray diffraction (PXRD) measurement using a Rigaku MiniFlex 600 diffractometer employing CuKα radiation (λ = 1.54184 Å).Microscopic observation of crystals
Optical microphotographs of interference color under crossed Nicols were obtained using a Nikon ECLIPSE E600POL or an Olympus BX53-P polarizing optical microscope equipped with a video camera system. Polarized absorption spectra were measured using the polarizing optical microscope equipped with a EBA JAPAN NH-2DK hyperspectral camera. The hyperspectral camera is capable of acquiring spectral information for each pixel of the captured image, but we used information averaged over about 2 μm2 to reduce errors. Light irradiation of the crystals was carried out using a super high-pressure mercury lamp (100 W; bandpass filter (405 nm light excitation)) attached to the polarizing optical microscope. The 405 nm light was applied to the entire crystal with uniform intensity. The power of the light irradiation was measured using a THORLABS PM160 optical power meter. The crystal thickness was measured using a KEYENCE VK-8700 laser scanning microscope. The interference color change accompanying the birefringence change was observed under crossed Nicols.Results and discussion
Progress of the photochemical reaction on the optical length scale
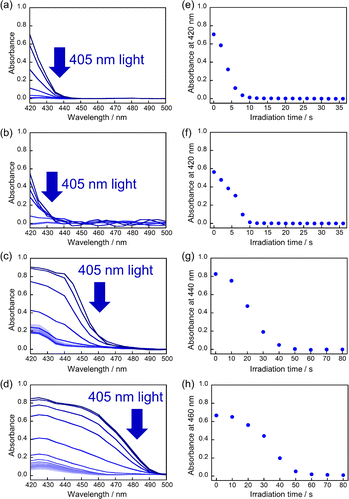
First, the single crystals of 9MA, 9AcA, 9CA, and 9AA were prepared by the procedures described in the Experimental section. The crystal thickness of the samples was in the range 1.0–3.0 μm as shown in Fig. S1.† Then, PXRD measurements were performed to characterize the molecular orientation of the single crystals (Fig. S2†). From the comparison of the experimental peaks with the calculated patterns using the CIF files (CCDC No. 1209376, 1139795, 1127855, 1103100) obtained by SCXRD measurements,30–33 the observed faces of the single crystals were determined to be the (100), (10-1), (120), and (002) faces for 9MA, 9AcA, 9CA, and 9AA, respectively (Fig. S3†).Next, we observed the single crystals of 9MA, 9AcA, 9CA, and 9AA under crossed Nicols using a polarized microscope (Fig. 2 and Movies S1–S4†). Before photoirradiation, the single crystals exhibited an interference color originating from the birefringence. The birefringence change is very sensitive to the photochemical reactions and proportional to the fractional conversion to the photoproducts.34 Therefore, observation of birefringence change during the reaction provides information about the spatial progress of the photochemical reaction.24,34,35 Upon irradiation with 405 nm light, the interference color changed as the photodimerization reaction proceeds. Interestingly, we found that there are two types of reaction progress. In the case of 9MA and 9AcA, the interference color changed uniformly across the entire crystal, i.e. homogeneously on the optical length scale. In contrast, the change in the interference color started from the edge to the center of the crystal in the case of 9CA and 9AA, indicating that the photodimerization reaction proceeded heterogeneously on the optical length scale. Note that the interference color of the single crystals of 9CA and 9AA became dark after completion of the photoreaction due to the loss of the crystallinity. In addition, we investigated the change in fluorescence intensity during photodimerization. In the case of 9MA and 9AcA, the fluorescence intensity decrease was spatially homogeneous (Movies S5 and S6†), while for 9CA and 9AA there was a clear phase front (Movies S7 and S8†). For both sets of molecules, the fluorescence evolution mirrored the change in birefringence. Thus, it was revealed that the progress of the photochemical reaction on the optical length scale depends on the compounds.
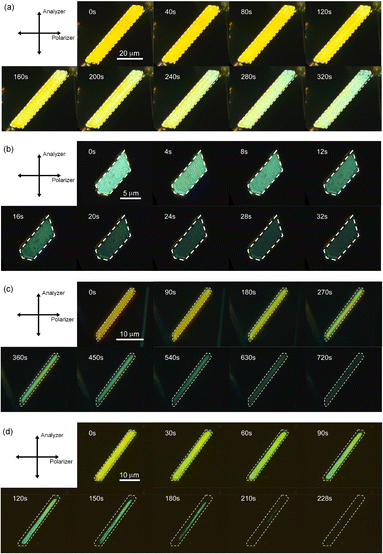 | ||
| Fig. 2 Interference color change of (a) 9MA, (b) 9AcA, (c) 9CA, and (d) 9AA single crystals observed under crossed Nicols upon irradiation with 405 nm light. | ||
Photochemical reaction kinetics on the molecular scale
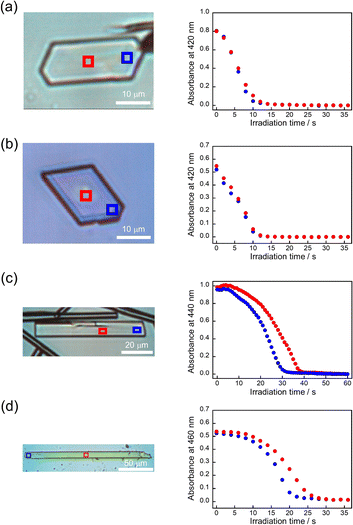
The absorbance changes due to the photodimerization reaction in single crystals of 9MA, 9AcA, 9CA, and 9AA were investigated using a hyperspectral camera that allows us to measure the absorbance changes at different spots in a single crystal. In all samples, the averaged absorbance across single crystals decreased as the photodimerization reaction proceeded (Fig. 3a–d). This is because the dimerization reaction destroys the conjugation of the anthracene ring.36Fig. 3e–h show the averaged absorbance decay profiles of 9MA, 9AcA, 9CA, and 9AA upon photoirradiation. In all cases, the decay profiles show some sigmoidal character, but those of 9CA and 9AA are much pronounced than those of 9MA and 9AcA. This suggests that the cooperative effect varies widely among the compounds.Furthermore, the absorbance decay profiles at different spatial locations in single crystals were also different depending on the compounds. In the case of 9MA and 9AcA, the absorbance change for separate spots across a single crystal were almost the same (Fig. 4a and b), whereas the absorbance attenuates first at the edges of the crystal in the case of 9CA and 9AA (Fig. 4c and d). This agrees with the results of the observation of interference color changes described above. In this way, from the results of absorbance changes at different spots, it was also confirmed that the photochemical reaction proceeds homogeneously on the optical length scale in the single crystals of 9MA and 9AcA but proceeds heterogeneously in single crystals of 9CA and 9AA.
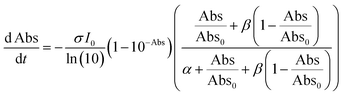
To quantitatively analyze the absorbance decay profiles, we first applied the commonly used JMAK equation (Johnson–Mehl–Avrami–Kolmogorov)37–40 (eqn (1))
| f = 1 − e−(kt)n | (1) |
Fig. S4–S6† show the results of the fitting of the change in conversion calculated from absorbance decay profiles of 9MA, 9AcA, 9CA, and 9AA with eqn (1). Note that the averaged absorbance across single crystals was used for the fitting and the fitting was performed 3 times using different samples. The parameters used for the fitting are summarized in Table 1. Fig. S7–S9† show the results of the fitting of absorbance decay in different single crystals of 9MA, 9AcA, 9CA, and 9AA. The n value ranged from 1.6–2.0 for 9MA, 1.8–2.2 for 9AcA, 2.4–2.9 for 9CA, and 2.8–3.2 for 9AA. The value of n increased sharply for 9CA and 9AA. Therefore, it can be said that the single crystals of 9AA and 9CA have a more pronounced cooperativity than those of 9AcA and 9MA.
| Sample | k (s−1) | n | |
|---|---|---|---|
| 9MA | 1 | 0.221 | 2.0 |
| 2 | 0.156 | 1.6 | |
| 3 | 0.270 | 1.8 | |
| 9AcA | 4 | 0.153 | 2.2 |
| 5 | 0.166 | 2.0 | |
| 6 | 0.146 | 1.8 | |
| 9CA | 7 | 0.039 | 2.4 |
| 8 | 0.035 | 2.9 | |
| 9 | 0.048 | 2.8 | |
| 9AA | 10 | 0.021 | 3.2 |
| 11 | 0.022 | 2.8 | |
| 12 | 0.026 | 3.2 |
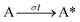
Next, to get more insights from the viewpoint of photochemistry, we applied the extended FW model that we developed previously.41,42 The extended FW model consists of four elementary reactions if A represents the monomer pair, and B the photodimer (eqn (2a)–(2d)).
 | (2a) |
 | (2b) |
 | (2c) |
 | (2d) |
 | (3) |
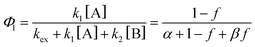 | (4a) |
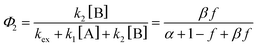 | (4b) |
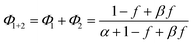 | (5) |
Note that if β = 1, Φ1+2 does not depend on f. Furthermore, as reported in our previous study, the Φ1+2,f=1/Φ1+2,f=0 is a useful quantity to parameterize the decay shape. When the value is relatively large, the curves have a definite induction period. On the other hand, as the ratio approaches unity, the curves are closer to single exponential. Therefore, we can evaluate the cooperativity quantitatively using the value of Φ1+2,f=1/Φ1+2,f=0.
Fig. S7–S9† show the results of the fitting of absorbance decay profiles in single crystals of 9MA, 9AcA, 9CA, and 9AA with eqn (3). Note that the averaged absorbance across single crystals was used for the fitting and the fitting was performed 3 times using different samples. The parameters used for the fitting are summarized in Table 2. The Φ1+2,f=1/Φ1+2,f=0 was in the range 2.8–4.6 for 9MA, 7.8–8.9 for 9AcA, 30.7–41.4 for 9CA, and 77.1–84.9 for 9AA. Thus, the value of Φ1+2,f=1/Φ1+2,f=0 increased in the order of 9MA, 9AcA, 9CA, and 9AA. This agrees with the results of the fitting using JMAK equation. Note that this trend holds for any value of σ in the range 1.5 × 10−18 to 1.5 × 10−16 cm2 per molecule, so it does not rely on the exact value of the absorption cross-section, which has some uncertainty. This analysis is more complicated than the JMAK model but provides additional parameters with clear chemical meaning. The data in Table 2 show that there is a dramatic difference between the 9MA/9AcA crystals and the 9CA/9AA crystals. In the latter crystals, the effective quantum yield increases by more than an order of magnitude as the reaction proceeds.
| Sample | α | β | Φ 1,f=0 | Φ 2,f=0 | Φ 1,f=1 | Φ 2,f=1 | Φ 1+2,f=1/Φ1+2,f=0 | |
|---|---|---|---|---|---|---|---|---|
| a σ was set to 1.5 × 10−17 cm2 per molecule. b I 0 was 3.9 × 1016 photons per cm per s. c I 0 was 2.7 × 1019 photons per cm per s. d I 0 was 1.8 × 1017 photons per cm per s. | ||||||||
| 9MA | 1 | 3.5 | 22.7 | 0.224 | 0.0 | 0.0 | 0.868 | 3.9 |
| 2 | 5.4 | 14.1 | 0.157 | 0.0 | 0.0 | 0.724 | 4.6 | |
| 3 | 2.0 | 25.6 | 0.333 | 0.0 | 0.0 | 0.928 | 2.8 | |
| 9AcA | 4 | 10.1 | 28.6 | 0.0900 | 0.0 | 0.0 | 0.739 | 8.2 |
| 5 | 10.0 | 24.7 | 0.0907 | 0.0 | 0.0 | 0.711 | 7.8 | |
| 6 | 11.5 | 29.0 | 0.0802 | 0.0 | 0.0 | 0.717 | 8.9 | |
| 9CA | 7 | 5.8 × 104 | 41.4 | 1.7 × 10−5 | 0.0 | 0.0 | 7.1 × 10−4 | 41.4 |
| 8 | 4.6 × 104 | 39.6 | 2.2 × 10−5 | 0.0 | 0.0 | 8.6 × 10−4 | 39.5 | |
| 9 | 3.5 × 104 | 30.7 | 2.9 × 10−5 | 0.0 | 0.0 | 8.9 × 10−4 | 30.7 | |
| 9AA | 10 | 1.3 × 103 | 85.7 | 7.9 × 10−4 | 0.0 | 0.0 | 6.3 × 10−2 | 80.4 |
| 11 | 1.2 × 103 | 82.3 | 8.3 × 10−4 | 0.0 | 0.0 | 6.4 × 10−2 | 77.1 | |
| 12 | 1.0 × 103 | 92.5 | 9.7 × 10−4 | 0.0 | 0.0 | 8.2 × 10−2 | 84.9 | |
Physical origin of cooperative reaction kinetics and spatially heterogeneous photochemical reactions
All crystals studied here exhibit some degree of cooperative kinetics in which the rate speeds up as the reaction proceeds. One possible explanation for this speed up could be photothermal heating that raises the crystal temperature during the illumination period. However, these crystals are only a few microns thick and are adhered to a thick glass substrate that acts as a heat sink. If we assume a thermal diffusivity of 10−7 m2 s−1,43 heat transfer across the crystal thickness occurs within milliseconds. Given the reactions occur on timescales of seconds, it is unlikely that non-equilibrated thermal gradients could build up during the observation period. It is also not clear why photothermal effects would be more pronounced for 9CA and 9AA as compared to 9MA and 9AcA. However, it would be interesting for future studies to investigate how the temperature (or heat) affects the reaction rate.To explain why the progress of the photochemical reaction on the optical length scale varies with compound, we instead focus on the molecular conformational change associated with the photodimerization reaction. In previous studies, the molecular structure and packing before and after the photodimerization reaction of 9MA, 9AcA, 9CA, and 9AA have been already reported.44–46 In the case of 9MA and 9AcA, they undergo a typical topotactic photodimerization reaction maintaining the head-to-tail packing of the monomer pair (Fig. 1a). On the other hand, 9CA and 9AA undergo an unusual photodimerization (non-topotactic) reaction that requires a large molecular conformational change from head-to-head to head-to-tail packing (Fig. 1b).47,48 It is not clear why the different substituents lead to different initial packing motifs, but we suspect that these motifs require large conformational changes for the 9CA and 9AA dimerization reactions, giving rise to their highly heterogeneous reaction kinetics.
We know that at least one 9CA/9AA molecule must flip in order to adopt the head-to-tail configuration that permits the photodimerization to occur. This can happen at defect sites, or in regions where the barrier to this flipping is much lower. Both of these conditions are more likely to occur at the crystal surface. The interior of the crystal is densely packed with monomer pairs, so dimerization requiring a large structural change, like the case of 9CA and 9AA, is unlikely to occur. Then, the dimerization of monomer pairs on the crystal surface results in the increase of the free volume of the surrounding monomer pairs, facilitating the dimerization reaction. By a series of such reactions, the photoreaction proceeds sequentially from the edge to the center of the crystal (Fig. 5). 9MA and 9AcA, on the other hand, have a head-to-tail packing that positions the molecules for facile photodimerization, so reactions in the interior occur at the same rate as those at the edges, leading to a spatially homogeneous transformation.
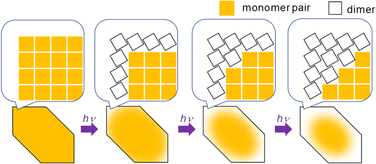 | ||
| Fig. 5 Schematic illustration of the mechanism of the heterogeneous photochemical reaction on the optical length scale. | ||
The induced defect mechanism for heterogeneous reaction dynamics can also qualitatively explain the dependence of the reaction yield on reaction progress (Table 2). If the reaction requires large rearrangements within a pristine crystal, then at the start of the reaction most of the incoming photons are “wasted” after being absorbed by molecules that cannot dimerize. Once a significant fraction has reacted and disrupted the original head-to-head lattice, molecular rotation and defects will become more widespread, and an excited molecule will be more likely to have the opportunity to dimerize. Therefore, both 9CA and 9AA require an induction period while disorder builds up in the crystal, which eventually increases the reaction quantum yield by a factor of 30-80. 9MA and 9AcA, in contrast, are already well-positioned for dimerization by the head-to-tail crystal packing, but still benefit from the reaction induced strain as the reaction proceeds. Interestingly, we found earlier that high defect densities in polycrystalline 9MA could actually slow down the reaction and lead to more sigmoidal kinetics.24 In that case, static structural disorder probably leads to misaligned 9MA pairs that must reconfigure to react, similar to the ordered packing in 9CA and 9AA, and thus leads to similar sigmoidal kinetics as well.
The results here suggest that molecular packing can be used not just to optimize the static properties of the crystalline solid (elastic modulus, conductivity) but also its dynamic behavior. This could be useful for designing stimuli-responsive materials. For example, in photomechanical crystals, the deformation is proportional to the fraction of reacted molecules. Crystals like 9MA and 9AcA, in which the molecules are pre-positioned for photodimerization, will change shape uniformly during the illumination. 9CA and 9AcA crystals, on the other hand, will require an induction period before such shape changes can occur because the build-up of product molecules requires more time. This type of delayed response could be useful to reduce the sensitivity to stray light or provide a photonic threshold for a photomechanical shape change. On the other hand, if we desire the photomechanical response to be strictly proportional to the photon dose, 9MA and 9AcA might be better candidates.
Our correlation of nonclassical kinetics and spatially heterogeneous reaction progress suggests several future research directions. First, it would be interesting to examine in greater detail what kind of molecular conformational changes give rise to the heterogeneous photochemical reaction progress. This would require investigating other types of photoresponsive molecular single crystals to determine the generality of this phenomenon. Eventually, we would like to develop a theoretical model capable of predicting both how the quantum yield evolves during the reaction and how this evolution gives rise to the heterogeneous reaction dynamics.
Conclusions
In this study, we compared and evaluated the reaction progress on the optical length scale and the photochemical reaction kinetics on the molecular scale in single crystals of four anthracene derivatives with different substituents at the 9-position. From the changes in birefringence of single crystals upon photoirradiation, it was confirmed that in 9MA and 9AcA, the photochemical reaction takes place homogeneously throughout the crystal, but in 9AA and 9CA, the photochemical reaction propagates from the edges to the center. Furthermore, the change in absorbance versus irradiation time showed different sigmoidal curves depending on the compound. Quantitative analysis of the absorbance decay profiles revealed that 9AA and 9CA have a more pronounced cooperativity in the photoreaction than those of 9AcA and 9MA. These results can be attributed to differences in the degree of molecular conformational and packing changes required for photodimerization. Namely, when the photodimerization reaction does not require large molecular packing changes (9MA and 9AcA), the photochemical reaction proceeds homogeneously throughout the crystal on the optical length scale and the photochemical reaction kinetics are close to first-order (exponential). In contrast, when the photodimerization reaction requires large molecular packing changes (9CA and 9AA), the photochemical reaction proceeds heterogeneously on the optical length scale (i.e., the photochemical reaction propagates from the edge toward the center of the crystal). This is due to the high reactivity at the crystal surface and the high cooperativity required for the photochemical reaction. Going forward, it will be important to determine what fraction of solid-state reactions support spatially heterogeneous reaction kinetics, because they may give rise to qualitatively new behavior. For example, our results suggest that it may be possible to design materials exhibiting desired functions at arbitrary timings after a stimulus is applied.Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Sogo Kataoka: investigation, formal analysis, visualization, writing – original draft; Daichi Kitagawa: conceptualization, methodology, formal analysis, project administration, resources, supervision, writing – original draft, writing – review & editing; Hikaru Sotome: formal analysis, writing – review & editing; Syoji Ito: formal analysis, writing – review & editing; Hiroshi Miyasaka: formal analysis, writing – review & editing; Christopher J. Bardeen: formal analysis, project administration, writing – review & editing; Seiya Kobatake: resources, project administration, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partly supported by JSPS KAKENHI Grant Numbers JP21K14603, JP23H01926 (D. K.), JP21H01888, JP23H03956, JP23H04877 (H. S.), JP21KK0092, JP22K19007 (S. I.), JP21H01889, JP21K18934 (H. M.), JP21H02016 (S. K.) and the U.S. National Science Foundation DMR-1810514 (C. J. B.).Notes and references
- S. P. Anthony, ChemPlusChem, 2012, 77, 518–531 CrossRef CAS.
- S.-J. Yoon, J. W. Chung, J. Gierschner, K. S. Kim, M.-G. Choi, D. Kim and S. Y. Park, J. Am. Chem. Soc., 2010, 132, 13675–13683 CrossRef CAS PubMed.
- S. Takamizawa and Y. Miyamoto, Angew. Chem., Int. Ed., 2014, 53, 6970–6973 CrossRef CAS PubMed.
- S. Takamizawa, Y. Takasaki, T. Sasaki and N. Ozaki, Nat. Commun., 2018, 9, 3984 CrossRef PubMed.
- G. Liu, J. Liu, X. Ye, L. Nie, P. Gu, X. Tao and Q. Zhang, Angew. Chem., Int. Ed., 2017, 56, 198–202 CrossRef CAS PubMed.
- P. Commins, H. Hara and P. Naumov, Angew. Chem., Int. Ed., 2016, 55, 13028–13032 CrossRef CAS PubMed.
- S. Bhunia, S. Chandel, S. K. Karan, S. Dey, A. Tiwari, S. Das, N. Kumar, R. Chowdhury, S. Mondal, I. Ghosh, A. Mondal, B. B. Khatua, N. Ghosh and C. M. Reddy, Science, 2021, 373, 321–327 CrossRef CAS PubMed.
- S. Mondal, P. Tanari, S. Roy, S. Bhunia, R. Chowdhury, A. K. Pal, A. Datta, B. Pal and C. M. Reddy, Nat. Commun., 2023, 14, 6589 CrossRef CAS PubMed.
- K. J. Msayib, D. Book, P. M. Budd, N. Chaukura, K. D. M. Harris, M. Helliwell, S. Tedds, A. Walton, J. E. Warren, M. Xu and N. B. McKeown, Angew. Chem., Int. Ed., 2009, 48, 3273–3277 CrossRef CAS PubMed.
- P. Naumov, S. Chizhik, M. K. Panda, N. K. Nath and E. Boldyreva, Chem. Rev., 2015, 115, 12440–12490 CrossRef CAS PubMed.
- W. M. Awad, D. W. Davies, D. Kitagawa, J. M. Halabi, M. B. Al-Handawi, I. Tahir, F. Tong, G. C. Alvarado, A. G. Shtukenberg, T. Alkhidir, Y. Hagiwara, M. Almehairbi, L. Lan, S. Hasebe, D. P. Karothu, S. Mohamed, H. Koshima, S. Kobatake, Y. Diao, R. Chandrasekar, H. Zhang, C. C. Sun, C. Bardeen, R. O. Al-Kaysi, B. Kahr and P. Naumov, Chem. Soc. Rev., 2023, 52, 3098–3169 RSC.
- Z. M. Png, C.-G. Wang, J. C. C. Yeo, J. J. C. Lee, N. E. Surat’man, Y. L. Tan, H. Liu, P. Wang, B. H. Tan, J. W. Xu, X. J. Loh and Q. Zhu, Mol. Syst. Des. Eng., 2023, 8, 1097–1129 RSC.
- Y. Ma, A. Zhang, X. Xue, D. Jiang, Y. Zhu and C. Zhang, Cryst. Growth Des., 2014, 14, 6101–6114 CrossRef CAS.
- M. Khalid, R. S. Ullah, M. A. Choudhary, M. N. Tahir, S. Murtaza, M. Hussain, B. Ali and Z. Ahmed, J. Mol. Struct., 2018, 1167, 57–68 CrossRef CAS.
- S. Kobatake, S. Takami, H. Muto, T. Ishikawa and M. Irie, Nature, 2007, 446, 778–781 CrossRef CAS PubMed.
- H. Koshima, K. Takechi, H. Uchimoto, M. Shiro and D. Hashizume, Chem. Commun., 2011, 47, 11423–11425 RSC.
- O. S. Bushuyev, A. Tomberg, T. Friščić and C. J. Barrett, J. Am. Chem. Soc., 2013, 135, 12556–12559 CrossRef CAS PubMed.
- T. Asahi, M. Suzuki and H. Masuhara, J. Phys. Chem. A, 2002, 106, 2335–2340 CrossRef CAS.
- J. M. McBride, B. E. Segmuller, M. D. Hollingsworth, D. E. Mills and B. A. Weber, Science, 1986, 234, 830–835 CrossRef CAS PubMed.
- N. M. Peachey and C. J. Eckhardt, J. Am. Chem. Soc., 1993, 115, 3519–3526 CrossRef CAS.
- I. Turowska-Tyrk, J. Phys. Org. Chem., 2004, 17, 837–847 CrossRef CAS.
- L. Bentea, M. A. Watzky and R. G. Finke, J. Phys. Chem. C, 2017, 121, 5302–5312 CrossRef CAS.
- J. B. Benedict and P. Coppens, J. Phys. Chem. A, 2009, 113, 3116–3120 CrossRef CAS PubMed.
- K. Morimoto, D. Kitagawa, F. Tong, K. Chalek, L. J. Mueller, C. J. Bardeen and S. Kobatake, Angew. Chem., Int. Ed., 2022, 61, e202114089 CrossRef CAS PubMed.
- K. Morimoto, D. Kitagawa, H. Sotome, S. Ito, H. Miyasaka and S. Kobatake, Angew. Chem., Int. Ed., 2022, 61, e202212290 CrossRef CAS PubMed.
- L. Li, P. Commins, M. B. Al-Handawi, D. P. Karothu, J. M. Halabi, S. Schramm, J. Weston, R. Rezgui and P. Naumov, Chem. Sci., 2019, 10, 7327–7332 RSC.
- A. Khalil, D. P. Karothu and P. Naumov, J. Am. Chem. Soc., 2019, 141, 3371–3375 CrossRef CAS PubMed.
- H. Chung, D. Dudenko, F. Zhang, G. D'Avino, C. Ruzie, A. Richard, G. Schweicher, J. Cornil, D. Beljonne, Y. Geerts and Y. Diao, Nat. Commun., 2018, 9, 278 CrossRef PubMed.
- D. W. Davies, B. Seo, S. K. Park, S. B. Shiring, H. Chung, P. Kafle, D. Yuan, J. W. Strzalka, R. Weber, X. Zhu, B. M. Savoie and Y. Diao, Nat. Commun., 2023, 14, 1304 CrossRef CAS PubMed.
- J. C. J. Bart and G. M. J. Schmidt, Isr. J. Chem., 1971, 9, 429–448 CrossRef CAS.
- K. Anderson, H. Becker, L. M. Engelhardt, L. Hansen and A. H. White, Aust. J. Chem., 1984, 37, 1337–1340 CrossRef.
- H. Rabaud and J. Clastre, Acta Crystallogr., 1959, 12, 911–915 CrossRef CAS.
- J. Trotter, Acta Crystallogr., 1959, 12, 922–928 CrossRef CAS.
- K. Morimoto, H. Tsujioka, D. Kitagawa and S. Kobatake, J. Phys. Chem. A, 2020, 124, 4732–4741 CrossRef CAS PubMed.
- K. Morimoto, H. Tsujioka, D. Kitagawa and S. Kobatake, Bull. Chem. Soc. Jpn., 2019, 92, 1299–1304 CrossRef CAS.
- A. S. Dvornikov and P. M. Rentzepis, Res. Chem. Intermed., 1996, 22, 115–128 CrossRef CAS.
- M. Bertmer, R. C. Nieuwendaal, A. B. Barnes and S. E. Hayes, J. Phys. Chem. B, 2006, 110, 6270–6273 CrossRef CAS PubMed.
- R. S. Bogadi, D. C. Levendis and N. J. Coville, J. Am. Chem. Soc., 2002, 124, 1104–1110 CrossRef CAS PubMed.
- R. Destro, E. Ortoleva, R. Soave, L. Loconte and L. Lo Presti, Phys. Chem. Chem. Phys., 2009, 11, 7181–7188 RSC.
- P. Naumov, P. Makreski, G. Petruševski, T. Runčevski and G. Jovanovski, J. Am. Chem. Soc., 2010, 132, 11398–11401 CrossRef CAS PubMed.
- T. Salzillo, S. Zaccheroni, R. G. Della Valle, E. Venuti and A. Brillante, J. Phys. Chem. C, 2014, 118, 9628–9635 CrossRef CAS.
- F. Tong, M. P. Hanson and C. J. Bardeen, Phys. Chem. Chem. Phys., 2016, 18, 31936–31945 RSC.
- W. Urbach, H. Hervet and F. Rondelez, Mol. Cryst. Liq. Cryst., 1978, 46, 209–221 CrossRef CAS.
- I. Zouev, T. Lavy and M. Kaftory, Eur. J. Org Chem., 2006, 18, 4164–4169 CrossRef.
- C. R. Theocharis and W. Jones, J. Chem. Soc., Faraday Trans., 1985, 1(81), 857–874 RSC.
- M. Ehrenberg, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1968, 24, 1123–1125 CrossRef CAS.
- D. Craig and P. Sarti-Fantoni, Chem. Commun., 1966, 742–743 RSC.
- A. Kawada and M. M. Labes, Mol. Cryst. Liq. Cryst., 1970, 11, 133–144 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Measurements of crystal thickness and powder X-ray diffraction, molecular packing diagrams in crystals, the results of fittings, and movies. See DOI: https://doi.org/10.1039/d4sc03060e |
| This journal is © The Royal Society of Chemistry 2024 |