Coherent spin-control of S = 1 vanadium and molybdenum complexes

Abstract

The burgeoning field of quantum sensing hinges on the creation and control of quantum bits. To date, the most well-studied quantum sensors are optically active, paramagnetic defects residing in crystalline hosts. We previously developed analogous optically addressable molecules featuring a ground-state spin-triplet centered on a Cr⁴⁺ ion with an optical-spin interface. In this work, we evaluate isovalent V³⁺ and Mo⁴⁺ congeners, which offer unique advantages, such as an intrinsic nuclear spin for V³⁺ or larger spin–orbit coupling for Mo⁴⁺, as optically addressable spin systems. We assess the ground-state spin structure and dynamics for each complex, illustrating that all of these spin-triplet species can be coherently controlled. However, unlike the Cr⁴⁺ derivatives, these pseudo-tetrahedral V³⁺ and Mo⁴⁺ complexes exhibit no measurable emission. Coupling absorption spectroscopy with computational predictions, we investigate why these complexes exhibit no detectable photoluminescence. These cumulative results suggest that design of future V³⁺ complexes should target pseudo-tetrahedral symmetries using bidentate or tridentate ligand scaffolds, ideally with deuterated or fluorinated ligand environments. We also suggest that spin-triplet Mo⁴⁺, and by extension W⁴⁺, complexes may not be suitable candidate optically addressable qubit systems due to their low energy spin-singlet states. By understanding the failures and successes of these systems, we outline additional design features for optically addressable V- or Mo-based molecules to expand the library of tailor-made quantum sensors.

---

Introduction

The second quantum revolution is driven by the design, creation, and control of quantum bits, or qubits, the fundamental units of quantum information processing.^1–10 Harnessing the power of quantum control, quantum sensors have provided unprecedented visualizations of nanoscale magnetic and electric fields in diverse physical environments.^11–14 In many impressive demonstrations – such as magnetic resonance of individual proteins,¹² detection of action potentials of individual neurons,¹⁵ or mapping electron flow in two-dimensional materials^16,17 – optically active, paramagnetic defects embedded in a crystalline host serve as the qubits.^3,7,18–22 The electronic structure of these color centers provides a valuable platform for quantum control. First, the ground state spin sublevels of these defects provide a two-level quantum system to act as the qubit. Crucially, the spin sublevel populations may be optically prepared into a non-thermal equilibrium state, i.e. initialized, while the spin state information may be read out using spin-dependent optical emission.^18,23 These combined features enable remote optical control and single qubit addressability, both of which are valuable features for quantum sensing technologies.^24,25

Although solid-state color centers offer incredible coherence properties and quantum control, deterministic spin localization and defect tunability remain major challenges.⁷ To complement existing top-down creation of these solid-state systems, molecular synthesis provides a bottom-up approach, offering a modular and scalable route to develop emerging quantum technologies.^5,7,26–31 To create bespoke quantum sensors, we sought to develop molecular analogues of solid-state color centers that host a similar optical-spin interface, but with their molecular nature facilitating bottom-up design and solution processibility towards specific sensor–analyte interactions.^32,33 In recapitulating this optical-spin interface, we needed (i) a ground state spin that can be coherently controlled, (ii) an electronic excited state that is ‘connected’ to this ground-state spin through a spin-selective optical process (e.g., excitation or relaxation, see ESI† for further discussion), (iii) radiative decay from the excited state to the ground state for optical readout, and (iv) a ground-state spin lifetime, or spin-lattice relaxation time (T₁), that is longer than the optical lifetime (τ_opt).³⁴ These criteria initially led us to spin-triplet (S = 1) transition metal complexes that share a similar electronic structure with optically addressable solid-state spins such as the anionic nitrogen vacancy center in diamond, divacancy defects in silicon carbide, or more similarly, tetravalent chromium (Cr⁴⁺) dopants in silicon carbide.^35–38

While these generic features provide a framework to build molecular color centers, S = 1 molecular systems pose two key challenges for spin-dependent optical readout. First, to achieve a spin-selective optical process and emission in S = 1 complexes, a ligand field that ensures that the first excited state is a spin-singlet excited state (¹ES) is desirable.³⁹ For resonant optical control (off-resonant optical control protocol addressed in the ESI†), the spin-flip transition from the ¹ES to the spin-triplet ground state (³GS) should exhibit limited vibronic coupling, allowing for both narrow optical linewidths for spin-selective optical excitation and radiative decay to the ground state.^34,40 This desired electronic structure requires a sufficiently strong ligand field around the spin-bearing metal center such that the first excited state is a ¹ES, eliminating lower energy ³ES's that provide non-radiative decay pathways.³⁹ Second, the ground-state spin must be capable of coherent control. However, the spin of S = 1 transition metal systems often cannot be coherently controlled with readily accessible microwave frequencies (i.e., 1–40 GHz). The inability to coherent drive the ground-state spin of these systems arises from both the integer spin and large zero-field splitting (ZFS) values, requiring high microwave frequencies (>95 GHz) to probe ground-state spin transitions.^41,42 This challenge may be overcome by designing orbitally non-degenerate, S = 1 ground states, wherein the spin-bearing ion resides in a (near) cubic ligand field.

Considering these design parameters, we previously demonstrated that pseudo-tetrahedral (T_d) Cr⁴⁺ molecules in a strong ligand field exhibit small ground-state ZFS values of 1.8–4.1 GHz for microwave control at X-band frequency (9–10 GHz), and an optical-spin interface.^34,40 Yet, the air-sensitivity, small spin–orbit coupling, and low percentage of nuclear spin-bearing isotopes of Cr⁴⁺-based systems may not be optimal for every sensing task. Herein, we aim to translate this combination of features from T_d Cr⁴⁺ systems into molecular hosts that offer (i) intrinsic nuclear spins, I, to serve as quantum memories for prolonged information storage,^7,43,44 and (ii) larger spin–orbit coupling for improved sensitivity to electric fields.^35,45 To that end, we turned to T_d trivalent vanadium (V³⁺) and tetravalent molybdenum (Mo⁴⁺) derivatives in the same ligand fields as their Cr⁴⁺ congeners. The vanadium-51 (i.e., ⁵¹V, I = 7/2, 99.8% abundance) center provides a potential nuclear spin memory that is intrinsically coupled to the electronic spin through hyperfine interactions,^42,46 while the Mo⁴⁺ center increases the spin–orbit coupling experienced by the electron spin, offering enhanced sensitivity of the spin Hamiltonian parameters to certain external fields through the Zeeman splitting term (e.g., strain or electric fields).^47,48 However, the metal ion substitution should substantially change both the electronic structure and spin dynamics that dictate the quantum sensor performance. To initiate our studies with these ions, we synthesized and evaluated three spin-triplet systems with V³⁺ and Mo⁴⁺ to compare with previously studied Cr⁴⁺ congeners. Coupling spectroscopic analysis with computational predictions, we evaluate how to design these systems, addressing their advantages and limitations. From these results, we suggest that reducing nearby high energy oscillators and using ligand scaffolds could enable both emission and low frequency microwave control for V³⁺ systems while Mo⁴⁺ systems may be fundamentally limited by their intrinsically low lying ¹ES.

Results and discussion

We synthesized [Li(THF)₄][V(o-tolyl)₄] (1, THF = tetrahydrofuran), Mo(o-tolyl)₄ (2),⁴⁹ and [Li(12-crown-4)₂][V(trimethylsilylmethyl)₄] (3) to directly compare with previous candidate color centers,^34,40 Cr(o-tolyl)₄ (4)⁵⁰ and Cr(trimethylsilylmethyl)₄ (5)⁵¹ (Fig. 1). Detailed synthetic procedures for 1 and 3 are outlined in the ESI† while 2, 4, and 5 were synthesized according to previously reported methods.^49–51 We also note that previous efforts to synthesize the molybdenum analogue of Cr(trimethylsilylmethyl)₄ resulted in the hexakis(trimethylsilylmethyl)dimolybdenum species, so we could not investigate the Mo⁴⁺ analogue of 5.^52,53

We first characterized the solid-state structure of 1 and 3 through single crystal X-ray diffraction, finding that their inner MC₄ coordination sphere remains close to ideal tetrahedral symmetry based on both the τ₄ and τ_4′ metrics (0.95–1.01).^54,552 had been previously characterized at room temperature and shows only a slight contraction in Mo–C bond lengths upon cooling to 100 K.⁴⁹ As such, these systems should exhibit relatively small, but non-zero, ZFS values. The ground-state structure may be approximated as a descent in symmetry from ideal T_d to C_2v, as discussed for [Li(THF)₄][V(mesityl)₄] and [Li(THF)₄] [V(pentachlorophenyl)₄].⁵⁶

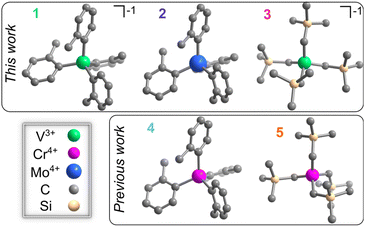Fig. 1 Molecular structures of 1, 2, 3, 4 (ref. 34), and 5 (ref. 40) determined at 100 K. Carbon, silicon, vanadium, chromium, and molybdenum given in gray, peach, green, pink, and blue, respectively. Hydrogen atoms and counter ions omitted for clarity.

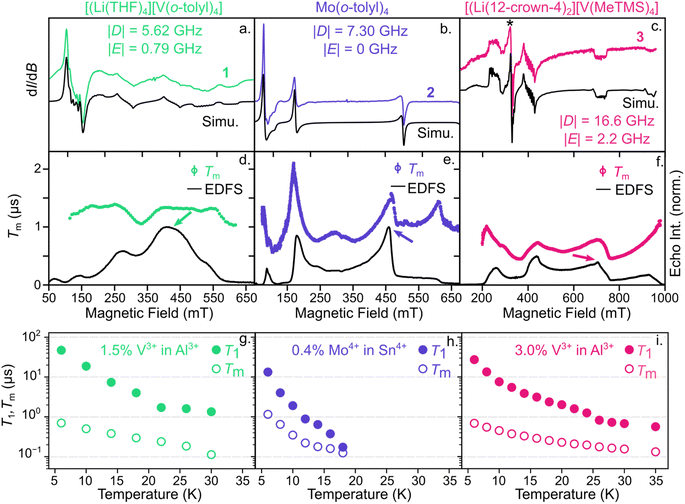
Microwave addressability remains a challenging parameter to design and tune in S = 1 compounds.^41,42 Thus, we initiated our investigation by probing the ground-state spin structure of these systems to determine if they are capable of ground-state spin control. We characterized 1–3 with both continuous-wave (cw) and pulsed electron paramagnetic resonance (EPR) to understand their ground-state spin structure and dynamics. To reduce decoherence from electron spin-electron spin interactions, we cocrystallized 1–3 in their corresponding isostructural, diamagnetic analogues, [Li(THF)₄][Al(o-tolyl)₄] (1-Al), Sn(o-tolyl)₄ (2-Sn),⁵⁷ and [Li(12-crown-4)₂][Al(trimethylsilylmethyl)₄] (3-Al), respectively (see ESI† for details). We denote the cocrystallized samples as 1′–3′ for all subsequent experiments with relative electron spin concentrations of 0.36–3% (Table S8†). From the X-band cw-EPR spectra in Fig. 2a–c, we find that the axial ZFS values, D, are larger for the V³⁺ and Mo⁴⁺ derivatives than the corresponding Cr⁴⁺ congeners.⁴⁰1′ and 2′ exhibit |D| values of 5.62 GHz and 7.3 GHz, respectively, while |D| for 4′ at 5 K is 3.63 GHz.³⁴ The largest contribution of the two-fold increase in |D| for 2′ likely arises from the increased spin–orbit coupling of the heavier Mo⁴⁺ ion, where the free ion spin–orbit coupling parameter, λ, is ∼425 and 167.5 cm⁻¹ for Mo⁴⁺ and Cr⁴⁺.⁵⁸ Given the similarity in λ for V³⁺ and Cr⁴⁺, the increase in |D| for 1′ more likely results from symmetry lowering around the V³⁺ center due to crystal packing with the [Li(THF)₄]⁺ cation. For example, |D| = 5.62 GHz for 1′ is similar to the |D| value of 5.55 GHz for Cr(o-tolyl)₄ (4) diluted in a lower symmetry (orthorhombic) host matrix.⁵⁹

Fig. 2 (top) cw-EPR spectra of (a) 1′, (b) 2′, and (c) 3′ at 5 K and 9.37–9.39 GHz with resulting D and E values. * denotes V⁴⁺ impurity in 3′, representing 1% of spin density in the sample. (middle) Magnetic field dependence of T_m (hollow symbols) at 6 K for (d) 1′, (e) 2′, and (f) 3 overlayed on the echo-detected field swept spectrum. Error bars are within the data points. (bottom) Temperature dependence of T₁ (filled circles) and T_m (hollow circles) for (g) 1′, (h) 2′, and (i) 3′ at X-band frequency and measured at the magnetic field indicated by the arrow in the (d–f).

While 1′ and 2′ show modest increases in |D| relative to their Cr⁴⁺ analogue (4′), 3′ exhibits a dramatic increase to 16.6 GHz, which is ∼13 times greater than its Cr⁴⁺ analogue (5′) where |D| = 1.23 GHz.⁴⁰ To understand this order-of-magnitude increase in |D| for 3′, we quantified the deviation from ideal T_d symmetry using the τ₄ and τ_4′ parameters^54,55 for 3′ and 5′. Between 3′ and 5′, the τ₄ and τ_4′ values vary by only 0.004 and 0.015, respectively. While these geometric deviations are small, the absolute spin splitting energies of 3′ and 5′ vary by only 63 μeV, suggesting that subtle structural changes may result in significant variations in |D|. However, variations in |D| may also arise from a convolution of competing effects, such as changes in SOC, ligand field strength, symmetry-driven coupling to excited states, and electron delocalization.^60,61 Thus, to maintain microwave addressability across diverse host media for sensing, it will be key to accurately predict and measure how growth on different surfaces or substrates affects local structure around the spin center and, consequently, |D|.⁶²

The two V³⁺ complexes, 1′ and 3′, also exhibit two advantageous features. First, the crystal symmetries of 1′ and 3′ result in non-zero transverse ZFS, |E|, values of 0.8 and 2.2 GHz, respectively. Non-zero |E| should result in clock-like transitions around zero magnetic field at frequencies of |D − E|, |D + E| and 2|E|, resulting from mixing of the M_S = +1 and −1 states (Fig. S1†).⁶³ Clock-like transitions show little variation in their transition frequency with small changes in applied magnetic field.^64,65 As a result, the clock transitions at zero magnetic field should exhibit longer coherence times, T_m, than typical Zeeman transitions, which exhibit a linear dependence on the external magnetic field.^{30,59,64–67} Second, the cw-EPR spectra in Fig. 2a and c exhibit hyperfine coupling to the ⁵¹V nucleus of 155 and 165 MHz for 1′ and 3′, respectively. Thus, the built-in ⁵¹V nuclear spin and relatively large hyperfine coupling to the electron spin provides a potential nuclear spin memory to prolong the storage time of quantum information.^44,68,69 For example, previous work with S = 1/2 V⁴⁺ as well as ¹⁷³Yb³⁺ molecular spins suggested that the coherence of strongly coupled nuclear spin may be prolonged beyond electronic spin coherence time by increasing the magnetic field strength.^46,70 As a result, both the clock-like transitions around zero field and the intrinsic nuclear spin of the V³⁺-based systems provide potential routes to lengthen coherence lifetimes.

To then determine the spin dynamics of these Mo⁴⁺ and V³⁺ systems in their isostructural matrices, we examined the temperature and magnetic field dependence on spin-lattice relaxation (T₁) and coherence (T_m) times for 1′–3′ at X-band frequency (9–10 GHz). In each case, these complexes exhibit shorter T₁ times (10–15 μs) at low temperature than 4′ or 5′, where we previously measured T₁ times of 2–3 ms at 5 K.⁴⁰ However, the concentration of both 1′ and 3′ were 1.5 and 3% in the spin-diluted lattice, which we have previously shown leads to a reduction in T₁ at low temperatures for 4′.⁴⁰ Thus, T₁ for 1′ and 3′ may likely be improved with further dilution. Notably, 1′ and 3′ exhibit T₁ times of >0.5 μs up to 30 K while 2′ shows a steep decline in T₁ < 0.5 μs by 18 K (Fig. 2g–i). These contrasting temperature dependencies likely arise from the larger spin–orbit coupling of the Mo⁴⁺-based spin centers, as well as lower energy phonon modes arising from the heavier metal center.^71,72

Turning to the T_m times, a key metric to evaluate the performance of qubit candidates, we find relatively similar temperature dependencies for 1′–3′. In general, each compound exhibits T_m times of approximately 1 μs at 6 K, likely limited by the high density of ¹H nuclei on the ligands.^23,73,74 To verify that the nuclear spin environment inhibits T_m, we also performed power-dependent Hahn-echo experiments to mitigate the influence of instantaneous diffusion from nearby paramagnetic spin centers in relatively spin concentrated samples.^64,75 We find that the T_m times of 1′ and 3′ show no significant change with decreasing power (Fig. S2†), suggesting that the nuclear spin environment of the matrix limits T_m in these samples. In contrast, the T_m time of 2′ approaches ∼2 μs at decreasing small microwave powers, which is similar to the T_m time previously measured for 4′ at similar concentrations⁴⁰ (see ESI† for further details). This analysis does not result in large increases in T_m times, indicating that coherence times reported here are likely limited by the ¹H nuclear spin environment. The T_m times then decrease with increasing temperature until the T_m times are limited by T₁. The larger spin–orbit coupling in 2′ likely leads to T₁-limited T_m times by 18 K while the V³⁺-based systems are measurable up to at least 30 K. However, both the T₁ and T_m times in 1′ and 3′ are shorter than their Cr⁴⁺ congeners, 4′ and 5′.⁴⁰ We posit that in these low field measurements, we may be either simultaneously driving multiple overlapping spin transitions (Fig. S1†) or driving a highly mixed spin transition, which has previously resulted in decreased spin-lattice relaxation times for an S = 5/2 Fe³⁺ complex.⁷⁶ However, this assertion requires a multifrequency EPR study for validation, which will be the subject of future work. Additionally, we note that the T₁ and T_m times reported here for 1′–3′ will vary substantially when measured in other matrices as the matrix tends to most strongly influence the spin dynamics of molecular qubits.⁷⁷

We further evaluate the magnetic field dependence of these T_m times. Similar to the behavior of 4′,⁴⁰ we find local maxima in T_m for 2′ at 170, 460, and 620 mT, where the applied field is parallel or perpendicular to the principal axis of the ZFS tensor (Fig. 2e). Across this field range, T_m changes by a factor of ∼4. For 1′ and 3′ where E > 0 and I = 7/2, the field dependence of T_m is less exaggerated since these systems exhibit are more transitions over a similar field range (Fig. S1†). As a result, T_m changes by less than a factor of 2 for 1′ over a similar field range to 2′. While the variation is less significant for 1′ and 3′, these data still highlight that no single value of T_m provides a complete picture of the spin relaxation, especially for anisotropic metal complexes. We similarly expect T₁ to show a strong magnetic field dependence for 1′–3′, as demonstrated with Cr(o-tolyl)₄.⁷⁸

Most importantly, even the maxima in T_m times measured here still fall well short of coherence times for state-of-the-art quantum sensors, such as anionic nitrogen vacancy centers in diamond (e.g., from 10 s to 100 s of microseconds).⁷⁹ In fact, low temperature (≤10 K) T_m times across most transition metal-based systems to date are ≤15 μs, regardless of spin state,^{30,73,77,80,81} ligand nuclear spin environment,^77,82 or magnetic field,^40,83 illustrating how the surrounding matrix promotes decoherence. Thus, introducing clock-like transitions (e.g., Fig. S1†) into molecular sensors while be critical to improve their coherence properties, and consequently their sensitivity,⁸⁴ in magnetically noisy matrices.^23,63

Turning to the excited state structure, we initially measured optical absorption spectra of these systems in solution at room temperature. The solution-phase UV-visible near-infrared spectra in Fig. 3a illustrate that the Mo⁴⁺ ion in 2 leads to both higher energy and more intense transitions than either of the first row congeners, 1 and 4. The UV-vis-NIR spectrum of 2 also appears qualitatively similar to 4, but the transitions in 2 are shifted to higher energy (Fig. S6†). This spectrum suggests that, similar to 4, the ¹ES of 2 is the lowest energy excited state, which should yield the correct energy level structure for optical-spin control.³⁴ Conversely, the V³⁺ ion in the pseudo-T_do-tolyl ligand field of 1 leads to lower energy transitions than both 2 or 4. In fact, 1 exhibits absorption extending well into the NIR, leading to substantial spectral overlap with aromatic C–H overtones (see green and blue shaded regions in Fig. 3a), which may provide a multi-phonon mediated non-radiative decay pathway.⁸⁵

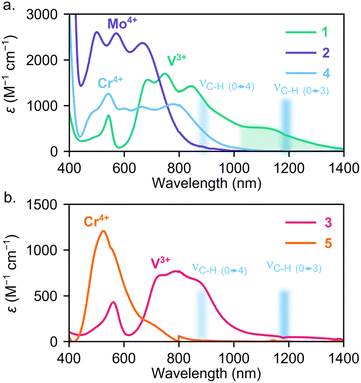Fig. 3 (a) Solution-state electronic absorption spectra of 1 and 2 compared with Cr⁴⁺ analogue, 4 (ref. 40). Green highlighted region indicates low energy absorption present for [V(aryl)₄]⁻ anions. (b) Solution-state electronic absorption spectra of 3 compared with Cr⁴⁺ analogue, 5 (ref. 40). Blue shaded region highlights energy of C–H stretching overtones that can mediate non-radiative decay.

When replacing the aryl ligands in 1 with (trimethylsilyl)methyl ligands in 3, we find that the absorption features from 1100–1400 nm are suppressed while the shorter wavelength transitions from 400–1000 nm appear similar between 1 and 3. The reduction in absorption between 1100–1400 nm for 3 suggests that either the stronger alkyl ligand field increases the transition energy of the ³ES manifold or the σ-only alkyl ligands do not mix with the lowest energy ³ES metal-centered transitions, resulting in very low oscillator strengths of the d–d transitions. We observed similar behavior in tetraaryl- and tetralkyl-Cr⁴⁺ systems. For example, 4 exhibits intense absorption between 600 and 800 nm while those transitions are present, but much weaker, for 5.⁴⁰

To determine if 1–3 exhibited emission from a ¹ES, we then performed steady-state photoluminescence measurements. When exciting pure, single-crystalline samples of 1–3 at 4 K with 660 or 785 nm excitation, we observe no emission in the range of 900–1700 nm. Even performing photoluminescence experiments on dilute single-crystalline samples of 1′–3′ or films of 5–10% (w/w) of 1–3 in polystyrene at 4 K yielded no emission. The lack of emission prevents optical readout of the ground-state spin, the essential component for molecular color centers. We sought to understand why some systems emit and other similar ones did not, to see if failure might serve as a guide for future systems.

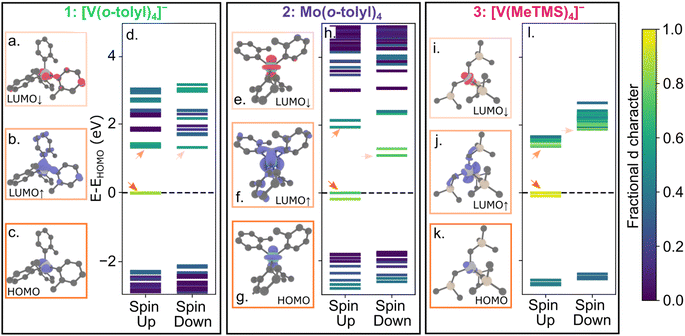
We performed spin polarized density functional theory calculations using VASP (Vienna Ab initio Simulation Package) 6.3.2 (ref. 86–89) with projector augmented wave pseudopotentials^90,91 and the PBE exchange correlation functional^92,93 (see ESI† for further details). For calculations of the charged molecules 1 and 3, we explicitly included counterions but, for clarity, we only highlight spin-bearing orbitals here. Fig. 4 shows the electronic structures of 1–3, highlighting the d character of the molecular orbitals. We visualized the highest occupied molecular orbital (HOMO) and spin up and down lowest unoccupied molecular orbital (LUMO) orbitals. Similar to 4 and 5,⁴⁰ all molecules have a HOMO and LUMO with significant d character. Thus, the qualitative picture of all five compounds is similar, yet only 4 and 5 exhibit measurable emission.

Fig. 4 Visualizations of selected molecular orbitals for 1 (a–c), 2 (e–g), and 3 (i–k). The color of the box around each molecular orbital visualization corresponds to the quantitative molecular orbital diagram for 1 (d), 2 (h), and 3 (l). The LUMO_↑ and LUMO_↓ orbitals represent the first spin-triplet (³ES) and first spin-singlet (¹ES) excited states, respectively.

To evaluate where the ¹ES lies relative to the ³GS manifold, we performed excited state calculations using the ΔSCF (delta self consistent field) method.^94,95 We calculated the ¹ES-³GS gap by subtracting the total energy of a constrained occupancy calculation, where the electron in the spin-up HOMO is promoted to the spin-down LUMO, from a standard ground-state DFT calculation (see ESI† for further details). We calculate ¹ES-³GS gaps of 0.355 eV, 0.319 eV, and 0.407 eV, eV for 1, 2, and 3, respectively. Previously, we estimated the ¹ES-³GS gap is 0.537 eV for 4 using the same methodology.⁶² Thus, the calculated ¹ES energies for 1, 2, and 3 are only 66, 59, and 76% of 4. Although these values have limited quantitative accuracy, the trend suggests that the ¹ES energy of 1 and 2 is significantly lower than 4. These results align with the expectation that the spin-pairing energetic penalty decreases with increasing ionic radii, such that the ¹ES energies should be Mo⁴⁺ < V³⁺ < Cr⁴⁺ in the same ligand field. We further find that 3 also exhibits a lower calculated ¹ES value than 4, despite the stronger alkyl ligand field of 3.

If we estimate hypothetical emission wavelengths by assuming the ratio between the calculated ¹ES and experimental emission energies is similar to 4, where calculated ¹ES/emission energy = 0.537/1.209 eV,^34,62 we find that 1, 2, and 3 would emit at roughly 1550, 1800, and 1400 nm. Considering this wavelength range, the lack of measurable emission may therefore be rationalized by four possible effects. First, any photons emitted at longer wavelengths than 1700 nm are outside of the range of commercially available InGaAs NIR detectors that are optimal for typical NIR emission measurements. Second, if any emission occurs in the measurement window, the higher strain sensitivity of 1–3 with lower symmetry or larger spin orbit couplings could result in broader emission than Cr⁴ derivatives, resulting in fewer photons counted per pixel in the CCD measurements, rendering the measurement less sensitive. Third, the posited lower energy ¹ES (≫1200 nm) may exhibit significant spectral overlap with high energy C–H stretching overtones (e.g., Fig. 3) that provide highly favorable non-radiative decay through multi-phonon mediated relaxation pathways. This potential explanation for the lack of emission could be ameliorated through selective deuteration or fluorination of the ligands.⁹⁶ Further experimental and theoretical studies are required to investigate this pathway. Fourth, the energy-gap law suggests that as the emissive state becomes lower in energy, non-radiative decay rates will increase.^97,98 In each compound, a combination of these effects may be operative, leading to no detectable emission. Based on the literature and our studies of similar compounds, we hypothesize that the C–H overtones are critical for quenching emission in this energy region.^96,99–101 These results suggest a pathway forward for the design of molecular color centers featuring depleted C–H modes for compounds that emit in the near-IR or telecom region.

Designing emissive V³⁺ systems with a microwave addressable ground-state spin

The aggregate of these results provides us with a series of new S = 1 molecules featuring coherent control over their ground-state spin and a set of design principles for next generation quantum sensors. Previous data illustrate that emissive V³⁺ systems may be achieved using trigonal bipyramidal or octahedral geometries.^102,103 However, trigonal bipyramidal or octahedral geometries with d² metal ions result in either a non-cubic (e.g., C_3v, D_3h) symmetry or an orbitally degenerate (³T₂) ground state, respectively. These features result in |D| values that well exceed frequencies of conventional microwave sources, making their ground-state spin control more challenging. Thus, we attempted to unify the emissive nature of five and six coordinate V³⁺ with the low |D| values of pseudo-T_d by introducing the V³⁺ ion into sufficiently strong ligand fields. However, we never observed emission for V³⁺ systems, even with the strong-field alkyl donors of 3. These results suggest that a stronger ligand field should be enforced through a rigid ligand coordination with, for example, C₃ symmetric ligand scaffolds (e.g. tris(pyridyl)methane, tris(N-heterocyclic carbene)borate) or C₂-symmetric bidentate ligand scaffolds (e.g. 1,1′-binaphthyl-2,2′-diamine).¹⁰⁴ Notably, increased rigidity is often ascribed to improved radiative efficiency of Cr³⁺ systems.⁹⁶ However, the hard nature and high charge of early transition metals likely necessitates using suitably hard, anionic ligand donors, precluding the use of softer strong field ligands such as phosphines. Additionally, the lower energy transitions in V³⁺ systems likely undergo rapid non-radiative decay mediated by nearby C–H groups. Thus, the spectral overlap of these modes with excited states may be mitigated through deuteration or fluorination, also demonstrated with Cr³⁺ systems to greatly enhance emission.^96,99,100 A similar approach may be employed with future systems to realize emission from these V³⁺ systems that feature generally small (e.g., <30 GHz) |D| values.

Designing emissive Mo/W systems with microwave addressable ground-state spin

In contrast to the V³⁺ analogues, Mo⁴⁺-based systems pose a unique challenge. The energy gap between the ¹ES and ³GS is generally quite small given the large size of the Mo⁴⁺ center. Additionally, to unlock the full potential of large spin–orbit coupling from the Mo⁴⁺ center to achieve enhanced sensitivities of the spin to electric field perturbations, the ion should sit in a polar molecular symmetry, such as C_3v.⁴⁵ For Mo⁴⁺ systems, these symmetries may simply yield an S = 0 complexes or prohibitively large |D| values. Thus, for Mo- and even W-based quantum sensors, an alternative spin-state may be better suited to enable strong spin-electric field coupling.^47,105 For example, Mo⁵⁺S = 1/2 defects in silicon carbide have demonstrated NIR emission¹⁰⁶ and may be capable of coherent optical control, similar to anionic tin vacancies in diamond.¹⁰⁷ Thus, future investigations with S = 1/2 Mo⁵⁺/W⁵⁺ systems may provide a more suitable framework to achieve a ground-state spin capable of coherent control connected to an emissive optical state than the S = 1 derivatives with second or third row metal ions.

Conclusions

In this work, we examined the electronic structure and spin dynamics of three novel V³⁺ and Mo⁴⁺ molecular color center candidates that could feature valuable spectroscopic handles for sensing. Notably, each system showed appropriately small ground-state anisotropy for coherent spin control. We demonstrated this control over a series of molecules, including a rare example of spin control in a second row transition metal with a spin-triplet ground state. We also suggest that the transverse anisotropy (i.e., |E| > 0) and nuclear spin of the V³⁺ analogues may offer two avenues to extend quantum coherence. Despite these potential advantageous features, none of the systems investigated here exhibited measurable emission, likely resulting from a combination of a low energy ¹ES and rapid non-radiative decay mediated by the C–H-rich ligand environment. Coupling experimental and computational insight, we suggest that the use of ligand scaffolds and deuteration/fluorination may result in emissive V³⁺ while maintaining ground-state spin control, while larger transition metal ions, such as Mo and W, in S = 1/2 states may be better suited for optical-spin control. Thus, we offer design considerations that will hopefully lead to the realization of V- or Mo-based molecular quantum sensors in future studies.

Data availability

The data underlying this work are available at https://doi.org/10.5281/zenodo.12794616. CCDC codes: 1 (2334908), 2 at 100 K (2334909), 3 (2334912), 1-Al (2334910), and 3-Al (2334911).

Author contributions

D. W. L., L. R. W., S. L. B., P. D. performed the experimental measurements. K. R. M. performed the computations. D. W. L. synthesized the compounds. D. D. A., J. M. R. and D. E. F. advised on all efforts. All authors contributed to the data analysis and manuscript preparation.

Conflicts of interest

The authors declare the following competing financial interests: D. W. L., S. L. B., D. E. F., and D. D. A. are inventors on patent application no. 63008589 submitted by the University of Chicago that covers chemically tunable optically addressable molecular-spin qubits and associated methods. S. L. B., P. D., D. W. L., D. E. F., and D. D. A. are inventors on patent application No. 22-T121 by the University of Chicago that covers enhancing quantum properties of optically addressable molecular qubits through host-matrix engineering.

Acknowledgements

We thank Dr Peter Mintun and Dr Berk Kovos for scientific discussion and comments on the manuscript. We thank Dr Yifan Quan and Rebecca Sponenburg for experimental assistance with pulsed EPR experiments and ICP-OES analysis, respectively. D. W. L. and D. E. F gratefully acknowledge support from the US Army Research Office under award number W911NF2010088 for the synthesis and design of new molecular color centers. This work used resources at the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231 using NERSC Award No. BES-ERCAP0020980. S. L. B. acknowledges support from UK Research and Innovation [grant number MR/W006928/1]. L. R. W. acknowledges the support from the University of Chicago/Advanced Institute for Materials Research Joint Research Center. Creating these molecules supports the work of Q-NEXT, one of the U.S. Department of Energy Office of Science National Quantum Information Science Research Centers, and will enable integration of these molecules into a larger quantum ecosystem. Work on magnetic dilution of these molecules, as a pathway for thin layer deposition was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under Award No. DE-SC0019356. This work made use of the IMSERC Crystallography facility at Northwestern University, which has received support from the Soft and Hybrid Nanotechnology Experimental (SHyNE) Resource (NSF ECCS-2025633), and Northwestern University. For the purpose of open access, the authors have applied a Creative Commons Attribution (CC BY) license to any Author Accepted Manuscript version arising from this submission.

References

1. L. M. K. Vandersypen, H. Bluhm, J. S. Clarke, A. S. Dzurak, R. Ishihara, A. Morello, D. J. Reilly, L. R. Schreiber and M. Veldhorst, Interfacing Spin Qubits in Quantum Dots and Donors—Hot, Dense, and Coherent, Npj Quantum Inf., 2017, 3, 1–10.
2. R. Li, L. Petit, D. P. Franke, J. P. Dehollain, J. Helsen, M. Steudtner, N. K. Thomas, Z. R. Yoscovits, K. J. Singh, S. Wehner, L. M. K. Vandersypen, J. S. Clarke and M. Veldhorst, A Crossbar Network for Silicon Quantum Dot Qubits, Sci. Adv., 2018, 4, eaar3960.
3. B. C. Rose, D. Huang, Z. H. Zhang, A. M. Tyryshkin, S. Sangtawesin, S. Srinivasan, L. Loudin, M. L. Markham, A. M. Edmonds, D. J. Twitchen, S. A. Lyon and N. P. de Leon, Observation of an Environmentally Insensitive Solid State Spin Defect in Diamond, Science, 2018, 361, 60–63.
4. E. J. Davis, G. Bentsen, L. Homeier, T. Li and M. H. Schleier-Smith, Photon-Mediated Spin-Exchange Dynamics of Spin-1 Atoms, Phys. Rev. Lett., 2019, 122, 10405.
5. M. Atzori and R. Sessoli, The Second Quantum Revolution: Role and Challenges of Molecular Chemistry, J. Am. Chem. Soc., 2019, 141, 11339–11352.
6. M. Kjaergaard, M. E. Schwartz, J. Braumüller, P. Krantz, J. I. J. Wang, S. Gustavsson and W. D. Oliver, Superconducting Qubits: Current State of Play, Annu. Rev. Condens. Matter Phys., 2020, 11, 369–395.
7. D. D. Awschalom, R. Hanson, J. Wrachtrup and B. B. Zhou, Quantum Technologies with Optically Interfaced Solid-State Spins, Nat. Photonics, 2018, 12, 516–527.
8. A. M. Ferrenti, N. P. de Leon, J. D. Thompson and R. J. Cava, Identifying Candidate Hosts for Quantum Defects via Data Mining, npj Comput. Mater., 2020, 6, 2–7.
9. I. Harris, C. J. Ciccarino, J. Flick, D. R. Englund and P. Narang, Group-III Quantum Defects in Diamond Are Stable Spin-1 Color Centers, Phys. Rev. B, 2020, 102, 195206.
10. H. S. Zhong, H. Wang, Y. H. Deng, M. C. Chen, L. C. Peng, Y. H. Luo, J. Qin, D. Wu, X. Ding, Y. Hu, P. Hu, X. Y. Yang, W. J. Zhang, H. Li, Y. Li, X. Jiang, L. Gan, G. Yang, L. You, Z. Wang, L. Li, N. L. Liu, C. Y. Lu and J. W. Pan, Quantum Computational Advantage Using Photons, Science, 2020, 370, 1460–1463.
11. F. Shi, Q. Zhang, P. Wang, H. Sun, J. J. Wang, X. Rong, M. Chen, C. Ju, F. Reinhard, H. Chen, J. Wrachtrup, J. J. Wang and J. Du, Single-Protein Spin Resonance Spectroscopy under Ambient Conditions, Science, 2015, 347, 1135–1138.
12. I. Lovchinsky, A. O. Sushkov, E. Urbach, N. P. de Leon, S. Choi, K. De Greve, R. Evans, R. Gertner, E. Bersin, C. Müller, L. McGuinness, F. Jelezko, R. L. Walsworth, H. Park and M. D. Lukin, Nuclear Magnetic Resonance Detection and Spectroscopy of Single Proteins Using Quantum Logic, Science, 2016, 351, 836–841.
13. A. A. Clerk, K. W. Lehnert, P. Bertet, J. R. Petta and Y. Nakamura, Hybrid Quantum Systems with Circuit Quantum Electrodynamics, Nat. Phys., 2020, 16, 257–267.
14. D. D. Awschalom, C. R. Du, R. He, F. Joseph Heremans, A. Hoffmann, J. Hou, H. Kurebayashi, Y. Li, L. Liu, V. Novosad, J. Sklenar, S. E. Sullivan, D. Sun, H. Tang, V. Tyberkevych, C. Trevillian, A. W. Tsen, L. R. Weiss, W. Zhang, X. Zhang, L. Zhao and C. H. W. Zollitsch, Quantum Engineering With Hybrid Magnonic Systems and Materials, IEEE Trans. Quantum Eng., 2021, 2, 5500836.
15. J. F. Barry, M. J. Turner, J. M. Schloss, D. R. Glenn, Y. Song, M. D. Lukin, H. Park and R. L. Walsworth, Optical Magnetic Detection of Single-Neuron Action Potentials Using Quantum Defects in Diamond, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 14133–14138.
16. M. J. H. Ku, T. X. Zhou, Q. Li, Y. J. Shin, J. K. Shi, C. Burch, L. E. Anderson, A. T. Pierce, Y. Xie, A. Hamo, U. Vool, H. Zhang, F. Casola, T. Taniguchi, K. Watanabe, M. M. Fogler, P. Kim, A. Yacoby and R. L. Walsworth, Imaging Viscous Flow of the Dirac Fluid in Graphene, Nature, 2020, 583, 537–541.
17. U. Vool, A. Hamo, G. Varnavides, Y. Wang, T. X. Zhou, N. Kumar, Y. Dovzhenko, Z. Qiu, C. A. C. Garcia, A. T. Pierce, J. Gooth, P. Anikeeva, C. Felser, P. Narang and A. Yacoby, Imaging Phonon-Mediated Hydrodynamic Flow in WTe₂, Nat. Phys., 2021, 17, 1216–1220.
18. F. J. Heremans, C. G. Yale and D. D. Awschalom, Control of Spin Defects in Wide-Bandgap Semiconductors for Quantum Technologies, Proc. IEEE, 2016, 104, 2009–2023.
19. M. W. Doherty, N. B. Manson, P. Delaney, F. Jelezko, J. Wrachtrup and L. C. L. Hollenberg, The Nitrogen-Vacancy Colour Centre in Diamond, Phys. Rep., 2013, 528, 1–45.
20. D. J. Christle, A. L. Falk, P. Andrich, P. V. Klimov, J. U. Hassan, N. T. Son, E. Janzén, T. Ohshima and D. D. Awschalom, Isolated Electron Spins in Silicon Carbide with Millisecond Coherence Times, Nat. Mater., 2015, 14, 160–163.
21. S. Chen, M. Raha, C. M. Phenicie, S. Ourari and J. D. Thompson, Parallel Single-Shot Measurement and Coherent Control of Solid-State Spins below the Diffraction Limit, Science, 2020, 370, 592–595.
22. P. Siyushev, K. Xia, R. Reuter, M. Jamali, N. Zhao, N. Yang, C. Duan, N. Kukharchyk, A. D. Wieck, R. Kolesov and J. Wrachtrup, Coherent Properties of Single Rare-Earth Spin Qubits, Nat. Commun., 2014, 5, 1–6.
23. G. Wolfowicz, F. J. Heremans, C. P. Anderson, S. Kanai, H. Seo, A. Gali, G. Galli and D. D. Awschalom, Quantum Guidelines for Solid-State Spin Defects, Nat. Rev. Mater., 2021, 6, 906–925.
24. D. P. DiVincenzo, The Physical Implementation of Quantum Computation, Fortschr. Phys., 2000, 48, 771–783.
25. C. L. Degen, F. Reinhard and P. Cappellaro, Quantum Sensing, Rev. Mod. Phys., 2017, 89, 1–39.
26. T. Yamabayashi, M. Atzori, L. Tesi, G. Cosquer, F. Santanni, M. E. Boulon, E. Morra, S. Benci, R. Torre, M. Chiesa, L. Sorace, R. Sessoli and M. Yamashita, Scaling Up Electronic Spin Qubits into a Three-Dimensional Metal-Organic Framework, J. Am. Chem. Soc., 2018, 140, 12090–12101.
27. A. M. Ariciu, D. H. Woen, D. N. Huh, L. E. Nodaraki, A. K. Kostopoulos, C. A. P. Goodwin, N. F. Chilton, E. J. L. McInnes, R. E. P. Winpenny, W. J. Evans and F. Tuna, Engineering Electronic Structure to Prolong Relaxation Times in Molecular Qubits by Minimising Orbital Angular Momentum, Nat. Commun., 2019, 10, 1–8.
28. I. Cimatti, L. Bondì, G. Serrano, L. Malavolti, B. Cortigiani, E. Velez-Fort, D. Betto, A. Ouerghi, N. B. Brookes, S. Loth, M. Mannini, F. Totti and R. Sessoli, Vanadyl Phthalocyanines on Graphene/SiC(0001): Toward a Hybrid Architecture for Molecular Spin Qubits, Nanoscale Horiz., 2019, 4, 1202–1210.
29. S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Electrically Driven Nuclear Spin Resonance in Single-Molecule Magnets, Science, 2014, 344, 1135–1138.
30. J. M. Zadrozny, A. T. Gallagher, T. D. Harris and D. E. Freedman, A Porous Array of Clock Qubits, J. Am. Chem. Soc., 2017, 139, 7089–7094.
31. C. J. Yu, M. D. Krzyaniak, M. S. Fataftah, M. R. Wasielewski and D. E. Freedman, A Concentrated Array of Copper Porphyrin Candidate Qubits, Chem. Sci., 2019, 10, 1702–1708.
32. M. S. Fataftah and D. E. Freedman, Progress towards Creating Optically Addressable Molecular Qubits, Chem. Commun., 2018, 54, 13773–13781.
33. C. J. Yu, S. Von Kugelgen, D. W. Laorenza and D. E. Freedman, A Molecular Approach to Quantum Sensing, ACS Cent. Sci., 2021, 7, 712–723.
34. S. L. Bayliss, D. W. Laorenza, P. J. Mintun, B. Diler, D. E. Freedman and D. D. Awschalom, Optically Addressable Molecular Spins for Quantum Information Processing, Science, 2020, 370, 1309–1312.
35. R. Schirhagl, K. Chang, M. Loretz and C. L. Degen, Nitrogen-Vacancy Centers in Diamond: Nanoscale Sensors for Physics and Biology, Annu. Rev. Phys. Chem., 2014, 65, 83–105.
36. A. L. Falk, B. B. Buckley, G. Calusine, W. F. Koehl, V. V. Dobrovitski, A. Politi, C. A. Zorman, P. X. L. Feng and D. D. Awschalom, Polytype Control of Spin Qubits in Silicon Carbide, Nat. Commun., 2013, 4, 1–7.
37. W. F. Koehl, B. Diler, S. J. Whiteley, A. Bourassa, N. T. Son, E. Janzén and D. D. Awschalom, Resonant Optical Spectroscopy and Coherent Control of Cr⁴⁺, Phys. Rev. B, 2017, 95, 035207.
38. B. Diler, S. J. Whiteley, C. P. Anderson, G. Wolfowicz, M. E. Wesson, E. S. Bielejec, F. Joseph Heremans and D. D. Awschalom, Coherent Control and High-Fidelity Readout of Chromium Ions in Commercial Silicon Carbide, Npj Quantum Inf., 2020, 6, 11.
39. N. B. Figgis and A. Hitchman, M. Tanabe-Sugano Diagrams, in Ligand Field Theory and Its Applications, Wiley-VCH, New York, 2000, pp 131–141.
40. D. W. Laorenza, A. Kairalapova, S. L. Bayliss, T. Goldzak, S. M. Greene, L. R. Weiss, P. Deb, P. J. Mintun, K. A. Collins, D. D. Awschalom, T. C. Berkelbach and D. E. Freedman, Tunable Cr⁴⁺ Molecular Color Centers, J. Am. Chem. Soc., 2021, 143, 21350–21363.
41. J. Krzystek, J. H. Park, M. W. Meisel, M. A. Hitchma, H. Stratemeier, L. C. Brunel and J. Telser, EPR Spectra from “EPR-Silent” Species: High-Frequency and High-Field EPR Spectroscopy of Pseudotetrahedral Complexes of Nickel(II), Inorg. Chem., 2002, 41, 4478–4487.
42. J. Krzystek, A. Ozarowski, J. Telser and D. C. Crans, High-Frequency and -Field Electron Paramagnetic Resonance of Vanadium(IV, III, and II) Complexes, Coord. Chem. Rev., 2015, 301–302, 123–133.
43. P. Neumann, R. Kolesov, B. Naydenov, J. Beck, F. Rempp, M. Steiner, V. Jacques, G. Balasubramanian, M. L. Markham, D. J. Twitchen, S. Pezzagna, J. Meijer, J. Twamley, F. Jelezko and J. Wrachtrup, Quantum Register Based on Coupled Electron Spins in a Room-Temperature Solid, Nat. Phys., 2010, 6, 249–253.
44. A. Ruskuc, C.-J. Wu, J. Rochman, J. Choi and A. Faraon, Nuclear Spin-Wave Quantum Register for a Solid-State Qubit, Nature, 2022, 602, 408–413.
45. F. Dolde, H. Fedder, M. W. Doherty, T. Nöbauer, F. Rempp, G. Balasubramanian, T. Wolf, F. Reinhard, L. C. L. Hollenberg, F. Jelezko and J. Wrachtrup, Electric-Field Sensing Using Single Diamond Spins, Nat. Phys., 2011, 7, 459–463.
46. S. Chicco, A. Chiesa, G. Allodi, E. Garlatti, M. Atzori, L. Sorace, R. De Renzi and S. Carretta, Controlled Coherent Dynamics of [VO(TPP)], a Prototype Molecular Nuclear Qudit with an Electronic Ancilla, Chem. Sci., 2021, 12, 12046–12055.
47. J. Liu, J. Mrozek, W. K. Myers, G. A. Timco, R. E. P. Winpenny, B. Kintzel, W. Plass and A. Ardavan, Electric Field Control of Spins in Molecular Magnets, Phys. Rev. Lett., 2019, 122, 37202.
48. Z. Liu, Y. Wang, Y. Fang, S. Qin, Z. Wang, S. Jiang and S. Gao, Electric Field Manipulation Enhanced by Strong Spin-Orbit Coupling: Promoting Rare-Earth Ions as Qubits, Natl. Sci. Rev., 2020, 7, 1557–1563.
49. J. Arnold, G. Wilkinson, B. Hussain and M. B. Hursthouse, Synthesis and X-Ray Crystal Structure of Tetra (2- Methylphenyl)Molybdenum(IV), Mo(2-MeC₆H₄)₄. Redox Chemistry of M(2-MeC₆H₄)₄ Compounds of Molybdenum Rhenium, Ruthenium, and Osmium, J. Chem. Soc., Dalton Trans., 1989, 2149–2153.
50. S. U. Koschmieder, B. S. McGilligan, G. McDermott, J. Arnold, G. Wilkinson, B. Hussain-Bates and M. B. Hursthouse, Aryl and Aryne Complexes of Chromium, Molybdenum, and Tungsten. X-Ray Crystal Structures of [Cr(2-MeC₆H₄)(μ-2-MeC₆H₄)(PMe₃)]₂, Mo(η²-2-MeC₆H₃)(2-MeC₆H₄)2(PMe₂Ph)₂, and W(η²-2,5-Me₂C₆H₂)(2,5-Me₂C₆H₃)₂-(PMe₃)₂, J. Chem. Soc., Dalton Trans., 1990,(11), 3427–3433.
51. C. Schulzke, D. Enright, H. Sugiyama, G. LeBlanc, S. Gambarotta, G. P. A. Yap, L. K. Thompson, D. R. Wilson and R. Duchateau, The Unusual Stability of Homoleptic Di- and Tetravalent Chromium Alkyls, Organometallics, 2002, 21, 3810–3816.
52. B. F. Huq, W. Mowat, A. Shortland, A. C. Skapski and G. Wilkinson, Crystal Structure of Hexakis (Trimethylsilylmethyl) Dimolybdenum, J. Chem. Soc. D, 1971, 1079–1080.
53. W. Mowat, A. Shortland, G. Yagupsky, N. J. Hill, M. Yagupsky and G. Wilkinson, Elimination Stabilized Alkyls. Part I. Chromium, Molybdenum, Tungsten, and Vanadium, J. Chem. Soc., Dalton Trans., 1972, 533–542.
54. L. Yang, D. R. Powell and R. P. Houser, Structural Variation in Copper(i) Complexes with Pyridylmethylamide Ligands: Structural Analysis with a New Four-Coordinate Geometry Index, T4, J. Chem. Soc., Dalton Trans., 2007,(9), 955–964.
55. A. Okuniewski, D. Rosiak, J. Chojnacki and B. Becker, Coordination Polymers and Molecular Structures among Complexes of Mercury(II) Halides with Selected 1-Benzoylthioureas, Polyhedron, 2015, 90, 47–57.
56. P. J. Alonso, J. Forniés, M. A. García-Monforte, A. Martín and B. Menjón, New Homoleptic Organometallic Derivatives of Vanadium(III) and Vanadium(IV): Synthesis, Characterization, and Study of Their Electrochemical Behaviour, Chem.–Eur. J., 2005, 11, 4713–4724.
57. C. Schneider-Koglin, B. Mathiasch and M. Dräger, Über Tetraaryl-Methan-Analoga in Der Gruppe 14. III. Ar₄Sn/Pb (Ar Ph, p-, m-, o-Tol, 2,4-Xyl Und 2,5-Xyl): Gegenüberstellung von Bindungslängen Und Winkeln, von NMR Chemischen Verschiebungen Und Kopplungskonstanten Und von Schwingungsdaten, J. Organomet. Chem., 1994, 469, 25.
58. B. N. Figgis and M. A. Hitchman, Spin-Orbit Coupling Constants, Ligand Field Theory and Its Applications, Wiley-VCH, New York, 2000, pp 108–110.
59. S. L. Bayliss, P. Deb, D. W. Laorenza, M. Onizhuk, G. Galli, D. E. Freedman and D. D. Awschalom, Enhancing Spin Coherence in Optically Addressable Molecular Qubits through Host-Matrix Control, Phys. Rev. X, 2022, 12, 031028.
60. S. Ye, F. Neese, A. Ozarowsk, D. Smirnov, J. Krzystek, J. Telser, J. H. Liao, C. H. Hung, W. C. Chu, Y. F. Tsai, R. C. Wang, K. Y. Chen and H. F. Hsu, Family of V(III)-Tristhiolato Complexes Relevant to Functional Models of Vanadium Nitrogenase: Synthesis and Electronic Structure Investigations by Means of High-Frequency and -Field Electron Paramagnetic Resonance Coupled to Quantum Chemical Computations, Inorg. Chem., 2010, 49, 977–988.
61. C. V. Stappen, D. Maganas, S. Debeer, E. Bill and F. Neese, Investigations of the Magnetic and Spectroscopic Properties of V (III) and V (IV) Complexes, Inorg. Chem., 2018, 57, 6421–6438.
62. K. R. Mullin, D. W. Laorenza, D. E. Freedman and J. M. Rondinelli, Quantum Sensing of Magnetic Fields with Molecular Color Centers, Phys. Rev. Res., 2023, 5, 1–9.
63. M. Onizhuk, K. C. Miao, J. P. Blanton, H. Ma, C. P. Anderson, A. Bourassa, D. D. Awschalom and G. Galli, Probing the Coherence of Solid-State Qubits at Avoided Crossings, PRX Quantum, 2021, 2, 010311.
64. G. Wolfowicz, A. M. Tyryshkin, R. E. George, H. Riemann, N. V. Abrosimov, P. Becker, H. J. Pohl, M. L. W. Thewalt, S. A. Lyon and J. J. L. Morton, Atomic Clock Transitions in Silicon-Based Spin Qubits, Nat. Nanotechnol., 2013, 8, 561–564.
65. K. C. Miao, J. P. Blanton, C. P. Anderson, A. Bourassa, A. L. Crook, G. Wolfowicz, H. Abe, T. Ohshima and D. D. Awschalom, Universal Coherence Protection in a Solid-State Spin Qubit, Science, 2020, 369, 1493–1497.
66. M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Enhancing Coherence in Molecular Spin Qubits via Atomic Clock Transitions, Nature, 2016, 531, 348–351.
67. K. Kundu, J. R. K. White, S. A. Moehring, J. M. Yu, J. W. Ziller, F. Furche, W. J. Evans and S. Hill, A 9.2-GHz Clock Transition in a Lu(II) Molecular Spin Qubit Arising from a 3,467-MHz Hyperfine Interaction, Nat. Chem., 2022, 14, 392–397.
68. G. Wolfowicz, C. P. Anderson, B. Diler, O. G. Poluektov, F. J. Heremans and D. D. Awschalom, Vanadium Spin Qubits as Telecom Quantum Emitters in Silicon Carbide, Sci. Adv., 2020, 6, eaaz1192.
69. C. E. Bradley, J. Randall, M. H. Abobeih, R. C. Berrevoets, M. J. Degen, M. A. Bakker, M. Markham, D. J. Twitchen and T. H. Taminiau, A Ten-Qubit Solid-State Spin Register with Quantum Memory up to One Minute, Phys. Rev. X, 2019, 9, 031045.
70. R. Hussain, G. Allodi, A. Chiesa, E. Garlatti, D. Mitcov, A. Konstantatos, K. S. Pedersen, R. De Renzi, S. Piligkos and S. Carretta, Coherent Manipulation of a Molecular Ln-Based Nuclear Qudit Coupled to an Electron Qubit, J. Am. Chem. Soc., 2018, 140, 9814–9818.
71. P. L. Scott and C. D. Jeffries, Spin-Lattice Relaxation in Some Rare-Earth Salts at Helium Temperatures; Observation of the Phonon Bottleneck, Phys. Rev., 1962, 127, 32–51.
72. M. Briganti, F. Santanni, L. Tesi, F. Totti, R. Sessoli and A. Lunghi, A Complete Ab Initio View of Orbach and Raman Spin-Lattice Relaxation in a Dysprosium Coordination Compound, J. Am. Chem. Soc., 2021, 143, 13633–13645.
73. A. Ardavan, O. Rival, J. J. L. Morton, S. J. Blundell, A. M. Tyryshkin, G. A. Timco and R. E. P. Winpenny, Will Spin-Relaxation Times in Molecular Magnets Permit Quantum Information Processing?, Phys. Rev. Lett., 2007, 98, 057201.
74. A. Bourassa, C. P. Anderson, K. C. Miao, M. Onizhuk, H. Ma, A. L. Crook, H. Abe, J. Ul-Hassan, T. Ohshima, N. T. Son, G. Galli and D. D. Awschalom, Entanglement and Control of Single Nuclear Spins in Isotopically Engineered Silicon Carbide, Nat. Mater., 2020, 19, 1319–1325.
75. S. Von Kugelgen, M. D. Krzyaniak, M. Gu, D. Puggioni, J. M. Rondinelli, M. R. Wasielewski and D. E. Freedman, Spectral Addressability in a Modular Two Qubit System, J. Am. Chem. Soc., 2021, 143, 8069–8077.
76. J. M. Zadrozny, M. J. Graham, M. D. Krzyaniak, M. R. Wasielewski and D. E. Freedman, Unexpected Suppression of Spin-Lattice Relaxation via High Magnetic Field in a High-Spin Iron(III) Complex, Chem. Commun., 2016, 52, 10175–10178.
77. J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, Millisecond Coherence Time in a Tunable Molecular Electronic Spin Qubit, ACS Cent. Sci., 2015, 1, 488–492.
78. N. P. Kazmierczak, K. M. Luedecke, E. T. Gallmeier and R. G. Hadt, T1 Anisotropy Elucidates Spin Relaxation Mechanisms in an S = 1 Cr(IV) Optically Addressable Molecular Qubit, J. Phys. Chem. Lett., 2023, 14, 7658–7664.
79. E. Bauch, S. Singh, J. Lee, C. A. Hart, J. M. Schloss, M. J. Turner, J. F. Barry, L. M. Pham, N. Bar-Gill, S. F. Yelin and R. L. Walsworth, Decoherence of Ensembles of Nitrogen-Vacancy Centers in Diamond, Phys. Rev. B, 2020, 102, 134210.
80. M. J. Amdur, K. R. Mullin, M. J. Waters, D. Puggioni, M. K. Wojnar, M. Gu, L. Sun, P. H. Oyala, J. M. Rondinelli and D. E. Freedman, Chemical Control of Spin-Lattice Relaxation to Discover a Room Temperature Molecular Qubit, Chem. Sci., 2022, 13, 7034–7045.
81. S. Lenz, H. Bamberger, P. P. Hallmen, Y. Thiebes, S. Otto, K. Heinze and J. Van Slageren, Chromium(III)-Based Potential Molecular Quantum Bits with Long Coherence Times, Phys. Chem. Chem. Phys., 2019, 21, 6976–6983.
82. C. E. Jackson, C. Y. Lin, S. H. Johnson, J. Van Tol and J. M. Zadrozny, Nuclear-Spin-Pattern Control of Electron-Spin Dynamics in a Series of V(IV) Complexes, Chem. Sci., 2019, 10, 8447–8454.
83. C. E. Jackson, C.-Y. Lin, J. van Tol and J. M. Zadrozny, Orientation Dependence of Phase Memory Relaxation in the V(IV) Ion at High Frequencies, Chem. Phys. Lett., 2020, 739, 137034.
84. J. F. Barry, J. M. Schloss, E. Bauch, M. J. Turner, C. A. Hart, L. M. Pham and R. L. Walsworth, Sensitivity Optimization for NV-Diamond Magnetometry, Rev. Mod. Phys., 2020, 92, 15004.
85. W. Robert, K. Johannes and M. Katja, Spin-flip Luminescence, Photochem. Photobiol. Sci., 2022, 21, 1309–1331.
86. G. Kresse and J. Hafner, Ab Initio Molecular Dynamics for Liquid Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
87. G. Kresse and J. Hafner, Ab Initio Molecular-Dynamics Simulation of the Liquid-Metal-Amorphous-Semiconductor Transition in Germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
88. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
89. G. Kresse and J. Furthmüller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6, 15–50.
90. G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
91. P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
92. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
93. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1997, 78, 1396.
94. J. Gavnholt, T. Olsen, M. Engelund and J. Schiøtz, Δ Self-Consistent Field Method to Obtain Potential Energy Surfaces of Excited Molecules on Surfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 75441.
95. A. Hellman, B. Razaznejad and B. I. Lundqvist, Potential-Energy Surfaces for Excited States in Extended Systems, J. Chem. Phys., 2004, 120, 4593–4602.
96. S. Otto, M. Dorn, C. Förster, M. Bauer, M. Seitz and K. Heinze, Understanding and Exploiting Long-Lived near-Infrared Emission of a Molecular Ruby, Coord. Chem. Rev., 2018, 359, 102–111.
97. R. Englman and J. Jortner, The Energy Gap Law for Radiationless Transitions in Large Molecules, Mol. Phys., 1970, 18, 285–287.
98. T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Spin-Vibronic Mechanism for Intersystem Crossing, Chem. Rev., 2018, 118, 6975–7025.
99. C. Wang, S. Otto, M. Dorn, E. Kreidt, J. Lebon, L. Sršan, P. Di Martino-Fumo, M. Gerhards, U. Resch-Genger, M. Seitz and K. Heinze, Deuterated Molecular Ruby with Record Luminescence Quantum Yield, Angew. Chem., Int. Ed., 2018, 57, 1112–1116.
100. C. Wegeberg and O. S. Wenger, Luminescent First-Row Transition Metal Complexes, JACS Au, 2021, 1, 1860–1876.
101. O. S. Wenger, Photoactive Complexes with Earth-Abundant Metals, J. Am. Chem. Soc., 2018, 140, 13522–13533.
102. M. S. Fataftah, S. L. Bayliss, D. W. Laorenza, X. Wang, B. T. Phelan, C. B. Wilson, P. J. Mintun, B. D. Kovos, M. R. Wasielewski, S. Han, M. S. Sherwin, D. D. Awschalom and D. E. Freedman, Trigonal Bipyramidal V³⁺ Complex as an Optically Addressable Molecular Qubit Candidate, J. Am. Chem. Soc., 2020, 142, 20400–20408.
103. M. Dorn, J. Kalmbach, P. Boden, A. Päpcke, S. Gómez, C. Förster, F. Kuczelinis, L. M. Carrella, L. A. Büldt, N. H. Bings, E. Rentschler, S. Lochbrunner, L. González, M. Gerhards, M. Seitz and K. Heinze, A Vanadium(III) Complex with Blue and NIR-II Spin-Flip Luminescence in Solution, J. Am. Chem. Soc., 2020, 142, 7947–7955.
104. D. Riegert, J. Collin, J. C. Daran, T. Fillebeen, E. Schulz, D. Lyubov, G. Fukin and A. Trifonov, Neutral Yttrium Tris(Amide) and Ate Complexes Coordinated by an (R)-N,N′-Diisopropyl-1,1′-Binaphthyl-2,2′-Diamido Ligand as Enantioselective Catalysts for Intramolecular Hydroamination, Eur. J. Inorg. Chem., 2007,(8), 1159–1168.
105. V. N. Golovach, M. Borhani and D. Loss, Electric-Dipole-Induced Spin Resonance in Quantum Dots, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 1–10.
106. T. Bosma, G. J. J. Lof, C. M. Gilardoni, O. V. Zwier, F. Hendriks, B. Magnusson, A. Ellison, A. Gällström, I. G. Ivanov, N. T. Son, R. W. A. Havenith and C. H. van der Wal, Identification and Tunable Optical Coherent Control of Transition-Metal Spins in Silicon Carbide, Npj Quantum Inf., 2018, 4, 48.
107. R. Debroux, C. P. Michaels, C. M. Purser, N. Wan, M. E. Trusheim, J. Arjona Martínez, R. A. Parker, A. M. Stramma, K. C. Chen, L. De Santis, E. M. Alexeev, A. C. Ferrari, D. Englund, D. A. Gangloff and M. Atatüre, Quantum Control of the Tin-Vacancy Spin Qubit in Diamond, Phys. Rev. X, 2021, 11, 041041.

---

Footnote

† Electronic supplementary information (ESI) available: Full experimental details, crystallographic data for 1-3, 1-Al, and 3-Al, additional EPR, optical, electrochemistry, and computational data and discussion. CCDC 2334908–2334912. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4sc03107e

---