Open Access Article
Open Access Article2D organic nanosheets of self-assembled guanidinium derivative for efficient single sodium-ion conduction: rationalizing morphology editing and ion conduction†
Anik Kumar
Dey
 ab,
Sam Sankar
Selvasundarasekar
c,
Subrata
Kundu
*c,
Amal Kumar
Mandal
ab,
Sam Sankar
Selvasundarasekar
c,
Subrata
Kundu
*c,
Amal Kumar
Mandal
 *ab,
Amitava
Das
*ab,
Amitava
Das
 *d and
Sumit Kumar
Pramanik
*d and
Sumit Kumar
Pramanik
 *ab
*ab
aAnalytical and Environmental Science Division and Centralized Instrument Facility, CSIR-Central Salt and Marine Chemicals Research Institute, Bhavnagar, Gujarat 364002, India. E-mail: sumitpramanik@csmcri.res.in; akmandal@csmcri.res.in
bAcademy of Scientific and Innovative Research (AcSIR), CSIR-Human Resource Development Centre, (CSIR-HRDC) Campus, Sector 19, Kamla Nehru Nagar, Ghaziabad, Uttar Pradesh 201 002, India
cElectrochemical Process Engineering (EPE) Division, CSIR-Central Electrochemical Research Institute (CECRI), Karaikudi, Tamil Nadu 630003, India. E-mail: skundu@cecri.res.in
dDepartment of Chemical Sciences, Indian Institute of Science Education and Research Kolkata, Mohanpur, 741 246, West Bengal, India. E-mail: amitava@iiserkol.ac.in
First published on 5th September 2024
Abstract
The resurgence of interest in sodium-ion batteries (SIBs) is largely driven by their natural abundance and favourable cost, apart from their comparable electrochemical performance when compared with lithium-ion batteries (LIBs). The uneven geographic distribution of the raw materials required for LIBs has also contributed to this. The solid-state electrolyte (SSE) is typically one of the vital components for energy storage in SIBs and for achieving high electrochemical performances. SSEs are preferred over liquid electrolytes primarily due to their enhanced safety and stability, apart from the option of achieving higher energy density. A single sodium-ion selective conductor minimises dendrite formation and cell polarisation, among many other benefits over binary ionic conductors in battery operation. Here, we demonstrate the first example of a sulfonated supramolecular organic two-dimensional (2D) nanosheet as a novel class of single sodium-ion conductors prepared from the self-assembly of a functionalised guanidinium ion (AD-1). Solvent-assisted exfoliation of the bulk powder in water yielded nanosheet morphology, whereas nanotube morphology was achieved in isopropanol (IPA). In contrast, self-assembly with systematic water/IPA solvent ratio variations produced marigold, sunflower, and nanorod morphologies. Thermodynamic parameters, crystallinity, elemental composition, and varying natures of hydrogen bonding in five distinct morphologies were determined using microscopic and spectroscopic studies. The single Na+ conducting properties of each morphology are correlated in terms of morphology, crystallinity, and the solvent used to achieve that specific morphology. Importantly, with high crystallinity and directional ion channels, 2D nanosheet morphology exhibits the highest single Na+-ion conductivity of 3.72 × 10−4 S cm−1 with an activation energy of 0.28 eV, showing a moderately high Na+-ion transference number of 0.83 at room temperature without incorporating any additional sodium salts and organic solvents. This report is believed to be the first to show the significance of nanostructure morphologies in achieving high single-Na+-ion transport.
Introduction
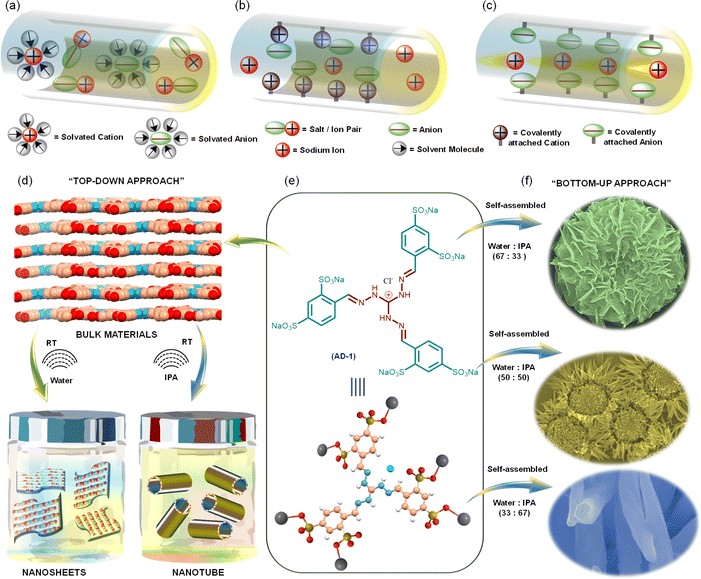
Emerging energy storage applications with increasing usage of smart portable electronics,1,2 electric vehicles,3,4 grid-level storage,5,6 and wearable soft electronics are driving the demand for safer and more energy-efficient power sources. Among various secondary batteries, lithium-ion batteries (LIBs) are the most viable ones due to their high gravimetric and volumetric energy density, high power output, and long cycling lifetime. However, unfavourable costs and uneven geographic distribution of the raw materials required for LIBs, as well as the environmental impacts associated with the LIB production process have led to the recent resurgence of SIBs. Apart from this, their physicochemical properties and similar battery chemistry make SIBs a primary alternative to LIBs.7–9 Although SIB full cells were developed in the 1980s, their practical application remained restricted due to their inferior performance in terms of energy density, rate performance, and long cycle life.10–14 Importantly, Na-ion anodes in SIBs, unlike Li-ion anodes in LIBs, use less dense aluminium rather than copper as a current collector, which contributes substantially to the total cell weight.15,16 This, together with the lower availability of copper, further drives the preference for SIBs compared with LIBs.17 Typical SIBs developed using organic liquid electrolytes suffer from liquid leakage, high volatilization and weak thermal stability, apart from the critical safety issues. These limitations have led to the development of the next generation of batteries: all-solid-state SIBs using solid-state electrolytes. Among various SSEs, electrolytes derived from tailored-made organic molecules offer the advantages of achieving stability within a certain electrochemical window, sufficiently high ionic conductivity, and favourable compatibility with various electrode materials.18,19Polymer-based SSEs like poly(ethylene oxide) (PEO),20–22 polyethylene glycol (PEG),23,24 and poly(vinylidene fluoride) (PVDF)25,26 can create a smoother interfacial surface with electrodes by employing an effective film-formation mechanism. However, their low ionic conductivity, low transference numbers, and narrow electrochemical windows restrain their practical application.27–31 Most of the earlier studies on SSEs used solvent or sodium salt in the framework, where both cations and counter anions are mobile species.32–34 The presence of free solvent molecules solvated the ions and, as a result, decreased the ion conductivity (Fig. 1a–c). Since the movement of cations is strongly connected with Lewis basic sites in the framework, anions typically move at least four times faster than cations. In the case of added salt, sodium ions contribute a small fraction of the overall ionic current.
Apart from this, free mobile anions collect at the interface between the electrode and electrolyte as there is no electrode reaction for anions, resulting in cell polarization and limited cycle life. To overcome such limitations, developing novel single Na-ion conductors is crucial. Recent knowledge based on supramolecular chemistry, binding synthons and building blocks has unfolded new options for designing unique supramolecular structures having properties that are otherwise unachievable. Self-assembled organic nanosheets (SONs) have drawn a lot of interest as a novel material for use as SSEs.35 Some critical features of SONs, like flexibility in the design and synthesis of purpose-driven target molecules for tuning the ion conductivity and reversible noncovalent interactions for tweaking mechanical strength make them an important class of materials for designing efficient SSEs. Despite their significance, systematic exploration in terms of the design of monomers and convenient preparation methods to attain SONs utilizing various noncovalent interactions during the self-assembly process remains challenging. Recently, we have reported an easy and facile self-assembly approach for preparing different nanostructures with a three-fold cationic guanidinium derivative.35–38 A self-assembled organic nanosheet of the zwitterionic form of this guanidinium derivative was used as a solid-state lithium-ion conductor with an ion conductivity of 5.14 × 10−4 S cm−1.38 To further improve the ion conductivity (3.42 × 10−4 S cm−1), we systematically altered the size and location of the directional channels with positional isomers in the SON framework. However, the presence of free anions in the framework resulted in an unsatisfactory lithium ion transference number (tLi+ = 0.49). It has been suggested recently that porous crystalline ion conductors can increase their ion transfer number by incorporating Lewis acidic frameworks. In some cases, the use of cationic or anionic frameworks has been explored to improve conductivity and transference numbers. To guarantee consistent ionic conductivity, they nevertheless continued to add free salts or organic solvents, which prevented them from achieving solid-state single-ion conduction behaviour.
Herein, we present a sodium sulfonated three-fold symmetric cationic guanidinium derivative (denoted as AD-1) as a new class of single Na-ion conductors (Fig. 1a–c). We anticipate two critical ideas for structural design: (1) the integration of the cationic guanidinium unit in the structure escalates ion-pair dissociation, enhancing Na-ion conductivity and the transference number and (2) the adroit design helps in maintaining the subtle balance between directional hydrogen bonding and cation–π interaction during the self-assembly process to achieve diverse nanostructured morphologies with well-defined directional channels for ion conduction. In the “top–down” approach, ultrasound-induced liquid-phase exfoliation of the bulk powder of AD-1 in water was used to generate free-standing nanosheet morphology, while nanotube morphology was achieved in isopropanol (IPA) (Fig. 1d). In the “bottom–up” approach, systematic variation of solvent polarity in a mixed solvent system (water/IPA, v/v) was used to prepare diverse flower shaped morphology through the self-assembly of AD-1 (Fig. 1f). The thermodynamic parameters and the association constant for this morphology evolution, through the delicate balance of multiple supramolecular interactions, were evaluated by variable temperature UV-vis spectroscopy and other standard characterization techniques. Finally, the resulting nanostructured morphologies were used to measure single Na-ion conduction at room temperature. Amon nanosheet, nanotube, and flower shaped morphologies, nanosheets display the highest single Na-ion conductivity (3.72 × 10−4 S cm−1) with a Na-ion transference number of 0.83 at 298 K. Presumably, this is the first demonstration that highlights an efficient strategy, articulates the structural design and explains the role of morphology in achieving exceptionally high single Na-ion conductivity in solvent-free SSEs.
Results and discussion
The purpose-built molecule AD-1 includes a positively charged guanidium ion having C3-symmetry, covalently coupled to three peripheral benzo-sodium sulfonated groups. The role of benzo-sodium sulfonated groups is to form hydrogen bonding and π–π stacking interactions in a concerted fashion during the self-assembly process. The central guanidinium unit was chosen due to its ability to form directional hydrogen bonds and to favour repulsive interlayer interactions during the exfoliation process.35–38 Sodium sulfonated tripodal guanidium derivate AD-1 was synthesized in a two-step reaction as outlined in the ESI (ESI, Fig. S1 and S2).† Most of the standard characterization details of the synthesized compounds are provided in ESI, Fig. S3–S9.† The elemental composition of AD-1 was confirmed by X-ray photoelectron spectroscopy (XPS). All elements were present in the XPS survey plot (ESI, Fig. S10†). High-resolution XPS spectra of C 1s were deconvoluted into three peaks at 284.8 eV, 286.0 eV, and 290.1 eV, which correspond to –C–C– and –C–S– and –C–N–, respectively. High-resolution XPS spectra unveil peaks with binding energies of 400.6 eV, 531.6 eV, and 1071.7 eV corresponding to core-level spectra of N 1s, O 1s, and Na 1s, respectively. High-resolution spectra of Cl 2p were deconvoluted into two peaks at 197.7 eV and 199.3 eV, which correspond to Cl 2p3/2 and Cl 2p1/2 states, respectively. XPS spectra of S 2p were deconvoluted into two peaks at 167.9 eV and 169.1 eV, which correspond to 2p3/2 of –S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O– and 2p1/2 of –S
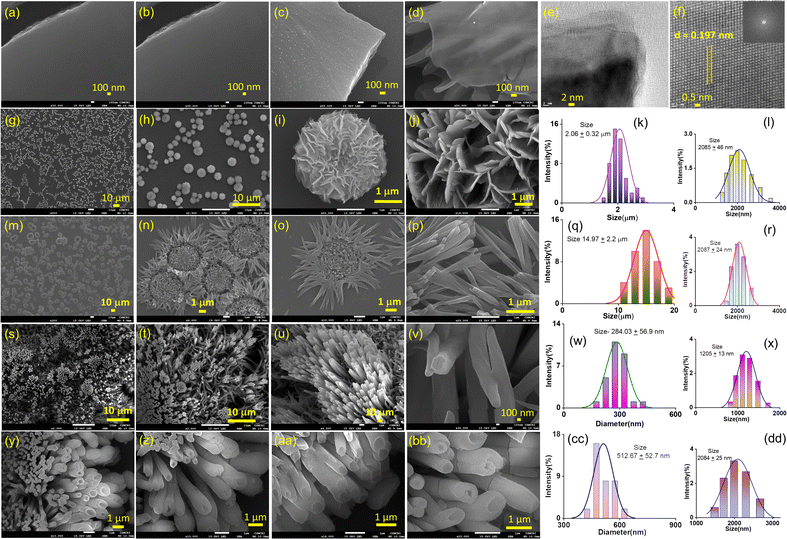
O– and 2p1/2 of –S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–, respectively (ESI, Fig. S11†). To prepare nanostructure morphology, in the “top–down” approach, the bulk powder of AD-1 was sonicated in water and isopropanol (IPA) for ten minutes, followed by thirty minutes of standing (ESI page 12†). A transverse component of ultrasonic waves can overcome weak interlayer connections between the layered structures of bulk AD-1 during this liquid-phase exfoliation process. Accordingly, the layers are gradually peeled off and assembled into the preferred morphology. An aliquot of this suspension in water produced nanosheet morphology, whereas in IPA, it produced nanotube morphology. Transmission electron microscopy images (TEM) and field-emission scanning electron microscopy (FE-SEM) images display the formation of large sheet-like structures in the order of several micrometres for nanosheet morphology (Fig. 2a–f). A high-resolution TEM image of the nanosheets reveals an ordered orientation of visible lattice fringes, with a measured lattice spacing of approximately 0.197 nm (Fig. 2f). Clear phases were seen in the corresponding selected area electron diffraction (SAED) pattern, indicating that nanosheets are highly crystalline (ESI, Fig. S13a†).
O–, respectively (ESI, Fig. S11†). To prepare nanostructure morphology, in the “top–down” approach, the bulk powder of AD-1 was sonicated in water and isopropanol (IPA) for ten minutes, followed by thirty minutes of standing (ESI page 12†). A transverse component of ultrasonic waves can overcome weak interlayer connections between the layered structures of bulk AD-1 during this liquid-phase exfoliation process. Accordingly, the layers are gradually peeled off and assembled into the preferred morphology. An aliquot of this suspension in water produced nanosheet morphology, whereas in IPA, it produced nanotube morphology. Transmission electron microscopy images (TEM) and field-emission scanning electron microscopy (FE-SEM) images display the formation of large sheet-like structures in the order of several micrometres for nanosheet morphology (Fig. 2a–f). A high-resolution TEM image of the nanosheets reveals an ordered orientation of visible lattice fringes, with a measured lattice spacing of approximately 0.197 nm (Fig. 2f). Clear phases were seen in the corresponding selected area electron diffraction (SAED) pattern, indicating that nanosheets are highly crystalline (ESI, Fig. S13a†).
Fig. 2y–bb reveals the FE-SEM images of nanotube morphology produced from exfoliation in IPA with an average tube diameter of 512.67 ± 52.7 nm. To establish a correlation between this morphology evolution from nanosheets to nanotubes, we have systematically varied the water/IPA content to produce nanostructures through the “bottom–up” self-assembly approach. In this process, a solution of AD-1 in water was exposed to varying amounts of IPA while maintaining a constant final concentration. To finish the automatic self-assembly process, the solution was thoroughly mixed and left undisturbed for around thirty minutes. Fig. 2g–j display the FE-SEM images of an aliquot of these suspensions after being drop-cast onto the silicon wafer surface. Self-assembly in the 67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 v/v water/IPA solvent system produced a marigold flower-like morphology (Fig. 2g–j). Detailed examination revealed that the collective alignment of nanosheet like petals growing radially from one centre produced this marigold flower-like structure with an average size of 2.06 ± 0.32 μm (Fig. 2k). A sunflower-like morphology with an average size of 14.97 ± 2.20 μm was created by self-assembly in a 50
33 v/v water/IPA solvent system produced a marigold flower-like morphology (Fig. 2g–j). Detailed examination revealed that the collective alignment of nanosheet like petals growing radially from one centre produced this marigold flower-like structure with an average size of 2.06 ± 0.32 μm (Fig. 2k). A sunflower-like morphology with an average size of 14.97 ± 2.20 μm was created by self-assembly in a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 v/v water/IPA solvent mixture, where nanorod-like petals extend from one centre to form this flower-like structure (Fig. 2q). Self-assembly in the 33
50 v/v water/IPA solvent mixture, where nanorod-like petals extend from one centre to form this flower-like structure (Fig. 2q). Self-assembly in the 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 v/v water/IPA solvent system produced vertically aligned nanorod morphology with an average diameter of 284.03 ± 56.9 nm (Fig. 2w). Dynamic light scattering measurements confirmed the dispersion with size distributions of 1.2–4.0 μm and 1.0–3.0 μm with average sizes of 2.08 ± 0.46 μm and 2.09 ± 0.24 μm for the as prepared marigold and sunflower-like morphologies, respectively (Fig. 2l and r). Likewise, for the as prepared nanorod and nanotube morphologies, size distributions of 0.8–2.0 μm and 1.5–3.0 μm with average sizes of 1.2 ± 0.13 μm and 2.08 ± 0.25 μm, respectively, were perceived (Fig. 2x and dd). The colloidal stability of all these nanostructures was visually confirmed by the clear Tyndall scattering of laser light.
67 v/v water/IPA solvent system produced vertically aligned nanorod morphology with an average diameter of 284.03 ± 56.9 nm (Fig. 2w). Dynamic light scattering measurements confirmed the dispersion with size distributions of 1.2–4.0 μm and 1.0–3.0 μm with average sizes of 2.08 ± 0.46 μm and 2.09 ± 0.24 μm for the as prepared marigold and sunflower-like morphologies, respectively (Fig. 2l and r). Likewise, for the as prepared nanorod and nanotube morphologies, size distributions of 0.8–2.0 μm and 1.5–3.0 μm with average sizes of 1.2 ± 0.13 μm and 2.08 ± 0.25 μm, respectively, were perceived (Fig. 2x and dd). The colloidal stability of all these nanostructures was visually confirmed by the clear Tyndall scattering of laser light.
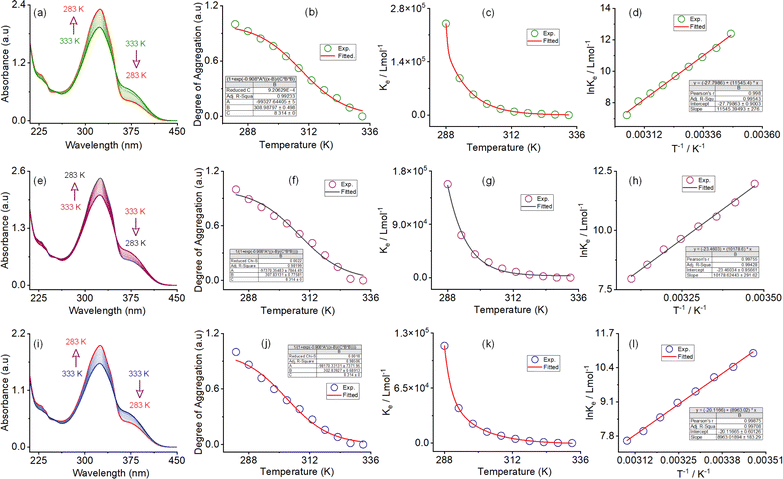
The self-assembly process in the IPA/water solvent system was systematically monitored by UV-vis spectroscopy. Upon increasing the percentage of IPA in water, the absorption maximum was decreased at 325 nm, with a simultaneous appearance of a new peak at 375 nm. The trend of spectral changes, with a distinct isosbestic point at 350 nm, indicates the transformation of the monomeric state to a self-assembled state with increasing IPA content. The thermodynamic parameters for this morphology evolution through the self-assembly process were evaluated using temperature-dependent UV-vis spectroscopy upon cooling the solution from 333 K to 283 K at a cooling rate of 5 K per five minutes (Fig. 3). In the self-assembly process in the 67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 v/v water/IPA solvent system, a continuous decrease in the absorbance maximum was found at 228 nm and 325 nm upon cooling. At the same time, the absorbance at 245 nm and 375 continuously increased. Three distinct isosbestic points at 239, 253, and 350 nm in the spectrum change trend indicate that the cooling process transforms the monomeric state into an aggregate state (Fig. 3a, ESI, Fig. S14†). A similar type of spectral trend was observed for the self-assembly process in the 50
33 v/v water/IPA solvent system, a continuous decrease in the absorbance maximum was found at 228 nm and 325 nm upon cooling. At the same time, the absorbance at 245 nm and 375 continuously increased. Three distinct isosbestic points at 239, 253, and 350 nm in the spectrum change trend indicate that the cooling process transforms the monomeric state into an aggregate state (Fig. 3a, ESI, Fig. S14†). A similar type of spectral trend was observed for the self-assembly process in the 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 v/v water/IPA and 33
50 v/v water/IPA and 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 v/v water/IPA solvent systems, upon cooling. The unique characteristics of the change in absorbance at 375 nm and the degree of aggregation (αagg) as a function of temperature are indicative of an isodesmic aggregation process, for all three self-assembly processes (Fig. 3b, f and j). By fitting the degree of aggregation with the thermal isodesmic aggregation model, aggregation association constants (Kiso) at different temperatures were found (Fig. 3c, g and k). The aggregation association constants (Kiso) of 5.4 × 104 M−1, 3.9 × 104 M−1, and 2.2 × 104 M−1 were estimated at 303 K for the self-assembly process in the 67
67 v/v water/IPA solvent systems, upon cooling. The unique characteristics of the change in absorbance at 375 nm and the degree of aggregation (αagg) as a function of temperature are indicative of an isodesmic aggregation process, for all three self-assembly processes (Fig. 3b, f and j). By fitting the degree of aggregation with the thermal isodesmic aggregation model, aggregation association constants (Kiso) at different temperatures were found (Fig. 3c, g and k). The aggregation association constants (Kiso) of 5.4 × 104 M−1, 3.9 × 104 M−1, and 2.2 × 104 M−1 were estimated at 303 K for the self-assembly process in the 67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 v/v; 50
33 v/v; 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 v/v and 33
50 v/v and 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 v/v water/IPA solvent systems. The van't Hoff plot of the reciprocal temperature and the logarithm of (Kiso) yielded the thermodynamic parameters for the three self-assembly processes (Fig. 3d, h and l). For the 67
67 v/v water/IPA solvent systems. The van't Hoff plot of the reciprocal temperature and the logarithm of (Kiso) yielded the thermodynamic parameters for the three self-assembly processes (Fig. 3d, h and l). For the 67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 v/v water/IPA solvent system, the standard enthalpy (ΔH0) and entropy (ΔS0) were estimated to be −95.98 (±0.2) kJ mol−1 and −231.1 (±0.9) J mol−1 K−1, respectively. Similarly, standard enthalpies of −84.62 (±0.2) kJ mol−1 and −74.51 (±0.1) kJ mol−1, and entropies of −195.0 (±0.9) J mol−1 K−1 and −167.2 (±0.6) J mol−1 K−1, were estimated for the self-assembly process in the 50
33 v/v water/IPA solvent system, the standard enthalpy (ΔH0) and entropy (ΔS0) were estimated to be −95.98 (±0.2) kJ mol−1 and −231.1 (±0.9) J mol−1 K−1, respectively. Similarly, standard enthalpies of −84.62 (±0.2) kJ mol−1 and −74.51 (±0.1) kJ mol−1, and entropies of −195.0 (±0.9) J mol−1 K−1 and −167.2 (±0.6) J mol−1 K−1, were estimated for the self-assembly process in the 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 v/v and 33
50 v/v and 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 v/v water/IPA solvent systems, respectively. The negative values of ΔH0 and ΔS0 confirm that all three self-assembly processes are enthalpy-driven. The trend of enthalpy and entropy values further suggests that the number of solvent molecules involved in the aggregation process decreases with increasing IPA content in the self-assembly process. Apart from this, the trend of aggregation association constant indicates that the stability of the self-assembled nanostructures increases with increasing water content.
67 v/v water/IPA solvent systems, respectively. The negative values of ΔH0 and ΔS0 confirm that all three self-assembly processes are enthalpy-driven. The trend of enthalpy and entropy values further suggests that the number of solvent molecules involved in the aggregation process decreases with increasing IPA content in the self-assembly process. Apart from this, the trend of aggregation association constant indicates that the stability of the self-assembled nanostructures increases with increasing water content.
To learn more about the molecular arrangements in various nanostructures, powder X-ray diffraction (PXRD) patterns were recorded after the sedimentation of the self-assembled morphology. Well-defined, sharp Bragg peaks for nanosheet morphology confirm the materials' crystalline structure (ESI, Fig. S15†). For nanosheet morphology, d-spacing values of 9.30 Å, 4.79 Å, 3.14 Å, and 2.35 Å correspond to characteristic reflection peaks at 2θ = 9.50°, 18.51°, 28.42°, and 38.18°, respectively; these values define diffraction from (001), (002), (003) and (004) planes, signifying ordered lamellar packing.38 Interestingly, the selected area electron diffraction pattern (SAED) of the stacked nanosheets matches very well with the d-spacing values corresponding to the reflection peaks at 2θ = 42.60° and 50.51°. Furthermore, the interplanar distance of 1.97 Å from the high-resolution TEM images correlates well with the reflection peak at 2θ = 45.89° (Fig. 2f). The findings of these two methods show a strong link, which supports the lamellar packing of nanosheet frameworks and the preservation of their structure in powder form. Likewise, for the self-assembled morphology in the 67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 v/v water/IPA solvent system, the characteristic reflection peaks at 2θ = 9.41°, d = 9.39 Å (001), 2θ = 18.42°, d = 4.81 Å (002), 2θ = 28.35°, d = 3.14 Å (003) and 2θ = 38.01°, d = 2.36 Å (004) suggest the layered crystal packing (Fig. S15†). Interestingly, a 24% decrease in the peak intensity corresponds to (001) and (004) planes observed with increasing IPA contents. For the self-assembled morphology in the 50
33 v/v water/IPA solvent system, the characteristic reflection peaks at 2θ = 9.41°, d = 9.39 Å (001), 2θ = 18.42°, d = 4.81 Å (002), 2θ = 28.35°, d = 3.14 Å (003) and 2θ = 38.01°, d = 2.36 Å (004) suggest the layered crystal packing (Fig. S15†). Interestingly, a 24% decrease in the peak intensity corresponds to (001) and (004) planes observed with increasing IPA contents. For the self-assembled morphology in the 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 v/v water/IPA solvent system, characteristic reflection peaks at 2θ = 9.86°, d = 8.96 Å; 2θ = 18.89°, d = 4.69 Å, and 2θ = 28.81°, d = 3.09 Å, corresponding to diffraction of (001), (002) and (003) planes, suggest the lamellar packing of the sunflower morphology. It is noteworthy that the distinctive reflection peak associated with the (004) plane is absent, whereas a ∼54% increase in peak intensity for the (001) plane was observed compared to the nanosheet morphology. It was observed that the peaks corresponding to the (001) and (004) planes vanish when the IPA concentration (33
50 v/v water/IPA solvent system, characteristic reflection peaks at 2θ = 9.86°, d = 8.96 Å; 2θ = 18.89°, d = 4.69 Å, and 2θ = 28.81°, d = 3.09 Å, corresponding to diffraction of (001), (002) and (003) planes, suggest the lamellar packing of the sunflower morphology. It is noteworthy that the distinctive reflection peak associated with the (004) plane is absent, whereas a ∼54% increase in peak intensity for the (001) plane was observed compared to the nanosheet morphology. It was observed that the peaks corresponding to the (001) and (004) planes vanish when the IPA concentration (33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 v/v water/IPA) is increased further, while the peak intensities for the (002) and (003) planes decrease by approximately 50%. The lack of distinct, sharp Bragg peaks in IPA alone suggests that the morphology is amorphous. This was also proved by the SAED image (ESI, Fig. S13b†). This result demonstrates that the water content in the solvent system has an important role in governing the crystallinity as well as the framework structure.
67 v/v water/IPA) is increased further, while the peak intensities for the (002) and (003) planes decrease by approximately 50%. The lack of distinct, sharp Bragg peaks in IPA alone suggests that the morphology is amorphous. This was also proved by the SAED image (ESI, Fig. S13b†). This result demonstrates that the water content in the solvent system has an important role in governing the crystallinity as well as the framework structure.
We used Fourier transform infrared spectroscopy (FT-IR) as a tool to gain information about the presence of solvents and their role in H-bonding interactions in the assembled structure. When analysing the nanosheet morphology of AD-1, notable peaks corresponding to –N–H, –O–H, and –C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N functionalities were observed at 3648 cm−1, 3244 cm−1, and 1638 cm−1, respectively (ESI, Fig. S16†). Two peaks corresponding to –S
N functionalities were observed at 3648 cm−1, 3244 cm−1, and 1638 cm−1, respectively (ESI, Fig. S16†). Two peaks corresponding to –S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds were observed at 1172 cm−1 and 1108 cm−1. The –O–H peaks of the associated solvent molecule appear at 3244 cm−1, whereas the corresponding peak for bending vibration presumably merges with the –C
O bonds were observed at 1172 cm−1 and 1108 cm−1. The –O–H peaks of the associated solvent molecule appear at 3244 cm−1, whereas the corresponding peak for bending vibration presumably merges with the –C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N peak. As the morphologies change from nanosheet to nanotube, the well-defined sharpness of the peak decreases and more broad peaks appear (ESI, Fig. S16a†). This suggests that the crystallinity of the respective morphology decreases with increasing IPA content. Analysis revealed that, for nanotube morphology, a blue shift of nearly 60 cm−1 for the –N–H peak was observed. This suggests that the –NH functionality in nanosheet morphology forms stronger and well-ordered H-bonds with water molecules compared to nanotube morphology. Apart from this, the percentage transmittance (75% for nanosheets and 95% for nanotube morphology) of the broad peak responsible for the –O-H functionality increases with increasing IPA content. This suggests that more solvent–solute interactions are observed with increasing water content or more solvent molecules are entangled during the self-assembly process through H-bonds. In addition, a systematic redshift of nearly 160 cm−1 of the broad peak (∼3244 to 3396 cm−1) responsible for the –OH functionality was observed with increasing IPA content or morphology evolution from nanosheets to nanotubes. Similarly, systematic redshifts of ∼40 cm−1 and ∼24 cm−1 of the two peaks for –S
N peak. As the morphologies change from nanosheet to nanotube, the well-defined sharpness of the peak decreases and more broad peaks appear (ESI, Fig. S16a†). This suggests that the crystallinity of the respective morphology decreases with increasing IPA content. Analysis revealed that, for nanotube morphology, a blue shift of nearly 60 cm−1 for the –N–H peak was observed. This suggests that the –NH functionality in nanosheet morphology forms stronger and well-ordered H-bonds with water molecules compared to nanotube morphology. Apart from this, the percentage transmittance (75% for nanosheets and 95% for nanotube morphology) of the broad peak responsible for the –O-H functionality increases with increasing IPA content. This suggests that more solvent–solute interactions are observed with increasing water content or more solvent molecules are entangled during the self-assembly process through H-bonds. In addition, a systematic redshift of nearly 160 cm−1 of the broad peak (∼3244 to 3396 cm−1) responsible for the –OH functionality was observed with increasing IPA content or morphology evolution from nanosheets to nanotubes. Similarly, systematic redshifts of ∼40 cm−1 and ∼24 cm−1 of the two peaks for –S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O functionality were observed with the change in morphology from nanosheets to nanotubes (ESI, Fig. S16b†).
O functionality were observed with the change in morphology from nanosheets to nanotubes (ESI, Fig. S16b†).
To explore solvent interactions and assess thermal stability, we conducted Thermogravimetric Analysis (TGA) experiments for all five morphologies. Each morphology exhibited a distinct four-step degradation profile. In the nanosheet morphology, initial degradation at 143 °C indicated the loss of lattice solvent molecules, followed by degradation at 394 °C attributed to the loss of –SO3Na groups. Subsequently, a sharp degradation peak at 535 °C indicated molecular decomposition (ESI, Fig. S17a†). Similar degradation patterns were observed for the marigold and sunflower morphologies. For the marigold morphology, degradation occurred at 126 °C, 396 °C, and 548 °C, while for the sunflower morphology, losses were observed at 121 °C, 366 °C, and 502 °C (ESI, Fig. S17b and c†). The percentage of isopropanol (IPA%) did not alter the degradation pattern. In the case of nanorod morphology, degradation peaks at 139 °C, 375 °C, and 504 °C corresponded to solvent molecule loss, –SO3Na group loss, and molecular decomposition, respectively (ESI, Fig. S17d†). Similarly, trends were observed with degradation peaks at 138 °C, 372 °C, and 491 °C (ESI, Fig. S17e†). Along with this, Differential Scanning Calorimetry (DSC) data were also recorded for all the respective morphologies (ESI, Fig. S18†). DSC plots for the respective morphologies mainly displayed two endothermic peaks and one exothermic peak (Table S2†). For nanosheet morphology, the first endothermic peak was attributed to the dissociation of the associated solvent with a broad maximum at 107.7 °C. The second endothermic peak at 466 °C was attributed to the melting temperature, while the exothermic peak appeared at 364.7 °C. For all other morphologies, the exothermic and endothermic peaks are detailed in Table S2.† The sharpness of the exothermic peaks increases as we move from nanosheet to nanotube morphology. This distinct difference in the DSC profile for the various morphologies signifies that the molecular arrangements of the associated molecules in their respective morphology are different. For nanosheet morphology, the loss of solvents was observed from room temperature to 119.9 °C. The data match well with the DSC data (ESI, Fig. S18a†). From this observation, it can be concluded that the upper-use temperature of nanosheet morphology was 119.9 °C. The loss of solvents for other morphologies is detailed in Table S3.† Consequently, upper-use temperatures for marigold, sunflower, nanorod and nanotube morphologies were observed at 135.1 °C, 132.0 °C, 136.5 °C, and 135.8 °C, respectively.
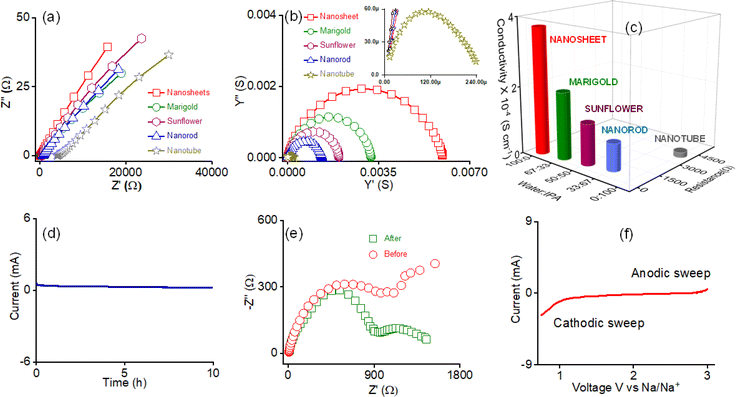
The highly crystalline phase-segregated nanostructure formed through the self-assembly of AD-1 inspired us to study the sodium ion conductivity properties. We prepared five different morphologies of AD-1, either through self-assembly or the exfoliation process in their respective solvent combinations without incorporating any additional Na-salts. The dispersed solution of the nanostructured morphologies was drop-cast on the surface of the Whatman filter membrane separator and the sample was dried at 50 °C for 2 h. The screw gauge method was used to calculate the separator's thickness (d = 0.095 cm). Following that, the dried separator was sandwiched between stainless steel electrodes. AC impedance spectroscopy was used to assess ionic conductivity in ambient settings, employing stainless-steel electrodes. The radius of the electrode surface was measured to be ∼7 mm, and the calculated area was 1.5386 cm2. A clear Warburg line can be seen in the Nyquist plots for each constructed morphology, as revealed by AC-impedance measurements, indicating that mass transfer is the main force behind a diffusion-controlled process (Fig. 4a). The charge transfer is therefore negligible. The relevant admittance plots for each morphology are displayed in Fig. 4b for easier comprehension. As the admittance plot is inversely correlated with the Z value, the kinetics approximation is predominantly concluded by observing the semicircle along with the steep line. Eventually, the formula σ = d/RA was applied to determine the associated ionic conductivity, where, d = thickness (cm), R = resistance (ohm), and A = area (cm2), respectively.
Fig. 4c displays the corresponding resistance and conductivity plots of the respective morphologies and the data are shown in Table 1. A Na-ion conductivity of 1.56 × 10−5 S cm−1 was observed for the nanotube morphology prepared in IPA. A 5-fold increase in the conductivity value of 8.11 × 10−5 S cm−1 was observed for the nanorod morphology prepared in 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 v/v water/IPA. The conductivity values of 1.22 × 10−4 S cm−1 and 1.98 × 10−4 S cm−1 for the sunflower and marigold-like flower shape morphology prepared in 33
67 v/v water/IPA. The conductivity values of 1.22 × 10−4 S cm−1 and 1.98 × 10−4 S cm−1 for the sunflower and marigold-like flower shape morphology prepared in 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 v/v and 50
67 v/v and 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 v/v water/IPA systems experienced an 8-fold and a 12-fold increase compared with the nanotube morphology. The nanosheet morphology generated in water had the maximum ion conductivity of 3.72 × 10−4 S cm−1, a 24-fold increase compared to that of the nanotube morphology. For nanosheet morphology, the activation energy was evaluated from the Arrhenius plot using data obtained from a temperature-dependent conductivity study (Fig. S19a†). It was observed that the conductivity of nanosheet morphology increases with increasing temperature (Table S5†). The activation energy (Ea) of Na-ion conductivity was analyzed from the Arrhenius plot presented in Fig. S19b.† In this case, the activation energy was found to be 0.28 eV. Interestingly, under identical conditions, a systematic upsurge in ion conductivity was observed with increasing water content in the solvent system during the preparation of the respective morphologies. Using a potentiostat polarization approach, the transference number (tNa+) was determined at room temperature to illustrate the single Na-ion conduction behaviour of the nanosheet morphology. Using the Bruce–Vincent approach, a symmetric cell Na/nanosheets/Na was built, and the DC was permitted to pass through the cell.
50 v/v water/IPA systems experienced an 8-fold and a 12-fold increase compared with the nanotube morphology. The nanosheet morphology generated in water had the maximum ion conductivity of 3.72 × 10−4 S cm−1, a 24-fold increase compared to that of the nanotube morphology. For nanosheet morphology, the activation energy was evaluated from the Arrhenius plot using data obtained from a temperature-dependent conductivity study (Fig. S19a†). It was observed that the conductivity of nanosheet morphology increases with increasing temperature (Table S5†). The activation energy (Ea) of Na-ion conductivity was analyzed from the Arrhenius plot presented in Fig. S19b.† In this case, the activation energy was found to be 0.28 eV. Interestingly, under identical conditions, a systematic upsurge in ion conductivity was observed with increasing water content in the solvent system during the preparation of the respective morphologies. Using a potentiostat polarization approach, the transference number (tNa+) was determined at room temperature to illustrate the single Na-ion conduction behaviour of the nanosheet morphology. Using the Bruce–Vincent approach, a symmetric cell Na/nanosheets/Na was built, and the DC was permitted to pass through the cell.
Solvent ratio (water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IPA) IPA) |
Morphology | Resistance (R) (ohm) | Na-ion conductivity (σ) (S cm−1) |
|---|---|---|---|
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
Nanosheet | 165.80 | 3.724 × 10−4 |
67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 33 |
Marigold | 311.58 | 1.981 × 10−4 |
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 50 |
Sunflower | 504.08 | 1.224 × 10−4 |
33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
Nanorod | 761.10 | 8.112 × 10−5 |
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
Nanotube | 3954.60 | 1.561 × 10−5 |
Fig. 4d displays the steady-state current obtained from the potentiostatic polarization study. The corresponding impedance spectra of this cell before and after the polarization study are shown in Fig. 4e. The stability plots also demonstrate the electrochemical stability of nanosheets, corresponding to reduced deterioration in this cell setup. The nanosheet morphology of AD-1 displays a sodium-ion transference number (tNa+) of 0.83 at room temperature (Table S6†). The high value of the Na-ion transference number confirms that there is no possibility of dissociation of Na-ions to dissolve in water, as previously observed for sodium salt of polystyrene sulfonate derivatives.39 Thus, in the present study, no free water is present in the framework that can help to dissolve Na-ions. Water molecules are present in the framework as a part of the structure. We conducted linear sweep voltammetry (LSV) for nanosheets of AD-1 with the Na/nanosheet/Ti asymmetric cell to examine the electrochemical stability. The sweep rate was set as 0.01 mV s−1 with a fixed voltage window (0.9 V to 3 V vs. Na/Na+) at room temperature. The identified stable anodic and cathodic behaviours suggest an electrochemical stability window of ca. 3 V for the nanosheets of AD-1 (Fig. 4f).
Improving Na-ion conductivity in solid conductors requires high Na-ion concentration and the easy mobility of these dissociated ions. The use of a cationic scaffold with a guanidinium core in the nanostructure in this study promotes the ion pair splitting to produce free mobile Na-ions. Furthermore, the directed channel formed by the nanostructured morphologies via H-bonding offers a means of transport for free ions. The increased ion conductivity of nanosheets under the same conditions compared to other morphologies suggests that coordinated solvent molecules are a significant factor influencing the conductivity value. A higher coordinated water content in the nanostructured morphologies promotes Na-ion release through hydration. The most coordinated water molecules among the various morphologies are found in nanosheets, which facilitate the production of a high concentration of hydrated Na-ions for mobility. This assertion is further supported by the thermodynamic parameter obtained from variable temperature UV-vis spectra, which show that the number of coordinated solvent molecules in the formed structure increases with increasing water percentage. In addition, the trend of the conductivity values indicates that, in contrast to other morphologies, the nanosheet morphology promotes the creation of a rigid, well-defined directional channel. PXRD and HR-TEM data also confirmed the nanosheet's highly crystalline nature compared to other morphologies. As a result, the finding shows that, among various morphologies, the greater Na-ion conductivity value for nanosheets is caused by high Na-ion concentration through hydration with coordinated water molecules and quick ionic movement through the directional channel. To the best of our knowledge, this is the first report showing such a high transference number and single Na-ion conductivity for self-assembled organic nanosheets. The observed ion conductivity value is much higher than that of recently reported solid Na-ion conductors, which either use externally added sodium salt or solvents for conductivity measurements (Fig. 5 and Table S4†).
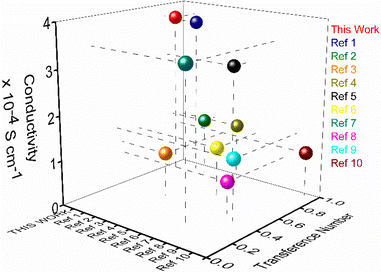 | ||
| Fig. 5 Performance comparison plot of sodium ion conductivity (room temperature) and transference number of the nanosheets of AD-1 with the reported solid sodium ion conductor (refer to ESI, Table S4†). | ||
Conclusions
In summary, we have demonstrated the efficacy of supramolecular cationic organic nanosheets as SSEs for single sodium-ion conduction. Sulfonated supramolecular organic 2D nanosheets were achieved through self-aggregation of a sulphonate-derivative of a cationic and C3-symmetric guanidinium core. The efficacy of these nanosheets as an SSE is examined. The role of the guanidinium ion as a cationic scaffold in the framework for improving the single sodium-ion conductivity is also discussed. A systematic variation in the water/IPA solvent ratio helped us in achieving three distinct morphologies; namely marigold, sunflower, and nanorod. We could establish a systematic correlation between the role of nanostructure morphologies and the solvent system responsible for achieving a specific morphology in influencing their efficiencies as an SSE. Following the top–down approach, solvent exfoliation of bulk powder produced nanosheets in water and nanotubes in IPA. Tyndall light scattering and DLS demonstrated the freestanding nature and dispersion stability. PXRD, HR-TEM, and SAED patterns identified the highly crystalline structure of the nanosheets among five distinct morphologies. The nanosheet morphology generated in water had a maximum ion conductivity of 3.72 × 10−4 S cm−1, a 24-fold increase in ion conductivity over the nanotube morphology. A sodium-ion transference number (tNa+) of 0.83 was evaluated at room temperature for nanosheet morphology. Thermodynamic parameters evaluated for the self-assembly process confirm that with an increase in the water content in the solvent system, the number of H-bonded solvent molecules in the nanostructured morphology increases. Finally, the single Na-ion conducting properties were explored for all morphologies without incorporating additional sodium salts and organic solvents. Among the five distinct morphologies studied, nanosheets displayed the highest single sodium-ion conductivity of 3.72 × 10−4 S cm−1. In this work, we have observed the maximum ionic conductivity value in water. For solid-state electrolytes, enhanced ion-pair dissociation and facile diffusion of the dissociated ions are crucial for improving ionic conductivity. Solvent molecules in the SSE framework help in sodium-ion release via hydration, thus boosting conductivity. Nanosheets, with the highest coordinated water content among all morphologies, facilitate the generation of a high concentration of hydrated Na-ions and enhance their mobility. These data are obtained using a temperature-dependent UV-vis study. Additionally, the highly crystalline nature of nanosheet morphology was ascertained from PXRD and HR-TEM data. A distinct difference in the SAED pattern of nanosheet and nanotube morphologies further corroborates the highly crystalline nature of the nanosheet morphology (Fig. S13†). Thus, with high crystallinity with directional ion channels, 2D nanosheet morphology exhibits the highest single Na+-ion conductivity. This highly crystalline nature of nanosheets for well-directional ordered channels favors high mobility of the sodium ions. The highly crystalline structure of the nanosheet morphology presumably accounts for the directional Na-ion conduction channels and the observed increase in ionic mobility. The significantly high number of H-bonded solvent molecules in the nanosheet framework contribute to the number density of the hydrated Na-ion in the channel. This is presumably attributed to the highest sodium ion conductivity among organic molecules, making it a suitable option for use as an SSE. This presents an enormous opportunity for further exploration of their ion-conducting characteristics. We believe that the strategy offers the opportunity to use such a design for the construction of next-generation solid-state SIBs.Data availability
All experimental data are available in the ESI.†Author contributions
Anik Kumar Dey: Scholar associated with synthesis, characterization, physicochemical studies, microscopic images. Sam Sankar Selvesundarasekar: electrochemical studies. Subrata Kundu: electrochemical studies, interpretation of all results of the electrochemical studies and writing of that part. Amal Kumar Mandal: interpretation of all characterization data and results of the material, data correlation and writing of this article. Amitava Das: interpretation and data correlation, overall coordination and writing of the article. Sumit Kumar Pramanik: interpretation and data correlation, overall coordination and writing of the article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
AKD thanks the CSIR for his research fellowship. AKM acknowledges funding from the Science and Engineering Research Board (SERB, India) grant SB/2019/F/6229-2020 and the Ministry of Mines, GOI, grant Met4-14/17/2022. A.D. acknowledges SERB (India) (JCB/2023/000005) and MoE (MoE-STARS: 2023-47) for supporting this research. We also thank the Analytical & Environment Science Division & Centralized Instrument Facility of CSIR-CSMCRI, Bhavnagar, for assistance with different analytical and spectroscopic measurements. The authors also wish to thank Dr Santoshkumar D Bhatt (CSIR-CECRI, Chennai Unit) for providing help in the temperature-dependent conductivity study. The authors also wish to thank Mr Arun Karmakar and Mr N. Sreenivasan (CSIR-CECRI) for their help with the temperature-dependent conductivity study. CSIR-CSMCRI PRIS no 158/2024.Notes and references
- Z. Bassyouni, A. Allagui and J. D. Abou Ziki, Adv. Mater. Technol., 2023, 8, 2200459 CrossRef CAS.
- X. Fan, C. Zhong, J. Liu, J. Ding, Y. Deng, X. Han, L. Zhang, W. Hu, D. P. Wilkinson and J. Zhang, Chem. Rev., 2022, 122, 17155–17239 CrossRef CAS PubMed.
- T. Watari, K. Nansai, K. Nakajima, B. C. McLellan, E. Dominish and D. Giurco, Environ. Sci. Technol., 2019, 53, 11657–11665 CrossRef CAS PubMed.
- D. Pulido-Sánchez, I. Capellán-Pérez, C. de Castro and F. Frechoso, Energy Environ. Sci., 2022, 15, 4872–4910 RSC.
- P. Poizot, J. Gaubicher, S. Renault, L. Dubois, Y. Liang and Y. Yao, Chem. Rev., 2020, 120, 6490–6557 CrossRef CAS PubMed.
- H. S. Hirsh, Y. Li, D. H. S. Tan, M. Zhang, E. Zhao and Y. S. Meng, Adv. Energy Mater., 2020, 10, 2001274 CrossRef CAS.
- P. K. Nayak, L. Yang, W. Brehm and P. Adelhelm, Angew. Chem., Int. Ed., 2018, 57, 102–120 CrossRef CAS PubMed.
- J.-M. Tarascon, Joule, 2020, 4, 1616–1620 CrossRef.
- K. M. Abraham, ACS Energy Lett., 2020, 5, 3544–3547 CrossRef CAS.
- C. Zhou, S. Bag and V. Thangadurai, ACS Energy Lett., 2018, 3, 2181–2198 CrossRef CAS.
- H.-L. Yang, B.-W. Zhang, K. Konstantinov, Y.-X. Wang, H.-K. Liu and S.-X. Dou, Adv. Energy Sustainability Res., 2021, 2, 2000057 CrossRef CAS.
- V. Thangadurai and B. Chen, Chem. Mater., 2022, 34, 6637–6658 CrossRef CAS.
- Z. Li, P. Liu, K. Zhu, Z. Zhang, Y. Si, Y. Wang and L. Jiao, Energy Fuels, 2021, 35, 9063–9079 CrossRef CAS.
- Y. Dong, P. Wen, H. Shi, Y. Yu and Z. S. Wu, Adv. Funct. Mater., 2024, 34, 2213584 CrossRef CAS.
- I. Hasa, S. Mariyappan, D. Saurel, P. Adelhelm, A. Y. Koposov, C. Masquelier, L. Croguennec and M. Casas-Cabanas, J. Power Sources, 2021, 482, 228872 CrossRef CAS.
- M. A. Sawhney, M. Wahid, S. Muhkerjee, R. Griffin, A. Roberts, S. Ogale and J. Baker, ChemPhysChem, 2022, 23, e202100860 CrossRef CAS PubMed.
- G. Kalimuldina, A. Nurpeissova, A. Adylkhanova, D. Adair, I. Taniguchi and Z. Bakenov, ACS Appl. Energy Mater., 2020, 3, 11480–11499 CrossRef CAS.
- S. Zhao, H. Che, S. Chen, H. Tao, J. Liao, X.-Z. Liao and Z.-F. Ma, Electrochem. Energy Rev., 2024, 7, 3 CrossRef CAS.
- Y. Wang, S. Song, C. Xu, N. Hu, J. Molenda and L. Lu, Nano Mater. Sci., 2019, 1, 91–100 CrossRef.
- C. Ma, K. Dai, H. Hou, X. Ji, L. Chen, D. G. Ivey and W. Wei, Adv. Sci., 2018, 5, 1700996 CrossRef PubMed.
- L. Xu, J. Li, W. Deng, L. Li, G. Zou, H. Hou, L. Huang and X. Ji, Mater. Chem. Front., 2021, 5, 1315–1323 RSC.
- X. Yu, L. Xue, J. B. Goodenough and A. Manthiram, Adv. Funct. Mater., 2021, 31, 2002144 CrossRef CAS.
- Y. Zheng, Q. Pan, M. Clites, B. W. Byles, E. Pomerantseva and C. Y. Li, Adv. Energy Mater., 2018, 8, 1801885 CrossRef.
- Y. Yao, Z. Wei, H. Wang, H. Huang, Y. Jiang, X. Wu, X. Yao, Z.-S. Wu and Y. Yu, Adv. Energy Mater., 2020, 10, 1903698 CrossRef CAS.
- W. Ling, N. Fu, J. Yue, X.-X. Zeng, Q. Ma, Q. Deng, Y. Xiao, L.-J. Wan, Y.-G. Guo and X.-W. Wu, Adv. Energy Mater., 2020, 10, 1903966 CrossRef CAS.
- X. Guo, Y. Li and H. Wang, ACS Appl. Energy Mater., 2024, 7, 1008–1014 CrossRef CAS.
- J.-K. Kim, Y. J. Lim, H. Kim, G.-B. Cho and Y. Kim, Energy Environ. Sci., 2015, 8, 3589–3596 RSC.
- Y. Yan, Z. Liu, T. Wan, W. Li, Z. Qiu, C. Chi, C. Huangfu, G. Wang, B. Qi and Y. Yan, Nat. Commun., 2023, 14, 3066 CrossRef CAS PubMed.
- X. Wang, C. Zhang, M. Sawczyk, J. Sun, Q. Yuan, F. Chen, T. C. Mendes, P. C. Howlett, C. Fu and Y. Wang, Nat. Mater., 2022, 21, 1057–1065 CrossRef CAS PubMed.
- H. Wan, J. P. Mwizerwa, X. Qi, X. Liu, X. Xu, H. Li, Y.-S. Hu and X. Yao, ACS Nano, 2018, 12, 2809–2817 CrossRef CAS PubMed.
- R. Tiwari, D. K. Verma, D. Kumar, S. Yadav, K. Kumar, P. Adhikary and S. Krishnamoorthi, Energy Fuels, 2022, 36, 6459–6467 CrossRef CAS.
- H. Hou, Q. Xu, Y. Pang, L. Li, J. Wang, C. Zhang and C. Sun, Adv. Sci., 2017, 4, 1700072 CrossRef PubMed.
- S. Chen, H. Che, F. Feng, J. Liao, H. Wang, Y. Yin and Z.-F. Ma, ACS Appl. Mater. Interfaces, 2019, 11, 43056–43065 CrossRef CAS PubMed.
- Q. Ma, J. Liu, X. Qi, X. Rong, Y. Shao, W. Feng, J. Nie, Y.-S. Hu, H. Li and X. Huang, J. Mater. Chem. A, 2017, 5, 7738–7743 RSC.
- A. Dey, V. R. Ramlal, S. S. Sankar, T. S. Mahapatra, E. Suresh, S. Kundu, A. K. Mandal and A. Das, ACS Appl. Mater. Interfaces, 2020, 12, 58122–58131 CrossRef CAS PubMed.
- A. Maity, M. Gangopadhyay, A. Basu, S. Aute, S. S. Babu and A. Das, J. Am. Chem. Soc., 2016, 138, 11113–11116 CrossRef CAS PubMed.
- A. Dey, A. Maity, T. Singha Mahapatra, E. Suresh, A. K. Mandal and A. Das, CrystEngComm, 2020, 22, 5117–5121 RSC.
- A. Dey, V. R. Ramlal, S. S. Sankar, S. Kundu, A. K. Mandal and A. Das, Chem. Sci., 2021, 12, 13878–13887 RSC.
- H. Cho, W. Cho, Y. Kim, J.-g. Lee and J. H. Kim, RSC Adv., 2018, 8, 29044–29050 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc03113j |
| This journal is © The Royal Society of Chemistry 2024 |