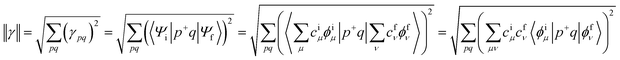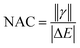Open Access Article
Open Access ArticleDiverse quantum interference regimes in intramolecular singlet fission chromophores with thiophene-based linkers†
Jonghwan
Lee
 a,
Sungsik
Eom
a and
Hyungjun
Kim
a,
Sungsik
Eom
a and
Hyungjun
Kim
 *ab
*ab
aDepartment of Chemistry and Research Institute of Basic Sciences, Incheon National University, Republic of Korea. E-mail: kim.hyungjun@inu.ac.kr
bDepartment of Chemistry, Hanyang University, Republic of Korea. E-mail: kimhyungjun@hanyang.ac.kr
First published on 9th October 2024
Abstract
An array of thiophene-based π-conjugated linkers in covalently linked pentacene dimers allow us to access diverse quantum interference (QI), modulating nonadiabatic coupling (NAC) in the singlet fission (SF) process. Simulations show that structural isomerism in terms of S atom orientation substantially alters NAC with relatively marginal impacts on energies. Extended curly arrow rules (ECARs) reveal sensitive dependence of QI on SF linker topologies and connectivity, categorizing regimes of constructive, destructive, and previously unrealized in SF research, shifted destructive QI. Drastic NAC changes in terms of S atom orientation are rationalized based on the nature of QI. Our results from nonequilibrium Green's function calculation using density functional theory corroborate the classification of QI regimes based on ECARs. Moreover, we found that the extent of charge resonance contribution in electronic states relevant to multiexciton formation and the appearance of optically allowed charge transfer excitation strongly depends on the operative QI regime. Notably, the magnitude of NAC effectively captures this influence. Our findings show that QI can rationalize and semi-quantitatively correlate with NAC for the multiexciton formation step in the SF process.
Introduction
Singlet fission (SF) is an intriguing photophysical process where two independent triplet excitons are generated from a high-energy singlet state.1,2 It is generally accepted that a multiexciton (ME) state consisting primarily of coupled triplets mediates this process,3–9 and meeting the thermodynamic requirement is highly desired for efficient exciton multiplications. By utilizing the thermally wasted part of high-energy photons to promote electronic excitations in neighboring chromophores, this phenomenon has the potential to significantly enhance the theoretical efficiency limits of single-junction photovoltaic devices, known as the Shockley–Queisser limit.10 However, the details of the mechanism remain under debate.11 In solid-state SF, structural heterogeneity limits mechanistic understanding.12,13 As an alternative approach, intramolecular SF (iSF) systems have been explored, where SF chromophores are covalently connected by a small molecule, linker. This allows definitive characterization of exciton dynamics on a single molecule level.14Numerous studies have shown that linkers play an integral role in modulating SF dynamics rather than simply holding chromophores together.14 Extensive investigations of iSF have elucidated how different linking topologies modify SF phenomena. Key discoveries demonstrate that the linkage pattern,15–20 conjugation type,21–23 distance,24–28 arrangement/packing structure,25,26,28–34 and extent of through-bond/through-space coupling26,31,34 alter triplet quantum yields, triplet lifetimes and SF rates. Such systematic linking strategies offer vital design guidelines to optimize iSF in acene dimers. In particular, chromophores attached at the phenylene linker in ortho, meta, and para positions show distinctive SF kinetics.15,35
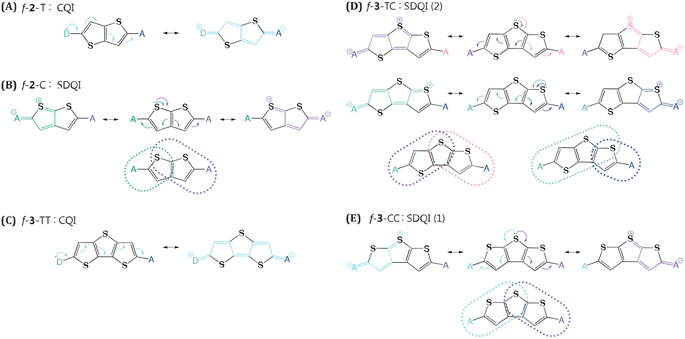
In molecular science, the communication between molecules is important. In particular, quantum interference (QI) has played a pivotal role in explaining conductance in molecular electronics.36–39 The function of various linkers has also been examined across research areas including electron transfer, spin coupling, and SF, revealing intriguing parallels.36 QI proves instrumental in analyzing SF kinetics.40,41 By examining iSF in pentacene dimers connected by various acene linkers, Campos et al. revealed that QI significantly impacts SF kinetics.40 Based on their proposed graphical model, they categorized these linking patterns into constructive and destructive QI, CQI and DQI, respectively. This rationalizes the previously observed dependence of SF kinetics on the attachment sites of chromophores at acene linkers.15,16,18,24
In this work, we employed an array of thiophene-based linkers to access diverse QI regimes through slight structural modifications, which surprisingly resulted in the tuning of electronic coupling over a wide range. Musser et al. recently showed that bithiophene linkers accelerate ME formation (MEF) versus phenylene linkers.31 As a five-membered ring, the thiophene allows us to probe how QI manifests in nonbipartite linker topologies. Furthermore, cis/trans isomerism for the sulfur atom enables exploring previously unrealized shifted destructive QI (SDQI) in MEF kinetics. We rationalize the nonintuitive structure–function trends obtained from quantum chemical simulations using extended curly arrow rules (ECARs) that categorize topological motifs featuring CQI, DQI, and SDQI.
ECARs are an effective method for predicting electron transmission in molecular electronic devices, developed as an advance to the original curly arrow rules (CARs).42–44 CARs use organic chemistry's curly arrow notation to predict electron transmission in alternant hydrocarbons, and ECARs expand this approach by considering electron-withdrawing and electron-donating groups. This improvement allows ECARs to predict the nature of QI in a wider range of molecules, including structures with cross-conjugation, heteroatoms, and/or nonalternant structures where the applicability of CARs is limited, thus offering a more comprehensive tool for understanding molecular conductance.45 Combined with high-level quantum chemical simulations and a molecular electronics model, we revealed that subtle structural modifications of the linkers can selectively control electronic couplings between chromophores.
Results
Model system and theoretical background
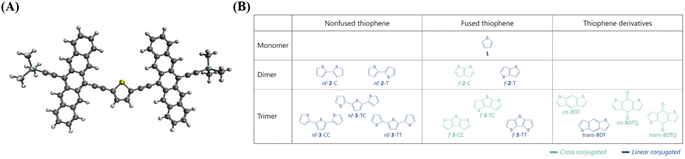
We designed a series of model systems of 6,6′-trimethylsilyl-pentacene (TMS-Pc) dimers connected via thiophene derivatives (Fig. 1A and S1†). We used an index f-#-X or nf-#-X to encode key topological details of the linkers, where f denotes fused, nf specifies nonfused chains, # indicates the number of repeating units, and X represents the relative sulfur atom orientation: cis (C) for the same direction, and trans (T) for the opposite direction (Fig. 1B). We performed restrictive active space with spin-flip (RAS-SF) calculations46–49 to obtain SF-relevant energetics, in particular, focusing on the MEF rate using a three-state kinetics model,50–52 and wavefunction decomposition.53 We also conducted nonequilibrium Green's function (NEGF) calculations using density functional theory (DFT) to describe electronic transmission through linkers. Further details regarding quantum chemical simulation are described in the ESI.†A deeper understanding into MEF kinetics is pursued based on quantum chemically computed nonadiabatic coupling (NAC) and thermodynamic driving force (ΔEMEF) (Fig. 2 and Table S1†). We quantified ΔEMEF as the electronic energy difference between a ME and the lowest optically allowed transition state. As suggested by Krylov et al., the norm of the reduced one-particle transition density matrix (‖γ‖) can be used to approximate NAC.54–56
Singlet fission kinetics
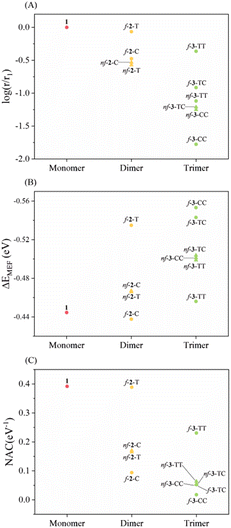
Before discussing the details, we would like to highlight the reliability of our theoretical approach. In previous experimental studies, Musser et al. measured MEF dynamics through the femtosecond transient absorption spectrum for f-2-T and nf-2-T. Experimentally determined time constants for MEF are 0.7 ps and 7 ps for nf-2-T, which further accelerates to 0.3 ps and 3.6 ps for f-2-T.31 Our simulations predict 3.2 times faster MEF rate for f-2-T compared to nf-2-T, which is comparable to experimental rate enhancements of 2.3 and 1.9. Moreover, the RAS-SF approach has been successful in describing relative changes in MEF kinetics of structurally similar systems.4,52 Krylov et al. conducted a comparative analysis between MEF rates from RAS-SF simulations and the experimental rates for a series of perylenediimide dimers, which shows a high correlation between them. This lends more confidence to the reliability of our simulations.RAS-SF calculations reveal that the magnitude of NAC varies significantly, with the maximum value (0.39 eV−1 for 1) being approximately 22 times larger than the minimum value (0.018 eV−1 for f-3-CC) (Fig. 2 and Table S1†). In contrast, the change in ΔEMEF is comparatively small, with a 26% difference between the minimum (−0.44 eV for 1) and maximum (−0.55 eV for f-3-CC) values. The substantial variation in NAC dominates over the influence of energy in determining the relative rate, and NAC is crucial for understanding the kinetics of the SF process, as established by various studies.54,55,57 Among the investigated thiophene derivatives, the monomer, 1, exhibits the strongest electronic coupling due to its shorter length compared to all other linkers, despite being thermodynamically unfavorable. As the number of linkers increases, the spatial separation between the pentacene chromophores expands, resulting in a highly anticipated decrease in NAC. Remarkably, the NAC value of f-2-T, the highest among dimers, is predicted to be of nearly the same magnitude as that of 1. The nonfused analogues (nf-2-T and nf-2-C) display similar values and exhibit inferior performance due to the rotatable single bond impeding conjugation between thiophene units, with f-2-C demonstrating the weakest NAC among the dimeric linkers. For the trimeric linkers, f-3-TT manifests the strongest electronic coupling, while the incorporation of even a single cis sulfur atom orientation induces a significant decline: 0.23 eV−1 for f-3-TT, 0.05 eV−1 for f-3-TC, and 0.02 eV−1 for f-3-CC. The NAC values of nonfused moieties (nf-3-TT, nf-3-TC, and nf-3-CC) lie approximately in the middle of the range observed for their fused counterparts. These findings lead to several key conclusions: (1) the overall trend of NAC with respect to the number of thiophene-based linkers follows the order: monomer > dimer > trimer; (2) the fused group exhibits a larger variation in NAC compared to the nonfused series; and (3) the presence of even a single cis sulfur atom orientation in fused linkers results in a significant deterioration of electronic coupling.
To elucidate this phenomenon, we initially sought to investigate the correlation between NAC and structural features. We hypothesized that increased interchromophoric distances would result in diminished NAC values. However, upon examining the relationship between NAC trends and geometric descriptors, such as the distance, in-plane angle, and dihedral angle between the chromophores (Fig. S4 and Table S2†), the estimated structural features were insufficient to fully rationalize the observed trends. Subsequently, we considered the bridge resonance effect proposed by Campos et al., which posits that energetic coherence between the frontier molecular orbitals of the chromophores and those of the bridge facilitates triplet pair formation, even for extended bridge lengths, ultimately enhancing the SF process.58–60 Notably, f-2-C and f-2-T exhibit comparable offset values, defined as the difference in frontier molecular orbital energies between pentacene and the thiophene-based linker, of 0.13 eV (Table S3†). Moreover, the offset values for the fused trimeric systems range from 0.07 eV to 0.18 eV, further indicating that the bridge resonance effect alone is insufficient to account for the observed variations in NAC. The comparable offset values within linkers containing the same number of repeating units indicate that the bridge resonance effect alone cannot fully explain the observed decrease in NAC upon the incorporation of cis-oriented thiophene moieties. In light of these findings, a robust and consistent theoretical framework is necessary to interpret the simulation results and provide a comprehensive understanding of the factors governing NAC and SF dynamics in these systems.
Quantum interference
QI offers a compelling explanation for the stark difference in NAC between f-2-T and f-2-C. We have applied ECARs to map the QI natures of representative thiophene linkers (Fig. 3). By replacing anchors (here, chromophores) with donor(D)/acceptor(A) groups and evaluating possible electron transfer pathways, ECARs predict whether wire will show CQI, DQI, or SDQI.45 Applying ECARs to f-2-T reveals that this linker features CQI. Quantum chemical simulations predict 76% drop in NAC of f-2-C relative to f-2-T. There is no continuous conjugated pathway for electron transfer between TMS-Pcs in f-2-C. However, the thiophene can function as a donor, enabling mediated electronic communication between TMS-Pcs. Based on ECARs, f-2-C falls into the SDQI regime which is less conductive than CQI, nicely accounting for the computed NAC decrease. Further investigation into the fused thiophene trimers unravels additional interesting findings. We found that f-3-TT has the largest NAC of 0.23 eV−1, readily understood by its CQI topology. The other structural isomers, f-3-TC and f-3-CC, both feature SDQI mediated by donor-like thiophene. Yet, this alone is insufficient to explain their ∼3-fold NAC difference. Closer inspection reveals that f-3-TC provides more pathways for SDQI than f-3-CC does. While both central thiophene and adjacent thiophene in cis orientation can participate in mediating electronic communication in f-3-TC, only the central thiophene can mediate electron transfer between chromophores in f-3-CC.This demonstrates the utility of ECAR analysis for both rationalizing NAC trends based on linker topology and semi-quantitatively discriminating variations in NAC magnitudes.
In addition to the pen-and-paper model predictions, the QI regime can be elucidated through the analysis of the computed electronic transmission. Quantum transport simulations yield the results that closely aligned with our expectations (Fig. 4). The f-3-TT linker exhibits a broad transmission curve above the Fermi energy level, which can be attributed to the CQI character. In contrast, both f-3-TC and f-3-CC linkers display masked Fano resonance peaks near 1.5 eV. These peaks likely originate from the presence of different transfer pathways that disrupt electronic communications between the electrodes, contributing to the appearance of SDQI.61 The simulated results demonstrate the robust predictive capability of ECARs and validate the QI characteristics derived from these rules, thereby reinforcing their reliability in predicting electronic transport properties.
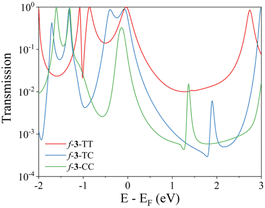 | ||
| Fig. 4 Transmission functions of pentacene dimers linked by fused trimers. Calculated transmission coefficients of Au-linker-Au junctions of f-3-TT, f-3-TC, and f-3-CC. | ||
Extended array of thiophene linkers
We have investigated the relationship between the magnitude of NAC and the operative QI character for an expanded array of thiophene-based linkers, including benzodithiophene (BDT) and its quinone derivative (BDTQ) (Fig. S6 and Table S1†). The NAC of trans-BDT is 2.63 times higher than that of cis-BDT, a phenomenon that can be rationalized using the ECARs model. ECAR analysis reveals that trans-BDT exhibits CQI, while cis-BDT corresponds to SDQI, in agreement with the observed NAC values and the rate of the MEF step. In contrast, trans-BDTQ and cis-BDTQ exhibit DQI and SDQI, respectively. This observation is further corroborated by the NAC values, which are nearly negligible at 0.026 eV−1 for cis-BDTQ and moderate at 0.084 eV−1 for trans-BDTQ. The consistent trends observed in both NAC and QI characters across this extended array of thiophene derivatives validate the generality of our proposed correlation between these two critical molecular properties.To further explore the generality of our findings, we have expanded the chromophore set to include 6,6′-TMS-tetracene (Tc) and 2,2′-TMS-pentacene (2,2′-TMS-Pc). The inclusion of 6,6′-TMS-Tc allows us to investigate whether our proposed correlation between NAC and QI characters remains valid for endothermic/isoergic MEF processes (Fig. S7 and Table S4†). Furthermore, the incorporation of 2,2′-TMS-Pc enables us to examine the influence of the linkage pattern between chromophores and linkers on our conclusions (Fig. S7 and Table S5†). Remarkably, for both chromophore systems, the overall trends in NAC and MEF rates closely resemble those observed for our original model system, 6,6′-TMS-Pc. Notably, the enhancement of NAC values in fused systems as the number of trans sulfur atom orientations increases is consistent with our main conclusion that fused linkers composed solely of trans S orientation exhibit a CQI character, resulting in large NAC values. While the energetic changes associated with different linkers are not significant for 2,2′-TMS-Pc, with differences less than 0.15 eV, the endo/exothermicity of the MEF process in the Tc-based systems appears to be dependent on the nature of the linker.
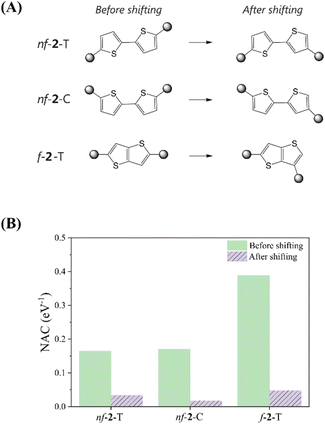
Bryce et al. conducted a study investigating the influence of varying the structural orientation of the anchoring group on the phenyl ring of 1-phenylpyrrole and biphenyl molecular wires, from para to meta positions.62 By employing ECARs, DFT simulations, and molecular conductance measurements, they showed that the meta positioning of the anchoring group led to a considerable deterioration of the electron transport pathway compared to the para orientation, strongly suggesting the manifestation of the DQI character. As implied by the electronic transmission study, for a QI-mediated mechanism, MEF kinetics should also be highly sensitive to subtle changes in the linkage between chromophores and linkers, as these modifications can completely invert the operative QI domain, for example, shifting from CQI to DQI, or vice versa. To validate this impact, we modified the bonding position of the chromophore attachment to the adjacent carbon atom in the cases of nf-2-T, nf-2-C, and f-2-T, which typically present CQI nature according to the ECARs (Fig. 5 and Table S6†). Generally, shifting the chromophore attachment site slightly favors ΔEMEF, but substantially reduces NAC since it shuts down CQI, leaving only the mediated pathway. The modification of the chromophore attachment position leads to a dramatic attenuation of NAC in both nonfused and fused systems. For nf-2-T and nf-2-C, the NAC values reduce by 81% and 88%, respectively, when the chromophore is connected to the adjacent carbon atom of the linker. Similarly, in fused systems, the NAC experiences a substantial 87% reduction upon altering the chromophore attachment site. Collectively, these examples demonstrate that MEF dynamics in thiophene-linked pentacene chromophores are principally dictated by the QI character determined from the linker topology, rather than energetics.
Discussion
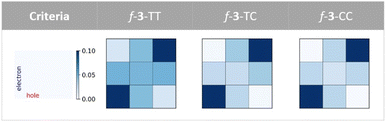
The physical origin of NAC variation can be understood based on the contribution of the charge resonance (CR) component. In the field of SF, it is widely recognized that the CR state plays an essential role in connecting the lowest excited singlet state (S1) which usually has a local exciton (LE) character and the multiexcitonic spin-correlated triplet pair state (TT).3,63–67 The CT electronic configuration can be coupled to both the local exciton and TT exciton via one-electron disposition, which facilitates the MEF mechanism. Mazumdar et al. employed the Pariser–Parr–Pople Hamiltonian and found that the para-connected SF chromophore exhibits a higher contribution of CR in both the lowest optically allowed singlet state and triplet–triplet ME states.17,68 A similar observation was reported based on the symmetry characters of molecular orbitals.41 Our RAS-SF adiabatic wavefunction decomposition also reveals an enhanced contribution of CR components for the pentacene dimers connected by fused thiophene linkers composed solely of trans-oriented sulfur atoms, in both the lowest optically allowed singlet excited state and ME states (Fig. 6 and Tables S7–S9†). For the former state which corresponds to S2 in the current model systems, the CR contribution of f-3-TT is 26.8%, which is 5.4 fold higher than that of f-3-CC. Also, in the ME adiabatic state, the CR ratio of f-3-TT surpasses that of f-3-CC by 3.6-fold. This substantial mixing of CR diabats into LE and ME adiabatic states facilitates the MEF step by enhancing electronic coupling. To further elucidate the role of one-electron coupling, we performed an electron–hole correlation diagram analysis calculated by time-dependent density functional theory (TDDFT) for the lowest optically allowed singlet excited state (Fig. 7 and S8†). For all cases, we observed a significant LE character within each chromophore, as evidenced by the strong correlation signatures at the bottom-left and top-right corners of the electron–hole correlation diagram matrix. Remarkably, the variations in charge-transfer (CT) elements are strikingly apparent across the series of molecules As the number of trans sulfur atoms increases, the color representing the CT ratio becomes more intense, indicating a rise in the CT contribution (bottom-center, middle-left, middle-right, and top-center regions of the matrix). For instance, f-3-TT, which exhibits CQI, displays much stronger CT contribution between the chromophores and the linkers compared to f-3-CC. Moreover, as noticed by Campos et al., we also found the relationship between the ground state absorption to an odd-parity CT state and the nature of the linker. We confirmed the presence of an optically allowed CT transition through our RAS-SF calculations (Tables S7–S9†). While the transition with the dominant CR character is completely forbidden in f-3-CC (i.e. zero oscillator strength), it becomes slightly accessible in f-3-TC, and f-3-TT exhibits the brightest CR state among the f-3 series. The extent of CR contribution is strongly associated with the operative QI mechanism.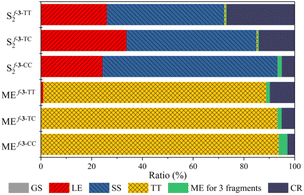 | ||
| Fig. 6 Wavefunction decomposition analysis. Composition of the lowest optically allowed singlet excited state (S2) and the multiexciton state (ME) from RAS-SF calculation. | ||
Subsequently, we aim to establish the correlation between the contribution of CR and the magnitude of NAC. The derivative coupling, a one-electron operator, can only couple the states whose wavefunctions are connected through one-electron excitation. The ME configuration differs by two-electron excitation from the local excited states, but they can be related by one-electron excitation through the CR components.1 Krylov et al. computed NAC by fully analytic formulation for several model SF systems, and compared trends.54,55 In their work, they remarked that the norm of one-particle transition density matrix can serve as a useful tool for analyzing the trends in coupling. Therefore, NAC successfully captures the contribution of CT/CR components in the MEF mechanism.50,54,64,69,70 This provides a more profound understanding of the intricate interrelationship between the linker topology, QI regime, CR component, and the magnitude of NAC.
Conclusions
In summary, this study advances comprehension of NAC control over iSF via QI. RAS-SF simulations of pentacene dimers linked with diverse thiophene derivatives enable comprehensive investigation into impacts of subtle structural modifications and linking pattern changes of conjugated linkers on MEF dynamics. Diverse QI regimes are accessed, categorizing motifs exhibiting CQI, DQI, and previously unrecognized SDQI in the MEF step, via ECARs. The rate of MEF is largely determined by the substantial effect of NAC, with energetics playing a relatively minor role in comparison. Drastic NAC variation up to 4-fold and 13-fold in dimeric and trimeric thiophenes can be understood with different operative QI regimes. The fully trans-configured f-3-TT exhibits the highest NAC magnitude of 0.23 eV−1, whereas introducing even one cis oriented thiophene unit reduces NAC to 0.052 eV−1 in the f-3-TC. When both thiophene units adopt a cis orientation, the NAC further diminishes to 0.018 eV−1, effectively approaching zero. NEGF calculation using DFT also corroborates the findings from ECARs. The calculated transmission function features a broad curve and a stark dip, which corresponds to CQI and SDQI, respectively, thus supporting the assignment of QI nature by ECARs. We extended our investigation to an expanded array of thiophene derivatives linkers and different chromophores, and confirmed that the structural isomerism of thiophene moieties in BDT and BDTQ profoundly changes QI properties and resulting MEF dynamics. In addition to pentacene, we included the tetracene chromophore to examine the influence of a nearly endothermic/isoergic MEF step on our proposed correlation between QI and NAC. This inclusion allowed us to assess the robustness of our argument under different energetic regimes. Furthermore, we modified the linkage patterns between pentacenes and linkers from the 2,2′ positions to the 6,6′ positions, and realized that our key observation holds for various chromophores.Having established the relationship between the nature of QI and the magnitude of NAC, we tried to unveil the physical origin of this observation. Our RAS-SF simulations revealed that the linkers exhibiting CQI demonstrate a significantly higher degree of CR character compared to the moieties indicative of DQI, with intensifications reaching up to 5 times higher in the lowest optically allowed singlet excited state and up to 4 times higher in the ME state. Moreover, these linkers feature an optically allowed CT transition, which is absent or significantly suppressed in linkers with DQI or SDQI regimes. Being a one-electron operator, approximate NAC can effectively capture the contribution of the CR component. Overall, QI determined by linker structures and linking patterns predominately dictates MEF kinetics over thermodynamic or geometric factors in these systems. The presented framework enables judiciously modulating electronic communication through engineered molecular connectivity and linker topology, delivering rational design principles for strategic control over the mechanism.
Data availability
The datasets supporting this article have been uploaded as part of the ESI.†Author contributions
H. K. conceived the project. J. L. and S. E. performed quantum chemical simulations. All authors discussed the results. J. L. and H. K. wrote the manuscript with input from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Research Foundation of Korea (NRF-2022R1C1C1010670), and Incheon National University Grant. The authors appreciate Dr Victor GarcíaSuárez for the advice regarding electronic transmission calculation and interpretation.References
- M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed.
- M. B. Smith and J. Michl, Annu. Rev. Phys. Chem., 2013, 64, 361–386 CrossRef CAS PubMed.
- H. Kim and P. M. Zimmerman, Phys. Chem. Chem. Phys., 2018, 20, 30083–30094 RSC.
- D. Casanova, Chem. Rev., 2018, 118, 7164–7207 CrossRef CAS PubMed.
- P. M. Zimmerman, C. B. Musgrave and M. Head-Gordon, Acc. Chem. Res., 2013, 46, 1339–1347 CrossRef CAS PubMed.
- K. Miyata, F. S. Conrad-Burton, F. L. Geyer and X.-Y. Zhu, Chem. Rev., 2019, 119, 4261–4292 CrossRef CAS PubMed.
- S. N. Sanders, A. B. Pun, K. R. Parenti, E. Kumarasamy, L. M. Yablon, M. Y. Sfeir and L. M. Campos, Chem, 2019, 5, 1988–2005 CAS.
- C. K. Yong, A. J. Musser, S. L. Bayliss, S. Lukman, H. Tamura, O. Bubnova, R. K. Hallani, A. Meneau, R. Resel, M. Maruyama, S. Hotta, L. M. Herz, D. Beljonne, J. E. Anthony, J. Clark and H. Sirringhaus, Nat. Commun., 2017, 8, 15953 CrossRef CAS PubMed.
- S. Lukman, J. M. Richter, L. Yang, P. Hu, J. Wu, N. C. Greenham and A. J. Musser, J. Am. Chem. Soc., 2017, 139, 18376–18385 CrossRef CAS PubMed.
- 1M. Einzinger, T. Wu, J. F. Kompalla, H. L. Smith, C. F. Perkinson, L. Nienhaus, S. Wieghold, D. N. Congreve, A. Kahn, M. G. Bawendi and M. A. Baldo, Nature, 2019, 571, 90–94 CrossRef PubMed.
- Y. Hong, J. Kim, D. Kim and H. Kim, J. Phys. Chem. A, 2021, 125, 875–884 CrossRef CAS PubMed.
- J. Kim, H. T. Teo, Y. Hong, Y. C. Liau, D. Yim, Y. Han, J. Oh, H. Kim, C. Chi and D. Kim, J. Am. Chem. Soc., 2023, 145, 19812–19823 CrossRef CAS PubMed.
- J. Kim, H. T. Teo, Y. Hong, J. Oh, H. Kim, C. Chi and D. Kim, Angew. Chem., Int. Ed., 2020, 59, 20956–20964 CrossRef CAS PubMed.
- N. V. Korovina, N. F. Pompetti and J. C. Johnson, J. Chem. Phys., 2020, 152, 040904 CrossRef CAS PubMed.
- J. Zirzlmeier, D. Lehnherr, P. B. Coto, E. T. Chernick, R. Casillas, B. S. Basel, M. Thoss, R. R. Tykwinski and D. M. Guldi, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5325–5330 CrossRef CAS PubMed.
- N. V. Korovina, J. Joy, X. Feng, C. Feltenberger, A. I. Krylov, S. E. Bradforth and M. E. Thompson, J. Am. Chem. Soc., 2018, 140, 10179–10190 CrossRef CAS PubMed.
- R. Chesler, S. Khan and S. Mazumdar, J. Phys. Chem. A, 2020, 124, 10091–10099 CrossRef CAS PubMed.
- H. Sakai, R. Inaya, H. Nagashima, S. Nakamura, Y. Kobori, N. V. Tkachenko and T. Hasobe, J. Phys. Chem. Lett., 2018, 9, 3354–3360 CrossRef CAS PubMed.
- N. Alagna, J. L. Pérez Lustres, N. Wollscheid, Q. Luo, J. Han, A. Dreuw, F. L. Geyer, V. Brosius, U. H. F. Bunz, T. Buckup and M. Motzkus, J. Phys. Chem. B, 2019, 123, 10780–10793 CrossRef CAS PubMed.
- O. Millington, S. Montanaro, A. Leventis, A. Sharma, S. A. Dowland, N. Sawhney, K. J. Fallon, W. Zeng, D. G. Congrave, A. J. Musser, A. Rao and H. Bronstein, J. Am. Chem. Soc., 2023, 145, 2499–2510 CrossRef CAS PubMed.
- E. Kumarasamy, S. N. Sanders, M. J. Y. Tayebjee, A. Asadpoordarvish, T. J. H. Hele, E. G. Fuemmeler, A. B. Pun, L. M. Yablon, J. Z. Low, D. W. Paley, J. C. Dean, B. Choi, G. D. Scholes, M. L. Steigerwald, N. Ananth, D. R. McCamey, M. Y. Sfeir and L. M. Campos, J. Am. Chem. Soc., 2017, 139, 12488–12494 CrossRef CAS PubMed.
- B. S. Basel, J. Zirzlmeier, C. Hetzer, B. T. Phelan, M. D. Krzyaniak, S. R. Reddy, P. B. Coto, N. E. Horwitz, R. M. Young, F. J. White, F. Hampel, T. Clark, M. Thoss, R. R. Tykwinski, M. R. Wasielewski and D. M. Guldi, Nat. Commun., 2017, 8, 15171 CrossRef CAS PubMed.
- B. S. Basel, J. Zirzlmeier, C. Hetzer, S. R. Reddy, B. T. Phelan, M. D. Krzyaniak, M. K. Volland, P. B. Coto, R. M. Young, T. Clark, M. Thoss, R. R. Tykwinski, M. R. Wasielewski and D. M. Guldi, Chem, 2018, 4, 1092–1111 CAS.
- S. N. Sanders, E. Kumarasamy, A. B. Pun, M. T. Trinh, B. Choi, J. Xia, E. J. Taffet, J. Z. Low, J. R. Miller, X. Roy, X.-Y. Zhu, M. L. Steigerwald, M. Y. Sfeir and L. M. Campos, J. Am. Chem. Soc., 2015, 137, 8965–8972 CrossRef CAS PubMed.
- Y. Matsui, S. Kawaoka, H. Nagashima, T. Nakagawa, N. Okamura, T. Ogaki, E. Ohta, S. Akimoto, A. Sato-Tomita, S. Yagi, Y. Kobori and H. Ikeda, J. Phys. Chem. C, 2019, 123, 18813–18823 CrossRef CAS.
- L. Ahrens, N. Wollscheid, J. Han, O. Kefer, F. Rominger, A. Roozbeh, J. Freudenberg, A. Dreuw, U. H. F. Bunz and T. Buckup, J. Phys. Chem. B, 2021, 125, 13235–13245 CrossRef CAS PubMed.
- A. B. Pun, A. Asadpoordarvish, E. Kumarasamy, M. J. Y. Tayebjee, D. Niesner, D. R. McCamey, S. N. Sanders, L. M. Campos and M. Y. Sfeir, Nat. Chem., 2019, 11, 821–828 CrossRef CAS PubMed.
- N. V. Korovina, S. Das, Z. Nett, X. Feng, J. Joy, R. Haiges, A. I. Krylov, S. E. Bradforth and M. E. Thompson, J. Am. Chem. Soc., 2016, 138, 617–627 CrossRef CAS PubMed.
- I. Papadopoulos, J. Zirzlmeier, C. Hetzer, Y. J. Bae, M. D. Krzyaniak, M. R. Wasielewski, T. Clark, R. R. Tykwinski and D. M. Guldi, J. Am. Chem. Soc., 2019, 141, 6191–6203 CrossRef CAS PubMed.
- B. S. Basel, C. Hetzer, J. Zirzlmeier, D. Thiel, R. Guldi, F. Hampel, A. Kahnt, T. Clark, D. M. Guldi and R. R. Tykwinski, Chem. Sci., 2019, 10, 3854–3863 RSC.
- K. Majumder, S. Mukherjee, N. A. Panjwani, J. Lee, R. Bittl, W. Kim, S. Patil and A. J. Musser, J. Am. Chem. Soc., 2023, 145, 20883–20896 CrossRef CAS PubMed.
- J. C. Dean, R. Zhang, R. K. Hallani, R. D. Pensack, S. N. Sanders, D. G. Oblinsky, S. R. Parkin, L. M. Campos, J. E. Anthony and G. D. Scholes, Phys. Chem. Chem. Phys., 2017, 19, 23162–23175 RSC.
- A. T. Gilligan, E. G. Miller, T. Sammakia and N. H. Damrauer, J. Am. Chem. Soc., 2019, 141, 5961–5971 CrossRef CAS PubMed.
- O. Kefer, L. Ahrens, J. Han, N. Wollscheid, E. Misselwitz, F. Rominger, J. Freudenberg, A. Dreuw, U. H. F. Bunz and T. Buckup, J. Am. Chem. Soc., 2023, 145, 17965–17974 CrossRef CAS PubMed.
- C. Hetzer, D. M. Guldi and R. R. Tykwinski, Chem.–Eur. J., 2018, 24, 8245–8257 CrossRef CAS PubMed.
- C. Herrmann, J. Phys. Chem. A, 2019, 123, 10205–10223 CrossRef CAS PubMed.
- C. J. Lambert, Chem. Soc. Rev., 2015, 44, 875–888 RSC.
- X. Li, Y. Zheng, Y. Zhou, Z. Zhu, J. Wu, W. Ge, Y. Zhang, Y. Ye, L. Chen, J. Shi, J. Liu, J. Bai, Z. Liu and W. Hong, J. Am. Chem. Soc., 2023, 145, 21679–21686 CrossRef CAS PubMed.
- P. Li, S. Hou, B. Alharbi, Q. Wu, Y. Chen, L. Zhou, T. Gao, R. Li, L. Yang, X. Chang, G. Dong, X. Liu, S. Decurtins, S.-X. Liu, W. Hong, C. J. Lambert, C. Jia and X. Guo, J. Am. Chem. Soc., 2022, 144, 15689–15697 CrossRef CAS PubMed.
- K. R. Parenti, R. Chesler, G. He, P. Bhattacharyya, B. Xiao, H. Huang, D. Malinowski, J. Zhang, X. Yin, A. Shukla, S. Mazumdar, M. Y. Sfeir and L. M. Campos, Nat. Chem., 2023, 15, 339–346 CrossRef CAS PubMed.
- S. Ito, T. Nagami and M. Nakano, J. Phys. Chem. A, 2016, 120, 6236–6241 CrossRef CAS PubMed.
- T. Stuyver, S. Fias, F. De Proft and P. Geerlings, J. Phys. Chem. C, 2015, 119, 26390–26400 CrossRef CAS.
- T. Stuyver, N. Blotwijk, S. Fias, P. Geerlings and F. De Proft, ChemPhysChem, 2017, 18, 3012–3022 CrossRef CAS PubMed.
- H. Hosoya, Curr. Org. Chem., 2015, 19, 293–310 CrossRef CAS.
- L. J. O'Driscoll and M. R. Bryce, Nanoscale, 2021, 13, 1103–1123 RSC.
- P. M. Zimmerman, F. Bell, M. Goldey, A. T. Bell and M. Head-Gordon, J. Chem. Phys., 2012, 137, 164110 CrossRef PubMed.
- D. Casanova and M. Head-Gordon, Phys. Chem. Chem. Phys., 2009, 11, 9779 RSC.
- D. Casanova, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1561 CAS.
- D. Casanova and A. I. Krylov, Phys. Chem. Chem. Phys., 2020, 22, 4326–4342 RSC.
- X. Feng, A. B. Kolomeisky and A. I. Krylov, J. Phys. Chem. C, 2014, 118, 19608–19617 CrossRef CAS.
- X. Feng, D. Casanova and A. I. Krylov, J. Phys. Chem. C, 2016, 120, 19070–19077 CrossRef CAS.
- M. H. Farag and A. I. Krylov, J. Phys. Chem. C, 2018, 122, 25753–25763 CrossRef CAS.
- D. Casanova and A. I. Krylov, J. Chem. Phys., 2016, 144, 014102 CrossRef PubMed.
- X. Feng, A. V. Luzanov and A. I. Krylov, J. Phys. Chem. Lett., 2013, 4, 3845–3852 CrossRef CAS.
- S. Matsika, X. Feng, A. V. Luzanov and A. I. Krylov, J. Phys. Chem. A, 2014, 118, 11943–11955 CrossRef CAS PubMed.
- M. Fumanal and C. Corminboeuf, J. Phys. Chem. Lett., 2021, 12, 7270–7277 CrossRef CAS PubMed.
- S. R. Yost, J. Lee, M. W. B. Wilson, T. Wu, D. P. McMahon, R. R. Parkhurst, N. J. Thompson, D. N. Congreve, A. Rao, K. Johnson, M. Y. Sfeir, M. G. Bawendi, T. M. Swager, R. H. Friend, M. A. Baldo and T. Van Voorhis, Nat. Chem., 2014, 6, 492–497 CrossRef CAS PubMed.
- K. R. Parenti, G. He, S. N. Sanders, A. B. Pun, E. Kumarasamy, M. Y. Sfeir and L. M. Campos, J. Phys. Chem. A, 2020, 124, 9392–9399 CrossRef CAS PubMed.
- Q. Van Nguyen, N. P. Van, H. Le Thi and G. Le Truong, ACS Appl. Nano Mater., 2022, 5, 16500–16508 CrossRef.
- T. Ohto, T. Inoue, H. Stewart, Y. Numai, Y. Aso, Y. Ie, R. Yamada and H. Tada, J. Phys. Chem. Lett., 2019, 10, 5292–5296 CrossRef CAS PubMed.
- R. Ferradás, V. M. García-Suárez and J. Ferrer, J. Phys.: Condens. Matter, 2013, 25, 325501 CrossRef PubMed.
- L. J. O'Driscoll, S. Sangtarash, W. Xu, A. Daaoub, W. Hong, H. Sadeghi and M. R. Bryce, J. Phys. Chem. C, 2021, 125, 17385–17391 CrossRef PubMed.
- N. Monahan and X.-Y. Zhu, Annu. Rev. Phys. Chem., 2015, 66, 601–618 CrossRef CAS PubMed.
- Y. Hong, J. Kim, W. Kim, C. Kaufmann, H. Kim, F. Würthner and D. Kim, J. Am. Chem. Soc., 2020, 142, 7845–7857 CrossRef CAS PubMed.
- S. Lukman, K. Chen, J. M. Hodgkiss, D. H. P. Turban, N. D. M. Hine, S. Dong, J. Wu, N. C. Greenham and A. J. Musser, Nat. Commun., 2016, 7, 13622 CrossRef CAS PubMed.
- S. Lukman, A. J. Musser, K. Chen, S. Athanasopoulos, C. K. Yong, Z. Zeng, Q. Ye, C. Chi, J. M. Hodgkiss, J. Wu, R. H. Friend and N. C. Greenham, Adv. Funct. Mater., 2015, 25, 5452–5461 CrossRef CAS.
- A. M. Alvertis, S. Lukman, T. J. H. Hele, E. G. Fuemmeler, J. Feng, J. Wu, N. C. Greenham, A. W. Chin and A. J. Musser, J. Am. Chem. Soc., 2019, 141, 17558–17570 CrossRef CAS PubMed.
- S. Khan and S. Mazumdar, J. Phys. Chem. C, 2020, 124, 1171–1177 CrossRef CAS.
- A. B. Kolomeisky, X. Feng and A. I. Krylov, J. Phys. Chem. C, 2014, 118, 5188–5195 CrossRef CAS.
- X. Feng and A. I. Krylov, Phys. Chem. Chem. Phys., 2016, 18, 7751–7761 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc03546a |
| This journal is © The Royal Society of Chemistry 2024 |