Open Access Article
Open Access ArticleA further focus on penetration indices of misfit van der Waals crusts
Jorge
Echeverría
 a and
Santiago
Alvarez
a and
Santiago
Alvarez
 b
b
aInstituto de Síntesis Química y Catalisis Homogénea (ISQCH) and Departmento de Química Inorgánica, Facultad de Ciencias, Universidad de Zaragoza, Pedro Cerbuna 12, 50009 Zaragoza, Spain. E-mail: Jorge.echeverria@unizar.es
bDepartment de Química Inorgànica i Orgànica, Secció de Química Inorgànica, and Institut de Química Teòrica i Computacional, Universitat de Barcelona, Martí i Franquès 1-11, 08028 Barcelona, Spain. E-mail: santiago@qi.ub.es
First published on 15th July 2024
Abstract
The recent proposal of the van der Waals crust as the spherical section comprised between the atomic radius and the van der Waals radius of an element generated a commentary by Grochala pointing out some supposed weaknesses of the approach (https://doi.org/10.1039/D3SC90191B). Our inital study is complemented herein by an analysis of the effects of the different size of the two interacting crusts, which shows that the penetration index defined earlier can adequately handle the misfit crust interactions.
In a recent paper published in this journal,1 we analysed in depth the potential application of a penetration index between the van der Waals crusts of two atoms A and B, pAB,2 as an alternative to the use of raw interatomic distances for the analysis of a variety of bonding situations, from weak van der Waals interactions all the way to strong multiple covalent bonds. The only pieces of information needed are the covalent and van der Waals radii of each of the two elements, rA,rB, vA and vB, as well as the interatomic distance dAB (Fig. 1a).
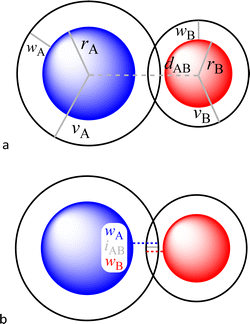 | ||
| Fig. 1 (a) Definition of the covalent (r) and van der Waals (v) radii, the width of the van der Waals crust (w) and the interatomic distance (d) for two nearby atoms A and B. (b) Parameters needed to define the penetration of atom A into the van der Waals crust of atom B and vice versa (eqn (4) and (5)). | ||
The interpenetration of the two crusts is defined as
| iAB = vA + vB − dAB | (1) |
Dividing the interpenetration by the sum of the van der Waals crust widths (wA and wB, Fig. 1a and eqn (2)), and multiplying by 100, we obtain the penetration index as a percentage of the sum of the two crust widths (eqn (3)).
| wA = vA − rA; wB = vB − rB | (2) |
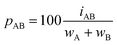 | (3) |
Simultaneously to the appearance of that paper, W. Grochala published a commentary warning about the problems that might arise when using such a penetration index for pairs of atoms with dissimilar sizes and different van der Waals crust widths.3
Although we had pinpointed such a possible problem in the text and given a simplified preliminary analysis in an Appendix, we think that the concern expressed by Grochala deserves a more detailed analysis that we present here.
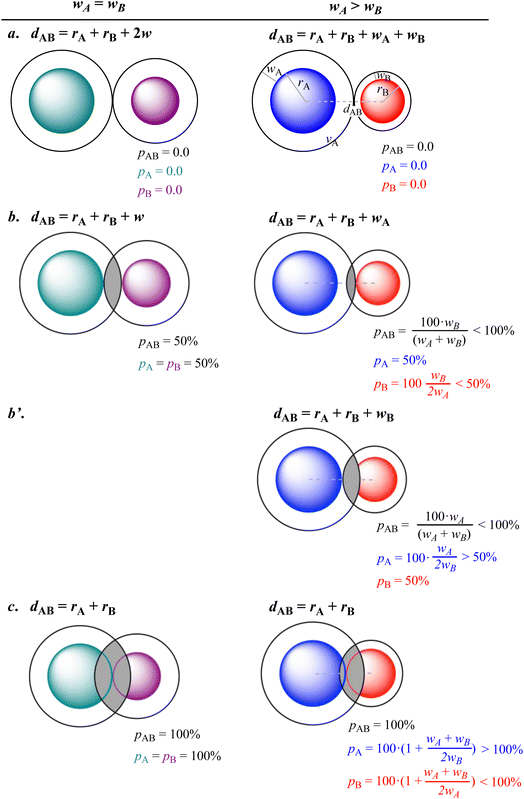
For an AB atom pair, we can differentiate the penetration of atom A into the van der Waals crust of atom B (pA, eqn (4)) from the penetration of atom B in the crust of atom A (pB, eqn (5)). Herewith we consider atom A to have a wider crust than atom B, regardless of the values of their covalent and van der Waals radii, i.e., wA ≥ wB.
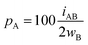 | (4) |
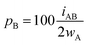 | (5) |
From eqn (4) and (5) it follows that pA ≥ pB in all cases. Notice also that the two degrees of penetration depend on the crust widths and on the distance, since iAB depends linearly on dAB, not on the atomic radii. Finally, it must be noted that pA and pB are calculated relative to the width of one crust each, whereas pAB is calculated with respect to the sum of the two widths, and for that reason we introduce a factor 2 in the denominator of eqn (4) and (5).
To explore the relationships between the three penetration parameters we compare in Fig. 2 their values at some special interatomic distances for the case of two crusts of the same width (left column) and for two misfit van der Waals crusts (right column), deduced by introducing the chosen distances into eqn (3)–(5). Notice that the expressions in the right hand column can incorporate the wA = wB cases (left hand side) by simply replacing in all the expressions the “<” and “>” symbols by “≤” and “≥”, respectively.
First, we consider the case in which two van der Waals spheres are barely in contact (Fig. 2a). By definition, the three penetration parameters are 0% both for crusts with the same width (Fig. 2a, left) or for misfit crusts (Fig. 2a, right). In a second case (Fig. 2b), the vdW crust of atom A reaches the valence sphere of atom B. The three penetration parameters adopt a value of 50% if the two crust widths are the same (Fig. 2b, left), but for misfit crusts only pA has that value, while pB is less than 50% (Fig. 2b, right).
For two misfit atoms, a further approach is required to get the VdW sphere of atom B in contact with the valence sphere of A (Fig. 2b′), giving pA > 50% and pB = 50%, while pAB is still less than 100%.
Finally, when the two valence spheres establish contact, i.e., when the interatomic distance is identical to the covalent radii sum (Fig. 2c), the interpenetration index pAB is 100% regardless of the widths of the two van der Waals crusts. The individual penetration pA reaches values higher than 100%, but those of pB are smaller than 100%.
All in all, it is seen that the evolution of the three penetration parameters as the interatomic distance decreases present each a clearly predictable behaviour. Still more interesting, the individual penetrations pA and pB can be obtained from the interpenetration index pAB according to eqn (6) and (7). Conversely, pAB can be obtained from the individual penetrations by means of eqn (8).
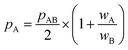 | (6) |
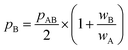 | (7) |
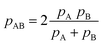 | (8) |
Those relationships are illustrated in Fig. 3, where we plot the individual penetration parameters pA and pB as a function of the interpenetration index pAB, for two atom pairs: one with practically identical crust widths, Ta–O (wTa = 0.83, wO = 0.84 Å), and one with very different widths, Zn–Te (wZn = 1.17 Å, wTe = 0.61 Å). In the first case (Fig. 2, left column), the individual penetrations pA and pB are equal to the interpenetration index pAB at any interatomic distance, whereas for atom pairs with different crust widths (e.g., Zn and Te) pA increases at a higher rate than pB as the interatomic distance decreases (i.e., as pAB increases).
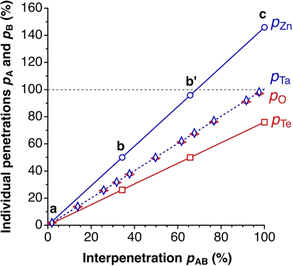 | ||
| Fig. 3 Dependence of the individual penetration parameters pA and pB on the penetration index pAB for the Zn–Te and O–Ta atom pairs, with crust width ratios wA/wB = 1.92 and 1.01, respectively. The points a, b, b′ and c correspond to the special distances specified in Fig. 2. All values calculated from standard covalent4 and van der Waals5 atomic radii at varying A–B distances. | ||
Conclusion
Even for misfit van der Waals crusts the interpenetration index pAB carries information on the different left-right (pA) and right-left (pB) penetrations. Those differences depend only on the relative widths of the two interpenetrating crusts (wA and wB), but not on the atomic sizes (rA, rB, vA and vB), as seen in eqn (6)–(8).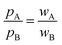 | (9) |
The deviation of the pA and pB values from pAB for an AB atom pair with misfit van der Waals crusts can be expressed by their quotient, which is found to be identical to the quotient of the crust widths (eqn (9)).
For those reasons, we think that it is advisable to use preferentially the interpenetration index pAB, which is conceptually clearer, implies no loss of information on the individual penetration indices pA and pB, and is simpler to use.
Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this comment.Author contributions
Both authors contributed to the discussion, writing and revision of the original draft.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Spanish Ministry of Economy and Competitiveness (PGC2018-093863-B-C21 and PID2022-140244NB-I00), the Spanish Structures of Excellence María de Maeztu program (grant MDM-2017-0767) and the Generalitat de Catalunya – AGAUR (grant 2017-SGR-1289). The allocation of computer time at CSUC is also acknowledged. J. E. is indebted to the Spanish MICCIN for a Ramón y Cajal research contract (RYC-2017-22853), and to the Gobierno de Aragón-ESF program (Research Group E07_23R) for financial support.References
- J. Echeverría and S. Alvarez, The Borderless World of Chemical Bonding Across the Van der Waals Crust, Chem. Sci., 2023, 14, 11647–11688 RSC.
- D. M. Gil, J. Echeverría and S. Alvarez, Tetramethylammonium Cation: Directionality and Covalency in Its Interactions with Halide Ions, Inorg. Chem., 2022, 61, 9082–9095 CrossRef CAS.
- W. Grochala, A focus on penetration index – a new descriptor of chemical bonding, Chem. Sci., 2023, 14, 11597–11600 RSC.
- B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Covalent Radii Revisited, Dalton Trans., 2008, 2832–2838 RSC.
- S. Alvarez, A Cartography of the Van der Waals Territory, Dalton Trans., 2013, 42, 8617–8636 RSC.
| This journal is © The Royal Society of Chemistry 2024 |