 Open Access Article
Open Access ArticleVesicular neurotransmitters exocytosis monitored by amperometry: theoretical quantitative links between experimental current spikes shapes and intravesicular structures†
Reina
Dannaoui
a,
Ren
Hu
 b,
Lihui
Hu
a,
Zhong-Qun
Tian
b,
Lihui
Hu
a,
Zhong-Qun
Tian
 b,
Irina
Svir
b,
Irina
Svir
 a,
Wei-Hua
Huang
a,
Wei-Hua
Huang
 c,
Christian
Amatore
c,
Christian
Amatore
 *ab and
Alexander
Oleinick
*ab and
Alexander
Oleinick
 *a
*a
aDépartement de Chimie, PASTEUR, Ecole Normale Supérieure, PSL Université, Sorbonne Université, CNRS, 24 rue Lhomond, Paris 75005, France. E-mail: christian.amatore@ens.psl.eu; oleksandr.oliynyk@ens.psl.eu
bState Key Laboratory of Physical Chemistry of Solid Surfaces, College of Chemistry and Chemical Engineering, Xiamen University, Xiamen 361005, P.R. China
cCollege of Chemistry and Molecular Sciences, Wuhan University, Wuhan 430072, P.R. China
First published on 31st July 2024
Abstract
Single cell amperometry has proven to be a powerful and well-established method for characterizing single vesicular exocytotic events elicited at the level of excitable cells under various experimental conditions. Nevertheless, most of the reported characteristics are descriptive, being mostly concerned with the morphological characteristics of the recorded current spikes (maximum current intensities, released charge, rise and fall times, etc.) which are certainly important but do not provide sufficient kinetic information on exocytotic mechanisms due to lack of quantitative models. Here, continuing our previous efforts to provide rigorous models rationalizing the kinetic structures of frequently encountered spike types (spikes with unique exponential decay tails and kiss-and-run events), we describe a new theoretical approach enabling a quantitative kinetic modeling of all types of exocytotic events giving rise to current spikes exhibiting exponential decay tails. This model follows directly from the fact that the condensation of long intravesicular polyelectrolytic strands by high concentrations of monocationic neurotransmitter molecules leads to a matrix structure involving two compartments in constant kinetic exchanges during release. This kinetic model has been validated theoretically (direct and inverse problems) and its experimental interest established by the analysis of the amperometric spikes relative to chromaffin and PC12 cells previously published by some of us.
Introduction
Neurons and secretory cells release molecular messengers including neurotransmitters stored inside intracellular vesicles through exocytosis. In these processes, a local fusion of the vesicle and cellular membranes occurs, creating a nanoscale fusion pore through which the vesicle content can be gradually released extracellularly (Fig. 1a) and detected by its oxidation at the tip of a carbon ultramicroelectrode in contact with the membrane of target neurons or neuroendocrine cells.1–3 These highly regulated activated processes depend significantly on cell types and/or their environment as well as the frequency and amplitude of activation pulses of adequate elicitors (e.g. Ca2+, Ba2+, K+, etc.). This allows recording of long-lasting amperometric traces consisting of large series of brief transient current spikes featuring sequential release events from individual vesicles.4 These informative traces encompass three major categories of current spikes which can be described based on their general shapes and whose relative proportions depend on the nature and conditions of the eliciting procedure as well as on the type of cell investigated. The most common category (>50–80%) contains well-defined current spikes involving a rapid increase in current intensity, primarily due to the opening of fusion pore, followed by a much longer monotonic decrease in current, termed hereafter the spike tail, leading to a gradual decrease while the current return to the baseline. A second category displays groups of accidental superposition of a few independent spikes from the first category when the local delay time between spikes is less than the average duration of their tails. The relative proportion of these overlapping signals can be significantly reduced by adequate modulation of the eliciting conditions. The peaks of this second category do not require specific theoretical analyzes since they can be easily modeled by statistical superpositions of peaks belonging to the first category. The third category, primarily observed for neurons probed under synapse-like conditions, represents complex events which could be precisely rationalized and quantitatively described as the result of flickering opening/closing sequences of fusion pores.5,6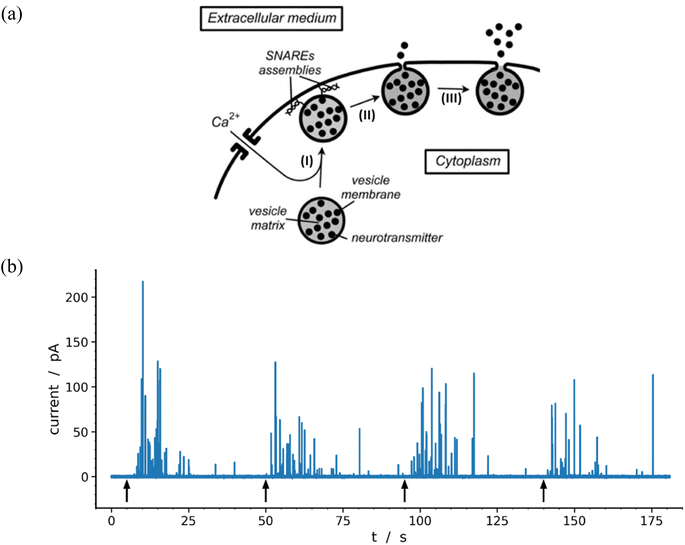 | ||
| Fig. 1 (a) Schematic representation of the main exocytotic release steps:7 (I) Ca2+-driven docking of a primed exocytotic vesicle; (II) opening of the fusion pore and beginning of release; (III) final opening of fusion pore and main releasing phase (for simplicity the SNAREs assemblies are only represented at the end of phase I because they play a crucial role in the docking mechanism;8,9 for the same reason the membrane cytoskeleton, see Fig. 3 in previous work,10 is not shown). (b) Representative amperometric data from a single PC12 cell with highly loaded vesicles11 recorded in HEPES buffer with 5 μm carbon fiber electrode held at +680 mV vs. Ag/AgCl. The 4 distinct groups of spikes seen in the trace were elicited by a series of 5 s duration 105 mM K+ puffs (each arrow indicates the beginning of K+ pulse for each group). Most of the events displayed in the trace (84%) were analyzable through the model developed here including 97 spikes exhibiting two-exponential tails and 9 single-exponential ones (see Table 1 and Fig. 7). | ||
Based on this categorization, it follows that most spikes containing kinetic information of interest for revealing general mechanistic features of exocytotic vesicular release control belong to the first category. This justifies the considerable efforts made to extract such fundamental biological information through physicochemical modeling and precise analyzes of this type of spikes.7,10,12–14 However, due to the absence so far of any rigorously established model and theory, these theoretical analyzes have necessarily been limited to spikes in the first category that exhibit a single exponential decay tail. But this omits spikes of the first category that exhibit two exponential tails although they generally represent a large proportion of events from this category and may even characterize most of them (see below for PC12 cells11,15). Such a particular shape has been qualitatively interpreted considering that it comes directly from non-isotropic intravesicular granular matrix structures (also known in the literature as “dense core” and “halo”16,17) that are expected to result from the imperfect condensation of the polyelectrolyte chromogranin by monocationic molecules.11,15,18,19 Indeed, as will be established therein, such granular structure implies the existence of complex kinetic exchange between differently condensed intravesicular domains while extracellular release of neurotransmitter proceeds.
Hereafter, we wish to establish theoretically and validate this new kinetic model based on the analyses of experimental spikes with two-exponential tails. A first scope is to rationalize theoretically the origin of these spikes as indicated above. A second objective is to develop a quantitative computational procedure based on this model to ensure precise extractions of structural, biophysical and kinetic information on intravesicular organization as well as on the size of fusion pores and their opening kinetics.
Results and discussion
Our main objective below is to describe and validate an original physicomathematical model aimed at accounting for the existence of the two types of current spikes of the first and most common class displayed in the amperometric traces recorded with carbon fiber microelectrodes from single neuroendocrine cells (see, e.g., Fig. 1b) in order to extract structural and kinetic features sustaining neurotransmitters (NT) release mechanism (Fig. 1a). The innovative contributions of the following report rest therefore essentially on theoretical and numerical bases. However, in order to validate this new model and document the efficiency of the resulting original extraction procedure, we will rely mainly on our previously published data relative to chromaffin cells1,7 or to PC12 cells containing vesicles with usual20 or high NT loads.11Definitions of spikes with single and two exponential decays
Fig. 1b displays a representative amperometric trace recorded from a PC12 cell which contains mostly current spikes of the first category (see Fig. 2). Similar traces are recorded from chromaffin cells and other neuroendocrine cells.20 The fast current rise of spikes of the first category mostly features the fusion pore opening dynamics.3 In contrast, the kinetics of descending branches is mainly controlled by diffusion-limited vesicle emptying, while the fusion pore radius has already reached its maximum value.10 It ensues that the existence of two types of spikes within the first category mostly evidences different kinetics of NT diffusional transport within the vesicles during release. These kinetics can be rigorously discriminated by plotting the spikes current in semi-log-scales as evidenced in Fig. 2B(a and b).15,21 Note that in order to simplify we use “diffusion” to represent the kinetically equivalent outcome of site-hopping exchange whereby a NT cation shifts from one chromogranin chelating site to an adjacent one. Indeed, as established for the similar situation in polymers,7,22–26 at a constant temperature, the corresponding kinetics are identical to those of a straightforward diffusion process.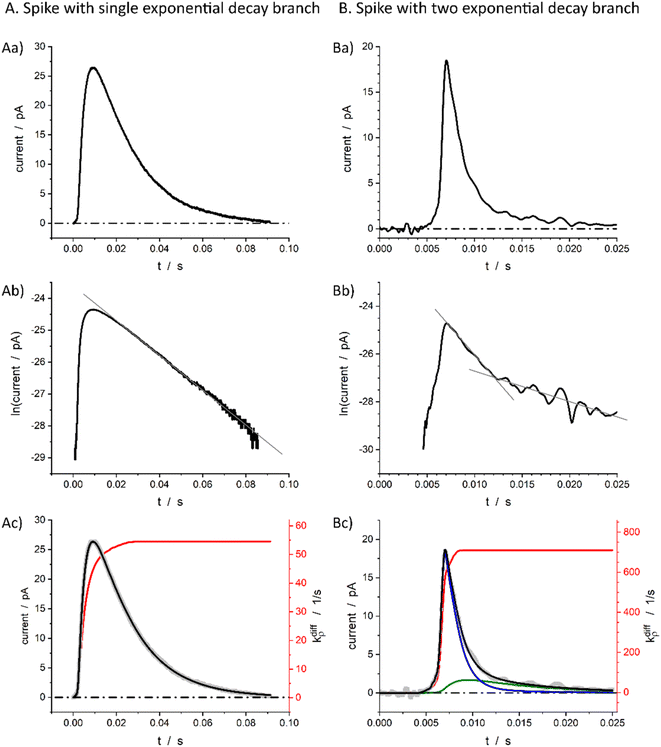 | ||
Fig. 2 Single (A) and double exponential (B) spikes in linear (a) and semi-log (b) scales; (c) shows simulations results of the spike current (black), its components (blue and green in (B(c)), see below for the meaning) and fusion pore opening dynamics (red, see text for kdiffρ(t) definition) with kdiffρmax = 54.5 s−1 in (A(c)) and kdiffρmax = 710.0 s−1 in (B(c)). The grey symbols are the overlayed experimental spikes shown in (a). The spike (A) was obtained from a chromaffin cell, while spike (B) is from a PC12 cell. Assuming Dves/rves2 = 415 s−1,27rves = 156 nm28 for chromaffin cells and Dves/rves2 = 5.8 × 103 s−1,29rves = 95 nm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29 for PC12 cells, the maximum pore opening can be evaluated as rmaxpore = 20 nm and rmaxpore = 12 nm, respectively. 29 for PC12 cells, the maximum pore opening can be evaluated as rmaxpore = 20 nm and rmaxpore = 12 nm, respectively. | ||
Let us first briefly recall the basics of the theoretical approach7,10,27 that we developed to analyze spikes with single-exponential current decay branches since, as will be made clear later, it is a simplified version of the physicochemical model developed in this work. Note that this previous model was carefully validated experimentally by analyzing several thousands of experimental amperometric spikes recorded from different cells (chromaffin, PC12, neurons, etc.).
First, we assume that the diffusional transport kinetics is essentially limited by the slow NT diffusion within the intravesicular matrix in order to reach the fusion pore and be released out. Indeed, for chromaffin or PC12 cells typical diffusion coefficients of NT inside the vesicle matrix is ca. 10−7 cm2 s−1,30 while it is ca. 10−5 cm2 s−1 in the extracellular solution.31 Since the vesicle radius is in the range of 80–300 nm (ref. 1 and 32) while the electrode – cell gaps are typically 100–200 nm,1 the diffusion times in the gaps (viz., a few μs) are negligible compared to that in the vesicular matrices (ca. a few tens of ms). Similarly, if the fusion pore connecting vesicle interior and extracellular space has not a flat toroid shape but a cylindrical one we have shown that the diffusion time through the cylindrical tube can be neglected (see section SM1 in ESI† in work1) unless the pore has length larger than vesicle size which, to the best of our knowledge, was never observed for NT release by cells.
Our former approach7 relies on Newton and Kelvin views to describe cooling of spherical bodies. This was previously validated for exocytotic vesicular release through accurate 3D numerical simulations for exocytotic vesicles.3,8 Interestingly, the approach proposed by Newton and Kelvin permits the use of ordinary differential equations to describe the temporal variations of intravesicular quantities over time periods exceeding a few tenths of the spikes rising times, i.e., as soon as a quasi-steady state diffusion regime prevails inside the whole vesicle.7,10,13 In addition to simplifying the physicomathematical formulations, this considerably reduces the duration of numerical analyzes of amperometric traces containing hundreds of spikes (Fig. 1b) to extract kinetic and structural information without any significant loss of precision compared to a 3D approach. Thus, a few seconds only are required per 2-exponential spike while the procedure is almost instantaneous for 1-exponential ones.
Spikes with single exponential tails
The instant NT released flux is given by:| dqout/dt = −dqves/dt | (1) |
| i(t) = nFdqout/dt = −nFdqves/dt | (2) |
| dqves/dt = −kdiffρ(t) × qves(t) | (3) |
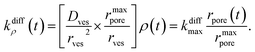 | (4) |
For the sake of presenting simply our approach, let us first assume that the fusion pore radius reaches its maximal value rmaxpore, i.e., ρ = ρmax = 1, faster than any other time scale of interest, then kdiffρ(t) is a constant noted as kdiffmax at all relevant times. Under these conditions, one obtains from eqn (3):
i(t) = nFkdiffmaxq0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−kdiffmaxt) exp(−kdiffmaxt) | (5) |
However, before the fusion pore radius reaches its maximal value one has from eqn (2) and (3):
| i(t) = nFkdiffρ(t)qves(t) | (6) |
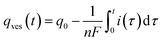 | (7) |
Additionally, from eqn (6) and (7) one obtains the fusion pore time opening function ρ(t):15
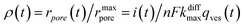 | (8a) |
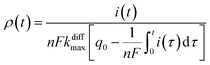 | (8b) |
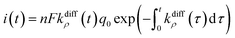 | (9) |
Fig. 2A(c) evidences the high precision of the spike current time-variations predicted by eqn (9) by comparing them to the experimental recording in Fig. 2A(a) (also overlaid onto the theoretical variations in Fig. 2A(c)). In Fig. 2A(c) is also shown the temporal dynamics of the fusion pore radius under the form of those of kdiffρ(t), which are proportional (eqn (4)).
Finally, let us recall that q0 whose value is required to evaluate numerically ρ(t) in eqn (8a) and (b) and i(t) in eqn (9) can be formally obtained by integrating the whole spike current taking into account that oxidation of NTs at the carbon electrode involves 2 F mole−1.33 However, it may happen that exponential decaying branches require a large time span to reach a situation where the current is sufficiently close to zero baseline level for neglecting any error due to the non-integrated part of the tail. In practice, this may happen because the tail current has a too low signal-to-noise value at the very end of the spike, and/or because a following spike current begins before this is achieved. In both cases the experimentally integrated q0 value would be underestimated. To overcome this problem, the exponential current tail was systematically extrapolated algebraically based on the equation of the linear fit of the spike tail in semi-log plot (see Fig. 2A(b)) in order to obtain a better estimation of q0.1 So, using Faraday's law, one obtains:
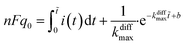 | (10) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) i(t) = (−kdiffmaxt + b) is the equation of the linear fit of the exponential segment in semi-log plot and
i(t) = (−kdiffmaxt + b) is the equation of the linear fit of the exponential segment in semi-log plot and ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) is the last time point where i(t) was measurable with a correct precision (see also ESI, Fig. A3).†
is the last time point where i(t) was measurable with a correct precision (see also ESI, Fig. A3).†
Model of individual exocytotic events featuring spikes with two exponential decays branches
The intravesicular matrix consists of strands of negatively charged polypeptides (from the chromogranin family) which are tightly packed through their association with the stored monoamine neurotransmitters cations,34 as well as by calcium ions, ATP, protons, neuropeptides, etc.35 Indeed, the presence inside of exocytotic vesicles of cations and of cationic molecules such as NTs prone to establish a dense network of hydrogen bonds with the charged chromogranin carboxylic groups, allows the whole matrix to condensate. Recent experimental works conducted by the Ewing group based on NanoSIMS investigations have demonstrated that the condensed matrices cannot always be regarded as homogeneous entities.17,36–38 In this context, molecular dynamics simulations have shown that truncated granin strands condense inhomogeneously, exhibiting both compacted and lacunar domains,39 as we assumed to rationalize some of our former experimental works.11,15 In fact, this is in full agreement with condensed matter physics18,19 which predicts that the degree of condensation of polyelectrolytes similar to the granins is strongly dependent on the cation charges. Accordingly, a total condensation into a single globular entity is only possible with multivalent cations,40,41 and even in this case this often gives rise to splitting of the intravesicular content between a low-condensed domain named “halo” by Ewing and others and highly-condensed one named “dense core” which release their content at different rates.12,42,43 Oppositely, monoamine NT are monocations so their electrostatic interaction energies with granins anionic groups are not sufficient to cause such a full condensation, even taking into account the network of hydrogen bonds, due to the large generated negative entropy.13,14 Under such conditions the intravesicular matrix is expected to adopt a folded “pearl necklace” structure (Fig. 3),4,10,14,44 whose “pearls” correspond to well-compacted blobs of chromogranin where the NT cations are strongly linked to the anionic sites of the polypeptides threaded by less compacted strands in which the NT cations are less associated with the granins backbones. In fact such dual organization has been observed by molecular dynamic investigations.39 Note that this obeys a similar physical principle to that involved for the creation of double layers in electrochemistry.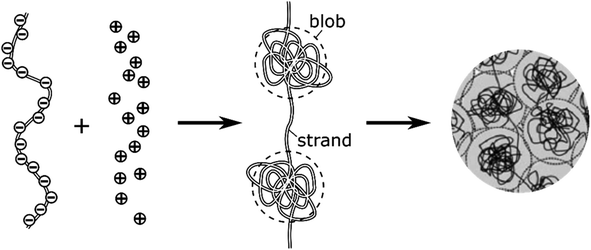 | ||
| Fig. 3 Schematic cartoon of the intravesicular structure of the secretory vesicle (the terminology “blob” vs. “strand” was introduced by de Gennes).44 | ||
NT diffusion by site-hopping is still feasible in the well-compacted domains, but is considerably slower than in the less compacted areas because any local reorganization of the assembly surrounding each site is more difficult. Nonetheless, molecules initially stored in these highly-compacted compartments may exchange with adjacent vacant sites present in the less compacted ones and be ultimately released through fast site-hopping diffusion up to the entrance of the fusion pore. In first approximation, this release contribution through exchange between the two phases (i.e., from highly- to less-packed domains that are labeled in the following for simplicity as slow and fast compartment, respectively) can be described by the following kinetic scheme (see ESI Section C† for a discussion justifying the consideration of an irreversible transfer):
 | (11a) |
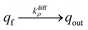 | (11b) |
At each given time the conservation of the chromogranin anionic sites in each compartment implies that qs + ∅s = q0s + ∅0s and qf + ∅f = q0f + ∅0f where the quantities before release begins (i.e. t = 0) are labeled with the superscript ‘0’. Assuming that at initial times the vesicles are fully loaded, viz., that the quantities of “free” sites ∅0f and ∅0s are negligible vs. q0f and q0s, the terms (q0s − qs) and (q0f − qf) represent the amounts of empty sites in each compartment. Taking advantage of our previous works,7,15 and following the same lines developed above for the single-exponential case, the release process in eqn (11a) and (b) can be formalized by the following set of non-linear ordinary differential equations:
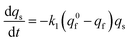 | (12a) |
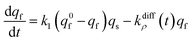 | (12b) |
Note that summation of eqn (12a) and (b) shows that the current, i(t), monitored at each instant t due to NT electrooxidation at the electrode surface is equal to nFkdiffρ(t)qf:
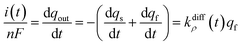 | (12c) |
Eqn (12a)–(c) are associated to the initial conditions:
| qt=0s = q0s, qt=0f = q0f, qt=0out = 0 | (12d) |
In addition, owing to the conservation of matter one has also:
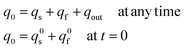 | (12e) |
It should be noted that eqn (6) and (8a) remain valid for the spikes with two exponential decay provided that qves(t) is replaced by qf(t), hence the fusion pore dynamics can be reconstructed exactly as was detailed above for single-exponential spikes as soon as the system (12a)–(d) is solved.
The system in eqn (12a) and (b) obeys two limits depending on the time. At short times, 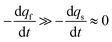 since by definition any release from the slow compartment necessarily lags behind that of the fast compartment. Hence, qs ≈ q0s and dqs/dt ≈ 0 so that at initial times eqn (12b) can be approximated by:
since by definition any release from the slow compartment necessarily lags behind that of the fast compartment. Hence, qs ≈ q0s and dqs/dt ≈ 0 so that at initial times eqn (12b) can be approximated by:
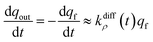 | (13a) |
Eqn (13a) shows that at initial times, as soon as the fusion pore radius has completed its expansion (viz., kdiffρ(t) = kdiffmax) NT release proceeds through a single exponential decay branch with a time constant τ1exp = 1/kdiffmax.1 In other words, up to when the slow compartments start to release significantly, the situation remains essentially identical to the case of single-exponential spikes.
Conversely, when the fast compartment is almost emptied, viz. when qf ≪ q0f and 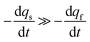 , the releasing rate is essentially controlled by the kinetics of transfer of NT molecules from the slow compartments into the fast one in which they can rapidly diffuse to the fusion pore. In other words, NT quantity in the fast compartment is under (quasi-)steady state, so that:
, the releasing rate is essentially controlled by the kinetics of transfer of NT molecules from the slow compartments into the fast one in which they can rapidly diffuse to the fusion pore. In other words, NT quantity in the fast compartment is under (quasi-)steady state, so that:
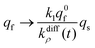 | (13b) |
Substituting eqn (13b) into (12c) shows that at long times:
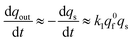 | (13c) |
This establishes that while time elapses the kinetics of the current decay progressively shifts from a single exponential mode described by eqn (13a) to another single exponential mode with a time constant τ2exp = 1/(k1q0f) as featured by eqn (13c). This is in perfect agreement with the experimental observations in Fig. 2B.
To conclude this section, we want to briefly discuss two modeling options that we have not considered above. One of them was proposed by Jackson et al.45 and amounts to considering that there exists a single NT isotropic distribution compartment whose release kinetics follows what our model attributes to the second exponential of the decay tails. Under such circumstances, the kinetic regime our model attributes to a two-step kinetic process involving a coupling between (i) the fusion pore opening phase followed by (ii) the first exponential release mode (see below sections I and II of Fig. 4b) would necessarily be replaced by a complex opening of the fusion pore involving a rapid enlargement followed by a slower shrinkage phase before reaching a constant value as obtained by Jackson et al.45 for vesicular release from chromaffin cells. However, we tend to favor our model firstly because it is perfectly consistent with de Gennes “blob” theory on soft matter,44 namely the necessary existence of an anisotropy during the condensation of polyelectrolytes by monocations as further elaborated by theoretical physics.13,14 Furthermore, the experimental reality of the two-phase structuring of the matrix of catecholamine vesicles cannot be disputed since it has been often observed by TEM imaging (see e.g., the following works14,16,46,47) as well as their granular organization by NanoSIMS.12 Secondly, because if the mechanism of initial opening of fusion pores seems already understood,48 that of a down-regulation of the radius of fusion pores after this phase (for example by synaptophysin-dynamin association49) remains still to be clarified.48,50
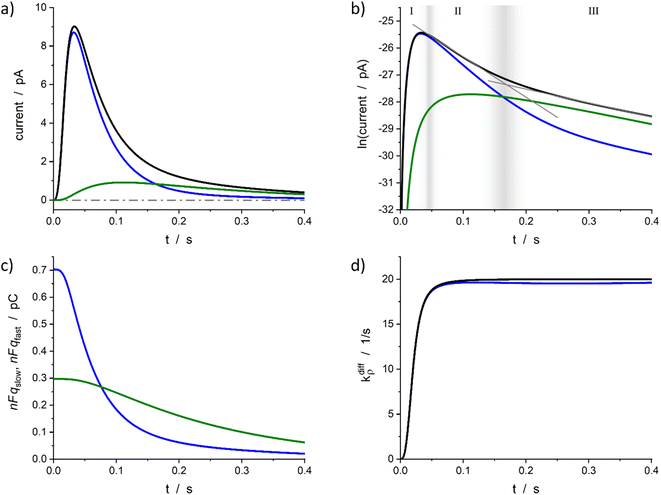 | ||
| Fig. 4 Simulated spike and its reconstructed components in real (a) and semi-log (b) scales. (c) Changes in the storage of neurotransmitter in fast and slow compartments. (d) Comparison between the imposed function (14) and its reconstruction. Simulation input parameters values (see eqn (12a)–(c)): a = 50, m = 3, Q0 = 2Fq0 = 1 pC, q0f/q0 = 0.7, k1q0f = 5 s−1, kdiffmax = 20 s−1; reconstructed parameters agreed within 1% except for kdiffmax value that was obtained with a −2% accuracy. Please refer to the text for a description of zones I–III in (b) and their gray gradient boundaries. | ||
Finally, if the existence of two main storage compartments were considered in accordance with the theoretical physics of polyelectrolyte condensation, but would be releasing in parallel, that is to say without any kinetic coupling, such as the observation of two-exponential decay tails may intuitively suggest, a completely different kinetic result inconsistent with the experimental data would be observed. This solution was therefore not explored in this work.
Validation of the model based on theoretically generated spikes
The above model was developed with the aim of rationalizing the existence in the first category of amperometric spikes with two-exponential tails and to extract the temporal variations of the main parameters, viz., qf(t), qs(t), and kdiffρ(t), which regulate NT release for these events (see ESI Section A† for details of the reconstruction procedure). Note that the model developed above for current spikes with two-exponential decay tails automatically includes the case of spikes exhibiting single-exponential decay branches, i.e., when k1 or q0s are negligible.1 The knowledge of q0f and q0s provides important information about the internal grainy structure of each analyzed vesicle while that of kdiffρ(t) time variations gives a direct access to the fusion pore opening rate as well as to its maximum radius value for each analyzed experimental current spike i(t).To proceed we wish first to validate the present model by showing that it allows quantitative analyses of two-exponential spikes with a high precision. For this purpose, we relied on the analyses of simulated theoretical spikes isim(t) corresponding to a series of arbitrarily selected values of k1, q0f, q0s and kdiffmax. To this aim, the time variations of kdiffρ(t) were assumed to obey the formulation in eqn (14) with:
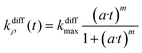 | (14) |
Fig. 4a represents a typical amperometric spike, i(t), simulated for the electrooxidative detection of a catecholamine (n = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33) based on the set of eqn (12a)–(c) for the set of k1, q0f, q0s, kdiffmax, a and m values given in its caption. The corresponding time variations of its two components, viz., −nF(dqf/dt) and −nF(dqs/dt) values, are also shown. Fig. 4b displays the same data presented in semi-logarithmic plots and illustrates the time ranges (zones II and III) of the two exponential regimes predicted above. Fig. 4c presents the time variations of the simulated qf(t) and qs(t) values which confirm that the unloading of the well-compacted domains starts to be visible only when more than 50% of the initial content of the less compacted domain has been released.
33) based on the set of eqn (12a)–(c) for the set of k1, q0f, q0s, kdiffmax, a and m values given in its caption. The corresponding time variations of its two components, viz., −nF(dqf/dt) and −nF(dqs/dt) values, are also shown. Fig. 4b displays the same data presented in semi-logarithmic plots and illustrates the time ranges (zones II and III) of the two exponential regimes predicted above. Fig. 4c presents the time variations of the simulated qf(t) and qs(t) values which confirm that the unloading of the well-compacted domains starts to be visible only when more than 50% of the initial content of the less compacted domain has been released.
Furthermore, for all cases tested as in Fig. 4a–c, the accuracy of the extraction procedure (see details in ESI Section A†) was better than 1% so that the time variations of the extracted time variations of i(t), qf(t), and qs(t) were impossible to differentiate graphically from the simulated ones. The only noticed slight discrepancy concerns the long time limit of kdiffρ(t) as evidenced in Fig. 4d, where the kdiffmax value was ca. 2% smaller than predicted. However, such slight discrepancy in the outcome of the invert problem was expected since in zone III the NT release flux depends essentially on (k1q0f) because the quantity qf(t) has almost reached its steady state value predicted by eqn (13b). Yet, the pore time-opening function, viz., kdiffρ(t), is perfectly reproduced in zone I and in the first part of zone II since in these zones the quantity qf(t) is still far from its steady state limit.
Altogether, these results validate the overall extraction procedure and demonstrate that it can be successfully applied for extracting all the parameters of interest based on the analysis of amperometric spikes with two-exponential tails. Remarkably, the fact that this relies on the solution of set of two coupled differential equations rather than on that of 3D partial derivative systems3,51 leads to typical execution times of 3–5 seconds per spike for each reconstruction procedure. This allows a facile and rapid analysis of individual current spikes present in amperometric traces within minutes.
Application to experimental spikes
The above section described the direct theoretical problem and, more interestingly, validated the quality of the procedure allowing the extraction of the important parameters that govern the release events giving rise to amperometric spikes with two-exponential tails. However, the second aspect was validated using simulated spikes which did not present any problem related to the presence of experimental noise although this may affect the accuracy of the reconstruction when analyzing small experimental spikes especially when their peak currents intensities are only a few times larger than the background noise. For this reason, in this section we wish to examine the accuracy of this extraction procedure when applied to real experimental spikes. To this end, we rely below on representative spikes from chromaffin or PC12 cells previously published by some of us.Fig. 5 illustrates reconstructed data for a spike measured from a single chromaffin cell.1,7 As can be seen the two current components (Fig. 5a and b), time variations of the neurotransmitter quantities in each domain (Fig. 5c) and fusion pore dynamics (Fig. 5d) can be successfully reconstructed to afford values of the four main parameters: Q0 = 4.6 pC, viz., q0 = 24 amol, q0f/q0 = 0.71, k1q0f = 7.2 s−1, kdiffmax = 41 s−1. Importantly, although the current in zone III (as defined in Fig. 4b) involves a significant contribution of the background noise (compare Fig. 5a and b), the accuracy of current measurements in the interzone II/III is sufficient to allow a full extraction of these parameters as well as the time variations of the fusion pore opening function (Fig. 5d).
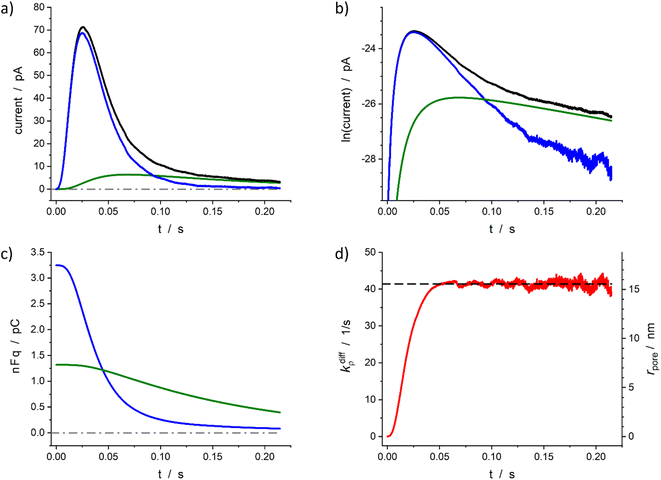 | ||
Fig. 5 Quantitative analysis of a typical amperometric spike featuring adrenaline release monitored at a chromaffin cell with carbon fiber electrode (CFE). Current spike and its reconstructed compartment-wise components in linear (a) and semi-log (b) scales. Variation of NT content in each domain (c) and reconstructed fusion pore dynamics (d). The dashed line in (d) represents kdiffmax; the right vertical axis indicates the corresponding rpore values which were evaluated assuming Dves/rves2 = 415 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27 and rves = 156 nm.28 27 and rves = 156 nm.28 | ||
Based on the value of Dves/r2ves = 415 s−1 determined in our previous works7,27 and that published for rves average value (156 nm)22 the time dependence of the fusion pore radius, rpore(t), was readily deduced from that of kdiffρ(t) using eqn (4) (see right vertical scale in Fig. 5d).
Fig. 6 demonstrates the reconstruction quality obtained for a typical experimental spike recorded at a single PC12 cell. Interestingly, although the spike chosen exhibits a pre-spike feature21,52 the extraction procedure yields excellent results (see below). The reconstructed parameters were: Q0 = 0.15 pC, viz., q0 = 0.78 amol, q0f/q0 = 0.7, kdiffmax = 2.2 × 103 s−1, k1q0f = 4.7 × 102 s−1. These results are in perfect agreement with the known smaller total vesicle content and faster rate constants for PC12 cells vs. chromaffin cells.32 It can be pointed out that although the spike current integrates a pre-spike feature (PSF)53 in the time range of 0.4 to 1.5 ms, and the noise of the background current has a visible impact on the spike current measurement (see Fig. 6a and b for t ≥ 4 ms), the reconstruction procedure converges extremely well over the whole current spike duration so kdiffρ(t) and rpore(t) time-dependent values can be extracted including their maxima values (Fig. 6d).
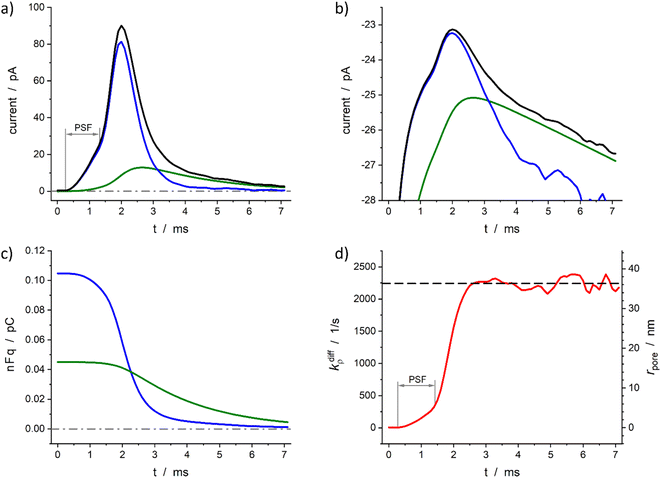 | ||
Fig. 6 Quantitative analysis of a typical amperometric spike featuring dopamine release monitored at a PC12 cell with CFE. Current spike and its reconstructed compartment-wise components in linear (a) and semi-log (b) scales. Variation of NT content in each domain (c) and reconstructed opening dynamics (d). The dashed line in (d) represents kdiffmax; the right vertical axis indicates the corresponding rpore values which were evaluated assuming Dves/rves2 = 5803 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29 and rves = 94 nm.29 PSF in (a) and (d) stands for “pre-spike feature”. 29 and rves = 94 nm.29 PSF in (a) and (d) stands for “pre-spike feature”. | ||
The typical results shown in full details in Fig. 5 and 6 validate the application of the extraction procedure to experimental amperometric spikes. In addition, Fig. 5c and 6c confirm that the exchange between the fast and slow domains may begin only when substantial amounts (ca. 50%) of NT cations initially present in the fast domain have been released. This validates a fortiori the fact that the transfer of NT is considered to be irreversible (eqn (11a)) in our model. To conclude, it must be emphasized that the present model makes it possible for the first time to quickly analyze all amperometric spikes of the first category within a time interval (a few seconds) compatible with the analysis of complete amperometric traces containing hundreds of peaks or more. This model is fundamentally based on the coexistence and kinetic interaction of two types of intravesicular domains. This central hypothesis is not only in agreement with the physicochemical behavior predicted for the condensation of polyelectrolytes similar to chromogranins18,19,34,35 but has recently received experimental support from the nanoSIMS experiments reported by Ewing's group.12
Quantitative kinetic analysis of a full amperometric trace data
The ca. 3 minutes long amperometric trace recorded from a single PC12 cell shown in Fig. 1b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11 contains 106 analyzable spikes of the first category (i.e. 84% of all individual events), of which 97 spikes had two-exponential tails and a very few ones (9) with single-exponential tails. One may be surprised by the very large proportion of spikes with two-exponential tails, but as will be clear in what follows, several of these would have appeared upon visual inspection to display single-exponential tails because their second exponential component was comparatively faint and would have been dismissed without plotting them in semi-logarithmic scales (compare Fig. 2). For this reason, considering that such situation may happen often unnoticed, all peaks of the first category were analyzed by the present procedure and their parameters extracted without any distinction.
11 contains 106 analyzable spikes of the first category (i.e. 84% of all individual events), of which 97 spikes had two-exponential tails and a very few ones (9) with single-exponential tails. One may be surprised by the very large proportion of spikes with two-exponential tails, but as will be clear in what follows, several of these would have appeared upon visual inspection to display single-exponential tails because their second exponential component was comparatively faint and would have been dismissed without plotting them in semi-logarithmic scales (compare Fig. 2). For this reason, considering that such situation may happen often unnoticed, all peaks of the first category were analyzed by the present procedure and their parameters extracted without any distinction.
Table 1 summarizes the results of this analysis for PC12 spikes11 with two-exponential decay tails, namely those whose analysis yielded q0f > q0s and k1q0f < kdiffmax within the precision of the determinations. The values in Table 1 are the median values of the reconstructed parameters for the 97 analyzed spikes with two-exponential tails whose distributions obeys log-normal statistics (see plots in Fig. 7). The total released amount of neurotransmitter q0 given in the Table 1 is somewhat higher than those reported in the literature for PC12 cells32 but fully agrees with our previous report.4
| Q 0/pC | q 0 /amol | q 0f/q0 | q 0s/q0 | k diffmax/s−1 | k 1 q 0f/s−1 |
|---|---|---|---|---|---|
a median total releasable amount of transmitter per vesicle. q0 is computed from Q0 using Faraday law Q0 [pC] = 10−6 × nFq0 [amol], with n = 2,33F = 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485.33 C mol−1. 485.33 C mol−1.
|
|||||
| 0.10 (0.07; 0.16) | 0.52 (0.35; 0.81) | 0.81 (0.76; 0.86) | 0.19 (0.14; 0.24) | 720 (510; 1100) | 180 (110; 280) |
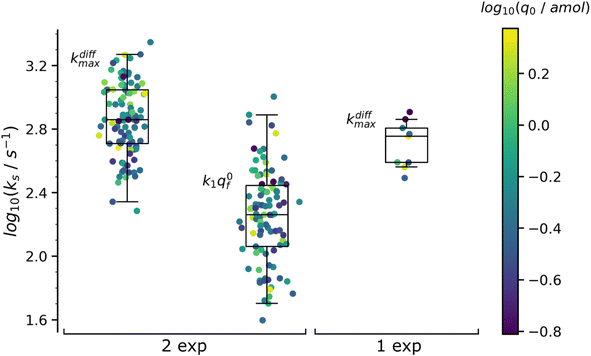 | ||
| Fig. 7 Box and whisker plots of the reconstructed kdiffmax and k1q0f values for the 97 spikes with two exponential decay and kdiffmax for the 9 spikes with single exponential decay (spikes from the trace in Fig. 1b). The color of each dot refers to the reconstructed releasable content of a vesicle q0 (in amol) as indicated by the color bar on the side. The different horizontal segments in each box and whisker plot represent, from top to bottom, the upper extreme (90%), upper quartile (75%), median (50%), lower quartile (25%) and lower extreme (10%) probabilities. | ||
Concerning the quantities q0, q0f and q0s shown in Table 1 is important to recall that they represent the median amounts of neurotransmitter released during spontaneous exocytotic events and not at all the total quantities stored in the vesicles before exocytosis occurs. Indeed, as release proceeds, the NT partition coefficient from the intravesicular matrix to the cell-electrode gap environment, PNTves→gap, must necessarily decrease to keep the vesicle integrity. On the one hand, PNTves→gap is initially very large to account for the extremely high initial values of intravesicular NT concentration.2,4,30,54,55 On the other hand, as the release progresses, the matrix/NT assembly is continually losing its initial structure due to the replacement of the NT cations by hydrated extracellular cations.3 The ensuing increase in the internal pressure of the vesicle necessarily causes a thermodynamic destabilization of the intravesicular matrix structure which should ultimately lead to its swelling40,54 as soon as it can no longer be compensated by the increase of the surface tension of the vesicular membrane.56–58 Therefore, in order to avoid possible membrane rupture or a complete fusion,30,59 the excess internal energy must be dissipated provoking a decrease of PNTves→gap while release proceeds with the consequence that release will stop before all initially stored NT quantities have been released. Note the release may stop before this situation is reached if the fusion pore closes although this seems quite rare except for intrasynaptic release.5,6,60 Consequently, to satisfy the intravesicular thermodynamics and maintain the vesicular structural integrity, a significant amount of NT remains inside the vesicle as already shown at several instances which evidenced that ca. 40 to 60% of the stored molecules remained stored inside vesicles at the end of release.6,16,43,54,61,62
The values in Table 1 need to be compared to those of q0 (0.27 amol) and kdiffmax (570 s−1) obtained for the 9 spikes exhibiting a single-exponential tail. Interestingly, upon assuming an identical NT concentration in both cases this population corresponds to vesicles with volumes being ca. half those of vesicles giving rise to a double-exponential behavior. This suggests that in order to structure into slow and fast domains the vesicles need to be sufficiently large. Hence, below a threshold size a single compartment is formed with structural properties lying presumably in between those of the fully compact and less compact domains. This is in full agreement with the fact that the value kdiffmax (570 s−1) for vesicles giving rise to spikes with single-exponential tails is less than that (720 s−1) determined for those leading to double-exponential release tails.
The distributions of the values reconstructed from spikes with one and two exponential decays as well as their statistics are plotted in Fig. 7. The color of each marker refers to the scale of the releasable NT content determined for the same vesicle, q0, shown on the right of the box and whisker plots. It is noted that the sampling time (0.1 ms![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11) used to record the amperometric trace in Fig. 1b was sufficiently small to record with sufficient accuracy the decay tails of all spikes including those with the largest kdiffmax values (ca. 2.2 × 103 s−1). On the other hand, the mean time separation between two successive spikes of each group of K+-elicited events was sufficiently wide (ca. 300 ms
11) used to record the amperometric trace in Fig. 1b was sufficiently small to record with sufficient accuracy the decay tails of all spikes including those with the largest kdiffmax values (ca. 2.2 × 103 s−1). On the other hand, the mean time separation between two successive spikes of each group of K+-elicited events was sufficiently wide (ca. 300 ms![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11) to allow recording the whole decay tail of each current spike even those with the largest time constants (ca. 30 ms). Hence the only possible experimental limitation which defined the set of 106 analyzed spikes was due to the background noise limit (0.3 pA
11) to allow recording the whole decay tail of each current spike even those with the largest time constants (ca. 30 ms). Hence the only possible experimental limitation which defined the set of 106 analyzed spikes was due to the background noise limit (0.3 pA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11) with the smallest peak intensity (ca. 5–7 pA) but that was taken care of by the extrapolation of the current tails which was used in evaluating q0 by eqn (10) or eqn (A.2)† (compare the outcome in Fig. 5 and 6). It may then be safely concluded that the distributions of kdiffmax and k1q0f values are not limited by the experimental recording of the amperometric traces and that they reflect biological properties characterizing each exocytotic event.
11) with the smallest peak intensity (ca. 5–7 pA) but that was taken care of by the extrapolation of the current tails which was used in evaluating q0 by eqn (10) or eqn (A.2)† (compare the outcome in Fig. 5 and 6). It may then be safely concluded that the distributions of kdiffmax and k1q0f values are not limited by the experimental recording of the amperometric traces and that they reflect biological properties characterizing each exocytotic event.
Fig. 8a suggests the existence of a correlation between the pairs of values kdiffmax and k1q0f determined for each of the 97 amperometric peaks presenting two exponential tails recorded in the trace shown in Fig. 1b (note that kdiffmax > k1q0f by definition so all datapoints lie below the first bisector shown by the dashed line). Fig. 9 (top) provides a quantitative confirmation of the correlation suggested in Fig. 8a by displaying a cumulative projection of all datapoints onto the axis perpendicular to the bisector (as shown by the black arrow in Fig. 8a). This projection gives strength to the correlation in Fig. 8a since it evidences that almost all datapoints fall within a relatively narrow interval centered around the relationship k1q0f ≈ 0.25kdiffmax. Moreover, it is noted that using a different experimental approach, Ewing et al.21 also hinted to the existence of a biologically-based relationship between two time constants that they used to characterize spikes decay tails in their investigation and which are somewhat related to 1/kdiffmax and 1/(k1q0f). So let's examine the logic behind this correlation to recognize its biological significance, if any.
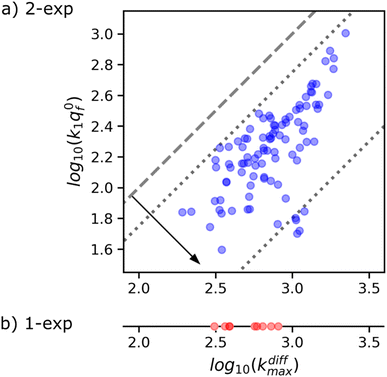 | ||
| Fig. 8 (a) Correlation between kdiffmax and k1q0f values characterizing each of the 97 spikes exhibiting two-exponential tails analyzed from the amperometric trace in Fig. 1b. These are put in perspective with the kdiffmax values (b) determined for the 9 spikes displaying a single-exponential tail recorded in the same amperometric trace. Slanted dotted lines delimit the region in which the spikes with two exponential tails may be quantitatively analyzed owing to the experimental constraints (see text and Fig. 9). | ||
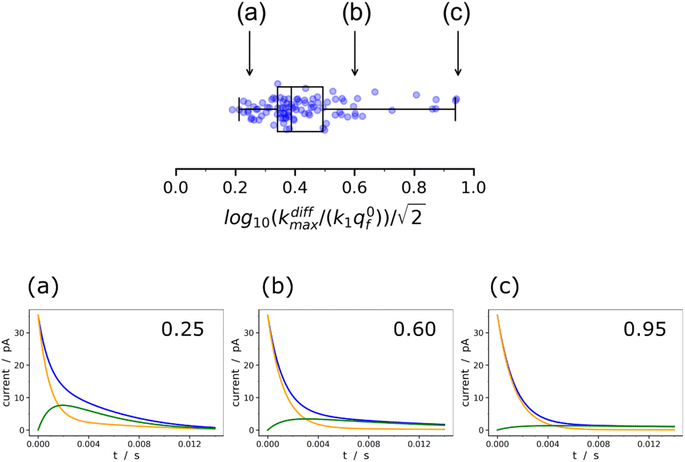 | ||
Fig. 9 Box and whisker plot together with the underlying distribution of the projections of the data points shown in Fig. 8a onto an axis perpendicular to the line with a unit slope (black arrow in Fig. 8a). The whiskers correspond to 1 and 99 percentiles. The total currents and its components are simulated for 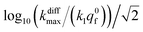 values shown in the sub-plots (a–c) as well as in box and whisker plot, for more details see text. Simulations in (a–c) were performed by imposing an instant fusion pore opening at t = 0 s in order to emphasize the effect of the intravesicular kinetics on the tail shapes. values shown in the sub-plots (a–c) as well as in box and whisker plot, for more details see text. Simulations in (a–c) were performed by imposing an instant fusion pore opening at t = 0 s in order to emphasize the effect of the intravesicular kinetics on the tail shapes. | ||
It is important to recall in this respect that in order to extract both values of kdiffmax and k1q0f from a single amperometric spike, its decay tail must display clear components of the first and second exponential behaviors or at least a recognizable kinetic mixture of these allowing their deconvolution with sufficient precision. However, such deconvolution process may be hampered at short time by a mixing of the fusion pore opening kinetics with the first exponential decay mode (compare Fig. 4a and b). Since the opening dynamics of the fusion pores being a priori unknown, the recording of a sufficient time trace linked to the first exponential mode is necessary. On the other hand, at large times, the second exponential behavior must give rise to a current flow large enough to be identified with sufficient precision from the background noise (compare Fig. 2B(a and b)). This is easily understood by examining the decay tails shown in Fig. 9a–c which were simulated using the following parameters: q0 = 0.52 amol, q0s = q0f = q0/2, log10(kdiffmax/s−1) = 2.85 (i.e. kdiffmax = 710 s−1, see Table 1), for three different values of log10(k1q0f/s−1) = 2.5, 2.0, 1.5 (i.e. k1q0f = 316, 100, 32 s−1) corresponding to the markers (a–c) shown in Fig. 9 (top) and assuming that the fusion pore opened instantly at t = 0 (assuming the same values as above, i.e., Dves/rves2 = 5.8 × 103 s−1,29rves = 95 nm;29 note that the radius of the instantly opened pore deduced from kdiffmax is then rmaxpore = 11 nm). This series of simulated current spikes shows that to extract both kdiffmax and k1q0f values from a single amperometric decay tail, these values must necessarily be commensurable. This is precisely what is observed experimentally in Fig. 8 and 9. Moreover, the current trace in Fig. 9a would evidently be strongly altered at short times by the fusion pore opening kinetics (compare Fig. 4a and b) so only (k1q0f) would be accessible. Likewise, the second exponential mode in Fig. 9c would be difficult to analyze due to the background noise (compare Fig. 2B), so only kdiffmax may be measurable.
This analysis actually requires that data points featuring all measurable |kdiffmax, k1q0f| pairs must fall within the area delimited by the two dotted lines parallel to the first bisector drawn in Fig. 8a as observed experimentally. It is therefore impossible to conclude with certainty whether this correlation has a biological significance or whether it is simply an artifact linked to the experimental impossibility of measuring datapoints located outside this area. However, given that less than 10% of the current spikes exhibited mono-exponential behavior while the remaining 90% could be analyzed with high accuracy in the double-exponential mode predicted by our theoretical model, we are inclined to consider this correlation as having a biological importance.
Conclusion
In this work, a novel theoretical model was proposed to take into account and analyze amperometric spikes corresponding to unique vesicular exocytotic events comprising decay tails obeying two exponential modes, which represent one of the main types of spikes. This model is based on an original concept according to which vesicular release involves a simultaneous exchange of the neurotransmitter between two types of intravesicular domains whose formation arises from the entropic constraints of condensation of polyelectrolytes by mono-charged ions such as most neurotransmitters.The predictive value of the present model and its importance in solving the inverse problem – namely the quantitative deconvolution of key physicochemical factors that determine the shape of amperometric spikes – have been carefully validated using theoretical and experimental data taken from our published work. This made it possible to design a robust automatic computational procedure to extract extremely rapidly the values of the main kinetic parameters that govern the release as well as the final fusion pore size and opening kinetics from the most common experimental amperometric spikes featuring single exocytotic release events from large amperometric datasets.
The present theoretical and computational framework can be formally generalized to the case of vesicular matrices containing more than the two condensed domains considered in this study, namely either “fully condensed” or “weakly condensed”. Indeed, even if the results of molecular dynamics simulations suggest that this is a simple but rather good description, formally there may exist a gradient of “more and more condensed” domains leading to amperometric spikes with more than two exponential decay tails. The corresponding amperometric spikes would then be analyzed through simple extensions of the current model, provided that their decay tail components could be deconvolved. However, this will be limited by the accuracy of the spike current numerical recordings and the relative amount of background noise, as has been highlighted here.
Data availability
This work is entirely theoretical and devoted to the analyses of previously published experimental data by some of us, as indicated whenever needed. We can confirm that no new experimental data was generated during this study. The only data gathered as the outcome of our theory is the set of statistical values reported in Table 1.Author contributions
R. D. – investigation (theoretical), software, formal analysis; R. H. – investigation (experimental); L. H. – investigation (experimental); Z. Q. T. – funding acquisition, supervision; I. S. – formal analysis; W. H. H. – funding acquisition, supervision; C. A. – conceptualization, supervision, writing – review & editing; A. O. – conceptualization, funding acquisition, supervision, software, writing – review & editing.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was supported in parts by CNRS, ENS – PSL University, Sorbonne University (UMR 8640 PASTEUR) in Paris and by the National Natural Science Foundation of China (NSFC) in Xiamen (grants MOST 2013CB933703 and NSFC 21303146) and Wuhan (grants 22090050, 22090051, and 21721005). All authors acknowledge the Sino-French IRP CNRS NanoBioCatEchem for the support. LH acknowledges her PhD scholarship by the Chinese Research Council; discussions with Dr J. Delacotte (LH PhD co-advisor) are acknowledged concerning LH experiments. CA thanks as well Xiamen University for his Distinguished Visiting Professor position.References
- C. Amatore, S. Arbault, M. Guille and F. Lemaître, Chem. Rev., 2008, 108, 2585–2621 CrossRef CAS PubMed.
- T. J. Schroeder, J. A. Jankowski, K. T. Kawagoe, R. M. Wightman, C. Lefrou and C. Amatore, Anal. Chem., 1992, 64, 3077–3083 CrossRef CAS PubMed.
- T. J. Schroeder, R. Borges, J. M. Finnegan, K. Pihel, C. Amatore and R. M. Wightman, Biophys. J., 1996, 70, 1061–1068 CrossRef CAS PubMed.
- R. M. Wightman, J. A. Jankowski, R. T. Kennedy, K. T. Kawagoe, T. J. Schroeder, D. J. Leszczyszyn, J. A. Near, E. J. Diliberto and O. H. Viveros, Proc. Natl. Acad. Sci. U. S. A., 1991, 88, 10754–10758 CrossRef CAS PubMed.
- Y.-T. Li, S.-H. Zhang, X.-Y. Wang, X.-W. Zhang, A. I. Oleinick, I. Svir, C. Amatore and W.-H. Huang, Angew. Chem., Int. Ed., 2015, 54, 9313–9318 CrossRef CAS PubMed.
- A. Larsson, S. Majdi, A. Oleinick, I. Svir, J. Dunevall, C. Amatore and A. G. Ewing, Angew. Chem., Int. Ed., 2020, 59, 6711–6714 CrossRef CAS PubMed.
- A. Oleinick, I. Svir and C. Amatore, Proc. R. Soc. A, 2017, 473, 20160684 CrossRef PubMed.
- L. Shi, Q.-T. Shen, A. Kiel, J. Wang, H.-W. Wang, T. J. Melia, J. E. Rothman and F. Pincet, Science, 2012, 335, 1355–1359 CrossRef CAS PubMed.
- Z. Wu, S. Thiyagarajan, B. O'Shaughnessy and E. Karatekin, Front. Mol. Neurosci., 2017, 10, 315 CrossRef PubMed.
- C. Amatore, A. I. Oleinick and I. Svir, ChemPhysChem, 2010, 11, 159–174 CrossRef CAS PubMed.
- R. Hu, B. Ren, C.-J. Lin, A. Oleinick, I. Svir, Z.-Q. Tian and C. Amatore, J. Electrochem. Soc., 2016, 163, H853–H865 CrossRef CAS.
- C. Amatore, S. Arbault, I. Bonifas, Y. Bouret, M. Erard and M. Guille, ChemPhysChem, 2003, 4, 147–154 CrossRef CAS PubMed.
- C. Amatore, A. I. Oleinick and I. Svir, ChemPhysChem, 2010, 11, 149–158 CrossRef CAS PubMed.
- A. Datta, C. L. Haynes and V. H. Barocas, Integr. Biol., 2017, 9, 248–256 CrossRef CAS PubMed.
- A. Oleinick, R. Hu, B. Ren, Z.-Q. Tian, I. Svir and C. Amatore, J. Electrochem. Soc., 2016, 163, H3014–H3024 CrossRef CAS.
- L. Ren, L. J. Mellander, J. Keighron, A.-S. Cans, M. E. Kurczy, I. Svir, A. Oleinick, C. Amatore and A. G. Ewing, Q. Rev. Biophys., 2016, 49, e12 CrossRef PubMed.
- J. Lovrić, J. Dunevall, A. Larsson, L. Ren, S. Andersson, A. Meibom, P. Malmberg, M. E. Kurczy and A. G. Ewing, ACS Nano, 2017, 11, 3446–3455 CrossRef PubMed.
- J. Wittmer, A. Johner and J. F. Joanny, J. Phys. II, 1995, 5, 635–654 CrossRef CAS.
- M. Muthukumar, J. Chem. Phys., 2004, 120, 9343–9350 CrossRef CAS PubMed.
- L. Hu, A. Savy, L. Grimaud, M. Guille-Collignon, F. Lemaître, C. Amatore and J. Delacotte, Biophys. Chem., 2019, 245, 1–5 CrossRef CAS PubMed.
- R. Trouillon and A. G. Ewing, ChemPhysChem, 2013, 14, 2295–2301 CrossRef CAS PubMed.
- I. Ruff and V. J. Friedrich, J. Phys. Chem., 1971, 75, 3297–3302 CrossRef CAS.
- I. Ruff, V. J. Friedrich, K. Demeter and K. Csillag, J. Phys. Chem., 1971, 75, 3303–3309 CrossRef CAS.
- C. P. Andrieux and J. M. Saveant, J. Electroanal. Chem., 1980, 111, 377–381 CrossRef CAS.
- R. W. Murray, Philos. Trans. R. Soc. London, Ser. A, 1981, 302, 253–265 CrossRef CAS.
- C. Amatore, F. Grün and E. Maisonhaute, Angew. Chem., Int. Ed., 2003, 42, 4944–4947 CrossRef CAS PubMed.
- A. Oleinick, F. Lemaître, M. G. Collignon, I. Svir and C. Amatore, Faraday Discuss., 2013, 164, 33 RSC.
- R. E. Coupland, Nature, 1968, 217, 384–388 CrossRef CAS PubMed.
- L. Ren, A. Oleinick, I. Svir, C. Amatore and A. G. Ewing, Angew. Chem., Int. Ed., 2020, 59, 3083–3087 CrossRef CAS PubMed.
- C. Amatore, Y. Bouret, E. R. Travis and R. M. Wightman, Biochimie, 2000, 82, 481–496 CrossRef CAS PubMed.
- G. Gerhardt and R. N. Adams, Anal. Chem., 1982, 54, 2618–2620 CrossRef CAS.
- R. H. S. Westerink and A. G. Ewing, Acta Physiol., 2007, 192, 273–285 CrossRef PubMed.
- E. L. Ciolkowski, K. M. Maness, P. S. Cahill, R. M. Wightman, D. H. Evans, B. Fosset and C. Amatore, Anal. Chem., 1994, 66, 3611–3617 CrossRef CAS.
- N. E. Preece, M. Nguyen, M. Mahata, S. K. Mahata, N. R. Mahapatra, I. Tsigelny and D. T. O'Connor, Regul. Pept., 2004, 118, 75–87 CrossRef CAS PubMed.
- R. Borges, J. Díaz-Vera, N. Domínguez, M. R. Arnau and J. D. Machado, J. Neurochem., 2010, 114, 335–343 CrossRef CAS PubMed.
- S. Rabasco, T. D. K. Nguyen, C. Gu, M. E. Kurczy, N. T. N. Phan and A. G. Ewing, Int. J. Mol. Sci., 2021, 23, 160 CrossRef PubMed.
- T. D. K. Nguyen, S. Rabasco, A. A. Lork, A. D. Toit and A. G. Ewing, Angew. Chem., Int. Ed., 2023, 62, e202304098 CrossRef CAS PubMed.
- T. D. K. Nguyen, L. Mellander, A. Lork, A. Thomen, M. Philipsen, M. E. Kurczy, N. T. N. Phan and A. G. Ewing, ACS Nano, 2022, 16, 4831–4842 CrossRef CAS PubMed.
- See https://www.ebi.ac.uk/pdbe/entry/pdb/1n2y and the molecular dynamics snapshots presented therein.
- P. E. Marszalek, B. Farrell, P. Verdugo and J. M. Fernandez, Biophys. J., 1997, 73, 1169–1183 CrossRef CAS PubMed.
- B. Prasai, G. J. Haber, M.-P. Strub, R. Ahn, J. A. Ciemniecki, K. A. Sochacki and J. W. Taraska, Nat. Commun., 2021, 12, 3970 CrossRef CAS PubMed.
- C. Amatore, S. Arbault, M. Guille and F. Lemaître, ChemPhysChem, 2007, 8, 1597–1605 CrossRef CAS PubMed.
- X. He and A. G. Ewing, Angew. Chem., Int. Ed., 2022, 61, e202116217 CrossRef CAS PubMed.
- P. G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca, New York, 1979, pp. 81–84 Search PubMed.
- M. B. Jackson, Y.-T. Hsiao and C.-W. Chang, Biophys. J., 2020, 119, 219–231 CrossRef CAS PubMed.
- H. Gu, C. Gu, N. Locker and A. G. Ewing, Angew. Chem., Int. Ed., 2024, 63, e202400422 CrossRef CAS PubMed.
- S. Ge, J. G. White and C. L. Haynes, Anal. Chem., 2009, 81, 2935–2943 CrossRef CAS PubMed.
- N. C. Harata, A. M. Aravanis and R. W. Tsien, J. Neurochem., 2006, 97, 1546–1570 CrossRef CAS PubMed.
- A. M. González-Jamett, X. Báez-Matus, M. A. Hevia, M. J. Guerra, M. J. Olivares, A. D. Martínez, A. Neely and A. M. Cárdenas, J. Neurosci., 2010, 30, 10683–10691 CrossRef PubMed.
- A. M. González-Jamett, F. Momboisse, M. J. Guerra, S. Ory, X. Báez-Matus, N. Barraza, V. Calco, S. Houy, E. Couve, A. Neely, A. D. Martínez, S. Gasman and A. M. Cárdenas, PLoS One, 2013, 8, e70638 CrossRef PubMed.
- C. Amatore, Y. Bouret and L. Midrier, Chem.–Eur. J., 1999, 5, 2151–2162 CrossRef CAS.
- C. Amatore, S. Arbault, I. Bonifas and M. Guille, Biophys. Chem., 2009, 143, 124–131 CrossRef CAS PubMed.
- C. Amatore, S. Arbault, I. Bonifas, M. Guille, F. Lemaître and Y. Verchier, Biophys. Chem., 2007, 129, 181–189 CrossRef CAS PubMed.
- X. Li, S. Majdi, J. Dunevall, H. Fathali and A. G. Ewing, Angew. Chem., Int. Ed., 2015, 54, 11978–11982 CrossRef CAS PubMed.
- N. Hillarp, Acta Physiol. Scand., 1960, 47, 271–279 CrossRef PubMed.
- F. Brochard-Wyart, P. G. de Gennes and O. Sandre, Phys. A, 2000, 278, 32–51 CrossRef CAS.
- C. Taupin, M. Dvolaitzky and C. Sauterey, Biochemistry, 1975, 14, 4771–4775 CrossRef CAS PubMed.
- O. Sandre, L. Moreaux and F. Brochard-Wyart, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 10591–10596 CrossRef CAS PubMed.
- C. Amatore, Y. Bouret, E. R. Travis and R. M. Wightman, Angew. Chem., Int. Ed., 2000, 39, 1952–1955 CrossRef CAS PubMed.
- L. J. Mellander, R. Trouillon, M. I. Svensson and A. G. Ewing, Sci. Rep., 2012, 2, 907 CrossRef PubMed.
- D. M. Omiatek, Y. Dong, M. L. Heien and A. G. Ewing, ACS Chem. Neurosci., 2010, 1, 234–245 CrossRef CAS PubMed.
- X.-K. Yang, F.-L. Zhang, X.-K. Jin, Y.-T. Jiao, X.-W. Zhang, Y.-L. Liu, C. Amatore and W.-H. Huang, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2219994120 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc04003a |
| This journal is © The Royal Society of Chemistry 2024 |
