Open Access Article
Open Access ArticleSalt-inclusion chalcogenides with d-orbital components: unveiling remarkable nonlinear optical properties and dual-band photoluminescence†
Shao-Min
Pei
ab,
Ming-Shu
Zhang
a,
Fan
Wu
ac,
Yan
Guo
ac,
Xiao-Ming
Jiang
 ab,
Bin-Wen
Liu
ab,
Bin-Wen
Liu
 *ab and
Guo-Cong
Guo
*ab and
Guo-Cong
Guo
 *ab
*ab
aState Key Laboratory of Structural Chemistry, Fujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences, Fuzhou, Fujian 350002, P. R. China. E-mail: gcguo@fjirsm.ac.cn; bwliu@fjirsm.ac.cn
bFujian Science & Technology Innovation Laboratory for Optoelectronic Information of China, Fuzhou, Fujian 350108, P. R. China
cCollege of Chemistry and Materials Science, Fujian Normal University, Fuzhou, Fujian 350007, P. R. China
First published on 31st July 2024
Abstract
Metals containing d-orbitals are typically characterized by strong deformation and polarization, yet they tend to induce narrow bandgaps that render them little-appreciated by high-power nonlinear optical (NLO) crystals. Incorporating highly electropositive polycations into d-orbital-containing chalcogenides to modify them into salt-inclusion chalcogenides (SICs) that are competitive in NLO materials, is a viable solution to this predicament. In the present work, two isostructural SICs [K4Cl][MGa9S16] (M = Mn, 1; Hg, 2) are successfully synthesized by the high-temperature molten-salt growth method. Both compounds demonstrate commendable second-harmonic-generation (SHG) responses (0.6–1.0 × AgGaS2 @1910 nm), which can be attributed to their well-designed [MGa9S16]3− anionic frameworks; and compound 2 exhibits the widest optical bandgap (3.41 eV) among the Hg-based NLO chalcogenides. Also, an interesting dual-band photoluminescence emission centered at ∼650 and ∼718 nm is detected in 1 at 77 K, with long lifetimes of 0.94 and 1.35 ms, respectively.
Introduction
Driven by keen interest in laser-related applications, nonlinear optical (NLO) crystal materials have enjoyed an exponential advancement, and are extensively utilized in numerous pivotal military and civilian sectors such as holography, semiconductor micromachining, medical examinations, etc.1–6 The predominant infrared NLO crystals including ZnGeP2, AgGaS2 (AGS), and AgGaSe2, however, either encounter formidable challenges in coping with the urgent demands of high-power and high-efficiency laser output due to their undesired two-photon absorption, or experience disequilibrium between second-harmonic generation (SHG) efficiencies and laser-induced damage thresholds (LIDTs).7 Therefore, the pioneering investigation of high-performance infrared NLO materials has captured considerable attention.With the notion of “structure steers property” firmly established, a significant number of endeavors have been dedicated to thoroughly investigating the structure–property relationship, which typically involves assigning functional motifs (FMs).8 For instance, the polar phosphorus chalcogenide cages β-P4Q3, and β-P4Q4 were considered to be the FMs that exerted a dominant influence on the outstanding NLO efficiencies exhibited by (CuBr)7(P4Q3)3 and (CuI)3(P4Q4) (Q = S, Se).9 Additionally, although the [MgQ6] units demonstrated a relatively diminished contribution to SHG responses, their favorable HOMO–LUMO gaps facilitated the achievement of wide optical bandgaps in AMg3Ga3Q8 (A = Ag, Li, Na, Cu),10 and AeMg6Ga6S16 (Ae = Ca, Sr, Ba).11 Accordingly, [MgQ6] units were largely acknowledged as be the FMs responsible for determining LIDT (positively correlated with the bandgap in chalcogenide). Therefore, the selection of appropriate FMs is a pivotal step in attaining the desired performances. Specially, the [MQ4] (M = metal containing d-electrons) tetrahedra are frequently chosen as fundamental building blocks due to their relatively strong distortion and polarization. Longitudinal comparisons reveal that compounds incorporating distorted [HgQ4] units especially manifest strong SHG intensities, as evidenced by Hg3P2S8,12 HgCuPS4,13 and Na2Hg3Si2Se8 (ref. 14) etc. Those structures adorned with [MnQ4] units exhibit not only decent NLO coefficients but also captivating photoluminescence (PL), encompassing K2MnGe3S8,15 Sr3MnSn2S8,16 Sr2MnGe2OS6,17etc. Additionally, [MnQ4]-based chalcogenides may demonstrate potential magnetic characteristics, endowing them with exceptional potential for exploring the intrinsic correlation between SHG effects and magnetic structures.18 However, the narrow bandgap remains a formidable obstacle impeding the extensive utilization of the above-mentioned compounds in the NLO field.19,20
Salt-inclusion chalcogenides (SICs) represent a burgeoning infrared NLO category that demonstrate comprehensive NLO performance owing to their advantageous dual-FMs configurations. On the one hand, the polycationic groups composed of alkali or alkaline-earth metals and halogens demonstrate native capabilities in broadening optical bandgaps; while on the other hand, the NLO FMs in anionic frameworks can be flexibly arranged to produce ideal SHG intensities. Particular attention has been paid to those Ga-based SIC, most of which are equipped with a neatly aligned structures to effectively counteract the potential degradation of SHG caused by increased bandgaps, as exemplified by Li[LiCs2Cl][Ga3S6] (0.7 × AGS, 4.18 eV),21 [ABa3Cl2][Ga5S10] (A = K, Rb, Cs) (∼1 × AGS, 3.3–3.35 eV),22 and [ABa2Cl][Ga4S8] (A = Rb, Cs) (0.9–1.0 × AGS, ∼4 eV).23
Inspired by the above, the incorporation of the [MnS4] and [HgS4] FMs into the Ga-based SIC system is worth exploring in order to acquire NLO crystals with satisfactory comprehensive performances. After numerous attempts, two isostructural SICs [K4Cl][MnGa9S16] (M = Mn, 1; Hg, 2) are successfully prepared by traditional high-temperature solid-state reactions. They are characterized by diamond-like frameworks consisting of distinct [Ga4S10] and [MGa3S10] T2-supertetrahedra. Predictably, both compounds exhibit excellent performances expected from applicable NLO materials, encompassing comparable SHG responses as well as dramatic LIDTs enabled by their wide bandgaps and exceptionally weak thermal expansion anisotropy (TEA). In addition, a remarkable dual-band phosphorescence (PL) emission centered at 650 and 718 nm at low-temperature is observed in compound 1.
Results and discussion
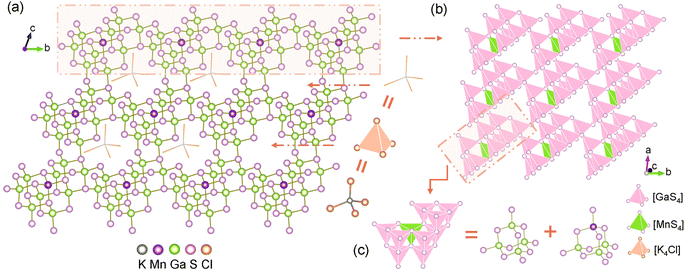
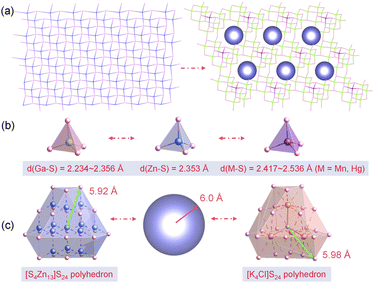
The conventional high-temperature solid-states method enables the acquisition of title compounds in high yields. Structural analysis unveiled that crystals 1–2 are isostructural to the previously reported, and all crystallize in the triclinic P1 space groups. A comprehensive structural description is provided below using Mn-based compound as an example. The asymmetric unit of 1 consists of four K atoms, one Cl atom, nine Ga atoms, one Mn atom, and sixteen S atoms. As depicted in Fig. 1a, the Mn and Ga atoms in 1 are tetra-coordinated with S atoms to form [GaS4] and [MnS4] tetrahedra. All the tetrahedra are linked by the common S atoms in a well-regulated fashion, ultimately giving rise to a “defective” diamond-like framework. The isolated [K4Cl]3+ polycations are held captive within the accessible cavity via K–S electrostatic interactions. The polyhedral stacking diagram of the independent 2D layer displays that each [MnS4] tetrahedra directs the adjacent nine [GaS4] tetrahedra to constitute a fundamental repeating unit (Fig. 1b), which can be further subdivided into two distinct types of [Ga4S10] and [MnGa3S10] T2-supertetrahedra (Fig. 1c). Detailed crystallographic parameters as well as a selection of bond lengths and bond angles of compounds 1–2 are attached to the ESI file (Tables S1, S2, and S3†).In essence, most of diamond-like chalcogenides extracted from experiments can be plausibly deduced to have evolved from zinc blende ZnS, which is accomplished by chemical substitutions. It has been demonstrated that tetrahedra of analogical dimensions can seamlessly interchange selected to supersede the [ZnS4] units (2.353 Å) in ZnS (Fig. 2b), fabricating the diamond-like [MGa9S16]3− (M = Mn, Hg) skeletons, which are suffused with abundant vacancies induced by unequal electrovalent substitution (Fig. 2a). A fictitious violet sphere is employed to depict the size and spatial distribution of vacancies. The thirteen neighboring [ZnS4] clusters can be perceived as a regular polyhedron with dimensions spanning from 4.50–5.92 Å, centered on [Zn13S4] and coordinated with 24 S atoms. Coincidently, the [K4Cl]S24 polyhedron with [K4Cl] serving as the pseudo-center exhibits strikingly similar configuration and dimension (4.37–5.98 Å) (Fig. 2c). Thus, the substitution of [K4Cl]S24 for [Zn13S4]S24 is logically deemed a viable strategic move. On one hand, the [K4Cl]3+ units serve to counterbalance the excessive negative charge within the frameworks, while on the other hand, the integration of alkali metal and halogen is advantageous for optimizing the optical bandgap. As a consequence, a multi-substitution abbreviated as [S4Zn13]S24 + 10[ZnS4] ⇒ [K4Cl]S24 + 9[GaS4] + [MS4] (M = Mn, Hg) facilitates the triumphant metamorphosis of ZnS into compounds 1–2.
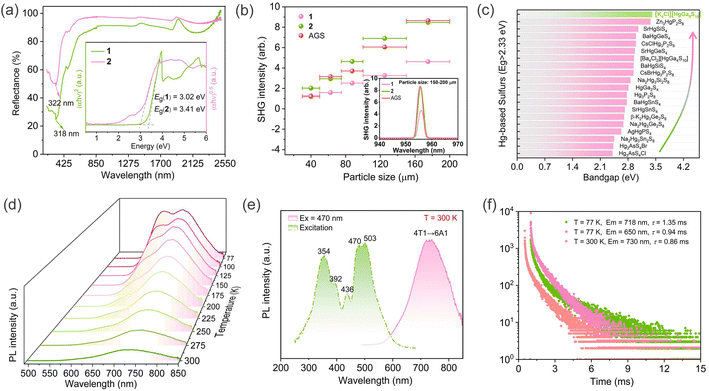
The purities of handpicked microcrystals 1–2 have been confirmed via powder X-ray diffraction prior to undergoing optical measurements (Fig. S2 and S3†). The acquired UV-vis-NIR diffuse reflectance spectra were processed using the Tauc plot method to investigate the optical bandgaps (Eg) of 1–2. As illustrated in Fig. 3a, compound 1 showed an indirect bandgap (infer from electronic band structure calculations) of 3.02 eV, which is wider than most of Mn-based chalcogenides, such as NaMn3Ga3S8 (2.5 eV),24 CaMn6Ga6S16 (2.64 eV),25 and comparable to those of Sr3MnSn2S8 (3.02 eV),16 [K3Cl][Mn2Ga6S12] (3.17 eV);26 while 2 possessed a direct bandgap of 3.41 eV, which was the widest bandgap among all the reported Hg-contained chalcogenide NLO materials (Fig. 3b and Table S4†).11,12,27–37 Unfortunately, crystals 1 and 2 obtained by spontaneous crystallization were insufficient for accurately estimating their infrared transmission regions. The infrared spectra of 1–2 measured with powder samples revealed no discernible absorption within the range of 2.5–25 μm (Fig. S4†), indicating their potentially broad transmission regions.
The intriguing PL properties observed in certain NLO materials, such as Ba3AGa5Se10Cl2 (A = Cs, Rb, K),38 NaMn3Ga3S8,24 and ACd4Ga5Te12 (A = K, Rb, Cs),39 prompt us to direct our attention towards the PL phenomenon exhibited by the title compounds. Indeed, a red luminescence was clearly observable in compound 1 under UV lamp in an ordinary environment. The emission value at 730 nm was utilized to establish the excitation spectra at room temperature. Five excitation peaks centered at 354, 392, 436, 470, and 503 nm can be observed in Fig. 3b, which were assigned to the transitions from 6A1(6S) fundamental energy level of Mn2+ to 4E(4D), 4T2(4D), [4E(4G), 4A1(4G)], 4T2(4G), and 4T1(4G), respectively. The emission spectrum performed at an excitation wavelength of 470 nm at 300 K was presented in the right side of Fig. 3e. The spectral emission spans from 575 nm (green) to 850 nm (infrared), with a broad peak at 730 nm, which corresponded to the characteristic luminescence arising from the 4T1 (4G) → 6A1 (6S) transition of Mn2+. The low temperature-dependent PL spectra in the temperature range of 77–300 K were presented in Fig. 3d, revealing the significant influence of temperature on the PL intensity. Specifically, as the temperature decreased, the emission peak position underwent a subtle redshift (730 nm → 718 nm). Simultaneously, a new conspicuous emission peak was found at low-temperature and quenched gradually above 200 K. Based on the previous analysis of the luminescence mechanism of SIC [Cs6Cl]NaGa6S12:Mn,40 we hypothesized that PL emission at lower wavelength (∼650 nm) in 1 may originate from Mn doping into the [GaS4] octahedral sites within the framework. The PL phenomena characterized by dual-band emission was more prevalent in organic–inorganic hybrid metal halides compared to inorganic metal chalcogenides.41,42 Several studies investigating the mechanism behind dual-band emission have demonstrated that structural modification or external stimuli like temperature change or pressure change may serve as the underlying incentives for the emergence of dual-band emission centers, highlighting the significant potential of dual-band emission in condition control for achieving tunable luminescence.43–45 For example, by reducing the temperature, it is possible to obtain fluorescence that differs from that observed at high temperatures. These low-temperature fluorescence phenomena find extensive applications in scientific research, substance identification, lighting technology, coatings development, and other related fields.46–48 Time-resolved fluorescence spectroscopy revealed that the decay time of 1 monitored at emission 730 nm was 0.86 ms under excitation of 470 nm at room temperature; while under cryogenic conditions (77 K), the decay times of dual-band emission centered on 718 nm and 650 nm were approximately 1.35 ms and 0.94 ms, respectively (Fig. 3f). The fluorescence quantum yield of 1 was measured to be 2.96% at 300 K. The investigation shows that low quantum yields (<10%) are common in chalcogenides, such as Ag8SnS6 nanoparticles (3.1%),49 Ag2S colloidal quantum dots (9%),50 CuInS2 nanoparticles (5%).51 Compound 1 may serve as a valuable reference case for researchers in the field of fluorescence and potentially inspire innovative doping and modification strategies aimed at enhancing its fluorescence quantum yield.
The non-centrosymmetric structures of compounds 1–2 have aroused our interest in their NLO properties. We have assessed the SHG responses and phase-matchable capabilities of compounds 1–2 and the benchmark AGS under a 1910 nm laser irradiation. As illustrated in Fig. 3b, compounds 1–2 presented pronounced phase-matchable behaviors, concretely, the SHG intensity showed a positive correlation with particle size. Additionally, compounds 1–2 with particle sizes ranging from 150–200 μm displayed optimal SHG responses, which corresponded to ∼0.6 and ∼1 times that of AGS, respectively. The obtained results indicate that compounds 1 and 2 have balanced NLO properties comparable to the reported SIC NLO candidates (Table S6†), such as [CsBa3X][B2S6] (X = Br, I) (0.5 × AGS, 2.65–2.71 eV),52 [Ba4Cl2][HgGa4S10] (1.5 × AGS, 2.95 eV),53 [K3Cl][Mn2Ga6S12] (0.8 × AGS),26 [ABa2Cl][Ga4S8] (A = Rb, Cs) (0.9–1.0 × AGS, 3.30–3.35 eV),22 and [Ba4Cl2][ZnGa4S10] (1.1 × AGS, 3.85 eV).54 The experimental effective nonlinear coefficient (deff) for 1 and 2 were 9.0 and 11.6 pm V−1, respectively, as determined based on the mathematic relation between SHG intensity (I2ω) and deff, namely, deff = deff,AGS (I2ω/I2ωAGS)1/2, where the deff,AGS is equal to 11.6 pm V−1.23
LIDT, as another decisive criterion for assessing the quality of NLO materials, is definitely worth discussing in the subsequent discourse. Nowadays, a majority of infrared NLO materials encounter the dilemma that large-size crystals are inaccessible via conventional spontaneous crystallization methods, hence, a microcrystal-based single-pulse method has been developed to estimate the LIDT of newly-acquired NLO crystals.55 As listed in Table S5,† the preliminarily measured LIDTs of crystals 1 and 2 were 20.8 and 21.3 MW cm−2, surpassing that of AGS (4.0 MW cm−2) by a factor of 5.2 and 5.3, respectively. In general, the damages caused by lasers with nanosecond pulse widths in crystals mainly involve thermally induced damage and dielectric breakdown, which are governed by lattice thermal effects and optical bandgap, respectively. The thermal expansion anisotropy (TEA, δ) symbolizes the ability to resist thermal shocks caused by intense laser radiation, and is calculated by the formula of δ = max [(αi − αj)/αi] (i, j = a, b, or c), and the thermal expansion coefficients (α) is determined by the formula αL = ΔL/LΔT, where ΔL/ΔT represents the slope of the fitted curve for the temperature-dependent lattice parameters, and L denotes the lattice parameter at T = 100 K. According to the (Fig. S5†), the α along a-, b-, c-axis were calculated as 9.860 × 10−6, 1.151 × 10−5, and 1.156 × 10−5 in 1, and 1.432 × 10−5, 1.750 × 10−5, and 1.780 × 10−5 in 2, respectively. Thus, the TEAs of 1 and 2 can be further extrapolated as 0.17 and 0.24, which were notably smaller in comparison to AGS (2.97).56 The superior LIDTs of the title compounds can be attributed to the combined effect of their wide optical bandgaps and small TEAs.
To elucidate the origin of optical properties, the electronic structures of compounds 1 and 2 have been investigated employing first-principles calculations based on density functional theory (DFT).57,58 The electronic band structure diagrams indicated that compound 1 possessed an indirect bandgap with theoretical value of 1.96 eV (Fig. 4a), whereas 2 was a direct bandgap compound with theoretical bandgap of 2.34 eV (Fig. 4b). The partial density of states (PDOS) analysis of 1 demonstrated that near the Fermi level, the valence-band maximums (VBMs) of the spin-up states were mainly occupied by S-p, Mn-d, and Cl-p states, and the conduction band minimums (CBMs) were dominated by Ga-s, Ga-p, and S-p states; whereas the VBMs of the spin-down states were contributed by S-p and Cl-p orbitals, and the Mn-d orbital was principally responsible for the CBMs. The PDOS of 2 revealed that the VBMs were predominantly influenced by S-p, Ga-p, and Cl-p states; while the CBMs primarily consist of Ga-s, Ga-p, and S-p states, with the Hg-s orbital playing a secondary role in CBMs. As can be inferred, the limited covalent interactions between K–S and K–Cl bonds resulted in the strong ionicity of [K4Cl]3+, thereby facilitating the occurrence of wide band gaps of 1 and 2. Additionally, the d–d transitions of Mn2+ (d5) exerted great negative influence on the bandgap of 1, while conversely, the Hg-d orbital played weak contribution in the vicinity of the Fermi level, resulting in a negligible effect on the bandgap of 2. These findings effectively elucidate the reason behind the experimental fact that 1 possesses a narrower bandgap compared to 2.
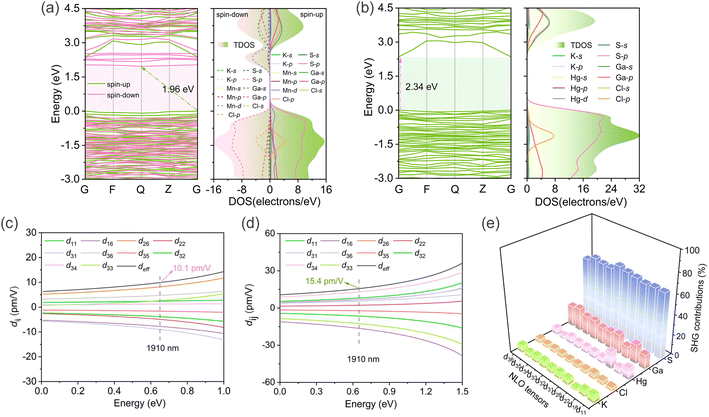 | ||
| Fig. 4 (a) Band structures (left) and partial density of states (right) of 1 (a) and 2 (b); calculated NLO tensors of 1 (c) and 2 (d); atom-resolved SHG contributions of 2 (e). | ||
The title compounds (P1 space group) possess ten non-zero independent NLO tensors based on the restriction of Kleinman symmetry. At a wavelength of 1910 nm (0.65 eV), the calculated d11, d16,d22, d26, d31, d32, d33, d34, d35, and d36 of 1 were −3.8, −7.8, −4.9, 8.2, 5.6, −9.0, 2.4, 2.6, −1.6, and 4.7 pm V−1, respectively (Fig. 4c), and the corresponding tensors in 2 were −6.5, −16.4, 2.3, 6.8, 6.5, −8.0, −12.6, 12.9, −2.2, and 5.6 pm V−1, respectively (Fig. 4d). The computed angular-averaged SHG susceptibility tensor (deff) for 1 and 2 were 10.1 and 15.4 pm V−1, respectively, exhibiting good agreement with the experimental values. To further analyze the provenance of NLO response, the atom-resolved SHG contributions of 2 were also calculated. As the Fig. 4e illustrated, K, Cl, Hg, Ga, and S atoms make the greatest contribution to the d36, d22, d22, d35, and d32 tensors, respectively. The maximum contribution to the overall NLO tensors was made by S atom (65.78%), followed by Ga (17.97%), Hg (7.18%), and K (5.48%) atoms, while Cl atom (3.59%) contributed minimally to the SHG response. These theoretical results suggested that the significant SHG response of compound 2 primarily arose from the anionic [HgGa9S16]3− formed by NLO-active [GaS4] and [HgS4] units and a similar conclusion was applicable to 1. The above results coincide with the original design concept for the development of SICs.
Conclusions
In conclusion, the successful incorporation of [MS4] units into the Ga-based SIC system has led to the synthesis of two isostructural SICs [K4Cl][MGa9S16] (M = Mn, 1; Hg, 2). The characterization of the optical properties demonstrates that both compounds have potential as infrared NLO candidates, as evidenced by their robust SHG responses (0.6–1.0 × AgGaS2 @1910 nm) and remarkable optical bandgaps (3.02–3.41 eV). Notably, the bandgap of 2 stood out the widest among mercury-chalcogenide NLO crystals to date. The atom-resolved SHG contributions revealed that [GaS4] and [MS4] (M = Mn, Hg) tetrahedra potentially serve as NLO-active FMs in the title compounds. Additionally, a red-emission with dual-emission centers (650 nm and 718 nm) at 77 K was observed in 1, accompanied by prolonged phosphorescence lifetimes of 0.94 and 1.35 ms, respectively. This work provides a novel concept for the design of high-performance infrared NLO and other optoelectronic functional materials.Data availability
All supplementary data for the results of this study are available in the article and its ESI file.† Any further relevant data are available from the authors upon reasonable request.Author contributions
Shao-Min Pei: writing – original draft, conceptualization, visualization; Ming-Shu Zhang: theoretical calculations, visualization; Fan Wu: data curation; Yan Guo: data curation; Bin-Wen Liu: writing – review & editing; Xiao-Ming Jiang: software, theoretical calculations; Guo-Cong Guo: writing – review & editing, supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (21827813, 21921001, 22175172, 22075283, 92161125, U21A20508), the Youth Innovation Promotion Association of Chinese Academy of Sciences (2020303, 2021300), and Fujian Science & Technology Innovation Laboratory for Optoelectronic Information of China (2020ZZ108). Postdoctoral Fellowship Program of FPSF (GZC20232667).Notes and references
- M. Mutailipu, J. Han, Z. Li, F. Li, J. Li, F. Zhang, X. Long, Z. Yang and S. Pan, Nat. Photonics, 2023, 17, 694–701 CrossRef CAS.
- X. Wang, X. Leng, Y. Kuk, J. Lee, Q. Jing and K. M. Ok, Angew. Chem., Int. Ed., 2023, e202315434 Search PubMed.
- X.-H. Li, Z.-H. Shi, M. Yang, W.-L. Liu and S.-P. Guo, Angew. Chem., Int. Ed., 2022, 61, e202115871 CrossRef CAS PubMed.
- Q. Wu, L. Kang and Z. Lin, Adv. Mater., 2023, 2309675 Search PubMed.
- M. Yan, R.-L. Tang, W.-D. Yao, W.-L. Liu and S.-P. Guo, Chem. Sci., 2024, 15, 2883–2888 RSC.
- L. Cao, H. Tian, D. Lin, C. Lin, F. Xu, Y. Han, T. Yan, J. Chen, B. Li, N. Ye and M. Luo, Chem. Sci., 2022, 13, 6990–6997 RSC.
- W.-F. Zhou and S.-P. Guo, Acc. Chem. Res., 2024, 57, 648–660 CAS.
- X.-M. Jiang, S.-Q. Deng, M.-H. Whangbo and G.-C. Guo, Natl. Sci. Rev., 2022, 9, nwac017 CrossRef CAS PubMed.
- S. Yang, C. Lin, H. Fan, K. Chen, G. Zhang, N. Ye and M. Luo, Angew. Chem., Int. Ed., 2023, e202218272 CAS.
- L. Luo, L. Wang, J. Chen, J. Zhou, Z. Yang, S. Pan and J. Li, J. Am. Chem. Soc., 2022, 144, 21916–21925 CrossRef CAS PubMed.
- J. Chen, Y. Zhang, H. Wu, Z. Hu, J. Wang, Y. Wu and H. Yu, Adv. Opt. Mater., 2022, 11, 2202147 CrossRef.
- Y. Chu, P. Wang, H. Zeng, S. Cheng, X. Su, Z. Yang, J. Li and S. Pan, Chem. Mater., 2021, 33, 6514–6521 CrossRef CAS.
- M. Li, Z. Ma, B. Li, X. Wu, H. Lin and Q. Zhu, Chem. Mater., 2020, 32, 4331–4339 CrossRef CAS.
- L. Gao, J. Xu, X. Tian, B. Zhang, X. Wu and K. Wu, Chem. Mater., 2022, 34, 5991–5998 CrossRef CAS.
- Z. Li, X. Jiang, C. Yi, M. Zhou, Y. Guo, X. Luo, Z. Lin, Y. Wu, Y. Shi and J. Yao, J. Mater. Chem. C, 2018, 6, 10042–10049 RSC.
- C. Liu, D. Mei, W. Cao, Y. Yang, Y. Wu, G. Li and Z. Lin, J. Mater. Chem. C, 2019, 7, 1146–1150 RSC.
- M. Ran, S. Zhou, B. Li, W. Wei, X. Wu, H. Lin and Q. Zhu, Chem. Mater., 2022, 34, 3853–3861 CrossRef CAS.
- R.-C. Xiao, D.-F. Shao, W. Gan, H.-W. Wang, H. Han, Z. G. Sheng, C. Zhang, H. Jiang and H. Li, npj Quantum Mater., 2023, 8, 62 CrossRef.
- S.-M. Pei, B.-W. Liu, W.-F. Chen, X.-M. Jiang and G.-C. Guo, Mater. Horiz., 2023, 10, 2921–2926 RSC.
- C. Li, X. Meng, Z. Li and J. Yao, Coord. Chem. Rev., 2022, 453, 214328 CrossRef CAS.
- B.-W. Liu, X.-M. Jiang, B.-X. Li, H.-Y. Zeng and G.-C. Guo, Angew. Chem., Int. Ed., 2020, 59, 4856–4859 CrossRef CAS PubMed.
- B.-W. Liu, H.-Y. Zeng, X.-M. Jiang and G.-C. Guo, CCS Chem., 2021, 3, 964–973 CrossRef CAS.
- B.-W. Liu, X.-M. Jiang, H.-Y. Zeng and G.-C. Guo, J. Am. Chem. Soc., 2020, 142, 10641–10645 CrossRef CAS PubMed.
- P. Yang, H. Wu, Z. Hu, J. Wang, Y. Wu and H. Yu, Mater. Today Chem., 2023, 33, 101727 CrossRef CAS.
- Y.-P. Zhang, S.-M. Pei, W.-F. Chen, B.-W. Liu, X.-M. Jiang and G.-C. Guo, Sci. China Chem., 2024 DOI:10.1007/s11426-024-2023-2.
- B.-W. Liu, S.-M. Pei, X.-M. Jiang and G.-C. Guo, Mater. Horiz., 2022, 9, 1513–1517 RSC.
- N. Umemura, T. Mikami and K. Kato, Opt. Commun., 2012, 285, 1394–1396 CrossRef CAS.
- K. Wu, Z. Yang and S. Pan, Chem. Mater., 2016, 28, 2795–2801 CrossRef CAS.
- J. Liao, G. Marking, K. Hsu, Y. Matsushita, M. Ewbank, R. Borwick, P. Cunningham, M. Rosker and M. Kanatzidis, J. Am. Chem. Soc., 2003, 125, 9484–9493 CrossRef CAS PubMed.
- Y. Guo, F. Liang, Z. Li, W. Xing, Z. Lin, J. Yao, A. Mar and Y. Wu, Inorg. Chem., 2019, 58, 10390–10398 CrossRef CAS PubMed.
- X. Zhang, H. Wu, Z. Hu, J. Wang, Y. Wu and H. Yu, Adv. Opt. Mater., 2023, 2301735 Search PubMed.
- W. Xing, N. Wang, C. Tang, C. Li, Z. Lin, J. Yao, W. Yin and B. Kang, J. Mater. Chem. C, 2021, 9, 1062–1068 RSC.
- Y. Chu, H. Wang, T. Abutukadi, Z. Li, M. Mutailipu, X. Su, Z. Yang, J. Li and S. Pan, Small, 2023, 19, 2305074 CrossRef CAS PubMed.
- Y. Zhang, H. Wu, Z. Hu, J. Wang, Y. Wu and H. Yu, Inorg. Chem. Front., 2022, 9, 4075–4080 RSC.
- F. Xu, X. Xu, B. Li, G. Zhang, C. Zheng, J. Chen and N. Ye, Inorg. Chem. Front., 2024, 11, 2105–2115 RSC.
- W. Xing, C. Tang, N. Wang, C. Li, E. Uykur, J. Wu, Z. Lin, J. Yao, W. Yin and B. Kang, Adv. Opt. Mater., 2021, 9, 2100563 CrossRef CAS.
- M. Yan, W.-D. Yao, W. -L Liu, R.-L. Tang and S.-P. Guo, Inorg. Chem., 2021, 60, 16917–16921 CrossRef CAS PubMed.
- P. Yu, L. Zhou and L. Chen, J. Am. Chem. Soc., 2012, 134, 2227–2235 CrossRef CAS PubMed.
- M. Sun, W. Xing, S. K. Chen, C. Li, W. Liu, M.-H. Lee and J. Yao, Chem. Mater., 2023, 35, 7218–7228 CrossRef CAS.
- A. A. Berseneva, L. W. Masachchi, L. G. Jacobsohn and H.-C. zur Loye, Chem. Mater., 2023, 35, 1417–1431 CrossRef CAS.
- H. Peng, T. Huang, B. Zou, Y. Tian, X. Wang, Y. Guo, T. Dong, Z. Yu, C. Ding, F. Yang and J. Wang, Nano Energy, 2021, 87, 106166 CrossRef CAS.
- Z. Li, Y. Li, P. Liang, T. Zhou, L. Wang and R. Xie, Chem. Mater., 2019, 31, 9363–9371 CrossRef CAS.
- K. Liu, L. Dong, F. Li, Y. Li, M. Zhao and J. Dai, Appl. Phys. Lett., 2023, 123, 202105 CrossRef CAS.
- Q. Li, B. Xu, Z. Chen, J. Han, L. Tan, Z. Luo, P. Shen and Z. Quan, Adv. Funct. Mater., 2021, 31, 2104923 CrossRef CAS.
- L. Lian, P. Zhang, G. Liang, S. Wang, X. Wang, Y. Wang, X. Zhang, J. Gao, D. Zhang, L. Gao, H. Song, R. Chen, X. Lan, W. Liang, G. Niu, J. Tang and J. Zhang, ACS Appl. Mater. Interfaces, 2021, 13, 22749–22756 CrossRef CAS PubMed.
- X. Zhao, N. Wang, M. Quan, A. Hou, K. Liu, Y. Cui, J. Zhao and Q. Liu, Inorg. Chem., 2024, 63, 10705–10712 CrossRef CAS PubMed.
- J. Du and D. Poelman, Adv. Opt. Mater., 2020, 8, 1901848 CrossRef CAS.
- H. Li, H. Wu, R. Pang, G. Liu, S. Zhang, L. Jiang, D. Li, C. Li, J. Feng and H. Zhang, J. Mater. Chem. C, 2021, 9, 1786 RSC.
- J. A. Adekoya, M. D. Kha, S. Mlow and N. Revaprasadu, Mater. Chem. Phys., 2023, 299, 127456 CrossRef CAS.
- H. M. Ju, D. Yoo and M.-J. Choi, Appl. Surf. Sci., 2023, 635, 157706 CrossRef CAS.
- A. C. Berends, F. T. Rabouw, F. C. M. Spoor, E. Bladt, F. C. Grozema, A. J. Houtepen, L. D. A. Siebbeles and C. de Mello Donegá, J. Phys. Chem. Lett., 2016, 7, 3503–3509 CrossRef CAS PubMed.
- J. Zhou, K. Hou, Y. Chu, Z. Yang, J. Li and S. Pan, Small, 2023, 2308806 Search PubMed.
- Y. Zhang, H. Wu, Z. Hu, J. Wang, Y. Wu and H. Yu, Inorg. Chem. Front., 2022, 9, 4075–4080 RSC.
- H. Chen, Y. Li, B. Li, P. Liu, H. Lin, Q. Zhu and X. Wu, Chem. Mater., 2020, 32, 8012–8019 CrossRef CAS.
- Z.-X. Qiu, Z.-X. Zheng, X.-M. Jiang, B.-W. Liu and G.-C. Guo, Chem. Sci., 2023, 14, 13568–13573 RSC.
- S.-F. Li, X.-M. Jiang, Y.-H. Fan, B.-W. Liu, H.-Y. Zeng and G.-C. Guo, Chem. Sci., 2018, 9, 5700–5708 RSC.
- S. Clark, M. Segall, C. Pickard, P. Hasnip, M. Probert, K. Refson and M. Payne, Z. Kristallogr. – Cryst. Mater., 2005, 220, 567–570 CrossRef CAS.
- S. Sharma and C. Ambrosch-Draxl, Phys. Scr., 2004, 128–134 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. Experimental section; theoretical calculations; crystallographic data, LIDT data, energy dispersive X-ray spectrometers, infrared spectra, and X-ray diffraction patterns of 1 and 2 (PDF). CCDC 2326388–2326389. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4sc04018j |
| This journal is © The Royal Society of Chemistry 2024 |