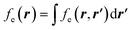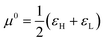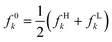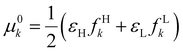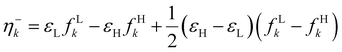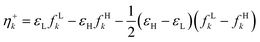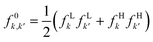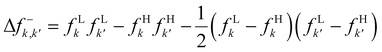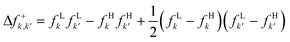Open Access Article
Open Access ArticleTemperature and external fields in conceptual density functional theory
Marco
Franco-Pérez
 *a,
Farnaz
Heidar-Zadeh
*a,
Farnaz
Heidar-Zadeh
 *b,
Paul W.
Ayers
*b,
Paul W.
Ayers
 *c,
Frank
De Proft
*c,
Frank
De Proft
 *d,
Alberto
Vela
*d,
Alberto
Vela
 *e,
José L.
Gázquez
*e,
José L.
Gázquez
 *f and
Paul
Geerlings
*f and
Paul
Geerlings
 *d
*d
aDepartamento de Física y Química Teórica, Facultad de Química, Universidad Nacional Autónoma, de México, Cd Universitaria, Ciudad de México, Mexico
bDepartment of Chemistry, Queen's University, Kingston, Ontario K7L-3N6, Canada
cDepartment of Chemistry, McMaster University, Hamilton, Ontario L8S 4L8, Canada
dResearch Group of General Chemistry (ALGC), Vrije Universiteit Brussel, Pleinlaan 2, B-1050 Brussels, Belgium
eDepartamento de Química, Centro de Investigación y de Estudio Avanzados (Cinvestav), Av. IPN 2508, San Pedro Zacatenco, 07360, CDMX, Mexico. E-mail: avela@cinvestav.mx
fDepartamento de Química, Universidad Autónoma Metropolitana-Iztapalapa, Av. San Rafael Atlixco, 186, 09340, CDMX, Mexico
First published on 29th October 2024
Abstract
Until quite recently, Conceptual DFT (CDFT) was mainly based on the energy functional, E[N,v], where the number of electrons N and the external potential v are state variables. One of the strengths of CDFT, however, is the ease with which additional and/or different state variables can be incorporated. Here, the incorporation of new variables—namely temperature and external fields—is discussed, outlining the motivation for these extensions, sketching their theoretical/computational context, and presenting some elucidative examples. Using the Grand Canonical Ensemble, finite temperature can be introduced, ameliorating the N-differentiability problem and leading to new well-behaved chemical reactivity concepts. Incorporating temperature as an additional fundamental variable enables us to formulate a novel suite of “thermodynamic” reactivity descriptors, including important concepts like the heat capacity of electronic systems. The mathematical structure underpinning the set of (well-behaved) finite-temperature reactivity indices can guide the formulation of plausible definitions for local analogs of global descriptors. This endeavor is especially significant in the case of local hardness, a concept that has remained elusive since the inception of CDFT. The ever-increasing portfolio of experimental reaction conditions to creatively synthesize new molecules, needs the introduction of various external “fields” like electric and magnetic fields (ε and B), mechanical forces (F) and pressure (P) to describe the state of the chemical system. The conventional energy functional can be expressed in a general form, E[N,v,X], where X denotes the “field”. Response functions to changes in the field can then be defined in analogy to classical thermodynamics. The electric field results display a case of a field-induced selectivity in a reaction channel of the Fukui function. Remarkably, atomic electronegativity and hardness in magnetic fields display a piecewise behavior in magnetic fields, associated to configurational jumps upon increasing field strength. The overall compression of their ranges for stronger fields may be insightful when investigating chemistry in extremely high fields. The electronegativity and hardness of diatomics under mechanical force can be traced back to changes in equilibrium distances in the neutral, cationic and anionic state, parallel with the evolution of an intrinsic atomic volume under pressure.
1. Introduction
Quantum Chemistry witnessed a breathtaking evolution in the last decades, both in wave function theory and density functional theory, enabling computational chemists and experimentalists to calculate the intrinsic properties of chemical systems at ever-increasing levels of theory. For practicing chemists, the interpretation of the results, preferably in terms of simple, often longstanding concepts, such as electronegativity, delocalization, and aromaticity,1 never lost its significance; on the contrary, Parr's dictum “To calculate a molecule is not to understand it”, formulated in 1985,2 did not lose its relevance.In wave function theory, the most traditional computational approaches, molecular-orbital (MO) and valence-bond (VB) theory, however, have a common shortcoming: wavefunctions which achieve quantitative agreement with experiment (e.g., configuration interaction calculations with millions of Slater determinants or Valence Bond calculations with thousands of resonance structures) obscure the elegant interpretative framework of simple qualitative MO and VB calculations. As Mulliken noted back in 1965, referring to discussions from a conference in 1958, “with old-fashioned chemical concepts…the more accurate the calculations became the more the concepts tended to vanish into thin air”.3
Starting around 1980, density functional theory (DFT),4 gained increasing acceptance by chemists as a valuable alternative to MO/VB-based computational methods. Concomitant with DFT's emergence as a computational workhorse in quantum chemistry, Parr and his coworkers developed a density-based framework for the interpretation (and ultimately prediction) of chemical phenomena, especially chemical reactivity, later termed Conceptual DFT (CDFT).5,6 In a natural way, “old-fashioned” concepts such as electronegativity,7 chemical hardness and softness,8 and Fukui functions9 (generalizing Fukui's frontier MO approach)10 reemerged from a rigorous mathematical framework based on a perturbation expansion of the energy functional (vide infra). The mathematical framework of CDFT concepts could then be used to elucidate known chemical rules (Sanderson's Electronegativity Equalization Principle,11 Pearson's fard and soft acids and bases principle,12 the Woodward–Hoffmann rules13,14) and to discover new rules (first, and most notably, Pearson's maximum hardness principle15). Applications in a variety of chemistry-subfields—from organic via organometallic to inorganic and materials chemistry, from catalysis to pharmaceutical and biochemistry—followed. Exhaustive reviews on both fundamental and applied aspects of CDFT are now available,16–24 as can be seen in the recently published comprehensive multi-author volume.25
One of the advantages of CDFT is its universality, stressed as one of the three pillars of its philosophy:19,26–28 CDFT tools do not depend on the type (and thus also the level) of the performed calculation; a Fukui function remains as simple to interpret whether it is calculated with using Hartree–Fock, DFT, or an enormous configuration interaction expansion.29,30 Another pillar of CDFT is its mathematical rigor, which means that all concepts arise from a well-defined, physical, theoretical framework. Specifically, CDFT can be developed from a perturbational approach in the influence of changes in the number of electrons, N, and/or the external potential v(r), (the potential felt by the electrons due to the nuclei when no external fields are present) are used to describe chemical changes, and reactivity indicators arise naturally as terms in the Taylor expansion of the energy functional E[N,v].5,16,21 (see Sections 2 and 5). The intrinsic part of these atomic or molecular responses—i.e., the infinitesimal response, where the magnitude and direction of the perturbation are usually immaterial—are response functions5,17,21 which can be written as 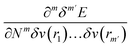 . Different types of response functions can now be discerned: global descriptors, the pure N-derivatives, independent of position such as the electronegativity
. Different types of response functions can now be discerned: global descriptors, the pure N-derivatives, independent of position such as the electronegativity 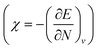 7 and the hardness
7 and the hardness 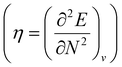 ;8 local descriptors, varying from place to place, such as the density itself
;8 local descriptors, varying from place to place, such as the density itself 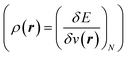 5,17,21 and the Fukui function
5,17,21 and the Fukui function 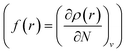 ;21 and finally non-local descriptors, which are functions of two or more position variables such as the linear response function χ(r,r′) defined as
;21 and finally non-local descriptors, which are functions of two or more position variables such as the linear response function χ(r,r′) defined as 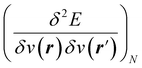 and also equal to
and also equal to 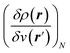 .5,31,32 These derivatives are commonly represented in a “response function tree”17,21 having at the left the global descriptors and then, moving to the right, the local and non-local descriptors, the order of the derivatives ascending when moving from the top to the bottom (see Section 3.1). Nearly all response functions up to n = 3 are now extensively documented and have been applied in a wide range of situations.16–23,25,31–37
.5,31,32 These derivatives are commonly represented in a “response function tree”17,21 having at the left the global descriptors and then, moving to the right, the local and non-local descriptors, the order of the derivatives ascending when moving from the top to the bottom (see Section 3.1). Nearly all response functions up to n = 3 are now extensively documented and have been applied in a wide range of situations.16–23,25,31–37
Until recently, the energy functional mentioned above and the corresponding response functions were considered with only N and v as independent variables, with one major exception. Spin was included quite early in the history of CDFT with two variants: 1° invoking spin polarization leading to a functional E[N,NS,v,B] where NS is the spin number (the difference between the number of α and β electrons) and B an external magnetic field;38,39 2° resolving the number of electrons and the external potential into its spin components E[Nα,Nβ,v,vβ].40 The evolution of a system when its spin state is perturbed, e.g., by a magnetic field either by spin transfer from its environment or by another reagent, can be scrutinized using this extension. A disadvantage of spin-resolved CDFT is the doubling of the reactivity descriptors and the concordant difficulties associated with their numerical evaluation.41–45 Nevertheless, its further development and use is essential, for example, when using CDFT to study transition metals and their role in catalysis and for studying radical systems and their reactions.
A more recent and natural extension is the inclusion of finite temperature by Franco-Perez, Ayers, Vela, and Gázquez46 to cope with the N-differentiability issues of the E[N,v] function(al).47 The exploration of the role temperature plays in CDFT was pioneered by Chattaraj, Cedillo, and Parr.48 It is indeed well-known that in the limit of 0 K, the E vs. N curve at constant v is a sequence of intersecting straight lines, leading to a discontinuity in the chemical potential and ill-defined behavior of all descriptors involving a second N derivative.47,49 In the first part of this Perspective, it will be shown that when passing to the grand canonical ensemble, a unified approach of CDFT chemical concepts can be formulated. Within this framework, both electronic energy and electron density can be expressed as analytical, continuous, and differentiable functions with respect to (w.r.t.) the number of electrons, alleviating several of the main limitations associated with the standard zero-temperature counterpart and offering temperature-dependent descriptors that resolve issues where they were previously ill-defined at absolute zero temperature. Relationships between descriptors that were previously only valid at 0 K are thus refined. These newly defined chemical concepts not only reconcile the mathematical rigor and chemical insight of CDFT, which are fundamental to the theory but also establish a general mathematical structure that forms the basis for the formulation of a plausible definition of local hardness, which inherently possesses a mathematical ambiguity, conjointly with other local counterparts of some global descriptors. Moreover, it is conceivable to validate and reformulate certain established reactivity principles, including the hard/soft acid/base (HSAB) principle, the maximum hardness principles, and the |Δμ| big is good rule,5 within a framework that considers temperature dependence.
The second part of this Perspective presents an extension of CDFT to variables other than spin and temperature. The motivation is no longer the need to formally supplement the traditional CDFT formalism, but the desire to treat, directly, external stimuli that are applied to molecules in state-of-the-art experimental studies. Present-day chemistry indeed shows an ever-increasing variability in new reaction conditions, including for example the presence of an external electric field,50,51 the application of an external mechanical force (mechanochemistry),52 and the creation of (very) high pressures.53 Inclusion of the corresponding variables (fields) in a CDFT description is useful, as it was shown by Chattaraj and Maiti for the interaction of a helium atom in its ground and excited electronic states with monochromatic and bichromatic laser pulses,54 the collision of a proton with two-electron atomic species,55 up to recent work by Liu and coworkers on the effect of an external electric field on the acidity and aromaticity of benzoic acids.56 The case of an (ε) is a counterpart of recent experimental and theoretical work on Oriented External Electric Fields (OEFFs), characterized by Shaik as “novel effectors of chemical change”.51 Its counterpart, the inclusion of external magnetic fields (B), though less prominent in the literature, has been receiving increased attention. For example, a groundbreaking study by Lange in 2005 revealed new bonding mechanisms (perpendicular paramagnetic bonding of H2 in magnetic fields on the order of 105 T).57 Its intrinsic importance in unveiling atomic behavior in white dwarfs and neutron stars with fields of the order of 102–105 T and 107–109 T,58 which hitherto has been a domain almost exclusively covered by atomic physicists, should not escape the attention of quantum chemists reflecting upon chemistry in (high) magnetic fields. The effect of an external magnetic field on several CDFT descriptors of confined atoms was analyzed by Chattaraj and his group.59
Although similar to electric and magnetic fields because it extends chemical reactivity in exciting ways, mechanochemistry—where molecules are subjected to an external mechanical force (F), is fundamentally different. Although existing in its macroscopic form for centuries (grinding, etc.), downscaling to the molecular level is recent.52 Thanks to ingenious experimental setups, unexpected chemistry has been revealed, for example, the overruling of the celebrated Woodward–Hoffmann rules for pericyclic reactions under external force.60,61 As the external force does not directly appear in the conventional quantum-mechanical Hamiltonian, an alternative computational framework is needed in which the directional character of the force is a leitmotiv in contrast to the isotropic nature of the pressure in the domain of “Chemistry at (Very) High Pressure”.53 This field, although finding its origins more than a century ago,62 also received particular interest in recent years thanks to a new generation of high-pressure devices (e.g. Diamond Anvil Cells) which bring pressures higher than 100 GPa into reach.63 From the computational side, XP-PCM64,65 and GOSTSHYP66 methods have been extremely instrumental in simulating/creating pressure in quantum-chemical studies of systems/reactions under pressure. Its extension to CDFT,67 is a natural sequel to the extension of classical work68 on the behavior of atomic and molecular systems under confinement to CDFT.69–73
The present Perspective aims at giving the reader an insight into how the above-mentioned extensions of CDFT to temperature, on the one hand, and external “fields”, on the other hand, (using the “field” terminology for the sake of brevity also for non-electromagnetic fields) were developed, and which new insights they led to based on few selected examples. Central in this endeavor is the extension from the standard N,v dependence of the energy functional to, at least formally (vide infra), an energy functional of the type E[N,v,T,X] with X = ε,B,F,P. An initial status report on the inclusion of external fields can be found in ref. 74.
The organization of the paper is as follows. After reviewing the underlying mathematical framework (Section 2), we consider including temperature within CDFT, starting from the observation that certain descriptors are ill-defined at zero temperature in the standard CDFT framework (Section 3). In Section 4, the introduction of the different “fields” will shortly be described. For the sake of brevity, in the latter part, we will only highlight some general and basic theoretical aspects and computational particularities without going into too many details. In each case, a few selected case studies are briefly presented. For more technical aspects, the reader is referred to the original papers and some CDFT reviews indicated in the text. Before summarizing, we make some notes about computational software and implementation.
2. Conceptual DFT with additional variables
Traditionally, the paramount variable in conceptual DFT is the ground-state electronic energy for an N-electrons system bound by an external potential, v(r). Invoking the variational principle, we have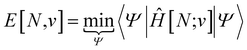 | (1) |
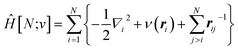 | (2) |
The response of the energy to changes in the external potential can be evaluated using standard perturbation theory, but responses to the number of electrons requires extending the formulation, either by allowing the wavefunction to have non-integer electron number (as in the Fock-space approach)75 or, more traditionally, by moving to the grand canonical ensemble.47,49,76,77 In the grand canonical ensemble, the density matrix replaces the wavefunction in the variational principle,
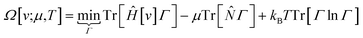 | (3) |
![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) is the number operator; the last term contains the von Neumann entropy,
is the number operator; the last term contains the von Neumann entropy,S[Γ] = −kBTr[Γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Γ] Γ] | (4) |
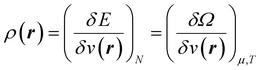 | (5) |
Early in the development of density-functional theory, researchers recognized that it would be useful to add additional variables to the fundamental framework. The first such attempts were related to resolving the spin-components of the electron density, imposing symmetry constraints, and targeting excited states, with subsequent work focused on providing a more rigorous foundation for meta- and hybrid-generalized gradient approximations.80–84 In principle, the strategy is simple: one adds a constraint to the minimization in eqn (1) or (3), thereby defining a new functional that depends on that property. For example, if one wishes to force the system to have specified values for one or more properties, χ, one can rewrite the grand-canonical variational principle as:85–92
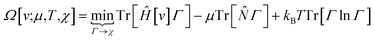 | (6) |
It was realized, relatively early on, that this poses challenges for the mathematical framework of DFT. First, the Hohenberg–Kohn theorem, which states that the ground-state density suffices to determine all the properties of the system, is now overloaded: one wishes to specify the density and χ, and these two quantities need not be compatible. For example, a meta-generalized gradient approximation depends simultaneously on the local kinetic energy, t(r), and the density, one discovers that there are choices for ρ(r) and t(r), that do not correspond to any fermionic system, and that the permissible choices are difficult to characterize.93 This N-representability problem can be removed when the constraints are nonconcave functionals of the density matrix because then one can use the Legendre transform to define a rigorous functional for any variable choice (though the functional will be infinite-valued where the variables are incompatible).94,95 This essentially, is what was done when deriving eqn (3): we chose to specify a specific particle number (described by a linear operator) and value for the entropy times minus one (so that it is described by a convex function); the conjugate variables (chemical potential and temperature, respectively) then entered into the functional.
The mathematics is simplest in the special case where the properties one wishes to specify, χ, are determined by linear operators/fields,
χ = Tr[![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) Γ] = 〈Ψ| Γ] = 〈Ψ|![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) |Ψ〉 |Ψ〉 | (7) |
We then have rigorous definitions for density functionals like,
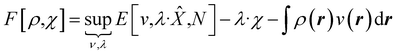 | (8) |
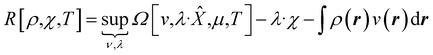 | (9) |
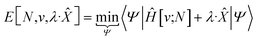 | (10) |
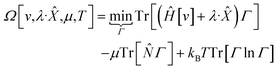 | (11) |
In eqn (10) and (11) one does not directly control the system's properties; one has to choose the field strengths, λ, to find the desired values of the field's conjugate properties, χ. When doing so, one must keep in mind that no such field may exist (this is the generalization of the v-representability problem in conventional DFT).
The functionals defined here are not the same as those which are used in normal conceptual DFT, but all the key mathematical strategies are still available because of their underlying reliance on the Legendre transform: it is only the difficulty of evaluating the state functions that impedes direct application of the theories. These difficulties are mitigated in cases where one wishes to control the fields, λ·![[X with combining circumflex]](https://www.rsc.org/images/entities/char_0058_0302.gif) , imposed on the system, rather than the targeted properties of the system, χ. In such cases, one can directly evaluate the energy and its functional derivatives, for example,
, imposed on the system, rather than the targeted properties of the system, χ. In such cases, one can directly evaluate the energy and its functional derivatives, for example,
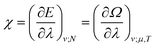 | (12) |
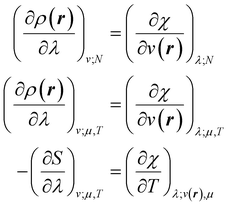 | (13) |
However, moving to the density-based picture in CDFT (e.g., examining the hardness kernel when there are additional basic variables) remains problematic because it requires one to deal with the non-standard density functionals, eqn (8) and (9).33,96 In addition, even within the theoretically straightforward framework founded by taking differentials of the energy or the grand potential, it is nontrivial to derive detailed working expressions and apply them to chemically relevant problems. The next sections review some key results along these lines.
3. Temperature
3.1 The N differentiability problem and the benefits of introducing temperature
As alluded to in the previous section, response functions, defined as the partial derivatives of the electronic energy E w.r.t. its independent variables, namely, the number of electrons and the external potential, play a fundamental role in CDFT.16,18,97 They are essential not only for predicting the chemical responses of electronic systems but also for establishing rules governing reactivity. However, it is important to note that proper definitions of these quantities require the electronic energy E to be a differentiable function of such variables. Unfortunately, the dependence of E on the number of electrons, at zero-temperature, exhibits a piecewise-continuous, straight-line behavior, which inherently results in a first-order derivative discontinuity.47,77 This phenomenon is known as the “N-differentiability problem” of electronic energy, and it is so fundamental that it hinders the development of unique and unequivocal working formulas for global reactivity descriptors (those that describe the molecule as a whole), such as the electronic chemical potential μ and the chemical hardness η, which are the first and second-order derivatives of E, respectively. Particularly, the chemical hardness has a Dirac delta behavior in the number of electrons, leading to a meaningless result for a real chemical property.98From the ensemble theorem,47 it is known that the electron density exhibits a dependence on the number of electrons similar to the electronic energy. Consequently, the electron density faces an equivalent “N-differentiability problem”, leading to significant implications in the development of working equations for local descriptors obtained from the derivatives of the electron density, such as the Fukui function and the dual descriptor99–101 (first and second-order derivatives of ρ, respectively).9,102 As the chemical hardness, the dual descriptor also exhibits a Dirac delta behavior in the number of electrons. Approximations such as finite differences or interpolation models are routinely used to address the N-differentiability problem on both the energy and the density. These approximations, while useful, can compromise the rigor and universality of CDFT theory.
Examining the E vs. N dependence, it becomes evident that the straight-line behavior is a consequence of how the fundamental N-states (electronic states with different numbers of electrons) are distributed at absolute zero temperature (0 K). At this condition, only one of them (for instance, the neutral species) will populate the ensemble, depending on the environmental conditions. To overcome the issue of derivative discontinuity, an alternative approach involves selecting a new theoretical framework that allows for the proper modulation of the distribution of electronic states with different particle numbers (electrons). A consistent approach is to adopt the rigorous framework of the grand potential, where the distribution of all possible quantum states can be controlled by manipulating the reservoir's temperature (T) and chemical potential (μBath).49,76 By doing so, for a given set of electronic states, the most probable energy value to be observed (E), the thermodynamic average energy, will exclusively depend on the environment (reservoir parameters). If the specified values for these free variables are established appropriately, a mixture of states will likely be observed. Consider a grand ensemble constituted by a mixture of states encompassing a neutral (N0), the first anion (N0 + 1), and the first cation (N0 − 1) species corresponding to a particular electronic system (atom or molecule). The average energy value relative to the corresponding neutral species is given by the following equation,103
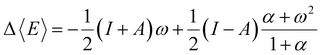 | (14) |
| α = (ω2 + 4(1 − ω2)exp[β(I − A)])1/2 | (15) |
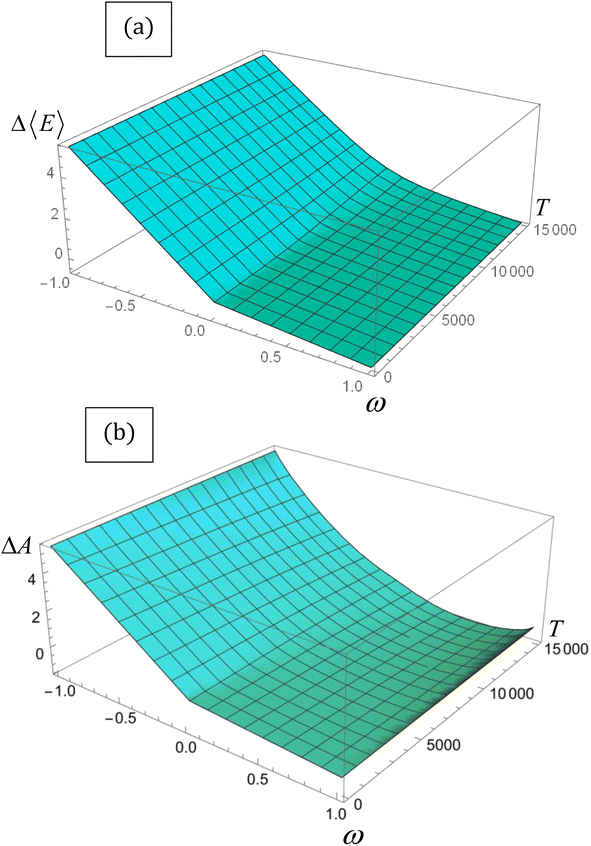 | ||
| Fig. 1 (a) ΔΔ〈E〉 vs. T and (b) Δ〈A〉 vs. T for the lithium atom obtained through eqn (14) and (16), respectively. Energy is in eV, and temperature in K. | ||
Recalling that each of the electronic states in the mixture owns an electron density, the average electron density relative to the density of the neutral species can be determined using the following equation,46
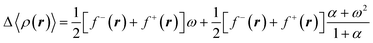 | (16) |
In the previous equation, f−(r) and f+(r) are commonly known as the directional Fukui functions, the former for an electrophilic and the second for a nucleophilic attack. Similar to the average energy (eqn (14), the average density in eqn (16) is N-differentiable to arbitrary order. Therefore, by introducing the temperature as a free variable within a grand potential framework, it is possible to resolve the N-differentiability problems in CDFT.
Despite its ad hoc nature, the parabolic approximation of the E vs. N profile has served as the foundational platform for computing most reactivity indexes.8,104–106 Moreover, it constitutes the theoretical underpinning for one of the most successful and widely used descriptors—the electrophilicity index. This index is defined as the negative disparity between the energy value at the minimum point of the approximated E vs. N profile and the energy associated with a reference state containing an integer number of electrons, typically the neutral state. Interpreted as the stabilization of maximum energy resulting from the acceptance of fractional electronic charge when the chemical species is immersed in a bath of electrons, it is essential to note that this interpretation may be misleading. This is particularly true since the exact E vs. N profile does not exhibit a minimum, even at temperature values different from zero, as discussed below. Nevertheless, considering that the concept of stabilization is inherently linked to equilibrium, where species evolve towards stable states, it becomes more convenient to utilize a thermodynamic state function instead of the electronic energy to describe the maximum stabilization of an electronic system due to the acceptance of electronic charge. An exhaustive inspection of the dependence of the Helmholtz free energy potential on the fractional charge (eqn (4)) reveals that this thermodynamic potential displays a convenient curvature (see Fig. 1b). This allows for the definition of a finite-temperature electrophilicity index analogous to the one defined at zero temperature. At temperature values consistent with β < (I − A), this dependence follows the analytical expression outlined below,
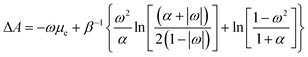 | (17) |
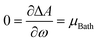 , which naturally implies the electron saturation situation. Moreover, our findings demonstrate the existence of a specific temperature condition under which the ΔA vs. ω profile closely resembles the parabolic approximation. Even more remarkably, under these circumstances, the finite temperature definitions of all reactivity indicators yield virtually identical results to their zero-temperature, parabolic counterparts. We have called this temperature condition the parabolic temperature Tparabol. Consequently, this analysis suggests that temperature has been “artificially” introduced into the conceptual chemical reactivity theory since its inception.
, which naturally implies the electron saturation situation. Moreover, our findings demonstrate the existence of a specific temperature condition under which the ΔA vs. ω profile closely resembles the parabolic approximation. Even more remarkably, under these circumstances, the finite temperature definitions of all reactivity indicators yield virtually identical results to their zero-temperature, parabolic counterparts. We have called this temperature condition the parabolic temperature Tparabol. Consequently, this analysis suggests that temperature has been “artificially” introduced into the conceptual chemical reactivity theory since its inception.
3.2 Towards well-behaved chemical reactivity concepts. Theoretical and computational ansatz and results
With explicit, continuous, and differentiable expressions for the electronic energy and the electron density as functions of the number of electrons, it is feasible to develop analytical working formulas for any of their corresponding response functions within the ensemble model composed of three fundamental electronic states. However, utilizing the chain rule for partial derivatives can establish a more general strategy. For example, the first-order derivative of E w.r.t. N, which represents the electronic chemical potential within a grand ensemble consisting of an arbitrary number of ionized, neutral, and excited states, is expressed as follows,107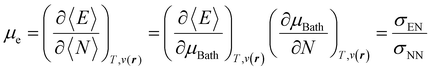 | (18) |
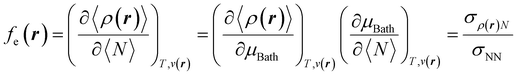 | (19) |
To use eqn (18) and (19), it is necessary to define the set of states constituting the grand ensemble. Nonetheless, in practice, it is still convenient to consider the ensemble model comprised by three fundamental electronic states, since, as shown earlier,109 the contribution of excited and highly ionized states is negligible at any temperature relevant to traditional chemistry. Alternatively, you can take the first-order derivative of eqn (14) and (16) w.r.t. the number of electrons ω, in any case resulting in,
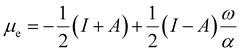 | (20) |
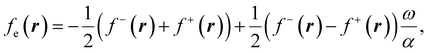 | (21) |
| ηe = (I − A)P(ω), | (22) |
| Δfe(r) = (f+(r) − f−(r))P(ω), | (23) |
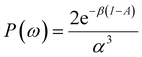 | (24) |
It was recently demonstrated that the chemical hardness in eqn (22) implies both the hard and soft acids and bases (HSAB) principle and the maximum hardness (MH) principle.110 As can be observed, all the quantities involved in such an equation depend, in addition to the grand potential free variables, on the quantity I − A, providing equivalent conclusions to the (approximated) zero-temperature computational scheme but on a different scale.110 One possible approach to address this scale discrepancy is to take the logarithm of the temperature-dependent quantities. This methodology aligns with the grand potential charge transfer models recently developed, wherein a chemical potential principle is defined for scenarios involving only two reagents engaged in a chemical reaction at an equimolar ratio. Notably, this method yielded electronegativity values for the resulting product that closely matched experimental results across nearly 40 reactions.111 Another, more elegant way to establish working formulas for the second order response functions is by defining their corresponding local or non-local counterparts by using the fluctuations ratio strategy conjointly with the chain rule for partial derivatives. To relate the global hardness to its local counterpart, the local hardness, through this procedure, it is first necessary to define the local counterpart of the chemical potential as follows,112
| μe = ∫μe(r)dr, |
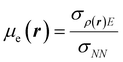 | (25) |
This way, μe(r), the local chemical potential, indicates how μe spreads over the molecular space. The low temperature working formulas for μe(r) are μ−e(r) = If−(r) and μ+e(r) = Af+(r) for the accepting and donating processes, respectively, while 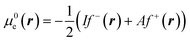 when the expected value of the fractional charge is zero. Taking the partial derivative of eqn (12) w.r.t. the average electrons ω one gets,
when the expected value of the fractional charge is zero. Taking the partial derivative of eqn (12) w.r.t. the average electrons ω one gets,
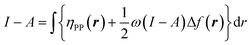 | (26) |
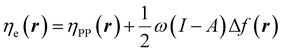 | (27) |
In eqn (26) and (27), ηPP(r) = If−(r) − Af+(r)) is called the Parr and Pearson local hardness while Δf(r) = f+(r) − f−(r) is the standard (zero temperature) definition of the dual descriptor. As it can be observed, the quantity P(ω) is absent in eqn (26). It was canceled out because it appears on both sides of the equation after differentiating eqn (25). The local hardness in eqn (27) describes how the quantity I − A is distributed across the molecular space. The corresponding low-temperature working formulas are 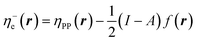 ,
, 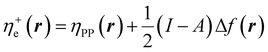 and η0e(r) = ηPP(r). It's important to mention that the local hardness has been a somewhat ambiguous quantity over the years due to its definition. However, employing the fluctuation ratio strategy within the finite temperature regime, it not only helps avoid the P(ω) quantity responsible for the Dirac delta behavior at absolute zero but also provides a plausible definition of local hardness.
and η0e(r) = ηPP(r). It's important to mention that the local hardness has been a somewhat ambiguous quantity over the years due to its definition. However, employing the fluctuation ratio strategy within the finite temperature regime, it not only helps avoid the P(ω) quantity responsible for the Dirac delta behavior at absolute zero but also provides a plausible definition of local hardness.
If this strategy is then applied to the Fukui function aiming to obtain a “well-behaved” definition of the dual descriptor, a non-local quantity (dependent on two positional vectors in space), denominated as the Fukui kernel, fe(r,r′), is thus obtained, i.e.,113
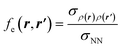 | (28) |
The low temperature working formulas for fe(r,r′) are f−e(r,r′) = f−(r)f−(r′), f+e(r,r′) = f+(r)f+(r′), and 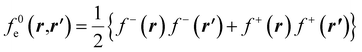 . The Fukui kernel is, in essence, a nearsighted descriptor, and it can be computed from the condensed Fukui functions of two adjacent atoms. This interpretation of the Fukui kernel characterizes it as a bond reactivity index, signifying the susceptibility of a specific chemical bond to engage in a charge transfer process. Now, taking the partial derivative w.r.t. the fractional charge at both sides of eqn (28), the following result is obtained,
. The Fukui kernel is, in essence, a nearsighted descriptor, and it can be computed from the condensed Fukui functions of two adjacent atoms. This interpretation of the Fukui kernel characterizes it as a bond reactivity index, signifying the susceptibility of a specific chemical bond to engage in a charge transfer process. Now, taking the partial derivative w.r.t. the fractional charge at both sides of eqn (28), the following result is obtained,
| Δf(r) = ∫Δfe(r,r′)dr′ | (29) |
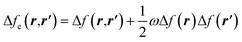 | (30) |
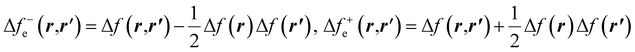 and Δf0e(r,r′) = Δf(r,r′). It is pertinent to mention that there are other temperature-dependent proposals for the (local) dual descriptor quantity; all of them provide a similar interpretation of the amphiphilic nature of chemical species at the local level.112,114
and Δf0e(r,r′) = Δf(r,r′). It is pertinent to mention that there are other temperature-dependent proposals for the (local) dual descriptor quantity; all of them provide a similar interpretation of the amphiphilic nature of chemical species at the local level.112,114
The suite of these new finite-temperature reactivity descriptors, encompassing both local and non-local indexes such as the local chemical potential, local hardness, as well as the Fukui and dual descriptor kernels, has demonstrated remarkable utility in characterizing, differentiating, and forecasting reactivity trends within diverse chemical species participating in an array of chemical reactions.112,113,115,116 It is worth noting that entirely equivalent definitions for these descriptors have been formulated using the zero-temperature (temperature-independent) formalism, strengthening their robustness and ensuring their versatility and applicability.117–121
The inclusion of temperature as a new independent variable to describe properties of the electronic reactive systems opens up the possibility of developing a novel family of response functions, particularly those associated with ensemble perturbations arising from temperature variations.122,123 Among these, the heat capacity of electronic systems stands out as a significant quantity that can offer valuable insights into reactive processes. By applying the chain rule for partial derivatives and the fluctuation ratio strategy, we derive the following definition and working equation for the heat capacity of a grand ensemble consisting of an arbitrary number of fundamental and excited states,122
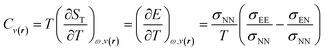 | (31) |
For the representative three-state ensemble model under low-temperature conditions, the heat capacity can be computed using the following expression,
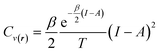 | (32) |
This equation is valid when the fractional charge equals zero (indicating the neutral species is predominant). For any other situation (at low temperatures), the quantity Cv(r) approaches zero. After an exhaustive analysis of eqn (31) and (32) it has been inferred that an energy transfer may occur before the exchange of electrons takes place. As an electronic system is “heated up”, its electrons become more labile and inclined to participate in charge transfer processes. Recent theoretical evidence suggests a close relationship between temperature, heat capacity, and the hardness properties of electronic systems.124 Notably, it has been demonstrated that at the temperature condition given by,
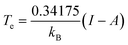 | (33) |
3.3 Chemical reactivity principles at finite temperature
In the zero-temperature CDFT formulation, reactivity principles are derived from certain response indices that explore the implications of achieving an equilibrium state. This is often expressed by considering the variation of the total electronic energy of all species involved in the reaction, equating to zero. In this context, the Chemical Potential Equalization Principle (CEP)7,11 posits that the exchange of electrons between two reacting species halts when their chemical potentials become identical. Similarly, the Maximum Hardness (MH) principle asserts that a reaction tends toward the maximum increase in chemical hardness.15,125,126 Under analogous considerations, the Hard and Soft Acids and Bases principles (HSAB) suggest that in a double substitution reaction, the most energetically favored process involves a soft acid interacting with a soft base, while a hard acid will react with a hard base.127–133Notably, a chemical potential equalization principle is inherently linked to the grand potential formalism, where a chemical species exchanges electrons until its chemical potential matches that of the reservoir. This scenario becomes apparent when a species is infinitely diluted or immersed in a second reagent, a concept previously leveraged in formulating a charge transference model under finite temperature conditions.111 The MH and HSAB principles find corroboration within a finite temperature regime by ensuring that the temperature-dependent definition of hardness eqn (22) is a monotonically increasing function of the standard Parr & Pearson hardness I − A.110 This guarantees that, for any pair of acids/bases, this definition of hardness identifies the same reagent as the hardest, as predicted by the zero-temperature chemical hardness. These findings offer robust theoretical support for their counterparts at zero temperature while concealing both theoretical frameworks.
In addition, it is important to mention that the dependence of the chemical potential on the temperature leads to an additional term in its differential given by
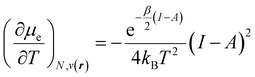 | (34) |
The development of reactivity principles remains an open and promising avenue within the grand canonical formalism. For instance, there is potential to establish a temperature equalization principle or reactivity rules focused on the (finite temperature) Fukui function or any of the presented response kernels. These propositions promise to provide novel and valuable insights into the reactivity of chemical species at the global, local, and chemical bonding levels.
3.4 Applications
Besides their theoretical rigor, chemical reactivity descriptors have demonstrated exceptional efficacy in accurately replicating equilibrium and reaction rate trends. In the subsequent discussion, we highlight instances where these descriptors successfully mirrored experimental trends and offered plausible explanations for the analyzed chemical processes. It is essential to acknowledge that, up to now, given the novelty of this theoretical framework, the capacity of some of these indices to describe the reactivity characteristics of chemical species has yet to be thoroughly tested.We also employed the Gaussian program144 with the PBE0 exchange–correlation energy functional145 and the 6-311G** basis set146,147 for geometry optimization of each considered molecule (neutral species). Default thresholds for Self-Consistent Field (SCF), geometry optimizations, and default grids for numerical integrations were utilized. Subsequently, deMon2k calculations were performed using the same optimized geometry, functional, and basis set as those in the Gaussian calculations. An auxiliary basis set GEN-A2* was used for the Hirshfeld population analysis.
In Fig. 2, we present the correlation between the electrophilic local chemical potential μ−k = εHfHk and experimental pKa values for a comprehensive set of 51 acids, comprising 17 phenols, 17 carboxylic acids, and 17 aniline derivatives.148,149 The condensed-to-atoms values for the “electrophilic” local chemical potential were computed at the appropriate protonation sites for each compound family—on the (deprotonated) acidic oxygen atom for phenols and carboxylic acids, and on the nitrogen atom in the amino moiety for anilines. The obtained regression coefficient demonstrates an acceptable fit and successfully captures the trend observed in experimental measurements. Notably, this local descriptor outperforms the “global” electrophilic chemical potential μ−e = εH, where a limited correlation (r2 = 0.417) was observed (see ref. 115). As highlighted earlier, local counterparts of global descriptors prove to be more convenient for analyzing the reactivity features of chemical species at the local level, especially when dealing with compounds that do not share identical functional reactive groups.
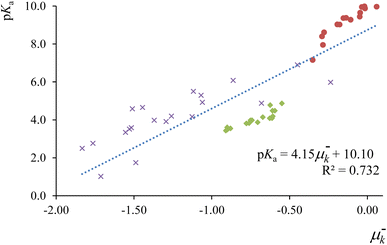 | ||
| Fig. 2 Correlation profiles between experimental pKa values of phenol (red circles), carboxylic acid (green diamonds) and aniline (purple crosses) derivatives, with the corresponding condensed to atom values for the local chemical potential at the protonation site. This figure has been reproduced from ref. 115 with permission from Springer Nature, copyright 2020. | ||
As a second illustrative example, we delved into the analysis of Markovnikov addition in nine distinct ethenes. Markovnikov's rule, governing the electrophilic addition of hydrogen halides (H–A) across a carbon–carbon double bond, posits that the hydrogen atom prefers to bind to the carbon atom with the highest number of hydrogen atoms attached, while the halide prefers the carbon bonded with fewer hydrogens.150,151 To explore this, we compared condensed-to-atom values of local hardness and local chemical potential at the C1 and C2 carbon atoms within the C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C2 double bond. These values were compared with the calculated reaction Er and activation energies Eact for the electrophilic addition of hydrogen chloride (HCl) to each ethylene derivative.152Fig. 3 illustrates the correlation profile between the local hardness ratio η−C2/η−C1 and the reaction energy ratio Er_C2/Er_C1 where Er_C1 and Er_C2 represent the reaction energies corresponding to hydrogen addition to C1 (Markovnikov addition) and C2 (anti-Markovnikov addition) carbon atoms, respectively. The obtained regression parameters indicate that the local hardness descriptor effectively discriminates between molecular sites that are most energetically susceptible to hard–hard and soft–soft interactions. This analysis strongly suggests that Markovnikov's rule emerges as a consequence of the Hard and Soft Acids and Bases (HSAB) principle.
C2 double bond. These values were compared with the calculated reaction Er and activation energies Eact for the electrophilic addition of hydrogen chloride (HCl) to each ethylene derivative.152Fig. 3 illustrates the correlation profile between the local hardness ratio η−C2/η−C1 and the reaction energy ratio Er_C2/Er_C1 where Er_C1 and Er_C2 represent the reaction energies corresponding to hydrogen addition to C1 (Markovnikov addition) and C2 (anti-Markovnikov addition) carbon atoms, respectively. The obtained regression parameters indicate that the local hardness descriptor effectively discriminates between molecular sites that are most energetically susceptible to hard–hard and soft–soft interactions. This analysis strongly suggests that Markovnikov's rule emerges as a consequence of the Hard and Soft Acids and Bases (HSAB) principle.
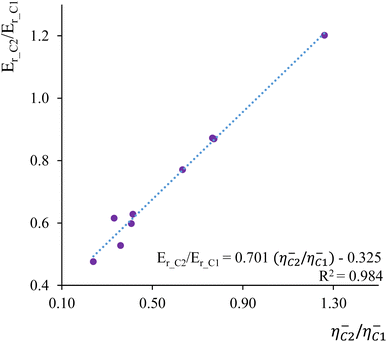 | ||
| Fig. 3 Correlation profile between the local hardness ratio η−C2/η−C1 and the reaction energy ratio Er_C2/Er_C1. | ||
As a third case study,113 we assessed bond stability by comparing our Fukui and Dual kernel descriptors with the experimentally determined bond enthalpies of 20 previously reported compounds.153 Bond enthalpy quantifies the strength of a chemical bond by measuring the energy needed for the homolytic dissociation of one mole of the bond. It is influenced by the bond's stability within the molecule and the fragments' ability to stabilize free radicals formed during dissociation.
The initial step in homolytic bond cleavage involves electron flow near the bonds, where fragments retain one bonding electron. Before using the Fukui kernel to analyze bond reactivity, studying how the bond order changes with the initial electron flux is essential. For this purpose, we used the τ-hyperdual kernel. Positive values of the τ-hyperdual kernel indicate increased bond order and resistance to homolytic cleavage, while negative values suggest weakened chemical bonding due to both the initial electron flux and bond breaking. Results in Table 1 of ref. 113 show that if one first uses Δf(2)k,k′ to classify the susceptibility/reluctance of a chemical bond toward its hemolytic cleavage, the calculated values for f0k,k′ then follows a similar trend to the experimental values of the bond enthalpies. Specifically, for bonds with Δf(2)k,k′ ≤ 0, ΔHbond, decreases if f0k,k′ increases. Conversely, for bonds with Δf(2)k,k′ ≥ 0, ΔHbond increases if f0k,k′ increases. Based on these classifications, we subsequently constructed the two correlation profiles presented in Fig. 4a and b, obtaining fairly high regression coefficients r2. As it is evident, delving into the analysis of bond stability and reactivity demands a more intricate examination. Moreover, bond cleavage constitutes a complex process involving various factors, for instance spin-recoupling, which falls beyond the scope of the bond descriptors under consideration.
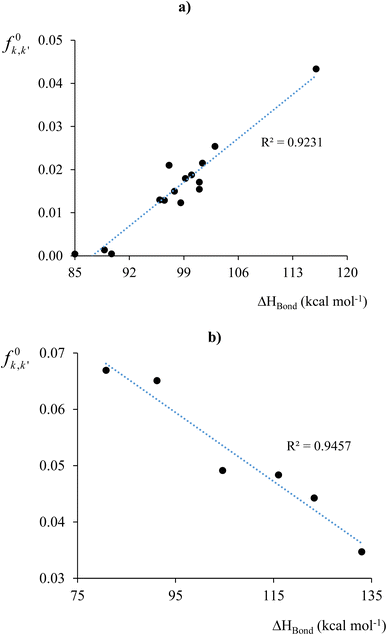 | ||
| Fig. 4 f 0 k,k′ vs. ΔHbond profiles for systems with molecular bonds for which (a) Δf(2)k,k′ < 0 (electron flux destabilized) and (b) Δf(2)k,k′ > 0 (electron flux stabilized). Figure (a) does not consider the data for the breaking of ethylene to methylene radicals (system 7, ref. 113) due to its large value for f0k,k′. Including this reaction would increase the correlation coefficient to 0.967. This figure has been reproduced from ref. 113 with permission from The Royal Society of Chemistry, copyright 2017. | ||
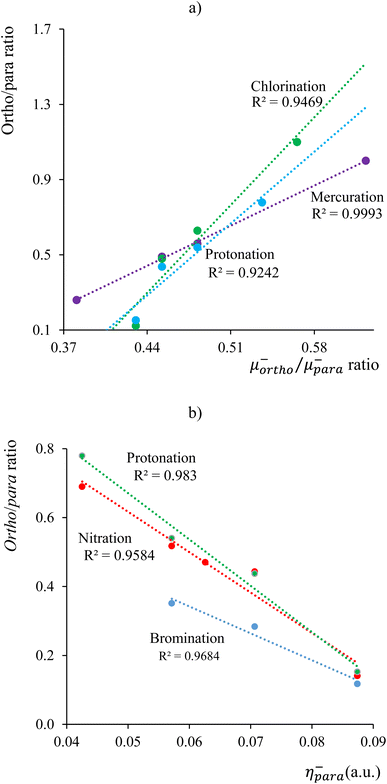
As a final case of study, we analyzed the electrophilic aromatic substitution, SEAr, occurring in 20 different chemical processes, encompassing chlorination,154,155 bromination,155 nitration,156,157 mercuration,158 and protonation159,160 of a set of benzene derivatives (bromine, chlorine, fluorine, iodine, methoxy, methyl, nitro, and hydroxy). SEAr proceeds by the formation of a sigma-complex intermediate, which is characterized by a non-aromatic six-membered ring with five sp2-hybridized carbon atoms and one sp3-hybridized carbon atom, forming sigma bonds with both the attacking electrophile and the departing substituent. The formation of the sigma-complex is generally the rate-limiting step for electrophilic aromatic substitution reactions.151,161 Our analysis revealed two patterns: one linking experimental ortho/para selectivity ratios to corresponding electrophilic local chemical potential ratios, μ−ortho/μ−para, Fig. 5a, and another associating ratios with local electrophilic hardness values at the para position, η−para, Fig. 5b. Fig. 5a shows that increasing the basicity of the ortho carbon favors ortho substitution, while Fig. 5b indicates a preference for para substitution when the para carbon's hardness exceeds that of the ortho carbon, aligning with the HSAB principle. These findings suggest that SEAr regioselectivity may be influenced by the (local) acid–base and hard–soft properties of ortho/para carbons. Specifically, if the ortho carbon is harder, the ortho/para ratio increases with its basicity. Conversely, the para adduct predominates with increasing para carbon hardness when the para carbon is harder.
4. External fields
4.1 Computational strategy (finite fields)
The overall strategy behind all calculations is a “finite field” approach,162i.e., atomic or molecular properties were calculated at different values of the field strength and constant geometry (constant external potential v(r)), and results are reported as such or in the form of derivatives at field strength zero, for the response functions. All calculations were done at 0 K, thereby avoiding the simultaneous presence of temperature and an external field in the energy functional. External fields are considered one at a time, so no mixed perturbations are treated. Details about the “single point” calculations, i.e., for a given field strength and at the geometry of the zero field calculation (the demand for constant v(r)) can be found in the original references.For an electric field with a linear term in the Hamiltonian, the response functions are mostly stopped at first order in the field justified by the relatively low field strengths used (usually from 0 to 0.02 a. u.).163 Note that 1 a. u. corresponds to 5.142 × 1011 V m−1, so e.g. a field of 0.01 a. u. (0.5 1011 V Å−1) is within the range corresponding to electric fields applied in STM experiments and in line with the typical field strengths experienced at the active sites of enzymes and zeolites.51,164,165 For magnetic fields, both the linear Zeeman term (involving the interaction with the total spin S and the total angular momentum L) and the quadratic diamagnetic term are taken into account, but also here, only first-order derivatives w.r.t. B are considered.166 The fields considered vary from 0 to 1 a. u. where 1 a. u. is 2.3505 × 105 T (also denoted as B0), comparable to the highest fields on white dwarfs. Note that this is still far below the very strong fields at which the so-called Landau regime sets in, where the magnetic interactions overrule the coulombic interactions.57 A non-perturbative implementation of current–density functional theory is used in these calculations.166
As already mentioned, in the two cases described above, the computational strategy is, at least in principle, straightforward provided that the inclusion of external electric and magnetic in the Hamiltonian is well defined; however, technically, it is much more complicated in the magnetic field case. The situation for mechanical forces and pressure is different as no corresponding terms in the Hamiltonian are available, so in both cases, an ad hoc computational strategy is used to define the change in external potential associated with the imposed constraint (more rigorously, one could determine the change in external potential using a variational principle like eqn (8), but this is generally impractical). Ergo, the mechanochemical calculations were performed with Beyer's COGEF (Constrained Geometries Simulate External Force) method167 in which the external force is simulated by imposing equilibrium distances r′ different from the field free equilibrium distance r of the diatomics discussed here. Through a number of single point calculations at different r′ values curves of the property considered as a function of F are obtained.168 The forces considered varied between −Fmax/2 and +Fmax/2 where Fmax is the maximum external pulling force that a molecule can resist.
The introduction of pressure was done with the XP-PCM method64,65 allowing simulations of pressures in the GPa range. Increasing pressure is achieved by compressing a molecular cavity with volume VC by reducing the radii of the spheres comprising this cavity. A scale factor f that is multiplied with a set of van der Waals radii starting from reference value f0 at standard conditions is gradually reduced. An energy vs. cavity volume curve is fitted to a Murnagham equation of state,169 and the pressure is obtained as P = −∂E/∂VC. Repeated molecular single-point calculations at different pressures then yield the desired property vs. pressure behavior. A pressure ranges up to the order of 100 GPa was considered, corresponding to the lower limit of the DAC based experiments mentioned above.
4.2 Results and discussion
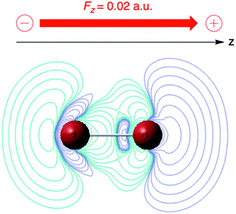 | ||
| Fig. 6 ∂ρ(r)/∂ε plot (in a. u.) for Br2 for a parallel field Fz of +0; 02 a. u. (blue: positive contours, green: negative contours). This figure has been reproduced from ref. 163 with permission from the PCCP Owner Societies, copyright 2021. | ||
As expected, the field polarizes the density with an accumulation of (negative) charge on the right-hand side of atom 1. The extent of polarization increases within the series of the four di-halogens F2, Cl2, Br2 and I2 as can be quantified to a certain extent by the distance of the outermost positive contour at the r.h.s. from nucleus 1 increasing from 1 (taken as unit) in F2, to 1.7 for Cl2, 1.8 for Br2 and 2.4 for I2, in line with the induced dipole moment, pointing in the −z direction with absolute values increasing from 0.30, to 2.20, 3.27 and 5.26 D. The increase in the corresponding parallel component of the polarizability (5.9, 43.4, 64.3, 103.5 a. u.) was shown to be in fair agreement with earlier studies. Condensing the density via a NPA analysis,170 an atom-condensed response function of the type ∂qA/∂ε is obtained, reflecting again the higher sensitivity of the atom when going down in the periodic table: 2.42, 5.25, 7.31 and 10.68 a. u. for F2, Cl2, Br2, I2, respectively. This sequence, which in its turn parallels the polarizability sequence of the halogen atoms, can be traced back to the early work by Coulson in Hückel theory on the atom–atom polarizability πr,s (∂qr/∂αs) where αs denotes the Coulomb integral of atom s.171 The role of the αs as modulator of the potential is taken over by the electric field ε. A similar analogy evolves between πr,s and the above-mentioned linear response function χ(r,r′) or ∂ρ(r)/∂v(r′), which in condensed form takes the form of a matrix with elements ∂qA/∂vB.172
In a second example, the Fukui function f+(r) for nucleophilic attack of formaldehyde is investigated, where the Fukui function f+ is evaluated as the difference in the electron density of the anion and the neutral system which already received ample interest in the literature due to its potential of describing the reactivity of aldehydes and ketones in their most typical reaction.173 In Fig. 7, the influence of a perpendicular electric field on f+ in the plane perpendicular to the molecular plane and containing the C2 axis(the higher field 0.2 is used for better visualization). The symmetry of the Fukui function w.r.t. the molecular plane is broken with contour lines stretching out more out on top of the molecule indicating a preference for a nucleophilic attack “from above”. Upon increasing the field, the Bürgi–Dunitz angle174 comes closer to 90° as compared to 107° for the field-free case. To rationalize the preference for an attack “from above” we decompose the Fukui function in two terms (eqn (35)). The difference between the Fukui function with and without field (f+(r;ε) − f+(r;0)), and the concomitant creation of asymmetry, can then be traced back to a difference in the deformation densities Δρ(r;ε) − Δρ(r;0) between the anion and the neutral system
| f+(r;ε) = f+(r;0) + [Δρ(−)(r;ε) − Δρ(0)(r;0)] | (35) |
| Δρ(r;ε) = ρ(r;ε) − ρ(r;0) | (36) |
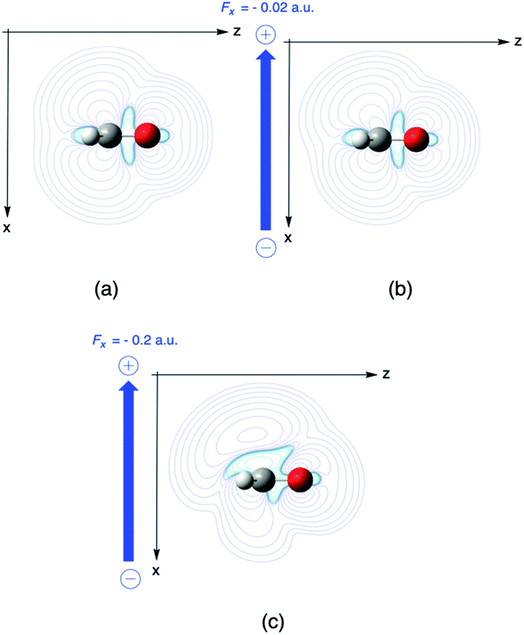 | ||
| Fig. 7 Fukui function for nucleophilic attack f+ for H2CO without electric field (a) and with perpendicular fields Fx of (b) −0.02 and (c) −0.2 a. u., respectively. This figure has been reproduced from ref. 163 with permission from the PCCP Owner Societies, copyright 2021. | ||
It should be remarked that this effect shows up locally but, remarkably, disappears when passing to an atom-condensed version of the Fukui function. The difference in deformation densities is a finite difference approach to the derivative of the Fukui function w.r.t. the electric field ∂f(r)/∂ε, a third order energy response function (∂3E/δv(r)∂N∂ε) further completing the response function tree (Scheme 1) together with the second order response function ∂ρ(r)/∂ε discussed above. In Fig. 8 the former function is shown in the finite difference approximation for Fx = −0.02 and −0.2 a. u., the latter case being used for magnifying the effect and improving the visualization of the asymmetry it induces.
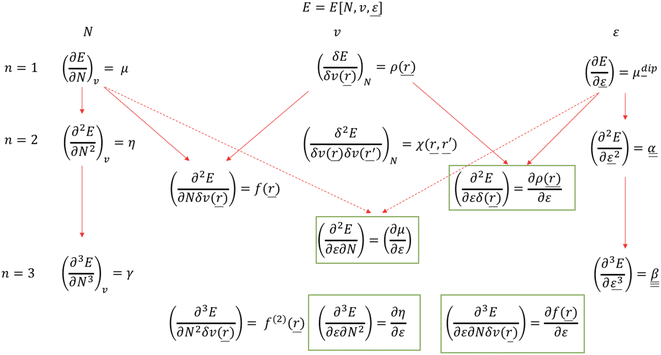 | ||
| Scheme 1 Extended response function tree for the E[N,v,ε] functional: first and second order (n = 1,2) and the most relevant third order (n = 3) cases. New electric field pertaining response functions163 are in green boxes (reproduced from ref. 163 with permission from the PCCP Owner Societies, copyright 2021). | ||
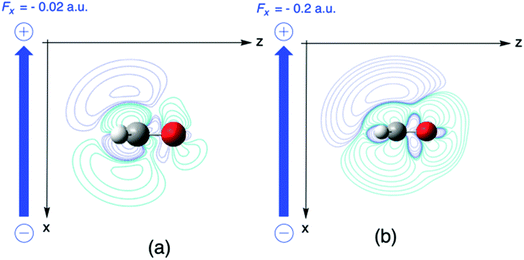 | ||
| Fig. 8 Difference between deformation densities for the H2CO anion and the neutral molecule field values (a) Fx = −0.02, and (b) −0.2 a. u. This figure has been reproduced from ref. 163 with permission from the PCCP Owner Societies, copyright 2021. | ||
This preference for a preferential side of attack may be taken further in the case of ketones or aldehydes with different substituents where a chiral system is then evolving upon attack of a suitable nucleophile. The preference for one side of attack may yield to the preference for forming one enantiomer, though the intricacies of an experimental setup with control of the orientation of the molecules and the field direction can hardly be overestimated.
As another recent example of the influence of an electric field on global DFT response functions, we refer to recent work where its influence on the philicity of radicals was studied varying from simple halogen atoms to diatomics and small polyatomics to aryl radical cations as a sequel to a previous study on electrophilicity/nucleophilicity trends in radicals in the absence of an electric field.175,176 The nucleophilic or electrophilic character was quantified by the global electrophilicity index ω. This global descriptor, not addressed in the Introduction yet, is a so-called derived CDFT descriptor,19 a combination of μ and η (see Section 4.2.3 for its evaluation), expressing the energy gain upon optimal uptake of electrons from an electron reservoir at zero chemical potential.177,178 In a parabolic approximation for the E(N) function it can be written as ω = μ2/ηω.
It turned out176 that the amplitude in the change of ω is dependent on the direction and strength of the applied field, where in most cases, the largest increase in ω is observed when a strong electric field is oriented parallel to the intrinsic dipole moment (in the positive direction) of the radical (e.g., OH, CF3) except when a low intrinsic dipole moment is accompanied by high polarizability as it is in the case of the aryl radical cations.
Finally, note that in Scheme 1, the new reactivity descriptors can be intertwined with the classical response functions used to describe the interaction of an atom or molecule with an electric field: the dipole moment μdip, the dipole polarizability tensor α and the first hyperpolarizability tensor β, containing only derivatives w.r.t. ε where ε has been separated from v as originally defined.
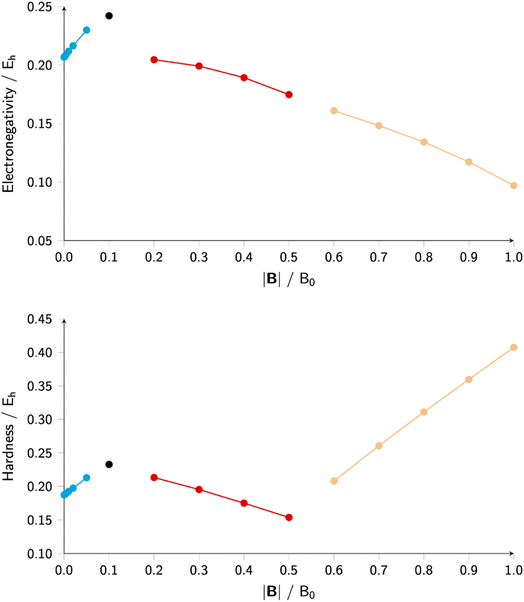
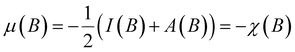 | (37) |
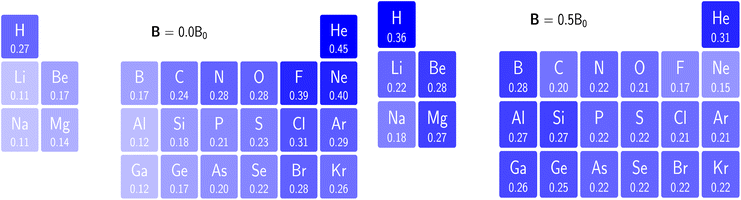
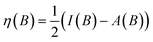 | (38) |
A case study, at Hartree Fock level and using an q-aug-cc-pVQZ basis,180 on the C-atom for a uniform magnetic field oriented along the z-axis varying between 0 and 1 a. u. (to enable a comparison with Schmelcher's earlier work181) reveals a particularity that was not discerned in the electric field studies making the case of the magnetic field much more intricate. Indeed, upon increasing field strength the valence-ground state electronic configuration 2sαβ2pβ−12pβ0 changes into 2sβ2pβ−12pβ02pβ+1 (at B = 0.2B0) and into 2sβ2pβ−12pβ03dβ−2 at B = 0.6B0 (due to the Zeeman term in the Hamiltonian the number of β electrons is maximized and the ML value is minimized). This type of configuration switching is obviously also at stake for the cationic and anionic species, with, in general, different switching points. Combining the behavior of the different species as in eqn (37) and (38) leads to an at first unexpected result of a piecewise behavior of both the electronegativity and hardness, leading to four compartments as shown in Fig. 9 within each compartment a different behavior of χ or η as a function of B: an almost nearly linear behavior shows up in each compartment, but with a different slope and sometimes with a different sign.
 | ||
| Fig. 9 Electronegativity and hardness vs. field strength for carbon (all values in a. u). Different colors correspond to different combinations of ground state configurations of neutral, anionic, and cationic systems. This figure has been reproduced from ref. 182 with permission from the Royal Society of Chemistry, copyright 2022. | ||
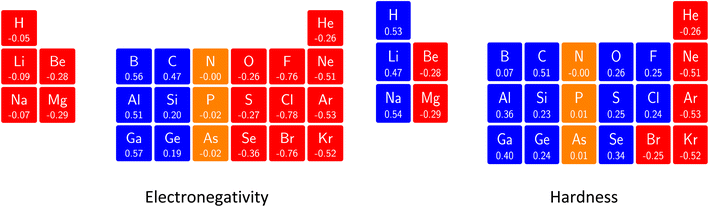
Comparing electronegativity and hardness as a function of B for different atoms thereby becomes extremely subtle as it turned out that the number and positions of the switching points differ from atom to atom. Two options can then be taken to gain nevertheless insight in how these CDFT descriptors vary along the periodic table: the evaluation of all quantities at a given B value for which the middle value of the considered range can be taken (B = 0.5B0), and the calculation of the χ or η derivatives at zero field in the spirit of the response functions discussed in the case of an electric field. With current DFT using the cTPSS exchange–correlation functional183,184 (benchmarked against high level ab initio calculations in strong magnetic fields185) both options were explored. Fig. 10 shows the periodic table for the electronegativity of the main group elements up to Kr at 0.5B0 compared with the field-free case.
 | ||
| Fig. 10 Schematic representation of the electronegativity values at B = 0.0B0 (left) and B = 0.5B0 (right)). Darker colors indicate higher electronegativity. This figure has been reproduced from ref. 182 with permission from the Royal Society of Chemistry, copyright 2022. | ||
The B = 0B0 case reflects well-known trends of increasing electronegativity from left to right and from bottom to top are retrieved at the B = 0 level. The high electronegativity for the noble gases is due to their extremely high ionization energies and negative electron affinities,186 which were set equal to zero as often done in Conceptual DFT studies.187 In the case of B = 0.5B0, now all anions turn out to be stable since the addition of β electrons further stabilizes the system due to the spin-Zeeman effect. The overall pattern now differs significantly from the field-free case. The first four columns, except carbon, show a strong increase in electronegativity, the elements of the fifth and sixth columns slightly decrease, and the halogens and the noble gases strongly decrease. The overall pattern that shows up is a compression of the electronegativity values into a smaller range in which the left-hand side of the periodic table generally shows higher electronegativities than the right hand side, which may yield to changes in the polarity of bonds and so unexpected, new chemistry.
The results for the derivatives ∂χ/∂B at zero field are given in Fig. 11. As no configuration jumps are expected in a finite field approach close to B = 0 yet (as checked for all atoms) this quantity enables a more straightforward comparison across the periodic table.
 | ||
| Fig. 11 Initial responses of the electronegativity and hardness in a magnetic field in a periodic table presentation showing both the numerical values (in a. u.) and categorizing them with a color code: blue (positive derivative), red (negative derivative) and yellow (derivative close to zero). This figure has been reproduced from ref. 182 with permission from the Royal Society of Chemistry, copyright 2022. | ||
The electronegativity derivatives for the s-block are negative (more outspoken for the earth-alkali atoms than for the alkali-atoms). When passing to the p-block strongly positive values occur for group 13 (B family), diminishing when passing to group 14 (C family), and becoming nearly zero for group 15 (N family). The remaining p-block groups show negative values, most notably for the halogens. In globo, one could say that the electronegativity of the elements at either end of the p-block is most sensitive to an external magnetic field leading to a large increase in electronegativity for elements at the left-hand side of this block and a large decrease in electronegativity at the right-hand side. Although the results in Fig. 11 are not directly comparable with the data depicted in Fig. 10, similar trends are retrieved for the p-block elements. Specifically, the increase in χ in Fig. 10 for the third and fourth groups aligns with the strongly positive derivatives in Fig. 11, the small change in the fifth group in Fig. 10 corresponds to the near zero derivative in Fig. 11, and the sometimes strong decrease in χ for the last two groups finds its equivalent in the negative derivatives shown Fig. 11. To put it otherwise: the overall tendency at B = 0 for increasing χ from bottom left to top right is attenuated by the decreasing χ response from left to right, the situation for the s-block elements being less clear-cut.
A similar analysis for the hardness182 reveals two striking tendencies: periodicity shows up again and overall the atoms with highest hardness at zero field have a tendency for decreased or unchanged hardness where most other atoms have a tendency to increase. Again, an overall compression along each period shows up. Finally note that, as in Section 4.2.1, the new response functions involving energy derivatives w.r.t. the magnetic field B can be placed in an extended response function tree alongside with the well-known “classical” pure energy derivatives w.r.t. B: the magnetic dipole moment ∂E/∂B and the magnetic susceptibility ∂2E/∂B2.
The results on atomic electronegativity and hardness can be used as a starting point to investigate the evolution of the polarity of bonds under the influence of a magnetic field. Fig. 12 shows a more detailed view of the evolution of the electronegativity of hydrogen and the halogens (F, Cl, Br) upon increasing magnetic field strength.188
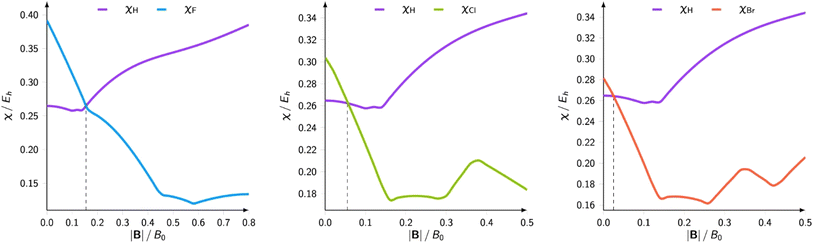 | ||
| Fig. 12 Electronegativities of H and F(left), Cl (center), and Br(right) as a function of the magnetic field strength. This figure has been reproduced from ref. 188 with permission from Informa UK Limited, trading as Taylor and Francis Group, copyright 2022. | ||
Not unexpected on the basis of Fig. 10 and 11, one observes a crossing between the H and halogen curves, which based on Huheey's equation,21,189 foreshadows an inversion in the polarity of the hydrogen halides, the field strength needed being of the order of 0.16, 0.05 and 0.03B0 for HF, HCl, HBr, respectively. The larger the initial dipole moment HX, the larger the magnetic field needed to invert it. It is tempting to see if this prediction, purely based on CDFT, would be confirmed by explicit dipole moment calculations. Fig. 13 indeed shows decreasing (absolute values) dipole moments (component along the bond axis) with increasing field. In all three cases a sign inversion occurs, again at a higher field for HF than for HBr, the HCl case at an intermediate field. Note that as opposed to the case of an electric field where the most important change in the dipole moment component along the bond is, as intuitively expected, provoked by a field along the bond axis, for a magnetic field the component perpendicular to the bond axis has by far the largest influence.
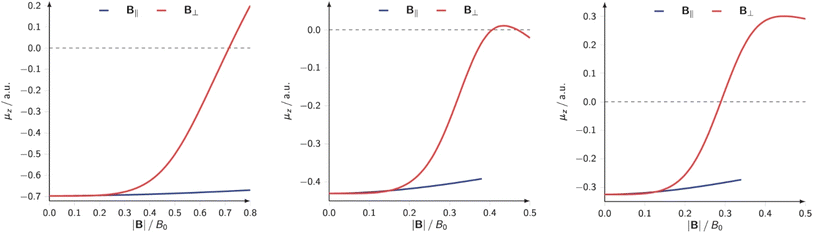 | ||
| Fig. 13 Electric dipole moment along the internuclear axis of HF (left), HCl(center) and HBr (right) as function of the external field strength applied parallel and perpendicular to the bond axis (all values in a. u.). This figure has been reproduced from ref. 188 with permission from Informa UK Limited, trading as Taylor and Francis Group, copyright 2022. | ||
This fundamental difference of the action of an electric and a magnetic field is remarkable and can be traced back to the evolution of the charge density. Fig. 14 reveals that for a parallel magnetic field, there is no charge transfer along the bond axis, mainly an accumulation of charge around the nuclei, whereas in the case of a perpendicular field, a clear and significant depletion of charge density around the F atom occurs with a concomitant accumulation of charge density around the hydrogen atom, providing further insight in the field-induced reversal of bond polarity. This study reveals a new local CDFT descriptor ∂ρ(r)/∂B in its finite difference form. For a detailed symmetry analysis, also more involved in the case of a magnetic field due to its time-reversal symmetry and the extension to small, σ-bonded polyatomics (H2O, NH3) the reader is referred to the original publication.188 The extension to π-bonded systems has been investigated recently.190
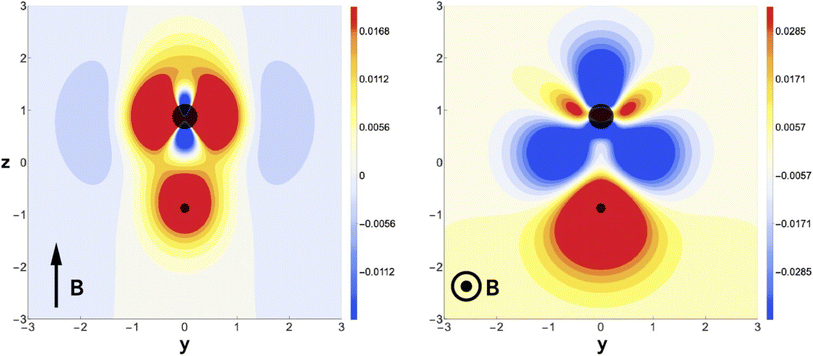 | ||
| Fig. 14 Difference in charge density for HF in a magnetic field of B = 0.8B0 applied field (left) and perpendicular (right) to the internuclear axis, relative to zero field. This figure has been reproduced from ref. 188 with permission from Informa UK Limited, trading as Taylor and Francis Group, copyright 2022. | ||
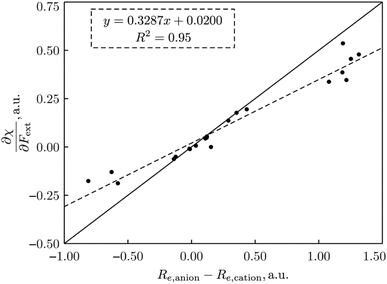 | ||
| Fig. 15 Plot of ∂χ/∂F vs. (re,anion − re,cation) for all 21 diatomics. All values in a. u. This figure has been reproduced from ref. 74 with permission from John Wiley and Sons, copyright 2023. | ||
This type of result, showing that the evolution of the electronegativity under force is governed by the (difference in) equilibrium distances between cationic and anionic species, can be carried over to the hardness, but with a slightly more complicated result, namely a proportionality with 2re,neutral − re,anion − re,cation, reminiscent of Pearson's hardness expression in terms of the energy of the neutral system, its anion and cation. Looking back, all this is not so unexpected. The derivative is a response function, so it should, as all other response functions in CDFT, be an intrinsic property of the system, independent of the magnitude of the external force. On a dimensional basis, it is easily seen that it should be a length or distance. Considering now, for example, the electronegativity in the Mulliken expression, which can be reduced to an energy difference between cation and anion, the proportionality between a difference in equilibrium distance between cation and anion appears in a natural way. Considering the quantitative side and concentrating first on the simplest case, the electronegativity, it was found that out of the 21 molecules mentioned, only seven molecules show a larger bond distance for the cation than for the anion (H2, HF, HCl, BN, LiF, NaCl, MgO; remark the appearance of the ionic systems) and all do show indeed a decrease in electronegativity upon applying a stretching force. The negative derivative can be traced back to the derivative of the ionization energy-component in χ which was seen to be strongly negative for the cases of an ionic bond and slightly negative for the hydrogen halides; in the case of these covalent bonds this negative sign can be interpreted in terms of the removal of an electron from a bonding orbital upon ionization (as opposed to the removal from an antibonding orbital of most other diatomics considered); in the case of an ionic bond, an electron is taken from an orbital that is localized on the (strongly) electronegative partner. All other diatomics have a larger bond distance in the anion relative to the cation and do show a positive first-order derivative of χ w.r.t. F, except for P2). As far as the hardness response is concerned, all molecules do show a negative value indicating that a rule of thumb can be formulated: hardness decreases when an external stretching force is exerted on a diatomic in agreement with the Maximum Hardness Principle in casu for pulling forces. Finally, note that similar reasonings have been put forward in the case of bending forces,191 and that applications have been presented on topology changes, the design of force probes, and achieving nucleophilic additions to ketones with “forbidden” reaction outcomes (anti-Felkin diastereoselectivity)192–194 for which we refer the reader to the original papers and a recent review.195
We would like to end this section with an interesting perspective by considering the response of the electrophilicity ω to a mechanical force (cf. the electric field case in Section 4.2.1). This response (∂ω/∂F) was evaluated based on the response functions for I and A as
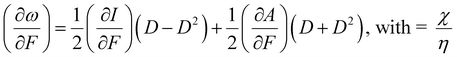 | (39) |
Returning to the expression for χ and η (eqn (37) and (38), dropping now the B dependence), the electron affinity A is mostly much smaller than the ionization energy (a ratio of 1/8 has been proposed in the literature196) D is close to 0.5 indicating that the (∂A/∂F) term is dominant in eqn (39), resulting in mostly positive values of (∂ω/∂F). Most diatomics are more prone to react with an electron-rich substrate when their bond is mechanically stretched. This tendency can be brought in line with studies by Baldus and Gräter197 on the redox behavior of the disulfide bond in the cysteine–cysteine dimer, where it was found that the redox potential increases with external pulling force, the order of magnitude being comparable with that measured upon mutation of thioredoxin. As the present authors pointed out,198,199 there is a positive correlation between reduction potentials and electrophilicity; the positive sign of (∂ω/∂F) is completely in line with the evolution of the reduction potential under external force and (insight in) the possibility of tuning redox potentials by mechanical forces is a natural sequel.
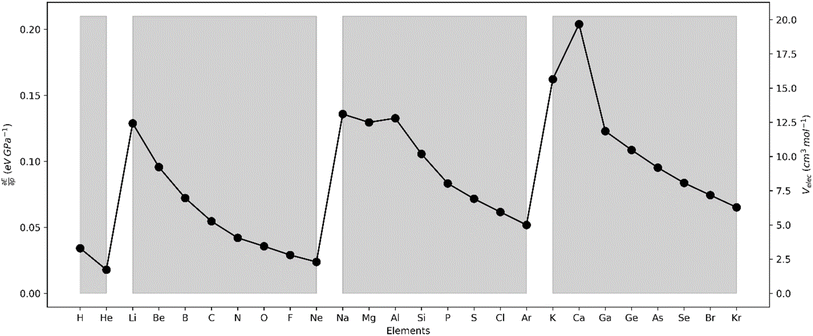
The results for the electronic volume show an overall periodic trend with a decrease throughout a period and increase in a column. To further establish the electronic atomic volume as a measure for the atom's size the corresponding pressure-sensitive radii, easily extracted from the electronic volume in the hypothesis of spherical symmetry, yield radii with an order of magnitude similar to well-known other sets of atomic radii such as those presented by Rahm,201 Bondi,202 Ghosh,203 with the best correlation for the Rahm set (R2 = 0.907), not surprisingly, as also these values are associated with isolated atoms, whereas other scales often refer to atoms in bonded situations. Periodicity, as expected, is retrieved.
Along these lines, the second derivative ∂2E/∂P2 can be identified, again in analogy with macroscopic thermodynamics,200 as directly related to an atomic compressibility
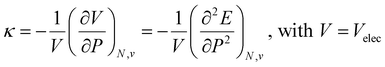 | (40) |
This expression is written in analogy to the inverse of the bulk modulus for macroscopic systems and modulates the second-order derivative by the volume to account for the difference in starting volume between atoms of different elements.
Passing now to electronegativity and hardness, a similar approach has been followed as in the cases of an electric and magnetic field, starting from evaluating I and A as a function of pressure.
Fig. 17 clearly shows that the electronegativity for all considered elements decreases with increasing pressure with a concave curve upward, leading to the at first sight unexpected result that the electronegativity becomes negative for some elements at high pressure. This behavior can be traced back to (1) the strong decrease in IP upon higher pressures leading, in the case of pressures outside the range considered here (50 to 90 GPa), to autoionization for K, Na and Li in agreement with the fact that alkali-atoms are most prone to electride formation;204 (2) to the strong decrease in electron affinity for all elements, becoming negative above 40 GPa (except for the halogens). The decreasing trend in χ agrees with the result obtained by Garza et al. in a confinement approach using a Dirichlet type confining potential,205 confirming that confinement studies can be seen as forerunners of pressure studies. Interesting to note is that more electronegative elements (at the reference conditions) display a less steep decrease than more electropositive elements. The increase in the range of electronegativities at higher pressure might yield an increase in the transfer of electrons upon bond formation, according to Huheey's expression189 based on the electronegativity equalization principle (cf. Section 4.2.2). For example, in view of the dramatic decrease of the electronegativity of the noble gases, as seen in Fig. 17, noble gases become more reactive w.r.t. electron-accepting bonding partners, as seen, for example, in the literature on the krypton–oxygen bond expected to yield stable compounds.206 Note that the general trend and shape of the curves in Fig. 17 agree with previous work by Rahm et al.201 based on the Allen scale. For an analogous discussion on the hardness, we refer to ref. 67.
 | ||
| Fig. 17 Electronegativity as a function of pressure for all main group elements from H to Kr. Colors of the curve indicate the group: Ia orange, IIa red, IIIa yellow, IVa black, Va green, via blue, VIIa purple, VIIIa magenta; the marker denotes the period (1 square, 2 diamond, 3 triangle, 4 cross) and the line style denotes the block (solid: s block, dashed: p-block, dotted: noble gases) this figure has been reproduced from ref. 67 with permission from the Royal Society of Chemistry, copyright 2022. | ||
Concentrating now on the derivative ∂χ/∂P in Fig. 18, periodicity shows up in the behavior along a period with, at first sight, some breaks when passing from the s-block to the p-block and in the nitrogen group. These particularities and the overall behavior of the black curve in Fig. 16 can be interpreted in a way that bears a strong analogy with the analysis of the χ and η derivatives w.r.t. an external force in Section 4.2.3. In the case of the electronegativity, the mixed second-order response function −∂2E/∂N∂P or ∂χ/∂P can be written as
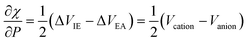 | (41) |
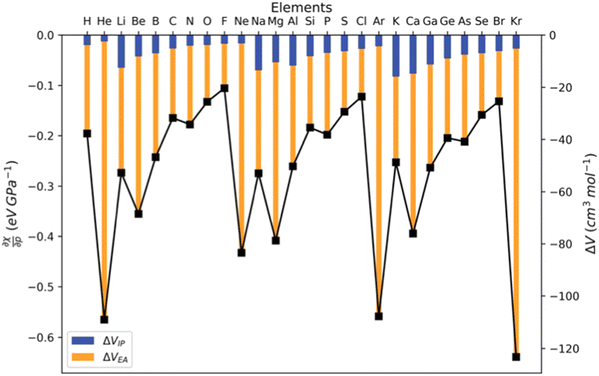 | ||
| Fig. 18 Derivative of the electronegativity w.r.t. the pressure at reference condition for all main group elements from H to Kr. The derivative is split into two volume terms: one involving the ionization energy (ΔVIE) and one involving the electron affinity (ΔVEA) (right axis). This figure has been reproduced from ref. 67 with permission from the Royal Society of Chemistry, copyright 2022. | ||
In analogy with the mechanical force case where ∂χ/∂P was found to be proportional to (ranion − rcation). ΔVIE is defined as the volume change associated with the loss of an electron (Vcation − Vanion) and ΔVEA is the opposite of the volume change associated with the addition of an electron (Vneutral − Vanion). It is easily seen that, as the volume in this context decreases when passing from an anion, to the neutral system and the cation, both ΔVIE and ΔVEA are negative, but that the absolute value for ΔVEA is by far larger than that of ΔVIE, resulting in a negative ∂χ/∂P derivative. Jumps or discontinuities in the curves can be traced back to the large volume expansion upon adding an electron to a noble gas, the removal of an electron from an alkali metal leading to the depletion of a subshell, the creation of a new subshell upon addition of an electron to the IIa metals, and the filling of the third p orbital in the anion of the IVa elements.
In analogy with the force derivatives, the dependence of the chemical hardness on the pressure, at least formally the third order mixed derivative (∂3E/∂N2∂P), can easily seen to be written as
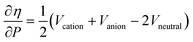 | (42) |
This quantity is always positive (Fig. 19), as can be foreseen by the relative order of magnitudes of the electronic volumes, further strengthening the electronic volume concept. As the hardness increases with increasing pressure, the softness (and also the polarizability) decreases with increasing pressure, retrieving the trend found in confinement studies thus further confirming the forerunner character of confinement to pressure studies.
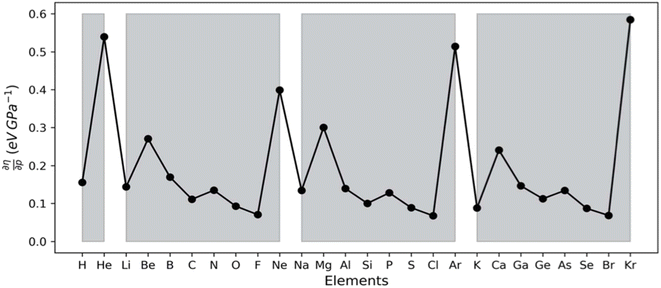 | ||
| Fig. 19 Derivative of the hardness w.r.t. the pressure at reference condition for all main group elements from H to Kr. This figure has been reproduced from ref. 67 with permission from the Royal Society of Chemistry, copyright 2022. | ||
For an extension of these studies to a local descriptor, the electron density, we refer the reader to the original literature.67 An information theory207 based approach on the radial distribution function thereby again revealed periodicity in an absolutely unbiased way in contrast with the authors' previous studies on atomic densities208 where a reference distribution had to be put in.
The behavior of atomic electronegativity and hardness under pressure has recently been used to interpret/predict the behavior the dipole moment of a series of diatomics under pressure, based on the Huheey equation,21,189 in complete analogy with the magnetic field case in Section 4.2.2.209
5. Generalized computational framework
Whether one models the energy of a chemical system (possibly with auxiliary fields, X = ε, B, F, P, etc.) using a standard interpolatory model106,196,210 or the grand canonical ensemble, the energy for a given (expected) number of electrons is always a linear combination of the energies of various eigenstates,106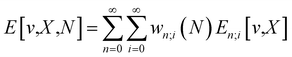 | (43) |
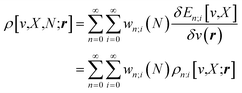 | (44) |
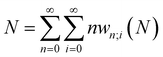 | (45) |
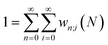 | (46) |
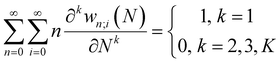 | (47) |
It is only in the ensemble case that the coefficients are nonnegative, wn;i ≥ 0, and the only interpolatory ensemble model is the zero-temperature grand canonical ensemble.211 Only three sensible choices for wn;i are known: piecewise linear interpolation (zero-temperature grand-canonical ensemble), (generalized) Lagrange polynomial interpolation, and the finite-temperature grand canonical ensemble.
Because eqn (43) is the only form for the energy that gives reasonable results, the response functions/reactivity indicators of the system are easily computed from the corresponding response functions of the system and the derivatives of the coefficients with respect to electron number106
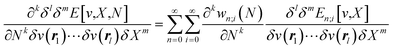 | (48) |
For example, eqn (18) and (19) can be derived as special cases of this general equation.
The corresponding reactivity indicators for the grand canonical ensemble (derivatives w.r.t μ and v(r)) are readily obtained by the Faà di Bruno formula37 (the same formula allows one to access derivatives with respect to the system's properties that are conjugate to the auxiliary fields). This sort of unified computational framework, which undergirds the implementation in ChemTools,37,212 has advantages over piecemeal implementations of individual reactivity indicators since it is readily extended to arbitrary-order descriptors.
6. Conclusions and outlook
Extending CDFT with temperature is the most elegant way to cope with the N-differentiability issues of the E[N,v] functional and concomitant ill-defined quantities. Passing to the grand canonical ensemble and using an ensemble model composed of the system's ground states with N0, N0 − 1, and N0 + 1 electrons, well-behaved and computable CDFT descriptors at finite temperature are put forward. These descriptors offer insights into the chemical reactivity of species across a range of temperature conditions and notably coincide with their approximate zero-temperature results at the limit of absolute zero. Within the finite temperature framework, it is possible to derive reasonable definitions for ambiguous quantities like local hardness. Additionally, a new series of indices has been formulated as partial derivatives of ensemble properties w.r.t. temperature. These indices yield fresh and valuable insights into the physicochemical processes taking place during the initial stages of a chemical interaction.The introduction of external “fields” (electric and magnetic fields, mechanical force, and external pressure, etc.) allows CDFT to adapt to the ever-increasing variability in the experimental reaction by augmenting the E[N,v] functional with additional field variables (in casu one at the time, although combinations are in principle possible) yielding formally functionals of the type E[N,v,X] with X = ε,B,F,P, etc. A finite field ansatz turns out, at this moment, the most practical way to compute the corresponding response functions, which formally can be seen as phenomenological parameters describing the field dependence of the energy at various orders. Overall, periodic trends showed up as a leitmotiv in the results. Symmetry breaking in reaction channels (electric field), segmented property curves and polarity inversion (magnetic fields), reactivity/potential energy curves intricacies (mechanical force), auto-ionization, and changing bonding characteristics (pressure) show up in a natural way in a conceptual DFT context. A variety of analogies emerge: first, between intrinsic, microscopic volume, and compressibility related descriptors and the volume and compressibility in macroscopic thermodynamics; second, between the electronegativity and hardness response to an external force and the pressure, related to shifts in equilibrium distances or changes in intrinsic volumes between a neutral system, its cation, and its anion.
Incorporating temperature as a new variable for the description of the chemical reactivity of the electronic systems may be attributed to the fact that, during chemical interactions, the molecular quantum states are perturbed and redistributed due to the presence of a second reagent. This redistribution can be partially modeled by modulating the temperature variable. Consequently, one can identify/search for temperature values that favor chemical interactions, as demonstrated in eqn (33). Furthermore, there is potential for developing a new theoretical framework rooted in non-equilibrium thermodynamics. This framework could be employed to study systems in the presence of oscillating fields, potentially bridging the two theoretical approaches presented here.
All in all, we hope that the present overview might be inspiring. For the temperature dependence, note that the introduction of this new free variable places CDFT derivatives and response functions on a solid mathematical footing. For the external field dependence, evaluating and analyzing an increasing diversity of response functions may lead to a better insight in the way atoms and molecules respond to a large variety of external conditions, thereby changing their intrinsic reactivity. These investigations may support experimentalists “in their endeavor of continuously extending their reaction conditions portfolio in the search for the synthesis of new molecules with unprecedented properties”.74
Data availability
All data reported in this Perspective is available in the original references cited.Author contributions
All authors contributed equally to the manuscript's design, writing, editing, and revision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors want to thank all colleagues who contributed in the past years to this exciting journey with joint publications listed in the bibliography: from master students to eminent senior scientists. So our most sincere regards to for part 1 (Temperature) Javier Carmona (UAM-Iztapalapa), Carlos Polanco (Xalapa), and for Part 2 (External Fields) (again in alphabetical order) to Mercedes Alonso (Brussels), Tom Bettens (Brussels), Roberto Cammi (Parma), Bo Chen (Donostia), Tom Clarys (Brussels), Jochen Eeckhoudt (Brussels), Robin Francotte (Brussels), Bang Huyng (Nottingham), Tom Irons(Nottingham), Thijs Stuyver(Paris), Andrew Teale(Nottingham). MFP, AV and JLG thank Conahcyt for grant Sinergia 1561802. FH acknowledges support from the Natural Sciences and Engineering Research Council (NSERC) of Canada and Digital Research Alliance of Canada. PWA thanks NSERC, the Canada Research Chairs, and the Digital Research Alliance of Canada for support. FDP acknowledges support from the Research Foundation Flanders (FWO) and the Vrije Universiteit Brussel through a Strategic Research Program awarded to his group.References
- M. J. Nye, From Chemical Philosophy to Theoretical Chemistry: Dynamics of Matter and Dynamics of Disciplines, 1800-1950, University of California Press, 1994 Search PubMed.
- R. G. Parr, in Density Functional Methods in Physics, ed. R. M. Dreizler and J. D. Providencia, Springer, New York, NY, 1985, pp. 141–158, DOI:10.1007/978-1-4757-0818-9.
- R. S. Mulliken, Molecular Scientists and Molecular Science - Some Reminiscences, J. Chem. Phys., 1965, 43, S002, DOI:10.1063/1.1701510.
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev. [Sect.] B, 1964, 136, B864–B871, DOI:10.1103/PhysRev.136.B864.
- R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, 1994 Search PubMed.
- R. G. Parr and W. Yang, Density-Functional Theory of the Electronic-Structure of Molecules, Annu. Rev. Phys. Chem., 1995, 46, 701–728, DOI:10.1146/annurev.pc.46.100195.003413.
- R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, Electronegativity - Density Functional Viewpoint, J. Chem. Phys., 1978, 68, 3801–3807, DOI:10.1063/1.436185.
- R. G. Parr and R. G. Pearson, Absolute Hardness - Companion Parameter to Absolute Electronegativity, J. Am. Chem. Soc., 1983, 105, 7512–7516, DOI:10.1021/ja00364a005.
- R. G. Parr and W. T. Yang, Density Functional-Approach to the Frontier-Electron Theory Oo Chemical-Reactivity, J. Am. Chem. Soc., 1984, 106, 4049–4050, DOI:10.1021/ja00326a036.
- K. Fukui, T. Yonezawa and H. Shingu, A Molecular Orbital Theory of Reactivity in Aromatic Hydrocarbons, J. Chem. Phys., 1952, 20, 722–725, DOI:10.1063/1.1700523.
- R. T. Sanderson, An Interpretation of Bond Lengths and a Classification of Bonds, Science, 1951, 114, 670–672, DOI:10.1126/science.114.2973.670.
- R. G. Pearson, The Principle of Maximum Hardness, Acc. Chem. Res., 1993, 26, 250–255, DOI:10.1021/ar00029a004.
- R. Hoffmann and R. B. Woodward, Conservation of Orbital Symmetry, Acc. Chem. Res., 1968, 1, 17–22, DOI:10.1021/ar50001a003.
- R. B. Woodward and R. Hoffmann, Conservation of Orbital Symmetry, Angew. Chem., Int. Ed., 1969, 8, 781–853, DOI:10.1002/anie.196907811.
- R. G. Pearson, Recent Advances in the Concept of Hard and Soft Acids and Bases, J. Chem. Educ., 1987, 64, 561–567, DOI:10.1021/ed064p561.
- P. W. Ayers, J. S. M. Anderson and L. J. Bartolotti, Perturbative perspectives on the chemical reaction prediction problem, Int. J. Quantum Chem., 2005, 101, 520–534, DOI:10.1002/qua.20307.
- H. Chermette, Chemical reactivity indexes in Density Functional Theory, J. Comput. Chem., 1999, 20, 129–154, DOI:10.1002/(sici)1096-987x(19990115)20:1<129::Aid-jcc13>3.0.Co;2-a.
- J. L. Gázquez, Perspectives on the Density Functional Theory of Chemical Reactivity, J. Mex. Chem. Soc., 2008, 52, 3–10 Search PubMed.
- P. Geerlings, E. Chamorro, P. K. Chattaraj, F. De Proft, J. L. Gázquez, S. B. Liu, C. Morell, A. Toro-Labbé, A. Vela and P. Ayers, Conceptual density functional theory: status, prospects, issues, Theor. Chem. Acc., 2020, 139, 36, DOI:10.1007/s00214-020-2546-7.
- P. Geerlings and F. De Proft, Conceptual DFT: the chemical relevance of higher response functions, Phys. Chem. Chem. Phys., 2008, 10, 3028–3042, 10.1039/b717671f.
- P. Geerlings, F. De Proft and W. Langenaeker, Conceptual Density Functional Theory, Chem. Rev., 2003, 103, 1793–1873, DOI:10.1021/cr990029p.
- P. Geerlings, S. Fias, Z. Boisdenghien and F. De Proft, Conceptual DFT: chemistry from the linear response function, Chem. Soc. Rev., 2014, 43, 4989–5008, 10.1039/c3cs60456j.
- S. B. Liu, Conceptual Density Functional Theory and Some Recent Developments, Acta Phys.-Chim. Sin., 2009, 25, 590–600, DOI:10.3866/PKU.WHXB20090332.
- F. De Proft, P. Geerlings, F. Heidar-Zadeh and P. W. Ayers, in Comprehensive Computational Chemistry, ed. M. Yáñez and R. J. Boyd, Elsevier, Oxford, 1st edn, 2024, pp. 306–321, DOI:10.1016/B978-0-12-821978-2.00025-8.
- S. Liu, Conceptual Density Functional Theory, 2 Volume Set: Towards a New Chemical Reactivity Theory, Wiley, 2022 Search PubMed.
- P. A. Johnson, L. J. Bartolotti, P. W. Ayers, T. Fievez and P. Geerlings, in Modern Charge-Density Analysis, ed. C. Gatti and P. Macchi, Springer, Netherlands, 2012, pp. 715–764 Search PubMed.
- F. De Proft, P. Geerlings and P. W. Ayers, in The chemical bond: Fundamental aspects of chemical bonding, ed. S. Shaik and G. Frenking, Wiley, Darmstadt, 2014, vol. 1, pp. 233–270 Search PubMed.
- P. W. Ayers, S. Fias and F. Heidar-Zadeh, The axiomatic approach to chemical concepts, Comput. Theor. Chem., 2018, 1142, 83–87, DOI:10.1016/j.comptc.2018.09.006.
- P. W. Ayers, R. C. Morrison and R. K. Roy, Variational principles for describing chemical reactions: Condensed reactivity indices, J. Chem. Phys., 2002, 116, 8731–8744, DOI:10.1063/1.1467338.
- J. Melin, P. W. Ayers and J. V. Ortiz, Removing electrons can increase the electron density: A computational study of negative Fukui functions, J. Phys. Chem. A, 2007, 111, 10017–10019, DOI:10.1021/jp075573d.
- S. Fias, P. W. Ayers, F. De Proft and P. Geerlings, Properties of the density functional response kernels and its implications on chemistry, J. Chem. Phys., 2022, 157, 114102, DOI:10.1063/5.0094653.
- B. Wang, P. Geerlings, C. Van Alsenoy, F. Heider-Zadeh, P. W. Ayers and F. De Proft, Investigating the Linear Response Function under Approximations Following the Coupled-Perturbed Approach for Atoms and Molecules, J. Chem. Theory Comput., 2023, 19, 3223–3236, DOI:10.1021/acs.jctc.3c00323.
- M. Berkowitz and R. G. Parr, Molecular hardness and softness, local hardness and softness, hardness and softness kernels, and relations among these quantities, J. Chem. Phys., 1988, 88, 2554–2557, DOI:10.1063/1.454034.
- P. Fuentealba and R. G. Parr, Higher-order derivatives in density-functional theory, especially the hardness derivative ∂η/∂N, J. Chem. Phys., 1991, 94, 5559–5564, DOI:10.1063/1.460491.
- P. Senet, Nonlinear electronic responses, Fukui functions and hardnesses as functionals of the ground-state electronic density, J. Chem. Phys., 1996, 105, 6471–6489, DOI:10.1063/1.472498.
- C. Cardenas, E. Echegaray, D. Chakraborty, J. S. M. Anderson and P. W. Ayers, Relationships between the third-order reactivity indicators in chemical density-functional theory, J. Chem. Phys., 2009, 130, 244105, DOI:10.1063/1.3151599.
- F. Heidar-Zadeh, M. Richer, S. Fias, R. A. Miranda-Quintana, M. Chan, M. Franco-Pérez, C. E. González-Espinoza, T. D. Kim, C. Lanssens, A. H. G. Patel, X. D. Yang, E. Vöhringer-Martinez, C. Cárdenas, T. Verstraelen and P. W. Ayers, An explicit approach to conceptual density functional theory descriptors of arbitrary order, Chem. Phys. Lett., 2016, 660, 307–312, DOI:10.1016/j.cplett.2016.07.039.
- M. Galván, J. L. Gázquez and A. Vela, Fukui Function - Spin-Density and Chemical-Reactivity, J. Chem. Phys., 1986, 85, 2337–2338, DOI:10.1063/1.451083.
- M. Galván, A. Vela and J. L. Gázquez, Chemical-Reactivity in Spin-Polarized Density Functional Theory, J. Phys. Chem., 1988, 92, 6470–6474, DOI:10.1021/j100333a056.
- T. K. Ghanty and S. K. Ghosh, Spin-Polarized Generalization of the Concepts of Electronegativity and Hardness and the Description of Chemical-Binding, J. Am. Chem. Soc., 1994, 116, 3943–3948, DOI:10.1021/ja00088a033.
- P. Pérez, E. Chamorro and P. W. Ayers, Universal mathematical identities in density functional theory:: Results from three different spin-resolved representations, J. Chem. Phys., 2008, 128, 204108, DOI:10.1063/1.2916714.
- J. Garza, R. Vargas, A. Cedillo, M. Galván and P. K. Chattaraj, Comparison between the frozen core and finite differences approximations for the generalized spin-dependent global and local reactivity descriptors in small molecules, Theor. Chem. Acc., 2006, 115, 257–265, DOI:10.1007/s00214-005-0002-3.
- R. A. Miranda-Quintana and P. W. Ayers, Systematic treatment of spin-reactivity indicators in conceptual density functional theory, Theor. Chem. Acc., 2016, 135, 1–18, DOI:10.1007/s00214-016-1995-5.
- M. Richer, F. Heidar-Zadeh, M. Ríos-Gutiérrez, X. D. Yang and P. W. Ayers, Spin-Polarized Conceptual Density Functional Theory from the Convex Hull, J. Chem. Theory Comput., 2024, 20, 4616–4628, DOI:10.1021/acs.jctc.4c00213.
- J. L. Gázquez, A. Vela and M. Galván, Fukui function, electronegativity and hardness in the Kohn-Sham theory, Struct. Bonding, 1987, 66, 79–97 CrossRef.
- J. L. Gázquez, M. Franco-Pérez, P. W. Ayers and A. Vela, Temperature-dependent approach to chemical reactivity concepts in density functional theory, Int. J. Quantum Chem., 2019, 119, e25797, DOI:10.1002/qua.25797.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Density-Functional Theory for Fractional Particle Number - Derivative Discontinuities of the Energy, Phys. Rev. Lett., 1982, 49, 1691–1694, DOI:10.1103/PhysRevLett.49.1691.
- P. K. Chattaraj, A. Cedillo and R. G. Parr, Chemical softness in model electronic systems: Dependence on temperature and chemical potential, Chem. Phys., 1996, 204, 429–437, DOI:10.1016/0301-0104(95)00276-6.
- E. P. Gyftopoulos and G. N. Hatsopoulos, Quantum-Thermodynamic definition of electronegativity, Proc. Natl. Acad. Sci. U.S.A., 1968, 60, 786–793, DOI:10.1073/pnas.60.3.786.
- S. Ciampi, N. Darwish, H. M. Aitken, I. Díez-Pérez and M. L. Coote, Harnessing electrostatic catalysis in single molecule, electrochemical and chemical systems: a rapidly growing experimental tool box, Chem. Soc. Rev., 2018, 47, 5146–5164, 10.1039/c8cs00352a.
- S. Shaik, R. Ramanan, D. Danovich and D. Mandal, Structure and reactivity/selectivity control by oriented-external electric fields, Chem. Soc. Rev., 2018, 47, 5125–5145, 10.1039/c8cs00354h.
- T. Stauch and A. Dreuw, Advances in Quantum Mechanochemistry: Electronic Structure Methods and Force Analysis, Chem. Rev., 2016, 116, 14137–14180, DOI:10.1021/acs.chemrev.6b00458.
- W. Grochala, R. Hoffmann, J. Feng and N. W. Ashcroft, The chemical imagination at work in very tight places, Angew. Chem., Int. Ed., 2007, 46, 3620–3642, DOI:10.1002/anie.200602485.
- P. K. Chattaraj and B. Maiti, Reactivity Dynamics in Atom−Field Interactions: A Quantum Fluid Density Functional Study, J. Phys. Chem. A, 2001, 105, 169–183, DOI:10.1021/jp0019660.
- P. K. Chattaraj and B. Maiti, HSAB Principle Applied to the Time Evolution of Chemical Reactions, J. Am. Chem. Soc., 2003, 125, 2705–2710, DOI:10.1021/ja0276063.
- M. Li, X. Wan, C. Rong, D. Zhao and S. Liu, Directionality and additivity effects of molecular acidity and aromaticity for substituted benzoic acids under external electric fields, Phys. Chem. Chem. Phys., 2023, 25, 27805–27816, 10.1039/D3CP02982D.
- K. K. Lange, E. I. Tellgren, M. R. Hoffmann and T. Helgaker, A Paramagnetic Bonding Mechanism for Diatomics in Strong Magnetic Fields, Science, 2012, 337, 327–331, DOI:10.1126/science.1219703.
- D. Lai, Matter in strong magnetic fields, Rev. Mod. Phys., 2001, 73, 629–661, DOI:10.1103/revmodphys.73.629.
- M. Khatua, U. Sarkar and P. K. Chattaraj, Reactivity dynamics of confined atoms in the presence of an external magnetic field, Eur. Phys. J. D, 2014, 68, 22 CrossRef.
- C. R. Hickenboth, J. S. Moore, S. R. White, N. R. Sottos, J. Baudry and S. R. Wilson, Biasing reaction pathways with mechanical force, Nature, 2007, 446, 423–427, DOI:10.1038/nature05681.
- M. T. Ong, J. Leiding, H. L. Tao, A. M. Virshup and T. J. Martínez, First Principles Dynamics and Minimum Energy Pathways for Mechanochemical Ring Opening of Cyclobutene, J. Am. Chem. Soc., 2009, 131, 6377–6379, DOI:10.1021/ja8095834.
- P. F. McMillan, Chemistry at high pressure, Chem. Soc. Rev., 2006, 35, 855–857, 10.1039/b610410j.
- J. K. Li, I. M. Chou, W. A. Bassett and X. Wang, A new type of hydrothermal diamond-anvil cell with cooling system, Rev. Sci. Instrum., 2020, 91, 053104, DOI:10.1063/1.5143596.
- R. Cammi, in Annual Reports in Computational Chemistry, ed. D. A. Dixon, 2017, vol. 13, pp. 117–135 Search PubMed.
- R. Cammi, V. Verdolino, B. Mennucci and J. Tomasi, Towards the elaboration of a QM method to describe molecular solutes under the effect of a very high pressure, Chem. Phys., 2008, 344, 135–141, DOI:10.1016/j.chemphys.2007.12.010.
- M. Scheurer, A. Dreuw, E. Epifanovsky, M. Head-Gordon and T. Stauch, Modeling Molecules under Pressure with Gaussian Potentials, J. Chem. Theory Comput., 2021, 17, 583–597, DOI:10.1021/acs.jctc.0c01212.
- J. Eeckhoudt, T. Bettens, P. Geerlings, R. Cammi, B. Chen, M. Alonso and F. De Proft, Conceptual density functional theory under pressure: Part I. XP-PCM method applied to atoms, Chem. Sci., 2022, 13, 9329–9350, 10.1039/d2sc00641c.
- A. Michels, J. De Boer and A. Bijl, Remarks concerning molecural interaction and their influence on the polarisability, Physica, 1937, 4, 981–994, DOI:10.1016/S0031-8914(37)80196-2.
- A. Borgoo, D. J. Tozer, P. Geerlings and F. De Proft, Influence of confinement on atomic and molecular reactivity indicators in DFT, Phys. Chem. Chem. Phys., 2008, 10, 1406–1410, 10.1039/b716727j.
- A. Borgoo, D. J. Tozer, P. Geerlings and F. De Proft, Confinement effects on excitation energies and regioselectivity as probed by the Fukui function and the molecular electrostatic potential, Phys. Chem. Chem. Phys., 2009, 11, 2862–2868, 10.1039/b820114e.
- P. Geerlings, D. J. Tozer and F. De Proft, in Chemical Reactivity in Confined Systems: Theory, Modelling and Applications, ed. P. K. Chattaraj and D. Chakraborty, Wiley, 2021, ch. 3 Search PubMed.
- D. J. Tozer and F. De Proft, Modeling temporary anions in density functional theory: Calculation of the Fukui function, J. Chem. Phys., 2007, 127, 034108, DOI:10.1063/1.2751158.
- D. Chakraborty and P. K. Chattaraj, Bonding, Reactivity, and Dynamics in Confined Systems, J. Phys. Chem. A, 2019, 123, 4513–4531, DOI:10.1021/acs.jpca.9b00830.
- P. Geerlings and F. De Proft, External fields in conceptual density functional theory, J. Comput. Chem., 2023, 44, 442–455, DOI:10.1002/jcc.26978.
- P. W. Ayers and M. Levy, Levy Constrained Search in Fock Space: An Alternative Approach to Noninteger Electron Number, Acta Phys.-Chim. Sin., 2018, 34, 625–630, DOI:10.3866/pku.Whxb201711071.
- N. D. Mermin, Thermal Properties of the Inhomogeneous Electron Gas, Phys. Rev., 1965, 137, 1441–1443, DOI:10.1103/PhysRev.137.A1441.
- Y. K. Zhang and W. T. Yang, Perspective on Density-functional theory for fractional particle number: derivative discontinuities of the energy Perdew JP, Parr RG, Levy M, Balduz Jr JL, Theor. Chem. Acc., 2000, 103, 346–348, DOI:10.1007/s002149900021.
- R. F. Nalewajski and T. S. Carlton, Legendre transforms and constrained search constructions of density functionals, J. Chem. Phys., 1983, 78, 1616–1618, DOI:10.1063/1.444858.
- R. F. Nalewajski and R. G. Parr, Legendre transforms and maxwell relations in density functional theory, J. Chem. Phys., 1982, 77, 399–407, DOI:10.1063/1.443620.
- P. W. Ayers and W. T. Yang, Legendre-transform functionals for spin-density-functional theory, J. Chem. Phys., 2006, 124, 224108, DOI:10.1063/1.2200884.
- A. Gorling, Symmetry in density-functional theory, Phys. Rev. A, 1993, 47, 2783–2799, DOI:10.1103/PhysRevA.47.2783.
- O. Gunnarsson and B. I. Lundqvist, Exchange and correlation in atoms, molecules, and solids by spin-density functional formalism, Phys. Rev. B: Solid State, 1976, 13, 4274–4298, DOI:10.1103/PhysRevB.13.4274.
- M. Levy and A. Nagy, Variational density-functional theory for an individual excited state, Phys. Rev. Lett., 1999, 83, 4361–4364, DOI:10.1103/PhysRevLett.83.4361.
- J. P. Perdew and A. Zunger, Self-interaction correction to density-functional approximations for many-electron systems, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079, DOI:10.1103/PhysRevB.23.5048.
- P. W. Ayers and M. Levy, Generalized density-functional theory:: Conquering the N-representability problem with exact functionals for the electron pair density and the second-order reduced density matrix, J. Chem. Sci., 2005, 117, 507–514, DOI:10.1007/bf02708356.
- P. W. Ayers and M. Levy, Time-independent (static) density-functional theories for pure excited states: Extensions and unification, Phys. Rev. A, 2009, 80, 012508, DOI:10.1103/PhysRevA.80.012508.
- P. W. Ayers, M. Levy and A. Nagy, Time-independent density-functional theory for excited states of Coulomb systems, Phys. Rev. A, 2012, 85, 042518, DOI:10.1103/PhysRevA.85.042518.
- K. Higuchi and M. Higuchi, Arbitrary choice of basic variables in density functional theory. II. Illustrative applications, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 165118, DOI:10.1103/PhysRevB.69.165118.
- K. Higuchi and M. Higuchi, Density functional theory with arbitrary basic variables, J. Magn. Magn. Mater., 2004, 272, 659–661, DOI:10.1016/j.jmmm.2003.11.244.
- K. Higuchi and M. Higuchi, Exchange-correlation energy functional and virial theorem in the extended constrained-search theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035116, DOI:10.1103/PhysRevB.71.035116.
- K. Higuchi and M. Higuchi, Kinetic energy contribution to the exchange-correlation energy functional of the extended constrained-search theory, Phys. Rev. A, 2009, 79, 022113, DOI:10.1103/PhysRevA.79.022113.
- M. Higuchi and K. Higuchi, Arbitrary choice of basic variables in density functional theory: Formalism, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 035113, DOI:10.1103/PhysRevB.69.035113.
- P. W. Ayers and S. B. Liu, Necessary and sufficient conditions for the N-representability of density functionals, Phys. Rev. A, 2007, 75, 022514, DOI:10.1103/PhysRevA.75.022514.
- P. W. Ayers and P. Fuentealba, Density-functional theory with additional basic variables: Extended Legendre transform, Phys. Rev. A, 2009, 80, 032510, DOI:10.1103/PhysRevA.80.032510.
- P. W. Ayers, S. Golden and M. Levy, Generalizations of the Hohenberg-Kohn theorem: I. Legendre transform constructions of variational principles for density matrices and electron distribution functions, J. Chem. Phys., 2006, 124, 054101, DOI:10.1063/1.2006087.
- B. G. Baekelandt, A. Cedillo and R. G. Parr, Reactivity indexes and fluctuation formulas in density-functional theory - isomorphic ensembles and a new measure of local hardness, J. Chem. Phys., 1995, 103, 8548–8556, DOI:10.1063/1.470165.
- S. B. Liu and R. G. Parr, Second-order density-functional description of molecules and chemical changes, J. Chem. Phys., 1997, 106, 5578–5586, DOI:10.1063/1.473580.
- P. W. Ayers, The dependence on and continuity of the energy and other molecular properties with respect to the number of electrons, J. Math. Chem., 2008, 43, 285–303, DOI:10.1007/s10910-006-9195-5.
- C. Morell, A. Grand and A. Toro-Labbé, New dual descriptor for chemical reactivity, J. Phys. Chem. A, 2005, 109, 205–212, DOI:10.1021/jp046577a.
- C. Morell, A. Grand and A. Toro-Labbé, Theoretical support for using the Δf(r) descriptor, Chem. Phys. Lett., 2006, 425, 342–346, DOI:10.1016/j.cplett.2006.05.003.
- P. W. Ayers, C. Morell, F. De Proft and P. Geerlings, Understanding the Woodward-Hoffmann rules by using changes in electron density, Chem.–Eur. J., 2007, 13, 8240–8247, DOI:10.1002/chem.200700365.
- P. W. Ayers, W. T. Yang and L. J. Bartolotti, in Chemical Reactivity Theory: A Density Functional View, ed. P. K. Chattaraj, CRC Press, Boca Raton, 2009, pp. 255–267 Search PubMed.
- M. Franco-Pérez, J. L. Gázquez, P. W. Ayers and A. Vela, Thermodynamic Justification for the Parabolic Model for Reactivity Indicators with Respect to Electron Number and a Rigorous Definition for the Electrophilicity: The Essential Role Played by the Electronic Entropy, J. Chem. Theory Comput., 2018, 14, 597–606, DOI:10.1021/acs.jctc.7b00940.
- R. Iczkowski and J. L. Margrave, Electronegativity, J. Am. Chem. Soc., 1961, 83, 3547, DOI:10.1021/ja01478a001.
- S. M. Valone, Quantum Mechanical Origins of the Iczkowski-Margrave Model of Chemical Potential, J. Chem. Theory Comput., 2011, 7, 2253–2261, DOI:10.1021/ct200283y.
- F. Heidar-Zadeh, R. A. Miranda-Quintana, T. Verstraelen, P. Bultinck and P. W. Ayers, When is the Fukui Function Not Normalized? The Danger of Inconsistent Energy Interpolation Models in Density Functional Theory, J. Chem. Theory Comput., 2016, 12, 5777–5787, DOI:10.1021/acs.jctc.6b00494.
- M. Franco-Pérez, J. L. Gázquez, P. W. Ayers and A. Vela, Revisiting the definition of the electronic chemical potential, chemical hardness, and softness at finite temperatures, J. Chem. Phys., 2015, 143, 154103, DOI:10.1063/1.4932539.
- M. Franco-Pérez, P. W. Ayers, J. L. Gázquez and A. Vela, Local and linear chemical reactivity response functions at finite temperature in density functional theory, J. Chem. Phys., 2015, 143, 244117, DOI:10.1063/1.4938422.
- M. Franco-Pérez, F. Heidar-Zadeh, P. W. Ayers, J. L. Gázquez and A. Vela, Going beyond the three-state ensemble model: the electronic chemical potential and Fukui function for the general case, Phys. Chem. Chem. Phys., 2017, 19, 11588–11602, 10.1039/c7cp00224f.
- R. A. Miranda-Quintana, M. Franco-Pérez, J. L. Gázquez, P. W. Ayers and A. Vela, Chemical hardness: Temperature dependent definitions and reactivity principles, J. Chem. Phys., 2018, 149, 124110, DOI:10.1063/1.5040889.
- M. Franco-Pérez, J. L. Gázquez, P. W. Ayers and A. Vela, Temperature-Dependent Approach to Electronic Charge Transfer, J. Phys. Chem. A, 2020, 124, 5465–5473, DOI:10.1021/acs.jpca.0c02496.
- M. Franco-Pérez, P. W. Ayers, J. L. Gázquez and A. Vela, Local chemical potential, local hardness, and dual descriptors in temperature dependent chemical reactivity theory, Phys. Chem. Chem. Phys., 2017, 19, 13687–13695, 10.1039/c7cp00692f.
- M. Franco-Pérez, C. A. Polanco-Ramírez, P. W. Ayers, J. L. Gázquez and A. Vela, New Fukui, dual and hyper-dual kernels as bond reactivity descriptors, Phys. Chem. Chem. Phys., 2017, 19, 16095–16104, 10.1039/c7cp02613g.
- M. Franco-Pérez, J. L. Gázquez, P. W. Ayers and A. Vela, Thermodynamic Dual Descriptor, Acta Phys.-Chim. Sin., 2018, 34, 683–691, DOI:10.3866/pku.Whxb201801031.
- M. Franco-Pérez, C. A. Polanco-Ramírez, J. L. Gázquez, P. W. Ayers and A. Vela, Study of organic reactions using chemical reactivity descriptors derived through a temperature-dependent approach, Theor. Chem. Acc., 2020, 139, 44, DOI:10.1007/s00214-020-2557-4.
- M. A. Pantoja-Hernández, M. Franco-Pérez, R. A. Miranda-Quintana and J. L. Gázquez, Perturbed reactivity descriptors in the grand canonical ensemble, Mol. Phys., 2023, e2199105, DOI:10.1080/00268976.2023.2199105.
- M. Franco-Pérez, C. A. Polanco-Ramírez, J. L. Gázquez and P. W. Ayers, Local and nonlocal counterparts of global descriptors: the cases of chemical softness and hardness, J. Mol. Model., 2018, 24, 285, DOI:10.1007/s00894-018-3823-4.
- M. Franco-Pérez, C. A. Polanco-Ramírez, J. L. Gázquez and P. W. Ayers, Reply to the "Comment on "Revisiting the definition of local hardness and hardness kernel by C. Morell, F. Guegan, W. Lamine, and H. Chermette, Phys. Chem. Chem. Phys., 2018, 20, 10.1039/C7CP04100D, Phys. Chem. Chem. Phys., 2018, 20, 9011–9014, 10.1039/c7cp07974e.
- E. A. Galván-García, E. Agacino-Valdés, M. Franco-Pérez and R. Gómez-Balderas, [Cu(H2O)n]2+ (n=1-6) complexes in solution phase: a DFT hierarchical study, Theor. Chem. Acc., 2017, 136, 29, DOI:10.1007/s00214-017-2056-4.
- C. A. Polanco-Ramírez, M. Franco-Pérez, J. Carmona-Espíndola, J. L. Gázquez and P. W. Ayers, Revisiting the definition of local hardness and hardness kernel, Phys. Chem. Chem. Phys., 2017, 19, 12355–12364, 10.1039/c7cp00691h.
- A. Robles, M. Franco-Pérez, J. L. Gázquez, C. Cárdenas and P. Fuentealba, Local electrophilicity, J. Mol. Model., 2018, 24, 245, DOI:10.1007/s00894-018-3785-6.
- M. Franco-Pérez, P. W. Ayers and J. L. Gázquez, Average electronic energy is the central quantity in conceptual chemical reactivity theory, Theor. Chem. Acc., 2016, 135, 199, DOI:10.1007/s00214-016-1961-2.
- M. Franco-Pérez, P. W. Ayers, J. L. Gázquez and A. Vela, Thermodynamic responses of electronic systems, J. Chem. Phys., 2017, 147, 094105, DOI:10.1063/1.4999761.
- M. Franco-Pérez, An electronic temperature definition for the reactive electronic species: Conciliating practical approaches in conceptual chemical reactivity theory with a rigorous ensemble formulation, J. Chem. Phys., 2019, 151, 074105, DOI:10.1063/1.5096561.
- R. G. Parr and P. K. Chattaraj, Principle of maximum hardness, J. Am. Chem. Soc., 1991, 113, 1854–1855, DOI:10.1021/ja00005a072.
- P. W. Ayers and R. G. Parr, Variational principles for describing chemical reactions: The Fukui function and chemical hardness revisited, J. Am. Chem. Soc., 2000, 122, 2010–2018, DOI:10.1021/ja9924039.
- R. G. Pearson, Hard and Soft Acids and Bases, Chem. Br., 1967, 3, 103–107 Search PubMed.
- R. G. Pearson, Acids and Bases, Science, 1966, 151, 172–177, DOI:10.1126/science.151.3707.172.
- R. G. Pearson, Hard and Soft Acids and Bases, J. Am. Chem. Soc., 1963, 85, 3533–3539, DOI:10.1021/ja00905a001.
- P. K. Chattaraj, H. Lee and R. G. Parr, HSAB Principle, J. Am. Chem. Soc., 1991, 113, 1855–1856, DOI:10.1021/ja00005a073.
- P. W. Ayers, The physical basis of the hard/soft acid/base principle, Faraday Discuss., 2007, 135, 161–190, 10.1039/b606877d.
- P. W. Ayers, R. G. Parr and R. G. Pearson, Elucidating the hard/soft acid/base principle: A perspective based on half-reactions, J. Chem. Phys., 2006, 124, 194107, DOI:10.1063/1.2196882.
- P. W. Ayers, An elementary derivation of the hard/soft-acid/base principle, J. Chem. Phys., 2005, 122, 141102, DOI:10.1063/1.1897374.
- R. A. Miranda-Quintana, P. W. Ayers and F. Heidar-Zadeh, Reactivity and Charge Transfer Beyond the Parabolic Model: the |Δμ| Big is Good Principle, ChemistrySelect, 2021, 6, 96–100, DOI:10.1002/slct.202004055.
- R. A. Miranda-Quintana and P. W. Ayers, The |Δμ| big is good rule, the maximum hardness, and minimum electrophilicity principles, Theor. Chem. Acc., 2019, 138, 44, DOI:10.1007/s00214-019-2435-0.
- R. A. Miranda-Quintana, F. Heidar-Zadeh and P. W. Ayers, Elementary Derivation of the |Δμ| Big Is Good Rule, J. Phys. Chem. Lett., 2018, 9, 4344–4348, DOI:10.1021/acs.jpclett.8b01312.
- R. A. Miranda-Quintana and P. W. Ayers, Dipolar cycloadditions and the |dμ| big is good rule: a computational study, Theor. Chem. Acc., 2018, 137, 177, DOI:10.1007/s00214-018-2391-0.
- F. L. Hirshfeld, Bonded-Atom Fragments for Describing Molecular Charge-Densities, Theor. Chim. Acta, 1977, 44, 129–138, DOI:10.1007/bf00549096.
- R. F. Nalewajski and R. G. Parr, Information theory, atoms in molecules, and molecular similarity, Proc. Natl. Acad. Sci. U.S.A., 2000, 97, 8879–8882, DOI:10.1073/pnas.97.16.8879.
- F. Heidar-Zadeh, P. W. Ayers, T. Verstraelen, I. Vinogradov, E. Vöhringer-Martinez and P. Bultinck, Information-Theoretic Approaches to Atoms-in-Molecules: Hirshfeld Family of Partitioning Schemes, J. Phys. Chem. A, 2018, 122, 4219–4245, DOI:10.1021/acs.jpca.7b08966.
- F. Heidar-Zadeh and P. W. Ayers, How pervasive is the Hirshfeld partitioning?, J. Chem. Phys., 2015, 142, 044107, DOI:10.1063/1.4905123.
- P. Bultinck, S. Fias, C. Van Alsenoy, P. W. Ayers and R. Carbó-Dorca, Critical thoughts on computing atom condensed Fukui functions, J. Chem. Phys., 2007, 127, 034102, DOI:10.1063/1.2749518.
- G. Geudtner, P. Calaminici, J. Carmona-Espíndola, J. M. del Campo, V. D. Domínguez-Soria, R. F. Moreno, G. U. Gamboa, A. Goursot, A. M. Köster, J. U. Reveles, T. Mineva, J. M. Vásquez-Pérez, A. Vela, B. Zúñinga-Gutierrez and D. R. Salahub, deMon2k, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 548–555, DOI:10.1002/wcms.98.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. A.03, 2016.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170, DOI:10.1063/1.478522.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, Self-Consistent Molecular-Orbital Methods .20. Basis Set for Correlated Wave-Functions, J. Chem. Phys., 1980, 72, 650–654, DOI:10.1063/1.438955.
- A. D. McLean and G. S. Chandler, Contracted Gaussian-Basis Sets for Molecular Calculations .1. 2nd Row Atoms, Z=11-18, J. Chem. Phys., 1980, 72, 5639–5648, DOI:10.1063/1.438980.
- A. Albert and E. P. Serjeant, Ionization Constants of Acids and Bases: A Laboratory Manual, Methuen, 1962 Search PubMed.
- W. M. Haynes, CRC Handbook of Chemistry and Physics, CRC Press, 2014 Search PubMed.
- W. Markownikoff, I. Ueber die Abhängigkeit der verschiedenen Vertretbarkeit des Radicalwasserstoffs in den isomeren Buttersäuren, Justus Liebigs Ann. Chem., 1870, 153, 228–259, DOI:10.1002/jlac.18701530204.
- J. McMurry and E. Simanek, Fundamentals of Organic Chemistry, Thomson-Brooks/Cole, 2007 Search PubMed.
- L. Meneses, A. Araya, F. Pilaquinga, R. Contreras and P. Fuentealba, Local hardness: An application to electrophilic additions, Chem. Phys. Lett., 2007, 446, 170–175, DOI:10.1016/j.cplett.2007.07.092.
- S. J. Blanksby and G. B. Ellison, Bond dissociation energies of organic molecules, Acc. Chem. Res., 2003, 36, 255–263, DOI:10.1021/ar020230d.
- J. M. Gnaim and R. A. Sheldon, Highly Regioselective Ortho-Chlorination of Phenol with Sulfuryl Chloride in the Presence of Amines, Tetrahedron Lett., 1995, 36, 3893–3896, DOI:10.1016/0040-4039(95)00592-z.
- G. A. Olah, S. J. Kuhn, B. A. Hardie and S. H. Flood, Aromatic Substitution .15. Ferric Chloride Catalyzed Bromination of Halobenzenes in Nitromethane Solution, J. Am. Chem. Soc., 1964, 86, 1044–1046, DOI:10.1021/ja01060a015.
- G. A. Olah and S. J. Kuhn, Aromatic Substitution .12. Steric Effects in Nitronium Salt Nitrations of Alkylbenzenes and Halobenzenes, J. Am. Chem. Soc., 1962, 84, 3684–3687, DOI:10.1021/ja00878a018.
- J. D. Roberts, J. K. Sanford, F. L. J. Sixma, H. Cerfontain and R. Zagt, Orientation in Aromatic Nitration Reactions, J. Am. Chem. Soc., 1954, 76, 4525–4534, DOI:10.1021/ja01647a005.
- P. Kovacic and J. J. Hiller, Ortho/Para Ratio in Electrophilic Aromatic Substitution . Mercuration and Alkylation of Chlorobenzene and Anisole . Evidence for a Coordination Effect, J. Org. Chem., 1965, 30, 1581–1588, DOI:10.1021/jo01016a060.
- C. Eaborn and R. Taylor, Aromatic Reactivity .16. Detritiation of Halogenobenzenes, J. Chem. Soc., 1961, 2388–2393, 10.1039/jr9610002388.
- W. F. K. Schnatter, D. W. Rogers and A. A. Zavitsas, Electrophilic Aromatic Substitution: Enthalpies of Hydrogenation of the Ring Determine Reactivities of C6H5X. The Direction of the C6H5-X Bond Dipole Determines Orientation of the Substitution, J. Phys. Chem. A, 2013, 117, 13079–13088, DOI:10.1021/jp409623j.
- J. Mortier, Arene Chemistry: Reaction Mechanisms and Methods for Aromatic Compounds, Wiley, New York, 2015 Search PubMed.
- H. D. Cohen and C. C. Roothaan, Electric Dipole Polarizability of Atoms by Hartree-Fock Method .I. Theory for Closed-Shell Systems, J. Chem. Phys., 1965, 43, S034–S038, DOI:10.1063/1.1701512.
- T. Clarys, T. Stuyver, F. De Proft and P. Geerlings, Extending conceptual DFT to include additional variables: oriented external electric field, Phys. Chem. Chem. Phys., 2021, 23, 990–1005, 10.1039/d0cp05277a.
- S. D. Fried, S. Bagchi and S. G. Boxer, Extreme electric fields power catalysis in the active site of ketosteroid isomerase, Science, 2014, 346, 1510–1514, DOI:10.1126/science.1259802.
- I. T. Suydam, C. D. Snow, V. S. Pande and S. G. Boxer, Electric fields at the active site of an enzyme: Direct comparison of experiment with theory, Science, 2006, 313, 200–204, DOI:10.1126/science.1127159.
- E. I. Tellgren, A. M. Teale, J. W. Furness, K. K. Lange, U. Ekström and T. Helgaker, Non-perturbative calculation of molecular magnetic properties within current-density functional theory, J. Chem. Phys., 2014, 140, 034101, DOI:10.1063/1.4861427.
- M. K. Beyer, The mechanical strength of a covalent bond calculated by density functional theory, J. Chem. Phys., 2000, 112, 7307–7312, DOI:10.1063/1.481330.
- T. Bettens, M. Alonso, P. Geerlings and F. De Proft, Implementing the mechanical force into the conceptual DFT framework: understanding and predicting molecular mechanochemical properties, Phys. Chem. Chem. Phys., 2019, 21, 7378–7388, 10.1039/c8cp07349j.
- F. D. Murnaghan, The compressibility of media under extreme pressures, Proc. Natl. Acad. Sci. U.S.A., 1944, 30, 244–247, DOI:10.1073/pnas.30.9.244.
- A. E. Reed, R. B. Weinstock and F. Weinhold, Natural-Population Analysis, J. Chem. Phys., 1985, 83, 735–746, DOI:10.1063/1.449486.
- C. A. Coulson and H. C. Longuethiggins, The Electronic Structure of Conjugated Systems .1. General Theory, Proc. R. Soc. London, Ser. A, 1947, 191, 39–60, DOI:10.1098/rspa.1947.0102.
- T. Stuyver, S. Fias, F. De Proft, P. W. Fowler and P. Geerlings, Conduction of molecular electronic devices: Qualitative insights through atom-atom polarizabilities, J. Chem. Phys., 2015, 142, 094103, DOI:10.1063/1.4913415.
- S. Patai and J. Zabicky, The Chemistry of the Carbonyl Group, Interscience Publishers, Chichester, New York, 1966 Search PubMed.
- H. B. Burgi, J. D. Dunitz, J. M. Lehn and G. Wipff, Stereochemistry of Reaction Paths at Carbonyl Centers, Tetrahedron, 1974, 30, 1563–1572, DOI:10.1016/s0040-4020(01)90678-7.
- F. De Vleeschouwer, V. Van Speybroeck, M. Waroquier, P. Geerlings and F. De Proft, Electrophilicity and nucleophilicity index for radicals, Org. Lett., 2007, 9, 2721–2724, DOI:10.1021/ol071038k.
- R. Van Lommel, R. H. Verschueren, W. M. De Borggraeve, F. De Vleeschouwer and T. Stuyver, Can the Philicity of Radicals Be Influenced by Oriented External Electric Fields?, Org. Lett., 2022, 24, 1–5, DOI:10.1021/acs.orglett.1c02935.
- P. K. Chattaraj, U. Sarkar and D. R. Roy, Electrophilicity index, Chem. Rev., 2006, 106, 2065–2091, DOI:10.1021/cr040109f.
- R. G. Parr, L. Von Szentpály and S. B. Liu, Electrophilicity index, J. Am. Chem. Soc., 1999, 121, 1922–1924, DOI:10.1021/ja983494x.
- R. S. Mulliken, A New Electroaffinity Scale; Together with Data on Valence States and on Valence Ionization Potentials and Electron Affinities, J. Chem. Phys., 1934, 2, 782–793, DOI:10.1063/1.1749394.
- B. P. Prascher, D. E. Woon, K. A. Peterson, T. H. Dunning and A. K. Wilson, Gaussian basis sets for use in correlated molecular calculations. VII. Valence, core-valence, and scalar relativistic basis sets for Li, Be, Na, and Mg, Theor. Chem. Acc., 2011, 128, 69–82, DOI:10.1007/s00214-010-0764-0.
- M. V. Ivanov and P. Schmelcher, Ground state of the carbon atom in strong magnetic fields, Phys. Rev. A, 1999, 60, 3558–3568, DOI:10.1103/PhysRevA.60.3558.
- R. Francotte, T. J. P. Irons, A. M. Teale, F. de Proft and P. Geerlings, Extending conceptual DFT to include external variables: the influence of magnetic fields, Chem. Sci., 2022, 13, 5311–5324, 10.1039/d1sc07263c.
- J. W. Furness, J. Verbeke, E. I. Tellgren, S. Stopkowicz, U. Ekström, T. Helgaker and A. M. Teale, Current Density Functional Theory Using Meta-Generalized Gradient Exchange-Correlation Functionals, J. Chem. Theory Comput., 2015, 11, 4169–4181, DOI:10.1021/acs.jctc.5b00535.
- J. M. Tao, Explicit inclusion of paramagnetic current density in the exchange-correlation functionals of current-density functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 205107, DOI:10.1103/PhysRevB.71.205107.
- J. M. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Climbing the density functional ladder: Nonempirical meta-generalized gradient approximation designed for molecules and solids, Phys. Rev. Lett., 2003, 91, 146401, DOI:10.1103/PhysRevLett.91.146401.
- J. Furtado, F. De Proft and P. Geerlings, The Noble Gases: How Their Electronegativity and Hardness Determines Their Chemistry, J. Phys. Chem. A, 2015, 119, 1339–1346, DOI:10.1021/jp5098876.
- C. Cárdenas, P. Ayers, F. De Proft, D. J. Tozer and P. Geerlings, Should negative electron affinities be used for evaluating the chemical hardness?, Phys. Chem. Chem. Phys., 2011, 13, 2285–2293, 10.1039/c0cp01785j.
- T. J. P. Irons, B. C. Huynh, A. M. Teale, F. De Proft and P. Geerlings, Molecular charge distributions in strong magnetic fields: a conceptual and current DFT study, Mol. Phys., 2022, e2145245, DOI:10.1080/00268976.2022.2145245.
- J. E. Huheey, Electronegativity of Groups, J. Phys. Chem., 1965, 69, 3284–3291, DOI:10.1021/j100894a011.
- M. Wibowo-Teale, B. C. Huynh, A. M. Wibowo-Teale, F. De Proft and P. Geerlings, Symmetry and reactivity of π-systems in electric and magnetic fields: a perspective from conceptual DFT, Phys. Chem. Chem. Phys., 2024, 26, 15156–15180, 10.1039/D4CP00799A.
- T. Bettens, M. Alonso, P. Geerlings and F. De Proft, The hunt for reactive alkynes in bio-orthogonal click reactions: insights from mechanochemical and conceptual DFT calculations, Chem. Sci., 2020, 11, 1431–1439, 10.1039/c9sc04507d.
- T. Bettens, M. Alonso, P. Geerlings and F. De Proft, Mechanochemical Felkin–Anh Model: Achieving Forbidden Reaction Outcomes with Mechanical Force, J. Org. Chem., 2023, 88, 2046–2056, DOI:10.1021/acs.joc.2c02318.
- T. Bettens, J. Eeckhoudt, M. Hoffmann, M. Alonso, P. Geerlings, A. Dreuw and F. De Proft, Designing Force Probes Based on Reversible 6π-Electrocyclizations in Polyenes Using Quantum Chemical Calculations, J. Org. Chem., 2021, 86, 7477–7489, DOI:10.1021/acs.joc.1c00482.
- T. Bettens, M. Hoffmann, M. Alonso, P. Geerlings, A. Dreuw and F. De Proft, Mechanochemically Triggered Topology Changes in Expanded Porphyrins, Chem.–Eur. J., 2021, 27, 3397–3406, DOI:10.1002/chem.202003869.
- M. Alonso, T. Bettens, J. Eeckhoudt, P. Geerlings and F. De Proft, Wandering through quantum-mechanochemistry: from concepts to reactivity and switches, Phys. Chem. Chem. Phys., 2023, 26, 21–35, 10.1039/d3cp04907h.
- R. G. Parr and L. J. Bartolotti, On the Geometric Mean Principle for Electronegativity Equalization, J. Am. Chem. Soc., 1982, 104, 3801–3803, DOI:10.1021/ja00378a004.
- I. B. Baldus and F. Gräter, Mechanical Force Can Fine-Tune Redox Potentials of Disulfide Bonds, Biophys. J., 2012, 102, 622–629, DOI:10.1016/j.bpj.2011.12.039.
- J. Moens, P. Geerlings and G. Roos, A conceptual DFT approach for the evaluation and interpretation of redox potentials, Chem.–Eur. J., 2007, 13, 8174–8184, DOI:10.1002/chem.200601896.
- J. Moens, G. Roos, P. Jaque, F. Proft and P. Geerlings, Can electrophilicity act as a measure of the redox potential of first-row transition metal ions?, Chem.–Eur. J., 2007, 13, 9331–9343, DOI:10.1002/chem.200700547.
- I. Prigogine and R. Defay, Chemical Thermodynamics, Longmans, London, 1954 Search PubMed.
- M. Rahm, R. Hoffmann and N. W. Ashcroft, Atomic and Ionic Radii of Elements 1-96, Chem.–Eur. J., 2016, 22, 14625–14632, DOI:10.1002/chem.201602949.
- A. Bondi, van der Waals Volumes and Radii,, J. Phys. Chem., 1964, 68, 441–451, DOI:10.1021/j100785a001.
- D. C. Ghosh and R. Biswas, Theoretical Calculation of Absolute Radii of Atoms and Ions. Part 1. The Atomic Radii, Int. J. Mol. Sci., 2002, 3, 87–113, DOI:10.3390/i3020087.
- M. S. Miao and R. Hoffmann, High Pressure Electrides: A Predictive Chemical and Physical Theory, Acc. Chem. Res., 2014, 47, 1311–1317, DOI:10.1021/ar4002922.
- J. Garza, R. Vargas, N. Aquino and K. D. Sen, DFT reactivity indices in confined many-electron atoms, J. Chem. Sci., 2005, 117, 379–386, DOI:10.1007/bf02708341.
- P. Zaleski-Ejgierd and P. M. Lata, Krypton oxides under pressure, Sci. Rep., 2016, 6, 1–7, DOI:10.1038/srep18938.
- S. Kullback and R. A. Leibler, On Information and Sufficiency, Ann. Math. Stat., 1951, 22, 79–86, DOI:10.1214/aoms/1177729694.
- A. Borgoo, M. Godefroid, K. D. Sen, F. De Proft and P. Geerlings, Quantum Similarity of atoms: a numerical Hartree-Fock and information theory approach, Chem. Phys. Lett., 2004, 399, 363–367, DOI:10.1016/j.cplett.2004.10.026.
- J. Eeckhoudt, M. Alonso, P. Geerlings and F. De Proft, Bond Lengths and Dipole Moments of Diatomic Molecules under Isotropic Pressure with XP-PCM and GOSTSHYP, J. Chem. Theory Comput., 2024, 20, 7430–7442, DOI:10.1021/acs.jctc.4c00665.
- P. Fuentealba and C. Cárdenas, On the exponential model for energy with respect to number of electrons, J. Mol. Model., 2013, 19, 2849–2853, DOI:10.1007/s00894-012-1708-5.
- R. A. Miranda-Quintana and P. W. Ayers, Interpolation of property-values between electron numbers is inconsistent with ensemble averaging, J. Chem. Phys., 2016, 144, 244112, DOI:10.1063/1.4953557.
- L. Pujal, A. Tehrani and F. Heidar-Zadeh, in Conceptual Density Functional Theory, ed. S. Liu, Wiley, 2022, ch. 32, pp. 649–661, DOI:10.1002/9783527829941.
| This journal is © The Royal Society of Chemistry 2024 |