Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ultrafast photophysics of para-substituted 2,5-bis(arylethynyl) rhodacyclopentadienes: thermally activated intersystem crossing†
Zilong
Guo
 b,
Yaxin
Wang
b,
Julia
Heitmüller
b,
Yaxin
Wang
b,
Julia
Heitmüller
 a,
Carolin
Sieck
c,
Andreas
Prüfer
d,
Philipp
Ralle
d,
Andreas
Steffen
a,
Carolin
Sieck
c,
Andreas
Prüfer
d,
Philipp
Ralle
d,
Andreas
Steffen
 d,
Petr
Henke
d,
Petr
Henke
 eg,
Peter R.
Ogilby
eg,
Peter R.
Ogilby
 *e,
Todd B.
Marder
*e,
Todd B.
Marder
 *cf,
Xiaonan
Ma
*cf,
Xiaonan
Ma
 *ba and
Tobias
Brixner
*ba and
Tobias
Brixner
 *af
*af
aInstitut für Physikalische und Theoretische Chemie, Julius-Maximilians-Universität Würzburg, Am Hubland, 97074 Würzburg, Germany. E-mail: tobias.brixner@uni-wuerzburg.de
bInstitute of Molecular Plus, Tianjin University, Tianjin 300072, P. R. China. E-mail: xiaonanma@tju.edu.cn
cInstitut für Anorganische Chemie, Julius-Maximilians-Universität Würzburg, Am Hubland, 97074 Würzburg, Germany. E-mail: todd.marder@uni-wuerzburg.de
dDepartment of Chemistry and Chemical Biology, TU Dortmund University, Otto-Hahn-Str. 6, 44227 Dortmund, Germany
eDepartment of Chemistry, Aarhus University, Aarhus DK-8000, Denmark. E-mail: progilby@chem.au.dk
fInstitute for Sustainable Chemistry and Catalysis with Boron (ICB), Julius-Maximilians-Universität Würzburg, Am Hubland, 97074 Würzburg, Germany
gFaculty of Science, Charles University, Hlavova 2030, 128 43 Prague 2, Czech Republic
First published on 15th August 2024
Abstract
2,5-Bis(phenylethynyl) rhodacyclopentadienes (RCPDs), as a type of Rh(III) complex, exhibit unusually intense fluorescence and slow intersystem crossing (ISC) due to weak metal–ligand interactions. However, details on their ultrafast photophysics and ISC dynamics are limited. In this work, electronic relaxation upon photoexcitation of two substituted RCPDs with two –CO2Me (A-RC-A) or –NMe2/–CO2Me (D-RC-A) end groups are comprehensively investigated using femtosecond transient absorption spectroscopy and theoretical analysis. Upon ultraviolet and visible excitation, dephasing of vibrational coherence, charge transfer, conformation relaxation, and ISC are observed experimentally. By calculating the spin–orbit coupling, reorganization energy, and adiabatic energy gap of plausible ISC channels, semi-classical Marcus theory revealed the dominance of thermally activated ISC (S1 → T2) for both D-RC-A and A-RC-A, while S1 → T1 channels are largely blocked due to high ISC barriers. With weak spin–orbit coupling, such differences in plausible ISC channels are predominately tuned by energetic parameters. Singlet oxygen sensitization studies of A-RC-A provide additional insight into the excited-state behavior of this complex.
Introduction
Organometallic complexes have attracted attention for a wide range of applications in photocatalysis,1–5 bioimaging,6–8 sensing,9,10 and organic light-emitting diode (OLED) devices.11–14 The spin-forbidden nature of the singlet–triplet transition often leads to slow intersystem crossing (ISC) in organic systems. However, by incorporating heavy transition metals, the ISC rate constant (kISC) can be significantly increased to typically greater than 1010 s−1,15 even up to 1013–1014 s−1 in Ru(II) complexes,16–19 leading to significant fluorescence quenching and enhanced phosphorescence emission. Efficient ISC can be primarily attributed to strong spin–orbit coupling (SOC) due to participation of the d-orbitals of heavy metals, which can significantly alter the photophysics due to strong metal–ligand interactions via metal-to-ligand charge transfer (MLCT) states that dominate electronic relaxation.20–24Unlike complexes with ultrafast ISC, 2,5-bis(phenylethynyl) rhodacyclopentadienes (RCPDs)25–27 incorporating Rh(III) exhibit up to 69% fluorescence quantum yields (Φf) with kISC = 107–108 s−1 which is several orders of magnitude slower than that in Ru(II) complexes.17 Intriguingly, by replacing Rh(III) with much heavier Ir(III), the corresponding iridacyclopentadienes28 are still highly fluorescent. Such photophysics was attributed to weakened SOC due to low d-orbital participation in the frontier orbitals and an enlarged S1–T1 energy gap (ΔEST).28,29 Meanwhile, the T2 state was reported to be an ISC destination through a thermally activated mechanism in RCPDs,28 which increased the complexity of their electronic relaxation. Investigations indicated that the fluorescence properties of RCPDs can be effectively tuned by introducing an electron donor (D) or acceptor (A) at the para-positions of the arylethynyl groups.28,30,31 In particular, symmetric substitution with A/A groups (–CO2Me or –BMes2) (Mes = mesityl = 2,4,6-Me3C6H2) at the para-positions leads to significantly higher Φf than corresponding D/A (–NMe2/–CO2Me) and unsubstituted RCPDs (see Table S1†). In a simple excited-state model, enhanced fluorescence emission can be attributed either to slow non-radiative relaxation of the S1 state via dark states or suppressed ISC to the triplet state.32,33 Although kISC of RCPDs was determined to be 107–108 s−1 using picosecond time-resolved infrared spectroscopy,30 a full picture of their S1 relaxation remains unclear. Therefore, a comprehensive picture of the photophysics of RCPDs with weak metal–ligand interactions might be helpful for future rational design of fluorescent emitters.
In general, the ISC rate constant kISC between singlet (Sm, m ≥ 1) and triplet (Tn, n ≥ 1) excited states can be expressed via the Fermi golden rule,34,35
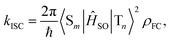 | (1) |
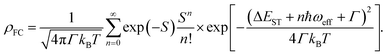 | (2) |
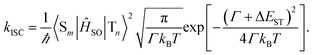 | (3) |
In cases of ultrafast ISC (kISC > 1012 s−1) of complexes with late transition metals, extremely high kISC is observed due to a large coupling term 〈Sm|ĤSO|Tn〉 up to several thousands of cm−1, which greatly amplifies the ISC rate associated with the ISC barrier (Ea) determined by Γ and ΔEST. However, RCPDs exhibit much slower ISC (kISC = 108–109 s−1) due to the lack of strong metal–ligand interactions,30i.e., 〈Sm|ĤSO|Tn〉 in eqn (3) is expected to be small and relatively sensitive to para-substitution on the aryl ligand. It is hypothesized that the kISC may vary significantly with the reorganization energy and adiabatic energy gap subject to para-substitution, which determine the ISC barrier (Ea) thermodynamically and can be discussed within the framework of Marcus theory.
In this work, two para-substituted 2,5- bis(arylethynyl)rhodacyclopentadiene complexes (Scheme 1) were investigated by using excitation-wavelength-(λex-)dependent femtosecond transient absorption (fs-TA) measurements and time-dependent density-functional theory (TD-DFT) calculations. Compared with A-RC-A (τS1 = 1.7 ns) substituted with two –CO2Me groups, the D-RC-A with –CO2Me/–NMe2 substitution exhibits a shorter (τS1 = 0.8 ns) lifetime of the S1 state in toluene solution.31 By resolving fs-TA data upon ultraviolet (UV) and visible excitation, the electronic relaxation channels of D-RC-A and A-RC-A are largely revealed. Moreover, by applying semi-classical Marcus theory, we determine that ISC of both D-RC-A and A-RC-A rely on a thermally activated S1 → T2 transition rather than the channel that directly populates the T1 state. We also report studies of singlet oxygen, O2(a1Δg), sensitization by A-RC-A, which provides additional insight into the excited-state behavior of this complex.
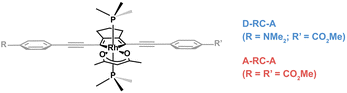 | ||
| Scheme 1 Chemical structures of investigated D-RC-A and A-RC-A. The Rh(III)–ligand core is illustrated in black while the peripheral groups are in gray. The phosphine ligand is PMe3. | ||
Results and discussion
Static absorption spectra
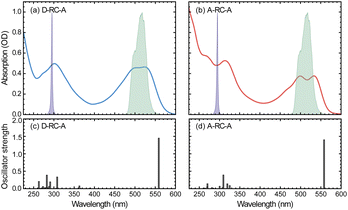
The static absorption spectra of D-RC-A and A-RC-A in THF are displayed in Fig. 1 along with the calculated vertical excitation energies and oscillator strengths, while the corresponding calculation results are listed in Table S2.† Note that the oscillator strength (f) here is not referenced to the transition probability for a freely oscillating electron in a single atom, but reflects only the transition dipole moment and the energy gap between two states of the RCPDs. For both D-RC-A and A-RC-A, the pronounced absorption in the 450–550 nm region can be attributed to the S1 excited state, while higher singlet (Sm, m > 1) states comprise the intense absorption in the UV region. As a result, upon visible (λex = 513 nm) and UV (λex = 295 nm) optical excitation, direct population of the S1 and Sm states can be expected in fs-TA experiments, as described in detail below.The observed S1 band of D-RC-A exhibits less pronounced vibronic progression than that of A-RC-A. Reduced vibronic progression might be attributed to stronger solute–solvent interaction due to excited-state charge transfer (CT) between substituted D and A groups, which was confirmed by natural transition orbital (NTO) analysis of the S1 state of both RCPDs. As illustrated in Fig. S1,† A-RC-A exhibits a symmetric distribution of both hole and electron density in the S1 state, indicating its locally excited (LE) nature. However, clear CT character is observed in the S1 state NTOs of D-RC-A, i.e., hole and electron density are asymmetrically distributed on D and A sides, respectively. A different S1 character (CT or LE) of D-RC-A and A-RC-A can also affect the corresponding S1 relaxation. The initially populated S1 state undergoes rapid decay leading to the relaxed CT state, which is observed in the fs-TA signal of D-RC-A and absent for A-RC-A. Furthermore, NTO analysis on the triplet states indicates that the T1 of D-RC-A is slightly mixed with CT character like the S1 state, while the corresponding T2 state and T1/T2 states of A-RC-A are all LE dominated.
On the other hand, NTO analysis indicates that the central Rh(III) in D-RC-A and A-RC-A is barely involved in the S0 → S1, S0 → T1, and S0 → T2 transitions, which is consistent with previous reports on electronic transitions of RCPDs,28,31i.e., the low-lying S1, T1, and T2 states of RCPDs are dominated by π–π* transitions of ligands with minimal contributions of Rh(III). The photophysics indicates the weak SOC of RCPDs, which is consistent with previous reports.25–28,30,31 Without pronounced metal–ligand interaction, ISC dynamics of RCPDs are largely determined by energetic parameters (Γ and ΔEST) and can thus be discussed in the framework of semi-classical Marcus theory.
Excitation-wavelength-dependent fs-TA
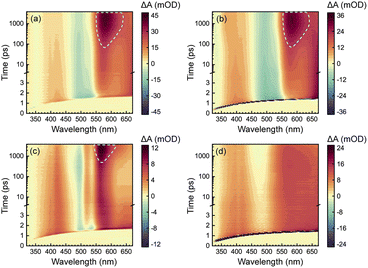
To acquire a full picture of electronic relaxation of RCPDs, we performed fs-TA experiments on D-RC-A and A-RC-A upon excitation by either UV (λex = 295 nm) or visible (λex = 513 nm) laser pulses as previously reported.50 The resulting TA signal in the probe range of λpr = 320–670 nm was recorded for delay times up to Δt = 3.8 ns and are displayed in Fig. 2.As shown in Fig. 2a and b, D-RC-A exhibits nearly identical fs-TA signals upon UV (λex = 295 nm) and visible (λex = 513 nm) excitation, respectively, in which at least three distinct bands can be distinguished. The negative band appears immediately after excitation in the λpr = 470–550 nm regime and agrees with the static absorption spectrum (S0 → S1), which can be attributed to the ground-state bleaching (GSB) signal. At the same time, two excited-state absorption (ESA) bands of the S1 state appear in the λpr = 360–460 nm and >550 nm regimes which, subsequently, exhibit relaxation simultaneously with the decay of the GSB band. Meanwhile, slow formation of a new positive band is observed with a center at λpr = 580 nm, which is superimposed on the decay of the long-lived ESA band in the λpr > 550 nm region, probably corresponding to ESA of an ISC-generated triplet state. However, the final destination (T1 or T2) of the observed ISC process is difficult to identify by fs-TA data itself. Instead, ISC rates of S1 → T1 and S1 → T2 need to be calculated to assign the observed ISC process. Thus, we tentatively denote the triplet state generated as the Tn (n ≥ 1) state.
Unlike D-RC-A, A-RC-A exhibits λex-dependent relaxation behavior. Upon UV excitation, a similar fs-TA signal as that for D-RC-A was recorded for A-RC-A, although the GSB displays a double peak at λpr = 500 nm and 535 nm, which is consistent with the pronounced vibronic progression exhibited in the static absorption spectrum. Meanwhile, triplet-state formation is also observed at λpr = 570 nm, with a substantially slower kISC than that of D-RC-A. As shown in Fig. S2,† preliminary fitting of triplet formation dynamics of D-RC-A (at λpr = 580 nm) and A-RC-A (at λpr = 570 nm) indicated that the observed ISC of D-RC-A (τISC < 350 ps) is one order of magnitude faster than ISC of A-RC-A (τISC > 3.5 ns). Thus, S1 state relaxation of D-RC-A might be dominated by ISC as it is much faster than radiative and non-radiative S1 → S0 channels. In contrast, considering the observed fluorescence lifetime (∼1.7 ns), the radiative and non-radiative S1 → S0 decay of A-RC-A might be comparable with ISC to triplet states.
Intriguingly, upon visible excitation, the triplet band of A-RC-A is absent in the fs-TA data up to the maximum delay time (3.8 ns), while the decay of ESA bands and refilling of the GSB band are still observable. In general, upon UV excitation, rapid internal conversion (IC) from initially populated Sm states leads to a vibrationally hot S1 state. Compared with the S1 state directly populated by resonant visible excitation, excess vibrational energy of the S1 state might be helpful to overcome the ISC barrier.51–54 Therefore, we believe that the ISC barrier (Ea) for A-RC-A should be higher than that for D-RC-A, which is also indicated by a slower rise of the ISC band of A-RC-A compared to that of D-RC-A upon UV excitation.
Ultrafast electronic relaxation
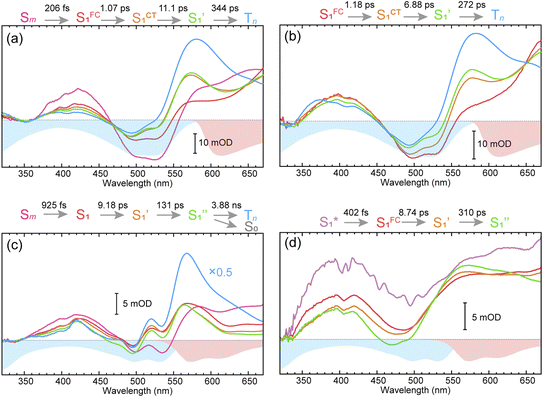
To obtain details on the electronic relaxation of the RCPDs, we performed target analysis on the corresponding λex-dependent fs-TA data. On ultrafast time scales, a sequential kinetic model including several independent species was employed for all fs-TA data, while a branched scheme was considered for the decay of the relaxed (CT and structural) S1 state, corresponding to competition between relaxation to the S0 state (S1 → S0) and ISC to triplet states (S1 → Tn). As discussed above, S1 relaxation of D-RC-A is dominated by the S1 → Tn channel, for which the S1 → S0 channel was correspondingly ignored in target analysis (Fig. S3†). However, for A-RC-A upon UV excitation, both the S1 → S0 and S1 → Tn channels were included in target analysis with a branch ratio of 0.5 (Fig. S3†). The extracted species-associated spectra (SAS) are displayed in Fig. 3, while the corresponding fitted time traces at selected λpr and the concentration evolution of each species can be found in Fig. S4 and S5,† respectively, in the ESI.†As mentioned above, D-RC-A exhibits similar relaxation dynamics upon UV and visible excitation. Upon UV excitation, the populated Sm states undergo rapid IC with a time constant of τ1 = 206 fs to reach the Franck–Condon region of the S1 state (Sm → S1FC), which is absent in the fs-TA data upon resonant visible excitation to the S1 state. The subsequent SAS exhibits a spectral depletion in the range λpr = 570–670 nm, which is consistent with fluorescence spectra of D-RC-A and can be attributed to the stimulated emission (SE) band of the S1 state. Pronounced solvatochromism of D-RC-A has been reported,31 implying CT character of the fluorescent bright state, which is also consistent with the NTO analysis mentioned above. Considering the observed SE signature in the SAS, we assigned the second SAS to the CT-relaxed S1 state (noted as S1CT), corresponding to a local minimum on the S1 potential energy surface (PES). Moreover, the fitted formation time of S1CT (S1FC → S1CT, ∼1 ps) is consistent with the reported formation time of the solvation-stabilized CT state of organic D–A-type chromophores in THF.55,56
During the subsequent relaxation (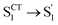 ) with a ∼10 ps time constant, the SAS exhibit only minimal changes of spectral features, which might be explained by structural relaxation in the S1 state. In order to obtain further details on S1 relaxation, we calculated the optimized structures of both D-RC-A and A-RC-A in their S1, T1, and T2 states to be compared with the S0 structure. As shown in Fig. S6 and S7,† large S0 → S1 twisting is observed for the peripheral phenyl and D/A groups of RCPDs, which can be quantified by the calculated twisting angles listed in Table S3.† Apart from the twisting angles, contributions of S0 → S1 conformational relaxation can be generalized in reorganization energy (ΓS1→S0).57,58 By summing over contributions from each vibrational mode (Fig. S8†), ΓS1→S0 of D-RC-A and A-RC-A were calculated to be 1519 cm−1 and 1944 cm−1, respectively. However, ΓS1→S0 contributed by vibrational modes is not able to provide the relative contribution of each structural part of the RCPDs to conformational relaxation. Therefore, we further calculated the root-mean-square displacement (RMSD) in Cartesian coordinates of the optimized S0 (xi, yi, zi) and S1 (
) with a ∼10 ps time constant, the SAS exhibit only minimal changes of spectral features, which might be explained by structural relaxation in the S1 state. In order to obtain further details on S1 relaxation, we calculated the optimized structures of both D-RC-A and A-RC-A in their S1, T1, and T2 states to be compared with the S0 structure. As shown in Fig. S6 and S7,† large S0 → S1 twisting is observed for the peripheral phenyl and D/A groups of RCPDs, which can be quantified by the calculated twisting angles listed in Table S3.† Apart from the twisting angles, contributions of S0 → S1 conformational relaxation can be generalized in reorganization energy (ΓS1→S0).57,58 By summing over contributions from each vibrational mode (Fig. S8†), ΓS1→S0 of D-RC-A and A-RC-A were calculated to be 1519 cm−1 and 1944 cm−1, respectively. However, ΓS1→S0 contributed by vibrational modes is not able to provide the relative contribution of each structural part of the RCPDs to conformational relaxation. Therefore, we further calculated the root-mean-square displacement (RMSD) in Cartesian coordinates of the optimized S0 (xi, yi, zi) and S1 (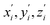 ) state structures,
) state structures,
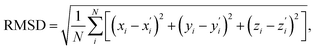 | (4) |
Summing over all atoms, i = 1, …, N. The calculation leads to RMSDS1/S0 = 0.156 Å for D-RC-A which is lower than that for A-RC-A (0.207 Å), consistent with the calculated ΓS1→S0. We further calculated the relative contributions of the peripheral groups (phenyls, C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C, and D/A, gray part in Scheme 1) and Rh(III)–ligand core (black part in Scheme 1). For D-RC-A, the RMSDS1/S0 was found to be dominated by twisting of the peripheral parts of the structure with ∼90% contribution. The rotational twisting around C–C single bonds has been widely reported to be nearly barrierless,59,60 which is consistent with the observed efficient relaxation (
C, and D/A, gray part in Scheme 1) and Rh(III)–ligand core (black part in Scheme 1). For D-RC-A, the RMSDS1/S0 was found to be dominated by twisting of the peripheral parts of the structure with ∼90% contribution. The rotational twisting around C–C single bonds has been widely reported to be nearly barrierless,59,60 which is consistent with the observed efficient relaxation (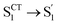 , ∼10 ps). Intriguingly, we found that the Rh(III)-ligand core contributes ∼40% to the RMSDS1/S0 of A-RC-A via its own framework distortion, which is comparable with the twisting of the peripheral parts (∼60%). Compared to the rapid twisting of the peripheral groups, the distortion of the molecular framework is normally much slower due to a high potential barrier. Therefore, a two-step conformational relaxation is expected to be observed in the fs-TA data of A-RC-A, which has been widely reported in organic fluorescent systems.61–63
, ∼10 ps). Intriguingly, we found that the Rh(III)-ligand core contributes ∼40% to the RMSDS1/S0 of A-RC-A via its own framework distortion, which is comparable with the twisting of the peripheral parts (∼60%). Compared to the rapid twisting of the peripheral groups, the distortion of the molecular framework is normally much slower due to a high potential barrier. Therefore, a two-step conformational relaxation is expected to be observed in the fs-TA data of A-RC-A, which has been widely reported in organic fluorescent systems.61–63
The extracted species 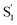 corresponds to a global minimum on the S1-state PES, which subsequently undergoes ISC leading to formation of a triplet state, featured by the rise of intense absorption centered at λpr = 580 nm and the disappearance of SE depletion (λpr = 570–670 nm). The formation time (
corresponds to a global minimum on the S1-state PES, which subsequently undergoes ISC leading to formation of a triplet state, featured by the rise of intense absorption centered at λpr = 580 nm and the disappearance of SE depletion (λpr = 570–670 nm). The formation time (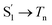 , ∼300 ps) of the triplet state corresponds to the ISC rate constant (kISC) of D-RC-A, which is consistent with the relatively low fluorescence quantum yield (Φf = 0.22) and sub-nanosecond fluorescence lifetime (τS1 = 0.8 ns) observed in toluene solution.31 Note that relaxation of the S1 state is contributed to by non-radiative decay to S0 (kNRS), radiative decay to S0 (kRS), and ISC to triplet states (kISC). Therefore, the S1 ESA decay and GSB refilling dynamics could be largely different with formation of the triplet band, i.e., S1 ESA and GSB include contributions of kNRS, kRS, and kISC, while rising of the triplet band is associated with kISC only. The full picture of the electronic relaxation of the RCPDs is summarized in Fig. 4.
, ∼300 ps) of the triplet state corresponds to the ISC rate constant (kISC) of D-RC-A, which is consistent with the relatively low fluorescence quantum yield (Φf = 0.22) and sub-nanosecond fluorescence lifetime (τS1 = 0.8 ns) observed in toluene solution.31 Note that relaxation of the S1 state is contributed to by non-radiative decay to S0 (kNRS), radiative decay to S0 (kRS), and ISC to triplet states (kISC). Therefore, the S1 ESA decay and GSB refilling dynamics could be largely different with formation of the triplet band, i.e., S1 ESA and GSB include contributions of kNRS, kRS, and kISC, while rising of the triplet band is associated with kISC only. The full picture of the electronic relaxation of the RCPDs is summarized in Fig. 4.
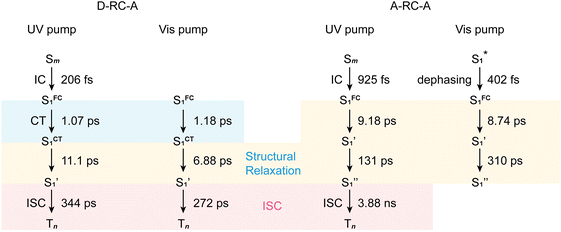 | ||
| Fig. 4 Electronic relaxation of D-RC-A (left two panels) and A-RC-A (right two panels) revealed by λex-dependent fs-TA measurements. | ||
In the fs-TA data for A-RC-A upon UV excitation, we observed electronic relaxation that is significantly different from D-RC-A. Without a D–A structure, the CT state signature was absent in the fs-TA of A-RC-A. After excitation, rapid IC (∼900 fs, Sm → S1FC) is followed by two-step conformational relaxation (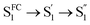 ), corresponding to a comparable contribution of the peripheral structure and metal–ligand core to the RMSDS1/S0 of A-RC-A. The first step (
), corresponding to a comparable contribution of the peripheral structure and metal–ligand core to the RMSDS1/S0 of A-RC-A. The first step (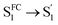 , ∼9 ps) exhibits a time constant similar to that of the corresponding step in D-RC-A (
, ∼9 ps) exhibits a time constant similar to that of the corresponding step in D-RC-A (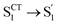 , ∼10 ps), which was attributed to barrierless twisting of the peripheral structure. Note that the observed twisting with a ∼10 ps time constant is unobservable in our previous time-resolved IR investigation due to the limitation of low temporal resolution (10–20 ps).30 The subsequent step (
, ∼10 ps), which was attributed to barrierless twisting of the peripheral structure. Note that the observed twisting with a ∼10 ps time constant is unobservable in our previous time-resolved IR investigation due to the limitation of low temporal resolution (10–20 ps).30 The subsequent step (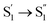 , ∼150 ps) accordingly corresponds to structural distortion of the Rh(III)–ligand framework. Furthermore, slower triplet formation (S1′′ → Tn, ∼3.88 ns) in A-RC-A than in D-RC-A was observed upon UV excitation, corresponding to a long-lived (τf = 1.7 ns) S1 state,31 which is discussed in detail below. Upon ∼25 fs visible excitation, A-RC-A exhibits largely different electronic relaxation (Fig. 3d) from the case with UV excitation (Fig. 3c). The target analysis extracted a short-lived species(noted as
, ∼150 ps) accordingly corresponds to structural distortion of the Rh(III)–ligand framework. Furthermore, slower triplet formation (S1′′ → Tn, ∼3.88 ns) in A-RC-A than in D-RC-A was observed upon UV excitation, corresponding to a long-lived (τf = 1.7 ns) S1 state,31 which is discussed in detail below. Upon ∼25 fs visible excitation, A-RC-A exhibits largely different electronic relaxation (Fig. 3d) from the case with UV excitation (Fig. 3c). The target analysis extracted a short-lived species(noted as 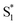 ) after excitation with a ∼400 fs time constant. As described above, rapid IC (∼900 fs, Sm → S1FC) was identified for A-RC-A upon UV excitation, while the observed visible-excitation-induced ∼400 fs relaxation obviously cannot be assigned to IC from Sm, as the visible excitation at λex = 513 nm employed is resonant with the S1 state of A-RC-A and, correspondingly, incapable of populating the Sm state. Moreover, as illustrated in Fig. S9,† we observed a beating behavior in the λpr = 400–550 nm wavelength regime of the fs-TA data, which is observed as an oscillatory modulation in both temporal (Fig. S4†) and frequency (Fig. S9†) domains. The beating-modulated TA spectra (Fig. S9†) observed in the initial few picoseconds are highly consistent with the extracted SAS of the
) after excitation with a ∼400 fs time constant. As described above, rapid IC (∼900 fs, Sm → S1FC) was identified for A-RC-A upon UV excitation, while the observed visible-excitation-induced ∼400 fs relaxation obviously cannot be assigned to IC from Sm, as the visible excitation at λex = 513 nm employed is resonant with the S1 state of A-RC-A and, correspondingly, incapable of populating the Sm state. Moreover, as illustrated in Fig. S9,† we observed a beating behavior in the λpr = 400–550 nm wavelength regime of the fs-TA data, which is observed as an oscillatory modulation in both temporal (Fig. S4†) and frequency (Fig. S9†) domains. The beating-modulated TA spectra (Fig. S9†) observed in the initial few picoseconds are highly consistent with the extracted SAS of the 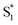 species with a ∼400 fs relaxation. We therefore attribute
species with a ∼400 fs relaxation. We therefore attribute 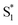 relaxation to dephasing of the coherent vibrational wave packet (noted as
relaxation to dephasing of the coherent vibrational wave packet (noted as 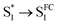 ). The dephasing of
). The dephasing of 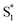 was not recognized as an independent species in the target analysis of D-RC-A upon visible excitation, which might be associated with a less modulated spectral shape and faster
was not recognized as an independent species in the target analysis of D-RC-A upon visible excitation, which might be associated with a less modulated spectral shape and faster 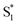 dephasing (Fig. S9†) of D-RC-A due to intense solute–solvent interactions. We further extracted beating signals by subtracting the fitted exponential components from the measured fs-TA data. The Fourier transformed power spectra of the beating signals (Fig. S10†) revealed a dominant vibrational mode at ∼250 cm−1 for both D-RC-A and A-RC-A. Considering that the beating frequency is independent of the 2,5-substitution, we speculate that the observed ∼250 cm−1 mode might originate from a distortion of the metal–ligand core.
dephasing (Fig. S9†) of D-RC-A due to intense solute–solvent interactions. We further extracted beating signals by subtracting the fitted exponential components from the measured fs-TA data. The Fourier transformed power spectra of the beating signals (Fig. S10†) revealed a dominant vibrational mode at ∼250 cm−1 for both D-RC-A and A-RC-A. Considering that the beating frequency is independent of the 2,5-substitution, we speculate that the observed ∼250 cm−1 mode might originate from a distortion of the metal–ligand core.
After rapid dephasing (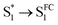 ), the S1 state of A-RC-A subsequently undergoes a two-step conformational relaxation (
), the S1 state of A-RC-A subsequently undergoes a two-step conformational relaxation (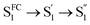 ) nearly identical with that of A-RC-A upon UV excitation. However, the rise of the Tn band observed in the fs-TA of A-RC-A upon UV excitation is absent upon visible excitation. Instead, we observe an isosbestic point at λpr = 530 nm in the fs-TA data of A-RC-A upon visible excitation, indicating that the TA bands located on the blue (GSB, λpr = 430–530 nm) and red (ESA, λpr = 530–670 nm) sides of the isosbestic point belong to an identical process, i.e., S1 relaxation. However, note that the fs-TA observation cannot fully exclude the existence of ISC of A-RC-A upon visible excitation due to the limitation of the fs-TA time window. Actually, upon visible excitation, slight spectral rising can be observed between 550 nm and 600 nm at long delays, which is consistent with the triplet band observed upon UV excitation. A plausible explanation is that visible excitation leads to an ultraslow ISC which is unobservable within our time window (3.8 ns).
) nearly identical with that of A-RC-A upon UV excitation. However, the rise of the Tn band observed in the fs-TA of A-RC-A upon UV excitation is absent upon visible excitation. Instead, we observe an isosbestic point at λpr = 530 nm in the fs-TA data of A-RC-A upon visible excitation, indicating that the TA bands located on the blue (GSB, λpr = 430–530 nm) and red (ESA, λpr = 530–670 nm) sides of the isosbestic point belong to an identical process, i.e., S1 relaxation. However, note that the fs-TA observation cannot fully exclude the existence of ISC of A-RC-A upon visible excitation due to the limitation of the fs-TA time window. Actually, upon visible excitation, slight spectral rising can be observed between 550 nm and 600 nm at long delays, which is consistent with the triplet band observed upon UV excitation. A plausible explanation is that visible excitation leads to an ultraslow ISC which is unobservable within our time window (3.8 ns).
By measuring the fluorescence quantum yield of A-RC-A upon UV (ΦfUV = 0.29) and visible (Φfvis = 0.33) excitation in THF (Table S4†) and assuming an unchanged radiative decay rate constant (kr) upon different excitation, the ISC time constant upon visible excitation was estimated to be ∼5.75 ns (ESI,† Section S4), which is accordingly unobservable in the fs-TA with time window of 3.8 ns. We also measured the fluorescence lifetime of A-RC-A upon UV (τS1UV) and visible (τS1vis) excitation, which leads to an unchanged lifetime of ∼1.6 ns (Fig. S11–S13†). However, quantitative estimation of the S1 state decay (ESI,† Section S4) indicated that τS1vis can be only <0.2 ns slower than τS1UV, which can be easily concealed by different temporal profiles of excitation sources in the UV and visible regimes. Therefore, we believe an ultraslow ISC that is beyond our fs-TA time window leads to the absence of triplet ESA in the fs-TA of A-RC-A upon visible excitation, which corresponds to an inaccessible barrier for ISC. In the next section, we further analyze the ISC energetic diagram of D-RC-A and A-RC-A in the framework of Marcus theory to understand the fundamental mechanism that leads to the different ISC dynamics of D-RC-A and A-RC-A.
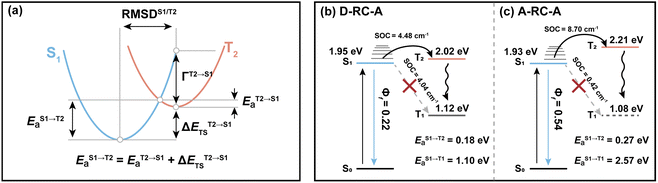
Marcus analysis of the ISC dynamics
As discussed above, upon identical excitation conditions, D-RC-A exhibited much faster ISC than A-RC-A, which is consistent with the reported lower Φf and shorter τS1 of D-RC-A compared to A-RC-A.31 For systems with weak SOC, i.e., 〈Sm|ĤSO|Tn〉 ≪ Ea, ISC can be simplified as a transition between non-adiabatic states and described by semi-classical Marcus theory.64–66 As the basis for our Marcus analysis, adiabatic excitation energies of the S1 and T2 states were calculated with TD-DFT for both D-RC-A and A-RC-A, while the corresponding T1 states were calculated using unrestricted DFT (UDFT). UDFT has been reported to be reliable for calculating T1 states of organic and organometallic complexes, but is inherently not able to treat higher lying triplet states.67–69Here, we first analyze the S1 → T1 channel that is regarded as the dominant ISC channel in common organic systems,70,71 for which the adiabatic excitation energies of the S1 and T1 states are required. The ISC barrier of the S1 → T1 channel (EaS1→T1) was estimated by a reorganization energy (ΓS1→T1) and corresponding adiabatic energy gap (ΔESTS1→T1) within the framework of Marcus theory. As listed in Table 1, ΔESTS1→T1 of RCPDs are comparable (0.829 eV for D-RC-A and 0.858 eV for A-RC-A) whereas D-RC-A features a higher ΓS1→T1 (0.115 eV) than A-RC-A (0.062 eV), leading to EaS1→T1 for D-RC-A (1.103 eV) and A-RC-A (2.574 eV), which are comparable with the adiabatic energies of the corresponding T1 states. Meanwhile, the SOC matrix elements 〈S1|ĤSO|T1〉 of D-RC-A and A-RC-A were calculated to be 4.045 cm−1 and 0.425 cm−1, respectively. The large ISC barrier (>1 eV) leads to virtually forbidden transitions of the S1 → T1 channel of D-RC-A and A-RC-A.
| D-RC-A | A-RC-A | |
|---|---|---|
| a Adiabatic excitation energy calculated by TD-DFT. b Adiabatic excitation energy calculated by UDFT. c Calculated by adiabatic energies of optimized geometries of corresponding electronic states, the adiabatic energy gap of an exothermic process was defined to be positive. d Estimated by reorganization energy and adiabatic energy gap of the corresponding transition by Marcus theory. e Calculated by EaS1→T2 = EaT2→S1 + ΔETST2→S1. | ||
| S1 excitation energya/eV | 1.952 | 1.939 |
| T1 excitation energyb/eV | 1.123 | 1.081 |
| T2 excitation energya/eV | 2.022 | 2.213 |
| RMSDS1/S0/Å | 0.156 | 0.207 |
| RMSDS1/T1/Å | 0.377 | 0.302 |
| RMSDS1/T2/Å | 0.853 | 0.325 |
| Γ S1→S0/eV | 0.188 | 0.241 |
| Γ S1→T1/eV | 0.115 | 0.062 |
| Γ T2→S1/eV | 0.558 | 0.257 |
| ΔESTS1→T1/eV | 0.829 | 0.858 |
| ΔESTS1→T2/eV | −0.070 | −0.274 |
| ΔETST2→S1/eV | 0.070 | 0.274 |
| 〈S1|ĤSO|T1〉/cm−1 | 4.045 | 0.425 |
| 〈S1|ĤSO|T2〉/cm−1 | 4.481 | 8.697 |
| E a S1→T1/eV | 1.103 | 2.574 |
| E a T2→S1/eV | 0.106 | <0.001 |
| E a S1→T2/eV | 0.177 | 0.274 |
| E a S1→T1/EaS1→T2 | 6.325 | 9.387 |
| k ISC S1→T2 (cal. DA)/kISCS1→T2 (cal. AA) | 7.774 | |
| k ISC (exp.)/ps−1 | 1/350 | 1/3900 |
| k ISC (exp. DA)/kISC (exp. AA) | 11.143 | |
Regarding the S1 → T2 channel, the calculated adiabatic energies of the S1 and T2 states indicate its endothermic nature with a negative ΔESTS1→T2 for both D-RC-A (−0.070 eV) and A-RC-A (−0.274 eV). Nevertheless, the S1 → T2 transition of RCPDs can still be accessible through a thermally activated mechanism as long as EaS1→T2 is small enough (normally <0.2 eV), which has been observed via temperature-dependent experiments for RCPDs.28 To estimate EaS1→T2, as illustrated in Fig. 5a, we calculated the reorganization energy (ΓT2→S1) and adiabatic energy gap (ΔETST2→S1) of its reverse transition T2 → S1. As an exothermic process, EaT2→S1 can be estimated by Marcus theory, leading to EaT2→S1 = 0.106 eV and <0.001 eV for D-RC-A and A-RC-A, respectively. Thus, EaS1→T2 can be approximated by the sum of EaT2→S1 and the adiabatic energy gap (ΔETST2→S1), i.e., 0.177 eV and 0.274 eV for D-RC-A (Fig. 5b) and A-RC-A (Fig. 5c), respectively.
With the calculated ISC barriers and SOC matrix elements of plausible ISC channels, we can discuss the ISC dynamics of D-RC-A (Fig. 5b) and A-RC-A (Fig. 5c) in detail. For both D-RC-A and A-RC-A, EaS1→T1 is substantially higher than EaS1→T2 (EaS1→T1/EaS1→T2 = 6.325 for D-RC-A and 9.387 for A-RC-A), leading to S1 → T2 as the dominant ISC channel of both D-RC-A and A-RC-A. Although S1 → T2 ISC is an endothermic process, the thermally accessible barriers (∼0.2 eV) lead to ISC dynamics at room temperature, which is consistent with our previously observed temperature-dependence.28 Furthermore, kISCS1→T2 of D-RC-A were calculated to be ∼7.7 times faster than kISCS1→T2 of A-RC-A, which is perfectly consistent with the ∼11 times faster ISC observed experimentally by fs-TA. The relatively fast ISC of D-RC-A also explains the lower Φf of D-RC-A than A-RC-A due to competition between radiative and non-radiative (including ISC) decay of the S1 state. Meanwhile, the calculated ISC barrier (EaS1→T2) of D-RC-A and A-RC-A also explains the λex-dependent fs-TA data of A-RC-A. For D-RC-A, the thermally accessible S1 → T2 channel at room temperature (EaS1→T2 = 0.177 eV) leads to the observed λex-independent ISC signature in the TA-data. However, EaS1→T2 of A-RC-A (0.274 eV) is ∼0.1 eV higher than that for the ISC channel of D-RC-A, leading to a hindered ISC (S1 → T2) via a thermally activated mechanism. As discussed above, triplet ESA was consequently unobservable in the fs-TA of A-RC-A upon visible excitation due to its slow formation (∼5.8 ns). However, upon UV excitation, initial IC (Sm → S1) decay may lead to more population being distributed in higher vibrational levels of the S1 state, leading to faster ISC that can be observed in the fs-TA data. Note that values of all ISC barriers listed in Table 1 were estimated by Marcus theory based on the TD-DFT-calculated energies of S1 and T2 states, and unrestricted DFT (UDFT)-calculated T1 state, which can have errors up to 0.3 eV. Thus, the S1 → T2 ISC barrier (EaS1→T2) can possibly be different between D-RC-A and A-RC-A, leading to different observations in the λex-dependent fs-TA data.
Last but not least, note that although the T2 state is heavily involved in the ISC dynamics of D-RC-A and A-RC-A, we believe that the observed triplet signal at λpr = 570–580 nm in the fs-TA data must be assigned to the T1 rather than the T2 state. Spin-allowed T2 → T1 transitions with ∼1 eV energy gaps are expected to be much faster than the corresponding S1 → T2 transitions, leading to limited accumulation of T2 species. Thus, the observed ESA bands should be assigned to the T1 states formed through rapid decay from the T2 state. Similarly, the ISC populated T2 states are energetically higher than the corresponding S1 states of D-RC-A and A-RC-A, leading to potential exothermic reverse ISC (RISC, T2 → S1). However, such an RISC process cannot be the dominant decay channel of the T2 state due to competition of spin-allowed internal conversion (T2 → T1).
Singlet oxygen sensitization
Having the above fs-TA and theoretical data in hand, we then examined the ability of photoexcited A-RC-A to sensitize singlet molecular oxygen, O2(a1Δg), and the associated kinetics for two reasons: (1) this would likely provide additional information on the formation of triplet states upon light irradiation, and (2) a compound which is both fluorescent and can generate O2(a1Δg) from its triplet state could be potentially useful for both bio-imaging and photodynamic therapy.72,73 Moreover, using the fluorescence, one has the advantage of being able to insure that the sensitizing compound was localized at the desired location in a heterogeneous biological system.74 We note that in our previous studies,28,30 we found that several related complexes are capable of simultaneous fluorescence and O2(a1Δg) sensitization, with reasonable quantum yields for both processes, often summing to ca. 1.Quantum yields of O2(a1Δg) production, ΦΔ, were obtained by monitoring the intensity of the 1275 nm O2(a1Δg) → O2(X3Σg−) phosphorescence in time-resolved experiments, as described previously.75,76 Experiments were performed upon irradiation of A-RC-A at 417 nm. The integrated intensity of the time-resolved O2(a1Δg) phosphorescence signal, measured as a function of incident laser power, was normalized by the sensitizer absorbance and the O2(a1Δg) lifetime. Although a bleaching experiment indicates that A-RC-A can react with O2(a1Δg) (Fig. S14†), all data were recorded under conditions where A-RC-A bleaching was negligible.
We first performed experiments in toluene-h8, using a solution that had been bubbled with a gas stream containing 2% oxygen and 98% N2 (the reasons for using low concentrations of oxygen will become apparent below when discussing the kinetics of the time-resolved O2(a1Δg) phosphorescence signal). In this case, we performed one set of experiments using 1H-phenalenone (PN) in benzene as the reference O2(a1Δg) photosensitizer (ΦΔ = 0.92 ± 0.03),77,78 and another using m-tetraphenylporphyrin (TPP) in benzene as the reference photosensitizer (ΦΔ = 0.66 ± 0.08).79 The results yield a value of ΦΔ for A-RC-A of 0.09 ± 0.01. The pertinent data are shown in Fig. S15 and S16.†
Singlet oxygen phosphorescence data recorded upon irradiation of A-RC-A show an increase in the value of ΦΔ with increasing oxygen concentration (Table 2). In contrast, corresponding data from the PN-sensitized production of O2(a1Δg) do not show an increase in ΦΔ with an increase in the oxygen concentration (Fig. 6a). These data indicate that, in the PN experiment, the lifetime of the O2(a1Δg) precursor (i.e., the PN triplet state) is sufficiently long that the entire 3PN population is effectively quenched at a low oxygen concentration, which is consistent with expectation. For the A-RC-A experiment, the data indicate that the O2(a1Δg) precursor, presumably the A-RC-A triplet state, is sufficiently short-lived that higher oxygen concentrations are needed to quench a larger fraction of the 3A-RC-A population.
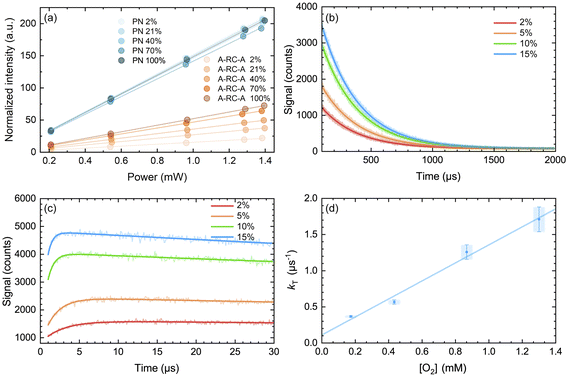 | ||
| Fig. 6 (a) Integrated intensity of the O2(a1Δg) phosphorescence signal upon irradiation at 417 nm, normalized by the sensitizer absorbance and the O2(a1Δg) lifetime, plotted as a function of laser power and collected over a range of O2 concentrations for both A-RC-A and for the reference standard, phenalenone (PN), in toluene-d8. The O2 concentration is represented as the percent of O2 in the O2/N2 gas mixture bubbled through the solution. The slopes of the linear fits are proportional to the O2(a1Δg) quantum yield. Representative time-resolved O2(a1Δg) phosphorescence traces used to obtain the A-RC-A data are shown in (b and c). (b) The data from 100 μs to 2000 μs were fitted by a single exponential decay function (solid lines) to obtain the lifetime of O2(a1Δg) (i.e., 1/kΔ). (c) Using kΔ as a fixed parameter, eqn (5) was used as a fitting function (solid lines) to obtain values of kT for a time domain where O2(a1Δg) was formed in the photosensitized reaction. (d) Plot of kT, obtained from the fits shown in (c) for the A-RC-A data, against the concentration of dissolved oxygen. The slope, (1.3 ± 0.1) × 109 M−1 s−1, is the bimolecular rate constant for oxygen quenching of the O2(a1Δg) precursor. The intercept yields a value of ∼9 μs for the lifetime of this O2(a1Δg) precursor in the absence of oxygen. Both of these numbers are consistent with expectation for oxygen quenching of a triplet state.74,82 | ||
Given that the lifetime of the S1 state of A-RC-A in oxygen-free toluene is 1.7 ns, the S1 state is so short-lived that it cannot be quenched by oxygen, even in an oxygen-saturated solution at atmospheric pressure. This can be confirmed in a calculation where one accepts that the quenching will occur at the diffusion controlled limit (i.e., kdiff = 3 × 1010 M−1 s−1). As such, we infer that the O2(a1Δg) precursor will be the A-RC-A triplet state (vide infra). We then chose to obtain information about the kinetics of the O2(a1Δg) precursor, again presumably the A-RC-A triplet state, using our time-resolved O2(a1Δg) phosphorescence data, as described below.
For the triplet-state-photosensitized production of O2(a1Δg) in homogeneous solutions, the intensity, I(t), of the time-resolved 1275 nm O2(a1Δg) → O2(X3Σg−) phosphorescence signal is generally modeled using a fitting function based on eqn (5)74,75,81
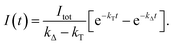 | (5) |
In Fig. 6d, we plot the values of kT thus obtained for A-RC-A against the oxygen concentration to yield the bimolecular rate constant for oxygen quenching of the O2(a1Δg) precursor. We determined oxygen concentrations using the mole fraction of oxygen in the bubbling gas (controlled by O2 and N2 flow meters) and Henry's Law constants published by Battino, et al.82 The value obtained for this quenching rate constant is (1.3 ± 0.1) × 109 M−1 s−1. As an independent control for this study on A-RC-A, we performed the same experiment using PN as the O2(a1Δg) sensitizer (Fig. S17†), and the results obtained provide credence for our results on A-RC-A. Specifically, our data for the quenching of 3PN by oxygen yield a rate constant of (2.2 ± 0.2) × 109 M−1 s−1, which is consistent with published data.78
The data obtained from Fig. 6d are consistent with the following assignment: the O2(a1Δg) precursor upon irradiation of A-RC-A is a triplet state whose lifetime in the absence of oxygen is ∼9 μs.
From Fig. 6b, the values of the O2(a1Δg) lifetime obtained (i.e., kΔ−1 = 296 ± 3 μs) are shorter than what is expected for the solvent-mediated deactivation of O2(a1Δg ) in toluene-d8. For the latter, we independently recorded a value of 326 ± 3 μs using PN as the sensitizer with the same batch of toluene-d8 used for the A-RC-A experiments. Using eqn (6), and with the A-RC-A concentration of 1.7 × 10−5 M used in our experiments, we obtain a rate constant of ∼1.8 × 107 M−1 s−1 for the deactivation/removal of O2(a1Δg) by A-RC-A. Given the magnitude of this rate constant, it is likely that the mechanism for A-RC-A-mediated deactivation of O2(a1Δg) involves some charge transfer from A-RC-A to O2(a1Δg).74,80 Moreover, based on an A-RC-A bleaching experiment (Fig. S14†), a small component of this rate constant reflects a chemical reaction between A-RC-A and O2(a1Δg).
| kobs.with A-RC-AΔ = kobs.without A-RC-AΔ + kq[A-RC-A] | (6) |
We also considered the interesting possibility that the O2(a1Δg) precursor might possibly be the T2 state. However, our data indicate that the O2(a1Δg) precursor upon irradiation of A-RC-A has quite a long lifetime (∼9 μs obtained from the intercept of the plot in Fig. 6d) and, as such, it must be the T1 state, as spin-allowed internal conversion from T2 to T1 is expected to be quite rapid (vide supra).
Conclusions
We investigated the ultrafast photophysics and intersystem crossing (ISC) dynamics of two para-substituted 2,5-bis(phenylethynyl) RCPDs (D-RC-A and A-RC-A) using excitation-wavelength-dependent fs-TA measurements and TD-DFT calculations. The electronic relaxation channels of the S1 state were revealed in detail, including charge transfer, conformational relaxation, vibrational dephasing, and ISC. By calculating the thermodynamic barrier and spin–orbit coupling, plausible ISC channels were revealed using semi-classical Marcus theory, i.e., ISC is dominated by the thermally activated S1 → T2 channel. With weak metal–ligand interactions, the plausible ISC channels of RCPDs are largely affected by ISC barriers. Studies of the sensitization of O2(a1Δg) by A-RC-A give quantum yields ΦΔ of up to ∼0.3 at high oxygen concentrations, consistent with the rate of ISC being competitive with that of fluorescence. The relatively long lifetime of the triplet state responsible for sensitization of O2(a1Δg) of ∼9 μs indicates that it must be T1, being formed rapidly from T2. Our work, especially the paradigm on ISC dynamics, might provide useful insight into the behavior of other fluorescent emitters.Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Zilong Guo: conceptualization, methodology, investigation, data curation, formal analysis, visualization and writing original draft; Yaxin Wang: data curation, formal analysis and validation; Julia Heitmüller: data curation and formal analysis; Carolin Sieck: investigation and data curation; Andreas Prüfer: investigation and data curation; Philipp Ralle: investigation and data curation; Andreas Steffen: conceptualization, methodology, investigation, writing – review and editing; Petr Henke: methodology, data curation, formal analysis and validation; Peter R. Ogilby: methodology, supervision, and writing – review and editing; Todd B. Marder: conceptualization, formal analysis, funding acquisition, supervision, and writing – review and editing; Xiaonan Ma: conceptualization, formal analysis, funding acquisition, supervision, and writing – review and editing; Tobias Brixner: conceptualization, formal analysis, funding acquisition, supervision, and writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
X. M. thanks the National Key R&D Program of China (No. 2020YFA0714603 and 2020YFA0714604) for funding. T. B. M. thanks the Julius-Maximilians-Universität Würzburg for support.Notes and references
- D. M. Arias-Rotondo and J. K. McCusker, Chem. Soc. Rev., 2016, 45, 5803–5820 RSC.
- D. A. Nicewicz and D. W. C. MacMillan, Science, 2008, 322, 77–80 CrossRef CAS PubMed.
- F. Strieth-Kalthoff, M. J. James, M. Teders, L. Pitzer and F. Glorius, Chem. Soc. Rev., 2018, 47, 7190–7202 RSC.
- Y. Du, R. M. Pearson, C.-H. Lim, S. M. Sartor, M. D. Ryan, H. Yang, N. H. Damrauer and G. M. Miyake, Chem.–Eur. J., 2017, 23, 10962–10968 CrossRef CAS PubMed.
- X. Zhao, Y. Hou, L. Liu and J. Zhao, Energy Fuels, 2021, 35, 18942–18956 CrossRef CAS.
- K. Y. Zhang, H.-W. Liu, M.-C. Tang, A. W.-T. Choi, N. Zhu, X.-G. Wei, K.-C. Lau and K. K.-W. Lo, Inorg. Chem., 2015, 54, 6582–6593 CrossRef CAS PubMed.
- A. Kazama, Y. Imai, Y. Okayasu, Y. Yamada, J. Yuasa and S. Aoki, Inorg. Chem., 2020, 59, 6905–6922 CrossRef CAS PubMed.
- D. Siegmund, N. Lorenz, Y. Gothe, C. Spies, B. Geissler, P. Prochnow, P. Nuernberger, J. E. Bandow and N. Metzler-Nolte, Dalton Trans., 2017, 46, 15269–15279 RSC.
- K. Y. Zhang, P. Gao, G. Sun, T. Zhang, X. Li, S. Liu, Q. Zhao, K. K.-W. Lo and W. Huang, J. Am. Chem. Soc., 2018, 140, 7827–7834 CrossRef CAS PubMed.
- X. Zhang, Y. Hou, X. Xiao, X. Chen, M. Hu, X. Geng, Z. Wang and J. Zhao, Coord. Chem. Rev., 2020, 417, 213371 CrossRef CAS.
- D. Di, A. S. Romanov, L. Yang, J. M. Richter, J. P. H. Rivett, S. Jones, T. H. Thomas, M. Abdi Jalebi, R. H. Friend, M. Linnolahti, M. Bochmann and D. Credgington, Science, 2017, 356, 159–163 CrossRef CAS PubMed.
- S.-F. Wang, B.-K. Su, X.-Q. Wang, Y.-C. Wei, K.-H. Kuo, C.-H. Wang, S.-H. Liu, L.-S. Liao, W.-Y. Hung, L.-W. Fu, W.-T. Chuang, M. Qin, X. Lu, C. You, Y. Chi and P.-T. Chou, Nat. Photonics, 2022, 16, 843–850 CrossRef CAS.
- Y.-C. Wei, S. F. Wang, Y. Hu, L.-S. Liao, D.-G. Chen, K.-H. Chang, C.-W. Wang, S.-H. Liu, W.-H. Chan, J.-L. Liao, W.-Y. Hung, T.-H. Wang, P.-T. Chen, H.-F. Hsu, Y. Chi and P.-T. Chou, Nat. Photonics, 2020, 14, 570–577 CrossRef CAS.
- S.-F. Wang, D.-Y. Zhou, K.-H. Kuo, C.-H. Wang, C.-M. Hung, J. Yan, L.-S. Liao, W.-Y. Hung, Y. Chi and P.-T. Chou, Angew. Chem., Int. Ed., 2024, 63, e202317571 CrossRef CAS PubMed.
- M. Chergui, Acc. Chem. Res., 2015, 48, 801–808 CrossRef CAS PubMed.
- W. Gawelda, A. Cannizzo, V.-T. Pham, F. van Mourik, C. Bressler and M. Chergui, J. Am. Chem. Soc., 2007, 129, 8199–8206 CrossRef CAS PubMed.
- A. Cannizzo, F. van Mourik, W. Gawelda, G. Zgrablic, C. Bressler and M. Chergui, Angew. Chem., Int. Ed., 2006, 45, 3174–3176 CrossRef CAS PubMed.
- Ch. Bressler, C. Milne, V.-T. Pham, A. ElNahhas, R. M. van der Veen, W. Gawelda, S. Johnson, P. Beaud, D. Grolimund, M. Kaiser, C. N. Borca, G. Ingold, R. Abela and M. Chergui, Science, 2009, 323, 489–492 CrossRef CAS PubMed.
- Q. Sun, S. Mosquera-Vazquez, L. M. Lawson Daku, L. Guénée, H. A. Goodwin, E. Vauthey and A. Hauser, J. Am. Chem. Soc., 2013, 135, 13660–13663 CrossRef CAS PubMed.
- A. J. Atkins and L. González, J. Phys. Chem. Lett., 2017, 8, 3840–3845 CrossRef CAS PubMed.
- Y. Sun, S. Doria, X. Xiao, L. Bussotti, Y. Li, J. Zhao and M. D. Donato, J. Organomet. Chem., 2024, 1006, 123004 CrossRef CAS.
- J. Moll, R. Naumann, L. Sorge, C. Förster, N. Gessner, L. Burkhardt, N. Ugur, P. Nuernberger, W. Seidel, C. Ramanan, M. Bauer and K. Heinze, Chem.–Eur. J., 2022, 28, e202201858 CrossRef CAS PubMed.
- R. D. Dill, R. I. Portillo, S. G. Shepard, M. P. Shores, A. K. Rappé and N. H. Damrauer, Inorg. Chem., 2020, 59, 14706–14715 CrossRef CAS PubMed.
- S. M. Fatur, S. G. Shepard, R. F. Higgins, M. P. Shores and N. H. Damrauer, J. Am. Chem. Soc., 2017, 139, 4493–4505 CrossRef CAS PubMed.
- C. Sieck, D. Sieh, M. Sapotta, M. Haehnel, K. Edkins, A. Lorbach, A. Steffen and T. B. Marder, J. Organomet. Chem., 2017, 847, 184–192 CrossRef CAS.
- J. P. Rourke, A. S. Batsanov, J. A. K. Howard and T. B. Marder, Chem. Commun., 2001, 2626–2627 RSC.
- A. Steffen, R. M. Ward, M. G. Tay, R. M. Edkins, F. Seeler, M. van Leeuwen, L.-O. Pålsson, A. Beeby, A. S. Batsanov, J. A. K. Howard and T. B. Marder, Chem.–Eur. J., 2014, 20, 3652–3666 CrossRef CAS PubMed.
- A. Steffen, K. Costuas, A. Boucekkine, M.-H. Thibault, A. Beeby, A. S. Batsanov, A. Charaf-Eddin, D. Jacquemin, J.-F. Halet and T. B. Marder, Inorg. Chem., 2014, 53, 7055–7069 CrossRef CAS PubMed.
- K. Li, Y. Chen, J. Wang and C. Yang, Coord. Chem. Rev., 2021, 433, 213755 CrossRef CAS.
- A. Steffen, M. G. Tay, A. S. Batsanov, J. A. K. Howard, A. Beeby, K. Q. Vuong, X.-Z. Sun, M. W. George and T. B. Marder, Angew. Chem., Int. Ed., 2010, 122, 2399–2403 CrossRef.
- C. Sieck, M. G. Tay, M.-H. Thibault, R. M. Edkins, K. Costuas, J.-F. Halet, A. S. Batsanov, M. Haehnel, K. Edkins, A. Lorbach, A. Steffen and T. B. Marder, Chem.–Eur. J., 2016, 22, 10523–10532 CrossRef CAS PubMed.
- T. Kumpulainen, B. Lang, A. Rosspeintner and E. Vauthey, Chem. Rev., 2017, 117, 10826–10939 CrossRef CAS PubMed.
- O. P. Dimitriev, Chem. Rev., 2022, 122, 8487–8593 CrossRef CAS PubMed.
- V. Lawetz, G. Orlandi and W. Siebrand, J. Chem. Phys., 1972, 56, 4058–4072 CrossRef CAS.
- G. W. Robinson and R. P. Frosch, J. Chem. Phys., 1963, 38, 1187–1203 CrossRef CAS.
- P. K. Samanta, D. Kim, V. Coropceanu and J.-L. Brédas, J. Am. Chem. Soc., 2017, 139, 4042–4051 CrossRef CAS PubMed.
- J.-L. Brédas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2004, 104, 4971–5004 CrossRef PubMed.
- K. Schmidt, S. Brovelli, V. Coropceanu, D. Beljonne, J. Cornil, C. Bazzini, T. Caronna, R. Tubino, F. Meinardi, Z. Shuai and J.-L. Brédas, J. Phys. Chem. A, 2007, 111, 10490–10499 CrossRef CAS PubMed.
- M. Bixon and J. Jortner, in Advances in Chemical Physics, John Wiley & Sons, Ltd, 1999, pp. 35–202 Search PubMed.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, Bioenerg., 1985, 811, 265–322 CrossRef CAS.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–610 CrossRef CAS.
- Y. Liu, M. Lin and Y. Zhao, J. Phys. Chem. A, 2017, 121, 1145–1152 CrossRef CAS PubMed.
- J. Stubbe, D. G. Nocera, C. S. Yee and M. C. Y. Chang, Chem. Rev., 2003, 103, 2167–2202 CrossRef CAS PubMed.
- E. Y.-T. Li, T.-Y. Jiang, Y. Chi and P.-T. Chou, Phys. Chem. Chem. Phys., 2014, 16, 26184–26192 RSC.
- T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Chem. Rev., 2018, 118, 6975–7025 CrossRef CAS PubMed.
- V. Pomogaev, S. Chiodo, K. Ruud, R. Kuznetsova and P. Avramov, J. Phys. Chem. C, 2020, 124, 11100–11109 CrossRef CAS.
- N. Aizawa, Y. Harabuchi, S. Maeda and Y.-J. Pu, Nat. Commun., 2020, 11, 3909 CrossRef CAS PubMed.
- K. Li, G. S. M. Tong, J. Yuan, C. Ma, L. Du, C. Yang, W.-M. Kwok, D. L. Phillips and C.-M. Che, Inorg. Chem., 2020, 59, 14654–14665 CrossRef CAS PubMed.
- Q. Zhu, S. Feng, X. Guo, X. Chen and J. Zhang, Spectrochim. Acta, Part A, 2019, 221, 117214 CrossRef CAS PubMed.
- X. Ma, J. Maier, M. Wenzel, A. Friedrich, A. Steffen, T. B. Marder, R. Mitrić and T. Brixner, Chem. Sci., 2020, 11, 9198–9208 RSC.
- A. O. Lykhin and S. A. Varganov, Phys. Chem. Chem. Phys., 2020, 22, 5500–5508 RSC.
- G. A. Zalesskaya, D. L. Yakovlev, E. G. Sambor and N. N. Bely, Phys. Chem. Chem. Phys., 2002, 4, 5634–5639 RSC.
- Y. Ide and T. Hikida, Chem. Phys., 1995, 194, 159–166 CrossRef CAS.
- K. Artmann, C. H. Pollok, C. Merten and P. Nuernberger, Phys. Chem. Chem. Phys., 2022, 24, 30017–30026 RSC.
- X. Niu, Z. Kuang, M. Planells, Y. Guo, N. Robertson and A. Xia, Phys. Chem. Chem. Phys., 2020, 22, 15743–15750 RSC.
- Z. Kuang, G. He, H. Song, X. Wang, Z. Hu, H. Sun, Y. Wan, Q. Guo and A. Xia, J. Phys. Chem. C, 2018, 122, 3727–3737 CrossRef CAS.
- Y. Wang, Z. Guo, Y. Gao, Y. Tian, Y. Deng, X. Ma and W. Yang, J. Phys. Chem. Lett., 2022, 13, 6664–6673 CrossRef CAS PubMed.
- Y. Wang, Y. Tian, Y. Gao, Z. Guo, Z. Xue, Y. Han, W. Yang and X. Ma, J. Phys. Chem. Lett., 2023, 14, 9665–9676 CrossRef CAS PubMed.
- A. Barak, N. Dhiman, F. Sturm, F. Rauch, Y. A. Lakshmanna, K. S. Findlay, A. Beeby, T. B. Marder and S. Umapathy, ChemPhotoChem, 2022, 6, e202200146 CrossRef CAS.
- A. Barak, N. Dhiman, F. Sturm, F. Rauch, Y. A. Lakshmanna, K. S. Findlay, A. Beeby, T. B. Marder and S. Umapathy, J. Phys. Chem. C, 2023, 127, 5855–5865 CrossRef CAS.
- W. Zhang, H. Song, J. Kong, Z. Kuang, M. Li, Q. Guo, C. Chen and A. Xia, J. Phys. Chem. C, 2019, 123, 19322–19332 CrossRef CAS.
- Y. Gao, Y. Wang, Z. Guo, Y. Wan, C. Li, B. Yang, W. Yang and X. Ma, J. Phys. Chem. B, 2022, 126, 2729–2739 CrossRef CAS PubMed.
- Y. Gao, Y. Wang, Z. Guo, Y. Wan, Z. Xue, Y. Han, W. Yang and X. Ma, Chem. Sci., 2024, 15, 6410–6420 RSC.
- Y. Lee, R. M. Malamakal, D. M. Chenoweth and J. M. Anna, J. Phys. Chem. Lett., 2020, 11, 877–884 CrossRef CAS PubMed.
- I. E. Serdiuk, M. Mońka, K. Kozakiewicz, B. Liberek, P. Bojarski and S. Y. Park, J. Phys. Chem. B, 2021, 125, 2696–2706 CrossRef CAS PubMed.
- M. Mońka, I. E. Serdiuk, K. Kozakiewicz, E. Hoffman, J. Szumilas, A. Kubicki, S. Y. Park and P. Bojarski, J. Mater. Chem. C, 2022, 10, 7925–7934 RSC.
- R. Schira and C. Latouche, Dalton Trans., 2021, 50, 746–753 RSC.
- Y. Guo, L. Zhang and Z. Qu, Molecules, 2023, 28, 3257 CrossRef CAS PubMed.
- J.-P. Malrieu and G. Trinquier, J. Chem. Phys., 2016, 144, 211101 CrossRef PubMed.
- C. M. Marian, Annu. Rev. Phys. Chem., 2021, 72, 617–640 CrossRef CAS PubMed.
- C. M. Marian, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 187–203 CAS.
- K. Božinović, D. Nestić, E. Michail, M. Ferger, M. Košćak, C. Lambert, D. Majhen, T. B. Marder and I. Piantanida, J. Photochem. Photobiol., B, 2022, 234, 112523 CrossRef PubMed.
- M. Ferger, C. Roger, E. Köster, F. Rauch, S. Lorenzen, I. Krummenacher, A. Friedrich, M. Košćak, D. Nestić, H. Braunschweig, C. Lambert, I. Piantanida and T. B. Marder, Chem.–Eur. J., 2022, 28, e202201130 CrossRef CAS PubMed.
- M. Bregnhøj, F. Thorning and P. R. Ogilby, Chem. Rev., 2024 DOI:10.1021/acs.chemrev.4c00105.
- M. Westberg, L. Holmegaard, F. M. Pimenta, M. Etzerodt and P. R. Ogilby, J. Am. Chem. Soc., 2015, 137, 1632–1642 CrossRef CAS PubMed.
- M. Bregnhøj, M. Prete, V. Turkovic, A. U. Petersen, M. B. Nielsen, M. Madsen and P. R. Ogilby, Methods Appl. Fluoresc., 2019, 8, 014001 CrossRef PubMed.
- R. Schmidt, C. Tanielian, R. Dunsbach and C. Wolff, J. Photochem. Photobiol., A, 1994, 79, 11–17 CrossRef CAS.
- C. Martí, O. Jürgens, O. Cuenca, M. Casals and S. Nonell, J. Photochem. Photobiol., A, 1996, 97, 11–18 CrossRef.
- F. Wilkinson, W. P. Helman and A. B. Ross, J. Phys. Chem. Ref. Data, 1993, 22, 113–262 CrossRef CAS.
- C. Schweitzer and R. Schmidt, Chem. Rev., 2003, 103, 1685–1758 CrossRef CAS PubMed.
- P. R. Ogilby, Chem. Soc. Rev., 2010, 39, 3181–3209 RSC.
- R. Battino, T. R. Rettich and T. Tominaga, J. Phys. Chem. Ref. Data, 1983, 12, 163–178 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc04306e |
| This journal is © The Royal Society of Chemistry 2024 |