Open Access Article
Open Access ArticleTheoretical insights into the generation and reactivity of hydride on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/h2_char_0031_0304.gif) 0) surface†
0) surface†
Xian-Yang
Zhang
a,
Zhi-Qiang
Wang
*a and
Xue-Qing
Gong
 *b
*b
aState Key Laboratory of Green Chemical Engineering and Industrial Catalysis, Centre for Computational Chemistry and Research Institute of Industrial Catalysis, School of Chemistry and Molecular Engineering, East China University of Science and Technology, 130 Meilong Road, Shanghai, 200237, China. E-mail: zhiqiangwang@ecust.edu.cn
bSchool of Chemistry and Chemical Engineering, Shanghai Jiao Tong University, 800 Dongchuan Road, Shanghai, 200240, China. E-mail: xqgong@sjtu.edu.cn
First published on 2nd August 2024
Abstract
ZnO is an important catalytic material for CO/CO2 hydrogenation. In this work, the pristine ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) and the surfaces with Zn–O dimer vacancies (ZnO(10
0) and the surfaces with Zn–O dimer vacancies (ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV) and oxygen vacancies are calculated. We find that the hydride (H−) species can be generated via heterolytic H2 dissociation on these surfaces, and that ZnO(10
0)–(Zn–O)DiV) and oxygen vacancies are calculated. We find that the hydride (H−) species can be generated via heterolytic H2 dissociation on these surfaces, and that ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV only needs to overcome the energy barrier of ∼0.10 eV. This is because the ZnO system has flexible orbitals for electron storage and release and the low-coordinated Zn3c atoms at the defect sites can form stable Zn–H− covalent bonds with high symmetry. Flexible Zn orbitals also impart the unique feature of activating multiple electrophilic adsorbates simultaneously as excess electrons exist. Moreover, we show that the covalent Zn–H− species can regulate the catalytic activity and selectivity for CO2 hydrogenation by preferentially producing *HCOO intermediates at Zn–O dimer vacancies. These results may help in the design of efficient Zn-based hydrogenation catalysts.
0)–(Zn–O)DiV only needs to overcome the energy barrier of ∼0.10 eV. This is because the ZnO system has flexible orbitals for electron storage and release and the low-coordinated Zn3c atoms at the defect sites can form stable Zn–H− covalent bonds with high symmetry. Flexible Zn orbitals also impart the unique feature of activating multiple electrophilic adsorbates simultaneously as excess electrons exist. Moreover, we show that the covalent Zn–H− species can regulate the catalytic activity and selectivity for CO2 hydrogenation by preferentially producing *HCOO intermediates at Zn–O dimer vacancies. These results may help in the design of efficient Zn-based hydrogenation catalysts.
Introduction
As a commonly used catalytic material, ZnO often plays crucial roles in catalyzing hydrogenation reactions, such as CO2 selective hydrogenation to methanol and conversion of syngas (mixture gas of CO/CO2/H2) to light olefins.1–4 A deep understanding of its catalytic activities would help construct Zn-based catalysts with better performances for these reactions, which may also contribute to the control of fossil fuel usage and the realization of carbon neutrality. However, a lot of debate still remains regarding the nature of the active site for the selective hydrogenation reactions.5–8 For example, for the CO2 selective hydrogenation catalyzed by the Cu/ZnO/Al2O3 catalyst, Behrens et al.9 suggested that the Cu–Zn alloys could form and promote the synthetic activity toward methanol, while the metal–oxide interface formed by Cu and ZnO was proposed as the active site by Kattel et al.10 Chen et al.11 found that the Cu/ZnO/ZrO2 catalyst can also be used for CO2 selective hydrogenation reactions, and they pointed out that the ZnO–ZrO2 interface is the active site, while the copper species plays the role of activating H2 and providing hydrogen for the reaction. In addition, Li and co-workers12 found that the single Cu atoms loaded on the ZnO surface can catalyze the selective hydrogenation of CO2 to methanol with the selectivity of ∼99.4%, and they also suggested that the water vapor in the system can act as a bridge between surface H and CO2 intermediates and has the regulatory role of increasing methanol selectivity. In general, catalysts containing ZnO have been extensively used in the selective hydrogenation reactions of CO2,8–13 and exploring its reaction mechanism is essential for further understanding their key features, especially the actual active site.In fact, there have already been many studies about selective hydrogenation reactions on clean ZnO surfaces, which were mainly focused on the activation mechanisms of H2 and CO2.13–15 Wöll and co-workers16 studied the CO2 adsorption and activation on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface with infrared reflection absorption spectroscopy (IRRAS) and showed that CO2 can be adsorbed along the [0001] direction and form the carbonate (CO3δ−) species. Ling et al.17 obtained the scanning tunneling microscope (STM) images of the heterolytically dissociated H2 on the ZnO(10
0) surface with infrared reflection absorption spectroscopy (IRRAS) and showed that CO2 can be adsorbed along the [0001] direction and form the carbonate (CO3δ−) species. Ling et al.17 obtained the scanning tunneling microscope (STM) images of the heterolytically dissociated H2 on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface under ambient pressure, and the adsorption structure was expected to be beneficial to the stabilization of the formed active H species. Peng and co-workers18 examined the mechanism of H2 activation on ZnO nanorods with and without surface oxygen vacancies by applying 17O nuclear magnetic resonance spectroscopy (NMR), and they found that more hydride species can be produced through homolytic and heterolytic dissociation at the oxygen vacancy sites of the reduced ZnO(10
0) surface under ambient pressure, and the adsorption structure was expected to be beneficial to the stabilization of the formed active H species. Peng and co-workers18 examined the mechanism of H2 activation on ZnO nanorods with and without surface oxygen vacancies by applying 17O nuclear magnetic resonance spectroscopy (NMR), and they found that more hydride species can be produced through homolytic and heterolytic dissociation at the oxygen vacancy sites of the reduced ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0). Theoretically, Tang et al.19 performed systematic on-site Coulomb interaction corrected density functional theory (DFT+U) calculations of the adsorption of CO2 and found that the adsorbed CO2 molecules tend to form linear structures on the polar ZnO facets (such as {0001} and {000
0). Theoretically, Tang et al.19 performed systematic on-site Coulomb interaction corrected density functional theory (DFT+U) calculations of the adsorption of CO2 and found that the adsorbed CO2 molecules tend to form linear structures on the polar ZnO facets (such as {0001} and {000![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) }), while the bending structures are produced on the nonpolar ZnO facets (such as {10
}), while the bending structures are produced on the nonpolar ZnO facets (such as {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}, {11
0}, {11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0} and {11
0} and {11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1}). Li and co-workers20 calculated the pathways of H2 activation on the pristine ZnO(10
1}). Li and co-workers20 calculated the pathways of H2 activation on the pristine ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface, and they determined the heterolytic dissociation of H2 rather than the homolytic one. Furthermore, through DFT calculations, Zhao et al.21 located the complete reaction routes of CO hydrogenation to methanol on the Zn-terminated ZnO(0001) surface and showed that CO would follow the route of being consecutively hydrogenated to formyl (HCO), formaldehyde (H2CO), and methoxy (H3CO) before the formation of methanol. Thus, we can find that the catalytic reactions at ZnO are closely related to its surface structures. However, the relationship between the unique electronic properties of ZnO and the catalytic activities in selective hydrogenation reactions has not been thoroughly investigated.
0) surface, and they determined the heterolytic dissociation of H2 rather than the homolytic one. Furthermore, through DFT calculations, Zhao et al.21 located the complete reaction routes of CO hydrogenation to methanol on the Zn-terminated ZnO(0001) surface and showed that CO would follow the route of being consecutively hydrogenated to formyl (HCO), formaldehyde (H2CO), and methoxy (H3CO) before the formation of methanol. Thus, we can find that the catalytic reactions at ZnO are closely related to its surface structures. However, the relationship between the unique electronic properties of ZnO and the catalytic activities in selective hydrogenation reactions has not been thoroughly investigated.
In this work, the wurtzite ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface, which has a rather low surface energy and exists under real catalytic conditions,9 was constructed for the DFT calculations. Both the pristine and defective surfaces were considered. Specifically, the surface defect structures were confirmed by the calculated p–T phase diagrams.6,11,22 Moreover, their electronic structures were also carefully studied, and the density of states (DOS) calculations showed a shrinkage of the unfilled dsp hybridized orbitals when excess electrons are present on the surfaces; at the same time, no new occupied states appear under the Fermi energy level (EF), indicating a unique strategy of electron storage and release by ZnO. Systematic calculations were then performed to investigate the generation of active H species on these surfaces and their reactivities in the CO2 selective hydrogenation reactions. It was found that the various vacancy defects are beneficial to the stabilization of the hydride species (H−), which can be generated through the heterolytic dissociation of H2. Interestingly, the calculated results also showed that the occurrence of H+ (proton) from heterolytic H2 dissociation on the ZnO(10
0) surface, which has a rather low surface energy and exists under real catalytic conditions,9 was constructed for the DFT calculations. Both the pristine and defective surfaces were considered. Specifically, the surface defect structures were confirmed by the calculated p–T phase diagrams.6,11,22 Moreover, their electronic structures were also carefully studied, and the density of states (DOS) calculations showed a shrinkage of the unfilled dsp hybridized orbitals when excess electrons are present on the surfaces; at the same time, no new occupied states appear under the Fermi energy level (EF), indicating a unique strategy of electron storage and release by ZnO. Systematic calculations were then performed to investigate the generation of active H species on these surfaces and their reactivities in the CO2 selective hydrogenation reactions. It was found that the various vacancy defects are beneficial to the stabilization of the hydride species (H−), which can be generated through the heterolytic dissociation of H2. Interestingly, the calculated results also showed that the occurrence of H+ (proton) from heterolytic H2 dissociation on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface can be involved in activating the adsorbed H on Zn to the hydride species, and it can also help enhance the adsorption of CO2 as well. This work revealed why the ZnO surface and its defects are favorable for catalyzing hydrogenation reactions as well as the ‘multifunction role’ of surface H in these reactions. It may provide some assistance for the rational design of Zn-based catalysts with high activities and selectivities.
0) surface can be involved in activating the adsorbed H on Zn to the hydride species, and it can also help enhance the adsorption of CO2 as well. This work revealed why the ZnO surface and its defects are favorable for catalyzing hydrogenation reactions as well as the ‘multifunction role’ of surface H in these reactions. It may provide some assistance for the rational design of Zn-based catalysts with high activities and selectivities.
Computational methods
In this work, all spin-polarized DFT calculations were carried out using the Vienna Ab initio Simulation Package (VASP).23 The projector augmented wave (PAW)24 method and the Perdew–Burke–Ernzerhof (PBE)25 functional under the generalized gradient approximation (GGA)26 were applied throughout the geometry and energy calculations. The kinetic energy cut-off was set to 400 eV, with H(1s), C(2s, 2p), O(2s, 2p) and Zn(3d, 4s) being treated as valence electrons. The force threshold in structure optimization was 0.02 eV Å−1. By adopting these calculation settings, the optimized lattice constants of ZnO are a = b = 3.26 Å and c = 5.24 Å, which is in good agreement with the experimental values of a = b = 3.25 Å, and c = 5.21 Å.27 For the model construction, we built a p(4 × 3) surface slab containing three O–Zn atomic layers for the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface, and the top two layers were allowed to fully relax, while the bottom O–Zn layer was kept fixed to mimic the bulk region. We used a large vacuum of ∼12 Å to eliminate the interactions between neighboring slabs, and hence a k-point mesh of 2 × 2 × 1 was applied to the system. Since the valence shells of Zn are filled with d and s electrons, which are strongly correlated, the properties relevant to the electronic structures were calculated by the hybrid functional raised by Heyd, Scuseria and Ernzerhof (HSE06),30 which may give reliable electronic information and avoid errors from the unique deep-lying 3d electron distribution of Zn.20,31
0) surface, and the top two layers were allowed to fully relax, while the bottom O–Zn layer was kept fixed to mimic the bulk region. We used a large vacuum of ∼12 Å to eliminate the interactions between neighboring slabs, and hence a k-point mesh of 2 × 2 × 1 was applied to the system. Since the valence shells of Zn are filled with d and s electrons, which are strongly correlated, the properties relevant to the electronic structures were calculated by the hybrid functional raised by Heyd, Scuseria and Ernzerhof (HSE06),30 which may give reliable electronic information and avoid errors from the unique deep-lying 3d electron distribution of Zn.20,31
The transition states (TSs) of surface reactions were located using a constrained optimization scheme and were verified when (i) all forces on the relaxed atoms vanish and (ii) the total energy is a maximum along the reaction coordinate, but it is a minimum with respect to the rest of the degrees of freedom.32,33
The adsorption energies of different species (X) on the surface (Eads(X)) were calculated with:
| Eads(X) = −(EX/slab − Eslab − EX) | (1) |
In addition, we also calculated the formation energies of different defects of ZnO surfaces.34 Firstly, the oxygen vacancy formation energy 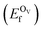 was calculated as:
was calculated as:
 | (2) |
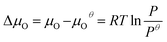 | (3) |
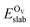 is the total energy of the surface containing a single oxygen vacancy,
is the total energy of the surface containing a single oxygen vacancy, 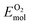 is the energy of a gas-phase O2 molecule and Epristineslab is the total energy of the pristine ZnO surface. To compare the formation energies of different defects, we used the chemical potential of oxygen in the gas phase to align the environmental effects.
is the energy of a gas-phase O2 molecule and Epristineslab is the total energy of the pristine ZnO surface. To compare the formation energies of different defects, we used the chemical potential of oxygen in the gas phase to align the environmental effects. 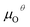 is the standard chemical potential of O, and R, T, and p represent the ideal gas constant, temperature, and the partial pressure of O2, respectively. Secondly, the Zn–O dimer vacancy formation energy
is the standard chemical potential of O, and R, T, and p represent the ideal gas constant, temperature, and the partial pressure of O2, respectively. Secondly, the Zn–O dimer vacancy formation energy 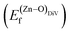 was calculated as:
was calculated as: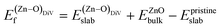 | (4) |
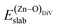 is the total energy of the surface with a Zn–O dimer vacancy, and EZnObulk is obtained by calculating the energy of a ‘Zn–O’ group in the bulk wurtzite-ZnO. Notably, we can find that the formation energy of the Zn–O dimer vacancy is constant under various conditions of oxygen potential. Finally, the zinc vacancy formation energy
is the total energy of the surface with a Zn–O dimer vacancy, and EZnObulk is obtained by calculating the energy of a ‘Zn–O’ group in the bulk wurtzite-ZnO. Notably, we can find that the formation energy of the Zn–O dimer vacancy is constant under various conditions of oxygen potential. Finally, the zinc vacancy formation energy 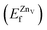 was calculated according to
was calculated according to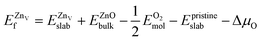 | (5) |
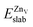 is the total energy of the surface with a single zinc vacancy.
is the total energy of the surface with a single zinc vacancy.
Notably, the choice for the size of the slab model has been systematically tested by the formation energy of different defects (Fig. S1†), and it was found that the formation energies of the various types of surface defects (OV and (Zn–O)DiV) largely converged with the size above p(4 × 3) (θ = 1/12 ML), which is also in agreement with previous reports.28,29
Results and discussion
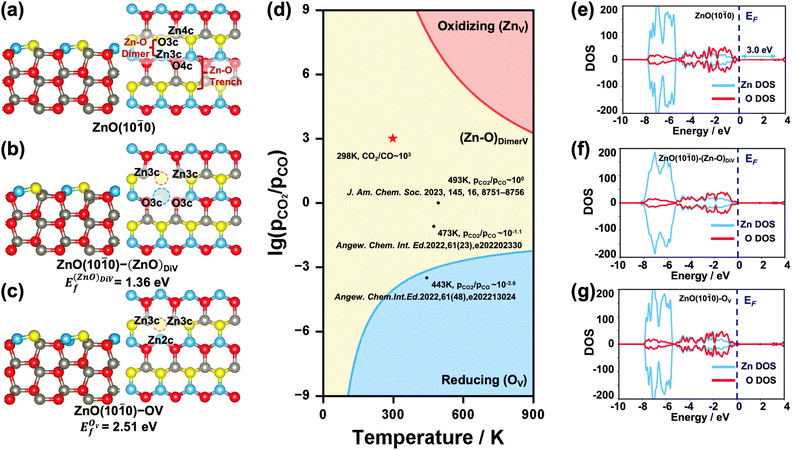
Pristine and defect ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/h3_char_0031_0304.gif) 0) surfaces
0) surfaces
The {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0} facet is the most stable one for ZnO in the hexagonal wurtzite phase.35 The surface Zn and O atoms on the ZnO(10
0} facet is the most stable one for ZnO in the hexagonal wurtzite phase.35 The surface Zn and O atoms on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface are three-fold coordinated (denoted as Zn3c and O3c), while the Zn and O atoms in the subsurface and bulk region are four-fold coordinated (denoted as Zn4c and O4c). The exposed surface Zn–O pairs can be recognized as the Zn–O dimer and Zn–O trench, as shown in Fig. 1a. When an O or Zn atom or Zn–O dimer is removed from the surface, the coordination number of the surface/subsurface Zn/O around the vacancy is reduced to 2 or 3. Considering that under real reaction conditions, the ZnO surface may have these different forms of defects,28,36i.e., zinc vacancy (denoted as ZnV), Zn–O dimer vacancy (denoted as (Zn–O)DiV, see Fig. 1b) and oxygen vacancy (denoted as OV, see Fig. 1c), we first systematically investigated their relative stabilities by calculating the formation energies of different defect ZnO(10
0) surface are three-fold coordinated (denoted as Zn3c and O3c), while the Zn and O atoms in the subsurface and bulk region are four-fold coordinated (denoted as Zn4c and O4c). The exposed surface Zn–O pairs can be recognized as the Zn–O dimer and Zn–O trench, as shown in Fig. 1a. When an O or Zn atom or Zn–O dimer is removed from the surface, the coordination number of the surface/subsurface Zn/O around the vacancy is reduced to 2 or 3. Considering that under real reaction conditions, the ZnO surface may have these different forms of defects,28,36i.e., zinc vacancy (denoted as ZnV), Zn–O dimer vacancy (denoted as (Zn–O)DiV, see Fig. 1b) and oxygen vacancy (denoted as OV, see Fig. 1c), we first systematically investigated their relative stabilities by calculating the formation energies of different defect ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces with respect to the oxygen chemical potentials (ΔμO) (Ef − ΔμO, Fig. S2†). The plotted equilibrium phase diagrams of these surfaces under different (pCO2/pCO) and T (Fig. 1d) showed that, consistent with the previously reported stable structures,34 both (Zn–O)DiV and OV surfaces (ZnO(10
0) surfaces with respect to the oxygen chemical potentials (ΔμO) (Ef − ΔμO, Fig. S2†). The plotted equilibrium phase diagrams of these surfaces under different (pCO2/pCO) and T (Fig. 1d) showed that, consistent with the previously reported stable structures,34 both (Zn–O)DiV and OV surfaces (ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV and ZnO(10
0)–(Zn–O)DiV and ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–OV, see Fig. 1b and c) can occur favorably under reaction conditions (T = 400–900 K, (pCO2/pCO) = 10−3–103).37,38 The (Zn–O)DiV is relatively more likely to form under atmospheric CO2/CO pressure ratio ((pCO2/pCO) ∼ 103, with the corresponding O2 partial pressure being 0.2 bar). In addition, it needs to be noted that the formation of an O vacancy will leave 2 excess electrons in the ZnO(10
0)–OV, see Fig. 1b and c) can occur favorably under reaction conditions (T = 400–900 K, (pCO2/pCO) = 10−3–103).37,38 The (Zn–O)DiV is relatively more likely to form under atmospheric CO2/CO pressure ratio ((pCO2/pCO) ∼ 103, with the corresponding O2 partial pressure being 0.2 bar). In addition, it needs to be noted that the formation of an O vacancy will leave 2 excess electrons in the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–OV system (Fig. 1c), which could help the adsorption of electrophilic species and its transformation into negatively charged species (such as the hydride).39,40 When the Zn–O dimer vacancy occurs, the ZnO(10
0)–OV system (Fig. 1c), which could help the adsorption of electrophilic species and its transformation into negatively charged species (such as the hydride).39,40 When the Zn–O dimer vacancy occurs, the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV surface remains charge balanced, though this defect surface obviously becomes more open for the adsorption and activation of relevant reactants.
0)–(Zn–O)DiV surface remains charge balanced, though this defect surface obviously becomes more open for the adsorption and activation of relevant reactants.
We also investigated the electronic properties of the pristine and various defect ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces by calculating the density of states (DOS) (Fig. 1e–g). The calculated band gap of the pristine ZnO(10
0) surfaces by calculating the density of states (DOS) (Fig. 1e–g). The calculated band gap of the pristine ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface was 3.0 eV, which largely agrees with the experimental result (3.3 eV).41 Further analysis of the partial DOS (pDOS) showed that most of the Zn 3d electrons lay deeply below the Fermi energy level (EF), clearly caused by the fully filled orbitals with strong correlations,42 and it also hints at a unique bonding pattern with other species. Besides, from the calculated DOS of the defect surface, we can clearly see that the bonding symmetry change caused by the Zn–O dimer vacancy also has a strong influence on the shape of Zn 3d orbitals (Fig. 1f and S2a†), which are broadened obviously. By contrast, the excess electrons contributed by the O vacancy do shrink the unoccupied dsp hybrid orbital (Fig. S3a†), but they do not change the shape of the Zn orbitals or bring about a new electronic state under EF, indicating a new way of storing electrons that is different from that of some reducible metal oxides,43,44 whose extra electrons would be localized at specific atomic orbitals. In fact, we have also determined that when the 2 electrons resulting from the formation of an oxygen vacancy are forced to be localized at the oxygen vacancy site, the corresponding vacancy formation energy is 0.70 eV higher than that when the 2 electrons are delocalized in the system (Fig. 2c and S3b†); and the pDOS calculation (Fig. S3b†) suggested that these excess electrons would exist within the hybrid orbitals throughout the ZnO bulk, just like the electrons from other atoms. Thus, the Zn orbitals appear to be rather flexible for electron storage.
0) surface was 3.0 eV, which largely agrees with the experimental result (3.3 eV).41 Further analysis of the partial DOS (pDOS) showed that most of the Zn 3d electrons lay deeply below the Fermi energy level (EF), clearly caused by the fully filled orbitals with strong correlations,42 and it also hints at a unique bonding pattern with other species. Besides, from the calculated DOS of the defect surface, we can clearly see that the bonding symmetry change caused by the Zn–O dimer vacancy also has a strong influence on the shape of Zn 3d orbitals (Fig. 1f and S2a†), which are broadened obviously. By contrast, the excess electrons contributed by the O vacancy do shrink the unoccupied dsp hybrid orbital (Fig. S3a†), but they do not change the shape of the Zn orbitals or bring about a new electronic state under EF, indicating a new way of storing electrons that is different from that of some reducible metal oxides,43,44 whose extra electrons would be localized at specific atomic orbitals. In fact, we have also determined that when the 2 electrons resulting from the formation of an oxygen vacancy are forced to be localized at the oxygen vacancy site, the corresponding vacancy formation energy is 0.70 eV higher than that when the 2 electrons are delocalized in the system (Fig. 2c and S3b†); and the pDOS calculation (Fig. S3b†) suggested that these excess electrons would exist within the hybrid orbitals throughout the ZnO bulk, just like the electrons from other atoms. Thus, the Zn orbitals appear to be rather flexible for electron storage.
Adsorption of a single H atom on different ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/h3_char_0031_0304.gif) 0) surfaces
0) surfaces
Previous studies showed that the hydride species is key to the CO/CO2 selective hydronation at metal oxides.45,46 To determine if one H adsorbed on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0), ZnO(10
0), ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–OV and ZnO(10
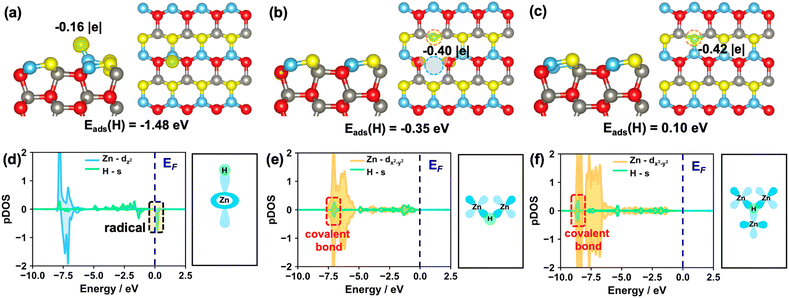
0)–OV and ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV surfaces can form a proton (H+), hydride (H−) or H radical (H˙), we performed the Bader charge analysis and calculated the corresponding spin charge density differences (Fig. 2 and S3†). Notably, the hydride species does not show net spin density, while for the H radical, it usually possesses a net spin density with the calculated Bader charge close to zero.
0)–(Zn–O)DiV surfaces can form a proton (H+), hydride (H−) or H radical (H˙), we performed the Bader charge analysis and calculated the corresponding spin charge density differences (Fig. 2 and S3†). Notably, the hydride species does not show net spin density, while for the H radical, it usually possesses a net spin density with the calculated Bader charge close to zero.
Firstly, we calculated the adsorption of one H atom at O sites on these surfaces. The calculated results showed that one electron from the H would preferentially transfer to the pristine and different defect ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces (Fig. S4†), and the corresponding Bader charges are +0.62, +0.63 and +0.66 |e| for the adsorbed H on the pristine, (Zn–O)DiV and OV surfaces, respectively, indicating that the proton species are formed. The calculated results also showed that the adsorption of the H atom at the O3c site on the ZnO(10
0) surfaces (Fig. S4†), and the corresponding Bader charges are +0.62, +0.63 and +0.66 |e| for the adsorbed H on the pristine, (Zn–O)DiV and OV surfaces, respectively, indicating that the proton species are formed. The calculated results also showed that the adsorption of the H atom at the O3c site on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV surface is exothermic by 1.28 eV. Such a favorable adsorption can be due to the fact that the adsorption location is rather open and the adsorbed H species can form the hydrogen bond with the neighboring O3c (the distance between O3c and H atoms is 2.05 Å, Fig. S4d†). The adsorption of one H atom at the O3c site on the ZnO(10
0)–(Zn–O)DiV surface is exothermic by 1.28 eV. Such a favorable adsorption can be due to the fact that the adsorption location is rather open and the adsorbed H species can form the hydrogen bond with the neighboring O3c (the distance between O3c and H atoms is 2.05 Å, Fig. S4d†). The adsorption of one H atom at the O3c site on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–OV surface was calculated to be exothermic by 0.71 eV only. This is mainly because the presence of the two excess electrons on the reduced ZnO(10
0)–OV surface was calculated to be exothermic by 0.71 eV only. This is mainly because the presence of the two excess electrons on the reduced ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface further increases the electron repulsion within the system. Notably, we can also find that the extra electron from an adsorbed H (Fig. S4c, f and i†) barely has any influence on the overall shape of the Zn orbitals of the various ZnO(10
0) surface further increases the electron repulsion within the system. Notably, we can also find that the extra electron from an adsorbed H (Fig. S4c, f and i†) barely has any influence on the overall shape of the Zn orbitals of the various ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces, which again suggests the flexibility of Zn orbitals in storing electrons.
0) surfaces, which again suggests the flexibility of Zn orbitals in storing electrons.
In addition, we also calculated the adsorption of one H atom at Zn sites on these surfaces. The results showed that the H species, as a radical, is barely adsorbed at the Zn site on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface since the adsorption is endothermic by 1.48 eV (Fig. 2a and d). By contrast, the H adsorbed on the ZnO(10
0) surface since the adsorption is endothermic by 1.48 eV (Fig. 2a and d). By contrast, the H adsorbed on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–OV surface can actually form three H–Zn bonds at the OV site, and it turns into a hydride species (Fig. 2c, the corresponding Bader charge is −0.42 |e|) with the exothermic adsorption energy of 0.10 eV. This result is largely consistent with the findings that the hydride species can form on some reduced metal oxide surfaces such as CeO2.39,45 For the adsorption of a single H atom at the Zn site on the ZnO(10
0)–OV surface can actually form three H–Zn bonds at the OV site, and it turns into a hydride species (Fig. 2c, the corresponding Bader charge is −0.42 |e|) with the exothermic adsorption energy of 0.10 eV. This result is largely consistent with the findings that the hydride species can form on some reduced metal oxide surfaces such as CeO2.39,45 For the adsorption of a single H atom at the Zn site on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV surface, the hydride, rather than a H radical, is also formed (Fig. 2b, the calculated Bader charge is −0.40 |e|), though this process is endothermic by 0.35 eV. In this case, the adsorbed H species would interact with the two Zn3c (Fig. 2e). Notably, the electronic analysis suggested that the hydrides on both the OV and (Zn–O)DiV surfaces occur via the covalent bonds contributed by the s electron from H and the multiple symmetric d electrons from Zn, in particular dx2−y2 (Fig. 2e and f), and the energy levels of the as-formed covalent Zn–H bonds at ZnO(10
0)–(Zn–O)DiV surface, the hydride, rather than a H radical, is also formed (Fig. 2b, the calculated Bader charge is −0.40 |e|), though this process is endothermic by 0.35 eV. In this case, the adsorbed H species would interact with the two Zn3c (Fig. 2e). Notably, the electronic analysis suggested that the hydrides on both the OV and (Zn–O)DiV surfaces occur via the covalent bonds contributed by the s electron from H and the multiple symmetric d electrons from Zn, in particular dx2−y2 (Fig. 2e and f), and the energy levels of the as-formed covalent Zn–H bonds at ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV and ZnO(10
0)–(Zn–O)DiV and ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)OV are far below EF.
0)–(Zn–O)OV are far below EF.
H2 dissociation on different ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/h3_char_0031_0304.gif) 0) surfaces
0) surfaces
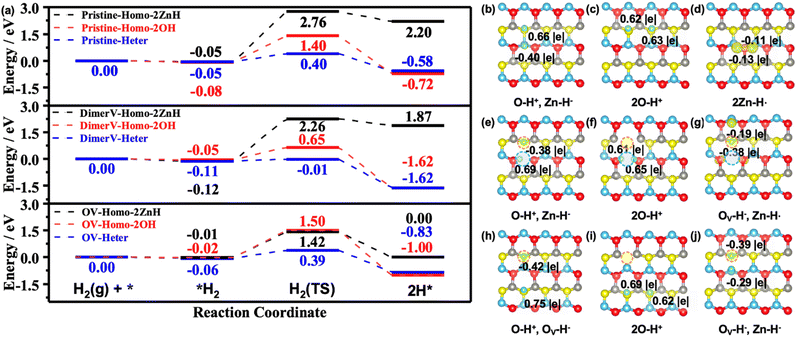
In real applications, the hydride species for selective hydrogenation reactions usually come from the dissociation of H2 molecules on the catalysts.42,47 Accordingly, we also systematically studied the possible pathways of the dissociative adsorption of H2 on the pristine and various defect ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces (Fig. 3, S5 and S6†), including the homolytic dissociation at (i) two O sites to produce two hydroxyl (O–H) groups or (ii) two Zn sites to produce two Zn–H species, as well as (iii) the heterolytic dissociation at the Zn and O sites for the formation of Zn–H and O–H species.
0) surfaces (Fig. 3, S5 and S6†), including the homolytic dissociation at (i) two O sites to produce two hydroxyl (O–H) groups or (ii) two Zn sites to produce two Zn–H species, as well as (iii) the heterolytic dissociation at the Zn and O sites for the formation of Zn–H and O–H species.
The calculated results showed that the homolytic dissociation of H2 to form two O–H species at O sites on the pristine, Zn–O dimer vacancies and oxygen vacancies of the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces needs to overcome the energy barriers of 1.48 eV, 0.70 eV and 1.52 eV (Fig. 3a and S6b, e and h†), respectively, and they are exothermic by 0.64 eV, 1.57 eV and 0.98 eV (Fig. 3a, c, f and i), respectively. Our results also showed that the homolytic H2 dissociation can produce two Zn–H species at adjacent Zn3c sites on the ZnO(10
0) surfaces needs to overcome the energy barriers of 1.48 eV, 0.70 eV and 1.52 eV (Fig. 3a and S6b, e and h†), respectively, and they are exothermic by 0.64 eV, 1.57 eV and 0.98 eV (Fig. 3a, c, f and i), respectively. Our results also showed that the homolytic H2 dissociation can produce two Zn–H species at adjacent Zn3c sites on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0), ZnO(10
0), ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV and ZnO(10
0)–(Zn–O)DiV and ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–OV surfaces, and the corresponding electronic analyses indicated that they are 2Zn–H˙, Zn–H˙ and Zn–H−, and OV–H− and Zn–H− species, respectively. Moreover, these processes need to overcome energy barriers as high as 2.81 eV, 2.38 eV and 1.43 eV, respectively (Fig. 3a and S6c, f and i†), and the calculated reaction energies also indicated that these processes are energetically unfavorable.
0)–OV surfaces, and the corresponding electronic analyses indicated that they are 2Zn–H˙, Zn–H˙ and Zn–H−, and OV–H− and Zn–H− species, respectively. Moreover, these processes need to overcome energy barriers as high as 2.81 eV, 2.38 eV and 1.43 eV, respectively (Fig. 3a and S6c, f and i†), and the calculated reaction energies also indicated that these processes are energetically unfavorable.
On the other hand, according to our calculated results, the heterolytic H2 dissociation on the different ZnO surfaces (ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0), ZnO(10
0), ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV and ZnO(10
0)–(Zn–O)DiV and ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–OV surfaces) can readily occur to form the Zn–H− and O–H species, which only need to overcome the small energy barriers of 0.45 eV, 0.10 eV and 0.45 eV (Fig. 3a and S6a, d and g†), respectively, and the corresponding processes are exothermic by 0.53 eV, 1.51 eV and 0.77 eV, which are consistent with those reported in previous experimental and theoretical studies.20,48,49 The stabilities could be attributed to the structural features of the transition states of the heterolytic H2 dissociations: the characteristic [H–O–Zn–H] four-membered ring at ZnO(10
0)–OV surfaces) can readily occur to form the Zn–H− and O–H species, which only need to overcome the small energy barriers of 0.45 eV, 0.10 eV and 0.45 eV (Fig. 3a and S6a, d and g†), respectively, and the corresponding processes are exothermic by 0.53 eV, 1.51 eV and 0.77 eV, which are consistent with those reported in previous experimental and theoretical studies.20,48,49 The stabilities could be attributed to the structural features of the transition states of the heterolytic H2 dissociations: the characteristic [H–O–Zn–H] four-membered ring at ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0), the [H–O–Zn–O–Zn–H] hexatomic ring at ZnO(10
0), the [H–O–Zn–O–Zn–H] hexatomic ring at ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV and a double [H–O–Zn–O–Zn–H] hexatomic ring at ZnO(10
0)–(Zn–O)DiV and a double [H–O–Zn–O–Zn–H] hexatomic ring at ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–OV.
0)–OV.
From the above results, we can find that H2 can be activated more readily through heterolytic dissociation rather than homolytic cleavage on the different ZnO surfaces, which is also consistent with the previously reported results on some other metal oxides.18,20,50 Specifically, among the different ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces, the (Zn–O)DiV surface is the most active one for the heterolytic H2 dissociation. This is because the low-coordinated O species around the ZnV site on the ZnO(10
0) surfaces, the (Zn–O)DiV surface is the most active one for the heterolytic H2 dissociation. This is because the low-coordinated O species around the ZnV site on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV surface are rather active for the transformation of the adsorbed H into stable protons, while the OV site on the (Zn–O)DiV surface can help produce the stable hydrides that interact with the surface through covalent Zn–H bonds. We also performed the density-functional perturbation theory (DFPT) calculations51,52 of the O–H and Zn–H species produced by the heterolytic H2 dissociation on the ZnO(10
0)–(Zn–O)DiV surface are rather active for the transformation of the adsorbed H into stable protons, while the OV site on the (Zn–O)DiV surface can help produce the stable hydrides that interact with the surface through covalent Zn–H bonds. We also performed the density-functional perturbation theory (DFPT) calculations51,52 of the O–H and Zn–H species produced by the heterolytic H2 dissociation on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) and ZnO(10
0) and ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV surfaces, and obtained the corresponding simulated infrared (IR) spectra (3550 (O–H) and 1773 (Zn–H) cm−1 for pristine ZnO(10
0)–(Zn–O)DiV surfaces, and obtained the corresponding simulated infrared (IR) spectra (3550 (O–H) and 1773 (Zn–H) cm−1 for pristine ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0); 3345 (O–H) and 1522 (Zn–H) cm−1 for ZnO(10
0); 3345 (O–H) and 1522 (Zn–H) cm−1 for ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV; see Fig. S7†). The wavenumber differences for the species on the pristine and (Zn–O)DiV surfaces are due to their different structures, i.e. on the (Zn–O)DiV surface, the O–H species can also form a hydrogen bond with the neighboring lattice O, and the hydride actually bonds with two Zn sites. These calculated wavenumbers are largely consistent with the reported experimental results that the pristine ZnO(10
0)–(Zn–O)DiV; see Fig. S7†). The wavenumber differences for the species on the pristine and (Zn–O)DiV surfaces are due to their different structures, i.e. on the (Zn–O)DiV surface, the O–H species can also form a hydrogen bond with the neighboring lattice O, and the hydride actually bonds with two Zn sites. These calculated wavenumbers are largely consistent with the reported experimental results that the pristine ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface gives rise to 3490 (O–H) and 1710 (Zn–H) cm−1 and the ZnO(10
0) surface gives rise to 3490 (O–H) and 1710 (Zn–H) cm−1 and the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV gives rise to 3400 (O–H) and 1475 (Zn–H) cm−1.48,53,54
0)–(Zn–O)DiV gives rise to 3400 (O–H) and 1475 (Zn–H) cm−1.48,53,54
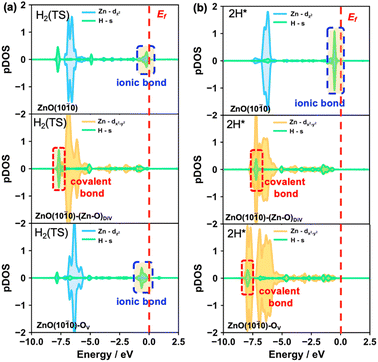
Besides, to further understand the energy barrier and product stability of heterolytic H2 dissociation on the different surfaces, we also calculated the partial DOS of the H species in the transition and final states of these processes (Fig. 4, S8 and S9†). The results indicated that the Zn–H ionic bonds occur in the transition states on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) and ZnO(10
0) and ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–OV surfaces (Fig. 4a). Moreover, the structural properties of the Zn–H bonds in the transition states (Fig. S8†) also showed that only a single asymmetric Zn–H bond forms on the pristine and OV surfaces, while the double symmetric Zn–H bond occurs on the (Zn–O)DiV surface. Accordingly, higher energy barriers were obtained on the pristine and OV surfaces (0.45 eV) compared with that on the (Zn–O)DiV surface (0.10 eV). Interestingly, stable covalent Zn–H bonds with relatively low energy levels can be formed on the defect surfaces, while Zn–H ionic bonds with relatively high energy levels were formed on the pristine ZnO(10
0)–OV surfaces (Fig. 4a). Moreover, the structural properties of the Zn–H bonds in the transition states (Fig. S8†) also showed that only a single asymmetric Zn–H bond forms on the pristine and OV surfaces, while the double symmetric Zn–H bond occurs on the (Zn–O)DiV surface. Accordingly, higher energy barriers were obtained on the pristine and OV surfaces (0.45 eV) compared with that on the (Zn–O)DiV surface (0.10 eV). Interestingly, stable covalent Zn–H bonds with relatively low energy levels can be formed on the defect surfaces, while Zn–H ionic bonds with relatively high energy levels were formed on the pristine ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface, leading to the different stabilities of the hydride species on the three surfaces.
0) surface, leading to the different stabilities of the hydride species on the three surfaces.
The corresponding Bader charge and spin charge density difference analyses (Fig. 3b–j) also supported that the heterolytic H2 dissociation on the various surfaces indeed produced a hydride and a hydroxyl species. The calculated Bader charges of the formed H+ and H− species are +0.66 |e| and −0.40 |e| at ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0), +0.69 |e| and −0.38 |e| at ZnO(10
0), +0.69 |e| and −0.38 |e| at ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV, and +0.75 |e| and −0.42 |e| at ZnO(10
0)–(Zn–O)DiV, and +0.75 |e| and −0.42 |e| at ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–OV. Interestingly, one can notice that the value of the calculated charge of H+ is approximately two times that of H− on the different ZnO(10
0)–OV. Interestingly, one can notice that the value of the calculated charge of H+ is approximately two times that of H− on the different ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces. This suggested that only some part of the charge contributed by the H during H2 dissociation is used to activate another H to form the hydride species, while the other part of the charge might be transferred to the ZnO(10
0) surfaces. This suggested that only some part of the charge contributed by the H during H2 dissociation is used to activate another H to form the hydride species, while the other part of the charge might be transferred to the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface (Table S2†). This is very different from some other metal oxides (e.g., MgO and CeO2), on which the calculated Bader charges of the H+ and H− species generated through heterolytic H2 dissociation are approximately equal.45,55
0) surface (Table S2†). This is very different from some other metal oxides (e.g., MgO and CeO2), on which the calculated Bader charges of the H+ and H− species generated through heterolytic H2 dissociation are approximately equal.45,55
For this unusual phenomenon, the calculated DOS (Fig. S8†) of the products of heterolytic H2 dissociation showed that the shapes of the Zn orbitals are almost unchanged, which is consistent with the situations of single H adsorption at surface O explored earlier on. In fact, the hydrides from these heterolytically dissociated H2 molecules can be recognized to evolve from the H adsorbing immediately following the H+ formation at the surface O site, in which case the electrons are released after storage. Therefore, it can also be concluded that the Zn orbitals are indeed quite flexible since they largely maintain the same shape during electron storage/release.
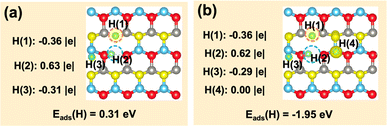
Finally, we further investigated if the transferred charge from the adsorbed H can be involved in the generation of multiple hydrides on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV surface (Fig. 5). The calculated results showed that, together with the surface H+, two hydride species can indeed occur, and their corresponding Bader charges are −0.36 |e| and −0.31 |e| (Fig. 5a). However, the charge contributed by one adsorbed H species cannot be used to activate more adsorbed H to the hydride species (e.g., the corresponding Bader charges of the three co-adsorbed H species are −0.36, −0.29 and 0.00 |e|, respectively, forming only two hydride species; Fig. 5b). Thus, we can expect that the charge released by the formation of a proton may perform dual functions for the simultaneous activation of two electrophilic adsorbates (e.g., CO2δ− and hydride).
0)–(Zn–O)DiV surface (Fig. 5). The calculated results showed that, together with the surface H+, two hydride species can indeed occur, and their corresponding Bader charges are −0.36 |e| and −0.31 |e| (Fig. 5a). However, the charge contributed by one adsorbed H species cannot be used to activate more adsorbed H to the hydride species (e.g., the corresponding Bader charges of the three co-adsorbed H species are −0.36, −0.29 and 0.00 |e|, respectively, forming only two hydride species; Fig. 5b). Thus, we can expect that the charge released by the formation of a proton may perform dual functions for the simultaneous activation of two electrophilic adsorbates (e.g., CO2δ− and hydride).
Selective CO2 hydrogenation on pristine and various defect ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/h3_char_0031_0304.gif) 0) surfaces
0) surfaces
To unveil the catalytic reactivities of the hydride species, we then proceeded to investigate the CO2 activation and hydrogenation on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0), ZnO(10
0), ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–Ov and ZnO(10
0)–Ov and ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV surfaces (Fig. 6 and S10–S19†). It is well known that the adsorption and activation of CO2 are the key steps of the overall CO2 reduction reactions.56,57 Our calculated results showed that the CO2 adsorptions on the ZnO(10
0)–(Zn–O)DiV surfaces (Fig. 6 and S10–S19†). It is well known that the adsorption and activation of CO2 are the key steps of the overall CO2 reduction reactions.56,57 Our calculated results showed that the CO2 adsorptions on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0), ZnO(10
0), ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–Ov and ZnO(10
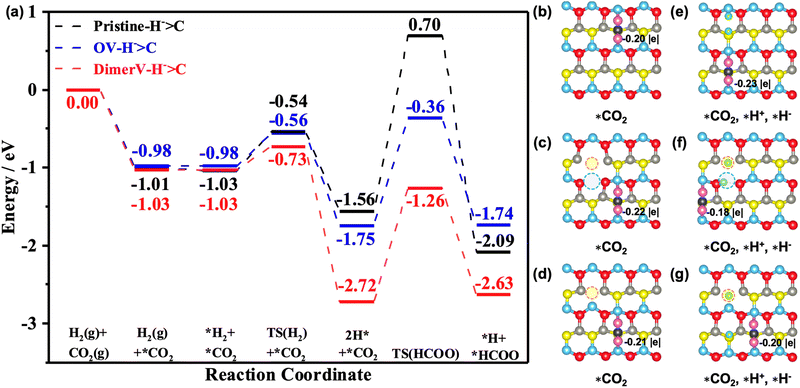
0)–Ov and ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV surfaces all lead to the formation of carbonate (CO32−)-like species, and these processes are exothermic by 1.01 eV, 0.98 eV and 1.03 eV, respectively (Fig. 6a). The Bader charge analysis also showed that the adsorbed CO2 is negatively charged on these surfaces (the corresponding Bader charges are −0.20 |e|, −0.22 |e| and −0.21 |e|, respectively (see Fig. 6b–d)).
0)–(Zn–O)DiV surfaces all lead to the formation of carbonate (CO32−)-like species, and these processes are exothermic by 1.01 eV, 0.98 eV and 1.03 eV, respectively (Fig. 6a). The Bader charge analysis also showed that the adsorbed CO2 is negatively charged on these surfaces (the corresponding Bader charges are −0.20 |e|, −0.22 |e| and −0.21 |e|, respectively (see Fig. 6b–d)).
Next, we calculated the further adsorption of H2 and found that it is generally rather weak on the pristine and different defect ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces with the pre-adsorbed CO2 (the corresponding adsorption energies are close to 0 eV; see Fig. 6a and S11†). The adsorbed H2 then undergoes heterolytic dissociation to produce one hydride and one proton species with the barriers of 0.49 eV, 0.30 eV and 0.42 eV on the pristine and defect ZnO(10
0) surfaces with the pre-adsorbed CO2 (the corresponding adsorption energies are close to 0 eV; see Fig. 6a and S11†). The adsorbed H2 then undergoes heterolytic dissociation to produce one hydride and one proton species with the barriers of 0.49 eV, 0.30 eV and 0.42 eV on the pristine and defect ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces, and the corresponding processes are exothermic by 0.53 eV, 1.69 eV and 0.77 eV. Interestingly, we also found that the adsorption energies of CO2 were enhanced by 0.18 eV and 0.06 eV on the pristine and (Zn–O)DiV surfaces, respectively, following the heterolytic dissociation of the H2, in comparison with the CO2 adsorbed alone. This is consistent with our findings above that the charges provided by the H that turns into a proton have ‘dual functions’ in activating multiple adsorbates.
0) surfaces, and the corresponding processes are exothermic by 0.53 eV, 1.69 eV and 0.77 eV. Interestingly, we also found that the adsorption energies of CO2 were enhanced by 0.18 eV and 0.06 eV on the pristine and (Zn–O)DiV surfaces, respectively, following the heterolytic dissociation of the H2, in comparison with the CO2 adsorbed alone. This is consistent with our findings above that the charges provided by the H that turns into a proton have ‘dual functions’ in activating multiple adsorbates.
We next considered two possible routes for CO2 activation, i.e. direct dissociation of CO2 and direct hydrogenation of CO2. The results indicated that the direct CO2 dissociation into co-adsorbed *CO and *O on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0), ZnO(10
0), ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV and ZnO(10
0)–(Zn–O)DiV and ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–Ov surfaces requires endothermic energies of 5.09 eV, 5.04 eV and 4.78 eV (Fig. S12†), respectively, and such high energy demands suggested that direct CO2 dissociation is unfavorable. In the route of direct hydrogenation of CO2, two possible pathways were then tested (Fig. 6 and S13–S15†). The first is the so-called COOH (carboxyl) pathway, in which the H+ or H− binds with the Oδ− of the adsorbed CO2 to form a *COOH species; the second is the so-called HCOO (formate) pathway, in which the H+ or H− reacts with the Cδ+ of the adsorbed CO2 to produce a *HCOO species. According to our calculated results, the processes with the H+ attacking the adsorbed CO2 to form the *HCOO species need to overcome enormously large energy barriers of 4.29 eV, 2.76 eV and 6.42 eV on the ZnO(10
0)–Ov surfaces requires endothermic energies of 5.09 eV, 5.04 eV and 4.78 eV (Fig. S12†), respectively, and such high energy demands suggested that direct CO2 dissociation is unfavorable. In the route of direct hydrogenation of CO2, two possible pathways were then tested (Fig. 6 and S13–S15†). The first is the so-called COOH (carboxyl) pathway, in which the H+ or H− binds with the Oδ− of the adsorbed CO2 to form a *COOH species; the second is the so-called HCOO (formate) pathway, in which the H+ or H− reacts with the Cδ+ of the adsorbed CO2 to produce a *HCOO species. According to our calculated results, the processes with the H+ attacking the adsorbed CO2 to form the *HCOO species need to overcome enormously large energy barriers of 4.29 eV, 2.76 eV and 6.42 eV on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0), ZnO(10
0), ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–Ov and ZnO(10
0)–Ov and ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV surfaces, respectively, and they are also highly endothermic (4.13 eV, 1.92 eV and 4.13 eV, respectively; Fig. S13a, e and i, and S14a, e and i†). When the H+ species attacks the Oδ− of the adsorbed CO2 to generate a *COOH species (Fig. S13c, g, and k, and S14c, g and k†), it also needs to overcome very large energy barriers (4.25 eV, 1.43 eV and 4.06 eV on the ZnO(10
0)–(Zn–O)DiV surfaces, respectively, and they are also highly endothermic (4.13 eV, 1.92 eV and 4.13 eV, respectively; Fig. S13a, e and i, and S14a, e and i†). When the H+ species attacks the Oδ− of the adsorbed CO2 to generate a *COOH species (Fig. S13c, g, and k, and S14c, g and k†), it also needs to overcome very large energy barriers (4.25 eV, 1.43 eV and 4.06 eV on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0), ZnO(10
0), ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–Ov and ZnO(10
0)–Ov and ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV surfaces, respectively) and these processes are highly endothermic (1.05 eV, 1.02 eV and 1.34 eV). Interestingly, for the processes with the H− species as the active H species to react with CO2, both the carboxylate and formate pathways can occur quite easily. For the pathway for the hydride species to attack the Cδ+ of the adsorbed CO2 to form the *HCOO species, the energy barriers are 2.26 eV, 1.39 eV and 1.46 eV on the pristine and the two defect ZnO(10
0)–(Zn–O)DiV surfaces, respectively) and these processes are highly endothermic (1.05 eV, 1.02 eV and 1.34 eV). Interestingly, for the processes with the H− species as the active H species to react with CO2, both the carboxylate and formate pathways can occur quite easily. For the pathway for the hydride species to attack the Cδ+ of the adsorbed CO2 to form the *HCOO species, the energy barriers are 2.26 eV, 1.39 eV and 1.46 eV on the pristine and the two defect ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces and they are exothermic by 0.53 eV and endothermic by 0.01 eV and 0.09 eV, respectively. At the same time, the reactions between H− and the Oδ− of the adsorbed CO2 (the COOH pathway) need to overcome the energy barriers of 2.42 eV, 1.40 eV and 1.71 eV, while they are endothermic by 0.09 eV, 0.05 eV and 0.67 eV.
0) surfaces and they are exothermic by 0.53 eV and endothermic by 0.01 eV and 0.09 eV, respectively. At the same time, the reactions between H− and the Oδ− of the adsorbed CO2 (the COOH pathway) need to overcome the energy barriers of 2.42 eV, 1.40 eV and 1.71 eV, while they are endothermic by 0.09 eV, 0.05 eV and 0.67 eV.
In addition, we also calculated the subsequent hydrogenation reaction steps in both the HCOO-to-methanol pathway and the COOH-to-methanol pathway (Fig. S16–19†) on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(ZnO)DiV surface. The results indicated that the HCOO-to-methanol pathway is more favorable than the COOH-to-methanol pathway in the formation of *H2CO species, where the maximum endothermic step (*HCOO + *H− → *HCOOH, ΔE = 0.78 eV) of the HCOO-to-methanol pathway is lower than that of the COOH-to-methanol pathway (*CO + *OH + *H+ → *CO + H2O(g), ΔE = 1.29 eV) (Fig. S16 and S18†). After the formation of the *H2CO species, the H2 dissociation into H+ and H− species releases an exothermic energy of 0.56 eV, while the formation of *H3CO is exothermic by 1.67 eV. The subsequent step of H2 adsorption and dissociation is exothermic by 0.18 eV, and the formation of *CH3OH species is highly exothermic by 1.89 eV. Therefore, it can be concluded that the *HCOO species is more readily formed and more stable during the CO2 hydrogenation to methanol reaction, and we believe that the *HCOO intermediate species is the most abundant reactive intermediate (MARI) in the CO2 hydrogenation reaction, which is consistent with other reports.58,59
0)–(ZnO)DiV surface. The results indicated that the HCOO-to-methanol pathway is more favorable than the COOH-to-methanol pathway in the formation of *H2CO species, where the maximum endothermic step (*HCOO + *H− → *HCOOH, ΔE = 0.78 eV) of the HCOO-to-methanol pathway is lower than that of the COOH-to-methanol pathway (*CO + *OH + *H+ → *CO + H2O(g), ΔE = 1.29 eV) (Fig. S16 and S18†). After the formation of the *H2CO species, the H2 dissociation into H+ and H− species releases an exothermic energy of 0.56 eV, while the formation of *H3CO is exothermic by 1.67 eV. The subsequent step of H2 adsorption and dissociation is exothermic by 0.18 eV, and the formation of *CH3OH species is highly exothermic by 1.89 eV. Therefore, it can be concluded that the *HCOO species is more readily formed and more stable during the CO2 hydrogenation to methanol reaction, and we believe that the *HCOO intermediate species is the most abundant reactive intermediate (MARI) in the CO2 hydrogenation reaction, which is consistent with other reports.58,59
From the above results, one can surely expect that the CO2 hydrogenation with the H− species on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV surface is more likely to follow the HCOO pathway, which may lead to the formation of CH3OH as the main product,60 and this stoichiometric surface with (Zn–O)DiV defects is more active than the reduced one with OV defects. This result is consistent with those reported recently by Ling et al.17 Moreover, the simulated infrared spectra (calculated by the DFPT method51,52) of formate (1355 and 1515 cm−1, Fig. S20†) are also consistent with the reported experimental results61,62 (1370 and 1595 cm−1). In general, we can learn from the calculated results in the current work that defects on the ZnO(10
0)–(Zn–O)DiV surface is more likely to follow the HCOO pathway, which may lead to the formation of CH3OH as the main product,60 and this stoichiometric surface with (Zn–O)DiV defects is more active than the reduced one with OV defects. This result is consistent with those reported recently by Ling et al.17 Moreover, the simulated infrared spectra (calculated by the DFPT method51,52) of formate (1355 and 1515 cm−1, Fig. S20†) are also consistent with the reported experimental results61,62 (1370 and 1595 cm−1). In general, we can learn from the calculated results in the current work that defects on the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface are key to its improved catalytic activities in H2 activation and CO2 hydrogenation, and the Zn–O dimer vacancy appears even more active than the usual O vacancy.
0) surface are key to its improved catalytic activities in H2 activation and CO2 hydrogenation, and the Zn–O dimer vacancy appears even more active than the usual O vacancy.
Conclusions
In summary, this study has systematically explored the catalytic roles of ZnO in CO2 hydrogenation to methanol, with a particular focus on the generation of active hydrogen species and their impact on catalysis. Our comprehensive computational analyses, based on density functional theory, have revealed the unique electronic properties of ZnO and their substantial influence on the catalytic processes. The characteristic ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0), ZnO(10
0), ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–OV and ZnO(10
0)–OV and ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV surfaces were constructed, and their stabilities were verified with the calculated equilibrium phase diagrams under reaction conditions. The calculated DOS further showed that for the pristine and various defect ZnO(10
0)–(Zn–O)DiV surfaces were constructed, and their stabilities were verified with the calculated equilibrium phase diagrams under reaction conditions. The calculated DOS further showed that for the pristine and various defect ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces, the size of the unfilled hybrid orbitals changes while the shape of the occupied orbitals remains unchanged when excess electrons exist, revealing the unique way of storing electrons for ZnO. We also determined that the hydride species can form through heterolytic H2 dissociation on the pristine and various defect ZnO(10
0) surfaces, the size of the unfilled hybrid orbitals changes while the shape of the occupied orbitals remains unchanged when excess electrons exist, revealing the unique way of storing electrons for ZnO. We also determined that the hydride species can form through heterolytic H2 dissociation on the pristine and various defect ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces. Among these surfaces, the ZnO(10
0) surfaces. Among these surfaces, the ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)–(Zn–O)DiV is the most active one for the heterolytic dissociation of H2, which demonstrates a notably low energy barrier (∼0.10 eV), largely due to the fact that the low-coordinated surface Zn3c is helpful for the stabilization of H− species. Moreover, it was found that the unique way of storing and releasing electrons in Zn orbitals gives ZnO the characteristic capacity of activating two electrophilic adsorbates simultaneously as excess electrons exist. Calculations of the key reaction steps further showed that the covalent Zn–H species can regulate the activities and selectivities in CO2 hydrogenation, by preferentially producing *HCOO intermediates, and revealed a lower reaction barrier on the Zn–O dimer vacancy surface. Our study provides valuable insights into the catalytic mechanisms of ZnO in hydrogenation reactions, highlighting the importance of its surface structures and electronic properties, and suggests the potential of the (Zn–O)DiV-containing ZnO surface as an efficient catalyst for hydrogenation reactions.
0)–(Zn–O)DiV is the most active one for the heterolytic dissociation of H2, which demonstrates a notably low energy barrier (∼0.10 eV), largely due to the fact that the low-coordinated surface Zn3c is helpful for the stabilization of H− species. Moreover, it was found that the unique way of storing and releasing electrons in Zn orbitals gives ZnO the characteristic capacity of activating two electrophilic adsorbates simultaneously as excess electrons exist. Calculations of the key reaction steps further showed that the covalent Zn–H species can regulate the activities and selectivities in CO2 hydrogenation, by preferentially producing *HCOO intermediates, and revealed a lower reaction barrier on the Zn–O dimer vacancy surface. Our study provides valuable insights into the catalytic mechanisms of ZnO in hydrogenation reactions, highlighting the importance of its surface structures and electronic properties, and suggests the potential of the (Zn–O)DiV-containing ZnO surface as an efficient catalyst for hydrogenation reactions.
Data availability
The data supporting this article have been included in the main article and the ESI.†Author contributions
X.-Y. Z. performed the DFT calculations, and collected and analyzed the DFT data. Z.-Q. W. supervised the research, analyzed the DFT data and provided constructive suggestions. X.-Q. G. conceived the ideas, supervised the research, and designed the present work. All authors contributed to the discussion and the manuscript writing.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work was supported by the National Key R&D Program of China (2023YFA1508500, 2021YFA1500700) and the National Natural Science Foundation of China (21825301, 92045303, 22203030).References
- G. Ertl, H. Knözinger and J. Weitkamp, Handbook of Heterogeneous Catalysis, VCH, 1997 Search PubMed.
- G. A. Olah, A. Goeppert and G. K. S. Prakash, Beyond Oil and Gas: The Methanol Economy, John Wiley & Sons, 2018 Search PubMed.
- M. Behrens, J. Catal., 2009, 267, 24–29 CrossRef CAS.
- S. A. Kondrat, P. J. Smith, P. P. Wells, P. A. Chater, J. H. Carter, D. J. Morgan, E. M. Fiordaliso, J. B. Wagner, T. E. Davies, L. Lu, J. K. Bartley, S. H. Taylor, M. S. Spencer, C. J. Kiely, G. J. Kelly, C. W. Park, M. J. Rosseinsky and G. J. Hutchings, Nature, 2016, 531, 83–87 CrossRef CAS PubMed.
- X. Liu, J. Luo, H. Wang, L. Huang, S. Wang, S. Li, Z. Sun, F. Sun, Z. Jiang, S. Wei, W.-X. Li and J. Lu, Angew. Chem., Int. Ed., 2022, 61, e202202330 CrossRef CAS PubMed.
- P. Amann, B. Klötzer, D. Degerman, N. Köpfle, T. Götsch, P. Lömker, C. Rameshan, K. Ploner, D. Bikaljevic, H.-Y. Wang, M. Soldemo, M. Shipilin, C. M. Goodwin, J. Gladh, J. Halldin Stenlid, M. Börner, C. Schlueter and A. Nilsson, Science, 2022, 376, 603–608 CrossRef CAS PubMed.
- S. Kuld, M. Thorhauge, H. Falsig, C. F. Elkjær, S. Helveg, I. Chorkendorff and J. Sehested, Science, 2016, 352, 969–974 CrossRef CAS PubMed.
- I. Kasatkin, P. Kurr, B. Kniep, A. Trunschke and R. Schlögl, Angew. Chem., Int. Ed., 2007, 46, 7324–7327 CrossRef CAS PubMed.
- M. Behrens, F. Studt, I. Kasatkin, S. Kühl, M. Hävecker, F. Abild-Pedersen, S. Zander, F. Girgsdies, P. Kurr, B.-L. Kniep, M. Tovar, R. W. Fischer, J. K. Nørskov and R. Schlögl, Science, 2012, 336, 893–897 CrossRef CAS PubMed.
- S. Kattel, P. J. Ramírez, J. G. Chen, J. A. Rodriguez and P. Liu, Science, 2017, 355, 1296–1299 CrossRef CAS PubMed.
- Y. Wang, S. Kattel, W. Gao, K. Li, P. Liu, J. G. Chen and H. Wang, Nat. Commun., 2019, 10, 1166 CrossRef PubMed.
- W. Wu, Y. Wang, L. Luo, M. Wang, Z. Li, Y. Chen, Z. Wang, J. Chai, Z. Cen, Y. Shi, J. Zhao, J. Zeng and H. Li, Angew. Chem., Int. Ed., 2022, 61, e202213024 CrossRef CAS PubMed.
- Y.-F. Shi, P.-L. Kang, C. Shang and Z.-P. Liu, J. Am. Chem. Soc., 2022, 144, 13401–13414 CrossRef CAS PubMed.
- J. C. Frost, Nature, 1988, 334, 577–580 CrossRef CAS.
- H. Shi, H. Yuan, Z. Li, W. Wang, Z. Li and X. Shao, J. Phys. Chem. C, 2019, 123, 13283–13287 CrossRef CAS.
- M. Buchholz, P. G. Weidler, F. Bebensee, A. Nefedov and C. Wöll, Phys. Chem. Chem. Phys., 2014, 16, 1672–1678 RSC.
- Y. Ling, J. Luo, Y. Ran, Z. Liu, W.-X. Li and F. Yang, J. Am. Chem. Soc., 2023, 145, 22697–22707 CrossRef CAS PubMed.
- B. Song, Y. Li, X.-P. Wu, F. Wang, M. Lin, Y. Sun, A. Jia, X. Ning, L. Jin, X. Ke, Z. Yu, G. Yang, W. Hou, W. Ding, X.-Q. Gong and L. Peng, J. Am. Chem. Soc., 2022, 144, 23340–23351 CrossRef CAS PubMed.
- Q.-L. Tang and Q.-H. Luo, J. Phys. Chem. C, 2013, 117, 22954–22966 CrossRef CAS.
- J. Luo, J.-X. Liu and W.-X. Li, J. Phys. Chem. C, 2022, 126, 9059–9068 CrossRef CAS.
- Y.-F. Zhao, R. Rousseau, J. Li and D. Mei, J. Phys. Chem. C, 2012, 116, 15952–15961 CrossRef CAS.
- W. Tu, P. Ren, Y. Li, Y. Yang, Y. Tian, Z. Zhang, M. Zhu, Y.-H. C. Chin, J. Gong and Y.-F. Han, J. Am. Chem. Soc., 2023, 145, 8751–8756 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- M. P. Teter, M. C. Payne and D. C. Allan, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 12255–12263 CrossRef PubMed.
- R. Escudero and R. Escamilla, Solid State Commun., 2011, 151, 97–101 CrossRef CAS.
- Y. Cao, J. Luo, W. Huang, Y. Ling, J. Zhu, W.-X. Li, F. Yang and X. Bao, J. Chem. Phys., 2020, 152, 074714 CrossRef CAS PubMed.
- K. Mun Wong, S. M. Alay-e-Abbas, A. Shaukat, Y. Fang and Y. Lei, J. Appl. Phys., 2013, 113, 014304 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Wróbel, K. J. Kurzydłowski, K. Hummer, G. Kresse and J. Piechota, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155124 CrossRef.
- A. Alavi, P. Hu, T. Deutsch, P. L. Silvestrelli and J. Hutter, Phys. Rev. Lett., 1998, 80, 3650–3653 CrossRef CAS.
- H.-F. Wang, D. Wang, X. Liu, Y.-L. Guo, G.-Z. Lu and P. Hu, ACS Catal., 2016, 6, 5393–5398 CrossRef CAS.
- R. Kovacik, B. Meyer and D. Marx, Angew. Chem., Int. Ed., 2007, 46, 4894–4897 CrossRef CAS PubMed.
- N. R. D'Amico, G. Cantele and D. Ninno, J. Phys. Chem. C, 2012, 116, 21391–21400 CrossRef.
- M.-H. Liu, Y.-W. Chen, T.-S. Lin and C.-Y. Mou, ACS Catal., 2018, 8, 6862–6869 CrossRef CAS.
- D. Li, F. Xu, X. Tang, S. Dai, T. Pu, X. Liu, P. Tian, F. Xuan, Z. Xu, I. E. Wachs and M. Zhu, Nat. Catal., 2022, 5, 99–108 CrossRef CAS.
- J. H. Seinfeld and S. N. Pandis, Atmospheric chemistry and physics: from air pollution to climate change, John Wiley & Sons, Hoboken, New Jersey, 3rd edn, 2016 Search PubMed.
- Z.-Q. Wang, D.-R. Chu, H. Zhou and X.-P. Wu, ACS Catal., 2022, 12, 624–632 CrossRef CAS.
- H. Zhou, X.-P. Wu and X.-Q. Gong, ChemCatChem, 2022, 14, e202101254 CrossRef CAS.
- Z. L. Wang, Mater. Today, 2004, 7, 26–33 CrossRef CAS.
- J.-J. Liu, Acta Phys. Sin., 2011, 60, 037102 CrossRef.
- Z.-Q. Wang, D. Wang and X.-Q. Gong, ACS Catal., 2020, 10, 586–594 CrossRef CAS.
- X.-P. Wu, X.-Q. Gong and G. Lu, Phys. Chem. Chem. Phys., 2015, 17, 3544–3549 RSC.
- Z.-Q. Wang, H.-H. Liu, X.-P. Wu, P. Hu and X.-Q. Gong, Catalysts, 2022, 12, 963 CrossRef CAS.
- S. Song, K. Yang, P. Zhang, Z. Wu, J. Li, H. Su, S. Dai, C. Xu, Z. Li, J. Liu and W. Song, ACS Catal., 2022, 12, 5997–6006 CrossRef CAS.
- H. Zhou, D. Wang and X.-Q. Gong, J. Phys. Chem. C, 2023, 127, 11040–11045 CrossRef CAS.
- D. R. Aireddy and K. Ding, ACS Catal., 2022, 12, 4707–4723 CrossRef CAS.
- G. Griffin, J. Catal., 1982, 73, 396–405 CrossRef CAS.
- H. Chen, L. Lin, Y. Li, R. Wang, Z. Gong, Y. Cui, Y. Li, Y. Liu, X. Zhao, W. Huang, Q. Fu, F. Yang and X. Bao, ACS Catal., 2019, 9, 1373–1382 CrossRef CAS.
- D. Karhánek, dakarhanek/VASP-infrared-intensities (version v1.0) Zenodo, 2020.
- S. Baroni, P. Giannozzi and A. Testa, Phys. Rev. Lett., 1987, 58, 1861–1864 CrossRef CAS PubMed.
- F. Boccuzzi, J. Catal., 1978, 51, 150–159 CrossRef CAS.
- R. P. Eischens, W. A. Pliskin and M. J. D. Low, J. Catal., 1962, 1, 180–191 CrossRef CAS.
- B. Yang, X.-M. Cao, X.-Q. Gong and P. Hu, Phys. Chem. Chem. Phys., 2012, 14, 3741–3745 RSC.
- C. Copéret, D. P. Estes, K. Larmier and K. Searles, Chem. Rev., 2016, 116, 8463–8505 CrossRef PubMed.
- Y. Wang, R. Kovacik, B. Meyer, K. Kotsis, D. Stodt, V. Staemmler, H. Qiu, F. Traeger, D. Langenberg, M. Muhler and C. Woll, Angew. Chem., Int. Ed., 2007, 46, 5624–5627 CrossRef CAS PubMed.
- W. Xiong, Z. Wu, X. Chen, J. Ding, A. Ye, W. Zhang and W. Huang, Sci. China: Chem., 2024, 67, 715–723 CrossRef CAS.
- X.-K. Wu, G.-J. Xia, Z. Huang, D. K. Rai, H. Zhao, J. Zhang, J. Yun and Y.-G. Wang, Appl. Surf. Sci., 2020, 525, 146481 CrossRef CAS.
- Q. Tang, Y. Lee, D.-Y. Li, W. Choi, C. W. Liu, D. Lee and D. Jiang, J. Am. Chem. Soc., 2017, 139, 9728–9736 CrossRef CAS PubMed.
- J. Wang, G. Li, Z. Li, C. Tang, Z. Feng, H. An, H. Liu, T. Liu and C. Li, Sci. Adv., 2017, 3, e1701290 CrossRef PubMed.
- Z. Feng, C. Tang, P. Zhang, K. Li, G. Li, J. Wang, Z. Feng and C. Li, J. Am. Chem. Soc., 2023, 145, 12663–12672 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc04344h |
| This journal is © The Royal Society of Chemistry 2024 |