Open Access Article
Open Access ArticleExtended conformations of bifurcating electron transfer flavoprotein constitute up to half the population, possibly mediating conformational change†
Sharique A.
Khan
 ab,
Alan
Hicks
b,
Wellington C.
Leite
b,
James
Byrnes
c,
Biswajit
Gorai
d,
Maria-Andrea
Mroginski
ab,
Alan
Hicks
b,
Wellington C.
Leite
b,
James
Byrnes
c,
Biswajit
Gorai
d,
Maria-Andrea
Mroginski
 d,
Hugh
O'Neill
*b and
Anne-Frances
Miller
d,
Hugh
O'Neill
*b and
Anne-Frances
Miller
 *a
*a
aDepartment of Chemistry, University of Kentucky, Lexington, KY 40506, USA. E-mail: afmill3r2@gmail.com
bNeutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA
cNational Synchrotron Light Source II, Brookhaven National Laboratory, Upton, NY 11973, USA
dDepartment of Chemistry, Technische Universität Berlin, 10623 Berlin, Germany
First published on 23rd October 2024
Abstract
Electron transfer bifurcation enables biological systems to drive unfavourable (endergonic) electron transfer by coupling it to favourable (exergonic) transfer of a second electron. In electron transfer flavoproteins (ETFs), a domain-scale conformational change is believed to sever the favourable pathway after a single electron has used it, thereby preventing the energy dissipation that would accompany exergonic transfer of the second electron. To understand the conformation change that participates in turnover, we have deployed small-angle neutron scattering (SANS) and computational techniques to characterize the bifurcating ETF from Acidaminococcus fermentans (AfeETF). SANS data reveal an overall radius of gyration (Rg) of 30.1 ± 0.2 Å and a maximum dimension (Dmax) of 100 Å for oxidized AfeETF. These measurements are 4 Å and 30 Å larger, respectively, than those of any published bifurcating ETF structure. Thus, we find that none of the reported ETF structures can explain the observed scattering, nor can any individual conformation generated by either of our molecular dynamics protocols. To optimize ensembles best able to explain the SANS data, we adapted a genetic algorithm. Successful ensembles contained a compact conformation comparable to one of the crystallographically documented conformations, accompanied by a much more extended one, and these two conformations sufficed to account for the data. The extended conformations identified all have Rgs at least 4 Å larger than those of any currently published ETF structures. However, they are strongly populated, constituting 20% of the population of reduced ETF and over 50% of the population of oxidized AfeETF. Thus, the published (compact) structures provide a seriously incomplete picture of the conformation of AfeETF in solution. Moreover, because the composition of the conformational ensemble changes upon reduction of AfeETF's flavins, interconversion of the conformations may contribute to turnover. We propose that the extended conformations can provide energetically accessible paths for rapid interconversion of the open and closed compact conformations that are believed essential at alternating points in turnover.
1 Introduction
Electron transfer bifurcation (‘bifurcation’) enhances energy efficiency in both aerobic and anaerobic organisms by coupling an unfavourable (endergonic) electron transfer to a favourable (exergonic) transfer as part of a coupled process. In effect, the energy of one electron is augmented at the expense of the other one. The high-energy electron is then transferred to a low reduction potential acceptor (low E°, strongly reducing), able to drive demanding reactions such as fixation of N2 or CO2. Bifurcation has been known since the 1970s, when it was elucidated by Mitchell et al. in the context of the respiratory chain bc1 complex.1–3 In that case, ubiquinol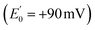 is the source of a pair of electrons, the Rieske iron-sulphur cluster protein
is the source of a pair of electrons, the Rieske iron-sulphur cluster protein  acquires one at high E° thereby ‘paying for’ direction of the other to cytochrome b as the low E° acceptor
acquires one at high E° thereby ‘paying for’ direction of the other to cytochrome b as the low E° acceptor  .
.
In 2008, Flavin-based electron bifurcation (FBEB) was identified by Buckel et al. in anaerobes.4 FBEB employs a flavin instead of a quinone as the site of bifurcation, with the lower E° of the flavin being consistent with the more reducing metabolism of anaerobes. Flavin adenine dinucleotide (FAD) or flavin mononucleotide (FMN) serves as the site of bifurcation and yields reduced low-potential electron carriers such as ferredoxin or flavodoxin (Fd or Fld),5 based on abundant but less reducing two-electron donors, including NADH, reduced coenzyme F420, H2, or formate.6 FBEB was first documented in Clostridium kluyveri, where the butyryl-CoA dehydrogenase (BCD) in combination with electron transfer flavoprotein (ETF) were demonstrated to couple endergonic reduction of ferredoxin  by NADH
by NADH  to the exergonic reduction of crotonyl-CoA
to the exergonic reduction of crotonyl-CoA 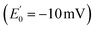 to butyryl-CoA.4 Since then, FBEB has been studied in numerous bifurcating ETFs (Bf-ETFs) from a growing diversity of species, including Acidaminococcus fermentans, Acetobacterium woodii, Rhodopseudomonas palustris, Pyrobaculum aerophilum and Thermotoga maritima.7–12
to butyryl-CoA.4 Since then, FBEB has been studied in numerous bifurcating ETFs (Bf-ETFs) from a growing diversity of species, including Acidaminococcus fermentans, Acetobacterium woodii, Rhodopseudomonas palustris, Pyrobaculum aerophilum and Thermotoga maritima.7–12
ETFs are heterodimeric FAD-binding proteins. They were originally discovered in mitochondria, where they associate with the inner membrane and contribute electrons to the respiratory electron transport chain.13 Mitochondrial ETFs, or ‘canonical’ ETFs, possess a single FAD that shuttles electrons from fatty acyl CoA dehydrogenases to the quinone pool14,15 and a bound AMP that is required for folding and stability.16,17 However, Bf-ETFs contain two FADs.18 The FAD that has no counterpart in canonical ETFs binds such that its AMP fragment is superimposable on the AMP of canonical ETFs.12 This, and conservation of residues nearby over both canonical and Bf-ETFs, indicate that canonical ETFs evolved from bifurcating predecessors.19 The FAD unique to Bf-ETFs is called the bifurcating FAD (Bf-FAD) and is the site of bifurcation.12,19 The FAD that is common to all known ETFs is called the ET-FAD because it mediates electron transfer (ET) to the high-E° partner proteins, including BCD.5,7,12,19–22
The ETF heterodimer comprises three domains. EtfA makes up domain I and domain II (N- and C-terminal halves of EtfA, respectively, Fig. 1). The smaller EtfB makes up domain III, but also contributes its C-terminal residues to domain II, henceforth called the ‘head’ (a.k.a. the shuttle). The flavin moiety of the Bf-FAD is situated in the interface between domains I and III, which together are called the ‘base’. The head associates with the base via a hydrophilic interface, besides being tethered to it by polypeptide linkers belonging to EtfA and B. The head also carries the ET-FAD, whose position relative to the Bf-FAD depends on the orientation of the head relative to the base20 (Fig. 1).
 | ||
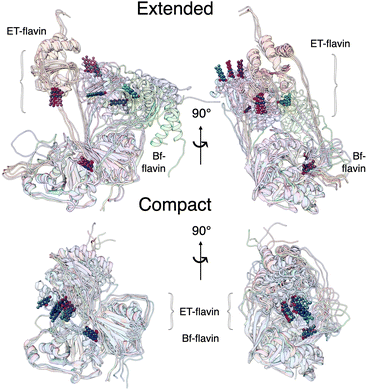
| Fig. 1 Comparison of the two conformations captured in crystal structures. Ribbon diagrams of AfeETF showing proximity of the two flavins in the closed conformation (left) vs. exposure of the ET-flavin in the open conformation (right). Based on their roles in turnover, the two conformations are also called ‘B-like’ because the closed state appears to approximate a conformation that would optimize bifurcation by enabling rapid electron transfer between ETF's two flavins, and ‘D’ because the open conformation positions the ET flavin to donate an electron to the dehydrogenase or quinone reductase partner.20 Structures are based on 4KPU (left) and 6FAH (right) and displayed from the same perspective with respect to the base (the lower portion, as shown). FADs are shown in ball and stick with ET-FAD in teal and BF-FAD in purple using the CPK convention for non-C atoms. The flavin headgroups are rendered with thicker bonds for visibility and labelled in the left-hand structure. Subunits are coloured in pale blue (chain A) and green (chain B), and domains I, II and III are labelled in the right-hand structure. The head and base are also indicated by coloured ovals, showing how the head's orientation relative to the base differs in the two cases. | ||
Crystal structures have revealed two conformations of ETFs, distinguished by the orientation of the head relative to the base.8,11,12,20,23–25 The closed25 conformation (also called B-like20) is exemplified by the crystal structure of ETF from Acidaminococcus fermentans (AfeETF, 4KPU, Fig. 1, left side),12 whereas the open conformation (also called ‘D’) is observed in the ETF from Clostridium difficile (CdiETF, 5OL2) in association with BCD,20 the Acetobacterium woodii Bf-ETF in complex with caffeoyl-CoA dehydrogenase (AwoETFCAR, 6FAH),11 the Bf-ETF of A. woodii's lactate dehydrogenase complex (AwoETFLDH7QH2),26 and the human canonical ETF in complex with medium chain acyl CoA dehydrogenase.25 In the closed conformation, the ET-flavin is 18 Å away from the Bf-flavin and partially occluded from solvent (Fig. 1). In contrast, the open conformation results from 80° rotation of the head domain that places the ET-FAD on an outward-facing surface accessible to interacting protein partners, and separates the two flavins by 37 Å. The two orientations of the head domain thereby cause the ET-flavin to alternate between positions close to the Bf-flavin, vs. accessible to partners. Thus, head orientation is proposed to regulate the ET-FAD's electron transfer activity, enabling ET between the ET-flavin and its partners in the open conformation, and possibly allowing for electron tunnelling between the ET- and Bf-flavins in the closed conformation.20 This echoes earlier findings on canonical ETFs, wherein pioneering SAXS studies demonstrated that these have a dynamic structure in solution.27,28 A conformation elucidated by cryo-electron microscopy (cryo-EM) of the ETF from Thermotoga maritima,8 places the flavin moieties 25 Å apart, suggesting an intermediate in the motional mechanism. An ‘ideal’ bifurcating conformation, facilitating electron tunnelling between the two flavins, remains to be observed. However, such a conformation need not be abundant or persistent, due to the rapidity of electron tunnelling. Regardless, the different captured conformations of ETF suggest that alternation between at least two orientations of the head plays a critical role in turnover. It is important to characterize these motions in solution, free of crystal packing constraints or freeze-trapping. Moreover in order to be functional, rotation of the head domain must be coordinated with other elements of catalysis to maximize efficiency of bifurcation.29
Domain scale motion essential to catalysis has been documented in many redox enzymes, including the respiratory bc1 complex,30,31 cytochrome P450 reductase (CPR)32,33 and the canonical ETFs.25 Studies of these systems revealed details of interactions between the protein domains and cofactors, and showed how protein conformations can modify the distance over which electron transfer occurs.25,34–38 However, a complete picture requires insight from a variety of different methods. Crystallization or cryo-EM can enrich certain conformations due to protein–protein interactions39,40 or protein-grid interactions,41 and thus produce a biased picture or fail to capture a functional conformation.42,43 Therefore, it is critical to also obtain information on proteins' structures in solution. Small-angle X-ray scattering (SAXS) is widely used to study protein conformation in solution44,45 but is problematic in the study of flavoproteins that may undergo redox-coupled conformation changes, because the X-rays used to make measurements can trigger flavin reduction.46–48 Förster resonance energy transfer (FRET) and other optical methods can provide detailed insights in solution49 but suffer similar challenges stemming from flavin photoreduction, in addition to complications in interpretation due to flavins being fluorophores themselves, as well as quenchers.50,51
Similar to SAXS, small-angle neutron scattering (SANS) is exceptionally well-suited for probing the domain-scale architecture of protein assemblies, enabling examination of internal reconfigurations and dynamics in solution.52 It has been used to study domain movements within CPR, NADPH-dependent sulphite reductases,53,54 and more complex entities such as the 70s ribosome.55,56 In the case of CPR, Freeman et al. were able to link domain scale motion to redox changes of the flavins.57 In subsequent work, they used SANS contrast matching with deuterated protein, to elucidate the solution structure of the complex between CPR and its electron transfer partner cytochrome c.58
In contrast to SAXS, SANS does not perturb the flavins. Because neutrons lack electrostatic charge and possess relatively low kinetic energy, they engage only weakly with molecules and do not produce the radiation damage or reduction that can complicate SAXS or cryo-EM.59 This and its applicability to dilute solutions of large complexes, beyond the scope of nuclear magnetic resonance (NMR) spectroscopy, make SANS ideal for studying ETF. Moreover, ongoing developments in computational modelling of SANS data enable elucidation of the solution structures of multidomain proteins and complexes, including Bf-ETFs.
Herein, we have used AfeETF to investigate domain scale motions in Bf-ETFs. We have delineated the resting conformation of Bf-ETF, proposing a structural ensemble in solution distinct from what has previously been reported.41 By contrasting SAXS and SANS data, we have demonstrated the tendency of ETF to populate different conformations under the influence of X-rays vs. neutrons. Leveraging molecular dynamics (MD) based modelling tools, we describe an equilibrium between extended and compact conformations of ETF, confirming a shift in this equilibrium upon reduction of the bound flavins.41
Based on the Bilbo-MD CHARMM workflow commonly employed for SAXS data modeling,60 we developed tools for analysing SANS data, implementing a genetic algorithm (GA) and metadynamics61,62 to explore conformational ensembles and identify those that best adhere to the data. Freeman et al.58 used MultiFOXS63 with SANS data to understand the flexibility of CPR upon reduction. By integrating such an approach with a GA, we were able to dramatically expand our conformational search space to explore possible advantages of integrating structures obtained by metadynamics with those identified by Bilbo-MD.64 Thus, we report a comprehensive investigation of the conformational landscape that may be explored by AfeETF, via sampling over a thousand conformations generated by Bilbo-MD and metadynamics simulations.
Finally, we explored the possible mechanistic significance of conformational change in ETF, testing for effects of two elements of catalytic turnover: reduction of the flavins or partner protein binding. The latter was made possible by selective deuteration and contrast variation techniques that are unique capabilities of SANS.56,65 Thus, we have advanced tools available for studying domain-scale movements in proteins by SANS, and used these to put forth a new proposal for the significance of extended conformations in enabling dynamic rearrangements of ETF. The SANS data could only be explained by invoking an ensemble of conformations wherein a very significant population explores extended conformations not previously examined. We propose that these extended conformations can provide critical paths between the open and closed compact conformations, thereby enabling their interconversion as required for catalytic competence.20
2 Experimental section
2.1. Production of AfeETF
The expression plasmid, pASG IBA33, containing the genes Acfer_0555 (encoding EtfB) and Acfer_0556 (encoding EtfA) was provided by R. Hille, with permission of Chowdhury et al. The plasmid was engineered to include a C-terminal 6X-His tag on EtfA.12 To produce the target protein, this plasmid was transformed into E. coli Nico21-DE3 cells (New England Biolabs C2529H).A preculture was cultivated in 10 mL of LB medium supplemented with carbenicillin at 100 μg μL−1, overnight at 37 °C and 220 rpm. For protein expression, 1 L of TB medium augmented with 100 μg μL−1 carbenicillin was prepared in a 3 L Erlenmeyer flask. This was inoculated with the 10 mL overnight preculture. Cells were grown at 37 °C and 200 rpm until reaching an OD600 of 0.6–0.8. At this point, the culture temperature and agitation were reduced to 18 °C and 180 rpm respectively, and protein expression was induced by addition of anhydrotetracycline to achieve a final concentration of 0.2 μg mL−1. The culture was grown for an additional 18 hours at 18 °C and 200 rpm before harvesting the cells and washing them with PBS (phosphate buffered saline: 137 mM NaCl, 2.7 mM KCl, 10 mM K2PO4 and 1.8 mM KPO4, pH 7.4) by centrifugation. Cell pellets (typically 14–15 g L−1 culture) were flash-frozen in liquid N2 and stored at −80 °C.
To obtain purified protein, frozen cells were thawed and suspended in a binding buffer composed of 50 mM HEPES, 10 mM imidazole at pH 7.5, augmented to be 1 mM PMSF (phenylmethylsulfonyl fluoride), 2 mM benzamidine, 1 mM NaF, benzonase nuclease (1 μL from Millipore sigma # 71205-3), recombinant lysozyme (1 μL, Millipore sigma #: 71110-4) and 1 mM FAD (2 mL binding buffer per g cell pellet). Cell lysis was accomplished using sonication in pulses of 5 seconds separated by 30 second pauses for a total of 30 cycles, with the cell suspension on ice. After centrifugation to remove debris and un-lysed cells (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 20 min), the resulting supernatant (clarified cell lysate) was loaded onto a gravity-propelled column containing Ni-nitrilotriacetate resin, pre-equilibrated with the binding buffer (5 mL resin for 15 g cell pellet). The column was washed with 20 column volumes (CV) of the binding buffer supplemented with 20 mM imidazole. Finally, the target protein was eluted from the column using 150 mM imidazole in the binding buffer.
000 rpm for 20 min), the resulting supernatant (clarified cell lysate) was loaded onto a gravity-propelled column containing Ni-nitrilotriacetate resin, pre-equilibrated with the binding buffer (5 mL resin for 15 g cell pellet). The column was washed with 20 column volumes (CV) of the binding buffer supplemented with 20 mM imidazole. Finally, the target protein was eluted from the column using 150 mM imidazole in the binding buffer.
The eluted protein was concentrated by centrifugation in an Amicon ultra centrifugal concentration device (3 kDa cut off) to a volume of 3 mL. This was exchanged into fresh buffer by gel filtration on a Biorad 10DG column (Econo-Pac 10DG Desalting Columns #7322010), which was pre-equilibrated with 50 mM KPO4 (potassium phosphate dibasic plus potassium phosphate monobasic) at pH 7.0. Excess FAD (to 1 mM) was added to restore any FAD lost in earlier steps, in the course of overnight incubation at 4 °C. Gel filtration on pre-equilibrated 10DG column was employed on the following day to remove any unbound FAD. The pure protein was concentrated to 12 mg mL−1 (0.18 mM) and rapidly frozen in liquid N2 for storage at −80 °C.
Protein purified and frozen at the University of Kentucky was shipped to Oak Ridge National Laboratory (ORNL) on dry ice. On the day of SANS data collection, protein was thawed and size exclusion chromatography (SEC) was used to capture the fraction containing individual EtfAB heterodimers, and remove any higher-order assemblies. SEC was performed on a AKTA GO purification system using a Cytiva Superdex 200 Increase 10/300 GL column pre-equilibrated with 50 mM KPO4 at pH 7.0. AfeETF eluted as a single peak in size exclusion chromatography (SEC), consistent with the 67.97 kDa mass expected for the heterodimeric protein (Fig. S1†). Only central fractions were employed for SANS. Such material was replete with FAD (FAD 2.1 ± 0.2 FAD per ETF heterodimer) and retained activity with its substrate NADH. This same-day resolution and data collection assured that the ETF used had accumulated minimal flavin modification or aggregates. As prepared and maintained in air-equilibrated buffers, it was deemed oxidized (OX) based on its optical spectrum which shows that both flavins were oxidized.66
2.2. BCD deuteration
The gene encoding BCD was generously provided by Chowdhury on the IBA33 plasmid. The plasmid was transformed into E. coli BL21(DE3) cell line for expression. For production of deuterated BCD, cells were initially grown in 6 L LB media at 37 °C until OD600 reached 0.6–0.8. The cells were then centrifuged in sterile centrifuge tubes at 4000×g for 30 min. The pellets were resuspended in 45 mL of 70% deuterated Enfors media67,68 and centrifuged at 4000×g for 10 min to remove residual LB media. Cell pellets were then resuspended in 2 L of 70% deuterated Enfors media, this time augmented with carbenicillin (100 μg mL−1 final), and gene expression was induced by addition of anhydrotetracycline to 0.2 μg mL−1 final. Expression of BCD in 70% D2O media was carried out for 18 hours at 18 °C.BCD was purified at 4 °C. Cell pellets were resuspended in the lysis buffer (50 mM Tris, 150 mM NaCl pH 7.5, augmented with one capsule of ‘cOmplete’ EDTA-free protease inhibitor cocktail (Roche, 11836170001), Benzonase nuclease (1 μL from Millipore sigma # 71205-3) recombinant lysozyme (1 μL, Millipore sigma #: 71110-4) and 1 mM FAD, at the ratio of 4 g cells per mL of buffer. Suspended cells were lysed by sonication using a Branson 450 Digital Sonicator at 40% amplitude for 30 cycles (pulse on for 5 s and off 30 s) on ice. The lysed cells were centrifuged at 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000×g for 20 min and the clarified lysate was filtered using 0.45 μm syringe filter. The rest of the purification steps were as for the ETF except that the final buffer was 50 mM Tris–HCl, 150 mM NaCl at pH 7.5.
000×g for 20 min and the clarified lysate was filtered using 0.45 μm syringe filter. The rest of the purification steps were as for the ETF except that the final buffer was 50 mM Tris–HCl, 150 mM NaCl at pH 7.5.
The complex of ETF and BCD was generated by mixing 200 μL of 4 mg mL−1 ETF with 300 μL of 3 mg mL−1 BCD. This yielded 500 μL of 23.55 μM ETF and 25.6 μM BCD. The mixture was resolved by SEC as above yielding and only central fractions were used (ESI Fig. S1†). The buffer was 75% D2O to null net scattering from dBCD.
2.3. SANS experiments and data collection
SANS data were collected at the Bio-SANS instrument,69 at the High-Flux Isotope Reactor (HFIR) at ORNL. SANS experiments were conducted with a single instrument configuration of the dual detector system, utilizing the Panel Scan feature70 of the data acquisition system. The main detector was positioned 7.0 meters from the sample position, while the wing detector was placed 1.13 meters from the sample and rotated at an angle of 1.4° with respect to the incoming neutron beam. In this configuration, the range of scattering vector (Q) was 0.007 < Q < 1 Å−1, where Q = 4π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ)/λ (2θ is the scattering angle and λ is the neutron wavelength). Neutrons with a wavelength of 6 Å and a relative wavelength spread (Δλ/λ) of 13.2% were utilized. The processed scattering data were circularly averaged and reduced to 1D scattering profiles using drtSANS software.71,72 Calibration of the SANS data to an absolute scale was performed by measuring a porous silica standard with known intensity at zero angle (extrapolated from a Debye–Bueche plot).
sin(θ)/λ (2θ is the scattering angle and λ is the neutron wavelength). Neutrons with a wavelength of 6 Å and a relative wavelength spread (Δλ/λ) of 13.2% were utilized. The processed scattering data were circularly averaged and reduced to 1D scattering profiles using drtSANS software.71,72 Calibration of the SANS data to an absolute scale was performed by measuring a porous silica standard with known intensity at zero angle (extrapolated from a Debye–Bueche plot).
SANS samples were contained in 1 mm pathlengths cylindrical cuvettes (Hellma 120-1 mm), with 320 μL of 3 mg mL−1 protein per sample. The cuvettes were customized with ground-glass airtight seals, ensuring that the reduced samples remained in their reduced state throughout the experiments. The reduced state samples were prepared with de-gassed buffers in a He-filled glove box (PLAS labs, Lansing Michigan). Solutions of NADH and dithionite were likewise prepared in the anaerobic box. NADH and dithionite were carefully added to the samples, in the glove box, to yield approximately 10-fold stoichiometric ratio vs. ETF. Samples thus comprised ETF at 44 μM accompanied by NADH at 480 μM based on absorbance of the NADH stock solution at 340 nm, or dithionite at 440 μM based absorbance of the dithionite stock solution at 315 nm. The cuvettes were tightly sealed to prevent any exposure to air upon removal from the box. Parafilm was then applied to secure the stoppers. Samples were at 10 °C in darkness during data collection.
2.4. SAXS experiments
Size exclusion chromatography coupled with Small-Angle X-ray Scattering (SEC-SAXS) was executed at the Life Sciences X-ray Scattering Beamline (LIX) at NSLSII (Brookhaven National Lab). Briefly, 60 μL of sample was injected onto a Superdex 200 Increase 5/150 GL column (Cytiva) using an Agilent 1260 Infinity II Bio Inert HPLC system. Samples in 50 mM potassium phosphate buffer (pH 7.0) were kept at 12 °C in the multisampler and run on the column at room temperature. The flow rate was set to 0.35 mL min−1 and eluate from the column was split 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 via a passive splitter between the X-ray flow cell and UV branch respectively.73 Small- and wide-angle X-ray scattering SAXS/WAXS images were collected simultaneously on a Pilatus 1 M (SAXS) and Pilatus 900K WAXS detector. The exposure time was 2 seconds, and 350 frames were collected. Data were merged, scaled and subtracted using LIX beamline software, py4xs and lixtools as described elsewhere.74
1 via a passive splitter between the X-ray flow cell and UV branch respectively.73 Small- and wide-angle X-ray scattering SAXS/WAXS images were collected simultaneously on a Pilatus 1 M (SAXS) and Pilatus 900K WAXS detector. The exposure time was 2 seconds, and 350 frames were collected. Data were merged, scaled and subtracted using LIX beamline software, py4xs and lixtools as described elsewhere.74
2.5. SANS data analysis and calculation of theoretical scattering
Initial SANS data analysis, including Guinier fits and pair-correlation, was performed using the BioXTAS RAW program and the ATSAS suite.75,76 The pairwise distance distribution function, P(r), was calculated using the indirect Fourier transform method in the GNOM program.77 The SANS data were fitted to theoretical scattering profiles generated from atomic model coordinates using Pepsi-SAXS/SANS.642.6. Augmentation of crystal structures to reflect actual proteins used
Because the available PDB structures of ETF did not include the unstructured termini or His6 tags, AlphaFold2 (AF2) was employed to add them, as well as to apply the amino acid sequence of AfeETF to the different published conformations, to permit more accurate comparison with our data. AF2-multimer models of the 4KPU, 6FAH, and 7KOE PDB conformations of the AfeETF were generated in ColabFold.78,79 The PDBs were used as the only templates with no MSA and with the unpaired-paired setting for alignment with the sequence of AfeETF. The pairwise all-atom RMSDs to the original PDB structures along with the other structures are shown in Table S1.† SAXS and SANS profiles were then calculated from the AF2 PDB models with Pepsi-SAXS/SANS64 with 500 q-vectors spanning from 0.0 to 0.5 Å−1 out to the 50th multipole order at 100% D2O. Deuterated PDBs for the Pepsi-SANS calculations were generated using the SCOMAP-XD deuteration algorithm80 at 100% solvent D2O.2.7. Genetic algorithm: ensemble optimization for SANS
To validate the application of GAs to SANS data, we developed an algorithm similar to that used in the minimum ensemble search of Bilbo-MD.60 Details are provided in the ESI.† In brief, our algorithm finds the minimum set of conformations that best fits the experimental scattering profile. The conformations present and the fractions of the population each represents are varied to generate candidate ensembles. Best performers are identified based on agreement between the SANS they predict and the data. Conformers were generated using the Bilbo-MD workflow and/or metadynamics. Both started from the 4KPU PDB structure with the His6 tag added, because 4KPU was obtained using AfeETF, the variant of Bf-ETF used in our SANS. The base domain was defined as EtfA1-205 and EtfB1-11,36-219, and designated as the fixed domain for Bilbo-MD sampling. The two flexible linkers between the base and head domains in EtfA and EtfB were left flexible, along with the loop, EtfB12-35. All other domains were held rigid. 1200 conformations were generated, split into six 3 Å Rg bins, with 200 conformations per bin. Another set of conformations was generated with the FADs in place, in their OX states, using metadynamics (Section 2.9 below).SAXS and SANS profiles were calculated from each of the ensembles as described above. These weighted ensemble scattering profiles were fit to experimental data using the lmfit module in python with the Nelder–Mead algorithm.
We ran the GA for 2-, 3-, and 4- conformer ensembles over 75 generations and 5 iterations. These settings were chosen as it was equally likely to find an optimal solution at 25 generations as it was at 100 generations (ESI Fig. S2†) 75 generations provided an efficient compromise permitting 5 repeat simulations with different initial conditions.
2.8. System preparation for metadynamics MD simulations
We started with the X-ray crystal structure of the closed conformer (B-like conformation) of AfeETF (code: 4KPU) but discarded water molecules and ions present in the structure. To append the His6-tag to the C-terminus of EtfA, we employed MODELLER 10.4.81 His-tagged AfeETF with both the flavins was placed at the centre of a dodecahedral box extending a minimum distance of 15 Å from any atom of the protein. The box was filled with TIP3P explicit water molecules82 and 19 sodium ions were added to neutralize the system. The system was minimized using the steepest-descent algorithm to remove any unusual geometry and steric clashes. We then equilibrated the system at 300 K for 500 ps using the Berendsen thermostat with a coupling time of 0.1 ps followed by equilibration at 1 atm. pressure for 5 ns using the Berendsen barostat. All H-bonds were constrained with the LINCS algorithm during system equilibrations.83 All-atom MD simulations were performed with a time-step of 2 fs with the Amber ff14sb force field using the GROMACS 2019.6 suite.84 GAFF compatible parameters for OX FAD were adapted from our previous work.852.9. Metadynamics simulations
We performed metadynamics simulations for 50 ns to sample plausible energetically favourable conformations that might be accessed from the closed conformer (ESI Fig. S3†).61,62 GROMACS patched with PLUMED 2.9 was employed to study the conformational transition of the protein.86 In this enhanced sampling method, a history dependent repulsive Gaussian shaped bias potential is deposited along a collective variable (CV): distance between the centre of masses of the Bf-FAD and ET-FAD based on their non-hydrogen atoms. Gaussians with heights of 0.1 kJ mol−1 and widths of 0.05 nm were deposited every 0.4 ps to fill the energy wells (local minima) and encourage the system to explore the whole free-energy surface in a reasonable computational time. Thus the process favours departure from the starting conformation but does not bias the system towards a predetermined end-point. In the production run, temperature and pressure were regulated using V-rescale and Parrinello-Rahman coupling methods, respectively.87 The coordinates from metadynamics simulations were saved at every 20 ps. We used Gromos' clustering algorithm with an RMSD cut-off value of 2 Å to cluster the conformations adopted by AfeETF during the simulation.88 400 conformations were thereby captured: 20 conformations from each of 20 different clusters.2.10. Analysis of selectively deuterated complexes
Bilbo-MD sampling for the ETF2·BCD2 complex was performed by freezing all the BCD atoms and using the same residue selections as were used for ETF alone. We sampled 1200 conformations with Rg bins between 45 to 55 Å. These 1200 conformations were added to the combined ensemble from the free AfeETF for the GA analysis. SANS profiles were calculated using Pepsi-SANS64 with the same inputs as above at 75% solvent D2O content. BCD non-exchangeable hydrogens were deuterated according to the 70% D2O growth conditions (∼51%), while the exchangeable hydrogens of the whole ETF2·BCD2 complex were deuterated at the 75% solvent D2O conditions with SCOMAP-XD.80 The GA was run as a 3-state model over 5 iterations and 75 generations.2.11. Structural analysis
For each conformation selected by the GA, FADs were restored to each of the head and base independently, based on overlays with the head domain of EtfA, or EtfB's contribution to the base (Etf33-199.B) because EtfB supplies almost all the binding contacts to the Bf-FAD. These overlays produced backbone RMSDs of 1.6 Å or less. The RFAD distance was then determined by calculating the minimum distance between any heavy atom in the isoalloxazine rings of the ET-FAD and Bf-FAD in VMD89 for Bilbo-MD derived structures, or mdtraj for the metadynamics ensembles. The Rg and the RMSD of both ensembles were calculated using mdtraj.90 The RMSD was calculated between backbone and CB atoms vs. the 4KPU or 6FAH structures to provide comparisons to the closed or open conformations, respectively.3 Results
3.1. ETF's scattering cannot be explained by the crystal structures
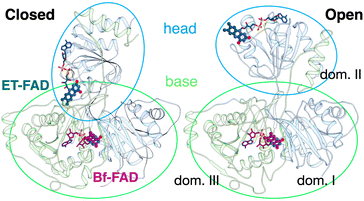
SANS of the OX state of AfeETF revealed complexity not evident from the crystal structures. Whereas pairwise distances approaching 100 ± 10 Å are evident from the pair distance distribution function, (P(r)), the theoretical SANS calculated based on the crystal structures yielded distances no longer than 80 Å, even when the models included the unstructured peptide termini (Fig. 2A, Experimental section 2.6). Neither 4KPU (closed conformation) nor 6FAH (open conformation) was able to explain the experimental profile, yielding χ2 values vs. the data of 86.7 and 96.7, respectively (A good fit is indicated by χ2 values approaching 1, but not larger than 10). The three published open conformation structures have RMSDs to one-another of ≤2.7 Å so they are similar, whereas the RMSD between 6FAH and the closed structure 4KPU is 10.4 Å, highlighting the distinction between open and closed (also see Fig. S4†). Modelling based on the ‘intermediate’ cryo-EM structure did not improve agreement either, as the χ2 of 138.2 was even higher (7KOE, Table 1). The high χ2 values are consistent with the fact that all of the open, intermediate, and closed conformations are compact, with theoretical radii of gyrations, Rgs, no larger than 26 Å (Table 1). Thus, the larger dimensions observed by SANS (Rg = 30.1 ± 0.2 Å and Dmax = 100 ± 10 Å) cannot be explained by any of the solid-state structures. More extended conformation(s) must be populated in solution. | ||
| Fig. 2 SANS demonstrates population of extended conformations in solution, depending on oxidation state. Panels A and B: pairwise distance distribution functions (P(r) profiles), wherein the prevalence (or probability) of scattering sites being separated by a particular distance is plotted vs. the distance separating the two scattering sites, r. Panels C and D: SANS profiles, with corresponding error-normalized residuals (panels E and F). The insets in panels C and D are Guinier fits. Results are compared for the oxidized (OX) state (panels A, C, and E), and the reduced (RED) state (panels B, D, and F). The data (circles) are compared with theoretical SANS and P(r) profiles calculated from the closed conformation (green, AfeETF's crystal structure, 4KPU, augmented to include the terminal His6 tag) and the open conformation (brown dashed line, based on AfeETF's sequence augmented with terminal His6 modelled on 6FAH). All data analyses were performed with Pepsi-SANS64 as described in the Experimental section. The open and closed conformations are compared in Fig. 1 and S4.† Error bars are shown as solid vertical lines. In the P(r) profiles (panels A and B) they are standard deviations based on multiple fits to the data using a series of Monte Carlo simulations,91 while for the SANS profiles (panels C and D), they are derived from counting statistics errors (N1/2/N), where N is the number of detector counts. | ||
| Samples | Oxidized | Reduced (NADH) | Reduced (dithionite) | Oxidized | Oxidized complex w. dBCD |
|---|---|---|---|---|---|
| Technique (solvent) | SANS | SANS (100% D2O) | SANS (100% D2O) | SEC-SAXS (H2O) | SANS (75% D2O) |
| a Errors in the Guinier and P(r) analysis are standard errors from the fits to the SANS and SAXS data. The error estimate for the Dmax is based on the range of input Dmax values that produced acceptable fits to the SANS data. b Theoretical scattering was computed for each structure after modelling the full sequence of AfeETF including N- and C-terminal unstructured amino acids and tags onto the structure in question. Predicted SANS profiles were generated using Pepsi-SANS.64 Due to the wide range of acceptable Dmax values for both RED and OX AfeETF, we fixed the Dmax at 100 for both oxidation states. c Deposited structures were augmented with a His6 tag prior to calculation of Dmax values. d 6FAH is used as a proxy for open conformations in general. RMSDs among different open conformations: 6FAH − 5OL2 = 1.3 Å across all 328 pairs. 6FAH − 7QH2 = 2.7 Å across all 326 pairs. 5OL2 − 7QH2 = 2.9 Å across all 323 pairs. Between open and closed conformations: 6FAH – 4KPU = 10.3 Å across all 327 pairs. e 7KOE has been described as an intermediate state between open and closed. f Values pertain to the ETF only. For the complex: Rg = 47.2 Å, Dmax = 164 Å. | |||||
| Guinier analysis | |||||
| I (0) (cm−1) | 0.577 ± 0.002 | 0.354 ± 0.001 | 0.445 ± 0.001 | 18.5 ± 0.1 | 0.124 ± 0.006 |
| R g (Å) | 30.3 ± 0.2 | 25.8 ± 0.1 | 25.9 ± 0.2 | 27.6 ± 0.1 | 48.7 ± 3.7 |
| Q × Rg range | 0.39–0.98 | 0.44–1.36 | 0.18–1.28 | 0.26–1.29 | 0.34–1.28 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| P(r) analysis | |||||
| I (0) (cm−1) | 0.570 ± 0.002 | 0.358 ± 0.001 | 0.448 ± 0.001 | 18.8 ± 0.1 | 0.122 ± 0.006 |
| R g (Å) | 29.9 ± 0.2 | 26.9 ± 0.1 | 26.8 ± 0.2 | 28.8 ± 0.1 | 53.3 ± 3.2 |
| D max (Å) | 100 ± 10 | 100 ± 10 | 100 ± 10 | 120 ± 10 | 185 ± 7 |
| Q × Rg range | 0.01–0.42 | 0.01–0.49 | 0.01–0.39 | 0.009–0.29 | 0.007–0.21 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| χ 2 of PDB fits | |||||
| χ 2 vs. 4KPU (Rg = 25.3 Å, Dmax = 95.3 Åc) | 86.7 | 22.8 | 23.6 | 7.7 | — |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ2vs.6FAHd (Rg = 25.3 Å, Dmax = 88.5 Å) χ2vs.6FAHd (Rg = 25.3 Å, Dmax = 88.5 Å) |
96.7 | 29.9 | 22.3 | 5.2 | — |
| χ 2 vs. 7KOE (Rg = 24.6 Å, Dmax = 87.9 Å) | 138.2 | 37.9 | 38.7 | 9.6 | — |
| χ 2 vs. 5OL2 (Rg = 25.7 Å, Dmax = 79.8 Å) | — | — | — | — | 2.7 |
3.2. Oxidation state affects the conformation of bifurcating ETF
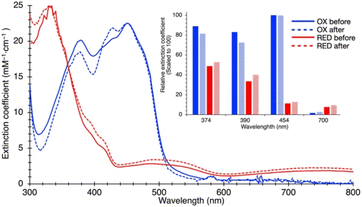
Because ETF's function involves alternation between oxidation states, we tested SANS' ability to detect a redox-coupled conformational change. Moreover, the above disagreement between dimensions detected by SANS and those obtained via X-ray crystallography/cryo-EM could be explained if flavin reduction causes contraction of the ETF, because both of the latter methods reduce the flavins, via the radiation used.46–48We used UV-visible spectra to test for full and sustained reduction of our reduced (RED) ETF samples. We contained our RED samples in custom sample cells with ground glass joints, loaded and sealed in an anaerobic chamber, to exclude air. Upon reduction with NADH, 10-fold diminution of absorbance at 454 nm vs. OX documented flavin reduction to the fully RED hydroquinone state (Fig. 3). Broad features attributable to RED Bf-flavin complexed with NAD+ (λ ≥ 650 nm) were also observed, and retained, documenting sustained reduction of our ETF over the entire period of data collection.
The SANS profile of RED AfeETF indicates a Rg of 25.8 ± 0.1 Å, approximately 4 Å smaller than that of OX AfeETF (Rg of 30.3 ± 0.2 Å, Table 1). There is also a very clear difference between the shapes of the P(r) curves produced by OX and RED samples (Fig. 2). The peak of the P(r) for OX has a shoulder at shorter distances from the maximum, which is not present for reduced AfeETF. Thus, SANS clearly discerns a change, even though flavin reduction is a structurally subtle event, corresponding to addition of a hydride (H−) to each flavin. However, our use of NADH as the reductant allows that binding of this dinucleotide could be the conformational trigger instead, or in addition. To test this, we also collected SANS on AfeETF reduced with the inorganic reductant dithionite. The results were not distinguishable from those obtained using NADH (Fig. S5† and Table 2), indicating that reduction of the flavin(s) suffices to produce the altered solution conformational behaviour, whereas bound nicotinamide dinucleotide is not required. Our finding that nicotinamide dinucleotide binding does not have a large effect is consistent with the fact that conformational dynamics are observed even in canonical ETFs, that do not bind NADH.25,92
| Sample | SAS technique | Source(s) of conformers | Extended conformationsa | Compact conformationsa | χ 2 | ||||
|---|---|---|---|---|---|---|---|---|---|
| Population | R g, (Å) | D max (Å) | Population | R g (Å) | D max (Å) | ||||
| a The extended and compact conformations obtained from each modelling method are listed. | |||||||||
| Oxidized ETF | SANS | Bilbo-MD | 0.52 | 32.3 | 130.3 | 0.48 | 25.1 | 79.7 | 2.7 |
| Metadynamics | 0.61 | 30.8 | 103.1 | 0.39 | 24.5 | 81.8 | 8.3 | ||
| Combined | 0.56 | 32.6 | 129.4 | 0.44 | 24.9 | 83.6 | 1.3 | ||
| Reduced ETF (NADH) | SANS | Bilbo-MD | 0.19 | 34.6 | 123.4 | 0.81 | 25.5 | 93.1 | 5.9 |
| Metadynamics | 0.28 | 30.5 | 101.7 | 0.72 | 25.2 | 84.8 | 13.5 | ||
| Combined | 0.19 | 34.8 | 125.5 | 0.81 | 25.5 | 93.1 | 5.9 | ||
| Reduced ETF (dithionite) | SANS | Bilbo-MD | 0.20 | 34.8 | 125.5 | 0.80 | 25.5 | 93.1 | 7.6 |
| Metadynamics | 0.29 | 30.5 | 101.7 | 0.71 | 25.2 | 84.8 | 19.5 | ||
| Combined | 0.20 | 34.8 | 125.5 | 0.80 | 25.5 | 93.1 | 7.6 | ||
| ‘Oxidized’ ETF | SEC-SAXS | Bilbo-MD | 0.22 | 34.7 | 127.6 | 0.78 | 25.0 | 80.0 | 10.3 |
| Metadynamics | 0.22 | 29.6 | 98.9 | 0.78 | 25.7 | 94.9 | 34.7 | ||
| Combined | 0.22 | 32.3 | 127.6 | 0.78 | 25.0 | 80.0 | 10.3 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| ETF-dBCD complex | |||||||||
| ETF2-dBCD2 complex | SANS | Combined | 0.46 | 29.3 | 107.1 | 0.21 | 25.6 | 96.6 | 0.8 |
| Free/singly bound ETF | 0 | NA | NA | 0.33 | 24.5 | 82.8 | |||
Although reduction of bound flavins produces relatively small local consequences, extensive work on CPR documents that this can drive long-range conformational changes.57 Thus, our finding that flavin reduction decreases the population of extended ETF conformations is consistent with similar conclusions in diverse other systems.54,93 We caution that the fully RED state of AfeETF, wherein both flavins are simultaneously in the HQ state, as well as the fully OX state where both flavins are OX, may have minor physiological relevance. Nevertheless, our comparison of these two oxidation states demonstrates that the system's conformational ensemble is coupled to the oxidation state of at least one of the two flavins.
As for the OX state, SANS of RED AfeETF were incompatible with the predictions of solid-state structures, yielding χ2 values of 22.4 vs.4KPU, and larger values vs. the other structures. Although the disagreement is less severe than for data from OX samples, none of the three static structures explain our RED state SANS profiles (Fig. 2). The SANS profiles display large deviations from the predictions made based on the static structures, especially in the mid-to-high-Q region (see Fig. 2E and F). Additionally, even though the experimental P(r) resembles the shape of the theoretical P(r) from 4KPU, it is unable to reproduce pairwise distances longer than 70 Å.
3.3. SANS-guided MD sampling of the conformational space of AfeETF
Although the SANS of RED AfeETF documents smaller contributions from extended conformations, it is still not explainable by any of the known structures 4KPU, 6FAH or 7KOE. Therefore, we employed two types of molecular dynamics (MD) methods to explore energetically accessible conformations of AfeETF and ensembles thereof, to identify solutions compatible with the data. (1) We modelled rigid body motions of connected domains using Bilbo-MD's CHARMM simulation engine,94,95 and (2) employed an advanced sampling method to accelerate comprehensive exploration of atomistic dynamics (metadynamics61,62). Both approaches initiated their conformational searches with the crystal structure of AfeETF 4KPU augmented to include unstructured residues and the purification tags (Experimental section 2.6).Bilbo-MD simulations explored a broad range of conformations as displayed in the distance between the two FADs (RFAD) plotted vs. the ETF Rg (Fig. 4A and C). Obtained conformations yielded average χ2 values vs. the SANS data of 20.5 and 30.1 for the OX and RED states, respectively. Thus, these explorations yielded improvements vs. the solid-state structures. Fig. 4 colour-codes the quality of fit to SANS data, with intense (dark) colours representing conformations that better fit the data, fits to OX-state data in panels A and B, and fits to RED-state data in panels C and D. The Bilbo conformers with Rg values similar to those of the exemplar structures (4KPU = closed, 6FAH = open and 7KOE is intermediate), had χ2 values from 57 to 107 vs. OX data (blue to light blue, Figure 4A) and 20 to 50 vs. RED data (red to light orange, Fig. 4C), respectively. Thus, the RED state is better described by conformations resembling the experimental structures. This could be because the experimental methods used produced partial reduction.
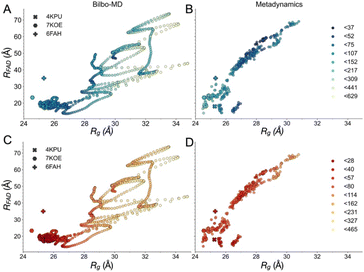 | ||
| Fig. 4 Map of fit to data onto conformational and function-related distances sampled by the Bilbo-MD and metadynamics ensembles. Each point is a structure representing a cluster that emerged from Bilbo-MD (panels A and C) or metadynamics (panels B and D), and is placed according to the minimum distance between any heavy atoms in the two FAD's isoalloxazine (‘flavin’) rings (RFAD, a distance related to speed of electron transfer between the flavins) and the radius of gyration (Rg, characterizing the degree of extension). In the top row, the points are coloured according to fit to OX data (A and B) vs. RED data below (C and D). χ2 values for the fits to the OX (blue to green to yellow) and RED (red to orange to yellow) data were then binned according to the upper limits shown in the legends, in order of low to high χ2. For reference, the values obtained from the exemplar crystal and cryo-EM structures 4KPU (closed), 7KOE (intermediate) and 6FAH (open) are displayed as well, using different symbols. | ||
Conversely, the conformer with the minimum χ2vs. the OX state data (46.2) had a Rg of 29.9 Å and a RFAD of 49.4 Å. The former is 4 Å larger than that of any of the solid-state structures available at the time of writing, and the latter is longer than yet observed in an ETF. In addition, despite the failure of solved structures to explain the larger pairwise distances observed, individual MD conformers that are more extended also failed, as conformers with Rg values greater than 29 Å displayed elevated χ2 values that increased with Rg, for both oxidation states. Thus, simply increasing the Rg of a single model did not yield an improved fit.
The conformers from metadynamics (Fig. 4B and D) covered similar ranges of RFAD and Rg as those covered by Bilbo-MD conformers, but did not sample the most expanded conformations. The best-fitting structures identified by metadynamics also had higher χ2 values than the best-fitting structures obtained by Bilbo-MD, but metadynamics obtained more structures with intermediate Rg and RFAD values (26–28 Å Rg) that produced relatively low values of χ2. Metadynamics also yielded conformers resembling all three of the experimental exemplars. Thus, the less extended RED state produced the same trend of lowest χ2s for shortest distances, for both Bilbo-MD and metadynamics. However, fits to the data from the more extended OX state did better with the intermediate-Rg structures that emerged from metadynamics. Nevertheless, the lowest values of χ2 obtained by individual structures were still unacceptably high (26.6 and 23.2 for the OX and RED states, from metadynamics), despite comprehensive exploration of conformation space.
Since the conformations with intermediate Rg and RFAD values produced some of the lowest χ2 to the OX data, it seemed possible that the correct model contains features of both the extended and compact conformations. Therefore, we quantified the ability of the average of the MD ensembles to describe the scattering data. For the RED state, the average of the conformational ensembles from Bilbo-MD and metadynamics provided similar χ2 values of 30.15 and 33.76, respectively, but these are higher than χ2 values produced by conformers close to the crystal structure (4KPU). However for the OX state, the average scattering profile from the entire ensemble of Bilbo-MD conformers (unweighted) fit the SANS data better (χ2 = 20.5) than did any of the solved structures, or the average of the profiles of the ensemble of metadynamics conformers (χ2 = 43.0).
These results suggest that the OX state, in particular, requires consideration of multiple conformers to describe the data. However, a simple average of all conformers does not account for the experimental results, even for the RED state. Thus, not all conformers are equally likely and/or conformations not sampled are required for a full description.
3.4. Identifying best-matching ensembles of conformers using a genetic algorithm
To determine the minimum number of conformations required to describe the SANS of AfeETF, we employed a genetic algorithm (GA) ensemble optimization search.96,97 We applied it to Bilbo-MD and metadynamics conformational ensembles separately, and combined. Our methodology was inspired by the Bilbo-MD framework,60 but we replaced calculation of SAXS with calculation of SANS, and retained a GA to identify structures and populations that optimize agreement between the simulated and observed SANS data.Optimized ensembles yielded greatly improved fits to data, for both oxidation states. In the OX state, the best ensemble based on Bilbo-MD-derived conformers included two conformations and fit the data with a χ2 value of 2.7 (Table 2). Ensembles with three and four conformations generally yielded larger χ2 values and were therefore not pursued (ESI Table S1†). The optimal 2-conformer model included an extended and a compact conformation with theoretical Rgs of 32.3 and 25.1 Å (Fig. S6A†), accounting for 52 and 48% of the population, respectively (Table 2).
For the RED state, two conformations from Bilbo-MD also sufficed to model the data, yielding a χ2 value of 5.9 for an ensemble in which an extended conformation (Rg = 34.6 Å) described 19% of the population and a compact conformation (Rg = 25.5 Å) was populated to 81%. The extended conformer identified for the RED state is different from than obtained for the OX state (Fig. 6, and S6†). However, the compact conformers identified for the RED and OX states are similar (RMSD of 4.9 Å).
The GA also identified two-conformer models based on conformers from metadynamics, obtaining χ2 values of 8.3 and 13.4 for the OX and RED states, respectively. Again, each optimized ensemble comprised an extended and a compact conformation. The extended conformer accounted for 61% of the population for the OX state but only 28% of the population for the RED state. The larger population of an extended conformation from metadynamics vs. Bilbo-MD could reflect the metadynamics-derived conformations' being less extended (smaller Rgs of 30.8 and 30.5 Å) than the extended conformations identified from the Bilbo-MD ensemble (Rgs of 32.2 and 34.8 Å) and therefore requiring greater population to achieve comparable fit.
When our GA protocol drew upon a pool of conformations derived from both MD methods (‘combined’), the results for the OX state again supported a two-conformer model. Its significantly smaller χ2 value of 1.3 is a 2.0- and 6.4-fold improvement in χ2 compared with models obtained from Bilbo-MD or metadynamics ensembles separately. The resulting model includes an extended conformer similar to the extended conformation obtained from Bilbo-MD alone. However, the compact conformer was selected from metadynamics simulations, from the same region of the χ2 landscape as the crystal structure (4KPU, RMSD of 8.2 Å). The fit to the RED state data was not significantly improved by application of the GA algorithm to a combined ensemble of Bilbo-MD and metadynamics conformations, as indicated by the obtained χ2 value of 5.9. As in the other attempts, a three-conformer model yielded no better fit to RED data, with a χ2 value of 6.0.
The χ2 values relied upon by the GA to optimize models were based on agreement between theoretical and observed scattering profiles. However, a more nuanced appreciation of the distinctions between the models is obtained by comparing theoretical predictions with pairwise distance profiles and Kratky plot presentations of the data (Fig. 5). The theoretical P(r) profiles calculated from GA models (Bilbo-MD, metadynamics, and combined) align well with experimental P(r) profiles for both OX and RED states (Fig. 5A and B, respectively). All three models capture the overall shape of the P(r) curves, including the peak position that represents the most probable distance between pairs of atoms within the protein. In addition, the dimensionless Kratky plots inform on flexibility (Fig. 5C and D). Specifically, the dimensionless Kratky plot for a single globular particle is a bell-shaped profile with a maximum normalized intensity of 1.1 at the normalized Rg of 1.73.98 However, AfeETF displays a maximum that is more elevated and shifted to longer Q × Rg, indicating that it has some degree of flexibility, especially in the OX state. Additionally, both the OX and RED state data show a prominent shoulder at longer Q × Rg ≈ 5 suggesting the presence of multiple domains, consistent with ETF's organization into distinct head and base domains.
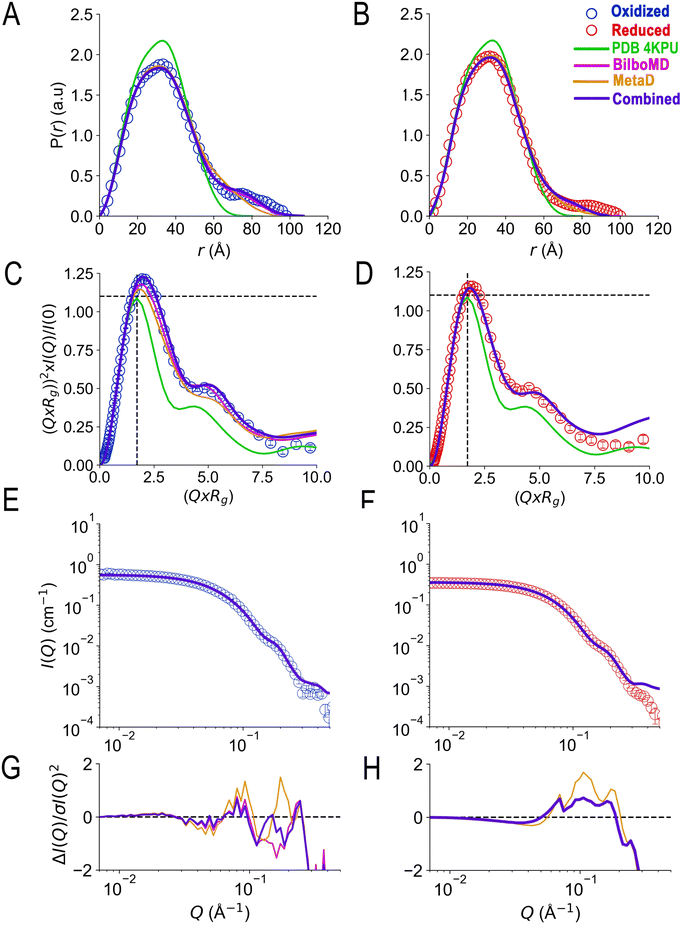 | ||
| Fig. 5 Agreement achieved with SANS data using a genetic algorithm and conformers from Bilbo-MD and metadynamics. Panels A and B compare the agreement with experimental P(r) profiles obtained by various fitting strategies wherein the prevalence (or probability) of scattering sites being separated by a particular distance is plotted vs. the distance separating the two scattering sites, r. Fits to OX P(r) are in panel A and those to RED (NADH) ETF's P(r) are in panel B, with the P(r) data shown as open circles in blue for OX and red for RED. Predictions of the best GA model for each state are the blue solid lines, and the models are those provided in Table 2 with χ2 = 1.3 (OX) and 5.9 (RED). For comparison, the predictions obtained when the GA drew only on subsets of the conformations are also shown: solid magenta lines depict the optimized ensembles employing two Bilbo-MD-derived conformations (χ2 = 2.7 for OX, 5.9 for RED) and gold lines depict those based on two metadynamics-derived conformations (χ2 = 8.3 for OX, and 13.4 for RED). The theoretical P(r) from the AfeETF crystal structure 4KPU is also shown as a green line. Panels C and D are the corresponding normalized Kratky plots. Panels E and F are the corresponding SANS profiles, with their normalized residuals in panels G and H, which also share the horizontal axes of E and F. Error bars are shown as solid vertical lines. For P(r) profiles (panels A and B) they are standard deviations based on multiple fits to the data using a series of Monte Carlo simulations.91 For normalized Kratky plots (panels C and D) they are standard errors propagated from SANS profiles. Errors for the SANS profiles (panels E and F) are derived from counting statistics errors (N1/2/N), where N is the number of detector counts. | ||
Although the GA algorithm achieved slightly better agreement with data when allowed to employ conformations from both Bilbo-MD and metadynamics, all the models employing two conformations greatly outperformed the crystal structures. Thus, we conclude that AfeETF in solution is best described as an ensemble of at least two conformations of which one is similarly compact to the crystal structures or cryo-EM models, but the other conformation is considerably more extended. Although prior work has equated extended conformation to the open conformation, we re-iterate that the structures of the open conformation have Rgs comparable to that of the closed conformation (25.3 Å for both of 6FAH and 4KPU, Table 1, Fig. S4†). Based on their theoretical scattering profiles (Fig. 2) the open and closed conformations documented in crystal structures are not distinguishable by our SANS data. The extended conformation shown by our GA to be essential to a complete description of AfeETF in solution, is an additional conformation.
3.5. Insight into the nature of the extended conformation(s)
Our two MD protocols provided examples of what the extended conformation might look like (Fig. 6). Although those arising from metadynamics retain interactions between the base and head domains, the predictions of the ensembles based on extended conformers from Bilbo-MD agree better with data (Fig. 5). Bilbo-MD-derived ensembles better reproduced observed Kratky plots and P(r) profiles, especially in the region of 70–100 Å (magenta in Fig. 5), than did predictions from models based on metadynamics-derived conformations (gold). This gives credibility to the extended conformations captured by Bilbo-MD, wherein the head domain is essentially detached from the base, only tethered translationally by linker polypeptides but free to rotate (Fig. 6, and S6†). Thus, the conformational ensemble of AfeETF, especially when OX, includes conformations in which the head domain enjoys extensive orientational freedom from the base.We do not claim that our best-fitting ensembles are unique solutions. Instead, we expect that the conformations that suffice to model the data could represent populations that fluctuate about the average conformation chosen by the GA as best fitting. However, the data themselves indicate distinct conformational ensembles for different oxidation states, so we are not surprised that the best-fitting extended conformers deviate from one another significantly. Additional work will be needed to characterize the heterogeneity and dynamic differences between the conformational ensembles populated by the different states of AfeETF.
3.6. Interaction of bifurcating ETF with partner enzyme butyryl CoA dehydrogenase
The open conformation of ETF has only been observed when ETF is complexed with a partner,11,20 suggesting that partner binding alters the relative stabilities of accessible conformers. To investigate the effect of partner binding on the conformation of ETF in solution, we performed SANS experiments using the ETF in complex with the binding partner BCD. To differentiate scattering from ETF from scattering from BCD, we used partially deuterated BCD (dBCD) in combination with protiated ETF at a (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) molar ratio (concentrations of 26 μM). We performed SANS measurements in a 75% D2O buffer to match the scattering from dBCD (minimal contrast between dBCD and the 75% D2O buffer, Fig. S7†). Under these conditions, scattering from protiated (1H) ETF dominates the data after subtraction of buffer contributions (including dBCD). Thus, differences between SANS of ETF vs. SANS from ETF·dBCD are dominated by effects due to conformational changes in ETF alone.
1) molar ratio (concentrations of 26 μM). We performed SANS measurements in a 75% D2O buffer to match the scattering from dBCD (minimal contrast between dBCD and the 75% D2O buffer, Fig. S7†). Under these conditions, scattering from protiated (1H) ETF dominates the data after subtraction of buffer contributions (including dBCD). Thus, differences between SANS of ETF vs. SANS from ETF·dBCD are dominated by effects due to conformational changes in ETF alone.
In the crystal structure of the ETF·BCD complex (5OL2), the BCD is a dimer. Each BCD binds an ETF, and the two ETFs are spatially separated on opposite sides of the BCD dimer (Fig. S8†20). Accordingly, the SANS-based P(r) profile of ETF in the complex indicated an asymmetrical bimodal distribution of molecular densities with peak positions at 28 Å and 125 Å, and higher molecular densities for the first peak than for the second one (Fig. 7). The first peak is consistent with the numerous shorter pairwise distances within each participating ETF. The second peak at longer distances is best explained by scattering between a scatterer in one ETF and a scattering partner in the other. The clear minimum between the modes at 75 Å is consistent with the separation of the two ETFs by an intervening BCD dimer, and the fact that BCD was deuterated and matched by the degree of buffer deuteration so that it would not contribute to the scattering observed. Thus, the position of the null corresponds to half the centre-to-centre distance between two separated ETFs.
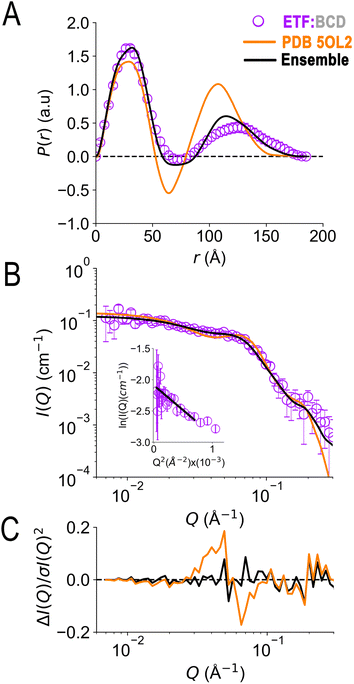 | ||
| Fig. 7 SANS of ETF in the presence of partner protein dBCD, and inadequacies of fits using either compact or extended ETF alone. Scattering from AfeETF is shown as magenta circles, stemming from ETF complexed with deuterated dBCD partner (the dBCD produces no net scattering and therefore does not contribute). Panel A: P(r) profiles, wherein the prevalence (or probability) of scattering sites being separated by a particular distance is plotted vs. the distance separating the two scattering sites, r. Panel B: SANS scattering profiles with Guinier plot as an inset. Panel C: residuals after fitting. The data are compared with the theoretical scattering predicted based the ETF2·BCD2 crystal structure in which the two ETFs are compact (orange lines, 5OL2), as well as predictions obtained from the optimal ensemble based on the combined pool of conformers and described in Table 2 (black lines). These two cases yield χ2 values of 2.7 and 0.8 respectively. Error bars are shown as solid vertical lines. For the P(r) profile (panel A) they are standard deviations based on multiple fits to the data using a series of Monte Carlo simulations,91 while for the SANS profile (panel B), they are derived from counting statistics errors (N1/2/N), where N is the number of detector counts. | ||
Although the longest pairwise distances observed were not predicted based on the crystal structure (>160 Å, Fig. 7) the scattering predicted based on 5OL2 (ref. 20) provided reasonably good agreement with the ETF2·dBCD2 SANS data. The fits were also reasonable when ETF was included in the structural model in a compact or an extended conformation derived from Bilbo-MD sampling. χ2 values of 2.7, 3.2, and 4.1 were obtained for a model based directly on 5OL2, a model allowing replacement of 5OL2's ETF with a Bilbo-MD compact or a model employing extended Bilbo-MD conformations, respectively. However, none of the models incorporating ETF in only one conformation could capture the higher probability densities within the first peak in the P(r) profile. This indicates that an additional scattering contribution for short-range distances must be included in the model. We interpreted this to reflect a small population of ETF that is either free or is bound to a dBCD2 alone, without a neighbouring ETF able to produce long inter-ETF distances. We treated these possibilities by including a population of uncomplexed ETF (since dBCD produces no net scattering).
To find a minimal ensemble of conformations able to describe the SANS of AfeETF complexed to dBCD, we applied our GA approach with 1200 conformations sampled from the BCD-ETF complex Bilbo-MD simulations as well as the 1600 conformations in our combined set of conformations of ETF alone. Therefore, our search considered an ensemble of conformations of two physically separated ETF dimers (bound to BCD) along with some free or singly bound ETF as required by the high probabilities of shorter pairwise distances. The best model is a mixture of 67% ETFs bound on opposite sides of BCD, in an extended (46%) or a compact conformation (21%), together with 33% of ETF in a compact conformation free or bound alone to dBCD. This ensemble yielded a χ2 value of 0.76 vs. the SANS (Table 2).
For the two ETFs in complex with dBCD, our data and analysis indicated a collective Rg of 53.3 ± 3.2 Å. This Rg is significantly larger than the Rg calculated from the 5OL2 starting conformation (Rg of 47.3 Å). Individual ETFs in the complex had Rgs of ≈ 25.6 Å (compact conformation) and ≈ 29 Å (extended). Although the distinction between extended and compact was less pronounced for the ETFs complexed to BCD than for free ETFs, complexation does not appear to trap better-defined conformations, since 69% of the bound ETF populates an extended conformation (vs. 56% of OX ETF in the absence of BCD, Table 2).
3.7. Comparison of SAXS and SANS: possible photoreduction of ETF
Our SANS results are distinct from recently-reported SAXS.41 To test whether the difference could reflect reduction of flavins during irradiation with X-rays,46–48 we compared SAXS data with SANS data in the different oxidation states. SAXS was done following in-line size exclusion chromatography (SEC-SAXS) in air-equilibrated buffers, as for SANS. Thus, AfeETF began the experiments in the OX state with ≈0.25 mM dissolved O2. The latter can reoxidize photoreduced ETF for a while, but may also yield reactive oxygen species in so doing.Analysis of the SEC-SAXS data produced RSAXSg = 27.6 ± 0.1 Å and DSAXSmax = 120 ± 10 Å. These values are distinct from those obtained by SANS (Rg = 30.3 ± 0.2 Å, Dmax = 100 ± 10 Å). Indeed, SAXS and SANS scattering profiles displayed large differences in the high-Q region (Fig. 8C). Specifically, the SANS profile displays a shoulder around 0.2 Å−1, which is much less pronounced in the SAXS profile. Furthermore, the P(r) profile from the SANS data indicates a shoulder at 20 Å in addition to the main peak at 40 Å, whereas the P(r) profile from SAXS indicates a single peak at 35 Å (Fig. 8A), as in our RED state SANS (Fig. 2). Moreover, the SAXS P(r) profile differs significantly from the OX SANS P(r) regarding population of long distances (and therefore the most extended conformations); instead, the SAXS resembles SANS of reduced AfeETF at long values of r. Finally, the normalized Kratky plot of SAXS data lacks the prominent shoulder near Q × Rg = 5 that reveals multiple domains with some degree of mobility relative to one-another, which was clearly observed in SANS experiments.
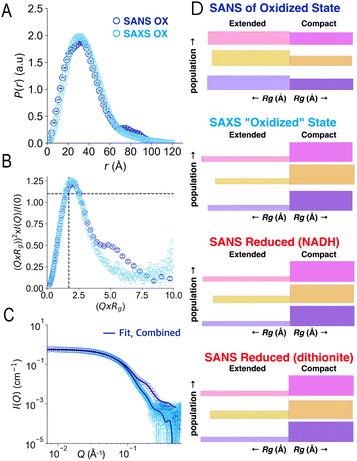 | ||
| Fig. 8 Comparison of SAXS and SANS of OX ETF. Panel A: P(r) profiles, wherein the prevalence (or probability) of scattering sites being separated by a particular distance is plotted vs. the distance separating the two scattering sites, r. Panel B: normalized Kratky plots. Panel C: scattering profiles. Panel D: graphical comparison of the SAXS analysis results (second from top) with those of SANS of the OX state (above) and the two RED states (below). In panel D, results of Bilbo-MD are in magenta/pink, those obtained from metadynamics are in amber/gold and those that were chosen from combined analyses are in violet, as in Fig. 5. In each case the lengths of the horizontal bars depict each conformer's Rg while the thickness (height) of the bar denotes the population of that conformation in the two-conformer ensemble. Thus, compact conformers are more populated in RED states (thicker bars), and the SAXS analysis produces a similar result, whereas fits to OX data yield higher populations of the extended conformations. Error bars are shown as solid vertical lines. For P(r) profiles (panel A) they are standard deviations based on multiple fits to the data using a series of Monte Carlo simulations.91 For normalized Kratky plots (panel B) they are standard errors propagated from SANS profiles. Errors for the SANS profiles (panel C) are derived from counting statistics errors (N1/2/N), where N is the number of detector counts. | ||
Accordingly, application of the GA to the SAXS data using conformations from the combined Bilbo-MD/metadynamics ensembles indicated the population of extended conformers to be only 22% in SAXS experiments. This differs markedly from our SANS results for OX ETF (56% extended) and is almost indistinguishable from our RED SANS results (20% extended, Fig. 8D). The same finding emerges when ensembles were constructed from conformers resulting from Bilbo-MD or from metadynamics (Fig. 8D), demonstrating that the result is independent of our analytical approach. Thus, the use of air-equilibrated buffers did not prevent samples exposed to X-ray rays from behaving as if partially RED. It is therefore simplest to conclude that a significant fraction of the ETF became reduced in the course of SAXS data collection, resulting in adoption of the associated distinct conformational equilibrium.
4 Discussion
4.1. Value of genetic algorithm to optimize ensemble descriptions
Catalytic turnover of ETF is believed to require alternation between two conformations, the closed (or B-like) conformation believed to enable bifurcating electron transfer from the Bf-flavin to the ET-flavin and another acceptor, and the open (or D) conformation in which further electron transfer is presumed to occur from the ET-flavin to a recipient dehydrogenase, BCD in the case of AfeETF.12,20,25,99 Therefore, crystal structures of closed12 and open11,20,26 Bf-ETF served as invaluable reference points for interpreting our SANS results. Indeed, it was the contrast between the predictions made by these structures vs. the SAXS and SANS of AfeETF that demonstrated that AfeETF in solution either adopts a novel conformation or exists in a conformational ensemble including at least one new conformation not known from any prior structural studies.41 Crucially, all ETF structures solved to-date are compact, with Rgs smaller than 26 Å.8,11,12,20,26 However our SANS data require that a substantial fraction of the population in solution must have a Rg of 30 Å or higher.Second, to learn whether conformational changes might be triggered by changes in flavin oxidation state, it is important to have a measurement technique that does not itself produce flavin reduction. This rules out methods that use electromagnetic radiation with wavelengths shorter than 800 nm, such as fluorescence, FRET, X-ray-crystallography and SAXS. Indeed, our results suggest that SAXS data describe partially RED AfeETF even when an OX sample and air-saturated buffer were used. Cryo-EM is also excluded by its use of an intense beam of electrons (reductants by definition). NMR is non-perturbative, but is challenging to apply to proteins larger than 40 kDa and requires high protein concentrations that can result in aggregation. SANS also probes nuclei, however scattering gains effectiveness with increasing molecular weight, making relatively dilute solutions sufficient for data acquisition. Crucially, SANS is compatible with physiological conditions and applies to biomolecules in solution where their propensity for conformational change is not constrained by the experiment.
Scattering projects a tumbling three-dimensional structure into a one-dimensional profile of scattering intensity vs. scattering vector, Q. Although it rarely suffices to define a structure de novo, it can often arbitrate between provided possibilities. Thus, interpretation of scattering data is greatly empowered by tools able to calculate the scattering expected from different structures.64,75 Moreover, such tools can now exploit the rapidly developing reliability of predicted and computed structures,78,100–102 using SANS to validate the structures consistent with observed solution behaviour.103 Thus, the shortcomings of SANS are now complemented by modern structure prediction/calculation, and SANS is positioned to provide the experimental tests that are critical to the credibility and intelligent use of a veritable flood of new structural models.
In the case of ETFs, scattering is also expanding our thinking, thanks to its capacity to test the descriptions provided by conformational ensembles. This requires not only identification of the best-supported structures, but also optimization of the abundance of each.60 We generated a large pool of candidate conformations using two contrasting approaches, to mitigate effects of bias or blind spots associated with individual methods. We used Bilbo-MD60 which maximizes ability to explore large-scale conformational variation by focusing on rigid body movement of domains relative to one-another. To also capture effects of movements within domains, we used the ‘metadynamics’ enhanced MD protocol, which accelerates sampling with respect to a selected collective variable.61 All-told, the combination of the two approaches provided 1600 candidate conformations of AfeETF which were used to model each of the data sets. Bilbo-MD was already validated for modelling SAXS data,60 so we adopted its workflow and generated a GA tool to interpret SANS data.
Our GA employs pools of MD-generated conformations in ensembles of stipulated sizes and compares their scattering predictions with data.60,63,97 Although more complex ensembles were tried, 2 conformations sufficed to minimize χ2, thanks to the structural diversity in our starting sets of conformations. The best fitting ensembles combined conformations generated from both Bilbo-MD and metadynamics that individually exhibited relatively high χ2 values vs. SANS of both OX and RED samples. Indeed, no individual conformation successfully described the scattering results, whereas GA optimized ensembles yielded significant improvement in the χ2 values vs. SANS data.
4.2. AfeETF in solution significantly populates an extended conformation not represented by any existing solid-state model
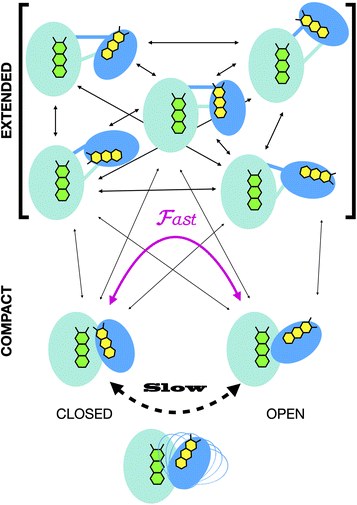
In all cases, the optimized ensembles included an ‘extended’ and a ‘compact’ conformation, so named because they have very different Rgs (as well as ). We do not claim that the ensembles and conformations chosen by the GA are unique solutions. However, we emphasize that all our data require (1) a description in terms of a conformational ensemble of at least two conformations and (2) substantial population of a conformation that is more extended than any previously solved structure. The latter represents more than 50% of the population of OX AfeETF, and is essential to achieve an acceptable description of the behaviour of AfeETF in solution.
). We do not claim that the ensembles and conformations chosen by the GA are unique solutions. However, we emphasize that all our data require (1) a description in terms of a conformational ensemble of at least two conformations and (2) substantial population of a conformation that is more extended than any previously solved structure. The latter represents more than 50% of the population of OX AfeETF, and is essential to achieve an acceptable description of the behaviour of AfeETF in solution.
Our extended conformations cannot be equated with either the open, closed or ‘intermediate’ conformations. This does not reflect avoidance of published structures, as some conformations very similar to published structures were chosen as the compact conformation, including both intermediate and closed conformations (Table 2, and Fig. 6). However, the very similar sizes and shapes of the open and closed conformations make them very difficult to distinguish by SANS (Fig. S4† and see their Rgs and 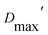 in Table 1). In contrast, none of the extended conformations resembles any published structure, based on their RMSDs vs. either 4KPU or 6FAH of 13.4 Å or higher, vs. RMSDs of 8.4 to 0.9 Å between compact conformers and 4KPU or 6FAH (Table S1†). Similarly, our extended conformers' Rg values for free ETF range from 30.5–34.8 Å, whereas the solid-state structures including both open and closed conformations have Rg values not larger than 25.9 Å (and as small as 24.6 Å).
in Table 1). In contrast, none of the extended conformations resembles any published structure, based on their RMSDs vs. either 4KPU or 6FAH of 13.4 Å or higher, vs. RMSDs of 8.4 to 0.9 Å between compact conformers and 4KPU or 6FAH (Table S1†). Similarly, our extended conformers' Rg values for free ETF range from 30.5–34.8 Å, whereas the solid-state structures including both open and closed conformations have Rg values not larger than 25.9 Å (and as small as 24.6 Å).
4.3. Observation of a reduction-triggered conformation change
Published mechanisms for ETF associate specific electron transfer events with each of the open and closed conformations, but do not exclude population of additional conformations that may play other roles. To interrogate possible mechanistic relevance for the proposed extended conformations, we tested for a correlation between their population and an element of enzymatic turnover: flavin redox state.In the OX state of ETF (both flavins oxidized), the optimized two-conformer ensemble had almost equal populations of the extended and compact conformers (Table 2). However upon reduction with NADH or dithionite, the population distribution shifted to some 80% in compact conformations. Thus, the conformational equilibrium is coupled to the redox states of the ETF's flavins, and hence elements of activity. The compact conformations obtained from the RED ETF data more closely approximate the crystallographic conformations of ETF than those obtained for OX ETF, possibly reflecting partial photoreduction of flavins during the X-ray data collection that led to the crystal structures.
Murray et al. also detected a shift towards more compact conformation upon reduction using NADH, based on SAXS of T. maritima ETF (TmaETF).41 Although they observed a less pronounced effect than we did, this could reflect our use of a fully OX reference state whereas they used as-isolated ETF as the reference, which is already partially reduced. Whilst fully OX ETF may have limited physiological relevance, it constitutes a well-defined reproducible starting point against which to assess changes. Moreover, this choice maximized our ability to detect effects produced by our SAXS conditions (Fig. 8). Thus, we observed a 4.5 Å smaller Rg upon reduction with NADH vs. 2.3 Å in TmaETF. We observed a similarly significant contraction upon reduction with dithionite, in contrast to TmaETF assessed vs. as-isolated. The TmaETF work's use of a reference state that is already partially reduced, and likely accrued additional photoreduction during data collection (Fig. 8), can explain the smaller effects produced by additional chemical reduction.
Nevertheless, our SAXS results agree well with those obtained on TmaETF, and qualitatively similar results were obtained with NADH for the two different ETFs, the AfeETF that partners with an acyl CoA dehydrogenase and TmaETF that partners with a quinone reductase.41 This confirms that the finding is both robust and general.
Our data also produce important insight. First, we noted that both the open and closed conformations are compact, with respect to not only their physical dimensions, but also their abilities to describe scattering data. Prior authors have equated their compact conformation in solution with the closed conformation and their extended conformation with the open conformation, on the basis of the distance between FADs.41 However, simple rotation of the head domain can separate the FADs from one-another without producing a large change in Rg or Dmax (Table 1). Extended conformations also separate the two FADs, but this is not the only way to achieve it. Moreover, neither SANS nor SAXS arbitrates on the proximity of the FADs, so we have only indirect evidence, via the conformance with data of conformations with different inter-FAD distances, to infer how far apart the FADs may be. Specifically, among our compact conformations we have short, intermediate, and long RFADs, so the closed, intermediate, open, and even the sought-after bifurcating conformation (‘true-B’) can be in that category, as required by the short Rg values of the published exemplars. We note that a large population of extended conformer is present in our complex with BCD, but the very large Rg value of the complex as a whole results in best-fitting models where the extended conformation of ETF is not snugly appressed to BCD as would be required to bring their two flavins close together and support electron transfer.
Instead, we emphasize that the extended conformations are novel, not corresponding to any of the previously solved open or closed structures (ESI Tables 1 and S1†).
Third, we find that the more compact behaviour of RED states can be explained by diminished population of extended conformations. Although the extended conformations selected by the GA varied considerably, as expected based on the greater freedom provided by the larger volume of space accessible to them, they always had a Rg at least 4.5 Å larger than that of the compact conformation that co-characterized the ensemble. What changed most with oxidation state was the extended conformation's population. Whereas the ratio of extended to compact was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in OX AfeETF (equivalent to an equilibrium constant of 1), the corresponding ratio was 0.25
1 in OX AfeETF (equivalent to an equilibrium constant of 1), the corresponding ratio was 0.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in the RED states. Thus, the equilibrium appears coupled to the oxidation state of at least one flavin.
1 in the RED states. Thus, the equilibrium appears coupled to the oxidation state of at least one flavin.
Even with minimal observed population of extended conformations, their effective equilibrium constant of 0.25 at 10 °C translates to an energy vs. compact of only 3.3 kJ mol−1 and demonstrates that extended conformations are readily accessible, energetically. Their substantial population increases the possibility that they can be physiologically relevant and contribute to function.
4.4. Functional relevance of models
Our proposed extended conformations may play a role in the accepted mechanism of Bf ETFs.12 This builds on Demmer et al.'s proposal for conformational change as part of turnover20 as refined in subsequent papers.8,11,26,41 In brief, the Bf-flavin is understood to accept a pair of electrons as hydride from NADH. The resulting RED Bf-Flavin then reduces both the ET-flavin and a low-potential acceptor (Fld or Fd) in tightly coupled single-electron transfers.5 This bifurcating event is held to occur in a hypothetical Bifurcating conformation approximated by the closed conformation of Bf-ETFs, where the proximity of the two flavins would maximize the efficiency of ET. The ET-flavin likely rests in its anionic semiquinone state (ASQ10,11) and therefore would assume the HQ state upon reduction (meanwhile the Bf-flavin would have returned to its OX state after also reducing Fld/Fd). To return the ET-flavin to its resting state and complete its catalytic cycle, the ETF must place the ET-flavin in contact with potential electron accepting partners. In the accepted mechanism, this is accomplished by the open (D) conformation.Our data suggest how the required large conformation change can occur. We propose that the extended conformations we observe in solution can mediate the conversion of closed ETF to the open conformation and back, in particular in ETFs that can dissociate from their high-potential partners. Kayastha et al.26 and others have presented a rotation-in-place possibility for the head domain, akin to a morph between the open and closed conformations via the intermediate conformation refined based on cryo-EM.8 Alternatively, or in addition, we suggest that the extended conformations revealed by SANS/SAXS reflect a dynamic conformational reservoir that provides almost friction-free paths between the compact open and closed conformations (Fig. 9).
In both oxidation states, AfeETF populates an ensemble of extended and compact conformations, based on the substantial amplitude of long-distance scattering. Extended conformations identified by the GA show that the newly exposed surfaces of the separated base and head are relatively hydrophilic, consistent with relatively facile detachment of the head, that nonetheless does not result in escape due to the flexible linkers. These properties of AfeETF rationalize the energetic accessibility of the extended conformations. In turn, the extended conformations enable the head domain to rotate freely with greatly diminished constraints (Fig. 6). Upon re-association with the base, the result can be the closed conformation even if the starting point was open, and vice versa.
In catalytic turnover, association with BCD or analogous partners could stabilize the open conformation, ‘extracting’ it from the conformational ensemble sampled via extended conformations. The RED state of the ET flavin could favour this via RED ETF's preference for compact conformations relative to extended. However, upon electron transfer to the BCD partner, the ET flavin would be reoxidized restoring higher preference for extended conformations, and thus detachment from BCD and equilibration with a closed conformation. The latter might then be trapped by binding of the next NADH. The conformational equilibrations would be accelerated by access to the extended conformations in which the energetic barrier between open and closed conformations would be greatly depressed. The fact that compact open conformations were not identified by our GA for our ETF in complex with BCD could be because our sample was fully OX, rather than the RED state of ETF expected to complex most strongly with BCD.
5 Conclusions
Electron bifurcation produces strong reductants at the expense of more weakly reducing starting material, in turn enabling enzymes to drive difficult reactions based on modest but abundant fuel. In Bf-ETFs, 80° rotation of a 25 kDa domain is believed to gate electron transfer to ensure that the high-energy electron is not dissipated. To examine conformational changes in Bf-ETF without perturbing the two flavins, we employed SANS, developing tools to leverage modern computational methods to interpret our data in terms of protein structures. Ensembles of two conformers were required to fit the SANS data, and their relative proportions proved responsive to the oxidation state of the ETF, arguing in favour of catalytic relevance. The extended conformations that emerge are not compatible with any of the previously published structures, open, closed, or intermediate. However, we propose that the ensemble of newly described extended conformations could provide conformational paths for interconversion between the compact open and closed conformations, lowering the kinetic barrier to domain rotation and accelerating a potentially rate-limiting step in catalytic turnover.Data availability
Data supporting this article have been included as part of the ESI.† Primary data have been submitted to the SimpleScattering data repository.Author contributions
SAK: methodology, investigation, validation, visualization, resources, writing – original draft, writing – review & editing. AH: methodology, investigation, validation, visualization, data curation, software, writing – original draft, writing – review & editing. WCL: methodology, investigation, validation, visualization, data curation, writing – original draft, writing – review & editing. JB: investigation, validation, resources. BG: investigation, writing – review & editing. MAM: resources, writing – review & editing, supervision. HON: conceptualization, resources, writing – review & editing, supervision, project administration, funding acquisition. AFM: conceptualization, validation, visualization, resources, writing – original draft, writing – review & editing, supervision, project administration, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
AFM and SAK gratefully acknowledge support from BES DOE under DE-SC0021283 and KY-EPSCoR PON2 635 2000003148 funding to AFM. This research was supported in part by an appointment to the Oak Ridge National Laboratory GRO Program, awarded to SAK and sponsored by Oak Ridge National Laboratory and administered by the Oak Ridge Institute for Science and Education. BG was supported by the Einstein Foundation of Berlin via EVF-2019-503-2 to AFM. AH acknowledges support from the Office of Biological & Environmental Research in the Department of Energy (DOE) Office of Science under project ERKPA14. We are grateful to Nilanjan Pal Chowdhury, Wolfgang Buckel and Russ Hille for sharing with us the expression systems for EtfAB and BCD. Anurag Priyadarshi provided a control, Joel Babbit prepared the customized banjo cells. Qiu Zhang and Kevin Weiss provided technical support for protein production and deuterium labeling. We acknowledge the help and support from Michael Hammel at the Sibyls beamline for access to the Bilbo-MD engine and SIBYLS computational resources. The LiX beamline is part of the Center for BioMolecular Structure (CBMS), which is primarily supported by the National Institutes of Health, National Institute of General Medical Sciences (NIGMS) through a P30 Grant (P30GM133893), and by the DOE Office of Biological and Environmental Research (KP1605010). LiX also received additional support from NIH Grant S10 OD012331. As part of NSLS-II, a national user facility at Brookhaven National Laboratory, work performed at the CBMS is supported in part by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences Program under contract number DE-SC0012704. SANS studies were performed using the Bio-SANS instrument of the Center for Structural Molecular Biology (FWP ERKP291) a Department of Energy Office of Biological and Environmental Research (OBER) Structural Biology Resource. This research used resources at the High Flux Isotope Reactor and Spallation Neutron Source, a U. S. DOE Basic Energy Sciences User Facility operated by the Oak Ridge National Laboratory (ORNL) via proposals IPTS-28650.1 and 29969.1. ORNL is operated by UT-Battelle, LLC under Contract No. DE-AC05-00OR22725 with the U.S. DOE. BG gratefully acknowledges the computing time granted by the Resource Allocation Board and provided on the supercomputers Lise at NHR@ZIB as part of the NHR infrastructure. The metadynamics simulations for this research were conducted with computing resources under the project ‘bec00272’. This manuscript has been coauthored by UT-Battelle, LLC, under contract no. DE-AC05-401 00OR22725 with the U.S. Department of Energy. The United States Government retains, and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for United States Government purposes. The Department of Energy will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan).References
- P. Mitchell, Possible molecular mechanisms of the protonmotive function of cytochrome systems, J. Theor. Biol., 1976, 62, 327–367 CrossRef CAS PubMed.
- P. Mitchell, Protonmotive redox mechanism of the cytochrome b-c1 complex in the respiratory chain: protonmotive ubiquinone cycle, FEBS Lett., 1975, 56, 1–6 CrossRef CAS PubMed.
- P. Mitchell, The protonmotive Q cycle: a general formulation, FEBS Lett., 1975, 59, 137–139 CrossRef CAS PubMed.
- G. Herrmann, E. Jayamani, G. Mai and W. Buckel, Energy conservation via electron-transferring flavoprotein in anaerobic bacteria, J. Bacteriol., 2008, 190, 784–791 CrossRef CAS PubMed.
- N. P. Chowdhury, J. Kahnt and W. Buckel, Reduction of ferredoxin or oxygen by flavin-based electron bifurcation in Megasphaera elsdenii, FEBS J., 2015, 282, 3149–3160 CrossRef CAS PubMed.
- W. Buckel and R. K. Thauer, Flavin-Based Electron Bifurcation, Ferredoxin, Flavodoxin, and Anaerobic Respiration With Protons (Ech) or NAD(+) (Rnf) as Electron Acceptors: A Historical Review, Front. Microbiol., 2018, 9, 401 CrossRef PubMed.
- H. D. Duan, C. E. Lubner, M. Tokmina-Lukaszewska, G. H. Gauss, B. Bothner, P. W. King, J. W. Peters and A. F. Miller, Distinct flavin properties underlie flavin-based electron bifurcation within a novel electron-transferring flavoprotein FixAB from Rhodopseudomonas palustris, J. Biol. Chem., 2018, 293, 4688–4701 CrossRef CAS PubMed.
- X. Feng, G. J. Schut, G. L. Lipscomb, H. Li and M. W. W. Adams, Cryoelectron microscopy structure and mechanism of the membrane-associated electron-bifurcating flavoprotein Fix/EtfABCX, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(2), e2016978118 CrossRef CAS PubMed.
- X. Ge, G. J. Schut, J. Tran, F. L. Poole Ii, D. Niks, K. Menjivar, R. Hille and M. W. W. Adams, Characterization of the Membrane-Associated Electron-Bifurcating Flavoenzyme EtfABCX from the Hyperthermophilic Bacterium Thermotoga maritima, Biochemistry, 2023, 62, 3554–3567 CrossRef CAS PubMed.
- G. J. Schut, N. R. Mohamed-Raseek, M. Tokmina-Lukaszewska, D. E. Mulder, D. M. N. Nguyen, G. L. Lipscomb, J. P. Hoben, A. Patterson, C. E. Lubner, P. W. King, J. W. Peters, B. Bothner, A. F. Miller and M. W. W. Adams, The catalytic mechanism of electron bifurcating electron transfer flavoproteins (ETFs) involves an intermediary complex with NAD+, J. Biol. Chem., 2019, 294, 3271–3283 CrossRef CAS PubMed.
- J. K. Demmer, J. Bertsch, C. Oppinger, H. Wohlers, K. Kayastha, U. Demmer, U. Ermler and V. Muller, Molecular basis of the flavin-based electron-bifurcating caffeyl-CoA reductase reaction, FEBS Lett., 2018, 592, 332–342 CrossRef CAS PubMed.
- N. P. Chowdhury, A. M. Mowafy, J. K. Demmer, V. Upadhyay, S. Koelzer, E. Jayamani, J. Kahnt, M. Hornung, U. Demmer, U. Ermler and W. Buckel, Studies on the mechanism of electron bifurcation catalyzed by electron transferring flavoprotein (Etf) and butyryl-CoA dehydrogenase (Bcd) of Acidaminococcus fermentans, J. Biol. Chem., 2014, 289, 5145–5157 CrossRef CAS PubMed.
- H. Beinert, Spectral characteristics of flavins at the semiquinoid oxidation level, J. Am. Chem. Soc., 1956, 78, 5323–5328 CrossRef CAS.
- C. Thorpe, in Chemistry and Biochemistry of Flavoenzymes, ed. F. Müller, CRC press, Boca Raton FL, 1991, ch. 18, vol. II, pp. 471–486 Search PubMed.
- N. J. Watmough and F. E. Frerman, The electron transfer flavoprotein: Ubiquinone oxidoreductases, Biochim. Biophys. Acta, 2010, 1797, 1910–1916 CrossRef CAS PubMed.
- K. Sato, Y. Nishina and K. Shiga, Electron-transferring flavoprotein has an AMP-binding site in addition to the FAD-binding site, J. Biochem., 1993, 114, 215–222 CrossRef CAS PubMed.
- E. R. DuPlessis, R. J. Rohlfs, R. Hille and C. Thorpe, Electron-transferring flavoproteins from pig and the methylotrophic bacterium W3A1 contains AMP as well as FAD, Biochem. Mol. Biol. Int., 1994, 32, 195–199 CAS.
- K. Sato, Y. Nishina and K. Shiga, Interaction between NADH and electron-transferring flavoprotein from Megasphaera elsdenii, J. Biochem., 2013, 153, 565–572 CrossRef CAS PubMed.
- N. Mohamed-Raseek, H. D. Duan, M. A. Mroginski and A. F. Miller, Spectroscopic, thermodynamic and computational evidence of the locations of the FADs in the nitrogen fixation-associated electron transfer flavoprotein, Chem. Sci., 2019, 10, 7762–7772 RSC.
- J. K. Demmer, N. P. Chowdhury, T. Selmer, U. Ermler and W. Buckel, The semiquinone swing in the bifurcating electron transferring flavoprotein/butyryl-CoA dehydrogenase complex from Clostridium difficile, Nat. Commun., 2017, 8, 1577 CrossRef PubMed.
- J. Sucharitakul, S. Buttranon, T. Wongnate, N. P. Chowdhury, M. Prongjit, W. Buckel and P. Chaiyen, Modulations of the reduction potentials of flavin-based electron bifurcation complexes and semiquinone stabilities are key to control directional electron flow, FEBS J., 2021, 288, 1008–1026 CrossRef CAS PubMed.
- W. Vigil Jr, J. Tran, D. Niks, G. J. Schut, X. Ge, M. W. W. Adams and R. Hille, The reductive half-reaction of two bifurcating electron-transferring flavoproteins: Evidence for changes in flavin reduction potentials mediated by specific conformational changes, J. Biol. Chem., 2022, 298, 101927 CrossRef PubMed.
- D. L. Roberts, F. E. Frerman and J. J. Kim, Three-dimensional structure of human electron transfer flavoprotein to 2.1-A resolution, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 14355–14360 CrossRef CAS PubMed.
- D. L. Roberts, D. Salazar, J. P. Fulmer, F. E. Frerman and J. J. Kim, Crystal structure of Paracoccus denitrificans electron transfer flavoprotein: structural and electrostatic analysis of a conserved flavin binding domain, Biochemistry, 1999, 38, 1977–1989 CrossRef CAS.
- H. S. Toogood, D. Leys and N. S. Scrutton, Dynamics driving function : new insights from electron transferring flavoproteins and partner complexes, FEBS J., 2007, 274, 5481–5504 CrossRef CAS PubMed.
- K. Kayastha, A. Katsyv, C. Himmrich, S. Welsch, J. M. Schuller, U. Ermler and V. Müller, Structure-based electron-confurcation mechanism of the Ldh-EtfAB complex, eLife, 2022, 11, e77095 CrossRef CAS PubMed.
- K. K. Chohan, M. Jones, J. G. Grossmann, F. E. Frerman, N. S. Scrutton and M. J. Sutcliffe, Protein dynamics enhance electronic coupling in electron transfer complexes, J. Biol. Chem., 2001, 276, 34142–34147 CrossRef CAS PubMed.
- M. Jones, J. Basran, M. J. Sutcliffe, J. G. Grossmann and N. S. Scrutton, X-ray scattering studies of Methylophilus methylotrophus (sp W(3)A(1)) electron-transferring flavoprotein – Evidence for multiple conformational states and an induced fit mechanism for assembly with trimethylamine dehydrogenase, J. Biol. Chem., 2000, 275, 21349–21354 CrossRef CAS PubMed.
- J. W. Peters, A. F. Miller, A. K. Jones, P. W. King and M. W. Adams, Electron bifurcation, Curr. Opin. Chem. Biol., 2016, 31, 146–152 CrossRef CAS PubMed.
- E. Darrouzet, M. Valkova-Valchanova, C. C. Moser, P. L. Dutton and F. Daldal, Uncovering the [2Fe2S] domain movement in cytochrome bc1and its implications for energy conversion, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 4567–4572 CrossRef CAS PubMed.
- G. Kurisu, M. Kusunoki, E. Katoh, T. Yamazaki, K. Teshima, Y. Onda, Y. Kimata-Ariga and T. Hase, Structure of the electron transfer complex between ferredoxin and ferredoxin-NADP(+) reductase, Nat. Struct. Biol., 2001, 8, 117–121 CrossRef CAS PubMed.
- C. Xia, S. P. Panda, C. C. Marohnic, P. Martasek, B. S. Masters and J. J. Kim, Structural basis for human NADPH-cytochrome P450 oxidoreductase deficiency, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 13486–13491 CrossRef CAS PubMed.
- M. Wang, D. L. Roberts, R. Paschke, T. M. Shea, B. S. Masters and J. J. Kim, Three-dimensional structure of NADPH-cytochrome P450 reductase: prototype for FMN- and FAD-containing enzymes, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 8411–8416 CrossRef CAS PubMed.
- N. G. Leferink, C. R. Pudney, S. Brenner, D. J. Heyes, R. R. Eady, S. Samar Hasnain, S. Hay, S. E. Rigby and N. S. Scrutton, Gating mechanisms for biological electron transfer: integrating structure with biophysics reveals the nature of redox control in cytochrome P450 reductase and copper-dependent nitrite reductase, FEBS Lett., 2012, 586, 578–584 CrossRef CAS PubMed.
- C. Feng, G. Tollin, M. A. Holliday, C. Thomas, J. C. Salerno, J. H. Enemark and D. K. Ghosh, Intraprotein electron transfer in a two-domain construct of neuronal nitric oxide synthase: the output state in nitric oxide formation, Biochemistry, 2006, 45, 6354–6362 CrossRef CAS PubMed.
- B. L. Greene, A. T. Taguchi, J. Stubbe and D. G. Nocera, Conformationally dynamic radical transfer within ribonucleotide reductase, J. Am. Chem. Soc., 2017, 139, 16657–16665 CrossRef CAS PubMed.
- V. L. Davidson, Protein control of true, gated, and coupled electron transfer reactions, Acc. Chem. Res., 2008, 41, 730–738 CrossRef CAS PubMed.
- K. Chen, J. Hirst, R. Camba, C. A. Bonagura, C. D. Stout, B. K. Burgess and F. A. Armstrong, Atomically defined mechanism for proton transfer to a buried redox centre in a protein, Nature, 2000, 405, 814–817 CrossRef CAS PubMed.
- Y. Hashizume, K. Inaka, N. Furubayashi, M. Kamo, S. Takahashi and H. Tanaka, Methods for Obtaining Better Diffractive Protein Crystals: From Sample Evaluation to Space Crystallization, Crystals, 2020, 10, 78 CrossRef CAS.
- W.-H. Chang, S.-H. Huang, H.-H. Lin, S.-C. Chung and I.-P. Tu, Cryo-EM Analyses Permit Visualization of Structural Polymorphism of Biological Macromolecules, Front. Bioinform., 2021, 1, 788308 CrossRef PubMed.
- D. T. Murray, X. Ge, G. J. Schut, D. J. Rosenberg, M. Hammel, J. C. Bierma, R. Hille, M. W. W. Adams and G. L. Hura, Correlating Conformational Equilibria with Catalysis in the Electron Bifurcating EtfABCX of Thermotoga maritima, Biochemistry, 2024, 63, 128–140 CrossRef CAS PubMed.
- S. Fieulaine, A. Boularot, I. Artaud, M. Desmadril, F. Dardel, T. Meinnel and C. Giglione, Trapping Conformational States Along Ligand-Binding Dynamics of Peptide Deformylase: The Impact of Induced Fit on Enzyme Catalysis, PLoS Biol., 2011, 9, e1001066 CrossRef CAS PubMed.
- E. D’Imprima and W. Kühlbrandt, Current limitations to high-resolution structure determination by single-particle cryoEM, Q. Rev. Biophys., 2021, 54, 1–15 CrossRef PubMed.
- J. Ellis, A. Gutierrez, I. L. Barsukov, W. C. Huang, J. G. Grossmann and G. C. K. Roberts, Domain motion in cytochrome P450 reductase: conformational equilibria revealed by NMR and small-angle x-ray scattering, J. Biol. Chem., 2009, 284, 36628–36637 CrossRef CAS PubMed.
- A. M. Bodenheimer, W. B. O'Dell, R. C. Oliver, S. Qian, C. B. Stanley and F. Meilleur, Structural investigation of cellobiose dehydrogenase IIA: Insights from small angle scattering into intra- and intermolecular electron transfer mechanisms, Biochim. Biophys. Acta, 2018, 1862, 1031–1039 CrossRef CAS PubMed.
- D. S. Berkholz, H. R. Faber, S. N. Savvides and P. A. Karplus, Catalytic cycle of human glutathione reductase near 1 A resolution, J. Mol. Biol., 2008, 382, 371–384 CrossRef CAS PubMed.
- R. Kort, H. Komori, S. Adachi, K. Miki and A. Eker, DNA apophotolyase from Anacystis nidulans: 1.8 A structure, 8-HDF reconstitution and X-ray-induced FAD reduction, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2004, 60, 1205–1213 CrossRef PubMed.
- R. Johansson, E. Torrents, D. Lundin, J. Sprenger, M. Sahlin, B.-M. Sjöberg and D. T. Logan, High-resolution crystal structures of the flavo-protein NrdI in oxidized and reduced states—an unusual flavodoxin, FEBS J., 2010, 277, 4265–4277 CrossRef CAS PubMed.
- B. Prevo and E. J. Peterman, Forster resonance energy transfer and kinesin motor proteins, Chem. Soc. Rev., 2014, 43, 1144–1155 RSC.
- K. Brunner, A. Tortschanoff, B. Hemmens, P. J. Andrew, B. Mayer and A. J. Kungl, Sensitivity of flavin fluorescence dynamics in neuronal nitric oxide synthase to cofactor-induced conformational changes and dimerization, Biochemistry, 1998, 37, 17545–17553 CrossRef CAS PubMed.
- S. D. M. Islam, T. Susdorf, A. Penzkofer and P. Hegemann, Fluorescence quenching of flavin adenine dinucleotide in aqueous solution by pH dependent isomerisation and photo-induced electron transfer, Chem. Phys., 2003, 295, 137–149 CrossRef CAS.
- R. Ashkar, H. Z. Bilheux, H. Bordallo, R. Briber, D. J. E. Callaway, X. Cheng, X. Q. Chu, J. E. Curtis, M. Dadmun, P. Fenimore, D. Fushman, F. Gabel, K. Gupta, F. Herberle, F. Heinrich, L. Hong, J. Katsaras, Z. Kelman, E. Kharlampieva, G. R. Kneller, A. Kovalevsky, S. Krueger, P. Langan, R. Lieberman, Y. Liu, M. Losche, E. Lyman, Y. Mao, J. Marino, C. Mattos, F. Meilleur, P. Moody, J. D. Nickels, W. B. O'Dell, H. O'Neill, U. Perez-Salas, J. Peters, L. Petridis, A. P. Sokolov, C. Stanley, N. Wagner, M. Weinrich, K. Weiss, T. Wymore, Y. Zhang and J. C. Smith, Neutron scattering in the biological sciences: progress and prospects, Acta Crystallogr., Sect. D: Struct. Biol., 2018, 74, 1129–1168 CrossRef CAS.
- D. T. Murray, K. L. Weiss, C. B. Stanley, G. Nagy and M. E. Stroupe, Small-angle neutron scattering solution structures of NADPH-dependent sulfite reductase, J. Struct. Biol., 2021, 213, 107724 CrossRef CAS PubMed.
- D. T. Murray, N. Walia, K. L. Weiss, C. B. Stanley, P. S. Randolph, G. Nagy and M. E. Stroupe, Neutron scattering maps the higher-order assembly of NADPH-dependent assimilatory sulfite reductase, Biophys. J., 2022, 121, 1799–1812 CrossRef CAS PubMed.
- R. Parfait, B. De Wolf and R. R. Crichton, Protein-RNA interactions in the Escherichia coli ribosome: L24 protein-23 S RNA complex, Arch. Int. Physiol. Biochim., 1976, 84, 404–405 CAS.
- R. R. Crichton, D. M. Engleman, J. Haas, M. H. Koch, P. B. Moore, R. Parfait and H. B. Stuhrmann, Contrast variation study of specifically deuterated Escherichia coli ribosomal subunits, Proc. Natl. Acad. Sci. U. S. A., 1977, 74, 5547–5550 CrossRef CAS PubMed.
- S. L. Freeman, A. Martel, E. L. Raven and G. C. K. Roberts, Orchestrated Domain Movement in Catalysis by Cytochrome P450 Reductase, Sci. Rep., 2017, 7, 9741 CrossRef PubMed.
- S. L. Freeman, A. Martel, J. M. Devos, J. Basran, E. L. Raven and G. C. K. Roberts, Solution structure of the cytochrome P450 reductase-cytochrome c complex determined by neutron scattering, J. Biol. Chem., 2018, 293, 5210–5219 CrossRef CAS PubMed.
- W. T. Heller and K. C. Littrell, in Micro and Nano Technologies in Bioanalysis, ed. J. W. Lee and R. S. Foote, Humana Press, 2009, vol. 544, pp. 293–305 Search PubMed.
- M. Pelikan, G. L. Hura and M. Hammel, Structure and flexibility within proteins as identified through small angle X-ray scattering, Gen. Physiol. Biophys., 2009, 28, 174–189 CrossRef CAS.
- G. Bussi and A. Laio, Using metadynamics to explore complex free-energy landscapes, Nat. Rev. Phys., 2020, 2, 200–212 CrossRef.
- A. Laio and M. Parrinello, Escaping free-energy minima, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS PubMed.
- D. Schneidman-Duhovny, M. Hammel, J. A. Tainer and A. Sali, FoXS, FoXSDock and MultiFoXS: Single-state and multi-state structural modeling of proteins and their complexes based on SAXS profiles, Nucleic Acids Res., 2016, 44, W424–W429 CrossRef CAS PubMed.
- S. Grudinin, M. Garkavenko and A. Kazennov, Pepsi-SAXS: an adaptive method for rapid and accurate computation of small-angle X-ray scattering profiles, Acta Crystallogr., Sect. D: Struct. Biol., 2017, 73, 449–464 CrossRef CAS PubMed.
- W. T. Heller, Small-angle neutron scattering and contrast variation: a powerful combination for studying biological structures, Acta Crystallogr., 2010, D66, 1213–1217 CrossRef.
- N. Mohamed-Raseek, C. van Galen, R. Stanley and A. F. Miller, Unusual reactivity of a flavin in a bifurcating electron-transferring flavoprotein leads to flavin modification and a charge-transfer complex, J. Biol. Chem., 2022, 298, 102606 CrossRef CAS PubMed.
- W. C. Leite, K. L. Weiss, G. Phillips, Q. Zhang, S. Qian, S. E. Tsutakawa, L. Coates and H. O'Neill, Conformational Dynamics in the Interaction of SARS-CoV-2 Papain-like Protease with Human Interferon-Stimulated Gene 15 Protein, J. Phys. Chem. Lett., 2021, 12, 5608–5615 CrossRef CAS PubMed.
- J. Marley, M. Lu and C. Bracken, A method for efficient isotopic labeling of recombinant proteins, J. Biomol. NMR, 2001, 20, 71–75 CrossRef CAS PubMed.
- W. T. Heller, V. S. Urban, G. W. Lynn, K. L. Weiss, H. M. O'Neill, S. V. Pingali, S. Qian, K. C. Littrell, Y. B. Melnichenko, M. V. Buchanan, D. L. Selby, G. D. Wignall, P. D. Butler and D. A. Myles, The Bio-SANS instrument at the High Flux Isotope Reactor of Oak Ridge National Laboratory, J. Appl. Crystallogr., 2014, 47, 1238–1246 CrossRef CAS.
- X. Yao, B. Avery, M. Bobrek, L. Debeer-Schmitt, X. Geng, R. Gregory, G. Guyotte, M. Harrington, S. Hartman, L. He, L. Heroux, K. Kasemir, R. Knudson, J. Kohl, C. Lionberger, K. C. Littrell, M. Pearson, S. V. Pingali, C. Pratt, S. Qian, M. Ruiz-Rodrigues, V. Sedov, G. Taufer, V. Urban and K. Vodopivec, A Unified User-Friendly Instrument Control and Data Acquisition System for the ORNL SANS Instrument Suite, Appl. Sci., 2021, 11, 1216 CrossRef CAS.
- O. Arnold, J. C. Bilheux, J. M. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. Ferraz Leal, M. A. Gigg, V. E. Lynch, A. Markvardsen, D. J. Mikkelson, R. L. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. G. Perring, P. F. Peterson, S. Ren, M. A. Reuter, A. T. Savici, J. W. Taylor, R. J. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Mantid—Data analysis and visualization package for neutron scattering and SR experiments, Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip., 2014, 764, 156–166 CrossRef CAS.
- W. T. Heller, J. Hetrick, J. Bilheux, J. M. B. Calvo, W.-R. Chen, L. DeBeer-Schmitt, C. Do, M. Doucet, M. R. Fitzsimmons, W. F. Godoy, G. E. Granroth, S. Hahn, L. He, F. Islam, J. Lin, K. C. Littrell, M. McDonnell, J. McGaha, P. F. Peterson, S. V. Pingali, S. Qian, A. T. Savici, Y. Shang, C. B. Stanley, V. S. Urban, R. E. Whitfield, C. Zhang, W. Zhou, J. J. Billings, M. J. Cuneo, R. M. F. Leal, T. Wang and B. Wu, Drtsans: The data reduction toolkit for small-angle neutron scattering at Oak Ridge National Laboratory, SoftwareX, 2022, 7, 101101 CrossRef.
- J. DiFabio, S. Chodankar, S. Pjerov, J. Jakoncic, M. Lucas, C. Krywka, V. Graziano and L. Yang, The Life Science X-ray Scattering Beamline at NSLS-II, AIP Conf. Proc., 2016, 1741, 030049 CrossRef.
- L. Yang, S. Antonelli, S. Chodankar, J. Byrnes, E. Lazo and K. Qian, Solution scattering at the Life Science X-ray Scattering (LiX) beamline, J. Synchrotron Radiat., 2020, 27, 804–812 CrossRef PubMed.
- D. Franke, M. V. Petoukhov, P. V. Konarev, A. Panjkovich, A. Tuukkanen, H. D. T. Mertens, A. G. Kikhney, N. R. Hajizadeh, J. M. Franklin, C. M. Jeffries and D. I. Svergun, ATSAS 2.8: a comprehensive data analysis suite for small-angle scattering from macromolecular solutions, J. Appl. Crystallogr., 2017, 50, 1212–1225 CrossRef CAS PubMed.
- J. B. Hopkins, R. E. Gillilan and S. Skou, BioXTAS RAW: improvements to a free open-source program for small-angle X-ray scattering data reduction and analysis, J. Appl. Crystallogr., 2017, 50, 1545–1553 CrossRef CAS PubMed.
- D. I. Svergun, Determination of the regularization parameter in indirect-transform methods using perceptual criteria, J. Appl. Crystallogr., 1992, 25, 495–503 CrossRef CAS.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Zidek, A. Potapenko, A. Bridgland, C. Meyer, S. A. A. Kohl, A. J. Ballard, A. Cowie, B. Romera-Paredes, S. Nikolov, R. Jain, J. Adler, T. Back, S. Petersen, D. Reiman, E. Clancy, M. Zielinski, M. Steinegger, M. Pacholska, T. Berghammer, S. Bodenstein, D. Silver, O. Vinyals, A. W. Senior, K. Kavukcuoglu, P. Kohli and D. Hassabis, Highly accurate protein structure prediction with AlphaFold, Nature, 2021, 596, 583–589 CrossRef CAS PubMed.
- M. Mirdita, K. Schutze, Y. Moriwaki, L. Heo, S. Ovchinnikov and M. Steinegger, ColabFold: making protein folding accessible to all, Nat. Methods, 2022, 19, 679–682 CrossRef CAS PubMed.
- A. Hicks, P. Abraham, W. Leite, Q. Zhang, K. L. Weiss, H. O'Neill, L. Petridis and J. C. Smith, SCOMAP-XD: atomistic deuterium contrast matching for small-angle neutron scattering in biology, Acta Crystallogr., 2023, D79, 420–434 Search PubMed.
- A. Šali and T. L. Blundell, Comparative protein modelling by satisfaction of spatial restraints, J. Mol. Biol., 1993, 234, 779–815 CrossRef.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of Simple Potential Functions for Simulating Liquid Water, J. Chem. Phys., 1983, 926–935 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- M. González-Viegas, R. K. Kar, A. F. Miller and M. A. Mroginski, Noncovalent interactions that tune the reactivities of the flavins in bifurcating electron transferring flavoprotein, J. Biol. Chem., 2023, 299, 104762 CrossRef PubMed.
- M. Bonomi, D. Branduardi, G. Bussi, C. Camilloni, D. Provasi, P. Raiteri, D. Donadio, F. Marinelli, F. Pietrucci, R. A. Broglia and M. Parrinello, PLUMED: A portable plugin for free-energy calculations with molecular dynamics, Comput. Phys. Commun., 2009, 180, 1961–1972 CrossRef CAS.
- G. Bussi, T. Zykova-Timan and M. Parrinello, Isothermal-isobaric molecular dynamics using stochastic velocity rescaling, J. Chem. Phys., 2009, 130, 074101 CrossRef PubMed.
- X. Daura, W. F. van Gunsteren, B. Jaun, A. E. Mark, K. Gademann and D. Seebach, Peptide Folding: When Simulation Meets Experiment, Angew. Chem., Int. Ed., 1999, 38, 236–240 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, VMD – Visual Molecular Dynamics, J. Mol. Graphics, 1996, 33–38 CrossRef CAS PubMed.
- R. T. McGibbon, K. A. Beauchamp, M. P. Harrigan, C. Klein, J. M. Swails, C. X. Hernández, C. R. Schwantes, L.-P. Wang, T. J. Lane and V. S. Pande, MDTraj: A Modern Open Library for the Analysis of Molecular Dynamics Trajectories, Biophys. J., 2015, 109, 1528–1532 CrossRef CAS PubMed.
- D. I. Svergun and J. S. Pedersen, Propagating Errors in Small Angle Scattering Data Treatment, J. Appl. Crystallogr., 1994, 27, 241–248 CrossRef CAS.
- D. Leys, J. Basran, F. Talfournier, M. J. Sutcliffe and N. S. Scrutton, Extensive conformational sampling in a ternary electron transfer complex, Nat. Struct. Biol., 2003, 10, 219–225 CrossRef CAS PubMed.
- G. Kang, A. T. Taguchi, J. Stubbe and C. L. Drennan, Structure of a trapped radical transfer pathway within a ribonucleotide reductase holocomplex, Science, 2020, 368, 424–427 CrossRef CAS PubMed.
- B. R. Brooks, R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan and M. Karplus, Charmm – a Program for Macromolecular Energy, Minimization, and Dynamics Calculations, J. Comput. Chem., 1983, 4, 187–217 CrossRef CAS.
- B. R. Brooks, C. L. Brooks, A. D. Mackerell, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, CHARMM: The Biomolecular Simulation Program, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS PubMed.
- G. Tria, H. D. T. Mertens, M. Kachala and D. I. Svergun, Advanced ensemble modelling of flexible macromolecules using X-ray solution scattering, IUCrJ, 2015, 2, 207–217 CrossRef CAS PubMed.
- P. Bernadó, E. Mylonas, M. V. Petroukhow, M. Blackledge and D. I. Svergun, Structural characterization of flexible proteins using small-angle X-ray scattering, J. Am. Chem. Soc., 2007, 129, 5656–5664 CrossRef PubMed.
- S. Da Vela and D. I. Svergun, Methods, development and applications of small-angle X-ray scattering to characterize biological macromolecules in solution, Curr. Res. Struct. Biol., 2020, 2, 164–170 CrossRef PubMed.
- H. S. Toogood, A. van Thiel, N. S. Scrutton and D. Leys, Stabilization of non-productive conformations underpins rapid electron transfer to electron transferring flavoprotein, J. Biol. Chem., 2005, 280, 30361–30366 CrossRef CAS PubMed.
- M. Baek, F. DiMaio, I. Abnishchenko, J. Dauparas, S. Ovchinnikov, G. R. Lee, J. Wang, Q. Cong, L. N. Kinch, R. D. Schaeffer, C. Millan, H. J. Park, C. Adams, C. R. Glassman, A. DeGiovanni, J. H. Pereira, A. V. Rodriques, A. A. van Dijk, A. C. Ebrecht, D. J. Opperman, T. Sagmeister, C. Buhlheller, T. Pavkov-Keller, M. K. Rathinaswamy, U. Dalwadi, C. K. Yip, J. E. Burke, K. C. Garcia, N. V. Grishin, P. D. Adams, R. J. Read and D. Baker, Accurate prediction of protein structures and interactions using a three-track neural network, Science, 2021, 373, 871–876 CrossRef CAS PubMed.
- I. Roterman, A. Sieradzan, K. Stapor, P. Fabian, P. Wesolowski and L. Konieczny, On the need to introduce environmental characteristics in ab initio protein structure prediction using a coarse-grained UNRES force field, J. Mol. Graphics Modell., 2022, 114, 108166 CrossRef CAS PubMed.
- S. M. Mortuza, W. Zheng, C. Zhang, Y. Li, R. Pearce and Y. Zhang, Improving fragment-based ab initio protein structure assembly using low-accuracy contact-map predictions, Nat. Commun., 2021, 12, 5011 CrossRef CAS PubMed.
- J. Trewhella, Small-angle scattering and 3D structure interpretation, Curr. Opin. Struct. Biol., 2016, 40, 1–7 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Technical considerations attending the genetic algorithm, a table and 7 figures. See DOI: https://doi.org/10.1039/d4sc04544k |
| This journal is © The Royal Society of Chemistry 2024 |