Revisiting a classic carbocation – DFT, coupled-cluster, and ab initio molecular dynamics computations on barbaralyl cation formation and rearrangements

Abstract

Density functional theory computations were used to model the formation and rearrangement of the barbaralyl cation (C₉H⁺₉). Two highly delocalized minima were located for C₉H⁺₉, one of C_s symmetry and the other of D_3h symmetry, with the former having lower energy. Quantum chemistry-based NMR predictions affirm that the lower energy structure is the best match with experimental spectra. Partial scrambling was found to proceed through a C₂ symmetric transition structure associated with a barrier of only 2.3 kcal mol⁻¹. The full scrambling was found to involve a C_2v symmetric transition structure associated with a 5.0 kcal mol⁻¹ barrier. Ab initio molecular dynamics simulations initiated from the D_3h C₉H⁺₉ structure revealed its connection to six minima, due to the six-fold symmetry of the potential energy surface. The effects of tunneling and boron substitution on this complex reaction network were also examined.

---

1 Introduction

A question driving many classic studies in the realm of physical organic chemistry is how many minima exist for a particular structure? For example, does a particular structure reside in one well or two on a potential energy surface (PES), with the two in the latter case rapidly interconverting through a low barrier? This question is intimately tied to the degree of delocalization in organic structures. The most famous examples of this type of issue involve “the nonclassical ion problem” (i.e., cyclic 3-center 2-electron delocalization)^1–6 and the search for “stable transition states” for Cope reactions (i.e., neutral homoaromaticity).^7–10 But if barriers between minima are very low (how low depends on the temperature) it doesn't really matter if these barriers exist, i.e., very shallow minima and a flat PES are not expected to show differences in dynamical behavior.¹¹ Consequently, some felt and feel that such issues were not worthy of investigation and even forcefully complained that discussions (which often devolved into viperous arguments) may well have irreparably damaged the field of physical organic chemistry. Nonetheless, the one-well-or-two issue has led to many insights into electronic structure and associated reactivity that remain relevant today, raising their heads in contexts ranging from natural product biosynthesis to transition metal-promoted C–H insertion.^12–15

Here we address structural and reactivity/dynamic issues for a classic carbocation with a putative nonclassical structure for which the number and identities of minima on its PES have long been uncertain: the barbaralyl cation (Scheme 1). As demonstrated by our computational results, this carbocation brings together the concepts of hyperconjugation (acyclic 3-center 2-electron delocalization),^16,17 nonclassical bridging (cyclic 3-center 2-electron delocalization),^1–6 through-bond coupling,¹⁸ homo/σ-aromaticity,^{7–10,19–22} sigmatropic shifts with low/no barriers (stable transition states?),^7–10,23 synchronicity,^24,25 entropic intermediates,²⁶ fluxionality,^14,27–29 non-statistical dynamic effects on calderas/mesas,^30–34 post-transition state bifurcations (PTSBs),^{11,30,35–39} inter-transition state roaming,^11,40,41 and tunneling.^42–45 While previous computational studies have elucidated scrambling mechanisms of some nonclassical carbocation rearrangements,^46–49 we cannot think of another carbocation, or any structure, that showcases so many principles of structure and reactivity, ranging from those appreciated a half-century ago or more to those only recently being recognized.

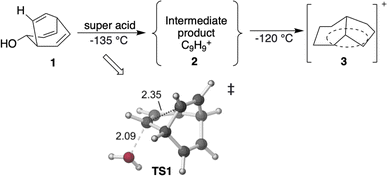Scheme 1 Previous experiments on C₉H⁺₉ cations.⁵⁰ The transition state TS1 is visualized using CYLview 1.0,⁵¹ with key bond lengths labeled in Å. The C–O bond breaks first, and the C–C bond formation occurs subsequently in an asynchronous manner (see ESI† for details).

1.1 C₉H⁺₉ barbaralyl cation

The C₉H⁺₉ barbaralyl cation has been studied both experimentally and computationally for decades. In 1970, Winstein and co-workers reported that C₉H⁺₉ (2) could be generated by reacting bicyclo[3.2.2]-nona-3,6,8-trien-2-ol (1) at −135 °C with superacid (FSO₃H-SO₂ClF in CD₂Cl₂) (Scheme 1) (following up on earlier solvolysis studies with a different substrate by Schleyer and co-workers).^50,52 Subsequently, NMR experiments led to various insights into the structure of 2. A key observation was that, at −135 °C both the ¹H and ¹³C NMR spectra of 2 contain only a single peak: a singlet at 6.6 ppm for ¹H and a peak at 118.5 ppm for ¹³C.^53,54 These results indicate that either nine CH groups are equivalent in the geometry of 2 or rapid equilibration during the NMR experiment leads to complete scrambling of all CHs. Since a regular polyhedron with nine vertices does not exist, and since cyclononatetraenyl cation possesses 8π electrons – a number associated with antiaromaticity or a Möbius topology,^20,21,55 it is very likely that fluxional isomerization is the cause of the simplicity of the NMR spectra.^53,54 In contrast, bullvalene (C₁₀H₁₀) only interchanges its CH groups when the temperature is raised to over 100 °C.⁵⁶ Moreover, as the temperature was decreased to −150 °C, the 118.5 ppm ¹³C NMR signal of 2 split to two peaks at 101 and 152 ppm with a 6 : 3 integration ratio, consistent with a rearrangement that slows at low temperature.^53,54 These experiments provide important constraints on the nature of the rearrangement and associated barrier heights.

While the first computational study was reported at the MINDO/3 level in 1989,⁵⁷ Cremer and co-workers proposed a “pound cake”-shaped PES with two types of minima and three transition structures (Fig. 1) in 1993 on the basis of the results of calculations conducted at the MP4(SDQ)/6-31G(d) level of theory.⁵⁸ More recently, Werstiuk revisited this PES along with QTAIM-DI-VISAB analysis at the B3PW91/aug-cc-pVTZ and CCSD(full)/6–31+G(d,p) levels of theory.⁵⁹ Other related works have examined the topology of the barbaralyl cation^12,60–62 and the less fluxional barbaralyl radical⁶¹ and barbaralone.^29,63

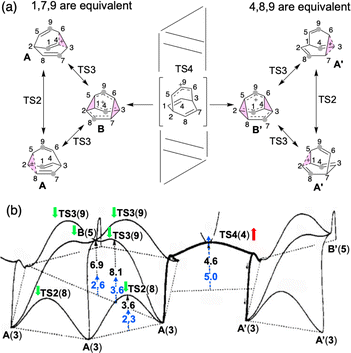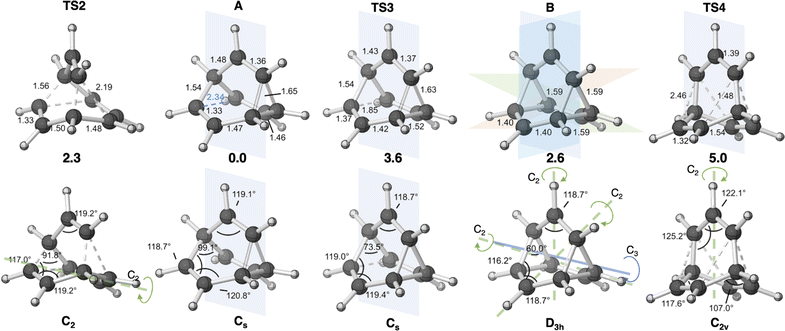
Fig. 1 (a) Outline of the computed mechanism of barbaralyl cation scrambling. The equivalent carbons in the middle are highlighted with grey circles for the partial scrambling process. (b) Energy profile depicted in 1993 based on MP4(SDQ)/6-31G(d) results (reproduced with permission from ref. 58). Relative free energies determined here with DLPNO-CCSD(T)/CBS//CAM-B3LYP/6-31G(d) at 138.15 K (−135 °C) have been added (blue). Green and red arrows also have been added to indicate whether the energies increased or decreased compared to the previous results. Numbers in parentheses are the structure numbers from ref. 58.

Here, we focus on the fluxionality of barbaralyl cation. A comprehensive benchmarking study using prevalent quantum mechanical methods was carried out, since the PES in question has rather flat regions. In addition, ab initio molecular dynamics (AIMD) simulations were used to characterize rearrangements.^{11,34,36–38,64–66} Our results indicate that the highly delocalized nature of C₉H⁺₉ structures gives rise to an unusual PES that supports complex dynamic effects. Beyond shedding light on the specific case of the barbaralyl cation itself, this study also points to potentially general considerations for the interplay of structure, stability, and dynamics in fluxional systems.^{7–9,14,27–29,67–69}

2 Computational methods

Initially, we performed geometry optimization using the M06-2X/def2-TZVP level of theory^70,71 with Gaussian 16 C.01,⁷² due to its widely acknowledged robustness for molecules composed of main group elements⁷³ and its previous use for carbocations.^74–78 Single point energy corrections were then computed at the DLPNO-CCSD(T)/CBS level of theory using ORCA 5.0.4.^79–81 Basis set extrapolation to the complete basis set (CBS) limit was performed using the focal point analysis approach employing def2-TZVPP and def2-QZVPP basis sets.^71,82,83 The TightPNO cutoff was used for the local coupled cluster calculations and iterative triples corrections were used.⁸⁴Quasi-harmonic thermochemical corrections were obtained using the GoodVibes package.^85,86 With this approach, one transition structure reported previously (TS2) was not found.^58,59 Consequently, an extensive benchmarking study was carried out. After examining geometries and energetics with density functionals and two basis sets, 6-31G(d) and def2-SVP (based on DLPNO-CCSD(T)/CBS//ωB97X-D/def2-TZVP results as TS2 cannot be located with M06-2X functional, see ESI† for details), it became clear that different functionals lead to divergent conclusions with regard to the relative energies of structures and existence of stationary points on PES. Although absolute energy differences were not large, i.e., the flatness of the PES was consistently reproduced, interpretation of NMR data requires quite accurate energies. Among the different levels of theory investigated, the CAM-B3LYP range-separated hybrid functional with the 6-31G(d) Pople basis set provided the best agreement with the relative electronic energies obtained at the DLPNO-CCSD(T)/CBS level for this specific system.^87–90 Consequently, results from this level of theory are discussed below (see ESI† for results from other levels, including AIMD results with M06-2X/6-31G(d)). Intrinsic Reaction Coordinate (IRC) calculations were carried out at the CAM-B3LYP/6-31G(d) level of theory.^91–93

To explore the dynamic behavior of C₉H⁺₉ cations, the Progdyn script developed by Singleton was employed.⁶⁶ Trajectories were propagated with a 1 fs time step using the Verlet algorithm at the CAM-B3LYP/6-31G(d) level. Both downhill (initiated at transition states) and uphill trajectories (initiated from minima using the “cannonball” approach, see ESI† for details) were collected. Metadynamics simulations were used to construct free energy surfaces using ORCA 5.0.4 (see ESI† for input details).^81,94

¹H and ¹³C NMR chemical shifts for the barbaralyl cation (C₉H⁺₉) were calculated using the revTPSS functional in combination with the pcSseg-1 basis set on structures optimized with CAM-B3LYP/6-31G(d).^95–97 To convert computed isotropic values to the conventional NMR scale, isotropic shielding values computed for tetramethylsilane (TMS) were used as a reference.

The effects of tunneling were investigated using the Gaussrate/Polyrate package developed by Truhlar.^98,99 Calculations were performed at the CAM-B3LYP/6-31G(d) level of theory. The tunneling contributions were quantified using two methods: small curvature tunneling (SCT) and zero curvature tunneling (ZCT).¹⁰⁰ Further details regarding the computational methodology employed can be found in the ESI.†

3 Results and discussion

3.1 Degenerate rearrangements

First, we reexamined the previously described C₉H⁺₉ PES using density functional theory (DFT) (Fig. 1 and 2). As shown in Scheme 1, carbocation A is generated following loss of water from protonated 1via transition structure TS1; C–O bond breakage and C–C bond formation occur asynchronously.^24,25,101

Fig. 2 Geometries (selected distances in Å) of A, B, and transition structures relevant to the fluxionality of C₉H⁺₉. Structures in top and bottom rows are the same. The rotational symmetry axes and planes of symmetry are shown along with point groups. Structures were optimized with CAM-B3LYP/6-31G(d). Relative free energies at the DLPNO-CCSD(T)/CBS//CAM-B3LYP/6-31G(d) level (thermochemical corrections from the lower level of theory included) are shown below each structure in the top row.

Carbocation A (+H₂O) is connected to transition structure TS1 (Scheme 1) by an IRC. This structure is set as the baseline for representing relative energies. The geometry of A is that of a “classic” non-classical carbocation with a cyclic 3-center 2-electron bonding array (highlighted in pink in line drawings).^{1–6,17,102–104} The barbaralyl cation A exhibits somewhat different electron delocalization than the 2-norbornyl cation, however, with its the 3-center/2-electron bonding array also interacting with the adjacent methine groups (see ESI† for details). From A, two distinct pathways are possible. One involves a C₂-symmetric transition structure (TS2) associated with a barrier of 2.3 kcal mol⁻¹, which converts A into an equivalent structure (identical in geometry but not identical in atomic positions). Alternatively, A can undergo ring closure viaTS3, which has a relative free energy of 3.6 kcal mol⁻¹ and leads to the D_3h symmetric carbocation B, which is 2.6 kcal mol⁻¹ higher in free energy than A. Only A and B were identified as minima on the portion of the C₉H⁺₉ PES relevant to fluxionality. The bonding in cation B is complex but can be formulated as involving three p-orbitals, one on each bridging carbon, containing a total of two electrons, that interact with each other through the cyclopropane rings that connect them.^18,105 Adaptive Natural Density Partitioning (AdNDP) using Multiwfn also supports this bonding picture (see ESI† for more details).^106,107 Each B is connected to six A structures viaTS3s. In this scenario, the bridging CHs cannot exchange with the bridgehead CHs (Fig. 1a). Consequently, TS2 and TS3 only result in partial scrambling of the barbaralyl cation.

Complete degeneracy of all CHs is achieved through another transition structure, TS4, with a computed overall barrier of 5.0 kcal mol⁻¹. This transition structure corresponds to a twist of one of the three bridges, converting B into a degenerate structure (B′). Thus, the combination of TS2, TS3, and TS4 allows for the interconversion of all nine CH groups. As illustrated in Fig. 1a, each TS4 enables the interconversion of groups of A and B structures. The qualitative nature of this PES matches that described by Cremer and co-workers three decades ago!⁵⁸

In Cremer and co-workers’ work, TS4 was found to have lower energy than TS3, while our calculations indicate that TS4 is the highest of the three transition states (see Fig. 1b; Werstiuk's energies differed considerably).^58,59 This difference arises from the comparatively lower energies of TS3 and B in our study. Nonetheless, both scenarios are consistent with the experimental observation of partial and total degeneracy at different temperatures. We also reached the same conclusion that TS4 involves a post-transition state bifurcation (PTSB) in both directions, which connects the two TS2 structures (IRCs can be found in the ESI†).^{11,30,35–37,91,92}

3.2 Escape from degeneracy

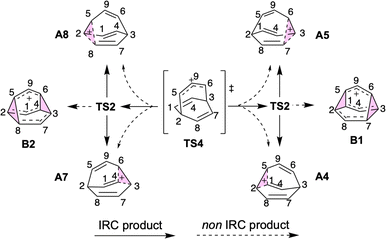
At elevated temperatures, the conversion of A to the lower energy cation C (previously formulated as 3, Scheme 1) can be achieved by the process shown in Fig. 3. TS5 and TS6 are different transition structures that connect A and C. TS5 corresponds to a 1,2-vinyl shift followed by cyclopropyl ring opening while TS6 corresponds to an apparent 1,3-vinyl shift. Subsequent hydride shifts through TS7–TS12 lead to other cations that are even lower in energy (D, E, G).§ The computed energy barriers are consistent with the experimental result as shown in Scheme 1, although the product is not neccessarily as homoconjugated as originally proposed.^50,53 At a temperature of −135 °C, the predicted half-life associated with the A to C conversion is ≥1.5 d, allowing A and B to be observed. When the temperature is increased to −120 °C, this predicted half-life decreases to 35 minutes, allowing C to be observed.⁵⁰ The subsequent 1,2-hydride shifts initiated by passage through TS7 are prevented by a 16.6 kcal mol⁻¹ barrier relative to C (predicted half-life of >3000 years).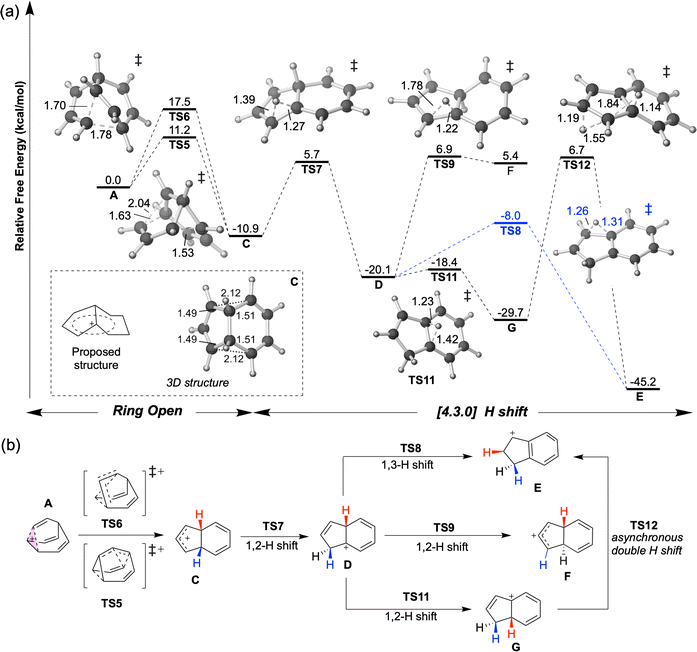

Fig. 3 (a) Energy profile of ring opening and hydride shift to form [4.3.0] structures at DLPNO-CCSD(T)/CBS//CAM-B3LYP/6-31G(d) level at 138.15 K. 3D structures of transition structures (visualized by CYLview 1.0)⁵¹ are close to their labels. The homoconjugated structure C is highlighted in a box. (b) Summary of the mechanism for generating [4.3.0] C₉H⁺₉ structures discovered in this study. Shifting hydrides are color-coded, with the exception of TS12, where red and blue Hs are swapped.

3.3 NMR computations

At the extremely low temperature of −150 °C, the half-life associated with complete scrambling is estimated to be 0.2 ms based on the computed overall barrier and Eyring equation (w/o tunneling effect) for A → TS4 (ΔG^‡ = 5.0 kcal mol⁻¹). Taking into account the height of the barrier, the associated partial scrambling is consistent with the observation of a 6 : 3 ratio of ¹³C peak splitting. As the temperature is elevated to −135 °C, the predicted half-life for complete scrambling is reduced to 20 μs, consistent with the observation of a single signal representing all CHs. Although tunneling accelerates the scrambling process, our analysis (below) demonstrates that it contributes only about 30% to the rate constant, which is equivalent to reducing the barrier only slightly, to 4.9 kcal mol⁻¹, in agreement with the estimated barrier of 5.0 kcal mol⁻¹ from the NMR experiment.⁵⁴ In Cremer and co-workers’ work, ¹³C NMR simulations at the IGLO/6-31G(d) level of theory suggested that the observed signals originate from the lower-energy structure A, but their computed difference between computed and experimental shifts was >6 ppm.⁵⁸ Our calculations using the revTPSS/pcSseg-1 level of theory reduced this deviation to 1.2 ppm for ¹³C (Table 1, left). In addition, the single ¹H signal exhibits a deviation of only 0.1 ppm at this level of theory. In contrast, structure B shows much larger deviations: a 0.4 ppm underestimation of the ¹H signal and a >20 ppm underestimation of the ¹³C signal (Table 1, right). Our results thus provide even more convincing evidence that the lower-energy carbocation isomer, A, is the species observed in the NMR experiments.

Table 1 Computed ¹H and ¹³C NMR shifts for A and B compared against the experimental results. The deviation of overall estimated chemical shifts (based on scrambling) relative to the experimental signals are in bold

C center	^13C shift	Pred (partial)	Pred (total)	^1H shift	Pred (total)	C center	^13C shift (pred partial)	Pred (total)	^1H shift	Pred (total)
4	221.7	153	119.7	9.99	6.7	4, 8, 9	132.8	95.5	6.5	6.2
8, 9	118.9			6.39
1	65.5	103		6.05		1, 2, 3, 5, 6, 7	76.8		6.0
2, 5	131.0			6.48
3	86.3			5.14
6, 7	102.1			6.56
Exp	—	152, 101	118.5	—	6.6	Exp	152, 101	118.5	—	6.6
Dev	—	+1, +2	+1.2	—	+0.1	Dev	−19.2, −24.2	−23	—	−0.4

---

3.4 Further exploration of the PES

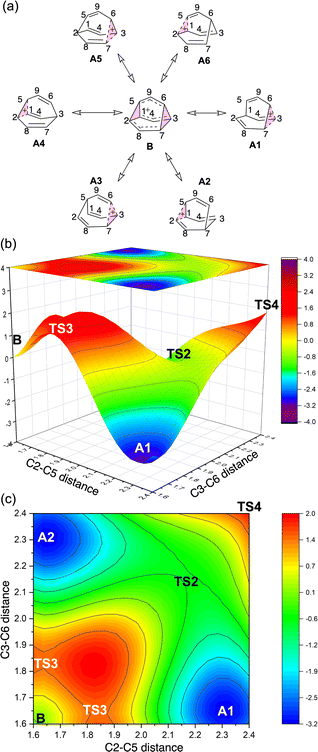
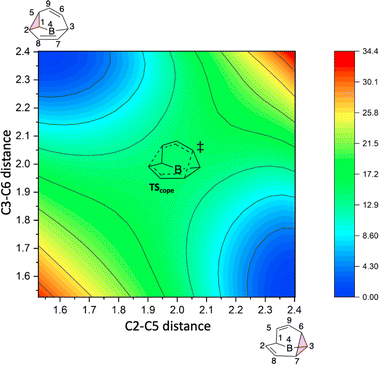
To better understand the C₉H⁺₉ PES, we conducted relaxed scans along the C2–C5 and C3–C6 bonds. Elongating the C2–C5 bond in B leads to the A1 isomer, whereas extending the C3–C6 bond results in the A2 isomer, both viaTS3s (Fig. 4a). These transformations lead to the symmetrical PES shown in Fig. 4b and c, which covers the region associated with partial scrambling. This surface also captures TS2, which interconverts the two As. TS4 resides at one corner. From the standpoint of TS4, proceeding downhill in either direction corresponding to its imaginary frequency leads to a bifurcation connecting two As. Metadynamics simulations gave a free energy surface of similar shape (see ESI†).

Fig. 4 (a) Six-fold symmetric reaction network that converts structure B into six equivalent As. (b) PES in terms of C2–C5 and C3–C6 distances (Å) and its 2D projection (above). (c) “Top view” of the 2D projection from (b), the energy color map is scaled in kcal mol⁻¹.

As the PESs shown in Fig. 4b and c represent only 1/6 of the network from Fig. 4a, it is instructive to duplicate and combine them to create a PES that covers the whole network. Such a PES is shown in Fig. 5. This PES can be considered a modern view of the “pound cake” PES depicted qualitatively by Cremer and co-workers (Fig. 1b).⁵⁸ Note that this surface only captures one B, however, with each TS4 leading toward others.

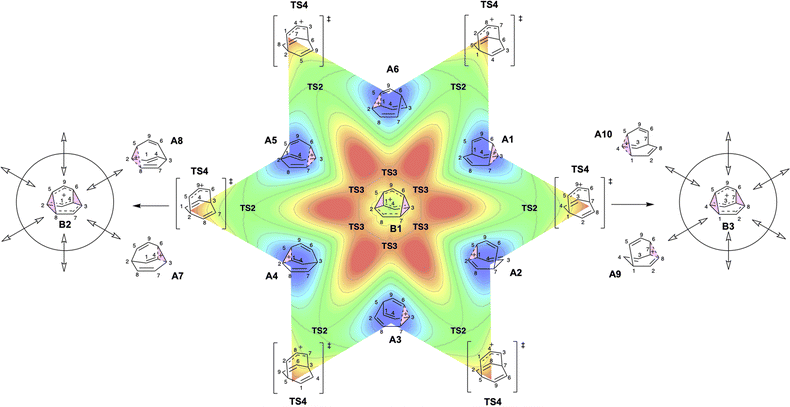Fig. 5 Six-fold symmetric 2D PES surrounding one B. Each 1/6 of this PES represents a 30-degree sheared, rescaled, and rotated version of the PES in Fig. 4. Key structures that are related to MD simulations are labeled with structure names, including A1–A8, B1, B2 and B3.

3.5 Uphill dynamics

To further understand the dynamic behavior governing the entire system, uphill AIMD simulations initiated from B1 were conducted. Overcoming TS3 from B1 at the CAM-B3LYP/6-31G(d) level requires 1.0 kcal mol⁻¹ of potential energy. We ran two sets of simulations, with 3 and 10 kcal mol⁻¹ of energy deposited into the starting points corresponding to the cleavage of the C2–C5 bond, i.e., the conversion of B1 to A1. Trajectories were propagated for 1000 fs and the minima encountered were recorded. The results are summarized in Fig. 6a. For both sets of simulations, even though energy is imparted to match the momentum associated with converting B1 to A1, other As can be accessed through this process in various amounts. As the extra energy associated with an A1-forming motion is increased, selectivity for forming A1 increases (see ESI† for results using 3 kcal mol⁻¹ of extra energy), but even with 10 kcal mol⁻¹ of extra energy, less than 70% of the trajectories reach A1 as the first minimum (Fig. 6b). Additional details can be found in the ESI.†

Fig. 6 (a) Distribution of the first minimum encountered for uphill simulations with 10 kcal mol⁻¹ excess energy. (b) Network visualization depicting minima encountered in uphill simulations from B1 towards A1. Sequential nodes from left to right denote successive minima encountered along each trajectory with 10 kcal mol⁻¹ excess energy. The thickness of lines reflects the relative population for different types of pathways, with denser populations of trajectories indicated by greater thickness.

Does this resistance to selectivity originate simply from the PES being flat (i.e., a gain in entropy)?^108,109 Yes and no, depending on one's preferred degree of subtlety. As shown in Fig. 7, inter-transition state roaming (through the red region of the PES) is actually observed.^11,40,41 For example, some trajectories initially explored the inter-transition state region between TS3s directly (Fig. 7c).

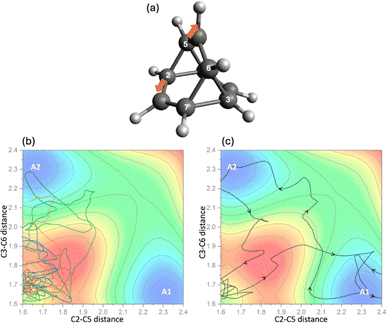Fig. 7 Projection of representative trajectories collected from uphill AIMD simulations (b and c) with 10 kcal mol⁻¹ external energy given to the stretch of bond C2–C5 (a).

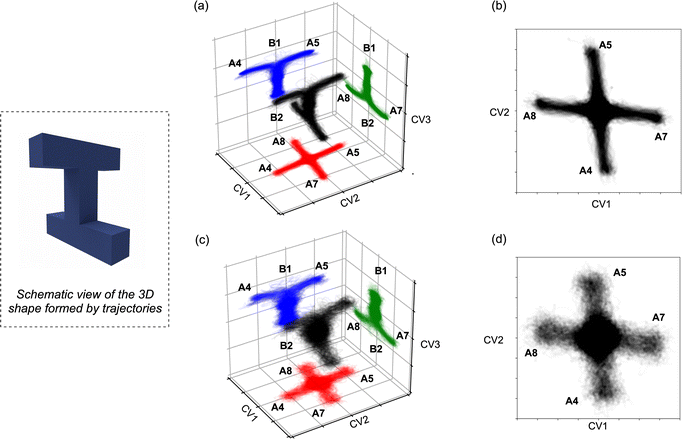
3.6 Complete scrambling in downhill dynamics

Given the reaction networks connected to each TS4, we sought to understand the dynamic behavior associated with descending from it. AIMD simulations initiated from TS4 revealed pathways that readily bridge a total of six minima, as illustrated in Scheme 2 (note that the labels A4 and A5 in this figure are the same as those in Fig. 4 and 5).

Scheme 2 Illustration of the pathways observed from downhill AIMD simulation initiated from TS4.

The trajectories from both quasi-classical (with zero-point energy) and classical (without zero-point energy) AIMD simulations are visualized in Fig. 8. The projection onto the three collective variables (CVs) clearly shows the states A4, A5, A7, and A8, as well as the associated states B1 and B2, being accessed by the trajectories in our simulations. The CVs chosen to plot the trajectories are based on the four bonds that dominate the geometric changes at TS4, including the C–C distances of bonds C4–C6, C5–C8, C6–C7, and C1–C5. The 3D shape produced by the trajectories resembles a twisted “H” structure, which is more apparent in the classical trajectories (Fig. 8a and c). Although the “cross” shape is not perfectly orthogonal (Fig. 8b and d), the reaction pathway that generates the four A structures (A4, A5, A7, and A8) exhibits four-fold symmetry. The tilted appearance of the cross is a result of the specific CV selection. For instance, the C4–C6 and C5–C8 distances are equivalent between A7 and A8, and consequently, the difference between these distances (CV2, C5–C8 − C4–C6) is inverted and close to, but not exactly equal to, zero.

Fig. 8 Trajectories (a and b: classical downhill AIMD; c and d: quasi-classical downhill AIMD) visualized with respect to the coordinates CV1, CV2, and CV3. CV1 is defined by R(C1,C5) − R(C6,C7); CV2 is defined by R(C5,C8) − R(C4,C6); and for CV3, (R(C1,C5) + R(C6,C7)) − (R(C5,C8) + R(C4,C6)). To better capture the six products, projections on each plane are distinctly colored in red, blue, and green. The schematic view at left describes the 3D shape of the trajectory bundle.

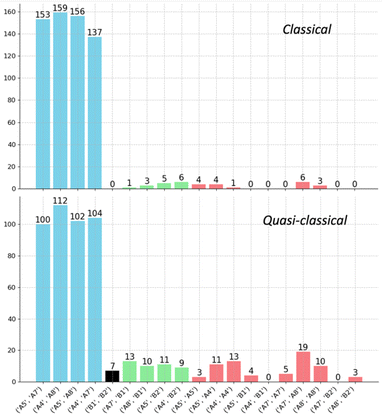
By analyzing the number of different types of trajectories, we confirmed that the ratio of trajectories connecting opposite A structures (A5–A7, A5–A8, A4–A7, A4–A8) is close to 1 : 1 : 1 : 1. As summarized in the histogram in Fig. 9, trajectories are classified into four groups: (1) trajectories connecting two A structures from different sides (blue); (2) trajectories connecting an A structure and a B structure from different sides (green); (3) recrossing trajectories that connect stationary points from the same side (red); and (4) trajectories that connect the opposite B1 and B2. When zero-point energy is deposited during the sampling process, notable increases in the proportions of type-2 and type-3 trajectories are observed. These increases manifest as a blurrier shape in Fig. 8c and d, indicating that classical trajectories have a higher probability of following the IRC under these conditions.^91–93 Another intriguing feature of the potential energy surface in Fig. 5 is the presence of minima B, which are in line with TS4 and TS3. These minima can be directly accessed with excess momentum before encountering the two A structures (for a different surface topography encountered at the M06-2X/6-31G(d) level of theory and the consequence to the dynamics, see ESI†).

Fig. 9 Histograms displaying the distribution of different trajectory types in classical (top) and quasi-classical (bottom) AIMD simulations initiated from TS4. Bars are colored blue (connecting two A structures from different sides), green (connecting an A structure and a B structure from different sides), red (recrossing), and black (connecting B1 and B2). The number of trajectories in each group is labeled on each bar.

3.7 Tunneling

Although both the nature of the C₉H⁺₉ PES and our dynamics simulations are consistent with the experimentally observed behavior of the barbaralyl cation, heavy-atom quantum mechanical tunneling may also contribute.^42–45,110 Tunneling in other carbocation rearrangements has been examined previously.⁴⁴ Here, both zero-curvature tunneling (ZCT) and small-curvature tunneling (SCT) were examined (see ESI† for details). Table 2 shows that large contributions from tunneling are expected for passage through transition structures under −135 °C, providing another route to scrambling, but the overall rate for the total scrambling process through TS4 is only accelerated by <30%. This acceleration is not substantial enough to invalidate the conclusion that, at temperatures below −150 °C, NMR spectroscopy can capture the partially scrambled structures. The tunneling effects only lower the effective barrier from 5.0 kcal mol⁻¹ to 4.9 kcal mol⁻¹ (see ESI† for detailed analysis).

Table 2 Tunneling contributions and including transmission coefficients (κ) for both ZCT and SCT. The results for temperatures used in NMR experiments are in bold

	T (K)	κ ZCT	κ SCT	Fraction of rate due to tunneling
				(ZCT)	(SCT)
TS2	138.15	1.08	1.34	7%	25%
	188.15	1.04	1.11	4%	10%
	273.15	1.02	1.04	2%	4%
TS3	138.15	1.76	1.87	43%	47%
	188.15	1.35	1.40	26%	28%
	273.15	1.15	1.17	13%	14%
TS4	138.15	1.28	1.39	22%	28%
	188.15	1.13	1.16	12%	14%
	273.15	1.06	1.07	6%	7%

---

3.8 Network neutrality

Although carbocations and boranes are isoelectronic, they display both similar and different behaviors. For example, while many boranes and boron clusters support 3-center 2-electron bonding, simple C⁺ → B substitution in carbocations can greatly reduce delocalization.¹¹¹ When performing such a replacement for C₉H⁺₉, a greatly simplified reaction network was observed (Fig. 10). The only transition structure we were able to locate resembling any of the structures from Fig. 2 was a transition structure for [3s,3s] sigmatropic shift (see ESI† for details) and this reaction was predicted to have a comparatively large barrier, 12.1 kcal mol⁻¹, a classic lack of fluxionality, which results from the absence of a yearning for charge delocalization.

Fig. 10 2D potential energy surface for [3s,3s] sigmatropic shift of BC₈H₉.

4 Conclusions

We delved into the complex behavior of the non-classical barbaralyl cation, shedding light on its formation and dynamic rearrangements through a multifaceted approach that integrates analysis of barriers, thermodynamics, non-statistical dynamic effects, and tunneling. The construction of the PES and AIMD simulations unveiled the importance of dynamic effects attributable to the flat and highly symmetrical nature of the energy surface on which the cation resides. Our results both validate the models of previous researchers and extend them to provide a rich picture of the reactivity of a fluxional carbocation at a level only achievable with modern theoretical methods. We look forward to similar studies on additional carbocations, both classic and newly conceived.

Data availability

Computational details and further supporting data are included in the ESI† (PDF). Optimized geometries are available through the ioChem-BD repository¹¹² at https://doi.org/10.19061/iochem-bd-6-371 (benchmark) and https://doi.org/10.19061/iochem-bd-6-375 (key structures).

Author contributions

W. G.: investigation, methodology, writing – original draft (lead), data analysis, and visualization. W.-Y. K.: investigation, benchmarking, writing – original draft (support), data analysis, and visualization. D. J. T.: supervision, funding acquisition, and writing – review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

D. J. T., W. G. and W.-Y. K. are grateful for financial (CHE-1856416, CHE-2154083) and computational (ACCESS, CHE-030089) support from the NSF. We also thank the Croucher Foundation for continued financial support to W.-Y. K. through a doctoral scholarship. We also thank Dr Croix J. Laconsay for insightful discussions.

Notes and references

1. H. C. Brown, The nonclassical ion problem, Springer, New York, NY, 1997.
2. R. V. Williams, Chem. Rev., 2001, 101, 1185–1204.
3. C. A. Grob, Acc. Chem. Res., 1983, 16, 426–431.
4. H. C. Brown, Acc. Chem. Res., 1983, 16, 432–440.
5. C. Walling, Acc. Chem. Res., 1983, 16, 448–454.
6. G. A. Olah, G. K. S. Prakash and M. Saunders, Acc. Chem. Res., 1983, 16, 440–448.
7. A. K. Cheng, F. A. L. Anet, J. Mioduski and J. Meinwald, J. Am. Chem. Soc., 1974, 96, 2887–2891.
8. R. V. Williams, Eur. J. Org. Chem., 2001, 2001, 227–235.
9. M. Seefelder, M. Heubes, H. Quast, W. D. Edwards, J. R. Armantrout, R. V. Williams, C. J. Cramer, A. C. Goren, D. A. Hrovat and W. T. Borden, J. Org. Chem., 2005, 70, 3437–3449.
10. R. V. Williams, A. G. Al-Sehemi, A. K. Meier, Z. Z. Brown and J. R. Armantrout, J. Org. Chem., 2017, 82, 4136–4147.
11. B. K. Carpenter, Chem. Rev., 2013, 113, 7265–7286.
12. C. J. Laconsay and D. J. Tantillo, J. Org. Chem., 2023, 88, 9056–9065.
13. Y. J. Hong and D. J. Tantillo, Helv. Chim. Acta, 2014, 97, 1475–1480.
14. M. Castiñeira Reis, C. S. López, O. Nieto Faza and D. J. Tantillo, Chem. Sci., 2019, 10, 2159–2170.
15. R. Properzi, P. S. J. Kaib, M. Leutzsch, G. Pupo, R. Mitra, C. K. De, L. Song, P. R. Schreiner and B. List, Nat. Chem., 2020, 12, 1174–1179.
16. R. S. Mulliken, C. A. Rieke and W. G. Brown, J. Am. Chem. Soc., 1941, 63, 41–56.
17. I. V. Alabugin, G. dos Passos Gomes and M. A. Abdo, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1389.
18. R. Hoffmann, Acc. Chem. Res., 1971, 4, 1–9.
19. H. Jiao, P. v. R. Schleyer and M. N. Glukhovtsev, J. Phys. Chem., 1996, 100, 12299–12304.
20. G. Merino, M. Solà, I. Fernández, C. Foroutan-Nejad, P. Lazzeretti, G. Frenking, H. L. Anderson, D. Sundholm, F. P. Cossío, M. A. Petrukhina, J. Wu, J. I. Wu and A. Restrepo, Chem. Sci., 2023, 14, 5569–5576.
21. R. Hoffmann, Am. Sci., 2015, 103, 1511.
22. W. J. Hehre, J. Am. Chem. Soc., 1974, 96, 5207–5217.
23. D. J. Tantillo, Acc. Chem. Res., 2016, 49, 741–749.
24. W. T. Borden, R. J. Loncharich and K. N. Houk, Annu. Rev. Phys. Chem., 1988, 39, 213–236.
25. D. J. Tantillo, J. Phys. Org. Chem., 2008, 21, 561–570.
26. O. M. Gonzalez-James, E. E. Kwan and D. A. Singleton, J. Am. Chem. Soc., 2012, 134, 1914–1917.
27. Y.-Y. Ma, M. Yan, H.-R. Li, Y.-B. Wu, X.-X. Tian, H.-G. Lu and S.-D. Li, Sci. Rep., 2019, 9, 17074.
28. R. Wodraszka and U. Manthe, J. Phys. Chem. Lett., 2015, 6, 4229–4232.
29. M. Sanz-Novo, M. Mato, Í. León, A. M. Echavarren and J. L. Alonso, Angew. Chem., Int. Ed. Engl., 2022, 61, e202117045.
30. B. K. Carpenter, Annu. Rev. Phys. Chem., 2005, 56, 57–89.
31. R. Hoffmann, S. Swaminathan, B. G. Odell and R. Gleiter, J. Am. Chem. Soc., 1970, 92, 7091–7097.
32. W. v. E. Doering, J. L. Ekmanis, K. D. Belfield, F.-G. Klärner and B. Krawczyk, J. Am. Chem. Soc., 2001, 123, 5532–5541.
33. W. Guo and D. J. Tantillo, J. Am. Chem. Soc., 2024, 146, 7039–7051.
34. C. Doubleday, Applied Theoretical Organic Chemistry, World Scientific, Europe, 2018, pp. 351–369.
35. D. H. Ess, S. E. Wheeler, R. G. Iafe, L. Xu, N. Celebi-Olçüm and K. N. Houk, Angew. Chem., Int. Ed. Engl., 2008, 47, 7592–7601.
36. J. Rehbein and B. Wulff, Tetrahedron Lett., 2015, 56, 6931–6943.
37. D. J. Tantillo, Advances in Physical Organic Chemistry, Elsevier, 2021, pp. 1–16.
38. D. Tantillo, Am. Sci., 2019, 107, 22–26.
39. S. R. Hare and D. J. Tantillo, Pure Appl. Chem., 2017, 89, 679–698.
40. Z. Feng and D. J. Tantillo, J. Am. Chem. Soc., 2021, 143, 1088–1097.
41. D. Townsend, S. A. Lahankar, S. K. Lee, S. D. Chambreau, A. G. Suits, X. Zhang, J. Rheinecker, L. B. Harding and J. M. Bowman, Science, 2004, 306, 1158–1161.
42. M. Saunders and H. A. Jimenez-Vazquez, Chem. Rev., 1991, 91, 375–397.
43. P. R. Schreiner, Trends Chem., 2020, 2, 980–989.
44. S. Kozuch, A. Karton, S. Jalife and G. Merino, Chem. Commun., 2021, 57, 10735–10738.
45. S. Kozuch, Phys. Chem. Chem. Phys., 2015, 17, 16688–16691.
46. S. Jalife, S. Mondal, E. Osorio, J. L. Cabellos, G. Martínez-Guajardo, M. A. Fernandez-Herrera and G. Merino, Org. Lett., 2016, 18, 1140–1142.
47. D. J. Tantillo and P. v. R. Schleyer, Org. Lett., 2013, 15, 1725–1727.
48. S. Jalife, I. Judy, C. Wu, G. Martínez-Guajardo, P. von Ragué Schleyer, M. A. Fernández-Herrera and G. Merino, Chem. Commun., 2015, 51, 5391–5393.
49. S. Jalife, S. Mondal, J. L. Cabellos, G. Martinez-Guajardo, M. A. Fernandez-Herrera and G. Merino, Chem. Commun., 2016, 52, 3403–3405.
50. P. Ahlberg, D. L. Harris and S. Winstein, J. Am. Chem. Soc., 1970, 92, 2146–2147.
51. C. Y. Legault, CYLview, 1.0b, https://www.cylview.org, 2009.
52. J. C. Barborak, J. Daub, D. M. Follweiler and P. v. R. Schleyer, J. Am. Chem. Soc., 1969, 91, 7760–7761.
53. P. Ahlberg, C. Engdahl and G. Jonsaell, J. Am. Chem. Soc., 1981, 103, 1583–1584.
54. C. Engdahl, G. Jonsaell and P. Ahlberg, J. Am. Chem. Soc., 1983, 105, 891–897.
55. D. Ajami, O. Oeckler, A. Simon and R. Herges, Nature, 2003, 426, 819–821.
56. G. Schröder, Angew. Chem., Int. Ed. Engl., 1963, 2, 481–482.
57. J. Bella, J. M. Poblet, A. Demoulliens and F. Volatron, J. Chem. Soc., Perkin Trans. 2, 1989, 37–42.
58. D. Cremer, P. Svensson, E. Kraka and P. Ahlberg, J. Am. Chem. Soc., 1993, 115, 7445–7456.
59. N. H. Werstiuk, Can. J. Chem., 2010, 88, 1195–1204.
60. P. E. Larsson and J. Linderberg, Theor. Chim. Acta, 1996, 93, 79–85.
61. A. Karton, Chem. Phys., 2022, 552, 111373.
62. A. Sanchez, A. Gurajapu, W. Guo, W.-Y. Kong, C. J. Laconsay, N. S. Settineri, D. J. Tantillo and T. J. Maimone, J. Am. Chem. Soc., 2023, 145, 13452–13461.
63. M. V. Makarova and S. G. Semenov, Russ. J. Gen. Chem., 2015, 85, 589–594.
64. W. Quapp, M. Hirsch and D. Heidrich, Theor. Chem. Acc., 1998, 100, 285–299.
65. D. J. Tantillo, J. Phys. Org. Chem., 2021, 34, e4202.
66. D. A. Singleton, C. Hang, M. J. Szymanski and E. E. Greenwald, J. Am. Chem. Soc., 2003, 125, 1176–1177.
67. G. Rasul, G. K. Surya Prakash and G. A. Olah, Chem. Phys. Lett., 2011, 517, 1–8.
68. D. A. Hrovat, E. C. Brown, R. V. Williams, H. Quast and W. T. Borden, J. Org. Chem., 2005, 70, 2627–2632.
69. M. L. McKee, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 943–951.
70. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
71. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
72. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 C.01, 2016.
73. Y. Wang, P. Verma, X. Jin, D. G. Truhlar and X. He, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 10257–10262.
74. H. Sato, B.-X. Li, T. Takagi, C. Wang, K. Miyamoto and M. Uchiyama, JACS Au, 2021, 1, 1231–1239.
75. H. Sato, T. Hashishin, J. Kanazawa, K. Miyamoto and M. Uchiyama, J. Am. Chem. Soc., 2020, 142, 19830–19834.
76. X. Tang, F. Zhang, T. Zeng, W. Li, S. Yin and R. Wu, ACS Chem. Biol., 2020, 15, 2820–2832.
77. D. T. Major, ACS Catal., 2017, 7, 5461–5465.
78. N. Tarannam, P. K. Gupta, S. Zev and D. T. Major, Beilstein J. Org. Chem., 2024, 20, 1189–1197.
79. C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106.
80. C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101.
81. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
82. F. Neese and E. F. Valeev, J. Chem. Theory Comput., 2011, 7, 33–43.
83. S. Zhong, E. C. Barnes and G. A. Petersson, J. Chem. Phys., 2008, 129, 184116.
84. Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov, L. Cavallo and F. Neese, J. Chem. Phys., 2018, 148, 011101.
85. S. Grimme, Chem.–Eur. J., 2012, 18, 9955–9964.
86. G. Luchini, J. V. Alegre-Requena, I. Funes-Ardoiz and R. S. Paton, F1000Research, 2020, 9, 291.
87. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
88. R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728.
89. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.
90. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
91. K. Fukui, Acc. Chem. Res., 1981, 14, 363–368.
92. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527.
93. S. Maeda, Y. Harabuchi, Y. Ono, T. Taketsugu and K. Morokuma, Int. J. Quantum Chem., 2015, 115, 258–269.
94. A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603.
95. M. T. de Oliveira, J. M. A. Alves, A. A. C. Braga, D. J. D. Wilson and C. A. Barboza, J. Chem. Theory Comput., 2021, 17, 6876–6885.
96. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, L. A. Constantin and J. Sun, Phys. Rev. Lett., 2009, 103, 026403.
97. F. Jensen, J. Chem. Theory Comput., 2015, 11, 132–138.
98. J. Zheng, J. L. Bao, S. Zhang, J. C. Corchado, R. Meana-Pañeda, Y.-Y. Chuang, E. L. Coitiño, B. A. Ellingson and D. G. Truhlar, Gaussrate 17, 2017.
99. J. Zheng, J. L. Bao, R. Meana-Pañeda, S. Zhang, B. J. Lynch, J. C. Corchado, Y.-Y. Chuang, P. L. Fast, W.-P. Hu, Y.-P. Liu, G. C. Lynch, K. A. Nguyen, C. F. Jackels, A. Fernandez Ramos, B. A. Ellingson, V. S. Melissas, I. V. J. Rossi, E. L. Coitiño, J. Pu, T. V. Albu, A. Ratkiewicz, R. Steckler, B. C. Garrett, A. D. Isaacson and D. G. Truhlar, Polyrate-version 2017-C, 2017.
100. W.-P. Hu, Y.-P. Liu and D. G. Truhlar, J. Chem. Soc., Faraday Trans., 1994, 90, 1715–1725.
101. P. R. Schreiner, P. v. R. Schleyer and H. F. Schaefer 3rd, J. Org. Chem., 1997, 62, 4216–4228.
102. C. J. Collins, J. Am. Chem. Soc., 1966, 88, 4117–4118.
103. B. P. Coppola, Chem. Intell., 1998, 4, 40–49.
104. G. A. Olah, G. K. Surya Prakash and M. Saunders, Acc. Chem. Res., 1983, 16, 440–448.
105. G. A. Olah, V. P. Reddy and G. K. S. Prakash, Chem. Rev., 1992, 92, 69–95.
106. D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217.
107. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
108. D. J. Tantillo, J. Am. Chem. Soc., 2022, 144, 13996–14004.
109. M. Bai, Z. Feng, J. Li and D. J. Tantillo, Chem. Sci., 2020, 9937–9944.
110. W. Guo, E. E. Robinson, R. J. Thomson and D. J. Tantillo, Org. Lett., 2024, 26, 4606–4609.
111. T. A. Hamlin, C. S. Hamann and D. J. Tantillo, J. Org. Chem., 2015, 80, 4046–4053.
112. M. Álvarez-Moreno, C. de Graaf, N. López, F. Maseras, J. M. Poblet and C. Bo, J. Chem. Inf. Model., 2015, 55, 95–103.

---

Footnotes

† Electronic supplementary information (ESI) available: Computational details and further supporting data. See DOI: https://doi.org/10.1039/d4sc04829f

‡ These authors contributed equally to this work.

§ It is worth noting that at the CAM-B3LYP/6-31G(d) level of theory, a minimum (H) and nearby transition structure (TS10) were optimized, suggesting a stepwise, two-step 1,2-H shift mechanism from structure D to structure E. However, when single-point energy corrections were performed using the higher-level DLPNO-CCSD(T)/CBS method, the energy of H was found to be higher than that of TS10, indicating that the stepwise mechanism is not viable. Instead, the higher-level calculations suggest that the transformation from D to E proceeds via an asynchronous concerted 1,3-H shift mechanism, with a relatively flat potential energy surface following the initial hydrogen shift (see the ESI† for details).

---