Open Access Article
Open Access ArticleData science-centric design, discovery, and evaluation of novel synthetically accessible polyimides with desired dielectric constants†
Mengxian
Yu
a,
Qingzhu
Jia
a,
Qiang
Wang
a,
Zheng-Hong
Luo
 b,
Fangyou
Yan
b,
Fangyou
Yan
 *a and
Yin-Ning
Zhou
*a and
Yin-Ning
Zhou
 *b
*b
aSchool of Chemical Engineering and Material Science, Tianjin University of Science and Technology, Tianjin 300457, P. R. China. E-mail: yanfangyou@tust.edu.cn
bDepartment of Chemical Engineering, School of Chemistry and Chemical Engineering, State Key Laboratory of Metal Matrix Composites, Shanghai Jiao Tong University, Shanghai 200240, P. R. China. E-mail: zhouyn@sjtu.edu.cn
First published on 4th October 2024
Abstract
Rapidly advancing computer technology has demonstrated great potential in recent years to assist in the generation and discovery of promising molecular structures. Herein, we present a data science-centric “Design–Discovery–Evaluation” scheme for exploring novel polyimides (PIs) with desired dielectric constants (ε). A virtual library of over 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 synthetically accessible PIs is created by extending existing PIs. Within the framework of quantitative structure–property relationship (QSPR), a model sufficient to predict ε at multiple frequencies is developed with an R2 of 0.9768, allowing further high-throughput screening of the prior structures with desired ε. Furthermore, the structural feature representation method of atomic adjacent group (AAG) is introduced, using which the reliability of high-throughput screening results is evaluated. This workflow identifies 9 novel PIs (ε >5 at 103 Hz and glass transition temperatures between 250 °C and 350 °C) with potential applications in high-temperature capacitive energy storage, and confirms these promising findings by high-fidelity molecular dynamics (MD) simulations.
000 synthetically accessible PIs is created by extending existing PIs. Within the framework of quantitative structure–property relationship (QSPR), a model sufficient to predict ε at multiple frequencies is developed with an R2 of 0.9768, allowing further high-throughput screening of the prior structures with desired ε. Furthermore, the structural feature representation method of atomic adjacent group (AAG) is introduced, using which the reliability of high-throughput screening results is evaluated. This workflow identifies 9 novel PIs (ε >5 at 103 Hz and glass transition temperatures between 250 °C and 350 °C) with potential applications in high-temperature capacitive energy storage, and confirms these promising findings by high-fidelity molecular dynamics (MD) simulations.
1 Introduction
The demand for dielectric materials is increasing dramatically along with the development of advanced fields such as semiconductors, energy storage and aerospace.1–4 Polymer dielectrics have become the material of choice for high voltage dielectric capacitors due to their high voltage resistance and ease of processing.5–7 PI8,9 is one of the important dielectric materials that can be applied in energy storage due to its excellent mechanical properties, reasonable dielectric loss and high breakdown strength. In application scenarios such as pulsed power systems, automobiles, geothermal power plants, and electrified aircraft, as well as oil and gas exploration, capacitors or electronic devices need to operate reliably at harsh temperatures ranging from 120 °C to more than 300 °C.9,10 Nevertheless, because PIs contain many highly conjugated structures, this leads to an exponential increase in conduction losses with increasing temperature and electric field.9 Therefore, the design of novel PIs with excellent dielectric properties has become a top priority while maintaining excellent high-temperature resistance.11–13Given that the multidimensional performance objectives of novel polymers desired in various fields differ, traditional empirically oriented structural design and performance optimization are hard to manage. Emerging data science14–18 exhibits tremendous potential for generating vast amounts of hypothetical chemical structures17,19–21 and discovering promising molecules,18,22–24 among others, which is expected to accelerate the development of novel polymers while easing the burden on researchers. Data-driven molecule generation strategies are ubiquitous and promising in the fields of drugs and chemistry,20,25–28 while their application in polymer design is rare.29,30 Polymers are generally stoichiometric molecules with long chain structures in contrast to small molecules, which may increase the complexity of designing polymers to some extent. Artificial intelligence (AI) algorithms for designing small molecules combined with polymer structure approximation representations (e.g., monomer, repeating unit, BigSMILES,31 and ring repeating unit32) allow for the creation of virtual polymer libraries.33–35
When confronted with the vast structural space, a strategy to rapidly optimize multiple properties of polymers to capture the candidate structures that meet productive life demands is sorely needed. Developed with the aid of machine learning (ML)11,18,21,36,37 algorithms, quantitative structure–property relationship (QSPR)18,38 models can predict the properties of target structures in seconds, which is widely recognized. This advantage of QSPR model is recently extended by applying it to high-throughput screening of unknown structural spaces to obtain ideal candidates.7,10,12,36,39 For instance, Chen et al.40 established a QSPR model for the dielectric constant (ε) of polymers with frequency, predicted 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 candidate polymers available for synthesis, and obtained 5 polymers with the desired ε for capacitors and microelectronic applications. In addition, Yang et al.41 developed a multi-task ML model to predict the permeability of gases such as H2, CO2, and CH4, screened more than 9 million hypothetical polymers, and identified thousands of high-performance hyper-permeable polymer membranes. In a recent eye-opening study, Gurnani et al.10 discovered a range of dielectrics in the polynorbornene and PI families using the AI scheme (including the frequency-dependent ε-QSPR model), expanding the temperature range for potential applications of electrostatic capacitors. Admittedly, the high-throughput screening paradigm based on the QSPR model greatly reduces the time required for discovering new materials,37,42 yet further validation of hundreds or thousands of promising candidate molecules still requires extensive experiments or density-functional theory (DFT) calculations.43
000 candidate polymers available for synthesis, and obtained 5 polymers with the desired ε for capacitors and microelectronic applications. In addition, Yang et al.41 developed a multi-task ML model to predict the permeability of gases such as H2, CO2, and CH4, screened more than 9 million hypothetical polymers, and identified thousands of high-performance hyper-permeable polymer membranes. In a recent eye-opening study, Gurnani et al.10 discovered a range of dielectrics in the polynorbornene and PI families using the AI scheme (including the frequency-dependent ε-QSPR model), expanding the temperature range for potential applications of electrostatic capacitors. Admittedly, the high-throughput screening paradigm based on the QSPR model greatly reduces the time required for discovering new materials,37,42 yet further validation of hundreds or thousands of promising candidate molecules still requires extensive experiments or density-functional theory (DFT) calculations.43
Considering that the vast structural screening space may exceed the predicted structural range of the QSPR model, this can lead to unreliable high-throughput screening results, which in turn increases the time for meaningless experiments or DFT calculation validation. Therefore, we introduce atomic adjacent groups (AAGs)44 to evaluate the reliability of high-throughput screening results. Both macromolecules and organic small molecules can be viewed as combinations of several groups (substructures). By confirming the distribution relationship between the molecules in the high-throughput screening structure library and the model-applicable structure space, the reliability of the high-throughput screening results will be evaluated. Furthermore, although high-throughput synthesis is a great and absolute way to extensively demonstrate the properties of target molecules, the consumption of raw materials and time remains overwhelming. If the designed monomers are hard or impossible to synthesize, it will be difficult to put the polymer candidates into application; therefore consideration of the synthetic accessibility for novel polymers is needed.45,46
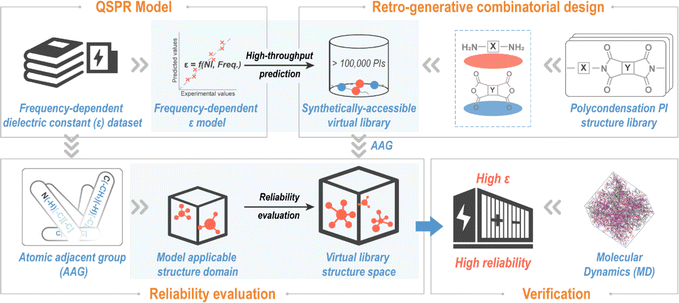
A “Design–Discovery–Evaluation” scheme for exploring novel PIs with desired ε, envisioned in this contribution, is shown in Fig. 1. To ensure synthetic accessibility of the novel PI, the virtual library was created by the virtual condensation polymerization of retro-generated diamines and dianhydrides, containing over 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 PIs. ε (ref. 47) is a key parameter for polymer dielectric materials.9,47,48 So, a frequency-dependent ε-QSPR model was developed and subjected to comprehensive validation procedures to provide performance parameters for various aspects (e.g., predictability and robustness) of the model. The ε-QSPR model was subsequently applied for high throughput predictions of polymers in the virtual library to obtain prior structures with potentially high ε. The reliability of the high-throughput screening results was evaluated on the basis of the spatial scope of the chemical structure of the polymer modelling dataset analyzed by AAG. Eventually, testable novel polymers for energy storage application were proposed, and high-fidelity molecular dynamics (MD) simulations were undertaken to verify the accuracy of the data science-centric “Design–Discovery–Evaluation” scheme.
000 PIs. ε (ref. 47) is a key parameter for polymer dielectric materials.9,47,48 So, a frequency-dependent ε-QSPR model was developed and subjected to comprehensive validation procedures to provide performance parameters for various aspects (e.g., predictability and robustness) of the model. The ε-QSPR model was subsequently applied for high throughput predictions of polymers in the virtual library to obtain prior structures with potentially high ε. The reliability of the high-throughput screening results was evaluated on the basis of the spatial scope of the chemical structure of the polymer modelling dataset analyzed by AAG. Eventually, testable novel polymers for energy storage application were proposed, and high-fidelity molecular dynamics (MD) simulations were undertaken to verify the accuracy of the data science-centric “Design–Discovery–Evaluation” scheme.
2 Methods
2.1 Datasets and feature engineering (norm descriptor)
Two linear PI datasets for developing the virtual library and establishing the QSPR model were collected from the extensive published literature and PolyInfo database. Among them, the modelling datapoints consist of 1256 dielectric constants at different frequencies for 287 PIs, whose range distribution is shown in Fig. S1.† It should be noted that only 25 data points are in the range of 4.77 to 5 and no data points are in the (3.92, 4.77) interval. Whether using 287 PIs or 1256 data points, the division of the training and test sets meets the 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. Details of the modelling datasets have been provided in the ESI.†
1 ratio. Details of the modelling datasets have been provided in the ESI.†
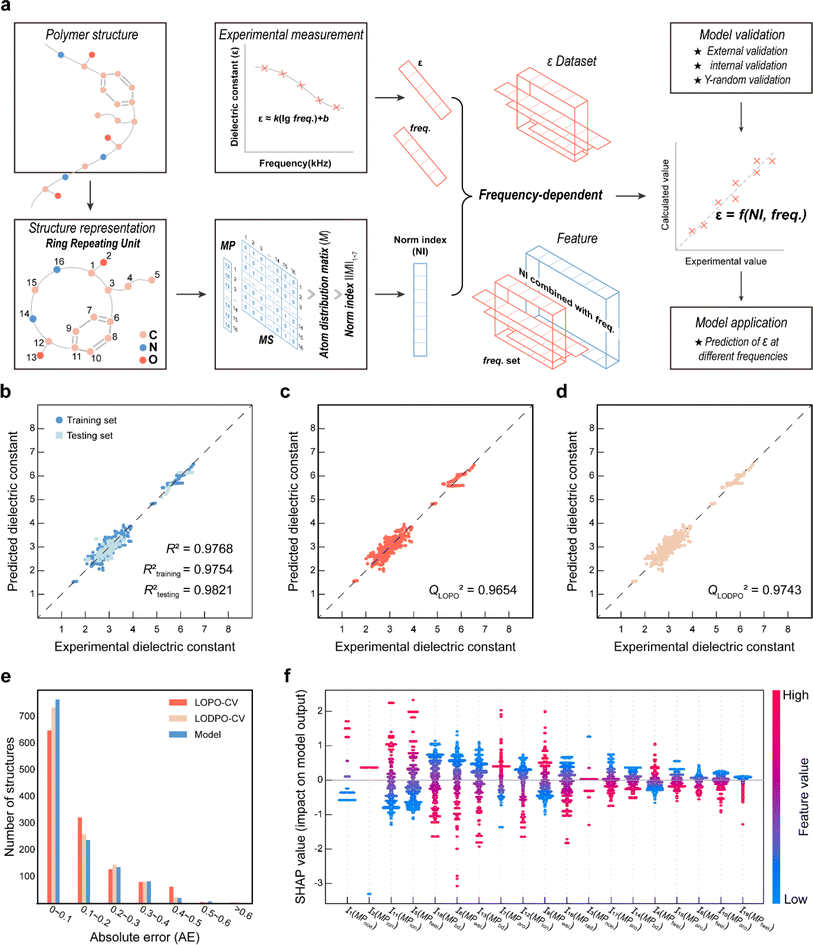
Norm descriptors are employed for feature engineering after the PI structure of the ring repeating unit (RRU) representation, which is implemented by calculating the norm indices (see ESI eqn (S1–S6†)) of the atomic distribution matrix M (consisting of hydrogen (H)-containing and H-suppressed structures). M is obtained from eqn (1) which is regarded as a combination of the step matrix (MS) and the property matrix (MP). Furthermore, MSs (seven in total, more details are listed in ESI eqn (S7–S13†)) are derived by mapping the position of each atom in the topology and its connectivity, while MPs are obtained by mapping the fundamental properties of each atom (see ESI Table S1†). Thus, norm descriptors comprehensively reflect the features of the chemical structure in a mathematical form.
 | (1) |
2.2 Model development, validation, and statistical parameters
Comprehensive validation procedures, including external validation, internal validation (i.e., leave-out-one cross-validation (LOO-CV)) and Y-random validation, are sufficient to ensure predictability and stability of the established model.26 In detail, given that the testing set is separate from the modelling process, it is utilized as an external validation object to assess the predictability of the model. LOO-CV is one of the methods used to validate model robustness. Since the modelling dataset contains ε at different frequencies for the same polymer, two LOO-CV methods are adopted: leave-one-polymer-out validation (LOPO-CV) and leave-one-data-point-out validation (LODPO-CV). LODPO-CV involves using each data point in the training set as a test set and the rest of the data points as a training set to evaluate the robustness of the model, while LOPO-CV involves using all the data points of each polymer in the training set as a test set and the data points of the rest of the polymers as a training set to evaluate the robustness of the model. The LOPO-CV method avoids the possibility of early appearance of structural features (descriptors) when the LODPO-CV method employs data points with different frequencies of the same polymer as a training set. For excluding chance correlation during modelling, Y-random validation is adopted.The SHapley Additive exPlanations (SHAP)49 model interpretation technique is a tool to understand the importance of the descriptors in the QSPR models. Derived from game theory, SHAP quantitatively explains the relationship between the descriptors and the final output by calculating the Shapley value to analyse the contribution of each descriptor to the prediction.
Statistical parameters involved in model development and validation processes, such as the squared correlation coefficient (R2), are defined in ESI Table S2.†
2.3 Atomic adjacent group (AAG)
AAG is a text-based representation of groups (substructures) in molecules. The AAG stems from the adjacency between atoms in a molecule. In the AAG representation rules, atoms in a molecule are classified into endpoint and connective atoms. An atom adjacent to only one non-hydrogen atom is regarded as an endpoint atom while an atom adjacent to more than one non-hydrogen atom is regarded as a connective atom. The AAG representation rule defines the types of bonds between atoms as “–”, “![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ”, “
”, “![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ”, “∼”, “≈”, “≋”, and “∷”, which correspond to single, double, and triple bonds in linear structures, and single, double, and triple bonds in ring structures, as well as the aromatic bonds unique to the benzene ring structure, respectively. Fig. S2a† shows some examples of AAG representations of endpoint and connective atoms and their bonding chemical bond types. In the AAG representation, endpoint atoms and their chemical bonds are described in “()” and connective atoms and their chemical bonds are described in “[]”. It should be noted that if there is a hydrogen atom directly bonded to the endpoint atom, it is written with the endpoint atom in “()”, e.g. (–CH3). As shown in Fig. S2b,† centred on a certain atom (i.e., the core atom), the AAG is written in the descriptive order of the core atom, its adjacent endpoint atoms and the type of chemical bonds, as well as its adjacent connective atoms and the type of chemical bonds.
”, “∼”, “≈”, “≋”, and “∷”, which correspond to single, double, and triple bonds in linear structures, and single, double, and triple bonds in ring structures, as well as the aromatic bonds unique to the benzene ring structure, respectively. Fig. S2a† shows some examples of AAG representations of endpoint and connective atoms and their bonding chemical bond types. In the AAG representation, endpoint atoms and their chemical bonds are described in “()” and connective atoms and their chemical bonds are described in “[]”. It should be noted that if there is a hydrogen atom directly bonded to the endpoint atom, it is written with the endpoint atom in “()”, e.g. (–CH3). As shown in Fig. S2b,† centred on a certain atom (i.e., the core atom), the AAG is written in the descriptive order of the core atom, its adjacent endpoint atoms and the type of chemical bonds, as well as its adjacent connective atoms and the type of chemical bonds.
2.4 Molecular dynamics (MD) simulation
The polarizability (α) was obtained from the Gaussian16W computational package.50 Geometry optimization and frequency calculations of the repeating units (RUs) were performed in the DFT framework using the B3LYP level of the 6-31G+(d) basis set,51 followed by obtaining the α for the lowest energy conformation.The molecular dynamics simulation was carried out with the COMPASS52 force field using the Forcite module in Materials Studio 2019 (Dassault Systemes, France) modelling software. The structure of the RUs was constructed using the visualization module and a polymer chain consisting of 20 RUs was built using the homopolymer tool.53 Optimization of their geometry was performed using a smart algorithm. 10 PI chains were packed into a periodic box in an amorphous cell structure with an initial density (ρ) of 1.0 g cm−3. Electrostatic interactions were calculated using the Ewald summation method and van der Waals interactions were calculated using an atom-based approach. The Norse thermostat54 and the Berenson barostat55 were applied to control the temperature and pressure with a Q-ratio of 0.01 and a decay constant of 0.1 ps.
After geometrical optimization of the established periodic box, 10 NVT annealing kinetic cycles were executed at 400–800 K to explore the global energy minimum conformation. A 500 ps NVT kinetic simulation was run at 298 K for the lowest energy conformation to remove internal stresses and stabilize the system temperature within 5% of the set temperature. Finally, an 800 ps NPT kinetic simulation was run to obtain the equilibrium density curve at 298 K and 0.0001 GPa.
2.5 Simulation theory of the high-frequency dielectric constant (ε)
Maxwell demonstrated that the high-frequency dielectric constant (ε∞) is related to the refractive index (nD), as shown in eqn (2).56 The refractive index is related to optical susceptibility (χ), i.e., eqn (3), and χ can be obtained from α viaeqn (4).57 Therefore, an approximate value of the dielectric constant can be deduced by obtaining α and ρ through DFT calculations and MD simulations.| ε∞ = nD2 | (2) |
| nD2 = 1 + 4πχ | (3) |
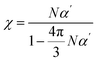 | (4) |
3 Results and discussion
3.1 Synthetically accessible polyimide (PI) virtual library
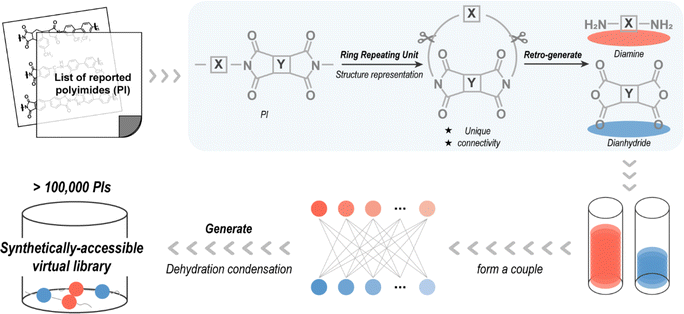
Referred to as “retro-generative combinatorial design”, this scheme enables virtual condensation polymerization to provide molecular structures for data scientific-centric property prediction, as shown in Fig. 2. Considering that the reactants of the reported molecules are easily purchased or synthesized, a step of retro-generation was added to improve the synthetic availability of the novel PIs. A total of 1280 reported PIs were pre-collected to reverse-generate diamine and dianhydride molecules after approximating their structures as RRU. RRU is a ring-like fragment formed by the head and tail of a RU that serves as an approximate structural representation for linear condensation polymers. By constructing “periodic boundaries”, the RRU incorporates the influence of adjacent RUs and is, thus, sufficient to find a complete characteristic group (–CO–N–CO–) on the RRU fragment. Since the collected PI is polymerized by condensation of diamine and dianhydride,8 two complete characteristic groups can be found on the RRU fragment. By cutting the RRU fragment at the position of the two characteristic groups and then filling in the H–O–H structure lost during the condensation process, PI is converted back to the possible reactants, e.g., diamine and dianhydride, completing the retro-generation process.Only one of the same diamines (or dianhydrides) was retained, giving unique 487 diamines and 210 dianhydrides from 1280 PIs. They were subjected to high-throughput virtual condensation subsequently and a PI virtual library was created prior to experimental synthesis. In detail, by simulating the condensation process of diamine and dianhydride, i.e., the hydrogen atoms in the amino group of the diamine are removed and the oxygen atom of ether group in the anhydride group of the dianhydride is replaced with a nitrogen atom, and then two-by-two splicing is performed, finally 102![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 270 novel PIs are generated. A complete list presented in the SMILES form, is available in the ESI.†
270 novel PIs are generated. A complete list presented in the SMILES form, is available in the ESI.†
3.2 Quantitative structure–property relationship (QSPR) model for polyimide (PI) dielectric constants (ε)
To capture the prior structures with desired performance from the virtual library, 1256 data points from 287 PIs (list in the ESI†) at different frequencies were collected from the literature to establish the ε-QSPR model. ε is influenced by the applied frequency as it is related to the electro polarization of the polymer within the alternating electric field. Generally, ε decreases with increasing applied frequency. For predicting the ε of polymers with frequency, without being limited to a specific ε at a single frequency, we introduce frequency-related variables into the QSPR model. Specifically, the prediction of ε at multiple frequencies for a given polymer is achieved by performing mathematical transformations of the norm descriptors of each PI-RRU structure with the frequencies corresponding to its data points, as shown in Fig. 3a. Subsequently, a bidirectional stepwise regression algorithm was adopted to reduce the dimensionality of features and a multiple linear regression (MLR) algorithm was used to develop the model.The PI-ε model developed in eqn (5) involves 19 variables, one of which is a frequency-dependent descriptor, which allows the model to predict ε of PI at multiple frequencies. The reported model descriptors (I) with their corresponding coefficients (b) are shown in ESI Table S3.†
ε(freq.) = α + β × log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) freq. freq. | (5) |
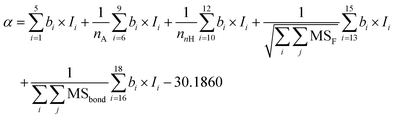 | (5a) |
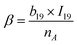 | (5b) |
| ntraining = 1013; Rtraining2 = 0.9754; AAEtraining = 0.1175. |
| ntesting = 243; Rtesting2 = 0.9821; AAEtesting = 0.1138. |
Fig. 3b displays the external validation results of the model. The data points are closely distributed on both sides of the diagonal line and the Rtesting2 value (i.e., 0.9821) is larger than the Rtraining2 value (i.e., 0.9754), which indicates that the model learns the underlying functional relationship between structural features and ε with high prediction accuracy. Fig. 3c–e show the validation results of LOPO-CV & LODPO-CV and their error distribution with the model. The Q2 values of 0.9654 and 0.9743 are the validation results of LOPO-CV and LODPO-CV, both of which indicate excellent stability of the model. Meanwhile, the absolute error (AE) is mostly concentrated in the range of 0–0.2 for internal validation and model results, which supports the good robustness of the established model. Furthermore, the validation results and error distribution plots show that the accuracy of LODPO-CV is higher than that of LOPO-CV, which is due to the model pre-learning the structural features, resulting in the “false high” phenomenon.
The Williams plot and the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Y-random validation results are shown in ESI Fig. S3a and b.† The prediction values of the developed model for most polymers were found to be reliable, as demonstrated by the Williams plot, which supports the satisfactory predictability of the model. As shown in Fig. S3b,† the average values of RY2 (0.0151) and QY2 (0.0331) of the model are much smaller than Rtraining2 and Q2, thus ruling out chance correlation in the modelling.
000 Y-random validation results are shown in ESI Fig. S3a and b.† The prediction values of the developed model for most polymers were found to be reliable, as demonstrated by the Williams plot, which supports the satisfactory predictability of the model. As shown in Fig. S3b,† the average values of RY2 (0.0151) and QY2 (0.0331) of the model are much smaller than Rtraining2 and Q2, thus ruling out chance correlation in the modelling.
To better understand the physical insight between the structure and properties captured by the model, the SHAP method was adopted to obtain the rankings of descriptor importance. As shown in Fig. 3f, the arrangement from left to right is the order of important to unimportant descriptors revealed by the SHAP method. An increase in the value of the feature (i.e., the scatter is red) results in a positive SHAP value, which usually indicates that the increase in the value of the descriptor leads to an increase in the target property value, i.e., the descriptor has a positive influence on the target properties. I1, I2 and I11 occupy the top 3 positions in the importance ranking and the number of outermost electrons (MPnoe) and ionization energy (MPion) of the atom in them may positively influence the ε of the PI. This may indicate that when designing high dielectric constant PIs, choosing atoms with larger ionization energies and a higher number of outermost electrons is more likely to be effective. Furthermore, we observe that the frequency-dependent descriptor I18 in the developed model has a negative effect on the ε of the PI, which is consistent with the experimental phenomenon that the dielectric constant decreases with frequency.
3.3 Reliability evaluation based on the atomic adjacent group (AAG)
The developed QSPR model was applied to predict the ε of 102![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 270 PIs in the virtual library at six specific frequencies (101 Hz, 102 Hz, 103 Hz, 104 Hz, 105 Hz, and 106 Hz) and identify the novel PIs with high ε. To address concerns that the vast structure screening space may exceed the QSPR model application domain, subsequently causing unreliable high-throughput screening results, a method based on AAG evaluation is proposed.
270 PIs in the virtual library at six specific frequencies (101 Hz, 102 Hz, 103 Hz, 104 Hz, 105 Hz, and 106 Hz) and identify the novel PIs with high ε. To address concerns that the vast structure screening space may exceed the QSPR model application domain, subsequently causing unreliable high-throughput screening results, a method based on AAG evaluation is proposed.
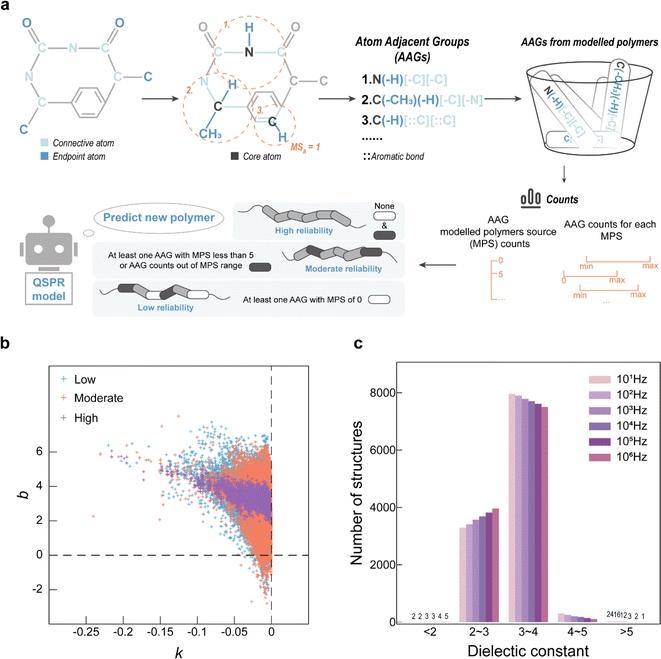
The AAG-based evaluation method workflow is shown in Fig. 4a, which evaluates the reliability of model prediction values by analysing the distribution of each AAG of the predicted polymer in the set of modelled AAGs. After distinguishing the connective atoms and the endpoint atoms in the PI-RRU structure, the connective atoms are sequentially designated as the core atoms. Centering on the core atom, the AAGs in the PI-RRU structure were divided according to the core atom, its adjacent endpoint atoms and the type of their chemical bonds, as well as its adjacent connective atoms and the type of their chemical bonds. With 55 unique AAGs for the polymers used in the modelling, Fig. S4–S6† illustrate the distribution of each AAGs, including the total number of occurrences of each AAG and the number of each AAG present in every single polymer. Benefiting from the polymer structure approximation represented by the RRU, it has connectivity and thus groups originating from the polymerization site are considered.
Based on the AAG distribution in the modelling dataset, AAG analysis was performed for 102![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 270 PIs in the virtual library to evaluate the reliability of their predicted values. To be specific, if one AAG of the predicted polymer does not appear in the modelling process, the predicted value is considered to have “low reliability”; if at least one of the AAGs in the predicted polymers occurs in fewer modelled substances (<5) or its number is outside the upper and lower limits of the AAG counts for the modelling substances, the predicted value is deemed to have “moderate reliability”; all other cases are classified as “high reliability”.
270 PIs in the virtual library to evaluate the reliability of their predicted values. To be specific, if one AAG of the predicted polymer does not appear in the modelling process, the predicted value is considered to have “low reliability”; if at least one of the AAGs in the predicted polymers occurs in fewer modelled substances (<5) or its number is outside the upper and lower limits of the AAG counts for the modelling substances, the predicted value is deemed to have “moderate reliability”; all other cases are classified as “high reliability”.
ε = b + k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) freq. freq. | (6) |
The variation of ε at multiple frequencies for the same PI in the modelling dataset is analysed, and the relationship between ε and frequency is approximated using eqn (6). Typically, ε decreases with the logarithmic exponential increase in frequency. Therefore, it is more realistic when the slope (k) in eqn (6) is negative. The intercept (b) in eqn (6) corresponds to ε when the frequency is 1 Hz. The dependence curves were obtained by fitting the predictedε values for each polymer against logarithmic exponential of their corresponding frequencies. As shown in Fig. 4b, the ε-frequency dependence curves of the PIs evaluated as “high reliability” have k-values less than 0, which is consistent with reality, and the b-values are between 2 and 7, which is minimal deviation from the ε-range of the modelling dataset (i.e., 1.49 to 6.53). In contrast, the ε-frequency dependence curves of the PIs evaluated as “low reliability”, and “moderate reliability” show too many outliers. Their ε-frequency dependence curves have b-values in the range of [−2, 8], which not only deviates significantly from the range of the modelling data but also appears unrealistic. This demonstrates that evaluating the reliability of QSPR model high-throughput screening results based on the AAG mitigates the issue of unreliability caused by predicted structures falling outside the judgement range of the model. The distribution of PI rated as “high reliability” at six specific frequencies of ε was analyzed to discover novel polymers with high ε potential, as seen in Fig. 4c. Even though most of the designed polymers have ε in the range of 2 to 5 at frequencies from 101 Hz to 106 Hz, there are still a few novel PIs showing high ε potential.
3.4 Novel polyimides (PIs) with desired dielectric constants (ε) and validated by molecular simulations
Because ε at 103 Hz is often taken as the performance parameter in applications, novel PIs with high ε and “high reliability” are identified and further analyzed. Fig. 5a illustrates 9 candidate PIs with ε greater than 5 at 103 Hz. This meets the dielectric performance requirements for polymer dielectric material in some demanding application scenarios (e.g., wind pitch control, pulsed power system, automobile, geothermal power plants, electrified aircraft, as well as oil and gas exploration). Furthermore, the glass transition temperature (Tg) of 9 PI candidate materials was predicted by employing our previously established PI-Tg QSPR model. The Tg of all 9 PI candidate materials was predicted to be greater than 250 °C. Thus, it is possible for all of them to work stably in application scenarios such as wind pitch control (maximum operating temperature of about 125 °C),10 hybrid vehicle inverters (140–150 °C), pulsed power systems (120–180 °C), and oil and gas exploration (170–250 °C).58 Furthermore, the PI_CD24351, PI_CD24529, PI_CD24352, PI_CD24603 and PI_CD24378 materials have the potential to have Tg in excess of 300 °C, which enables them to work in application scenarios such as geothermal power plants (200–300 °C) and electrified aircraft (180–300 °C). The AAG analysis of the RUs for the 9 candidate PIs confirms that the AAG type involved in each candidate PI has appeared in at least 6 modelling PIs. Meanwhile, the number of each AAG type involved in each PI candidate lies between the minimum and maximum of the AAG number of the modelling PI (i.e., the green line in Fig. 5a lies between the blue and orange lines). This confirms the “high reliability” of the high-throughput screening results for the 9 PI candidates.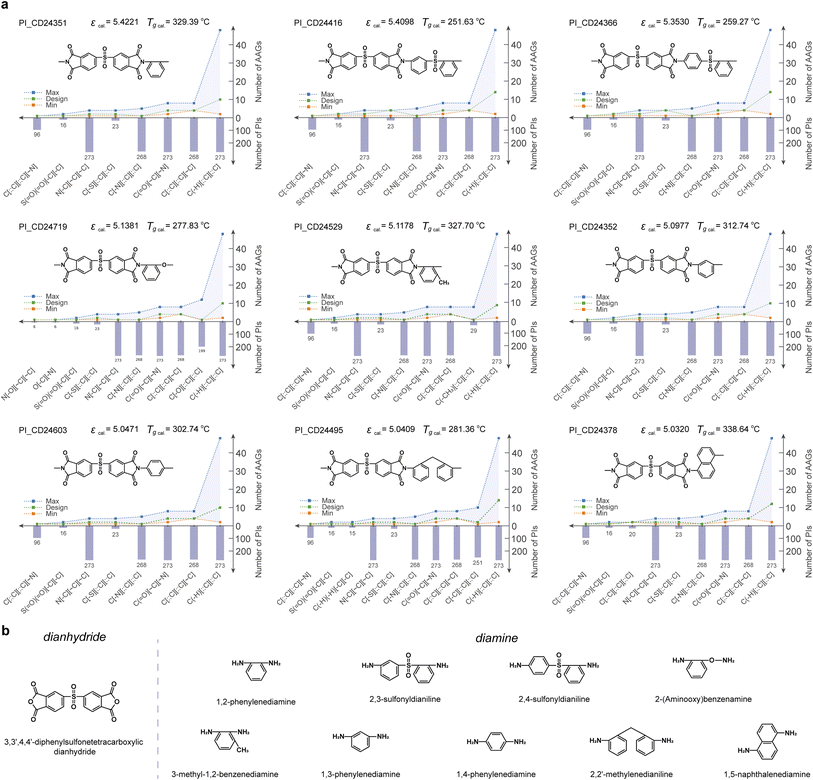 | ||
| Fig. 5 (a) The analysis of the 9 candidate PIs with “high reliability”; (b) possible dianhydride and diamine feedstocks for the 9 candidate PIs. | ||
Fig. 5b summarises the possible diamine and dianhydride feedstocks for the 9 candidate PIs. Notably, the source of dianhydride for all 9 candidate PIs is likely to be 3,3′,4,4′-diphenylsulfonetetracarboxylic dianhydride. Of the 9 diamine sources, both 2,3-sulfonyldianiline and 2,4-sulfonyldianiline involve a sulfonyl group. This suggests that an increased number of sulfonyl groups in the polymerised main chain increases internal rotation, allowing easy rotation of the polymer chain, lower proximity interactions and reduced dipole moments, thus contributing to the high ε. This ensures that the phenyl groups on the main chain enhance the rigidity of the polymer, making the polymer chain segments less prone to mobility. This may explain the emergence of new PIs with high ε potential. Also, the polymerisation of the 6 potential diamine sources increases the asymmetry of the polymer chains, which enhances the polarization of the polymer and contributes to the high ε. Furthermore, these feedstocks can all be synthesized or even purchased, especially 1,2-phenylenediamine, 1,3-phenylenediamine, and 1,4-phenylenediamine, which are common dianhydride feedstocks. As a common source of dianhydride for the 9 candidate polymers, 3,3′,4,4′-diphenylsulfonetetracarboxylic dianhydride, is also an easily available feedstock. This somewhat reduces the challenge for synthesizing candidate PIs.
To further confirm the identified PIs with high ε, the RU structures of these 9 PIs were established; DFT calculations and all-atom molecular dynamics simulations were carried out for the nine novel PIs. For obtaining the values of α needed for the calculation of ε, geometrical optimization and frequency calculations were performed by the DFT method. Of note, the end saturated non-hydrogen atoms of the bonded RUs were added to the optimized RUs considering the periodicity and connectivity characteristics of the polymer (see ESI Text† for the Cartesian coordinates). The ρ values used to calculate ε were acquired by all-atom molecular dynamics simulations. The amorphous cells of 9 PI candidate materials were constructed by placing 10 polymer chains containing 20 repeating units into a periodic box with an initial ρ of 1.0 g cm−3, as shown in Fig. S7a–S15a.† Subsequently, 10 NVT annealing kinetic cycles were executed at 400–800 K to explore the global energy minimum conformation. Based on the lowest energy conformation, 500 ps NVT kinetic simulations were run to remove internal stresses and stabilize the system temperature within 5% of the set temperature. The energy stability curves of the 9 PI candidates at 298 K are shown in Fig. S7b–S15b.† After ensuring the energy stability of the systems, NPT kinetic simulations were run for 800 ps to obtain equilibrium ρ curves. As shown in Fig. S7c–S15c,† the ρ of each system increased dramatically in the first 100 ps and the ρ of each system remained essentially stable in the last 200 ps. Lastly, the average of the last 100 ps of the NPT kinetic simulation was calculated as the ρ value used to calculate ε. The molar mass of RU (Mw), α, and ρ for the derivation of ε are listed in Table 1.
| PI | α | ρ | M w | α′ | N | χ | n D | ε DFT | ε QSPR | diff.g |
|---|---|---|---|---|---|---|---|---|---|---|
| a The unit of polarizability (α) is a.u., where 1 a.u. = 1.6487772754 × 10−41 C2 m2 J−1. The unit of density (ρ) is g cm−3, and that of Mw is g mol−1, of polarizability volume (α′) is 10−29 C2 m2 J−1, of molecular number density (N) is 1027 m−3. The rest are dimensionless quantities. b Calculated using density functional theory (DFT). c Calculated by molecular dynamics (MD) simulation. d Optical susceptibility (χ). e Refractive index (nD). f When the frequency is greater than 1014 Hz, i.e., the polarization time is 10−14 s, both orientation polarization and atomic polarization are less likely to occur, in which case ε = nD2. Thus, εQSPR is the predicted value of the model at 1014 Hz. g diff. = |εQSPR − εDFT|. | ||||||||||
| PI_CD24351 | 340.2053 | 1.32 | 432.41 | 5.0439 | 1.8007 | 0.1466 | 1.6854 | 2.9035 | 3.0517 | 0.1482 |
| PI_CD24416 | 437.5390 | 1.362 | 572.56 | 6.4870 | 1.4325 | 0.1521 | 1.7060 | 2.9104 | 4.0504 | 1.1400 |
| PI_CD24366 | 442.9503 | 1.285 | 572.56 | 6.5672 | 1.3515 | 0.1412 | 1.6655 | 2.7740 | 3.9935 | 1.2195 |
| PI_CD24719 | 336.6686 | 1.361 | 448.41 | 4.9914 | 1.8277 | 0.1476 | 1.6894 | 2.8540 | 2.9090 | 0.0550 |
| PI_CD24529 | 352.9113 | 1.277 | 446.43 | 5.2322 | 1.7226 | 0.1447 | 1.6787 | 2.8181 | 2.9704 | 0.1523 |
| PI_CD24352 | 341.5917 | 1.344 | 432.41 | 5.0644 | 1.8717 | 0.1572 | 1.7245 | 2.9740 | 2.7273 | 0.2467 |
| PI_CD24603 | 346.5003 | 1.341 | 432.41 | 5.1372 | 1.8676 | 0.1603 | 1.7361 | 3.0139 | 2.6768 | 0.3371 |
| PI_CD24495 | 423.0180 | 1.274 | 522.53 | 6.2716 | 1.4683 | 0.1499 | 1.6977 | 2.8822 | 3.5412 | 0.6590 |
| PI_CD24378 | 388.1433 | 1.3 | 482.47 | 5.7546 | 1.6226 | 0.1533 | 1.7104 | 2.9255 | 3.1764 | 0.2509 |
As shown in Table 1, the molecular simulation results show that the differences (diff.) between the calculated (εDFT) and model-predicted (εQSPR) values for most of the novel PIs are within the AAE of the model, i.e., less than 0.6, indicating trustworthiness of predictions from the model. This difference may arise not only from the polymer structure, but also from errors caused by the molecular simulation method.59,60 It is noteworthy that the εDFT. of PI_CD24603 is 3.0139, which is higher than the εDFT. of the remaining 8 candidate PIs, and its potential as an energy storage material is great.
4 Conclusion
A holistic “Design–Discovery–Evaluation” scheme is suggested in this work, which includes the creation of a synthetically accessible PI virtual library, the development of the ε-QSPR model and the reliability evaluation for high-throughput screening results based on the AAG method. At first, the retro-generative combinatorial method for designing novel PIs is presented. Given that the novel PIs generated have traceable raw materials for synthesis, their structural validity and synthesizability can be ensured. Next, by combining specific frequencies of datapoints and structural descriptors, frequency-dependent features were obtained, which led to the QSPR model that predicts ε at multiple frequencies. Following multifaceted validations, the model exhibited good predictability (R2 = 0.9768) and stability (Q2 = 0.9654), as well as a satisfactory AAE (i.e., 0.1168). The ε-QSPR model is applied to the high-throughput screening of PIs in virtual libraries, and an AAG-based evaluation method to assess the reliability of the screening results is proposed. The AAG-based evaluation method not only distinguishes the predicted values of the model with “high reliability”, “medium reliability” and “low reliability”, but also provides insights into the design and screening of novel polymers and organics in the future by AAG analysis. In the context of the predicted values with “high reliability”, the ε values of novel PIs at six specific frequencies are analysed, and 9 novel PIs with high ε potential (ε >5 at 103 Hz and Tg between 250 °C and 350 °C) are identified for energy storage applications. In summary, the proposed “Design–Discovery–Evaluation” scheme for novel PIs with the desired ε could be further generalized towards the design of other linear polycondensation polymers.Abbreviations
| PI | Polyimide |
| ε | Dielectric constant |
| QSPR | Quantitative structure–property relationship |
| AAG | Atomic adjacent group |
| MD | Molecular dynamics |
| AI | Artificial intelligence |
| ML | Machine learning |
| DFT | Density functional theory |
| RRU | Ring repeating unit |
| M | Atomic distribution matrix |
| MS | Step matrix |
| MP | Property matrix |
| LOO-CV | Leave-out-one cross-validation |
| LOPO-CV | Leave-one-polymer-out cross-validation |
| LODPO-CV | Leave-one-data-point-out cross-validation |
| SHAP | SHapley additive exPlanations |
| RU | Repeating unit |
| n D | Refractive index |
| χ | Optical susceptibility |
| α | Polarizability |
| ρ | Density |
| M w | The molar mass of RU |
| ε 0 | Vacuum permittivity |
| N A | Avogadro's constant |
| MLR | Multiple linear regression |
| R 2 | The squared correlation coefficient |
| Q 2 | The squared correlation coefficient for leave-one-out cross validation (QLOO2) |
| AE | Absolute error |
| T g | Glass transition temperature |
Data availability
More details on the creation of virtual libraries, datasets for model development, model statistical parameters, and the applicability evaluation based on the atomic adjacent group (AAG) method can be found in the ESI.† Besides, the following four parts of information can be further viewed in the ESI:† (1) the SMILES strings of 487 diamine and 210 dianhydride molecular structures generated in reverse; (2) the SMILES strings of 102![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 270 novel PI structures designed through the combination of 487 diamine and 210 dianhydride molecules; (3) the PI-ε dataset used for QSPR model development, including the collected 1257 experimental values of ε from the literature, the predicted values of the QSPR model, and the division between the training and test sets; and (4) an example of the application of the developed model in the form of Excel formulae.
270 novel PI structures designed through the combination of 487 diamine and 210 dianhydride molecules; (3) the PI-ε dataset used for QSPR model development, including the collected 1257 experimental values of ε from the literature, the predicted values of the QSPR model, and the division between the training and test sets; and (4) an example of the application of the developed model in the form of Excel formulae.
Author contributions
M. X. Y. and Q. Z. J. conceived the problem and carried out detailed studies. M. X. Y., F. Y. Y and Y.-N. Z. analyzed the problem and designed the method. M. X. Y., F. Y. Y co-analyzed the results. M. X. Y. wrote the manuscript and F. Y. Y and Y.-N. Z. made modifications. Q. W. and Z.-H. L. provided strategic guidance. All authors contributed to useful discussions.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (22222807 and 22278319).References
- Y. Zheng, S. Zhang, J. B.-H. Tok and Z. Bao, J. Am. Chem. Soc., 2022, 144, 4699–4715 CrossRef CAS.
- Q.-K. Feng, S.-L. Zhong, J.-Y. Pei, Y. Zhao, D.-L. Zhang, D.-F. Liu, Y.-X. Zhang and Z.-M. Dang, Chem. Rev., 2021, 122, 3820–3878 CrossRef PubMed.
- J. Wei and L. Zhu, Prog. Polym. Sci., 2020, 106, 101254 CrossRef CAS.
- J. Anguita, C. Smith, T. Stute, M. Funke, M. Delkowski and S. Silva, Nat. Mater., 2020, 19, 317–322 CrossRef CAS PubMed.
- H. Tran, R. Gurnani, C. Kim, G. Pilania, H.-K. Kwon, R. P. Lively and R. Ramprasad, Nat. Rev. Mater., 2024, 1–21 Search PubMed.
- C. Wu, L. Chen, A. Deshmukh, D. Kamal, Z. Li, P. Shetty, J. Zhou, H. Sahu, H. Tran and G. Sotzing, ACS Appl. Mater. Interfaces, 2021, 13, 53416–53424 CrossRef CAS.
- R. Wang, Y. Zhu, J. Fu, M. Yang, Z. Ran, J. Li, M. Li, J. Hu, J. He and Q. Li, Nat. Commun., 2023, 14, 2406 CrossRef CAS.
- D.-J. Liaw, K.-L. Wang, Y.-C. Huang, K.-R. Lee, J.-Y. Lai and C.-S. Ha, Prog. Polym. Sci., 2012, 37, 907–974 CrossRef CAS.
- J.-W. Zha, Y. Tian, M.-S. Zheng, B. Wan, X. Yang and G. Chen, Mater. Today Energy, 2023, 31, 101217 CrossRef CAS.
- R. Gurnani, S. Shukla, D. Kamal, C. Wu, J. Hao, C. Kuenneth, P. Aklujkar, A. Khomane, R. Daniels and A. A. Deshmukh, Nat. Commun., 2024, 15, 6107 CrossRef CAS.
- A. Chen, X. Zhang and Z. Zhou, InfoMat, 2020, 2, 553–576 CrossRef CAS.
- G. Bradford, J. Lopez, J. Ruza, M. A. Stolberg, R. Osterude, J. A. Johnson, R. Gomez-Bombarelli and Y. Shao-Horn, ACS Cent. Sci., 2023, 9, 206–216 CrossRef CAS PubMed.
- L. Chen, C. Kim, R. Batra, J. P. Lightstone, C. Wu, Z. Li, A. A. Deshmukh, Y. Wang, H. D. Tran, P. Vashishta, G. A. Sotzing, Y. Cao and R. Ramprasad, npj Comput. Mater., 2020, 6, 61 CrossRef CAS.
- R. Pollice, G. Dos Passos Gomes, M. Aldeghi, R. J. Hickman, M. Krenn, C. Lavigne, M. Lindner-D'Addario, A. Nigam, C. T. Ser, Z. Yao and A. Aspuru-Guzik, Acc. Chem. Res., 2021, 54, 849–860 CrossRef CAS PubMed.
- T. Zhou, Z. Song and K. Sundmacher, Engineering, 2019, 5, 1017–1026 CrossRef CAS.
- D. J. Walsh, W. Zou, L. Schneider, R. Mello, M. E. Deagen, J. Mysona, T. S. Lin, J. J. de Pablo, K. F. Jensen, D. J. Audus and B. D. Olsen, ACS Cent. Sci., 2023, 9, 330–338 CrossRef CAS.
- Z. Tu, T. Stuyver and C. W. Coley, Chem. Sci., 2023, 14, 226–244 RSC.
- M. Aldeghi and C. W. Coley, Chem. Sci., 2022, 13, 10486–10498 RSC.
- J. P. Liles, C. Rouget-Virbel, J. L. H. Wahlman, R. Rahimoff, J. M. Crawford, A. Medlin, V. S. O’Connor, J. Li, V. A. Roytman, F. D. Toste and M. S. Sigman, Chem, 2023, 9, 1518–1537 CAS.
- M. Moret, L. Friedrich, F. Grisoni, D. Merk and G. Schneider, Nat. Mach. Intell., 2020, 2, 171–180 CrossRef.
- E. Shim, J. A. Kammeraad, Z. Xu, A. Tewari, T. Cernak and P. M. Zimmerman, Chem. Sci., 2022, 13, 6655–6668 RSC.
- Y. Amamoto, Polym. J., 2022, 54, 957–967 CrossRef CAS.
- J. Lyu, Y. Li, Z. Li, P. Polanowski, J. K. Jeszka, K. Matyjaszewski and W. Wang, Angew Chem. Int. Ed. Engl., 2023, 62, e202212235 CrossRef CAS PubMed.
- H. Kim, H. Choi, D. Kang, W. B. Lee and J. Na, Chem. Sci., 2024, 15, 7908–7925 RSC.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Science, 2018, 361, 360–365 CrossRef CAS PubMed.
- A. Bender, N. Schneider, M. Segler, W. Patrick Walters, O. Engkvist and T. Rodrigues, Nat. Rev. Chem, 2022, 6, 428–442 CrossRef PubMed.
- T. Gensch, G. Dos Passos Gomes, P. Friederich, E. Peters, T. Gaudin, R. Pollice, K. Jorner, A. Nigam, M. Lindner-D'Addario, M. S. Sigman and A. Aspuru-Guzik, J. Am. Chem. Soc., 2022, 144, 1205–1217 CrossRef CAS PubMed.
- W. P. Walters and R. Barzilay, Acc. Chem. Res., 2021, 54, 263–270 CrossRef CAS PubMed.
- S. Wu, Y. Kondo, M.-a. Kakimoto, B. Yang, H. Yamada, I. Kuwajima, G. Lambard, K. Hongo, Y. Xu, J. Shiomi, C. Schick, J. Morikawa and R. Yoshida, npj Comput. Mater., 2019, 5, 66 CrossRef.
- A. Nagoya, N. Kikkawa, N. Ohba, T. Baba, S. Kajita, K. Yanai and T. Takeno, Macromolecules, 2022, 55, 3384–3395 CrossRef CAS.
- T. S. Lin, C. W. Coley, H. Mochigase, H. K. Beech, W. Wang, Z. Wang, E. Woods, S. L. Craig, J. A. Johnson, J. A. Kalow, K. F. Jensen and B. D. Olsen, ACS Cent. Sci., 2019, 5, 1523–1531 CrossRef CAS.
- M. Yu, Y. Shi, Q. Jia, Q. Wang, Z. H. Luo, F. Yan and Y. N. Zhou, J. Chem. Inf. Model., 2023, 63, 1177–1187 CrossRef CAS.
- T. S. Lin, N. J. Rebello, H. K. Beech, Z. Wang, B. El-Zaatari, D. J. Lundberg, J. A. Johnson, J. A. Kalow, S. L. Craig and B. D. Olsen, J. Chem. Inf. Model., 2021, 61, 1150–1163 CrossRef CAS.
- R. Ma and T. Luo, J. Chem. Inf. Model., 2020, 60, 4684–4690 CrossRef CAS.
- R. Gurnani, D. Kamal, H. Tran, H. Sahu, K. Scharm, U. Ashraf and R. Ramprasad, Chem. Mater., 2021, 33, 7008–7016 CrossRef CAS.
- J. Yang, L. Tao, J. He, J. R. McCutcheon and Y. Li, Sci. Adv., 2022, 8, eabn9545 CrossRef CAS PubMed.
- Y. Chung and W. H. Green, Chem. Sci., 2024, 15, 2410–2424 RSC.
- T. Le, V. C. Epa, F. R. Burden and D. A. Winkler, Chem. Rev., 2012, 112, 2889–2919 CrossRef CAS PubMed.
- H. Qiu, J. Wang, X. Qiu, X. Dai and Z.-Y. Sun, Macromolecules, 2024, 57, 3515–3528 CrossRef CAS.
- L. Chen, C. Kim, R. Batra, J. P. Lightstone, C. Wu, Z. Li, A. A. Deshmukh, Y. Wang, H. D. Tran and P. Vashishta, npj Comput. Mater., 2020, 6, 61 CrossRef CAS.
- J. Yang, L. Tao, J. He, J. R. McCutcheon and Y. Li, Sci. Adv., 2022, 8, eabn9545 CrossRef CAS.
- A. M. Diaz-Rovira, H. Martin, T. Beuming, L. Diaz, V. Guallar and S. S. Ray, J. Chem. Inf. Model., 2023, 63, 1668–1674 CrossRef CAS PubMed.
- R. Ma, H. Zhang, J. Xu, L. Sun, Y. Hayashi, R. Yoshida, J. Shiomi, J.-x. Wang and T. Luo, Mater. Today Phys., 2022, 28, 100850 CrossRef CAS.
- F. Yan, D. Cao, X. Feng, J. Xiong, Q. Wang, Q. Jia and S. Xia, Chem. Eng. Sci., 2023, 280, 118990 CrossRef CAS.
- H. Taniwaki and H. Kaneko, Macromol. Theory Simul., 2023, 32, 2300011 CrossRef CAS.
- K. Sankaranarayanan and K. F. Jensen, Chem. Sci., 2024, 15, 10221–10231 RSC.
- W. Volksen, R. D. Miller and G. Dubois, Chem. Rev., 2010, 110, 56–110 CrossRef CAS PubMed.
- Q. Li, L. Chen, M. R. Gadinski, S. Zhang, G. Zhang, U. Li, E. Iagodkine, A. Haque, L. Q. Chen, N. Jackson and Q. Wang, Nature, 2015, 523, 576–579 CrossRef CAS PubMed.
- S. M. Lundberg and S.-I. Lee, Adv. Neural Inf. Process. Syst., 2017, 30, 4765–4774 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- A. Modelli, L. Mussoni and D. Fabbri, J. Phys. Chem. A, 2006, 110, 6482–6486 CrossRef CAS PubMed.
- H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364 CrossRef CAS.
- X. Ma, F. Zheng, C. G. C. E. van Sittert and Q. Lu, J. Phys. Chem. B, 2019, 123, 8569–8579 CrossRef CAS PubMed.
- D. J. Evans and B. L. Holian, J. Chem. Phys., 1985, 83, 4069–4074 CrossRef CAS.
- R. Faller and J. J. de Pablo, J. Chem. Phys., 2002, 116, 55–59 CrossRef CAS.
- S. S. Park, S. Lee, J. Y. Bae and F. Hagelberg, Chem. Phys. Lett., 2011, 511, 466–470 CrossRef CAS.
- S. Lee and S. S. Park, J. Phys. Chem. B, 2011, 115, 12571–12576 CrossRef CAS PubMed.
- H. Li, Y. Zhou, Y. Liu, L. Li, Y. Liu and Q. Wang, Chem. Soc. Rev., 2021, 50, 6369–6400 RSC.
- H. Lei, X. Li, J. Wang, Y. Song, G. Tian, M. Huang and D. Wu, Chem. Phys. Lett., 2022, 786, 139131 CrossRef CAS.
- X. He, S. Zhang, Y. Zhou, F. Zheng and Q. Lu, Polymer, 2022, 254 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc05000b |
| This journal is © The Royal Society of Chemistry 2024 |