Entropy in catalyst dynamics under confinement

Abstract

Entropy during the dynamic structural evolution of catalysts has a non-trivial influence on chemical reactions. Confinement significantly affects the catalyst dynamics and thus impacts the reactivity. However, a full understanding has not been clearly established. To investigate catalyst dynamics under confinement, we utilize the active learning scheme to effectively train machine learning potentials for computing free energies of catalytic reactions. The scheme enables us to compute the reaction free energies and entropies of O₂ dissociation on Pt clusters with different sizes confined inside a carbon nanotube (CNT) at the timescale of tens of nanoseconds while keeping ab initio accuracy. We observe an entropic effect owing to liquid-to-solid phase transitions of clusters at finite temperatures. More importantly, the confinement effect enhances the structural dynamics of the cluster and leads to a lower melting temperature than those of the bare cluster and cluster outside the CNT, consequently facilitating the reaction to occur at lower temperatures and preventing the catalyst from forming unfavorable oxides. Our work reveals the important influence of confinement on structural dynamics, providing useful insight into entropy in dynamic catalysis.

---

Introduction

The concept of active sites in heterogeneous catalysis was proposed nearly a century ago;¹ many experimental and theoretical studies have been devoted to exploring the nature of active sites and the origin of catalytic reactivity and selectivity.^2,3 The active sites are often regarded as certain fixed structures with special atomic arrangements, and thus in literature the few, most stable configuration of a catalytic site due to its abundance, or a low abundance coordination site with high activity, is commonly considered in theoretical treatment to understand catalytic reactions. In recent years, more and more studies, both experimental and theoretical, have turned to elucidating the dynamic nature of catalytic sites under reaction conditions,^4–6 and found that dynamic interconversion between catalyst configurations may produce some metastable structures that are more active in catalyzing the chemical reactions.^7–9

Generally speaking, it is challenging to observe the catalyst dynamics at high temperatures and pressures experimentally, and even harder to obtain the thermodynamic and kinetic information of elementary catalytic reactions. The latter is essential to obtain quantitative understanding on entropic effects of structural dynamics on catalysis. Computation with ab initio accuracy and efficient statistical sampling of configurational space, on the other hand, can provide a feasible means to investigate the underlying mechanisms of dynamic catalysis and obtain detailed thermodynamic data on elementary steps.¹⁰

For complex supported catalysts such as metal nanoparticles confined in porous frameworks (e.g., carbon nanotube (CNT), zeolite, and metal–organic framework), the channels pose restraints on the morphology and structural dynamics of catalysts,^11,12 which, in turn, may result in non-trivial entropic effects. Many theoretical studies have shown that spatial confinement can modify the catalytic performances due to the geometric and electronic effects.^13,14 However, prevalent works have searched for the most stable structures using static geometry optimization,^15,16 and very few have considered the structural dynamics of confined systems under reaction conditions and the corresponding entropic effects. Recently, Sautet and coworkers have considered different isomers of sub-nanometer cluster catalysts using the global optimization method, whereas reaction calculations were still carried out for given stable structures of catalysts.^8,17 Notably, Cheng and coworkers have used ab initio molecular dynamics (AIMD) and free energy calculation method to study the dynamic behaviors of sub-nanometer metal cluster catalysts and rigorously compute the reaction free energies and entropies of dynamic surface reactions, fully accounting for the contributions of metastable cluster isomers with sufficient statistical sampling.^18–20 It is interesting that anomalous non-linear, peak-shaped relationships of reaction entropy with temperature have been discovered, and they are attributable to the adsorption-induced phase transitions of clusters along the reaction pathways, which can facilitate the chemical reactions. A similar non-linear temperature dependence of free energy for N₂ dissociation on Fe(111) has been subsequently reported by Parrinello et al.⁹

It is evident that AIMD that combines electronic structure calculation and configurational sampling is essential to treat catalyst dynamics. However, the time scale and the model size affordable by AIMD is often limited to tens of pico-seconds (ps) and hundreds of atoms, respectively.^21–23 Thus, it is insufficient to study the dynamic processes of large-sized models of relevance to catalysis at realistic conditions. The classical force field methods can be used for large-scale simulations and have been used to study dynamic behaviors of metal nanoparticles.^24–26 However, classical force fields are generally not suitable for treating chemical reactions. Thus, one of the main challenges for modeling catalyst dynamics is to develop an efficient approach that allows for computation of catalytic processes at much greater sizes and time scales while keeping ab initio accuracy. Machine learning potentials (MLPs) utilize datasets generated by density functional theory (DFT) to train ML models that inherit the accuracy of DFT with a very small fraction of its computational cost,^27,28 and have become an effective computational tool to study complex chemistries such as surface reaction networks.^29–31

In this work, we develop a MLP based reaction free energy calculation workflow to simulate O₂ dissociation on subnanometer Pt₁₅ and Pt₂₇ clusters confined within a CNT channel, which is a synthetic catalytic system found in applications in oxygen reduction^32,33 and hydrocarbon oxidation reactions.^34–36 The reason for choosing Pt₁₅ and Pt₂₇ is that their global minimum structures in the gas phase are characterized as magic number clusters.^37,38 The Pt₁₅ is representative of clusters without core atoms, and the Pt₂₇ has the most popular one-atom core structures. Since the gas phase clusters have been well studied using the traditional static geometry optimization, they can serve as a good initial reference for comparison with the case under confinement. We calculate the reaction free energies (barriers) at various temperatures, and compare them with those at the bare cluster as well as the cluster outside the CNT. Our results show that these catalysts undergo liquid-to-solid phase transitions at certain intermediate temperatures, which gives rise to a reverse peak-shaped entropy curve. More importantly, the confinement imposed by the CNT substrate increases the structural dynamics of clusters, while the support effect to the cluster outside the CNT decreases the catalyst dynamics. Consequently, dynamic confinement effectively shifts the transitions of free energy and entropy to lower temperature ranges, thus facilitating the reaction to occur under milder conditions. Our work provides a computationally affordable approach to investigate the influence of entropy arising from structural dynamics of realistic confined catalysts on reactions, and offers a new dimension to understanding the dynamic confinement effect in catalysis.

Results and discussion

Automated workflow for ML-accelerated free energy calculation

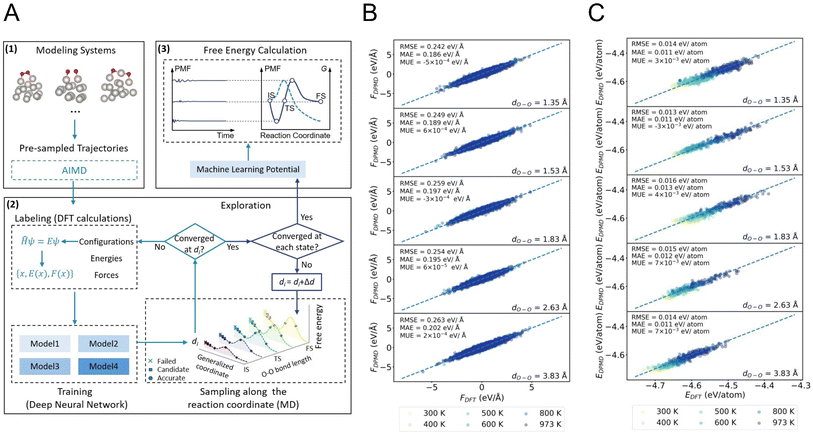
Fig. 1A shows the automated workflow for free energy calculation, incorporating the concurrent learning and potential of mean force (PMF) method.³⁹ Our workflow involves three steps: initialization, training, and free energy calculation. First, the initial structures are randomly selected from AIMD trajectories and calculated using density functional theory (DFT). In the training step, four MLPs are trained, followed by a series of restrained MD simulations along the predefined reaction coordinate at different temperatures to enhance sampling. For the studied O₂ dissociation reaction in this work, the collective variable is chosen as O–O distance. According to the obtained model deviation at a given O–O distance, an error indicator proposed by Zhang et al.,^40,41 those candidate structures falling within the defined bounds are added to the training datasets to obtain MLPs with improved performance. This iterative process continues until the accuracy of the MLP at each O–O distance along the reaction coordinate reaches the trusted level, i.e., no candidate structures are generated, resulting in a MLP that accurately predicts free energy surfaces. Finally, the reaction free energies and barriers are computed by integrating the mean force along the reaction coordinate using the converged MLP.

Fig. 1 (A) Schematic illustration of the workflow of the MLP-accelerated free energy calculation method. The comparison between the atomic forces (B) and energies (C) along the O–O bond length at different temperatures predicted by the generated MLP model and those calculated from DFT. The insets represent the errors towards atomic forces (unit: eV Å⁻¹) and energies (unit: eV) for validation data.

To evaluate the validity of the obtained MLP, we selected over ∼4000 structures from the simulated trajectories along the O–O bond lengths at various temperatures for DFT calculations. The root-mean-squared-error (RMSE) and mean-absolute-error (MAE) of predicted energies by MLP are about ∼0.01 eV per atom, and the RMSE and MAE of predicted atomic forces are about ∼0.2 eV Å⁻¹ for all O–O bond lengths. These results indicate that both forces and energies fitted by our MLP have ab initio level accuracy, thus confirming the reliability of our constructed MLP (Fig. 1B, C and S1–S3 in the ESI†). With this accurate MLP, we proceed to determine the free energy profile of O₂ dissociation on the Pt₁₅ cluster and compare the results with those obtained from AIMD simulations. At the same time scale of ∼5 ps, the mean forces derived from machine learning accelerated molecular dynamics (MLMD) and AIMD exhibit good agreement, further demonstrating that our MLP is very reliable (see inset in Fig. S4A in the ESI†). However, when extending to the longer time scale, the mean forces obtained by MLMD converge to a different value (Fig. S4B and C in the ESI†), indicating the insufficient timescale of AIMD for describing structural dynamics and highlighting the importance and necessity of MLMD. It should be emphasized that in our works, to guarantee the convergence of the average force and free energy, we sample a total of about ∼thirty million configurations in MLMD trajectories of each catalytic system (Fig. S5 in the ESI†).

Entropy in catalyst dynamics

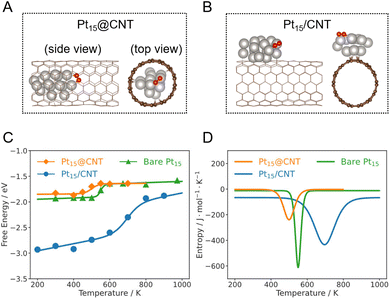
To unveil the effect of structural dynamics on catalytic reaction, we calculate the free energies of O₂ dissociation on a bare Pt₁₅ cluster at varying temperatures using the obtained MLP. To ensure the reliability of our result, we further estimate the statistical errors of mean forces and energies at each constrained O–O bond length (Fig. S6 in the ESI†). The statistical errors of mean forces and free energies are less than 0.3 eV Å⁻¹ and 0.08 eV, respectively. Our results show that the barrier (ΔG^‡) exhibits minimal dependence on temperature, while the reaction free energy (Δ_rG) displays a non-linear relationship with increasing temperature (Fig. S7A in the ESI†). Notably, there exists a steep increase at an intermediate temperate range, suggesting that it is inappropriate to extrapolate the catalytic performance from experiment and theory at low temperatures to high temperature conditions. Furthermore, entropy, which plays an important role in catalyst dynamics, can be rigorously computed by the temperature derivative of free energy. We notice that the reaction entropy changes (Δ_rS) show a reverse peak in the temperature range of 450–700 K, while the activation entropies (ΔS^‡) are not so sensitive to temperature (Fig. S7B in the ESI†).

To study catalyst dynamics under confinement, we calculate the free energy profiles of O₂ dissociation on a confined Pt₁₅ cluster in a CNT (Pt₁₅@CNT) at different temperatures using MLMD. Fig. 2A gives a representative snapshot of the Pt₁₅@CNT from the MLMD trajectory. For comparison, we also investigate the O₂ dissociation on the Pt₁₅ cluster supported outside the CNT (Pt₁₅/CNT) (Fig. 2B). It is worth noting that the temperature dependence of the Δ_rG and Δ_rS for the confined and supported clusters are very similar to those for the bare Pt₁₅ cluster (Fig. 2C, D and S8–S12 in the ESI†), in which significant increases in Δ_rG and reverse peaks in Δ_rS are observed in the intermediate temperature range for all three systems.

Fig. 2 Free energies of O₂ dissociation on Pt₁₅@CNT, bare Pt₁₅ and Pt₁₅/CNT calculated from MLMD. Representative snapshots of structures for O₂ adsorbed on Pt₁₅@CNT (A) and Pt₁₅/CNT (B). The silver and red balls are Pt and O atoms. (C) The reaction free energies (Δ_rG) of O₂ dissociation on Pt₁₅@CNT, bare Pt₁₅, and Pt₁₅/CNT as a function of temperature. The solid lines are fitted curves. (D) The reaction entropy changes (Δ_rS) of O₂ dissociation on the Pt₁₅@CNT, bare Pt₁₅, and Pt₁₅/CNT as a function of temperature.

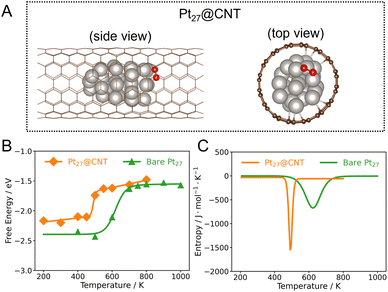
Considering that the catalytic activity is dramatically sensitive to catalyst size, we further investigate the dynamic effect of Pt clusters with different sizes confined inside the CNT. We herein calculate the reaction free energy and entropy of the Pt₂₇@CNT (Fig. S13 in the ESI†). The trends in the change of Δ_rG and Δ_rS with temperature on the Pt₂₇@CNT are similar to those of the Pt₁₅@CNT (Fig. 3), showing the generality of the unusual entropy changes under confinement. A similar temperature dependence has recently been reported for the CO₂ dissociation on Cu clusters and attributed to the phase transitions of clusters during the reaction.¹⁹

Fig. 3 (A) Representative snapshots of structures for O₂ adsorbed on Pt₂₇@CNT. The silver and red balls are Pt and O atoms. (B) The reaction free energies (Δ_rG) of O₂ dissociation on Pt₂₇@CNT and bare Pt₂₇ as a function of temperature. The solid lines are fitted curves. (C) The reaction entropy changes (Δ_rS) of O₂ dissociation on the Pt₂₇@CNT and bare Pt₂₇ as a function of temperature.

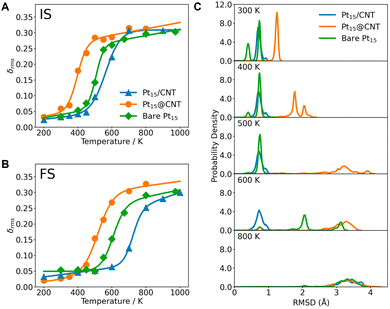
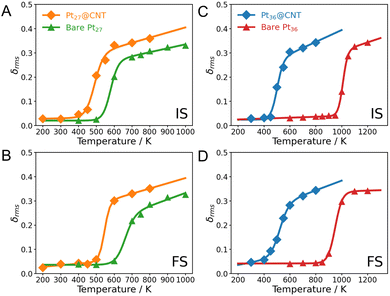
We, therefore, analyze the phase transition behaviors of clusters at the initial (IS), transition (TS), and final states (FS) by monitoring their root-mean-squared bond length fluctuation (δ_rms). It is a sensitive descriptor used to illustrate the phase transition behaviors of small clusters.^42,43 The CNT substrate significantly influences the melting temperatures (T_melt) of clusters. The Pt₁₅@CNT exhibits the lowest melting temperature, followed by the bare Pt₁₅ cluster, while the Pt₁₅/CNT has the highest melting temperature (Fig. 4A and B). Also, for the larger-sized Pt₂₇ and Pt₃₆ clusters, their melting temperatures decrease when they are confined inside the CNT channel (Fig. 5). It is shown that the decrease in melting temperature due to the confinement effect does not occur only in specific sizes but in all sizes of clusters.

Fig. 4 Phase transition behaviors of Pt₁₅@CNT, Pt₁₅/CNT, and bare Pt₁₅ at the IS (A) and FS (B). The calculated values are represented by points, and the corresponding fitted curves are shown by lines. (C) The probability density of RMSD of Pt atomic position at the FS for the Pt₁₅@CNT, bare Pt₁₅, and Pt₁₅/CNT at different temperatures. The RMSD of Pt atomic positions is calculated along the MD trajectories with respect to the first frame.

Fig. 5 Phase transition behaviors of Pt₂₇ and Pt₃₆ inside CNT as well as bare clusters at the IS (A and C) and FS (B and D). The calculated values are represented by points, and the corresponding fitted curves are shown by lines.

The reverse peak in reaction entropy change of bare Pt₁₅ can be justified by the difference in phase transitions between the IS and the FS, with the corresponding mechanism shown in Fig. S14A in the ESI.† In the low temperature range, the IS and FS are solid-like states, and their structures do not change much. As a result, the entropies of the two states can be largely canceled, leading to a minor change in the Δ_rS. However, in the intermediate temperature range, the structures of the IS and FS appear to differ markedly; the IS first enters the coexistent region, in which the entropy of the IS suddenly increases, causing a decrease in the Δ_rS. When the FS also moves into the coexistent region, the entropy of the FS then starts to compensate for the entropy of the IS. As a consequence, the Δ_rS starts to increase with temperature. In contrast, the ΔS^‡ remains constant with increasing temperature due to the almost similar phase transition behaviors between the IS and the TS (Fig. S14B in the ESI†). Similarly, the reverse peaks observed in the Pt₁₅@CNT, Pt₂₇@CNT, and Pt₁₅/CNT can be attributed to the different melting temperatures of the IS and FS, indicating that such abnormal entropic effect may happen on realistic confined and supported catalysts (Fig. S15–S17 in the ESI†). It is worth noting that the observed reverse peak in the Δ_rS curve indicates that the O₂ dissociation on Pt clusters is more likely to occur at lower temperatures. In contrast, its reverse reaction performance can be facilitated through the phase transitions of catalysts. By understanding how phase transitions affect the catalytic properties, researchers can explore strategies to either leverage the positive effects or mitigate the negative ones.

Dynamic effect under confinement

Upon comparing the Δ_rG curves of the confined, supported, and bare Pt₁₅ cluster catalysts, it can be seen that the Δ_rG on Pt₁₅/CNT is lower than that of Pt₁₅@CNT and bare Pt₁₅ in the low and medium temperature ranges, suggesting that O₂ dissociation on supported Pt₁₅ more easily occurs than that on confined and bare Pt₁₅ (Fig. 2C). The reason for the difference is that the local environments in cluster structures are quite different in these temperature ranges, where the Pt₁₅/CNT with a low Pt–Pt coordination number has a stronger O binding energy (Fig. S18 in the ESI†), causing the final state to be stabilized. It is consistent with the static calculated results; the adsorption energy of O on the supported Pt₁₅ cluster is −5 eV, which is higher than that on the confined Pt₁₅ cluster of −4.6 eV (Table S1 in the ESI†). This implies that the cluster supported on the carbon surface is more likely to be oxidized to form a stable oxide, causing the deactivation of the catalyst. On the other hand, the confinement imposed by the CNT protects the Pt cluster from being oxidized, which is consistent with some experimental evidence obtained from in situ EXAFS of Pt catalysts during toluene oxidation.³⁴ Interestingly, at high temperatures, the reaction free energies for the three catalysts are close to each other. Note that the Pt clusters have already melted, suggesting the structural dynamics of the catalysts outweighs the support effects as a primary factor affecting the activity in the high temperature range.

Furthermore, comparison of the Δ_rS curves shows that the temperature at peak position (T_s) of the Pt₁₅@CNT shifts to a lower temperature (∼500 K) compared to that of the bare Pt₁₅ (∼550 K), while the T_s of the Pt₁₅/CNT is the highest (∼700 K) (Fig. 2D and S19 in the ESI†). Similarly, the Pt₂₇@CNT also has a lower T_s than bare Pt₂₇ (Fig. 3C). One wonders what caused this change in temperature. We speculate that the influence of the CNT substrate on the phase transition behaviors of the clusters, as mentioned before, may be the key. We further investigate this by examining the correlation between T_s and the melting temperature T_melt. The result demonstrates that this trend in the T_s is consistent with their corresponding T_melt (Fig. S20 in the ESI†), suggesting that the confinement can increase the entropic contribution to the reaction free energy at lower temperatures because the confined Pt clusters have the lowest melting temperature. In contrast, for Pt clusters sitting outside the CNT, the support effect increases the melting temperature of the cluster, and a higher temperature is required to trigger the favorable entropic response from phase transition.

In order to understand how the CNT changes the melting temperature of the cluster, we further analyze the dynamic fluctuation of bond length of each Pt atom in the three types of Pt₁₅ systems. We notice that the strong binding of two oxygen atoms on the Pt₁₅ cluster outside the CNT leads to formation of a rigid Pt₃O₂ unit that anchors the cluster surface and significantly reduces the dynamic behavior of the cluster, as indicated by the lower δ_rms of the three Pt atoms bound to two oxygen atoms rather than other Pt atoms (Fig. S21 in the ESI†). The rigid unit is not observed on the confined and bare clusters because of weaker adsorption of oxygen (Fig. S22 and S23 in the ESI†). Thus, the oxygen atoms are capable of facile diffusion on the surface, rendering the cluster structure more dynamic. This is consistent with the previous work on other metal clusters, e.g. Au, Ag, and Cu.^19,44 Furthermore, compared to the supported Pt₁₅, when the cluster is confined within the CNT channel, all Pt atoms can interact with C atoms, showing a higher Pt–C coordination number (Fig. S24 in the ESI†). As a result, the confinement imposed by the CNT enables the cluster to change its configuration more easily, as can be seen from the δ_rms of each Pt atom (Fig. S23 in the ESI†). In other words, the confined cluster can have access to a larger configurational space and thus has greater entropic contribution to surface catalysis. To further understand the structural dynamics of the cluster, we analyze the probability distribution of the root-mean-square deviation (RMSD) of Pt atomic position. At temperatures below 400 K, all Pt clusters in the Pt₁₅@CNT, bare Pt₁₅, and Pt₁₅/CNT show very narrow distributions, indicating the solid-like structures. While at 500 K, the Pt₁₅@CNT shows significantly broader distributions compared to the Pt₁₅/CNT and bare Pt₁₅ (Fig. 4C). A similar trend is observed in the initial state (Fig. S25 and S26 in the ESI†). These structural analyses indicate that the Pt cluster inside the CNT generally shows higher structural dynamics.

There are plenty of experimental studies showing that dynamic structural changes of confined catalysts can affect catalytic performances. For example, Corma et al.⁴⁵ investigated the structural evolution of the PtSn cluster within the zeolite framework using in situ spectroscopic techniques and observed that the subtle changes in the cluster structure can have significant impact on the catalytic activity for propane dehydrogenation. Bao et al.⁴⁶ showed that the dynamic confinement of SAPO-17 cages can enhance the ethylene selectivity in syngas conversion. These studies highlight the importance of the confinement of the porous frameworks on the structural dynamics of nanosized catalysts and their performances. However, a connection between catalyst dynamics under confinement and catalytic performances has yet to be established.

Our results show that confinement enhances the structural dynamics and lowers the melting temperatures of metal clusters, which can promote catalytic reactions to occur under milder conditions. There is some experimental evidence in the literature that hints at the correlation between the activity and melting temperature of a catalyst. For example, methane dissociation on the Cu(111) surface occurs at a temperature close to the melting temperature of the Cu surface.⁴⁷ Interestingly, a similar behavior can also be found in enzyme catalysis, where the glycosylation reaction reaches the optimum rate when operated at the melting point of mesophilic α-amylase.⁴⁸ In view that the confined metal cluster has a lower melting temperature, we suggest that confinement can help lower the optimal working temperature of the catalytic reaction. This is supported by a recent study showing that the toluene oxidation catalyzed by Pt nanoclusters within the CNT channels occurs at a temperature of ∼420 K, which is close to our calculated melting temperature.³⁴ Thus, it is conceivable that there may exist a connection between the optimal reaction temperature and the melting temperature of the catalyst, which may be used as a guideline for finding the optimum temperatures for some specific catalytic reactions, and help optimize catalysts more efficiently. Considering the complexity in catalysis, the melting temperature may be a potential descriptor influencing reactivity, rather than the sole factor. Further investigation into the specific mechanisms of reactions and the influence of phase transitions is necessary to fully understand their impact on catalytic activity.

Conclusions

To summarize, we investigate the confinement effect on dynamic catalysis by using machine learning molecular dynamics and free energy calculation. Through detailed analyses on free energies, entropies, and structural dynamics, we demonstrate for the first time how entropy in catalyst dynamics under confinement can affect the activity and how the structural dynamics and melting temperatures of confined catalysts may connect to the optimal reaction temperatures. Our work opens up a new perspective to the understanding of the dynamic confinement effect, and would inspire future investigations on microscopic mechanisms of dynamic catalysis under confinement.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Author contributions

J. C. conceived and designed the project. Q.-Y. F. and H.-X. Z. performed the calculations. Y.-P. L. analyzed the data. All authors discussed the results and wrote the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

J. C. thanks the support by the National Natural Science Foundation of China (Grant No. 22225302, 92161113, 21991151, 21991150, and 22021001), the Fundamental Research Funds for the Central Universities (Grant No. 20720220009 and 20720230090), and Laboratory of AI for Electrochemistry (AI4EC), IKKEM (Grant No. RD2023100101 and RD2022070501). Q.-Y. F. thanks the support by the Natural Science Research Foundation of Shanxi Province (Grant No. 202303021212005).

References

1. H. S. Taylor, Proc. R. Soc. London, Ser. A, 1925, 108, 105–111.
2. J. K. Nørskov, T. Bligaard, B. Hvolbæk, F. Abild-Pedersen, I. Chorkendorff and C. H. Christensen, Chem. Soc. Rev., 2008, 37, 2163–2171.
3. I. E. Wachs and C. A. Roberts, Chem. Soc. Rev., 2010, 39, 5002–5017.
4. Y. Zhou, C. Jin, Y. Li and W. Shen, Nano Today, 2018, 20, 101–120.
5. A. Bergmann and B. R. Cuenya, ACS Catal., 2019, 9, 10020–10043.
6. Z. Zhang, B. Zandkarimi and A. N. Alexandrova, Acc. Chem. Res., 2020, 53, 447–458.
7. G. Collinge, S. F. Yuk, M.-T. Nguyen, M.-S. Lee, V.-A. Glezakou and R. Rousseau, ACS Catal., 2020, 10, 9236–9260.
8. G. Sun and P. Sautet, J. Am. Chem. Soc., 2018, 140, 2812–2820.
9. L. Bonati, D. Polino, C. Pizzolitto, P. Biasi, R. Eckert, S. Reitmeier, R. Schlögl and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2313023120.
10. R. H. Lavroff, H. T. Morgan, Z. Zhang, P. Poths and A. N. Alexandrova, Chem. Sci., 2022, 13, 8003–8016.
11. M. A. Newton, Chem. Soc. Rev., 2008, 37, 2644–2657.
12. L. Liu and A. Corma, Nat. Rev. Mater., 2020, 6, 244–263.
13. W. Chen, Z. Fan, X. Pan and X. Bao, J. Am. Chem. Soc., 2008, 130, 9414–9419.
14. J. Xiao, X. Pan, S. Guo, P. Ren and X. Bao, J. Am. Chem. Soc., 2015, 137, 477–482.
15. J. Xiao, X. Pan, F. Zhang, H. Li and X. Bao, Chem. Sci., 2017, 8, 278–283.
16. L. Yu, W.-X. Li, X. Pan and X. Bao, J. Phys. Chem. C, 2012, 116, 16461–16466.
17. G. Sun, A. N. Alexandrova and P. Sautet, ACS Catal., 2020, 10, 5309–5317.
18. J.-J. Sun and J. Cheng, Nat. Commun., 2019, 10, 5400.
19. Q.-Y. Fan, J.-J. Sun, F. Wang and J. Cheng, J. Phys. Chem. Lett., 2020, 11, 7954–7959.
20. Q.-Y. Fan, Y. Wang and J. Cheng, J. Phys. Chem. Lett., 2021, 12, 3891–3897.
21. K. F. Kalz, R. Kraehnert, M. Dvoyashkin, R. Dittmeyer, R. Glaser, U. Krewer, K. Reuter and J. D. Grunwaldt, ChemCatChem, 2017, 9, 17–29.
22. Y. He, J.-C. Liu, L. Luo, Y.-G. Wang, J. Zhu, Y. Du, J. Li, S. X. Mao and C. Wang, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 7700.
23. H. Guo, P. Sautet and A. N. Alexandrova, J. Phys. Chem. Lett., 2020, 11, 3089–3094.
24. H. Akbarzadeh and A. N. Shamkhali, RSC Adv., 2015, 5, 23160–23173.
25. H. Wei, S. Wei, X. Zhu and X. Lu, J. Phys. Chem. C, 2017, 121, 12911–12920.
26. H. Akbarzadeh, M. Abbaspour, S. Salemi and M. Abroodi, Phys. Chem. Chem. Phys., 2015, 17, 12747–12759.
27. J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401.
28. L. Zhang, J. Han, H. Wang, R. Car and W. E, Phys. Rev. Lett., 2018, 120, 143001.
29. S. Ma and Z.-P. Liu, ACS Catal., 2020, 10, 13213–13226.
30. M. Galib and D. T. Limmer, Science, 2021, 371, 921–925.
31. M. Yang, U. Raucci and M. Parrinello, Nat. Catal., 2023, 6, 829–836.
32. A. G. Hubert and M. M. Nenad, Science, 2009, 324, 48–49.
33. K. Yamamoto, T. Imaoka, W.-J. Chun, O. Enoki, H. Katoh, M. Takenaga and A. Sonoi, Nat. Chem., 2009, 1, 397–402.
34. F. Zhang, F. Jiao, X. Pan, K. Gao, J. Xiao, S. Zhang and X. Bao, ACS Catal., 2015, 5, 1381–1385.
35. S. A. Miners, G. A. Rance and A. N. Khlobystov, Chem. Soc. Rev., 2016, 45, 4727–4746.
36. X. Gao, S. Wang, D. Gao, Z. Chen, W. Liu, M. Wang and S. Wang, Chem. Eng. Technol., 2016, 39, 960–968.
37. X. Wang and D. Tian, Comput. Mater. Sci., 2009, 46, 239–244.
38. G.-F. Wei and Z.-P. Liu, J. Chem. Theory Comput., 2016, 12, 4698–4706.
39. E. A. Carter, G. Ciccotti, J. T. Hynes and R. Kapral, Chem. Phys. Lett., 1989, 156, 472–477.
40. L. Zhang, D.-Y. Lin, H. Wang, R. Car and W. E, Phys. Rev. Mater., 2019, 3, 023804.
41. Y. Zhang, H. Wang, W. Chen, J. Zeng, L. Zhang, H. Wang and W. E, Comput. Phys. Commun., 2020, 253, 107206.
42. H. S. De, S. Krishnamurty, D. Mishra and S. Pal, J. Phys. Chem. C, 2011, 115, 17278–17285.
43. X. Liu, X. Wen and R. Hoffmann, ACS Catal., 2018, 8, 3365–3375.
44. F.-Q. Gong, Y.-X. Guo, Q.-Y. Fan and J. Cheng, Next Nanotechnology, 2023, 1, 100002.
45. L. Liu, M. Lopez-Haro, C. W. Lopes, S. Rojas-Buzo, P. Concepcion, R. Manzorro, L. Simonelli, A. Sattler, P. Serna, J. J. Calvino and A. Corma, Nat. Catal., 2020, 3, 628–638.
46. H. Wang, F. Jiao, Y. Ding, W. Liu, Z. Xu, X. Pan and X. Bao, Natl. Sci. Rev., 2022, 9, nwac146.
47. P. Li, X. Zeng and Z. Li, JACS Au, 2022, 2, 443–452.
48. J. Sočan, M. Purg and J. Åqvist, Nat. Commun., 2020, 11, 2644.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc05399k

‡ These authors contributed equally to this work.

---