Open Access Article
Open Access ArticleLow temperature decoherence dynamics in molecular spin systems using the Lindblad master equation†
Timothy J.
Krogmeier
 ab,
Anthony W.
Schlimgen
ab,
Anthony W.
Schlimgen
 ab and
Kade
Head-Marsden
ab and
Kade
Head-Marsden
 *ab
*ab
aDepartment of Chemistry, Washington University in St. Louis, St. Louis, MO 61630, USA. E-mail: khm@umn.edu
bDepartment of Chemistry, University of Minnesota, Minneapolis, MN 55455, USA
First published on 11th November 2024
Abstract
Understanding the spin dynamics in low-temperature settings is crucial to designing and optimizing molecular spin systems for use in emerging quantum technologies. At low temperatures, irreversible loss occurs due to ensemble dynamics facilitated by electronic–nuclear spin interactions. We develop a combined open quantum systems and electronic structure theory capable of predicting trends in relaxation rates in molecular spin ensembles. We use the Gorini–Kossakowski–Sudarshan–Lindblad master equation and explicitly include electronic structure information in the decoherence channels. We apply this theory to several molecular systems pertinent to contemporary quantum technologies. Our theory provides a framework to describe irreversible relaxation effects in molecular spin systems with applications in quantum information science, quantum sensing, molecular spintronics, and other spin systems dominated by spin–spin relaxation.
Introduction
Molecular spin systems are centerpieces of a variety of emerging technologies including quantum computing, sensing, single-molecule magnets, and spintronics.1–9 In addition to technological applications, molecular spin systems are fundamental components of contemporary problems in experimental and theoretical chemistry across many fields. In cold chemistry, for example, the nuclear spin states of ultracold molecular collisions can influence the branching ratios of product channels.10–13 Other recent experiments characterize the spin dynamics in molecular systems by measuring the spin–lattice, T1, and spin–spin, T2, relaxation rates.14–21 In the context of quantum computing magnetic molecules could serve as quantum bits, or qubits, due to their optical addressability, synthetic tunability, and potential for high-temperature operation.22–26 Fundamental understanding of the electron dynamics and the manipulation and control of the electronic state are essential for effective use of molecular spin systems in practical settings.The dynamics, and therefore control, of these molecular systems are complicated by the ensemble nature of experiments performed in solution or solid phase. From a computational perspective, modeling ensembles requires an understanding of the distribution of configurations and how the individual molecular dynamics differ from one another in the ensemble. Additionally, experiments performed on single molecules still require detailed knowledge of these factors, as measurements of these single-molecule quantum systems must be performed many times to produce accurate statistics of the measurement outcomes.27 Furthermore modeling the T2 relaxation, or dephasing, requires characterization of the connection between ensemble-averaged dynamics and loss of phase information. Modeling these relaxation processes is therefore a significant computational challenge because a Hilbert space containing every molecule in a solution is intractable. However, accurate modeling of ensemble dephasing would be a boon in informing experimental design and predicting T2 relaxation times in molecular spin systems in contemporary technologies.
In many technological applications, including molecular qubits and single molecule magnets, a two-level system is generated via an external magnetic field interacting with an unpaired electron. For practical use of a superposition of the parallel and antiparallel states, relative phase information must be long-lived. Dephasing occurs due to spin–lattice and spin–spin relaxation; at high temperatures, T1 is expected to dominate, while at low temperatures T2 dominates.15,18–21
In this article, we develop a phenomenological model capable of describing ensemble dynamics of molecular spin systems interacting with an environment. Because these systems undergo relaxation, one natural approach is to use an open quantum system perspective. We focus on the low-temperature setting using the Gorini–Kossakowski–Sudarshan–Lindblad (GKSL) equation to simulate the quantum dynamics.28–31 We incorporate the geometric and dynamic distributions present in ensemble systems to predict T2 relaxation. Specifically, we use ab initio electronic structure to determine the GKSL decoherence rates for non-interacting ensembles of molecular spins. We demonstrate the utility of this approach by simulating the decoherence dynamics of two molecular spin systems. This approach is general to cold molecular spin systems undergoing decoherence dynamics with applications in a wide array of emerging quantum technologies.
Theory and methods
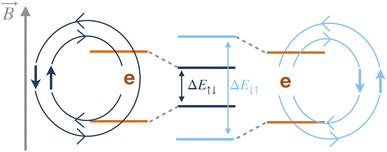
One mechanism that leads to T2 relaxation is nuclear spins coupled through a dipolar magnetic interaction, Ĥdip, which connects the low-spin states of the two nuclei, and is proportional to r−3 where r is the internuclear distance.32–34 This coupling induces an exchange of spin orientation between two antiparallel nuclear spins in a pair-wise flip-flop of magnetization, for example when the spin state changes from |↑↓〉 to |↓↑〉. In a molecular spin system a given spin state of the nuclear pair will induce a different magnetic field at the location of the electron, compared to the corresponding flip-flop state. Therefore, the flip-flop of a nuclear spin pair that are hyperfine coupled to the electron results in a time-dependent magnetic field at the electron, as shown in Fig. 1. In either a time- or ensemble-averaged experiment, this time-dependent magnetic field rescales the Zeeman energy of the electron, broadening the energy states by dynamically changing the precession frequency of the electron. In a spin echo experiment at low temperatures, decoherence due to static inhomogeneities of an external magnetic field is removed, but the dynamic flip-flop broadening processes will remain. The time-dependent field induced by the nuclear spin flip-flops is therefore the most significant remaining contributor to dephasing.35–38 Modeling the ensemble spin-decoherence in these systems is therefore challenging due to the influence of the static electronic structure along with the irreversible nature of the electron broadening process.Here, we use the GKSL equation enhanced with ab initio electronic structure to model the spin decoherence of an ensemble of molecules. The GKSL equation is a commonly used open quantum system master equation derived under the Born–Markov approximation, meaning it can be used to capture the dissipative dynamics in quantum systems weakly coupled to quickly relaxing environments.28–31 This equation has found application in many fields including quantum biology, quantum information, quantum optics, and condensed matter physics.31,39–44 A major benefit of the GKSL equation is that, by construction, it preserves the positivity of the density matrix.28–31 This equation takes the form,
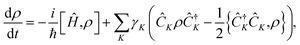 | (1) |
In typical ensemble experiments measurements will sample a distribution of molecular configurations or geometries. For non-interacting systems at low temperature, the distribution of geometries can be approximated from the zero-point vibrational modes of a molecule. To simulate such an ensemble, we sample the zero-point vibrational modes of each molecule using density functional theory (DFT), which results in a distribution of local magnetic environments for the nuclear spins. Computing this distribution is an important part of our approach because it estimates the broadening of the rescaled Zeeman energy in Fig. 1 which is the source of the irreversible decoherence in a molecular ensemble. For each molecule we generate 2·(3N − 6) different geometries from the normal modes.
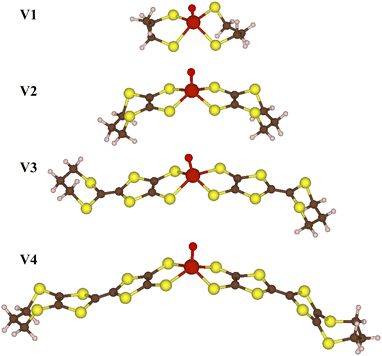
We carry out all electronic structure calculations using the ORCA 5 quantum chemistry software package.45 Since the vanadium-oxo complexes are not strongly correlated, DFT is sufficient to describe their electronic structure. We used the B3LYP hybrid functional, in addition to a triple-ζ polarized basis set for the carbon, hydrogen, oxygen, and sulfur, with a core-polarized CP(PPP) basis set for the vanadium ion, in addition to an auxiliary basis set.46–48 For each molecule V1–V4 in Fig. 2, we optimized geometries optimized, and from those equilibrium geometries, we calculated vibrational modes calculated. We followed the same process for CuS and CuSe, using the M06L functional with an ANO-RCC-DZP basis for the carbon and hydrogen, and an ANO-RCC-TZP basis for the copper, sulfur, and selenium, in addition to auxiliary basis sets.49–54 The functionals and basis sets were chosen following previous work which qualitatively matches experimentally measured spin densities.55,56
During each calculation, we computed hyperfine tensors, taking into account dipole–dipole interactions, spin–orbit coupling, and the Fermi contact interaction between the electron and the spin-active hydrogen and vanadium nuclei in the molecules. We computed the hyperfine tensors via an expectation value taken over the spin density of each molecule.32–34,45 We used the resulting hyperfine tensors to compute the difference in magnetic environment between two nuclear spins i and j as Δij = |Ai − Aj|, with full details for electronic structure methods and computation of hyperfine tensors shown in the (ESI).†
Following an analogous process for nuclear spin lattices with defects,57 we calculate the flip-flop rate for each nuclear pair i, j in a specific geometry according to,
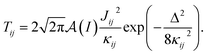 | (2) |
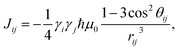 | (3) |
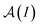 is a normalization factor, and Δij = |Ai − Aj| is the hyperfine energy difference between nuclei i and j. κij is given by
is a normalization factor, and Δij = |Ai − Aj| is the hyperfine energy difference between nuclei i and j. κij is given by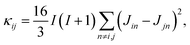 | (4) |
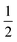 in the present work. For this work, vanadium and copper are approximated as a spin-
in the present work. For this work, vanadium and copper are approximated as a spin-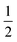 nucleus. This is not expected to be a significant source of error for the present model, as the difference in hyperfine energy between the vanadium and copper metal ions and the distal hydrogens is so large that nuclear flip-flops between the vanadium and other spin-active nuclei are prevented, and therefore do not contribute to decoherence of the electron.
nucleus. This is not expected to be a significant source of error for the present model, as the difference in hyperfine energy between the vanadium and copper metal ions and the distal hydrogens is so large that nuclear flip-flops between the vanadium and other spin-active nuclei are prevented, and therefore do not contribute to decoherence of the electron.
This equation is derived by considering the lineshape of a nuclear pair in a nuclear magnetic resonance (NMR) experiment.57κij represents broadening of the NMR lineshape of a nuclear pair because of the dipolar interactions between the nuclear flip-flop pair and all other spin-active nuclei. The broadening of the lineshape allows the flip-flop process to occur even when the Zeeman energy of each nuclei differs.58–62 The terms Ai and Aj represent the center of each feature in the NMR lineshape, or the chemical shift, of the two nuclei, and are taken from the hyperfine tensors calculated with the electronic structure methods described above. Flip-flop rates were generated by setting Δ = Δ0 = 0 and Δ = Δij = |Ai − Aj| in eqn (2). For each pair ij the distribution of flip-flop rates present in an ensemble solution is given by the set {Tij}, from which the standard deviation of flip-flop rates, σ{Tij} for each pair in an ensemble is calculated. Calculating the distribution of flip-flop rates and their use as the decay parameter for molecular spin decoherence is a major contribution of this work. This provides a relationship between ab initio quantum chemistry and the rate of nuclear spin flip-flops in molecular spin systems.
To account for the irreversible loss of coherence due to ensemble dephasing of the electron in an ensemble of molecular spin systems the GKSL equation, eqn (1) was used. The standard deviation of the flip-flop rates described above, σ{Tij}are used as the decay rates, γK, each of which correspond to a Lindbladian channel ĈK which is chosen to be the Pauli-Z operator, Ŝz. The use of rates of transitions between states, such as the transition between flip-flop states, as the decay rates in the GKSL equation has been previously used.63 Each nuclear pair ij in the molecule is assigned a loss channel and the associated decay rate corresponding to the standard deviation of the flip-flop rate of that nuclear pair.
To treat the Liouvillian part of the dynamics, some approximation is necessary. The vanadium-oxo molecular systems contain 13 spin-active nuclei, in addition to the electron, which amounts to a 214 dimensional Hilbert space, while the copper systems contain 9 spin-active nuclei in addition to the electron, for a 210 dimensional Hilbert space. To minimize this cost, the Hamiltonian is factorized into clusters of nuclear spins in their interactions with the central electron, following the master equation cluster-correlation expansion (ME-CCE).64–70 A major contribution of this work is the physically-motivated derivation of the decay rates γK, where previous approaches as well as implementations of ME-CCE have used γK as an adjustable parameter to match experiment.38,69 Here, no adjustable parameters are present, and qualitative experimental agreement is achieved. For the purposes of this work, clusters of two nuclear spins are sufficient since the mechanism of dephasing being considered here is the pairwise flip-flop of two nuclear spins at a time.68 Finally, the Hamiltonian parameters that were factorized using CCE were taken from the equilibrium geometry of each molecule calculated using DFT. Additional details on the calculation of spin dynamics is included in the ESI.†
Results
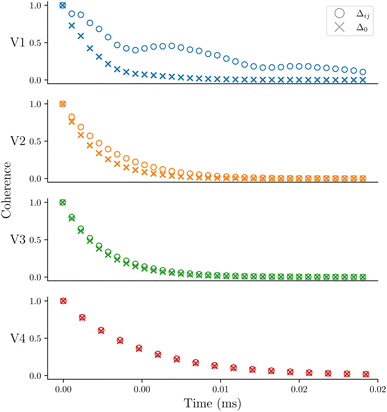
The first system we consider is a series of vanadium-oxo structures V1–V4 shown in Fig. 2. The T2 spin–spin relaxation in these molecules has been experimentally measured, and the results highlight the counter-intuitive relationship between electron-nuclear distance and electron decoherence.16 The longest coherence was observed in the smallest molecule, V1, even though this molecule has the strongest hyperfine coupling interactions. These results were explained using the concept of the spin diffusion barrier, a phenomenon in which nuclei close to a strong magnetic moment, in this case an electron, are energetically detuned relative to one another such that nuclear flip-flops are no longer energy conserving and become suppressed, thereby stifling decoherence.56,71–76 In other words, for hyperfine tensors Ai and Aj, when Δij = |Ai − Aj| is very large, flip-flops and decoherence are both suppressed. If Ai = Aj then Δ = Δ0 = 0 and there is no suppression of flip-flops or decoherence due to the spin diffusion barrier.In Fig. 3 we show the calculated coherence profiles using the GKSL equation for each ensemble of V1–V4, with the experimental data shown in the inset.16 Experimental decoherence profiles are generally fit to an empirical equation (see ESI†) which provides an estimate of the decay constant. Following this procedure, Table 1 shows the resulting decay constants which are fit from our simulated data. Our simulated results agree qualitatively with experiment, notably showing that V1 has the longest-lived coherence, followed by V2–V4 with faster decoherence. The simulations predict that V2–V4 have similar decay constants, which is also in good agreement with the experiment.
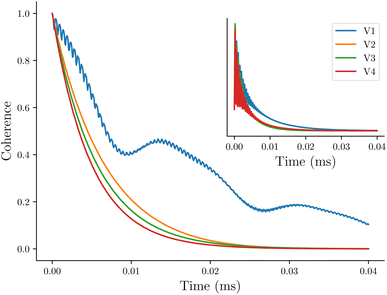 | ||
| Fig. 3 Simulated decoherence of the vanadium-oxo series using the GKSL equation, with experimental data reproduced from ref. 16 shown in the inset. | ||
| Δ ij | Exp. | Δ 0 | |
|---|---|---|---|
| V1 | 0.0274 | 0.01011 | 0.00834 |
| V2 | 0.0111 | 0.00602 | 0.00997 |
| V3 | 0.0110 | 0.00659 | 0.00996 |
| V4 | 0.00972 | 0.00595 | 0.00936 |
To test the influence of the Δ parameter in eqn (2), the dynamics are recalculated with Δ = Δ0. The coherence profiles for V1–V4 are shown in Fig. 4 comparing the coherence of each molecular ensemble with Δ0 and Δij. The decay time constants for the profiles with Δ0 are included in Table 1. Fig. 4 demonstrates that Δij is crucial to reproduce the correct experimental trend. For Δ0, V1 has the fastest decoherence time, whereas with Δij it is longest-lived, which is what is observed in experiment.
To further evaluate the impact of Δ on the spread of flip-flop rates, σ{Tij}is plotted in Fig. 5 with Δij and Δ0 for the nuclear pairs that have σ{Tij} > 5 kHz. σ{Tij}for all nuclear spins are shown in the ESI.† We show that V1 has the greatest change in σ{Tij}when changing from Δij to Δ0, V2 shows a slight change, followed by V3, and finally V4 shows an even smaller change. This highlights the sensitivity of V1, and to a much lesser extent, V2–V4, to the Δ term. The Δ parameter encodes the hyperfine energy difference between each nuclei undergoing the mutual flip-flop process, and is therefore a measure of the different magnetic environments that each nuclei occupies.
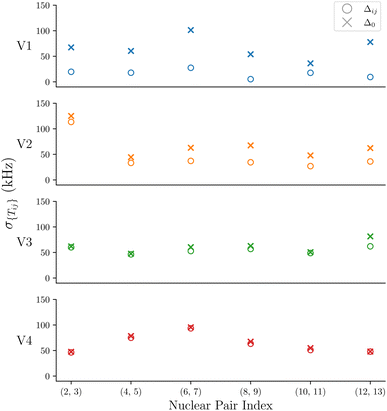 | ||
| Fig. 5 The standard deviations of the flip-flop rates for each ensemble V1–V4 for Δ0 and Δij are shown for the geminal hydrogens. | ||
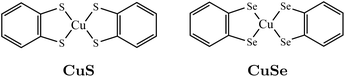
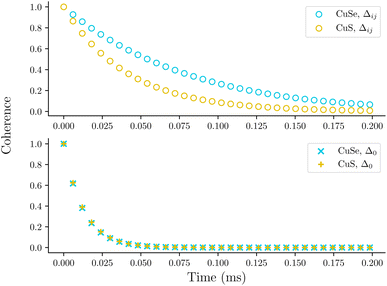
The example of the vanadium ensembles demonstrates the importance of the location of the spin-active nuclei relative to the electron in determining decoherence. Altering the local magnetic environment of the electron can also be achieved by changing the ligand that is bonded to the metal center. To demonstrate this we compare the coherence profiles of a copper molecular spin system with sulfur- or selenium-based ligands shown in Fig. 6, labelled as CuS and CuSe, respectively. Experiments show that CuSe has a longer-lived coherence due to increased copper-ligand covalency, indicating that the electron is delocalized on to the selenium ligand.55 Computed spin densities for each molecule using the previously described DFT parameters are shown in the ESI.†
Fig. 7 shows simulated decoherence for these two molecular species using either Δij or Δ0. The decay constants taken from fits to the calculated profiles are shown in Table 2. Similar to the vanadium-oxo series, simulated decoherence trends are qualitatively comparable to experiments. Namely, the selenium based series has slower decoherence due to the delocalized copper-selenium σ-bond. This behavior is not seen when the local magnetic environment is neglected, i.e. when Δ = Δ0. This highlights the importance of including the hyperfine energy difference in the calculation of the flip-flop rates for nuclear spin pairs.
| Δ ij | Exp. | Δ 0 | |
|---|---|---|---|
| CuS | 0.0411 | 0.002048 | 0.0128 |
| CuSe | 0.0766 | 0.003183 | 0.0125 |
Discussion and conclusions
Through these two sets of molecular spin systems, we have shown that the GKSL equation qualitatively reproduces experimental trends in spin decoherence. Importantly, the local magnetic environment of the decohering spin through electronic structure calculations which directly relates to the decoherence rate of molecular spin ensembles. The magnetic environment can be tuned in various ways, for example through increased metal–ligand covalency or through the internuclear distance of the spins. As an example of the former, we compare two copper molecules to show how increasing metal–ligand covalency can impact spin–spin decoherence. Increased metal–ligand covalency, or delocalization of the electron onto the selenium ligands, increases the hyperfine coupling via the Fermi contact and dipole–dipole interactions between the electron and the nuclear spins in the copper molecules. As an example of the latter, we compare a series of vanadium-oxo complexes showing the smallest complex exhibited the longest coherence time. Our results validate conventional understanding of decoherence in these molecular species; namely, that a spin diffusion barrier mitigates decoherence processes when nuclear spins are near the electronic spin. Our approach naturally incorporates the distinct magnetic environments of each nuclei by using ab initio electronic structure in its treatment of the nuclear pair flip-flop process. In doing so, the presence of the spin diffusion barrier is a natural outcome, providing a theoretical justification for its use in explaining observed molecular T2 trends.It is important to emphasize that the GKSL equation only includes the T2 decoherence process, and does not include T1 spin–lattice relaxation. The ensemble averaging over geometries via sampling of vibrational trajectories generates the distribution of flip-flop rates which yields the GKSL decay rate, but does not describe any coupling between the electron and lattice vibrations. Furthermore, the utility of the GKSL equation model in these systems is in describing trends, and informing experimental ligand choices for long-lived coherence times. While quantitative agreement with experiment is unlikely using this model, we obtain qualitative prediction of trends in coherence time with changes in electron-nuclear distance as well as atomic or ligand substitutions.
It is necessary for the master equation approach to encode the different magnetic environments of each nuclei in a spin pair to produce experimentally comparable results. This method explicitly incorporates the electronic structure of each molecule, and the distribution of flip-flop rates, into the decay rate in the GKSL equation. This approach is general to any molecular system at low temperature in a spin–spin dominated relaxation regime. This approach can be extended to strongly correlated transition metal systems, provided that the electronic structure can be computed accurately. The development of this genuinely open systems framework for molecular spin systems unlocks the possibility of modeling these systems with qualitative agreement with experimental results.
Data availability
Additional data and code that support the findings of this study are available from the corresponding author upon reasonable request and on the Head-Marsden group's GitHub repository.Author contributions
Timothy J. Krogmeier: data curation, formal analysis, methodology, validation, visualization, writing – original draft, writing – review & editing, software; Anthony W. Schlimgen: conceptualization, formal analysis, methodology, software, supervision, writing – original draft, writing – review & editing; Kade Head-Marsden: conceptualization, formal analysis, funding acquisition, methodology, project administration, resources, software, supervision, writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts to declare.References
- A. Zabala-Lekuona, J. M. Seco and E. Colacio, Single-molecule magnets: From Mn12-ac to dysprosium metallocenes, a travel in time, Coord. Chem. Rev., 2021, 441, 213984 CrossRef CAS.
- D. Aravena and E. Ruiz, Spin dynamics in single-molecule magnets and molecular qubits, Dalton Trans., 2020, 49, 9916 RSC.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, 2006 Search PubMed.
- R. Clérac, Molecular cluster magnets, Angew. Chem., Int. Ed., 2012, 51, 7079–7080 CrossRef.
- D. G. Cristiano Benelli, Introduction to Molecular Magnetism, John Wiley & Sons, Ltd, 2015, ch. 4, pp. 51–67 Search PubMed.
- K. R. Mullin, D. W. Laorenza, D. E. Freedman and J. M. Rondinelli, Quantum sensing of magnetic fields with molecular color centers, Phys. Rev. Res., 2023, 5, L042023 CrossRef CAS.
- S. Sanvito, Molecular spintronics, Chem. Soc. Rev., 2011, 40, 3336 RSC.
- M. R. Wasielewski, M. D. E. Forbes, N. L. Frank, K. Kowalski, G. D. Scholes, J. Yuen-Zhou, M. A. Baldo, D. E. Freedman, R. H. Goldsmith, T. Goodson, M. L. Kirk, J. K. McCusker, J. P. Ogilvie, D. A. Shultz, S. Stoll and K. B. Whaley, Exploiting chemistry and molecular systems for quantum information science, Nat. Rev. Chem, 2020, 4, 490 CrossRef CAS PubMed.
- S. L. Bayliss, P. Deb, D. W. Laorenza, M. Onizhuk, G. Galli, D. E. Freedman and D. D. Awschalom, Enhancing spin coherence in optically addressable molecular qubits through host-matrix control, Phys. Rev. X, 2022, 12, 031028 CAS.
- R. Hermsmeier, X. Xing and T. V. Tscherbul, Nuclear spin relaxation in cold atom–molecule collisions, J. Phys. Chem. A, 2023, 127, 4511 CrossRef CAS PubMed.
- L. D. Carr, D. DeMille, R. V. Krems and J. Ye, Cold and ultracold molecules: science, technology and applications, New J. Phys., 2009, 11, 055049 CrossRef.
- J. L. Bohn, A. M. Rey and J. Ye, Cold molecules: Progress in quantum engineering of chemistry and quantum matter, Science, 2017, 357, 1002 CrossRef CAS PubMed.
- N. R. Hutzler, Polyatomic molecules as quantum sensors for fundamental physics, Quantum Sci. Technol., 2020, 5, 044011 CrossRef.
- D. W. Laorenza, A. Kairalapova, S. L. Bayliss, T. Goldzak, S. M. Greene, L. R. Weiss, P. Deb, P. J. Mintun, K. A. Collins, D. D. Awschalom, T. C. Berkelbach and D. E. Freedman, Tunable Cr4+ molecular color centers, J. Am. Chem. Soc., 2021, 143, 21350 CrossRef CAS PubMed.
- M. J. Amdur, K. R. Mullin, M. J. Waters, D. Puggioni, M. K. Wojnar, M. Gu, L. Sun, P. H. Oyala, J. M. Rondinelli and D. E. Freedman, Chemical control of spin–lattice relaxation to discover a room temperature molecular qubit, Chem. Sci., 2022, 13, 7034 RSC.
- M. J. Graham, C.-J. Yu, M. D. Krzyaniak, M. R. Wasielewski and D. E. Freedman, Synthetic approach to determine the effect of nuclear spin distance on electronic spin decoherence, J. Am. Chem. Soc., 2017, 139, 3196 CrossRef CAS PubMed.
- K. R. Mullin, R. B. Greer, M. J. Waters, M. J. Amdur, L. Sun, D. E. Freedman and J. M. Rondinelli, Detrimental increase of spin-phonon coupling in molecular qubits on substrates, ACS Appl. Mater. Interfaces, 2024, 16, 40160 CrossRef CAS PubMed.
- R. Mirzoyan and R. G. Hadt, The dynamic ligand field of a molecular qubit: decoherence through spin–phonon coupling, Phys. Chem. Chem. Phys., 2020, 22, 11249 RSC.
- S. K. Hoffmann and S. Lijewski, Raman electron spin–lattice relaxation with the debye-type and with real phonon spectra in crystals, J. Magn. Reson., 2013, 227, 51 CrossRef CAS PubMed.
- A. J. Fielding, S. Fox, G. L. Millhauser, M. Chattopadhyay, P. M. Kroneck, G. Fritz, G. R. Eaton and S. S. Eaton, Electron spin relaxation of copper (II) complexes in glassy solution between 10 and 120K, J. Magn. Reson., 2006, 179, 92 CrossRef CAS PubMed.
- M. Atzori, L. Tesi, E. Morra, M. Chiesa, L. Sorace and R. Sessoli, Room-temperature quantum coherence and rabi oscillations in vanadyl phthalocyanine: Toward multifunctional molecular spin qubits, J. Am. Chem. Soc., 2016, 138, 2154 CrossRef CAS PubMed.
- G. A. Timco, S. Carretta, F. Troiani, F. Tuna, R. J. Pritchard, C. A. Muryn, E. J. L. McInnes, A. Ghirri, A. Candini, P. Santini, G. Amoretti, M. Affronte and R. E. P. Winpenny, Engineering the coupling between molecular spin qubits by coordination chemistry, Nat. Nanotechnol., 2009, 4, 173 CrossRef CAS PubMed.
- A. Chiesa, P. Santini, E. Garlatti, F. Luis and S. Carretta, Molecular nanomagnets: a viable path toward quantum information processing?, Rep. Prog. Phys., 2024, 87, 034501 CrossRef CAS PubMed.
- R. H. Lavroff, D. L. Pennington, A. S. Hua, B. Y. Li, J. A. Williams and A. N. Alexandrova, Recent innovations in solid-state and molecular qubits for quantum information applications, J. Phys. Chem. A, 2021, 125, 9567 CrossRef CAS PubMed.
- H. Mao, G. J. Pažėra, R. M. Young, M. D. Krzyaniak and M. R. Wasielewski, Quantum gate operations on a spectrally addressable photogenerated molecular electron spin-qubit pair, J. Am. Chem. Soc., 2023, 145, 6585 CrossRef CAS PubMed.
- S. Chicco, G. Allodi, A. Chiesa, E. Garlatti, C. D. Buch, P. Santini, R. De Renzi, S. Piligkos and S. Carretta, Proof-of-concept quantum simulator based on molecular spin qudits, J. Am. Chem. Soc., 2024, 146, 1053 CrossRef CAS PubMed.
- R. de Sousa, Electron spin as a spectrometer of nuclear-spin noise and other fluctuations, in Electron Spin Resonance and Related Phenomena in Low-Dimensional Structures, ed. M. Fanciulli, Springer Berlin Heidelberg, Berlin, Heidelberg, 2009, pp. 183–220 Search PubMed.
- H.-P. Breuer and F. Petruccione, The Theory of Open Quantum Systems, Oxford University Press, 2007 Search PubMed.
- V. Gorini, A. Kossakowski and E. C. G. Sudarshan, Completely positive dynamical semigroups of N-level systems, J. Math. Phys., 1976, 17, 821 CrossRef.
- G. Lindblad, On the generators of quantum dynamical semigroups, Commun. Math. Phys., 1976, 48, 119 CrossRef.
- D. Manzano, A short introduction to the Lindblad master equation, AIP Adv., 2020, 10, 025106 CrossRef.
- N. F. Ramsey, Electron coupled interactions between nuclear spins in molecules, Phys. Rev., 1953, 91, 303 CrossRef CAS.
- A. Soncini and P. Lazzeretti, Nuclear spin-spin coupling density in molecules, J. Chem. Phys., 2003, 118, 7165 CrossRef CAS.
- N. F. Ramsey and E. M. Purcell, Interactions between nuclear spins in molecules, Phys. Rev., 1952, 85, 143 CrossRef CAS.
- E. L. Hahn, Spin echoes, Phys. Rev., 1950, 80, 580 CrossRef.
- W. Yao, R.-B. Liu and L. J. Sham, Theory of electron spin decoherence by interacting nuclear spins in a quantum dot, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 195301 CrossRef.
- N. Zhao, S.-W. Ho and R.-B. Liu, Decoherence and dynamical decoupling control of nitrogen vacancy center electron spins in nuclear spin baths, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 115303 CrossRef.
- K. Aruachan, Y. J. Colón, D. Aravena and F. Herrera, Semi-empirical Haken–Strobl model for molecular spin qubits, New J. Phys., 2023, 25, 093031 CrossRef.
- D. A. Lidar, I. L. Chuang and K. B. Whaley, Decoherence-free subspaces for quantum computation, Phys. Rev. Lett., 1998, 81, 2594 CrossRef CAS.
- M. B. Plenio and S. F. Huelga, Dephasing-assisted transport: quantum networks and biomolecules, New J. Phys., 2008, 10, 113019 CrossRef.
- B. Kraus, H. P. Büchler, S. Diehl, A. Kantian, A. Micheli and P. Zoller, Preparation of entangled states by quantum markov processes, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 78, 042307 CrossRef.
- E. M. Gauger, E. Rieper, J. J. L. Morton, S. C. Benjamin and V. Vedral, Sustained quantum coherence and entanglement in the avian compass, Phys. Rev. Lett., 2011, 106, 040503 CrossRef PubMed.
- T. c. v. Prosen, Open xxz spin chain: Nonequilibrium steady state and a strict bound on ballistic transport, Phys. Rev. Lett., 2011, 106, 217206 CrossRef PubMed.
- G. McCauley, B. Cruikshank, D. I. Bondar and K. Jacobs, Accurate lindblad-form master equation for weakly damped quantum systems across all regimes, Npj Quantum Inf., 2020, 6, 74 CrossRef.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- F. Weigend, Accurate coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8, 1057 RSC.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- G. L. Stoychev, A. A. Auer and F. Neese, Automatic generation of auxiliary basis sets, J. Chem. Theory Comput., 2017, 13, 554 CrossRef CAS PubMed.
- P.-O. Widmark, P.-Å. Malmqvist and B. O. Roos, Density matrix averaged atomic natural orbital (ANO) basis sets for correlated molecular wave functions, Theor. Chim. Acta, 1990, 77, 291 CrossRef CAS.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, Main group atoms and dimers studied with a new relativistic ANO basis set, J. Phys. Chem. A, 2004, 108, 2851 CrossRef CAS.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, New relativistic ANO basis sets for transition metal atoms, J. Phys. Chem. A, 2005, 109, 6575 CrossRef CAS PubMed.
- S. Lenz, K. Bader, H. Bamberger and J. van Slageren, Quantitative prediction of nuclear-spin-diffusion-limited coherence times of molecular quantum bits based on copper (II), Chem. Commun., 2017, 53, 4477 RSC.
- M. S. Fataftah, M. D. Krzyaniak, B. Vlaisavljevich, M. R. Wasielewski, J. M. Zadrozny and D. E. Freedman, Metal–ligand covalency enables room temperature molecular qubit candidates, Chem. Sci., 2019, 10, 6707 RSC.
- J. Chen, C. Hu, J. F. Stanton, S. Hill, H.-P. Cheng and X.-G. Zhang, Decoherence in molecular electron spin qubits: Insights from quantum many-body simulations, J. Phys. Chem. Lett., 2020, 11, 2074 CrossRef CAS PubMed.
- R. de Sousa and S. Das Sarma, Theory of nuclear-induced spectral diffusion: Spin decoherence of phosphorus donors in Si and GaAs quantum dots, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 115322 CrossRef.
- E. Dikarov, O. Zgadzai, Y. Artzi and A. Blank, Direct measurement of the flip-flop rate of electron spins in the solid state, Phys. Rev. Appl., 2016, 6, 044001 CrossRef.
- J. M. Steiner, P. Hautle and W. T. Wenckebach, Relaxation of nuclear dipolar energy, J. Magn. Reson., 2021, 333, 107099 CrossRef CAS PubMed.
- G. Parker, Nuclear magnetic resonance line shapes in solids, Am. J. Phys., 1970, 38, 1432 CrossRef CAS.
- K. Schaumburg, E. Shabanova and J. Sellschop, NMR studies of orientation-dependent nuclear spin-spin relaxation and lineshapes in 13C-enriched diamonds, J. Magn. Reson., Ser. A, 1995, 112, 176 CrossRef CAS.
- P. W. Anderson and P. R. Weiss, Exchange narrowing in paramagnetic resonance, Rev. Mod. Phys., 1953, 25, 269 CrossRef CAS.
- S. Mehl and D. P. DiVincenzo, Noise analysis of qubits implemented in triple quantum dot systems in a Davies master equation approach, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 195309 CrossRef.
- W. Yang and R.-B. Liu, Quantum many-body theory of qubit decoherence in a finite-size spin bath, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 085315 CrossRef.
- W. Yang and R.-B. Liu, Quantum many-body theory of qubit decoherence in a finite-size spin bath. II. ensemble dynamics, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115320 CrossRef.
- N. Zhao, S.-W. Ho and R.-B. Liu, Decoherence and dynamical decoupling control of nitrogen vacancy center electron spins in nuclear spin baths, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 115303 CrossRef.
- Z.-S. Yang, Y.-X. Wang, M.-J. Tao, W. Yang, M. Zhang, Q. Ai and F.-G. Deng, Longitudinal relaxation of a nitrogen-vacancy center in a spin bath by generalized cluster-correlation expansion method, Ann. Phys., 2020, 413, 168063 CAS.
- W. Yao, R.-B. Liu and L. J. Sham, Theory of electron spin decoherence by interacting nuclear spins in a quantum dot, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 195301 CrossRef.
- M. Onizhuk, Y.-X. Wang, J. Nagura, A. A. Clerk and G. Galli, Understanding central spin decoherence due to interacting dissipative spin baths, Phys. Rev. Lett., 2024, 132, 250401 CrossRef CAS PubMed.
- M. Onizhuk and G. Galli, Decoherence of solid-state spin qubits: a computational perspective, arXiv, 2024, preprint, arXiv:2405.18535 [quant-ph], DOI:10.48550/arXiv.2405.18535.
- N. Bloembergen, On the interaction of nuclear spins in a crystalline lattice, Physica, 1949, 15, 386 CrossRef CAS.
- W. E. Blumberg, Nuclear spin-lattice relaxation caused by paramagnetic impurities, Phys. Rev., 1960, 119, 79 CrossRef CAS.
- G. R. Khutsishvili, Spin diffusion and magnetic relaxation of nuclei, J. Exptl. Theoret. Phys., 1962, 42, 1311–1318 CAS.
- G. R. Khutsishvili, Spin diffusion and nuclear magnetic relaxation in a crystal containing a magnetic impurity, Sov. Phys. Usp., 1969, 11, 802 CrossRef.
- H. Rorschach, Nuclear relaxation in solids by diffusion to paramagnetic impurities, Physica, 1964, 30, 38 CrossRef CAS.
- R. Guichard, S. J. Balian, G. Wolfowicz, P. A. Mortemousque and T. S. Monteiro, Decoherence of nuclear spins in the frozen core of an electron spin, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 214303 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: The full standard deviation of the flip-flop rate for each nuclear pair in the ensembles V1–V4. The fitting function information used to extract decay times from simulated data is also provided. Additional details on the electronic structure methods used and the ME-CCE method used are provided, including the computed spin densities of each molecule, calculation of hyperfine tensors, and the effective spin Hamiltonian used to calculate spin dynamics. See DOI: https://doi.org/10.1039/d4sc05627b |
| This journal is © The Royal Society of Chemistry 2024 |