Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Preparation of superstructured comb polymers based on tadpole-shaped single-chain nanoparticles†
Yangjing
Chen
 a,
Zhiyu
Hu
a,
Zhigang
Shen
b,
Xiaoqiang
Xue
a,
Zhiyu
Hu
a,
Zhigang
Shen
b,
Xiaoqiang
Xue
 c and
Hongting
Pu
c and
Hongting
Pu
 *a
*a
aDepartment of Polymer Materials, School of Materials Science & Engineering, Tongji University, Shanghai, 201804, China. E-mail: puhongting@tongji.edu.cn
bSinopec Shanghai Research Institute of Petrochemical Technology Co., LTD., Shanghai, 201208, China
cIndustrial College of Carbon Fiber and New Materials, School of Chemical Engineering and Materials, Changzhou Institute of Technology, Changzhou, Jiangsu 213000, China
First published on 3rd October 2024
Abstract
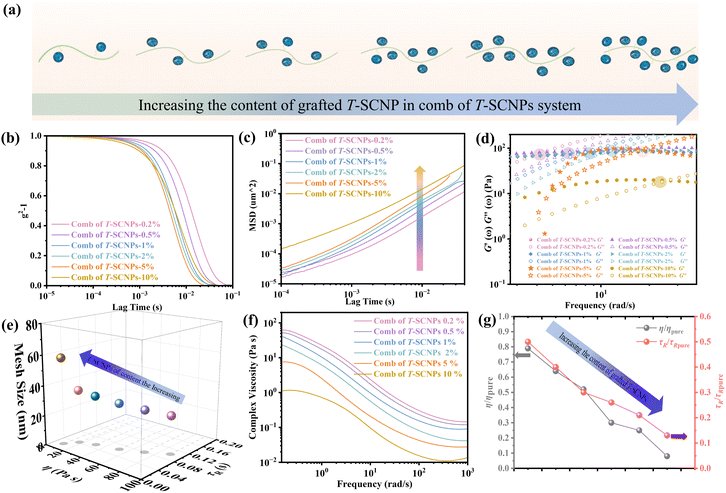
Compared with the formation of individual elements, the creation of superstructures often yields exceptional properties. This approach has been applied to assemble diverse synthetic building blocks (molecules, macromolecules, inorganic nanoparticles, etc.) into highly organized constructs. In the present study, a novel comb polymer superstructure is developed via the grafting of tadpole-shaped single-chain nanoparticles (T-SCNPs) onto a high-molecular-weight linear backbone (H-LP). The resulting superstructure (comb of T-SCNPs), which utilizes T-SCNPs as building blocks, exhibits distinct rheological behavior in solution. The influences of the microstructure and related parameters (specifically the relaxation time (τR) and mesh size (ξ) of the entangled chains) on the macroscopic properties (modulus and viscosity) of this complex topological structure in solution are investigated. Compared with conventional comb macromolecules (comb of F-LPs) and blends of SCNPs with high-molecular-weight polymers (SCNPs&H-LP), T-SCNP combs exhibit significantly reduced chain entanglement, faster τR, and larger ξ in solution, resulting in a substantially decreased viscosity (up to 90%). Furthermore, our research underscores the intricate relationship between these rheological properties and the size and concentration of grafted T-SCNPs. As the size or concentration of T-SCNPs increases, the mesh size of the entangled chains expands, which leads to increased τR and decreased viscosity.
Introduction
Complex polymer architectures, such as star-shaped,1 dendritic,2 grafted,3 bottle-brushed,4 or hyperbranched polymers,5 exhibit additional complexity that imparts unique physical properties. This inherent complexity and the resulting properties have facilitated the widespread application of complex polymer architectures in diverse fields, including drug delivery,6 bioimaging,7 catalysis,8 nanotemplates,9,10 photonics,11 and superelastomers.12 Therefore, polymer topology, including branching, cyclic, and cross-linked structures, is crucial in studying and designing the mechanical and rheological properties of bulk polymer materials.13,14 Among various topological structures, comb shaped polymers, which consist of a single backbone with multiple side chains, have recently garnered significant attention for their tailored and unique softening mechanical properties.15–17 These grafted polymers can encode mechanical properties through structural parameters such as backbone length, side chain length, and branch point spacing, thereby mimicking the mechanical characteristics of various soft materials.18–21 However, the fundamental chemical characteristics of these polymers, including intermolecular forces, conformational features, phase separation patterns, and crystalline structures, often hinder the ability to design their mechanical properties topologically.22 As a result, the task of understanding and engineering mechanical properties based on polymer topology remains a formidable challenge.23In recent years, nanobuilding blocks (NBBs), which are composed of nanoparticle (NP) cores and precisely defined polymer chains, have emerged as innovative “colloidal molecules” for the bottom-up fabrication of functional materials and devices.24 These NBBs have shown promise in mechanically reinforcing polymer networks through the utilization of nanoparticles such as Fe3+,25 BaTiO3+,26 and metal–organic cages27 as cross-linking agents. Despite considerable1–23 advancements in this area, the design and synthesis of NBBs with precise structures, particularly those featuring specific NP core geometries and topologies, are still in the nascent stage, with only a few successful examples reported. Current synthetic methods of NBBs, such as selective surface modification,28 kinetically controlled synthesis,29 post-functionalization on cage-like inorganic compounds,30 and encapsulation,31 primarily involve complex synthesis processes, multiple preparation or purification stages, and insufficient control over the dimensions of both NP cores and polymer structures. A promising strategy for creating well-defined NBBs is the self-collapse of individual polymer chains through intramolecular cross-linking, as developed by Hawker's group.32 At very low concentrations, coil-to-globule transitions driven by various intramolecular reactions occur solely within individual polymer chains, resulting in what are known as single-chain nanoparticles (SCNPs).33–38 SCNPs, characterized by their ultrafine sizes and “secondary” structures, have attracted considerable interest due to their applications in sensing,39 catalysis,40,41 bioimaging,42 and drug delivery.43
Furthermore, Hawker et al. demonstrated that the single chain polymer chemistry could be extended to linear block copolymers where the coil-to-globule transition only occurred within one block containing cross-linkable groups. This gave rise to the formation of a tadpole-shaped NBB (T-SCNP) where the crosslinked block formed the “head”, attached by an un-cross-linked polymer “tail”.44 This provides the possibility of preparing more complex topological structures using T-SCNPs, as the cross-linked “tail” can be functionalized and grafted into the linear polymer skeleton through grafting methods, forming a novel comb shaped polymer. Interestingly, when internal crosslinking of T-SCNPs occurs via dynamic covalent bonds, this unique comb-shaped polymer can reversibly transform into traditional comb-shaped polymers. This process offers a platform for developing novel topology-reversible transition materials.
Moreover, using T-SCNPs as grafting units allows for orthogonal control over the interaction of the “heads” with the surface and the properties of the comb. Consequently, this method can achieve tasks that existing methods cannot.45 Compared with traditional comb polymers, comb polymers with special topological structures prepared by grafting T-SCNPs with specific sizes and shapes as grafting units can significantly alter the chain entanglement behavior of the system and the relaxation process of chain segments due to the size effect of their side chains. This, in turn, affects their macroscopic properties, especially the change in rheological behavior. To the best of our knowledge, there has been limited exploration into how the topological structure and size of the side chains attached to comb polymers affect their microstructure, including entanglement behavior of chain segments, relaxation rate, and mesh size of the entangled chain. The topic of chain entanglement has been of interest to polymer scientists for decades, as it has significant implications for adjusting macroscopic properties through the microstructure of the system.46–48
Results and discussion
The synthetic method utilized in this study is depicted in Scheme 1. A random copolymer (F-LP) containing methyl methacrylate (MMA), anthracenyl methacrylate (AMA), and an aldehyde end group was synthesized via atom transfer radical polymerization (ATRP), employing CHO–PMMA–Br as a macroinitiator (Scheme 1a and b). The successful preparation of CHO–PMMA–Br was verified using gel permeation chromatography (GPC), proton nuclear magnetic resonance (1H NMR), and mass spectrometry (MALDI-TOF MS). The SEC curve of the polymer (CHO–PMMA–Br) exhibited a single peak with a small dispersity index (Đ) (Fig. S3 in the ESI†), which is characteristic of ATRP. In the 1H NMR spectrum (Fig. S4 in the ESI†), proton peaks corresponding to the polymer were evident, and the number-average molecular weight (Mn) calculated from NMR data was 2700 g mol−1, which is consistent with the GPC result (3200 g mol−1). The mass spectrum of CHO–PMMA–Br showed a Gaussian distribution (Fig. S5 in the ESI†), with the main peak corresponding to a molecule where the bromine end group was replaced by a sodium ion and adjacent major peaks differing by 100.1, corresponding to the MMA monomeric unit. Minor peaks represented molecules with a potassium ion at the chain end, with adjacent minor peaks also differing by 100.1. The collapse process of the liner precursor was conducted using a copolymer (F-LP) through the photodimerization of pendant anthracene groups at a low polymer concentration (c = 1 mg mL−1) to produce tadpole-shaped single-chain nanoparticles (T-SCNPs). In this process, functional copolymers were excited, leading to internal dimerization of the highly aromatic pendant groups under an inert atmosphere (Scheme 1c). The composition of the F-LP was ascertained using NMR calculations, which revealed the ratio of the methylene protons of methyl methacrylate units at 3.51 ppm and the overall aromatic protons of the anthracene segments ranging from 7.51–8.52 ppm, confirming that the copolymer (F-LP) comprised 10 mol% of the anthracene segments. Following dimerization, the signals for the aromatic protons of the anthracene segments shifted from 7.51–8.52 ppm to 6.89 ppm, as shown by 1H NMR analysis (Fig. S6 in the ESI†).Table S1 (in the ESI†) lists the molecular weights (Mn and Mw), dispersity index (Đ), sizes (Rh), and glass transition temperatures (Tg) of both F-LP and T-SCNP. The intramolecular anthracene dimerization process resulted in a decrease in the hydrodynamic radius (Rh) of the resulting T-SCNPs, leading to a noticeable reduction in Mn due to a transition from a coil to a globe structure. Additionally, the SEC trace of the T-SCNPs indicated a longer retention time than that of its linear precursor after the photoinduced internal crosslinking process (Fig. S7 in the ESI†). The UV-Vis spectra of F-LP exhibit a characteristic absorption peak for anthracene moieties between 325 and 400 nm. Following irradiation, the intensity of the absorption peak decreased indicating the dimerization of pendant anthracene units, as depicted in Fig. S8 (in the ESI†). The glass transition temperature (Tg) is a critical property influencing the processing performance of polymers. It represents the temperature at which amorphous polymers transition from a glassy state to a highly elastic state. The movement of chain segments in T-SCNPs is restricted, leading to reduced degrees of freedom of the chains. Fig. S9 (in the ESI†) compares the Tg values of T-SCNPs and F-LP. Compared with that of F-LP (Tg 122 °C), the Tg of T-SCNPs was found to be 132 °C, indicating that the internal crosslinking structure of SCNPs restricts chain segment mobility.
The tadpole-shaped SCNP (T-SCNP), featuring a segment with an aldehyde functional group at the terminal, is capable of reacting with high-Mw linear polymers (H-LPs) that contain hydrazide side groups, facilitating the grafting of T-SCNPs onto the linear backbone. The structure of the H-LP was characterized using 1H NMR and GPC, as indicated in Fig. S10 and S11 in the ESI.† The SEC curve exhibited a single peak with a Đ of 1.92 and Mw of 10.8 kDa, which is consistent with the characteristics of conventional free radical polymerization. The positions of each peak in the NMR spectrum correspond to the protons of the polymer.
Additionally, comprehensive characterization via1H NMR, DLS, SEC, SAXS, and diffusion-ordered NMR spectroscopy (DOSY NMR) provided substantial evidence for the successful synthesis of a superstructure comb polymer (comb of T-SCNPs) using T-SCNPs as graft units. The complete reaction between the aldehyde and hydrazide groups was confirmed by the disappearance of the aldehyde proton peak and the appearance of new peaks representing hydrazone bonds in the NMR spectrum (Fig. S12 in the ESI†). The NMR results revealed that the positions of the two spectral lines were almost identical, with minor variations in the relative intensities of the peaks. With the formation of the comb of T-SCNPs, the disappearance of peak a (10.08 ppm), which corresponds to the hydrogen peak of the –CHO– group of F-SCNPs, was noted. Moreover, new peaks b′ and c′ in the spectrum of the comb of T-SCNPs were identified, corresponding to the protons of the –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH– (10.72 ppm) and NH (8.31 ppm) groups, respectively.
NH– (10.72 ppm) and NH (8.31 ppm) groups, respectively.
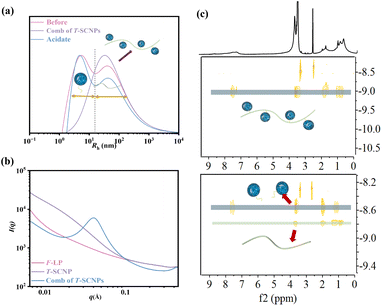
The SEC curves before and after the grafting reaction indicated a transformation from two distinct peaks, corresponding to the T-SCNPs and the high-Mw linear polymer (H-LP), to a single peak, indicating the transition from two separate components to one unified component (Fig. S13 in the ESI†). However, a notably higher Đ was observed, potentially due to variations in the grafting efficiency across different chains, resulting in diverse hydrodynamic volumes in solution. The dynamic light scattering (DLS) results support the SEC data, showing a transition from two peaks to a single peak with an expanded size distribution after the reaction (Fig. 1a). Remarkably, the acylhydrazone bond serves as a dynamic covalent bond. Upon the addition of a small amount of acid, coupled with a system pH of about 6.5, the acylhydrazone bond is cleaved, resulting in the detachment of T-SCNPs from the H-LP. This dissociation is evidenced by a return from a single peak to the original two peaks in the DLS results.
Fig. 1b displays the one-dimensional (1D) SAXS intensity results for the F-LP, T-SCNPs, and comb of T-SCNPs. The SAXS experiment was performed at the BL16B beamline of the Shanghai Synchrotron Radiation Facility (China). Initially, the results indicate a qualitative difference between linear polymers and SCNPs. The extended polymer precursor exhibited a region of linear decrease at low q values, whereas the compact SCNP presented higher order structures. This phenomenon is described by the relationship I(q) ∝ qp, where p is the Porod exponent. A Porod exponent of 4 indicates an ideal sphere, a range of 3 < p < 4 suggests a flexible protein, a value of 2 corresponds to an unfolded, random chain, and p = 1 signifies a fully extended chain.49 For the comb of T-SCNPs, the 1D SAXS curve displays a distinct peak at 0.47 nm, reflecting the locally ordered structure of the T-SCNPs. Additionally, the distance between the T-SCNP domains within the comb of the T-SCNPs was precisely determined to be 13.36 nm, as calculated using Bragg's equation (d = 2π/q).
Finally, the effectiveness of grafting T-SCNPs onto the H-LP was evaluated using DOSY NMR, a technique that exploits the exponential decay of signals due to molecular self-diffusion. DOSY NMR provides a two-dimensional analysis where the first dimension (F2) reflects conventional chemical shifts and the second dimension (F1) corresponds to the self-diffusion coefficient (D).50 This method is highly sensitive and adept at detecting even trace amounts in complex mixtures. For this study, DOSY NMR of the resulting comb of T-SCNPs and its precursors was conducted in dilute DMSO. As depicted in the DOSY map (Fig. 1c), distinct diffusion coefficients are observed in the SCNP&H-LP mixture, indicating separate compositions of T-SCNP and H-LP. The uniform diffusion coefficients across all the protons within the comb of T-SCNPs confirmed the efficient grafting of T-SCNPs onto the H-LP.
The inclusion of nanoparticles, whether inorganic,51 grafted with SiO2,52 or dendrimers,53 alters the rheological properties of polymers, causing a significant decrease in system viscosity. Several theories, such as the free volume effect, nanoconfinement effect, nanoparticle surface slip effect, shear banding effect, and shear thinning effect induced by nanoparticles, have been proposed to explain this change. However, Goldansaz and colleagues,54 in their study of dendritic polyethylene/polystyrene composites, concluded that these effects alone cannot fully explain the viscosity reduction observed. This underscores the complexity arising from interactions between nanoparticles and polymer chains in heterogeneous composite systems, further compounded by chemical compositional differences. Therefore, developing broadly applicable theoretical models across different systems remains challenging. In nanoparticle–polymer composites, both the kinetic properties of the polymer chains and the dynamic behaviors of the nanoparticles play critical roles. The diffusion kinetics of nanoparticles are closely linked to their size relative to the characteristic length of polymer chains, with different types of nanoparticles exhibiting distinct diffusion mechanisms within the polymer melt.
Mackay et al.55 incorporated SCNPs of polystyrene into a polystyrene melt, resulting in an 80% viscosity reduction with just a 1% volume of SCNPs, despite their chemical similarity to the polymer chains. This phenomenon, which occurs without specific enthalpic interactions between the nanoparticles and melt chains, remains inadequately explained by current theories. Recent molecular dynamics simulations by Qian and colleagues indicate that the reduced internal degrees of freedom within SCNPs lead to decreased friction on the surrounding molten polymer chains.56 This insight illustrates the mechanism responsible for viscosity reduction in polymer systems due to SCNPs.
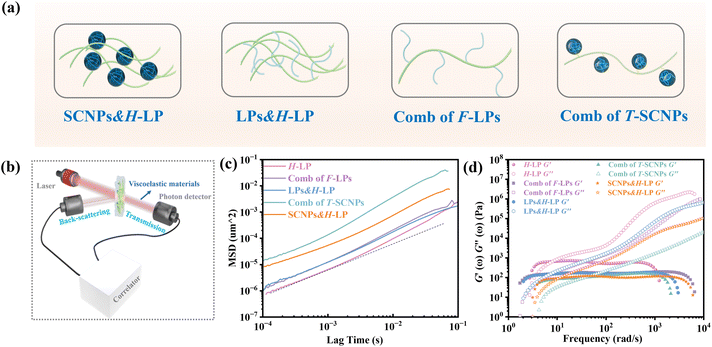
We investigated the direct grafting of T-SCNPs onto linear main chains via an aldehyde–acylhydrazone reaction, contrasting this with the simple addition of SCNPs to polymer melts or solutions in composite form. Our focus was on exploring the potential performance of novel comb topological polymers in solution. For comparison, mixtures of SCNPs with high Mw linear matrix polymers (SCNPs&H-LP) and traditional comb polymers (comb of F-LPs) were prepared, where T-SCNP precursor polymers were grafted onto the main chains of the H-LP. Additionally, mixtures of SCNP precursor polymers with the H-LP (LPs&H-LP) were prepared (Fig. 2a). The amount of grafted F-LP corresponded to the molar quantity of T-SCNPs in the comb of the T-SCNP system, which was consistent with the molar quantities of SCNPs and LPs added to the two composite systems (SCNPs&H-LP and LPs&H-LP). The structural details of the LPs, SCNPs, and comb of F-LPs are provided in the ESI, as illustrated in Fig. S14–S16 in the ESI.†
Microrheological experiments were conducted to explore the varied rheological behaviors exhibited by these systems in solution, aiming to further understand chain entanglement, restricted chain mobility, and disentanglement effects induced by SCNPs grafted onto high Mw linear polymers. A contemporary microrheology technique involves tracking the movement of a small particle probe, typically a colloidal microsphere, to minimize mechanical disturbance of the medium (Fig. 2b).57 Colloidal particles are ideal probes because they induce minimal perturbations in the structure and dynamics of soft matter at thermal energies of about kBT (where kB is Boltzmann's constant and T is the absolute temperature). This characteristic enables precise measurement of the rheological properties of materials at scales ranging from micrometers to submicrometers. In contrast to conventional rotational mechanical rheometers, microrheology studies impose virtually negligible strain on the material during measurement.52
Fig. S17 in the ESI† illustrates the ICF curves of various systems, showing that the interchain friction coefficient in each system decays to 0 over time, indicating complete chain relaxation. The H-LP system demonstrated prolonged relaxation due to extensive interchain entanglement; however, the addition of SCNPs to the system significantly decreased the chains' relaxation rate, consistent with previous findings.56 Interestingly, the comb of the T-SCNP system exhibited a notably faster relaxation rate compared to the SCNPs&H-LP system. We hypothesize that grafting SCNPs into the H-LP not only reduces friction between linear chains through steric effects but also reduces chain density around SCNPs, thereby increasing system free volume. The comb of F-LPs and LPs&H-LP systems show minimal differences; however, compared with that of the H-LP system, the relaxation rate of entangled chains in the two systems is enhanced, possibly because of the plasticizing effect of the low Mw linear polymers.
To characterize the translational dynamics of polymer chains, we calculated the MSD of tracer particles in polymer solutions across different systems on the basis of the velocity autocorrelation function for a Brownian particle (eqn (1) and (2))
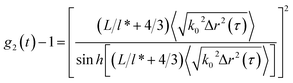 | (1) |
| 〈Δr2(τ)〉 = δ2(1 − e(−τ/τc)a) | (2) |
Fig. 2c displays MSD curves of tracer particles (TiO2, 360 nm) in the polymer solutions of various systems. Initially, at short lag times, the MSDs exhibit a linear trend proportional to the lag time (Δr2(τ)–τ), indicating pure diffusive motion of the tracer particles and a microenvironment resembling a viscous liquid. In the entangled regime (at intermediate lag times), MSDs display a power-law behavior with lag time, with a slope slightly less than one (Δr2(τ)–τ0.85), indicative of polymer entangled network cage formation characteristic of viscoelastic behavior. The tracer particles in the comb of the T-SCNP system exhibit much higher MSD values than those in other systems, corresponding to the highest diffusion coefficient. The Laplace transform of the MSD corresponds to the complex shear modulus (G*), which is evaluated using the generalized Stokes–Einstein equation (eqn (3)).58 This connection facilitates the computation of the storage modulus (G′) and loss modulus (G′′) using eqn (4).
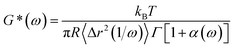 | (3) |
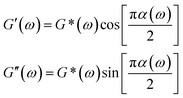 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ] and Γ is the gamma function.
τ] and Γ is the gamma function.
Fig. 2d depicts the frequency-dependent modulus variation across several systems. This demonstrates that the reduced chain entanglement within the system leads to decreased friction during the disentanglement process. Consequently, the comb of the T-SCNP system has the lowest G′′, which is consistent with MSD findings across different systems.
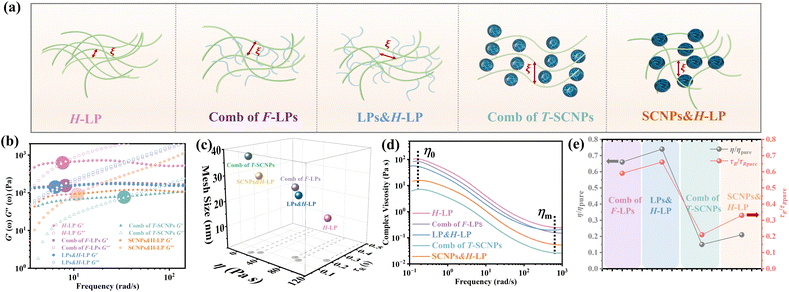
Therefore, we believe that integrating SCNPs into a linear polymer matrix through grafting induces substantial alterations in the system's microstructure, resulting in discernible variations in the macroscopic properties. The macroscopic behavior of polymers is intricately linked to their microstructural configuration. The unique rheological characteristics observed in the T-SCNP comb system in solution stem from an enlarged mesh size (ξ) between the interlocked chains. As depicted in Fig. 3a, grafting T-SCNPs onto high Mw linear main chains is believed to increase the distance between these chains, thereby reducing chain entanglement. Similarly, incorporating mixed-form SCNPs into high Mw linear resins is anticipated to yield a comparable effect. However, SCNPs feature internal loops and clusters of small loops referred to as “domains,” which are essential for filling space at higher polymer concentrations. These entanglements are thought to be minimized within the T-SCNP comb structure. In contrast, in the comb of F-LPs and LPs&H-LP systems, intermolecular entanglements persist between low Mw linear polymers and high molecular weight matrix resins, limiting effective reduction of chain entanglement.
In DWS, the plateau modulus G0 is related to the diffusivity of tracer particles through the equation G0 = kBT/(6παδ2). Additionally, the mesh size ξ, which denotes the spacing between entangled polymer chains, can be determined using eqn (5).59
| ξ = (kBT/G0)1/3 | (5) |
The introduction of SCNPs into the H-LP system (SCNPs&H-LP) led to a significant increase in ξ, from 17.32 to 31.07 nm (as indicated in Table 1), indicating that SCNPs increase the free volume within the system. In the comb of the T-SCNP system, ξ further increases to 35.83 nm compared with that of the SCNPs&H-LP system. Moreover, higher chain entanglement within the system hinders chain segment relaxation due to intermolecular friction, resulting in longer relaxation times. A crossover of the G′ and G′′ is observed along with the determination of the terminal relaxation time (τR), which is the reciprocal of the crossover frequency.60 For long linear chains, G′ and G′′ curves typically intersect at low frequencies, reflecting chain disentanglement. Comparing relaxation times (τR) of H-LP, LPs&H-LP, and the comb of F-LP systems, τR decreases from 0.2 s to 0.13 s and 0.12 s for LPs&H-LP and the comb of F-LP systems, respectively, as shown in Fig. 3b. However, there is a minimal difference in τR between LPs&H-LP and F-LP systems. Notably, the τR of the T-SCNP comb system is significantly reduced, showing a fivefold decrease compared with that of the H-LP and a twofold decrease compared with that of SCNPs&H-LP, as detailed in Fig. 3c and Table 1. Thus, the impact of SCNPs on viscosity primarily arises from its size effect, which increases the free volume around linear resins, thereby reducing the friction coefficient.
| Samples | 6δ2 × 105a (μm2) | η 0 (Pa s) | η m × 102a (Pa s) | G 0 (Pa) | τ R × 102b (s) | Mesh sizec (nm) |
|---|---|---|---|---|---|---|
| a Data acquired from DWS. b Data acquired from the crossover of G′ and G′′. c Data acquired from the corresponding theoretical calculation using eqn (5). | ||||||
| H-LP | 1.05 | 111.8 | 29.2 | 780 | 20.3 | 17.32 |
| Comb of F-LPs | 5.46 | 73.8 | 12.9 | 185 | 12.1 | 27.98 |
| LP&H-LP | 7.29 | 83.1 | 19.8 | 238 | 13.5 | 25.71 |
| Comb of T-SCNPs | 16.32 | 16.7 | 5.8 | 88 | 4.3 | 35.83 |
| SCNPs&H-LP | 12.12 | 27.9 | 8.9 | 135 | 7.2 | 31.07 |
The viscosity curves (Fig. 3d) demonstrate that the comb of the T-SCNP system has the lowest zero-shear viscosity (η0). As the frequency increases, chains begin to disentangle, leading to the viscosity reduction characteristic of a Newtonian fluid. At higher frequencies, where chain entanglements are fully resolved, viscosity stabilizes. In this regime, viscosity is solely influenced by the intrinsic structure of polymers, as entangled chains are fully released from interaction. The viscosity curve indicates that ηm of the T-SCNP comb is one-fifth that of the H-LP polymer, highlighting the significant impact of T-SCNPs on the polymer conformation in solution. Fig. 3e presents the ratios of zero-shear viscosities (η/ηpure) and relaxation times (τR/τR pure) of various systems compared to their respective matrix polymer chains. For the comb of F-LPs and F-LPs&H-LP systems, the viscosity is moderately reduced with ratios of η/ηpure = 0.66 and 0.75, respectively. In contrast, the viscosity ratio for the SCNP&H-LP system is significantly reduced to 0.25. This ratio can be further decreased to 0.15 with the comb of the T-SCNP system. These findings align well with the reduction in relaxation time, where the τR/τR pure of the T-SCNP comb system is 0.21, indicating a substantial increase in the chain segment disentanglement rate. This accelerated chain dynamics is likely attributable to the disentanglement effect induced by T-SCNPs on the side chains.
To test our hypothesis that the size effect of T-SCNPs introduces additional free volume, accelerating the disentanglement of polymer chains and reducing viscosity, we synthesized T-SCNPs of varying sizes by adjusting the crosslinking group content in linear precursors (F-LPs) and grafting them onto high Mw linear polymers. Fig. S18 and S19,† along with Table S2 (in the ESI†), detail GPC and DLS data for three T-SCNPs of different sizes, demonstrating that increased crosslinking led to more compact T-SCNPs with smaller Rh and, consequently, lower Mn (Table S2 in the ESI†). The UV spectra of these T-SCNPs showed that a relatively high anthracene content increased the absorption peak intensity at 360–400 nm (Fig. S20 in the ESI†). However, upon nanoparticle formation, the absorption peak intensity decreased due to the combination of pendant anthracene units after irradiation. 1H NMR analysis of F-LPs with varying anthracene contents and T-SCNPs of different sizes indicated that higher anthracene content increased the proton peak intensity at 7.21–8.52 ppm. The dimerization of anthracene caused a shift in the peak toward 6.53 ppm, suggesting extensive involvement of anthracene rings in the dimerization reaction (Fig. S21 in the ESI†).
Finally, we evaluated the folding of linear polymers containing different AMA groups using characteristic viscosity, the Zimm branching factor g′, and the Stokes ratio Rg/Rh. Increasing the content of the linear polymer AMA led to enhanced internal crosslinking, enabling SCNPs to adopt a more spherical three-dimensional structure and reducing interchain entanglement. T-SCNP3, which has the highest degree of internal crosslinking, presented lower viscosity and g′ values than T-SCNP1, T-SCNP2, and their linear precursors (Fig. S22 and S23 in the ESI†). Additionally, Rg/Rh is critical for describing molecular configuration in solution. A lower Rg/Rh value indicates a more compact structure in solution.61 As shown in Fig. S24,†Rg/Rh values for F-LP1-3 ranged from 1.2–1.4, whereas those for T-SCNP1-3 varied from 0.5 to 0.8, demonstrating that SCNPs adopt a more compact structure in solution than their linear analogs. Notably, T-SCNP-3, with the highest degree of internal crosslinking, exhibited the lowest Rg/Rh value, highlighting its exceptionally compact molecular configuration.
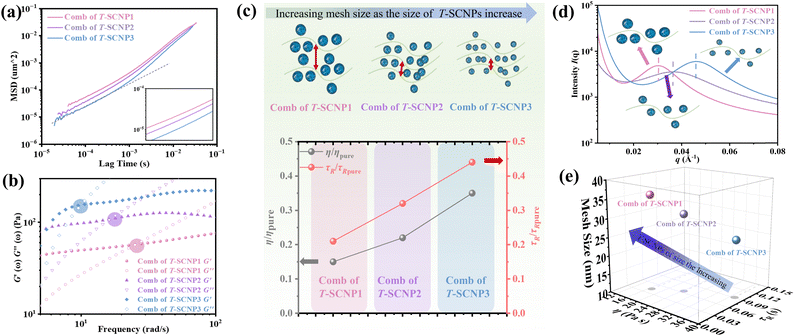
According to microrheological studies, enlarging the size of T-SCNPs leads to an increase in the MSD of tracer particles across three different systems (Fig. 4a). For example, the MSD for the comb of T-SCNP1 is 16.32 × 10−5 μm2, almost threefold greater than that for the comb of T-SCNP3, which is 6.39 × 10−5 μm2. Additionally, the τR values vary significantly across these systems, with Fig. 4b displaying τR values for each system. The τR for the comb of T-SCNP1 is 0.043 s, considerably faster than that for the comb of T-SCNP2 (0.065 s) and T-SCNP3 (0.089 s). The viscosity ratio for the comb of T-SCNP1, τR/τR pure, is 0.21, whereas it increases to 0.32 for the comb of T-SCNP2 and further to 0.44 with the smaller T-SCNP3. These findings align well with the viscosity data (Fig. 4c).
It is hypothesized that maintaining the same SCNP concentration with increased SCNP volume necessitates greater distances between polymer chains, thereby reducing the local chain concentration and accelerating the chain relaxation process. The low-q SAXS peak measurements reveal d-spacings for the comb of T-SCNP1, T-SCNP2, and T-SCNP3 at 21.5 nm, 17.3 nm, and 13.9 nm, respectively, indicating that larger SCNPs must be spaced further apart to maintain a constant T-SCNP concentration (Fig. 4d). This is supported by G0 calculations of polymer entanglement mesh size, with the ξ for the comb of T-SCNP1 being 35.83 nm, larger than those for the comb of T-SCNP2 (31.15 nm) and T-SCNP3 (25.52 nm) systems. Fig. 4e and S25 (in the ESI†) indicate the lowest viscosity in the comb of T-SCNP1, which is consistent with fewer intermolecular entanglements.
Previous studies have shown that adding SCNPs reduces the viscosity of the polymer solution by increasing the free volume at the polymer/SCNP boundary. In contrast, past reports have documented that incorporating inorganic nanoparticles into polymer melts increases the system's viscosity once the nanoparticle loading exceeds a certain threshold, leading to the formation of NP aggregates that significantly impede melt chain relaxation.62 Here, the rheological properties of combs of T-SCNPs with different grafting densities were examined, as shown in Fig. 5a. It is believed that increasing the grafting density of T-SCNPs reduces the entanglement density among polymer chains due to steric hindrance. The ICF curves in Fig. 5b demonstrate that higher grafting densities accelerate the relaxation rate of the system. Concurrently, the most intense Brownian motion within the system correlates with higher MSD values (Fig. 5c). The modulus versus the frequency curve (Fig. S26 in the ESI†) shows a marked decrease in G′′ with increasing T-SCNP grafting content, with the intersection point of the two moduli moving toward higher frequencies, indicating quicker τR (Fig. 5d). As indicated in Fig. 5e and Table S3 (in the ESI†), the G0 of the system decreases as T-SCNP grafting content increases. At a 10% grafting rate, the ξ significantly increased from 17.32 nm for the pure H-LP to 57.82 nm. This finding suggests that the grafting of SCNPs into the main chain prevents nanoparticle aggregation in solution, unlike in traditional NP/polymer melt composite systems, due to the bonding effect. The viscosity curves (Fig. 5f) demonstrate that increasing T-SCNP content results in a progressive decrease in system viscosity, indicating the easier occurrence of chain entanglements. The minimum viscosity ratio (η/ηpure) reaches 0.08 at a 10% grafting content, reflecting a viscosity reduction of over 90%. Moreover, the τR/τR pure ratio decreases to 0.13 as the grafted content of the T-SCNPs increases (Fig. 5g). Thus, the rheological behavior exhibited by the comb of T-SCNPs in solution is intricately linked not only to the size of the SCNPs but also to their grafting density.
Conclusions
In this study, the rheological properties of a specialized superstructure polymer, referred to as the comb of T-SCNPs, were examined. This polymer utilizes tadpole-type SCNPs (T-SCNPs) with active end chains as reaction units. A comb of T-SCNPs was synthesized, with a focus on parameters such as the relaxation time of the chains (τR) and mesh size (ξ). The microstructure of these polymers is critical in determining their macroscopic properties. Compared with traditional SCNP and linear matrix resin composites (SCNPs&H-LP) as well as traditional comb polymers (comb of F-LPs), the comb of T-SCNPs results in a smaller ξ and faster τR. These characteristics result in fewer entanglements among chains within the comb of the T-SCNP system, leading to reduced viscosity and loss modulus. The introduction of SCNPs into the system through grafting effectively decreases the local density of chains, thereby accelerating the disentanglement time with increasing frequency. Furthermore, the findings establish a direct correlation between the rheological behavior of the comb of T-SCNPs and the size and content of grafted SCNPs, suggesting that larger sizes or higher contents of grafted SCNPs result in lighter chain entanglement, quicker chain relaxation time, larger system mesh size, and decreased loss modulus and viscosity.Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Hongting Pu planned and designed the project. Yangjing Chen conducted all of the experiments. Zhiyu Hu, Zhigang Shen, and Xiaoqiang Xue helped synthesize the materials. Zhiyu Hu helped characterize the samples. Yangjing Chen and Hongting Pu analyzed the data and wrote the paper. All authors reviewed the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported by the Fundamental Research Funds for the Central Universities (China) (0500219216) and National Natural Science Foundation of China (21144006).References
- J. H. Vrijsen, C. O. Medeiros, J. Gruber and T. Junkers, Polym. Chem., 2019, 10, 1591–1598 RSC
.
- A. W. Bosman, H. M. Janssen and E. W. Meijer, Chem. Rev., 1999, 99, 1665–1688 CrossRef CAS
.
- C. Feng, Y. Li, D. Yang, J. Hu, X. Zhang and X. Huang, Chem. Soc. Rev., 2011, 40, 1282–1295 RSC
.
- S. S. Sheiko, B. S. Sumerlin and K. Matyjaszewski, Prog. Polym. Sci., 2008, 33, 759–785 CrossRef CAS
.
- X. Q. Xue, Y. J. Chen, W. Y. Li, K. Liang, W. Y. Huang, H. J. Yang, L. Jiang, Q. M. Jiang, F. L. Chen and T. Jiang, Chem. Commun., 2021, 57, 399–402 RSC
.
- A. Kakkar, G. Traverso, O. C. Farokhzad, R. Weissleder and R. Langer, Nat. Rev. Chem, 2017, 1, 0063–0080 CrossRef CAS
.
- M. A. Sowers, J. R. McCombs, Y. Wang, J. T. Paletta, S. W. Morton, E. C. Dreaden, M. D. Boska, M. F. Ottaviani, P. T. Hammond, A. Rajca and J. A. Johnson, Nat. Commun., 2014, 5, 5460–5469 CrossRef PubMed
.
- T. Terashima, M. Kamigaito, K.-Y. Baek, T. Ando and M. Sawamoto, J. Am. Chem. Soc., 2003, 125, 5288–5289 CrossRef CAS
.
- Y. Zheng, H. L. Cao, B. Newland, Y. X. Dong, A. Pandit and W. X. Wang, J. Am. Chem. Soc., 2011, 133, 13130–13137 CrossRef CAS PubMed
.
- Y. S. Gao, D. Z. Zhou, T. Y. Zhao, X. Wei, S. McMahon, J. O'Keeffe Ahern, W. Wang, U. Greiser, B. J. Rodriguez and W. X. Wang, Macromolecules, 2015, 48, 6882–6889 CrossRef CAS
.
- B. R. Sveinbjörnsson, R. A. Weitekamp, G. M. Miyake, Y. Xia, H. A. Atwater and R. H. Grubbs, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14332–14336 CrossRef
.
- M. Vatankhah-Varnosfaderani, A. N. Keith, Y. Cong, H. Liang, M. Rosenthal, M. Sztucki, C. Clair, S. Magonov, D. A. Ivanov, A. V. Dobrynin and S. S. Sheiko, Science, 2018, 359, 1509–1513 CrossRef CAS PubMed
.
- J. Lopez, D. G. Mackanic, Y. Cui and Z. Bao, Nat. Rev. Mater., 2019, 4, 312–330 CrossRef CAS
.
- C. R. López-Barrón, A. H. Tsou, J. R. Hagadorn and J. A. Throckmorton, Macromolecules, 2018, 51, 6958–6966 CrossRef
.
- G. Xu, Y. Xiao, W. J. Wang, B. G. Li and P. Liu, Macromolecules, 2023, 56, 3064–3072 CrossRef CAS
.
- M. Hayashi, K. Shibata and S. Nobukawa, Polymer, 2021, 236, 124316 CrossRef CAS
.
- W. Wang, W. Lu, A. Goodwin, H. Wang, P. Yin, N. G. Kang, K. Hong and J. W. Mays, Prog. Polym. Sci., 2019, 95, 1–31 CrossRef CAS
.
- A. N. Keith, C. Clair, A. Lallam, E. A. Bersenev, D. A. Ivanov, Y. Tian, A. V. Dobrynin and S. S. Sheiko, Macromolecules, 2020, 53, 9306–9312 CrossRef CAS
.
- Y. L. Deng, S. Dwaraknath, W. O. Ouyang, C. J. Matsumoto, S. Ouchida and Y. Lu, Angew. Chem., Int. Ed., 2023, 62, e202215719 CrossRef CAS PubMed
.
- M. Dhar, A. Das, D. Parbat and U. Manna, Angew. Chem., Int. Ed., 2022, 61, e202116763 CrossRef CAS PubMed
.
- M. Vatankhah-Varnosfaderani, W. F. Daniel, M. H. Everhart, A. A. Pandya, H. Liang, K. Matyjaszewski, A. V Dobrynin and S. S. Sheiko, Nature, 2017, 549, 497–501 CrossRef PubMed
.
- M. Ebe, A. Soga, K. Fujiwara, B. J. Ree, H. Marubayashi, K. Hagita, A. Imasaki, M. Baba, T. Yamamoto and K. Tajima, Angew. Chem., Int. Ed., 2023, 135, e202304493 CrossRef
.
- Z. Liu, Z. Yang, X. Chen, R. Tan, G. Li, Z. Gan, Y. Shao, J. He, Z. Zhang and W. Li, JACS Au, 2020, 1, 79–86 CrossRef
.
- Y. Ohya, R. Dohi, F. Seko, Y. Nakazawa, K. I. Mizuguchi, K. Shinzaki, T. Yasui, H. Ogawa, S. Kato and Y. Yoshizaki, Angew. Chem., Int. Ed., 2024, 136, e202317045 CrossRef
.
- J. Lee, K. Chang, S. Kim, V. Gite, H. Chung and D. Sohn, Macromolecules, 2016, 49, 7450–7459 CrossRef CAS
.
- Q. Li and J. A. Lewis, Adv. Mater., 2003, 15, 1639–1643 CrossRef CAS
.
- A. V. Zhukhovitskiy, M. Zhong, E. G. Keeler, V. K. Michaelis, J. E. Sun, M. J. Hore, D. J. Pochan, R. G. Griffin, A. P. Willard and J. A. Johnson, Nat. Chem., 2016, 8, 33–41 CrossRef CAS
.
- X. Xu, N. L. Rosi, Y. Wang, F. Huo and C. A. Mirkin, J. Am. Chem. Soc., 2006, 128, 9286–9287 CrossRef CAS PubMed
.
- D. Zanchet, C. M. Micheel, W. J. Parak, D. Gerion and A. P. Alivisatos, Nano Lett., 2001, 1, 32–35 CrossRef CAS
.
- X. Yu, W. B. Zhang, K. Yue, X. Li, H. Liu, Y. Xin, C. L. Wang, C. Wesdemiotis and S. Z. Cheng, J. Am. Chem. Soc., 2012, 134, 7780–7787 CrossRef CAS PubMed
.
- J. M. Hu, T. Wu, G. Y. Zhang and S. Y. Liu, J. Am. Chem. Soc., 2012, 134, 7624–7627 CrossRef CAS PubMed
.
- E. Harth, B. Van Horn, V. Y. Lee, D. S. Germack, C. P. Gonzales, R. D. Miller and C. J. Hawker, J. Am. Chem. Soc., 2002, 124, 8653–8660 CrossRef CAS
.
- F. Wang, H. T. Pu and X. Che, Chem. Commun., 2016, 52, 3516–3519 RSC
.
- F. Wang, H. T. Pu, M. Jin and D. C. Wan, Macromol. Rapid Commun., 2016, 37, 330–336 CrossRef CAS
.
- X. Jiang, H. T. Pu and P. Wang, Polymer, 2011, 52, 3597–3602 CrossRef CAS
.
- J. P. Wang, R. Wang, Y. G. Gu, Y. Gu, A. Sourakov, B. D. Olsen and J. A. Johnson, Chem. Sci., 2019, 10, 5332–5337 RSC
.
- S. Mavila, O. Eivgi, I. Berkovich and N. G. Lemcoff, Chem. Rev., 2016, 116, 878–961 CrossRef CAS PubMed
.
- M. Gonzaĺez-Burgos, A. Latorre-Sanchez and J. A. Pomposo, Chem. Soc. Rev., 2015, 44, 6122–6142 RSC
.
- M. A. J. Gillissen, I. K. Voets, E. W. Meijer and A. R. A. Palmans, Polym. Chem., 2012, 3, 3166–3174 RSC
.
- T. Terashima, T. Mes, T. F. De Greef, M. A. Gillissen, P. Besenius, A. R. Palmans and E. W. Meijer, J. Am. Chem. Soc., 2011, 133, 4742–4745 CrossRef CAS
.
- M. Artar, T. Terashima, M. Sawamoto, E. W. Meijer and A. R. A. Palmans, J. Polym. Sci., Part A: Polym. Chem., 2014, 52, 12–20 CrossRef CAS
.
- J. Willenbacher, K. N. R. Wuest, J. O. Mueller, M. Kaupp, H. A. Wagenknecht and C. Barner-Kowollik, ACS Macro Lett., 2014, 3, 574–579 CrossRef CAS
.
- E. H. H. Wong, S. J. Lam, E. Nam and G. G. Qiao, ACS Macro Lett., 2014, 3, 524–528 CrossRef CAS PubMed
.
- W. K. Li, S. Thanneeru, I. Kanyo, B. Liu and J. He, ACS Macro Lett., 2015, 4, 736–740 CrossRef CAS
.
- X. Y. Zhao, D. H. Li, J. Zhu, Y. B. Fan, J. Y. Xu, X. Y. Huang, Z. H. Nie and D. Y. Chen, ACS Macro Lett., 2024, 13, 882–888 CrossRef CAS
.
- Y. J. Chen, Z. Y. Hu and H. T. Pu, Macromolecules, 2023, 56, 9277–9288 CrossRef CAS
.
- S. Chandra, C. C. Wang, S. B. Tor, U. Ramamurty and X. P. Tan, Nat. Commun., 2024, 15, 3094–3108 CrossRef CAS PubMed
.
- Y. J. Chen, Z. Y. Hu, D. P. Wang, X. Q. Xue and H. T. Pu, ACS Macro Lett., 2023, 12, 1311–1316 CrossRef CAS PubMed
.
- R. Upadhya, N. S. Murthy, C. L. Hoop, S. Kosuri, V. Nanda, J. Kohn, J. Baum and A. J. Gormley, Macromolecules, 2019, 52, 8295–8304 CrossRef CAS
.
- Y. Bakkour, V. Darcos, F. Coumes, S. Li and J. Coudane, Polymer, 2013, 54, 1746–1754 CrossRef CAS
.
- H. Tan, Y. Lin, J. Zheng, J. Gong, J. Qiu, H. Xing and T. Tang, Soft Matter, 2015, 11, 3986–3993 RSC
.
- L. Zheng, R. J. Farris and E. B. Coughlin, Macromolecules, 2001, 34, 8034–8039 CrossRef CAS
.
- S. Mariya, J. J. Barr, P. Sunthar and J. R. Prakash, Soft Matter, 2024, 20, 993–1008 RSC
.
- H. Goldansaz, F. Goharpey, F. Afshar-Taromi, I. Kim, F. J. Stadler, E. Van Ruymbeke and V. Karimkhani, Macromolecules, 2015, 48, 3368–3375 CrossRef CAS
.
- M. E. Mackay, T. T. Dao, A. Tuteja, D. L. Ho, B. Van Horn, H. C. Kim and C. J. Hawker, Nat. Mater., 2003, 2, 762–766 CrossRef CAS
.
- T. Chen, H. Zhao, R. Shi, W. Lin, X. Jia, H. Qian, Z. Lu, X. Zhang, Y. Li and Z. Sun, Nat. Commun., 2019, 10, 5552 CrossRef CAS
.
- E. Sarmiento-Gomez, I. N. Santamaría-Holek and R. Castillo, J. Phys. Chem. B, 2014, 118, 1146–1158 CrossRef CAS
.
- S. Morozova, E. Hitimana, S. Dhakal, K. G. Wilcox and D. Estrin, J. Appl. Phys., 2021, 129, 071101 CrossRef CAS
.
- C. Oelschlaeger, M. Schopferer, F. Scheffold and N. Willenbacher, Langmuir, 2009, 25, 716–723 CrossRef CAS PubMed
.
- J. H. van Zanten, S. Amin and A. A. Abdala, Macromolecules, 2004, 37, 3874–3880 CrossRef CAS
.
- H. Kumari, S. R. Kline and J. L. Atwood, Chem. Sci., 2014, 5, 2554–2559 RSC
.
- Z. Chen, Y. Chao, S. Sayyar, T. Tian, K. Wang, Y. Xu, G. Wallace, J. Ding and C. Wang, Adv. Sci, 2023, 10, 2302844 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc05650g |
| This journal is © The Royal Society of Chemistry 2024 |