Open Access Article
Open Access ArticleThe impact of analyte size on SERS enhancement location, enhancement factor, excitation wavelength, and spectrum
Yanjun
Yang
 a,
Xinyi
Chen
a,
Xinyi
Chen
 b,
Bin
Ai
b,
Bin
Ai
 b and
Yiping
Zhao
b and
Yiping
Zhao
 *a
*a
aDepartment of Physics and Astronomy, The University of Georgia, Athens, GA 30602, USA. E-mail: zhaoy@uga.edu
bSchool of Microelectronics and Communication Engineering, Chongqing Key Laboratory of Bio-perception & Intelligent Information Processing, Chongqing University, Chongqing, 400044, P.R. China
First published on 22nd March 2024
Abstract
The study systematically explores the connection between analyte particle size and the hot-spot in Au nanoparticle (NP) dimer systems. Contrary to the conventional understanding tied to localized surface plasmon resonance (LSPR), we show that depending on the analyte particle's size, the location to produce surface-enhanced Raman scattering (SERS), defined as effective hot-spot, is different from the gap based hot-spot, where the electric field reaches maximum intensity, and the corresponding resonant wavelength is also shifted significantly from LSPR wavelength. This effective hot-spot occurs primarily at the point where the Au NP contacts the analyte particle, covering a larger area than the traditional hot-spot and having a significantly smaller enhancement factor. Moreover, different effective hot-spots can be activated under various polarizations. The local electric field versus distance relationship decays significantly slower, complicating the interpretation of SERS spectra of large analyte particles. This complexity offers tunability, allowing for a more precise representation of unique molecular features of the analyte. Consequently, our findings demonstrate the necessity for SERS substrate design rules to be contingent on analyte particle size. Although interpreting SERS spectra is intricate, it can be refined to effectively capture distinctive molecular characteristics. These insights pave a new way to tailor SERS substrate design specifically catering to large analyte particles.
1. Introduction
In recent years, surface-enhanced Raman scattering (SERS) spectroscopy has gained widespread applications in chemical and biological detection, significantly augmenting diagnostic capabilities.1 In comparison to conventional fluorescence spectroscopy techniques commonly employed in the fields of biology and health sciences, SERS offers several distinct advantages, including enhanced sensitivity, the ability for multiplexing, chemical specificity, and a reduction in autofluorescence. Moreover, SERS enables label-free, high-resolution, and quantitative analysis, making it an invaluable tool in various applications. At the core of SERS applications lies the SERS enhancement mechanisms, particularly the electromagnetic (EM) enhancement.2,3 This mechanism primarily arises from the formation of high-quality hot-spots within SERS-active substrates, where a substantial local electric field, generated within nanostructures by external laser excitation, is concentrated.1–3 As long as the target molecules can adsorb onto these hot-spot locations, the SERS enhancement factor (EF) is proportionally related to |Eloc/E0|4, where Eloc and E0 represent the magnitude of the local and incident electric fields. Consequently, the resulting SERS spectrum is dominated by the signals generated within these hot-spots. Therefore, numerous publications in SERS substrate design and mechanism explanation implement the imperative nature of identifying or designing hot-spots through diverse numerical methods.3,4 As outlined in a recent review paper,3 three distinct categories of hot-spots have been identified. The first-generation hot-spots encompasses individual nano-objects like Au or Ag NPs, nanorods, and nano-stars,2etc. where the side surfaces or sharp tips of these NPs serve as hot-spots. The second-generation hot-spots are characterized by controlled nanogaps resulting from the electromagnetic coupling of nano-objects, with these gaps being exceptionally narrow (≤5 nm) between two or more nano-objects. The third generation hot-spots are formed by nanogaps between nano-objects and thin films. In this case, the coupling between the EM response of the NPs and the reflected EM fields from the thin film gives rise to the EM enhancement. From a geometric perspective, these three types of hot-spots can be classified into two general configurations: the open hot-spot of a single NP system and the gap hot-spots, encompassing both the second- and third-generation hot-spots. If the analyte molecules are located inside the hot-spot areas, under near-resonant excitation wavelength λ0, the substrate can produce the highest SERS signals.However, in the context of biological-based SERS detection5–7 or some other detections (such as microplastics),8,9 certain target analytes possess physical dimensions comparable to or even greater than the dimensions of hot-spots. For instance, proteins like BSA typically have a nominal size of 7.1 nm,10 viruses span diameters ranging from 20 nm to 250–400 nm (with the SARS-CoV-2 virus being approximately 100 nm in diameter),11 bacteria exhibit considerable size of around or larger than 1 μm,12 while microplastics shows particle size varying from tens of nanometers to a few micrometers.13 For open hot-spots, as long as the hot-spot locations can be adsorbed on the surface of the large analyte, they can generate good SERS signal. Such a situation has been discussed in detail in ref. 14. However, for gap hot-spot, since the size (gap) of the hot-spots could be significantly smaller than the size of the analyte, the target analytes cannot physically infiltrate the hot-spot gaps or can only expose a fraction of their surface to tip-based hot-spots. Thus, the SERS signal generated from these SERS substrates for large size analytes cannot come from gap hot-spot. Though some literature has raised this issue, no systematic investigation has been done.15–17 For example, Rastogi et al. used self-assembled gold nanoparticle cluster arrays to achieve impressive picomolar detection limits for both a small molecule (1-naphthalene thiol) and a large biomolecule (streptavidin, a protein) by systematically adjust the gap size of the cluster arrays.16 Liu et al. applied V-shape substrate to show that the effective SERS EF decreased monotonically with the size of PMMA microsphere.17 Several fundamental questions need to be addressed or clarified for the gap hot-spot bio-detection scenario: 1) how can one redefine an effective hot-spot (EHS) where the SERS enhancement is actually coming from when the analyte's size is comparable to or surpasses the size of conventionally defined hot-spots? 2) How does this EHS alter SERS performance, such as EF (i.e., sensitivity), excitation wavelength, spectral characteristics, and others? 3) How can one comprehend the resulting SERS spectra in such a situation?
In this paper, we will define the EHS for large sized analytes in the case of gap hot-spot using an Au nanosphere dimer as an example and use finite-difference time-domain (FDTD) calculation to illustrate the impact of analyte size on SERS hot-spots and spectra. Our findings will elucidate that, for gap hot-spot SERS substrates, the EHS location and the excitation wavelength are contingent on the analyte's size. Furthermore, the SERS EF undergoes significant alterations in response to varying analyte sizes. Finally, we will demonstrate that the geometry and size of the gap hot-spot can influence the spectral shape due to the inherent heterogeneity of microorganisms.
2. FDTD calculations
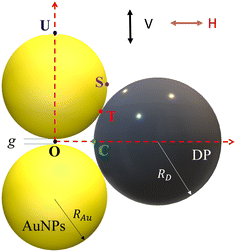
A typical gap hot-spot system is a nanosphere dimer with a very narrow gap, as shown in Fig. 1, which represents a typical hot-spot configuration in SERS community.18,19 This system is selected since it is a very simple representative of a gap hot-spot and some of the results can be easily interpreted. Since the problem we consider here is a size exclusion case, some of the results obtained here can be extended to other gap hot-spot configurations. Each sphere has the same radius RAu. When the excitation laser wavelength λex is tuned to be near the localized plasmon resonance (LSPR) wavelength λLSPR of the dimer, locations of very high local E-fields appear, and these locations are called hot-spot. Due to the shape anisotropy and plasmon hybridization, the dimer has two longitudinal LSPR modes and one transverse mode.20 When excited near the bonding longitudinal mode (λex ≈ λbLSPR) with a vertical polarization (V-polarization, the black arrow in Fig. 1), the hot-spot is presented in the center of the gap, i.e., the O location (black dot in Fig. 1); when λex is near the anti-bonding mode λaLSPR with V-polarization, the hot-spots are at the two ends of the dimer along the long-axis direction, i.e., U location (blue spot); if the excitation wavelength is near the transverse mode λex ≈ λtLSPR with a horizontal polarization (H-polarization, the purple arrow), the highest local E-field appears at the left and right sides of the two Au nanospheres, i.e., the S location (purple dot). Given the anisotropic optical properties of the Au NP dimer, potential hot-spot locations are not confined solely to the gap but may also include the side surfaces of the nanoparticles. Furthermore, in real SERS measurements, the orientations of the Au dimers in the measurement system may exhibit randomness with respect to the polarization direction of the excitation laser. Therefore, investigation on the excitation polarization of the hot-spot becomes crucial. The analyte, we assume to be a large dielectric particle (DP), can also be treated as a sphere with a radius RD. In principle, the DP can be randomly attached to all the accessible outer surfaces of the dimer, such as U or S, where λex ≈ λaLSPR & V-polarization or λex ≈ λtLSPR & H-polarization can excite the hot-spot at these contact locations. Among all these possible contact locations, the DP contacts to both dimer spheres may represent a configuration that most likely to generate the highest SERS signals. The DP and the dimer have two contact points T (red dot). In addition, it is likely the location C (green dot) on the DP, which is closest to O location, may also experience a high local-E-field. The locations T, C, S, and U could potentially serve as EHS.A commercial software package (FDTD Solutions version 8.16.931, Lumerical Solutions Inc.) was used to calculate the localized electric field (E-field) distribution of the AuNP-DP clusters. In the FDTD calculation, RAu = 50 nm, g = 5 nm, RD varies from 3 nm to 100 nm, with an increment of 10 nm. The dielectric function of the DP is treated as a constant, εD = 1.55, and the dielectric functions of Au were taken from Johnson and Christy.21 The entire structure was surrounded by the dielectric environment of vacuum. Linearly polarized light with the wavelength from 250 nm to 1000 nm was applied, which is consistent with normal SERS measurement configuration. Two polarization directions, i.e., V-polarization and H-polarization, were used in the calculations. Perfectly matched layer (PML) absorbing boundaries were applied in all directions. To ensure the convergence of the calculations, a mesh size of 1 nm × 1 nm × 1 nm was chosen. A monitor of “frequency-domain field profile” was set up to calculate the localized E-field distributions and the obtained E-fields were normalized to the magnitude of the incident E-fields. A MATLAB program was used to extract the E-field distribution and the LSPR wavelength results from the FDTD calculations.
3. Results and discussion
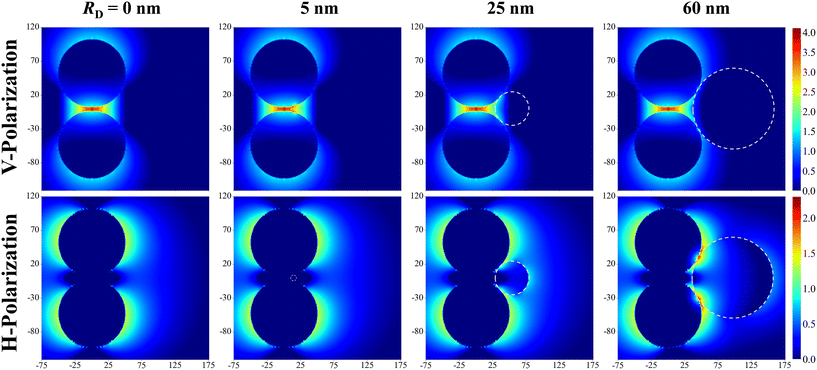
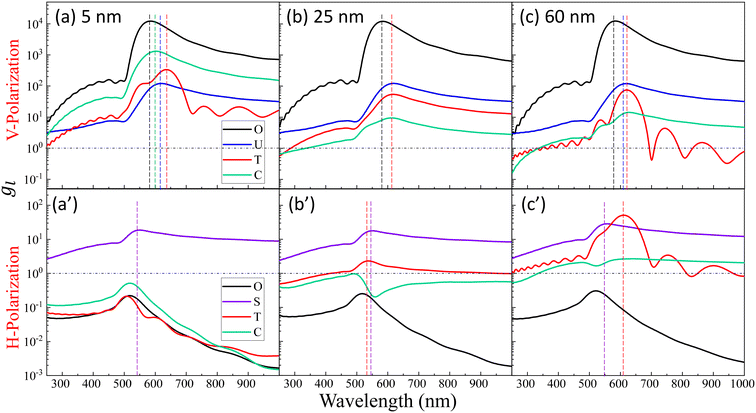
Fig. 2 shows the typical local electric field distributions gl = |Eloc/E0|2 (in logarithmic scale) for the dimer-DP system under λbLSPR & V-polarization and under λtLSPR & H-polarization for RD = 0, 5, 25, and 60 nm, respectively. Regardless of the viral particle size, the general trends of the gl under these two conditions agree well with results from previous publications: at λbLSPR & V-polarization, a hot-spot appears at O with extremely high gl (denoted as gmaxl), with gmaxl ∼ 1.2 × 104, and λbLSPR ≈ 584–585 nm, which is invariant with RD. At λtLSPR & H-polarization, apparently the gl distribution is almost invariant at very small RD (≤5 nm). When RD = 25 nm, the gl distribution around the contacts between AuNPs and DP starts to deviate the gl distribution of the AuNP dimer only case. At RD = 60 nm, the deviation becomes more serious. Not only much higher local gl appears around the contacts between AuNPs and DP, but also the local fields penetrate into the DP, which could significantly attenuate the SERS spectral shape (see later distance dependent discussion). The gmaxl at S is around 17.7–18.7 for RD ≤ 25 nm, while λtLSPR ≈ 550 nm. When RD = 60 nm, the gmaxl at S increases significantly, to ∼28.5, and λtLSPR redshifts to 556 nm. Under this condition, the contact point T is very close to S.Though the highest gmaxl appears at O under λbLSPR & V-polarization regardless of the size of DP, this location is inaccessible to DP due to the size exclusion, which means this hot-spot location would play no role to SERS signal of DP. Rather, the locations T and/or C in Fig. 1 and/or areas around these two locations have the most potentials to contribute to the SERS enhancement, whose gmaxl is expected to be significantly smaller than that at O. In addition, since these locations really depend on the size of the analyte particle, their gl shall be size dependent, so should be the corresponding resonant wavelength λT0 or λC0, at which the gl at corresponding locations reach maximum (which will determine how to adjust λex to gain the strongest SERS signal). Fig. 3 shows the glversus λ at O, U, T, C for V-polarization (Fig. 3a–c) and O, S, T, C for H-polarization (Fig. 3a′–c′) for RD = 5, 25, and 60 nm, respectively. The corresponding gmaxl and resonance wavelength λ0 are indicated in the figure with the same color and summarized in Table 1. As can be seen from Fig. 3a–c, for V-polarization, the amplitudes of gl spectra at other locations are significantly lower than that at O, and corresponding λ0 redshifts with respect to λbLSPR, i.e., at C, λC0 shifts from λbLSPR = 585 nm to 602 nm at RD = 5 nm; then to 618 nm at RD = 25 nm; and finally to 628 nm at RD = 60 nm, while gmaxl decreases monotonically, from 1.2 × 104 to 1312, 54, and 14, respectively. Similarly, λT0 changes to 636, 612, and 620 nm while gmaxl varies from 336, 9.5, to 75 correspondingly. That is, if the DP is tangent to both dimer spheres, the EHS location, local field strength, and resonant wavelength depend strongly on RD, i.e., under V-polarization, for RD ≤ 50 nm, the EHS for a DP is at C; while when RD = 60 nm, the EHS changes to T. However, one shall notice that the gmaxl at U is almost invariant with RD, and the λ0 corresponding to this location is λaLSPR = 618–620 nm. It is expected that when a DP is attached to U location, it can also serve as an EHS. For H-polarization, a different trend is observed (Fig. 3a′–c′): For a small DP, RD = 5 nm, at both C and T, gmaxl < 1, which means no enhancement of DP can be observed with the configuration shown in Fig. 1, i.e., the EHS is at S. However, when RD increases, to be 60 nm, the gmaxl (= 51) at T is almost double the value at S (= 28.5). The corresponding λ0 changes to 611 nm, compared to λSLSPR 556 nm. Clearly, when DP is large, the EHS location is at T. Note that at O location, gmaxl is always smaller than 1.
| Location | No virus | R D = 5 nm | R D = 25 nm | R D = 60 nm | |
|---|---|---|---|---|---|
| V-Polarization | T | 336 | 9.5 | 75 | |
| 636 nm | 612 nm | 620 nm | |||
| C | 1312 | 54 | 14 | ||
| 602 nm | 618 nm | 428 nm | |||
| U | 120 | 120 | 122 | 120 | |
| 617 nm | 620 nm | 618 nm | 618 nm | ||
| O | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 658 658 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 234 234 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 136 136 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 402 402 |
|
| 584 nm | 585 nm | 584 nm | 584 nm | ||
| H-Polarization | T | 0.21 | 2.3 | 51 | |
| 508 nm | 537 nm | 611 nm | |||
| C | 0.52 | 0.97 | 2.7 | ||
| 518 nm | 490 nm | 641 nm | |||
| O | 0.22 | 0.23 | 0.25 | 0.31 | |
| 517 nm | 517 nm | 517 nm | 521 nm | ||
| S | 18.7 | 18.7 | 17.7 | 28.5 | |
| 550 nm | 550 nm | 550 nm | 556 nm |
The examples above illustrate a strong dependence of both the EHS location and the resonance wavelength λ0 on the size of DP. To gain a deeper understanding of how both gmaxl and λ0 vary with different positions as a function of RD, comprehensive FDTD calculations with RD from 3 nm to 100 nm were performed. The resulting gmaxl and λ0 values versus RD for different positions O, U, T, C under V-polarization and O, S, T, C under H-polarization are plotted in Fig. 4. In Fig. 4a, under V-polarization, the O location consistently exhibits the highest gmaxl, varying from 1.20 × 104 to 1.29 × 104, corresponding to the conventional hot-spot. The λbLSPR only changes slightly, from 583 nm to 595 nm. However, this location is inaccessible for a large DP. An alternative EHS with high gmaxl is found at U, with gmaxl values ranging from 120 to 4 and λ0 fluctuating between 618 nm and 640 nm. Additionally, C and T are also identified as EHS locations. At RD ≤ 15 nm, both gmaxl at C (ranging from 2600 to 130) and T (ranging from 720 to 58) exceed those at U, and the corresponding λ0 (∼600 nm to 612 nm) at C is very close to that at U while at Tλ0 fluctuates from 603 nm to 654 nm. In this RD region, we can treat the spherical cap formed between C and T as an EHS area (see Fig. 5a). At RD > 15 nm, gmaxl at U still is the highest, but C and T may have comparable strengths. For example, at 15 < RD ≤ 55 nm, gmaxl at C (ranging from 73 to 17) surpasses that at T (ranging from 17 to 3), but their differences are within one order of magnitude. The corresponding λ0 varies from 600–630 nm. Similarly, when 55 < RD ≤ 100 nm, gmaxl at T (ranging from 75 to 7) is larger than that at C (ranging from 14 to 7), while λ0 fluctuates from 520–620 nm.
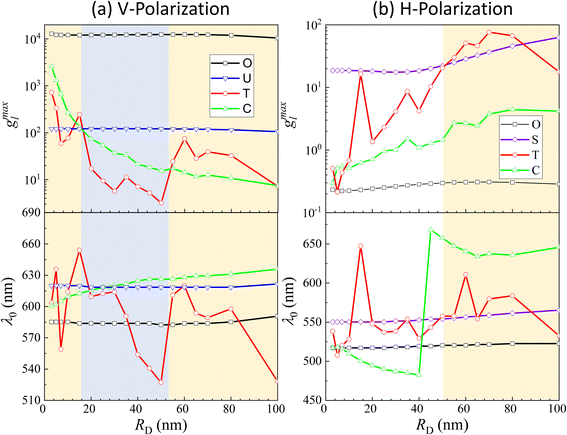 | ||
| Fig. 4 g maxl and λ0 as a function of RD at (a) O, U, T, C for V-polarization and (b) O, S, T, C for H-polarization. | ||
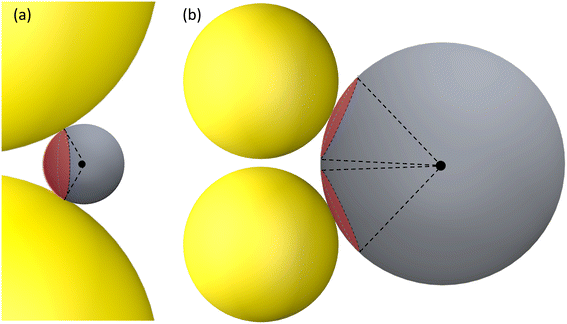 | ||
| Fig. 5 The hot-spot area on a DP for (a) RD ≤ 15 nm and V-polarization and (b) RD > 50 nm and H-polarization. The red spherical caps indicate the possible hot-spot area. | ||
Under H-polarization (see Fig. 5b), gmaxl at O shows the lowest gmaxl. At RD < 50 nm, gmaxl at S is the highest, with almost a constant value (∼17–20), while gmaxl at T increases almost monotonically from 0.5 to 25. At RD > 50 nm, the gmaxl at S increases gradually to 63 at RD = 100 nm, while gmaxl at T surpasses the value at S in most cases, varying from 30 to 76, with λ0 primarily varying between 557 and 580 nm. It is worth noting that at S, λ0 changes slightly, varying from 550 nm to 560 nm. This suggests the possibility of two spherical caps between T and S becoming a potential EHS area (Fig. 5b).
The concept of a EHS area remains applicable even when RD > 15 nm under V-polarization, where the T location exhibits the largest gmaxl. In spherical coordinates centered at one (top) AuNP in question, the surfaces of entire top half hemisphere (or bottom half hemisphere for the bottom AuNP) displays gmaxl values ranging from 10 to 80. Locations closer to T exhibit higher gmaxl values. Therefore, these hemispheres can be considered as EHS areas. Similarly, for RD < 50 nm under H-polarization, the spherical caps surrounding the S locations (of which there are 4) can also be designated as EHS areas.
We notice that regardless of the polarization, the maximum gmaxl at various potential EHS locations is consistently around 102, and the corresponding λ0 has relatively substantial variations, ranging from 520 nm to 630 nm, in contrast to the fixed value of 585 nm for the O hot-spot. When defining EHS based on locations with the highest gmaxl, especially for large DPs, multiple EHS locations may emerge on the SERS substrate or even form an area rather than a single specific point. This property leads to two significant consequences: first, following the principles of SERS, the SERS intensity ISERS can be expressed as
| ISERS = GFσSERSNI0, | (1) |
Another crucial observation arises when considering the typical conditions for exciting a conventional hot-spot in AuNP dimers. Such conditions demand strict polarization and resonance wavelength matching. However, with larger-sized analytes, the necessity for stringent polarization conditions might be alleviated. This relaxation is due to the fact that both U and S locations can act as EHS candidates under various polarization states. These findings suggest a fundamental shift in the designing criteria for SERS substrates when dealing with larger analyte particles. These criteria should be to maximize the local electric fields of locations that are accessible to the analyte particle while simultaneously to optimize the EHS's overall surface area to accommodate larger analyte particles effectively. This, in turn, enhances the potential for successful SERS measurements on larger analyte particles.
Based on above discussion, the EHSs for large DP are not in the location of gmaxl where the LSPR wavelength produced (we term this location as traditional hot-spot location). Then some other properties of traditional hot-spot may not hold. One particular property is the distance dependent local field decay. It has been reported that for a spherical particle, 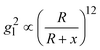 , where R is the radius of the spherical plasmonic particle, and x is the radial-distance away from the particle surface.22 Masango et al. experimentally measured the distance dependent SERS enhancement factor on bare silver film over nanospheres substrate (AgFON), and demonstrated
, where R is the radius of the spherical plasmonic particle, and x is the radial-distance away from the particle surface.22 Masango et al. experimentally measured the distance dependent SERS enhancement factor on bare silver film over nanospheres substrate (AgFON), and demonstrated 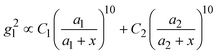 , where a1 and a2 are the short-range and long-range radii of curvature of AgFON features, and C1 and C2 are related constant.23 Both situations neglect the analyte particle size effect, i.e., RD is assumed to be very small compared to the SERS surface features. However, due to the size effect, since both the gmaxl and λ0 change, it is expected that the g2l–x relationship can also be altered, which can ultimately affect the interpretation of the SERS spectra.
, where a1 and a2 are the short-range and long-range radii of curvature of AgFON features, and C1 and C2 are related constant.23 Both situations neglect the analyte particle size effect, i.e., RD is assumed to be very small compared to the SERS surface features. However, due to the size effect, since both the gmaxl and λ0 change, it is expected that the g2l–x relationship can also be altered, which can ultimately affect the interpretation of the SERS spectra.
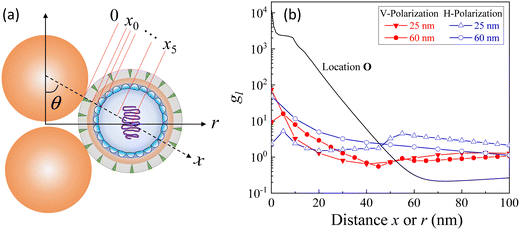
Based on the above discussion, it is evident that for analytes of varying sizes, location T may emerge as the EHS location. The g2l–x along the center of one Au NP and the center of the analyte particle is explored, as shown in Fig. 6a. The g2l–x relationship for RD = 25 and 60 nm at both V- and H-polarizations are shown in Fig. 6b. Here x = 0 nm at T. The g2l–x relationship at O is also plotted to serv as a reference. Compared to the fast decay at O location, the g2l–x at the contact location T shows a much slow decay. In fact, for RD = 60 nm, we can fit the g2l–x using the function 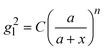 , and obtain a = 2.5 and 4.6 nm, n = 1.5 ± 0.2 and 1.3 ± 0.1 for V- and H-polarizations, respectively. This implies that the enhancement factor shall follow
, and obtain a = 2.5 and 4.6 nm, n = 1.5 ± 0.2 and 1.3 ± 0.1 for V- and H-polarizations, respectively. This implies that the enhancement factor shall follow 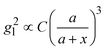 or
or 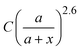 . Such a slow distance-dependent local field can significantly change the interpretation of the SERS spectrum of large analyte particles. If the analyte particle is a virus particle as shown in Fig. 6a, it can be treated as a layered structure at the contact point T between the viral particle and the Au NP dimer. For example, if the viral particle is a SARS-CoV-2 or flu virus, at the contact point, the 1st layer consists of pike proteins; the 2nd layer is the viral envelop (lipid bilayer); the 3rd layer is matrix protein; and the 4th or 5th layer comprises of nucleocapsid proteins and RNA.24 Thus, the SERS intensity can be expressed as,
. Such a slow distance-dependent local field can significantly change the interpretation of the SERS spectrum of large analyte particles. If the analyte particle is a virus particle as shown in Fig. 6a, it can be treated as a layered structure at the contact point T between the viral particle and the Au NP dimer. For example, if the viral particle is a SARS-CoV-2 or flu virus, at the contact point, the 1st layer consists of pike proteins; the 2nd layer is the viral envelop (lipid bilayer); the 3rd layer is matrix protein; and the 4th or 5th layer comprises of nucleocapsid proteins and RNA.24 Thus, the SERS intensity can be expressed as,
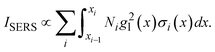 | (2) |
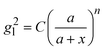 and assume that σi is independent of x in ith layer, eqn (2) can change to
and assume that σi is independent of x in ith layer, eqn (2) can change to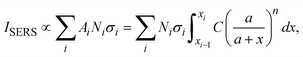 | (3) |
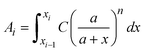 is a linear coefficient depending strongly on a and n according to eqn (3).
is a linear coefficient depending strongly on a and n according to eqn (3).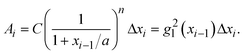 | (4) |
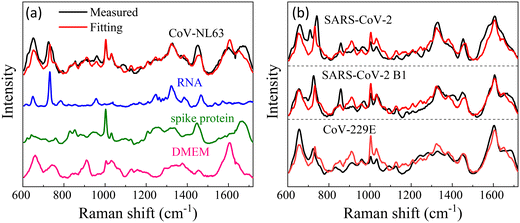
While we lack experimental data for virus detection on AuNP-dimers or gap hot-spots, the same principle can be extended to open hot-spot substrates. One example is silver nanorod (AgNR) array substrate made by oblique angle deposition.15 Our previous work showed that the hot-spots of this substrate were located between the nanorods as well as at the tip of the nanorods. The SERS spectra of various respiratory viruses utilizing AgNR array substrate have been obtained.25Fig. 7a show an averaged SERS spectrum of a coronavirus, CoV-NL 63. In the figure, we present the SERS spectra of the virus's key components—the spike protein and RNA—on AgNR substrates, alongside the SERS spectrum of the buffer solution (DMEM) in which the viruses are suspended. According to eqn (2), the SERS spectrum of CoV-NL 63 can be expressed as a linear combination of the SERS spectra of DMEM, spike protein, and RNA, i.e., Ivirus = dIDMEM + sISpike + rIRNA, where d, s, and r are fitting constants. The red curve in Fig. 7a represents the fitted spectrum using above equation, with d = 0.55, s = 0.38, and r = 0.18, respectively. The Pearson's correlation coefficient Cp is about 0.85 between the fitted and experimentally measured spectra. As can be seen from Fig. 7a, nearly all the spectral features in the measured virus spectrum are captured by the fitted spectrum. Notably, the r value is approximately half of the s value, indicating substantial contributions from RNA. Similar data analysis can be conducted for other coronaviruses, as shown in Fig. 7b for CoV-229E, SARS-CoV-2 B1, SARS-CoV-2, HMPV-B with d = 0.74, 0.63, 0.72, s = 0.35, 0.31, 0.2, r = 0.13, 0.17, 0.2, and Cp = 0.83, 0.82, 0.81, respectively. In all cases, d > s ≥ r. The larger contribution from DMEM is understandable because the buffer contains small biomolecules that can easily access normal hot-spot locations. Yet, for all the fittings, r is about half of the s or even the same. All these results suggest that the sharp distance dependent relationship for G may not be applicable for the detection of large analytes.
Though the investigations here are focused on NP dimers, the conclusions drawn from the dimer shall be very general and are applicable for other gap hot-spot configurations such as clusters and NP on a film. The analysis of size effects on the Au NP dimer yields several significant findings, especially when the size of the analyte is sufficiently large: firstly, the EHS shall be defined as the region where the analyte particle attaches to the SERS substrate with the highest local electric field. Secondly, the resonance frequency/wavelength to excite this EHS location can exhibit notable shifts compared to this to excite the original gap hot-spot. Thirdly, both the EHS location and resonant frequency exhibit strong dependencies on the size of the analytes. Moreover, the relationship of distance-dependent EF for SERS undergoes substantial modifications, with components inside the analyte particle potentially contributing significantly to the measured SERS spectra. These conclusions are anticipated to be applicable to other gap hot-spot configurations with slight modifications, as certain configurations may be complicated. For instance, in NP clusters with multiple gaps, the field enhancements at different gap locations could vary. Notably, studies have shown that the middle gap in a gold NP tetramer chain structure had the highest electromagnetic enhancement among the three gaps,26 while calculations by Ding et al. suggested a distribution of electromagnetic enhancements in gaps of clusters made of multiple NPs.27 Consequently, when an analyte particle is situated near different gap locations, the effective EF and change in optical property are anticipated to differ. Particularly in scenarios where the number of NPs in a cluster is substantial but the number of analyte particles attached to the cluster is minimal, the optical properties of the cluster may not undergo significant changes, yet the EF and distance-dependent SERS effects may be altered markedly. Similar arguments can be extended to third-generation hot spots.
4. Conclusions
In summary, our study explored the impact of analyte particle size on the gap hot-spot within the Au NP dimer system for a SERS substrate. Our findings reveal a strong dependence between the EHS location, where the local E-field reaches its maximum, and the resonant wavelength necessary to achieve this local E-field, on the size of the analyte particle. Interestingly, the local E-field strength can be considerably weaker than the conventional gap hot-spot when excited at the LSPR wavelength. And the resonant wavelength for these intensified local E-fields can significantly shift, either red- or blue-shifted, in comparison to the LSPR wavelength.In the specific case of the Au NP dimer configuration, the EHS predominantly occurs at the contact point between the Au NP and the analyte particle. This EHS can cover a larger area than the conventional hot-spot and is excitable at various polarizations. Moreover, these changes impact the distance-dependent relationship of the local E-field, leading to a much slower decay compared to the conventional hot-spot scenario. Consequently, interpreting the SERS spectrum of large analyte particles needs consideration of molecular compositions from the outer surface to the inner contents, offering richer information for discrimination and quantification.
Our results imply two key considerations: first, for large analyte particles, since the location of the EHS, enhancement factor, and resonance wavelength all change with analyte particle size, SERS substrate design rules should be size-dependent. To achieve the highest EF, the SERS substrate's accessible surfaces for analyte particles should align with the maximum local E-fields, and for SERS measurements, the excitation laser should closely match the resonance wavelength of the EHS' accessible area.
Secondly, interpreting the SERS spectrum of large analyte particles might be intricate, but the spectrum can be tuned to better represent the analyte particle's unique molecular characteristics. The maximum local field enhancement and distance effects change based on the SERS nanostructure, incident polarization, and analyte size. To enhance classification and quantification, particularly for microorganisms with distinctive internal molecular features, adjusting the power index n of the g2l–x relationship to a smaller value allows multiple layers of the analyte to contribute to the spectra. We anticipate that our findings will pave the way for innovative SERS substrate designs tailored for large analyte particles.
Declaration of generative AI and AI-assisted technologies in the writing process
During the preparation of this work the authors used ChatGPT in order to proof-write the manuscript, i.e., to get rid of possible grammar errors and change the sentence structures. After using this tool/service, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.Author contributions
Y. Y.: FDTD calculations, data analysis, writing – review & editing. Xinyi Chen: MATLAB code for data analysis. Bin Ai: writing – review & editing. Y. Z.: conceptualization, data analysis, funding acquisition, supervision, project administration, writing – original draft, writing – review & editing.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
Y. Y. and Y. Z. are funded by USDA NIFA Grant number 2023-67015-39237.References
- Y. Wang, Principles and Clinical Diagnostic Applications of Surface-Enhanced Raman Spectroscopy, Elsevier, 2022 Search PubMed.
- J. Langer, D. Jimenez de Aberasturi, J. Aizpurua, R. A. Alvarez-Puebla, B. Auguié, J. J. Baumberg, G. C. Bazan, S. E. J. Bell, A. Boisen, A. G. Brolo, J. Choo, D. Cialla-May, V. Deckert, L. Fabris, K. Faulds, F. J. García de Abajo, R. Goodacre, D. Graham, A. J. Haes, C. L. Haynes, C. Huck, T. Itoh, M. Käll, J. Kneipp, N. A. Kotov, H. Kuang, E. C. Le Ru, H. K. Lee, J.-F. Li, X. Y. Ling, S. A. Maier, T. Mayerhöfer, M. Moskovits, K. Murakoshi, J.-M. Nam, S. Nie, Y. Ozaki, I. Pastoriza-Santos, J. Perez-Juste, J. Popp, A. Pucci, S. Reich, B. Ren, G. C. Schatz, T. Shegai, S. Schlücker, L.-L. Tay, K. G. Thomas, Z.-Q. Tian, R. P. Van Duyne, T. Vo-Dinh, Y. Wang, K. A. Willets, C. Xu, H. Xu, Y. Xu, Y. S. Yamamoto, B. Zhao and L. M. Liz-Marzán, ACS Nano, 2020, 14, 28–117 CrossRef CAS.
- S.-Y. Ding, E.-M. You, Z.-Q. Tian and M. Moskovits, Chem. Soc. Rev., 2017, 46, 4042–4076 RSC.
- A. Shiohara, Y. Wang and L. M. Liz-Marzán, J. Photochem. Photobiol., C, 2014, 21, 2–25 CrossRef CAS.
- S. Shanmukh, L. Jones, J. Driskell, Y. P. Zhao, R. Dluhy and R. A. Tripp, Nano Lett., 2006, 6, 2630–2636 CrossRef CAS.
- F. Saviñon-Flores, E. Méndez, M. López-Castaños, A. Carabarin-Lima, K. A. López-Castaños, M. A. González-Fuentes and A. Méndez-Albores, Biosensors, 2021, 11, 66 CrossRef.
- P. A. Mosier-Boss, Biosensors, 2017, 7, 51 CrossRef.
- L. Mikac, I. Rigó, L. Himics, A. Tolić, M. Ivanda and M. Veres, Appl. Surf. Sci., 2023, 608, 155239 CrossRef CAS.
- Q. Chen, J. Wang, F. Yao, W. Zhang, X. Qi, X. Gao, Y. Liu, J. Wang, M. Zou and P. Liang, Microchim. Acta, 2023, 190, 465 CrossRef CAS PubMed.
- B. Alberts, A. Johnson, J. Lewis, M. Raff, K. Roberts and P. Walter, Molecular biology of the cell, Garland Science/Taylor & Francis LLC, New York, 4th edn, 2002 Search PubMed.
- Medical Microbiology, ed. S. Baron, The University of Texas Medical Branch at Galveston, Galveston, 4th edn, 1996 Search PubMed.
- P. A. Levin and E. R. Angert, Cold Spring Harbor Perspect. Biol., 2015, 7, a019216 CrossRef PubMed.
- E. Uurasjärvi, S. Hartikainen, O. Setälä, M. Lehtiniemi and A. Koistinen, Water Environ. Res., 2020, 92, 149–156 CrossRef PubMed.
- Y. Zhao, Nanomaterials, 2023, 13, 2998 CrossRef CAS PubMed.
- Y. Zhao, A. Kumar and Y. Yang, Chem. Soc. Rev., 2024, 53, 1004–1057 RSC.
- R. Rastogi, E. A. Dogbe Foli, R. Vincent, P.-M. Adam and S. Krishnamoorthy, ACS Appl. Mater. Interfaces, 2021, 13, 9113–9121 CrossRef CAS.
- J. Liu, G. Xu, X. Ruan, K. Li and L. Zhang, Front. Environ. Sci. Eng., 2022, 16, 143 CrossRef CAS.
- C. E. Talley, J. B. Jackson, C. Oubre, N. K. Grady, C. W. Hollars, S. M. Lane, T. R. Huser, P. Nordlander and N. J. Halas, Nano Lett., 2005, 5, 1569–1574 CrossRef CAS PubMed.
- K. D. Alexander, M. J. Hampton, S. Zhang, A. Dhawan, H. Xu and R. Lopez, J. Raman Spectrosc., 2009, 40, 2171–2175 CrossRef CAS.
- N. Zohar, L. Chuntonov and G. Haran, J. Photochem. Photobiol., C, 2014, 21, 26–39 CrossRef CAS.
- P. B. Johnson and R.-W. Christy, Phys. Rev. B: Solid State, 1972, 6, 4370 CrossRef CAS.
- R. Aroca, Surface-Enhanced Vibrational Spectroscopy, John Wiley & Sons, Ltd, Chichester, England, 2006 Search PubMed.
- S. S. Masango, R. A. Hackler, N. Large, A.-I. Henry, M. O. McAnally, G. C. Schatz, P. C. Stair and R. P. Van Duyne, Nano Lett., 2016, 16, 4251–4259 CrossRef CAS.
- M. Y. Wang, R. Zhao, L. J. Gao, X. F. Gao, D. P. Wang and J. M. Cao, Front. Cell. Infect. Microbiol., 2020, 10, 587269 CrossRef CAS.
- Y. J. Yang, B. B. Xu, J. Murray, J. Haverstick, X. Y. Chen, R. A. Tripp and Y. P. Zhao, Biosens. Bioelectron., 2022, 217, 114721 CrossRef CAS.
- P. A. Mercadal, J. C. Fraire and E. A. Coronado, J. Phys. Chem. C, 2022, 126, 10524–10533 CrossRef CAS.
- S.-Y. Ding, J. Yi, J.-F. Li, B. Ren, D.-Y. Wu, R. Panneerselvam and Z.-Q. Tian, Nat. Rev. Mater., 2016, 1, 16021 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |