Kuttsukigami: sticky sheet design

Abstract

Shaping 3D objects from 2D sheets enables form and function in diverse areas from art to engineering. Here we introduce kuttsukigami, which exploits sheet-sheet adhesion to create structure. The technique allows thin sheets to be sculpted without requiring sharp folds, enabling structure in a broad range of materials for a versatile and reconfigurable thin-sheet engineering design scheme. Simple closed structures from cylindrical loops to complex shapes like the Möbius loop are constructed and modeled through the balance between deformation and adhesion. Importantly, the balance can be used to create experimental measurements of elasticity in complex morphologies. More practically, kuttsukigami is demonstrated to encapsulate objects from the kitchen to micro scales and to build on-demand logic gates through sticky electronic sheets for truly reusable, reconfigurable devices.

---

1 Introduction

Origami has allowed artists to create intricate sculptures from single sheets of paper for centuries. In this artform, structure is created through a process of sharply folding and creasing flat sheets like paper or other polymeric materials and often requires steps of unfolding and refolding to reach the desired end state. More recently, researchers have noted many real-world engineering problems such as efficient packing and deployment of solar cells,^1,2 collapsible arterial stents,³ robotics,^4–6 and encapsulation^7,8 can be addressed with methods mimicking origami and kirigami.

One basic underlying principle of origami is the need to create a permanent hinge for the desired structure to form. Origami hinges are typically created through irreversible, plastic deformation in areas of high local curvature (as in creased paper) but can also be engineered through local changes in material properties,^9,10 mechanical mechanisms,^11–13 or the addition of plasticizers as in wet origami.¹⁴ In these cases, the sheet retains memory of the fold so if a first design is unfolded then a second different design will be influenced by the first. Furthermore, any additional functional layers must accommodate the extreme curvatures at the location of the crease, which may cause fracture or loss of function. Creating hinges can also be challenging in elastic materials like rubber which do not readily plastically deform, though are often used in stretchable electronics and soft robotics. These challenges with origami hinges can limit reconfigurability, necessitate designs which carefully place functional material, and limit material selection. Overcoming these challenges presents opportunities to vastly expand the library of possible 3D structures in a greater selection of materials for reconfigurable and functional material systems.

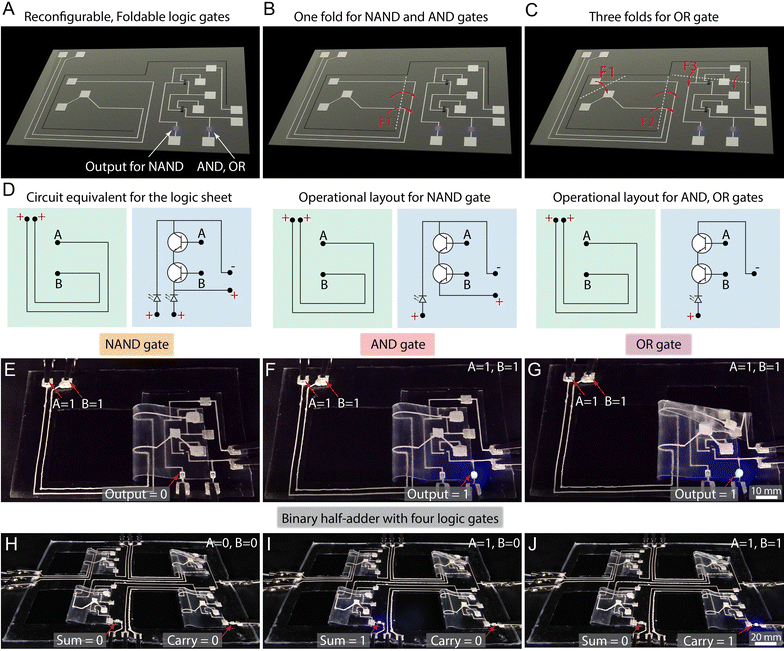
Adding adhesion (stickiness) to a sheets surface creates an overlooked paradigm for design with thin sheets. Here we introduce sticky-sheet structuring, which we call kuttsukigami (see ESI,† Section I), which overcomes hinge limitations in origami design and enables new materials to be used and new curved shapes to be sculpted (Fig. 1). When a sticky sheet is bent into self-contact, a low curvature structure arises (a racquet fold, see Fig. 1(D)), which maintains the far-field geometric outcome of a crease without incurring the high local strains found in a crease. Kuttsukigami widens the design space beyond traditional origami materials to materials such as hydrogels or elastomers because plastic damage or programmed hinges are no longer a requirement. Stable, smooth shapes are now possible, for example a cylinder, Möbius strip, and cone (Fig. 1(E)–(G)). Hybrid structures such as shapes created using adhesion and creasing (i.e. Origami) are also possible (Fig. 1(H)). Additionally, kuttsukigami, can create reconfigurable, reusable designs in elastic materials without preprogramming. For example, a soft electronic sheet created from a silicone elastomer with internal conductive traces of liquid metal can be used to “fold” a fox, then a fish and then a boat shape (Fig. 1(I)–(L)). The fox is formed first using smooth “racquet” bends rather than sharp creases. When the fox is unfolded, there is no memory as the sheet was not damaged or programmed to create a fox, enabling subsequent folding into different objects (fish, boat) and the embedded circuit elements continue to function in the different configurations. As these geometries are the result of a balance between mechanical and interfacial energies, kuttsukigami is a versatile tool for mechanical energy measurement (metrology). A shape will not stay closed if the adhesion energy does not exceed the mechanical energy. Finally, kuttsukigami can encapsulate objects across micro to macro scales and can build reusable, reconfigurable on-demand logic gates from sticky electronic sheets.

Fig. 1 Examples of kuttsukigami design. (A) 3D sculpture created through selectively adhesive regions. Inset shows a racquet shape held by adhesive. (B) A set of sheets adhered at alternating edges under the action of gravity. (C) A sharply folded sheet of hydrogel fails through fracture. (D) A hydrogel racquet shape does not fracture. (E)–(H) New structures formed through adhesive design: (E) a cylinder, (F) a Möbius strip, (G) a cone, (H) a shape created using adhesion and creasing. (I)–(L) Reconfigurable kuttsukigami circuit: (I) reusable electronic sheet integrated with soft conductive traces and LEDs. (J) A “fox” state. (K) A “fish” state. (L) A “boat” state.

2 Methods

2.1 Polydimethylsiloxane

Sylgard 184 was used as received to create thin elastomer films. The system is a two part polydimethylsiloxane (PDMS) mixture, in which prepolymer is mixed by weight ratio with a cross-linker. In this work we use weight ratios of 10 : 1 and 30 : 1, prepolymer to crosslinker respectively. Solutions were mixed vigorously by hand for 10 minutes, then degassed in a vacuum oven.

In order to create thin films the uncured PDMS was coated onto polyacrylic acid (PAA) coated glass slides and placed onto a spincoater (Laurell Technologies Corporation Model WS-400BZ-6NPP/LITE) and quickly rotated to create a thin, uniform film on the slide. PDMS films created by spin coating were on the order of tens of microns in thickness. Thicker samples (over a hundred microns in thickness) were created by drop-casting uncured PDMS onto a PAA coated glass slide.

The film samples were then placed in a vacuum oven at a vacuum pressure of 25 inHg for approximately 20 minutes to remove any air bubbles incurred during the casting process. Samples then were annealed at 85 °C for 90 minutes. Samples were allowed to cool and then scored into strips with a scalpel blade. The glass slide containing the samples was then submerged in MilliQ (Millipore Inc) filtered water in order to dissolve the PAA release layer and allow the film to float to the water surface. Floating films were gently placed onto kimwipes to dry overnight in a closed container.

Thickness values for each sample were determined using three-dimensional scanning confocal microscopy (Olympus FLUOVIEW FV1000) or atomic force microscopy (Veeco Dimension 3100). Each film sample was placed on a glass slide and the height of the film from the glass surface was scanned at three locations around the perimeter. The average was reported as the thickness.

2.2 Polystyrene

Polystyrene with a molecular weight of 192 000 Daltons was dissolved in Optima grade toluene to various weight ratios, both materials were used as received from Fisher Scientific. Samples were allowed to rest over several days to ensure complete dissolution. Solutions were then deposited on freshly cleaved mica sheets which were fixed to a spin coater chuck. Different combinations of angular speed, acceleration, and polystyrene : toluene weight ratio were used to create films of various thicknesses. The films shown in Fig. 3(M) and (N), for example, were coated at 3000 rpm from a 1% solution.

Polystyrene packets were made by floating a spin-coated film off its mica substrate onto a Milli-Q water surface. Films could be loaded with cargo at this stage, or could be removed from the water surface with a Kim wipe and loaded after drying. For the demonstration of ESI,† Movie 2 Nile Red (a crystalline solid at room temperature) was deposited on a film. Nile red is a colorful dye which is visible to the naked eye at even a few parts per million in a solution. Once the cargo was deposited the film was folded by hand, halving its visible area, and van der Waals forces held it in contact. The corners of the racquet packet are compressed by tweezers such that plastic failure occurs and the racquet is destroyed. The flat-folded ends of the packet are then held closed by van der Waals forces.

2.3 Gelatin

JELL-O Gelatin was used as received. 12 ounces of powdered gelatin was mixed with two and one-half cups of boiling filtered water in a glass vessel and gently stirred until dissolution. Thin films were cast on tin foil or waxed paper in order to aid release, and then cooled to approximately 4 °C overnight. Samples were then cut into strips with a Henckels knife. Thicknesses were measured through image analysis of calibrated images taken with a digital camera.

2.4 Double-sided adhesive sheets

8′′ × 10′′ double-sided adhesive sheets were trimed to various sizes and otherwise used as received from ArtGrafixUSA through Etsy.com.

2.5 Thin film circuits

A two part silicone Ecoflex 30 (Smooth-On Inc.) was mixed in a high shear centrifugal mixer (FlackTek Inc.) and cast into a 6 in. × 6 in. sheet with a thin film applicator (Proceq ZUA 2000) on a glass slide to achieve a 400 μm thickness. After curing in a convection oven at 60 °C for 2 hours, copper tape is attached with silicone glue (Sil-poxy, Smooth-On) at predetermined locations for interfacing with power supply. Then, conductive traces are screen-printed with a PET stencil of 75 μm thickness and using a semi-solid paste made by adding 7 vol% of copper particles into liquid metal (EGaIn). LEDs are placed in the circuit and the whole sheet is encapsulated with a 700 μm layer of Ecoflex 30 with a white pigment (Silc pig, Smooth-On) for 2 hours.

2.6 Foldable electronic sheets

The substrate material was made by creating a solution of 40% volume fraction of styrene-isoprene-styrene (SIS) block copolymer and 60 vol% of polybutadiene (PBD) in toluene. SIS and PBD were purchased from Sigma Aldrich and toluene from Fisher Scientific. Solid pellets of SIS were added to liquid PBD and toluene and mixed at 2000 rpm in the FlackTek mixer to dissolve the pellets and form a homogeneous solution. This solution was cast into molds and left overnight in a fumehood to remove the toluene. The result is a ∼300 μm soft and flexible adhesive substrate. Small chain length PBD is typically used as a plasticizer for natural and synthetic rubbers and elastomers. When added to SIS at a volume fraction ≤40%, PBD leads to a decrease in modulus of SIS thereby increasing the softness and flexibility among other effects. Above 40 vol%, it acts an a tackifier enhancing the stickiness of the SIS elastomer. Conductive traces and connecting pads were designed in solidworks and an stl file was used for direct ink writing of liquid metal-silver flakes-SIS ink on a Hyrel Engine SR 3D printer with SDS-10 head. Silver flakes (SF160) were purchased from Ames Goldsmith Advanced Materials. A 0.26 mm diameter steel nozzle was utilized to dispense the ink with a target thickness of 200 μm on the substrate. The conductive traces were cured in a convection oven at 40 °C for 4 hours. Bipolar junction transistors (Rohm semiconductor) and blue LEDs (Everlight Electronics Co Ltd) were purchased from Digikey electronics. These components were placed at the predetermined locations and connected to the circuit by adding extra ink at the component terminals followed by curing at 40 °C for 30 min. To prevent any undesired electrical shorting of the conductive traces when folded, a thin (∼30 μm) polyurethane coating (Humiseal, 1A33) was applied to selected regions of the circuit as encapsulation that may overlap. Cuts were made on these soft adhesive sheets using a razor blade at the desired locations to allow for folding mechanism.

3 Results and discussion

3.1 Elasticity

Rather than a sharp crease, a sheet brought into self-contact under the influence of adhesion (Fig. S1, ESI†) finds equilibrium by adopting a loop geometry commonly known as a ‘racquet’ shape (Fig. 2(A)) which can be used to construct a wide array of structures (Fig. S2, ESI†). The shape (defined formally in Fig. S3, ESI†) results from a balance between bending (increasing energy cost as the loop diameter decreases) and adhesion (decreasing energy cost by closing the loop). Assuming an inextensible sheet for simplicity, the shape can be accurately calculated through variational means.^15,16 For example, if a racquet is formed with a thin film and placed on a substrate the calculation of Glassmaker and Hui shows the width of a racquet (Fig. 2(A)):

W = ηl_ea, (1)

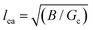where η is a numerical constant related to the difference between self and substrate adhesion, is the elastoadhesive length, B = Et³/12(1 − ν²) is the bending modulus, E is the Youngs modulus, t the film thickness, ν the Poisson ratio and G_c is the critical energy release rate, a measure of adhesion energy (see ESI,† Section II). Direct measurement of the shape (or just the loop width) coupled with knowledge of the material properties of the film yields a measurement of the adhesion energy in the system.

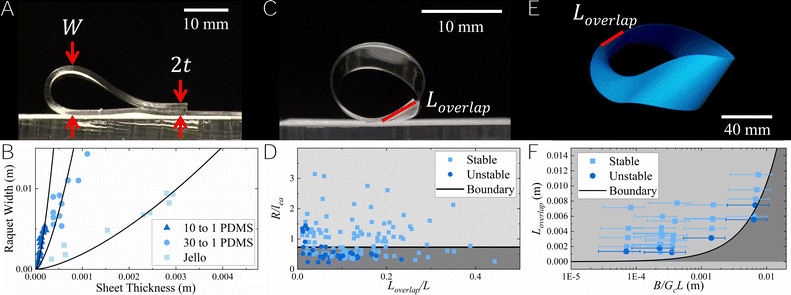Fig. 2 Selected geometries formed with sticky sheets. (A) A racquet shape formed by a PDMS film. (B) Plot of racquet width as a function of film thickness showing data from 10 : 1 PDMS, 30 : 1 PDMS and a hydrogel. Linear least squares fits to scaling law W = at^3/2 − as described in the text are shown as solid lines. a is a fit constant equal to 1960 ± 140, 640 ± 50, and 60 ± 3 for 10 : 1, 30 : 1 and gelatin respectively. (C) A cylinder formed from a sticky sheet. (D) A plot of the scaled cylinder radius against the overlap length, scaled by the overall sheet length. Solid line indicates a fit to (eqn (2)) through a binary weighted edge fit as discussed in the text. Solid symbols indicate experimental observations. (E) A Möbius strip showing a small overlap region. (F) A plot of the length of overlap in a Möbius strip as a function of bending modulus, B, divided by the energy release rate, G_c and overall film length L. Solid line is a linear least squares fit of the scaling function described in the text (eqn (3)) the unstable data. The slope of the linear function was found to be 1.0 ± 0.14.

Fig. 2(A) shows a typical racquet formed from a polydimethylsiloxane (PDMS) elastomer, and Fig. 2(B) shows the widths of racquets formed from two different PDMS elastomers as well as a hydrogel as a function of film thickness. Assuming minimal adhesion to the substrate, η ∼ 1.25 and eqn (1) can be fit to each set of data. Using established Youngs moduli of 1.7 × 10⁶, 2.1 × 10⁵, and 3.6 × 10⁴ Pa^17,18 for the 10 : 1, 30 : 1 and gelatin respectively, we find a work of adhesion for each to be G_c = 7.6 × 10⁻², 8.7 × 10⁻² and 1.8 N m⁻¹.^17,18 The work of adhesion for the two PDMS samples is slightly low, but compares reasonably well with the literature.¹⁷ A reliable published value for the self-adhesion of gelatin could not be found.

The width of the racquet shape will impact how some origami patterns are mimicked. In equilibrium, for example, a flat folded state cannot be reached. However, elastic materials can be used so compression will still allow flat folded states to be reached if desired. Additionally, the racquet shape can be modified by combining it with kirigami to decrease its natural length (removing bending cost).¹⁹ Local changes in modulus could also be designed into sheets as could localized changes in adhesion.^9–13,20 It must be acknowledged that the inclusion of higher-order features would come at the cost of reduced reconfigurability of a system.

Adhesion based design is not limited to recreating traditional origami models using racquet bends but enables geometries that are either fundamentally inaccessible or are prohibitively difficult to create with origami. The most basic demonstration of this idea can be seen when a sheet is curved into a cylinder (Fig. 2(C)). With adhesion, a small overlap length (L_overlap) can hold the cylindrical shape indefinitely if adhesion energy dominates the bending energy. Using a local energy balance at the crack tip, one would conclude that a cylinder would be unstable whenever

R < l_ea. (2)

This scaling estimate assumes a large radius of curvature and small overlap such that the shape remains close to circular (see ESI,† Section V). In a more detailed treatment, in which the loop is modeled as an elastica and contact includes a boundary condition on the curvature, some deviation from this prediction is inevitable. The calculation is lengthy, so we defer it to a separate publication.

Fig. 2(D) shows data from several different loops which either remain closed, or open spontaneously. The solid line is a fit to the scaling discussed above, i.e. R/l_ea = a, where a is a constant. The fit is reached through the maximization of a weighted binary metric. In detail, each stable point is assigned −1 or +1 depending on if they are above or below the fit line, the sum is taken and normalized by the number of points in the ensemble. If all stable points were below the best fit line, the metric would be 1. The opposite metric is assigned to unstable points (+1 if above, −1 if below) and again the sum is normalized by number of points. Both averages are added and maximized to find the best fit to the edge of the data set. In so doing, we identify a = 0.73.

When the two edges of the sheet are adhered at an imperfect angle, the adhered area is not rectangular and overall a cone shape rather than a cylinder will result. A related shape, the developable cone (d-cone), can be created in an ordinary sheet by “folding” a singular “core” (say by pushing a sheet into a cup with a pencil). In this case, the core is not developable and comes at an increased energetic cost due to the change in Gaussian curvature.^21–23 Interestingly, higher-order structures created with racquet edges (such as the fox in Fig. 1(J)) will also create the localized d-cone structure and incur increased energetic costs during assembly. In a highly compact state (as in the fox) the energy of the localized core is negligible when compared to the very large bending energy incurred by bending the doubly thick sheet. Essentially the core scales as B of the sheet, but the bending energy scales as 8B/W times the length of the second bend. The numerical factor is from the effective double thickness of the sheet for the second bend.²⁴ More importantly, the high curvatures of the core will lead to plasticity and failure in some materials. The advantage of using kuttsukigami methods is that a highly elastic material may be used (as we do in Fig. 1(J)). With an elastic material, damage can be avoided and the sheet will return to its original flat state, unscathed by the stress concentration occurring at the d-cone core.

Origami schemes, such as the famed Miura Ori pattern, are often used to create stable and highly compacted configurations.^1–3 Such structures necessarily require high curvatures and stresses at the many repeated vertex locations. Kuttsukigami methods introduce additional design schemes that can dramatically reduce the amount of stress stored while at the same time creating a highly compact state for a sheet. Consider a sheet that is simply rolled into a tight spiral. Without adhesion the sheet unrolls when released, however if adhesion is present the structure may remain stable in the rolled, Archimedean spiral state. We point out that the same balance between curvature and adhesion occur at the crack tip in the spiral state, so the same criteria above will determine its stability.

Another example of a curved shape that can be created with kuttsukigami is the Möbius strip. This fascinating, single-surfaced geometry has entertained mathematicians and children alike for centuries^25,26 and more recently has found application, for example, in novel resonator designs.²⁷ The structure can easily be constructed with a sticky strip having an aspect ratio (width, w to length, L) below 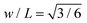, by twisting the strip and then overlapping some small amount of the two ends (Fig. 2(E)). The structure is smooth, but has localized curvature which can become extreme as the aspect ratio approaches 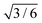and a folded triple-covered equilateral triangle emerges.

The closure of the Möbius strip will again depend on the balance between the energy stored in the adhesion of the overlap and the mechanical energy stored in the body of the strip. In this case the energy is stored both in bending and torsion of the material, and becomes highly localized as the aspect ratio becomes large. This means that a simple balance at the crack tip will not be easily relatable to macroscopic measures such as an approximate radius. Here we opt for a broad argument – the energy stored in the entire structure must be greater than that stored by adhesion for the shape to be unstable. While imperfect, this provides some guide to the stability of the strip. Calculating the total energy stored in a Möbius strip is a challenging problem, but recently two efforts have reported results.^25,26 Starostin and van der Heijden use a variational bicomplex formalism to solve a set of elastic equations and find the resulting shape and mechanical energy of the structure. They show that the predicted mechanical energy scales as U_m ∼ (w/L)B but the scaling has never been experimentally verified. The principles of kuttsukigami offer a direct test of the predicted energy scaling changing either the strength of adhesion, or more easily, the contact area of the overlap region allows a measurement of the systems mechanical energy. The length of the overlap region, L_overlap, can be determined by assuming an energy balance between the energy stored in the overlapping region, which scales as U_a ∼ L_overlap wG_c, and the mechanical energy stored in the deformed strip. The result,

L_overlap ∼ B/G_cL, (3)

is plotted alongside data from several different thicknesses and aspect ratios of PDMS Möbius strips in Fig. 2(F). In these experiments a given strip was tested with decreasing amounts of overlap until such time as the Möbius strip would spontaneously open. The scaling prediction matches the data reasonably well, supporting the predictions of Starostin and van der Heijden and demonstrating kuttsukigami as a powerful measurement tool (see ESI,† Section VI). A more detailed theoretical treatment will certainly increase the accuracy of the prediction, so we caution that the simple energy comparison made here is not expected to be precise.

3.2 Encapsulation

Encapsulation and targeted release of a cargo is an end goal for many technologies including origami.^7,8,16,28 The motivation is to protect a cargo from its environment until such time as it arrives at a desired location and can be released. A solid, however, cannot smoothly be wrapped by an inextensible sheet, particularly if the sheet must inhibit a surrounding fluid environment from contacting the cargo.^7,8,16,28 While partial solutions involving sheets have been demonstrated, kuttsukigami methods allow for the design of simpler packages which can be made sensitive to a broad range of stimuli. In fact, encapsulation by folding a sheet around a solid cargo using an adhesive has been a mainstay of the packaging and food industries for centuries. Fig. 3(A)–(H) demonstrates several examples of sticky sheet encapsulation found in packaging tea and coffee, as well as pierogi, pasta, wontons and spring rolls. These macroscopic examples require mechanical effort (tearing or chewing) to release their cargo, for example, at the right time to change the flavour profile experienced by a subject (see demonstrations in ESI,† Section VIII). Chewing or tearing is not the only response that can be used to open a packet. We demonstrate packages created with hydrogel sheets (Fig. 3(I)–(L)) which swell and open when submerged in water (or dilute acetic acid) and packages created from sub 100 nm thick polystyrene films which dissolve in organic solvents such as toluene or acetone but not polar solvents such as water (ESI,† Movies 1 and 2). Countless possibilities exist for other “switchable” adhesive systems.²⁹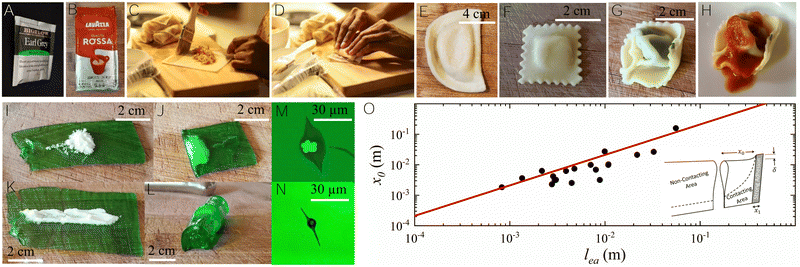

Fig. 3 Encapsulation with sticky sheets. (A) A tea bag in a packet. (B) Packaged ground coffee. (C) A spring roll as an egg-wash adhesive is applied. (D) The spring roll sealed closed. (E) A perogy encapsulating potato and cheese. (F) A ravioli encapsulating cheese. (G) A tortelloni encapsulating cheese and spinach, showing secondary structure formed through additional adhesion. (H) The secondary structure of the tortelloni allows sauce to be captured. (I) A hydrogel sheet with sodium bicarbonate. (J) The sheet is closed into a packet state. (K) A hydrogel film with sodium bicarbonate. (L) The same sheet in a “scroll” which also encapsulates the sodium bicarbonate. (M) Several 3 μm scale polystyrene particles on a silicon substrate encapsulated by a 100 nm thick polystyrene sheet. (N) A single 3 μm particle encapsulated by a 100 nm polystyrene sheet showing symmetry broken by packaging direction. (O) The length x₀ as a function of the elasto-adhesive length l_ea. Solid line shows a linear least squares fit to the linear model (eqn (4)) discussed in the text and supplement. Data is from PDMS and adhesive sheets in which corners have been forced closed with a clamp or epoxy adhesive. Slope was found to be 2.1 ± 0.2. Inset shows the schematic geometry. Strong adhesion indicates a region which has a larger adhesion than the far field ‘ordinary’ film or only a racquet shape would form. The region below the dotted line labeled ‘contacting area’ indicates where the sheet would be in contact with itself and under the influence of ‘ordinary’ adhesion.

A simple encapsulation geometry can be created from a sticky sheet in a modified racquet shape by simply forcing the open ends of the racquet to close with a stronger adhesive or a physical clamp. The inset of Fig. 3(O) and Fig. S4 (ESI†) show the region of increased adhesion in a darkened color, which extends a distance x₁ from the sheet edge. The strain created along the apex of the racquet can be estimated by comparing the length of the hypotenuse of a triangle with sides x₀ and δ to the unstretched length x₀. The racquet shape is a developable surface and closing the ends requires a change in Gaussian curvature if the center of the packet remains in the racquet shape. The change in Gaussian curvature means that in plane stretching must be occurring in the sheet in addition to the increased bending. The stretching is more easily accommodated by a soft elastomer due to its lower elastic modulus (Fig. 3(J)) as a truly inextensible sheet cannot adopt this geometry. Another possibility is using a material that yields plastically during processing such as foil, wet paper, or noodle (Fig. 3(E)–(G)).

Pinching the ends of the racquet closed creates a geometry that is analogous to a “stretching ridge” a structure which forms between two developable cones.²² In this case the ridge forms between the pinch point and a point some distance away, x₀, which has a fixed curvature of order 1/W. If the ridge is held in place by adhesion, then

x₀ ∼ l_ea, (4)

as one might expect given the problem becomes a balance of bending and adhesion in this limit. Fig. 3(O) shows a fit of eqn (4) to data collected from PDMS and double-sided sticky sheets. In most cases, the strong adhesive used to close the racquet ends was a clamp, though Epoxy was occasionally used. We find the clamp avoids the thickness of the adhesive layer itself, which we do not account for. A similar scaling is observed in the case of a film draped over a particle, where a ridge is formed with a curvature set by the particle on one end and infinity at the other. Fig. 3(M) and (N) show the result of draping a thin ∼100 nm polystyrene film over one or several 3.5 micron radius polystyrene spheres. The sheet forms a symmetry breaking shape which extends in two directions from the sphere.

3.3 Reconfigurable electronics

One of the limitations with using origami to enable other technologies can be demonstrated with a thin-film electronic layer added to a sheet. Consider a simple circuit created by depositing a copper wire on a polyimide sheet (inset ESI,† Fig. S5). When the sheet is sharply creased, opened and flattened, and creased again, resistivity jumps to infinity after approximately 20 repetitions (only 5 if the sheet is creased in opposite directions each cycle). While there has been a great effort to create methods which can accommodate the high strains often exerted on thin film and wearable electronic devices, many of these devices may still not survive the extreme curvatures created in a crease.³⁰ Kuttsukigami offers a very simple way to protect a device while still allowing a larger structure to be assembled. Using a similar circuit but adhering it in a racquet shape to avoid a crease, the circuit continues to maintain a low resistivity for over 500 bending per flattening cycles (ESI,† Section IX and Fig. S5).

The ability of kuttsukigami to create reconfigurable, reusable designs with purely elastic materials is demonstrated in a mechanical logic scheme. As illustrated in Fig. 4(A), a single functional sheet using conductive traces integrated with transistors and LEDs (details in ESI† and Fig. S6). When this functional sheet is folded once along F1, it can realize a NAND or an AND logic gate (Fig. 4(B)). Additionally, when folded along F1, F2 and F3 as indicated in Fig. 4(C) schematic, an OR logic gate is created. The layout for the logic sheet is presented in Fig. 4(D) with operational layouts and power supply points for inputs (A, B). The green side is flipped to blue side such that the A, B input pads come in contact to realize logic (ESI,† Section X and Fig. S6). Implementation of these gates is recorded and presented in ESI† (Movies 3–5). Images for each gate with logic inputs A = 1, B = 1 are presented in Fig. 4(E)–(G). The ON state of LED indicates output of 1 and the OFF state 0.

Fig. 4 Reconfigurable, foldable logic through kuttsukigami. (A) Schematic of the reconfigurable logic gate circuit with LEDs to indicate binary output of the folding logicwith fold lines and folding directional arrows for (B) NAND and AND logic gates. (C) OR logic gate. (D) Circuit equivalent for the logic sheet and operational layouts for individual gates, green represents the input and blue the transistor side. (E)–(G) Images of the fabricated circuit and folds showing the outputs for inputs A = 1, B = 1 for the respective gates. (H)–(J) Implementation of binary half-adder circuit using four individual reconfigurable circuits the LEDs at the bottom left and the bottom right circuits indicate the sum and carry outputs for the half-adder for different input A, B combinations.

Further, multiple “units” of these refoldable, reconfigurable functional sheets can be combined to demonstrate material-level operations. Fig. 4(H) illustrates such a complex four-unit circuit in which each unit can be configured or reconfigured into one of NAND, AND, and OR gates on-demand. In one configuration, by folding one unit as a NAND gate, two units as AND gates, and the fourth unit as an OR gate, this circuit functions as a binary half-adder that can add two binary digits. The two output digits sum and carry are indicated by the state of the respective blue LEDs (ON for 1 and OFF for 0). Inputs A = 0, B = 0 will result in output = 0 for both sum (left bottom LED) and carry (right bottom LED) as indicated by OFF state for both LEDs in Fig. 4(H). If either of the inputs is 1, the result will be 1 for sum and 0 for carry as shown in Fig. 4(I) and both inputs of 1 result in a sum of 0 and carry of 1 (Fig. 4(J)).

4 Conclusions

Through sheet-sheet adhesion, a stable yet reconfigurable 3D structuring technique was developed that can embed different functionalities and morphologies into diverse materials and across vast length scales. This approach was shown to enable sculpting in elastic materials, relying on adhesion to sustain shapes, instead of plasticity or heterogeneous material structures. This enabled flat functional sheets such as soft electronic devices to be created which can maintain various stable configurations, while still maintaining reversibility or reconfigurability back to a flat sheet.

Kuttsukigami opens possibilities for measuring material properties. This can provide a methodology to measure relative contributions between mechanical deformation (i.e. bending) and adhesion in difficult to evaluate structures. Similar to techniques such as the JKR approach,³¹ Kuttsukigami can measure adhesion energy and elastic modulus. Such possibilities may be particularly useful when considering complex structures where the energy landscape could be difficult to measure (i.e. the Möbius). We also see kuttsukigami as synergistic with other approaches such as origami and kirigami. Such multimodal combinations could allow for deploying into architectures set by folds or cuts once adhesion is released or generating both smooth and discrete curved geometries to open further 3D shape possibilities and functions. Future work could explore these synergies. Additionally, the incorporation of actuation mechanisms could enable shape reconfiguration without human input,^6,32 and represents a future pathway for autonomous reconfiguration. Therefore, these combinations could enable future applications in areas such as biomedical devices, soft robotics, and deployable structures.

Author contributions

Conceptualization: ABC, TT, MB; methodology: ABC, TT, MB, RT; investigation: TT, WZ, RT; visualization: ABC, TT, RT, MB; funding acquisition: ABC, MB; project administration: ABC, MB; supervision: ABC, MB; writing – original draft: ABC, TT; writing – review & editing: ABC, TT, MB, RT.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

TT and ABC gratefully acknowledge funding through the National Science Foundation (NSF) (award no.: CMMI-2011681). RT, WZ, and MB acknowledge support through NSF (award no.: CMMI-2054409). WZ acknowledges support through the – Virginia Tech ICTAS Doctoral Scholars Program. The authors thank the late Daniel King and an anonymous reviewer for help coining the Kuttsukigami name.

References

1. R. Tang, H. Huang, H. Tu, H. Liang, M. Liang, Z. Song, Y. Xu, H. Jiang and H. Yu, Appl. Phys. Lett., 2014, 104, 083501.
2. T. Chen, O. R. Bilal, R. Lang, C. Daraio and K. Shea, Phys. Rev. Appl., 2019, 11, 064069.
3. K. Kuribayashi, K. Tsuchiya, Z. You, D. Tomus, M. Umemoto, T. Ito and M. Sasaki, Mater. Sci. Eng., A, 2006, 419, 131–137.
4. S. Li, D. M. Vogt, D. Rus and R. J. Wood, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 13132–13137.
5. J. Rogers, Y. Huang, O. G. Schmidt and D. H. Gracias, MRS Bull., 2016, 41, 123–129.
6. D. Hwang, E. J. Barron III, A. T. Haque and M. D. Bartlett, Sci. Robot., 2022, 7, eabg2171.
7. J.-H. Cho and D. H. Gracias, Nano Lett., 2009, 9, 4049–4052.
8. A. Azam, K. E. Laflin, M. Jamal, R. Fernandes and D. H. Gracias, Biomed. Microdevices, 2011, 13, 51–58.
9. Y. Liu, J. K. Boyles, J. Genzer and M. D. Dickey, Soft Matter, 2012, 8, 1764–1769.
10. J.-H. Na, A. A. Evans, J. Bae, M. C. Chiappelli, C. D. Santangelo, R. J. Lang, T. C. Hull and R. C. Hayward, Adv. Mater., 2015, 27, 79–85.
11. E. Hawkes, B. An, N. M. Benbernou, H. Tanaka, S. Kim, E. D. Demaine, D. Rus and R. J. Wood, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12441–12445.
12. B. An, N. Benbernou, E. D. Demaine and D. Rus, Robotics, 2011, 29, 87–102.
13. M. T. Tolley, S. M. Felton, S. Miyashita, D. Aukes, D. Rus and R. J. Wood, Smart Mater. Struct., 2014, 23, 094006.
14. B. Y. Ahn, D. Shoji, C. J. Hansen, E. Hong, D. C. Dunand and J. A. Lewis, Adv. Mater., 2010, 22, 2251–2254.
15. N. Glassmaker and C. Hui, J. Appl. Phys., 2004, 96, 3429–3434.
16. C. Py, P. Reverdy, L. Doppler, J. Bico, B. Roman and C. N. Baroud, Phys. Rev. Lett., 2007, 98, 156103.
17. T. Elder, T. Twohig, H. Singh and A. B. Croll, Soft Matter, 2020, 16, 10611–10619.
18. G. Henderson Jr, D. Campbell, V. Kuzmicz and L. Sperling, J. Chem. Educ., 1985, 62, 269.
19. M. Liu, L. Domino and D. Vella, Soft Matter, 2020, 16, 7739–7750.
20. T. Twohig and A. B. Croll, Soft Matter, 2021, 17, 9170–9180.
21. E. Cerda, S. Chaieb, F. Melo and L. Mahadevan, Nature, 1999, 401, 46–49.
22. A. Lobkovsky, S. Gentges, H. Li, D. Morse and T. A. Witten, Science, 1995, 270, 1482–1485.
23. E. Cerda and L. Mahadevan, Phys. Rev. Lett., 1998, 80, 2358.
24. T. Elder, D. Rozairo and A. B. Croll, Macromolecules, 2019, 52, 690–699.
25. L. Mahadevan and J. B. Keller, Proc. R. Soc. London, Ser. A, 1993, 440, 149–162.
26. E. L. Starostin and G. H. van der Heijden, Nat. Mater., 2007, 6, 563–567.
27. J. K. Hamilton, I. R. Hooper and C. R. Lawrence, Sci. Rep., 2021, 11, 9045.
28. H.-W. Huang, M. W. Tibbitt, T.-Y. Huang and B. J. Nelson, Soft Robot., 2019, 6, 150–159.
29. A. B. Croll, N. Hosseini and M. D. Bartlett, Adv. Mater. Technol., 2019, 4, 1900193.
30. S.-I. Park, J.-H. Ahn, X. Feng, S. Wang, Y. Huang and J. A. Rogers, Adv. Funct. Mater., 2008, 18, 2673–2684.
31. K. L. Johnson, K. Kendall and A. Roberts, Proc. R. Soc. London, Ser. A, 1971, 324, 301–313.
32. D. Shah, B. Yang, S. Kriegman, M. Levin, J. Bongard and R. Kramer-Bottiglio, Adv. Mater., 2021, 33, 2002882.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01403g

‡ These authors contributed equally to this work.

---