Interfacial energy as an approach to designing amphipathic surfaces during photopolymerization curing

Abstract

Photopolymerization induced phase separation (PIPS) is a platform capable of creating heterogeneous materials from initially miscible resin solutions, where both the reaction's governing thermodynamics and kinetics significantly influence the resulting phase composition and morphology. Here, PIPS is used to develop materials in a single photopolymerization step that are hydrophobic on one face and hydrophilic on the other. These two faces possess a water contact angle difference of 50°, bridged by a bulk-scale chemical gradient. The impact of the PIPS-triggering inert additive is investigated by increasing the loading of poly(methyl methacrylate) (PMMA) in an acrylonitrile/1,6-hexanediol diacrylate comonomer resin. The extent of phase separation in the sample network depends on this loading, with increasing PMMA corresponding to macroscale domains that are more chemically and mechanically distinct. A significant period between the onsets of phase separation and reaction deceleration, determined using in situ FT-IR, facilitates this enhanced phase segregation in PMMA-modified samples. Spatially directed domain formation can be further promoted using multiple interface types in the sample mold, here, glass and stainless steel. With multiple interface types, interfacial rearrangements to minimize surface energy during resin photopolymerization result in a hydrophobic face that is nitrile-rich and a hydrophilic face that is nitrile-poor (e.g., acrylate-rich). Using this strategy, patterned wettability on a single face can also be engineered. This study illustrates the capabilities of PIPS for complex surface design and in applications requiring stark differences in surface character without sharp interfaces.

---

1 Introduction

Heterogeneity within the bulk volume of a polymer introduces a complexity not attainable through solely homogeneous materials, expanding the horizon of what is possible in soft matter research. Heterogeneous polymer systems are leveraged to increase toughness by modifying stress distributions throughout a bulk material^1–3 and also to finely control gloss, antifouling, and extreme wettabilities^4–6 not attainable using homogeneous counterparts. There exist a range of synthesis methods to produce and manipulate heterogeneity in polymeric materials, including but not limited to chemical reaction driven phase separation^7–11 and the self assembly of block copolymers.^12–15

One type of chemical-reaction-driven phase separation is photoolymerization induced phase separation (PIPS), where the reaction of initially miscible components (monomers, inert additives, etc.) causes a decrease in Gibbs free energy during polymerization, promoting phase separation. While the reduction in Gibbs free energy during polymerization is a thermodynamic driving force promoting phase separation, with PIPS, the kinetics of polymerization also has a significant role, impacting the ease at which molecules diffuse to form distinct phase domains. As one example, if the reaction kinetics correspond with a rapid onset of gelation and/or vitrification of the network, the mobility of immiscible domains will be hindered and phase separation can be suppressed.¹⁶ The interplay between kinetics and thermodynamics is complex, with the relationship between the two discussed below.

The thermodynamic driving force for phase separation is ultimately dictated by the change in Gibbs free energy of mixing, ΔG_mix, which is in turn determined by the system's enthalpy, ΔH_mix, entropy, ΔS_mix, and absolute temperature, T (eqn (1)). If the free energy (ΔG_mix) of a system is negative, the mixture will remain in a well-mixed, single-phase state. However, a positive ΔG_mix indicates that spontaneous de-mixing of the components is thermodynamically favorable. Enthalpic-driven phase separation occurs from a lack of compatibility between the mixture components, resulting in conditions where there is a higher preference for aggregation of similar species as opposed to equal mixing of different species. Alternatively, entropic-driven phase separation occurs from changes in the system's available degrees of freedom. The number of possible distinct configurations Ω available to a system influences ΔG_mix in that more configurations enables a larger entropy, related through the Boltzmann constant k_B (eqn (2)).¹⁷ In a polymerizing system, the growth of polymer chains from initial monomers gradually reduces the degrees of freedom, decreasing S.¹⁸ ΔG_mix > 0 can be linked to the combination of decreased miscibility between developing species and a reduction of available macromolecular conformational states.¹⁹

ΔG_mix = ΔH_mix − TΔS_mix (1)

S = k_B ln(Ω) (2)

However, as mentioned, thermodynamic equilibrium as dictated by ΔG_mix is not the only determining factor on the final morphology of phase separated polymer networks; reaction kinetics also play a significant role.^20,21 The evolving physical state of a sample undergoing PIPS can constrain or limit phase separation by impacting the mobility of reactive species. Most significantly, cross-linking events and the introduction of inert additives will influence mobility within the system.¹⁰ Both a solution's initial viscosity as a function of its resin chemistry and its change in viscosity as monomer converts into polymer result in a wide range of time dependent viscosity environments that are possible in a polymerizing system.²² Since the viscosity environment impacts diffusion of immiscible species within a system, it has a direct influence on the final microstructure formed from PIPS. Transient changes to the local viscosity environment can be probed via reaction kinetics, typically via characterization of overall rate of polymerization (R_p). This type of kinetic analysis can identify the onset of diffusion–limitations during a polymerization, i.e. the moment where the viscosity environment is such that diffusion is limited for all reactive species. As highlighted in previous works, resin compositions and reaction conditions (e.g., rate of initiation) can be adjusted to tailor the final polymer morphology attained via phase separation.^2,4,16 For instance, a system with a low initial resin viscosity will take longer to reach this upper limit viscosity threshold during polymerization, and thus can be employed to favor extensive phase diffusion.²³ Understanding the impact of the available kinetic parameters can ultimately be a powerful tool, as manipulation of reaction kinetics is one strategy to tailor PIPS to yield diverse morphologies and phase structures, as phase separation can be halted or frozen in a non-equilibrium state.

This phase separation can come about by either spinodal decomposition or nucleation and growth, both of which are influenced by the thermodynamic and kinetic environment of the developing polymer. Both mechanisms can result in a multi-domain morphology but their associated thermodynamic stability and deviation from equilibrium differ from one another.^24,25 On one hand, the nucleation and growth mechanism follows a meta-stable increase in domain size, while spinodal decomposition is inherently unstable and forms distinct domains from local fluctuations. When considering crosslinking polymerizations, domain development competes with the actively reacting network, as discussed in the kinetics section. Therefore, the phase separation mechanism can be manipulated via reaction kinetics, with slower rates allowing for a more equilibrium nucleation and growth approach while fast rates prevent thermodynamic equilibrium from being reached and instead favors spinodal decomposition.¹⁶ Manipulating the mechanism of phase separation presents an approach to tailor morphology, as nucleation and growth typically results in isolated domains within a matrix whereas spinodal decomposition is associated with more co-continuous morphologies.^16,24

While controlling heterogeneity via phase separation involves complex interactions between thermodynamics and kinetics, the applications of these phenomena provide an avenue to create and tailor exemplary compositional gradients in materials. Such gradients can be leveraged for enhanced mechanical properties. A number of organisms in nature already make use of such gradients in their bodily systems across a range of length scales, including mussel filaments (centimeter), squid beaks (millimeter), and human teeth (micrometer).^26–30 These gradients in a given mechanical property, such as modulus or toughness, can be facilitated by a gradient in chemical concentration.^28,31 Having a chemical concentration change gradually over a distance as opposed to a sharp interface between the two endpoint concentrations has the benefits of reducing stresses that can lead to fracture as well as increasing overall toughness by preventing crack propagation.^26,32 Despite the advantages associated with chemical gradients and heterogeneity in natural systems, there still exist challenges in creating similar gradients on the order of hundreds of microns in engineered materials. The majority of research in obtaining chemical gradients via phase separation focus largely on nanometer to micrometer thick samples.^33,34 This limitation in length scale minimizes the benefit of such compositional gradients in terms of stress dissipation. Prior works have demonstrated that PIPS can be leveraged to engineer chemical gradients in phase separating resins by providing the relevant controls over the reaction, but such gradients have yet to be demonstrated on larger length scales.

This study demonstrates how PIPS can be employed to create macroscale chemical gradients in photopolymerized materials, ultimately creating surfaces with contrasting wettabilities. The rapidly formed acrylate networks with inert poly(methyl methacrylate) additions examined here develop chemical gradients without lengthy processing procedures. By varying the chemical component ratios and the UV curing conditions, the resins undergo macro-scale phase separation yielding chemical gradients spanning several hundred micrometers. Furthermore, spatially-directed bulk phase separation is achieved by tailoring the interfacial energies between the polymer resin and the sample mold configuration. This results in a final material where the location of phase domains is guided by the interfacial energies present between the developing polymer and the sample mold materials. Specifically, two different interfacial environments employed here (glass and stainless steel) impart hydrophobic character to one side of the formed polymer while the other possesses hydrophilic character. This work demonstrates the application of knowledge on thermodynamic compatibility between chemical species and the impact of reaction kinetics in developing phase separated polymer materials with macroscale gradients and dissimilar chemical domains. We develop spatially-resolved domains over large length-scales and generate stark differences in surface character from initially miscible resins in a single step procedure, opening avenues for streamlining complex surface manufacture.

2 Experimental

2.1 Materials

Co-monomer formulations consisted of acrylonitrile (AN, Sigma Aldrich) and 1,6-hexanediol diacrylate (HDDA, Sigma Aldrich), with HDDA acting as a cross-linker (Fig. 1). In certain resin formulations, an inert polymer additive, poly(methyl methacrylate) (PMMA; M_w = ∼120 000 g mol⁻¹, Sigma Aldrich) was included to promote phase separation during polymerization. 2,2-Dimethoxy-2-phenylacetophenone (DMPA, Sigma Aldrich) was employed in all formulations as photoinitiator (0.5 wt%). All chemicals were used as received and without further purification.

Fig. 1 Chemical structures of species included in resin formulations (left to right): acrylonitrile (AN comonomer), 1,6-hexanediol diacrylate (HDDA – crosslinker), poly(methyl methacrylate) (PMMA – inert additive), and 2,2-dimethoxy-2-phenylacetophenone (DMPA – photoinitiator).

2.2 Resin preparation

Resin formulations in this study contained varying weight fractions (wt%) of components AN, HDDA, and PMMA, as described in Table 1. In all resins, DMPA loading was held at 0.5 wt% relative to the combined weight of the other species. To further increase the free energy in the system and promote phase separation, PMMA was incorporated in increasing amounts up to 20 wt%. For ease of reference throughout the following text, sample names are listed as A_aX_bP_c, where A corresponds to acrylonitrile, X corresponds to the cross-linker 1,6-hexanediol diacrylate, and P corresponds to PMMA. The subscript values indicate the weight fractions present, where a and b are the wt% values of AN and HDDA relative to one another within the comonomer resin, respectively, and c is the wt% of PMMA relative to the whole resin sans DMPA.

Table 1 Full compositions of resins with nomenclature

	AN (wt%)	HDDA (wt%)	PMMA (wt%)	DMPA (wt%)
A70X30P0	69.65	29.85	—	0.50
A70X30P5	66.17	28.86	4.98	0.50
A70X30P10	62.69	26.86	9.95	0.50
A70X30P20	55.72	23.88	19.90	0.50

---

To prepare resins, DMPA was first massed in a glass vial, and if necessary, PMMA was subsequently added to the same vial. These solids were then allowed to completely dissolve in the appropriate mass of AN and HDDA following the resin formulation. Haziness in the solution was not observed for any of the samples in the monomer state, indicating good mixing and macroscopic miscibility. After magnetic agitation for 30 minutes at ambient temperature, resins were degassed via N₂ bubbling for 10 minutes prior to photopolymerization to eliminate any inhibition effects as a result of dissolved oxygen.

2.3 Viscosity measurement

The viscosity of the 4 A₇₀X₃₀P_c resins at ambient conditions was measured using a sine-wave vibration viscometer SV-10A (A&D Company Ltd, Tokyo, Japan). For each resin formulation, 15 mL was added to the well for measurement, with each formulation tested three times.

2.4 Bulk photopolymerization

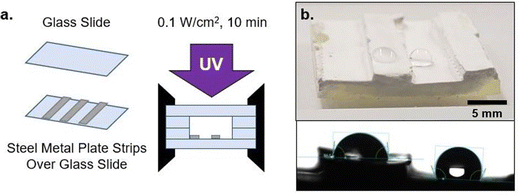
To investigate multiple length scales of phase separation behavior using mechanical testing and surface characterization techniques, rectangular samples were made. For these bulk sample photopolymerizations, 1 mL of the desired resin formulation was injected into a rectangular mold consisting of glass slides (two glass substrates with glass spacers), creating samples with approximate dimensions of 10 mm × 25 mm × 2 mm (length × width × thickness) (Fig. 2a). The glass mold was clamped together on both ends to prevent delamination. Samples were then immediately cured using a UV lamp (UVitron, Intelliry 600) with the 365 nm intensity (I₀) value at the sample interface recorded using a handheld radiometer (Excelitas, OmiCure R2000 with Cure Site Detector attachment). Exposure time was 10 minutes with I₀ = 0.1 W cm⁻².

Fig. 2 Two mold geometries were utilized in curing the resins to manipulate surface energy gradients. One geometry consisted completely of 1 mm thick glass slides (a) and in the other, a stainless steel plate replaced the bottom face (b). In both geometries, resin was injected into the open cavity left by the glass slides, and all polymerizations proceeded upon exposure to 0.1 W cm⁻² irradiation of 365 nm light for 10 minutes.

To investigate directionally-guided macro phase separation, the molds used for bulk photopolymerization were modified to introduce a difference in interfacial energies at the mold interfaces. In these cases, bulk samples were made using a procedure similar to that described above, however one of the glass substrates was replaced with a stainless steel plate (Fig. 2b). Samples were oriented so that the metal substrate was on the bottom to allow UV light to pass through the upper glass substrate and interact with the resin to facilitate curing.

2.5 Dynamic mechanical analysis (DMA)

Thermo-mechanical properties of polymerized specimens without PMMA were assessed using a dynamic mechanical analyzer (DMA, TA Instruments, Discovery DMA850). Samples were measured in a three-point-bending configuration, with 15 mm between the outer points. An initial preload force of 0.01 N was selected, with a 20.0 μm amplitude and 1.0 Hz frequency selected for the duration of the run. A temperature ramp of 5.0 °C min⁻¹ was employed to scan over a range of 20 °C to 200 °C. To ensure that residual, unreacted monomer in the photocured samples did not influence the collected data, all specimens were annealed for 1 hour at 150 °C prior to analysis. The annealing temperatures was chosen based on the reported T_g of poly(acrylonitrile) in the range of 75 °C to 105 °C.^35,36

2.6 Raman spectroscopy

To better characterize chemical gradients, cross sections of polymerized samples were imaged using Raman spectroscopy (Horiba Jobin Yvon LabRAM HR). 2D chemical mapping of the cross sections allowed for confirmation of optically-observed phase separation. After an initial Si calibration, scans at 10× magnification were carried out over a 0.5 mm × 2.0 mm mapping area. A 785 nm laser was used with a 750 nm grating to excite the sample. Spectra were collected along a 25 × 100 point grid, collecting a total of 2500 data points. 2D maps were generated based off of the nitrile C≡N functional group peak at 2250 cm⁻¹, present only where polyacrylonitrile has formed in the sample. Raman mapping of the sample cross section was performed by stitching together multiple screening areas to compile the whole observed area.

2.7 Small angle X-ray scattering (SAXS)

To check for nanoscale phase separation, 5 mm diameter, 0.5 mm thick sections were taken from bulk rectangle samples after curing to collect small angle scattering data (12-ID-B beamline, Advanced Photon Source, Argonne National Lab). The incident X-ray beam used was set at 13.3 keV (λ = 0.935 angstrom). The sample/detector distance was 2.1 m for all measurements, corresponding to a range of scattering wave vector (q) of 0.003–0.9 Å⁻¹. A two-dimensional (2D) Pilatus 2 M detector was used. The scattering angles were calibrated with silver behenate and the absolute scattering intensity was determined from a glassy carbon standard. Polymer samples were secured to a solid sample plate using clear tape. SAXS measurements were taken of the clear tape by itself to provide a spectrum for background subtraction to yield the polymer material spectra. The corresponding d-spacing was calculated by taking the inverse of q and multiplying by a factor of 2π.

2.8 Real time Fourier-transform infrared spectroscopy (FT-IR)

Real time Fourier-transform infrared spectroscopy (FTIR, ThermoNicolet, Nicolet iS50) was employed to monitor real-time photopolymerization kinetics of select formulations. For in situ photopolymerizations, the desired formulation was injected into a rectangular mold comprised of glass slides with a spacer of 0.1 mm thickness. The molds were designed to limit atmosphere exposure during testing; the glass slides were clamped together to prevent delamination. Samples were placed in the sample chamber with a UV light source (EFOS Ultracure 100ss Plus, λ ∼ 320–500 nm) equipped with a flexible light guide directed to irradiate the sample area (I₀ = 0.01 W cm⁻² measured at sample surface), to enable simultaneous UV exposure and collection of FTIR spectra. All samples were angled to ensure that the incoming UV light was perpendicular to the specimen while maintaining transmittance of the IR beam. This was done to mitigate the cosine error associated with light intensity experienced by non-perpendicular surfaces, where the intensity experienced at the surface decays as a Lambertian function with an increased change in the incident angle.³⁷ The FTIR sample chamber was kept dark throughout the experiment by folding thick absorbent pads over the opening. Real-time conversion curves were generated by monitoring the integral area between 6100 cm⁻¹ and 6240 cm⁻¹, corresponding to the C=C vinyl peak at 6165 cm⁻¹.

2.9 Contact angle measurements

The wettability of sample surfaces was characterized via water contact angles (θ) measured using a goniometer (Kruss, Drop Shape Analyzer – DSA30). Prior to measurement, each side of the sample was washed with water for cleaning and gently wiped with a Kimwipe to dry. Contact angle values were calculated from a 2.0 μL sessile drop mechanically deposited by syringe. 5 images were collected per drop, and 5 drops were measured across the sample surface to obtain an average value. Contact angles were measured using an ellipse-tangent fit between the drop and surface. Surface energy values (γ) were calculated using the OWRK model pairing the water contact angle with a toluene contact angle to calculate polar and disperse contributions.³⁸

Surface free energy of initial comonomers were characterized using the pendant drop method, where 6.0 μL of monomer liquid was suspended from the deposition needle and calculated from the drop's shape factor.

3 Results and discussion

Phase separation in the 70 wt% acrylonitrile 30 wt% 1,6-hexanediol diacrylate system with increasing poly(methyl methacrylate) additions (denoted as A₇₀X₃₀P_c) was robustly investigated using optical (macro-imaging), thermomechanical (DMA), surface (contact angle), and spectroscopy (Raman, SAXS) characterization techniques. Combining the performed analyses enabled assembly of a full picture of PIPS. This determined how domain formation and its manipulation can be utilized to establish stark chemical gradients over large length scales using rapid photopolymerizations.

3.1 PIPS system domain structures as a function of PMMA loading

To ensure that the PIPS observed in the platform studied here is due to the increase in entropy via addition of the inert prepolymer (PMMA), it was necessary to first ensure that the base copolymer matrix (AN:HDDA) formed a single-phase network. With this design, a homogeneous control (AN:HDDA network) is easily defined and the proclivity for phase separation is tailored via PMMA addition. It should be noted that crosslinked networks formed via free radical polymerization have an intrinsic degree of heterogeneity in their structure.^39,40 The heterogeneity arises from the mechanism of nanosized gel formation, clusters of which form quickly after radical initiation. These local variations in network structure are different than discrete domains formed via phase separation observed in PIPS systems, and typically differ in length scales (nano vs. micro scale domains).

Ultimately, the A₇₀X₃₀P_c comonomer system was chosen as the base formulation as it does not undergo phase separation during polymerization (e.g., A₇₀X₃₀P₀ forms a random copolymer network). This selection of comonomer system was determined by investigating the photopolymerization behavior of a series of AN:HDDA copolymers (e.g., A_xX_yP₀) consisting of 5 wt% to 100 wt% HDDA. The visual opacity of each copolymer network was used as an initial indicator for microscale phase separation^2,41 (Fig. S1, ESI†). From this analysis, it was clear that an HDDA loading of 30 wt% (e.g., A₇₀X₃₀P₀) presented the smallest fraction of crosslinker that did not have associated phase separation of the copolymer network.

Specifically, A₇₀X₃₀P₀ samples were fully transparent after curing at I₀ = 0.1 W cm⁻², indicating a lack of phase separation at a domain size larger than the wavelength of the interacting visible light^2,41 (Fig. 3ai). Furthermore, thermomechanical characterization via DMA testing revealed a single, symmetric peak in the tan δ profile, indicative of a well-mixed homopolymer network with a single glass transition temperature (T_g = 110 °C, Fig. S2, ESI†). This T_g confirms that the base copolymer network is glassy at ambient conditions. Consistent with prior works highlighting nanoscale heterogeneities in networks formed via free-radical polymerization,^39,40 some domains between 70 and 100 nm in size are observed in the A₇₀X₃₀P_c system via small-angle X-ray scattering (SAXS) Fig. S3 (ESI†). These local fluctuations in sample density are in line with previous descriptions of this behavior.⁴²

As demonstrated in prior works,^22,43 the addition of an inert additive to a polymerizing resin can increase the viscosity environment, thus limiting reaction kinetics, while also modifying free energy conditions to promote phase separation. Implementing a similar design, in this study PMMA was employed as an inert additive based on its miscibility with the comonomers investigated (AN and HDDA), ensuring a stable and homogeneous precursor resin that does not phase separate prior to polymerization. PMMA loadings of 0 wt%, 5 wt%, 10 wt%, and 20 wt% were explored (i.e., A₇₀X₃₀P₀, A₇₀X₃₀P₅, A₇₀X₃₀P₁₀, and A₇₀X₃₀P₂₀). The influence of PMMA on the viscosity of the precursor resins was characterized to better understand the starting conditions for each formulation (Table 2). Unsurprisingly, viscosity increases with increased PMMA loading, resulting in a viscosity range from 0.66 mPa s for the comonomer control (A₇₀X₃₀P₀) to 45.1 mPa s at maximum PMMA loading (A₇₀X₃₀P₂₀).

Table 2 Viscosity of uncured resins

	Viscosity (mPa s)
A70X30P0	0.66 ± 0.03
A70X30P5	1.61 ± 0.03
A70X30P10	5.64 ± 0.06
A70X30P20	45.1 ± 0.3

---

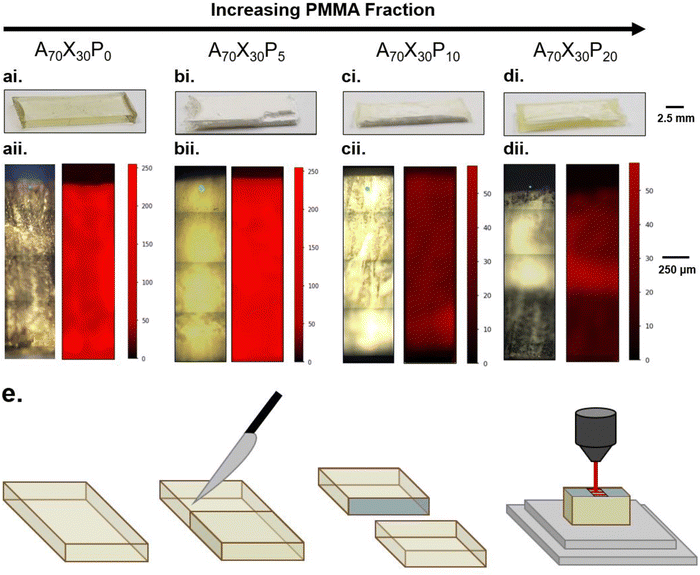
The integration of PMMA also impacts the compositional gradients that arise after photopolymerization, as depicted in Fig. 3. All resins were polymerized with standardized UV irradiation of 0.1 W cm⁻² for 10 minutes. The compositional gradients that arise in PMMA-modified formulations, despite the initial precursor formulations being macroscopically homogeneous, confirms that PIPS occurs in this system. After photopolymerization, the control A₇₀X₃₀P₀ sample is macroscopically homogeneous with yellow-tinted transparency (Fig. 3ai). Initial addition of PMMA (5 wt%, e.g. A₇₀X₃₀P₅) changes the sample appearance dramatically. A₇₀X₃₀P₅ is defined by a chalky, opaque white phase that is uniform throughout the macroscopic volume. Increasing the PMMA loading to 10 wt% (A₇₀X₃₀P₁₀) results in a marbling appearance (Fig. 3cii). At this loading level, the sample is no longer uniform in appearance, indicating that distinct macroscale domains have formed, however, their spatial distribution is irregular. The transparent, yellow-tinted domains appear like those observed in the control comonomer sample and the opaque white domains appear like those observed in A₇₀X₃₀P₅. The maximum PMMA loading studied here, (e.g., 20 wt%, A₇₀X₃₀P₂₀) resulted in full phase separation, consisting of an exterior, yellow-tinted transparent region and an interior opaque white region (Fig. 3dii). The structure after polymerization of A₇₀X₃₀P₂₀ is of particular interest, as stark phase domains on the macroscale have yet to be reported in rapidly-forming, glassy phase-separated materials.

Fig. 3 By increasing the PMMA loading in the A₇₀X₃₀P_c system, the phase separated domains increase in size until reaching the macroscale. Bulk samples have a stark change in morphology (top row) with increasing PMMA fraction, starting with the transparent A₇₀X₃₀P₀ (ai) which transitions to contain an opaque white phase in samples A₇₀X₃₀P₅ (bi), A₇₀X₃₀P₁₀ (ci), and A₇₀X₃₀P₂₀ (di). Raman imaging confirms that the macroscopic observations are related to phase separation. Bright red regions indicate high concentrations of nitrile functional groups. In A₇₀X₃₀P₀ (aii) and A₇₀X₃₀P₅ (bii), the uniform bright red throughout the entire cross section indicate domains rich in poly(acrylonitrile), containing a nitrile intensity of 50 or higher. A₇₀X₃₀P₁₀ (cii) and A₇₀X₃₀P₂₀ (dii) have domain segregation, with the regions of highest nitrile concentration located within the sample interior. These latter two samples exhibit lower total nitrile concentrations than the two former. All Raman analyses were conducted with the scanning laser perpendicular to sample cross-sections (e).

Analyzing the cross-section of the samples in Fig. 3 revealed that the opaque domains (observed in A₇₀X₃₀P₅, A₇₀X₃₀P₁₀ and A₇₀X₃₀P₂₀) had a rough, powdery texture similar to chalk. Meanwhile, the translucent domains (observed in A₇₀X₃₀P₀, A₇₀X₃₀P₁₀ and A₇₀X₃₀P₂₀) were glassy, hard, and smooth with no discernible texture. This noted rigidity in the translucent domains and lack of such in the opaque domains indicate a difference in the relative degree of crosslinking present in those domains of the sample. Additionally, based on light scattering interactions, the opacity of the powdery region indicates a degree of microscale phase separation is likely occurring within these domains. These observations signify that two scales of phase separation occurring within a single sample: macro- and microscale.

Raman spectroscopy confirms the suspected compositional gradients made from optical observation of the A₇₀X₃₀P_c samples with varied PMMA loadings, particularly on the macroscale. 2D maps of the nitrile content were constructed from the exposed cross section of each sample (Fig. 3e), enabling classification of macroscopic domains as nitrile-rich or nitrile-poor. The nitrile functionality was chosen for mapping since it is a functional group unique to the acrylonitrile (AN) monomer within the resin system. In the Raman maps, regions with bright red indicate domains rich in poly(acrylonitrile) and thus dark regions correspond to domains with relatively lower local concentrations. A₇₀X₃₀P₀ and A₇₀X₃₀P₅ samples exhibit uniform concentrations of the nitrile group distributed across the entire sample volume (Fig. 3aii and bii). It is of note that though there are similar concentrations of C≡N throughout these two samples, they have very different optical appearances, transitioning from completely clear to opaque with the initial addition of PMMA, which may indicate microscale variations within the sample volume. With higher PMMA loadings in A₇₀X₃₀P₁₀ and A₇₀X₃₀P₂₀, more distinct chemical segregation is apparent from the Raman maps. The dramatic interior/exterior bulk phase separation noted in A₇₀X₃₀P₂₀ is verified to consist of two bulk domains with varying nitrile content (Fig. 3dii). The interior has a higher local concentration of nitrile groups and it is thus assumed that the acrylate species preferentially migrate to the glass mold interface. Additional experiments discussed in the next section leverage this observed chemical segregation to explicitly direct where domain formation occurs by changing the mold configuration used during curing.

Chemical segregation on a macroscopic length scale, as observed in Fig. 3d for the A₇₀X₃₀P_c system, is of particular note since prior studies have emphasized phase separation-driven polymer morphologies in submicron systems, primarily thin films with thicknesses less than 0.1 mm.^16,33,34,44 Within these submicron examples, the difference in interfacial energies during fabrication, such as glass vs. exposed atmosphere, allows for a steep chemical gradient due to the extremely small distance between the two employed interfaces. For example, Vitale et al.³³ demonstrated stark contrast in wettability on differing faces of photopolymerized films (10–200 μm) due to the segregation of siloxane oligomers throughout the film thickness. The results in Fig. 3 highlight how similar guiding principles, e.g. variations in surface energy, can be leveraged in larger samples, with thicknesses on the order of 10² μm. Specifically, the two prominent domains observed in A₇₀X₃₀P₂₀, nitrile-rich interior and nitrile-poor exterior, are visible to the eye without the need of microscopy. Leveraging PIPS allows this patterning to span a sample volume of multi-millimeter thicknesses, which has yet to be highlighted.

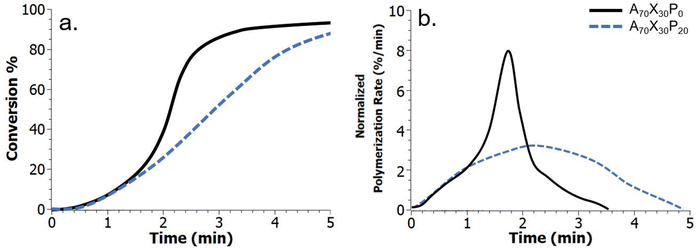
The observed macroscale phase segregation, particularly at higher PMMA loadings (e.g., A₇₀X₃₀P₂₀) is significantly influenced by the kinetic environment. Specifically, macroscale phase separation is enabled by a decreased polymerization rate and delay in autodeceleration, predominantly due to the addition of the inert PMMA additive, which can be tracked via FTIR spectroscopy (Fig. 4). Real-time kinetic data including extent of double bond conversion and overall polymerization rate (R_p), which is taken as the first derivative of the conversion data, were characterized for both the control comonomer matrix – A₇₀X₃₀P₀, and the A₇₀X₃₀P₂₀ resin with macroscale phase separation. In this analysis, R_p was normalized by initial double bond concentration to account for the reduction in overall concentration of double bonds within the polymerizing system due to the introduction of inert PMMA. In the control comonomer resin A₇₀X₃₀P₀, an initial sharp increase in double bond conversion, and thus an associated increase in R_p is observed throughout the first 1.5 minutes of polymerization. After this period, R_p decreases for the remainder of the reaction and the double-bond conversion eventually plateaus at approximately 90% (solid black series, Fig. 4b). This is consistent with autoacceleration behavior of free-radical photopolymerizations. Analysis of PMMA-modified resins (e.g., A₇₀X₃₀P₂₀, dashed blue series Fig. 4) reveals a similar period of increasing R_p during the first minute of UV exposure. However, after 1 min the R_p behavior of A₇₀X₃₀P₀ and A₇₀X₃₀P₂₀ deviates. Ultimately, A₇₀X₃₀P₂₀ has a longer period of autoacceleration (e.g., increasing R_p); an overall decrease in polymerization rate is not observed until much later (roughly 2.2 min) (Fig. 4b). This onset of autodeceleration, e.g. the period during the reaction where R_p steadily decreases, provides critical insight on diffusivity within the reactive medium. At the onset of autodeceleration, diffusion of all reactive species is significantly hindered, which manifests as a steady decline in observed reaction events.

Fig. 4 The reaction kinetics for A₇₀X₃₀P_c systems are characterized by monitoring the disappearance of the C=C bond peak at 6165 cm⁻¹ for the duration of the 0.1 W cm⁻² UV cure (a). A sharp Sshaped curve is observed in the Conversion % vs. time plot for A₇₀X₃₀P₀. Addition of PMMA in the A₇₀X₃₀P₂₀ resin results in a slower reaction. The curve shape is consistent with autoacceleration behavior characteristic of the acrylate crosslinker used. The rate of polymerization (R_p) is obtained by taking the derivative of the Conversion % plot with respect to time, and the rate is normalized by the initial C=C concentration (b). The maximum polymerization rate is reached earlier for the non-PIPS control resin, which also has a larger observed rate maximum. The overall rate is halved for A₇₀X₃₀P₂₀, and the rate maximum and onset of deceleration occurs later in the reaction timeline.

Taking the maximum in R_p as the onset of deceleration,^45,46 we estimate this transition occurs at 1.7 and 2.2 minutes after initial UV exposure for the A₇₀X₃₀P₀ and A₇₀X₃₀P₂₀ resins, respectively. This delay in onset of viscous and diffusive limitations within the reactive medium supports the stark phase segregation observed in Fig. 3d; there is ample time for phase separating domains to diffuse within the bulk system to minimize free energy prior to becoming kinetically trapped. It is important to note that the free-radical photopolymerizations employed here are exothermic in nature, impacting the morphology by both decreasing viscosity, which improves diffusion of components, and increasing mixing through the inverse relationship of temperature with the Flory–Huggins mixing parameter. The thermal evolution for select resins was characterized during curing and confirms the exothermic nature of the polymerizations (Fig. S4, ESI†). However, the results also highlight that a larger exotherm evolves in the control resin, A₇₀X₃₀P₀, which experiences a larger maximum temperature (T_max) during polymerization initiated by incident irradiation of 0.1 W cm⁻². If phase domain formation was merely dictated by changes in the viscosity and the associated impact on diffusivity of immiscible domains in a polymerizing resin, one would expect a higher exotherm in samples with distinct, macroscale phase domains (e.g. PMMA-modified samples). However, since a larger exotherm arises in the non-phase separated control – A₇₀X₃₀P₀, it is clear that other factors, including the evolution of R_p plays a significant role. It is difficult to fully resolve the two competing factors of viscosity and thermodynamic mixing (Flory–Huggins parameter) when considering the influence of temperature generated by the reaction, especially given that the Flory–Huggins parameter is also constantly changing due to propagation and termination events that impact molecular weight of resin constituents.

It is expected that other phase separating resins, i.e. A₇₀X₃₀P₅ and A₇₀X₃₀P₁₀, also have a delayed onset of autodeceleration. However, this was not probed directly as the phase separation in A₇₀X₃₀P₅ and A₇₀X₃₀P₁₀ resins resulted in samples that become IR opaque, thus giving only partial in situ FT-IR conversion curves (Fig. S5, ESI†). Cessation of IR transmission indicates the formation of domains capable of scattering IR irradiation. For both A₇₀X₃₀P₅ and A₇₀X₃₀P₁₀ samples, the IR signal from the measured 1620 nm wavelength (corresponding to the C=C vinyl peak at 6165 cm⁻¹) stops approximately 1.4 minutes after initial UV light exposure, indicating that phase separation is ongoing at least by 15% conversion (Fig. S5a, ESI†) This is important, as it indicates that phase segregation on the microscale is ongoing prior to any observable onset of autodeceleration (e.g., decrease in R_p). An important distinction here is that phase domains of size below this threshold likely form at earlier timepoints in the reaction, but are not fully detected with this specific wavelength of irradiation. Even though complete, dynamic in situ FTIR measurements were not possible for A₇₀X₃₀P₅ and A₇₀X₃₀P₁₀, the extent of conversion for these two systems can still be estimated via gravimetric analysis. In brief, cured samples were placed in toluene for 2 days and dried, and the associated change in mass was recorded (Table S1, ESI†), yielding 75% and 71% conversion, respectively. This was also performed for the A₇₀X₃₀P₀ and A₇₀X₃₀P₂₀ resins, with final conversions matching those recorded from FT-IR (Fig. 4). The non-monotonic nature of these extents of conversion is related to the viscosities of the A₇₀X₃₀P_c resins. Formulations with higher initial viscosities enhance autoacceleration and thus enable higher extent of conversion, which is observed with A₇₀X₃₀P₂₀ (Table 2).

To address the impact of this developing opacity on the photopolymerization, and it's associated impact on the resulting phase domains, PIPS resins were optically monitored throughout curing with subsequent video analysis in ImageJ to relate opacity and polymerization rate (Fig. S6, ESI†). For samples A₇₀X₃₀P₀ and A₇₀X₃₀P₂₀, it has already been established that R_p is roughly the same at the beginning of the polymerization and these two curves do not deviate until after 1.1 minutes of UV exposure (Fig. 4b). However, characterization of the optical evolution during polymerization reveals that the onset of optical opacity for A₇₀X₃₀P₂₀ occurs between 0.28 and 0.35 minutes (a similar onset in opacity is observed for A₇₀X₃₀P₅ and A₇₀X₃₀P₁₀, see Fig. S6, ESI†). Since R_p evolution does not deviate between the control comonomer system (A₇₀X₃₀P₀) and samples undergoing PIPS (such as A₇₀X₃₀P₂₀) during this initial period of increasing opacity (first 1.5 mins of polymerization), we conclude that the opacity is not a significant hindrance on the photopolymerization of these resins. Furthermore, given the rapid onset of opacity (e.g. slope of the absorbance data at the onset of opacity), we suspect that phase separation arises from an unstable state and follows the spinodal decomposition mechanism. This data does not point to a steady and consistent growth of scattering domains that would be expected from a nucleation and growth process.

To determine the influence of PMMA addition on the free energy state of each of the PIPS resins, theoretical estimates of each systems’ ΔG_mix was performed (Table S2 and Fig. S7, ESI†). This was achieved by calculating the derivative of ΔG_mix from (eqn (1)) at multiple points throughout the polymerization using estimations provided by the energy of cohesion for the developing molecules, with further details found in the Supplemental.^47–50 The difference in 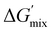between the A₇₀X₃₀P_c resins is minimal when tracking the changing favorability for phase separation, particularly at high degrees of polymerization. Given that molecular weight builds rapidly in free-radical network polymerizations, the observed similarities in 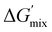further emphasizes that the kinetic environment is a determining factor in the phase morphologies observed here.

3.2 Guiding domain formation though use of glass and steel molds

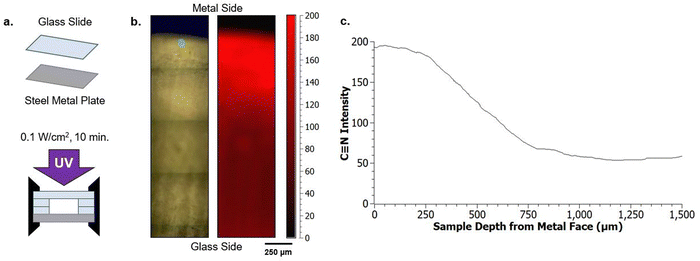
The phase separation behavior probed thus far uses glass as the surrounding mold, which results in nitrile-rich domains migrating towards the center of the sample. This migration, which reduces the contact between nitrile-domains and glass, becomes more significant with increasing PMMA loading (wt%) due to the reduced polymerization rate (Fig. 4b). To further explore the phase domain length scales possible from interface-driven phase segregation, curing molds were delibrately modified to have significant variations in surface energy within the mold geometry. Specifically, one substrate was modified to be a steel metal plate (Fig. 5a). This produced two types of interfaces: glass against resin and metal against resin.

Fig. 5 Preferential segregation of resin constituents is possible using substrates of differing surface energy, such as glass and stainless steel (a). After photopolymerization of A₇₀X₃₀P₅ samples (0.1 W cm⁻²) in this configuration, a 2D Raman map (b) reveals that nitrile functional group containing polymers preferentially migrate to the metal interface, leaving the majority of the acrylate-containing regions at the glass interface. This results in a 2 mm thick sample with two faces of different chemical character. (c) The gradual change in the nitrile intensity occurs over a 500 μm region between the maximum and minimum values, one quarter of the total 2 mm thickness.

With this modification, directional segregation during the photopolymerization process driven by the surface energy imbalance from the two different mold materials was leveraged to design particular compositional gradients. With two different interfaces present, one resin/glass and the other resin/metal, the final morphology adopted by a resin undergoing PIPS minimizes the interfacial free energy at both faces (Fig. 5b and c). This is demonstrated by the polymerization of A₇₀X₃₀P₅ in this configuration, where the separate mold materials further promote phase segregation and drive macroscale phase separation. This is in stark contrast to that observed during polymerization of A₇₀X₃₀P₅ within a uniform curing mold (Fig. 3b). In the new configuration, the nitrile-rich domains are preferentially located near the metal interface (Fig. 5b), compared to being positioned in the center of the sample when only glass was used in the molds. This introduction of multiple interface types in the mold configuration serves as an additional driving force to promote phase separation.

This long-range phase segregation, which was not possible for the A₇₀X₃₀P₅ sample when cured in a uniform glass mold, is achieved through deliberate selection of the mold materials. Specifically, incorporating a contacting mold surface with a characteristic surface energy can direct segregation of phase domains to minimize overall free energy.^51,52 The surface energies (γ) of the two substrates (glass and steel) are sufficiently distinct, and they can be quantiatively determined using the OWRK model from water and toluene contact angles (θ) (eqn (3)).³⁸ With this approach, a linear regression is used to calculate the polar (γ^p) and dispersive (γ^d) parts of the total substrate surface energy using two reference liquids (water and toluene) with known polar (γ^p_L) and dispersive (γ^d_L) components. Using this method, untreated glass had a γ of 72.4 mJ m⁻², and the stainless steel a γ of 36.0 mJ m⁻² (Table 3). These γ values are consistent with previous reports (Fig. S8, ESI†).^53–58 The ratio between polar and dispersive components for the stainless steel and glass substrates are rather similar, with the greatest difference between these two substrates being the total net surface energy value. As such, the significant difference in total net surface energy suffices in driving phase segregation, not the specifics of polar vs dispersive character.

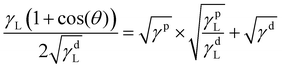Table 3 Substrate contact angle (water θ_w and toluene θ_t) and surface energy measurements (total surface energy γ, polar component γ^p, and dispersive component γ^d)

Substrate	θ w (°)	θ t (°)	γ (mJ m^−2)	γ ^p (mJ m^−2)	γ ^d (mJ m^−2)
Plain glass	9.8 ± 0.5	9.8 ± 1.4	72.4 ± 0.6	44.3 ± 0.4	28.1 ± 0.2
Stainless steel	68.0 ± 5.9	9.8 ± 4.3	36.0 ± 6.7	17.8 ± 5.1	18.2 ± 1.6

---

Given the surface energy calculations (Table 3), the compositional gradients observed in the A₇₀X₃₀P₅ sample (Fig. 5) are a result of minimizing system energy through selective migration of lower energy moieties to lower energy interfaces and likewise for higher energy moieties to higher energy interfaces. This phenomenon has previously been explored in both thin films from polymer melts and thin films from ongoing polymerization reactions.^59–61 Directing phase separation in each of these scenarios is accomplished via deliberate selection of polymer components and substrates used for forming the thin film. By using different monolayer coatings of a substrate, researchers Genzer and Kramer could switch which of two polymer phases migrated to a substrate face depending on which polymer/substrate monolayer combination minimized interfacial free energy.⁵⁹ These cited examples use the interplay between minimizing interfacial free energy and mixture phase separation to predict a polymer system's final morphology.

Here, nitrile groups migrating to the steel substrate while acrylate groups migrate to the glass substrate can be explained by the monomer surface energies relative to the two available mold interfaces. Pendant drop analysis of the individual monomers recorded γ of 9.5 mJ m⁻² for AN and γ of 26.4 mJ m⁻² for HDDA (Table 4). The lower energy AN monomer selectively diffuses to wet the lower energy metal substrate while the higher energy HDDA selectively diffuses to wet the higher energy glass substrate, forming a depthwise gradient in nitrile composition. The established chemical gradient also results in a mechanical gradient between the two sample faces. From characterization of the phases in Fig. 3, the nitrile-rich domains have a lower local modulus than the acrylate-rich domain. The acrylate crosslinker forms a more rigid network at the glass substrate interface compared to the monofunctional nitrile monomer. Compared to the results highlighted in Fig. 3, here a stark compositional gradient is achieved with a reduced inert additive loading (A₇₀X₃₀P₅) due to the influence of the differing surface energy environments imparted by the mold materials (steel and glass). This is important, as it broadens the range of resin compositions over which macroscale, stark gradients can be achieved. Furthermore, the gradual chemical gradient accompanied with a gradual modulus change (e.g. variation in cross-linking density) has potential benefits in applications where biomimetic stress dissipation is desired.

Table 4 Surface free energy measurements of resin comonomers

Comonomer	γ (mJ m^−2)
AN	9.5 ± 0.2
HDDA	26.4 ± 0.5

---

3.3 Tuning surface wettabilities as a function of PMMA loading

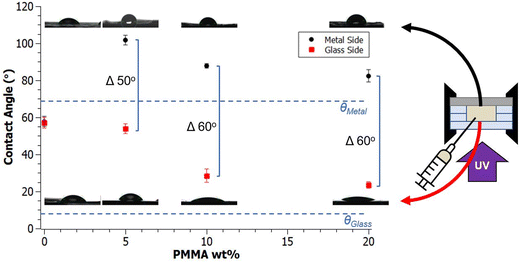
Introducing a mold interface with distinctly different surface energy from glass, such as metal explored here when curing A₇₀X₃₀P_c resins, drives the opaque nitrile-rich phase to the metal surface and the transparent nitrile-poor phase to the glass surface. In addition to the compositional gradients afforded by this design (Fig. 5b), this segregation also results in differing wettabilities on each face. As highlighted in Fig. 6, the measured contact angles of sample surfaces varied based on both the PMMA wt% loading and the surface energy of the mold interface (e.g., glass or metal).

Fig. 6 Chemical gradients arising from phase separation driven by intrinsic differences in substrate free energy results in an extreme difference in contact angles of the two sample faces. In the non-phase separating control A₇₀X₃₀P₀, the difference in surface energy of the two substrates did not impact the surface contact angle as it was equivalent on all faces of the sample (57°). With the introduction of PMMA and phase separation, stark contrasts in wettability are observed, with the interface contacting metal adopting a more hydrophobic character (and the glass interface hydrophilic). The metal-contacting surface of A₇₀X₃₀P₅ possessed the most hydrophobic behavior within this set of resin formulations. A slight decline is observed with increased PMMA loading as the contact angle for the metal interface dips below 90°. This reduction is also present on the glass interface, dropping from its initial 57° to 23° with increased PMMA wt%. Both of the two main sample surfaces trended towards the surface character of the mold substrates with increasing PMMA loading.

The control homopolymer network, A₇₀X₃₀P₀ had a consistent water contact angle of 57° measured on both faces of the sample. Given that no macroscale phase separation occurs in this resin formulation, a uniform contact angle on all sample faces is not surprising. As PMMA is introduced to the resin system, a stark difference in wettability between the two sample faces emerges. The nitrile-rich phase of A₇₀X₃₀P₅ had a water contact angle of 106° while the nitrile poor phase had a water contact angle of 53°. The two surfaces here straddle the transition from hydrophilic to hydrophobic behavior. A higher PMMA fraction in A₇₀X₃₀P₁₀ drops the recorded contact angle values, reducing the metal side by ∼20° and the glass side ∼30° relative to A₇₀X₃₀P₅. Increasing PMMA loading beyond 10 wt% in A₇₀X₃₀P₂₀ does not appear to change the contact angle values significantly compared to the previous additions of PMMA. A₇₀X₃₀P₅ possessed the most hydrophobic surface within the formulations explored.

Building upon this behavior, macroscale wettability design/patterning is possible via select application of steel plate sections on a glass substrate. This enables a single face of a sample to exhibit spatially-dependent wettability. Both hydrophilic and hydrophobic character can be imparted onto a given surface depending on the initial arrangement of the metal as depicted in Fig. 7. This mold arrangement illustrates that the phase separation in A₇₀X₃₀P_c is not limited to the z-direction depth, rather, discrete regions of a given face can have differing wettabilities.

Fig. 7 Surface energy gradients can be utilized to create local variations across a single interface, expanding potential future applications of using metal as a way of patterning wettability in polymer materials. This has been illustrated by creating striped line design using metal ribbons arranged in parallel on the bottom glass substrate before assembling the mold (a). After curing, phase segregation in the A₇₀X₃₀P_c sample here is not merely in the z-direction, but can be selectively engineered to guide chemical domain formation across a single surface (b).

The addition of PMMA produced a significant contact angle difference of ∼50°–60° between the two sample surfaces in the A₇₀X₃₀P_c PIPS systems. While changing the PMMA loading appears to shift the absolute value of the contact angles of the faces in contact with the glass and metal substrates, a similar difference between the two values is maintained. This demonstrates an opportunity to move the absolute values of the high and low contact angle values without sacrificing the distinct contrast in wettability between domains, maintaining a large window between the two faces. Increasing concentrations of PMMA lead to contact angles that trend towards the intrinsic contact angles of the glass and metal substrates, a phenomenon noted in literature focused on interfaces of polymer melts cast against different mold materials.⁴⁴

From the contact angle behavior observed in Fig. 6, a balance is observed between introducing PMMA to induce PIPS and the associated decrease in the fraction of copolymer network in the overall formulation based on this modification. Specifically, higher PMMA loading increases the thermodynamic driving force for phase separation, however this comes at the cost of available nitrile content per volume. It is established that phase separation of the A₇₀X₃₀P_c resins yield chemically distinct domains. Furthermore, the specific compositions and concentrations of these domains depends on the PMMA loading fraction, as highlighted in Fig. 3e–h. Given that the nitrile-rich domains are responsible for the sample's hydrophobicity, the variable composition of the nitrile-rich phase as a function of PMMA loading conditions results in variable wettability. Increased PMMA loading leads to nitrile-poor domains having a greater composition of unbounded free polymer chains. The increase in free polymer chains facilitates an increased ability of the nitrile-poor domain to reorient chains and side groups to better match the surface of the mold material, resulting in differing wettability (Fig. 6). Polymer rearrangement at different interfaces has been documented in previous literature to have a significant impact on the final surface character for a given sample.^44,62 A relevant example of this from Chihani et al. shows how the melt of a random copolymer containing both polar and non-polar functional groups had different ways of arranging itself at the interface depending on the polar character of said interface.

The ability of polymers present at the resin/mold interface to reorient in an attempt to increase compatibility between the sample and mold is supported by contact angle measurements taken 2 months after sample photopolymerization, removal from the curing mold, and storage under ambient conditions (Fig. S9, ESI†). After the elapsed time, samples with higher PMMA loading (e.g., A₇₀X₃₀P₁₀, A₇₀X₃₀P₂₀) have a larger increase between the initially measured contact angle associated with the glass substrate (e.g., hydrophilic side) and that measured 2 months later. For the A₇₀X₃₀P₂₀ sample, this change was 24° to 62°, and for A₇₀X₃₀P₁₀ a smaller change from 28° to 38° was observed. No significant change in the contact angle on the hydrophilic face was noted for A₇₀X₃₀P₅. During curing in the mold, we suspect that HDDA domains initially migrate to the glass interface and reorient functional groups for interfacial energy reduction, yielding a relatively low contact angle. However, once this glass substrate is removed after curing and the sample is left untouched for several months, a gradual reorientation that minimizes the surface energy of the sample/air interface occurs. The new contact angle values measured on the hydrophilic face after 2 months can be rationalized when considering that acrylic polymers, such as PMMA are known to have water contact angles around 70° to 90°, a range supported by both previous literature and our own measurements of a pure PMMA film.⁶³

At the same time, the contact angles for the hydrophobic faces (e.g. faces in contact with the steel substrate that are nitrile-rich) did not change for A₇₀X₃₀P₁₀ and A₇₀X₃₀P₂₀, but did for A₇₀X₃₀P₅ where the contact angle dropped from 102° to roughly 85°. Still, the contact angles of the nitrile-rich domains remained hydrophobic and did not revert to the highly hydrophilic wettability as would be expected of generic poly(acrylonitrile). This is most likely due to the presence of the chains of PMMA present in the nitrile-rich domains, able to maintain hydrophobicity.

This concept of environmentally-influenced surface energy is demonstrated here by uniting the measured surface properties with the distribution of nitrile and acrylate groups within the A₇₀X₃₀P_c system sample volumes (Fig. 5c and 6). While pure poly(acrylonitrile) is commonly though of as a more hydrophilic polymer and pure PMMA is commonly thought of as a more hydrophobic polymer, the polymerization environment can modify how these polymer surfaces present themselves. It is possible for the intrinsic surface behavior of these polymers to be influenced by the substrate material as shown in Fig. 6. Referring to the kinetics studies of this system in Fig. 4, in phase-separated systems there is an enhanced period for domain formation allowing developing polymers to adopt an energy-minimizing arrangement prior to being kinetically trapped by the crosslinked network.

4 Conclusions

In this work, macroscale heterogeneity from homogeneous starting resins is demonstrated in nitrile-acrylate photopolymerizing systems, forming domains of differing wettability bridged by a bulk chemical gradient. The network morphology and resulting surface properties can be tailored by varying the polymerization mold materials and chemical ratios within a four component resin system. No macroscale phase separation occurred in the control sample A₇₀X₃₀P₀, however, the addition of 5 wt%, 10 wt% and 20 wt% PMMA in the resins A₇₀X₃₀P₅, A₇₀X₃₀P₁₀, and A₇₀X₃₀P₂₀ caused photoinitiated PIPS to occur. This separation is due to the increase in ΔG_mix that occurs during the polymerization. The domains in A₇₀X₃₀P_c from PIPS were confirmed with optical microscopy and Raman spectroscopy, consisting of a transparent, glassy, nitrile-poor domain and an opaque, chalky, nitrile-rich phase. Under the highest PMMA loading condition, A₇₀X₃₀P₂₀, macroscale phase separation was observed, with the chalky nitrile-rich phase preferentially migrating to the center of the sample surrounded by the glassy nitrile-poor phase on the exterior at the interface between the sample and the glass molds.

Further experiments investigated the role of interfacial energies on resulting phase-separated morphology by modifying the mold materials used during curing. Differences in interfacial energies within the mold geometry provide an additional driving force to form distinct gradients via phase separation. Replacing one interface of the curing mold with a substrate of differing surface energy, such as stainless steel, spatially directed the resulting phase separation and created chemical gradients spanning 500 μm. In the case of A₇₀X₃₀P₅, the guided phase separation resulted in a hydrophobic face with a contact angle of 101° from the nitrile-rich phase at the metal interface and a hydrophilic face with a contact angle of 53° from the nitrile-poor phase at the glass interface. The placement of these domains is driven by mitigation of the interfacial energy, with the low surface energy acrylonitrile (γ = 9.5 mJ m⁻²) migrating to the low energy metal surface (γ = 36.0 mJ m⁻²) and the high surface energy 1,6-hexanediol diacrylate (γ = 26.4 mJ m⁻²) migrating to the high energy glass surface (γ = 72.4 mJ m⁻²). The relationship between PMMA loading and wettability properties is explained by recognizing two aspects of this resin system: (1) there is a delay between the onset of phase separation and onset of deceleration, enabling domains to migrate within the sample volume, and (2) polymers at the mold interfaces are capable of orienting themselves to increase compatibility between the resin sample and the glass or metal surface, resulting in samples with a contact angle difference of ∼50°–60° between its two faces. These two findings allow for increased control over the polymerization design. Systems can be engineered to have a lengthened period prior to autodeceleration to allow for domain coalescence and significant phase separation by increasing the inert additive fraction, as demonstrated in A₇₀X₃₀P₂₀ samples. Additionally, in systems where the delay is not as significant, changes in surface energy of the substrate can help further drive the phase separation as demonstrated in A₇₀X₃₀P₅ using multiple interfaces, facilitating development of macroscale domains.

Future implementation of this work has potential for streamlining surface patterning while simultaneously reducing energy and waste associated with templating materials. Steel can be reclaimed and reformed into sheets much easier compared to frequently-used crosslinked silicone polymer photomasks.^64–66 Using steel substrates as opposed to plastic photomasks can make the recycling and reuse of mold materials more efficient while still maintaining robust patterning abilities. The surface energies of the glass and metal used require no additional modification or functionalization to spatially direct bulk phase segregation. This approach serves as a facile method for developing macroscale chemical gradients across a range of wettability characteristics in a single polymerization procedure, without the need for separate steps of patterning and depositing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by start-up funds from Michigan State University. This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science user facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. Furthermore, Prof. Shiwang Cheng is acknowledged for insightful feedback on SAXS results and analysis.

References

1. S. C. Ligon-Auer, M. Schwentenwein, C. Gorsche, J. Stampfl and R. Liska, Toughening of photo-curable polymer networks: a review, Polym. Chem., 2016, 7, 257–286.
2. S. C. Leguizamon, J. Powers, J. Ahn, S. Dickens, S. Lee and B. H. Jones, Polymerization-Induced Phase Separation in Rubber-Toughened Amine-Cured Epoxy Resins: Tuning Morphology from the Nano-to Macro-scale, Macromolecules, 2021, 54(17), 7796–7807.
3. J. P. Gong, Why are double network hydrogels so tough?, Soft Matter, 2010, 6, 2583–2590.
4. I. Calvez, C. R. Szczepanski and V. Landry, Hybrid Free-Radical/Cationic Phase-Separated UV-Curable System: Impact of Photoinitiator Content and Monomer Fraction on Surface Morphologies and Gloss Appearance, Macromolecules, 2022, 3129–3139.
5. Z. Li, G. Wang, Y. Wang and H. Li, Reversible Phase Transition of Robust Luminescent Hybrid Hydrogels, Angew. Chem., 2018, 2(130), 2216–2220.
6. C. R. Szczepanski, T. Darmanin and F. Guittard, Spontaneous, Phase-Separation Induced Surface Roughness: A New Method to Design Parahydrophobic Polymer Coatings with Rose Petal-like Morphology, ACS Appl. Mater. Interfaces, 2016, 2(8), 3063–3071.
7. F. Abedin, Q. Ye, H. J. Good, R. Parthasarathy and P. Spencer, Polymerization- and solvent-induced phase separation in hydrophilic-rich dentin adhesive mimic, Acta Biomater., 2014, 10, 3038–3047.
8. L. H. Sperling, Interpenetrating polymer networks and related materials, Springer Science & Business Media, 2012.
9. C. R. Szczepanski and J. W. Stansbury, Stress reduction in phase-separated, cross-linked networks: influence of phase structure and kinetics of reaction, J. Appl. Polym. Sci., 2014, 10, 131.
10. E. Hasa, J. P. Scholte, J. L. P. Jessop, J. W. Stansbury and C. A. Guymon, Kinetically Controlled Photoinduced Phase Separation for Hybrid Radical/Cationic Systems, Macromolecules, 2019, 4(52), 2975–2986,  DOI:10.1021/acs.macromol.9b00177.
11. H. Nakanishi, M. Satoh, T. Norisuye and Q. Tran-Cong-Miyata, Generation and Manipulation of Hierarchical Morphology in Interpenetrating Polymer Networks by Using Photochemical Reactions, Macromolecules, 2004, 11(37), 8495–8498,  DOI:10.1021/ma048657i.
12. F. S. Bates and G. H. Fredrickson, Block copolymers-designer soft materials, Phys. Today, 1999, 52, 32–38.
13. L. Cheng, J. W. Simonaitis, K. R. Gadelrab, M. Tahir, Y. Ding and A. Alexander-Katz, et al., Imparting Superhydrophobicity with a Hierarchical Block Copolymer Coating, Small., 2020, 16(1), 1905509,  DOI:10.1002/smll.201905509.
14. M. Li and C. K. Ober, Block copolymer patterns and templates, Mater. Today, 2006, 9(9), 30–39.
15. M. Byun, W. Han, B. Li, X. Xin and Z. Lin, An Unconventional Route to Hierarchically Ordered Block Copolymers on a Gradient Patterned Surface through Controlled Evaporative Self-Assembly, Angew. Chem., Int. Ed., 2013, 1(52), 1122–1127,  DOI:10.1002/anie.201208421 Available from: .
16. N. Kimura, K. Kawazoe, H. Nakanishi and T. Norisuye, Influences of wetting and shrinkage on the phase separation process of polymer mixtures induced by photopolymerization, pubsrscorg, 2013. Available from: https://rsc.66557.net/en/content/articlehtml/2013/sm/c3sm51203g.
17. E. T. Jaynes, Gibbs vs. Boltzmann entropies, Am. J. Phys., 1965, 33(5), 391–398.
18. C. R. Szczepanski and J. W. Stansbury, Accessing photo-based morphological control in phase-separated, cross-linked networks through delayed gelation, Eur. Polym. J., 2015, 67, 314–325.
19. G. E. Molau, Heterogeneous polymer systems. III. Phase separation in styrene-acrylonitrile copolymers, J. Polym. Sci., Part B: Polym. Lett., 1965, 3(12), 1007–1015.
20. L. Tian, B. Li, X. Li and Q. Zhang, Janus dimers from tunable phase separation and reactivity ratios, Polym. Chem., 2020, 11(28), 4639–4646.
21. K. S. Anseth, C. M. Wang and C. N. Bowman, Reaction behaviour and kinetic constants for photopolymerizations of multi (meth) acrylate monomers, Polymer, 1994, 35(15), 3243–3250.
22. C. R. Szczepanski, C. S. Pfeifer and J. W. Stansbury, A new approach to network heterogeneity: polymerization induced phase separation in photo-initiated, free-radical methacrylic systems, Polymer, 2012, 53(21), 4694–4701.
23. C. R. Szczepanski and J. W. Stansbury, Modification of linear prepolymers to tailor heterogeneous network formation through photo-initiated polymerization-induced phase separation, Polymer, 2015, 6(70), 8–18.
24. T. Inoue, Reaction-induced phase decomposition in polymer blends, Prog. Polym. Sci., 1995, 1(20), 119–153.
25. A. S. Kulkarni and G. Beaucage, Reaction induced phase-separation controlled by molecular topology, Polymer, 2005, 46(12), 4454–4464.
26. A. Miserez, T. Schneberk, C. Sun, F. W. Zok and J. H. Waite, The transition from stiff to compliant materials in squid beaks, Science, 2008, 319(5871), 1816–1819.
27. J. D. Fox, J. R. Capadona, P. D. Marasco and S. J. Rowan, Bioinspired water-enhanced mechanical gradient nanocomposite films that mimic the architecture and properties of the squid beak, J. Am. Chem. Soc., 2013, 135(13), 5167–5174.
28. C. Sun and J. H. Waite, Mapping chemical gradients within and along a fibrous structural tissue, mussel byssal threads, J. Biol. Chem., 2005, 280(47), 39332–39336.
29. K. A. DeRocher, P. J. Smeets, B. H. Goodge, M. J. Zachman, P. V. Balachandran and L. Stegbauer, et al., Chemical gradients in human enamel crystallites, Nature, 2020, 583(7814), 66–71.
30. J. H. Waite, H. C. Lichtenegger, G. D. Stucky and P. Hansma, Exploring molecular and mechanical gradients in structural bioscaffolds, Biochemistry, 2004, 43(24), 7653–7662.
31. K. U. Claussen, T. Scheibel, H. W. Schmidt and R. Giesa, Polymer gradient materials: can nature teach us new tricks?, Macromol. Mater. Eng., 2012, 297(10), 938–957.
32. S. Suresh, Graded materials for resistance to contact deformation and damage, Science, 2001, 292(5526), 2447–2451.
33. A. Vitale, S. Touzeau, F. Sun and R. Bongiovanni, Compositional Gradients in Siloxane Copolymers by Photocontrolled Surface Segregation, Macromolecules, 2018, 51, 4023–4031.
34. Y. Gan, X. Jiang and J. Yin, Self-Wrinkling Patterned Surface of Photocuring Coating Induced by the Fluorinated POSS Containing Thiol Groups (F-POSS-SH) as the Reactive Nanoadditive, Macromolecules, 2012, 9(45), 7520–7526,  DOI:10.1021/ma301439g.
35. J. R. Rumble, CRC handbook of chemistry and physics, (Internet Version 2022), CRC Press, Taylor & Francis, Boca Raton, FL, 2022.
36. M. Minagawa, H. Kanoh, S. Tanno and M. Satoh, Glass-Transition Temperature (T_g) of Free-Radically Prepared Polyacrylonitrile by Inverse Gas Chromatography, 2. Molecular-Weight Dependence of Tg of Two Different Types of Aqueous Polymers, Macromol. Chem. Phys., 2002, 203(17), 2481–2487.
37. J. Michalsky, L. Harrison and W. Berkheiser III, Cosine response characteristics of radiometric and photometric sensors, State Univ. of New York, Albany, NY (United States). Atmospheric Sciences, 1992.
38. D. K. Owens and R. Wendt, Estimation of the surface free energy of polymers, J. Appl. Polym. Sci., 1969, 13(8), 1741–1747.
39. V. M. Litvinov and A. A. Dias, Real-Time NMR. How Fast Can We Do It?, Macromolecular Symposia, 2005, 230(1), 20–25,  DOI:10.1002/masy.200551137.
40. Z. Guo, H. Sautereau and D. Kranbuehl, Evidence for spatial heterogeneities observed by frequency dependent dielectric and mechanical measurements in vinyl/dimethacrylate systems, Polymer, 2005, 46(26), 12452–12459.
41. Y. Lin, E. Bilotti, C. W. Bastiaansen and T. Peijs, Transparent semi-crystalline polymeric materials and their nanocomposites: a review, Polym. Eng. Sci., 2020, 60(10), 2351–2376.
42. F. Di Lorenzo and S. Seiffert, Nanostructural heterogeneity in polymer networks and gels, Polym. Chem., 2015, 6(31), 5515–5528.
43. G. L. Batch and C. W. Macosko, Kinetic model for crosslinking free radical polymerization including diffusion limitations, J. Appl. Polym. Sci., 1992, 44(10), 1711–1729.
44. R. Cuthrell, Environment-influenced surface layer in polymers, J. Appl. Polym. Sci., 1967, 11(8), 1495–1507.
45. C. S. Pfeifer, N. D. Wilson, Z. R. Shelton and J. W. Stansbury, Delayed gelation through chain-transfer reactions: mechanism for stress reduction in methacrylate networks, Polymer, 2011, 52(15), 3295–3303.
46. L. G. Lovell, J. W. Stansbury, D. C. Syrpes and C. N. Bowman, Effects of composition and reactivity on the reaction kinetics of dimethacrylate/dimethacrylate copolymerizations, Macromolecules, 1999, 32(12), 391321.
47. Z. Wang, Q. Ran, R. Zhu and Y. Gu, Reaction-induced phase separation in a bisphenol A-aniline benzoxazine-N,N-(2,2,4-trimethylhexane-1,6-diyl)bis(maleimide)-imidazole blend: the effect of changing the concentration on morphology, Phys. Chem. Chem. Phys., 2014, 3(16), 5326–5331.
48. D. W. V. Krevelen and K. T. Nijenhuis, Cohesive Properties and Solubility, Elsevier, 2009, pp. 189–227.
49. J. A. Lanasa, A. Neuman, R. A. Riggleman and R. J. Hickey, Investigating Nanoparticle Organization in Polymer Matrices during Reaction-Induced Phase Transitions and Material Processing, ACS Appl. Mater. Interfaces, 2021, 9(13), 42104–42113.
50. J B, EH I, EA G, editors. v11 Exhibit 1011-Polymer Handbook. vol. 89. 4th edn. John Wiley Sons Inc, 2003.
51. S. Ghaffari, P. K. Chan and M. Mehrvar, Long-range surface-directed polymerization-induced phase separation: a computational study, Polymers, 2021, 1(13), 1–19.
52. M. Tabatabaieyazdi, P. K. Chan and J. Wu, A computational study of long range surface-directed phase separation in polymer blends under a temperature gradient, Comput. Mater. Sci., 2016, 1(111), 387–394.
53. D. Brian and M. Eslamian, Analysis of impact dynamics and deposition of single and multiple PEDOT:PSS solution droplets, Exp. Fluids, 2019, 60, 1–15.
54. K. Mader-Arndt, Z. Kutelova, R. Fuchs, J. Meyer, T. Staedler and W. Hintz, et al., Single particle contact versus particle packing behavior: model based analysis of chemically modified glass particles, Granular Matter, 2014, 16, 359–375.
55. M. Kruszelnicki, I. Polowczyk and P. B. Kowalczuk, Control of glass surface wettability via esterification with n-alkyl alcohols, Physicochem. Probl. Miner. Process., 2022, 58, 145147.
56. S. Tang, O. J. Kwon, N. Lu and H. S. Choi, Surface free energy changes of stainless steel after one atmospheric pressure plasma treatment, Korean J. Chem. Eng., 2004, 21, 1218–1223.
57. J. Heil, B. Mohammadian, M. Sarayloo, K. Bruns and H. Sojoudi, Relationships between surface properties and snow adhesion and its shedding mechanisms, Appl. Sci., 2020, 10(16), 5407.
58. L. Boulange-Petermann, J. C. Joud and B. Baroux, Wettability parameters controlling the surface cleanability of stainless steel. Contact angle, wettability and adhesion Leiden, VSP, 2008, pp. 139–151.
59. J. Genzer and E. J. Kramer, Wetting of substrates with phase-separated binary polymer mixtures, Phys. Rev. Lett., 1997, 78(26), 4946.
60. T. Murashige, H. Fujikake, H. Sato, H. Kikuchi, T. Kurita and F. Sato, Polymer wall formation using liquidcrystal/polymer phase separation induced on patterned polyimide Films, Jpn. J. Appl. Phys., 2004, 43(12B), L1578.
61. N. Kimura, K. Kawazoe, H. Nakanishi, T. Norisuye and Q. Tran-Cong-Miyata, Influences of wetting and shrinkage on the phase separation process of polymer mixtures induced by photopolymerization, Soft Matter, 2013, 9(35), 8428–8437.
62. T. Chihani, P. Bergmark and P. Flodin, Surface modification of ethylene copolymers moulded against different mould surfaces-1. Surface enrichment by functional groups, J. Adhesion Sci. Technol., 1993, 7(4), 327–341.
63. D. Briggs, H. Chan, M. Hearn, D. McBriar and H. Munro, The contact angle of poly(methyl methacrylate) cast against glass, Langmuir, 1990, 6(2), 420–424.
64. P. Zheng and T. J. McCarthy, Rediscovering silicones: molecularly smooth, low surface energy, unfilled, UV/vis-transparent, extremely cross-linked, thermally stable, hard, elastic pdms, Langmuir, 2010, 26(24), 18585–18590.
65. B. Rupasinghe and J. C. Furgal, Full circle recycling of polysiloxanes via room-temperature fluoride-catalyzed depolymerization to repolymerizable cyclics, ACS Appl. Polym. Mater., 2021, 3(4), 1828–1839.
66. G. Parker, Encyclopedia of materials: science and technology, Elsevier, 2001.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01528a

---