Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dynamics of individual inkjet printed picoliter droplet elucidated by high speed laser speckle imaging†
Riccardo
Antonelli
a,
Remco
Fokkink
a,
Joris
Sprakel
b and
Thomas E.
Kodger
 *a
*a
aPhysical Chemistry and Soft Matter, Wageningen University & Research, Stippeneng 4, Wageningen, The Netherlands. E-mail: thomas.kodger@wur.nl
bLaboratory of Biochemistry, Wageningen University & Research, The Netherlands
First published on 8th February 2024
Abstract
Inkjet printing is a ubiquitous consumer and industrial process that involves concomitant processes of droplet impact, wetting, evaporation, and imbibement into a substrate as well as consequential substrate rearrangements and remodeling. In this work, we perform a study on the interaction between ink dispersions of different composition on substrates of increasing complexity to disentangle the motion of the liquid from the dynamic response of the substrate. We print three variations of pigmented inks and follow the ensuing dynamics at millisecond and micron time and length scales until complete drying using a multiple scattering technique, laser speckle imaging (LSI). Measurements of the photon transport mean free path, l*, for the printed inks and substrates show that the spatial region of information capture is the entire droplet volume and a depth within the substrate of a few μm beneath the droplet. Within this spatial confinement, LSI is an ideal approach for studying the solid–liquid transition at these small length and time scales by obtaining valid g2 and d2 autocorrelation functions and interpreting these dynamic changes under through kymographs. Our in situ LSI results show that droplets undergo delamination and cracking processes arising during droplet drying, which are confirmed by post mortem SEM imaging.
Ink-jet printing is probably the most widespread and versatile technological application based on microfluidics1–3 as it is an extremely adaptable technique, which besides the common everyday application of printing documents on paper, can serve numerous purposes in fundamental research. Scientists have used this technique for printing DNA,4 cells and living tissues,5 electrical circuits,6 transistor,7 solar panels and much more.7–10 This technique allows the printing of thousands of very small picoliter-sized ink droplets per second, reaching high performances in resolution and color fidelity. Inks are multi-component colloidal dispersions, usually containing water or some other suspending solvent, colloidal pigment particles, colloidal latex particles as film formers, glycerol as a drying modifier, surfactants as stabilizers, rheology modifiers, and wetting agents.11,12 With this complex composition, the ink performance in terms of uniform droplet spreading and drying during inkjet printing is difficult to predict. Additionally, this predictability is deeply affected by the widely varying substrates used for printing; these are often porous, such as paper or fabric, and thus imbibe the fluid and a fraction of the solid particles depending on their porosity and wettability. However, when new inks are developed or new substrates tested, problems occur in the performance of the final product including unwanted droplet spreading leading to loss of print resolution, full substrate imbibement leading to loss of coloration, and incomplete ink latex coalescence leading to poor mechanical stability on the substrate.
While the fluid dynamics of droplet formation in the inkjet nozzle have been studied in detail,3,13 much less is known what happens to the droplet after impacting a substrate and drying. Experimentally observing and quantifying how picoliter droplets evolve in the micro-, milli-, to seconds after impacting the surface remain challenging due to the small dimensions and the high temporal evolution at which the drying process occurs. For this reason, the majority of research is focused on numerical simulation and theoretical studies on drop formation, involving complex fluid physics calculations.14,15 While such studies have elucidated the complexity of this process, there are inherent assumptions in terms of substrate homogeneity and often difficult to interpret geometric boundary conditions, such as contact line pinning.16–18
An experimental technique that could provide picoliter dynamical information is laser speckle imaging, or LSI, the spatially-resolved, i.e. imaging technique, equivalent of diffusing wave spectroscopy (DWS).19 LSI has been used mostly in the medical field, for example, to monitor blood flow in tissues20 or in the brain,21,22 and in some cases it has been used as a complementary technique to Doppler echo scans for quantitative fluid velocimetry.23,24 More recently, LSI has been developed outside of the medical field being applied in a variety of material science experiments25–27 including studies on film formation and cracks propagation in paints, droplets, and other liquid to solid transitions. In these works, the authors use LSI to generate quantitative data on the internal dynamics and their associated timescales, in these complex composite material systems. In other works, LSI has been used to study fracture initiation in soft solids and the dynamics of thin (10 μm) films of turbid media.26,28 LSI has also been used in the field of art painting restoration, to quantify the plasticizing effects that varnish removal operations have on the underlying oil painting layers.29 In this last case, l* ranges from only 7 to 21 μm, which is comparable to the length scale of ink-jet printed droplets.
In this work, we explore the use of LSI to resolve this challenge, by using high speed laser speckle imaging (HS-LSI)30 to quantify the internal dynamics of picoliter droplets immediately after they impinge on a substrate. With HS-LSI, we record time-series of 2D speckle patterns which contain information on the colloidal dynamics occurring within the ink and the fiber swelling dynamics in the substrate. To disentangle these signals, we gradually increase the complexity of the experiment by printing both water and pigmented inks on both non-adsorbing and non-swelling substrates, and on real paper substrates which imbibe the water and undergo fiber swelling. We show that speckle motion after printing is observed in all cases, notably also in the case of water printed on Teflon, where, surprisingly the motion occurs due to a change in droplet interface shape. Interestingly, we also observe ink cracking and substrate delamination events with HS-LSI which occur in situ during the droplet consolidation and confirmed by SEM.
1 Materials and methods
For the present study, three simplified commercial inks were supplied by Canon production printing and labelled as A, B and C. In these series of experiments, all inks contained the same latex particles. All inks were printed on five different substrates of increasing complexity discussed below. The composition of the inks can be found in Table S1 in the ESI.† MilliQ water droplets are used as a control reference.1.1 Transport mean free path, l*
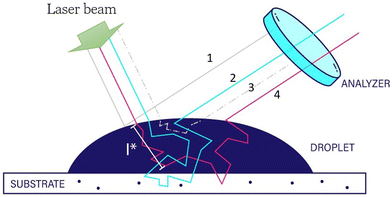
A key parameter when utilizing multiple scattered light is the photon transport mean-free path, l*; this is especially in the case of experiments on thin samples. This parameter, and how it changes within time, correlates with the physical length into the sample that light can explore by multiple scattering. When the sample thickness is smaller than l*, then the light cannot be considered to be in the multiple scattering regime, and cannot be assumed to take diffusive paths, which is a crucial condition for LSI experiments, potentially leading to misinterpretation of the 2D speckle image. Crucially, l* is a scalar quantity that expresses the extent of the multiple scattering in a material.19,31 It expresses the distance photons travel before their original orientation is randomized, which depending on the material, can range from several millimeters for only mildly opaque materials down to single microns for highly scattering matrices.32 The magnitude of l* depends on the size of the scatterers, their concentration, their spatial organisation, and the refractive index contrast between scatterers and surrounding medium. It also depends on polarization effects of the scatters, if their optical properties are not isotropic, such as when they are formed from crystalline polymers. Since l*, cannot be accurately calculated a priori for composite materials due to the large variety of factors that contribute, and knowledge of its value is crucial for the quantitative interpretation of multiple scattering experiments, it is essential to measure l* for each sample studied.Therefore, following the procedure reported in ref. 19, we built an instrument in order to evaluate this parameter. The setup consist of a laser source generating a coherent beam impinging on the sample of known thickness L, and unknown l*. A single mode fiber optic collectes photons in a transmission orientation and guides photons to a PMT to record the intensity. An analyzer is placed in cross scheme to the laser to ensure only multiply scattered photons are measured. The number of photons that arrive to the detector, measured as normalized intensity, is related to the mean free path l* of the light inside the material. It has been demonstrated that the transmitted intensity and l* parameter, when light absorption is negligible, are related through the equation:19,33–35
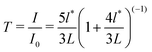 | (1) |
Therefore, by using the same optical/geometrical components among different samples, an unknown l* value may be calculated when the transmission light intensity, the sample thickness L, and l* are known for different samples. A sample of known l* is used as a reference: a 1 wt% aqueous polystyrene dispersion of precisely 400 nm in diameter, with polydispersity <1%, (NIST standard from Duke Scientific). The sample appears of white in color and does not absorb the incident laser wavelength of 532 nm. The l* of this particular sample has being studied by other authors.36,37
With this setup, l* is measured for both liquid and solid samples. For inks, l* is measured to be ∼5–8 μm and l* ∼ 10 μm in the case of solid samples, which here serves as printing substrates. During inkjet printing, a precise volume of 10 pL is generated corresponding to, based on the calculation of a hemispherical cap of a droplet assuming a contact angle of 90 degrees, a radius, r = 17 μm. This length implies that in principle, LSI could be applied to the scenario of picoliter droplets, as r > l*, remaining just within the diffusing wave approximation. Photons may also be scattered by the underlying substrate, yet not contributing to decorrelation as the substrate is not dynamic.
When light impinges on a resting droplet, a fraction of the laser light explores at least one or more l* lengths given the magnitude of l*. We have observed that when an ink film of 150 μm thickness dries, l* initially decreases faster than mass loss, typically reaching a final value 2.5 times smaller; for ink A, initially l* = 5.1 μm ± 0.9 which reduces to l* = 1.95 μm when fully dry after 6000 seconds. We assume that this dynamic range in l* also occurs for picoliter droplets, however, with decreased time scales due to increased drying rate.
1.2 LSI and printing setup
A laser speckle imaging setup was mounted on a custom made ink-jet printer, as described in detail elsewhere.30 A high-speed camera (Fastec Hi-Spec1) and illuminating laser, operating at 200 mW, was located above a commercial print-head (Fujifilm Dimatix DMC-11610) which moved at the linear velocity of 1 m s−1 over the sample holder consisting of a thin steel plate with a 2 cm circle hole within which the ink was printed onto chosen substrate held flat and fixed in space. A series of picoliter droplet were generated, using a computer programmed pulse sequence, falling toward the substrate; given the physical dimensions and translational velocity of the print-head, data recording began after the print head cleared the impinging laser path, which occurred 110 ± 10 ms after droplet release. The ink droplet was then illuminated with 200 mW of coherent green laser light at 532 nm. The photons impinge and explore the sample and eventually, after having travelled inside the ink and substrate a distance![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (3l*), they are scattered enough times to be considered to be in the multiple scattering regime. If there was no motion inside the sample, the resulting speckle patterns were static, i.e. they do not change over time. By contrast, due to internal motion inside the droplet and substrate, the speckle pattern fluctuated in both space and in time. The emerging speckles patterns were recorded by a high-speed camera at 2000 fps. Even though, the camera was capable of higher full speed capacities, a faster acquisition rate would require a higher intensity laser light, resulting in a temperature of the sample >35 °C causing enhanced drying not consistent with commercial printing conditions.
(3l*), they are scattered enough times to be considered to be in the multiple scattering regime. If there was no motion inside the sample, the resulting speckle patterns were static, i.e. they do not change over time. By contrast, due to internal motion inside the droplet and substrate, the speckle pattern fluctuated in both space and in time. The emerging speckles patterns were recorded by a high-speed camera at 2000 fps. Even though, the camera was capable of higher full speed capacities, a faster acquisition rate would require a higher intensity laser light, resulting in a temperature of the sample >35 °C causing enhanced drying not consistent with commercial printing conditions.
A key component of the optical system is a polarizer placed in the analyzer position in front of the high-speed camera, which is set crossed polarization with respect to the laser beam. This analyser, especially for experiments performed in this backscattering LSI geometry is fundamentally important to block photons that have been reflected from the surface, or have scattered an insufficient number of times to lose their initial polarization, as shown in Fig. 1. This ensures that the majority of light collected by the camera is multiply scattered.26,32,38
Speckle patterns were saved and analyzed, using a custom-made MATLAB script, by means of a spatially averaged auto-correlation function. The auto-correlation function used in this work was d2(t, τ, x, y), since this form of correlation function performed better with respect to others considering the case of limited number of speckles within the limited spatial field of view:39
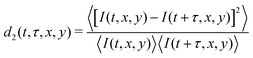 | (2) |
1.3 Inks and substrate
All simplified commercial inks contain the same weight fraction, 5 wt%, of yellow pigment and contain the same latex particles, at 12 wt%, which have a native glass transition temperature (Tg) of 55 °C, well above room temperature. This means that the latex particles are not likely to coalesce and form thin contiguous films during the experiment. Variations among the inks are found in the different concentrations of other components: water, glycerol, and surfactant; the bulk properties of the inks under study are shown in Table S1 of the ESI.† Ink A contains 82% of water, 1% of glycerol and no surfactant. Ink B contains additional glycerol at 17%. The net effect is an increasing of the bulk viscosity which likely slows down dynamics and evaporation processes. Ink C contains the same glycerol content as A, but 2% of the water is this time replaced by a commercial grade ink-jet printing surfactant. In addition to a change in surface tension from 68 mN m−1 of A to 30 mN m−1 of C, a secondary effect is that the Tg of the latex decreases from 55 to 25 °C degrees, which becomes around room temperature, allowing for partial coalescence of the latex particles. When the surface tension is lower, a droplet is expected to spread more on a given substrate, increasing the contact area,40,41 the length of the contact line between liquid and substrate; consequently, the evaporation rate of the volatile component of the liquid is also likely to increase.42,43Inkjet printing occurred with pure water and these three inks onto five different substrate: mylar, Teflon, glass frits, Teslin paper, and Sappi Magno paper. Mylar, also known as BoPET (biaxially-oriented polyethylene terephthalate) is a special type of stretched polyester film, which does not imbibe nor swell. The thickness is h = 500 μm. Teflon (PTFE) is a synthetic fluoropolymer of tetrafluoroethylene. The thickness is h = 3 mm. Glass frits (produced by Duran) are made of fused borosilicate glass powder with a certain particle size distribution resulting in a porous and imbibing, solid body. The nominal pore size for the frits is 1 to 1.6 μm, similar to commercial paper. The thickness is h = 4 mm. Teslin is a waterproof, single-layer, uncoated, porous, synthetic printing paper (produced by PPG Industries); thickness is h = 100 μm. Sappi Magno is a glossy cellulosic paper made up of fibers coated with layer of calcium carbonate of approximately 5 μm thick. The total thickness is h = 50 μm. Value of l* for some of these substrates are listed in Table 1. Importantly, while individual droplet drying occurrences are shown in subsequent figures, these constitute representative results as hundreds of individual droplet were analyzed for each ink–substrate combination.
| Sample | l* (μm) |
|---|---|
| Ink A | 6.5 ± 0.7 |
| Ink B | 5.1 ± 0.9 |
| Ink C | 7.9 ± 1.2 |
| Sappi Magno paper | 4.2 ± 0.2 |
| Teslin paper | 4.9 ± 0.2 |
| Mylar | 9.7 ± 0.5 |
Measurements of the contact angle for millimeter size droplets was performed to assess the wetting and spreading behaviour of the three inks over the five chosen substrates, as reported in Table S3 (ESI†).
Their behaviour, overall, was as expected: inks A and B exhibited similar contact angles on the all substrates with values similar to MilliQ water, implying that the surface tension among these fluids is similar. Teflon and Teslin are predominately hydrophobic substrates as the contact angles were greater than 90 degrees for water and inks A and B. As a consequence, the contact area between liquid and substrates was smaller, as is the contact line. As the evaporation rate is greater at the contact lines, a decreased evaporation rates for these two substrates is expected. Additionally, for ink A, the higher glycerol content drastically increases the viscosity and therefore spreading time-scale and evaporation rate, due to an interface enriched composition of glycerol which has been studied numerically and experimentally.14,44,45 For ink C which contains surfactant, the contact angle was consistently smaller, implying increased spreading on all of the considered substrates, therefore increased contact area and line, implying an increased evaporation rate.
2 Results and discussion
The complex drying dynamics of inkjet printed droplets is dependent on the physical interactions of ink with substrate where these substrates are often heterogeneous in structure and wettability on the length scale of the picoliter droplets. Cellulosic paper is a porous material with ink capable of both imbibing into the pores and swelling individual fibers. However, commercial printing occurs on many substrates including non-swelling synthetic paper and coated paper containing an inorganic, low permeability, glossy coating of typically calcium carbonate. To explore this substrate variety, multiple substrates are chosen for this study ranging in their properties. In addition to paper, mylar and Teflon are wetting and non-wetting impermeable substrates, respectively, therefore the only LSI detectable motion is given by the motion within the ink itself. Increasing substrate complexity, porous fused glass frits are used which constitute an immobile solid, wetting substrate, that allows imbibition but does not swell. Lastly, commercial papers with two trade names papers Teslin and Sappi Magno are used which both allow imbibition, with no fiber swelling and fiber swelling respectively. With this framework of multiple substrates, we aim to utilize LSI to untangle the dynamics after droplet formation arising from the liquid phase only, expected for the Mylar and Teflon, and within the underlying substrate, expected for porous glass frit, and papers, Teslin or Sappi Magno. Additionally, these latter substrates may also undergo internal structural rearrangements when imbibed, causing additional speckle decorrelation. These changes may alter the dynamic imbibition of the liquid component of the ink; disentangling the motion of the liquid from that of the substrate may be possible with LSI.2.1 Autocorrelation spatial maps – activation areas
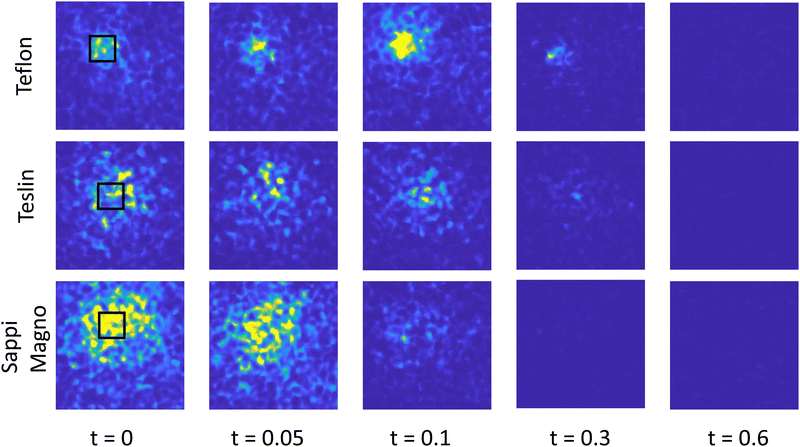
To separate these concommitant physical effects during printing, picoliter droplets of water and the three inks are printed on the selected substrates and the resulting spatially-varying dynamics recorded as a speckle pattern movie at 2000 frames per second. Each printing experiment, which last in general only a few seconds, produces 3 to 4 gigabytes worth of raw image data; the amount of information from each printing process is large and only partially discussed here.To visualize the printed area, in which motion is expected to occur, the auto-correlation function d2(t, τ, x, y) is used to generate spatial maps, averaging over 20 consecutive images, spaced at a fixed value of correlation time, τ = 0.01 s. In this framework, the spatial coordinates are retained at the price of visualizing results for a fixed correlation time; an example of this analysis is shown for ink C on Teslin paper in Fig. 2. From the known printing volume of ink, 10 pL, and the measured, albeit, macroscopic contact angle, there is an anticipated contact area for each ink–substrate combination. A small area of higher (red) d2 values corresponds well to the expected area of the liquid cap sitting on the substrate, and an external area of lower activity (yellow) which extends outside the physical droplet, surrounded by a very low activity (blue) corresponding to the bare substrate. For the non-imbibing substrates, namely Mylar and Teflon, this external region of low activation is smaller and less pronounced. For imbibing substrates, this external region of low activation outside the spherical cap of the droplet is likely due to the liquid imbibing into the substrate giving rise to structural rearrangement within the substrate. While these fiber rearrangements are small in magnitude, note that LSI is highly sensitive to displacements of nanometric amplitudes.26 Using these d2 images, the area is calculated of the high activation region for all the combinations of liquid and substrate, reported in the Table S4. The black square in Fig. 2, represents this area of the region of image/droplet used for all subsequent analyses.
2.2 Printing water and ink picoliter droplets
By averaging over the region-of-interest (ROI), using eqn (2), kymographs show how the droplet dynamics evolve over time, which visualize the dynamics as a function of sample age, t and correlation time, τ. The resulting d2(τ, t) kymograph images for combinations of water and inks, and substrates are shown in Fig. 3. A constant area of 25 × 25 μm among all the repetitions is used for all experiments despite the different substrate contact angles to ensure similar statistical averaging. The y-axis of the kymographs is the age of the droplet, where t = 0 is the time when we start the acquisition, while on the x-axis is the correlation time τ between frames. The magnitude of the d2(t, τ) scales by definition from 0 to 1 and represents the activity occurring within the area of averaging; the dynamics recorded are the cumulative activity of the fluid and the substrate. As l* of the ink, which is a measure of how much deep photons penetrate into the sample, is comparable to the radius of the droplet itself, the majority of d2(t, τ) activity arises from the motion of the liquid droplet, yet some scattering arises from the substrate. However, if the printed fluid contains little to no scattering particles, e.g. water, then the observed d2 arises from motions within the substrate. A limited series of experiments is shown in Fig. 3, consisting of water, and three inks A, B and C, interacting with three substrates; additional results for the other two substrates are shown in Fig. 3.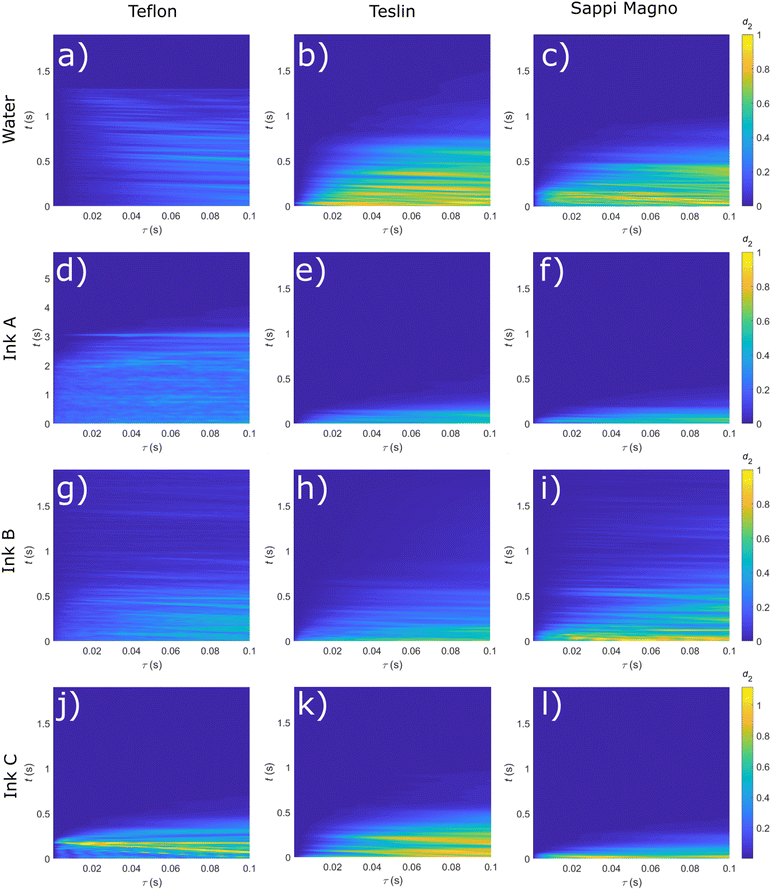 | ||
| Fig. 3 d 2 activity kymographs for combinations of inks and substrates with the experimental time, or age of the sample, versus the correlation time between frames, τ. Color bar is from 0 to 1, as the range that the d2 autocorrelation function. For the sake of space, we report only the results for three out of the five studied substrates with others shown in the ESI.† | ||
By printing water as a control fluid, the impinging laser beam has a negligible interaction as no scatterers are present in this liquid, thus, the biggest contribution to the observed motion arises from the movement within the substrate. As the water droplet is printed on the surface, the shape of droplet interface changes over time from a spherical cap shape to eventually reach a flat surface after evaporation if the contact line is pinned by the substrate.46,47 In this case, changes in the droplet shape could alter the angle on which the laser beam hits the surface resulting in a moving speckle pattern. Photons entering the air–water interface at an angle, traverse the droplet and impinge the sample. Some time later, when traversing the droplet, photons experience a different interface, resulting in a low frequency change in the recorded speckle pattern intensity. Note that this effect is also present in pigmented droplets, however, the scattering due to the pigment lessens the magnitude. The top panel of Fig. 3(a) shows this effect with Teflon being a non-absorbing, non-swelling substrate: the water printed on this material can only evaporate, thus all the calculated d2 motion originates from change in shape of the droplet. Additionally, a fast Fourier analysis of the d2 at 5 chosen values of τ is used to search for any periodicity in time, yet no such periodicity is observed. The predominately horizontal lines in Fig. 3(a) may represent the damped, but not periodic, oscillatory motion of the droplet after landing on the substrate. The d2 motion ends abruptly on Teflon, and likely occurs when the water is fully evaporated. The contribution of shorter correlation times, τ < 0.01, meaning fast motion, is absent for this sample, supporting the hypothesis that d2 motion arises from the relatively slow change in droplet shape rather than other effects. Additionally, the same abrupt end of motion also for water printed on Mylar surface, see Fig. S1 (ESI†).
By contrast, the d2 motion behavior does not end abruptly on paper. On Teslin and Sappi Magno paper, a high initial value for the d2 is seen, indicating higher activity in the region of averaging. This is followed by a gradual decrease in d2 activity compared to non-imbibing substrates, with d2 → 0 at t ≈ 0.6–0.7 s after printing as seen in of Fig. 3(b) and (c). At this age, most of the water has likely evaporated or imbibed. Additionally, the magnitude of d2 for τ < 0.01, meaning faster dynamics, are present for water printed on Sappi Magno paper, and still present, but with lower intensity on Teslin paper. The water printed on Teslin and Sappi Magno also imbibes into the substrate, causing motion of the substrate itself. Thus large magnitude of d2 is mostly caused by rearrangement of the fiber in the case of Teslin paper, and of the calcium carbonate coating in the case of the Sappi Magno.
Commercial inks nearly universally contain scattering particles, as pigment and as film-forming latex colloids, which directly effects the contribution of the speckle decorrelation. Additionally, these inks often contain higher concentration of glycerol, which decreases the drying rate and practically reduces both nozzle clogging and ink surface cracking.45 For a low glycerol content ink, ink A, the resulting d2 activity is shown in Fig. 3(d)–(g); note that for Fig. 3d, ink A, the timescale has been extended up to t = 6 s. This is the only ink–substrate combination of liquid and substrate in which d2 persists for extended t. This combination of ink composition and hydrophobicity for this substrate likely allows for an particulate film, or skin, to form on the interface of the droplet restricting the evaporation of the volatile ink components from droplet and substrate, retaining d2 motion inside the droplet to be present for longer t. By contrast, the same ink printed on Teslin and Sappi Magno papers imbibes into the substrate, accelerating the drying process, as seen in Fig. 3e and f. By adding glycerol to the ink, the resulting d2 motion for ink B has reduced evaporation rate, increasing the total time, t, during which d2 > 0.1 for all three substrate well over t > 1 s, as shown in Fig. 3(g)–(i). The magnitude of this increase in drying time, is up to five time longer as seen in Fig. 3(i) compared to Fig. 3(f); this result is consistent with previous studies that found a heterogeneous composition within the drying droplet, a glycerol rich interface which slows the drying rate, even with only a low fraction of added glycerol, only 17 vol%.44
In addition to glycerol, commercial ink also contain surfactants, which aid in increasing the ink wettability on the often heterogeneous-wetting substrate; surfactant and other additives also reduce the Tg of the latex. The resulting data for surfactant containing ink C is shown in Fig. 3j–l. Compared to inks without surfactant, the evaporation rate is increased with d2 decreasing to zero at t < 0.5 for all τ, as seen in Fig. 3j–l. Both the decreased contact angle and Tg of the latex promote the faster evaporation and fixation of this ink on all tested substrates. This ink is the most representative of a commercial ink, where timescales for picoliter droplet to dry, i.e. d2 < 0.1, are shorter than a second with the largest change in d2 motion found in the first 0.5 s after deposition. A magnification in t for these three ink–substrate combinations is shown in Fig. 4. Interestingly, for the combination of ink C on Teflon, there are linear oblique lines of slope value −1; with kymograph dimensions being t and τ, this slope indicates a constant velocity. These high d2 motions of constant velocity likely arise from quick and sudden motions such as delamination of the ink phase from the substrate. Similar constant velocity lines appear in the d2 motion, albeit with a lower intensity, for droplets printed on Teslin paper, in the middle panel of Fig. 4. This lower observed d2 magnitude is likely due to the d2 signal also resulting from heterogeneous motions within the Teslin paper substrate. These motions effectively obscure the abrupt nature of the delamination process seen in the Teflon case. Additionally, in Fig. 4 Teflon, there are periodic in τ, damped d2 motions which arise from substrate vibration due to the deceleration of the inkjet print head occurring at 0 < t < 0.1 s.
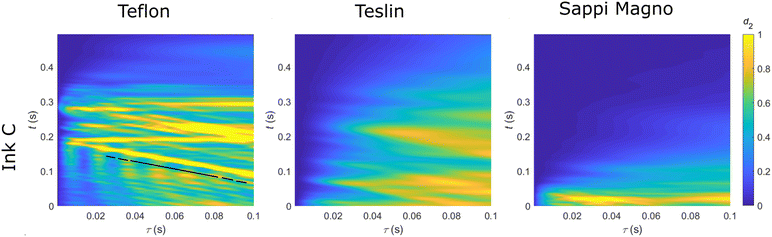 | ||
| Fig. 4 LSI kymographs of Ink C for the three substrates at higher temporal magnification and shorter age of the ink-jet printed droplets. The black line in the first image indicates a slope s = 1. | ||
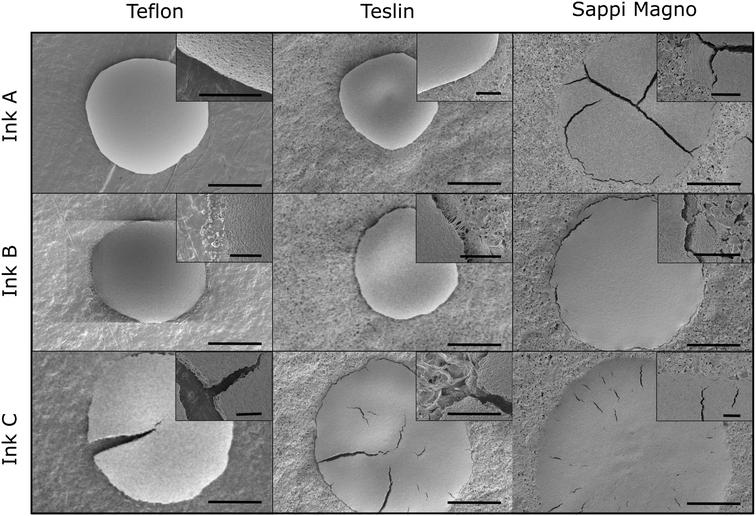
While the kinetic LSI measurements shown here follow ink–substrate interactions during drying, typically post-mortem analyses are performed to assess the ink-jet process; SEM images relative to the combination of these three inks printed on Teflon, Teslin and Sappi Magno are shown in Fig. 5. The combination of both kinetic and post-mortem experiments is a way to deepen the understanding and interpretion of the ultrafast drying processes seen for picoliter ink droplet. These images provide a visual confirmation of the studied LSI kinetics. Ink A on Teflon and Teslin appear as a solid drop, with no cracks and no receding contact line, supporting the formation of a film on the drop surface which cannot recede or form cracks. The same ink printed on Sappi Magno paper shows diametrical cracks, which may indicate a high evaporation rate, corresponding to the LSI data, as seen in Fig. 3(c). Droplets printed using ink B, which contains glycerol, exhibit no cracks within the droplet, however, there is evidence of a moving contact line with cracks observed at the periphery of the droplets, as seen in the inset images of Fig. 5. These droplets tend to shrink at some stage during their drying, implying, as observed with LSI, an overall longer drying time, observed as d2(t) > 0.1 s. However, this moving contact line is not observed in the LSI analyses due to the restricted region of interest of the spatially averaged d2 analyses. Interestingly, the delamination process of ink C on Teflon and Teslin substrates is also observable in post-mortem SEM images taken hours after printing. Additionally, this ink spreads more, with an increasing contact area with the substrate respect to the other formulation due to the surfactant. This ink containing a surfactant, and therefore a decreased latex Tg, is expected to promote latex particle coalescence and subsequently decrease crack formation during drying. Interestingly, this is not observed in the SEM images, nor in the LSI d2 motions in Fig. 4, and a true plasticizer or lower Tg polymer comprising the latex is needed.
3 Conclusion
In this paper, we have studied the interaction of picoliter inkjetted droplets with a series of selected substrates using high-speed LSI. The impinging laser light in these multiple scattering experiments explores the sample to a depth of approximately![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (3l*) ∼ 9–15 μm. If the hemispherical ink droplet radii are much larger than this penetration depth, the diffusion approximation for light paths is valid and the measured speckle information originates from within the droplet itself. It is however possible, since ink l* values and the physical dimensions of the picoliter droplets are comparable, that a fraction of the d2 information arises not from within the ink, but also from the substrate underneath. By printing picoliter-sized droplets of water, and inks of different composition, on substrates of increasing structural complexity, we can disentangle the contribution of the measured decorrelation originating in the ink versus within the substrate. Motion within the picoliter drops is observed in all the cases, notably also in the case of water printed on Teflon, where motion recorded accounts for the change in interfacial shape of the droplet. The addition of glyercol slows down drying dynamics and, by contrast, when surfactant is present, dynamics are faster respect to the other inks, given the increased wetting properties of such liquid. This highlights the importance of substrate wetting and imbibition in drying dynamics during inkjet printing. Finally, we have demonstrated that with LSI can detect when cracks and substrate delamination events occur during the droplet consolidation. These processes are marked by oblique line with slope of unity in the (t, τ) kymographs, confirmed by post-mortem SEM imaging. These in situ LSI observations of inkjet printed picoliter droplet drying enable a deep understanding of the short-time processes occurring within such exceedingly small pL droplets that has otherwise remained hidden.
(3l*) ∼ 9–15 μm. If the hemispherical ink droplet radii are much larger than this penetration depth, the diffusion approximation for light paths is valid and the measured speckle information originates from within the droplet itself. It is however possible, since ink l* values and the physical dimensions of the picoliter droplets are comparable, that a fraction of the d2 information arises not from within the ink, but also from the substrate underneath. By printing picoliter-sized droplets of water, and inks of different composition, on substrates of increasing structural complexity, we can disentangle the contribution of the measured decorrelation originating in the ink versus within the substrate. Motion within the picoliter drops is observed in all the cases, notably also in the case of water printed on Teflon, where motion recorded accounts for the change in interfacial shape of the droplet. The addition of glyercol slows down drying dynamics and, by contrast, when surfactant is present, dynamics are faster respect to the other inks, given the increased wetting properties of such liquid. This highlights the importance of substrate wetting and imbibition in drying dynamics during inkjet printing. Finally, we have demonstrated that with LSI can detect when cracks and substrate delamination events occur during the droplet consolidation. These processes are marked by oblique line with slope of unity in the (t, τ) kymographs, confirmed by post-mortem SEM imaging. These in situ LSI observations of inkjet printed picoliter droplet drying enable a deep understanding of the short-time processes occurring within such exceedingly small pL droplets that has otherwise remained hidden.
Conflicts of interest
The authors declare that there are no conflicts of interest.Acknowledgements
The authors acknowledge funding support from Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO) through the Open Technology Program, grant #15777.Notes and references
- M. P. Brenner, S. Hilgenfeldt and D. Lohse, Rev. Mod. Phys., 2002, 74, 425 CrossRef CAS.
- M. Draijer, E. Hondebrink, T. van Leeuwen and W. Steenbergen, Lasers Med. Sci., 2009, 24, 639–651 CrossRef PubMed.
- D. Lohse, Annu. Rev. Fluid Mech., 2022, 54, 349–382 CrossRef.
- T. Xu, J. Jin, C. Gregory, J. J. Hickman and T. Boland, Biomaterials, 2005, 26, 93–99 CrossRef CAS.
- J. T. Delaney, P. J. Smith and U. S. Schubert, Soft Matter, 2009, 5, 4866–4877 RSC.
- S. Chen, M. Su, C. Zhang, M. Gao, B. Bao, Q. Yang, B. Su and Y. Song, Adv. Mater., 2015, 27, 3928–3933 CrossRef CAS PubMed.
- H. Minemawari, T. Yamada, H. Matsui, J. Tsutsumi, S. Haas, R. Chiba, R. Kumai and T. Hasegawa, Nature, 2011, 475, 364–367 CrossRef CAS.
- R. P. Tortorich and J.-W. Choi, Nanomaterials, 2013, 3, 453–468 CrossRef CAS.
- H. Sirringhaus and T. Shimoda, MRS Bull., 2003, 28, 802–806 CrossRef.
- P. Calvert, Chem. Mater., 2001, 13, 3299–3305 CrossRef CAS.
- C. Yoon and J.-h Choi, Color. Technol., 2008, 124, 355–363 CAS.
- S. Magdassi, The chemistry of inkjet inks, 2010, pp. 19–41 Search PubMed.
- N. F. Morrison and O. G. Harlen, Rheol. Acta, 2010, 49, 619–632 CrossRef CAS.
- C. Diddens, J. Comput. Phys., 2017, 340, 670–687 CrossRef CAS.
- D. Siregar, J. G. Kuerten and C. Van Der Geld, J. Colloid Interface Sci., 2013, 392, 388–395 CrossRef CAS PubMed.
- V. Joekar-Niasar and S. Hassanizadeh, Crit. Rev. Environ. Sci. Technol., 2012, 42, 1895–1976 CrossRef CAS.
- X. Yin, H. Aslannejad, E. de Vries, A. Raoof and S. Hassanizadeh, Transp. Porous Media, 2018, 125, 239–258 CrossRef CAS PubMed.
- H. Tan, C. Diddens, P. Lv, J. G. Kuerten, X. Zhang and D. Lohse, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8642–8647 CrossRef CAS PubMed.
- D. J. Pine, D. A. Weitz, P. M. Chaikin and E. Herbolzheimer, Phys. Rev. Lett., 1988, 60, 1134 CrossRef CAS PubMed.
- H. Cheng, Q. Luo, S. Zeng, S. Chen, J. Cen and H. Gong, J. Biomed. Opt., 2003, 8, 559–564 CrossRef PubMed.
- B. Weber, C. Burger, M. Wyss, G. Von Schulthess, F. Scheffold and A. Buck, Eur. J. Neurosci., 2004, 20, 2664–2670 CrossRef CAS PubMed.
- A. K. Dunn, H. Bolay, M. A. Moskowitz and D. A. Boas, J. Cereb. Blood Flow Metab., 2001, 21, 195–201 CrossRef CAS.
- I. Fredriksson, M. Hultman, T. Strömberg and M. Larsson, J. Biomed. Opt., 2019, 24, 016001 Search PubMed.
- D. Briers, D. D. Duncan, E. Hirst, S. J. Kirkpatrick, M. Larsson, W. Steenbergen, T. Stromberg and O. B. Thompson, J. Biomed. Opt., 2013, 18, 066018 CrossRef.
- A. Amon, A. Mikhailovskaya and J. Crassous, Rev. Sci. Instrum., 2017, 88, 051804 CrossRef PubMed.
- H. M. van der Kooij, S. Dussi, G. T. van de Kerkhof, R. A. Frijns, J. van der Gucht and J. Sprakel, Sci. Adv., 2018, 4, eaar1926 CrossRef PubMed.
- H. M. van der Kooij, S. A. Semerdzhiev, J. Buijs, D. J. Broer, D. Liu and J. Sprakel, Nat. Commun., 2019, 10, 3501 CrossRef.
- L. Vitomir, J. Sprakel and J. Van Der Gucht, Sci. Rep., 2017, 7, 16879 CrossRef PubMed.
- L. Baij, J. Buijs, J. J. Hermans, L. Raven, P. D. Iedema, K. Keune and J. Sprakel, Sci. Rep., 2020, 10, 10574 CrossRef CAS.
- R. Antonelli, R. Fokkink, N. Tomozeiu, J. Sprakel and T. Kodger, Rev. Sci. Instrum., 2021, 92, 083906 CrossRef CAS.
- F. Scheffold, S. Skipetrov, S. Romer and P. Schurtenberger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 061404 CrossRef CAS PubMed.
- R. Lenke and G. Maret, Scattering in polymeric and colloidal systems, 2000, pp. 1–73 Search PubMed.
- C. Bonnet, M. Corredig and M. Alexander, J. Agric. Food Chem., 2005, 53, 8600–8606 CrossRef CAS PubMed.
- M. Alexander, L. Rojas-Ochoa, M. Leser and P. Schurtenberger, J. Colloid Interface Sci., 2002, 253, 35–46 CrossRef CAS PubMed.
- D. Durian, D. Weitz and D. Pine, Science, 1991, 252, 686–688 CrossRef CAS.
- D. Pine, D. Weitz, P. Chaikin and E. Herbolzheimer, Photon Correlation Techniques and Applications, 1988, p. QONC35 Search PubMed.
- P. Kaplan, M. H. Kao, A. Yodh and D. J. Pine, Appl. Opt., 1993, 32, 3828–3836 CrossRef CAS.
- H. M. van der Kooij, A. Susa, S. J. Garca, S. van der Zwaag and J. Sprakel, Adv. Mater., 2017, 29, 1701017 CrossRef.
- K. Schätzel, Appl. Phys. B: Photophys. Laser Chem., 1987, 42, 193–213 CrossRef.
- D. Y. Kwok and A. W. Neumann, Adv. Colloid Interface Sci., 1999, 81, 167–249 CrossRef CAS.
- A. Clarke, T. Blake, K. Carruthers and A. Woodward, Langmuir, 2002, 18, 2980–2984 CrossRef CAS.
- K. Sefiane, Adv. Colloid Interface Sci., 2014, 206, 372–381 CrossRef CAS.
- R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2000, 62, 756 CrossRef CAS PubMed.
- C. Diddens, J. Kuerten, C. van der Geld and H. Wijshoff, J. Colloid Interface Sci., 2017, 487, 426–436 CrossRef CAS.
- M. Rump, U. Sen, R. Jeurissen, H. Reinten, M. Versluis, D. Lohse, C. Diddens and T. Segers, Phys. Rev. Appl., 2023, 19, 054056 CrossRef CAS.
- T. Pham and S. Kumar, Langmuir, 2017, 33, 10061–10076 CrossRef CAS PubMed.
- Z. Wang, L. Espn, F. S. Bates, S. Kumar and C. W. Macosko, Chem. Eng. Sci., 2016, 146, 104–114 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01701j |
| This journal is © The Royal Society of Chemistry 2024 |